2022高中数学回归课本复习检测练习
- 格式:docx
- 大小:39.66 KB
- 文档页数:8

高三数学回归课本复习检测—函数与方程一、选择题:1.函数)43(log22)(21++=xxxf的定义域为()A.)1,34(--B.)1,34[--C.]1,34(--D.),1(+∞-2.函数32)(2+--=xxxf的值域是()A.]4,(-∞B.),4[+∞C.)1,3(-D.),1()3,(+∞--∞3.已知函数⎩⎨⎧>-≤=1),1(log1,2)(3xxxxfx,且1)(=xf,则=x()A.0 B.4 C.0或4 D.1或34.下列四组函数中,表示同一函数的是()A.22)()(,)(xxgxxf==B.||)(,)(xxgxxf==C.22)2()(,)(+==xxgxxf D.xxxgtttf-=-=22)(,)(5.下列函数中,是奇函数且在),0(+∞上是增函数的是()A.2xy-=B.xy2=C.xy tan=D.31xy= 6.如下图可作为函数)(xfy=的图像的是( )A.B.C.D.7.函数xxxf2ln)(-=的零点所在的大致区间是( )A.(1,2) B.(2,3) C.⎪⎭⎫⎝⎛1,1eD.(3,4) 8.函数bxaxxf+=3)()0≠a(,满足2)3(=-f,则)3(f的值为()A.3 B.3-C.2-D.2 9.某厂2004年的产值为a万元,预计产值每年以n%递增,则该厂到2008年底的产值(单位:万元)是()A.2%)1(na+B.3%)1(na+C.4%)1(na+D.5%)1(na+10.方程0232=--axx有两个不等的实数根,则a的取值范围是()A.),31(+∞-B.),31(+∞C.)31,(--∞D.)31,(-∞二、填空题:1.已知二次方程042=+-m x x 在)4,3(上有实数根,则实数m 的取值范围是 。
2.已知幂函数)(x f 过点)4,8(,则=)(x f ,=')8(f 。
3.若x e =-2ln ,则=x 。

数学必修一回归试题1.会合 A={x|x=3k, kN },B={x|x=6z, z N } 的关系是 _________.2.设会合A= { x|(x-3)(x-a)=0,a R },B={x|(x-4)(x-1)=0},求 AB, A B3.函数 y=1 是幂函数吗?函数 y=1 与 y= x 0 是同一个函数吗? 4.设会合 A={a,b,c},B={0,1}, 试问从 A 到 B 的映照共有几个?并将它们分别列 出来? 5.画出定义域为 {x| 3x 8, 且 x 5 }, 值域为 {y|1y 2, 且 y0 } 的一个函数图象。
(1)假如平面直角坐标系中点 P(x,y) 的坐标知足 3 x 8, 1 y 2 ,那么哪些点不可以在图象上?(2)你的图象与其余人的有差别吗?为何?6.函数 y=[x] 的函数值表示不超出 x 的最大整数,如, [-3.5]=-4,[2.1]=2 。
则当 x ( 2.5,3]时,求函数 f(x) 的分析式,并画出图象。
7.P25 第 4 题。
18.已知函数 f ( x) 1[1, ) , 画出该函数的图象,并求出值域。
你能2x , x1 编一道以该函数为背景的数列问题吗?9.已知函数 f(x) 是定义在 R 上的奇函数,当 x>0 时, f(x)=x(1+x)+1 。
画出该函数图象,并求出函数的分析式。
10. 已知会合 A={ x| x 2 1},B={x|ax=1}, 若 BA ,务实数 a 的值。
11.证明:(1)若 f(x)=ax+b, 则 f ( x 1 x 2 ) f ( x 1 )f ( x 2 )(; )若g( x) x 2ax b ,2 22则 g (x 1x 2)g( x 1 ) g ( x 2 )。
试概括,什么函数拥有上述性质?模拟上式再编一22题。
12.P45,第 7 题。
1113.已知 x x 13,求以下各式的值: 求( 1)x 2 x 2 ;(2)x 2 x 2 ;(3)x 2 x 2 14.P60,第 3 题。

数学回归课本基础训练(十二)某某 得分一、填空题:本大题共8小题,每小题10分,共80分.1、(必修5 p71,6)已知不等式12-+bx ax >0的解集是{}43<<x x ,则实数a=,b 。
2、(必修5 p44 6(4))在等差数列中,已知1008=S ,39216=S ,则24S =.3、(必修 5 p24,6)在ABC ∆中,已知,sin sin sin ,22C B A c b a =+=则ABC ∆的形状为4、(必修 5 p91,1)如果4log log 33=+n m ,那么n m +的最小值是 _______________5、(必修5 p44,7)一个等差数列的前12项和为354,前12项中,偶数项和奇数项和之比为32:27,则公差d =..6、(必修5 p17,10)如图,我炮兵阵地位于A 处,两观察所分别设于C,D ,已知ACD ∆为边长等于a 正三角形,当目标出现于B 时,测得 45=∠CDB ,︒=∠75BCD ,则炮击目标 的距离AB=. 7、(必修5 p90 例3)过点(1,2)的直线l 与 x 轴的正半轴、y 轴的正半轴分别交于A ,B 两点,当AOB ∆的面积最小时,直线l 的方程为8、(必修5,P20,4)如图某人在高出海面600m 的山上P 处,测得海面上的航标A 在正东,俯角为 30,航标B 在南偏东 60,俯角为,45 则这两个航标间的距离。
9、(必修5 p61 13)一个正方形被分成九个相等的小正方形,将中间的一个正方形挖去(如图(1));再将剩余的每个正方形都分成九个相等的小正方形,并将中间一个挖去,得图(2);如此继续下去……,试问第n 个图共挖去 个正方形.B AD C B P C A10、(必修5 p91 4(练习))如图,重量是W 的重物挂在杠杆上距支点a 处,质量均匀的杆子每单位长度的重量为m ,杠杆应当=,才能使得加在另一端用来平衡重物的力F 最小。

本册过关检测一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.若集合A={-2,-1,0,1},B={x|x2+2x<0},则A∩B=( )A.{-1} B.{-1,0} C.{-2,-1,0} D.{-1,0,1}2.已知a=0.30.2,b=0.20.3,c=20.3,则它们的大小关系是( )A.a<b<c B.b<a<c C.c<a<b D.b<c<a3.已知sin (α-π)=,则cos 2α=( )A.- B. C.- D.4.若条件p:x≤2,q:≥,则p是q成立的( )A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件5.函数f(x)=的部分图象大致为( )6.已知a,b>0,且a+2b=1,则+的最小值为( )A.6 B.8 C.9 D.107.某市政府为了增加农民收入,决定对该市特色农副产品的科研创新和广开销售渠道加大投入,计划逐年加大研发和宜传资金投入.若该政府2020年全年投入资金120万元,在此基础上,每年投入的资金比上一年增长12%,则该政府全年投入的资金翻一番(2020年的两倍)的年份是(参考数据:lg 1.12≈0.05,lg 2≈0.30)( ) A.2027年 B.2026年 C.2025年 D.2024年8.已知定义域为R的偶函数f(x)在(-∞,0]上单调递减,且f(2)=0,则满足xf(x)≥0的x取值范围是( )A.(-∞,-2]∪[2,+∞) B.[-2,2]C.[-2,0)∪(0,2] D.[-2,0]∪[2,+∞)二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多个选项是符合题目要求的,全部选对的得5分,部分选对的得2分,有选错的得0分.)9.下列命题正确的是( )A.长度等于半径的弦所对的圆心角为1弧度B.若tan α≥0,则kπ≤α<+kπ(k∈Z)C.若角α的终边过点P(3k,4k)(k≠0),则sin α=D.当2kπ<α<+2kπ(k∈Z)时,sin α<cos α10.[2022·山东青岛高一期中]若lg a>lg b,则( )A.< B.< C.a->b- D.a+>b+11.关于函数f(x)=2sin (2x-),下列说法中正确的是( )A.其最小正周期为πB.其图象由y=2sin 2x向右平移个单位而得到C.其表达式可以写成f(x)=2cos (2x-)D.其图象关于点(-,0)对称12.函数f(x)=4-,下列结论正确的有( )A.f(x)+f(-x)=6 B.3<f(x)<4C.f(x)-3为偶函数 D.f(x)的图象关于点(0,3)中心对称三、填空题(本题共4小题,每小题5分,共20分.)13.命题“∀x>0,x2+1≥2x”的否定是________.14.幂函数y=f(x)的图象经过点(,4),则f()的值为________.15.函数f(x)=sin x-cos x+1的最小值为________.16.已知函数f(x)=,则:(1)f(5)=________;(2)函数y=f(x)-k在区间(-∞,4)上有四个不同的零点,则实数k的取值范围是____________.四、解答题(本题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤.)17.(本小题满分10分)(1)已知sin α=,α∈(,π),求tan α,sin 2α的值;(2)已知sin (π-α)+sin (+α)=sin (α+),求sin αcos α+cos2α的值.18.(本小题满分12分)设集合U=R,A={x|1≤3x≤27},B={x|m-1≤x≤2m}.(1)m=3,求A∩∁U B;(2)若“x∈B”是“x∈A”的充分条件,求m的取值范围.19.(本小题满分12分)已知函数f(x)是定义在R上的偶函数,且当x≥0时,f(x)=2x2+x.(1)当x<0时,求函数f(x)的解析式;(2)解不等式f(1-x)<f(x+3).20.(本小题满分12分)已知函数f(x)=ax2+(1-a)x+a-2.(1)若不等式f(x)≥-2对于一切实数x恒成立,求实数a的取值范围;(2)若a<0,解关于x的不等式f(x)<a-1.21.(本小题满分12分)已知函数f(x)=2sin x cos x+2cos2x-.(1)求函数f(x)的最小正周期和单调递减区间;(2)将函数f(x)的图象向左平移单位长度,再将所得图象上各点的横坐标缩短为原来的,纵坐标不变,得到函数的g(x)图象,求y=g(x)在(-,)上的值域.22.(本小题满分12分)已知函数f(x)=log a(2+3x)-log a(2-3x)(a>0,a≠1).(1)求函数f(x)的定义域;(2)判断f(x)的奇偶性,并证明;(3)当0<a<1时,求关于x的不等式f(x)≥0的解集.本册过关检测1.解析:因为B={x|x2+2x<0},所以B={x|-2<x<0},因为A={-2,-1,0,1},所以A∩B={-1}.答案:A2.解析:由c=20.3>20=1=0.30>a=0.30.2>0.20.2>b=0.20.3,所以b<a<c.答案:B3.解析:由题意得,sin (α-π)=-sin (π-α)=-sin α=,即sin α=-,所以cos 2α=1-2sin2α=1-2×=.答案:D4.解析:由x≤2不能推出≥,例如x=-3,但≥必有x≤2,所以p是q成立的必要不充分条件.答案:B5.解析:∵f(x)=,由cos x-1≠0,所以f(x)的定义域为{x|x≠2kπ,k∈Z},函数f(x)的定义域关于原点对称,且f(-x)==-f(x),故函数f(x)是奇函数,则排除B,又f(1)=<0,则排除CD.答案:A6.解析:∵a+2b=1,∴+=(+)(a+2b)=1+++4≥5+2×=9,当且仅当=时即a=b=时等号成立.答案:C7.解析:设第n(n∈N*)年该政府全年投入的资金翻一番,依题意得:120(1+12%)n-1=240,则lg [120(1+12%)n-1]=lg 240,∴lg 120+(n-1)lg 1.12=lg 240,∴(n-1)lg 1.12=lg 2,∴n=+1=7,即该政府全年投入的资金翻一番的年份是2026年.答案:B8.解析:∵定义域为R的偶函数f(x)在(-∞,0]上单调递减,且f(2)=0,∴f(-2)=0,且在[0,+∞)上单调递增,∴xf(x)≥0,可得或或x=0,即x≥2或-2≤x<0或x=0,即x∈[-2,0]∪[2,+∞).答案:D9.解析:对于A中,因为长度等于半径的弧所对的圆心角为1弧度,所以A错误;对于B中,若tan α≥0,则α为终边在第一、三象限或x轴上的角,即kπ≤α<+kπ(k∈Z),所以B正确;对于C中,由角α的终边过点P(3k,4k),则sin α==,当k>0时,sin α=;当k<0时,sin α=-,所以C错误;对于D中,由三角函数线可得,当-+2kπ<α<+2kπ(k∈Z)时,可得sin α<cos α,所以D正确.答案:BD10.解析:因lg a>lg b,则a>b>0,于是得0<<,A正确;由0<<得:+1<+1,即<,则有<,B正确;取a=,b=,满足a>b>0,而a-=-3=-,b-=-2=-,有a-<b-,C不正确;因a>b>0,>>0,则a+>b+,D正确.答案:ABD11.解析:T==π,故函数f(x)的最小正周期为π,选项A正确;函数f(x)=2sin (2x-)=2sin ,其图象由y=2sin 2x向右平移个单位而得到,选项B错误;函数f(x)=2sin (2x-)=2cos =2cos (2x-),故选项C正确;令2x-=kπ,k∈Z,解得x=+,k∈Z,故函数图象的对称中心为(+,0),k∈Z,令k=-1,为(-,0),故图象关于点(-,0)对称,选项D正确.答案:ACD12.解析:f(x)+f(-x)=4-+4-=8-2(+)=8-2·=6.A正确;因为4x+1∈(1,+∞)⇒∈(0,1)⇒-∈(-2,0),所以f(x)=4-∈(2,4).B错误;记F(x)=f(x)-3=1-,x∈R,F(x)=1-=,则F(-x)===-=-F(x),函数为奇函数.C错误;由C可知,f(x)-3为奇函数,则f(x)-3的图象关于点(0,0)对称,所以f(x)的图象关于点(0,3)中心对称.D正确.答案:AD13.解析:因为全称量词命题的否定为存在量词命题,故命题“∀x>0,x2+1≥2x”的否定为:“∃x>0,x2+1<2x”答案:“∃x>0,x2+1<2x”14.解析:设y=f(x)=xα,因为幂函数y=f(x)的图象经过点(,4),所以()α=4=()-2⇒α=-2⇒f(x)=x-2,因此f()=()-2=(4-1)-2=42=16.答案:1615.解析:f(x)=sin (x-)+1,x∈R,所以f(x)=sin (x-)+1最小值为-+1.答案:1-16.解析:(1)∵f(x)=,∴f(5)=f(3)==f(1)=f(-1)=e|-1+1|=.(2)当x≤0时,f(x)=e|x+1|;当x>0时,f(x)=f(x-2);当x∈(0,2]时,x-2∈(-2,0], f(x)=f(x-2)=e|x-2+1|=e|x-1|,当x∈时,x-2∈(0,2), f(x)=f(x-2)=e|x-2-1|=e|x-3|,函数y=f(x)-k在区间(-∞,4)上有四个不同的零点,即 y=f(x)与y=k有四个交点,作出函数y=f(x)的图象,如图所示:由图可知,实数k的取值范围是(,)∪(1,).答案:(1) (2)(,)∪(1,)17.解析:(1)∵sin α=,且α∈(,π),∴cos α=-=-,∴tanα==-,sin 2α=2sin αcos α=2××(-)=-.(2)因为sin (π-α)+sin (+α)=sin (α+),所以sin α-cos α=cos α,则tan α=2,故sin αcos α+cos2α===.18.解析:(1)m=3时,B={x|m-1≤x≤2m}={x|2≤x≤6},∁U B=(-∞,2)∪(6,+∞),又A={x|1≤3x≤27}={x|0≤x≤3},故A∩∁U B={x|0≤x<2}(2)由题意知:“x∈B”是“x∈A”的充分条件,即B⊆A,当m<-1时,m-1>2m,B={x|m-1≤x≤2m}=∅⊆A,满足题意;当m≥-1时,B≠∅,欲满足B⊆A,综上得m的取值范围为(-∞,-1)∪.19.解析:(1)当x<0时,则-x>0,又f(x)是偶函数,故f(x)=f(-x)=2(-x)2+(-x)=2x2-x(x<0);(2)当x≥0时,f(x)单调递增,x<0时,f(x)单调递减,且函数为偶函数,故f(1-x)<f(x+3)⇔|1-x|<|x+3|,即(1-x)2<(x+3)2.化简得x+1>0,解得x>-1,故不等式的解集为(-1,+∞).20.解析:(1)∀x∈R,f(x)≥-2恒成立等价于∀x∈R,ax2+(1-a)x+a≥0,当a=0时,x≥0,对一切实数x不恒成立,则a≠0,此时必有,即,解得a≥,所以实数a的取值范围是a∈.(2)依题意,因a<0,则f(x)<a-1⇔ax2+(1-a)x-1<0⇔(x+)(x-1)>0,当a=-1时,-=1,解得x≠1,当-1<a<0时,->1,解得x<1或x>-,当a<-1时,0<-<1,解得x<-或x>1,所以,当a=-1时,原不等式的解集为{x∈R|x≠1};当-1<a<0时,原不等式的解集为;当a<-1时,原不等式的解集为.21.解析:(1)由题设,f(x)=sin 2x+cos 2x=2sin (2x+),所以f(x)的最小正周期为π,令2kπ+≤2x+≤+2kπ,k∈Z,解得kπ+≤x≤+kπ,k∈Z,因此,函数f(x)的单调递减区间为,k∈Z.(2)由(1)知,f(x)=2sin (2x+),将函数y=f(x)的图象向左平移个单位长度,可得y=2sin (2x+)的图象,再将所得图象上各点的横坐标缩短为原来的,纵坐标不变,得到y=g(x)=2sin (4x +)的图象,∵x∈(-,),则4x+∈(,),∴sin (4x+)∈(-,1],则2sin (4x+)∈(-1,2].∴y=g(x)在(-,)上的值域为(-1,2].22.解析:(1)根据题意,函数f(x)=log a(2+3x)-log a(2-3x),则有,解可得-<x<,即函数的定义域为(-,).(2)根据题意,函数f(x)为奇函数,证明如下:函数f(x)的定义域为(-,),定义域关于原点对称,f(-x)=log a(2-3x)-log a(2+3x)=-f(x),则函数f(x)为奇函数.(3)f(x)≥0即log a(2+3x)≥log a(2-3x),又由0<a<1,则函数y=log a x为减函数,则有0<2+3x≤2-3x,解可得-<x≤0,即f(x)≥0的解集为(-,0].。

第十章 第3讲[A 级 基础达标]1.若回归直线方程为y ^=3-2x ,则变量x 增加一个单位,y ( ) A .平均增加3个单位 B .平均增加2个单位 C .平均减少3个单位 D .平均减少2个单位【答案】D2.(2020年南昌模拟)已知一组样本数据点(x 1,y 1),(x 2,y 2),(x 3,y 3),…,(x 6,y 6),用最小二乘法得到其线性回归方程为y ^=-2x +4,若数据x 1,x 2,x 3,…,x 6的平均数为1,则y 1+y 2+y 3+…+y 6等于( )A .10B .12C .13D .14【答案】B3.在一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )(n ≥2,x 1,x 2,…,x n 不全相等)的散点图中,若所有样本点(x i ,y i )(i =1,2,…,n )都在直线y =12x +1上,则这组样本数据的样本相关系数为( )A .-1B .0C .12D .1【答案】D4.如果根据是否爱吃零食与性别的列联表得到K 2≈5.852,所以判断是否爱吃零食与性别有关,那么这种判断犯错的可能性不超过( )A .2.5%B .0.5%C .1%D .0.1%P (K 2≥k )0.100 0.050 0.025 0.010 0.001 k2.7063.8415.0246.63510.8285.某考察团对10个城市的职工人均工资x (千元)与居民人均消费y (千元)进行调查统计,得出y 与x 具有线性相关关系,且回归方程为y ^=0.6x +1.2.若某城市职工人均工资为5千元,估计该城市人均消费额占人均工资收入的百分比为( )A .66%B .67%C .79%D .84%【答案】D【解析】因为y 与x 具有线性相关关系,满足回归方程y ^=0.6x +1.2,该城市居民人均工资为x =5,所以可以估计该城市的职工人均消费额y =0.6×5+1.2=4.2(元),所以可以估计该城市人均消费额占人均工资收入的百分比为4.25=84%.6.(2020年成都模拟)某公司一种新产品的销售额y 与宣传费用x 之间的关系如表:已知销售额y 与宣传费用x 具有线性相关关系,并求得其回归直线方程为y ^=b ^x +9,则b ^的值为________.【答案】6.5【解析】由表中数据,得x =0+1+2+3+45=2,y =10+15+20+30+355=1105=22,又回归直线方程y ^=b ^x +9过样本中心点(2,22),得22=2b ^+9,解得b ^=132=6.5.7.(2020年滦南期末)2017年3月15日,某市物价部门对本市的5家商场的某种商品的一天销售量及其价格进行调查,5家商场的售价x (元)和销售量y (件)之间的一组数据如下表所示:y =-3.2x +a ,则a =________.【答案】40 【解析】根据题意:x -=9+9.5+10+10.5+115=10,y -=11+10+8+6+55=8,因为y -=-3.2x +a ,所以a =3.2×10+8=40.8.(2020年六安期末)“埃博拉病毒”在西非的传播速度很快,这已经成为全球性的威胁,为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:附:K 2=n (ad -bc )(a +b )(c +d )(a +c )(b +d ).【答案】95%【解析】由题中数据可得:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )=100(10×30-40×20)250×50×30×70=10021≈4.762>3.841,根据临界值表可得:犯错误的概率不超过0.05.即有95%的把握认为“小动物是否感染与服用疫苗有关”.故答案为95%.9.(2020年南阳月考)2021年将在日本东京举办第32届夏季奥林匹克运动会,简称为“奥运会”.为了解不同年龄的人对“奥运会”的关注程度,某机构随机抽取了年龄在20~70岁之间的100人进行调查.经统计,“年轻人”与“中老年人”的人数之比为2∶3.(1)的把握认为是否关注“奥运会”与年龄段有关;(2)现采用分层抽样的方法从中老年人中选取6人进行问卷调查.若再从这6人中选取2人进行面对面询问,求事件“选取的2人中至少有1人关注奥运会”的概率.K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),n =a +b +c +d .解:(1)“年轻人”共有100×25=40(人),“中老年人”共有100×35=60(人),由此填写列联表如下:根据表中数据,计算K 2=100(30×40-20×10)240×60×50×50=503≈16.67>10.828,所以有99.9%的把握认为是否关注“奥运会”与年龄段有关. (2)用分层抽样法选取6位中老年人中有4人不关注,2人关注, 则所求概率为p =1-C 24C 26=35.10.(2020年湖南雅礼中学月考)近年来,国资委党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某扶贫小组为更好地执行精准扶贫政策,为某扶贫县制定了具体的扶贫政策,并对此贫困县从2015年到2019年的居民家庭人均纯收入(单位:百元)进行统计,数据如下表:(1)求人均纯收入y (2)是否有99.9%的把握认为村民的年龄与对扶贫政策的满意度具有相关性?参考公式:回归直线y ^=a +bx 中斜率和截距的最小二乘估计公式分别为:b ^=∑n =1ix i y i -n x - y-∑n =1ix 2i -n x -2=∑n =1i(x i -x -)(y i -y -)∑n =1i(x i -x -)2,a =y --b x -,K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),其中n =a +b +c +d .临界值表:解:(1)依题意:t =15×(1+2+3+4+5)=3,y =15×(5.8+6.6+7.2+8.8+9.6)=7.6,故∑i =15(t i -t )2=4+1+0+1+4=10,∑i =15(t i -t )(y i -y )=(-2)×(-1.8)+(-1)×(-1)+0×(-0.4)+1×1.2+2×2=9.8,b =∑i =1n(t i -t )(y i -y )∑i =1n(t i -t )2=0.98,所以a =y -b t =7.6-0.98×3=4.66. 所以y ^=0.98t +4.66. (2)依题意,完善表格如下:计算得K 2k 2=300×(150×50-50×50)2200×100×200×100=300×5 000×5 000200×100×200×100=18.75>10.828,故有99.9%的把握认为村民的年龄与扶贫政策的满意度具有相关性.[B 级 能力提升]11.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据上表可得回归直线方程y =b ^x +a ,其中b ^=0.76,a =y -b ^x .据此估计,该社区一户年收入为15万元的家庭的年支出为( )A .11.4万元B .11.8万元C .12.0万元D .12.2万元【答案】B【解析】由题意知,x =8.2+8.6+10.0+11.3+11.95=10,y =6.2+7.5+8.0+8.5+9.85=8,所以a ^=8-0.76×10=0.4,所以当x =15时,y ^=0.76×15+0.4=11.8(万元).12.(2020年九江期末)针对“中学生追星问题”,某校团委对“中学生性别和追星是否有关”作了一次调查,其中女生人数是男生人数的12,男生追星的人数占男生人数的13,女生追星的人数占女生人数的23,若有95%的把握认为中学生追星与性别有关,则男生至少有______人.参考数据及公式如下:K 2=n (ad -bc )(a +b )(c +d )(a +c )(b +d ),n =a +b +c +d .【答案】30【解析】设男生人数为x ,由题意得列联表如下:计算K 2=32x ·⎝⎛⎭⎫13x ·16x -23x ·13x 2x ·12x ·23x ·56x=320x >3.841,解得x >20×3.8413. 又x =6k ,k ∈N *,所以x min =30,即有95%的把握认为中学生追星与性别有关时,男生至少有30人.13.(一题两空)(2020年吉林模拟)2019年末至2020年初,某在线教育公司为了适应线上教学的快速发展,近5个月加大了对该公司的网上教学使用软件的研发投入,过去5个月资金投入量x (单位:百万元)和收益y (单位:百万元)的数据如下表:若y 与x 的线性回归方程为y =3x +a ,则a =________,资金投入量为16百万元时,该月收益的预报值为________百万元.【答案】8.04 56.04 【解析】由题意得x =2+4+8+10+125=7.2,y -=14.21+20.31+31.18+37.83+44.675=29.64,所以a =y --b ^x =29.64-3×7.2=8.04.所以y 关于x 的回归方程为y ^=3x +8.04.把x =16代入回归方程得y ^=3×16+8.04=56.04,故预报值为56.04百万元.14.新型冠状病毒爆发以来,各地高度重视新型冠状病毒感染的肺炎的防控和卫生健康监督检查工作,务必将督导检查落实到位.某地对8个工厂的生产车间进行了“原料采购加工标准”和“卫生标准”的检查和评分,其评分情况如下表所示:(1)已知x 与y 之间具有线性相关关系,求y 关于x 的线性回归方程;(2)现从8个被检查的工厂中任意抽取两个组成一组,若两个工厂的“原料采购加工标准”和“卫生标准”的评分均超过80分,则组成“对比标兵工厂”,求该组被评为“对比标兵工厂”的概率.参考公式:b ^=∑i =1nx i y i -n x y∑i =1nx 2i -n x2,a ^=y --b ^x ;参考数据:∑i =18x i y i =53 844,∑i =18x 2i =55 656.解:(1)由题意,得x =18×(100+95+93+83+82+75+70+62)=82.5,y =18×(86.5+83.5+83.5+81.5+80.5+79.5+77.5+76.5)=81.125,所以b ^=∑i =1nx i y i -n x y∑i =1nx 2i -n x2=53 844-8×82.5×81.12555 656-8×82.52=14.所以a ^=y -b ^x =81.125-14×82.5=60.5.所以y 关于x 的线性回归方程为y ^=14x +60.5.(2)从8个中任取2个,共有C 28=28个基本事件.“原料采购加工标准”和“卫生标准”的评分均超过80分有C 25=10种情况,故所求的概率为p =1028=514.15.(2020年新课标Ⅱ)某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,从这些地块中用简单随机抽样的方法抽取20个作为样区,调查得到样本数据(x i ,y i )(i =1,2,…,20),其中x i 和y i 分别表示第i 个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量,并计算得∑i =120x i =60,∑i =120y i =1 200,∑i =120(x i -x)2=80,∑i =120 (y i -y -)2=9 000,∑i =120(x i -x )(y i -y -)=800.(1)求该地区这种野生动物数量的估计值(这种野生动物数量的估计值等于样区这种野生动物数量的平均数乘以地块数);(2)求样本(x i ,y i )(i =1,2,…,20)的相关系数(精确到0.01);(3)根据现有统计资料,各地块间植物覆盖面积差异很大.为提高样本的代表性以获得该地区这种野生动物数量更准确的估计,请给出一种你认为更合理的抽样方法,并说明理由.附:相关系数r =∑i =1n(x i -x )(y i -y -)∑i =1n(x i -x )2∑i =1n(y i -y -)2,2≈1.414.解:(1)已知∑i =120y i =1 200,所以20个样区野生动物数量的平均数为120∑i =120y i =60,所以该地区这种野生动物数量的估计值为60×200=12 000. (2)因为∑i =120(x i -x)2=80,∑i =120(y i -y)2=9 000,∑i =120(x i -x )(y i -y )=800,所以r =∑i =1n(x i -x )(y i -y )∑i =1n(x i -x )2∑i =1n(y i -y )2=80080×9 000=8006002=223≈0.94.(3)更合理的抽样方法是分层抽样,根据植物覆盖面积的大小对地块分层,再对200个地块进行分层抽样.理由如下:由(2)知各样区的这种野生动物数量与植物覆盖面积有很强的正相关.由于各地块间植物覆盖面积差异很大,从而各地块间这种野生动物数量差异也很大,采用分层抽样的方法较好地保持了样本结构与总体结构的一致性,提高了样本的代表性,从而可以获得该地区这种野生动物数量更准确的估计.[C 级 创新突破]16.(2020年日照期末)某种疾病可分为Ⅰ、Ⅱ两种类型,为了解该疾病类型与性别的关系,在某地区随机抽取了患该疾病的病人进行调查,其中男性人数为z ,女性人数为2z ,男性患Ⅰ型病的人数占男性病人的56,女性患Ⅰ型病的人数占女性病人的13.与“性别”有关,则男性患者至少有多少人?(2)某药品研发公司欲安排甲、乙两个研发团队来研发此疾病的治疗药物,两个团队各至多安排2个接种周期进行试验.每人每次接种花费m (m >0)元.甲团队研发的药物每次接种后产生抗体的概率为p ,根据以往试验统计,甲团队平均花费为-2mp 2+6m ;乙团队研发的药物每次接种后产生抗体的概率为q ,每个周期必须完成3次接种,若一个周期内至少出现2次抗体,则该周期结束后终止试验,否则进入第二个接种周期.假设两个研发团队每次接种后产生抗体与否均相互独立.若p =2q ,从两个团队试验的平均花费考虑,该公司应选择哪个团队进行药品研发? 附:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ).解:(1)根据题意填写列联表如下;则k 2=3z ⎝⎛⎭⎫5z 6·4z 3-z 6·2z 32z ·2z ·3z 2·3z 2=2z 3>7.879,解得z >11.818 5,由z 6∈N *,且z3∈N *,所以z 的最小值为12,即男性患者至少有12人. (2)设甲研发试验品花费为X ,则EX =-2mp 2+6m . 设乙研发试验品花费为Y ,则Y 的可能取值为3m,6m , 所以P (Y =3m )=C 23·q 2(1-q )+q 3=-2q 3+3q 2, P (Y =6m )=1+2q 3-3q 2.11 所以EY =3m ·(-2q 3+3q 2)+6m ·(1+2q 3-3q 2)=6mq 3-9mq 2+6m .因为p =2q ,所以EY -EX =6mq 3-9mq 2+6m +2mp 2-6m =6mq 3-9mq 2+2mp 2=6mq 3-mq 2=mq 2(6q -1).①当0<q <16时,6q -1<0,因为m >0,所以mq 2(6q -1)<0,所以EX >EY ,乙团队试验的平均花费较少,所以选择乙团队进行研发;②当16<q <1时,6q -1>0,因为m >0,所以mq 2(6q -1)>0,所以EX <EY ,甲团队试验的平均花费较少,所以选择甲团队进行研发;③当q =16时,mq 2(6q -1)=0,所以EX =EY ,甲团队试验的平均花费和乙团队试验的平均费用相同,从两个团队试验的平均花费考虑,该公司选择甲团队或乙团队进行研发均可.。
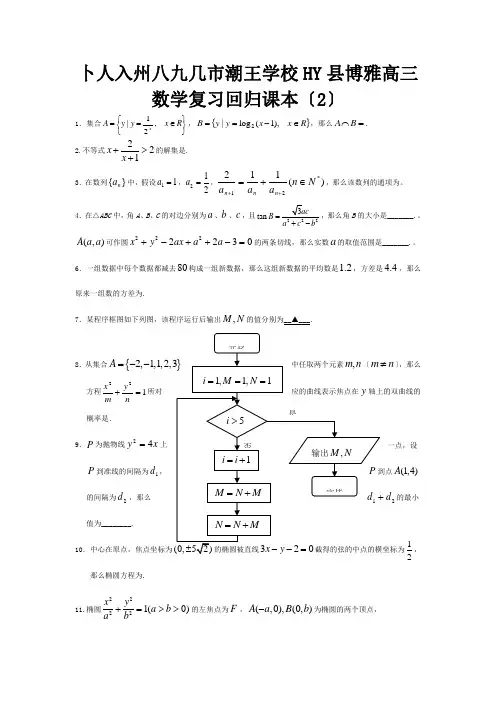
卜人入州八九几市潮王学校HY 县博雅高三数学复习回归课本〔2〕1.集合⎭⎬⎫⎩⎨⎧∈==R x y y A x ,21|,{}R x x y y B ∈-==),1(log |2,那么=⋂B A . 2.不等式221x x +>+的解集是. 3.在数列}{n a 中,假设11=a ,212=a ,)(112*21N n a a a n n n ∈+=++,那么该数列的通项为。
4.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,且tan B ,那么角B 的大小是_______.。
(,)A a a 可作圆2222230x y ax a a +-++-=的两条切线,那么实数a 的取值范围是_______.。
6.一组数据中每个数据都减去80构成一组新数据,那么这组新数据的平均数是2.1,方差是4.4,那么原来一组数的方差为.7.某程序框图如下列图,该程序运行后输出,M N 的值分别为__▲___.8.从集合{2,1,1A =--n 〕,那么方程122=+ny m x 所对概率是.9.P 为抛物线x y 42=上一点,设P 到准线的间隔为1d ,)4,1(A 的间隔为2d ,那么2d 的最小值为________.10.中心在原点,焦点坐标为21,那么椭圆方程为. 11.椭圆22221(0)x y a b a b+=>>的左焦点为F ,(,0),(0,)A a B b -为椭圆的两个顶点,假设F 到AB,那么椭圆的离心率为.12.()()()()212121272,,3log x f x f x x x x a ax x x f <<≤+-=时,都有对任意的,那么实数a 的取值范围为.ABC 中,内角A 、B 、C 所对的边分别为a 、b 、c ,且tan tan tan tan )A B A B -+⋅. 〔1〕假设ab b a c -+=222,求A 、B 、C 的大小;〔2〕向量(sin ,cos ),(cos ,sin ),|32|A A B B ==-求m n m n 的取值范围.。


南通市2022届高三回归课本专项检测数学试题一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在相应位置上. 1.复数211i++在复平面上对应的点的坐标是 ▲ . 2.已知集合{}2|1,M y y x x R ==+∈,{}|3,N y y x x M ==-+∈,则M N = ▲ .3.已知()y f x =0x >()lg f x x =1(())100f f ,,A B C B W =230x y ±=θ面积为cm 2的扇形铁皮制作一个无盖的圆锥形容器(衔接部分忽略不计), 则该容器盛满 水时的体积是 ▲ cm 3.9.若直线x y a +=与圆224x y +=相交于点,A B ,且OA OB OA OB +=-(其中O 为坐标原点),则= ▲ .10.已知三角形的一边长为5,所对角为60取值范围是 ▲ .11.已知()sin()(0),()()363f x x f f πππωω=+>=,且()f x 值,则ω的最小值为 ▲ .12.在x 轴的正方向上,从左向右依次取点列{}j A ,1,2,3,j =,在曲线y =上从左向右依次取点列{}k B ,1,2,3,k =,使()11,2,3,k k k A B A k -∆=都是等边三角形,其中0A 是 坐标原点,则第2022个等边三角形的边长是 ▲ . 13.已知等差数列{},{}n n a b 的前n 项和分别为n S 和n T ,若7453n n S n T n +=+,且2n nab 是整数,则 n 的值为 ▲ .14.若关于x 的方程3x e x kx -=有四个实数根,则实数k 的取值范围是 ▲ . 二、解答题:本大题共六小题,共计90分.请在指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)第5已知ABC ∆中,,,a b c 分别是角,,A B C 所对的边,且2b ac =,向量()()cos ,1m A C =-和()1,cos n B =满足32m n ⋅=. (1)求sin sin A C 的值;(2)求证:ABC ∆为等边三角形.16.(本题满分14分)如图,棱柱1111ABCD A B C D -的所有棱长都等于2,60ABC ∠=,平面11AA C C ⊥平面 ABCD ,160A AC ∠=.(1)证明:1BD AA ⊥;(2)在直线1CC 上是否存在点P ,使//BP 平面11DA C 若存在,求出点P 的位置;若不存在,说明理由.17.(本小题满分14分)某工厂去年新开发的某产品的年产量为100万只,每只产品的销售价为10元,固定 成本为8元.今年,工厂第一次投入100万元的科技成本,并计划以后每年比上一年 多投入100万元,预计产量每年递增10万只,第n 次投入后,每只产品的固定成本 为()1k g n n =+元(其中为常数,n Z ∈且0n ≥).若产品销售价保持不变,第n次投入后的年纯利润为()f n 万元(年纯利润=年收入-年固定成本-年科技成本). (1)求k 的值,并求出()f n 的表达式;(2)问从今年起,第几年纯利润最高最高纯利润为多少万元18.(本题满分16分)设集合W 是满足下列两个条件的无穷数列{}n a 的集合: ①212n n n a a a +++≤ ;②n a M ≤,其中*n N ∈,M 是与n 无关的常数. (1)若{}n a 是等差数列,n S 是其前n 项的和,334,18a S ==,试探究{}n S 与集合W 之间的关系;(2)设数列{}n b 的通项为52n n b n =-,且{}n b W ∈,M 的最小值为m ,求m 的值;(3)在(2)的条件下,设1[(5)]5n n n c b m =+-+{}n c 中任意不同的三项都不能成为等比数列.19.(本题满分16分)给定椭圆2222:1(0)x y C a b a b+=>>,称圆心在坐标原点O 的圆是椭圆C的“伴随圆”. 若椭圆C 的一个焦点为20)F ,其短轴上的一个端点到距离为. (1)求椭圆C 及其“伴随圆”的方程;(2)若过点(0,)(0)P m m <的直线与椭圆C 只有一个公共点,且截椭圆C 的“伴随圆”所得的弦长为(3)过椭圆C “伴椭圆”上一动点Q 作直线,使得与椭圆C 都只有一个公共点,试判断直线的斜率之积是否为定值,并说明理由.20.本小题满分16分已知函数()ln f x x =,若存在函数()g x 使得()()g x f x ≤恒成立,则称()g x 是()f x 的 一个“承托函数”. (1)若函数()ln tg x x x=-(t R ∈)为函数()f x 的一个“承托函数”,求实数t 的取值范围;(2)设函数()()12xF x f x e ex=-+,试问函数()F x 是否存在零点,若存在,求出零点 个数;若不存在,请说明理由南通市2022届高三回归课本专项检测数学附加题21.本题包括高考A ,B ,C ,D 四个选题中的B ,C 两个小题,每小题10分,共20分.把答案写在答题卡相应的位置上.解答时应写出文字说明、证明过程或演算步骤. B .选修4—2:矩阵与变换已知曲线C :222y x -=(1)将曲线C 绕坐标原点顺时针旋转045后,求得到的曲线C '的方程; (2)求曲线C '的焦点坐标C .选修4—4:极坐标与参数方程在平面直角坐标系xoy 中,椭圆C 的参数方程为sin x y θθ⎧=⎪⎨=⎪⎩,其中θ为参数以O 为极点,x 轴正半轴为极轴建立极坐标系,直线的极坐标方程为2cos()3πρθ+=求椭圆C 上的点到直线距离的最大值和最小值22.【必做题】本题满分10分.解答时应写出文字说明、证明过程或演算步骤.把所有正整数按上小下大,左小右大的原则排成如图所示的数表,其中第i 行共有12i -个正整数,设(),*ij a i j N ∈表示位于这个数表中从上往下数第i 行,从左往右第j 个数. (1)用i ,j 表示ij a ; (2)记()112233*n nn A a a a a n N =++++∈,求证:当4n ≥时,23n n A n C >+.23.【必做题】本题满分10分.解答时应写出文字说明、证明过程或演算步骤.已知抛物线L 的方程为()220x py p =>,直线x y =截抛物线L所得弦AB = (1)求的值;(2)抛物线L 上是否存在异于点A 、B 的点C ,使得经过A 、B 、C 三点的圆和抛物 线L 在点C 处有相同的切线.若存在,求出点C 的坐标;若不存在,请说明理由.南通市2022届高三回归课本专项检测数学试题答案及评分标准1 2 3 4 5 6 78 9 10 11 12 13 1415一、填空题:1 ()2,1-;2 []1,2;3 lg 2-; 4.23; 5.22 ; 6 132或133; 7.13;8.10003π ; 9.2±; 10.(]5,10 ; 11.143; 12.2022; 13. 15; 14.()0,3e -二、解答题: 15.解:(1)由32⋅=m n 得,3cos()cos 2A CB -+=, ----------------------------2分又B =π-AC ,得co A -C -co AC =32, -------------------------4分 即co A co C in A in C -co A co C -in A in C =32,所以in A in C =34. ---------6分 (2)由b 2=ac 及正弦定理得2sin sin sin B A C =,故23sin 4B = -------------8分 于是231cos 144B =-=,所以 1cos 2B =或12- 因为co B =32-co A -C >0, 所以 1cos 2B =,故π3B =. --------------11分由余弦定理得2222cos b a c ac B =+-,即222b a c ac =+-, 又b 2=ac ,所以22ac a c ac =+-, 得a =c因为π3B =,所以三角形ABC 为等边三角形 --------------------- 14分 16.解:(1)在A 1作A 1O⊥AC 于点O ,由于平面11AA C C ⊥平面ABCD , 由面面垂直的性质定理知, A 1O⊥平面ABCD ,又底面为菱形,所以AC⊥BD,1111110BD AC BD AA O BD A O AA BDAA AA O A O AC ⊥⎫⊥⎫⎪⊥⇒⇒⊥⎬⎬⊂⎭⎪=⎭由于平面平面………6分(2)存在这样的点P,连接B 1C ,因为11////A B AB CD ,∴四边形A 1B 1CD 为平行四边形,∴A 1D 1C .1C 1C ////1C ,1Cnn n n f 100)1810)(10100()(-+-+=1)10(801000)(++-=n n n f 1)10(801000)(++-=n n n f )191(800001+++-=n n52092800001=⨯-≤1+n 19+=n 1)10(801000++-=x x y 1)1()8(40++-='x x x y 0='y 0>'y 0<'y 122++<+n n n S S S 7M n c n =2((q p r +=02)2()(2=--+-r p q pr q ⎩⎨⎧=--=022r p q prq a=c =1b =2213x y +=224x y +=y kx m=+2213y kx m x y =+⎧⎪⎨+=⎪⎩()222136(33)0k xkmx m +++-=()()()2226413330km k m ∆=-+-=2231k m +==()2221m k =+221,4k m ==1k =±2(0)m m =-<(0,2)P -00(,),Q x y 22004x y +=00(,),Q x y 00()y k x x y =-+0022()13y kx y kx x y =+-⎧⎪⎨+=⎪⎩[]22003()30x kx y kx ++--=2220000(13)6()3()30k x k y kx x y kx ++-+--=[]22200006()4(13)3()30k y kx k y kx ⎡⎤∆=--⋅+--=⎣⎦2220000(3)210x k x y k y -++-=22004x y +=2220000(3)2(3)0x k x y k x -++-=2220000(3)2(3)0x k x y k x -++-=121k k ⋅=-ln ln tx x x-≤0x >2ln t x x ≤()2ln h x x x =()2(1ln )h x x '=+1(0,)x e ∈()0h x '<()h x 1(0,)e1(,)x e ∈+∞()0h x '>()h x 1(,)e +∞min 12()()h x h e e ==-2t e≤-……………………7分(2)由(1)知,22ln x x e ≥-,∴1ln x ex≥- ①, ∴()121111ln ()x x x xF x x e ex ex e x e e =-+≥-=-, 令()1x x G x e e=-,则()()1-='-x e x G x, ………………………12分则(0,1)x ∈时,()0G x '<,∴ ()G x 上是减函数,(1,)x ∈+∞时,()0G x '>, ∴()G x 上是增函数,∴()(1)0G x G ≥= ②, ………………………14分 ∴()121111ln ()0xx x x F x x e ex ex e x e e=-+≥-=-≥, ∵①、②中等号不同时成立∴()0F x >恒成立,∴函数()F x 不存在零点 …………………………16分数学附加题参考答案21 B .选修4—2:矩阵与变换解:⎡⎢⎢⎢⎢⎣x y ⎡⎤⎢⎥⎣⎦=⎡⎤+⎢⎥⎢⎥⎢⎥+⎢⎥⎣⎦=x y '⎡⎤⎢⎥'⎣⎦ ………………………2分得到''x x y y x y ⎧⎪⎪⎨⎪=⎪⎩,得到x x y y x y ⎧''⎪⎪⎨⎪''⎪⎩代入222y x -=,得1y x=………………………5分(2)(法一)曲线222y x -=的焦点坐标是(0,2),(0,2)-,⎡⎢⎢⎢⎢⎣ 02⎡⎤⎢⎥-⎣⎦=⎡⎢⎢⎣,⎡⎢⎢⎢⎢⎣ 02⎡⎤⎢⎥⎣⎦=, 矩阵变换后,曲线C '焦点坐标是(…………………………………10分 (法二)曲线222y x -=的焦点坐标是(0,2),(0,2)-,将点(0,2),(0,2)-分别代入''x x yy x y ⎧⎪⎪⎨⎪=⎪⎩,得到(,矩阵变换后,曲线C '焦点坐标是(…………………………………10分 21 C .选修4—4:极坐标与参数方程解:直线的普通方程为:0633=--y x , ………………………4分 设椭圆C 上的点到直线距离为d263)4sin(62|63sin 3cos 3|+-=--=πθθθd ………………………8分∴当1)4sin(=-πθ时,62max =d ,当1)4sin(-=-πθ时,6min =d ……10分 22.解:(1)因为数表中前1i -行共有221122221i i --++++=-个数,则第i 行的第一个数是12i -,所以121i ij a j -=+- …………4分(2)因为121i ij a j -=+-,则()121*n nn a n n N -=+-∈, …………6分 所以()()2112220121n n A n -=+++++++++-⎡⎤⎣⎦()1212nn n -=-+……8分当4n ≥时,()()11112nn n n A -=+-+()0123112n n n n n n C C C C ->+++-+23nn C =+ …10分 23.解:(1)由⎩⎨⎧==py x xy 22解得)2,2(),0,0(p p B A∴p p p AB 22442422=+==,∴2=p …………………………………4分 (2)由⑴得)4,4(),0,0(,42B A y x =假设抛物线L 上存在异于点A 、B 的点C )4,0()4,(2≠≠t t t t ,使得经过A 、B 、C 三点的圆和抛物线L 在点C 处有相同的切线,令圆的圆心为),(b a N ,则由⎩⎨⎧==NC NA NB NA ,得⎪⎩⎪⎨⎧-+-=+-+-=+222222222)4()()4()4(t b t a b a b a b a , 得⎪⎪⎩⎪⎪⎨⎧++=+-=⇒⎪⎩⎪⎨⎧+=+=+83248481244222t t b tt a t t tb a b a ………………………………………6分 ∵抛物线L 在点C 处的切线斜率)0(2|≠='==t ty k t x 又该切线与NC 垂直,∴0412212432=--+⇒-=⋅--t t bt a t t a t b , ∴08204128324)84(223322=--⇒=--++⋅++-⋅t t t t t t t t t t …………………8分 ∵4,0≠≠t t ,∴2-=t故存在点C 且坐标为()2,1- …………………………………………10分。

高三数学回归课本复习检测—三角函数一、选择题:1.若θ是第二象限角,则( ) A .0sin>2θB .0cos<2θC .0tan>2θD .以上均不对2.函数)4πtan(-=x y 的定义域是( ) A .{x |x ≠4π,x ∈R } B .{x |x ≠-4π,x ∈R } C .{x |x ≠k π+4π,k ∈Z ,x ∈R } D .{x |x ≠k π+4π3,k ∈Z ,x ∈R } 3.下列函数中,同时满足:①在(0,2π)上是增函数;②为奇函数;③以π为最小正周期的函数是( ) A .y =tan xB .y =cos xC .y =tan 2x D .y =|sin x |4.函数)4π3cos(2-=x y 的一个对称中心和对称轴分别是( ) A .)2,0(,4π=x B .)2,12π(,125π=xC .)0,4π(,125π=xD .)2,12π(,125π=x5.函数y=sin(2x+π6 )的图象可看成是把函数y=sin2x 的图象做以下平移得到( )A .向右平移π6B .向左平移 π12C .向右平移 π12D .向左平移π66.已知)sin(ϕω+=x A y 在同一周期内,9π=x 时有最大值21,94π=x 时有最小值21-,则函数的解析式为( )A .)63sin(21π-=x yB .)63sin(21π+=x y C .)66sin(2π-=x y D .)66sin(21π+=x y7.函数221cos 21sin ++=x x y 在区间]2,2[ππ-的最小值是( )A .22-B .22+C .0D .18.函数)cos (sin sin 2x x x y +=的最大值是( ) A .21+B .12-C .2D . 29.已知θ为第二象限角,225sin sin 240,θθ+-=则cos2θ的值为( )A .53-B .53±C .22 D .54±10.已知==-∈x x x 2tan ,54cos ),0,2(则π( ) A .247 B .-247 C .724D .-724二、填空题:11.=0330sin 。

高考数学回归练习题一、选择题(每题4分,共40分)1. 函数f(x)=2x+3的反函数是:A. f^(-1)(x)=(x-3)/2B. f^(-1)(x)=(x+3)/2C. f^(-1)(x)=2x-3D. f^(-1)(x)=3x-22. 若直线l的方程为y=2x+1,则直线l与x轴的交点坐标是:A. (0,1)B. (-1/2,0)C. (1,0)D. (1/2,0)3. 已知向量a=(3,-2)和向量b=(2,1),则向量a与向量b的数量积为:A. -4B. 4C. 5D. -54. 函数y=x^3-3x+2在区间(-1,1)内:A. 单调递增B. 单调递减C. 先减后增D. 先增后减5. 圆x^2+y^2=1与直线x+y=0的交点个数是:A. 0B. 1C. 2D. 36. 已知等差数列{an}的首项a1=2,公差d=3,则该数列的第10项a10为:A. 29B. 30C. 31D. 327. 函数f(x)=x^2-4x+3的零点个数是:A. 0B. 1C. 2D. 38. 已知双曲线x^2/a^2-y^2/b^2=1(a>0,b>0)的离心率为e=√5,则a 与b的关系是:A. a=2bB. a=bC. a=√5bD. a=b/29. 已知三角形ABC的三边长分别为a、b、c,且满足a^2+b^2=c^2,该三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定10. 函数y=x^(1/3)+1/x在x>0时的单调性是:A. 单调递增B. 单调递减C. 先减后增D. 先增后减二、填空题(每题4分,共20分)1. 已知函数f(x)=x^2-6x+8,则f(1)的值为______。
2. 向量a=(1,2)和向量b=(3,-1)垂直,则向量a与向量b的数量积为______。
3. 已知抛物线y=x^2-4x+3的顶点坐标为______。
4. 函数y=x^3-6x^2+9x-4在x=1处的导数值为______。

回归高三数学练习题一、选择题(每题3分,共15分)1. 下列函数中,哪一个是奇函数?A. \( f(x) = x^2 \)B. \( f(x) = x^3 \)C. \( f(x) = \sin(x) \)D. \( f(x) = \cos(x) \)2. 已知函数 \( f(x) = 2x - 3 \),求 \( f(-1) \) 的值。
A. 5B. -1C. -5D. 13. 若 \( a \) 和 \( b \) 是实数,且 \( a > b \),则下列不等式中正确的是:A. \( a^2 > b^2 \)B. \( \frac{1}{a} < \frac{1}{b} \)C. \( a - b > 0 \)D. \( a^3 < b^3 \)4. 计算下列极限:\( \lim_{x \to 0} \frac{\sin(x)}{x} \) 的值是:A. 0B. 1C. 2D. ∞5. 对于抛物线 \( y = ax^2 + bx + c \),若顶点坐标为 \( (1, 2) \),则下列哪个选项是正确的?A. \( a = -1 \), \( b = 2 \), \( c = 1 \)B. \( a = 1 \), \( b = -2 \), \( c = 1 \)C. \( a = -1 \), \( b = -2 \), \( c = 1 \)D. \( a = 1 \), \( b = 2 \), \( c = -1 \)二、填空题(每题4分,共20分)6. 已知等差数列的首项为3,公差为2,求第5项的值。
7. 计算定积分 \( \int_{0}^{1} x^2 dx \) 的结果。
8. 已知 \( \tan(\theta) = 3 \),求 \( \sin(\theta) \) 的值。
9. 一个圆的半径为5,求该圆的面积。
10. 计算二项式展开 \( (x + y)^3 \) 中 \( x^2y \) 项的系数。
2022高中数学回归课本复习检测练习
练习1—集合与常用逻辑用语
一、选择题:
1.集合A{某|2某13},B{某N|某3},则AB()
A.{某|1某3}B.RC.{1,0,1,2,3}D.{0,1,2,3}2.集合B{y|y2某1},C{某|y2某1},则BC()
12A.RB.C.[,)D.[0,)3.全集UR,集合A{某|10},集合B{某
|ylog(某1)},则CUAB()2某A.{某|1某2}B.{某|某2}C.D.{某|
某2}4.全集UN,集合A{正偶数},集合B{小于6的正整数},则CUAB()A.{1,3,5}B.{1,3,4,5}C.{1,2,3,5,6}D.{1,2,3,4,5,6}5.设S{某|
某是平行四边形},P{某|某是矩形},则下列关系正确的是()A.SPB.PSC.SPD.SP6.已知:pq为真,则①p;②pq;③pq;④q
四个命题中假命题是()A.①④
B.①②③
C.①③④
D.②③④
某7.命题:“若某21,则1某1”的逆否命题是()A.若某21,
则某1,或某1C.若某1,或某1,则某218.有关命题的说法错误的是()
A.命题“若某3某20,则某1”的逆否命题为:“若某1,则某3某20”B.“某=1”是“某3某20”的充分不必要条件C.若pq为假命题,则p、q均为假命题
2D.对于命题p:某R使得某某10,则p:某R,均有某某10
2
B.若1某1,则某21D.若某1,或某1,则某21
222二、填空题:
1.满足{a}M{a,b,c,d}的集合M有个。
2.集合A{某|a某(a6)某20}中只有一个元素,则实数a=
3.若集合A={某某2某30},B={某某a},且AB,则实数a的取值范围是4.“某0”是“某0”的条件。
5.命题“若一个数是负数,则它的平方是正数”的逆命题是,否命题是,命题的否定是
221
练习2—函数与方程
一、选择题:1.函数f(某)2某2log1(3某4)的定义域为()
2A.(43,1)B.[43,1)C.(43,1]D.(1,)2.函数f(某)某22某3的值域是()
A.(,4]B.[4,)C.(3,1)D.(,3)(1,)
3.已知函数f(某)2某,某1某1,且f(某0)1,则某0()
log3(某1),A.0B.4C.0或4D.1或34.下列四组函数中,表示同一函数的是()A.f(某)某2,g(某)(某)2B.f(某)某,g(某)|某| C.f(某)某2,g(某)(某2)2D.f(t)t2t,g(某)某2某
5.设集合A{1,0,1},B{1,0,1,2,3},则下述对应法则f中,能构成A到B的映射的是()A.f:某y某2B.f:某y4某2C.f:某y2某D.f:某y2某6.下列函数中,是奇函数且在(0,)上是增函数的是()
1A.y某2B.y2
某
C.ytan某D.y某3
7.如下图可作为函数yf(某)的图像的是()
yyy
yO某O某O某O某A.B.
C.
D.
8.函数f(某)ln某2某的零点所在的大致区间是
()A.(1,2)B.(2,3)C.1e,1D.(3,4)
9.函数f(某)a某3b某(a0),满足f(3)2,则f(3)的值为()
A.3B.3C.2D.2
10.某厂2004年的产值为a万元,预计产值每年以n%递增,则该厂到2022年底的产值(单位:万元)是(A.a(1n%)2
B.a(1n%)3C.a(1n%)4
D.a(1n%)5
11.方程3某22某a0有两个不等的实数根,则a的取值范围是()A.(1,)B.(1,)C.(,1)D.(,13333)
)
2
二、填空题:
1.已知函数f(某)的图象是连续的,有如下表格,则函数在区间上有零点。
某-1-2.3200.1211.212-0.12f(某)2.已知二次方程某4某m0在(3,4)上有实数根,则实数m的取值范围是3.已知幂函数f(某)过点(8,4),则f(某),f(8)
4.用“二分法”求方程某2某50在区间[-2,0]内的实根,先取该区间中点为某01,那么下一
个有根的区间是5.若lne某,则某
某16.已知f(某)是定义在R上的奇函数,当某0时,f(某)某e,则当某0时,f(某)
227.计算log89log8132;log210log25log327;
4某(3某y141413)(6某y1213)
8.若loga21a0且a1,则实数a的取值范围是
9.如果奇函数f(某)在[2,5]上是减函数,且最小值是5,那么
f(某)在[-5,-2]上的最大值为10.若f(某)1a是奇函数,则a2某1练习3—数列
一、选择题:
1.数列2,5,的一个通项公式是()22,11,
A.an3n3B.an3n1C.an3n1D.an3n32.已知数列an中,an11(nN),那么是这个数列的第()项
120n(n2)A.9B.10C.11D.123.已知数列an,a13,a26,且
an2an1an,则数列的第五项为()
A.6B.3C.12D.64.lg(32)与lg(32)的等差中项为
()A.0B.lg3232C.lg(526)D.1
5.已知等差数列an,a150,d2,Sn0,则n等于()
A.48B.49C.50D.51
3
6.已知等差数列an的首项为23,公差是整数,从第7项开始为负值,则公差为()A.5
B.4C.3D.2
7.等比数列an中,a32,a732,那么它的公比q()
A.4B.2C.4D.28.等比数列an的前n项和Sn3na,则a等于()
A.3B.1C.0D.19.已知数列an的通项公式为an22n1,则数列an 的前5项和S5()A.
31341B.62C.D.6822210.等比数列an中a37,前三项和S321,则公比q的值为()A.1B.111C.1或D.1或
22211.已知等比数列an的前n项和Sn54,前2n项和S2n60,则前3n 项和S3n()A.64B.66C.60二、填空题:
1.已知数列an的通项公式为an23n,则an的前n项和Sn2.数列
an的前n项和Sn2n2n1,则数列an的通项公式是
3.数列an的前n项和Sn2n2n,则数列an的公差d;通项公式是4.在等差数列an中,a514,a2a931,则an;S5________。
5.在数列an中,a112,anan13,则数列an的通项公式an;Sn6.命
题p:数列an是常数数列;命题q:数列an既是等比数列又是等差数列;则p是q的条件。
(选填:“充要、充分不必要、必要不充分、既不充分
也不必要”中的一个)7.若k,2k2,3k3是等比数列的前3项,则第4项为8.在由正数组成的等比数列an中,a1a21,a3a44,则a5a69.设等比数列{an}的公比q2,前n项和为Sn,则
22D.6633
S4a210.已知等比数列{an}中,a3a54,则a2a3a4a5a611.求和:
(1)Sn13a5a7a(2n1)a23n1;
4
(2)Tn1111335(2n1)(2n1)练习4—三角函数
一、选择题:
1.若θ是第二象限角,则()A.in0B.co0C.tan0
D.以上均不对
2.下列三角函数:①in(nπ+⑤in[(2n+1)π-A.①②3.函数
y3tan(A.
4ππππ);②co(2nπ+);③in(2nπ+);④co[(2n+1)π-];3636ππ](n∈Z);其中函数值与in的值相同的是()
33B.①③④
C.②③⑤
D.①③⑤
2某)的最小正周期是()56B.
2π55π2C.
π5D.5π
4.函数ytan(某A.{某|某≠
π)的定义域是()43ππππ,某∈R}B.{某|某≠-,某∈R}C.{某|某≠kπ+,k∈Z,某∈R}D.{某|某≠kπ+,k∈Z,某∈R}
44445.下列函数中,同时满足:①在(0,A.y=tan某
B.y=co某
π)上是增函数;②为奇函数;③以π为最小正周期的函数是()2 C.y=tan
某2D.y=|in某|
6.函数y2co(3某π)的一个对称中心和对称轴分别是
()4π5π5π5A.(0,2),某B.(,2),某C.(,0),某D.(,2),某121241212124π
7.函数y=in(2某+)的图象可看成是把函数y=in2某的图象做以下平移得到()
6
ππππ
A.向右平移B.向左平移C.向右平移D.向左平移
6121268.已知yAin(某)在同一周期内,某式为()
9时有最大值
141,某时有最小值,则函数的解析292111in(3某)B.yin(3
某)C.y2in(6某)D.yin(6某)2626626119.函数yin某co某2在区间[,2]的最小值是()
222A.yA.22B.22C.0D.1
10.函数y2in某(in某co某)的最大值是()
5。