2020-2021高三数学上期末模拟试卷带答案

2020-2021高三数学上期末试卷(含答案)(1)一、选择题1．已知数列{}n a 的前n 项和为n S ，且1142n n a -⎛⎫=+- ⎪⎝⎭，若对任意*N n ∈，都有()143n p S n ≤-≤成立，则实数p 的取值范围是（ ）A ．()2,3B ．[]2,3C ．92,2⎡⎤⎢⎥⎣⎦D ．92,2⎡⎫⎪⎢⎣⎭2．数列{}n a 满足()11nn n a a n ++=-⋅，则数列{}n a 的前20项的和为( ) A ．100 B ．-100C ．-110D ．1103．在ABC ∆中,,,a b c 分别为角,,A B C 所对的边,若 2?a bcos C =,则此三角形一定是( ) A ．等腰直角三角形 B ．直角三角形C ．等腰三角形D ．等腰三角形或直角三角形 4．已知在中，，，分别为角，，的对边，为最小角，且，，，则的面积等于（ ） A ．B ．C ．D ．5．已知x ，y 满足2303301x y x y y +-≤⎧⎪+-≥⎨⎪≤⎩，z ＝2x +y 的最大值为m ，若正数a ，b 满足a +b ＝m ，则14a b+的最小值为（ ） A ．3B ．32C ．2D ．526．设变量,x y 、满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩，则目标函数2z x y =+的最大值为（ ）A ．2B ．3C ．4D ．97．已知,,a b R +∈且115a b a b+++=,则+a b 的取值范围是（ ） A ．[1,4]B ．[)2,+∞C ．(2,4)D ．(4,)+∞8．“0x >”是“12x x+≥”的 A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件9．已知数列{a n }满足331log 1log ()n n a a n N +++=∈且2469a a a ++=，则15793log ()a a a ++的值是( )A ．－5B ．－15C ．5D ．1510．已知点(),M a b 与点()0,1N -在直线3450x y -+=的两侧，给出以下结论：①3450a b -+>；②当0a >时，+a b 有最小值，无最大值；③221a b +>；④当0a >且1a ≠时，11b a +-的取值范围是93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭，正确的个数是（ ） A ．1B ．2C ．3D ．411．设数列{}n a 的前n 项和为n S ，若2，n S ，3n a 成等差数列，则5S 的值是（ ） A ．243-B ．242-C ．162-D ．24312．在ABC ∆中，a ，b ，c 分别是角A ，B ，C 的对边，若2b c =，a =7cos 8A =，则ABC ∆的面积为（ ） AB ．3CD二、填空题13．若,a b ∈R ，0ab >，则4441a b ab++的最小值为___________.14．已知n S 为数列{a n }的前n 项和，且22111n n n a a a ++-=-，21313S a =，则{a n }的首项的所有可能值为______15．已知锐角三角形的边长分别为1，3，a ，则a 的取值范围是__________．16．△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若acosB ＝5bcosA ，asinA ﹣bsinB ＝2sinC ，则边c 的值为_______．17．已知x ，y 满足3010510x y x y x y +-≤⎧⎪-+≥⎨⎪-+≤⎩，则2z x y =+的最大值为______.18．数列{}n a 满足10a =，且()1*11211n nn N a a +-=∈--，则通项公式n a =_______．19．数列{}n a 满足：1a a =（a R ∈且为常数），()()()*13343n n n n n a a a n N a a +⎧->⎪=∈⎨-≤⎪⎩，当100a =时，则数列{}n a 的前100项的和100S 为________.20．已知数列{}n a (*n ∈N )，若11a =，112nn n a a +⎛⎫+= ⎪⎝⎭，则2lim n n a →∞= ． 三、解答题21．在ABC ∆中，,,a b c 分别是角,,A B C 所对的边，且2sin 3tan c B a A =.（1）求222b c a+的值； （2）若2a =，求ABC ∆面积的最大值. 22．已知数列中，，. （1）求证：是等比数列，并求的通项公式； （2）数列满足，求数列的前项和.23．设数列{}n a 满足()*164n n n a a n a +-=∈-N ，其中11a =. （Ⅰ）证明：32n n a a ⎧⎫-⎨⎬-⎩⎭是等比数列； （Ⅱ）令112n n b a =--，设数列{}(21)n n b -⋅的前n 项和为n S ，求使2019n S <成立的最大自然数n 的值.24．在数列{}n a 中, 已知11a =，且数列{}n a 的前n 项和n S 满足1434n n S S +-=, n *∈N . （1）证明数列{}n a 是等比数列；（2）设数列{}n na 的前n 项和为n T ，若不等式3()1604nn aT n+⋅-<对任意的n *∈N 恒成立, 求实数a 的取值范围. 25．己知数列的前n 项和为，且．（1）求数列的通项公式；（2）设，求数列的前n 项和．26．在等差数列{}n a 中，2723a a +=-，3829a a +=-． （1）求数列{}n a 的通项公式．（2）若数列{}n n a b +的首项为1，公比为q 的等比数列，求{}n b 的前n 项和n S ．【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【解析】11111444222n n S -⎛⎫⎛⎫⎛⎫=+-++-+⋅⋅⋅++- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭11221244133212nnn n ⎛⎫-- ⎪⎛⎫⎝⎭=+=+-⋅- ⎪⎛⎫⎝⎭-- ⎪⎝⎭()143n p S n ≤-≤Q即22113332n p ⎛⎫⎛⎫≤-⋅-≤ ⎪ ⎪ ⎪⎝⎭⎝⎭对任意*n N ∈都成立， 当1n =时，13p ≤≤ 当2n =时，26p ≤≤当3n =时，443p ≤≤ 归纳得：23p ≤≤故选B点睛：根据已知条件运用分组求和法不难计算出数列{}n a 的前n 项和为n S ，为求p 的取值范围则根据n 为奇数和n 为偶数两种情况进行分类讨论，求得最后的结果2．B解析：B 【解析】 【分析】数列{a n }满足1(1)nn n a a n ++=-⋅，可得a 2k ﹣1+a 2k ＝﹣（2k ﹣1）．即可得出．【详解】∵数列{a n }满足1(1)nn n a a n ++=-⋅，∴a 2k ﹣1+a 2k ＝﹣（2k ﹣1）．则数列{a n }的前20项的和＝﹣（1+3+……+19）()101192⨯+=-=-100．故选：B ． 【点睛】本题考查了数列递推关系、数列分组求和方法，考查了推理能力与计算能力，属于中档题．3．C解析：C 【解析】在ABC ∆中，222222cos ,2cos 222a b c a b c C a b C b ab abQ +-+-=∴==⋅，2222a a b c ∴=+-，,b c ∴=∴此三角形一定是等腰三角形，故选C.【方法点睛】本题主要考查利用余弦定理判断三角形形状，属于中档题.判断三角形状的常见方法是：（1）通过正弦定理和余弦定理，化边为角，利用三角变换得出三角形内角之间的关系进行判断；(2)利用正弦定理、余弦定理，化角为边，通过代数恒等变换，求出边与边之间的关系进行判断；（3）根据余弦定理确定一个内角为钝角进而知其为钝角三角形.4．C解析：C 【解析】 【分析】根据同角三角函数求出；利用余弦定理构造关于的方程解出，再根据三角形面积公式求得结果. 【详解】由余弦定理得：，即解得：或为最小角本题正确选项： 【点睛】本题考查余弦定理解三角形、三角形面积公式的应用、同角三角函数关系，关键是能够利用余弦定理构造关于边角关系的方程，从而求得边长.5．B解析：B 【解析】 【分析】作出可行域，求出m ，然后用“1”的代换配凑出基本不等式的定值，从而用基本不等式求得最小值． 【详解】作出可行域，如图ABC ∆内部（含边界），作直线:20l x y +=，平移该直线，当直线l 过点(3,0)A 时，2x y +取得最大值6，所以6m =．1411414143()()(5)(52)6662b a b a a b a b a b a b a b +=++=++≥+⨯=，当且仅当4b a a b =，即12,33a b ==时等号成立，即14a b +的最小值为32． 故选：B. 【点睛】本题考查简单的线性规划，考查用基本不等式求最值，解题关键是用“1”的代换凑配出基本不等式的定值，从而用基本不等式求得最小值．6．D解析：D 【解析】 【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论. 【详解】画出满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩的可行域，如图，画出可行域ABC ∆，(2,0)A ，(1,1)B ，(3,3)C ， 平移直线2z x y =+，由图可知，直线2z x y =+经过(3,3)C 时 目标函数2z x y =+有最大值，2z x y =+的最大值为9.故选D. 【点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.7．A解析：A 【解析】分析：,a b R +∈，由22a b ab +⎛⎫≥ ⎪⎝⎭，可得()214ab a b ≥+，又115a b a b +++=，可得()()()214151a b a b ab a b ⎛⎫⎛⎫ ⎪++=≥++ ⎪ ⎪⎝⎭+⎝⎭，化简整理即可得出. 详解：,a b R +∈，由22a b ab +⎛⎫≥ ⎪⎝⎭，可得()214ab a b ≥+，又115a b a b+++=， 可得()()()214151a b a b ab a b ⎛⎫⎛⎫ ⎪++=≥++ ⎪ ⎪⎝⎭+⎝⎭， 化为()()2540a b a b +-++≤， 解得14a b ≤+≤， 则+a b 的取值范围是[]1,4. 故选：A.点睛：本题考查了基本不等式的性质、一元二次不等式的解法，考查了推理能力与计算能力，属于中档题.8．C解析：C 【解析】先考虑充分性,当x>0时，12x x +≥=，当且仅当x=1时取等.所以充分条件成立.再考虑必要性，当12 xx+≥时，如果x>0时，22210(1)0x x x-+≥∴-≥成立，当x=1时取等.当x<0时，不等式不成立. 所以x>0.故选C.9．A解析：A【解析】试题分析：331313log1log log log1n n n na a a a+++=∴-=Q即13log1nnaa+=13nnaa+∴=∴数列{}n a是公比为3的等比数列335579246()393a a a q a a a∴++=++=⨯=15793log()5a a a∴++=-．考点：1．等比数列的定义及基本量的计算；2．对数的运算性质．10．B解析：B【解析】【分析】【详解】∵点M(a,b)与点N(0,−1)在直线3x−4y+5=0的两侧,∴()()34530450a b-+⨯++<，即3450a b-+<，故①错误；当0a>时,54a b+>，a+b即无最小值，也无最大值，故②错误；设原点到直线3x−4y+5=0的距离为d,则22513(4)==+-d,则22a b+>1，故③正确；当0a>且a≠1时,11ba+-表示点M(a,b)与P(1,−1)连线的斜率．∵当0a=,b=54时,51194114ba++==---,又直线3x−4y+5=0的斜率为34，故11ba+-的取值范围为93,,44⎛⎫⎛⎫-∞-⋃+∞⎪ ⎪⎝⎭⎝⎭，故④正确.∴正确命题的个数是2个. 故选B.点睛：本题是常规的线性规划问题，线性规划问题常出现的形式有：①直线型，转化成斜截式比较截距，要注意z 前面的系数为负时，截距越大，z 值越小；②分式型，其几何意义是已知点与未知点的斜率；③平方型，其几何意义是距离，尤其要注意的是最终结果应该是距离的平方；④绝对值型，转化后其几何意义是点到直线的距离.11．B解析：B 【解析】 【分析】 【详解】因为2,,3n n S a 成等差数列，所以223n n S a =+，当1n =时，111223,2S a a =+∴=-；当2n ≥时，1113333112222n n n n n n n a S S a a a a ---=-=+--=-，即11322n n a a -=，即()132nn a n a -=≥，∴数列{}n a 是首项12a =-，公比3q =的等比数列，()()55151213242113a q S q---∴===---，故选B.12．D解析：D 【解析】 【分析】三角形的面积公式为1sin 2ABC S bc A ∆=，故需要求出边b 与c ，由余弦定理可以解得b 与c . 【详解】解：在ABC ∆中，2227cos 28b c a A bc +-==将2b c =，a =22246748c c c +-=， 解得：2c =由7cos 8A =得sin A ==所以，11sin 2422ABC S bc A ∆==⨯⨯=故选D. 【点睛】三角形的面积公式常见形式有两种：一是12（底⨯高），二是1sin 2bc A .借助12（底⨯高）时，需要将斜三角形的高与相应的底求出来；借助1sin 2bc A 时，需要求出三角形两边及其夹角的正弦值.二、填空题13．4【解析】（前一个等号成立条件是后一个等号成立的条件是两个等号可以同时取得则当且仅当时取等号）【考点】均值不等式【名师点睛】利用均指不等式求最值要灵活运用两个公式（1）当且仅当时取等号；（2）当且仅解析：4 【解析】44224141144a b a b ab ab ab ab +++≥=+≥= ，（前一个等号成立条件是222a b =，后一个等号成立的条件是12ab =，两个等号可以同时取得，则当且仅当2224a b ==时取等号）. 【考点】均值不等式【名师点睛】利用均指不等式求最值要灵活运用两个公式，（1）22,,2a b a b ab ∈+≥R ，当且仅当a b =时取等号；（2）,a b R +∈ ，a b +≥ ，当且仅当a b =时取等号；首先要注意公式的使用范围，其次还要注意等号成立的条件；另外有时也考查利用“等转不等”“作乘法”“1的妙用”求最值.14．【解析】【分析】根据题意化简得利用式相加得到进而得到即可求解结果【详解】因为所以所以将以上各式相加得又所以解得或【点睛】本题主要考查了数列的递推关系式应用其中解答中利用数列的递推关系式得到关于数列首解析：34，- 【解析】 【分析】根据题意，化简得22111n n n a a a ++-=-，利用式相加，得到2213113112S a a a --=-，进而得到211120a a --=，即可求解结果.【详解】因为22111n n n a a a ++-=-，所以22111n n n a a a ++-=-， 所以2222222213321313121,1,,1a a a a a a a a a -=--=--=-L ，将以上各式相加，得2213113112S a a a --=-，又21313S a =，所以211120a a --=，解得13a =-或14a =.【点睛】本题主要考查了数列的递推关系式应用，其中解答中利用数列的递推关系式，得到关于数列首项的方程求解是解答的关键，着重考查了推理与运算能力，属于中档试题.15．【解析】由三角形中三边关系及余弦定理可得应满足解得∴实数的取值范围是答案：点睛：根据三角形的形状判断边满足的条件时需要综合考虑边的限制条件在本题中要注意锐角三角形这一条件的运用必须要考虑到三个内角的解析：a <<【解析】由三角形中三边关系及余弦定理可得a 应满足22222222224130130310a a a a <<⎧⎪+->⎪⎨+->⎪⎪+->⎩，解得a << ∴实数a的取值范围是．答案： 点睛：根据三角形的形状判断边满足的条件时，需要综合考虑边的限制条件，在本题中要注意锐角三角形这一条件的运用，必须要考虑到三个内角的余弦值都要大于零，并由此得到不等式，进一步得到边所要满足的范围．16．3【解析】【分析】由acosB ＝5bcosA 得由asinA ﹣bsinB ＝2sinC 得解方程得解【详解】由acosB ＝5bcosA 得由asinA ﹣bsinB ＝2sinC 得所以故答案：3【点睛】本题主要解析：3 【解析】 【分析】由acosB ＝5bcosA 得22223a b c -=，由asinA ﹣bsinB ＝2sinC 得222a b c -=，解方程得解. 【详解】由acosB ＝5bcosA 得22222222225,223a cb bc a a b a b c ac bc +-+-⋅=⋅∴-=.由asinA ﹣bsinB ＝2sinC 得222a b c -=，所以222,33c c c =∴=. 故答案：3 【点睛】本题主要考查正弦定理和余弦定理解三角形，意在考查学生对这些知识的理解掌握水平和分析推理能力.17．5【解析】【分析】画出不等式表示的可行域利用目标函数的几何意义当截距最小时取z 取得最大值求解即可【详解】画出不等式组表示的平面区域(如图阴影所示)化直线为当直线平移过点A 时z 取得最大值联立直线得A （解析：5 【解析】 【分析】画出不等式表示的可行域，利用目标函数的几何意义当截距最小时取z 取得最大值求解即可 【详解】画出不等式组表示的平面区域(如图阴影所示)，化直线2z x y =+为122z y x =-+ 当直线平移过点A 时，z 取得最大值，联立直线3010x y x y +-=⎧⎨-+=⎩得A （1,2），故max 145z =+=故答案为：5【点睛】本题考查画不等式组表示的平面区域、考查数形结合求函数的最值，是基础题18．【解析】【分析】构造数列得到数列是首项为1公差为2的等差数列得到【详解】设则数列是首项为1公差为2的等差数列故答案为【点睛】本题考查了数列的通项公式的求法构造数列是解题的关键意在考查学生对于数列通项解析：2221n n -- 【解析】 【分析】构造数列11n nb a =-，得到数列n b 是首项为1公差为2的等差数列21n b n =-，得到2221n n a n -=-. 【详解】 设11n n b a =-，则12n n b b +-=，11111b a ==- 数列n b 是首项为1公差为2的等差数列1222121121n n n b n n a n n a -=⇒=--⇒--= 故答案为2221n n -- 【点睛】本题考查了数列的通项公式的求法，构造数列11n nb a =-是解题的关键，意在考查学生对于数列通项公式的记忆，理解和应用.19．【解析】【分析】直接利用分组法和分类讨论思想求出数列的和【详解】数列满足：（且为常数）当时则所以（常数）故所以数列的前项为首项为公差为的等差数列从项开始由于所以奇数项为偶数项为所以故答案为：【点睛】 解析：1849【解析】 【分析】直接利用分组法和分类讨论思想求出数列的和. 【详解】数列{}n a 满足：1a a =（a R ∈且为常数），()()()*13343n n n n n a a a n N a a +⎧->⎪=∈⎨-≤⎪⎩， 当100a =时，则1100a =， 所以13n n a a +-=-（常数）， 故()10031n a n =--，所以数列的前34项为首项为100，公差为3-的等差数列. 从35项开始，由于341a =，所以奇数项为3、偶数项为1， 所以()()1001001346631184922S +⨯=+⨯+=，故答案为：1849 【点睛】本题考查了由递推关系式求数列的性质、等差数列的前n 项和公式，需熟记公式，同时也考查了分类讨论的思想，属于中档题.20．【解析】【分析】由已知推导出=(=1+（）从而-=-由此能求出【详解】∵数列满足：∴（）+（）+……+（）=++……+==(∴=(；又+……+（）=1+++……+=1+=1+（）即=1+（）∴-=-解析：23-【解析】 【分析】 由已知推导出2n S =23(11)4n -，21n S -=1+13（1114n --），从而22n n a S =-21n S -=21132n -n -23，由此能求出2lim n n a →∞【详解】 ∵数列{}n a 满足：1 1a =，112nn n a a +⎛⎫+= ⎪⎝⎭， ∴（12a a +）+（34 a a +）+……+（212 n n a a -+）=12+312⎛⎫ ⎪⎝⎭+……+2112n -⎛⎫ ⎪⎝⎭=11124114n ⎛⎫- ⎪⎝⎭-=23(11)4n-， ∴2n S =23(11)4n -； 又12345a a a a a +++++……+（2221 n n a a --+）=1+212⎛⎫ ⎪⎝⎭+412⎛⎫ ⎪⎝⎭+……+2212n -⎛⎫ ⎪⎝⎭=1+2111124114n -⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭-=1+13（1114n --），即21n S -=1+13（1114n --） ∴22n n a S =-21n S -=21132n -n -23∴2211lim lim(32n n n n a n -→∞→∞=-2)3=-23，故答案为：-2 3【点睛】本题考查数列的通项公式的求法，数列的极限的求法，考查逻辑思维能力及计算能力，属于中档题．三、解答题21．（1）2224b c a+=（2 【解析】 【分析】（I ）由题意2sin 3tan c B a A =，利用正、余弦定理化简得2224b c a +=，即可得到答案. （II ）因为2a =，由（I ）知222416b c a +==，由余弦定理得6cos A bc=，进而利用基本不等式，得到6cos bc A =，且(0,)2A π∈，再利用三角形的面积公式和三角函数的性质，即可求解面积的最大值. 【详解】解：（I ）∵2sin 3tan c B a A =， ∴2sin cos 3sin c B A a A =， 由正弦定理得22cos 3cb A a =，由余弦定理得22222?32b c a cb a bc+-=，化简得2224b c a +=，∴2224b c a+=. （II ）因为2a =，由（I ）知222416b c a +==，∴由余弦定理得2226cos 2b c a A bc bc+-==， 根据重要不等式有222b c bc +≥，即8bc ≥，当且仅当b c =时“=”成立， ∴63cos 84A ≥=. 由6cos A bc =，得6cos bc A =，且0,2A π⎛⎫∈ ⎪⎝⎭， ∴ABC ∆的面积116sin sin 3tan 22cos S bc A A A A==⨯⨯=. ∵2222222sin cos sin 11tan 1cos cos cos A A A A A A A++=+==，∴tan 3A =≤=∴3tan S A =≤∴ABC ∆的面积S . 【点睛】本题主要考查了利用正弦定理和三角函数的恒等变换求解三角形问题，对于解三角形问题，通常利用正弦定理进行“边转角”寻求角的关系，利用“角转边”寻求边的关系，利用余弦定理借助三边关系求角，利用两角和差公式及二倍角公式求三角函数值. 利用正、余弦定理解三角形问题是高考高频考点，经常利用三角形内角和定理，三角形面积公式，结合正、余弦定理解题.22．(1)答案见解析；(2).【解析】试题分析：⑴根据数列的递推关系，结合等比数列的定义即可证明是等比数列，并求的通项公式，⑵利用错位相减法即可求得答案；解析：（1）∵∴∴，∵，，∴是以为首项，以4为公比的等比数列∴，∴，∴，（2），∴①②①-②得∴.23．（Ⅰ）证明见解析（Ⅱ）6 【解析】 【分析】（Ⅰ）由递推公式凑出1132n n a a ++--与32n n a a --的关系，即可得证（Ⅱ）由（Ⅰ）可得2111222n n n n n a b a a --=-==--，即可得到{}(21)n n b -⋅的通项公式，再用错位相减法求和，证明其单调性，可得得解. 【详解】 解：（Ⅰ）()*164n n n a a n a +-=∈-N Q 1163346224n n n n n n a a a a a a ++----∴=---- 6312628n n n n a a a a --+=--+2(3)(2)n n a a --=--322n n a a -=- 32n n a a ⎧⎫-∴⎨⎬-⎩⎭是首项为113132212a a --==--，公比为2的等比数列（Ⅱ）由（Ⅰ）知，322n n n a a -=-， 即2111222n n n n n a b a a --=-==--， 21212n n n b n ∴-⋅=-⋅（）（）123S 123252...(21)2n n n =⋅+⋅+⋅++-⋅①23412S 123252...(21)2n n n +=⋅+⋅+⋅++-⋅②，①减②得11231142S 122(22...2)(21)222(21)212n n n n n n n +++--=⋅+++--⋅=+⋅--⋅-1(32)26n n +=-⋅-. 1S (23)26n n n +∴=-⋅+2111S S (21)2(23)22210n n n n n n n n ++++∴-=-⋅--⋅=+>（），S n ∴单调递增.76S 92611582019=⨯+=<Q ， 87S 112628222019=⨯+=>.故使S 2019n <成立的最大自然数6n =. 【点睛】本题考查利用递推公式证明函数是等比数列，以及错位相减法求和，属于中档题. 24．(1)见解析(2) (,20)-∞ 【解析】分析：（1）利用1434n n S S +-=推出134n n a a +=是常数，然后已知2134a a =，即可证明数列{}n a 是等比数列；（2）利用错位相减法求出数列{}n na 的前n 项和为n T n ，化简不等式31604nn aT n⎛⎫+⋅-< ⎪⎝⎭，通过对任意的*n N ∈恒成立，求实数a 的取值范围．详解：(1) Q 已知*1434,n n S S n N +-=∈,∴ 2n ≥时, 143 4.n n S S --= 相减得1430n n a a +-=. 又易知0,n a ≠134n n a a +∴=. 又由*1434,n n S S n N +-=∈得()121434,a a a +-=22133,44a a a ∴=∴=. 故数列{}n a 是等比数列.(2)由(1)知1133144n n n a --⎛⎫⎛⎫=⨯= ⎪⎪⎝⎭⎝⎭.01133312444n n T n -⎛⎫⎛⎫⎛⎫∴=⨯+⨯++⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭L ,123333124444nn T n ⎛⎫⎛⎫⎛⎫∴=⨯+⨯++⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭L . 相减得213113333341344444414nn n nn T n n -⎛⎫- ⎪⎛⎫⎛⎫⎛⎫⎛⎫⎝⎭=++++-⨯=-⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭-L ,331616444n nn T n ⎛⎫⎛⎫∴=-⨯-⨯ ⎪ ⎪⎝⎭⎝⎭, ∴不等式31604n n a T n ⎛⎫+⨯-< ⎪⎝⎭为33316164160444n n na n n⎛⎫⎛⎫⎛⎫-⨯-⨯+⨯-< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 化简得2416n n a +>. 设()2416f n n n =+,*n N ∈Q ()()120min f n f ∴==.故所求实数a 的取值范围是(),20-∞.点睛：本题考查等比数列的判断，数列通项公式与前n 项和的求法，恒成立问题的应用，考查计算能力． 25．（1）；（2）【解析】 【分析】 （1）运用，证明数列是等比数列，计算通项，即可。

2020-2021高三数学上期末一模试题及答案(1)一、选择题1．若函数y ＝f (x )满足：集合A ＝{f (n )|n ∈N *}中至少有三个不同的数成等差数列，则称函数f (x )是“等差源函数”，则下列四个函数中，“等差源函数”的个数是( ) ①y ＝2x ＋1；②y ＝log 2x ；③y ＝2x＋1；④y ＝sin44x ππ+（）A ．1B ．2C ．3D ．42．已知等比数列{}n a 的公比为正数，且239522,1a a a a ⋅==，则1a = ( )A ．12B ．2 CD ．23．“干支纪年法”是中国历法上自古以来就一直使用的纪年方法，干支是天干和地支的总称，把干支顺序相配正好六十为一周，周而复始，循环记录，这就是俗称的“干支表”甲、乙、丙、丁、戊、己、庚、辛、癸等十个符号叫天干，子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥等十二个符号叫地支，如公元1984年农历为甲子年，公元1985年农历为乙丑年，公元1986年农历为丙寅年，则公元2047年农历为 A ．乙丑年B ．丙寅年C ．丁卯年D ．戊辰年4．已知实数,x y 满足0{20x y x y -≥+-≤则2y x -的最大值是( )A ．-2B ．-1C ．1D ．2 5．在等差数列{}n a 中，若1091a a <-，且它的前n 项和n S 有最大值，则使0n S >成立的正整数n 的最大值是（ ） A ．15B ．16C ．17D ．146．若a 、b 、c >0且a (a ＋b ＋c )＋bc ＝4－，则2a ＋b ＋c 的最小值为( )A ．1B ．1C ．＋2D ．27．已知正项等比数列{}n a 的公比为3，若229m n a a a =，则212m n+的最小值等于（ ） A ．1B ．12C ．34 D ．328．已知数列{}n a 的前n 项和为n S ，点(,3)n n S +*()n N ∈在函数32xy =⨯的图象上，等比数列{}n b 满足1n n n b b a ++=*()n N ∈，其前n 项和为n T ，则下列结论正确的是（ ）A ．2n n S T =B ．21n n T b =+C ．n n T a >D ．1n n T b +<9．在ABC ∆中，a ，b ，c 分别是角A ，B ，C 的对边，若2b c =，a =7cos 8A =，则ABC ∆的面积为（ ） A ．17B ．3C ．15D ．15210．在R 上定义运算：A()1B A B =-，若不等式()x a -()1x a +<对任意的实数x ∈R 恒成立，则实数a 的取值范围是( ) A ．11a -<<B ．02a <<C ．1322a -<< D ．3122a -<< 11．在△ABC 中，若1tan 15013A C BC ︒===，，，则△ABC 的面积S 是( ) A ．338- B ．334- C ．338+ D ．334+ 12．等差数列{}n a 中，34512a a a ++=，那么{}n a 的前7项和7S =（ ） A ．22B ．24C ．26D ．28二、填空题13．已知x y ，满足20030x y y x y -≥⎧⎪≥⎨⎪+-≤⎩，，，，则222x y y ++的取值范围是__________.14．数列{}21n-的前n 项1,3,7..21n-组成集合{}()*1,3,7,21nn A n N=-∈，从集合nA中任取()1,2,3?··n k k =个数，其所有可能的k 个数的乘积的和为（若只取一个数，规定乘积为此数本身），记12n n S T T T =++⋅⋅⋅+，例如当1n =时，{}1111,1,1===A T S ；当2n =时，{}21221,2,13,13,13137A T T S ==+=⨯=++⨯=，试写出n S =___15．已知数列{}n a 中，45n a n =-+，等比数列{}n b 的公比q 满足1(2)n n q a a n -=-≥，且12b a =，则12n b b b +++=__________．16．在等差数列{}n a 中，12a =，3510a a +=，则7a = ．17．若实数,x y 满足约束条件200220x y x y x y +≥⎧⎪-≤⎨⎪-+≥⎩，则3z x y =-的最小值等于_____．18．设，，若，则的最小值为_____________.19．设122012(1)(1)(1)n n n x x x a a x a x a x ++++++=++++，其中n *∈N ，且2n ≥，若0121022n a a a a ++++=，则n =_____20．数列{}n a 满足10a =，且()1*11211n nn N a a +-=∈--，则通项公式n a =_______．三、解答题21．ABC 的内角A 、B 、C 所对的边分别为a b c ，，，且sin sin sin 2sin a A b B c C a B +=+()1求角C ；()2求3sin cos 4A B π⎛⎫-+ ⎪⎝⎭的最大值． 22．等差数列{}n a 中，71994,2a a a ==. (1)求{}n a 的通项公式； (2)设1n nb na =，求数列{}n b 的前n 项和n S . 23．已知S n 为等差数列{a n }的前n 项和，a 1>0，a 8﹣a 4﹣a 3=1，a 4是a 1和a 13的等比中项. （1）求数列{a n }的通项公式； （2）证明：对一切正整数n .有1211134n S S S +++<. 24．在ABC ∆中，内角,,A B C 的对边分别为,,a b c ，设平面向量()()sin cos ,sin ,cos sin ,sin p A B A q B A B =+=-，且2cos p q C ⋅=（Ⅰ）求C ； （Ⅱ）若3,23c a b =+=，求ABC ∆中边上的高h .25．已知各项均为正数的等比数列{}n a 的首项为12，且()3122123a a a -=+。

2020-2021郑州市高三数学上期末模拟试题(含答案)一、选择题1．已知点(),M a b 与点()0,1N -在直线3450x y -+=的两侧，给出以下结论：①3450a b -+>；②当0a >时，+a b 有最小值，无最大值；③221a b +>；④当0a >且1a ≠时，11b a +-的取值范围是93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭，正确的个数是（ ） A ．1B ．2C ．3D ．42．若正实数x ，y 满足141x y +=，且234yx a a +>-恒成立，则实数a 的取值范围为（ ） A ．[]1,4-B ．()1,4-C ．[]4,1-D ．()4,1-3．已知数列{}n a 的前n 项和2n S n =，()1nn n b a =-则数列{}n b 的前n 项和n T 满足（ ） A ．()1nn T n =-⨯ B ．n T n =C ．n T n =-D ．,2,.n n n T n n ⎧=⎨-⎩为偶数，为奇数4．ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，已知2b =，6B π=，4C π=，则ABC ∆的面积为（ ） A．2+B1C．2D15．若直线()100,0ax by a b ++=>>把圆()()224116x y +++=分成面积相等的两部分，则122a b+的最小值为( ) A ．10B ．8C ．5D ．46．已知点(),P x y 是平面区域()4{04y x y x m y ≤-≤≥-内的动点, 点()1,1,A O -为坐标原点, 设()OP OA R λλ-∈u u u r u u u r的最小值为M ,若M ≤恒成立, 则实数m 的取值范围是（ ）A ．11,35⎡⎤-⎢⎥⎣⎦B ．11,,35⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭C ．1,3⎡⎫-+∞⎪⎢⎣⎭D ．1,2⎡⎫-+∞⎪⎢⎣⎭7．数列{}{},n n a b 为等差数列，前n 项和分别为,n n S T ，若3n 22n n S T n +=，则77a b =（ ） A ．4126B ．2314C ．117 D ．1168．若直线()10,0x ya b a b+=>>过点(1,1)，则4a b +的最小值为（ ） A ．6B ．8C ．9D ．109．设x y ，满足约束条件70310,350x y x y x y +-⎧⎪-+⎨⎪--⎩，，„„…则2z x y =-的最大值为（ ）.A ．10B ．8C ．3D ．210．在ABC ∆中，内角,,A B C 所对的边分别为,,a b c ，且()cos 4cos a B c b A =-，则cos2A =（ ）A ．78B ．18C ．78-D ．18-11．在等差数列{a n }中，a 1＞0，a 10·a 11＜0，若此数列的前10项和S 10＝36，前18项的和S 18＝12，则数列{|a n |}的前18项和T 18的值是 （ ） A ．24B ．48C ．60D ．8412．等差数列{}n a 中，34512a a a ++=，那么{}n a 的前7项和7S =（ ） A ．22B ．24C ．26D ．28二、填空题13．已知实数，且，则的最小值为____14．在等差数列{}n a 中，首项13a =，公差2d =，若某学生对其中连续10项进行求和，在遗漏掉一项的情况下，求得余下9项的和为185，则此连续10项的和为 ．15．数列{}n a 满足14a =，12nn n a a +=+，*n N ∈，则数列{}n a 的通项公式n a =______.16．设函数2()1f x x =-，对任意2,3x ⎡⎫∈+∞⎪⎢⎣⎭，24()(1)4()x f m f x f x f m m ⎛⎫-≤-+⎪⎝⎭恒成立，则实数m 的取值范围是 .17．ABC ∆内角A 、B 、C 的对边分别是a ，b ，c ，且2cos (32)cos b C a c B =-.当42b =，2a c =，ABC ∆的面积为______.18．设，，若，则的最小值为_____________.19．已知x y 、满足约束条件1{1,22x y x y x y +≥-≥--≤若目标函数()0,0z ax by a b =+>>的最大值为7，则34a b+的最小值为_______． 20．已知数列{}n a 满足51()1,62,6n n a n n a a n -⎧-+<⎪=⎨⎪≥⎩，若对任意*n N ∈都有1n n a a +>，则实数a 的取值范围是_________.三、解答题21．已知等差数列{}n a 的前n 项和为254,12,16n S a a S +==． (1)求{}n a 的通项公式； (2)数列{}n b 满足141n n n b T S =-，为数列{}n b 的前n 项和，是否存在正整数m ，()1k m k <<，使得23k m T T =?若存在，求出m ，k 的值；若不存在，请说明理由．22．已知函数()21f x x =-. （1）若不等式121(0)2f x m m ⎛⎫+≥+> ⎪⎝⎭的解集为][(),22,-∞-⋃+∞，求实数m 的值； （2）若不等式()2232y yaf x x ≤+++对任意的实数,x y R ∈恒成立，求正实数a 的最小值.23．设数列{}n a 的前n 项和n S 满足：2(1)n n S na n n =--，等比数列{}n b 的前n 项和为n T ，公比为1a ，且5352T T b =+．（1）求数列{}n a 的通项公式;（2）设数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n M ，求证：1154n M ≤<．24．在△ABC 中，角A B C 、、的对边分别为a b c 、、，已知3cos()16cos cos B C B C --=，（1）求cos A （2）若3a =，△ABC的面积为求b c 、25．在公差不为0的等差数列{}n a 中，1a ，3a ，9a 成公比为3a 的等比数列，又数列{}n b 满足*2,21,()2,2,n a n n k b k N n n k ⎧=-=∈⎨=⎩． （1）求数列{}n a 的通项公式； （2）求数列{}n b 的前2n 项和2n T ．26．在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且22222230a c b ac +-+=. （1）求cos B 的值；（2）求sin 24B π⎛⎫+⎪⎝⎭的值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【解析】 【分析】 【详解】∵点M (a ,b )与点N (0,−1)在直线3x −4y +5=0的两侧,∴()()34530450a b -+⨯++<，即3450a b -+<，故①错误； 当0a >时,54a b +>，a +b 即无最小值，也无最大值，故②错误； 设原点到直线3x −4y +5=0的距离为d ,则22513(4)==+-d ,则22a b +>1，故③正确；当0a >且a ≠1时,11b a +-表示点M (a ,b )与P (1,−1)连线的斜率． ∵当0a =,b =54时,51194114b a ++==---,又直线3x −4y +5=0的斜率为34， 故11b a +-的取值范围为93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭，故④正确.∴正确命题的个数是2个. 故选B.点睛：本题是常规的线性规划问题，线性规划问题常出现的形式有：①直线型，转化成斜截式比较截距，要注意z 前面的系数为负时，截距越大，z 值越小；②分式型，其几何意义是已知点与未知点的斜率；③平方型，其几何意义是距离，尤其要注意的是最终结果应该是距离的平方；④绝对值型，转化后其几何意义是点到直线的距离.2．B解析：B 【解析】 【分析】 根据1444y y x x x y ⎛⎫⎛⎫+=++ ⎪ ⎪⎝⎭⎝⎭，结合基本不等式可求得44yx +≥，从而得到关于a 的不等式，解不等式求得结果. 【详解】 由题意知：1442444y y x yx x x y y x⎛⎫⎛⎫+=++=++ ⎪ ⎪⎝⎭⎝⎭ 0x Q >，0y > 40x y ∴>，04yx>424x y y x ∴+≥=（当且仅当44x y y x =，即4x y =时取等号） 44yx ∴+≥ 234a a ∴-<，解得：()1,4a ∈- 本题正确选项：B 【点睛】本题考查利用基本不等式求解和的最小值问题，关键是配凑出符合基本不等式的形式，从而求得最值.3．A解析：A 【解析】 【分析】先根据2n S n =,求出数列{}n a 的通项公式,然后利用错位相减法求出{}n b 的前n 项和n T .【详解】解:∵2n S n =,∴当1n =时,111a S ==;当2n ≥时,()221121n n n a S S n n n -=-=--=-, 又当1n =时,11a =符合上式,∴21n a n =-, ∴()()()1121nnn n b a n =-=--,∴()()()()()123113151121nn T n =⨯-+⨯-+⨯-+⋅⋅⋅+--①,∴()()()()()2341113151121n n T n +-=⨯-+⨯-+⨯-+⋅⋅⋅+--②,①-②,得()()()()()()23412121111211n n n T n +⎡⎤=-+⨯-+-+-+⋅⋅⋅+---⨯-⎣⎦()()()()()()211111122112111n n n n n -+⎡⎤---⎣⎦=-+⨯--⨯-=---,∴()1nn T n =-,∴数列{}n b 的前n 项和()1nn T n =-.故选:A . 【点睛】本题考查了根据数列的前n 项和求通项公式和错位相减法求数列的前n 项和,考查了计算能力,属中档题.4．B解析：B 【解析】试题分析：根据正弦定理，，解得，，并且，所以考点：1．正弦定理；2．面积公式．5．B解析：B 【解析】 【分析】由于直线将圆平分，故直线过圆的圆心，将圆心坐标代入直线方程，利用“1”的代换的方法以及基本不等式，求得所求和的最小值. 【详解】圆的圆心为()4,1--，由于直线将圆平分，故直线过圆心，即410a b --+=，即41a b +=，故()121288444282222b a b a a b a b a b a b a b⎛⎫+=++=++≥+⋅= ⎪⎝⎭，当且仅当82b aa b =，即11,82a b ==时，取得最小值为8.故选B. 【点睛】本小题主要考查直线和圆的位置关系，考查利用“1”的代换和基本不等式求解和式的最小值问题.直线能将圆平分成面积相等的两个部分，则这条直线是经过圆心的.要注意的是，圆的标准方程是()()222x a y b r -+-=，圆心是(),a b ，所以本题的圆心是()4,1--，而不是()4,1.6．C解析：C 【解析】试题分析：直线()4x m y =-恒过定点(0,4)，当0m >时，约束条件()4{04y x y x m y ≤-≤≥-对应的可行域如图，则()OP OA R λλ-∈u u u r u u u r的最小值为0M=，满足2M ≤，当0m =时，直线()4x m y =-与y 轴重合，平面区域()4{04y x y x m y ≤-≤≥-为图中y 轴右侧的阴影区域，则()OP OA R λλ-∈u u u r u u u r的最小值为0M =，满足2M ≤，当0m <时，由约束条件()4{04y x y x m y ≤-≤≥-表示的可行域如图，点P 与点B 重合时，()OP OA R λλ-∈u u u r u u u r的最小值为M OB =u u u r ，联立{(4)y x x m y ==-，解得44(,)11m mB m m --，所以421m OB m =-u u u r ，由4221m m ≤-，解得1135m -≤≤，所以103m -≤≤，综上所述，实数m 的取值范围是1,3⎡⎫-+∞⎪⎢⎣⎭，故选C.考点：简单的线性规划.【方法点晴】本题主要考查了二元一次不等式组所表示的平面区域、简单的线性规划求最值问题，着重考查了数形结合思想方法及分类讨论的数学思想方法的应用，关键是正确的理解题意，作出二元一次不等式组所表示的平面区域，转化为利用线性规划求解目标函数的最值，试题有一定的难度，属于难题.7．A解析：A 【解析】依题意，113713113713132412226132a a a Sb b b T +⋅===+⋅.8．C解析：C 【解析】 【详解】 因为直线()10,0x y a b a b+=>>过点()1,1,所以11+1a b = ,因此1144(4)(+)5+529b a b aa b a b a b a b+=+≥+⋅= ,当且仅当23b a ==时取等号,所以选C.点睛：在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误.9．B解析：B 【解析】 【分析】作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数即可求解. 【详解】 作出可行域如图：化目标函数为2y x z =-， 联立70310x y x y +-=⎧⎨-+=⎩，解得5,2A（）. 由图象可知，当直线过点A 时，直线在y 轴上截距最小，z 有最大值25-28⨯=. 【点睛】本题主要考查了简单的线性规划，数形结合的思想，属于中档题.10．C解析：C 【解析】 【分析】根据题目条件结合三角形的正弦定理以及三角形内角和定理可得sin A ，进而利用二倍角余弦公式得到结果. 【详解】∵()cos 4cos a B c b A =-． ∴sin A cos B ＝4sin C cos A ﹣sin B cos A 即sin A cos B +sin B cos A ＝4cos A sin C ∴sin C ＝4cos A sin C ∵0＜C ＜π，sin C ≠0． ∴1＝4cos A ，即cos A 14=， 那么27cos2218A cos A =-=-． 故选C 【点睛】本题考查了正弦定理及二倍角余弦公式的灵活运用，考查计算能力，属于基础题．11．C解析：C 【解析】试题分析：∵11011101100000a a a d a a ⋅∴＞，＜，＜，＞，＜， ∴18110111810181060T a a a a S S S =+⋯+--⋯-=--=（），选C . 考点：1.等差数列的求和；2.数列的性质.12．D解析：D 【解析】试题分析：由等差数列的性质34544123124a a a a a ++=⇒=⇒=，则考点：等差数列的性质二、填空题13．3+54【解析】【分析】由a+b ＝2得出b ＝2﹣a 代入代数式中化简后换元t ＝2a ﹣1得2a ＝t+1得出1＜t ＜3再代入代数式化简后得出2t6t-(t2+5)然后在分式分子分母中同时除以t 利用基本不等 解析：【解析】 【分析】由a +b ＝2得出b ＝2﹣a ，代入代数式中，化简后换元t ＝2a ﹣1，得2a ＝t +1，得出1＜t ＜3，再代入代数式化简后得出，然后在分式分子分母中同时除以t ，利用基本不等式即可求出该代数式的最小值． 【详解】解：由于a +b ＝2，且a ＞b ＞0，则0＜b ＜1＜a ＜2， 所以，，令t ＝2a ﹣1∈（1，3），则2a ＝t +1， 所以，． 当且仅当，即当时，等号成立． 因此，的最小值为．故答案为：．【点睛】本题考查利用基本不等式求最值，解本题的关键就是对代数式进行化简变形，考查计算能力，属于中等题．14．200【解析】试题分析：等差数列中的连续10项为遗漏的项为且则化简得所以则连续10项的和为考点：等差数列解析：200 【解析】试题分析：等差数列{}n a 中的连续10项为*+129,,,,,()x x x x a a a a x N ++⋯∈，遗漏的项为*+,x n a n N ∈且19,n ≤≤则9()10(18)10(2)22x x x x x n x a a a a a a n +++⨯++⨯-=-+，化简得4494352x n ≤=+≤，所以5x =，511a =，则连续10项的和为(1111+18)10=2002+⨯.考点：等差数列.15．【解析】【分析】由题意得出利用累加法可求出【详解】数列满足因此故答案为：【点睛】本题考查利用累加法求数列的通项解题时要注意累加法对数列递推公式的要求考查计算能力属于中等题 解析：22n +【解析】 【分析】由题意得出12nn n a a +-=，利用累加法可求出n a .【详解】数列{}n a 满足14a =，12n n n a a +=+，*n N ∈，12nn n a a +∴-=，因此，()()()211213214222n n n n a a a a a a a a --=+-+-++-=++++L L ()121242212n n --=+=+-.故答案为：22n +. 【点睛】本题考查利用累加法求数列的通项，解题时要注意累加法对数列递推公式的要求，考查计算能力，属于中等题.16．【解析】【分析】【详解】根据题意由于函数对任意恒成立分离参数的思想可知递增最小值为即可知满足即可成立故答案为解析：33,,22⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢ ⎪⎝⎦⎣⎭【解析】 【分析】 【详解】根据题意，由于函数2()1f x x =-，对任意2,3x ⎡⎫∈+∞⎪⎢⎣⎭，24()(1)4()x f m f x f x f m m ⎛⎫-≤-+ ⎪⎝⎭恒成立，22222()4(1)(1)11xm x x m m--≤--+-，分离参数的思想可知，,递增，最小值为53，即可知满足33,⎛⎫-∞⋃+∞ ⎪ ⎪⎝⎦⎣⎭即可成立故答案为33,22⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎦⎣⎭．17．【解析】【分析】由利用正弦定理得到再用余弦定理求得b 可得ac 利用面积公式计算可得结果【详解】由正弦定理可化为所以在三角形中所以因为所以又所以由余弦定理得又所以有故的面积为故答案为【点睛】本题考查了正 解析：3257【解析】 【分析】由()2cos 32cos b C a c B =-，利用正弦定理得到2cos 3B =，再用余弦定理求得b ，可得a 、c ，利用面积公式计算可得结果. 【详解】由正弦定理()2cos 32cos b C a c B =-可化为2sin cos 3sin cos 2sin cos B C A B C B =-， 所以()2sin 3sin cos B C A B +=， 在三角形中，()sin sin B C A +=，所以2sin 3sin cos A A B =，因为sin 0A ≠，所以2cos 3B =， 又0B π<<，所以25sin 1cos B B =-=， 由余弦定理得2224323b a c ac =+-=，又2a c =，所以有2967c =. 故ABC ∆的面积为22196965325sin sin sin 27737S ac B c B c B =====⨯=. 故答案为325. 【点睛】本题考查了正弦定理、余弦定理的应用，考查了三角形面积计算公式，考查了推理能力与计算能力，属于中档题．18．3+22【解析】【分析】由已知可得a-1+b=1从而有2a-1+1b=(2a-1+1b)(a-1+b)展开后利用基本不等式即可求解【详解】由题意因为a>1b>2满足a+b=2所以a-1+b=1且a- 解析：【解析】 【分析】 由已知可得，从而有，展开后利用基本不等式，即可求解. 【详解】由题意，因为满足，所以，且，则，当且仅当且，即时取得最小值.【点睛】本题主要考查了利用基本不等式求最值问题的应用，其中解答中根据题意配凑基本不等式的使用条件，合理利用基本不等式求得最值是解答的关键，着重考查了分析问题和解答问题的能力，属于中档试题.19．7【解析】试题分析：作出不等式表示的平面区域得到及其内部其中把目标函数转化为表示的斜率为截距为由于当截距最大时最大由图知当过时截距最大最大因此由于当且仅当时取等号考点：1线性规划的应用；2利解析：7【解析】试题分析：作出不等式表示的平面区域，得到及其内部，其中把目标函数转化为，表示的斜率为，截距为，由于当截距最大时，最大，由图知，当过时，截距最大，最大，因此，，由于，当且仅当时取等号，.考点：1、线性规划的应用；2、利用基本不等式求最值.20．【解析】【分析】由题若对于任意的都有可得解出即可得出【详解】∵若对任意都有∴∴解得故答案为【点睛】本题考查了数列与函数的单调性不等式的解法考查了推理能力与计算能力属于中档题解析：17,212⎛⎫⎪⎝⎭【解析】 【分析】由题若对于任意的*n N ∈都有1n n a a +>，可得5610012a a a a -＜，＞，＜＜． 解出即可得出． 【详解】∵511,62,6n n a n n a a n -⎧⎛⎫-+<⎪ ⎪=⎝⎭⎨⎪≥⎩，若对任意*n N ∈都有1n n a a +>， ∴5610012a a a a -＜，＞，＜＜．． ∴11 0()510122a a a a --⨯+＜，＞，＜＜ ， 解得17 212a ＜＜． 故答案为17,212⎛⎫⎪⎝⎭．【点睛】本题考查了数列与函数的单调性、不等式的解法，考查了推理能力与计算能力，属于中档题．三、解答题21．（1）*21,n a n n N =-∈（2）存在，2,12m k ==【解析】 【分析】（1）设等差数列{}n a 的公差为d ，由等差数列的通项公式与前n 项和公式得112512238a d a d +=⎧⎨+=⎩，解得112a d =⎧⎨=⎩，从而求出21n a n =-； （2）由（1）得()2122n n n S n n -=+⨯=，由211114122121n b n n n ⎛⎫==- ⎪--+⎝⎭，利用裂项相消法得21n n T n =+，若23k m T T =，则()2232121k m k m =++，整理得223412m k m m =+-，由1k m >>得11m <<+，从而可求出答案． 【详解】解：（1）设等差数列{}n a 的公差为d ， 由2541216a a S +=⎧⎨=⎩得112512238a d a d +=⎧⎨+=⎩，解得112a d =⎧⎨=⎩，()*12121,n a n n n N ∴=+-=-∈；（2）()2122n n n S n n -=+⨯=，211114122121n b n n n ⎛⎫∴==- ⎪--+⎝⎭，1211111111111123352321212122121n n n T b b b n n n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫∴=++⋅⋅⋅+=-+-+⋅⋅⋅+-+-=-= ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥---+++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ，若23k m T T =，则()2232121k m k m =++，整理得223412m k m m=+-， 又1k m >>，2234121m m m m m ⎧>⎪∴+-⎨⎪>⎩，整理得222104121m m m m m ⎧-->⎪+-⎨⎪>⎩，解得11m << 又*m N ∈，2m ∴=，12k ∴=， ∴存在2,12m k ==满足题意． 【点睛】本题主要考查等差数列的性质与求和，考查裂项相消法求和，属于中档题．22．(1) 32m =；(2)4. 【解析】试题分析：（Ⅰ）先根据绝对值定义解不等式解集为][(),22,-∞-⋃+∞，再根据解集相等关系得122m +=，解得32m =．（Ⅱ）不等式恒成立问题，一般转化为对应函数最值问题，即()max212322y y ax x --+≤+，根据绝对值三角不等式可得()max21234x x --+=，再利用变量分离转化为对应函数最值问题：()max242y ya ⎡⎤≥-⎣⎦，根据基本不等式求最值： ()()224224242y yy y ⎡⎤+-⎢⎥-≤=⎢⎥⎣⎦，因此4a ≥，所以实数a 的最小值为4．试题解析：（Ⅰ）由题意知不等式221(0)x m m ≤+>的解集为][(),22,-∞-⋃+∞． 由221x m ≤+，得1122m x m --≤≤+， 所以，由122m +=，解得32m =． （Ⅱ）不等式()2232y y a f x x ≤+++等价于212322yya x x --+≤+， 由题意知()max212322y y ax x --+≤+． 因为()()212321234x x x x --+≤--+=， 所以242y y a +≥，即()242y y a ⎡⎤≥-⎣⎦对任意y R ∈都成立，则()max 242y ya ⎡⎤≥-⎣⎦．而()()224224242y yy y⎡⎤+-⎢⎥-≤=⎢⎥⎣⎦，当且仅当242y y =-，即1y =时等号成立， 故4a ≥，所以实数a 的最小值为4． 23．(1) 43n a n =-;(2)证明见解析. 【解析】 【分析】 【详解】（1）∵2(1)n n S na n n =--①， ∴11(1)2(1)n n S n a n n ++=+-+②， ②-①，11(1)4n n n a n a na n ++=+--，∴14n n a a +-=，又∵等比数列{}n b ，5352T T b =+，∴535452T T b b b -=⇐=，1q =，∴11a =，∴数列{}n a 是1为首项，4为公差的等差数列， ∴14(1)43n a n n =+-=-；（2）由（1）可得111111()(43)(41)44341n n a a n n n n +==--+-+， ∴11111111(1)(1)45594341441n M n n n =-+-+⋅⋅⋅+-=--++，∴111(1)454n M -≤<， 即1154n M ≤<． 考点：1．等差等比数列的运算；2．列项相消法求数列的和． 24．：（1）1cos 3A =（2）3{2b c ==或23b c =⎧⎨=⎩【解析】：（1）由3cos()16cos cos B C B C --=得3(cos cos sin sin )1B C B C -=- 即1cos()3B C +=-从而cos A 1cos()3B C =-+= （2）由于0,A π<<1cos 3A =，所以sin A =又ABC S =V1sin 2bc A =6bc =由余弦定理2222cos a b c bc A =+-，得2213b c += 解方程组2213{6b c bc +==，得3{2b c ==或23b c =⎧⎨=⎩ 25．（1）n a n =；（2）22(41)2(1)3n n T n n -=++ 【解析】 【分析】（1）根据条件列方程组解得公差与首项，即得数列{}n a 的通项公式；（2）根据分组求和法得结果. 【详解】（1）公差d 不为0的等差数列{}n a 中，1a ，3a ，9a 成公比为3a 的等比数列，可得2319a a a =，313a a a =，可得2111(2)(8)a d a a d +=+，11a =，化简可得11a d ==，即有n a n =；（2）由（1）可得2,212,2n n n k b n n k ⎧=-=⎨=⎩，*k N ∈；前2n 项和212(28322)(48124)n n T n -=+++⋯+++++⋯+2(14)12(41)(44)2(1)1423n n n n n n --=++=++-． 【点睛】本题考查等差数列通项公式以及分组求和法求和，考查基本分析求解能力，属中档题. 26．（1）34-（2）16【解析】试题分析：（1）利用余弦定理表示出cosB ，将已知等式代入即可求出cosB 的值；（2）由cosB 可求出sin 2,cos 2B B 的值，然后利用两角和的余弦公式可得结果. 试题解析：（1）由22222230a c b ac +-+=，得22232a cb ac +-=-， 根据余弦定理得222332cos 224aca cb B ac ac -+-===-； （2）由3cos 4B =-，得sin B =∴sin22sin cos B B B ==21cos22cos 18B B =-=，∴1sin 2sin2cos cos2sin 44428816B B B πππ⎫⎛⎫+=+=-+=⎪ ⎪⎪⎝⎭⎝⎭．。

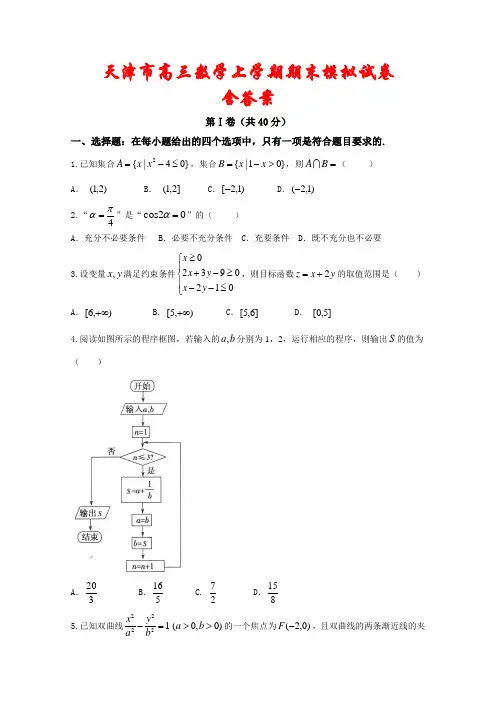
天津市高三数学上学期期末模拟试卷含答案第Ⅰ卷（共40分）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合}04|{2≤-=x x A ，集合}01|{>-=x x B ，则=B A （ ） A ． )2,1( B ． ]2,1( C ．)1,2[- D ．)1,2(- 2.“4πα=”是“02cos =α”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要3.设变量y x ,满足约束条件⎪⎩⎪⎨⎧≤--≥-+≥01209320y x y x x ，则目标函数y x z 2+=的取值范围是（ ）A ．),6[+∞B ．),5[+∞C ．]6,5[D ． ]5,0[4.阅读如图所示的程序框图，若输入的b a ,分别为1，2，运行相应的程序，则输出S 的值为（ ）A ．320 B ．516 C. 27 D ．815 5.已知双曲线22221x y a b-=(0,0)a b >>的一个焦点为)0,2(-F ，且双曲线的两条渐近线的夹角为060，则双曲线的方程为（ ）A ．1322=-y x B ．12622=-y x C. 1322=-y x 或1322=-y x D ．1322=-y x 或12622=-y x 6.在ABC ∆中，内角,,A B C 的对边分别为,,a b c ，已知B C 2sin sin =，且2=b ，3=c ，则a 等于（ ） A ．21B ．3 C. 2 D ．32 7.如图，平面四边形ABCD 中，090=∠=∠ADC ABC ，2==CD BC ，点E 在对角线AC 上，44==AE AC ，则ED EB •的值为（ ）A ． 17B ．13 C. 5 D ．18.已知函数xxe e xf -+=)(（其中e 是自然对数的底数），若当0>x 时，1)(-+≤-m e x mf x恒成立，则实数m 的取值范围为（ ）A ．)31,0( B ．]31,(--∞ C. ),31[+∞ D ．]31,31[-第Ⅱ卷（共110分）二、填空题（每题5分，满分30分，将答案填在答题纸上）9.已知i 为虚数单位，则=+-ii12 ． 10.在6)12(xx -的展开式中2x 的系数为 ．（用数字作答） 11.一个四棱柱的三视图如图所示，该四棱柱的体积为 ．12.已知曲线3x y =与直线)0(>=k kx y 在第一象限内围成的封闭图形的面积为4，则=k ．13.在平面直角坐标系xOy 中，已知抛物线⎩⎨⎧==t y t x 442（t 为参数）的焦点为F ，动点P 在抛物线上，动点Q 在圆⎩⎨⎧=+=ααsin cos 3y x （α为参数）上，则||||PQ PF +的最小值为 ．14.已知函数⎪⎩⎪⎨⎧>≤+=0|,ln |0,131)(x x x x x f ，若函数0)(=-ax x f 恰有3个零点，则实数a 的取值范围为 ．三、解答题 （本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.）15.已知函数x x x x x f cos sin 32sin cos )(22+-=，R x ∈.（1）求)(x f 的最小正周期； （2）求)(x f 在区间]4,6[ππ-上的最大值与最小值. 16.某大学现有6名包含A 在内的男志愿者和4名包含B 在内的女志愿者，这10名志愿者要参加第十三届全运会支援服务工作，从这些人中随机抽取5人参加田赛服务工作，另外5人参加径赛服务工作.（1）求参加田赛服务工作的志愿者中包含A 但不包含B 的概率；（2）设X 表示参加径赛服务工作的女志愿者人数，求随机变量X 的分布列与数学期望.17. 在如图所示的几何体中，AC DE //，90=∠=∠ACD ACB ，32==DE AC ，2=BC ，1=DC ，二面角E AC B --的大小为060.（1）求证：⊥BD 平面ACDE ；（2）求平面BCD 与平面BAE 所成的角（锐角）的大小；（3）若F 为AB 的中点，求直线EF 与平面BDE 所成的角的大小. 18. 已知}{n a 是等比数列，满足21=a ，且432,2,a a a +成等差数列. （1）求}{n a 的通项公式；（2）设n n na b 2=，数列}{n b 的前n 项和为n S ，4792)(2-+-=n S n n n g ),2(*N n n ∈≥，求正整数k 的值，使得对任意2≥n 均有)()(n g k g ≥.19. 设椭圆22221(0)x y a b a b +=>>的左焦点为1F ，离心率为21，1F 为圆0152:22=-++x y x M 的圆心.（1）求椭圆的方程；（2）已知过椭圆右焦点2F 的直线l 交椭圆于B A ,两点，过2F 且与l 垂直的直线1l 与圆M 交于D C ,两点，求四边形ACBD 面积的取值范围. 20. 已知函数)1(ln )(x a x x f -+=，R a ∈. （1）讨论)(x f 的单调性；（2）当21-=a 时，令)(21)(2x f x x g --=，其导函数为)('x g ，设21,x x 是函数)(x g 的两个零点，判断221x x +是否为)('x g 的零点？并说明理由.高三数学（理）参考答案一、选择题: 1－8CABDC CDB 二、填空题： 9．1322i - 10．240 11．36 12．4 13．3 14．11,3e ⎡⎫⎪⎢⎣⎭三、解答题：（15）解：（Ⅰ）()22cos sin cos f x x x x x =-+cos 22x x =+12cos 2sin 22sin 2226x x x π⎛⎫⎛⎫=+=+ ⎪ ⎪ ⎪⎝⎭⎝⎭所以22T ππ==，所以()f x 的最小正周期为π． （Ⅱ）由,64x ππ⎡⎤∈-⎢⎥⎣⎦，得22,663x πππ⎡⎤+∈-⎢⎥⎣⎦， 所以当2,662x πππ⎡⎤+∈-⎢⎥⎣⎦，即,66x ππ⎡⎤∈-⎢⎥⎣⎦时，函数()f x 单调递增； 当22,623x πππ⎡⎤+∈⎢⎥⎣⎦，即,64x ππ⎡⎤∈⎢⎥⎣⎦时，函数()f x 单调递减； 且当266x ππ+=-，即6x π=-时，1sin 262x π⎛⎫+=- ⎪⎝⎭，此时()=1f x -； 当262x ππ+=，即6x π=时，sin 216x π⎛⎫+= ⎪⎝⎭，此时()=2f x ;当2263x ππ+=，即4x π=时，sin 262x π⎛⎫+= ⎪⎝⎭，此时()f x 所以当6x π=-时，()f x 取得最小值1-；当6x π=时，()f x 取得最大值2（16）解：（I ）记参加田赛服务工作的志愿者中包含A 但不包含B 的事件为M ， 则基本事件的总数为510C ，事件M 包含基本事件的个数为48C ，则()48510518C P M C ==.(II)由题意知X 可取的值为：0,1,2,3,4.则()5651010,42C P X C === ()416451051,21C C P X C === ()3264510102,21C C P X C ===()236451053,21C C P X C === ()146451014,42C C P X C ===因此X 的分布列为X 的数学期望是()()()()()()0011223344E X P X P X P X P X P X =⨯=+⨯=+⨯=+⨯=+⨯==151******** 2.4221212142⨯+⨯+⨯+⨯+⨯= （17）解：方法一：（I ）因为90ACB ACD ∠=∠=，则AC CD ⊥，AC CB ⊥， 所以BCD ∠为二面角B AC E --的平面角，即60BCD ∠=， 在BCD ∆中，2BC =，1DC =，60BCD ∠=，所以214122132BD =+-⨯⨯⨯=，所以222BD DC BC +=，即BD DC ⊥， 由AC CD ⊥，AC CB ⊥，且BC DC C =，可知AC ⊥平面BCD ，又BD ⊂平面BCD ，所以AC BD ⊥， 又因为ACDC C =，AC ⊂平面ACDE ，DC ⊂平面ACDE ，所以BD ⊥平面ACDE ．（II ）由BD ⊥平面ACDE 得BD DC ⊥，BD DE ⊥，又AC CD ⊥，即DB ，DC ，DE 两两垂直，则以DB ，DC ，DE 分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系，如图所示．由（I ）知3BD =则()0,0,0D ，)30,0B，()0,1,0C ，由23AC DE ==得30,0,2E ⎛⎫⎪⎝⎭，()0,1,3A 依题意30,1,2AE ⎛⎫=--⎪⎝⎭，()31,3AB =--，设平面BAE 的一个法向量为(),,n x y z =，则00n AE n AB ⎧⋅=⎪⎨⋅=⎪⎩，即302330y z x y z ⎧--=⎪--=，不妨设3y =，可得()3,3,2n =--，由AC ⊥平面BCD 可知平面BCD 的一个法向量为()0,0,3AC = 设平面BCD 与平面BAE 所成的角（锐角）为θ，所以61cos cos ,432n AC n AC n ACθ⋅====⨯，于是=3πθ， 所以平面BCD 与平面BAE 所成的角（锐角）为3π． （III ）若F 为AB 的中点，则由（II ）可得313,,222F ⎛⎫⎪ ⎪⎝⎭，所以31,,022EF ⎛⎫= ⎪ ⎪⎝⎭，依题意CD ⊥平面BDE ，可知平面BDE 的一个法向量为()0,1,0DC =， 设直线EF 与平面BDE 所成角为α，则1sin cos ,2DC EF DC EF DC EFα⋅===，所以直线EF 与平面BDE 所成角的大小6π．方法二：（I ）因为90ACB ACD ∠=∠=，则AC CD ⊥，AC CB ⊥， 所以BCD ∠为二面角B AC E --的平面角，即60BCD ∠=， 在BCD ∆中，2BC =，1DC =，60BCD ∠=，所以214122132BD =+-⨯⨯⨯=，所以222BD DC BC +=，即BD DC ⊥， 由AC CD ⊥，AC CB ⊥，且BC DC C =，可知AC ⊥平面BCD ，又BD ⊂平面BCD ，所以AC BD ⊥， 又因为ACDC C =，AC ⊂平面ACDE ，DC ⊂平面ACDE ，所以BD ⊥平面ACDE ．（Ⅱ）令CD AE ,的延长线的交点为G ，连BG 。

2020-2021高三数学上期末一模试题(含答案)(5)一、选择题1．数列{}n a 满足()11nn n a a n ++=-⋅，则数列{}n a 的前20项的和为( )A ．100B ．-100C ．-110D ．1102．已知等比数列{}n a 的公比为正数，且239522,1a a a a ⋅==，则1a = ( )A ．12B ．2 CD．23．设x y ，满足约束条件10102x y x y y -+≤⎧⎪+-⎨⎪≤⎩＞，则yx 的取值范围是（ ）A ．()[),22,-∞-+∞UB ．(]2,2-C ．(][),22,-∞-+∞UD ．[]22-,4．已知实数x 、y 满足约束条件00134x y x ya a⎧⎪≥⎪≥⎨⎪⎪+≤⎩，若目标函数231x y z x ++=+的最小值为32，则正实数a 的值为（ ） A ．4B ．3C ．2D ．15．在ABC V 中，A ，B ，C 的对边分别为a ，b ，c ，2cos 22C a b a+=，则ABC V 的形状一定是( ) A ．直角三角形B ．等边三角形C ．等腰三角形D ．等腰直角三角形6．设数列{}n a 是以2为首项，1为公差的等差数列，{}n b 是以1为首项，2为公比的等比数列，则1210b b b a a a ++⋯+=（ ） A ．1033B ．1034C ．2057D ．20587．在ABC ∆中，,,a b c 是角,,A B C 的对边，2a b =，3cos 5A =，则sinB =（ ） A ．25B ．35C ．45 D ．858．设实数,x y 满足242210x y x y x -≤⎧⎪+≤⎨⎪-≥⎩，则1y x +的最大值是（ ）A ．-1B ．12C ．1D ．329．已知等比数列{}n a 的各项均为正数，前n 项和为n S ，若26442,S 6a S a =-=，则5a = A ．4B ．10C ．16D ．3210．已知数列{}n a 中，()111,21,n n na a a n N S *+==+∈为其前n 项和，5S的值为（ ） A ．63B ．61C ．62D ．5711．ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，已知2b =，6B π=，4C π=，则ABC ∆的面积为（ ）A ．2+B 1C ．2D 112．在△ABC 中，若1tan 15013A C BC ︒===，，，则△ABC 的面积S 是( )A ．38- B ．34- C ．38+ D 二、填空题13．在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c .2C A π-=，1sin 3A =，3a =，则b =______.14．已知数列{}n a 的前n 项和为2*()2n S n n n N =+∈，则数列{}n a 的通项公式n a =______．15．若正数,a b 满足3ab a b =++，则+a b 的取值范围_______________。

2020-2021高三数学上期末一模试卷及答案(2)一、选择题1．下列结论正确的是（ ） A ．若a b >，则22ac bc > B ．若22a b >，则a b > C ．若,0a b c ><，则a c b c +<+ D<a b <2．若0a b <<,则下列不等式恒成立的是 A ．11a b> B ．a b -> C ．22a b > D ．33a b <3．若正项递增等比数列{}n a 满足()()()243510a a a a R λλ+-+-=∈，则89a a λ+的最小值为（ ） A ．94-B ．94C ．274D ．274-4．若直线()100,0ax by a b ++=>>把圆()()224116x y +++=分成面积相等的两部分，则122a b+的最小值为( ) A ．10B ．8C ．5D ．45．设,x y 满足约束条件3002x y x y x -+≥⎧⎪+≥⎨⎪≤⎩, 则3z x y =+的最小值是 A ．5-B ．4C ．3-D ．116．若n S 是等差数列{}n a 的前n 项和，其首项10a >，991000a a +>，991000a a ⋅< ，则使0n S >成立的最大自然数n 是（ ） A ．198 B ．199C ．200D ．2017．若直线()10,0x ya b a b+=>>过点(1,1)，则4a b +的最小值为（ ） A ．6B ．8C ．9D ．108．在等差数列{}n a 中，若1091a a <-，且它的前n 项和n S 有最大值，则使0n S >成立的正整数n 的最大值是（ ） A ．15B ．16C ．17D ．149．已知,,a b R +∈且115a b a b+++=,则+a b 的取值范围是（ ） A ．[1,4]B ．[)2,+∞C ．(2,4)D ．(4,)+∞10．若a 、b 、c >0且a (a ＋b ＋c )＋bc ＝4－2a ＋b ＋c 的最小值为( ) A．1B．1C ．23＋2D ．23－211．设,x y 满足约束条件0,20,240,x y x y x y -≥⎧⎪+-≥⎨⎪--≤⎩则2z x y =+的最大值为（ ）A ．2B ．3C ．12D ．1312．已知数列{}n a 的前n 项和为n S ，且()*21n n S a n N =-∈，则5a 等于（ ）A ．16-B ．16C ．31D ．32二、填空题13．已知实数，且，则的最小值为____14．已知lg lg 2x y +=，则11x y+的最小值是______.15．在ABC ∆中，角,,A B C 所对的边为,,a b c ，若23sin c ab C =，则当b aa b+取最大值时，cos C =__________；16．已知平面四边形ABCD 中，120BAD ∠=︒，60BCD ∠=︒，2AB AD ==，则AC 的最大值为__________．17．已知0,0a b >>，且20a b +=，则lg lg a b +的最大值为_____． 18．设无穷等比数列{}n a 的公比为q ，若1345a a a a =+++…，则q =__________________．19．已知x ，y 满足3010510x y x y x y +-≤⎧⎪-+≥⎨⎪-+≤⎩，则2z x y =+的最大值为______.20．设(32()lg 1f x x x x =++，则对任意实数,a b ，“0a b +≥”是“()()0f a f b +≥”的_________条件．（填“充分不必要”.“必要不充分”.“充要”.“既不充分又不必要”之一）三、解答题21．已知函数()()22f x x x a x R =++∈（1）若函数()f x 的值域为[0,)+∞，求实数a 的值；（2）若()0f x >对任意的[1,)x ∈+∞成立，求实数a 的取值范围。

2020-2021高三数学上期末一模试题带答案(3)一、选择题1．记n S 为等比数列{}n a 的前n 项和.若2342S S S =+，12a =，则2a =（ ）A ．2B ．-4C ．2或-4D ．42．在ABC ∆中，2AC =,BC =135ACB ∠=o ，过C 作CD AB ⊥交AB 于D ，则CD =( ) ABCD3．等比数列{}n a 的前n 项和为n S ，若36=2S =18S ，，则105S S 等于( ) A ．－3B ．5C ．33D ．－314．已知实数,x y 满足0{20x y x y -≥+-≤则2y x -的最大值是( )A ．-2B ．-1C ．1D ．25．已知函数223log ,0(){1,0x x f x x x x +>=--≤，则不等式()5f x ≤的解集为 ( )A ．[]1,1-B ．[]2,4-C ．(](),20,4-∞-⋃D ．(][],20,4-∞-⋃ 6．在ABC ∆中，,,a b c 是角,,A B C 的对边，2a b =，3cos 5A =，则sinB =（ ） A ．25B ．35C ．45 D ．857．若直线()10,0x ya b a b+=>>过点(1,1)，则4a b +的最小值为（ ） A ．6B ．8C ．9D ．108．已知数列{}n a 中，()111,21,n n na a a n N S *+==+∈为其前n 项和，5S的值为（ ）A ．63B ．61C ．62D ．579．已知x ，y 均为正实数，且111226x y +=++，则x y +的最小值为（ ） A ．20B ．24C ．28D ．3210．如图，为了测量山坡上灯塔CD 的高度，某人从高为=40h 的楼AB 的底部A 处和楼顶B 处分别测得仰角为=60βo，=30αo ，若山坡高为=35a ，则灯塔高度是（ ）A ．15B ．25C ．40D ．6011．设x y ，满足约束条件70310,350x y x y x y +-⎧⎪-+⎨⎪--⎩，，„„…则2z x y =-的最大值为（ ）.A ．10B ．8C ．3D ．212．等差数列{}n a 中，34512a a a ++=，那么{}n a 的前7项和7S =（ ） A ．22B ．24C ．26D ．28二、填空题13．已知实数，且，则的最小值为____14．要使关于x 的方程()22120x a x a +-+-=的一根比1大且另一根比1小，则a 的取值范围是__________．15．已知0,0a b >>，且20a b +=，则lg lg a b +的最大值为_____．16．已知x ，y 满足3010510x y x y x y +-≤⎧⎪-+≥⎨⎪-+≤⎩，则2z x y =+的最大值为______.17．若ABC ∆的三个内角45A =︒，75B =︒，60C =︒，且面积623S =+，则该三角形的外接圆半径是______ 18．数列{}n a 满足10a =，且()1*11211n nn N a a +-=∈--，则通项公式n a =_______．19．在等比数列中，，则__________．20．已知数列{}n a (*n ∈N )，若11a =，112nn n a a +⎛⎫+= ⎪⎝⎭，则2lim n n a →∞= ． 三、解答题21．设{}n a 是等比数列，公比不为1．已知113a =，且1a ，22a ，33a 成等差数列． （1）求{}n a 的通项公式；（2）设数列n na ⎧⎫⎨⎬⎩⎭的前n 项和为n T ，求n T ． 22．在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转，如图，小卢利用图形的旋转设计某次活动的徽标，他将边长为a 的正三角形ABC 绕其中心O 逆时针旋转θ到三角形A 1B 1C 1，且20,3πθ⎛⎫∈ ⎪⎝⎭.顺次连结A ，A 1，B ，B 1，C ，C 1，A ，得到六边形徽标AA 1BB 1CC 1 .(1)当θ＝6π时，求六边形徽标的面积； (2)求六边形徽标的周长的最大值.23．设ABC V 的内角A ，B ，C 的对边分别为a ，b ，c .若2cos cos cos c C a B b A =+. （1）求角C .（2）若ABC V 的面积为S ，且224()S b a c =--，2a =，求S .24．已知各项均为正数的等比数列{}n a 的首项为12，且()3122123a a a -=+。

2020-2021高三数学上期末模拟试卷(含答案)(1)一、选择题1．若0a b <<,则下列不等式恒成立的是A ．11a b> B ．a b -> C ．22a b > D ．33a b <2．在ABC ∆中，2AC =,22BC =,135ACB ∠=o ，过C 作CD AB ⊥交AB 于D ，则CD =( ) A ．25B ．2C ．3D ．53．设x y ，满足约束条件10102x y x y y -+≤⎧⎪+-⎨⎪≤⎩＞，则yx 的取值范围是（ ）A ．()[),22,-∞-+∞UB ．(]2,2-C ．(][),22,-∞-+∞UD ．[]22-,4．设变量,x y 、满足约束条件236y xx y y x ≤⎧⎪+≥⎨⎪≥-⎩，则目标函数2z x y =+的最大值为（ ）A ．2B ．3C ．4D ．95．设,x y 满足约束条件0,20,240,x y x y x y -≥⎧⎪+-≥⎨⎪--≤⎩则2z x y =+的最大值为（ ）A ．2B ．3C ．12D ．136．在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c ，若∠C=120°，c=a ，则A ．a ＞bB ．a ＜bC ．a ＝bD ．a 与b 的大小关系不能确定7．已知正项等比数列{}n a 的公比为3，若229m n a a a =，则212m n+的最小值等于（ ） A ．1B ．12C ．34 D ．328．已知点(),M a b 与点()0,1N -在直线3450x y -+=的两侧，给出以下结论：①3450a b -+>；②当0a >时，+a b 有最小值，无最大值；③221a b +>；④当0a >且1a ≠时，11b a +-的取值范围是93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭，正确的个数是（ ） A ．1B ．2C ．3D ．49．设数列{}n a 的前n 项和为n S ，若2，n S ，3n a 成等差数列，则5S 的值是（ ） A ．243-B ．242-C ．162-D ．24310．若变量x ，y 满足约束条件1358x y x x y ≥-⎧⎪≥⎨⎪+≤⎩，，，则2yz x =-的取值范围是（ ） A ．113⎡⎤-⎢⎥⎣⎦，B ．11115⎡⎤--⎢⎥⎣⎦，C ．111153⎡⎤-⎢⎥⎣⎦， D ．3153⎡⎤-⎢⎥⎣⎦，11．一个递增的等差数列{}n a ，前三项的和12312a a a ++=，且234,,1a a a +成等比数列，则数列{}n a 的公差为 ( ) A ．2±B ．3C ．2D ．112．已知函数1()2xf x ⎛⎫= ⎪⎝⎭，则不等式()24(3)f a f a ->的解集为( )A ．(4,1)-B ．(1,4)-C ．(1,4)D ．(0,4)二、填空题13．已知0a >，0b >，当()214a b ab++取得最小值时，b =__________． 14．已知数列{}n a 的前n 项和为21nn S =-，则此数列的通项公式为___________．15．计算：23lim 123n n nn→+∞-=++++L ________16．ABC ∆内角A 、B 、C 的对边分别是a ，b ，c ，且2cos (32)cos b C a c B =-.当b =2ac =，ABC ∆的面积为______.17．在等差数列{}n a 中，12a =，3510a a +=，则7a = ．18．设,x y 满足约束条件0{2321x y x y x y -≥+≤-≤，则4z x y =+的最大值为 .19．已知等差数列{}n a 的公差为()d d 0≠，前n 项和为n S，且数列也为公差为d 的等差数列，则d =______．20．已知二次函数f （x ）=ax 2+2x+c （x ∈R ）的值域为[0，+∞），则11a c c a+++的最小值为_____．三、解答题21．已知等差数列{}n a 的前n 项和为n S ，且满足37a =，999S =. （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）若()2n n n a b n N *=∈，求数列{}n b 的前n 项和n T .22．已知数列中，，.（1）求证：是等比数列，并求的通项公式；（2）数列满足，求数列的前项和.23．设{}n a是等比数列，公比不为1．已知11 3a=，且1a，22a，33a成等差数列．（1）求{}n a的通项公式；（2）设数列nna⎧⎫⎨⎬⎩⎭的前n项和为nT，求nT．24．在平面内，将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转，如图，小卢利用图形的旋转设计某次活动的徽标，他将边长为a的正三角形ABC 绕其中心O逆时针旋转θ到三角形A1B1C1，且20,3πθ⎛⎫∈ ⎪⎝⎭.顺次连结A，A1，B，B1，C，C1，A，得到六边形徽标AA1BB1CC1 .(1)当θ＝6π时，求六边形徽标的面积；(2)求六边形徽标的周长的最大值.25．在等比数列{}n a中，125a a+=，且2320a a+=.（1）求{}n a的通项公式；（2）求数列{}3n na a+的前n项和nS.26．等差数列{a n}的前n项和为S n，且3a=9，S6=60．（I）求数列{a n}的通项公式；（II）若数列{b n}满足b n+1﹣b n=n a（n∈N+）且b1=3，求数列1nb⎧⎫⎨⎬⎩⎭的前n项和T n．【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【解析】 ∵0a b << ∴设1,1a b =-= 代入可知,,A B C 均不正确对于D ，根据幂函数的性质即可判断正确 故选D2．A解析：A 【解析】 【分析】先由余弦定理得到AB 边的长度，再由等面积法可得到结果. 【详解】根据余弦定理得到22222AC BC AB AC BC +-=-⨯⨯将2AC =,BC =,代入等式得到AB=再由等面积法得到11222CD CD ⨯=⨯⇒=故答案为A. 【点睛】这个题目考查了解三角形的应用问题，涉及正余弦定理，面积公式的应用，在解与三角形有关的问题时，正弦定理、余弦定理是两个主要依据.解三角形时，有时可用正弦定理，有时也可用余弦定理，应注意用哪一个定理更方便、简捷一般来说 ,当条件中同时出现ab 及2b 、2a 时，往往用余弦定理，而题设中如果边和正弦、余弦函数交叉出现时，往往运用正弦定理将边化为正弦函数再结合和、差、倍角的正余弦公式进行解答.3．A解析：A 【解析】 【分析】根据题意，作出可行域，分析yx的几何意义是可行域内的点(),x y 与原点O 连线的斜率，根据图象即可求解. 【详解】作出约束条件表示的可行域，如图所示，yx的几何意义是可行域内的点(),x y 与原点O 连线的斜率，由102x y y -+=⎧⎨=⎩，得点A 的坐标为()1,2，所以2OA k =，同理，2OB k =-，所以yx 的取值范围是()[),22,-∞-+∞U . 故选：A 【点睛】本题考查简单的线性规划，考查斜率型目标函数问题，考查数形结合思想，属于中等题型.4．D解析：D 【解析】 【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论. 【详解】画出满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩的可行域，如图，画出可行域ABC ∆，(2,0)A ，(1,1)B ，(3,3)C ， 平移直线2z x y =+，由图可知，直线2z x y =+经过(3,3)C 时 目标函数2z x y =+有最大值，2z x y =+的最大值为9.故选D. 【点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.5．C解析：C 【解析】 【分析】由约束条件可得可行域，将问题变成1122y x z =-+在y 轴截距最大问题的求解；通过平移直线可确定最大值取得的点，代入可得结果. 【详解】由约束条件可得可行域如下图所示：当2z x y =+取最大值时，1122y x z =-+在y 轴截距最大 平移直线12y x =-，可知当直线1122y x z =-+过图中A 点时，在y 轴截距最大由240y xx y =⎧⎨--=⎩得：()4,4A max 42412z ∴=+⨯= 故选：C 【点睛】本题考查线性规划中最值问题的求解，关键是能够将问题转化为直线在y 轴截距最值问题的求解，属于常考题型.6．A解析：A 【解析】 【分析】由余弦定理可知c 2＝a 2+b 2﹣2ab cos C ，进而求得a ﹣b 的表达式，根据表达式与0的大小，即可判断出a 与b 的大小关系． 【详解】解：∵∠C ＝120°，ca ，∴由余弦定理可知c 2＝a 2+b 2﹣2ab cos C ，（）2＝a 2+b 2+ab ．∴a 2﹣b 2＝ab ，a ﹣b ，∵a ＞0，b ＞0， ∴a ﹣b ，∴a ＞b 故选A ． 【点睛】本题考查余弦定理，特殊角的三角函数值，不等式的性质，比较法，属中档题．7．C解析：C 【解析】∵正项等比数列{}n a 的公比为3，且229m n a a a =∴2224222223339m n m n a a a a --+-⋅⋅⋅=⋅=∴6m n +=∴121121153()()(2)(2)62622624m n m n m n n m ⨯++=⨯+++≥⨯+=，当且仅当24m n ==时取等号. 故选C.点睛：利用基本不等式解题的注意点：（1）首先要判断是否具备了应用基本不等式的条件，即“一正、二正、三相等”，且这三个条件必须同时成立．（2）若不直接满足基本不等式的条件，需要通过配凑、进行恒等变形，构造成满足条件的形式，常用的方法有：“1”的代换作用，对不等式进行分拆、组合、添加系数等． （3）多次使用基本不等式求最值时，要注意只有同时满足等号成立的条件才能取得等号．8．B解析：B 【解析】 【分析】【详解】∵点M (a ,b )与点N (0,−1)在直线3x −4y +5=0的两侧,∴()()34530450a b -+⨯++<，即3450a b -+<，故①错误； 当0a >时,54a b +>，a +b 即无最小值，也无最大值，故②错误； 设原点到直线3x −4y +5=0的距离为d ,则22513(4)==+-d ,则22a b +>1，故③正确；当0a >且a ≠1时,11b a +-表示点M (a ,b )与P (1,−1)连线的斜率． ∵当0a =,b =54时,51194114b a ++==---,又直线3x −4y +5=0的斜率为34， 故11b a +-的取值范围为93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭，故④正确.∴正确命题的个数是2个. 故选B.点睛：本题是常规的线性规划问题，线性规划问题常出现的形式有：①直线型，转化成斜截式比较截距，要注意z 前面的系数为负时，截距越大，z 值越小；②分式型，其几何意义是已知点与未知点的斜率；③平方型，其几何意义是距离，尤其要注意的是最终结果应该是距离的平方；④绝对值型，转化后其几何意义是点到直线的距离.9．B解析：B 【解析】 【分析】 【详解】因为2,,3n n S a 成等差数列，所以223n n S a =+，当1n =时，111223,2S a a =+∴=-；当2n ≥时，1113333112222n n n n n n n a S S a a a a ---=-=+--=-，即11322n n a a -=，即()132nn a n a -=≥，∴数列{}n a 是首项12a =-，公比3q =的等比数列，()()55151213242113a q S q---∴===---，故选B.10．A解析：A 【解析】 【分析】画出满足条件的平面区域，求出角点的坐标，结合2yz x =-的几何意义求出其范围，即可得到答案. 【详解】由题意，画出满足条件的平面区域，如图所示：由358y x x y =⎧⎨+=⎩，解得11A (，)，由1x y x =-⎧⎨=⎩，解得(11)B --，， 而2yz x =-的几何意义表示过平面区域内的点与0(2)C ，的直线斜率， 结合图象，可得1AC k =-，13BC k =，所以2y z x =-的取值范围为113⎡⎤-⎢⎥⎣⎦，， 故选：A.【点睛】本题主要考查了简单的线性规划问题，其中解答中作出约束条件所表示的平面区域，结合图象确定出目标函数的最优解是解答的关键，着重考查了数形结合思想，以及计算能力，属于基础题.11．C解析：C 【解析】 【分析】【详解】解：∵234,,1a a a +成等比数列， ∴，∵数列{}n a 为递增的等差数列，设公差为d ， ∴，即，又数列{}n a 前三项的和，∴，即，即d ＝2或d ＝−2（舍去）， 则公差d ＝2． 故选：C ．12．B解析：B 【解析】 【分析】先判断函数1()2xf x ⎛⎫= ⎪⎝⎭的单调性，把()24(3)f a f a ->转化为自变量的不等式求解.【详解】可知函数()f x 为减函数，由2(4)(3)f a f a ->，可得243a a -<，整理得2340a a --<，解得14a -<<，所以不等式的解集为(1,4)-． 故选B. 【点睛】本题考查函数不等式，通常根据函数的单调性转化求解，一般不代入解析式.二、填空题13．【解析】【分析】根据均值不等式知即再由即可求解注意等号成立的条件【详解】（当且仅当等号成立）（当且仅当等号成立）（当且仅当等号成立）故答案为【点睛】本题主要考查了均值不等式不等式等号成立的条件属于中 解析：14【解析】 【分析】根据均值不等式知，4a b +≥=()2416a b ab +≥，再由41684ab a b +≥=⋅即可求解，注意等号成立的条件. 【详解】4a b +≥=Q （当且仅当4a b =等号成立），()2416a b ab ∴+≥（当且仅当4a b =等号成立），()2444a b a b ∴++≥⋅8=（当且仅当4a b =等号成立）， ()224281a a a∴+=⇒=. 故答案为14b =. 【点睛】本题主要考查了均值不等式，不等式等号成立的条件，属于中档题.14．【解析】【分析】由数列的前项和为得时得出;验证时是否满足即可【详解】当时当时又所以故答案为:【点睛】本题考查了由数列的前项和公式推导通项公式的计算问题;解题时需验证时是否满足是基础题解析：12n n a -=【解析】 【分析】由数列{}n a 的前n 项和为23nn S =-，得2n >时1123n n S --=-,，得出1n n n a S S -=-;验证1n =时11a S =是否满足n a 即可. 【详解】当1n =时,11211a S ==-=, 当2n ≥时,()11121212nn n n n n a S S ---=-=---=,又1121-=,所以12n n a -=. 故答案为:12n n a -=.【点睛】本题考查了由数列{}n a 的前n 项和公式n S 推导通项公式n a 的计算问题;解题时，需验证1n =时11a S =是否满足n a ，是基础题.15．【解析】【详解】结合等差数列前n 项和公式有：则： 解析：6【解析】 【详解】结合等差数列前n 项和公式有：()11232n n n +++++=L ，则：()()226231362lim lim lim lim61123111n n n n n n n n n n n n n n n→+∞→+∞→+∞→+∞----====+++++++L . 16．【解析】【分析】由利用正弦定理得到再用余弦定理求得b 可得ac 利用面积公式计算可得结果【详解】由正弦定理可化为所以在三角形中所以因为所以又所以由余弦定理得又所以有故的面积为故答案为【点睛】本题考查了正【解析】 【分析】由()2cos 32cos b C a c B =-，利用正弦定理得到2cos 3B =，再用余弦定理求得b ，可得a 、c ，利用面积公式计算可得结果. 【详解】由正弦定理()2cos 32cos b C a c B =-可化为2sin cos 3sin cos 2sin cos B C A B C B =-， 所以()2sin 3sin cos B C A B +=， 在三角形中，()sin sin B C A +=，所以2sin 3sin cos A A B =，因为sin 0A ≠，所以2cos 3B =， 又0B π<<，所以sin B == 由余弦定理得2224323b a c ac =+-=，又2a c =，所以有2967c =. 故ABC ∆的面积为2219696sin sin sin 277S ac B c B c B ======. 【点睛】本题考查了正弦定理、余弦定理的应用，考查了三角形面积计算公式，考查了推理能力与计算能力，属于中档题．17．8【解析】【分析】【详解】设等差数列的公差为则所以故答案为8解析：8 【解析】 【分析】 【详解】设等差数列{}n a 的公差为d ， 则351712610a a a a a d +=+=+=， 所以71101028a a =-=-=，故答案为8.18．【解析】试题分析：约束条件的可行域如图△ABC 所示当目标函数过点A(11)时z 取最大值最大值为1+4×1=5【考点】线性规划及其最优解解析：【解析】 .试题分析：约束条件的可行域如图△ABC 所示.当目标函数过点A(1，1)时，z 取最大值，最大值为1+4×1=5.【考点】线性规划及其最优解.19．【解析】【分析】表示出再表示出整理并观察等式列方程组即可求解【详解】等差数列的公差为前项和为设其首项为则=又数列也为公差为的等差数列首项为所以=即：整理得：上式对任意正整数n 成立则解得：【点睛】本题 解析：12【解析】 【分析】表示出n S n S n + 【详解】等差数列{}n a 的公差为()0d d ≠，前n 项和为n S ，设其首项为1a ， 则n S =()112n n na d -+，又数列{}n S n +也为公差为d 1111S a +=+n S n +()111a n d +-()()111112n n na d n a n d -++=+-()()2222111121122d d n a n d n a d dn a d⎛⎫+-+=++-++- ⎪⎝⎭上式对任意正整数n 成立，则)2120122d d d da d d⎧=⎪=⎪-+=⎪⎩，解得：12d =，134a =-【点睛】本题主要考查了等差数列的前n 项和及通项公式，考查了方程思想及转化思想、观察能力，属于中档题．20．4【解析】【分析】先判断是正数且把所求的式子变形使用基本不等式求最小值【详解】由题意知则当且仅当时取等号∴的最小值为4【点睛】】本题考查函数的值域及基本不等式的应用属中档题解析：4 【解析】 【分析】先判断a c 、是正数，且1ac =，把所求的式子变形使用基本不等式求最小值． 【详解】由题意知，044010a ac ac c =-=∴=V ＞，，，＞，则111111 2224a c a c a c c a c c a a c a c a +++=+++=+++≥+=+=（）（），当且仅当1a c ==时取等号．∴11a c c a +++的最小值为4． 【点睛】】本题考查函数的值域及基本不等式的应用．属中档题.三、解答题21． （Ⅰ）21n a n =+，n *∈N （Ⅱ）2552n nn T +=- 【解析】试题分析：（1）先根据条件列出关于首项与公差的方程组,解得首项与公差,代入等差数列通项公式即可（2）利用错位相减法求和, 利用错位相减法求和时，注意相减时项的符号变化，中间部分利用等比数列求和时注意项数，最后要除以1q -试题解析：（Ⅰ）由题意得：1127989992a d a d +=⎧⎪⎨⨯+=⎪⎩,解得132a d =⎧⎨=⎩ , 故{}n a 的通项公式为21n a n =+，*n N ∈ （Ⅱ）由（Ⅰ）得：212n nn b +=23435792122222n n n T +=++++⋯+ ① 234113572121222222n n n n n T +-+=+++⋯++ ② ①－②得：23411311112122222222n n n n T ++⎛⎫=++++⋯+- ⎪⎝⎭ 152522n n ++=- 故2552n nn T +=-点睛：用错位相减法求和应注意的问题(1)要善于识别题目类型，特别是等比数列公比为负数的情形；(2)在写出“n S ”与“n qS ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“n n S qS -”的表达式；(3)在应用错位相减法求和时，若等比数列的公比为参数，应分公比等于1和不等于1两种情况求解. 22．(1)答案见解析；(2) .【解析】试题分析：⑴根据数列的递推关系，结合等比数列的定义即可证明是等比数列，并求的通项公式，⑵利用错位相减法即可求得答案；解析：（1）∵ ∴ ∴，∵，，∴是以为首项，以4为公比的等比数列∴，∴， ∴，（2），∴① ②①-②得∴.23．（1）13nn a ⎛⎫= ⎪⎝⎭； （2）13(21)34n n n T ++-⋅=【解析】 【分析】（1）由等差中项可得21343a a a =+,设数列{}n a 的公比为()1q q ≠,则211143a q a a q ⋅=+⋅,可解得q ,即可求得通项公式；（2）由（1）可得3n nnn a =⋅,再利用错位相减法求解即可. 【详解】解:（1）设数列{}n a 的公比为()1q q ≠,且1a ,22a ,33a 成等差数列,所以21343a a a =+,即211143a q a a q ⋅=+⋅,解得13q =, 因为113a =,所以13nn a ⎛⎫= ⎪⎝⎭（2）由（1）知，13nn a ⎛⎫= ⎪⎝⎭，所以3n nn n a =⋅, 所以1231323333nn T n =⨯+⨯+⨯++⋅L ,则234131323333n n T n +=⨯+⨯+⨯++⋅L ,作差可得,1231233333n n n T n +-=++++-⋅L则()+13312331n n nT n --=-⋅-，即1132322n n T n +⎛⎫-=-⋅- ⎪⎝⎭,所以()132134n n n T ++-⋅=【点睛】本题考查等差中项的应用,考查等比数列的通项公式,考查错位相减法求数列的和.24．(1)234a ；(2) 【解析】 【分析】（1）连接OB ,则123AOB πθ∠=-,由等边三角形ABC 的边长为a ,可得OA OB ==,再利用三角形面积公式求解即可； （2）根据三角形的对称性可得12sin sin 232AA OA a θθ==,112sin sin 3232222A B OB πθθθ⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭,则周长为关于θ的函数,进而求得最值即可 【详解】（1）Q 等边三角形ABC 的边长为a ,OA OB ∴==, 连接OB ,123AOB πθ∴∠=-,22123sin sin sin 2326S OA ππθθθ⎡⎤⎛⎫⎛⎫∴=⨯+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦, ∴当6πθ=时,六边形徽标的面积为234S a =（2）在1AOA V 中,12sinsin 232AA OA a θθ==,在1BOA V 中,112sin cos sin 3232222A B OB a πθθθ⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭,设周长为()f q ,则()()113sin 23f AA A B θπθ⎛⎫=+=+ ⎪⎝⎭,20,3θπ⎛⎫∈ ⎪⎝⎭,当且仅当232θππ+=,即3πθ=时,()max fθ=【点睛】本题考查三角形面积的应用,考查正弦型函数的最值问题,考查三角函数在几何中的应用,考查数形结合思想25．（1）14n n a -=；（2）n S 4121n n =-+-.【解析】 【分析】（1）由数列{}n a 是等比数列，及125a a +=，且2320a a +=，两式相除得到公比q ，再代入125a a +=可求1a ，则通项公式可求.（2）利用分组求和求出数列{}3n n a a +的前n 项和n S . 【详解】解：（1）因为等比数列{}n a 中，125a a +=，且2320a a +=. 所以公比23124a a q a a +==+， 所以12155a a a +==， 即11a =， 故14n n a -=.（2）因为14n n a -=所以113342n n n n a a --+=⋅+，所以141231412n nn S --=⨯+--4121n n =-+- 422n n =+-. 【点睛】本题考查等比数列的通项公式的计算与等比数列前n 项和公式的应用，属于基础题. 26．（Ⅰ）a n =2n+3；（Ⅱ）31142(1)2(2)n n --++. 【解析】试题分析：（Ⅰ）设出等差数列的首项和公差，利用通项公式、前n 项和公式列出关于首项和公差的方程组进行求解；（Ⅱ）利用迭代法取出数列{}n b 的通项公式，再利用裂项抵消法进行求和.试题解析：（Ⅰ）设等差数列{a n }的公差为d ，∵a 3=9，S 6=60．∴，解得．∴a n =5+（n ﹣1）×2=2n+3． （Ⅱ）∵b n+1﹣b n =a n =2n+3，b 1=3，当n≥2时，b n =（b n ﹣b n ﹣1）+…+（b 2﹣b 1）+b 1 =[2（n ﹣1）+3]+[2（n ﹣2）+3]+…+[2×1+3]+3=．当n=1时，b 1=3适合上式，所以．∴．∴= =点睛：裂项抵消法是一种常见的求和方法，其适用题型主要有： （1）已知数列的通项公式为1(1)n a n n =+，求前n 项和：111(1)1n a n n n n ==-++；（2）已知数列的通项公式为1(21)(21)n a n n =-+，求前n 项和：1111()(21)(21)22121n a n n n n ==--+-+；（3）已知数列的通项公式为1n a n n =++n 项和:.11n a n n n n ==+++。

2020-2021高三数学上期末试卷(带答案)(8)一、选择题1．记n S 为等比数列{}n a 的前n 项和.若2342S S S =+，12a =，则2a =（ ）A ．2B ．-4C ．2或-4D ．42．设,x y 满足约束条件 202300x y x y x y --≤⎧⎪-+≥⎨⎪+≤⎩，则46y x ++的取值范围是A ．3[3,]7- B ．[3,1]- C ．[4,1]-D ．(,3][1,)-∞-⋃+∞3．等差数列{}n a 中，已知70a >，390a a +<，则{}n a 的前n 项和n S 的最小值为（ ） A ．4SB ．5SC ．6SD ．7S4．程大位《算法统宗》里有诗云“九百九十六斤棉，赠分八子做盘缠.次第每人多十七，要将第八数来言.务要分明依次弟，孝和休惹外人传.”意为：996斤棉花，分别赠送给8个子女做旅费，从第一个开始，以后每人依次多17斤，直到第八个孩子为止.分配时一定要等级分明，使孝顺子女的美德外传，则第八个孩子分得斤数为（ ） A ．65 B ．184 C ．183 D ．1765．在ABC ∆中，2AC =,22BC =,135ACB ∠=o ，过C 作CD AB ⊥交AB 于D ，则CD =( ) A ．25B ．2C ．3D ．56．在等差数列{}n a 中，若1091a a <-，且它的前n 项和n S 有最大值，则使0n S >成立的正整数n 的最大值是（ ） A ．15 B ．16C ．17D ．147．在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c ，若∠C=120°，c=a ，则A ．a ＞bB ．a ＜bC ．a ＝bD ．a 与b 的大小关系不能确定8．在等差数列{a n }中，a 1＞0，a 10·a 11＜0，若此数列的前10项和S 10＝36，前18项的和S 18＝12，则数列{|a n |}的前18项和T 18的值是 （ ） A ．24B ．48C ．60D ．849．已知01x <<，01y <<，则()()()()222222221111x y x y x y x y ++--+-+- ）A 5B ．2C 10D ．2310．设数列{}n a 的前n 项和为n S ，若2，n S ，3n a 成等差数列，则5S 的值是（ ） A ．243- B ．242- C ．162- D ．24311．在中，，，，则A ．B ．C ．D ．12．已知数列{}n a 的前n 项和为n S ，1112n n a S a +＝，＝， 则n S ＝( )A ．12n -B ．13()2n -C ．12()3n - D ．112n - 二、填空题13．已知,x y 满足约束条件420y x x y y ≤⎧⎪+≤⎨⎪+≥⎩，则2z x y =+的最大值为__________．14．已知函数1()f x x x=-，数列{}n a 是公比大于0的等比数列，且61a =，1239101()()()()()f a f a f a f a f a a +++⋅⋅⋅++=-，则1a =_______.15．已知变量,x y 满足约束条件2{41y x y x y ≤+≥-≤，则3z x y =+的最大值为____________．16．已知数列{}n a 中，45n a n =-+，等比数列{}n b 的公比q 满足1(2)n n q a a n -=-≥，且12b a =，则12n b b b +++=L __________．17．若正数,a b 满足3ab a b =++，则+a b 的取值范围_______________。

2020-2021高三数学上期末一模试卷(含答案)(6)一、选择题1．记n S 为等比数列{}n a 的前n 项和.若2342S S S =+，12a =，则2a =（ ）A ．2B ．-4C ．2或-4D ．42．已知在中，，，分别为角，，的对边，为最小角，且，，，则的面积等于（ ） A ．B ．C ．D ．3．等比数列{}n a 的前n 项和为n S ，若36=2S =18S ，，则105S S 等于( ) A ．－3B ．5C ．33D ．－314．设等比数列{}n a 的前n 项和为n S ，若633S S =， 则96S S =（ ） A ．2B ．73C ．83D ．35．已知实数,x y 满足0{20x y x y -≥+-≤则2y x -的最大值是( )A ．-2B ．-1C ．1D ．26．设数列{}n a 是以2为首项，1为公差的等差数列，{}n b 是以1为首项，2为公比的等比数列，则1210b b b a a a ++⋯+=（ ） A ．1033B ．1034C ．2057D ．20587．已知ABC ∆的三个内角、、A B C 所对的边为a b c 、、，面积为S ，且223tan 2S B =+，则A 等于（ ）A ．6π B ．4π C ．3π D ．2π 8．数列{}n a 为等比数列，若11a =，748a a =，数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ，则5(S = )A ．3116B ．158C ．7D ．319．已知x ，y 均为正实数，且111226x y +=++，则x y +的最小值为（ ） A ．20B ．24C ．28D ．3210．在R 上定义运算：A()1B A B =-，若不等式()x a -()1x a +<对任意的实数x ∈R 恒成立，则实数a 的取值范围是( ) A ．11a -<<B ．02a <<C ．1322a -<< D ．3122a -<< 11．设x y ，满足约束条件70310,350x y x y x y +-⎧⎪-+⎨⎪--⎩，，………则2z x y =-的最大值为（ ）.A ．10B ．8C ．3D ．212．一个递增的等差数列{}n a ，前三项的和12312a a a ++=，且234,,1a a a +成等比数列，则数列{}n a 的公差为 ( ) A ．2±B ．3C ．2D ．1二、填空题13．若,a b ∈R ，0ab >，则4441a b ab++的最小值为___________.14．数列{}n a 满足14a =，12nn n a a +=+，*n N ∈，则数列{}n a 的通项公式n a =______.15．已知数列{}n a 中，其中199199a =，11()an n a a -=，那么99100log a =________16．已知数列{}n a 的首项12a =，且满足()*12n n n a a n N +=∈，则20a =________． 17．已知锐角三角形的边长分别为1，3，a ，则a 的取值范围是__________．18．已知n S 为数列{}n a 的前n 项和，且13a =，131n n a S +=+，*n ∈N ，则5S =______.19．已知数列{}n a 为正项的递增等比数列，1582a a +=，2481a a =g ，记数列2n a ⎧⎫⎨⎬⎩⎭的前n 项和为n T ，则使不等式112020|1|13n nT a -->成立的最大正整数n 的值是__________．20．已知二次函数f （x ）=ax 2+2x+c （x ∈R ）的值域为[0，+∞），则11a c c a+++的最小值为_____．三、解答题21．已知在ABC ∆中，角A ，B ，C 的对边分别是a ，b ，c 且2cos 2a C c b +=. （1）求角A 的大小；（2）若1a =，求ABC ∆面积的最大值。

山东省济南市2021届高三第一学期期末检测数学试卷一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上） 1．设集合{}2A |60x x x =−−≤，{}B |10x x =−<，则AB =A ．{}|3x x ≤B ．{}|31x x −≤<C ．{}|21x x −≤<−D ．{}|21x x −≤< 2．已知复数i1i z =+（其中i 为虚数单位），则z 的共轭复数为 A ．11i 22−+ B ．11i 22−− C ．11i 22+ D ．11i 22−3．已知直线l 过点(2，2)，则“直线l 的方程为y ＝2”是“直线l 与圆224x y +=相切”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．十二生肖是中国特有的文化符号，有着丰富的内涵，它们是成对出现的，分别为鼠和牛、虎和兔、龙和蛇、马和羊、猴和鸡、狗和猪六对．每对生肖相辅相成，构成一种完美人格．现有十二生肖的吉祥物各一个，按照上面的配对分成六份．甲、乙、丙三位同学依次选一份作为礼物，甲同学喜欢牛和马，乙同学喜欢牛、狗和羊，丙同学所有的吉祥物都喜欢．如果甲、乙、丙三位同学选取的礼物中均包含自己喜欢的生肖，则不同的选法种数共有A ．12种B ．16种C ．20种D ．24种5．已知菱形ABCD 的边长为2，∠BAD ＝120°，点E ，F 分别在边BC ，CD 上，且满足BEEC =，CD 2CF =，则AE AF +=AB ．3C ．D ．46．把物体放在空气中冷却，如果物体原来的温度是1C θ︒，空气的温度是0C θ︒，那么min t后物体的温度θ（单位：C ︒）满足公式010()e kt θθθθ−=+−（其中k 为常数）．现有52C ︒的物体放在12C ︒的空气中冷却，2min 后物体的温度是32C ︒．则再经过4min 该物体的温度可冷却到A ．12C ︒B ．14.5C ︒ C ．17C ︒D ．22C ︒7．已知双曲线C ：22221(00)x y a b a b−=>>，的左、右顶点分别为A ，B ，其中一条渐近线与以线段AB 为直径的圆在第一象限内的交点为P ，另一条渐近线与直线PA 垂直，则C 的离心率为A ．3B ．2C D8．已知函数()(1)e x f x a x x =+−，若存在唯一的正整数0x ，使得0()0f x <，则实数a 的取值范围是 A ．[12e −，334e ) B ．[334e ，223e ) C ．[223e ，12e ) D ．[12e ，12) 二、 多项选择题（本大题共4小题，每小题5分， 共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）9．为落实《山东省学生体质健康促进条例》的要求，促进学生增强体质，健全人格，锤炼意志，某学校随机抽取了甲、乙两个班级，对两个班级某一周内每天的人均体育锻炼时间（单位：分钟）进行了调研．根据统计数据制成折线图如下：下列说法正确的是A ．班级乙该周每天的人均体育锻炼时间的众数为30B ．班级甲该周每天的人均体育锻炼时间的中位数为72C ．班级甲该周每天的人均体育锻炼时间的极差比班级乙的小D ．班级甲该周每天的人均体育锻炼时间的平均值比班级乙的大10．已知函数12()sin(2)cos(2)f x a x b x ϕϕ=+++(()f x 不恒为0)，若()06f π=，则下列说法一定正确的是A ．()12f x π−为奇函数 B ．()f x 的最小正周期为πC ．()f x 在区间[12π−，125π]上单调递增 D ．()f x 在区间[0，2021π]上有4042个零点 11．如图，在正四棱柱ABCD—A 1B 1C 1D 1中，AA 1＝2AB ＝2，点P 为线段AD 1上一动点，则下列说法正确的是 A ．直线PB 1∥平面BC 1DB ．三棱锥P—BC 1D 的体积为13C ．三棱锥D 1—BC 1D 外接球的表面积为32π D ．直线PB 1与平面BCC 1B 112．已知红箱内有5个红球、3个白球，白箱内有3个红球、5个白 第11题球，所有小球大小、形状完全相同．第一次从红箱内取出一球后再放回去，第二次从与第一次取出的球颜色相同的箱子内取出一球，然后再放回去，依次类推，第k ＋1次从与第k 次取出的球颜色相同的箱子内取出一球，然后再放回去．记第n 次取出的球是红球的概率为n P ，则下列说法正确的是A ．21732P =B ．117232n n P P +=+C ．211221()2n n n n n n P P P P P P ++++−=−+D ．对任意的i ，j N *∈且1i j n ≤<≤，11111()()(14)(14)22180n n i ji j nP P −−≤<≤−−=−−∑ 三、填空题（本大题共4小题， 每小题5分，共计20分．请把答案填写在答题卡相应位置上）13．已知1sin()63απ+=，则5sin()6απ−的值为 ． 14．若实数x ，y 满足lg lg lg()x y x y +=+，则xy 的最小值为 ． 15．已知奇函数()f x 在(0，+∞ )上单调递减，且(4)0f =，则不等式(1)0xf x +>的解集为 ．16．已知直线l 与抛物线C ：28y x =相切于点P ，且与C 的准线相交于点T ，F 为C 的焦点，连接PF 交C 于另一点Q ，则△PTQ 面积的最小值为 ；若|TF |5=，则|PQ |的值为 ．（本小题第一空2分，第二空3分）四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）在平面四边形ABCD 中，AB ＝2，BC ＝5，∠ABC ＝120°，AD，∠ADC ＝2∠ACD ，求△ACD 的面积． 18．（本小题满分12分）已知数列{}n a 的前n 项和2n S n =． （1）求数列{}n a 的通项公式； （2）在①218()n n n nb a a +=⋅，②2n n n b a =⋅，③(1)n n n b S =−⋅这三个条件中任选一个，补充在下面的问题中，并求解该问题．若 ，求数列{}n b 的前n 项和n T ．注：如果选择多个条件分别解答，按第一个解答计分．19．（本小题满分12分）如图，在三棱柱ABC—A 1B 1C 1中，AB ＝AC ＝2，D 为BC 的中点，平面BB 1C 1C ⊥平面ABC ，设直线l 为平面AC 1D 与平面A 1B 1C 1的交线．（1）证明：l ⊥平面BB 1C 1C ；（2）已知四边形BB 1C 1C 为边长为2的菱形，且∠B 1BC ＝60°，求二面角D—AC 1—C 的余弦值．某县在实施脱贫工作中因地制宜，着力发展枣树种植项目．该县种植的枣树在2020年获得大丰收，依据扶贫政策，所有红枣由经销商统一收购．为了更好的实现效益，县扶贫办从今年收获的红枣中随机选取100千克，进行质量检测，根据检测结果制成如图所示的频率分布直方图．右表是红枣的分级标准，其中一级品、二级品统称为优质品．经销商与某农户签订了红枣收购协议，规定如下：从一箱红枣中任取4个进行检测，若4个均为优质品，则该箱红枣定为A 类；若4个中仅有3个优质品，则再从该箱中任意取出1个，若这一个为优质品，则该箱红枣也定为A 类；若4个中至多有一个优质品，则该箱红枣定为C 类；其它情况均定为B 类．已知每箱红枣重量为10千克，A 类、B 类、C 类的红枣价格分别为每千克20元、16元、12元．现有两种装箱方案：方案一：将红枣采用随机混装的方式装箱；方案二：将红枣按一、二、三、四等级分别装箱，每箱的分拣成本为1元． 以频率代替概率解决下面的问题．（1）如果该农户采用方案一装箱，求一箱红枣被定为A 类的概率； （2）根据所学知识判断，该农户采用哪种方案装箱更合适，并说明理由．21．（本小题满分12分）已知椭圆C ：22221(0)x y a b a b+=>>（1）求椭圆C 的标准方程；（2）若折线0)y k x =≠与C 相交于A ，B 两点（点A 在直线x =的右侧），设直线OA ，OB 的斜率分别为1k ，2k ，且212k k −=，求k 的值．22．（本小题满分12分）已知函数()ln(1)f x a x x =−+． （1）讨论()f x 的单调性； （2）若1()e 1x f x x −≥−+对任意的x ∈(0，+∞)恒成立，求实数a 的取值范围．山东省济南市2021届高三第一学期期末检测数学试卷一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上） 1．设集合{}2A |60x x x =−−≤，{}B |10x x =−<，则AB =A ．{}|3x x ≤B ．{}|31x x −≤<C ．{}|21x x −≤<−D ．{}|21x x −≤< 答案：D解析：{}2A |60x x x =−−≤＝[﹣2，3]，{}B |10x x =−<＝(−∞，1)，故AB =[﹣2，1)．选D ．2．已知复数i1i z =+（其中i 为虚数单位），则z 的共轭复数为 A ．11i 22−+ B ．11i 22−− C ．11i 22+ D ．11i 22−答案：D解析：i i(1i)1i1i (1i)(1i)22z −===+++−，则1i 22z =−．选D ． 3．已知直线l 过点(2，2)，则“直线l 的方程为y ＝2”是“直线l 与圆224x y +=相切”的 A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案：A解析：“直线l 的方程为y ＝2”⇒“直线l 与圆224x y +=相切”, “直线l 与圆224x y += 相切”“直线l 的方程为y ＝2”，故选A ．4．十二生肖是中国特有的文化符号，有着丰富的内涵，它们是成对出现的，分别为鼠和牛、虎和兔、龙和蛇、马和羊、猴和鸡、狗和猪六对．每对生肖相辅相成，构成一种完美人格．现有十二生肖的吉祥物各一个，按照上面的配对分成六份．甲、乙、丙三位同学依次选一份作为礼物，甲同学喜欢牛和马，乙同学喜欢牛、狗和羊，丙同学所有的吉祥物都喜欢．如果甲、乙、丙三位同学选取的礼物中均包含自己喜欢的生肖，则不同的选法种数共有A ．12种B ．16种C ．20种D ．24种答案：B解析：甲若选牛，则有1124C C 种；甲若选马，则有1124C C 种．故共有16种，选B ．5．已知菱形ABCD 的边长为2，∠BAD ＝120°，点E ，F 分别在边BC ，CD 上，且满足BEEC =，CD 2CF =，则AE AF +=AB ．3 C．D ．4答案：B解析：由题意知△AEF 的等边三角形，故AE AF +=3，选B ．6．把物体放在空气中冷却，如果物体原来的温度是1C θ︒，空气的温度是0C θ︒，那么min t后物体的温度θ（单位：C ︒）满足公式010()e kt θθθθ−=+−（其中k 为常数）．现有52C ︒的物体放在12C ︒的空气中冷却，2min 后物体的温度是32C ︒．则再经过4min 该物体的温度可冷却到A ．12C ︒B ．14.5C ︒ C ．17C ︒D ．22C ︒ 答案：C解析：221321240e e 2k k −−=+⇒=，6311240e 1240()172k θ−=+=+⨯=，故选C ． 7．已知双曲线C ：22221(00)x y a b a b−=>>，的左、右顶点分别为A ，B ，其中一条渐近线与以线段AB 为直径的圆在第一象限内的交点为P ，另一条渐近线与直线PA 垂直，则C 的离心率为A ．3B ．2CD 答案：B解析：将直线AP 与斜率为正数的渐近线方程联立：()a y x a bb y x a ⎧=+⎪⎪⎨⎪=⎪⎩，解得P(322a b a −，222a b b a −)，因为OP ＝a ，则322222222()()a a b a b a b a+=−−，化简得2222222334a b a c a c a =⇒=−⇒=2e ⇒=，选B ．8．已知函数()(1)e x f x a x x =+−，若存在唯一的正整数0x ，使得0()0f x <，则实数a 的取值范围是 A ．[12e −，334e ) B ．[334e ，223e ) C ．[223e ，12e ) D ．[12e ，12) 答案：C解析：0()0f x <，参变分离得：000(1)e x x a x <+，令000()(1)(1)e x x g x x x =≥+，2000201()0(1)e x x x g x x +−'=−<+，所以0()g x 在[1，+∞)且0x Z ∈单调递增， 求得1(1)2e g =，22(2)3eg =，故要使存在唯一的正整数0x ，使得0()0f x <， 则223e ≤a ＜12e，选C ． 二、 多项选择题（本大题共4小题，每小题5分， 共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）9．为落实《山东省学生体质健康促进条例》的要求，促进学生增强体质，健全人格，锤炼意志，某学校随机抽取了甲、乙两个班级，对两个班级某一周内每天的人均体育锻炼时间（单位：分钟）进行了调研．根据统计数据制成折线图如下：下列说法正确的是A ．班级乙该周每天的人均体育锻炼时间的众数为30B ．班级甲该周每天的人均体育锻炼时间的中位数为72C ．班级甲该周每天的人均体育锻炼时间的极差比班级乙的小D ．班级甲该周每天的人均体育锻炼时间的平均值比班级乙的大 答案：AC解析：班级甲该周每天的人均体育锻炼时间的中位数为65，故B 错误；班级甲该周每天的人均体育锻炼时间的平均值比班级乙的小，故D 错误．综上选AC ．10．已知函数12()sin(2)cos(2)f x a x b x ϕϕ=+++(()f x 不恒为0)，若()06f π=，则下列说法一定正确的是 A ．()12f x π−为奇函数 B ．()f x 的最小正周期为π C ．()f x 在区间[12π−，125π]上单调递增 D ．()f x 在区间[0，2021π]上有4042个零点答案：BD解析：()12f x π−为偶函数，故A 错误；()f x 在区间[12π−，125π]上单调，但不一定是单调递增，故C 错误．综上选BD ．11．如图，在正四棱柱ABCD—A 1B 1C 1D 1中，AA 1＝2AB ＝2，点P 为线段AD 1上一动点，则下列说法正确的是A ．直线PB 1∥平面BC 1DB ．三棱锥P—BC 1D 的体积为13C ．三棱锥D 1—BC 1D 外接球的表面积为32πD ．直线PB 1与平面BCC 1B 1答案：ABD解析：因为平面AB 1D 1∥平面BC 1D ，PB 1⊂平面AB 1D 1，所以直线PB 1∥平面BC 1D ，A 正确；V P—BC1D ＝V A—BC1D ＝V C1—ABD ＝111112=323⨯⨯⨯⨯，故B 正确；三棱锥D 1—BC 1D=S 球＝246ππ=，故C 错误；PB 1min 点P 到平面BCC 1B 1的距离为1，所以直线PB 1与平面BCC 1B 1所成角的正弦值的最，故D 正确．综上选ABD ．12．已知红箱内有5个红球、3个白球，白箱内有3个红球、5个白球，所有小球大小、形状完全相同．第一次从红箱内取出一球后再放回去，第二次从与第一次取出的球颜色相同的箱子内取出一球，然后再放回去，依次类推，第k ＋1次从与第k 次取出的球颜色相同的箱子内取出一球，然后再放回去．记第n 次取出的球是红球的概率为n P ，则下列说法正确的是A ．21732P =B ．117232n n P P +=+C ．211221()2n n n n n n P P P P P P ++++−=−+D ．对任意的i ，j N *∈且1i j n ≤<≤，11111()()(14)(14)22180n n i ji j nP P −−≤<≤−−=−−∑ 答案：ACD解析：第n 此取出球是红球的概率为n P ，则白球概率为(1)n P −，对于第1n +次，取出红球有两种情况． ①从红箱取出1(1)58n n P P +=⋅（条件概率）， ②从白箱取出2(1)3(1)8n nP P +=−⋅， 对应121(1)(1)3184n n n n P P P P +++=+=+（转化为数列问题）， 所以1111()242n n P P +−=−， 令12n n a P =−，则数列{n a 为等比数列，公比为14，因为158P =，所以118a =， 故2(21)2n n a −+=即对应(21)122n n P −+=+， 所以21732P =，故选项A 正确； [2(1)1](21)231111112[2]222224n n n n n P P −++−+−−+−=+−⨯+=−，故117232n n P P +=+不成立，故选项B 错误； 经验证可得，211221()2n n n n n n P P P P P P ++++−=−+，故选项C 正确；1(21)(21)11111()()2222n ni j i j i j n i j i P P −−+−+<==+−−=⋅∑∑∑ 1(21)(23)(23)142[22]3n i i n i −−+−+−+==⋅−∑11(44)(23)(21)114[222]3n n i n i i i −−−+−+−+===−∑∑ 844(23)3214164[(22)2(22)]3153n n n −−−−+−−−=−−⋅− 424141122218045369n n n −−−=−⋅−⋅+⋅ 421(14252)180n n −−=+⋅−⋅ 221(142)(12)180n n −−=−⋅−11(14)(14)180n n −−=−−，故D 正确． 三、填空题（本大题共4小题， 每小题5分，共计20分．请把答案填写在答题卡相应位置上）13．已知1sin()63απ+=，则5sin()6απ−的值为 ． 答案：13解析：51sin()sin[()]sin()6663ππαπααπ−=−+=+=． 14．若实数x ，y 满足lg lg lg()x y x y +=+，则xy 的最小值为 ．答案：4解析：11lg lg lg()1x y x y xy x y x y+=+⇒=+⇒+=， 11()()24y xxy x y x y x y x y=+=++=++≥，当且仅当x ＝y ＝2时取“＝”．15．已知奇函数()f x 在(0，+∞ )上单调递减，且(4)0f =，则不等式(1)0xf x +>的解集为 ．答案：(0，3)(﹣5，﹣1)解析：0(1)0(1)0x xf x f x >⎧+>⇒⎨+>⎩或003(1)0x x f x <⎧⇒<<⎨+<⎩或51x −<<−，故原不等式的解集为(0，3)(﹣5，﹣1)．16．已知直线l 与抛物线C ：28y x =相切于点P ，且与C 的准线相交于点T ，F 为C 的焦点，连接PF 交C 于另一点Q ，则△PTQ 面积的最小值为 ；若|TF |5=，则|PQ |的值为 ．（本小题第一空2分，第二空3分）答案：16，252解析：当PQ 为抛物线通径时△PTQ 的面积最小，为16；当TF ＝5时，可得线段PQ 中点的纵坐标为3或﹣3，故PQ 的斜率为43或43−，故PQ ＝2228254sin 2()5p α==． 四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤） 17．（本小题满分10分）在平面四边形ABCD 中，AB ＝2，BC ＝5，∠ABC ＝120°，AD，∠ADC ＝2∠ACD ，求△ACD 的面积．解：在△ABC 中，由余弦定理可得：所以在△ACD 中，由正弦定理可得：，即所以所以 因为，所以所以所以18．（本小题满分12分）已知数列{}n a 的前n 项和2n S n =． （1）求数列{}n a 的通项公式； （2）在①218()n n n nb a a +=⋅，②2n n n b a =⋅，③(1)n n n b S =−⋅这三个条件中任选一个，补充在下面的问题中，并求解该问题．若 ，求数列{}n b 的前n 项和n T ．注：如果选择多个条件分别解答，按第一个解答计分． 解：（1）因为所以所以当时，适合上式，所以（2）若选①： 因为所以若选②：因为所以则两式相减可得：所以若选③：当n为偶数时，当n为奇数时，综上：19．（本小题满分12分）如图，在三棱柱ABC—A1B1C1中，AB＝AC＝2，D为BC的中点，平面BB1C1C⊥平面ABC，设直线l为平面AC1D与平面A1B1C1的交线．（1）证明：l⊥平面BB1C1C；（2）已知四边形BB1C1C为边长为2的菱形，且∠B1BC＝60°，求二面角D—AC1—C的余弦值．解：（1）证明：因为AB＝AC＝2，D为BC的中点，所以AD⊥BC，又因为平面BB1C1C⊥平面ABC，且平面BB1C1C平面ABC＝BC，AD 平面ABC，所以AD⊥平面BB1C1C，而AD∥平面A1B1C1，且AD⊂平面AC1D，平面AC1D平面A1B1C1＝l，所以AD∥l，所以l⊥平面BB1C1C；（2）因为AD⊥平面BB1C1C，AD⊂平面AC1D，所以平面AC1D⊥平面BB1C1C，在平面BB1C1C内，过C作CH⊥DC1于点H，则CH⊥平面AC1D，过C作CG⊥AC1于点G，则G为线段AC1的中点，连接HG，则∠CGH就是二面角D—AC1—C的平面角，在直角中，在中，，在中，，在直角中，，所以所以二面角D—AC1—C的余弦值为20．（本小题满分12分）某县在实施脱贫工作中因地制宜，着力发展枣树种植项目．该县种植的枣树在2020年获得大丰收，依据扶贫政策，所有红枣由经销商统一收购．为了更好的实现效益，县扶贫办从今年收获的红枣中随机选取100千克，进行质量检测，根据检测结果制成如图所示的频率分布直方图．右表是红枣的分级标准，其中一级品、二级品统称为优质品．经销商与某农户签订了红枣收购协议，规定如下：从一箱红枣中任取4个进行检测，若4个均为优质品，则该箱红枣定为A 类；若4个中仅有3个优质品，则再从该箱中任意取出1个，若这一个为优质品，则该箱红枣也定为A 类；若4个中至多有一个优质品，则该箱红枣定为C 类；其它情况均定为B 类．已知每箱红枣重量为10千克，A 类、B 类、C 类的红枣价格分别为每千克20元、16元、12元．现有两种装箱方案：方案一：将红枣采用随机混装的方式装箱；方案二：将红枣按一、二、三、四等级分别装箱，每箱的分拣成本为1元． 以频率代替概率解决下面的问题．（1）如果该农户采用方案一装箱，求一箱红枣被定为A 类的概率；（2）根据所学知识判断，该农户采用哪种方案装箱更合适，并说明理由． 解：（1）从红枣中任意取出一个，则该红枣为优质品的概率是，记“如果该农户采用方案一装箱，一箱红枣被定为A 类”为事件A ，则（2）记“如果该农户采用方案一装箱，一箱红枣被定为B 类”为事件B ，“如果该农户采用方案一装箱，一箱红枣被定为C 类”为事件C ，则所以如果该农户采用方案一装箱，每箱红枣收入的数学期望为：元；由题意可知，如果该农户采用方案二装箱，则一箱红枣被定为A 类的概率为，被定为C 类的概率也为，所以如果该农户采用方案二装箱，每箱红枣收入的数学期望为： 元；所以该农户采用方案二装箱更合适．21．（本小题满分12分）已知椭圆C ：22221(0)x y a b a b+=>>（1）求椭圆C 的标准方程；（2）若折线0)y k x =≠与C 相交于A ，B 两点（点A 在直线x =的右侧），设直线OA ，OB 的斜率分别为1k ，2k ，且212k k −=，求k 的值．解：（1）由题可知22c a b a⎧=⎪⎪⎨⎪=⎪⎩，又因为，所以所以椭圆C 的标准方程为（2）因为折线与椭圆C 相交于A ，B 两点，设点B 关于x 轴的对称点为B′， 则直线与椭圆C 相交于A ，B′两点，设则由得所以所以整理得解得22．（本小题满分12分）已知函数()ln(1)f x a x x =−+． （1）讨论()f x 的单调性；（2）若1()e 1x f x x −≥−+对任意的x ∈(0，+∞)恒成立，求实数a 的取值范围． 解：（1）若，，此时在上单调递减；若，由得，此时在上单调递减，在上单调递增；综上所述，，在上单调递减；，在上单调递减，在上单调递增；（2）因为记所以在上单调递增，所以，所以恒成立；若不合题意；若，由（1）知，在上单调递减，所以不合题意；若，记记所以在上单调递增，所以所以符合题意；综上实数a的取值范围是．。

2020-2021高三数学上期末模拟试题(附答案)一、选择题1．已知数列121,,,4a a 成等差数列，1231,,,,4b b b 成等比数列，则212a ab -的值是 ( ) A ．12B ．12-C ．12或12- D ．142．在ABC ∆中,,,a b c 分别为角,,A B C 所对的边,若 2?a bcos C =,则此三角形一定是( ) A ．等腰直角三角形 B ．直角三角形C ．等腰三角形D ．等腰三角形或直角三角形3．程大位《算法统宗》里有诗云“九百九十六斤棉，赠分八子做盘缠.次第每人多十七，要将第八数来言.务要分明依次弟，孝和休惹外人传.”意为：996斤棉花，分别赠送给8个子女做旅费，从第一个开始，以后每人依次多17斤，直到第八个孩子为止.分配时一定要等级分明，使孝顺子女的美德外传，则第八个孩子分得斤数为（ ） A ．65 B ．184C ．183D ．1764．已知在中，，，分别为角，，的对边，为最小角，且，，，则的面积等于（ ） A ．B ．C ．D ．5．设数列{}n a 是以2为首项，1为公差的等差数列，{}n b 是以1为首项，2为公比的等比数列，则1210b b b a a a ++⋯+=（ ） A ．1033 B ．1034C ．2057D ．20586．若直线()10,0x ya b a b+=>>过点(1,1)，则4a b +的最小值为（ ） A ．6 B ．8 C ．9 D ．107．已知等比数列{}n a 的各项都是正数，且13213,,22a a a 成等差数列，则8967a a a a +=+ A ．6B ．7C ．8D ．98．在等差数列{a n }中，a 1＞0，a 10·a 11＜0，若此数列的前10项和S 10＝36，前18项的和S 18＝12，则数列{|a n |}的前18项和T 18的值是 （ ） A ．24B ．48C ．60D ．849．已知数列{a n }满足331log 1log ()n n a a n N +++=∈且2469a a a ++=，则15793log ()a a a ++的值是( )A ．－5B ．－15C ．5D ．1510．设数列{}n a 的前n 项和为n S ，若2，n S ，3n a 成等差数列，则5S 的值是（ ） A ．243-B ．242-C ．162-D ．24311．已知数列{}n a 中，()111,21,n n na a a n N S *+==+∈为其前n 项和，5S的值为（ ） A ．63B ．61C ．62D ．5712．在等差数列 {}n a 中， n S 表示 {}n a 的前 n 项和，若 363a a += ，则 8S 的值为（ ）A ．3B ．8C ．12D ．24二、填空题13．已知lg lg 2x y +=，则11x y+的最小值是______. 14．若为等比数列的前n 项的和，，则=___________15．如图，在ABC V 中，,43C BC π==时，点D 在边AC 上， AD DB =，DE AB ⊥，E 为垂足若22DE =，则cos A =__________16．若正数,a b 满足3ab a b =++，则+a b 的取值范围_______________。

2020-2021高三数学上期末一模试卷(及答案)(6)一、选择题1．等差数列{}n a 中，已知70a >，390a a +<，则{}n a 的前n 项和n S 的最小值为（ ） A ．4SB ．5SC ．6SD ．7S2．若,x y 满足1010330x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩，则2z x y =+的最大值为( )A ．8B ．7C ．2D ．13．在ABC ∆中，,,a b c 分别为角,,A B C 的对边，若,1,3A bπ==ABC ∆的面积为3，则a 的值为（ ） A ．2B ．3C ．32D ．14．程大位《算法统宗》里有诗云“九百九十六斤棉，赠分八子做盘缠.次第每人多十七，要将第八数来言.务要分明依次弟，孝和休惹外人传.”意为：996斤棉花，分别赠送给8个子女做旅费，从第一个开始，以后每人依次多17斤，直到第八个孩子为止.分配时一定要等级分明，使孝顺子女的美德外传，则第八个孩子分得斤数为（ ） A ．65B ．184C ．183D ．1765．等比数列{}n a 的前n 项和为n S ，若36=2S =18S ，，则105S S 等于( ) A ．－3B ．5C ．33D ．－316．我国的《洛书》中记载着世界上最古老的一个幻方：将1，2，...，9填入33⨯的方格内，使三行、三列、两对角线的三个数之和都等于15 (如图）.一般地，将连续的正整数1，2，3，…，2n 填入n n ⨯的方格内，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n 阶幻方.记n 阶幻方的一条对角线上数的和为n N (如：在3阶幻方中，315N =)，则10N =（ ）A ．1020B ．1010C ．510D ．5057．设,x y 满足约束条件0,20,240,x y x y x y -≥⎧⎪+-≥⎨⎪--≤⎩则2z x y =+的最大值为（ ）A ．2B ．3C ．12D ．138．已知等比数列{}n a 的各项都是正数，且13213,,22a a a 成等差数列，则8967a a a a +=+ A ．6B ．7C ．8D ．99．已知点(),M a b 与点()0,1N -在直线3450x y -+=的两侧，给出以下结论：①3450a b -+>；②当0a >时，+a b 有最小值，无最大值；③221a b +>；④当0a >且1a ≠时，11b a +-的取值范围是93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭，正确的个数是（ ） A ．1B ．2C ．3D ．410．已知x 、y 满足约束条件50{03x y x y x -+≥+≥≤，则24z x y =+的最小值是（ ）A ．6-B ．5C ．10D ．10-11．已知数列{}n a 中，()111,21,n n na a a n N S *+==+∈为其前n 项和，5S的值为（ ） A ．63B ．61C ．62D ．5712．在直角梯形ABCD 中，//AB CD ，90ABC ∠=o ，22AB BC CD ==，则cos DAC ∠=（ ）ABCD．10二、填空题13．在ABC ∆中，角,,A B C 所对的边为,,a b c ，若23sin c ab C =，则当b aa b+取最大值时，cos C =__________；14．已知数列{}n a 的首项12a =，且满足()*12n n n a a n N +=∈，则20a =________．15．已知函数()2xf x =，等差数列{}n a 的公差为2，若()2468104f a a a a a ++++=，则()()()()212310log f a f a f a f a ⋅⋅⋅⋅=⎡⎤⎣⎦L ___________.16．已知锐角三角形的边长分别为1，3，a ，则a 的取值范围是__________． 17．已知数列{}{}n n a b 、满足ln n n b a =，*n ∈N ，其中{}n b 是等差数列，且431007e a a ⋅=，则121009b b b +++=L ________．18．设n S 是等差数列{}n a 的前n 项和，若510S =，105S =-，则公差d =（___）． 19．已知等比数列{}n a 满足232,1a a ==，则12231lim ()n n n a a a a a a +→+∞+++=L ________________.20．已知0,0a b >>，且20a b +=，则lg lg a b +的最大值为_____．三、解答题21．设 的内角 的对边分别为 已知．（1）求角 ；（2）若，，求的面积．22．已知等差数列{}n a 的所有项和为150，且该数列前10项和为10，最后10项的和为50.（1）求数列{}n a 的项数； （2）求212230a a a ++⋅⋅⋅+的值.23．已知函数f(x)＝x 2－2ax －1＋a ，a∈R. (1)若a ＝2，试求函数y ＝()f x x(x>0)的最小值； (2)对于任意的x∈[0，2]，不等式f(x)≤a 成立，试求a 的取值范围． 24．已知{}n a 为等差数列，且36a =-，60a =． （1）求{}n a 的通项公式；（2）若等比数列{}n b 满足18b =-，2123b a a a =++，求数列{}n b 的前n 项和公式． 25．已知函数()11f x x x =-++． （1）解不等式()2f x ≤；（2）设函数()f x 的最小值为m ，若a ，b 均为正数，且14m a b+=，求+a b 的最小值．26．在四边形ABCD 中，120BAD ︒∠=，60BCD ︒∠=，1cos 7D =-，2AD DC ==.(1) 求cos DAC ∠及AC 的长； (2) 求BC 的长.【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】 【分析】先通过数列性质判断60a <，再通过数列的正负判断n S 的最小值. 【详解】∵等差数列{}n a 中，390a a +<，∴39620a a a +=<，即60a <.又70a >，∴{}n a 的前n 项和n S 的最小值为6S . 故答案选C 【点睛】本题考查了数列和的最小值，将n S 的最小值转化为{}n a 的正负关系是解题的关键.2．B解析：B 【解析】试题分析：作出题设约束条件可行域，如图ABC ∆内部（含边界），作直线:20l x y +=，把直线l 向上平移，z 增加，当l 过点(3,2)B 时，3227z =+⨯=为最大值．故选B ．考点：简单的线性规划问题．3．B解析：B 【解析】试题分析：由已知条件及三角形面积计算公式得131sin ,2,232c c π⨯⨯=∴=由余弦定理得考点：考查三角形面积计算公式及余弦定理．4．B解析：B 【解析】分析：将原问题转化为等差数列的问题，然后结合等差数列相关公式整理计算即可求得最终结果.详解：由题意可得，8个孩子所得的棉花构成公差为17的等差数列，且前8项和为996， 设首项为1a ，结合等差数列前n 项和公式有：811878828179962S a d a ⨯=+=+⨯=， 解得：165a =，则81765717184a a d =+=+⨯=. 即第八个孩子分得斤数为184. 本题选择B 选项.点睛：本题主要考查等差数列前n 项和公式，等差数列的应用，等差数列的通项公式等知识，意在考查学生的转化能力和计算求解能力.5．C解析：C 【解析】 【分析】由等比数列的求和公式结合条件求出公比，再利用等比数列求和公式可求出105S S . 【详解】设等比数列{}n a 的公比为q （公比显然不为1），则()()61636333111119111a q S q q q S qa q q---===+=---，得2q =， 因此，()()101105510555111111233111a q S q q q S q a qq---===+=+=---，故选C. 【点睛】本题考查等比数列基本量计算，利用等比数列求和公式求出其公比，是解本题的关键，一般在求解等比数列问题时，有如下两种方法：（1）基本量法：利用首项和公比列方程组解出这两个基本量，然后利用等比数列的通项公式或求和公式来进行计算；（2）性质法：利用等比数列下标有关的性质进行转化，能起到简化计算的作用．解析：D 【解析】n阶幻方共有2n个数，其和为()2221 12...,2n nn n++++=Q阶幻方共有n行，∴每行的和为()()2221122n nn nn++=，即()()2210110101,50522nn nN N+⨯+=∴==，故选D. 7．C解析：C【解析】【分析】由约束条件可得可行域，将问题变成1122y x z=-+在y轴截距最大问题的求解；通过平移直线可确定最大值取得的点，代入可得结果.【详解】由约束条件可得可行域如下图所示：当2z x y=+取最大值时，1122y x z=-+在y轴截距最大平移直线12y x=-，可知当直线1122y x z=-+过图中A点时，在y轴截距最大由240y xx y=⎧⎨--=⎩得：()4,4Amax42412z∴=+⨯=故选：C【点睛】本题考查线性规划中最值问题的求解，关键是能够将问题转化为直线在y轴截距最值问题的求解，属于常考题型.8．D解析：D【解析】设各项都是正数的等比数列{a n }的公比为q ，（q ＞0），由题意可得关于q 的式子，解之可得q ，而所求的式子等于q 2，计算可得． 【详解】设各项都是正数的等比数列{a n }的公比为q ，（q ＞0）由题意可得31212322a a a ⨯=+， 即q 2-2q-3=0， 解得q=-1（舍去），或q=3，故()26728967679a a qa a q a a a a ．++===++ 故选：D ． 【点睛】本题考查等差数列和等比数列的通项公式，求出公比是解决问题的关键，属基础题．9．B解析：B 【解析】 【分析】 【详解】∵点M (a ,b )与点N (0,−1)在直线3x −4y +5=0的两侧,∴()()34530450a b -+⨯++<，即3450a b -+<，故①错误； 当0a >时,54a b +>，a +b 即无最小值，也无最大值，故②错误； 设原点到直线3x −4y +5=0的距离为d ,则22513(4)==+-d ,则22a b +>1，故③正确；当0a >且a ≠1时,11b a +-表示点M (a ,b )与P (1,−1)连线的斜率． ∵当0a =,b =54时,51194114b a ++==---,又直线3x −4y +5=0的斜率为34， 故11b a +-的取值范围为93,,44⎛⎫⎛⎫-∞-⋃+∞ ⎪ ⎪⎝⎭⎝⎭，故④正确.∴正确命题的个数是2个. 故选B.点睛：本题是常规的线性规划问题，线性规划问题常出现的形式有：①直线型，转化成斜截式比较截距，要注意z 前面的系数为负时，截距越大，z 值越小；②分式型，其几何意义是已知点与未知点的斜率；③平方型，其几何意义是距离，尤其要注意的是最终结果应该是距离的平方；④绝对值型，转化后其几何意义是点到直线的距离.10．A解析：A 【解析】 【分析】 【详解】作出不等式50{03x y x y x -+≥+≥≤所表示可行域如图所示，作直线:24l z x y =+，则z 为直线l 在y 轴上截距的4倍， 联立3{x x y =+=，解得3{3x y ==-，结合图象知，当直线l 经过可行域上的点()3,3A -时，直线l 在y 轴上的截距最小， 此时z 取最小值，即()min 23436z =⨯+⨯-=-，故选A. 考点：线性规划11．D解析：D 【解析】解：由数列的递推关系可得：()11121,12n n a a a ++=++= ，据此可得：数列{}1n a + 是首项为2 ，公比为2 的等比数列，则：1122,21n n n n a a -+=⨯⇒=- ，分组求和有：()5521255712S ⨯-=-=- .本题选择D 选项.12．C解析：C 【解析】 【分析】设1BC CD ==，计算出ACD ∆的三条边长，然后利用余弦定理计算出cos DAC ∠． 【详解】如下图所示，不妨设1BC CD ==，则2AB =，过点D 作DE AB ⊥，垂足为点D ， 易知四边形BCDE 是正方形，则1BE CD ==，1AE AB BE ∴=-=， 在Rt ADE ∆中，222AD AE DE =+=，同理可得225AC AB BC =+=，在ACD ∆中，由余弦定理得2222310cos 2252AC AD CD DAC AC AD +-∠===⋅⨯⨯， 故选C ．【点睛】本题考查余弦定理求角，在利用余弦定理求角时，首先应将三角形的边长求出来，结合余弦定理来求角，考查计算能力，属于中等题．二、填空题13．【解析】【分析】由余弦定理得结合条件将式子通分化简得再由辅助角公式得出当时取得最大值从而求出结果【详解】在中由余弦定理可得所以其中当取得最大值时∴故答案为：【点睛】本题考查解三角形及三角函数辅助角公 213【解析】 【分析】由余弦定理得2222cos c a b ab C =+-，结合条件23sin c ab C =，将式子b aa b+通分化简得3sin 2cos C C +，再由辅助角公式得出b aa b +()13sin C ϕ=+，当2C πϕ+=时，b aa b +取得最大值，从而求出结果. 【详解】在ABC ∆中由余弦定理可得2222cos c a b ab C =+-，所以2222cos 3sin 2cos 3sin 2cos b a a b c ab C ab C ab C C C a b ab ab ab++++====+()13sin C ϕ=+，其中213sin ϕ=，313cos ϕ=， 当b a a b +132C πϕ+=，∴213cos cos sin 213C πϕϕ⎛⎫=-== ⎪⎝⎭．213【点睛】本题考查解三角形及三角函数辅助角公式，考查逻辑思维能力和运算能力，属于常考题.14．512【解析】【分析】利用已知将n 换为n+1再写一个式子与已知作比得到数列的各个偶数项成等比公比为2再求得最后利用等比数列的通项公式即可得出【详解】∵anan+1=2n （）∴an+1an+2=2n+解析：512 【解析】 【分析】利用已知将n 换为n +1，再写一个式子，与已知作比，得到数列{}n a 的各个偶数项成等比，公比为2，再求得2=1a ，最后利用等比数列的通项公式即可得出． 【详解】∵a n a n +1=2n ，（*n N ∈） ∴a n +1a n +2=2n +2．（*n N ∈）∴22n na a +=,（*n N ∈），∴数列{}n a 的各个奇数项513...a a a ，，成等比，公比为2， 数列{}n a 的各个偶数项246...a a a ，，成等比，公比为2，又∵a n a n +1=2n ，（*n N ∈），∴a 1a 2=2,又12a =，∴2=1a ，可得：当n 为偶数时，1222n n a a -=⋅∴a 20＝1•29＝512．故答案为：512．【点睛】本题考查了等比数列的通项公式、数列递推关系，考查了推理能力与计算能力，属于中档题． 15．【解析】【分析】根据指数运算出再利用等差中项的性质得出并得出然后再利用等差数列的性质和指数对数的运算法则求出的值【详解】依题意有且则而因此故答案为【点睛】本题考查等差数列基本性质的计算同时也考查了等 解析：6-【解析】【分析】根据指数运算出2468102a a a a a ++++=，再利用等差中项的性质得出625a =，并得出56825a a =-=-，然后再利用等差数列的性质和指数、对数的运算法则求出()()()()212310log f a f a f a f a ⋅⋅⋅⋅⎡⎤⎣⎦L 的值.【详解】依题意有246810625a a a a a a ++++==，625a ∴=，且56282255a a =-=-=-. 则()()()110123101105610825556255a a a a a a a a a a +⎛⎫++++==+=+=⨯-+=- ⎪⎝⎭L ， 而()()()()1231061231022a a a a f a f a f a f a ++++-⋅⋅⋅⋅==L L ，因此，()()()()62123102log log 26f a f a f a f a -⋅⋅⋅⋅==-⎡⎤⎣⎦L .故答案为6-.【点睛】 本题考查等差数列基本性质的计算，同时也考查了等差数列的定义以及指数、对数的运算，解题时充分利用等差中项的性质，可简化计算，考查计算能力，属于中等题.16．【解析】由三角形中三边关系及余弦定理可得应满足解得∴实数的取值范围是答案：点睛：根据三角形的形状判断边满足的条件时需要综合考虑边的限制条件在本题中要注意锐角三角形这一条件的运用必须要考虑到三个内角的解析：a <<【解析】由三角形中三边关系及余弦定理可得a 应满足22222222224130130310a a a a <<⎧⎪+->⎪⎨+->⎪⎪+->⎩，解得a << ∴实数a的取值范围是．答案：点睛：根据三角形的形状判断边满足的条件时，需要综合考虑边的限制条件，在本题中要注意锐角三角形这一条件的运用，必须要考虑到三个内角的余弦值都要大于零，并由此得到不等式，进一步得到边所要满足的范围．17．2018【解析】【分析】数列{an}{bn}满足bn ＝lnann ∈N*其中{bn}是等差数列可得bn+1﹣bn ＝lnan+1﹣lnan ＝ln 常数t 常数et ＝q ＞0因此数列{an}为等比数列由可得a1解析：2018【解析】【分析】数列{a n }、{b n }满足b n ＝lna n ，n ∈N *，其中{b n }是等差数列，可得b n +1﹣b n ＝lna n +1﹣lna n ＝ln 1n n a a +=常数t ．1n na a +=常数e t ＝q ＞0，因此数列{a n }为等比数列．由431007e a a ⋅=， 可得a 1a 1009＝a 2a 1008431007a a e =⋅==L ．再利用对数运算性质即可得出．【详解】解：数列{a n }、{b n }满足b n ＝lna n ，n ∈N *，其中{b n }是等差数列，∴b n +1﹣b n ＝lna n +1﹣lna n ＝ln 1n na a +=常数t ． ∴1n na a +=常数e t ＝q ＞0， 因此数列{a n }为等比数列．且431007e a a ⋅=，∴a 1a 1009＝a 2a 1008431007a a e =⋅==L ．则b 1+b 2+…+b 1009＝ln （a 1a 2…a 1009）==lne 2018＝2018．故答案为：2018．【点睛】本题考查了等比数列的通项公式与性质、对数运算性质，考查了推理能力与计算能力，属于中档题．18．【解析】【分析】根据两个和的关系得到公差条件解得结果【详解】由题意可知即又两式相减得【点睛】本题考查等差数列和项的性质考查基本分析求解能力属基础题解析：1-【解析】【分析】根据两个和的关系得到公差条件，解得结果.【详解】由题意可知，10551015S S -=--=-，即67891015a a a a a ++++=-，又1234510a a a a a ++++=，两式相减得2525d =-，1d =-.【点睛】本题考查等差数列和项的性质，考查基本分析求解能力，属基础题.19．【解析】【分析】求出数列的公比并得出等比数列的公比与首项然后利用等比数列求和公式求出即可计算出所求极限值【详解】由已知所以数列是首项为公比为的等比数列故答案为【点睛】本题考查等比数列基本量的计算同时 解析：323【解析】【分析】求出数列{}n a 的公比，并得出等比数列{}1n n a a +的公比与首项，然后利用等比数列求和公式求出12231n n a a a a a a ++++L ，即可计算出所求极限值.【详解】 由已知3212a q a ==，23112()()22n n n a --=⨯=，3225211111()()()2()2224n n n n n n a a ----+=⋅==⋅，所以数列{}1n n a a +是首项为128a a =，公比为1'4q =的等比数列， 11223118[(1()]3214[1()]13414n n n n a a a a a a -+-+++==--L ， 1223132132lim ()lim [1()]343n n n n n a a a a a a +→+∞→∞+++=-=L . 故答案为323. 【点睛】本题考查等比数列基本量的计算，同时也考查了利用定义判定等比数列、等比数列求和以及数列极限的计算，考查推理能力与计算能力，属于中等题.20．【解析】【分析】由为定值运用均值不等式求的最大值即可【详解】当且仅当时等号成立即而当且仅当时等号成立故的最大值为2故答案为：2【点睛】本题主要考查了基本不等值求积的最大值对数的运算属于中档题解析：2【解析】【分析】由0,0a b >>，20a b +=为定值，运用均值不等式求ab 的最大值即可.【详解】0,0a b ∴>>,20a b +=,202a b ab ∴=+≥,当且仅当10a b ==时，等号成立，即100ab ≤，而lg lg lg lg1002a b ab +=≤=，当且仅当10a b ==时，等号成立，故lg lg a b +的最大值为2，故答案为：2【点睛】本题主要考查了基本不等值求积的最大值，对数的运算，属于中档题.三、解答题21．（1） （2）【解析】【分析】（1）直接利用正弦定理和三角函数关系式的恒等变换求出结果．（2）利用（1）的结论，余弦定理及三角形的面积公式求出结果．【详解】（1）∵b=a （cosC ﹣sinC ），∴由正弦定理得sinB=sinAcosC ﹣sinAsinC ，可得sin （A+C ）=sinAcosC+cosAsinC=sinAcosC ﹣sinAsinC ，∴cosAsinC=﹣sinAsinC ，由sinC≠0，得sinA+cosA=0，∴tanA=﹣1，由A 为三角形内角，可得．（2）因为， 所以由正弦定理可得b=c ， 因为a 2=b 2+c 2﹣2bccosA ，， 可得c=，所以b=2， 所以．【点睛】 本题考查的知识要点：三角函数关系式的恒等变换，正弦定理和余弦定理的应用，三角形面积公式的应用．22．（1）50；（2）30【解析】【分析】(1)根据条件结合等差数列的性质可得16n a a +=,再根据{}n a 的所有项和为150,即可求出项数n 的值;(2)根据(1)求出{}n a 的首项1a 和公差d ,然后将212230a a a ++⋅⋅⋅+用1a 和d 表示,再求出其值.【详解】解:(1)由题意,得1231010a a a a +++⋅⋅⋅+=,12950n n n n a a a a ---+++⋅⋅⋅+=,∴()()()()1213210960n n n n a a a a a a a a ---++++++⋅⋅⋅++=,根据等差数列性质,可知12132109n n n n a a a a a a a a ---+=+=+=⋅⋅⋅=+,∴()11060n a a +=,∴16n a a +=,又{}n a 的所有项和为150,∴()11502n n a a +=, ∴50n =,即数列{}n a 的项数为50.(2)由(1)知,1501610910102a a a d +=⎧⎪⎨⨯+=⎪⎩,即112496292a d a d +=⎧⎨+=⎩,∴11120110a d ⎧=⎪⎪⎨⎪=⎪⎩, ∴()2122233021305a a a a a a +++⋅⋅⋅+=+()15249a d =+11152492010⎛⎫=⨯+⨯ ⎪⎝⎭30=. 【点睛】本题考查了等差数列的性质和前n 项和公式,考查了转化思想和方程思想,属基中档题.23．（1）2-；（2）3,4⎡⎫+∞⎪⎢⎣⎭【解析】【分析】（1）根据基本不等式求最值，注意等号取法，（2）先化简不等式，再根据二次函数图像确定满足条件的不等式，解不等式得结果.【详解】(1)依题意得y=()f x x =2-41x x x+=x+1x -4. 因为x>0,所以x+1x ≥2.当且仅当x=1x时, 即x=1时,等号成立.所以y≥-2. 所以当x=1时,y=()f x x的最小值为-2. (2)因为f(x)-a=x 2-2ax-1, 所以要使得“对任意的x∈[0,2],不等式f(x)≤a 成立”只要“x 2-2ax-1≤0在[0,2]恒成立”.不妨设g(x)=x 2-2ax-1,则只要g(x)≤0在[0,2]上恒成立即可.所以(0)0,(2)0,g g ≤⎧⎨≤⎩ 即0-0-10,4-4-10,a ≤⎧⎨≤⎩解得a≥34,则a 的取值范围为3,4∞⎡⎫+⎪⎢⎣⎭. 【点睛】在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误.24．(1)212n a n =-;(2)4(13)n n S =-.【解析】【分析】【详解】本试题主要是考查了等差数列的通项公式的求解和数列的前n 项和的综合运用．、 （1）设{}n a 公差为d ，由已知得1126{50a d a d +=-+=解得110{2a d =-=, 212n a n =-（2）21232324b a a a a =++==-Q ，∴等比数列{}n b 的公比212438b q b -===- 利用公式得到和8(13)4(13)13n n n S -⨯-==--．25．（Ⅰ）[]1,1-； （Ⅱ）92. 【解析】【分析】 （Ⅰ）分段去绝对值求解不等式即可；（Ⅱ）由绝对值三角不等式可得2m =，再由()122a b a b a b ⎛⎫+=++⎪⎝⎭，展开利用基本不等式求解即可.【详解】 （Ⅰ）Q ()2121121x x f x x x x -≤-⎧⎪=-<≤⎨⎪>⎩，，， ∴ 122x x ≤-⎧⎨-≤⎩ 或 1122x -<≤⎧⎨≤⎩ 或 122x x >⎧⎨≤⎩∴ 11x -≤≤,∴不等式解集为[]1,1-.（Ⅱ） Q ()()11112x x x x -++≥--+=,∴ 2m =, 又142a b+=,0,0a b >>, ∴1212a b +=,∴ ()125259222222a b a b a b a b b a ⎛⎫+=++=++≥+= ⎪⎝⎭, 当且仅当1422a b b a ⎧+=⎪⎨⎪=⎩即323a b ⎧=⎪⎨⎪=⎩时取等号,所以()min 92a b +=. 【点睛】绝对值不等式的常见解法：①利用绝对值不等式的几何意义求解，体现了数形结合的思想；②利用“零点分段法”求解，体现了分类讨论的思想；③通过构造函数，利用函数的图象求解，体现了函数与方程的思想．26．(1) cos DAC ∠=AC =(2) 3 【解析】【分析】（1）用余弦定理求AC ，再求cos DAC ∠；（2）先求出sin BAC ∠和sin B ，再用正弦定理可求得BC ．【详解】（1）ACD ∆中，由余弦定理可得：222164222277AC ⎛⎫=⨯-⨯⨯-= ⎪⎝⎭，解得AC =11272cos 2AC DAC AD ∴∠=== （2）设DAC DCA α∠==∠，由（1）可得：cos sin 77αα==， ()sin sin 120BAC α︒∴∠=-1272714=+⨯=， ()sin sin()sin 1802B BAC BCA α︒=∠+∠=-sin 22777α==⨯= 在BAC V 中，由正弦定理可得：sin sin BC AC BAC B=∠，37BC ⨯∴==. 【点睛】本题考查余弦定理，正弦定理，考查两角和与差的正弦公式，诱导公式，二倍角公式等．本题属于中档题．解三角形注意公式运用：①利用正弦定理可解决两类三角形问题：一是已知两角和一角的对边，求其他边或角；二是已知两边和一边的对角，求其他边或角；②利用余弦定理可解决两类三角形问题：一是已知两边和它们的夹角，求其他边或角；二是已知三边求角．由于这两种情形下的三角形是唯一确定的，所以其解也是唯一的．。

2020-2021高三数学上期末模拟试题(附答案)(1)一、选择题1．已知正数x 、y 满足1x y +=，且2211x y m y x +≥++，则m 的最大值为（ ） A ．163B ．13C ．2D ．42．已知等比数列{}n a 的公比为正数，且239522,1a a a a ⋅==，则1a = ( )A ．12B ．2 CD．23．设等比数列{}n a 的前n 项和为n S ，若633S S =， 则96S S =（ ） A ．2B ．73C ．83D ．34．设x y ，满足约束条件10102x y x y y -+≤⎧⎪+-⎨⎪≤⎩＞，则yx 的取值范围是（ ）A ．()[),22,-∞-+∞UB ．(]2,2-C ．(][),22,-∞-+∞UD ．[]22-,5．已知等差数列{}n a 满足244a a +=，3510a a +=，则它的前10项的和10S =（ ） A ．138B ．135C ．95D ．236．设变量,x y 、满足约束条件236y xx y y x ≤⎧⎪+≥⎨⎪≥-⎩，则目标函数2z x y =+的最大值为（ ）A ．2B ．3C ．4D ．97．若a 、b 、c >0且a (a ＋b ＋c )＋bc ＝4－，则2a ＋b ＋c 的最小值为( ) A．1 B．1 C ．＋2D ．28．已知正项等比数列{}n a 的公比为3，若229m n a a a =，则212m n+的最小值等于（ ） A ．1B ．12C ．34 D ．329．等差数列{}n a 中，已知611a a =，且公差0d >，则其前n 项和取最小值时的n 的值为( ) A ．6B ．7C ．8D ．910．已知x 、y 满足约束条件50{03x y x y x -+≥+≥≤，则24z x y =+的最小值是（ ）A ．6-B ．5C ．10D ．10-11．已知数列{}n a 的前n 项和2n S n n =-，数列{}n b 满足1sin2n n n b a π+=，记数列{}n b 的前n 项和为nT，则2017T =（ ） A ．2016B ．2017C ．2018D ．201912．在ABC ∆中，a ，b ，c 分别是角A ，B ，C 的对边，若2b c =，a =7cos 8A =，则ABC ∆的面积为（ ） AB ．3CD二、填空题13．若首项为1a ，公比为q （1q ≠）的等比数列{}n a 满足21123lim()2n n a q a a →∞-=+，则1a 的取值范围是________.14．已知x y ，满足20030x y y x y -≥⎧⎪≥⎨⎪+-≤⎩，，，，则222x y y ++的取值范围是__________.15．已知n S 为数列{a n }的前n 项和，且22111n n n a a a ++-=-，21313S a =，则{a n }的首项的所有可能值为______16．设0a >，若对于任意满足8m n +=的正数m ，n ，都有1141a m n ++≤，则a 的取值范围是______.17．已知n S 为数列{}n a 的前n 项和，且13a =，131n n a S +=+，*n ∈N ，则5S =______. 18．设(3()lg f x x x =+，则对任意实数,a b ，“0a b +≥”是“()()0f a f b +≥”的_________条件．（填“充分不必要”.“必要不充分”.“充要”.“既不充分又不必要”之一）19．已知不等式250ax x b -+>的解集是{}|32x x -<<-，则不等式250bx x a -+>的解集是_________.20．已知数列{}n a 为正项的递增等比数列，1582a a +=，2481a a =g ，记数列2n a ⎧⎫⎨⎬⎩⎭的前n 项和为n T ，则使不等式112020|1|13n nT a -->成立的最大正整数n 的值是__________．21．在条件①()(sin sin )()sin a b A B c b C +-=-，②sin cos()6a Bb A π=+，③sinsin 2B Cb a B +=中任选一个，补充到下面问题中，并给出问题解答. 在ABC ∆中，角,,A B C 的对边分别为,,a bc ，6b c +=，a =， . 求ABC ∆的面积.22．已知等差数列{}n a 的公差为()0d d ≠，等差数列{}n b 的公差为2d ，设n A ，n B 分别是数列{}n a ，{}n b 的前n 项和，且13b =，23A =，53A B =. （1）求数列{}n a ，{}n b 的通项公式； （2）设11n n n n c b a a +=+•，数列{}n c 的前n 项和为n S ，证明：2(1)n S n <+.23．设}{n a 是等差数列，公差为d ，前n 项和为n S . （1）设140a =，638a =，求n S 的最大值.（2）设11a =，*2()na nb n N =∈，数列}{n b 的前n 项和为n T ，且对任意的*n N ∈，都有20n T ≤，求d 的取值范围.24．已知在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，sin tan cos sin tan cos b B C b B a A C a A -=-． （1）求证：A B =；（2）若c =3cos 4C =，求ABC ∆的周长．25．设递增等比数列{a n }的前n 项和为S n ，且a 2＝3，S 3＝13，数列{b n }满足b 1＝a 1，点P （b n ，b n +1）在直线x ﹣y +2＝0上，n ∈N *. （1）求数列{a n }，{b n }的通项公式； （2）设c n nnb a =，求数列{c n }的前n 项和T n . 26．已知等差数列{}n a 的前n 项和为254,12,16n S a a S +==． (1)求{}n a 的通项公式； (2)数列{}n b 满足141n n n b T S =-，为数列{}n b 的前n 项和，是否存在正整数m ，()1k m k <<，使得23k m T T =?若存在，求出m ，k 的值；若不存在，请说明理由．【参考答案】***试卷处理标记，请不要删除1．B 解析：B 【解析】 【分析】由已知条件得()()113x y +++=，对代数式2211x y y x +++变形，然后利用基本不等式求出2211x y y x +++的最小值，即可得出实数m 的最大值. 【详解】正数x 、y 满足1x y +=，则()()113x y +++=，()()()()()()222222221212111111111111y x y x y x x y y x y x y x y x +-+-⎡⎤⎡⎤----⎣⎦⎣⎦+=+=+=+++++++++444444141465111111y x x y y x x y x y =+-+++-+=+++-=+-++++++()()14441111525311311y x x y x y x y ⎛⎫⎛⎫++=++++-=++-⎡⎤ ⎪ ⎪⎣⎦++++⎝⎭⎝⎭412533⎛≥⨯+-= ⎝， 当且仅当12x y ==时，等号成立，即2211x y y x +++的最小值为13，则13m ≤. 因此，实数m 的最大值为13. 故选：B. 【点睛】本题考查利用基本不等式恒成立求参数，对代数式合理变形是解答的关键，考查计算能力，属于中等题.2．D解析：D 【解析】设公比为q ，由已知得()22841112a q a q a q ⋅=，即22q=，又因为等比数列{}n a 的公比为正数，所以q 212a a q ===，故选D. 3．B解析：B【分析】首先由等比数列前n项和公式列方程，并解得3q，然后再次利用等比数列前n项和公式，则求得答案．【详解】设公比为q，则6163 63313(1)1113(1)11a qS qqqa qS qq---===+=---，∴32q=，∴93962611271123S qS q--===--．故选：B．【点睛】本题考查等比数列前n项和公式，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力，求解时也可以利用连续等长片断的和序列仍然成等比数列，进行求解.4．A解析：A【解析】【分析】根据题意，作出可行域，分析yx的几何意义是可行域内的点(),x y与原点O连线的斜率，根据图象即可求解.【详解】作出约束条件表示的可行域，如图所示，yx的几何意义是可行域内的点(),x y与原点O连线的斜率，由102x yy-+=⎧⎨=⎩，得点A的坐标为()1,2，所以2OAk=，同理，2OBk=-，所以yx的取值范围是()[),22,-∞-+∞U.故选：A本题考查简单的线性规划，考查斜率型目标函数问题，考查数形结合思想，属于中等题型.5．C解析：C 【解析】 试题分析：∵24354{10a a a a +=+=，∴1122{35a d a d +=+=，∴14{3a d =-=， ∴1011091040135952S a d ⨯=+⨯=-+=． 考点：等差数列的通项公式和前n 项和公式．6．D解析：D 【解析】 【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论. 【详解】画出满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩的可行域，如图，画出可行域ABC ∆，(2,0)A ，(1,1)B ，(3,3)C ， 平移直线2z x y =+，由图可知，直线2z x y =+经过(3,3)C 时 目标函数2z x y =+有最大值，2z x y =+的最大值为9.【点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.7．D解析：D 【解析】由a (a ＋b ＋c )＋bc ＝4－，得(a ＋c )·(a ＋b )＝4－ ∵a 、b 、c >0.∴(a ＋c )·(a ＋b )≤22b c 2a ++⎛⎫ ⎪⎝⎭(当且仅当a ＋c ＝b ＋a ，即b ＝c 时取“＝”)，∴2a ＋b ＋c ＝1)＝－2. 故选：D点睛：在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误8．C解析：C 【解析】∵正项等比数列{}n a 的公比为3，且229m n a a a =∴2224222223339m n m n a a a a --+-⋅⋅⋅=⋅=∴6m n +=∴121121153()()(2)(2)62622624m n m n m n n m ⨯++=⨯+++≥⨯+=，当且仅当24m n ==时取等号. 故选C.点睛：利用基本不等式解题的注意点：（1）首先要判断是否具备了应用基本不等式的条件，即“一正、二正、三相等”，且这三个条件必须同时成立．（2）若不直接满足基本不等式的条件，需要通过配凑、进行恒等变形，构造成满足条件的形式，常用的方法有：“1”的代换作用，对不等式进行分拆、组合、添加系数等． （3）多次使用基本不等式求最值时，要注意只有同时满足等号成立的条件才能取得等号．9．C解析：C因为等差数列{}n a 中，611 aa =，所以6116111150,0,,2a a a a a d =-=-，有2[(8)64]2n dS n =--， 所以当8n =时前n 项和取最小值.故选C. 10．A解析：A 【解析】 【分析】 【详解】作出不等式50{03x y x y x -+≥+≥≤所表示可行域如图所示，作直线:24l z x y =+，则z 为直线l 在y 轴上截距的4倍， 联立3{x x y =+=，解得3{3x y ==-，结合图象知，当直线l 经过可行域上的点()3,3A -时，直线l 在y 轴上的截距最小， 此时z 取最小值，即()min 23436z =⨯+⨯-=-，故选A. 考点：线性规划11．A解析：A 【解析】 【分析】由2n S n n =-得到22n a n =-，即n b =2(1)cos2n n π-，利用分组求和法即可得到结果. 【详解】由数列{}n a 的前n 项和为2n S n n =-，当1n =时，11110a S ==-=；当2n …时，1n n n a S S -=-22(1)(1)22n n n n n ⎡⎤=-----=-⎣⎦，上式对1n =时也成立， ∴22n a n =-， ∴cos2n n n b a π==2(1)cos 2n n π-， ∵函数cos 2n y π=的周期242T ππ==，∴()2017152013T b b b =++++L (26b b +)2014b ++L ()()3720154820162017b b b b b b b +++++++++L L02(152013)0=-+++++L 2(3+72015)045042016+++=⨯=L ，故选：A. 【点睛】本题考查的知识要点：数列的通项公式的求法及应用，利用分组法求数列的和，主要考查学生的运算能力和转化能力，属于中档题．12．D解析：D 【解析】 【分析】三角形的面积公式为1sin 2ABC S bc A ∆=，故需要求出边b 与c ，由余弦定理可以解得b 与c . 【详解】解：在ABC ∆中，2227cos 28b c a A bc +-==将2b c =，a =22246748c c c +-=， 解得：2c =由7cos 8A =得sin A ==所以，11sin 2422ABC S bc A ∆==⨯⨯=故选D. 【点睛】三角形的面积公式常见形式有两种：一是12（底⨯高），二是1sin 2bc A .借助12（底⨯高）时，需要将斜三角形的高与相应的底求出来；借助1sin 2bc A 时，需要求出三角形两边及其夹角的正弦值.二、填空题13．【解析】【分析】由题意可得且即且化简可得由不等式的性质可得的取值范围【详解】解：故有且化简可得且即故答案为：【点睛】本题考查数列极限以及不等式的性质属于中档题解析：33(0,)(,3)22U【解析】 【分析】由题意可得1q <且0q ≠，即11q -<<且0q ≠，211232a a a =+，化简可得13322a q =+由不等式的性质可得1a 的取值范围. 【详解】解：21123lim()2n n a q a a →∞-=+Q 21123lim 2n a a a →∞∴=+，lim 0nn q →∞= 故有11q -<<且0q ≠，211232a a a =+ 化简可得13322a q =+ 103a ∴<<且132a ≠即133(0,)(,3)22a ∈U 故答案为：33(0,)(,3)22U 【点睛】本题考查数列极限以及不等式的性质，属于中档题.14．；【解析】【分析】利用表示的几何意义画出不等式组表示的平面区域求出点到点的距离的最值即可求解的取值范围【详解】表示点到点的距离则三角形为等腰三角形则点到点的距离的最小值为：1最大值为所以的最小值为：解析：[]0,9； 【解析】 【分析】 利用()()2201x y -++表示的几何意义，画出不等式组表示的平面区域，求出点(0,1)A -到点(,)x y 的距离的最值，即可求解222x y y ++的取值范围.【详解】()()22222011x y y x y ++=-++-()()2201x y -++表示点(0,1)A -到点(,)x y 的距离1AO =，1910,9110AD AC =+==+=ACD 为等腰三角形则点(0,1)A -到点(,)x y 的距离的最小值为：110 所以222x y y ++的最小值为：2110-=，最大值为：101=9-故222x y y ++的取值范围为[]09，故答案为：[]09，【点睛】本题主要考查了求平方和型目标函数的最值，属于中档题.15．【解析】【分析】根据题意化简得利用式相加得到进而得到即可求解结果【详解】因为所以所以将以上各式相加得又所以解得或【点睛】本题主要考查了数列的递推关系式应用其中解答中利用数列的递推关系式得到关于数列首解析：34，- 【解析】 【分析】根据题意，化简得22111n n n a a a ++-=-，利用式相加，得到2213113112S a a a --=-，进而得到211120a a --=，即可求解结果.【详解】因为22111n n n a a a ++-=-，所以22111n n n a a a ++-=-， 所以2222222213321313121,1,,1a a a a a a a a a -=--=--=-L ，将以上各式相加，得2213113112S a a a --=-，又21313S a =，所以211120a a --=，解得13a =-或14a =.【点睛】本题主要考查了数列的递推关系式应用，其中解答中利用数列的递推关系式，得到关于数列首项的方程求解是解答的关键，着重考查了推理与运算能力，属于中档试题.16．【解析】【分析】由题意结合均值不等式首先求得的最小值然后结合恒成立的条件得到关于a 的不等式求解不等式即可确定实数a 的取值范围【详解】由可得故：当且仅当即时等号成立故只需又则即则的取值范围是【点睛】在 解析：[)1,+∞【解析】 【分析】由题意结合均值不等式首先求得141m n ++的最小值，然后结合恒成立的条件得到关于a 的不等式，求解不等式即可确定实数a 的取值范围. 【详解】由8m n +=可得19m n ++=，故：()1411411411419191n m m n m n m n m n +⎛⎫⎛⎫+=+++=+++ ⎪ ⎪+++⎝⎭⎝⎭11419⎛⨯++= ⎝≥， 当且仅当12141n mn m mn +=⎧⎪+⎨=⎪+⎩，即3m =，5n =时等号成立，故只需11a≤，又0a >，则1a ≥. 即则a 的取值范围是[)1,+∞. 【点睛】在应用基本不等式求最值时，要把握不等式成立的三个条件，就是“一正——各项均为正；二定——积或和为定值；三相等——等号能否取得”，若忽略了某个条件，就会出现错误．17．853【解析】【分析】由与的关系可得即进而得到是以为首项为公比的等比数列可得令即可得到的值【详解】由题即则是以为首项为公比的等比数列即当时故答案为：853【点睛】本题考查等比数列通项公式考查由与的关解析：853 【解析】【分析】由n S 与n a 的关系可得,131n n n S S S +-=+,即141n n S S +=+,进而得到13n S ⎧+⎫⎨⎬⎩⎭是以103为首项,4为公比的等比数列,可得1101433n n S -=⋅-,令5n =,即可得到5S 的值 【详解】由题,1131n n n n a S S S ++=-=+,即141n n S S +=+,则()14n n S S λλ++=+143n n S S λ+∴=+,13λ∴=13a =Q ,111110333S a ∴+=+=,∴13n S ⎧+⎫⎨⎬⎩⎭是以103为首项,4为公比的等比数列,∴1110433n n S -+=⋅,即1101433n n S -=⋅- 当5n =时,51510110142568533333S -=⨯-=⨯-= 故答案为：853 【点睛】本题考查等比数列通项公式,考查由n S 与n a 的关系求n S ,根据1n n S k S b +=⋅+,可构造数列{}n S λ+为等比数列,公比为k18．充要【解析】所以为奇函数又为单调递增函数所以即是的充要条件点睛：充分必要条件的三种判断方法1定义法：直接判断若则若则的真假并注意和图示相结合例如⇒为真则是的充分条件2等价法：利用⇒与非⇒非⇒与非⇒非解析：充要 【解析】33()()lg(()lg(lg10f x f x x x x x +-=++-+-== ，所以()f x 为奇函数，又()f x 为单调递增函数，所以0()()()()()()0a b a b f a f b f a f b f a f b +≥⇔≥-⇔≥-⇔≥-⇔+≥ ，即“0a b +≥”是“()()0f a f b +≥”的充要条件点睛：充分、必要条件的三种判断方法．1．定义法：直接判断“若p 则q ”、“若q 则p ”的真假．并注意和图示相结合，例如“p ⇒q ”为真，则p 是q 的充分条件．2．等价法：利用p ⇒q 与非q ⇒非p ，q ⇒p 与非p ⇒非q ，p ⇔q 与非q ⇔非p 的等价关系，对于条件或结论是否定式的命题，一般运用等价法．3．集合法：若A ⊆B ，则A 是B 的充分条件或B 是A 的必要条件；若A ＝B ，则A 是B 的充要条件．19．【解析】【分析】根据不等式的解集是求得的值从而求解不等式的解集得到答案【详解】由题意因为不等式的解集是可得解得所以不等式为即解得即不等式的解集为【点睛】本题主要考查了一元二次不等式的解法其中解答中根解析：11(,)23--【解析】 【分析】根据不等式250ax x b -+>的解集是{}|32x x -<<-，求得,a b 的值，从而求解不等式250bx x a -+>的解集，得到答案.【详解】由题意，因为不等式250ax x b -+>的解集是{}|32x x -<<-，可得53(2)(3)(2)a b a ⎧-+-=⎪⎪⎨⎪-⨯-=⎪⎩，解得1,6a b =-=-，所以不等式250bx x a -+>为26510x x --->， 即2651(31)(21)0x x x x ++=++<，解得1123x -<<-， 即不等式250bx x a -+>的解集为11(,)23--. 【点睛】本题主要考查了一元二次不等式的解法，其中解答中根据三个二次式之间的关键，求得,a b 的值是解答的关键，着重考查了推理与运算能力，属于基础题.20．8【解析】【分析】根据求得再求出带入不等式解不等式即可【详解】因为数列为正项的递增等比数列由解得则整理得：使不等式成立的最大整数为故答案为：【点睛】本题主要考查了等比数列的性质和等比数列的求和同时考解析：8 【解析】 【分析】根据1524158281a a a a a a +=⎧⎨==⎩，求得15181a a =⎧⎨=⎩，13-=n n a .再求出13(1)3n n T =-，带入不等式112020|1|13n nT a -->，解不等式即可.【详解】因为数列{}n a 为正项的递增等比数列，由1524158281a a a a a a +=⎧⎨==⎩，解得15181a a =⎧⎨=⎩.则3q =，13-=n n a .1(1)1323(1)1313n n n T -=⨯=--. 112020|1|13n n T a -->⇒1112020|11|133n n ---->. 整理得：38080n <.使不等式成立的最大整数n 为8. 故答案为：8 【点睛】本题主要考查了等比数列的性质和等比数列的求和，同时考查了学生的计算能力，属于中档题.三、解答题21．见解析 【解析】 【分析】若选①：利用正弦定理可得(a b)()(c b)a b c +-=-,即222b c a bc +-=,再利用余弦定理求得cos A ,进而求得bc ,从而求得面积；若选②：利用正弦定理可得sin sin sin cos()6A B B A π=+,化简可得tan A =,即6A π=,利用余弦定理求得bc ,从而求得面积；若选③：根据正弦定理得sin sin sin sin 2B CB A B +=,整理可得3A π=,进而求得面积 【详解】 解：若选①：由正弦定理得(a b)()(c b)a b c +-=-， 即222b c a bc +-=，所以2221cos 222b c a bc A bc bc +-===，因为(0,)A π∈，所以3A π=.又2222()3a b c bc b c bc =+-=+-，a =6bc +=，所以4bc =，所以11sin 4sin 223ABC S bc A π∆==⨯⨯= 若选②：由正弦定理得sin sin sin cos()6A B B A π=+.因为0B π<<，所以sin 0B ≠，sin cos()6A A π=+，化简得1sin sin 2A A A =-，即tan A =，因为0A π<<，所以6A π=.又因为2222cos6a b c bc π=+-，所以2222bc =，即24bc =-所以111sin (246222ABC S bc A ∆==⨯-⨯=- 若选③：由正弦定理得sin sinsin sin 2B CB A B +=， 因为0B π<<，所以sin 0B ≠， 所以sin sin 2B CA +=，又因为BC A +=π-， 所以cos2sin cos 222A A A =， 因为0A π<<，022A π<<，所以cos 02A≠， 1sin22A ∴=，26A π=，所以3A π=. 又2222()3a b c bc b c bc =+-=+-，a =6bc +=，所以4bc =，所以11sin 4sin 223ABC S bc A π∆==⨯⨯= 【点睛】本题考查正弦定理与余弦定理处理三角形中的边角关系,考查三角形面积公式的应用,考查运算能力22．（1）n a n =，21n b n =+；（2）见解析【解析】 【分析】（1）由等差数列的通项公式及求和公式列1a d ，的方程组求解则n a n =可求，进而得21n b n =+（2）利用()111212111n c n n n n n n ⎛⎫=++=++- ⎪⋅++⎝⎭分组求和即可证明【详解】（1）因为数列{}n a ，{}n b 是等差数列，且23A =，53A B =，所以112351096a d a d d+=⎧⎨+=+⎩.整理得1123549a d a d +=⎧⎨+=⎩，解得111a d =⎧⎨=⎩，所以()11?n a a n d n =+-=，即n a n =，()11221n b b n d n =+-⋅=+，即21n b n =+.综上，n a n =，21n b n =+. （2）由（1）得()111212111n c n n n n n n ⎛⎫=++=++- ⎪⋅++⎝⎭，所以()11111352112231n S n n n ⎡⎤⎛⎫⎛⎫⎛⎫=++⋯+++-+-+⋯+- ⎪ ⎪ ⎪⎢⎥+⎝⎭⎝⎭⎝⎭⎣⎦， 即()()22211211111n S n n n n n n =++-=+-<+++. 【点睛】本题考查等差数列的通项公式及求和公式，裂项相消求和，考查推理计算能力，是中档题 23．（1）2020（2）29-,log 10⎛⎤∞ ⎥⎝⎦【解析】 【分析】（1）运用等差数列的通项公式可得公差d ，再由等差数列的求和公式，结合配方法和二次函数的最值求法，可得最大值；（2）由题意可得数列{b n }为首项为2，公比为2d 的等比数列，讨论d ＝0，d ＞0，d ＜0，判断数列{b n }的单调性和求和公式，及范围，结合不等式恒成立问题解法，解不等式可得所求范围． 【详解】（1）a 1＝40，a 6＝38，可得d 61255a a -==-， 可得S n ＝40n 12-n （n ﹣1）2155=-（n 2012-）2220120+，由n 为正整数，可得n ＝100或101时，S n 取得最大值2020；（2）设()*112na n ab n N ==∈，，数列{b n }的前n 项和为T n，可得a n ＝1+（n ﹣1）d ，数列{b n }为首项为2，公比为2d 的等比数列， 若d ＝0，可得b n ＝2；d ＞0，可得{b n }为递增数列，无最大值； 当d ＜0时，T n ()21221212dn dd-=--＜，对任意的n ∈N *，都有T n ≤20，可得20212d≥-，且d ＜0， 解得d ≤29log 10． 【点睛】本题考查等差数列和等比数列的通项公式和求和公式的运用，考查数列不等式恒成立问题解法，注意运用转化思想，考查化简运算能力，属于中档题． 24．（1）证明见解析；（2）． 【解析】 【分析】（1）利用三角函数恒等变换的应用化简已知等式可求in 0()s A B -=，可得()A B k k Z π-=∈，结合范围A ，(0,)B π∈，即可得证A B =．（2）由（1）可得a b =，进而根据余弦定理可求a b ==ABC ∆的周长．【详解】（1）sin tan cos sin tan cos b B C b B a A C a A -=-Q ，∴sin sin sin sin cos cos cos cos b B C a A Cb B a A C C-=-，sin sin cos cos sin sin cos cos b B C b B C a A C a A C ∴-=-， cos()cos()a A C b B C ∴+=+，又A B C π++=Q ，cos cos a B b A ∴-=-，sin cos sin cos A B B A ∴-=-， sin()0A B ∴-=，()A B k k Z π∴-=∈，又A Q ，(0,)B π∈，A B ∴=． （2）Q 由（1）可知A B =，可得a b =，又c =Q 3cos 4C =，∴2232342a a-==， 226a b ∴==，可得a b ==ABC ∆∴的周长a b c ++=【点睛】本题考查三角函数恒等变换的应用、余弦定理在解三角形中的综合应用，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力，求解时注意三角函数求值时，要先写出角的范围．25．（1）a n ＝3n ﹣1，b n ＝2n ﹣1（2）T n ＝3﹣（n +1）•（13）n ﹣1 【解析】 【分析】(1)利用基本量法求解n a ,再代入()1,n n P b b +到直线20x y -+=可得{}n b 为等差数列,再进行通项公式求解即可. (2)利用错位相减求和即可. 【详解】（1）递增等比数列{a n }的公比设为q ,前n 项和为S n ,且a 2＝3,S 3＝13, 可得a 1q ＝3,a 1+a 1q +a 1q 2＝13,解得q ＝3或q 13=, 由等比数列递增,可得q ＝3,a 1＝1,则13-=n n a ； P （b n ,b n +1）在直线x ﹣y +2＝0上,可得b n +1﹣b n ＝2, 且b 1＝a 1＝1,则b n ＝1+2（n ﹣1）＝2n ﹣1； （2）c n nn b a ==（2n ﹣1）•（13）n ﹣1, 前n 项和T n ＝1•1+3•13+5•19++L （2n ﹣1）•（13）n ﹣1, 13T n ＝1•13+3•19+5•127++L （2n ﹣1）•（13）n , 相减可得23T n ＝1+2（1139+++L （13）n ﹣1）﹣（2n ﹣1）•（13）n＝1+2•111133113n -⎛⎫- ⎪⎝⎭--（2n ﹣1）•（13）n , 化简可得T n ＝3﹣（n +1）•（13）n ﹣1.【点睛】本题主要考查了等比等差数列的通项公式求解以及错位相减的求和方法,属于中档题.26．（1）*21,n a n n N =-∈（2）存在，2,12m k ==【解析】 【分析】（1）设等差数列{}n a 的公差为d ，由等差数列的通项公式与前n 项和公式得112512238a d a d +=⎧⎨+=⎩，解得112a d =⎧⎨=⎩，从而求出21n a n =-；（2）由（1）得()2122n n n S n n -=+⨯=，由211114122121n b n n n ⎛⎫==- ⎪--+⎝⎭，利用裂项相消法得21n n T n =+，若23k m T T =，则()2232121k m k m =++，整理得223412m k m m =+-，由1k m >>得11m <<+，从而可求出答案． 【详解】解：（1）设等差数列{}n a 的公差为d ， 由2541216a a S +=⎧⎨=⎩得112512238a d a d +=⎧⎨+=⎩，解得112a d =⎧⎨=⎩，()*12121,n a n n n N ∴=+-=-∈；（2）()2122n n n S n n -=+⨯=，211114122121n b n n n ⎛⎫∴==- ⎪--+⎝⎭，1211111111111123352321212122121n n n T b b b n n n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫∴=++⋅⋅⋅+=-+-+⋅⋅⋅+-+-=-= ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥---+++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦ ，若23k m T T =，则()2232121k m k m =++，整理得223412m k m m=+-， 又1k m >>，2234121m m m m m ⎧>⎪∴+-⎨⎪>⎩，整理得222104121m m m m m ⎧-->⎪+-⎨⎪>⎩，解得112m <<+， 又*m N ∈，2m ∴=，12k ∴=， ∴存在2,12m k ==满足题意． 【点睛】本题主要考查等差数列的性质与求和，考查裂项相消法求和，属于中档题．。

2020-2021高三数学上期末试卷(带答案)(1)一、选择题1．已知数列{}n a 的前n 项和为n S ，且1142n n a -⎛⎫=+- ⎪⎝⎭，若对任意*N n ∈，都有()143n p S n ≤-≤成立，则实数p 的取值范围是（ ）A ．()2,3B ．[]2,3C ．92,2⎡⎤⎢⎥⎣⎦D ．92,2⎡⎫⎪⎢⎣⎭2．在ABC ∆中，,,a b c 分别为角,,A B C 的对边，若,1,3A b π==ABC ∆的面积为3，则a 的值为（ ） A ．2B ．3C ．3 D ．13．设,x y 满足约束条件3002x y x y x -+≥⎧⎪+≥⎨⎪≤⎩, 则3z x y =+的最小值是 A ．5-B ．4C ．3-D ．114．正项等比数列中，的等比中项为，令，则（ ） A ．6B ．16C ．32D ．645．在ABC ∆中，2AC =,22BC =135ACB ∠=o ，过C 作CD AB ⊥交AB 于D ，则CD =( ) A 25B 2C 3D 56．在ABC V 中，A ，B ，C 的对边分别为a ，b ，c ，2cos 22C a b a+=，则ABC V 的形状一定是( ) A ．直角三角形 B ．等边三角形C ．等腰三角形D ．等腰直角三角形7．若直线()10,0x ya b a b+=>>过点(1,1)，则4a b +的最小值为（ ） A ．6 B ．8 C ．9 D ．10 8．已知ABC ∆的三个内角、、A B C 所对的边为a b c 、、，面积为S ，且223tan 2S B =+，则A 等于（ ）A ．6π B ．4π C ．3π D ．2π9．已知,,a b R +∈且115a b a b+++=,则+a b 的取值范围是（ ） A ．[1,4]B ．[)2,+∞C ．(2,4)D ．(4,)+∞10．等差数列{}n a 中，已知611a a =，且公差0d >，则其前n 项和取最小值时的n 的值为( ) A ．6B ．7C ．8D ．911．在ABC ∆中，a ，b ，c 分别是角A ，B ，C 的对边，若2b c =，a =7cos 8A =，则ABC ∆的面积为（ ） AB ．3CD．212．设x y ，满足约束条件70310,350x y x y x y +-⎧⎪-+⎨⎪--⎩，，„„…则2z x y =-的最大值为（ ）.A ．10B ．8C ．3D ．2二、填空题13．在ABC ∆中，角,,A B C 所对的边为,,a b c ，若23sin c ab C =，则当b aa b+取最大值时，cos C =__________；14．已知0a >，0b >，当()214a b ab++取得最小值时，b =__________． 15．已知数列{}n a 满足：11a =，{}112,,,n n n a a a a a +-∈⋅⋅⋅()*n ∈N ，记数列{}n a 的前n 项和为n S ，若对所有满足条件的{}n a ，10S 的最大值为M 、最小值为m ，则M m +=______.16．若实数,x y 满足约束条件200220x y x y x y +≥⎧⎪-≤⎨⎪-+≥⎩，则3z x y =-的最小值等于_____．17．已知数列{}n a 满足51()1,62,6n n a n n a a n -⎧-+<⎪=⎨⎪≥⎩，若对任意*n N ∈都有1n n a a +>，则实数a 的取值范围是_________.18．设(3()lg f x x x =+，则对任意实数,a b ，“0a b +≥”是“()()0f a f b +≥”的_________条件．（填“充分不必要”.“必要不充分”.“充要”.“既不充分又不必要”之一）19．已知数列{}n a (*n ∈N )，若11a =，112nn n a a +⎛⎫+= ⎪⎝⎭，则2lim n n a →∞= ． 20．已知是数列的前项和，若，则_____．三、解答题21．设函数()112f x x =+＋|x |(x ∈R)的最小值为a . (1)求a ；(2)已知两个正数m ，n 满足m 2＋n 2＝a ，求11m n+的最小值. 22．在条件①()(sin sin )()sin a b A B c b C +-=-，②sin cos()6a Bb A π=+，③sinsin 2B Cb a B +=中任选一个，补充到下面问题中，并给出问题解答. 在ABC ∆中，角,,A B C 的对边分别为,,a bc ，6b c +=，6a =， . 求ABC ∆的面积.23．已知等差数列{}n a 的公差为()0d d ≠，等差数列{}n b 的公差为2d ，设n A ，n B 分别是数列{}n a ，{}n b 的前n 项和，且13b =，23A =，53A B =. （1）求数列{}n a ，{}n b 的通项公式； （2）设11n n n n c b a a +=+•，数列{}n c 的前n 项和为n S ，证明：2(1)n S n <+.24．已知函数()()22f x x x a x R =++∈（1）若函数()f x 的值域为[0,)+∞，求实数a 的值；（2）若()0f x >对任意的[1,)x ∈+∞成立，求实数a 的取值范围。

2020-2021高三数学上期末一模试卷及答案(5)一、选择题1．在ABC ∆中,,,a b c 分别为角,,A B C 所对的边,若 2?a bcos C =,则此三角形一定是( ) A ．等腰直角三角形 B ．直角三角形 C ．等腰三角形 D ．等腰三角形或直角三角形2．在ABC ∆中，2AC =,22BC =,135ACB ∠=o ，过C 作CD AB ⊥交AB 于D ，则CD =( ) A ．25B ．2C ．3D ．53．“干支纪年法”是中国历法上自古以来就一直使用的纪年方法，干支是天干和地支的总称，把干支顺序相配正好六十为一周，周而复始，循环记录，这就是俗称的“干支表”甲、乙、丙、丁、戊、己、庚、辛、癸等十个符号叫天干，子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥等十二个符号叫地支，如公元1984年农历为甲子年，公元1985年农历为乙丑年，公元1986年农历为丙寅年，则公元2047年农历为 A ．乙丑年B ．丙寅年C ．丁卯年D ．戊辰年4．设变量,x y 、满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩，则目标函数2z x y =+的最大值为（ ）A ．2B ．3C ．4D ．95．我国的《洛书》中记载着世界上最古老的一个幻方：将1，2，...，9填入33⨯的方格内，使三行、三列、两对角线的三个数之和都等于15 (如图）.一般地，将连续的正整数1，2，3，…，2n 填入n n ⨯的方格内，使得每行、每列、每条对角线上的数的和相等，这个正方形就叫做n 阶幻方.记n 阶幻方的一条对角线上数的和为n N (如：在3阶幻方中，315N =)，则10N =（ ）A ．1020B ．1010C ．510D ．5056．已知,,a b R +∈且115a b a b+++=,则+a b 的取值范围是（ ） A ．[1,4]B ．[)2,+∞C ．(2,4)D ．(4,)+∞7．设,x y 满足约束条件0,20,240,x y x y x y -≥⎧⎪+-≥⎨⎪--≤⎩则2z x y =+的最大值为（ ）A ．2B ．3C ．12D ．138．已知等比数列{}n a 的各项均为正数，前n 项和为n S ，若26442,S 6a S a =-=，则5a = A ．4B ．10C ．16D ．329．已知数列{}n a 的前n 项和为n S ，点(,3)n n S +*()n N ∈在函数32x y =⨯的图象上，等比数列{}n b 满足1n n n b b a ++=*()n N ∈，其前n 项和为n T ，则下列结论正确的是（ ）A ．2n n S T =B ．21n n T b =+C ．n n T a >D ．1n n T b +<10．在ABC ∆中，a ，b ，c 分别是角A ，B ，C 的对边，若2b c =，a =7cos 8A =，则ABC ∆的面积为（ ） AB ．3CD11．设x y ，满足约束条件70310,350x y x y x y +-⎧⎪-+⎨⎪--⎩，，„„…则2z x y =-的最大值为（ ）.A ．10B ．8C ．3D ．212．在直角梯形ABCD 中，//AB CD ，90ABC ∠=o ，22AB BC CD ==，则cos DAC ∠=（ ）ABCD．10二、填空题13．△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若acosB ＝5bcosA ，asinA ﹣bsinB ＝2sinC ，则边c 的值为_______． 14．观察下列的数表： 2 4 68 10 12 1416 18 20 22 24 26 28 30 …… ……设2018是该数表第m 行第n 列的数，则m n ⋅=__________． 15．在钝角ABC V中，已知1AB AC ==，若ABC V的面积为2BC 的长为______．16．若变量,x y满足约束条件{241yx yx y≤+≥-≤，则3z x y=+的最小值为_____．17．设122012(1)(1)(1)n nnx x x a a x a x a x++++++=++++L L，其中n*∈N，且2n≥，若0121022na a a a++++=L，则n=_____18．数列{}n a满足：1a a=（a R∈且为常数），()()()*13343n nnn na aa n Na a+⎧->⎪=∈⎨-≤⎪⎩，当100a=时，则数列{}n a的前100项的和100S为________.19．若log41,ab=-则+a b的最小值为_________.20．设正项数列{}n a的前n项和是n S，若{}n a和{}n S都是等差数列，且公差相等，则1a＝_______．三、解答题21．已知数列中，，.（1）求证：是等比数列，并求的通项公式；（2）数列满足，求数列的前项和.22．设的内角的对边分别为已知．（1）求角；（2）若，，求的面积．23．己知数列的前n项和为，且．（1）求数列的通项公式；（2）设，求数列的前n项和．24．如图，在四边形ABCD中，7,2,AC CD AD==2.3ADCπ∠=（1）求CAD∠的正弦值；（2）若2BAC CAD∠=∠，且△ABC的面积是△ACD面积的4倍，求AB的长. 25．在ABC∆中，内角,,A B C的对边分别为,,a b c，设平面向量()()sin cos ,sin ,cos sin ,sin p A B A q B A B =+=-v v ，且2cos p q C ⋅=v v（Ⅰ）求C ；（Ⅱ）若c a b =+=ABC ∆中边上的高h .26．在△ABC 中，角A B C 、、的对边分别为a b c 、、，已知3cos()16cos cos B C B C --=，（1）求cos A （2）若3a =，△ABC 的面积为求b c 、【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【解析】在ABC ∆中，222222cos ,2cos 222a b c a b c C a b C b ab abQ +-+-=∴==⋅，2222a a b c ∴=+-，,b c ∴=∴此三角形一定是等腰三角形，故选C.【方法点睛】本题主要考查利用余弦定理判断三角形形状，属于中档题.判断三角形状的常见方法是：（1）通过正弦定理和余弦定理，化边为角，利用三角变换得出三角形内角之间的关系进行判断；(2)利用正弦定理、余弦定理，化角为边，通过代数恒等变换，求出边与边之间的关系进行判断；（3）根据余弦定理确定一个内角为钝角进而知其为钝角三角形.2．A解析：A 【解析】 【分析】先由余弦定理得到AB 边的长度，再由等面积法可得到结果. 【详解】根据余弦定理得到22222AC BC AB AC BC +-=-⨯⨯将2AC =,BC =,代入等式得到AB=再由等面积法得到11222CD CD ⨯=⨯⇒=故答案为A. 【点睛】这个题目考查了解三角形的应用问题，涉及正余弦定理，面积公式的应用，在解与三角形有关的问题时，正弦定理、余弦定理是两个主要依据.解三角形时，有时可用正弦定理，有时也可用余弦定理，应注意用哪一个定理更方便、简捷一般来说 ,当条件中同时出现ab 及2b 、2a 时，往往用余弦定理，而题设中如果边和正弦、余弦函数交叉出现时，往往运用正弦定理将边化为正弦函数再结合和、差、倍角的正余弦公式进行解答.3．C解析：C 【解析】记公元1984年为第一年，公元2047年为第64年，即天干循环了十次，第四个为“丁”，地支循环了五次，第四个为“卯”,所以公元2047年农历为丁卯年. 故选C.4．D解析：D 【解析】 【分析】由约束条件作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，把最优解的坐标代入目标函数得结论. 【详解】画出满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩的可行域，如图，画出可行域ABC ∆，(2,0)A ，(1,1)B ，(3,3)C ， 平移直线2z x y =+，由图可知，直线2z x y =+经过(3,3)C 时 目标函数2z x y =+有最大值，2z x y =+的最大值为9.故选D.【点睛】本题主要考查线性规划中，利用可行域求目标函数的最值，属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值.5．D解析：D 【解析】n 阶幻方共有2n 个数，其和为()222112...,2n n n n ++++=Q 阶幻方共有n 行，∴每行的和为()()2221122n n n n n++=，即()()2210110101,50522n n n N N+⨯+=∴==，故选D.6．A解析：A 【解析】分析：,a b R +∈，由22a b ab +⎛⎫≥ ⎪⎝⎭，可得()214ab a b ≥+，又115a b a b +++=，可得()()()214151a b a b ab a b ⎛⎫⎛⎫ ⎪++=≥++ ⎪ ⎪⎝⎭+⎝⎭，化简整理即可得出. 详解：,a b R +∈，由22a b ab +⎛⎫≥ ⎪⎝⎭，可得()214ab a b ≥+，又115a b a b+++=， 可得()()()214151a b a b ab a b ⎛⎫⎛⎫ ⎪++=≥++ ⎪ ⎪⎝⎭+⎝⎭， 化为()()2540a b a b +-++≤， 解得14a b ≤+≤， 则+a b 的取值范围是[]1,4. 故选：A.点睛：本题考查了基本不等式的性质、一元二次不等式的解法，考查了推理能力与计算能力，属于中档题.7．C解析：C 【解析】 【分析】由约束条件可得可行域，将问题变成1122y x z =-+在y 轴截距最大问题的求解；通过平移直线可确定最大值取得的点，代入可得结果. 【详解】由约束条件可得可行域如下图所示：当2z x y =+取最大值时，1122y x z =-+在y 轴截距最大 平移直线12y x =-，可知当直线1122y x z =-+过图中A 点时，在y 轴截距最大由240y xx y =⎧⎨--=⎩得：()4,4A max 42412z ∴=+⨯=故选：C 【点睛】本题考查线性规划中最值问题的求解，关键是能够将问题转化为直线在y 轴截距最值问题的求解，属于常考题型.8．C解析：C 【解析】由64S S -=6546a a a +=得，()22460,60q q a q q +-=+-=，解得2q =，从而3522=28=16a a =⋅⨯，故选C.9．D解析：D 【解析】 【分析】 【详解】由题意可得：332,323n nn n S S +=⨯=⨯- ，由等比数列前n 项和的特点可得数列{}n a 是首项为3，公比为2的等比数列，数列的通项公式：132n n a -=⨯ ，设11n nb b q -= ，则：111132n n n b q b q --+=⨯ ，解得：11,2b q == ，数列{}n b 的通项公式12n nb -= ，由等比数列求和公式有：21nn T =- ，考查所给的选项：13,21,,n n n n n n n n S T T b T a T b +==-<< .本题选择D 选项.10．D解析：D 【解析】 【分析】三角形的面积公式为1sin 2ABC S bc A ∆=，故需要求出边b 与c ，由余弦定理可以解得b 与c . 【详解】解：在ABC ∆中，2227cos 28b c a A bc +-==将2b c =，a =22246748c c c +-=， 解得：2c =由7cos 8A =得sin 8A ==所以，11sin 2422ABC S bc A ∆==⨯⨯=故选D. 【点睛】三角形的面积公式常见形式有两种：一是12（底⨯高），二是1sin 2bc A .借助12（底⨯高）时，需要将斜三角形的高与相应的底求出来；借助1sin 2bc A 时，需要求出三角形两边及其夹角的正弦值.11．B解析：B 【解析】 【分析】作出可行域，化目标函数为直线方程的斜截式，数形结合得到最优解，联立方程组求得最优解的坐标，代入目标函数即可求解. 【详解】 作出可行域如图：化目标函数为2y x z =-，联立70310x y x y +-=⎧⎨-+=⎩，解得5,2A（）. 由图象可知，当直线过点A 时，直线在y 轴上截距最小，z 有最大值25-28⨯=. 【点睛】本题主要考查了简单的线性规划，数形结合的思想，属于中档题.12．C解析：C 【解析】 【分析】设1BC CD ==，计算出ACD ∆的三条边长，然后利用余弦定理计算出cos DAC ∠． 【详解】如下图所示，不妨设1BC CD ==，则2AB =，过点D 作DE AB ⊥，垂足为点D ， 易知四边形BCDE 是正方形，则1BE CD ==，1AE AB BE ∴=-=， 在Rt ADE ∆中，222AD AE DE =+=，同理可得225AC AB BC =+=，在ACD ∆中，由余弦定理得2222310cos 2252AC AD CD DAC AC AD +-∠===⋅⨯⨯， 故选C ．【点睛】本题考查余弦定理求角，在利用余弦定理求角时，首先应将三角形的边长求出来，结合余弦定理来求角，考查计算能力，属于中等题．二、填空题13．3【解析】【分析】由acosB ＝5bcosA 得由asinA ﹣bsinB ＝2sinC 得解方程得解【详解】由acosB ＝5bcosA 得由asinA ﹣bsinB ＝2sinC 得所以故答案：3【点睛】本题主要解析：3 【解析】 【分析】由acosB ＝5bcosA 得22223a b c -=，由asinA ﹣bsinB ＝2sinC 得222a b c -=，解方程得解. 【详解】由acosB ＝5bcosA 得22222222225,223a cb bc a a b a b c ac bc +-+-⋅=⋅∴-=.由asinA ﹣bsinB ＝2sinC 得222a b c -=，所以222,33c c c =∴=. 故答案：3 【点睛】本题主要考查正弦定理和余弦定理解三角形，意在考查学生对这些知识的理解掌握水平和分析推理能力.14．4980【解析】【分析】表中第行共有个数字此行数字构成以为首项以2为公差的等差数列根据等差数列求和公式及通项公式确定求解【详解】解：表中第行共有个数字此行数字构成以为首项以2为公差的等差数列排完第行解析：4980 【解析】 【分析】表中第n 行共有12n -个数字，此行数字构成以2n 为首项，以2为公差的等差数列．根据等差数列求和公式及通项公式确定求解. 【详解】解：表中第n 行共有12n -个数字，此行数字构成以2n 为首项，以2为公差的等差数列．排完第k 行，共用去1124221k k -+++⋯+=-个数字， 2018是该表的第1009个数字， 由19021100921-<<-，所以2018应排在第10行，此时前9行用去了921511-=个数字， 由1009511498-=可知排在第10行的第498个位置， 即104984980m n =⨯=g， 故答案为：4980 【点睛】此题考查了等比数列求和公式，考查学生分析数据，总结、归纳数据规律的能力，关键是找出规律，要求学生要有一定的解题技巧．15．【解析】【分析】利用面积公式可求得再用余弦定理求解即可【详解】由题意得又钝角当为锐角时则即不满足钝角三角形故为钝角此时故即故答案为：【点睛】本题主要考查了解三角形中面积公式与余弦定理的运用属于中等题 解析：10 【解析】 【分析】 利用面积公式可求得A ,再用余弦定理求解BC 即可. 【详解】由题意得, 61671sin sin 27A A =⨯⨯⨯⇒=. 又钝角ABC V ,当A 为锐角时,261cos 177A ⎛⎫=-= ⎪ ⎪⎝⎭,则21712777BC =+-⨯=,即7BC =不满足钝角三角形.故A 为钝角.此时261cos 177A ⎛⎫=--=- ⎪ ⎪⎝⎭.故217127107BC =++⨯=. 即10BC =故答案为：10【点睛】本题主要考查了解三角形中面积公式与余弦定理的运用,属于中等题型.16．8【解析】【分析】【详解】作出不等式组表示的平面区域得到如图的△ABC 及其内部其中A （22）B （）C （32）设z=F （xy ）=3x+y 将直线l ：z=3x+y 进行平移当l 经过点A （22）时目标函数z 达解析：8【解析】【分析】【详解】作出不等式组表示的平面区域，得到如图的△ABC 及其内部，其中A （2，2），B （53,22）,C （3，2）设z =F （x ，y ）=3x +y ，将直线l ：z =3x +y 进行平移，当l 经过点A （2，2）时，目标函数z 达到最小值∴z 最小值=F （2，2）=8故选：C17．9【解析】【分析】记函数利用等比数列求和公式即可求解【详解】由题：记函数即故答案为：9【点睛】此题考查多项式系数之和问题常用赋值法整体代入求解体现出转化与化归思想解析：9【解析】【分析】记函数122012()(1)(1)(1)n n n f x x x x a a x a x a x =++++++=++++L L ，012222(1)2n n f a a a a =+++=++++L L ，利用等比数列求和公式即可求解.【详解】由题：记函数212012()(1)(1)(1)n n n f x a a x a x a x x x x =++++=++++++L L ，021222(12)(21)212n nn f a a a a -=++++++=-=+L L ， 即1221022n +-=，121024,9n n +==故答案为：9【点睛】 此题考查多项式系数之和问题，常用赋值法整体代入求解，体现出转化与化归思想. 18．【解析】【分析】直接利用分组法和分类讨论思想求出数列的和【详解】数列满足：（且为常数）当时则所以（常数）故所以数列的前项为首项为公差为的等差数列从项开始由于所以奇数项为偶数项为所以故答案为：【点睛】 解析：1849【解析】【分析】直接利用分组法和分类讨论思想求出数列的和.【详解】数列{}n a 满足：1a a =（a R ∈且为常数），()()()*13343n n n n n a a a n N a a +⎧->⎪=∈⎨-≤⎪⎩， 当100a =时，则1100a =，所以13n n a a +-=-（常数），故()10031n a n =--，所以数列的前34项为首项为100，公差为3-的等差数列.从35项开始，由于341a =，所以奇数项为3、偶数项为1，所以()()1001001346631184922S +⨯=+⨯+=，故答案为：1849【点睛】本题考查了由递推关系式求数列的性质、等差数列的前n 项和公式，需熟记公式，同时也考查了分类讨论的思想，属于中档题.19．1【解析】试题分析：由得所以（当且仅当即时等号成立）所以答案应填1考点：1对数的运算性质；2基本不等式解析：1【解析】试题分析：由log 41,a b =-得104a b =>，所以114a b b b +=+≥=（当且仅当14b b =即12b =时，等号成立） 所以答案应填1.考点：1、对数的运算性质；2、基本不等式.20．【解析】分析：设公差为d 首项利用等差中项的性质通过两次平方运算即可求得答案详解：设公差为d 首项和都是等差数列且公差相等即两边同时平方得：两边再平方得：又两数列公差相等即解得：或为正项数列故答案为：点 解析：14【解析】分析：设公差为d ，首项1a ，利用等差中项的性质，通过两次平方运算即可求得答案. 详解：设公差为d ，首项1a ，Q {}n a 和都是等差数列，且公差相等，∴=，即=，两边同时平方得：()1114233a d a a d +=+++14a d +=两边再平方得：()221111168433a a d d a a d ++=+， ∴2211440a a d d -+=，12d a =，又两数列公差相等，2112a a d a =-==，即1111222a a a a +-=，解得：114a =或10a =， Q {}n a 为正项数列， ∴114a =. 故答案为：14. 点睛：本题考查等差数列的性质，考查等差中项的性质，考查化归与方程思想.三、解答题21．(1)答案见解析；(2) .【解析】试题分析：⑴根据数列的递推关系，结合等比数列的定义即可证明是等比数列，并求的通项公式，⑵利用错位相减法即可求得答案； 解析：（1）∵∴∴， ∵，， ∴是以为首项，以4为公比的等比数列 ∴， ∴， ∴， （2），∴①②①-②得∴.22．（1）（2）【解析】【分析】（1）直接利用正弦定理和三角函数关系式的恒等变换求出结果．（2）利用（1）的结论，余弦定理及三角形的面积公式求出结果．【详解】（1）∵b=a（cosC﹣sinC），∴由正弦定理得sinB=sinAcosC﹣sinAsinC，可得sin（A+C）=sinAcosC+cosAsinC=sinAcosC﹣sinAsinC，∴cosAsinC=﹣sinAsinC，由sinC≠0，得sinA+cosA=0，∴tanA=﹣1，由A为三角形内角，可得．（2）因为，所以由正弦定理可得b=c，因为a2=b2+c2﹣2bccosA，，可得c=，所以b=2，所以．【点睛】本题考查的知识要点：三角函数关系式的恒等变换，正弦定理和余弦定理的应用，三角形面积公式的应用．23．（1）；（2） 【解析】【分析】（1）运用，证明数列是等比数列，计算通项，即可。