计算机仿真实验报告
- 格式:doc
- 大小:418.00 KB
- 文档页数:22
基于Simulink 控制系统仿真与综合设计一、实验目的(1) 熟悉Simulink 的工作环境及其功能模块库; (2) 掌握Simulink 的系统建模和仿真方法; (3) 掌握Simulink 仿真数据的输出方法与数据处理;(4) 掌握利用Simulink 进行控制系统的时域仿真分析与综合设计方法; (5) 掌握利用 Simulink 对控制系统的时域与频域性能指标分析方法。
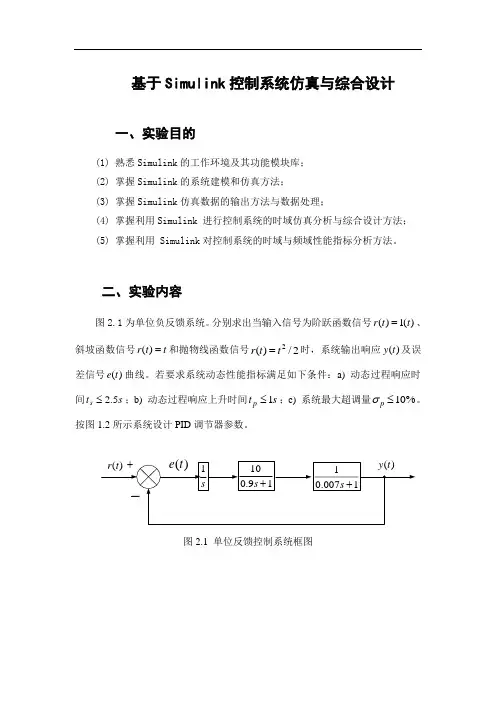
二、实验内容图2.1为单位负反馈系统。
分别求出当输入信号为阶跃函数信号)(1)(t t r =、斜坡函数信号t t r =)(和抛物线函数信号2/)(2t t r =时,系统输出响应)(t y 及误差信号)(t e 曲线。
若要求系统动态性能指标满足如下条件:a) 动态过程响应时间s t s 5.2≤;b) 动态过程响应上升时间s t p 1≤;c) 系统最大超调量%10≤p σ。
按图1.2所示系统设计PID 调节器参数。
图2.1 单位反馈控制系统框图图2.2 综合设计控制系统框图三、实验要求(1) 采用Simulink系统建模与系统仿真方法,完成仿真实验;(2) 利用Simulink中的Scope模块观察仿真结果,并从中分析系统时域性能指标(系统阶跃响应过渡过程时间,系统响应上升时间,系统响应振荡次数,系统最大超调量和系统稳态误差);(3) 利用Simulink中Signal Constraint模块对图2.2系统的PID参数进行综合设计,以确定其参数;(4) 对系统综合设计前后的主要性能指标进行对比分析,并给出PID参数的改变对闭环系统性能指标的影响。
四、实验步骤与方法4.1时域仿真分析实验步骤与方法在Simulink仿真环境中,打开simulink库,找出相应的单元部件模型,并拖至打开的模型窗口中,构造自己需要的仿真模型。
根据图2.1 所示的单位反馈控制系统框图建立其仿真模型,并对各个单元部件模型的参数进行设定。
所做出的仿真电路图如图4.1.1所示。

一、实验内容:实验三 利用欧拉法、梯形数法和二阶显式Adams 法对RLC 串联电路的仿真1前向欧拉法状态方程:Du CX y Bu AX X m +=+=+•1 然后根据前向欧拉法(其中h 为步长)•++=m m m hX X X 1即可得到系统的差分方程2后向欧拉法根据前向欧拉法得到的系统状态方程,结合后向欧拉法(其中h 为步长)•+++=11m m m hX X X 即可得到系统的差分方程3梯形法由前面的系统状态方程,结合梯形法)(211+••+++=m m m m X X h X X 即可得到系统的差分方程4二阶显式Adams 方法由前面的状态方程,结合二阶显式Adams 方法)51623(12211--++-+=m m m m m F F F h X X 即可得到系统的差分方程但是二阶显式Adams 法不能自起步,要使方程起步,需要知道开始的三个值,但是我们只知道第一个值。
经过分析后,二阶显式Adams 方法精度是二阶的,而梯形法精度也是二阶的,因此我们可以先借助梯形法得到输出的前三个值,以达到起步的目的,然后借助上面得到的差分方程对其进行求解。
二、实验波形:下图为前向欧拉法、后向欧拉法、梯形法、二阶显式Adams 方法的系统差分方程得到相应的输出波形:图1 h=410 时四种方法的输出波形图2 h=56-⨯时四种方法的输出波形10图3 h=510-时四种方法的输出波形图4 h=610-时四种方法的输出波形三、实验分析:由输出波形可以看到各种方法的特点(在图中蓝色线均表示连续系统模型的实际输出波形,红色线表示在对应方法下系统的输出波形。
):1前向欧拉法和二阶显式Adams方法对步长的要求很强。
步长太大,最后的到的结果不是绝对收敛,而是发散。
在小步长下才显得收敛,这也从另一方面验证,步长越小,截断误差越小;2步长不能太小,太小的步长相应的舍入误差和累积误差也会增大;3前向欧拉法也可称为显式欧拉法,后向欧拉法也可称为隐式欧拉法,可以看到,后向欧拉法的稳定域要比前向欧拉法大,计算精度也要高一些。

第1篇一、实验背景与目的随着现代科技的发展,虚拟仿真技术在各个领域得到了广泛应用。
它能够在计算机上模拟真实环境,降低实验成本,提高实验效率。
本实验旨在通过虚拟仿真软件搭建一个简单的电路系统,验证其基本功能,并探讨虚拟仿真在实验教学中的应用。
二、实验器材与软件1. 实验器材:- 电脑一台- 虚拟仿真软件(如Multisim、LTspice等)2. 实验软件:- 选择Multisim软件进行虚拟仿真实验三、实验步骤1. 软件安装与启动:- 在电脑上安装Multisim软件- 启动Multisim软件2. 搭建电路:- 打开Multisim软件,选择“原理图”模块- 从元件库中选取所需的元件,如电阻、电容、二极管、晶体管等- 使用导线连接元件,搭建所需电路3. 设置参数:- 设置电源电压、元件参数等- 设置仿真时间、步进等参数4. 仿真实验:- 点击仿真按钮,观察电路的仿真结果- 分析仿真结果,与理论计算进行对比5. 结果分析:- 对仿真结果进行详细分析,总结实验现象- 分析实验误差,探讨改进措施6. 实验报告撰写:- 按照实验报告格式,撰写实验报告四、实验结果与分析1. 电路搭建:- 搭建了一个由电阻、电容、二极管组成的简单电路- 电路包括一个整流电路和一个滤波电路2. 仿真结果:- 仿真结果显示,电路能够正常工作- 整流电路将交流电源转换为直流电源- 滤波电路对直流电源进行滤波,输出稳定的电压3. 结果分析:- 仿真结果与理论计算基本一致- 电路搭建过程中,元件选择和参数设置合理- 仿真软件在电路搭建和仿真实验中发挥了重要作用五、实验讨论1. 虚拟仿真在实验教学中的应用:- 虚拟仿真技术能够降低实验成本,提高实验效率- 在虚拟仿真环境中,学生可以自由搭建电路,进行实验操作 - 虚拟仿真有助于提高学生的动手能力和创新意识2. 实验误差分析:- 仿真软件的精度对实验结果有一定影响- 元件参数的误差也可能导致实验误差- 实验过程中,应尽量减少误差,提高实验精度3. 改进措施:- 提高仿真软件的精度,降低实验误差- 优化元件参数选择,提高电路性能- 加强实验操作规范,提高实验效果六、结论本实验通过虚拟仿真搭建了一个简单的电路系统,验证了其基本功能。

第1篇实验名称:仿真程序开发与应用实验时间:2023年X月X日实验地点:计算机实验室实验人员:XXX、XXX、XXX一、实验目的1. 熟悉仿真程序开发的基本流程和常用工具。
2. 学习使用仿真软件进行系统建模、仿真实验和分析。
3. 提高编程能力和解决实际问题的能力。
二、实验内容1. 仿真软件的选择与安装2. 系统建模与仿真3. 仿真实验与分析4. 仿真结果可视化与报告撰写三、实验步骤1. 仿真软件的选择与安装(1)根据实验要求,选择合适的仿真软件,如MATLAB、Simulink等。
(2)下载并安装仿真软件,确保软件版本与实验要求相符。
2. 系统建模与仿真(1)根据实验题目要求,确定仿真系统的组成和功能。
(2)在仿真软件中建立系统模型,包括输入、输出、中间变量等。
(3)设置仿真参数,如仿真时间、初始条件等。
(4)进行仿真实验,观察系统性能。
3. 仿真实验与分析(1)对仿真实验结果进行分析,包括性能指标、稳定性、可靠性等。
(2)根据分析结果,对系统模型进行优化和改进。
4. 仿真结果可视化与报告撰写(1)将仿真结果以图表、曲线等形式进行可视化展示。
(2)根据实验内容和结果,撰写实验报告,包括实验目的、步骤、结果和分析等内容。
四、实验结果与分析1. 仿真软件的选择与安装实验中选择了MATLAB仿真软件,该软件具有强大的仿真功能和丰富的工具箱,能够满足本次实验的要求。
2. 系统建模与仿真根据实验题目要求,建立了系统模型,并进行了仿真实验。
实验结果显示,系统性能符合预期,稳定性较好。
3. 仿真实验与分析通过对仿真实验结果的分析,发现以下问题:(1)系统在某些条件下存在波动,需要进一步优化。
(2)系统响应速度较慢,需要提高系统性能。
4. 仿真结果可视化与报告撰写将仿真结果以图表、曲线等形式进行可视化展示,并撰写实验报告,详细描述实验目的、步骤、结果和分析等内容。
五、实验总结本次仿真程序开发实验,使我们对仿真软件的使用和系统建模有了更深入的了解。


第1篇一、实验背景随着计算机技术的飞速发展,仿真技术在各个领域得到了广泛应用。
仿真模型实验作为科学研究的重要手段,能够有效模拟复杂系统的运行过程,为理论研究和工程设计提供有力支持。
本报告总结了近期参与的仿真模型实验,旨在总结实验过程、分析实验结果,并对实验方法进行评价。
二、实验内容本次实验涉及多个领域,主要包括以下三个方面:1. 电力系统仿真实验:通过PSCAD软件搭建电力系统仿真模型,分析发电机在三相对称短路故障下的暂态响应。
2. 高速数字系统设计与实践仿真实验:设计并优化一个满足特定要求的微带线结构,分析其在不同频率下的传输特性。
3. 计算机组成原理仿真实验:使用Proteus仿真软件,验证寄存器的存储功能。
三、实验过程1. 电力系统仿真实验:- 搭建仿真模型:在PSCAD软件中,根据实验要求搭建包含发电机、变压器、负荷和故障装置的电力系统仿真模型。
- 设置参数:根据实验要求,设置发电机的参数、变压器的参数、负荷的参数以及故障装置的参数。
- 运行仿真:启动仿真,观察短路故障发生时的电压、电流等暂态响应。
2. 高速数字系统设计与实践仿真实验:- 确定阻抗:根据设计要求,确定微带线的阻抗,作为设计基准。
- 优化参数:在满足阻抗要求的前提下,优化信号导体宽度、导体间距和介质厚度等参数,以满足插入损耗、远端串扰和近端串扰等设计指标。
- 运行仿真:根据优化后的参数,运行仿真,分析微带线在不同频率下的传输特性。
3. 计算机组成原理仿真实验:- 连接电路:根据电路图,在Proteus软件中搭建实验电路,包括寄存器、三态门、发光二极管等元件。
- 设置参数:根据实验要求,设置寄存器的参数,以及控制信号的参数。
- 运行仿真:启动仿真,观察寄存器的存储功能是否正常。
四、实验结果与分析1. 电力系统仿真实验:- 短路故障发生时,短路电流和励磁电流迅速增大,随后逐渐衰减。
- 考虑阻尼绕组时,短路电流衰减速度较快,说明阻尼绕组能够有效抑制短路电流。

第1篇实验名称:仿真软件操作实验实验目的:1. 熟悉仿真软件的基本操作和界面布局。
2. 掌握仿真软件的基本功能,如建模、仿真、分析等。
3. 学会使用仿真软件解决实际问题。
实验时间:2023年X月X日实验地点:计算机实验室实验器材:1. 仿真软件:XXX2. 计算机一台3. 实验指导书实验内容:一、仿真软件基本操作1. 打开软件,熟悉界面布局。
2. 学习软件菜单栏、工具栏、状态栏等各个部分的功能。
3. 掌握文件操作,如新建、打开、保存、关闭等。
4. 熟悉软件的基本参数设置。
二、建模操作1. 学习如何创建仿真模型,包括实体、连接器、传感器等。
2. 掌握模型的修改、删除、复制等操作。
3. 学会使用软件提供的建模工具,如拉伸、旋转、镜像等。
三、仿真操作1. 设置仿真参数,如时间、步长、迭代次数等。
2. 学习如何进行仿真,包括启动、暂停、继续、终止等操作。
3. 观察仿真结果,包括数据、曲线、图表等。
四、分析操作1. 学习如何对仿真结果进行分析,包括数据统计、曲线拟合、图表绘制等。
2. 掌握仿真软件提供的分析工具,如方差分析、回归分析等。
3. 将仿真结果与实际数据或理论进行对比,验证仿真模型的准确性。
实验步骤:1. 打开仿真软件,创建一个新项目。
2. 在建模界面,根据实验需求创建仿真模型。
3. 设置仿真参数,启动仿真。
4. 观察仿真结果,进行数据分析。
5. 将仿真结果与实际数据或理论进行对比,验证仿真模型的准确性。
6. 完成实验报告。
实验结果与分析:1. 通过本次实验,掌握了仿真软件的基本操作,包括建模、仿真、分析等。
2. 在建模过程中,学会了创建实体、连接器、传感器等,并能够进行模型的修改、删除、复制等操作。
3. 在仿真过程中,成功设置了仿真参数,启动了仿真,并观察到了仿真结果。
4. 在分析过程中,运用了仿真软件提供的分析工具,对仿真结果进行了数据分析,并与实际数据或理论进行了对比,验证了仿真模型的准确性。

《计算机仿真技术》实验报告实验一 数字仿真方法验证一、实验目的1.掌握基于数值积分法的系统仿真、了解各仿真参数的影响; 2.掌握基于离散相似法的系统仿真、了解各仿真参数的影响; 3.掌握SIMULINK 动态仿真;4.熟悉MATLAB 语言及应用环境。
二、实验环境网络计算机系统,MATLAB 语言环境三、实验内容、要求(一)试将示例1的问题改为调用ode45函数求解,并比较结果。
示例1:设方程如下,取步长 h =0.1。
上机用如下程序可求出数值解。
调用ode45函数求解: 1)建立一阶微分方程组 du=u-2*t/u2)建立描述微分方程组的函数m 文件 function du=sy11vdp(t,u) du=u-2*t/u3)调用解题器指令ode45求解y[t,u]=ode45('sy11vdp',[0 1],1) plot(t,u,'r-'); xlabel('t'); ylabel('u'); 结果对比:euler 法:t=1,u=1.7848; RK 法:t=1,u=1.7321; ode45求解:t=1,u=1.7321;[]1,01)0(2∈⎪⎩⎪⎨⎧=-=t u u t u dt duode45求解t-u 图:00.10.20.30.40.50.60.70.80.9111.11.21.31.41.51.61.71.8tu(二)试用四阶RK 法编程求解下列微分方程初值问题。
仿真时间2s ,取步长h=0.1。
⎪⎩⎪⎨⎧=-=1)0(2y t y dt dy 四阶RK 法程序:clear t=2; h=0.1; n=t/h; t0=0; y0=1;y(1)=y0; t(1)=t0;for i=0:n-1 k1=y0-t0^2;k2=(y0+h*k1/2)-(t0+h/2)^2; k3=(y0+h*k2/2)-(t0+h/2)^2 k4=(y0+h*k3)-(t0+h)^2;y1=y0+h*(k1+2*k2+2*k3+k4)/6; t1=t0+h; y0=y1; t0=t1;y(i+2)=y1; t(i+2)=t1;end y tplot(t,y,'r'); 结果:t=2,y=2.61090.511.522.511.21.41.61.822.22.42.62.83:(三)试求示例3分别在周期为5s 的方波信号和脉冲信号下的响应,仿真时间20s ,采样周期Ts=0.1。

计算机仿真技术实验报告今天我要给大家讲一讲我做的计算机仿真技术实验。
这个实验可有趣啦,就像玩一场超级神奇的游戏。
我做这个实验的目的呢,就是想看看计算机怎么能像变魔术一样模拟出真实的东西。
我用到的工具就是学校电脑室里的电脑,那电脑的屏幕大大的,闪着光,好像在等着我去探索它的秘密。
实验开始的时候,我打开了一个专门做仿真的软件。
这个软件的界面花花绿绿的,有好多小图标。
我点了一个看起来像小房子的图标,屏幕上就出现了一个简单的小房子模型。
这个小房子就像我们用积木搭起来的一样,方方正正的,还有个三角形的屋顶。
我可以用鼠标拖着它转来转去,从各个角度看这个小房子,就像我真的围着小房子在走一样。
然后呢,我想让这个小房子变得更像真的。
我就在软件里找到了一个可以给小房子加颜色的功能。
我给房子的墙涂成了白色,就像我们家的房子一样。
屋顶呢,我涂成了红色,就像圣诞老人的帽子。
这时候的小房子看起来漂亮多了,就像从童话里走出来的一样。
接着,我又想给小房子周围加点东西。
我就在软件里找啊找,发现了可以加树的工具。
我在小房子前面加了几棵大树,那些大树有粗粗的树干和绿绿的树叶。
我还在树下加了一些小花,五颜六色的小花在风中好像还会轻轻晃动呢。
现在小房子看起来就像是住在森林里的小木屋,感觉特别温馨。
在这个实验里,我还发现了一些特别有趣的事情。
比如说,我可以让太阳在小房子的上空移动。
当太阳慢慢升起的时候,阳光洒在小房子和树上,小房子和树的影子就会慢慢变短。
当太阳慢慢落下的时候,影子又会变长。
这就像我们在外面玩的时候,早上和傍晚影子长长的,中午影子短短的一样。
我还能让天空中的云动起来。
我加了一些白白的云,那些云就像棉花糖一样。
我让风一吹,云就慢慢地飘走了,有的云还会变成各种形状,像小兔子,像小绵羊。
这个计算机仿真技术实验真的太好玩了。
它就像一个魔法世界,我可以在这个世界里创造出我想要的东西。
通过这个实验,我也明白了计算机好厉害呀,它能做出这么像真的东西。

计算机仿真技术实验报告1. 引言计算机仿真技术是一种基于计算机模型的虚拟实验手段,通过对真实系统的建模和仿真运行,可以模拟系统在不同条件下的行为和性能,从而实现系统优化、预测和决策支持等目的。
本实验旨在通过一个简单的例子,介绍计算机仿真技术的基本原理和应用。
2. 实验目的掌握计算机仿真技术的基本原理和方法,通过实际操作了解模型建立、参数设置和结果分析等相关内容。
3. 实验过程3.1 模型建立选择一个适合的仿真软件,如Arena、Simulink等,并根据实际需要,在软件中建立相应的仿真模型。
模型的建立包括确定系统的输入、输出、变量和参数,并定义其关系和约束条件。
3.2 参数设置为了保证仿真结果的准确性和可靠性,需要对模型中的参数进行设置。
根据实际情况,选择合适的参数值,并考虑不同参数对仿真结果的影响。
3.3 仿真运行设置好参数后,可以运行仿真程序,观察系统在不同条件下的运行情况。
可以通过改变输入、输出、变量和参数等相关参数,来模拟不同的系统行为。
3.4 结果分析根据仿真运行的结果,进行相应的数据分析和结果评估。
可以通过绘制柱状图、折线图、散点图等,直观地展示系统的性能和行为。
4. 实验结果与讨论根据实际情况,展示实验的结果,并进行相应的讨论。
可以比较不同参数下的仿真结果,分析其差异和影响因素。
在讨论时,可以考虑系统的稳定性、效率、安全性等方面。
5. 实验结论通过本次实验,我们深入了解了计算机仿真技术的基本原理和方法,并通过实际操作,掌握了模型建立、参数设置和结果分析等相关技能。
计算机仿真技术具有广泛的应用领域,包括交通运输、物流管理、生产调度、风险评估等,可以帮助我们理解和优化现实系统的运行和性能。
6. 参考文献[1] Robert, J. (2007). Simulation Modeling and Analysis. Boston: McGraw-Hill.[2] Banks, J., Carson, J., Nelson, B. L., & Nicol, D. M. (2000). Discrete-Event System Simulation. New Jersey: Prentice Hall.7. 致谢感谢实验指导教师对本次实验的支持和指导,也感谢实验中的所有参与人员的付出和帮助。

第1篇一、实验目的1. 了解仿真软件的基本操作和功能。
2. 掌握仿真建模的基本方法。
3. 通过仿真实验,加深对理论知识的理解。
4. 培养实验设计、数据分析及问题解决的能力。
二、实验背景(简要介绍仿真技术的基本概念、应用领域及实验所使用的仿真软件)三、实验设备与软件1. 实验设备:计算机、网络连接等。
2. 仿真软件:[软件名称],版本号:[版本号]。
四、实验内容1. 仿真软件的基本操作- 界面介绍:熟悉仿真软件的界面布局,包括菜单栏、工具栏、视图窗口等。
- 基本命令:学习并掌握仿真软件的基本命令,如新建项目、打开项目、保存项目等。
2. 仿真建模- 模型建立:根据实验要求,建立仿真模型,包括实体模型、参数设置等。
- 模型验证:对建立的模型进行验证,确保模型的准确性和可靠性。
3. 仿真实验- 设置仿真参数:根据实验要求,设置仿真参数,如仿真时间、步长等。
- 运行仿真:启动仿真实验,观察仿真结果。
- 结果分析:对仿真结果进行分析,与理论预期进行比较。
五、实验步骤1. 准备工作- 安装仿真软件,并进行环境配置。
- 熟悉实验要求和仿真软件的基本操作。
2. 建立仿真模型- 根据实验要求,确定仿真模型的类型和结构。
- 使用仿真软件进行模型搭建,包括添加元件、连接线路等。
3. 设置仿真参数- 根据实验要求,设置仿真参数,如仿真时间、步长等。
- 确保参数设置合理,符合实验要求。
4. 运行仿真实验- 启动仿真实验,观察仿真结果。
- 记录实验数据和关键信息。
5. 结果分析- 对仿真结果进行分析,与理论预期进行比较。
- 解释仿真结果,并探讨实验过程中的问题。
六、实验结果与分析1. 实验数据记录- [实验数据表格,包括时间、参数、结果等]2. 仿真结果分析- [对仿真结果的详细分析,包括图表、曲线等]3. 与理论预期比较- [仿真结果与理论预期的比较,分析误差原因]七、实验讨论1. 实验中遇到的问题及解决方法- [记录实验过程中遇到的问题及解决方法]2. 实验结果的启示- [总结实验结果对理论知识的启示和实际应用的意义]八、实验总结1. 实验收获- [总结实验过程中的收获,包括理论知识、操作技能等]2. 实验不足与改进建议- [分析实验过程中的不足,并提出改进建议]九、附录1. 仿真软件截图- [展示仿真软件界面、模型搭建、仿真结果等截图]2. 参考文献- [列出实验过程中参考的书籍、文章等]十、实验报告撰写说明1. 实验报告应结构完整,逻辑清晰。
计算机网络仿真实验报告一、实验目的本次计算机网络仿真实验的主要目的是深入理解计算机网络的工作原理和性能特点,通过仿真工具对网络模型进行构建和分析,观察不同参数设置对网络性能的影响,从而为实际网络的设计、优化和故障诊断提供理论依据和实践经验。
二、实验环境本次实验使用了具体仿真软件名称作为仿真工具,该软件具有强大的网络建模和性能分析功能,能够支持多种网络协议和拓扑结构的模拟。
实验在 Windows 10 操作系统上进行,计算机配置为处理器型号、内存大小、硬盘容量。
三、实验内容(一)网络拓扑结构的构建首先,我们构建了一个简单的星型网络拓扑结构,包括一个中心节点和多个边缘节点。
中心节点作为服务器,边缘节点作为客户端。
通过设置不同的链路带宽和延迟参数,模拟了不同网络环境下的数据传输情况。
(二)网络协议的配置在构建好网络拓扑结构后,我们配置了常用的网络协议,如 TCP/IP 协议。
设置了 IP 地址、子网掩码、网关等参数,确保网络的连通性。
(三)流量生成与性能监测为了测试网络的性能,我们使用了流量生成工具,模拟了不同类型的网络流量,如文件传输、视频流、语音通话等。
同时,通过内置的性能监测模块,实时监测网络的吞吐量、延迟、丢包率等关键性能指标。
四、实验步骤1、打开仿真软件,创建一个新的项目。
2、在项目中绘制星型网络拓扑结构,添加中心节点和边缘节点,并连接它们之间的链路。
3、为链路设置带宽和延迟参数,例如,将某些链路的带宽设置为10Mbps,延迟设置为 50ms。
4、配置网络协议,为每个节点设置 IP 地址、子网掩码和网关。
5、启动流量生成工具,选择流量类型和流量强度,例如,生成一个持续的文件传输流量,速率为 5Mbps。
6、运行仿真实验,观察网络性能指标的变化。
7、调整参数,如增加链路带宽、减少延迟、改变流量类型和强度等,重复实验,比较不同参数设置下的网络性能。
五、实验结果与分析(一)带宽对网络性能的影响当链路带宽增加时,网络的吞吐量显著提高,延迟和丢包率降低。
计算机仿真实验报告计算机仿真实验报告引言:计算机仿真是一种利用计算机模拟实际系统行为的方法。
它通过建立数学模型,运用计算机算法和技术,模拟和分析系统的运行过程,以便更好地理解和预测系统的行为。
本文将探讨计算机仿真实验的概念、目的、方法和应用。
一、概念与目的计算机仿真实验是指利用计算机技术对实际系统进行模拟和分析,以研究系统的行为、性能和优化方法的一种实验方法。
其目的在于通过模拟实验,提供对实际系统的理解和预测,以便进行决策和改进。
二、方法与技术1. 建立数学模型:计算机仿真实验的第一步是建立数学模型,即将实际系统抽象为数学表达式或算法。
这需要对系统的结构、行为和性能进行深入分析和理解。
2. 数据采集与预处理:收集实际系统的数据,并对数据进行预处理,以便在计算机中进行仿真实验。
这包括数据清洗、数据转换和数据校正等步骤。
3. 编程与算法设计:根据建立的数学模型,使用计算机编程语言编写仿真程序,并设计相应的算法。
这需要熟悉计算机编程和算法设计的基本原理和方法。
4. 参数设置与验证:根据实际系统的特点和需求,设置仿真实验的参数,并进行验证。
这需要对实际系统的数据进行分析和比对,以确保仿真实验的准确性和可靠性。
5. 仿真运行与结果分析:运行仿真程序,观察和分析仿真结果。
这包括对系统行为、性能和优化方法的分析,以及对仿真结果的可视化和统计。
三、应用与案例计算机仿真实验在各个领域都有广泛的应用。
以下是一些典型的案例:1. 交通仿真:通过模拟城市交通流量和交通信号灯的运行,优化交通信号配时方案,提高交通效率和减少拥堵。
2. 生物仿真:通过模拟生物系统的行为和进化过程,研究生物多样性、环境适应性和生物进化机制。
3. 金融仿真:通过模拟金融市场的价格波动和交易行为,预测市场趋势和风险,辅助投资决策和风险管理。
4. 工程仿真:通过模拟工程系统的设计和运行过程,优化工程结构和工艺参数,提高工程效率和质量。
5. 医学仿真:通过模拟人体器官的结构和功能,研究疾病的发生机制和治疗方法,辅助医学研究和临床决策。
计算机仿真实验报告实验名称叠加定理的验证串联RLC电路时域相应的测试学生姓名学号所在学院教师叠加定理的验证一、实验目的1. 进一步掌握直流稳压电源和万用表的使用方法。
2. 掌握直流电压与直流电流的测试方法。
3.进一步加深对叠加定理的理解。
二、实验原理叠加定理叠加定理指出全部电源在线性电路中产生的任一电压或电流,等于每一个电源单独作用时产生的相应电压或电流的代数和。
三、测试方法1. 直流电压的测试;2. 直流电流的测试。
四、实验内容1. 实验电路图验证R3两端的电压之和等于V1和V2分别作用在R3上的电压U1与U2之和。
两个电压源都不为零时:a.R3上的电压U0=13.2V;将电压源V1置零后:b.电压源V1置零后R3上的电压: U1=6V,I1=1mA;将电压源V2置零后:c.电压源V2置零后R3上的电压U2=7.2,I2=1.201mA。
经验证:U0=13.2V=U1+U2;I0=I1+I1=2.201mA故叠加定理得到验证。
五、实验器材电压源面包板万用表导线RLC串联谐振电路的测试一、实验目的1. 进一步理解谐振电路的谐振特点。
2.掌握谐振频率、品质因数的测试方法。
3.掌握串联谐振电路频率特性的测试方法。
二、实验原理1.RLC串联谐振电路的条件:含有电阻、电容和电感元件的单口网络,在某些工作频率上,出现端口电压和电流波形相位相同的情况时,称为电路发生谐振。
如图所示RLC串联电路,电路的转移函数电压转移比为H(jω)=U RU=RR+jωL+1jωC=11+j(ωLR−1RωC)因此,电路的谐振角频率和谐振频率分别为:ω0=√LC f0=2π√LC2.RLC串联电路谐振特性(1)谐振时,RLC串联回路的输入阻抗为纯电阻,激励电压与回路电流同相,电阻电压相同与电源电压相同且同相。
(2)谐振时,电感上的电压与电容上的电压幅值相等且反相(实际电路中,因电感有串联等效电阻、电容有并联等效电阻,因此电感两端的电压略高于电容电压),若品质因数Q>1,则谐振时,电容、电感电压是激励电压的Q部,可实现电压放大。
计算机仿真实验报告《计算机仿真实验报告》摘要:本实验利用计算机仿真技术对某一特定系统进行了模拟实验,通过对系统的运行状态、性能参数等进行观测和分析,得出了一系列有意义的结论。
本报告将详细介绍实验的背景、目的、方法、结果和结论,以及对实验过程中遇到的问题和解决方法进行总结。
1. 背景随着计算机技术的不断发展,计算机仿真技术已经成为了科学研究和工程实践中不可或缺的一部分。
通过对实际系统的建模和仿真,可以更好地理解系统的运行规律,优化系统设计,提高系统的性能和可靠性。
2. 目的本实验旨在利用计算机仿真技术对某一特定系统进行模拟实验,通过观测和分析系统的运行状态和性能参数,得出有意义的结论,为系统的优化设计提供参考。
3. 方法本实验选取了某一特定系统作为研究对象,首先对系统进行了建模,并利用计算机软件进行了仿真实验。
在实验过程中,通过改变系统的参数和条件,观测系统的运行状态和性能参数的变化,并记录实验数据。
4. 结果通过实验观测和数据分析,得出了一系列有意义的结论:系统在不同参数和条件下的运行状态、系统的性能参数随时间的变化趋势等。
这些结论为系统的优化设计提供了重要的参考依据。
5. 结论本实验利用计算机仿真技术对某一特定系统进行了模拟实验,通过观测和分析系统的运行状态和性能参数,得出了一系列有意义的结论。
这些结论为系统的优化设计提供了重要的参考依据,具有一定的理论和实际意义。
6. 实验过程中遇到的问题和解决方法在实验过程中,我们遇到了一些问题,如系统建模的复杂性、仿真实验的参数选择等。
通过认真分析和讨论,我们采取了一些解决方法,最终顺利完成了实验。
综上所述,本实验利用计算机仿真技术对某一特定系统进行了模拟实验,通过观测和分析系统的运行状态和性能参数,得出了一系列有意义的结论,为系统的优化设计提供了重要的参考依据。
同时,我们也总结了实验过程中遇到的问题和解决方法,为今后的研究和实践提供了一定的借鉴。
计算机仿真技术综合实验实验目的:熟悉使用动态系统仿真工具SimuLink的方法实验要求:1.练习启动SimuLink2.熟悉SimuLink模型窗口3. 练习使用鼠标和键盘操作1)对模块操作2)对直线操作3)对信号标签操作4) 对模型注释操作4. 练习使用以下模块库中的模块用SimuLink建立仿真模型的过程,可以理解为将模块库中的模块搭在一起。
模块库中的模块可以用SimuLink库浏览器得到。
●Source 系统输入模块●Sinks 系统输出模块●Discrete 离散时间系统模块库●Continuous 连续时间系统模块库●Discontinuities 不连续系统模块库●Math Operations 数学运算库●Signal Attributes 信号特性模块库●Signal Routing 信号路由模块●Look-Up Tables 表函数模块库5.用SimuLink建立一个仿真模型,要求仿真模型应该有模型本身、输入和输出部分。
并运行仿真模型得到仿真结果。
实验原理:用SimuLink对通信中2ASK信号进行解调的仿真解调:指从携带消息的已调信号中恢复消息的过程。
在各种信息传输或处理系统中,发送端用所欲传送的消息对载波进行调制,产生携带这一消息的信号。
接收端必须恢复所传送的消息才能加以利用。
2ASK(二进制振幅键控):振幅键控是正弦载波的幅度随数字基带信号而变化的数字调制.当数字基带信号为二进制时,则为二进制振幅键控。
幅度键控可以通过乘法器和开关电路来实现。
载波在数字信号1或0的控制下通或断,在信号为1的状态载波接通,此时传输信道上有载波出现;在信号为0的状态下,载波被关断,此时传输信道上无载波传送。
那么在接收端我们就可以根据载波的有无还原出数字信号的1和0。
对于二进制幅度键控信号的频带宽度为二进制基带信号宽度的两倍。
二进制振幅键控信号解调器原理框图实验内容:对2ASK信号进行解调(1) 建立simulink模型方框图相干解调也叫同步解调,就是用已调信号恢复出载波——既同步载波。
目录实验一Matlab语言编程 (1)一.实验目的 (1)二.具体实验内容、步骤、要求: (1)实验二数值积分算法及函数调用练习 (3)一.实验目的 (3)二.实验实例介绍: (3)实验三控制工具箱与SIMULINK软件应用 (9)一.实验目的 (9)二.实验预习要求: (9)三.学会调出、运行已由SIMULINK建立的仿真模型。
(9)四.实验设计题目与要求: (10)实验一 Matlab 语言编程一. 实验目的熟悉Matlab 语言及其编程环境,掌握编程方法 要求认真听取实验指导老师讲解与演示二. 具体实验内容、步骤、要求:1.运行交互式学习软件,学习Matlab 语言2.在Matlab 的命令窗口下输入如下命令:INTRO,然后根据显示出来的幻灯片右面按钮进行操作,可按START —>NEXT —>NEXT 按钮,一步步运行,观察。
3.自编程序并完成上机编辑、调试、运行,存盘。
(1). 用Matlab 命令完成矩阵的各种运算,例如:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=44434241343332312423222114131211A 求出下列运算结果,并上机验证。
A(:,1),A(2,:),A(1:2,2:3),A(2:3,2:3),A(:,1:2),A(2:3), A(:),A(:,:),ones(2,2), eye(2)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=41312111A(:,1)[]24232221:)A(2,=⎥⎦⎤⎢⎣⎡=232213123):2,2:A(1 ⎥⎦⎤⎢⎣⎡=333223223):3,2:A(2⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=42413231222112112):A(:,1[]31213):A(2=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=44342414433323134232221241312111A(:)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=44434241343332312423222114131211:)A(:,⎥⎦⎤⎢⎣⎡=1111)2,2(ones ⎥⎦⎤⎢⎣⎡=1001)2(eye(2). 绘制数学函数图形t=0:0.1:8;y=1-2*t.*sin(t); plot(t,y)12345678-15-10-551015时间t输出y绘制数学函数图形4.理解命令文件和函数文件的区别,并自编函数文件并调用。
计算机仿真实验报告班级:姓名:学号:指导教师:昆明理工大学信息工程与自动化学院2012年12月实验一常微分方程的求解及系统数学模型的转换一.实验目的通过实验熟悉计算机仿真中常用到的Matlab指令的使用方法,掌握常微分方程求解指令和模型表示及转换指令,为进一步从事有关仿真设计和研究工作打下基础。
二. 实验设备个人计算机,Matlab软件。
三. 实验准备预习本实验有关内容(如教材第2、3、5章中的相应指令说明和例题),编写本次仿真练习题的相应程序。
四. 实验内容1. Matlab中常微分方程求解指令的使用题目一:请用MATLAB的ODE45算法分别求解下列二个方程。
要求:1.编写出Matlab 仿真程序;2.画出方程解的图形并对图形进行简要分析;3.分析下列二个方程的关系。
1.2.方程1:M文件:function xprim=xprim(t,x)xprim=-x^2程序:[t,x]=ode45('xprim',[0,1],1);plot(t,x,'o',t,x,'-');xlabel('time t0=0,tt=1');ylabel('X values X(0)=1');grid图像:方程2:M文件:function xprim=xprim2(t,x) xprim=x^2程序:[t,x]=ode45('xprim2',[0,1],-1); plot(t,x,'o',t,x,'-');xlabel('time t0=0,tt=1'); ylabel('X values X(0)=-1'); grid图像:题目二:下面方程组用在人口动力学中,可以表达为单一化的捕食者-被捕食者模式(例如,狐狸和兔子)。
其中1x 表示被捕食者, 2x 表示捕食者。
如果被捕食者有无限的食物,并且不会出现捕食者。
于是有1'1x x ,则这个式子是以指数形式增长的。
大量的被捕食者将会使捕食者的数量增长;同样,越来越少的捕食者会使被捕食者的数量增长。
而且,人口数量也会增长。
请分别调用ODE45、ODE23算法求解下面方程组。
要求编写出Matlab 仿真程序、画出方程组解的图形并对图形进行分析和比较。
题目二程序及其运行结果: ODE45算法: M 文件:function fun=fun(t,x)fun=[x(1)-0.1*x(1)*x(2)+0.01*t;-x(2)+0.02*x(1)*x(2)+0.04*t]; 程序:[t,x]=ode45('fun',[0,20],[30;20]);plot(t,x);xlabel('time t0=0,tt=20');ylabel('x values x1(0)=30,x2(0)=20');ODE23解法:M文件:function fun=fun(t,x)fun=[x(1)-0.1*x(1)*x(2)+0.01*t;-x(2)+0.02*x(1)*x(2)+0.04*t]; 程序:[t,x]=ode23('fun',[0,20],[30;20]);plot(t,x);xlabel('time t0=0,tt=20');ylabel('x values x1(0)=30,x2(0)=20');2. Matlab 中模型表示及模型转换指令的使用题目三:若给定系统的的传递函数为1132106126)(23423+++++++=s s s s s s s s G 请用MATLAB 编程求解其系统的极零点模型。
程序:num=[6,12,6,10];den=[1,2,3,1,1];[z,p,k]=tf2zp(num,den);sys=zpk(z,p,k) 运行结果:题目四:习题2.4 num=[1,4,5]; den=[1,6,11,6]; sys=tf(num,den); canon(sys,'modal')题目五:习题5.8程序:D=zpk(0,[0.1,0.2],1,0.02)D2=d2d(D,0.1)程序运行结果:>> D=zpk(0,[0.1,0.2],1,0.02)Zero/pole/gain:z---------------(z-0.1) (z-0.2)Sampling time: 0.02>> D2=d2d(D,0.1)Zero/pole/gain:1.3881 (z+0.0002381)----------------------(z-1e-005) (z-0.00032) Sampling time: 0.1 五.总结与体会通过本次实验了解了计算机仿真中常用到的Matlab 指令的使用方法,掌握了常微分方程求解指令和模型表示及转换指令,为进一步学习仿真设计打下了基础。
实验二 Matlab 优化工具箱的使用一.实验目的通过上机操作熟悉Matlab 优化工具箱的主要功能及其使用方法,掌握优化工具箱中常用函数的功能和语法,并利用其进行极值运算、求解线性和非线性问题等,为进一步的仿真设计和研究打下基础。
二. 实验设备个人计算机,Matlab 软件。
三. 实验准备预习本实验有关内容(如教材第6章中的相应指令说明和例题),编写本次仿真练习题的相应程序。
四. 实验内容1. 应用Matlab 优化工具箱求解优化问题例题6.6~6.10,选做2题,要求自行修改方程系数,并比较运行结果。
例题6.7(原):min 432142x x x x +++ s.t. 8434321≤-++x x x x 6324321≤+-+x x x x 94431≤++x x x 0,,,4321≥x x x x 解:f=[2 4 1 1];A=[1 3 4 -1;2 1 -3 1;1 0 4 1]; b=[8 6 9];LBnd=[0 0 0 0];[x,fval]=linprog(f,A,b,[],[],LBnd,[]) Optimization terminated.x =1.0e-012* 0.0078 0.0259 0.2098 0.0860fval =4.1508e-0136.7(修改):min 432122x x x x +++ s.t. 62424321≤-++x x x x 8324321≤+-+x x x x 622431≤++x x x 0,,,4321≥x x x x 解:f=[1 2 2 1];A=[1 2 4 -2;2 1 -3 1;1 0 2 2]; b=[6 8 6];LBnd=[0 0 0 0];[x,fval]=linprog(f,A,b,[],[],LBnd,[]) Optimization terminated. x =1.0e-009 *0.2255 0.0452 0.0324 0.0467fval =4.2736e-0106.9 (原)求解下面的约束非线性规划问题s.t. 12212122121212min ()(42421)1.50100x f x e x x x x x x x x x x x =+++++--≤--≤function [f,g]=fun(x)f=exp(x(1))*(4*x(1)^2+2*x(2)^2+4*x(1)*x(2)+2*x(2)+1); g(1)=1.5+x(1)*x(2)-x(1)-x(2); g(2)=-x(1)*x(2)-10; 调用:x0=[-1 1];options=[];[x,options]=constr('fun',x0,options) x =-9.5474 1.0474options =Columns 1 through 150 0.0001 0.0001 0.0000 0 0 0 0.0236 0 29.0000 10.0000 10.0000 0 200.0000 0Columns 16 through 180.0000 0.1000 1.0000输出最优解为options(8)=0.02366.9(修改)求解下面的约束非线性规划问题s.t.12212122121212min()(221)1.50100xf x e x x x x xx x x xx x=+++++--≤--≤function [f,g]=fun(x)f=exp(x(1))*(2*x(1)^2+x(2)^2+2*x(1)*x(2)+x(2)+1);g(1)=1.5+x(1)*x(2)-x(1)-x(2);g(2)=-x(1)*x(2)-10;调用:x0=[-1 1];options=[];[x,options]=constr('fun',x0,options)x =-9.5474 1.0474options =Columns 1 through 150 0.0001 0.0001 0.0000 0 00 0.0118 0 25.0000 9.0000 9.0000 0 200.0000 0Columns 16 through 180.0000 0.1000 1.0000输出最优解为options(8)=0.0118对修改前后分析可以看出,前七列的值相同,后六列的值也相同,同时最优解均出现在第八列上。
2. 应用Matlab优化工具箱求解极值问题已知函数f(x)=10*exp(-x)*cos(x) ,求函数的极值。
(1)x∈[2,5]时,求函数的最小值,并画出函数的曲线。
(2)x∈[3,9]时,求函数的最大值,并画出函数的曲线。
(1)f='10*exp(-x)*cos(x)';fplot(f,[2,5])X=fmin('10*exp(-x)*cos(x)',2,5)X =2.3562Y=10*exp(-2.3562)*cos(2.3562)Y =-0.6702(2)f='10*exp(-x)*cos(x)';fplot(f,[3,9]);X=fmin('-10*exp(-x)*cos(x)',3,9)X =5.4978Y=10*exp(-5.4978)*cos(5.4978)Y =0.0290五.总结与体会通过这次实验让我对matlab优化工具箱有了一定的了解,对一些函数的使用基本比较熟悉了,像线性规划、最大最小值函数、约束条件下的优化函数都能使用它们来解决一些问题,特别是习题中的问题,对它们的功能和语法都掌握了。