2017年丰台一模试题

丰台区2017年高三年级第二学期综合练习（一）高三语文2017.03本试卷满分共150分。

考试时间150分钟。

注意事项：1.答题前，考生务必先将答题卡上的学校、年级、班级、姓名、准考证号用黑色字迹签字笔填写清楚，并认真核对条形码上的准考证号、姓名，在答题卡的“条形码粘贴区”贴好条形码。

2.本次考试所有答题均在答题卡上完成。

选择题必须使用2B铅笔以正确填涂方式将各小题对应选项涂黑，如需改动，用橡皮擦涂干净后再选涂其它选项。

非选择题必须使用标准黑色字迹签字笔书写，要求字体工整、字迹清楚。

3.请严格按照答题卡上题号在相应答题区内作答，超出答题区域书写的答案无效，在试题、草稿纸上答题无效。

4.请保持答题卡卡面清洁，不要装订、不要折叠、不要破损。

一、本大题共8小题，共24分。

阅读下面的材料，完成1—8题。

材料一2011年以来，中国大气污染加重，雾霾覆盖面不断增加，出现时间不断增长，程度不断加深。

有关研究表明：中国近些年大气污染加重的直接原因在于大气主要污染物排放总量及其集聚程度上升；在工业化速度快的地区，工业废气（二氧化硫、工业烟尘等）是最大的污染源。

工业废气产生量主要集中在中东部几个省市。

2013年，工业烟尘产生量排名前五的是河南、山东、山西、河北与江苏。

工业二氧化硫产生量前六名是山东、内蒙古、江苏、山西、河北与河南。

2013年12月，中国环境监测总站的全国城市空气质量实时发布平台显示，中国雾霾严重的城市主要分布在京津冀、河南、山东等地区。

其中，京津冀最为严重，除了气候干燥之外，与工业废气污染源过于集中有很大关系。

在地级与副省级城市的工业烟尘产生量排名中，河北的沧州、邯郸．．与石家庄分别排在第一、第二与第六位。

中国雾霾严重的地区分布与工业废气的地区集聚、城市集聚状况非常一致。

导致中国城市工业废气集聚的原因很多，其中，非均衡的工业化是中国城市工业废气集聚最根本的原因。

中国工业化进程中的非均衡主要包括两个方面：首先是工业化的地区不均衡——不同城市与地区之间工业化进程与速度存在很大差异。

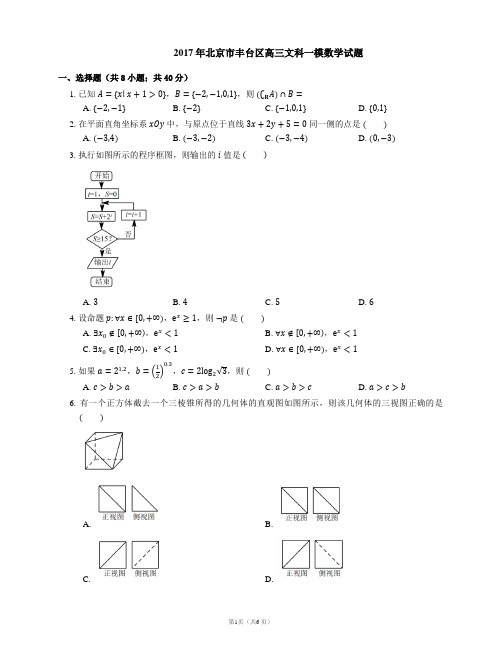
2017年北京市丰台区高三文科一模数学试题一、选择题（共8小题；共40分）1. 已知，，则 ______A. B. C. D.2. 在平面直角坐标系中，与原点位于直线同一侧的点是A. B. C. D.3. 执行如图所示的程序框图，则输出的值是A. B. C. D.4. 设命题，，则是A. ，B. ，C. ，D. ，5. 如果，，，则A. B. C. D.6. 有一个正方体截去一个三棱锥所得的几何体的直观图如图所示，则该几何体的三视图正确的是A. B.C. D.7. 已知函数，点，都在曲线上，且线段与曲线有五个公共点，则的值是A. B. C. D.8. 一次猜奖游戏中，1，2，3，4 四扇门里摆放了a，b，c，d 四件奖品（每扇门里仅放一件），甲同学说：1 号门里是 b，3 号门里是 c；乙说：2 号门里是 b，3 号门里是 d；丙说：4 号门里是 b，2 号门里是 c；丁说：4 号门里是 a，3 号门里是 c．如果他们每人都猜对了一半，那么4 号门里是A. aB. bC. cD. d二、填空题（共6小题；共30分）9. 在复平面内，复数对应的点到原点的距离是______．10. 抛物线的准线方程是______．11. 设，，为常数，且的最大值为，则等于______．12. 如图，在直角梯形中，，，，，是的中点，则 ______．13. 已知点，，若直线上存在点，满足，则的取值范围是______．14. 已知函数．（1）若，，则的值域为______；（2）若恰有三个零点，则实数的取值范围是______．三、解答题（共6小题；共78分）15. 在中，角，，的对应边分别是，，，且，．（1）若，求；（2）若的面积为，求，．16. 已知是各项均为正数的等比数列，设，且，．（1）求证：数列是以为公差的等差数列；（2）设数列的前项和为，求的最大值．17. 如图1，平行四边形中，，，现将沿折起，得到三棱锥（如图 2），且，点为侧棱的中点．（1）求证：平面平面；（2）求三棱锥的体积；（3）在的角平分线上是否存在点，使得 平面?若存在，求出的长；若不存在，请说明理由．18. 某学校营养餐由A，B两家配餐公司配送．学校为了解学生对这两家配餐公司的满意度，采用问卷的形式，随机抽取了名学生对这两家公司分别评分．根据收集的分问卷的评分，得到A公司满意度评分的频率分布直方图和B公司满意度评分的频数分布表：A公司满意度评分分组频数（1）根据A公司的频率分布直方图，估计该公司满意度评分的中位数；（2）从满意度高于分的问卷中随机抽取两份，求这两份问卷都是给A公司评分的概率；（3）请从统计角度，对 A，B两家公司做出评价．19. 已知是椭圆上一点，点到椭圆的两个焦点的距离之和为．（1）求椭圆的方程；（2）设，是椭圆上异于的两点，直线与直线交于点，是否存在点，使得?若存在，求出点的坐标；若不存在，请说明理由．20. 已知函数，，是曲线上不同的两点．（1）求的单调区间，并写出实数的取值范围；（2）证明：．答案第一部分1. A2. A3. B4. C5. D6. D7. A8. A第二部分9.10.11.12.13.14. （1）；（2）第三部分15. （1）由正弦定理可知：．从而求得．（2）由的面积等于，可知．从而由余弦定理可得联立得．16. （1）设等比数列的公比为，则，因此数列是等差数列．又，，又等差数列的公差，即．即数列是以为公差的等差数列．（2）设等差数列的前项和为，则，于是当时，有最大值，最大值为．17. （1）在平行四边形中，，又因为为侧棱的中点，所以；又因为，，且，所以平面．又因为平面，所以；因为，所以平面，又因为平面，所以平面平面．（2）因为，平面，所以是三棱锥的高，故，又因为，，，所以，所以有．（3）取中点，连接并延长至点，使得，连接，，．，所以射线是的角平分线．又因为点是中点，所以，因为平面，平面，所以 平面．因为，互相平分，故四边形为平行四边形，有．又因为，所以有，又因为，故．18. （1）设A公司调查的份问卷的中位数为，则有解得：所以，估计该公司满意度得分的中位数为．（2）满意度高于分的问卷共有份，其中份评价A公司，设为，，，，份评价B公司，设为，．从这份问卷中随机取份，所有可能的结果有：，，，，，，，，，，，，，，，共有种．其中份问卷都评价A公司的有以下种：，，，，，．设两份问卷均是评价A公司为事件，则．（3）由所给两个公司的调查满意度得分知：A公司得分的中位数低于B公司得分的中位数，A公司得分集中在这组，而B公司得分集中在和两个组，A公司得分的平均数低于B公司得分的平均数，A公司得分比较分散，而B公司得分相对集中，即A公司得分的方差高于B公司得分的方差．19. （1）由椭圆过点可得．又点到两焦点距离和为，可得．所以椭圆的方程．（2）设，依题意得：直线的斜率存在．则直线的方程为：．令，，即．又等价于且点在轴的右侧，从而．因为点在轴的右侧，所以，解得，由点在椭圆上，解得：，于是存在点，使得．20. （1）的定义域为．．由得，．由得，．由的，．所以的单调增区间为，单调减区间为．的取值范围是．（2）由（Ⅰ）知，，要证，只需证．因为，所以只需证，只需证，只需证．令，则，因为，所以在上单调递减，所以，所以在上单调递增，所以，所以，故．。

丰台区2017年高三年级第二学期综合练习（一）理科综合物理试题2017. 0312、根据卢瑟福提出的原子核式结构模型解释α粒子散射实验，使极少数α粒子发生大角度偏转的作用力是A、原子核对α粒子的库仑引力B、原子核对α粒子的库仑斥力C、核外电子对α粒子的库仑引力D、核外电子对α粒子的库仑斥力14.已知一束可见光m是由a、b、c三种单色光组成的，光束m通过三棱镜的传播情况如图所示，则比较a、b、c三种单色光，下列说法正确的是A、a色光的折射率最大B、c色光的频率最小C、b色光在玻璃中的传播速度最大D、c色光发生全反射的临界角最小15.某质量为M、半径为R的行星表面附近有一颗质量为m的卫星，卫星绕行星的运动可视为匀速圆周运动，其角速度大小为 ，线速度大小为v；若在该行星表面上用弹簧测力计测量一质量为m0的物体重力，物体静止时，弹簧测力计的示数为F0万有引力常量为G，忽略该行星自转。

根据已知条件，下列表达式中不正确的是16、在如图所示电路中，电源内阻不可忽略。

开关S闭合后，在滑动变阻器R2的滑动端由b向a缓慢滑动的过程中，下列说法正确的是A.电流表的示数增大B.电压表的示数减小C.电容器C的电容增大D.电容器C所带电荷量增大17、质量不同、电荷量相同的粒子，不计重力，垂直于电场线射入同一个勻强电场。

若它们离开电场时速度方向改变的角度相同，则它们在进入电场前必然具有相同的A.速度B.动量C.动能D.动量或动能均可以18、如图所示，一水平面内固定两根足够长的光滑平行金属导轨，导轨上面横放着两根完全相同的铜棒a b和cd，构成矩形回路，在整个导轨平面内都有竖直向上的匀强磁场B。

开始时，棒cd静止，棒a b有一个向左的初速度v0，则关于两棒以后的运动，下列说法正确的是A.a b棒做匀减速直线运动，cd棒做勻加速直线运动B.a b棒减小的动量等于cd棒增加的动量C、a b棒减小的动能等于cd棒增加的动能D、两棒一直运动，机械能不断转化为电能19、某同学想要描绘标有“2.5 V，0.3 A”字样的小灯泡的伏安特性曲线，要求测M数据尽量精确，绘制曲线完整。

北京市丰台区2017年高三年级第二学期综合练习（一模）英语2017. 03第二部分知识运用（共两节45分）第一节单项填空（共15小题；每小题1分，共15分）从每题所给的A、B、C、D四个选项中，选出可以填入空白处的最佳选项，并在答题卡上将该项涂黑。

21. Congratulations on the great progress you ________ since last year.A. makeB. have madeC. were makingD. will have made22. According to the author, those ________ enjoy reading will never feel lonely.A. whenB. whoC. whereD. which23. —Have I filled out the application correctly, Mr. Smith?—Well, you ________ one questionhere.A. missedB. missC. will missD. are missing24. The key point is not who said the words, but ________ they are true or not.A. whatB. whenC. thatD. whether25. It ________ for two weeks, and the whole area is flooded.A. had rainedB. rainsC. would rainD. has been raining26. It’s an excellent job offer. Don’t let such a good opportunity ________ through your fingers.A. slippedB. to slipC. slipD. slipping27. The sponsors agreed that they would support us ________ we didn’t break the rules.A. as well asB. as soon asC. as far asD. as long as28. When ________, the project will help to greatly improve the air quality in the community.A. finishingB. to finishC. finishD. finished29. ________ they should do about the hole in their roof is their most pressing problem.A. ThatB. How oftenC. WhatD. Why30. The delivery of the goods ________ because of the heavy snow storm.A. is putting offB. was put offC. had been put offD. would put off31. Life is not predictable; even the worst ________ become the best.A. shallB. mightC. mustD. need32. ________ which club to attend, Jane asked her friends for advice.A. Not knowingB. Not knowC. Not knownD. Not to know33. —Have you seen the film Avatar?—Of course, I have. It was in our hometown ________ the film was made.A. whenB. whyC. thatD. which34. I wish I ________ the lecture yesterday, but I missed it.A. had attendedB. would attendC. have attendedD. attended35. We really appreciate our learning environment, ________ we can have open and friendlycommunication.A. whoseB. whichC. whereD. what第二节完形填空（共20小题；每小题1.5分，共30分）阅读下面短文，掌握其大意，从每题所给的A、B、C、D四个选项中，选出最佳选项，并在答题卡上将该项涂黑。

北京市丰台区2017年高三年级第二学期综合练习第一部分听力理解（共三节30分）第一节（共5小题；每小题1.5分，共7.5分）听下面5段对话。

每段对话后有一道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听完每段对话后，你将有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话你将听一遍。

1. What is the man’s plan for his holiday?A.To go to Hawaii.B. To go to HongKong.C. To stay at home.2. What pet does the man decide to keep finally?A. A dog.B. A cat.C. A rabbit.3. What time will the woman leave?A. At 13:00.B. At 14:30.C. At 16:20.4. Where does this conversation take place?A. On the train.B. In the airplane.C. In the hotel.5. What is the woman doing?A. Offering the man some advice.B. Telling the man some bad news.C. Playing a joke on the man.第二节（共10小题；每小题1.5分，共15分）听下面4段对话或独白。

每段对话或独白后有几道小题，从每题所给的A、B、C三个选项中选出最佳选项。

听每段对话或独白前，你将有5秒钟的时间阅读每小题。

听完后，每小题将给出5秒钟的作答时间。

每段对话或独白你将听两遍。

听下面一段对话，回答第6至7两道小题。

6. What is Lucy’s New Year resolution?A. To take more exercise.B. To make big money.C. To do better in Chinese.7.What is the relationship between the two speakers?A. Family members.B. Friends.C. Classmates.听下面一段对话，回答第8至9两道小题。

丰台区2017年高三年级第二学期综合练习（一）高三语文2017.03本试卷满分共150分。

考试时间150分钟。

一、本大题共8道小题，共24分。

1. D【解析】与原文“中国目前正处于重化工业阶段下半场，这种状况短期内难以发生根本性改变。

”不相符。

(3分)2. C【解析】原文表述为“工业内部结构的不均衡包括技术含量低、粗放式发展的工业比例过高”。

(3分)3.C【解析】“付诸东流”的“诸”是“之于”的意思。

(2分)4.B【解析】滞后：（事物）落在形势发展的后面；落后：发展水平较低，不进步。

改变：改换，更动；改善：改变原有情况使好一些。

拓宽：开拓使宽广，拓展：开拓发展。

(2分)5.A【解析】从材料二第一段“大气污染防治法并未考虑到与其他环境要素保护法律之间的衔接、配合，缺乏系统性”，可以明确2000年《大气污染防治法》并未与其他环境保护法协同配合。

(3分)6.A【解析】材料二第三段说“综观草案，其修订仍然以污染防治为导向，鲜有涉及大气环境保护的规定”，因此，题干“不再以污染防治为导向，需要涉及大气环境保护的规定”表述是错误的。

(3分)7. D【解析】“开发大气污染预测系统”这一技术能够检测、把握大气环境质量，但不能实现“低排放”，控制污染源。

(3分)8.①工业发展过程中，想方设法走工业均衡发展的道路。

②制定并不断完善适应新时期大气污染问题的相关法律。

③倡导公众参与大气环境治理，切实建立起公众参与大气污染防治的相关制度。

④借鉴国外先进经验，改进国家治理大气措施。

○5充分利用科技手段控制污染源，加强对污染的监测。

【评分标准】共5个要点，答及1点1分，2点2分，3点3分,4点5分。

答满4点即给满分。

意思对即可。

二、本大题共7道小题，共24分。

9. C【解析】所以：用来……的。

（3分）10.A【解析】A也，语气词，表判断。

B介词，在；介词，对于。

C代词，你，你们；副词，像，好像D词尾，……的样子；连词，但是(3分)11.B【解析】所谓：所说的。

2017年北京市丰台区高考数学一模试卷（文科）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．如果集合A={x∈Z|﹣2≤x＜1}，B={﹣1，0，1}，那么A∩B=（）A．{﹣2，﹣1，0，1}B．{﹣1，0，1}C．{0，1}D．{﹣1，0}2．在平面直角坐标系xOy中，与原点位于直线3x+2y+5=0同一侧的点是（）A．（﹣3，4）B．（﹣3，﹣2）C．（﹣3，﹣4）D．（0，﹣3）3．执行如图所示的程序框图，则输出的i的值是（）A．3 B．4 C．5 D．64．设命题p：∀x∈[0，+∞），e x≥1，则￢p是（）A．∃x0∉[0，+∞）， B．∀x∉[0，+∞），e x＜1C．∃x0∈[0，+∞），D．∀x∈[0，+∞），e x＜15．如果，那么（）A．c＞b＞a B．c＞a＞b C．a＞b＞c D．a＞c＞b6．由一个正方体截去一个三棱锥所得的几何体的直观图如图所示，则该几何体的三视图正确的是（）A．B．C．D．7．已知函数，点A（m，n），B（m+π，n）（|n|≠1）都在曲线y=f（x）上，且线段AB与曲线y=f（x）有五个公共点，则ω的值是（）A．4 B．2 C．D．8．某校举行了以“重温时代经典，唱响回声嘹亮”为主题的“红歌”歌咏比赛．该校高一年级有1，2，3，4四个班参加了比赛，其中有两个班获奖．比赛结果揭晓之前，甲同学说：“两个获奖班级在2班、3班、4班中”，乙同学说：“2班没有获奖，3班获奖了”，丙同学说：“1班、4班中有且只有一个班获奖”，丁同学说：“乙说得对”．已知这四人中有且只有两人的说法是正确的，则这两人是（）A．乙，丁B．甲，丙C．甲，丁D．乙，丙二、填空题共6小题，每小题5分，共30分．9．在复平面内，复数z=1﹣2i对应的点到原点的距离是．10．抛物线y2=2x的准线方程是．11．设a+b=M（a＞0，b＞0），M为常数，且ab的最大值为2，则M等于．12．如图，在直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=CD=1，P是AB的中点，则=．13．已知点A（1，0），B（3，0），若直线y=kx+1上存在点P，满足PA⊥PB，则k的取值范围是．14．已知函数（1）若a=0，x ∈[0，4]，则f （x ）的值域是 ；（2）若f （x ）恰有三个零点，则实数a 的取值范围是 ．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．在△ABC 中，角A ，B ，C 对应的边长分别是a ，b ，c ，且，c=4．（Ⅰ）若，求a ；（Ⅱ）若△ABC 的面积等于，求a ，b ．16．已知{a n }是各项均为正数的等比数列，a 11=8，设b n =log 2a n ，且b 4=17． （Ⅰ）求证：数列{b n }是以﹣2为公差的等差数列； （Ⅱ）设数列{b n }的前n 项和为S n ，求S n 的最大值．17．如图1，平行四边形ABCD 中，AC ⊥BC ，BC=AC=1，现将△DAC 沿AC 折起，得到三棱锥D ﹣ABC （如图2），且DA ⊥BC ，点E 为侧棱DC 的中点． （Ⅰ）求证：平面ABE ⊥平面DBC ； （Ⅱ）求三棱锥E ﹣ABC 的体积；（Ⅲ）在∠ACB 的角平分线上是否存在点F ，使得DF ∥平面ABE ？若存在，求DF 的长；若不存在，请说明理由18．某校学生营养餐由A 和B 两家配餐公司配送．学校为了解学生对这两家配餐公司的满意度，采用问卷的形式，随机抽取了40名学生对两家公司分别评分．根据收集的80份问卷的评分，得到如图A 公司满意度评分的频率分布直方图和如表B 公司满意度评分的频数分布表：（Ⅰ）根据A公司的频率分布直方图，估计该公司满意度评分的中位数；（Ⅱ）从满意度高于90分的问卷中随机抽取两份，求这两份问卷都是给A公司评分的概率；（Ⅲ）请从统计角度，对A、B两家公司做出评价．19．已知P（0，1）是椭圆C：=1（a＞b＞0）上一点，点P到椭圆C的两个焦点的距离之和为2．（Ⅰ）求椭圆C的方程；（Ⅱ）设A，B是椭圆C上异于点P的两点，直线PA与直线x=4交于点M，是=？若存在，求出点A的坐标；若不存在，请说否存在点A，使得S△ABP明理由．20．已知函数，A（x1，m），B（x2，m）是曲线y=f（x）上两个不同的点．（Ⅰ）求f（x）的单调区间，并写出实数m的取值范围；（Ⅱ）证明：x1+x2＞0．2017年北京市丰台区高考数学一模试卷（文科）参考答案与试题解析一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．如果集合A={x∈Z|﹣2≤x＜1}，B={﹣1，0，1}，那么A∩B=（）A．{﹣2，﹣1，0，1}B．{﹣1，0，1}C．{0，1}D．{﹣1，0}【考点】交集及其运算．【分析】先分别求出集合A和B，由此利用交集定义能求出A∩B．【解答】解：∵集合A={x∈Z|﹣2≤x＜1}={﹣2，﹣1，0}，B={﹣1，0，1}，∴A∩B={﹣1，0}．故选：D．2．在平面直角坐标系xOy中，与原点位于直线3x+2y+5=0同一侧的点是（）A．（﹣3，4）B．（﹣3，﹣2）C．（﹣3，﹣4）D．（0，﹣3）【考点】二元一次不等式（组）与平面区域．【分析】二元一次不等式的表示的平面区域表示的点的特点判断即可．【解答】解：当x=0，y=0时，0+0+5＞0，对于A：当x=﹣3，y=4时，﹣9+8+5＞0，故满足，对于B：当x=﹣3，y=﹣2时，﹣9﹣4+5＜0，故不满足，对于C：x=﹣3，y=﹣4，﹣9﹣8+5＜0，故不满足，对于D：x=﹣3，y=﹣2时，0﹣6+5＜0，故不满足，故选：A3．执行如图所示的程序框图，则输出的i的值是（）A．3 B．4 C．5 D．6【考点】程序框图．【分析】由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量i的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【解答】解：第一次执行循环体后，S=2，不满足退出循环的条件，i=2；再次执行循环体后，S=6，不满足退出循环的条件，i=3；再次执行循环体后，S=14，不满足退出循环的条件，i=4；再次执行循环体后，S=30，满足退出循环的条件，故输出的i值为4，故选：B．4．设命题p：∀x∈[0，+∞），e x≥1，则￢p是（）A．∃x0∉[0，+∞）， B．∀x∉[0，+∞），e x＜1C．∃x0∈[0，+∞），D．∀x∈[0，+∞），e x＜1【考点】命题的否定．【分析】利用全称命题的否定是特称命题，可以求出￢p．【解答】解：因为命题p是全称命题，所以利用全称命题的否定是特称命题可得：￢p：∃x0∈[0，+∞），．故选：C5．如果，那么（）A．c＞b＞a B．c＞a＞b C．a＞b＞c D．a＞c＞b【考点】对数值大小的比较．【分析】利用指数与对数函数的单调性即可得出．【解答】解：a=21.2＞2，＜1，c=2=log23∈（1，2）．∴a＞c＞b．故选：D．6．由一个正方体截去一个三棱锥所得的几何体的直观图如图所示，则该几何体的三视图正确的是（）A．B．C．D．【考点】简单空间图形的三视图．【分析】画物体的三视图的口诀为：主、俯：长对正；主、左：高平齐；俯、左：宽相等．依此画出该几何体的三视图．【解答】解：根据三视图的画法，可得俯视图、侧视图，故选D．7．已知函数，点A（m，n），B（m+π，n）（|n|≠1）都在曲线y=f（x）上，且线段AB与曲线y=f（x）有五个公共点，则ω的值是（）A．4 B．2 C．D．【考点】y=Asin（ωx+φ）中参数的物理意义．【分析】由题意，2T=π，利用周期公式可得结论．【解答】解：由题意，2T=π，∴T=，∴ω=4，故选A．8．某校举行了以“重温时代经典，唱响回声嘹亮”为主题的“红歌”歌咏比赛．该校高一年级有1，2，3，4四个班参加了比赛，其中有两个班获奖．比赛结果揭晓之前，甲同学说：“两个获奖班级在2班、3班、4班中”，乙同学说：“2班没有获奖，3班获奖了”，丙同学说：“1班、4班中有且只有一个班获奖”，丁同学说：“乙说得对”．已知这四人中有且只有两人的说法是正确的，则这两人是（）A．乙，丁B．甲，丙C．甲，丁D．乙，丙【考点】进行简单的合情推理．【分析】根据题意，假设乙的说法是正确的，分析可得丁也是正确的，那么甲丙的说法都是错误的，分析可得乙的说法相矛盾，即可得假设乙的说法是正确是错误的，从而可得丁的说法也是错误的，从而可得说法正确的是甲、丙，即可得答案．【解答】解：根据题意，由于甲乙丙丁四人中有且只有两人的说法是正确的，假设乙的说法是正确的，则丁也是正确的，那么甲丙的说法都是错误的，如果丙同学说：“1班、4班中有且只有一个班获奖”是错误的，那么1班、4班都获奖或1班、4班都没有获奖，与乙的说法矛盾，故乙的说法是错误，则丁同学说：“乙说得对”也是错误的；故说法正确的是甲、丙，故选：B．二、填空题共6小题，每小题5分，共30分．9．在复平面内，复数z=1﹣2i对应的点到原点的距离是．【考点】复数的代数表示法及其几何意义．【分析】利用复数的几何意义、两点之间的距离公式即可得出．【解答】解：复数z=1﹣2i对应的点（1，﹣2）到原点的距离d==．故答案：．10．抛物线y2=2x的准线方程是．【考点】抛物线的简单性质．【分析】先根据抛物线方程求得p，进而根据抛物线的性质，求得答案．【解答】解：抛物线y2=2x，∴p=1，∴准线方程是x=﹣故答案为：﹣11．设a+b=M（a＞0，b＞0），M为常数，且ab的最大值为2，则M等于2．【考点】基本不等式．【分析】由基本不等式，ab≤（）2=可求ab的最大值，结合已知即可求解M【解答】解：∵a+b=M（a＞0，b＞0），由基本不等式可得，ab≤（）2=，∵ab的最大值为2，∴=2，M＞0，∴M=2，故答案为：．12．如图，在直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=CD=1，P是AB的中点，则=﹣1．【考点】平面向量数量积的运算．【分析】由题意可得△BCD为等腰直角三角形，求得BD的长，运用中点的向量表示和向量数量积的性质：向量的平方即为模的平方，计算即可得到所求值．【解答】解：在直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=CD=1，可得△BCD为等腰直角三角形，则BD=，且P是AB的中点，可得=（+），=（+）•（﹣）=（2﹣2）=[（）2﹣22]=﹣1．故答案为：﹣1．13．已知点A（1，0），B（3，0），若直线y=kx+1上存在点P，满足PA⊥PB，则k的取值范围是．【考点】直线的一般式方程与直线的垂直关系．【分析】以AB为直径圆的方程为：（x﹣1）（x﹣3）+y2=0，把y=kx+1代入上述方程可得：（1+k2）x2+（2k﹣4）x+4=0，根据直线y=kx+1上存在点P，满足PA⊥PB，可得△≥0，解出即可得出．【解答】解：以AB为直径圆的方程为：（x﹣1）（x﹣3）+y2=0，把y=kx+1代入上述方程可得：（1+k2）x2+（2k﹣4）x+4=0，∵直线y=kx+1上存在点P，满足PA⊥PB，∴△=（2k﹣4）2﹣16（1+k2）≥0，化为：3k2+4k≤0．解得0，则k的取值范围是．故答案为：．14．已知函数（1）若a=0，x∈[0，4]，则f（x）的值域是[﹣1，1] ；（2）若f（x）恰有三个零点，则实数a的取值范围是（﹣∞，0）．【考点】函数零点的判定定理；函数的值．【分析】（1）求出f（x）在[﹣4，4]上的单调性，利用单调性求出最值即可得出值域；（2）对x讨论，分别求出f（x）的零点，令其零点分别在对应的定义域上即可．【解答】解：（1）a=0时，f（x）=，∴f（x）在[0，1]上单调递减，在（1，4]上单调递增，∵f（0）=0，f（1）=﹣1，f（4）=1，∴f（x）在[0，1]上的值域是[﹣1，0]，在（1，4]上的值域是（0，1]，∴f（x）在[0，4]上的值域是[﹣1，1]．（2）当x≤1时，令f（x）=0得x=2a或x=a，当x＞1时，令f（x）=0得=1﹣a，∴x=（1﹣a）2（1﹣a＞1），∵f（x）恰好有三个解，∴，解得a＜0．故答案为：[﹣1，1]；（﹣∞，0）．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．在△ABC中，角A，B，C对应的边长分别是a，b，c，且，c=4．（Ⅰ）若，求a；（Ⅱ）若△ABC的面积等于，求a，b．【考点】余弦定理；正弦定理．【分析】（Ⅰ）由已知及正弦定理即可计算得解a的值．（Ⅱ）由已知及三角形面积公式可求ab=16，利用余弦定理可得，16=a2+b2﹣ab，联立即可解得a，b的值．【解答】（本小题共13分）解：（Ⅰ）由正弦定理可知：，从而求得…（Ⅱ）由△ABC的面积等于，可知，从而ab=16①，由余弦定理c2=a2+b2﹣2abcosC可得，16=a2+b2﹣ab②，联立①②得a=b=4．…16．已知{a n}是各项均为正数的等比数列，a11=8，设b n=log2a n，且b4=17．（Ⅰ）求证：数列{b n}是以﹣2为公差的等差数列；（Ⅱ）设数列{b n}的前n项和为S n，求S n的最大值．【考点】等差数列与等比数列的综合．【分析】（Ⅰ）利用等比数列以及对数的运算法则，转化证明数列{b n}是以﹣2为公差的等差数列；（Ⅱ）求出数列的和，利用二次函数的性质求解最大值即可．【解答】（本小题共13分）解：（Ⅰ）证明：设等比数列{a n}的公比为q，则b n﹣b n=log2a n+1﹣log2a n==log2q，+1因此数列{b n}是等差数列．又b11=log2a11=3，b4=17，又等差数列{b n}的公差，即b n=25﹣2n．即数列{b n}是以﹣2为公差的等差数列．…（Ⅱ）设等差数列{b n}的前n项和为S n，则n==（24﹣n）n=﹣（n﹣12）2+144，于是当n=12时，S n有最大值，最大值为144．…17．如图1，平行四边形ABCD中，AC⊥BC，BC=AC=1，现将△DAC沿AC折起，得到三棱锥D﹣ABC（如图2），且DA⊥BC，点E为侧棱DC的中点．（Ⅰ）求证：平面ABE⊥平面DBC；（Ⅱ）求三棱锥E﹣ABC的体积；（Ⅲ）在∠ACB的角平分线上是否存在点F，使得DF∥平面ABE？若存在，求DF的长；若不存在，请说明理由【考点】棱柱、棱锥、棱台的体积；直线与平面平行的判定；平面与平面垂直的判定．【分析】（Ⅰ）证明AE⊥CD；结合AC⊥BC，AD⊥BC，推出BC⊥平面ACD．得到AE⊥BC；证明AE⊥平面BCD，即可推出平面ABE⊥平面BCD．（Ⅱ）利用V E﹣ABC =V B﹣ACE，结合BC是三棱锥的高，求解．（Ⅲ）取AB中点O，连接CO并延长至点F，使CO=OF，连接AF，DF，BF．说明射线CO是角∠ACB的角分线．正面OE∥DF，推出DF∥平面ABE．然后最后求解DF即可．【解答】（本小题共14分）解：（Ⅰ）证明：在平行四边形ABCD中，有AD=BC=AC，又因为E为侧棱DC的中点，所以AE ⊥CD ；又因为AC ⊥BC ，AD ⊥BC ，且AC ∩AD=A ，所以BC ⊥平面ACD ． 又因为AE ⊂平面ACD ，所以AE ⊥BC ； 因为BC ∩CD=C ， 所以AE ⊥平面BCD ， 又因为AE ⊂平面ABE ， 所以平面ABE ⊥平面BCD ．…（Ⅱ）解：因为V E ﹣ABC =V B ﹣ACE ，BC ⊥平面ACD ，所以BC 是三棱锥的高，故，又因为BC=1，，，所以，所以有…（Ⅲ）解：取AB 中点O ，连接CO 并延长至点F ，使CO=OF ，连接AF ，DF ，BF ．因为BC=AC ，所以射线CO 是角∠ACB 的角分线．又因为点E 是的CD 中点，所以OE ∥DF ， 因为OE ⊂平面ABE ，DF ⊄平面ABE ， 所以DF ∥平面ABE ． 因为AB 、FC 互相平分，故四边形ACBF 为平行四边形，有BC ∥AF ． 又因为DA ⊥BC ，所以有AF ⊥AD ，又因为AF=AD=1，故．…18．某校学生营养餐由A 和B 两家配餐公司配送．学校为了解学生对这两家配餐公司的满意度，采用问卷的形式，随机抽取了40名学生对两家公司分别评分．根据收集的80份问卷的评分，得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表：（Ⅰ）根据A公司的频率分布直方图，估计该公司满意度评分的中位数；（Ⅱ）从满意度高于90分的问卷中随机抽取两份，求这两份问卷都是给A公司评分的概率；（Ⅲ）请从统计角度，对A、B两家公司做出评价．【考点】众数、中位数、平均数；古典概型及其概率计算公式．【分析】（Ⅰ）设出中位数，根据频率分布直方图求出中位数的值即可；（Ⅱ）意度高于9的问卷共有6份，其中4份评价A公司，设为a1，a2，a3，a4，2份评价B公司，设为b1，b2，求出满足条件的个数，求出满足条件的概率即可；（Ⅲ）根据A公司得分的中位数低于B公司得分的中位数，A公司得分的平均数数低于B公司得分的平均数，得出结论即可．【解答】解：（Ⅰ）设A公司调查的40份问卷的中位数为x，则有0.015×10+0.025×10+0.03×（x﹣70）=0.5解得：x≈73.3所以，估计该公司满意度得分的中位数为73.3 …（Ⅱ）满意度高于9的问卷共有6份，其中4份评价A公司，设为a1，a2，a3，a4，2份评价B公司，设为b1，b2．从这6份问卷中随机取2份，所有可能的结果有：（a1，a2），（a1，a3），（a1，a4），（a1，b1），（a1，b2），（a2，a3），（a2，a4），（a2，b1），（a2，b2），（a3，a4），（a3，b1），（a3，b2），（a4，b1），（a4，b2），（b1，b2），共有15种．其中2份问卷都评价A公司的有以下6种：（a1，a2），（a1，a3），（a1，a4），（a2，a3），（a2，a4），（a3，a4）．设两份问卷均是评价A公司为事件C，则有．…（Ⅲ）由所给两个公司的调查满意度得分知：A公司得分的中位数低于B公司得分的中位数，A公司得分集中在[70，80）这组，而B公司得分集中在[70，80）和[80，90）两个组，A公司得分的平均数数低于B公司得分的平均数，A公司得分比较分散，而B公司得分相对集中，即A公司得分的方差高于B公司得分的方差．…19．已知P（0，1）是椭圆C：=1（a＞b＞0）上一点，点P到椭圆C的两个焦点的距离之和为2．（Ⅰ）求椭圆C的方程；（Ⅱ）设A，B是椭圆C上异于点P的两点，直线PA与直线x=4交于点M，是=？若存在，求出点A的坐标；若不存在，请说否存在点A，使得S△ABP明理由．【考点】圆锥曲线的存在性问题；椭圆的标准方程；直线与椭圆的位置关系．【分析】（Ⅰ）由椭圆C：过点P（0，1）可得b=1，然后求解a，即可求解椭圆的方程．（Ⅱ）设A（m，n），直线PA的方程为：，求出M，通过等价于且点A在y轴的右侧，党的，求出A（，），可得结果．【解答】（本小题共14分）解：（Ⅰ）由椭圆C：过点P（0，1）可得b=1，又点P到两焦点距离和为，可得，所以椭圆C的方程．…（Ⅱ）设A（m，n），依题意得：直线PA的斜率存在，则直线PA的方程为：，令x=4，，即M，又等价于且点A在y轴的右侧，从而，因为点A在y轴的右侧，所以，解得，由点A在椭圆上，解得：，于是存在点A（，），使得．…20．已知函数，A（x1，m），B（x2，m）是曲线y=f（x）上两个不同的点．（Ⅰ）求f（x）的单调区间，并写出实数m的取值范围；（Ⅱ）证明：x1+x2＞0．【考点】利用导数研究函数的单调性．【分析】（Ⅰ）求出函数的导数，解关于导函数的不等式，求出函数的单调区间，得到m的范围即可；（Ⅱ）问题转化为证f（x1）＜f（﹣x1），只需证（x1∈（﹣1，0）），令h（x）=（x﹣1）e2x+x+1＜0，则h'（x）=（2x﹣1）e2x+1，根据函数的单调性证明即可．【解答】解：f（x）的定义域为R．（Ⅰ），由f'（x）=0得，x=0，由f'（x）＞0得，x＜0，由f'（x）＜0得，x＞0，所以f（x）的单调增区间为（﹣∞，0），单调减区间为（0，+∞），m的取值范围是（0，1）．…（Ⅱ）由（Ⅰ）知，x1∈（﹣1，0），要证x2＞﹣x1＞0，只需证f（x2）＜f（﹣x1）因为f（x1）=f（x2）=m，所以只需证f（x1）＜f（﹣x1），只需证，只需证（x1∈（﹣1，0））令h（x）=（x﹣1）e2x+x+1＜0，则h'（x）=（2x﹣1）e2x+1，因为（h'（x））'=4xe2x＜0，所以h'（x）在（﹣1，0）上单调递减，所以h'（x）＞h'（0）=0，所以h（x）在（﹣1，0）上单调递增，所以h（x）＜h（0）=0，所以，故x1+x2＞0…2017年4月15日。

2017北京市丰台区初三（一模）语文一、基础·运用（共18分）1．阅读下面的文字，完成（1）-（3）题。

（共7分）脸谱是中国戏曲独有的、在舞台演出中使用的一种化妆造型艺术。

从戏曲的角度来讲，它是性格化的；从美术的角度来看，它是图案式的。

在漫长的岁月里，脸谱随着戏曲艺术的发展孕育形成，逐渐成熟，并以谱式的方法相对固定下来。

京剧脸谱一般用于净丑行．当，以夸张的色彩和醒目的图案来表现舞台角色迥异于常人的性格特征。

它大胆借鉴民间艺术的装饰技法和用色原则，通过对各种艺术元素的提（练、炼）、加工、转化，形成了独特的艺术风格。

京剧脸谱用色根据传统的民族习惯和心理感受，赋予色彩极强的象征意义。

红脸含有褒义，代表忠勇；黑脸为中性，代表猛智；蓝脸和绿脸也为中性，代表草莽英雄；黄脸和白脸含贬义，代表奸诈凶恶；金脸和银脸是神秘，代表神妖。

用色注重色彩的强烈对比，如京剧舞台上包拯这一角色的脸谱，在黑色的整脸上，独勾出两条扭曲的白眉，黑色的额头上勾画出一弯白色的月形，形成强烈的黑白对比，用以体现角色铁面无私、爱憎．分明的性格特点。

（1）对文中划线字笔顺和横线处选填汉字判断全都正确的一项是（2分）A. “式”字的笔顺是：练B. “式”字的笔顺是：练C. “式”字的笔顺是：炼D. “式”字的笔顺是：炼（2）文中加点字注音都正确的一项是（2分）A．行．（hánɡ）当爱憎．（zēnɡ）分明B．行．（xínɡ）当爱憎．（zēnɡ）分明C．行．（hánɡ）当爱憎．（zènɡ）分明D．行．（xínɡ）当爱憎．（zènɡ）分明（3）为了让传统京剧在现代社会焕发新的生机，艺术家们将我国的传统戏曲元素巧妙地融入到歌曲之中，使整首歌听起来琅琅上口，亦歌亦戏，这就是戏歌。

下面是戏歌《说唱脸谱》里面的歌词节选，选择【甲】【乙】【丙】中任意一处，为人物脸谱配色，并阐明理由。

（3分）蓝脸的窦尔敦盗御马红脸的关公战长沙黄脸的典韦【甲】的曹操【乙】的张飞叫喳喳……紫色的天王托宝塔绿色的魔鬼斗夜叉【丙】的猴王银色的妖怪灰色的精灵笑哈哈……选择：脸谱颜色：理由：2．梅兰芳、荀慧生、程砚秋、尚小云被誉为“京剧四大名旦”，他们开启了京剧舞台的鼎盛时代。

北京丰台区高三年级2016-2017学年度第一次综合练习数学试卷（文科）2017．3一、选择题：共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．如果集合{}21A x Z x =∈-≤<，{}101B =-， ， ，那么A B =（ ）A ．{}2101--， ， ，B ．{}101-， ，C ．{}01，D ．{}10-，2．在平面直角坐标系xOy 中，与原点位于直线3250x y ++=同一侧的点是（ ） A ．()34-，B ．()32--，C ．()34--，D ．()03-，3．执行如图所示的程序框图，则输出的i 的值是（ ） A ．3 B ．4 C ．5D ．64．设命题[):01xp x e ∀∈+∞≥，，，则p ⌝是（ ） A ．[)0001xx e ∃∉+∞<，，B ．[)01xx e ∀∉+∞<，，C ．[)0001xx e ∃∈+∞<，，D ．[)01xx e ∀∈+∞<，，5．如果0.31.22122log 2a b c ⎛⎫=== ⎪⎝⎭，， ）A ．c b a >>B ．c a b >>C ．a b c >>D ．a c b >>6．由一个正方体截去一个三棱锥所得的几何体的直观图如图所示，则该几何体的三视图正确的是（ ）A ．B ．C ．D ．7．已知函数()sin 3f x x πω⎛⎫=-⎪⎝⎭，点()A m n ，，()B m n π+，（1n ≠）都在曲线()y f x =上，且线段AB 与曲线()y f x =有五个公共点，则()x ω的值是（ ） A ．4B ．2C ．12D ．148．某校举行了以“重温时代经典，唱响回声嘹亮”为主题的“红歌”歌咏比赛．该校高一年级有1234， ， ， 四个班参加了比赛，其中有两个班获奖．比赛结果揭晓之前，甲同学说：“两个获奖班级在2班、3班、4班中”，乙同学说：“2班没有获奖，3班获奖了”，丙同学说：“1班、4班中有且只有一个班获奖”，丁同学说：“乙说得对”．已知这四人中有且只有两人的说法是正确的，则这两人是（ ） A ．乙，丁B ．甲，丙C ．甲，丁D ．乙，丙二、填空题共6小题，每小题5分，共30分．9．在复平面内，复数12z i =-对应的点到原点的距离是_________． 10．抛物线22y x =准线方程是_________．11．设()00a b M a b M +=>>，，为常数，且ab 的最大值为2，则M 等于_________．12．如图，在直角梯形ABCD 中，//AD BC ，90ADC ∠=，21AD BC CD ===，，P 是AB 的中点，则DP AB ⋅=_________．13．已知点()()1030A B ， ，， ，若直线1y kx =+上存在点P ，满足PA PB ⊥，则k 的取值范围是_________．14．已知函数()()()2111x a a x x f x a x --≤⎧⎪=->，，（1）若[]004a x =∈，， ，则()f x 的值域是_________； （2）若()f x 恰有三个零点，则实数a 的取值范围是_________．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题满分13分）在ABC ∆中，角A B C ，，对应的边长分别是a b c ，，，且43C c π==，．（Ⅰ）若3sin 4A =，求a ；（Ⅱ）若ABC ∆的面积等于a b ，．已知{}n a 是各项均为正数的等比数列，118a =，设2log n n b a =，且417b =． （Ⅰ）求证：数列{}n b 是以2-为公差的等差数列； （Ⅱ）设数列{}n b 的前n 项和为n S ，求n S 的最大值．如图1，平行四边形ABCD 中，1AC BC BC AC ⊥==，，现将DAC ∆沿AC 折起，得到三棱锥D ABC -（如图2），且DA BC ⊥，点E 为侧棱DC 的中点．（Ⅰ）求证：平面ABE ⊥平面DBC ； （Ⅱ）求三棱锥E ABC -的体积；（Ⅲ）在ACB ∠的角平分线上是否存在点F ，使得//DF 平面ABE ？若存在，求DF 的长；若不存在，请说明理由（Ⅰ）根据B公司的频率分布直方图，估计该公司满意度评分的中位数；（Ⅱ）从满意度高于90分的问卷中随机抽取两份，求这两份问卷都是给A公司评分的概率；，两家公司做出评价．（Ⅲ）请从统计角度，对A B已知()01P ， 是椭圆()2222:=10x y C a b a b+>>上一点，点P 到椭圆C 的两个焦点的距离之和为（Ⅰ）求椭圆C 的方程；（Ⅱ）设A B ，是椭圆C 上异于点P 的两点，直线PA 与直线4x =交于点M ，是否存在点A ，使得12ABP ABM S S ∆∆=？若存在，求出点A 的坐标；若不存在，请说明理由．已知函数()()()121xx f x A x m B x m e +=，，，，是曲线()y f x =上两个不同的点． （Ⅰ）求()f x 的单调区间，并写出实数m 的取值范围； （Ⅱ）证明：120x x +>．2017年北京市丰台区高考数学一模试卷（文科）参考答案与试题解析一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）如果集合A={x∈Z|﹣2≤x＜1}，B={﹣1，0，1}，那么A∩B=（）A．{﹣2，﹣1，0，1} B．{﹣1，0，1} C．{0，1} D．{﹣1，0}【解答】解：∵集合A={x∈Z|﹣2≤x＜1}={﹣2，﹣1，0}，B={﹣1，0，1}，∴A∩B={﹣1，0}．故选：D．2．（5分）在平面直角坐标系xOy中，与原点位于直线3x+2y+5=0同一侧的点是（）A．（﹣3，4）B．（﹣3，﹣2）C．（﹣3，﹣4）D．（0，﹣3）【解答】解：当x=0，y=0时，0+0+5＞0，对于A：当x=﹣3，y=4时，﹣9+8+5＞0，故满足，对于B：当x=﹣3，y=﹣2时，﹣9﹣4+5＜0，故不满足，对于C：x=﹣3，y=﹣4，﹣9﹣8+5＜0，故不满足，对于D：x=﹣3，y=﹣2时，0﹣6+5＜0，故不满足，故选：A3．（5分）执行如图所示的程序框图，则输出的i的值是（）A．3 B．4 C．5 D．6【解答】解：第一次执行循环体后，S=2，不满足退出循环的条件，i=2；再次执行循环体后，S=6，不满足退出循环的条件，i=3；再次执行循环体后，S=14，不满足退出循环的条件，i=4；再次执行循环体后，S=30，满足退出循环的条件，故输出的i值为4，故选：B．4．（5分）设命题p：∀x∈[0，+∞），e x≥1，则￢p是（）A．∃x0∉[0，+∞），＜B．∀x∉[0，+∞），e x＜1C．∃x0∈[0，+∞），＜D．∀x∈[0，+∞），e x＜1【解答】解：因为命题p是全称命题，所以利用全称命题的否定是特称命题可得：￢p：∃x0∈[0，+∞），＜．故选：C5．（5分）如果，，，那么（）A．c＞b＞a B．c＞a＞b C．a＞b＞c D．a＞c＞b【解答】解：a=21.2＞2，＜1，c=2=log23∈（1，2）．∴a＞c＞b．故选：D．6．（5分）由一个正方体截去一个三棱锥所得的几何体的直观图如图所示，则该几何体的三视图正确的是（）A．B．C．D．【解答】解：根据三视图的画法，可得俯视图、侧视图，故选D．7．（5分）已知函数，点A（m，n），B（m+π，n）（|n|≠1）都在曲线y=f（x）上，且线段AB与曲线y=f（x）有五个公共点，则ω的值是（）A．4 B．2 C．D．【解答】解：由题意，2T=π，∴T=，∴ω=4，故选A．8．（5分）某校举行了以“重温时代经典，唱响回声嘹亮”为主题的“红歌”歌咏比赛．该校高一年级有1，2，3，4四个班参加了比赛，其中有两个班获奖．比赛结果揭晓之前，甲同学说：“两个获奖班级在2班、3班、4班中”，乙同学说：“2班没有获奖，3班获奖了”，丙同学说：“1班、4班中有且只有一个班获奖”，丁同学说：“乙说得对”．已知这四人中有且只有两人的说法是正确的，则这两人是（）A．乙，丁B．甲，丙C．甲，丁D．乙，丙【解答】解：根据题意，由于甲乙丙丁四人中有且只有两人的说法是正确的，假设乙的说法是正确的，则丁也是正确的，那么甲丙的说法都是错误的，如果丙同学说：“1班、4班中有且只有一个班获奖”是错误的，那么1班、4班都获奖或1班、4班都没有获奖，与乙的说法矛盾，故乙的说法是错误，则丁同学说：“乙说得对”也是错误的；故说法正确的是甲、丙，故选：B．二、填空题共6小题，每小题5分，共30分．9．（5分）在复平面内，复数z=1﹣2i对应的点到原点的距离是．【解答】解：复数z=1﹣2i对应的点（1，﹣2）到原点的距离d==．故答案：．10．（5分）抛物线y2=2x的准线方程是．【解答】解：抛物线y2=2x，∴p=1，∴准线方程是x=﹣故答案为：﹣11．（5分）设a+b=M（a＞0，b＞0），M为常数，且ab的最大值为2，则M等于2．【解答】解：∵a+b=M（a＞0，b＞0），由基本不等式可得，ab≤（）2=，∵ab的最大值为2，∴=2，M＞0，∴M=2故答案为：．12．（5分）如图，在直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=CD=1，P是AB的中点，则=﹣1．【解答】解：在直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=CD=1，可得△BCD为等腰直角三角形，则BD=，且P是AB的中点，可得=（+），=（+）•（﹣）=（2﹣2）=[（）2﹣22]=﹣1．故答案为：﹣1．13．（5分）已知点A（1，0），B（3，0），若直线y=kx+1上存在点P，满足P A⊥PB，则k的取值范围是，．【解答】解：以AB为直径圆的方程为：（x﹣1）（x﹣3）+y2=0，把y=kx+1代入上述方程可得：（1+k2）x2+（2k﹣4）x+4=0，∵直线y=kx+1上存在点P，满足P A⊥PB，∴△=（2k﹣4）2﹣16（1+k2）≥0，化为：3k2+4k≤0．解得0，则k的取值范围是，．故答案为：，．14．（5分）已知函数，，＞（1）若a=0，x∈[0，4]，则f（x）的值域是[﹣1，1]；（2）若f（x）恰有三个零点，则实数a的取值范围是（﹣∞，0）．【解答】解：（1）a=0时，f（x）=，，＞，∴f（x）在[0，1]上单调递减，在（1，4]上单调递增，∵f（0）=0，f（1）=﹣1，f（4）=1，∴f（x）在[0，1]上的值域是[﹣1，0]，在（1，4]上的值域是（0，1]，∴f（x）在[0，4]上的值域是[﹣1，1]．（2）当x≤1时，令f（x）=0得x=2a或x=a，当x＞1时，令f（x）=0得=1﹣a，∴x=（1﹣a）2（1﹣a＞1），∵f（x）恰好有三个解，，解得a＜0．∴＞＞故答案为：[﹣1，1]；（﹣∞，0）．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（13分）在△ABC中，角A，B，C对应的边长分别是a，b，c，且，c=4．（Ⅰ）若，求a；（Ⅱ）若△ABC的面积等于，求a，b．【解答】（本小题共13分）解：（Ⅰ）由正弦定理可知：，从而求得…（6分）（Ⅱ）由△ABC的面积等于，可知△ ，从而ab=16①，由余弦定理c2=a2+b2﹣2abcosC可得，16=a2+b2﹣ab②，联立①②得a=b=4．…（13分）16．（13分）已知{a n}是各项均为正数的等比数列，a11=8，设b n=log2a n，且b4=17．（Ⅰ）求证：数列{b n}是以﹣2为公差的等差数列；（Ⅱ）设数列{b n}的前n项和为S n，求S n的最大值．【解答】（本小题共13分）解：（Ⅰ）证明：设等比数列{a n}的公比为q，则b n+1﹣b n=log2a n+1﹣log2a n==log2q，因此数列{b n}是等差数列．又b11=log2a11=3，b4=17，又等差数列{b n}的公差，即b n=25﹣2n．即数列{b n}是以﹣2为公差的等差数列．…（6分）（Ⅱ）设等差数列{b n}的前n项和为S n，则n==（24﹣n）n=﹣（n﹣12）2+144，于是当n=12时，S n有最大值，最大值为144．…（13分）17．（14分）如图1，平行四边形ABCD中，AC⊥BC，BC=AC=1，现将△DAC沿AC折起，得到三棱锥D ﹣ABC（如图2），且DA⊥BC，点E为侧棱DC的中点．（Ⅰ）求证：平面ABE⊥平面DBC；（Ⅱ）求三棱锥E﹣ABC的体积；（Ⅲ）在∠ACB的角平分线上是否存在点F，使得DF∥平面ABE？若存在，求DF的长；若不存在，请说明理由【解答】（本小题共14分）解：（Ⅰ）证明：在平行四边形ABCD中，有AD=BC=AC，又因为E为侧棱DC的中点，所以AE⊥CD；又因为AC⊥BC，AD⊥BC，且AC∩AD=A，所以BC⊥平面ACD．又因为AE⊂平面ACD，所以AE⊥BC；因为BC∩CD=C，所以AE⊥平面BCD，又因为AE⊂平面ABE，所以平面ABE⊥平面BCD．…（5分）（Ⅱ）解：因为V E﹣ABC=V B﹣ACE，BC⊥平面ACD，所以BC是三棱锥的高，故△ ，又因为BC=1，，，所以△ ，所以有△ …（9分）（Ⅲ）解：取AB中点O，连接CO并延长至点F，使CO=OF，连接AF，DF，BF．因为BC=AC，所以射线CO是角∠ACB的角分线．又因为点E是的CD中点，所以OE∥DF，因为OE⊂平面ABE，DF⊄平面ABE，所以DF∥平面ABE．因为AB、FC互相平分，故四边形ACBF为平行四边形，有BC∥AF．又因为DA⊥BC，所以有AF⊥AD，又因为AF=AD=1，故．…（14分）18．（13分）某校学生营养餐由A和B两家配餐公司配送．学校为了解学生对这两家配餐公司的满意度，采用问卷的形式，随机抽取了40名学生对两家公司分别评分．根据收集的80份问卷的评分，得到如图A 公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表：（Ⅰ）根据A公司的频率分布直方图，估计该公司满意度评分的中位数；（Ⅱ）从满意度高于90分的问卷中随机抽取两份，求这两份问卷都是给A公司评分的概率；（Ⅲ）请从统计角度，对A、B两家公司做出评价．【解答】解：（Ⅰ）设A公司调查的40份问卷的中位数为x，则有0.015×10+0.025×10+0.03×（x﹣70）=0.5解得：x≈73.3所以，估计该公司满意度得分的中位数为73.3 …（4分）（Ⅱ）满意度高于9（0分）的问卷共有6份，其中4份评价A公司，设为a1，a2，a3，a4，2份评价B公司，设为b1，b2．从这6份问卷中随机取2份，所有可能的结果有：（a1，a2），（a1，a3），（a1，a4），（a1，b1），（a1，b2），（a2，a3），（a2，a4），（a2，b1），（a2，b2），（a3，a4），（a3，b1），（a3，b2），（a4，b1），（a4，b2），（b1，b2），共有15种．其中2份问卷都评价A公司的有以下6种：（a1，a2），（a1，a3），（a1，a4），（a2，a3），（a2，a4），（a3，a4）．设两份问卷均是评价A公司为事件C，则有．…（9分）（Ⅲ）由所给两个公司的调查满意度得分知：A公司得分的中位数低于B公司得分的中位数，A公司得分集中在[70，80）这组，而B公司得分集中在[70，80）和[80，90）两个组，A公司得分的平均数数低于B公司得分的平均数，A公司得分比较分散，而B公司得分相对集中，即A公司得分的方差高于B公司得分的方差．…（13分）19．（14分）已知P（0，1）是椭圆C：=1（a＞b＞0）上一点，点P到椭圆C的两个焦点的距离之和为2．（Ⅰ）求椭圆C的方程；（Ⅱ）设A，B是椭圆C上异于点P的两点，直线P A与直线x=4交于点M，是否存在点A，使得S△ABP=△ ？若存在，求出点A的坐标；若不存在，请说明理由．【解答】（本小题共14分）解：（Ⅰ）由椭圆C：＞＞过点P（0，1）可得b=1，又点P到两焦点距离和为所以椭圆C的方程．…（4分）（Ⅱ）设A（m，n），依题意得：直线P A的斜率存在，则直线P A的方程为：，令x=4，，即M，，又△ △ 等价于且点A在y轴的右侧，从而，因为点A在y轴的右侧，所以，解得，由点A在椭圆上，解得：，于是存在点A（，），使得△ △ ．…（14分）20．（13分）已知函数，A（x1，m），B（x2，m）是曲线y=f（x）上两个不同的点．（Ⅰ）求f（x）的单调区间，并写出实数m的取值范围；（Ⅱ）证明：x1+x2＞0．【解答】解：f（x）的定义域为R．（Ⅰ），由f'（x）=0得，x=0，由f'（x）＞0得，x＜0，由f'（x）＜0得，x＞0，所以f（x）的单调增区间为（﹣∞，0），单调减区间为（0，+∞），m的取值范围是（0，1）．…（6分）（Ⅱ）由（Ⅰ）知，x1∈（﹣1，0），要证x2＞﹣x1＞0，只需证f（x2）＜f（﹣x1）因为f（x1）=f（x2）=m，所以只需证f（x1）＜f（﹣x1），只需证＜，只需证＜（x1∈（﹣1，0））令h（x）=（x﹣1）e2x+x+1＜0，则h'（x）=（2x﹣1）e2x+1，因为（h'（x））'=4xe2x＜0，所以h'（x）在（﹣1，0）上单调递减，所以h'（x）＞h'（0）=0，所以h（x）在（﹣1，0）上单调递增，所以h（x）＜h（0）=0，所以＞，故x1+x2＞0…（13分）。

丰台区2017年初三毕业及统一练习数学试卷2017. 05一、选择题（本题共30分，每小题3分）下列各题均有四个选项，其中只有一个．．是符合题意的． 1．随着“一带一路”的建设推进，北京丰台口岸进口货值业务量加速增长，2016年北京丰台口岸进口货值飙升至189 000 000美元，比上一年翻了三倍，创下历史新高．将189 000 000用科学记数法表示应为 A ．610189⨯ B ．610891⨯. C ．710918⨯. D ．810891⨯. 2．实数a ，b 在数轴上的对应点的位置如图所示，则正确的结论是A ．b a >B ．a b <C ．a a <-D ．a b <-3．北京教育资源丰富，高校林立，下面四个高校校徽主体图案是中心对称图形的是北京林业大学 北京体育大学 北京大学 中国人民大学A ．B ．C ．D ．4．如图，香港特别行政区标志紫荆花图案绕中心旋转n °后能与原来的图案互相重合，则n 的最小值为A ．45B ．60C ．72D ．1445．在与国际友好学校交流活动中，小敏打算制做一个正方体礼盒送给外国朋友，每个面上分别书写一种中华传统美德，一共有“仁义礼智信孝”六个字．如图是她设计的礼盒平面展开图，那么“礼”字对面的字是 A ．义 B ．仁C ．智D ．信6. 如果0222=-+m m ，那么代数式2442+⋅⎪⎭⎫ ⎝⎛++m m m m m 的值是 A ．-2 B ．-1 C ．2 D ．3◇仁 ◇义◇礼 ◇智 ◇信 ◇孝0a b132-1-2-347．如图，比例规是一种画图工具，它由长度相等的两脚AC 和BD 交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方（即同时使OA =3OC ，OB =3OD ），然后张开两脚，使A ，B 两个尖端分别在线段a 的两个端点上，当CD =1.8cm 时，则AB 的长为A ．7.2 cmB ．5.4 cmC ．3.6 cmD ．0.6 cm8．如图，这是小新在询问了父母后绘制的去年全家的开支情况扇形统计图，如果他家去年总开支为6万元，那么用于教育的支出为 A ．3万元 B ．35万元 C ．2.4万元 D ．2万元9．如图，在正方形网格中，如果点A （1，1），B （2，0），那么点C 的坐标为 A ．（-3，-2）B ．（3，-2）C ．（-2，-3）D ．（2，-3）10．近年来由于空气质量的变化，以及人们对自身健康的关注程度不断提高，空气净化器成为很多家庭的新电器．某品牌的空气净化器厂家为进一步了解市场，制定生产计划，根据2016年下半年销售情况绘制了如下统计图，其中同比增长率%1001⨯⎪⎪⎭⎫⎝⎛-=去年同月销售量当月销售量，下面有四个推断： ①2016年下半年各月销售量均比2015年同月销售量增多 ②第四季度销售量占下半年销售量的七成以上 ③下半年月均销售量约为16万台④下半年月销售量的中位数不超过10万台其中合理的是 A ．①② B ．①④ C ．②③ D ．③④二、填空题（本题共18分，每小题3分）某品牌空气净化器下半年销售情况统计图10203040销售量/万台-10%0%10%20%30%40%同比增长率销售量同比增长率销售量89.39.813.419.736同比增长率-2.3%6.5%5.2%15.1%20.7%35.9%7月8月9月10月11月12月ABC教育医疗食品交通娱乐其它120°55°100°35°30°aA BD C11．如果二次根式4 x 有意义，那么x 的取值范围是__________．12．右图中的四边形均为矩形，根据图形的面积关系，写出一个正确的等式：_____________________．13．一天上午林老师来到某中学参加该校的校园开放日活动，他打算随机听一节九年级的课程，下表是他拿到的当天上午九年级的课表，如果每一个班级的每一节课被听的可能性是一样的，那么听数学课的可能性是__________．班级 节次 1班 2班 3班 4班 第1节 语文 数学 外语 化学 第2节 数学 政治 物理 语文 第3节 物理 化学 体育 数学 第4节外语语文政治体育14．如下图，小量角器的0°刻度线在大量角器的0°刻度线上，且小量角器的中心在大量角器的外缘边上．如果它们外缘边上的公共点P 在大量角器上对应的度数为40°，那么在小量角器上对应的度数为______________．（只考虑小于90°的角度）15．众所周知，中华诗词博大精深，集大量的情景情感于短短数十字之间，或豪放，或婉约，或思民生疾苦，或抒发己身豪情逸致，文化价值极高．而数学与古诗词更是有着密切的联系．古诗中，五言绝句是四句诗，每句都是五个字；七言绝句是四句诗，每句都是七个字．有一本诗集，其中五言绝句比七言绝句多13首，总字数却反而少了20个字．问两种诗各多少首？设七言绝句有x 首，根据题意，可列方程为____________________．16．在数学课上，老师提出如下问题：a nm c b P小姗的作法如下：老师说：“小姗的作法正确”．请回答：得到△ABC 是等腰三角形的依据是：____________________________． 三、解答题（本题共72分，第17~26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明、演算步骤或证明过程. 17．计算：()3360cos 4120--︒+--π．18．解不等式组：()⎪⎩⎪⎨⎧-≤-->-.3951 106 2 x x x x ，19．如图，四边形ABCD 中，AB ∥DC ，∠B = 90º，F 为DC 上一点，且AB =FC ，E 为AD 上一点，EC 交AF 于点G ，EA = EG ． 求证：ED = EC ．20．已知关于x 的一元二次方程0432=-+-k kx x ．如图，（1）作线段BC =a ；（2）作线段BC 的垂直平分线MN 交线段BC 于点D ； （3）在MN 上截取线段DA =b ，连接AB ，AC ．所以，△ABC 就是所求作的等腰三角形．已知：线段a ，b ． 求作：等腰△ABC ，使AB =AC ，BC =a ，BC 边上的高为b ． G F ED CBAa bMNAB CD（1）判断方程根的情况；（2）若此方程有一个整数根，请选择一个合适的k 值，并求出此时方程的根．21．如图，在平面直角坐标系xOy 中，直线m x y +-=3与双曲线xky =相交于点A （m ，2）． （1）求双曲线xky =的表达式；（2）过动点P (n ，0)且垂直于x 轴的直线与直线m x y +-=3及双曲线xky =的交点分别为B 和C ，当点B 位于点C 下方时，求出n 的取值范围．22．课题学习：设计概率模拟实验．yx2A O在学习概率时，老师说：“掷一枚质地均匀的硬币，大量重复实验后，正面朝上的概率约是21．”小海、小东、小英分别设计了下列三个模拟实验：小海找来一个啤酒瓶盖（如图1）进行大量重复抛掷，然后计算瓶盖口朝上的次数与总次数的比值；小东用硬纸片做了一个圆形转盘，转盘上分成8个大小一样的扇形区域，并依次标上1至8个数字（如图2），转动转盘10次，然后计算指针落在奇数区域的次数与总次数的比值；小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子（如图3），其中有三枚是白子，一枚是黑子，从中随机同时摸出两枚棋子，并大量重复上述实验，然后计算摸出的两枚棋子颜色不同的次数与总次数的比值．图1 图2 图3 根据以上材料回答问题：小海、小东、小英三人中，哪一位同学的实验设计比较合理，并简要说出其他两位同学实验的不足之处．23．如图，在四边形ABCD 中，∠ABC =90°，DE ⊥AC 于点E ，且AE = CE ，DE =5，EB =12． （1）求AD 的长；（2）若∠CAB =30°，求四边形ABCD 的周长．24．阅读下列材料：67854321ABCD E由于发展时间早、发展速度快，经过20多年大规模的高速开发建设，北京四环内，甚至五环内可供开发建设的土地资源越来越稀缺，更多的土地供应将集中在五环外，甚至六环外的远郊区县．据中国经济网2017年2月报道，来自某市场研究院的最新统计，2016年，剔除了保障房后，在北京新建商品住宅交易量整体上涨之时，北京各区域的新建商品住宅交易量则是有涨有跌．其中，昌平、通州、海淀、朝阳、西城、东城六区下跌，跌幅最大的为朝阳区，新建商品住宅成交量比2015年下降了46.82%．而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨，涨幅最大的为顺义区，比2015年上涨了118.80%．另外，从环线成交量的占比数据上，同样可以看出成交日趋郊区化的趋势．根据统计，2008年到2016年，北京全市成交的新建商品住宅中，二环以内的占比逐步从3.0%下降到了0.2%；二、三环之间的占比从5.7%下降到了0.8%；三、四环之间的占比从12.3%下降到了2.3%；四、五环之间的占比从21.9%下降到了4.4%．也就是说，整体成交中位于五环之内的新房占比，从2008年的42.8%下降到了2016年的7.7%，下滑趋势非常明显．由此可见，新房市场的远郊化是北京房地产市场发展的大势所趋．（注：占比，指在总数中所占的比重，常用百分比表示）根据以上材料解答下列问题： （1）补全折线统计图；（2）根据材料提供的信息，预估 2017年位于北京市五环之内新建商品住宅成交量占比约_________，你的预估理由是________________________________．2008年和2016年新建商品住宅环线成交量占比折线统计图0%10%20%30%40%50%60%70%80%90%100%二环以内二、三环之间三、四环之间四、五环之间五环以外环线成交量占比2008年2016年25．如图，AB 是⊙O 的直径，C ，D 为⊙O 上两点，CF ⊥AB 于点F ，CE ⊥AD 交AD 的延长线于点E ，且CE =CF ．（1）求证：CE 是⊙O 的切线；（2）连接CD ，CB ．若AD =CD =a ，写出求四边形ABCD 面积的思路．26．【问题情境】已知矩形的面积为a （a 为常数，0>a ），当该矩形的长为多少时，它的周长最小?最小值是多少?【数学模型】设该矩形的长为x ，周长为y ，则y 与x 的函数表达式为⎪⎭⎫⎝⎛+=x a x y 2()0>x ． 【探索研究】小彬借鉴以前研究函数的经验，先探索函数xx y 1+=的图象性质． （1）结合问题情境，函数xx y 1+=的自变量x 的取值范围是0>x ，下表是y 与x 的几组对应值． x … 41 31211 2 3 m … y…414 313 212 2 212 313 414 …①写出m 的值；②画出该函数图象，结合图象，得出当x =______时，y 有最小值，y 最小=________； 【解决问题】（2）直接写出“问题情境”中问题的结论．O FE DCBAOyx1243124327．在平面直角坐标系xOy 中，抛物线()01242≠-+-=m m mx mx y 与平行于x 轴的一条直线交于A ，B 两点．（1）求抛物线的对称轴；（2）如果点A 的坐标是（-1，-2），求点B 的坐标；（3）抛物线的对称轴交直线AB 于点C ， 如果直线AB 与y 轴交点的纵坐标为-1，且抛物线顶点D 到点C 的距离大于2，求m 的取值范围．Oyx-1-2-4-3-5-1-2-4-5-3124351243528．在边长为5的正方形ABCD 中，点E ，F 分别是BC ，DC 边上的两个动点（不与点B ，C ，D 重合），且AE ⊥EF ．（1）如图1，当BE = 2时，求FC 的长；（2）延长EF 交正方形ABCD 外角平分线CP 于点P ．①依题意将图2补全；②小京通过观察、实验提出猜想：在点E 运动的过程中，始终有AE =PE ．小京把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的三种想法：想法1：在AB 上截取AG =EC ，连接EG ，要证AE =PE ，需证△AGE ≌△ECP ． 想法2：作点A 关于BC 的对称点H ，连接BH ，CH ，EH ．要证AE =PE ， 需证△EHP 为等腰三角形．想法3：将线段BE 绕点B 顺时针旋转90°，得到线段BM ，连接CM ，EM ， 要证AE =PE ，需证四边形MCPE 为平行四边形． 请你参考上面的想法，帮助小京证明AE =PE ．（一种方法即可）图1 图229．在平面直角坐标系xOy 中，对于任意三点A ，B ，C ，给出如下定义：FA BCD EF A BCDE如果矩形的任何一条边均与某条坐标轴平行，且A ，B ，C 三点都在矩形的内部或边界上，则称该矩形为点A ，B ，C 的覆盖矩形．点A ，B ，C 的所有覆盖矩形中，面积最小的矩形称为点A ，B ，C 的最优覆盖矩形．例如，下图中的矩形A 1B 1C 1D 1，A 2B 2C 2D 2，AB 3C 3D 3都是点A ，B ，C 的覆盖矩形，其中矩形AB 3C 3D 3是点A ，B ，C 的最优覆盖矩形．（1）已知A (-2，3)，B (5，0)，C (t ，-2)．①当2=t 时，点A ，B ，C 的最优覆盖矩形的面积为_____________； ②若点A ，B ，C 的最优覆盖矩形的面积为40，求直线AC 的表达式；（2）已知点D (1，1)．E (m ，n )是函数)0(4>=x xy 的图象上一点，⊙P 是点O ，D ，E 的一个面积最小的最优覆盖矩形的外接圆，求出⊙P 的半径r 的取值范围．D 3B 3C 3A 2D 2D 1C 2B 1C 1B 2A 1A BC Oyx-1-1-212435124365丰台区2017年初三毕业及统一练习数 学 参 考 答 案一、选择题（本题共30分，每小题3分） 题号 1 2 3 4 5 6 7 8 9 10 答案DABCACBDBC二、填空题（本题共18分，每小题3分）11. 4-≥x ； 12. 答案不唯一，如：()()nc nb na mc mb ma c b a n m +++++=+++； 13. 163； 14. 70°； 15. ()20132028=+-x x ；16. 垂直平分线上的点到线段两个端点距离相等；到线段两个端点距离相等的点在这条线段的垂直平分线上； 有两条边相等的三角形是等腰三角形. 三、解答题（本题共30分，每小题5分） 17．解：原式=3321132+-+-…………………………………………………………4分 =2733-．……………………………………………………………………5分18．解：解不等式①，得2>x ．……………………………………………………………2分解不等式②，得3≥x ． ……………………………………………………………4分 ∴原不等式组的解集是3≥x ． ……………………………………………………5分19．证明：∵AB ∥DC ，FC=AB ，∴四边形A B C F 是平行四边形．…………………………………………………1分∵∠B =90°，∴四边形A B C F 是矩形．………………………………………………………2分∴∠AFC =90°，∴∠D =90°-∠D A F ，∠E C D =90°-∠C G F ．………………………3分 ∵EA=EG ，∴∠EAG =∠EGA ．………………………………………………………………4分 ∵∠EGA =∠CGF ，∴∠DAF =∠CGF ． ∴∠D =∠ECD ．∴E D =E C ．……………………………………………………………………5分20．解：（1）∵Δ=()()01264812412222>+-=+-=---k k k k k ）（．…………2分∴方程有两个不等的实数根．…………………………………………………3分 （2）当k =4时，Δ=16，方程化为0432=-x x ，∴01=x ，342=x ；……………………………5分 或当k =8时，Δ=16，方程化为04832=+-x x ，∴21=x ，322=x ．………………………5分 21.解：（1）∵点A （m ，2）在直线m x y +-=3上，∴m m +-=32，m = -1．……………………………………………………1分 ∴A （-1，2）. ∵点A 在双曲线xky =上， ∴12-=k，k =-2. ∴xy 2-=.………………………………………………………………………2分（2）令x x 213-=--，得到11-=x ，322=x ．………………………………3分根据图形，点B 位于点C 下方，即反比例函数大于一次函数时， ∴01<<-n 或32>n .………………………………………………………5分 22. 解：小英设计的模拟实验比较合理. ……………………………………………………2分小海选择的啤酒瓶盖质地不均匀；小东操作转盘时没有用力转动，而且实验次数 太少，没有进行大量重复实验. ……………………………………………………5分23. 解：（1）∵∠ABC =90°，AE = CE ，EB =12，∴EB =AE =CE =12. ∵DE ⊥AC ，DE =5， ∴在Rt △ADE 中， 由勾股定理得AD =22DE AE +=22512+=13．…………………2分（2）∵在Rt △ABC 中，∠CAB =30°，AC =AE +CE =24，∴BC =12，AB =AC ·cos30°=123．………………………………………3分 ∵DE ⊥AC ，AE =CE ，∴AD =DC =13． ………………………………………………………………4分∴四边形ABCD 的周长为AB +BC +CD +AD =38+123．…………………5分24. 解：（1）正确画出折线. …………………………………………………………………3分（2）预估理由须包含材料中提供的信息，且支撑预估的数据. ………………5分 25.（1）证明：连接OC ，AC ．∵CF ⊥AB ，CE ⊥AD ，且CE =CF ．∴∠CAE =∠CAB . ……………………………………………………………… 1分 ∵OC = OA ， ∴∠CAB =∠OCA . ∴∠CAE =∠OCA . ∴OC ∥AE ．∴∠OCE +∠AEC =180°， ∵∠AEC =90°，∴∠OCE =90°即OC ⊥CE ，∵OC 是⊙O 的半径，点C 为半径外端，∴CE 是⊙O 的切线．………………………………………………………………2分（2）求解思路如下：①由AD =CD =a ，得到∠DAC =∠DCA ，于是∠DCA =∠CAB ，可知DC ∥AB ； ②由OC ∥AE ，OC=OA ，可知四边形AOCD 是菱形；③由∠CAE =∠CAB ，得到CD=CB ，DC=BC=a ，可知△OBC 为等边三角形； ④由等边△OBC 可求高CF 的长，进而可求四边形ABCD 面积. ………………………5分 26. 解：（1）①m = 4；…………………………………………………………………………1分 ②图象如图. ……………………………………………………………………2分2008年和2016年新建商品住宅环线成交量占比折线统计图0%10%20%30%40%50%60%70%80%90%100%二环以内二、三环之间三、四环之间四、五环之间五环以外环线成交量占比2008年2016年ABCDE FO ⌒ ⌒1；2. …………………………………………………………………………4分 （2）根据小彬的方法可知，当xax =时，y 有最小值，即a x =时，a y 4=最小．…………………5分 27. 解：（1）∵抛物线()12212422---=-+-=m x m m mx mx y ，∴对称轴为x = 2．………………………………………………………………2分（2）①∵抛物线是轴对称图形，∴点A 点B 关于x = 2轴对称，∵A (﹣1，-2) ，∴B （5，-2）．……………………………………………3分②∵抛物线()12212422---=-+-=m x m m mx mx y ，∴顶点D （2，﹣2m -1）． …………………………………………………4分 ∵直线AB 与y 轴交点的纵坐标为-1，∴C （2，-1）． ……………………………………………………………5分∵顶点D 到点C 的距离大于2， ∴﹣2m ﹣1 +1 > 2或﹣1+ 2m +1 > 2，∴m <﹣1或m > 1．………………………………………………………… 7分28. 解：（1）∵正方形ABCD 的边长为5， BE =2， ∴EC =3.∵四边形ABCD 是正方形， ∴∠B =∠C= 90°， ∴∠1+∠3=90°，∵AE ⊥EF ，∴∠2+∠3=90°， ∴∠1=∠2. ∴△ABE ∽△ECF ，∴FC CE BE AB =，即FC 325= ∴FC =56. ………………………………………………………………………2分（2）①依题意补全图形. ……………………………………………………………3分②法1：证明：在AB 上截取AG =EC ，连接EG . ∵AB = BC ，∴GB =EB .y=x+1xOyx12431243 DA F PG 1 F A DC BE132∵∠B =90°，∴∠BGE =45°，∴∠AGE =135°. ∵∠DCB =90°，CP 是正方形ABCD 外角平分线， ∴∠ECP =135°. ∴∠AGE =∠ECP .又∵∠1=∠2，∴△AGE ≌△ECP .∴AE =PE . ………………………………………………………………7分法2：证明：作点A 关于BC 的对称点H ，连接BH ，CH ，EH . ∴AB =BH=BC ，∠1=∠4，∠ABE =∠HBE =90°. ∴∠BHC =∠BCH =45°，∠4+∠5=45°.∵∠1=∠2，∴∠2+∠5=45°. ∵∠ECP =135°，∴∠HCP =180°，点H ，C ，P 在同一条直线上.∵∠6=∠2+∠P =45°，∴∠5 =∠P .∴AE =PE . ………………………………………………………………7分法3：证明：将线段BE 绕点B 顺时针旋转90°，得到线段BM ，连接CM ，EM . ∴MB =EB ，∴∠MEB =45°，∠MEC =135°. 由法1∠ECP =135°，∴∠MEC =∠ECP . ∴ME ∥PC .又∵AB =BC ，∠ABC =∠MBC =90°. ∴△ABE ≌△CBF .∴∠1=∠BCM ，MC =AE .∴MC ∥EP .∴四边形MCPE 为平行四边形. ∴MC =PE .∴AE =PE . ………………………………………………………………7分29. 解：（1）①35；……………………………………………………………………………1分②∵点A ，B ，C 的最优覆盖矩形的面积为40，∴由定义可知，t =-3或6，即点C 坐标为（-3，-2）或（6，-2）.B CE D A FP M112 BC E DA F P H4 5 6设AC 表达式为b kx y +=，∴⎩⎨⎧+-=-+-=.b k ,b k 3223或⎩⎨⎧+=-+-=.b k ,b k 6223∴⎩⎨⎧==.b ,k 135或⎪⎩⎪⎨⎧=-=.b ,k 4785∴135+=x y 或4785+-=x y .……………………………………………4分（2）如图1，OD 所在的直线交双曲线于点E ，矩形OFEG 是点O ，D ，E 的一个面 积最小的最优覆盖矩形，∵点D （1，1），∴OD 所在的直线表达式为y =x ， ∴点E 的坐标为（2，2）， ∴OE =22， ∴⊙H 的半径r =2， 如图2，∵当点E 的纵坐标为1时，1=4x，解得x =4， ∴OE =2241+=17， ∴⊙H 的半径r =217， ∴2172≤≤r ．……………………………………………………8分图2图1 GFDEOyxDGFE Oyx。

丰台区2017 年初三毕业及统一练习英语试卷2017.05听力理解（共30 分）一、听对话，从下面各题所给的A、B、C 三幅图片中选择与对话内容相符的图片。

每段对话你将听两遍。

（共5 分，每小题1 分）二、听对话或独白，根据对话或独白的内容，从下面各题所给的A、B、C 三个选项中选择最佳选项。

每段对话或独白你将听两遍。

（共15 分，每小题1.5 分）请听一段对话，完成第6 至第7 小题。

6. What does the man want to buy?A. A coat.B. A shirt.C. A dress.7. When does the woman ask him to come again?A. Tomorrow.B. Next week.C. Next month.请听一段对话，完成第8 至第9 小题。

8. What’s wrong with the woman?A. She feels tired easily.B. She has a headache.C. She has a bad cold.9. What does the doctor tell her to do?A. Take some medicine.B. Have enough sleep.C. Finish work early.请听一段对话，完成第10 至第11 小题。

10. Where does the man want to go?A. Apple Street.B. King Street.C. The Town Hall.11. How long will it take the man to get there by bus?A. About 10 minutes.B. About 20 minutes.C. About 30 minutes.请听一段对话，完成第12 至第13 小题。

12. What are the speakers mainly talking about?A. Their hometowns.B. Their trip plans.C. Their holiday trips.13. What can we learn about the man?A. He is a good football player.B. He never went diving before.C. He will taste the local tea soon.请听一段独白，完成第14 至第15 小题。

2017年北京市丰台区中考数学一模试卷一、选择题（本题共30分，每小题3分）下列各题均有四个选项，其中只有一个是符合题意的．1．随着“一带一路”的建设推进，北京丰台口岸进口货值业务量加速增长，2016年北京丰台口岸进口货值飙升至189 000 000美元，比上一年翻了三倍，创下历史新高．将189 000 000用科学记数法表示应为（）A．189×106B．1.89×106C．18.9×107D．1.89×1082．实数a，b在数轴上的对应点的位置如图所示，则正确的结论是（）A．|a|＞b B．|b|＜a C．﹣a＜a D．﹣b＜a3．北京教育资源丰富，高校林立，下面四个高校校徽主体图案是中心对称图形的是（）A．北京林业大学B．北京体育大学 C．北京大学 D．中国人民大学4．如图，香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合，则n 的最小值为（）A．45 B．60 C．72 D．1445．在与国际友好学校交流活动中，小敏打算制做一个正方体礼盒送给外国朋友，每个面上分别书写一种中华传统美德，一共有“仁义礼智信孝”六个字．如图是她设计的礼盒平面展开图，那么“礼”字对面的字是（）A．义B．仁C．智D．信6．如果m2+2m﹣2=0，那么代数式（m+）•的值是（）A．﹣2 B．﹣1 C．2 D．37．如图，比例规是一种画图工具，它由长度相等的两脚AC和BD交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方（即同时使OA=3OC，OB=3OD），然后张开两脚，使A，B两个尖端分别在线段a的两个端点上，当CD=1.8cm时，则AB的长为（）A．7.2 cm B．5.4 cm C．3.6 cm D．0.6 cm8．如图，这是小新在询问了父母后绘制的去年全家的开支情况扇形统计图，如果他家去年总开支为6万元，那么用于教育的支出为（）A．3万元B．万元C．2.4万元D．2万元9．如图在正方形网格中，若A（1，1），B（2，0），则C点的坐标为（）A．（﹣3，﹣2） B．（3，﹣2）C．（﹣2，﹣3） D．（2，﹣3）10．近年来由于空气质量的变化，以及人们对自身健康的关注程度不断提高，空气净化器成为很多家庭的新电器．某品牌的空气净化器厂家为进一步了解市场，制定生产计划，根据2016年下半年销售情况绘制了如下统计图，其中同比增长率=（﹣1）×100%，下面有四个推断：①2016年下半年各月销售量均比2015年同月销售量增多②第四季度销售量占下半年销售量的七成以上③下半年月均销售量约为16万台④下半年月销售量的中位数不超过10万台其中合理的是（）A．①② B．①④ C．②③ D．③④二、填空题（本题共18分，每小题3分）11．如果二次根式有意义，那么x的取值范围是．12．图中的四边形均为矩形，根据图形的面积关系，写出一个正确的等式：．13．一天上午林老师来到某中学参加该校的校园开放日活动，他打算随机听一节九年级的课程，下表是他拿到的当天上午九年级的课表，如果每一个班级的每一节课被听的可能性是一样的，那么听数学课的可能性是．14．如图，小量角器的0°刻度线在大量角器的0°刻度线上，且小量角器的中心在大量角器的外缘边上．如果它们外缘边上的公共点P在大量角器上对应的度数为40°，那么在小量角器上对应的度数为．（只考虑小于90°的角度）15．众所周知，中华诗词博大精深，集大量的情景情感于短短数十字之间，或豪放，或婉约，或思民生疾苦，或抒发己身豪情逸致，文化价值极高．而数学与古诗词更是有着密切的联系．古诗中，五言绝句是四句诗，每句都是五个字；七言绝句是四句诗，每句都是七个字．有一本诗集，其中五言绝句比七言绝句多13首，总字数却反而少了20个字．问两种诗各多少首？设七言绝句有x首，根据题意，可列方程为．16．在数学课上，老师提出如下问题：已知：线段a，b（如图1）．求作：等腰△ABC，使AB=AC，BC=a，BC边上的高为b．小姗的作法如下：如图2，（1）作线段BC=a；（2）作线段BC的垂直平分线MN交线段BC于点D；（3）在MN上截取线段DA=b，连接AB，AC．所以，△ABC就是所求作的等腰三角形．老师说：“小姗的作法正确”．请回答：得到△ABC是等腰三角形的依据是：．三、解答题（本题共72分，第17～26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明、演算步骤或证明过程.17．（5分）计算：﹣（4﹣π）0+cos60°﹣|﹣3|．18．（5分）解不等式组：．19．（5分）如图，四边形ABCD中，AB∥DC，∠B=90°，F为DC上一点，且AB=FC，E为AD上一点，EC交AF于点G，EA=EG．求证：ED=EC．20．（5分）已知关于x的一元二次方程3x2﹣kx+k﹣4=0．（1）判断方程根的情况；（2）若此方程有一个整数根，请选择一个合适的k值，并求出此时方程的根．21．（5分）如图，在平面直角坐标系xOy中，直线y=﹣3x+m与双曲线y=相交于点A（m，2）．（1）求双曲线y=的表达式；（2）过动点P（n，0）且垂直于x轴的直线与直线y=﹣3x+m及双曲线y=的交点分别为B 和C，当点B位于点C下方时，求出n的取值范围．22．（5分）课题学习：设计概率模拟实验．在学习概率时，老师说：“掷一枚质地均匀的硬币，大量重复实验后，正面朝上的概率约是．”小海、小东、小英分别设计了下列三个模拟实验：小海找来一个啤酒瓶盖（如图1）进行大量重复抛掷，然后计算瓶盖口朝上的次数与总次数的比值；小东用硬纸片做了一个圆形转盘，转盘上分成8个大小一样的扇形区域，并依次标上1至8个数字（如图2），转动转盘10次，然后计算指针落在奇数区域的次数与总次数的比值；小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子（如图3），其中有三枚是白子，一枚是黑子，从中随机同时摸出两枚棋子，并大量重复上述实验，然后计算摸出的两枚棋子颜色不同的次数与总次数的比值．根据以上材料回答问题：小海、小东、小英三人中，哪一位同学的实验设计比较合理，并简要说出其他两位同学实验的不足之处．23．（5分）如图，在四边形ABCD中，∠ABC=90°，DE⊥AC于点E，且AE=CE，DE=5，EB=12．（1）求AD的长；（2）若∠CAB=30°，求四边形ABCD的周长．24．（5分）阅读下列材料：由于发展时间早、发展速度快，经过20多年大规模的高速开发建设，北京四环内，甚至五环内可供开发建设的土地资源越来越稀缺，更多的土地供应将集中在五环外，甚至六环外的远郊区县．据中国经济网2017年2月报道，来自某市场研究院的最新统计，2016年，剔除了保障房后，在北京新建商品住宅交易量整体上涨之时，北京各区域的新建商品住宅交易量则是有涨有跌．其中，昌平、通州、海淀、朝阳、西城、东城六区下跌，跌幅最大的为朝阳区，新建商品住宅成交量比2015年下降了46.82%．而延庆、密云、怀柔、平谷、门头沟、房山、顺义、大兴、石景山、丰台十区的新建商品住宅成交量表现为上涨，涨幅最大的为顺义区，比2015年上涨了118.80%．另外，从环线成交量的占比数据上，同样可以看出成交日趋郊区化的趋势．根据统计，2008年到2016年，北京全市成交的新建商品住宅中，二环以内的占比逐步从3.0%下降到了0.2%；二、三环之间的占比从5.7%下降到了0.8%；三、四环之间的占比从12.3%下降到了2.3%；四、五环之间的占比从21.9%下降到了4.4%．也就是说，整体成交中位于五环之内的新房占比，从2008年的42.8%下降到了2016年的7.7%，下滑趋势非常明显．由此可见，新房市场的远郊化是北京房地产市场发展的大势所趋．（注：占比，指在总数中所占的比重，常用百分比表示）根据以上材料解答下列问题：（1）补全折线统计图；（2）根据材料提供的信息，预估 2017年位于北京市五环之内新建商品住宅成交量占比约，你的预估理由是．25．（5分）如图，AB是⊙O的直径，C，D为⊙O上两点，CF⊥AB于点F，CE⊥AD交AD的延长线于点E，且CE=CF．（1）求证：CE是⊙O的切线；（2）连接CD，CB．若AD=CD=a，写出求四边形ABCD面积的思路．26．（5分）【问题情境】已知矩形的面积为a（a为常数，a＞0），当该矩形的长为多少时，它的周长最小？最小值是多少？【数学模型】设该矩形的长为x，周长为y，则y与x的函数表达式为y=2（x+）（x＞0）．【探索研究】小彬借鉴以前研究函数的经验，先探索函数y=x+的图象性质．（1）结合问题情境，函数y=x+的自变量x的取值范围是x＞0，如表是y与x的几组对应值．①写出m的值；②画出该函数图象，结合图象，得出当x= 时，y有最小值，y最小= ；【解决问题】（2）直接写出“问题情境”中问题的结论．27．（7分）在平面直角坐标系xOy中，抛物线y=mx2﹣4mx+2m﹣1（m≠0）与平行于x轴的一条直线交于A，B两点．（1）求抛物线的对称轴；（2）如果点A的坐标是（﹣1，﹣2），求点B的坐标；（3）抛物线的对称轴交直线AB于点C，如果直线AB与y轴交点的纵坐标为﹣1，且抛物线顶点D到点C的距离大于2，求m的取值范围．28．（7分）在边长为5的正方形ABCD中，点E，F分别是BC，DC边上的两个动点（不与点B，C，D重合），且AE⊥EF．（1）如图1，当BE=2时，求FC的长；（2）延长EF交正方形ABCD外角平分线CP于点P．①依题意将图2补全；②小京通过观察、实验提出猜想：在点E运动的过程中，始终有AE=PE．小京把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的三种想法：想法1：在AB上截取AG=EC，连接EG，要证AE=PE，需证△AGE≌△ECP．想法2：作点A关于BC的对称点H，连接BH，CH，EH．要证AE=PE，需证△EHP为等腰三角形．想法3：将线段BE绕点B顺时针旋转90°，得到线段BM，连接CM，EM，要证AE=PE，需证四边形MCPE为平行四边形．请你参考上面的想法，帮助小京证明AE=PE．（一种方法即可）29．（8分）在平面直角坐标系xOy中，对于任意三点A，B，C，给出如下定义：如果矩形的任何一条边均与某条坐标轴平行，且A，B，C三点都在矩形的内部或边界上，则称该矩形为点A，B，C的覆盖矩形．点A，B，C的所有覆盖矩形中，面积最小的矩形称为点A，B，C的最优覆盖矩形．例如，下图中的矩形A1B1C1D1，A2B2C2D2，AB3C3D3都是点A，B，C 的覆盖矩形，其中矩形AB3C3D3是点A，B，C的最优覆盖矩形．（1）已知A（﹣2，3），B（5，0），C（t，﹣2）．①当t=2时，点A，B，C的最优覆盖矩形的面积为；②若点A，B，C的最优覆盖矩形的面积为40，求直线AC的表达式；（2）已知点D（1，1）．E（m，n）是函数y=（x＞0）的图象上一点，⊙P是点O，D，E 的一个面积最小的最优覆盖矩形的外接圆，求出⊙P的半径r的取值范围．2017年北京市丰台区中考数学一模试卷参考答案与试题解析一、选择题（本题共30分，每小题3分）下列各题均有四个选项，其中只有一个是符合题意的．1．随着“一带一路”的建设推进，北京丰台口岸进口货值业务量加速增长，2016年北京丰台口岸进口货值飙升至189 000 000美元，比上一年翻了三倍，创下历史新高．将189 000 000用科学记数法表示应为（）A．189×106B．1.89×106C．18.9×107D．1.89×108【考点】1I：科学记数法—表示较大的数．【分析】用科学记数法表示较大的数时，一般形式为a×10﹣n，其中1≤|a|＜10，n为整数，据此判断即可．【解答】解：189 000 000=1.89×108．故选：D．【点评】此题主要考查了用科学记数法表示较大的数，一般形式为a×10﹣n，其中1≤|a|＜10，确定a与n的值是解题的关键．2．实数a，b在数轴上的对应点的位置如图所示，则正确的结论是（）A．|a|＞b B．|b|＜a C．﹣a＜a D．﹣b＜a【考点】29：实数与数轴．【分析】根据数轴上点的位置，利用相反数，绝对值的性质判断即可．【解答】解：根据数轴上点的位置得：a=﹣2，1＜b＜2，则|a|=2＞b，|b|＞a，﹣a＞a，﹣b＞a，故选A【点评】此题考查了实数与数轴，相反数，绝对值，熟练掌握各自的性质是解本题的关键．3．北京教育资源丰富，高校林立，下面四个高校校徽主体图案是中心对称图形的是（）A．北京林业大学B．北京体育大学 C．北京大学 D．中国人民大学【考点】R5：中心对称图形．【分析】根据中心对称图形的概念对各选项分析判断即可得解．【解答】解：A、不是中心对称图形，故本选项错误；B、是中心对称图形，故本选项正确；C、不是中心对称图形，故本选项错误；D、不是中心对称图形，故本选项错误．故选B．【点评】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后两部分重合．4．如图，香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合，则n 的最小值为（）A．45 B．60 C．72 D．144【考点】R3：旋转对称图形．【分析】该图形被平分成五部分，因而每部分被分成的圆心角是72°，并且圆具有旋转不变性，因而旋转72度的整数倍，就可以与自身重合．【解答】解：该图形被平分成五部分，旋转72°的整数倍，就可以与自身重合，故n的最小值为72．故选：C．【点评】本题考查旋转对称图形的概念：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角．5．在与国际友好学校交流活动中，小敏打算制做一个正方体礼盒送给外国朋友，每个面上分别书写一种中华传统美德，一共有“仁义礼智信孝”六个字．如图是她设计的礼盒平面展开图，那么“礼”字对面的字是（）A．义B．仁C．智D．信【考点】I8：专题：正方体相对两个面上的文字．【分析】利用正方体及其表面展开图的特点解题．【解答】解：这是一个正方体的平面展开图，共有六个面，其中“礼”字对面的字是义．故选：A．【点评】本题考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．6．如果m2+2m﹣2=0，那么代数式（m+）•的值是（）A．﹣2 B．﹣1 C．2 D．3【考点】6D：分式的化简求值．【分析】先把括号内通分，再把分子分解后约分得到原式=m2+2m，然后利用m2+2m﹣2=0进行整体代入计算．【解答】解：原式=•=• =m （m+2）=m 2+2m ，∵m 2+2m ﹣2=0，∴m 2+2m=2，∴原式=2．【点评】本题考查了分式的化简求值：先把分式化简后，再把分式中未知数对应的值代入求出分式的值．在化简的过程中要注意运算顺序和分式的化简．化简的最后结果分子、分母要进行约分，注意运算的结果要化成最简分式或整式．7．如图，比例规是一种画图工具，它由长度相等的两脚AC 和BD 交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方（即同时使OA=3OC ，OB=3OD ），然后张开两脚，使A ，B 两个尖端分别在线段a 的两个端点上，当CD=1.8cm 时，则AB 的长为（ ）A ．7.2 cmB ．5.4 cmC ．3.6 cmD ．0.6 cm【考点】SA ：相似三角形的应用．【分析】首先根据题意利用两组对边的比相等且夹角相等的三角形是相似三角形判定相似，然后利用相似三角形的性质求解．【解答】解：∵OA=3OC ，OB=3OD ，∴OA ：OC=OB ：OD=3：1，∠AOB=∠DOC ，∴△AOB ∽△COD ，∴==，∴AB=3CD=3×1.8=5.4（cm ）．故选B ．【点评】本题考查的是相似三角形的应用，利用相似三角形的相似比，列出方程，通过解方程求解即可，体现了数形转化思想的应用．8．如图，这是小新在询问了父母后绘制的去年全家的开支情况扇形统计图，如果他家去年总开支为6万元，那么用于教育的支出为（）A．3万元B．万元C．2.4万元D．2万元【考点】VB：扇形统计图．【分析】利用总开支乘以对应的比例即可求解．【解答】解：6×=2（万）．故选D．【点评】本题考查扇形统计图及相关计算．在扇形统计图中，每部分占总部分的百分比等于该部分所对应的扇形圆心角的度数与360°的比．9．如图在正方形网格中，若A（1，1），B（2，0），则C点的坐标为（）A．（﹣3，﹣2） B．（3，﹣2）C．（﹣2，﹣3） D．（2，﹣3）【考点】D3：坐标确定位置．【分析】根据A（1，1），B（2，0），再结合图形即可确定出点C的坐标．【解答】解：∵点A的坐标是：（1，1），点B的坐标是：（2，0），∴点C的坐标是：（3，﹣2）．故选B．【点评】本题主要考查了点的坐标．点坐标就是在平面直角坐标系中，坐标平面内的点与一对有序实数是一一对应的关系，这对有序实数则为这个点的坐标点的坐标．10．近年来由于空气质量的变化，以及人们对自身健康的关注程度不断提高，空气净化器成为很多家庭的新电器．某品牌的空气净化器厂家为进一步了解市场，制定生产计划，根据2016年下半年销售情况绘制了如下统计图，其中同比增长率=（﹣1）×100%，下面有四个推断：①2016年下半年各月销售量均比2015年同月销售量增多②第四季度销售量占下半年销售量的七成以上③下半年月均销售量约为16万台④下半年月销售量的中位数不超过10万台其中合理的是（）A．①② B．①④ C．②③ D．③④【考点】VD：折线统计图；VC：条形统计图；W4：中位数．【分析】①根据题意求得7月的同比增长率是﹣2.3%，于是得到2016年7月销售量比2015年同月销售量减小；②通过计算即可得到结果；③列式计算即可得到结果；④根据中位数的定义即可得到结论．【解答】解：①∵7月的同比增长率是﹣2.3%，∴2016年7月销售量比2015年同月销售量减小；故①错误；②∵≈0.73，∴第四季度销售量占下半年销售量的七成以上，故②正确；③∵（8+9.3+9.8+13.4+19.7+36）≈16万台，故③正确；④下半年月销售量的中位数=≈11.1万台＞10万台，故④错误；故选C．【点评】本题考查了折线统计图，条形统计图，中位数的定义，正确的识别图形是解题的关键．二、填空题（本题共18分，每小题3分）11．如果二次根式有意义，那么x的取值范围是x≥﹣4 ．【考点】72：二次根式有意义的条件．【分析】根据二次根式有意义的条件列出不等式，解不等式即可．【解答】解：由题意得，x+4≥0，解得，x≥﹣4，故答案为：x≥﹣4．【点评】本题考查的是二次根式有意义的条件，掌握二次根式中的被开方数必须是非负数是解题的关键．12．图中的四边形均为矩形，根据图形的面积关系，写出一个正确的等式：（m+n）（a+b+c）=ma+mb+mc+na+nb+nc ．【考点】4B：多项式乘多项式．【分析】根据图中，从两个角度计算面积即可得出答案．【解答】解：（m+n）（a+b+c）=ma+mb+mc+na+nb+nc；故答案：（m+n）（a+b+c）=ma+mb+mc+na+nb+nc（答案不唯一）【点评】本题考查多项式乘以多项式，解题的关键是熟练运用运算法则，本题属于基础题型．13．一天上午林老师来到某中学参加该校的校园开放日活动，他打算随机听一节九年级的课程，下表是他拿到的当天上午九年级的课表，如果每一个班级的每一节课被听的可能性是一样的，那么听数学课的可能性是．【考点】X2：可能性的大小．【分析】根据概率公式可得答案．【解答】解：由表可知，当天上午九年级的课表中听一节课有16种等可能结果，其中听数学课的有3种可能，∴听数学课的可能性是，故答案为：． 【点评】本题考查的可能性的大小．用到的知识点为：概率=所求情况数与总情况数之比．14．如图，小量角器的0°刻度线在大量角器的0°刻度线上，且小量角器的中心在大量角器的外缘边上．如果它们外缘边上的公共点P 在大量角器上对应的度数为40°，那么在小量角器上对应的度数为 70° ．（只考虑小于90°的角度）【考点】M1：圆的认识．【分析】设大量角器的左端点为A ，小量角器的圆心为B ．利用三角形的内角和定理求出∠PBA 的度数．然后根据圆的知识可求出小量角器上对应的度数．【解答】解：设大量角器的左端点是A ，小量角器的圆心是B ，连接AP ，BP ，则∠APB=90°，∠PAB=20°，因而∠PBA=90°﹣20°=70°，在小量角器中弧PB所对的圆心角是70°，因而P在小量角器上对应的度数为70°．故答案为：70°；【点评】本题主要考查了直径所对的圆周角是90度．能把实际问题转化为数学问题是解决本题的关键．15．众所周知，中华诗词博大精深，集大量的情景情感于短短数十字之间，或豪放，或婉约，或思民生疾苦，或抒发己身豪情逸致，文化价值极高．而数学与古诗词更是有着密切的联系．古诗中，五言绝句是四句诗，每句都是五个字；七言绝句是四句诗，每句都是七个字．有一本诗集，其中五言绝句比七言绝句多13首，总字数却反而少了20个字．问两种诗各多少首？设七言绝句有x首，根据题意，可列方程为28x﹣20（x+13）=20 ．【考点】89：由实际问题抽象出一元一次方程．【分析】利用五言绝句与七言绝句总字数之间的关系得出等式进而得出答案．【解答】解：设七言绝句有x首，根据题意，可列方程为：28x﹣20（x+13）=20．故答案为：28x﹣20（x+13）=20．【点评】此题主要考查了由实际问题抽象出一元一次方程，正确得出等量关系是解题关键．16．在数学课上，老师提出如下问题：已知：线段a，b（如图1）．求作：等腰△ABC，使AB=AC，BC=a，BC边上的高为b．小姗的作法如下：如图2，（1）作线段BC=a；（2）作线段BC的垂直平分线MN交线段BC于点D；（3）在MN上截取线段DA=b，连接AB，AC．所以，△ABC就是所求作的等腰三角形．老师说：“小姗的作法正确”．请回答：得到△ABC是等腰三角形的依据是：垂直平分线上的点到线段两个端点距离相等；有两条边相等的三角形是等腰三角形．【考点】N3：作图—复杂作图；KG：线段垂直平分线的性质；KJ：等腰三角形的判定与性质．【分析】利用垂直平分线的性质得到AB=CB，从而可判断△ABC为满足条件的等腰三角形．【解答】解：由作法得MN垂直平分BC，则AB=AC．故答案为垂直平分线上的点到线段两个端点距离相等；有两条边相等的三角形是等腰三角形．【点评】本题考查了作图﹣复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法．解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．也考查了线段垂直平分线的性质．三、解答题（本题共72分，第17～26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明、演算步骤或证明过程.17．计算：﹣（4﹣π）0+c os60°﹣|﹣3|．【考点】2C：实数的运算；6E：零指数幂；T5：特殊角的三角函数值．【分析】首先计算乘方和开方，然后从左向右依次计算，求出算式﹣（4﹣π）0+cos60°﹣|﹣3|的值是多少即可．【解答】解：﹣（4﹣π）0+cos60°﹣|﹣3|==【点评】此题主要考查了实数的运算，零指数幂以及特殊角的三角函数值，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．18．解不等式组：．【考点】CB：解一元一次不等式组．【分析】分别求出每个不等式的解集，再求其解集的公共部分即可．【解答】解：解不等式①，得x＞2．解不等式②，得x≥3．∴原不等式组的解集是x≥3．【点评】此题考查了不等式组的解法，求不等式组的解集要根据以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．19．如图，四边形ABCD中，AB∥DC，∠B=90°，F为DC上一点，且AB=FC，E为AD上一点，EC交AF于点G，EA=EG．求证：ED=EC．【考点】LD：矩形的判定与性质．【分析】先证明四边形ABCF是平行四边形．再证出四边形ABCF是矩形．得出∠AFC=90°，得出∠D=90°﹣∠DAF，∠ECD=90°﹣∠CGF．由等腰三角形的性质得出∠EAG=∠EGA．由对顶角相等得出∠DAF=∠CGF．证出∠D=∠ECD．即可得出结论．【解答】证明：∵AB∥DC，FC=AB，∴四边形ABCF是平行四边形．∵∠B=90°，∴四边形ABCF是矩形．∴∠A FC=90°，∴∠D=90°﹣∠DAF，∠ECD=90°﹣∠CGF．∵EA=EG，∴∠EAG=∠EGA．∵∠EGA=∠CGF，∴∠DAF=∠CGF．∴∠D=∠ECD．∴ED=EC．【点评】本题考查了矩形的判定与性质、等腰三角形的判定与性质、直角三角形的性质、对顶角相等的性质；熟练掌握矩形的判定与性质是解决问题的关键．20．已知关于x的一元二次方程3x2﹣kx+k﹣4=0．（1）判断方程根的情况；（2）若此方程有一个整数根，请选择一个合适的k值，并求出此时方程的根．【考点】AA：根的判别式．【分析】（1）先求出△的值，再根据根的判别式即可得出方程根的情况；（2）根据方程有整数根，可知△是完全平方数，利用求根公式选择k=4（答案不唯一），求出方程的根即可．【解答】解：（1）∵△=（﹣k）2﹣12（k﹣4）=k2﹣12k+48=（k﹣6）2+12＞0，∴方程有两个不等的实数根；（2）当k=4时，△=16，方程化为3x2﹣4x=0，解得x1=0，x2=．【点评】本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式△=b2﹣4ac：当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．也考查了一元二次方程的解法．21．如图，在平面直角坐标系xOy中，直线y=﹣3x+m与双曲线y=相交于点A（m，2）．（1）求双曲线y=的表达式；（2）过动点P（n，0）且垂直于x轴的直线与直线y=﹣3x+m及双曲线y=的交点分别为B 和C，当点B位于点C下方时，求出n的取值范围．【考点】G8：反比例函数与一次函数的交点问题．【分析】（1）由点A的坐标利用一次函数图象上点的坐标特征即可求出m值，进而可得出点A的坐标，再由点A的坐标利用待定系数法即可求出双曲线的表达式；（2）令﹣3x﹣1=﹣，可求出两函数图象交点的横坐标，再根据两函数图象的上下位置关系即可得出当点B位于点C下方时，n的取值范围．【解答】解：（1）∵点A（m，2）在直线y=﹣3x+m上，∴2=﹣3m+m，解得：m=﹣1，∴A（﹣1，2）．∵点A在双曲线上，∴，k=﹣2，∴双曲线的表达式为y=﹣．（2）令y=﹣3x﹣1=﹣，解得：x1=﹣1，x2=．。

2017年北京市丰台区中考数学一模试卷一、选择题（本题共30分，每小题3分）下列各题均有四个选项,其中只有一个是符合题意的．1．随着“一带一路”的建设推进，北京丰台口岸进口货值业务量加速增长，2016年北京丰台口岸进口货值飙升至189 000 000美元，比上一年翻了三倍，创下历史新高．将189 000 000用科学记数法表示应为（）A．189×106 B．1。

89×106C．18。

9×107D．1.89×1082．实数a，b在数轴上的对应点的位置如图所示,则正确的结论是( )A．|a|＞b B．|b｜＜a C．﹣a＜a D．﹣b＜a3．北京教育资源丰富，高校林立，下面四个高校校徽主体图案是中心对称图形的是( ) A．北京林业大学B．北京体育大学C．北京大学D．中国人民大学4．如图，香港特别行政区标志紫荆花图案绕中心旋转n°后能与原来的图案互相重合，则n 的最小值为（)A．45 B．60 C．72 D．1445．在与国际友好学校交流活动中，小敏打算制做一个正方体礼盒送给外国朋友，每个面上分别书写一种中华传统美德，一共有“仁义礼智信孝”六个字．如图是她设计的礼盒平面展开图,那么“礼"字对面的字是（)A．义 B．仁 C．智 D．信6．如果m2+2m﹣2=0,那么代数式（m+）•的值是( ）A．﹣2 B．﹣1 C．2 D．37．如图，比例规是一种画图工具，它由长度相等的两脚AC和BD交叉构成，利用它可以把线段按一定的比例伸长或缩短．如果把比例规的两脚合上，使螺丝钉固定在刻度3的地方（即同时使OA=3OC,OB=3OD），然后张开两脚，使A,B两个尖端分别在线段a的两个端点上，当CD=1.8cm时，则AB的长为( ）A．7。

2 cm B．5。

4 cm C．3.6 cm D．0.6 cm8．如图，这是小新在询问了父母后绘制的去年全家的开支情况扇形统计图，如果他家去年总开支为6万元，那么用于教育的支出为（)A．3万元B．万元C．2.4万元 D．2万元9．如图在正方形网格中，若A（1，1）,B（2，0）,则C点的坐标为( ）A．（﹣3，﹣2) B．（3，﹣2) C．（﹣2，﹣3）D．（2，﹣3）10．近年来由于空气质量的变化,以及人们对自身健康的关注程度不断提高，空气净化器成为很多家庭的新电器．某品牌的空气净化器厂家为进一步了解市场，制定生产计划，根据2016年下半年销售情况绘制了如下统计图，其中同比增长率=(﹣1）×100%，下面有四个推断:①2016年下半年各月销售量均比2015年同月销售量增多②第四季度销售量占下半年销售量的七成以上③下半年月均销售量约为16万台④下半年月销售量的中位数不超过10万台其中合理的是( ）A．①②B．①④C．②③D．③④二、填空题（本题共18分，每小题3分）11．如果二次根式有意义，那么x的取值范围是．12．图中的四边形均为矩形，根据图形的面积关系，写出一个正确的等式：．13．一天上午林老师来到某中学参加该校的校园开放日活动，他打算随机听一节九年级的课程，下表是他拿到的当天上午九年级的课表，如果每一个班级的每一节课被听的可能性是一样的，那么听数学课的可能性是．班级节次1班2班3班4班第1节语文数学外语化学第2节数学政治物理语文第3节物理化学体育数学第4节外语语文政治体育14．如图，小量角器的0°刻度线在大量角器的0°刻度线上,且小量角器的中心在大量角器的外缘边上．如果它们外缘边上的公共点P在大量角器上对应的度数为40°，那么在小量角器上对应的度数为．（只考虑小于90°的角度）15．众所周知，中华诗词博大精深，集大量的情景情感于短短数十字之间,或豪放,或婉约,或思民生疾苦，或抒发己身豪情逸致，文化价值极高．而数学与古诗词更是有着密切的联系．古诗中，五言绝句是四句诗，每句都是五个字；七言绝句是四句诗,每句都是七个字．有一本诗集,其中五言绝句比七言绝句多13首，总字数却反而少了20个字．问两种诗各多少首？设七言绝句有x首，根据题意,可列方程为．16．在数学课上，老师提出如下问题：已知：线段a，b（如图1)．求作：等腰△ABC,使AB=AC，BC=a，BC边上的高为b．小姗的作法如下：如图2，（1)作线段BC=a;（2）作线段BC的垂直平分线MN交线段BC于点D；（3)在MN上截取线段DA=b，连接AB,AC．所以，△ABC就是所求作的等腰三角形．老师说：“小姗的作法正确”．请回答:得到△ABC是等腰三角形的依据是: ．三、解答题（本题共72分，第17～26题,每小题5分，第27题7分,第28题7分，第29题8分）解答应写出文字说明、演算步骤或证明过程.17．(5分）计算：﹣（4﹣π）0+cos60°﹣|﹣3｜．18．（5分）解不等式组：．19．（5分)如图,四边形ABCD中，AB∥DC，∠B=90°，F为DC上一点，且AB=FC,E为AD上一点,EC交AF于点G,EA=EG．求证：ED=EC．20．（5分）已知关于x的一元二次方程3x2﹣kx+k﹣4=0．(1）判断方程根的情况；（2)若此方程有一个整数根,请选择一个合适的k值，并求出此时方程的根．21．(5分）如图,在平面直角坐标系xOy中,直线y=﹣3x+m与双曲线y=相交于点A（m，2)．（1)求双曲线y=的表达式；（2）过动点P（n，0）且垂直于x轴的直线与直线y=﹣3x+m及双曲线y=的交点分别为B和C，当点B位于点C下方时，求出n的取值范围．22．（5分）课题学习：设计概率模拟实验．在学习概率时,老师说：“掷一枚质地均匀的硬币，大量重复实验后,正面朝上的概率约是．”小海、小东、小英分别设计了下列三个模拟实验：小海找来一个啤酒瓶盖（如图1）进行大量重复抛掷,然后计算瓶盖口朝上的次数与总次数的比值；小东用硬纸片做了一个圆形转盘,转盘上分成8个大小一样的扇形区域，并依次标上1至8个数字(如图2)，转动转盘10次，然后计算指针落在奇数区域的次数与总次数的比值;小英在一个不透明的盒子里放了四枚除颜色外都相同的围棋子（如图3),其中有三枚是白子，一枚是黑子，从中随机同时摸出两枚棋子，并大量重复上述实验,然后计算摸出的两枚棋子颜色不同的次数与总次数的比值．根据以上材料回答问题：小海、小东、小英三人中，哪一位同学的实验设计比较合理，并简要说出其他两位同学实验的不足之处．23．(5分）如图，在四边形ABCD中,∠ABC=90°，DE⊥AC于点E，且AE=CE，DE=5,EB=12．（1)求AD的长;（2)若∠CAB=30°,求四边形ABCD的周长．24．（5分）阅读下列材料：由于发展时间早、发展速度快，经过20多年大规模的高速开发建设，北京四环内，甚至五环内可供开发建设的土地资源越来越稀缺，更多的土地供应将集中在五环外，甚至六环外的远郊区县．据中国经济网2017年2月报道,来自某市场研究院的最新统计，2016年，剔除了保障房后，在北京新建商品住宅交易量整体上涨之时,北京各区域的新建商品住宅交易量则是有涨有跌．其中，昌平、通州、海淀、朝阳、西城、东城六区下跌，跌幅最大的为朝阳区,新建商品住宅成交量比2015年下降了46。

2017届北京市丰台区高三数学（文）一模试题答案一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．如果集合A={x∈Z|﹣2≤x＜1}，B={﹣1，0，1}，那么A∩B=（）A．{﹣2，﹣1，0，1}B．{﹣1，0，1}C．{0，1}D．{﹣1，0}【解答】解：∵集合A={x∈Z|﹣2≤x＜1}={﹣2，﹣1，0}，B={﹣1，0，1}，∴A∩B={﹣1，0}．故选：D．2．在平面直角坐标系xOy中，与原点位于直线3x+2y+5=0同一侧的点是（）A．（﹣3，4）B．（﹣3，﹣2）C．（﹣3，﹣4）D．（0，﹣3）【解答】解：当x=0，y=0时，0+0+5＞0，对于A：当x=﹣3，y=4时，﹣9+8+5＞0，故满足，对于B：当x=﹣3，y=﹣2时，﹣9﹣4+5＜0，故不满足，对于C：x=﹣3，y=﹣4，﹣9﹣8+5＜0，故不满足，对于D：x=﹣3，y=﹣2时，0﹣6+5＜0，故不满足，故选：A3．执行如图所示的程序框图，则输出的i的值是（）A．3 B．4 C．5 D．6【解答】解：第一次执行循环体后，S=2，不满足退出循环的条件，i=2；再次执行循环体后，S=6，不满足退出循环的条件，i=3；再次执行循环体后，S=14，不满足退出循环的条件，i=4；再次执行循环体后，S=30，满足退出循环的条件，故输出的i值为4，故选：B．4．设命题p：∀x∈[0，+∞），e x≥1，则￢p是（）A．∃x0∉[0，+∞）， B．∀x∉[0，+∞），e x＜1C．∃x0∈[0，+∞），D．∀x∈[0，+∞），e x＜1【解答】解：因为命题p是全称命题，所以利用全称命题的否定是特称命题可得：￢p：∃x0∈[0，+∞），．故选：C5．如果，那么（）A．c＞b＞a B．c＞a＞b C．a＞b＞c D．a＞c＞b【解答】解：a=21.2＞2，＜1，c=2=log23∈（1，2）．∴a＞c＞b．故选：D．6．由一个正方体截去一个三棱锥所得的几何体的直观图如图所示，则该几何体的三视图正确的是（）A．B．C．D．宽相等．依此画出该几何体的三视图．【解答】解：根据三视图的画法，可得俯视图、侧视图，故选D．7．已知函数，点A（m，n），B（m+π，n）（|n|≠1）都在曲线y=f（x）上，且线段AB与曲线y=f（x）有五个公共点，则ω的值是（）A．4 B．2 C．D．【解答】解：由题意，2T=π，∴T=，∴ω=4，故选A．8．某校举行了以“重温时代经典，唱响回声嘹亮”为主题的“红歌”歌咏比赛．该校高一年级有1，2，3，4四个班参加了比赛，其中有两个班获奖．比赛结果揭晓之前，甲同学说：“两个获奖班级在2班、3班、4班中”，乙同学说：“2班没有获奖，3班获奖了”，丙同学说：“1班、4班中有且只有一个班获奖”，丁同学说：“乙说得对”．已知这四人中有且只有两人的说法是正确的，则这两人是（）A．乙，丁B．甲，丙C．甲，丁D．乙，丙【解答】解：根据题意，由于甲乙丙丁四人中有且只有两人的说法是正确的，假设乙的说法是正确的，则丁也是正确的，那么甲丙的说法都是错误的，如果丙同学说：“1班、4班中有且只有一个班获奖”是错误的，那么1班、4班都获奖或1班、4班都没有获奖，与乙的说法矛盾，故乙的说法是错误，则丁同学说：“乙说得对”也是错误的；故说法正确的是甲、丙，故选：B．二、填空题共6小题，每小题5分，共30分．9．在复平面内，复数z=1﹣2i对应的点到原点的距离是．【解答】解：复数z=1﹣2i对应的点（1，﹣2）到原点的距离d==．故答案：．10．抛物线y2=2x的准线方程是．【解答】解：抛物线y2=2x，∴p=1，∴准线方程是x=﹣故答案为：﹣11．设a+b=M（a＞0，b＞0），M为常数，且ab的最大值为2，则M等于2．【考点】基本不等式．【分析】由基本不等式，ab≤（）2=可求ab的最大值，结合已知即可求解M【解答】解：∵a+b=M（a＞0，b＞0），由基本不等式可得，ab≤（）2=，∵ab的最大值为2，∴=2，M＞0，∴M=2，故答案为：．12．如图，在直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=CD=1，P是AB的中点，则=﹣1．【解答】解：在直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=CD=1，可得△BCD为等腰直角三角形，则BD=，且P是AB的中点，可得=（+），=（+）•（﹣）=（2﹣2）= [（）2﹣22]=﹣1．故答案为：﹣1．13．已知点A（1，0），B（3，0），若直线y=kx+1上存在点P，满足PA⊥PB，则k的取值范围是．【解答】解：以AB为直径圆的方程为：（x﹣1）（x﹣3）+y2=0，把y=kx+1代入上述方程可得：（1+k2）x2+（2k﹣4）x+4=0，∵直线y=kx+1上存在点P，满足PA⊥PB，∴△=（2k﹣4）2﹣16（1+k2）≥0，化为：3k2+4k≤0．解得0，则k的取值范围是．故答案为：．14．已知函数（1）若a=0，x∈[0，4]，则f（x）的值域是[﹣1，1] ；（2）若f（x）恰有三个零点，则实数a的取值范围是（﹣∞，0）．【解答】解：（1）a=0时，f（x）=，∴f（x）在[0，1]上单调递减，在（1，4]上单调递增，∵f（0）=0，f（1）=﹣1，f（4）=1，∴f（x）在[0，1]上的值域是[﹣1，0]，在（1，4]上的值域是（0，1]，∴f（x）在[0，4]上的值域是[﹣1，1]．（2）当x≤1时，令f（x）=0得x=2a或x=a，当x＞1时，令f（x）=0得=1﹣a，∴x=（1﹣a）2（1﹣a＞1），∵f（x）恰好有三个解，∴，解得a＜0．故答案为：[﹣1，1]；（﹣∞，0）．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．在△ABC中，角A，B，C对应的边长分别是a，b，c，且，c=4．（Ⅰ）若，求a；（Ⅱ）若△ABC的面积等于，求a，b．【解答】（本小题共13分）解：（Ⅰ）由正弦定理可知：，从而求得…（Ⅱ）由△ABC的面积等于，可知，从而ab=16①，由余弦定理c2=a2+b2﹣2abcosC可得，16=a2+b2﹣ab②，联立①②得a=b=4．…16．已知{a n}是各项均为正数的等比数列，a11=8，设b n=log2a n，且b4=17．（Ⅰ）求证：数列{b n}是以﹣2为公差的等差数列；（Ⅱ）设数列{b n}的前n项和为S n，求S n的最大值．【解答】（本小题共13分）解：（Ⅰ）证明：设等比数列{a n}的公比为q，﹣b n=log2a n+1﹣log2a n==log2q，则b n+1因此数列{b n}是等差数列．又b11=log2a11=3，b4=17，又等差数列{b n}的公差，即b n=25﹣2n．即数列{b n}是以﹣2为公差的等差数列．…（Ⅱ）设等差数列{b n}的前n项和为S n，则n==（24﹣n）n=﹣（n﹣12）2+144，于是当n=12时，S n有最大值，最大值为144．…17．如图1，平行四边形ABCD中，AC⊥BC，BC=AC=1，现将△DAC沿AC折起，得到三棱锥D﹣ABC（如图2），且DA⊥BC，点E为侧棱DC的中点．（Ⅰ）求证：平面ABE⊥平面DBC；（Ⅱ）求三棱锥E﹣ABC的体积；（Ⅲ）在∠ACB的角平分线上是否存在点F，使得DF∥平面ABE？若存在，求DF的长；若不存在，请说明理由【解答】（本小题共14分）解：（Ⅰ）证明：在平行四边形ABCD中，有AD=BC=AC，又因为E为侧棱DC的中点， 所以AE ⊥CD ；又因为AC ⊥BC ，AD ⊥BC ，且AC ∩AD=A ，所以BC ⊥平面ACD ． 又因为AE ⊂平面ACD ，所以AE ⊥BC ； 因为BC ∩CD=C ， 所以AE ⊥平面BCD ， 又因为AE ⊂平面ABE ， 所以平面ABE ⊥平面BCD ．…（Ⅱ）解：因为V E ﹣ABC =V B ﹣ACE ，BC ⊥平面ACD ，所以BC 是三棱锥的高， 故，又因为BC=1，，，所以，所以有…（Ⅲ）解：取AB 中点O ，连接CO 并延长至点F ，使CO=OF ，连接AF ，DF ，BF ．因为BC=AC ，所以射线CO 是角∠ACB 的角分线．又因为点E 是的CD 中点，所以OE ∥DF ， 因为OE ⊂平面ABE ，DF ⊄平面ABE ， 所以DF ∥平面ABE ． 因为AB 、FC 互相平分，故四边形ACBF 为平行四边形，有BC ∥AF ． 又因为DA ⊥BC ，所以有AF ⊥AD ， 又因为AF=AD=1，故．…18．某校学生营养餐由A 和B 两家配餐公司配送．学校为了解学生对这两家配餐公司的满意度，采用问卷的形式，随机抽取了40名学生对两家公司分别评分．根据收集的80份问卷的评分，得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表：频数满意度评分分组[50，60）2[60，70）8[70，80）14[80，90）14[90，100]2（Ⅰ）根据A公司的频率分布直方图，估计该公司满意度评分的中位数；（Ⅱ）从满意度高于90分的问卷中随机抽取两份，求这两份问卷都是给A公司评分的概率；（Ⅲ）请从统计角度，对A、B两家公司做出评价．Array【解答】解：（Ⅰ）设A公司调查的40份问卷的中位数为x，则有0.015×10+0.025×10+0.03×（x﹣70）=0.5解得：x≈73.3所以，估计该公司满意度得分的中位数为73.3 …（Ⅱ）满意度高于9的问卷共有6份，其中4份评价A公司，设为a1，a2，a3，a4，2份评价B公司，设为b1，b2．从这6份问卷中随机取2份，所有可能的结果有：（a1，a2），（a1，a3），（a1，a4），（a1，b1），（a1，b2），（a2，a3），（a2，a4），（a2，b1），（a2，b2），（a3，a4），（a3，b1），（a3，b2），（a4，b1），（a4，b2），（b1，b2），共有15种．其中2份问卷都评价A公司的有以下6种：（a1，a2），（a1，a3），（a1，a4），（a2，a3），（a2，a4），（a3，a4）．设两份问卷均是评价A公司为事件C，则有．…（Ⅲ）由所给两个公司的调查满意度得分知：A公司得分的中位数低于B公司得分的中位数，A公司得分集中在[70，80）这组，而B公司得分集中在[70，80）和[80，90）两个组，A公司得分的平均数数低于B公司得分的平均数，A公司得分比较分散，而B公司得分相对集中，即A公司得分的方差高于B公司得分的方差．…19．已知P（0，1）是椭圆C：=1（a＞b＞0）上一点，点P到椭圆C的两个焦点的距离之和为2．（Ⅰ）求椭圆C的方程；（Ⅱ）设A，B是椭圆C上异于点P的两点，直线PA与直线x=4交于点M，是=？若存在，求出点A的坐标；若不存在，请说否存在点A，使得S△ABP明理由．【解答】（本小题共14分）解：（Ⅰ）由椭圆C：过点P（0，1）可得b=1，又点P到两焦点距离和为，可得，所以椭圆C的方程．…（Ⅱ）设A（m，n），依题意得：直线PA的斜率存在，则直线PA的方程为：，令x=4，，即M，又等价于且点A在y轴的右侧，从而，因为点A在y轴的右侧，所以，解得，由点A在椭圆上，解得：，于是存在点A（，），使得．…20．已知函数，A（x1，m），B（x2，m）是曲线y=f（x）上两个不同的点．（Ⅰ）求f（x）的单调区间，并写出实数m的取值范围；（Ⅱ）证明：x1+x2＞0．【解答】解：f（x）的定义域为R．（Ⅰ），由f'（x）=0得，x=0，由f'（x）＞0得，x＜0，由f'（x）＜0得，x＞0，所以f（x）的单调增区间为（﹣∞，0），单调减区间为（0，+∞），m的取值范围是（0，1）．…（Ⅱ）由（Ⅰ）知，x1∈（﹣1，0），要证x2＞﹣x1＞0，只需证f（x2）＜f（﹣x1）因为f（x1）=f（x2）=m，所以只需证f（x1）＜f（﹣x1），只需证，只需证（x1∈（﹣1，0））令h（x）=（x﹣1）e2x+x+1＜0，则h'（x）=（2x﹣1）e2x+1，因为（h'（x））'=4xe2x＜0，所以h'（x）在（﹣1，0）上单调递减，所以h'（x）＞h'（0）=0，所以h（x）在（﹣1，0）上单调递增，所以h（x）＜h（0）=0，所以，故x1+x2＞0…第11页（共11页）。

丰台区2017年高三年级第二学期综合练习（一）数学（理科）2017. 03（本试卷满分共150分，考试时间120分钟）第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1. 如果集合21A x x Z，101B ,,，那么AB =（A ）2101,,,（B ）101,,（C ）01,（D ）10,2.已知,a b R ，则“0b ”是“复数abi i 是纯虚数”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件3. 定积分311(2)d xx x=（A ）10ln 3（B ）8ln 3（C ）223（D ）6494. 设E ，F 分别是正方形ABCD 的边AB ，BC 上的点，且1=2AE AB ，2=3BF BC ，如果=+EF mAB nAC uu u r uu u r uuu r（m n ，为实数），那么mn 的值为（A ）12（B ）0 （C ）12（D ）15. 执行如图所示的程序框图，若输出的S 的值为64，则判断框内可填入的条件是（A ）3?k（B ）3?k （C ）4?k （D ）4?k k=0,S=1开始结束是否k=k +1 输出S S=S ×2k第5题第6题6. 某几何体的三视图如图所示，则该几何体的体积为（A ）56（B ）23（C ）12（D ）137.小明跟父母、爷爷奶奶一同参加《中国诗词大会》的现场录制，5人坐成一排.若小明的父母至少有一人与他相邻，则不同坐法的总数为（A ）60 （B ）72（C ）84（D ）968.一次猜奖游戏中，1,2,3,4四扇门里摆放了,,a b c d ,四件奖品（每扇门里仅放一件）.甲同学说：1号门里是b ，3号门里是c ；乙同学说：2号门里是b ，3号门里是d ；丙同学说：4号门里是b ，2号门里是c ；丁同学说：4号门里是a ，3号门里是c . 如果他们每人都猜对了一半，那么4号门里是（A ）a（B ）b（C ）c（D ）d第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分．9.抛物线22yx 的准线方程是．10. 已知n a 为等差数列，n S 为其前n 项和. 若22a ，99S ，则8a ．11.在△ABC 中，若2bac ，3B，则A =．12.若x y ,满足20701,,xy xy x,则y x的取值范围是．13.在平面直角坐标系xOy 中，曲线14C x y：，曲线21cos ,sinx C y：（为参数），过原点O 的直线l 分别交1C ，2C 于A ，B 两点，则OAOB 的最大值为．14. 已知函数()ee xxf x ，下列命题正确的有_______．（写出所有正确命题的编号）①()f x 是奇函数；②()f x 在R 上是单调递增函数；③方程2()2f x xx 有且仅有1个实数根；④如果对任意(0)x，，都有()f x kx ，那么k 的最大值为 2.三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15.（本小题共13分）已知函数()sin()f x A x (0)的图象如图所示.（Ⅰ）求()f x 的解析式；（Ⅱ）若()()cos(2)6g x f x x，求()g x 在[0]2,上的单调递减区间.16.（本小题共14分）如图1，平面五边形ABCDE 中，AB ∥CD ，90BAD，=2AB ，=1CD ，△AD E是边长为2的正三角形. 现将△ADE 沿AD 折起，得到四棱锥EABCD (如图2)，且DEAB .（Ⅰ）求证：平面ADE平面ABCD ；（Ⅱ）求平面BCE 和平面ADE 所成锐二面角的大小；（Ⅲ）在棱AE 上是否存在点F ，使得DF ∥平面BCE ？若存在，求EF EA的值；若不存在，请说明理由.17.（本小题共13分）某公司购买了A ，B ，C 三种不同品牌的电动智能送风口罩.为了解三种品牌口罩的电池性能，现采用分层抽样的方法，从三种品牌的口罩中抽出25台，测试它们一次完全充电后的连续待机时长，统计结果如下（单位：小时）：A 4 4 4.5 5 5.5 6 6B 4.5 5 6 6.5 6.5 7 7 7.5 C555.566777.588（Ⅰ）已知该公司购买的C 品牌电动智能送风口罩比B 品牌多200台，求该公司购买的B 品牌电动智能送风口罩的数量；（Ⅱ）从A 品牌和B 品牌抽出的电动智能送风口罩中，各随机选取一台，求A 品牌待机时长高于B 品牌的概率；（Ⅲ）再从A ，B ，C 三种不同品牌的电动智能送风口罩中各随机抽取一台，它们的待机时长分别是a ，b ，c （单位：小时）.这3个新数据与表格中的数据构成的新样本的平均数记为1，表格中数据的平均数记为.若01，写出a+b+c 的最小值（结论不要求证明）.18.（本小题共13分）已知函数1()ln()(0)f x kx k kx.（Ⅰ）求()f x 的单调区间；（Ⅱ）对任意12[]x k k，，都有ln()1x kx kxmx ，求m 的取值范围.19.（本小题共14分）已知椭圆C ：222210x y a bab的离心率为22，右焦点为F ，点01，B 在椭圆C 上．（Ⅰ）求椭圆C 的方程；（Ⅱ）过点F 的直线交椭圆C 于M ，N 两点，交直线2x于点P ，设=P M MF u u u r u u u r，=PN NF u u u r u u u r，求证：为定值．20.（本小题共13分）对于*N n，若数列n x 满足11nn x x ，则称这个数列为“K 数列”．（Ⅰ）已知数列：1，m+1，m 2是“K 数列”，求实数m 的取值范围；（Ⅱ）是否存在首项为-1的等差数列n a 为“K 数列”，且其前n 项和n S 满足2*1(N )2nS nn n ？若存在，求出n a 的通项公式；若不存在，请说明理由；（Ⅲ）已知各项均为正整数的等比数列n a 是“K 数列”，数列12n a 不是“K 数列”，若11nna b n ，试判断数列n b 是否为“K 数列”，并说明理由．（考生务必将答案答在答题卡上，在试卷上作答无效）丰台区2016~2017学年度第二学期一模练习高三数学（理科）参考答案及评分参考2017．03一、选择题共8小题，每小题5分，共40分．题号 1 2 3 4 5 6 7 8 答案DBBCAACA二、填空题共6小题，每小题5分，共30分．9．12x10．011．312．9,6513．21414．①②④三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15.（本小题共13分）解：（1）由图象可知2A，设函数()f x 的周期为T ，则ππ3()424T ，求得πT，从而=2，所以()2sin 2f x x5分（2）因为π()2sin2cos(2+)6g x x x =23sin2cos2sin 2x x x=311sin 4cos4222xx =π1sin(4)62x，所以ππ3π+2π42π262k xk ，即ππππ+12232k k x ，kZ令0k，得ππ123x，所以()g x 在π[0,]2上的单调递减区间为ππ[,]123. .………………13分16.（本小题共14分）（Ⅰ）证明：由已知得，.因为，所以平面.又平面，所以平面平面..………………4分（Ⅱ）设的中点为，连接.因为△ADE 是正三角形，所以，所以.因为平面平面，平面平面，平面，所以平面.以为原点，所在的直线为轴，在平面内过垂直于的直线为轴，所在的直线为轴，建立空间直角坐标系，如图所示.由已知，得，，.所以，.设平面的法向量. 则所以令，则，所以.又平面的一个法向量(0,1,0)n ，所以.所以平面和平面所成的锐二面角大小为. ………………10分（Ⅲ）在棱上存在点，使得∥平面，此时.理由如下：设的中点为，连接，，则∥，.ABAD AB DE ADDED ABADE AB ABCD ADEABCD AD O EO EAED EOAD ADE ABCD ADE ABCD AD EOADE EOABCD O OA x ABCD OAD y OE z Oxyz (0,0,3)E (1,2,0)B (1,1,0)C (1,1,3)CE(2,1,0)CBBCE (,,)=x y z m 0,0.CE CB m m 30,20.x y z xy 1x 2, 3yz (1,2,3)=m ADE 2cos ,2m n m nm nBCE ADE 4AE F DF BCE 12EF EABE G CG FG FG AB 12FGAB GBDCEA yxO z F因为∥，且12CD AB ，所以∥,且，所以四边形是平行四边形，所以∥. 因为平面，且平面，所以∥平面. .………………14分17．（本小题共13分）解：（Ⅰ）设该公司购买的B 品牌电动智能送风口罩的数量为x 台，则购买的C 品牌电动智能送风口罩为54x 台，由题意得52004xx，所以800x.答：该公司购买的B 品牌电动智能送风口罩的数量为800台..………………5分（Ⅱ）设A 品牌待机时长高于B 品牌的概率为P ，则71788P.答：在A 品牌和B 品牌抽出的电动智能送风口罩中各任取一台，A 品牌待机时长高于B 品牌的概率为18...………………10分（Ⅲ）18 .………………13分18．（本小题共13分）解：由已知得，()f x 的定义域为(0,).（Ⅰ）21()x f x x，.令()0f x ，得1x ，令()0f x ，得01x.所以函数()f x 的单调减区间是(0,1)，单调增区间是(1,)...………………5分（Ⅱ）由ln()1x kx kx mx ，得1ln()kx km x，即()max mf x .由（Ⅰ）知，（1）当2k 时，()f x 在12[,]k k 上单调递减，所以1()()0maxf x f k，所以0m；.（2）当01k时，()f x 在12[,]k k 上单调递增，所以2()()ln22maxk f x f k，所以ln 22k m；AB CD FG CD FGCD CDFG DF CG CGBCE DFBCE DF BCE（3）当12k时，()f x 在1[,1)k上单调递减，在2(1,]k上单调递增，所以12()(),()max f x max f f k k .又1()0f k，2()ln22k f k ,①若21()()f f kk ，即ln 202k ，所以12ln 2k，此时2()()ln22maxk f x f k，所以ln 22k m .②若21()()f f kk，即ln 202k ，所以2ln 22k，此时max()0f x ，所以0m综上所述，当2ln 2k时，0m ；当02ln 2k时，ln 22k m...………………13分19.（本小题共14分）（Ⅰ）解：因为点(01)B ,在椭圆C ：22221xy ab上，所以211b，即1b .又因为椭圆C 的离心率为22，所以22c a，由222abc ，得2a.所以椭圆C 的方程为2212x y....………………5分（Ⅱ）证明：由已知得,直线的斜率存在.设直线MN 的方程为(1)y k x ，11(,)M x y ，22(,)N x y ，则(2,)P k . 由PM MF ，PNNF ,得121222,11x x x x ，所以121212121212223()2411()1x x x x x x x x x x x x ，.联立221,2(1),yk x xy得2222(12)4220k xk xk.所以2122412kx x k ，21222212kx x k .因为221212224223()243241212kkx x x x kk222212444812kk kk0，所以0为定值．...………………14分20．（本小题共13分）解：（Ⅰ）由题意得(1)11m ，①(1,0)F MN2(1)1mm ，②解①得1m ；解②得1m 或2m．所以2m，故实数m 的取值范围是2m．..………………4分（Ⅱ）假设存在等差数列符合要求，设公差为d ，则1d，由11a ，得(1)2nn n S n d ，.由题意，得2(1)122n n n dnn 对nN 均成立，即(1)n d n ．①当1n 时，d R ; ②当1n 时，1nd n ，因为1=1+111n nn ，所以1d ，与1d 矛盾，故这样的等差数列{}n a 不存在．..………………8分（Ⅲ）设数列{}n a 的公比为q ，则11n na a q ，因为{}n a 的每一项均为正整数，且1(1)10nnn nn a a a qa a q ，所以10a ，且1q . 因为111()nnnn nn a a q a a a a ，所以在1{}nn a a 中，“21a a ”为最小项．同理，在111{}22nn a a 中，“211122a a ”为最小项．由{}n a 为“K 数列”，只需211a a ，即1(1)1a q ，又因为1{}2n a 不是“K 数列”，且“211122a a ”为最小项，所以2111122a a ，即1(1)2a q ，由数列{}n a 的每一项均为正整数，可得1(1)2a q，所以11,3a q 或12,2a q.①当11,3a q时，13n na ，则31nnb n ，令*1()n nn c b b n N ，则13321321(1)(2)n nnnn c nn nn ，又1232133(2)(3)(1)(2)n nnn n n n n 2348602(1)(3)nn nn nn，所以{}n c 为递增数列，即121nnnc c c c ，{}n a所以111221n n nnnnb b b b b b b b ．因为21333122b b ，所以对任意的*nN ，都有11n n b b ，即数列{}n c 为“K 数列”．②当12,2a q时，2nna ，则121n nb n ．因为21213b b ，所以数列{}n b 不是“K 数列”．综上：当13n na 时，数列{}nb 为“K 数列”，当2nna 时，数列{}nb 不是“K 数列”．..………………13分（若用其他方法解题，请酌情给分）。

丰台区2017年初三毕业及统一练习数 学 参 考 答 案二、填空题（本题共18分，每小题3分）11. 4-≥x ； 12. 答案不唯一，如：()()nc nb na mc mb ma c b a n m +++++=+++； 13.163； 14. 70°； 15.()20132028=+-x x ； 16. 垂直平分线上的点到线段两个端点距离相等；到线段两个端点距离相等的点在这条线段的垂直平分线上； 有两条边相等的三角形是等腰三角形.三、解答题（本题共30分，每小题5分） 17．解：原式=3321132+-+-…………………………………………………………4分 =2733-．……………………………………………………………………5分18．解：解不等式①，得2>x ．……………………………………………………………2分解不等式②，得3≥x ． ……………………………………………………………4分 ∴原不等式组的解集是3≥x ． ……………………………………………………5分19．证明：∵AB ∥DC ，FC=AB ，∴四边形ABCF 是平行四边形．…………………………………………………1分∵∠B =90°，∴四边形ABCF 是矩形．………………………………………………………2分∴∠AFC =90°，∴∠D =90°-∠DAF ，∠ECD =90°-∠CGF ．………………………3分 ∵EA=EG ，∴∠EAG =∠EGA ．………………………………………………………………4分 ∵∠EGA =∠CGF ，∴∠DAF =∠CGF ． ∴∠D =∠ECD ．∴ED=EC ．……………………………………………………………………5分20．解：（1）∵Δ=()()01264812412222>+-=+-=---k k k k k ）（．…………2分∴方程有两个不等的实数根．…………………………………………………3分 （2）当k =4时，Δ=16，方程化为0432=-x x ，∴01=x ，342=x ；……………………………5分 或当k =8时，Δ=16，方程化为04832=+-x x ，∴21=x ，322=x ．………………………5分 21.解：（1）∵点A （m ，2）在直线m x y +-=3上，∴m m +-=32，m = -1．……………………………………………………1分 ∴A （-1，2）. ∵点A 在双曲线xky =上， ∴12-=k，k =-2. ∴xy 2-=.………………………………………………………………………2分（2）令x x 213-=--，得到11-=x ，322=x ．………………………………3分根据图形，点B 位于点C 下方，即反比例函数大于一次函数时， ∴01<<-n 或32>n .………………………………………………………5分 22. 解：小英设计的模拟实验比较合理. ……………………………………………………2分小海选择的啤酒瓶盖质地不均匀；小东操作转盘时没有用力转动，而且实验次数 太少，没有进行大量重复实验. ……………………………………………………5分23. 解：（1）∵∠ABC =90°，AE = CE ，EB =12，∴EB =AE =CE =12. ∵DE ⊥AC ，DE =5， ∴在Rt △ADE 中， 由勾股定理得AD =22DE AE +=22512+=13．…………………2分（2）∵在Rt △ABC 中，∠CAB =30°，AC =AE +CE =24，∴BC =12，AB =AC ·cos30°=123．………………………………………3分 ∵DE ⊥AC ，AE =CE ，∴AD =DC =13． ………………………………………………………………4分∴四边形ABCD 的周长为AB +BC +CD +AD =38+123．…………………5分（2）预估理由须包含材料中提供的信息，且支撑预估的数据. ………………5分25.（1）证明：连接OC ，AC ．∵CF ⊥AB ，CE ⊥AD ，且CE =CF ．∴∠CAE =∠CAB . ……………………………………………………………… 1分 ∵OC = OA ， ∴∠CAB =∠OCA . ∴∠CAE =∠OCA . ∴OC ∥AE ．∴∠OCE +∠AEC =180°， ∵∠AEC =90°，∴∠OCE =90°即OC ⊥CE ，∵OC 是⊙O 的半径，点C 为半径外端，∴CE 是⊙O 的切线．………………………………………………………………2分（2）求解思路如下：①由AD =CD =a ，得到∠DAC =∠DCA ，于是∠DCA =∠CAB ，可知DC ∥AB ； ②由OC ∥AE ，OC=OA ，可知四边形AOCD 是菱形；③由∠CAE=∠CAB ，得到CD=CB ，DC=BC=a ，可知△OBC 为等边三角形；④由等边△OBC 可求高CF 的长，进而可求四边形ABCD 面积. ………………………5分⌒ ⌒②图象如图. ……………………………………………………………………2分1；2. …………………………………………………………………………4分 （2）根据小彬的方法可知，当xax =时，y 有最小值，即a x =时，a y 4=最小．…………………5分 27. 解：（1）∵抛物线()12212422---=-+-=m x m m mx mx y ，∴对称轴为x =2．………………………………………………………………2分（2）①∵抛物线是轴对称图形，∴点A 点B 关于x = 2轴对称，∵A (﹣1，-2) ，∴B （5，-2）． (3)分②∵抛物线()12212422---=-+-=m x m m mx mx y ，∴顶点D （2，﹣2m -1）． (4)分∵直线AB 与y 轴交点的纵坐标为-1，∴C （2，-1）． ……………………………………………………………5分∵顶点D 到点C 的距离大于2，∴﹣2m ﹣1 +1 > 2或﹣1+ 2m +1 > 2，∴m <﹣1或m > 1．…………………………………………………………7分28. 解：（1）∵正方形ABCD 的边长为5， BE =2， ∴EC =3.∵四边形ABCD 是正方形， ∴∠B =∠C= 90°， ∴∠1+∠3=90°，∵AE ⊥EF ，∴∠2+∠3=90°， ∴∠1=∠2.1xFA DCBE132∴△ABE ∽△ECF ，∴FC CE BE AB =，即FC325= ∴FC =56. ………………………………………………………………………2分（2）①依题意补全图形. ……………………………………………………………3分②法1：证明：在AB 上截取AG =EC ，连接EG . ∵AB = BC ，∴GB =EB .∵∠B =90°，∴∠BGE =45°，∴∠AGE =135°. ∵∠DCB =90°，CP 是正方形ABCD 外角平分线， ∴∠ECP =135°. ∴∠AGE =∠ECP .又∵∠1=∠2，∴△AGE ≌△ECP .∴AE =PE . ………………………………………………………………7分法2：证明：作点A 关于BC 的对称点H ，连接BH ，CH ，EH . ∴AB =BH=BC ，∠1=∠4，∠ABE =∠HBE =90°. ∴∠BHC =∠BCH =45°，∠4+∠5=45°.∵∠1=∠2，∴∠2+∠5=45°. ∵∠ECP =135°，∴∠HCP =180°，点H ，C ，P 在同一条直线上.∵∠6=∠2+∠P =45°，∴∠5 =∠P .∴AE =PE . ………………………………………………………………7分法3：证明：将线段BE 绕点B 顺时针旋转90°，得到线段BM ，连接CM ，EM . ∴MB =EB ，∴∠MEB =45°，∠MEC =135°. 由法1∠ECP =135°，∴∠MEC =∠ECP . ∴ME ∥PC .又∵AB =BC ，∠ABC =∠MBC =90°. ∴△ABE ≌△CBF .∴∠1=∠BCM ，MC =AE .BCEDA F P G 1 2B CE DA F P112BCE DA F P H4 5 6∴MC ∥EP .∴四边形MCPE 为平行四边形. ∴MC =PE .∴AE =PE . ………………………………………………………………7分29. 解：（1）①35；……………………………………………………………………………1分②∵点A ，B ，C 的最优覆盖矩形的面积为40，∴由定义可知，t =-3或6，即点C 坐标为（-3，-2）或（6，-2）. 设AC 表达式为b kx y +=，∴⎩⎨⎧+-=-+-=.b k ,b k 3223或⎩⎨⎧+=-+-=.b k ,b k 6223∴⎩⎨⎧==.b ,k 135或⎪⎩⎪⎨⎧=-=.b ,k 4785 ∴135+=x y 或75+-=x y .……………………………………………4分。