(完整版)青岛版四年级数学上册知识点整理
- 格式:doc
- 大小:36.92 KB
- 文档页数:9
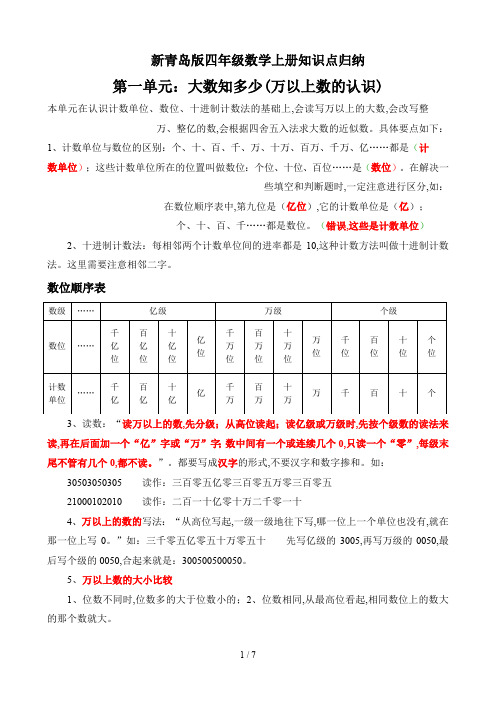
新青岛版四年级数学上册知识点归纳第一单元:大数知多少(万以上数的认识)本单元在认识计数单位、数位、十进制计数法的基础上,会读写万以上的大数,会改写整万、整亿的数,会根据四舍五入法求大数的近似数。
具体要点如下:1、计数单位与数位的区别:个、十、百、千、万、十万、百万、千万、亿……都是(计数单位);这些计数单位所在的位置叫做数位:个位、十位、百位……是(数位)。
在解决一些填空和判断题时,一定注意进行区分,如:在数位顺序表中,第九位是(亿位),它的计数单位是(亿);个、十、百、千……都是数位。
(错误,这些是计数单位)2、十进制计数法:每相邻两个计数单位间的进率都是10,这种计数方法叫做十进制计数法。
这里需要注意相邻二字。
数位顺序表3、读数:“读万以上的数,先分级;从高位读起;读亿级或万级时,先按个级数的读法来读,再在后面加一个“亿”字或“万”字;数中间有一个或连续几个0,只读一个“零”,每级末尾不管有几个0,都不读。
”。
都要写成汉字的形式,不要汉字和数字掺和。
如:30503050305 读作:三百零五亿零三百零五万零三百零五21000102010 读作:二百一十亿零十万二千零一十4、万以上的数的写法:“从高位写起,一级一级地往下写,哪一位上一个单位也没有,就在那一位上写0。
”如:三千零五亿零五十万零五十先写亿级的3005,再写万级的0050,最后写个级的0050,合起来就是:300500500050。
5、万以上数的大小比较1、位数不同时,位数多的大于位数小的;2、位数相同,从最高位看起,相同数位上的数大的那个数就大。
6、改写成以“万”作单位的数,把万位后面的4个0去掉,加上一个“万”字。
改写成以“亿”作单位的数,把亿位后面的8个0去掉,加上一个“亿”字。
求一个大数的近似数,要看尾数的最高位是几,用“四舍五入”法确定是“舍”(0 1 2 3 4)还是“入”(5 6 7 8 9).数的改写与求近似数的区别:相同点:都要写成用“万”或者“亿”做单位的数。

数学四年级上册青岛版青岛版数学四年级上册知识点汇总一、数与代数1. 大数的认识•在青岛版数学四年级上册中,学生开始深入学习大数。
大数的读写是重要内容。
例如,读一个数时,要先分级,从高位读起。
像123456789读作一亿二千三百四十五万六千七百八十九。
写数时也是从高位写起,哪一位上没有数字就写0占位。
•比较大数的大小,先看位数,位数多的数大;如果位数相同,从最高位比起,最高位上的数字大的那个数就大,如果最高位相同,就比较下一位,以此类推。
2. 三位数乘两位数•计算方法是先用两位数个位上的数去乘三位数,得数的末位和两位数的个位对齐;再用两位数十位上的数去乘三位数,得数的末位和两位数的十位对齐;最后把两次乘得的积加起来。
例如:123×45,先计算123×5 = 615,再计算123×40 = 4920,最后615+4920 = 5535。
•在解决实际问题时,我们可以根据乘法的意义来列式。
如,一辆汽车每小时行驶60千米,4小时行驶多少千米?就是求4个60是多少,列式为60×4 = 240千米。
3. 除数是两位数的除法•试商是除法计算中的关键步骤。
例如计算196÷28时,我们把28看作30来试商,因为196里面大约有6个30,所以试商6,28×6 = 168,196• 168 = 28,余数等于除数,说明商小了,改商7,28×7 = 196,正好除尽。
•在解决实际问题中,如将240个苹果平均分给30个小朋友,每个小朋友分得几个?列式为240÷30 = 8个。
二、图形与几何1. 角的度量•认识角的度量单位“度”,用符号“°”表示。
量角器是度量角的工具。
量角时,量角器的中心与角的顶点重合,0°刻度线与角的一条边重合,角的另一条边所对的量角器上的刻度,就是这个角的度数。
例如,一个角的一条边与量角器的0°刻度线重合,另一条边指向80°,这个角就是80°。

四年级数学上册知识点汇总一.计算器1、计算器是一种运算快、操作简便的计算工具。
2、开机按ON/OFF键;如果要清屏按C键;要关机按ON/OFF键。
二.用字母表示数1、简便写法9× x 或x×9 可以简写成9 • x或x•9(把乘号用点代替),也可以简写成9x(特别注意省略乘号时必须把数字写在前面)。
1×x或x×1可以简写成x。
*注意:只有在含有字母的乘法式子里,数字和字母、字母和字母之间的乘号才能省略,其他的运算中的运算符号不能省略。
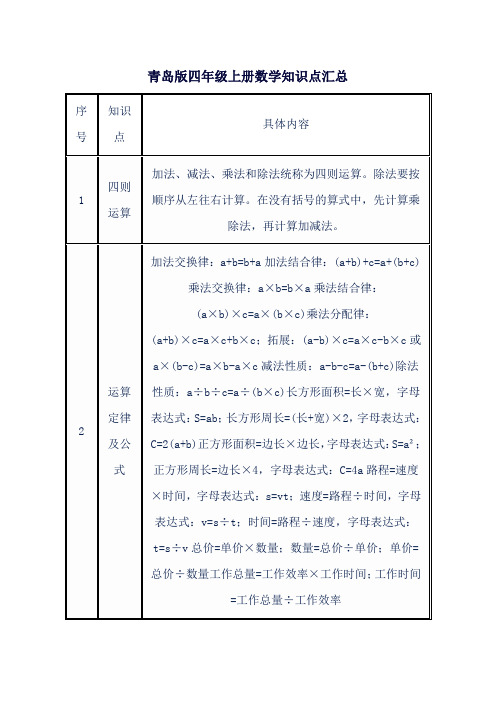
2、用字母表示运算公式长方形:周长=(长+宽)×2C=(a+b)×2面积=长×宽S=a×b正方形:周长=边长×4C=4a面积=边长×边长S=a×a 3、数量关系:路程=速度×时间s=vt速度=路程÷时间v=s÷t 时间=路程÷速度t=s÷v总价=单价×数量单价=总价÷数量数量=总价÷单价工作总量=工作效率×工作时间工作时间=工作总量÷工作效率工作效率=工作总量÷工作时间4、2a表示两个a相加。
a²表示两个a相乘,读作a的平方。
4、求含字母的式子的值把字母表示的数代入式子中按运算顺序计算即可,特别要注意代入的格式必须先抄代数式,再代入计算。
例:当a=3,b=5时求2a+6b的值。
解:当a=3,b=5时2a+6b=2×3+6×5=6+30=36注意:不加单位。
三.运算律运算律:1、加法交换律:交换两个加数的位置和不变。
用字母表示:a+b=b+a2、加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,和不变。
用字母表示:(a+b)+c=a+(b+c)3、乘法交换律:两个因数相乘,交换因数的位置,积不变。
用字母表示为a • b=b • a4、乘法结合律:三个数相乘,先乘前两个数或先乘后两个数积不变。

四年级上册数学书青岛版知识点
1. 认识数字和数的大小关系:包括认识0-99以内的数字,认识数的比较大小,认识数的顺序关系。
2. 位数与数的意义:理解个、十位数的概念,并能用公式表示出一个两位数的十位数与个位数。
3. 正整数的加法与减法:学习超过十的两位正整数的加法与减法,包括不进位、进位的运算。
4. 相邻数与数的估算:学习相邻数及相邻数的关系,利用相邻数进行数的估算。
5. 两位数的乘法与除法:学习带有0的乘法和除法,解决两位数的乘法和除法问题。
6. 变量与算式:学习带变量的算式,理解不同常量与变量的关系。
7. 分数的认识与简单运算:了解分数的概念,进行简单的分数计算。
8. 分数的比较与转化:学习分数的比较,通过比较将分数转化为相同分母的分数进行比较。
9. 长度的认识和测量:学习常用长度单位,进行长度的测量与换算。
10. 重量的认识与测量:学习常用重量单位,进行重量的测量与换算。
11. 时间的认识与折算:学习钟表的读时与写时,进行时间的换算和相关问题的解决。
12. 周期的认识与折算:学习每个周期的概念,进行周期的换算和相关问题的解决。
13. 数据的收集与整理:学习收集数据的方法,进行数据的整理和简单的统计。
14. 几何图形的认识:认识常见的几何图形,了解几何图形的性质和分类。
15. 方位与方向的认识:学习方位词和方向词的含义,了解方位与方向的关系。
这些是四年级上册数学书青岛版的主要知识点。
具体的章节和内容会根据教材的具体安排有所不同。

四年级数学上册知识点汇总一.计算器1、计算器是一种运算快、操作简便的计算工具。
2、开机按 ON/OFF 键;如果要清屏按 C 键;要关机按 ON/OFF 键。
二.用字母表示数1、简便写法9× x 或 x×9 可以简写成9 • x或x•9(把乘号用点代替),也可以简写成9x(特别注意省略乘号时必须把数字写在前面)。
1×x或x×1可以简写成x。
*注意:只有在含有字母的乘法式子里,数字和字母、字母和字母之间的乘号才能省略,其他的运算中的运算符号不能省略。
2、用字母表示运算公式长方形:周长=(长+宽)×2 C=(a+b)×2 面积=长×宽 S=a×b正方形:周长=边长×4 C=4a 面积=边长×边长 S=a×a3、数量关系:路程=速度×时间s=vt 速度=路程÷时间v=s÷t 时间=路程÷速度t=s÷v 总价=单价×数量单价=总价÷数量数量=总价÷单价工作总量=工作效率×工作时间工作时间=工作总量÷工作效率工作效率=工作总量÷工作时间4、2a表示两个a相加。
a²表示两个a相乘,读作a的平方。
4、求含字母的式子的值把字母表示的数代入式子中按运算顺序计算即可,特别要注意代入的格式必须先抄代数式,再代入计算。
例:当a=3,b=5时求2a+6b的值。
解:当a=3,b=5时 2a+6b=2×3+6×5=6+30=36注意:不加单位。
三.运算律运算律:1、加法交换律:交换两个加数的位置和不变。
用字母表示:a+b=b+a2、加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,和不变。
用字母表示:(a+b)+c=a+(b+c)3、乘法交换律:两个因数相乘,交换因数的位置,积不变。

【最新整理,下载后即可编辑】青岛版四年级上册期末复习材料第一单元:大数知多少(万以上数的认识)本单元在认识计数单位、数位、十进制计数法的基础上,会读写万以上的大数,会改写整万、整亿的数,会根据四舍五入法求大数的近似数。
具体要点如下:1、计数单位与数位的区别:个、十、百、千、万、十万、百万、千万、亿……都是(计数单位);这些计数单位所在的位置叫做数位:个位、十位、百位……是(数位)。
在解决一些填空和判断题时,一定注意进行区分,如:在数位顺序表中,第九位是(亿位),它的计数单位是(亿);个、十、百、千……都是数位。
(错误,这些是计数单位)2、十进制计数法:每相邻两个计数单位间的进率都是10,这种计数方法叫做十进制计数法。
这里需要注意相邻二字。
数位顺序表3、读数:“读万以上的数,先分级;从高位读起;读亿级或万级时,先按个级数的读法来读,再在后面加一个“亿”字或“万”字;数中间有一个或连续几个0,只读一个“零”,每级末尾不管有几个0,都不读。
”。
都要写成汉字的形式,不要汉字和数字掺和。
如:30503050305 读作:三百零五亿零三百零五万零三百零五21000102010 读作:二百一十亿零十万二千零一十4、万以上的数的写法:“从高位写起,一级一级地往下写,哪一位上一个单位也没有,就在那一位上写0。
”如:三千零五亿零五十万零五十先写亿级的3005,再写万级的0050,最后写个级的0050,合起来就是:300500500050。
5、万以上数的大小比较1、位数不同时,位数多的大于位数小的;2、位数相同,从最高位看起,相同数位上的数大的那个数就大。
6、改写成以“万”作单位的数,把万位后面的4个0去掉,加上一个“万”字。
改写成以“亿”作单位的数,把亿位后面的8个0去掉,加上一个“亿”字。
求一个大数的近似数,要看尾数的最高位是几,用“四舍五入”法确定是“舍”(0 1 2 3 4)还是“入”(5 6 7 8 9).数的改写与求近似数的区别:相同点:都要写成用“万”或者“亿”做单位的数。

青岛版四年级数学上册知识点帮助。
四年级数学知识点梳理1.直线、射线、角直线:向两端无限延伸的线,直线无端点。
射线:能像一个方向延伸的线,射线有一个端点。
线段:不能延伸的线,线段有两个端点。
具有公共端点的两条射线组成的图形叫做角。
这个公共端点叫做角的顶点,这两条射线叫做角的两条边。
2.直线、射线与线段的联系和区别1)直线和射线都可以无限延伸,因此无法量出长短。
2)线段可以量出长度。
3)线段有两个端点,直线没有端点,射线只有一个端点。
3.角的特征角有一个顶点,两条边四年级上册数学练习知识点一、填空。
1、我们学过的四边形有()、()、()和()。
2、两条直线相交成()度时,这两条直线互相垂直。
3、平行四边形具有()。
4、长方形相邻的两条边互相()。
相对的两条边互相()。
5、以平行四边形的一条边为底,能作出()条高,这些高的长度都()。
6、在同一平面内,()的两条直线叫做平行线。
7、()和()都是特殊的平行四边形。
8、等腰梯形()一组对边平行。
9、平行四边形()轴对称图形。
10、任意四边形的内角和都是()度。
二、选择。
1、从平行四边形的一条边上的一点到对边可以引()垂线。
A、一条B、两条C、无数条2、两个完全一样的三角形一定可以拼成一个()。
A、平行四边形B、梯形C、长方形3、下面图形中,不是轴对称图形的是()。
A、长方形B、圆形C、平行四边形D、等腰梯形4、长方形中有()组对边平行。
A、1B、2C、4三、判断。
1、两个梯形可以拼成一个平行四边形。
()2、有四个角是直角的图形一定是长方形。
()3、过一点可以画一条直线。
()4、只有一组对边平行的四边形一定是梯形。
()5、只要不相交就一定是平行线。
()6、两条直线相交就一定是垂直。
()四年级技巧一、让活动带领学生走进数学殿堂。
兴趣是的老师,兴趣是的动力。
学生的求知兴趣一旦被调动起来,他们就会积极参与,努力探索,专心倾听的学习习惯是学生主动参与学习过程,提高课堂学习效率的前提,而兴趣也是专心倾听的根本。

青岛版四年级数学上册知识点整理(一)10个一万是十万,10个十万是一百万,10个一百万是一千万,10个一千万是一亿。
(另一种说法:十万里面有10个一万,一百万里面有10个十万,一千万里面有10个一百万,一亿里面有10个一千万)(二)数位:个位、十位、百位、千位、……个级万位、十万位、百万位、千万位、……万级亿位、十亿位、百亿位、千亿位……亿级一个数从右边起,每4个数位是一级。
(三)计数单位:个(一)、十、百、千、万、十万、百万、千万、亿、十亿、百亿、千亿……(四)每相邻两个计数单位间的进率都是10,这种计数方法叫做十进制计数法。
(五)改写成用“万”作单位的数:末尾去掉4个0,加一个“万”;改写成用“亿”作单位的数:末尾去掉8个0,加一个“亿”。
(六)四舍五入法省略万位后面的位数求近似数:看千位,千位大于4,进1,后面省去,加一个“万”;千位小于或等于4,后面直接省去,加一个“万”。
省略亿位后面的位数求近似数:看千万位,千万位大于4,进1,后面省去,加一个“亿”;千万位小于或等于4,后面直接省去,加一个“亿”;第二单元线和角(一)线段有2个端点,可以度量;射线有1个端点,无限长;直线没有端点,无限长。
(二)从一点引出两条射线所组成的图形叫作角。
角通常用符号∠来表示,例如∠1,读作“角一”。
(三)角的计量单位是“度”,用符号“。
”表示。
(四)锐角大于0度,小于90度;直角是90度;钝角大于90度,小于180度;平角是180度;周角是360度。
1平角=2直角1周角=2平角=4直角第三单元三位数乘两位数一个因数不变,另一个因数乘几,得到的积就等于原来的积乘几;一个因数不变,另一个因数除以几,得到的积就等于原来的积除以几。
第四单元平行与相交(一)在同一平面内,不相交的两条直线互相平行,其中一条直线是另一条直线的平行线。
(二)两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,两条直线的交点叫作垂足。

第一学期期末数学复习材料第一单元:大数知多少本单元在认识计数单位、数位、十进制计数法的基础上,会读写万以上的大数,会改写整万、整亿的数,会根据四舍五入法求大数的近似数。
具体要点如下:1、计数单位与数位的区别:个、十、百、千、万、十万、百万、千万、亿……都是(计数单位);这些计数单位所在的位置叫做数位:个位、十位、百位……是(数位)。
在解决一些填空和判断题时,一定注意进行区分,如:在数位顺序表中,第九位是(亿位),它的计数单位是(亿);个、十、百、千……都是数位。
(错误,这些是计数单位)2、十进制计数法:每相邻两个计数单位间的进率都是10,这种计数方法叫做十进制计数法。
这里需要注意相邻二字。
3、读数:“读大数,先分级;高位起,依次读;亿万级,同个级;读完后,加个字;末尾0,都不读;连续0,读一个”。
都要写成汉字的形式,不要汉字和数字掺和。
如:30503050305 读作:三百零五亿零三百零五万零三百零五21000102010 读作:二百一十亿零十万二千零一十4、写数:“写大数,高位起;找亿万,分好级;亿万级,同个级;位不足,0补齐。
”如:三千零五亿零五十万零五十先写亿级的3005,再写万级的0050,最后写个级的0050,合起来就是:300500500050。
5、数的改写与求近似数的区别:相同点:都要写成用“万”或者“亿”做单位的数。
不同点:数的改写大小不变,用=连接;求近似数大小变化,用≈连接。
如:87330000=8733万8733200省略万位后面的尾数(只看千位上的数字),大约是873万,而不是800万或者900万。
6、拓展平台关于数字编码:身份证编码中倒数第二位是性别码,男单女双。
这类问题要把所提供的信息读明白后再完成,如:某学校四年级八班学号为12号的学生的编号为40812,请你为五年级二班学号为9号的学生设计编码(50209),不要写成(5209)。
第二单元:线和角(1) 线段有两个端点,不能向两端无限延伸。

青岛版四年级数学上册知识点总结知识点总结第一单元:大数知多少(万以上数的认识)本单元在认识计数单位、数位、十进制计数法的基础上,会读写万以上的大数,会改写整万、整亿的数,会根据四舍五入法求大数的近似数。
具体要点如下:1、计数单位与数位的区别:个、十、百、千、万、十万、百万、千万、亿……都是(计数单位);这些计数单位所在的位置叫做数位:个位、十位、百位……是(数位)。
在解决一些填空和判断题时,一定注意进行区分,如:在数位顺序表中,第九位是(亿位),它的计数单位是(亿);个、十、百、千……都是数位。
(错误,这些是计数单位)2、十进制计数法:每相邻两个计数单位间的进率都是10,这种计数方法叫做十进制计数法。
这里需要注意相邻二字。
3、读数:“读万以上的数,先分级;从高位读起;读亿级或万级时,先按个级数的读法来读,再在后面加一个“亿”字或“万”字;数中间有一个或连续几个0,只读一个“零”,每级末尾不管有几个0,都不读。
”。
都要写成汉字的形式,不要汉字和数字掺和。
如:30503050305 读作:三百零五亿零三百零五万零三百零五21000102010 读作:二百一十亿零十万二千零一十4、万以上的数的写法:“从高位写起,一级一级地往下写,哪一位上一个单位也没有,就在那一位上写0。
”如:三千零五亿零五十万零五十先写亿级的3005,再写万级的0050,最后写个级的0050,合起来就是:300500500050。
5、万以上数的大小比较1、位数不同时,位数多的大于位数小的;2、位数相同,从最高位看起,相同数位上的数大的那个数就大。
6、改写成以“万”作单位的数,把万位后面的4个0去掉,加上一个“万”字。
改写成以“亿”作单位的数,把亿位后面的8个0去掉,加上一个“亿”字。
求一个大数的近似数,要看尾数的最高位是几,用“四舍五入”法确定是“舍”(0 1 2 3 4)还是“入”(5 6 7 8 9).数的改写与求近似数的区别:相同点:都要写成用“万”或者“亿”做单位的数。

青岛版小学数学四年级数学上册全册知识点梳理汇总第一单元:大数知多少本单元在认识计数单位、数位、十进制计数法的基础上,会读写万以上的大数,会改写整万、整亿的数,会根据四舍五入法求大数的近似数。
具体要点如下:1、计数单位与数位的区别:个、十、百、千、万、十万、百万、千万、亿……都是(计数单位);这些计数单位所在的位置叫做数位:个位、十位、百位……是(数位)。
在解决一些填空和判断题时,一定注意进行区分,如:在数位顺序表中,第九位是(亿位),它的计数单位是(亿);个、十、百、千……都是数位。
(错误,这些是计数单位)2、十进制计数法:每相邻两个计数单位间的进率都是10,这种计数方法叫做十进制计数法。
这里需要注意相邻二字。
3、读数:“读大数,先分级;高位起,依次读;亿万级,同个级;读完后,加个字;末尾0,都不读;连续0,读一个”。
都要写成汉字的形式,不要汉字和数字掺和。
如:30503050305 读作:三百零五亿零三百零五万零三百零五21000102010 读作:二百一十亿零十万二千零一十4、写数:“写大数,高位起;找亿万,分好级;亿万级,同个级;位不足,0补齐。
”如:三千零五亿零五十万零五十先写亿级的3005,再写万级的0050,最后写个级的0050,合起来就是:300500500050。
5、数的改写与求近似数的区别:相同点:都要写成用“万”或者“亿”做单位的数。
不同点:数的改写大小不变,用=连接;求近似数大小变化,用≈连接。
如:87330000=8733万 8733200省略万位后面的尾数(只看千位上的数字),大约是873万,而不是800万或者900万。
6、拓展平台关于数字编码:身份证编码中倒数第二位是性别码,男单女双。
这类问题要把所提供的信息读明白后再完成,如:某学校四年级八班学号为12号的学生的编号为40812,请你为五年级二班学号为9号的学生设计编码(50209),不要写成(5209)。
第二单元:线和角(1)(1)线段有两个端点,不能向两端无限延伸。

新青岛版四年级数学上册全册知识点归纳材料第一单元:大数知多少(万以上数的认识)本单元在认识计数单位、数位、十进制计数法的基础上,会读写万以上的大数,会改写整万、整亿的数,会根据四舍五入法求大数的近似数。
具体要点如下:1、计数单位与数位的区别:个、十、百、千、万、十万、百万、千万、亿……都是(计数单位);这些计数单位所在的位置叫做数位:个位、十位、百位……是(数位)。
在解决一些填空和判断题时,一定注意进行区分,如:在数位顺序表中,第九位是(亿位),它的计数单位是(亿);个、十、百、千……都是数位。
(错误,这些是计数单位)2、十进制计数法:每相邻两个计数单位间的进率都是10,这种计数方法叫做十进制计数法。
这里需要注意相邻二字。
数位顺序表3、读数:“读万以上的数,先分级;从高位读起;读亿级或万级时,先按个级数的读法来读,再在后面加一个“亿”字或“万”字;数中间有一个或连续几个0,只读一个“零”,每级末尾不管有几个0,都不读。
”。
都要写成汉字的形式,不要汉字和数字掺和。
如:30503050305 读作:三百零五亿零三百零五万零三百零五21000102010 读作:二百一十亿零十万二千零一十4、万以上的数的写法:“从高位写起,一级一级地往下写,哪一位上一个单位也没有,就在那一位上写0。
”如:三千零五亿零五十万零五十先写亿级的3005,再写万级的0050,最后写个级的0050,合起来就是:300500500050。
5、万以上数的大小比较1、位数不同时,位数多的大于位数小的;2、位数相同,从最高位看起,相同数位上的数大的那个数就大。
6、改写成以“万”作单位的数,把万位后面的4个0去掉,加上一个“万”字。
改写成以“亿”作单位的数,把亿位后面的8个0去掉,加上一个“亿”字。
求一个大数的近似数,要看尾数的最高位是几,用“四舍五入”法确定是“舍”(0 1 2 3 4)还是“入”(5 6 7 8 9).数的改写与求近似数的区别:相同点:都要写成用“万”或者“亿”做单位的数。

青岛版四年级上册数学知识点青岛版四年级上册数学知识点(一)口算除法1、整十数除整十数或几百几十的数的口算方法。
(1)算除法,想乘法;比方60÷30=()就可以想(2)×30=60(2)利用表内除法计算。
利用除法运算的性质:将被除数和除数同时扩大或缩小一样的倍数,商不变。
如:200÷50想20÷5=4,所以200÷50=4。
2、两位数除两位数或三位数的估算方法:除法估算一般是把算式中不是整十数或几百几十的数用“四舍五入”法估算成整十数或几百几十的数,再进展口算。
注意结果用“≈”号。
(二)笔算除法1、除数是两位数的笔算除法计算方法:从被除数的高位除起,先用除数试除被除数的前两位,假如前两位数比除数小,就看前三位。
除到被除数的哪一位,商就写在那一位的上面。
每次除后余下的数必须比除数小。
2、除数不是整十数的两位数的除法的试商方法:假如除数是一个接近整十数的两位数,就用“四舍五入”法把除数看做与它接近的整十数试商,也可以把除数看做与它接近的几十五,再利用一位数的乘法直接确定商。
3、商一位数:(1)两位数除以整十数,如:62÷30;(2)三位数除以整十数,如:364÷70(3)两位数除以两位数,如:90÷29(把29看做30来试商)(4)三位数除以两位数,如:324÷81(把81看做80来试商)(5)三位数除以两位数,如:104÷26(把26看做25来试商)(6)同头无除商七九,如:404÷42(被除数的位和除数的位一样,即“同头”,被除数的前两位除以除数不够除,即“无除”,不是商8就是商9。
)(7)除数折半商四五,如:252÷48(除数48的一半24,和被除数的前两位25很接近,不是商4就是商5。
)4、商两位数:(三位数除以两位数)(1)前两位有余数,如:576÷18(2)前两位没有余数,如:930÷315、判断商的位数的方法:被除数的前两位除以除数不够除,商是一位数;被除数的前两位除以除数够除,商是两位数。

青岛版(六年制)四年级数学上册知识手册学校________________班级________________姓名________________一大数知多少——万以上数的认识百万位、亿级表示多少个“亿”。
、十、百、千、万、十万、百万、10个十万是一百万,10个一百万是一千万,10个一千万是一亿。
整数没有最大的计数单位。
计数单位与数位的区别:计数单位是指计算物体个数的单位;数位是指一个数中每个数字所占的位置。
易错点:计数单位之间的进率都是10,这是不对的,一定要注意“相邻”二字。
读数方法可以概括为一句话:“一画二看三说四读”。
“一画”是指从右边起,按每四位一级画虚线;“二看”是指看这个数包含哪几级;“三说”是指说出最高位上是几;“四读”是指读出这个数。
读。
思路分析:看清算盘的个位是哪一位,每一位上分别有几个上珠,几个下珠,一个上珠表示5,一个下珠表示1。
答案:250781369 二亿五千零七十八万一千三百六十九73062000305 七百三十亿六千二百万零三百零五2. 2013年年初以来,我国发生大范围持续雾霾天气,通过四舍五入估计约有6亿人受影响。
受影响的最多有()人,最少有( )人。
思路分析:如果是通过“四舍”得到的6亿,那么这个数千万位上的数是0、1、2、3、4中的一个,把这个数舍去尾数后是6亿,原数就比6亿大;如果是通过“五入”得到的,那么这个数千万位上的数是5、6、7、8、9中的一个,这个数是5亿多。
而6亿多比5亿多大,因此,要求的最大数是通过“四舍法”求得近似数的,那么这个数千万位上最大是4,其他数位上最大都是9,那么这个数最大是二繁忙的工地——线和角线段、射线和直线的区别:线段有两个端点;射线线。
2. 线段、射线和直线的特点。
(1)线段有两个端点,不能向两端无限延长,可以度量长度。
读作 :线段AB或线段BA。
(2)射线有一个端点,可以向一端无限延长,不能度量长度,过一点可以画无数条射线。

四年级上册数学素材知识点汇总青岛版第一单元万以上数的认识一、数的认识(一)整数1、自然数整数的意义用来表示物体个数的1,2,3……叫做自然数。
一个物体也没有,用0表示。
0也是自然数它们差不多上整数。
最小的自然数是0,没有最大的自然数。
自然数的个数是无限的。
2、计数单位一(个)、十、百、千、万、十万、百万、千万、亿……差不多上计数单位。
其中“一”是计数的差不多单位。
3、十进制计数法10个1是10,10个10是100……每相邻两个计数单位之间的进率差不多上10。
如此的计数法叫做十进制计数法。
4、数位计数单位按照一定的顺序排列起来,它们所占的位置叫做数位。
5、整数的读法:从高位到低位,一级一级地读。
读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万”字。
每一级末尾的0都不读出来,其它数位连续有几个0都只读一个零。
6、整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
7、万以上数的写法:(1)一个数含有万级和亿级,应从最高位写起,一级一级地往下写。
(2)写数时哪一位上是几就在那一位上写几,遇到哪一位上一个单位也没有,就在那一位上写0占位。
8、比较两个数的大小:(1)假如位数不同,位数多的那个数就大,位数少的那个数就小;(2)假如位数相同,就从最高位开始比较,最高位数大的那个数就大;假如第一位相同就看下一位,以此类推。
9、整万、整亿数的改写:(1)改写成以“万”为单位的数,把万位后面的4个0去掉,加上一个“万”字即可。
(2)改写成以“亿”为单位的数,把亿位后面的8个0去掉,加上一个“亿”字即可。
10、近似数与准确数:有些数的前面有“约”字,都不是准确数,像如此的数我们称做为“近似数”。
“四舍五入法”:在取近似数的时候,按要求保留到哪一位,这一位后面的数称为“尾数”。
假如尾数的最高位数字小于5,就把尾数去掉。
假如尾数的最高位数字大于或等于5,就把尾数舍去并向它的前一位进“1”,这种取近似数的方法叫做四舍五入法。

青岛版数学四年级上册全部知识点第一部分:计算涉及的单元:第三单元:三位数乘两位数,第五单元:除数是两位数的除法一、直接写得数:(1)乘法口算:1、两位数×一位数的进位口算:18×3=54(建议:先乘十位,1×3=3,接着算3×8=24,把十位算得的3加进位的2,写积的十位5,再写积的个位4,算完并写完)2、整百数×整十数的口算:400×20=8000(建议:数零法——先算数,算4×2=8;再数零——数出两个因数一共有几个零;再写零——在8的末尾写3个零)(2)除法口算:1、两位数÷一位数的口算:96÷6=16(建议:从高位除起,9÷6商1在十位,余3个十,与个位的6合为36,用36÷6得6,写在个位上,算完并写完)2、三位数÷两位数的口算:540÷60=9(建议:消零法——被除数和除数的末尾都有零,先把被除数和除数消掉相等个数的零,再计算,54÷6=9。
)二、竖式计算:(1)多位数乘多位数计算方法:从低到高逐位算积, 从上到下对位加积(2)多位数除以多位数计算方法:从高到低逐位算商, 从上到下对位减积(算除法要运用到加减乘除四种运算)试商的方法:两位数除数的个位是1、2、3的看成比它小的相邻的整十数进行试商。
(如:21、22、23看成20。
)两位数除数的个位是7、8、9的看成比它大的相邻的整十数进行试商。
(如:27、28、29看成30。
)两位数除数的个位是4、5、6的看成个位是5的两位数进行试商。
(如:24、25、26看成25。
)(注意:1、竖式计算中上下必须对齐数位。
试商的本领是由乘法水平决定的,试商时要既要看除数的十位也要看个位,才能方便试商。
)23×18+82×23=23×(18+82)=23×100=2300三、脱式计算:运算顺序:先乘除,后加减;有括号,先括号。

完整版)青岛版四年级数学上册知识点整理第一单元:万以上数的认识1.十万由10个一万组成,一百万由10个十万组成,一千万由10个一百万组成,一亿由10个一千万组成。
(另一种说法:十万里面有10个一万,一百万里面有10个十万,一千万里面有10个一百万,一亿里面有10个一千万)2.数位包括个位、十位、百位、千位……个级、万位、十万位、百万位、千万位……万级、亿位、十亿位、百亿位、千亿位……亿级。
每4个数位是一级。
3.计数单位包括个、十、百、千、万、十万、百万、千万、亿、十亿、百亿、千亿……。
4.十进制计数法中,每相邻两个计数单位间的进率都是10.5.改写用“=”号:末尾去掉连续4个数位,加一个“万”;末尾去掉连续8个数位,加一个“亿”。
6.四舍五入法用“≈”号表示。
省略万位后面的数位求近似数:看千位,千位大于4,进1,后面省去,加一个“万”;千位小于或等于4,后面直接省去,加一个“万”。
省略亿位后面的数位求近似数:看千万位,千万位大于4,进1,后面省去,加一个“亿”;千万位小于或等于4,后面直接省去,加一个“亿”。
7.最大的一位数是9,最小的自然数是1.8.编码:身份证号xxxxxxxxxxxxxxxx14,出生于()年()月()日,年龄()岁,性别()。
第二单元:线和角1.线段有2个端点,可以度量;射线有1个端点,无限长;直线没有端点,无限长。
射线和线段是直线的一部分。
2.把线段的一端无限延长,就得到了一条射线,过一点可以画无数条射线,过两点可以画1条直线。
把线段的两端无限延长,就得到一条直线,过一点可以画无数条直线。
3.从一点引出两条射线所组成的图形叫作角。
角通常用符号“∠”来表示,例如∠1,读作“角一”。
角的计量单位是“度”,用符号“°”表示。
把半圆平均分成180份(或把半圆分成180等分),每一份所对的角就是1度,记作“1°”。
10×2×3 = 60在一个乘法算式中,一个因数乘a(a为任何数),得到的积是原来的积乘a的平方。
第一单元万以上数的认识(一)10个一万是十万,10个十万是一百万,10个一百万是一千万,10个一千万是一亿。
(另一种说法:十万里面有10个一万,一百万里面有10个十万,一千万里面有10个一百万,一亿里面有10个一千万)(二)数位:个位、十位、百位、千位……个级万位、十万位、百万位、千万位……万级亿位、十亿位、百亿位、千亿位……亿级一个数从右边起,每4个数位是一级。
(三)计数单位:个(一)、十、百、千、万、十万、百万、千万、亿、十亿、百亿、千亿……(四)每相邻两个计数单位间的进率都是10,这种计数方法叫做十进制计数法。
(五)改写用“=”号改写成用“万”作单位的数:末尾去掉连续4个0,加一个“万”;例: 5600000=560万 45000000000=4500000万改写成用“亿”作单位的数:末尾去掉连续8个0,加一个“亿”。
例: 82000000000=820亿(六)四舍五入法:用“≈”号省略万位后面的位数求近似数:看千位千位大于4,进1,后面省去,加一个“万”;65270≈7万 898300≈90万千位小于或等于4,后面直接省去,加一个“万”。
64270≈6万 8733200≈873万省略亿位后面的位数求近似数:看千万位千万位大于4,进1,后面省去,加一个“亿”;178680000≈2万 388888000≈4万千万位小于或等于4,后面直接省去,加一个“亿”;148889000≈1亿 5948565425≈59亿(七)最大的一位数是9,最小的自然数是0,最小的一位数是1。
(八)编码身份证号370204************,出生于()年()月()日年龄()岁,性别()。
第二单元线和角(一)线段有2个端点,可以度量;射线有1个端点,无限长;直线有0个(没有)端点,无限长。
射线和线段是直线的一部分。
(二)把线段的一端无限延长,就得到了一条射线,过一点可以画无数条射线,过两点可以画1条直线。
把线段的两端无限延长,就得到一条直线,过一点可以画无数条直线。
(三)从一点引出两条射线所组成的图形叫作角。
角通常用符号“∠”来表示,例如∠1,读作“角一”。
角的计量单位是“度”,用符号“°”表示。
把半圆平均分成180份(或把半圆分成180等分),每一份所对的角就是1度,记作“1°”(四)用量角器量角时,量角器的中心点与角的顶点重合,“0°”刻度线和角的一条边重合,另一条边在量角器上所对的刻度就是角的刻度。
(五)锐角大于0度,小于90度;直角是90度;钝角大于90度,小于180度;(区别:钝角大于90度√/ 大于90度的角是钝角×)平角是180度;周角是360度。
1平角=2直角 1周角=2平角=4直角(六)一副三角板的度数为:45度,45度,90度。
30度,60度,90度。
三角板有两条边互相垂直。
三角形的三个角的和是180度。
第三单元三位数乘两位数(一)口算:先把0前面的数相乘,再看两个因素一共有几个“0”,就在积的末尾添上相应个数的“0”。
例: 20×600=12000(二)估算:估算无定法,根据实际情况选择估算的方法。
一般按照“四舍五入”估成接近的整十或整百数。
与钱有关的估算,要估大。
例:羽毛球拍每副97元,买4副大约需要多少钱?(97估成100)网球拍每副202元,买3副大约需要多少钱?(202估成210)(两个数只估一个数即可)(三)笔算:1、三位数在上,两位数在下。
相同数位要对齐。
用第二个因数的个位去乘第一因数,乘积的末尾跟个位对齐;再用第二个因数的十位去乘第一个因数,乘积的末尾跟十位对齐;两次的乘积相加就是最终的乘积。
5 3 2× 2 84 256 8×5321 0 6 4 20×532=106401 4 8 9 6 4256+106402、末尾有0的乘法(优化算法)5 3 0 2 6× 2 3 × 5 0 01 5 9 1 3 0 0 01 0 6虚线不画1 2 1 9 0(四)积的变化规律初级版:在一个乘法算式中,一个因数不变,另一个因数乘几,得到的积就等于原来的积乘几;例:10 × 5 = 5010 ×(5×5)= 50×5在一个乘法算式中,一个因数不变,另一个因数除以几,得到的积就等于原来的积除以几。
例: 10 × 5 = 50(10÷5)× 5 = 50 ÷ 5中级版:在一个乘法算式中,一个因数乘a(a为任何数),另一个因数乘b(b 为任何数),得到的积是原来的积乘a再乘b。
例: 10 × 5 = 50(10×3)×(5×2) = 50×3×2在一个乘法算式中,一个因数除以a(a是不为0的任何数),另一个因数除以b(b是不为0任何数),得到的积是原来的积除以a再除以b。
例: 10 × 5 = 50(10÷ 2)× (5 ÷ 5) = 50 ÷2 ÷5高级版:在一个乘法算式中,一个因数乘a(a为任何数),另一个因数除以b (b是不为0任何数),得到的积是原来的积乘a再除以b。
例: 10 × 5 = 50(10×2)×(5÷5)= 50×2÷5特殊情况:在一个乘法算式中,一个因数乘几,另一个因数除以相同的数,积不变。
例: 10 × 5 = 50(10×5)×(5÷5)= 50(积不变)第四单元平行与相交(一)在同一平面内,不相交的两条直线互相平行,其中一条直线是另一条直线的平行线。
在同一平面内,两条直线的位置关系是相交或平行。
或者:在同一平面内,两条直线的位置关系要么平行要么相交。
(二)两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,两条直线的焦点叫作垂足。
(三)同一平面内,如果两条直线都与第三条直线平行,那么这两条直线互相平行;(自己画出图)同一平面内,如果两条直线都与第三条直线垂直,那么这两条直线互相平行。
(自己画出图)(另一种说法:在同一平面内,平行于同一条直线的两条直线互相平行,垂直于同一条直线的两条直线互相平行)(四)两点之间线段的长度就是两点间的距离。
或者:两点之间线段最短。
(五)从直线外一点到这条直线所画的垂直线段最短,它的长度叫作点到直线的距离。
或者:点到直线的距离垂直线段最短。
(六)两条直线相交有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点。
(七)在长方形、书本、课桌中,相邻的两条边互相垂直,有4组垂直线段,相对的两条边互相平行,有2组平行线。
第五单元除数是两位数的除法(一)商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商不变。
(二)三位数乘两位数,积可能是四位数,也可能是五位数;三位数除以两位数,商可能是一位数,也可能是两位数。
(三)商的变化规律初级:被除数和除数同时乘或除以相同的数(0除外),商不变。
例: 30 ÷ 6 = 5(30×2)÷(6×2)= 5(30÷3)÷(6÷3)= 5中级:被除数不变,除数乘几,商就除以几。
例:60 ÷ 6 = 1060 ÷(6 ×2)= 10 ÷2被除数不变,除数除以几,商就乘几。
例:60 ÷ 6 = 1060 ÷(6÷3)= 10× 3被除数乘几,除数不变,商就乘几。
例:60 ÷ 6 =10(60×2)÷ 6 =10×2被除数除以几,除数不变,商就除以几。
例:60 ÷ 6 = 10(60÷2)÷ 6 = 10 ÷ 2高级:(稍难,根据个人情况选择性理解)被除数乘几,除数除以几,商就分别乘几再乘几。
例:60 ÷ 6 = 10(60×2)÷(6÷3)= 10×2×3被除数除以几,除数乘几,商就分别除以几再除以几例:60 ÷ 6 = 10(60÷5)÷(6×2)= 10÷5÷2第六单元解决问题(一)像“每分钟行驶900米”可以写作“900米/分”,读作“900米每分”,属于速度。
单位时间内所行驶的路程叫做速度。
(二)速度×时间= 路程路程÷时间= 速度路程÷速度= 时间(三)新课堂95、96页1、2、3、4四种典型题看懂★★★(四)相遇问题常见类型1.相向而行 = 相对而行求路程:速度和×时间(相遇时用的时间)=路程2.相背而行=相反而行求路程:速度和×时间(同时用的时间)=路程3.同向而行(速度有快有慢)求相距的距离:速度差×时间(同时用的时间)=相差的路程例:甲乙两车同时从A地开往B地,甲车每小时行89千米,乙车每小时行77千米,12小时后,两车相距多少千米?4.同向而行(相遇一次)求路程:速度和×时间(同时用的时间)÷2例:两辆车同时从A地开往B地,甲车每小时行58千米,乙车每小时行驶42千米,甲车到达B地后立即返回,两车行驶6小时后第一次相遇。
求A,B两地之间的距离。
第七单元混合运算(一)在一个算式里,先算乘除,后算加减;先算小括号,再算中括号。
(二)单价×数量= 总价总价÷数量= 单价总价÷单价= 数量第八单元条形统计图条形统计图需要注意的地方:1.横轴、纵轴各代表什么;2.一个格表示多少个单位;3.注意单位名称;4.分析时,需分析最多的一项和最少的一项各是什么;5.合计,就是把所有的项目加起来;算平均数,就是用合计的总数除以有几个项目。
6.作图时,注意纵轴的单位数量,把格子涂实。
智慧广场植树问题(一)两端都栽的情况:间隔数+1 = 棵数(二)一端不栽的情况:间隔数= 棵数(圆形花坛,封闭图形属于一端不栽)(三)两端不栽的情况:间隔数- 1 = 棵数(锯木头)。