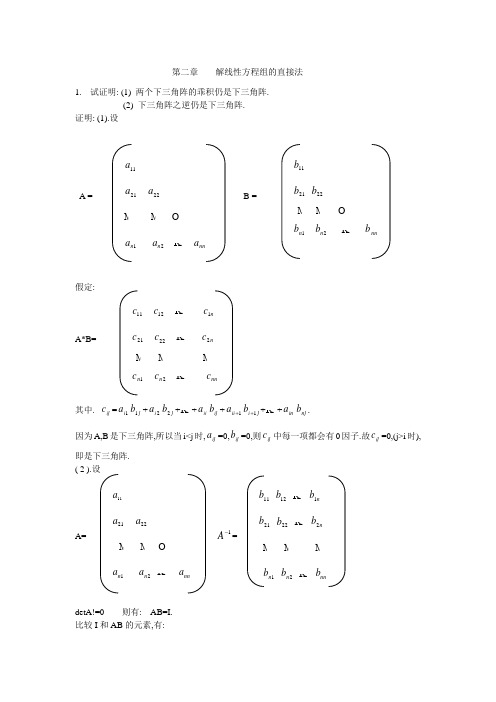
第二章 解线性方程组的直接法1. 试证明: (1) 两个下三角阵的乖积仍是下三角阵. (2) 下三角阵之逆仍是下三角阵. 证明: (1).设A =B =假定:A*B=其中.ij c =1i a j b 1+2i a j b 2+K +ii a ij b +1+ii a j i b 1++K +in a nj b .因为A,B 是下三角阵,所以当i<j 时,ij a =0,ij b =0,则ij c 中每一项都会有0因子.故ij c =0,(j>i 时),即是下三角阵.( 2 ).设A=1-A =detA!=0 则有: AB=I. 比较I 和AB 的元素,有:11a21a 22aMM O 1n a 2n a K nn a11b21b 22bM M O1n b 2n b K nn b11c 12c K n c 1 21c 22c K n c 2 M M M1n c 2n c K nn c 11a 21a 22aM M O 1n a 2n a K nn a 11b 12b K n b 1 21b 22b K n b 2MMM 1n b 2n b K nn b1=n b a b a b a b a 1111311121111110,,0,0,===K K 因为detA!=0, 可得0!,,0!,0!2211===nn a a a K 所以.0,,0,011312===n b b b K 依此类推下去,对其它行,当i<j 时,都是0=ij b . 故B 是下三角阵.2. 用Gauss 消去法求解方程组. 1x + 2x -44x =1 -1x + 2x + 3x +34x =-2 1x +32x +53x -44x =-4 2x -4x =-2 解: 消元过程:回代过程可得:4x =0,3x =-1,2x =0,1x =1.1 1 0 -4 1 -1 1 1 3 -2 13 5 -4 -4 0 1 2 -1 -2 1 1 0 -4 1 0 2 1 -1 -1 0 25 0 -5 0 1 2 -1 -21 1 0 -4 1 02 1 -1 -1 0 0 4 1 -4 0 0 1.5 0.5 -1.5 1 1 0 -4 1 0 2 1 -1 -1 0 0 4 1 -4 0 0 0 0.125 03.试写Gauss 消去法的算法:解: Gauss 消去法算法分为消元过程和回代过程,其中: 对k=1,2,K ,n-1 i=k+1,k+2,K ,n n x =n b /nn a消 ik m =ik a /kk a 回对i=n-1,n-2,K ,1 元 j=k+1,k+2,K ,n代i x =(i b -∑ijaxj)/ii a过 ij a =ija -ik m kj a 程 i b=i b -ik m k b4,用Gauss 列主元素消去法解方程组.=解:1 2 1 -2 -1 2 5 3 -2 3 2 5 3 -2 3 0 3 6 3 18 -2 -2 3 5 15 0 -0.5 -0.5 -1 -2.5 1 3 2 5 9 0 0.5 0.5 6 7.5 2 5 3 -2 3 交换1,2行 2 5 3 -2 3 1 2 1 -2 -1 Gauss 消去 0 3 6 3 18 -2 -2 3 5 15 一步 0 0 0.5 -0.5 0.5 1 3 2 5 9 0 0 -0.5 5.5 4.5 2 5 3 -2 3 2 5 3 -2 3 0 -0.5 -0.5 -1 -2.5 交换2,3行. 0 3 6 3 18 0 3 6 3 18 Gauss 消去一步 0 0 0.5 -0.5 0.5 0 0.5 0.5 6 7.5 0 0 0 5 5 回代求解得:.3,1,2,11234-====x x x x1 2 1 -2 2 5 3 -2 -2 -2 3 5 1 3 2 5 4321x x x x-13 15 95.某一装置运动轨迹为一圆锥曲线2x +bxy+c 2y +dx+ey+f=0在运动轨上测得5个不同点:1c :(14.38,3.94),2c :(11.38,2.79),)59.2,81.8(:),11.5,38.6(:),07.3,42.7(:543c c c 试写出b,c,d,e,f 所满足的方程,并用列主元素消去法求出b,c,d,e,f 的近似值. 解:依题义得方程组: 祥见教材第270页.6.设A=n n ij a *)(是实对称阵,且ii a !=0.经过Gauss 消去法一步后,A 约化为 .其中,是阶方阵.证明是对称阵. 证明:A== ;而=11aα0 2A11a 12a 13a K n a 121a 22a 23a K n a 231a 32a 33a K n a 3 M M M1n a 2n a 3n a K a 11a 12a 13a K n a 10 )2(22a )2(23a K )2(2n aMM M M 0 )2(2n a )2(3n a K )2(nn a11a α0 2A1-1121a a1 M O -11a a nnK 1 11a 12a K n a 121a 22a K n a 2M M M1n a 2n a K nn a=其中:1111)2(a a a a a j i ij ij -=,i,j=2,3,K ,n.A=T A ,ji ij a a =,i,j=1,2,K ,n..,,3,2,,)2(11111111)2(n j i a a a a a a a a a aji j i ji j i ij ijK ==-=-=亦得证2A 是对称的. 7.证明: (1) k L =的逆阵:(2)11a 12a K n a 10 11122122a a a a -K 111212a a a a n n - M M M 0 111212a a a a n n -K 1111a aa a n n nn - 1 O1k k l ,1+- 1 M O k n l ,- k1 O1k k l ,1+ 1MO nk l 1121l 131l 32l 1 M O1n l 2n l 3n l K 1=----111211n L L L K证明:(1)直接验证I L L k k =-1.=-1k k L L= I.(2).用有限归纳法证明:I n L L L L L L n n )2(111211111211--+++=--------K K .1),当k=2时.=--1211L L==I L L )12(1211-++--2),假若k=m 时成立,要让k=m+1时成立mIL L L L L m mI mL L L L L m L L L L L L L I m L L L L L L L I m L L L L L L m m m m m m m m m m m m m m m m +++++=---++++=--+++=--+++=--+++=------+-+----+-+--+--+--+----+---------1111211111112111111111121111111121111112111121111211)1()1(])1([)1(ΛK K K K K K .所以结论成立.8设nn a A ij )(=实方阵,若对i=1,2,K n.∑==>nij j ijii aa !1成立,则称A(行)严格对角占优.试证明:若严格对角占优,则A 非奇异.1 O1k k l ,1+- 1M O k n l ,- 11 O 1k k l ,1+ 1M Ok n l , 11 21l 1 31l 0 1M M O1n l 0 K 111 32l 1MO 2n l 1121l 1 31l 32l 1M M O1n l2n l证明:A 严格对角占优,所以0211>=>∑=nj ijaaGauss 消去一步得:, 且有严格对角化.n i a a a a a a a a nij j i ij j i ii ,,3,2.,2!11111111K =->-∑= 1111,2!111,2!,2!1111,2!,2!1111?a a a a a a a a a a a a a aj i nij j nij ijnij j i nij ij ni j j i ij-+=+≤-∑∑∑∑∑=====111111111111,1!1111,2!?a a a a a a a a a a a a a a a a j i ii j i ii j i nij ij j i nij ij -≤-<-=-+<∑∑==由2A 严格对角占优0!)2(22=a ,Gauss 消去法一步类似的证3A 严格对角优化.0!)3(33=a 仿此做下去可推得:0!)(=n nn a 又由0!det )()3(33)2(2211==n nn a a a a A K 亦得证A 严格对角占优.则非奇异9.设Ax= b,其中.A=b=用Dollitle 方法解此方程组.解:先求A=LU 分解,由Dolittle 分解算法.L= U== 得y=11a α 0 2A5 7 9 106 8 10 97 1089 5 7 6 5 2618 22 911.2 11.4 -0.5 11 0 0.6 15 7 9 10-0.4 -0.8 -3 -5 -6.5 -1.111.2 1 1.4-0.5 11 0 0.6 1 4321y y y y 26 18 22 926 -13.2 -21 -4.4=得x=10.用追赶法解三对角方程组AX=F,其中:A= ,F=解:先求三角分解:=由公式(6.6),(6.8)解得i i i y ,,βα)3,2,1()4,3,2(,)4,3,2(111===-====-i c i a b b i a ii i i i i i i i αββααγ (6.6)(6.8)i i α i β i γ 1 2 1/2 -3/2 2 7/2 2/7 15/7 3 26/7 7/26 83/26 4 45/25 -35 7 9 10-0.4 -0.8 -3-5 -6.5 -1.1 4321x x x x 26 -13.2 -21 -4.4 -8 5 -1 42 1 0 0 1 4 1 0 0 1 4 1 0 0 1 2 -3 6 14 -2 1b 1c 2a 2b 2c 3a 3b 3c 4a 4b1α 2γ 2α3γ 3α4λ 4α1 1β1 2β 1 3β 1)4,3,2(1111=-==-i y a f y f y ii i i i αα再公式(6.10)44y x =1+-=i i i i x y x β i=3,2,1 (6.10)得到: 2,1,4,31234-===-=x x x x。
