二次函数的图象与系数的关系(例题加练习绝对经典)

二次函数中各项系数a ，b ，c 与图像的关系一、首先就y=ax 2+bx+c （a≠0）中的a ，b ，c 对图像的作用归纳如下：1 a 的作用：决定开口方向：a > 0开口向上；a < 0开口向下；决定张口的大小：∣a ∣越大，抛物线的张口越小．2 b 的作用：b 和a 与抛物线图像的对称轴、顶点横坐标有关．b 与a 同号，说明02<-a b ，则对称轴在y 轴的左边； b 与a 异号，说明−b 2a >0，则对称轴在y 轴的右边；特别的，b = 0，对称轴为y 轴．3 c 的作用：c 决定了抛物线与y 轴的交点纵坐标．抛物线与y 轴的交点（0，c ）c > 0 抛物线与y 轴的交点在y 轴的正半轴；c < 0 抛物线与y 轴的交点在y 轴的负半轴；特别的，c = 0，抛物线过原点．4 a,b,c 共同决定判别式?=b 2−4ac 的符号进而决定图象与x 轴的交点b 2−4ac >0 与x 轴两个交点b 2−4ac =0 与x 轴一个交点b 2−4ac <0 与x 轴没有交点5 几种特殊情况：x=1时，y=a + b + c ；x= -1时，y=a - b + c ．当x = 1时，① 若y > 0，则a + b + c >0；② 若y < 时0，则a + b + c < 0当x = -1时，① 若y > 0，则a - b + c >0；② 若y < 0，则a - b + c < 0．扩：x=2, y=4a + 2b + c ；x= -2, y=4a -2b + c ； x=3, y=9a +3 b + c ；x= -3, y=9a -3b + c 。

一．选择题（共8小题）1．已知二次函数y=ax 2+bx +c 的图象大致如图所示，则下列关系式中成立的是（ ）A ．a ＞0B ．b ＜0C ．c ＜0D ．b +2a ＞02．如果二次函数y=ax 2+bx +c （a ≠0）的图象如图所示，那么下列不等式成立的是（ ）A ．a ＞0B ．b ＜0C ．ac ＜0D ．bc ＜0．3．已知二次函数y=ax 2+bx +c （a ≠0）的图象如图所示，有下列4个结论：①abc ＞0；②b ＜a +c ；③4a +2b +c ＞0；④b 2﹣4ac ＞0；其中正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个4．二次函数y=ax 2+bx +c （a ≠0）的图象如图所示，对于下列结论：①a ＜0；②b ＜0；③c ＞0；④2a +b=0；⑤a ﹣b +c ＜0，其中正确的个数是（ ）A ．4个B ．3个C ．2个D ．1个第3题图 第4题图 第5题图 第6题图5．二次函数y=ax 2+bx +c （a ≠0）的图象如图，给出下列四个结论：：①a ＜0；②b ＞0；③b 2﹣4ac ＞0；④a +b +c ＜0；其中结论正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个6．如图所示，抛物线y=ax 2+bx +c 的顶点为（﹣1，3），以下结论：①b 2﹣4ac ＜0；②4a ﹣2b +c ＜0；③2c﹣b=3；④a+3=c，其中正确的个数（）A．1 B．2 C．3 D．47．如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为直线x=﹣1，下列给出四个结论中，正确结论的个数是（）个①c＞0；②若点B（﹣，y1）、C（﹣，y2）为函数图象上的两点，则y1＜y2；③2a﹣b=0；④＜0；⑤4a﹣2b+c＞0．A．2 B．3 C．4 D．58．二次函数y=ax2+bx+c的图象如图所示，以下结论：①abc＞0；②4ac＜b2；③2a+b＞0；④当x＜时，y随x的增大而减小；⑤a+b+c＞0．其中正确的有（）A．5个 B．4个 C．3个 D．2个二．填空题（共4小题）9．如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③3a+c＞0；④当y＞0时，x的取值范围是﹣1≤x＜3；⑤当x＜0时，y随x增大而增大；其中结论正确有．10．一抛物线和抛物线y=﹣2x2的形状、开口方向完全相同，顶点坐标是（﹣1，3），则该抛物线的解析式为．11．抛物线y=ax2+12x﹣19顶点横坐标是3，则a=．12．将二次函数y=x2+6x+5化为y=a（x﹣h）2+k的形式为．三．解答题（共7小题）13．已知：抛物线y=﹣x2+bx+c经过点B（﹣1，0）和点C（2，3）．（1）求此抛物线的表达式；（2）如果此抛物线沿y轴平移一次后过点（﹣2，1），试确定这次平移的方向和距离．14．函数y=（m+2）是关于x的二次函数，求：（1）满足条件的m值；（2）m为何值时，抛物线有最低点？求出这个最低点．这时，当x为何值时，y随x的增大而增大？（3）m为何值时，函数有最大值？最大值是多少？这时，当x为何值时，y随x的增大而减小．15．已知二次函数的图象经过（0，0）（﹣1，﹣1），（1，9）三点．（1）求这个函数的解析式；（2）求这个函数图象的顶点坐标．16．已知抛物线的顶点坐标是（1，﹣4），且经过点（0，﹣3），求与该抛物线相应的二次函数表达式．17．已知二次函数y=x2﹣4x+5．（1）将y=x2﹣4x+5化成y=a （x﹣h）2+k的形式；（2）指出该二次函数图象的对称轴和顶点坐标；（3）当x取何值时，y随x的增大而增大？18．如图，二次函数的图象的顶点坐标为（1，），现将等腰直角三角板直角顶点放在原点O，一个锐角顶点A在此二次函数的图象上，而另一个锐角顶点B在第二象限，且点A的坐标为（2，1）．（1）求该二次函数的表达式；（2）判断点B是否在此二次函数的图象上，并说明理由．19．已知二次函数y=a（x﹣h）2，当x=4时有最大值，且此函数的图象经过点（1，﹣3）．（1）求此二次函数的解析式；（2）当x为何值时，y随x的增大而增大？。

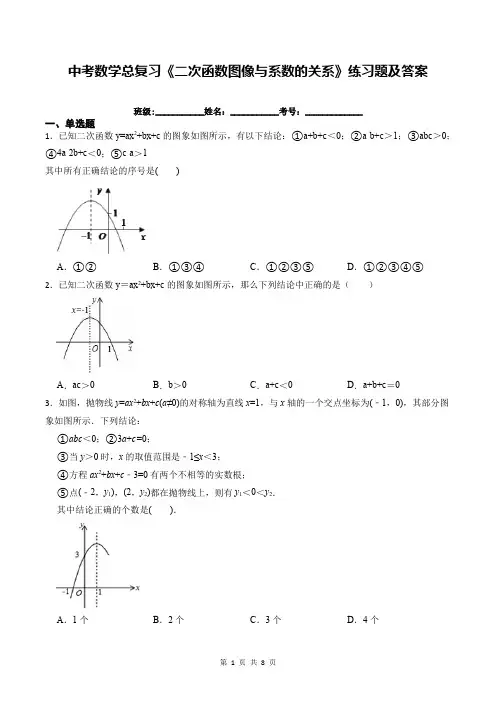
中考数学总复习《二次函数图像与系数的关系》练习题及答案班级:___________姓名：___________考号：_____________一、单选题1．已知二次函数y=ax2+bx+c的图象如图所示，有以下结论：①a+b+c＜0；②a-b+c＞1；③abc＞0；④4a-2b+c＜0；⑤c-a＞1其中所有正确结论的序号是()A．①②B．①③④C．①②③⑤D．①②③④⑤2．已知二次函数y＝ax2+bx+c的图象如图所示，那么下列结论中正确的是（）A．ac＞0B．b＞0C．a+c＜0D．a+b+c＝03．如图，抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1，与x轴的一个交点坐标为(﹣1，0)，其部分图象如图所示．下列结论：①abc＜0；②3a+c=0；③当y＞0时，x的取值范围是﹣1≤x＜3；④方程ax2+bx+c﹣3=0有两个不相等的实数根；⑤点(﹣2，y1)，(2，y2)都在抛物线上，则有y1＜0＜y2．其中结论正确的个数是()．A．1个B．2个C．3个D．4个4．在平面直角坐标系xOy中，开口向下的抛物线y＝ax2＋bx＋c的一部分图象如图所示，它与x轴交于A(1，0)，与y轴交于点B(0，3)，则a的取值范围是（）A．a＜0B．－3＜a＜0C．a<−32D．−92<a<−325．在同一坐标系内，一次函数y=ax+b与二次函数y=ax2+8x+b的图象可能是A．B．C．D．6．已知b＜0时，二次函数y=ax2+bx+a2-1的图象如下列四个图之一所示．根据图象分析，a的值等于()A．－2B．－1C．1D．27．对于二次函数y=﹣（x+1）2﹣3，下列结论正确的是（）A．函数图象的顶点坐标是（﹣1，﹣3）B．当x＞﹣1时，y随x的增大而增大C．当x=﹣1时，y有最小值为﹣3D．图象的对称轴是直线x=18．二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：x…-5-4-3-2-10…y…40-2-204…A．抛物线的开口向下B．当时，y随x的增大而增大C．二次函数的最小值是D．抛物线的对称轴是直线9．二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论中正确的是（）A．a＞0B．当x≥1时，y随x的增大而增大C．c＜0D．当﹣1＜x＜3时，y＞010．如图，在同一平面直角坐标系中，函数y=ax+2(a≠0)与y=−ax2−2x(a≠0)的图象可能是（）．A．B．C．D．11．已知二次函数y=﹣（x+k）2+h，当x＞﹣2时，y随x的增大而减小，则函数中k的取值范围是（）A．k≥﹣2B．k≤﹣2C．k≥2D．k≤212．已知：二次函数y＝ax2+bx+c的图象如图，则下列答案正确的是（）A．a＞0，b＞0，c＞0，△＜0B．a＜0，b＞0，c＜0，△＞0C．a＞0，b＜0，c＜0，△＞0D．a＜0，b＜0，c＞0，△＜0二、填空题13．二次函数y=ax2+bx+c（a≠0）的图象如图（虚线部分为对称轴），给出以下6个结论：①abc＞0；②a﹣b+c＞0；③4a+2b+c＞0；④2a＜3b；⑤x＜1时，y随x的增大而增大；⑥a+b＜m（am+b）（m为实数且m≠1）其中正确的结论有（填上所有正确结论的序号）14．已知二次函数y=ax2+bx+c的图象如图所示，则由此可得a0，b0，c 0.（填“<”或“>”）15．老师给出一个二次函数，甲，乙，丙三位同学各指出这个函数的一个性质：甲：函数的图象经过第一、二、四象限；乙：当x＜2时，y随x的增大而减小．丙：函数的图象与坐标轴只有两个交点．已知这三位同学叙述都正确，请构造出满足上述所有性质的一个函数．16．如果抛物线y＝（m﹣1）x2有最低点，那么m的取值范围为．17．已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（-1，0），（3，0）．对于下列命题：①b-2a=0；②abc＜0；③a-2b+4c＜0；④8a+c＞0．其中正确的有。

二次函数的图象与性质大题（五大题型）通用的解题思路：题型一．二次函数的性质二次函数y＝ax2+bx+c（a≠0）的顶点坐标是（﹣，），对称轴直线x＝﹣，二次函数y＝ax2+bx+c （a≠0）的图象具有如下性质：①当a＞0时，抛物线y＝ax2+bx+c（a≠0）的开口向上，x＜﹣时，y随x的增大而减小；x＞﹣时，y随x的增大而增大；x＝﹣时，y取得最小值，即顶点是抛物线的最低点．②当a＜0时，抛物线y＝ax2+bx+c（a≠0）的开口向下，x＜﹣时，y随x的增大而增大；x＞﹣时，y随x的增大而减小；x＝﹣时，y取得最大值，即顶点是抛物线的最高点．③抛物线y＝ax2+bx+c（a≠0）的图象可由抛物线y＝ax2的图象向右或向左平移|﹣|个单位，再向上或向下平移||个单位得到的．题型二．二次函数图象与系数的关系二次函数y＝ax2+bx+c（a≠0）①二次项系数a决定抛物线的开口方向和大小．当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；|a|还可以决定开口大小，|a|越大开口就越小．②一次项系数b和二次项系数a共同决定对称轴的位置．当a与b同号时（即ab＞0），对称轴在y轴左侧；当a与b异号时（即ab＜0），对称轴在y轴右侧．（简称：左同右异）③．常数项c决定抛物线与y轴交点．抛物线与y轴交于（0，c）．④抛物线与x轴交点个数．△＝b2﹣4ac＞0时，抛物线与x轴有2个交点；△＝b2﹣4ac＝0时，抛物线与x轴有1个交点；△＝b2﹣4ac ＜0时，抛物线与x轴没有交点．题型三．待定系数法求二次函数解析式（1）二次函数的解析式有三种常见形式：①一般式：y＝ax2+bx+c（a，b，c是常数，a≠0）；②顶点式：y＝a（x﹣h）2+k（a，h，k是常数，a≠0），其中（h，k）为顶点坐标；③交点式：y＝a（x﹣x1）（x﹣x2）（a，b，c是常数，a≠0）；（2）用待定系数法求二次函数的解析式．在利用待定系数法求二次函数关系式时，要根据题目给定的条件，选择恰当的方法设出关系式，从而代入数值求解．一般地，当已知抛物线上三点时，常选择一般式，用待定系数法列三元一次方程组来求解；当已知抛物线的顶点或对称轴时，常设其解析式为顶点式来求解；当已知抛物线与x轴有两个交点时，可选择设其解析式为交点式来求解．题型四．抛物线与x轴的交点求二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标，令y＝0，即ax2+bx+c＝0，解关于x 的一元二次方程即可求得交点横坐标．（1）二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）的交点与一元二次方程ax2+bx+c＝0根之间的关系．△＝b2﹣4ac决定抛物线与x轴的交点个数．△＝b2﹣4ac＞0时，抛物线与x轴有2个交点；△＝b2﹣4ac＝0时，抛物线与x轴有1个交点；△＝b2﹣4ac＜0时，抛物线与x轴没有交点．（2）二次函数的交点式：y＝a（x1）（x﹣x2）（a，b，c是常数，a≠0），可直接得到抛物线与x轴的交点坐标（x1，0），（x2，0）．题型五．二次函数综合题（1）二次函数图象与其他函数图象相结合问题解决此类问题时，先根据给定的函数或函数图象判断出系数的符号，然后判断新的函数关系式中系数的符号，再根据系数与图象的位置关系判断出图象特征，则符合所有特征的图象即为正确选项．（2）二次函数与方程、几何知识的综合应用将函数知识与方程、几何知识有机地结合在一起．这类试题一般难度较大．解这类问题关键是善于将函数问题转化为方程问题，善于利用几何图形的有关性质、定理和二次函数的知识，并注意挖掘题目中的一些隐含条件．（3）二次函数在实际生活中的应用题从实际问题中分析变量之间的关系，建立二次函数模型．关键在于观察、分析、创建，建立直角坐标系下的二次函数图象，然后数形结合解决问题，需要我们注意的是自变量及函数的取值范围要使实际问题有意义．题型一．二次函数的性质（共3小题）1．（2024•石景山区校级模拟）在平面直角坐标系xOy 中，1(A x ，1)y ，2(B x ，2)y 是抛物线2(0)y x bx b =−+≠上任意两点，设抛物线的对称轴为直线x h =． （1）若抛物线经过点(2,0)，求h 的值；（2）若对于11x h =−，22x h =，都有12y y >，求h 的取值范围；（3）若对于121h x h −+……，221x −−……，存在12y y <，直接写出h 的取值范围． 【分析】（1）根据对称轴2bx a=−进行计算，得2b h =，再把(2,0)代入2(0)y x bx b =−+≠，即可作答．（2）因为1(A x ，1)y ，2(B x ，2)y 是抛物线2(0)y x bx b =−+≠上的点，所以把11x h =−，22x h =分别代入，得出对应的1y ，2y ，再根据12y y >联立式子化简，计算即可作答；（3）根据121h x h −+……，221x −−……，存在12y y <，得出当221h −<−<−或者211h −<+<−，即可作答． 【解答】解：（1）抛物线的对称轴为直线x h =， 22b bh ∴=−=−， 即2b h =，∴抛物线22y x hx =−+，把(2,0)代入22y x hx =−+， 得0422h =−+⨯， 解得1h =；（2）由（1）知抛物线22y x hx =−+，1(A x ，1)y ，2(B x ，2)y 是抛物线22y x hx =−+上任意两点，221(1)2(1)1y h h h h ∴=−−+−=−，22(2)220y h h h =−+⨯=，对于11x h =−，22x h =，都有12y y >， 210h ∴−>，解得1h >或1h <−；（3）1(A x ，1)y ，2(B x ，2)y 是抛物线22y x hx =−+上任意两点，对于121h x h −+……，221x −−……，存在12y y <，且1(2,)h y −关于直线x h =的对称点为1(2,)h y +，1(1,)h y +关于直线x h =的对称点为1(1,)h y −，∴当221h −<−<−时，存在12y y <，解得01h <<，当221h −<+<−时，存在12y y <， 解得43h −<<−，当211h −<+<−时，存在12y y <， 解得32h −<<−，当211h −<−<−时，存在12y y <， 解得10h −<<，综上，满足h 的取值范围为41h −<<且0h ≠．【点评】本题考查了二次函数的图象性质、增减性，熟练掌握二次函数的图象和性质是解决本题的关键． 2．（2024•鹿城区校级一模）已知二次函数223y x tx =−++． （1）若它的图象经过点(1,3)，求该函数的对称轴． （2）若04x ……时，y 的最小值为1，求出t 的值．（3）如果(2,)A m n −，(,)C m n 两点都在这个二次函数的图象上，直线2y mx a =+与该二次函数交于1(M x ，1)y ，2(N x ，2)y 两点，则12x x +是否为定值？若是，请求出该定值；若不是，请说明理由．【分析】（1）把(1,3)代入解析式求出12t =，再根据对称轴公式求出对称轴； （2）根据抛物线开口向下，以及0x =时3y =，由函数的性质可知，当4x =时，y 的最小值为1，然后求t 即可；（3）(2,)A m n −，(,)C m n 两点都在这个二次函数的图象上，有对称轴公式得出1m t −=，再令2232x tx mx a −++=+，并转化为一般式，然后由根与系数的关系求出122x x +=−．【解答】解：（1）将(1,3)代入二次函数223y x tx =−++，得3123t =−++， 解得12t =， ∴对称轴直线为21122t x t =−==−⨯； （2）当0x =时，3y =，抛物线开口向下，对称轴为直线x t =， ∴当x t =时，y 有最大值，04x ……时，y 的最小值为1，∴当4x =时，16831y t =−++=，解得74t =； （3）12x x +是定值，理由：(2,)A m n −，(,)C m n 两点都在这个二次函数的图象上， 212m mx t m −+∴===−， 1m t ∴−=，令2232x tx mx a −++=+， 整理得：22()30x m t x a +−+−=，直线2y mx a =+与该二次函数交于1(M x ，1)y ，2(N x ，2)y 两点， 1x ∴，2x 是方程22()30x m t x a +−+−=的两个根，122()2()21m t x x m t −∴+=−=−−=−是定值． 【点评】本题考查了二次函数的性质，二次函数图象上点的坐标特征等知识，关键是掌握二次函数的性质． 3．（2024•拱墅区一模）在平面直角坐标系中，抛物线2(2)2y ax a x =−++经过点(2,)A t −，(,)B m p ． （1）若0t =，①求此抛物线的对称轴；②当p t <时，直接写出m 的取值范围；（2）若0t <，点(,)C n q 在该抛物线上，m n <且5513m n +<−，请比较p ，q 的大小，并说明理由． 【分析】（1）①当0t =时，点A 的坐标为(2,0)−，将其代入函数解析式中解得1a =−，则函数解析式为抛物线的解析式为22y x x =−−+，再根据求对称轴的公式2bx a=−即可求解； ②令0y =，求出抛物线与x 轴交于(2,0)−和(1,0)，由题意可得0p <，则点B 在x 轴的下方，以此即可解答； （2）将点A 坐标代入函数解析式，通过0t <可得a 的取值范围，从而可得抛物线开口方向及对称轴，根据点B ，C 到对称轴的距离大小关系求解．【解答】解：（1）①当0t =时，点A 的坐标为(2,0)−，抛物线2(2)2y ax a x =−++经过点(2,0)A −， 42(2)20a a ∴+++=，1a ∴=−，∴抛物线的解析式为22y x x =−−+， ∴抛物线的对称轴为直线112(1)2x −=−=−⨯−；②令0y =，则220x x −−+=， 解得：11x =，22x =−，∴抛物线与x 轴交于(2,0)−和(1,0)，点(2,0)A −，(,)B m p ，且0p <， ∴点(,)B m p 在x 轴的下方，2m ∴<−或1m >．（2）p q <，理由如下：将(2,)t −代入2(2)2y ax a x =−++得42(2)266t a a a =+++=+，0t <， 660a ∴+<， 1a ∴<−，∴抛物线开口向下，抛物线对称轴为直线(2)1122a x a a −+=−=+， 1a <−，110a∴−<<， 1111222a ∴−<+<， m n <且5513m n +<−，∴1312102m n +<−<−， ∴点(,)B m p 到对称轴的距离大于点(,)C n q 到对称轴的距离，p q ∴<．【点评】本题考查二次函数的综合应用，解题关键是掌握二次函数的性质，掌握二次函数与方程及不等式的关系．题型二．二次函数图象与系数的关系（共8小题）4．（2023•南京）已知二次函数223(y ax ax a =−+为常数，0)a ≠． （1）若0a <，求证：该函数的图象与x 轴有两个公共点． （2）若1a =−，求证：当10x −<<时，0y >．（3）若该函数的图象与x 轴有两个公共点1(x ，0)，2(x ，0)，且1214x x −<<<，则a 的取值范围是 ．【分析】（1）证明240b ac −>即可解决问题． （2）将1a =−代入函数解析式，进行证明即可． （3）对0a >和0a <进行分类讨论即可．【解答】证明：（1）因为22(2)43412a a a a −−⨯⨯=−， 又因为0a <，所以40a <，30a −<， 所以24124(3)0a a a a −=−>，所以该函数的图象与x 轴有两个公共点． （2）将1a =−代入函数解析式得，2223(1)4y x x x =−++=−−+，所以抛物线的对称轴为直线1x =，开口向下． 则当10x −<<时，y 随x 的增大而增大， 又因为当1x =−时，0y =， 所以0y >．（3）因为抛物线的对称轴为直线212ax a−=−=，且过定点(0,3)， 又因为该函数的图象与x 轴有两个公共点1(x ，0)，2(x ，0)，且1214x x −<<<， 所以当0a >时，230a a −+<， 解得3a >， 故3a >．当0a <时，230a a ++<，解得1a <−， 故1a <−．综上所述，3a >或1a <−． 故答案为：3a >或1a <−．【点评】本题考查二次函数的图象和性质，熟知二次函数的图象和性质是解题的关键．5．（2024•南京模拟）在平面直角坐标系xOy 中，点1(1,)y ，2(3,)y 在抛物线222y x mx m =−+上． （1）求抛物线的顶点(,0)m ； （2）若12y y <，求m 的取值范围；（3）若点0(x ，0)y 在抛物线上，若存在010x −<<，使102y y y <<成立，求m 的取值范围． 【分析】（1）利用配方法将已知抛物线解析式转化为顶点式，可直接得到答案； （2）由12y y <，得到221296m m m m −+<−+，解不等式即可； （3）由题意可知012032m m +⎧<⎪⎪⎨+⎪>⎪⎩或112132m m −+⎧<⎪⎪⎨−+⎪>⎪⎩，解不等式组即可．【解答】解：（1）抛物线222()y x mx m x m =−+=−． ∴抛物线的顶点坐标为(,0)m ．故答案为：(,0)m ；（2）点1(1,)y ，2(3,)y 在抛物线222y x mx m =−+上，且12y y <， 221296m m m m ∴−+<−+，2m ∴<；（3）点0(x ，0)y 在抛物线上，存在010x −<<，使102y y y <<成立， ∴012032m m +⎧<⎪⎪⎨+⎪>⎪⎩或112132m m −+⎧<⎪⎪⎨−+⎪>⎪⎩，解得302m <<． 【点评】本题考查了二次函数与系数的关系，二次函数图象上点的坐标特征，熟知二次函数的性质是解题的关键．6．（2024•北京一模）在平面直角坐标系中，已知抛物线23y ax bx =++经过点(2,3)a −． （1）求该抛物线的对称轴（用含有a 的代数式表示）；（2）点(2,)M t m −，(2,)N t n +，(,)P t p −为该抛物线上的三个点，若存在实数t ，使得m n p >>，求a 的取值范围．【分析】（1）将点(2,3)a −代入抛物线23y ax bx =++中，然后根据二次函数的对称轴公式代入数值，即可得出答案；（2）分类讨论当0a >和0a <，利用数形结合以及二次函数的性质就可以得出a 的取值范围． 【解答】解（1）抛物线23y ax bx =++经过点(2,3)a −， ∴把(2,3)a −代入23y ax bx =++得2(2)233a a ab ⨯−−+=，22b a ∴=，2223y ax a x ∴=++，∴抛物线的对称轴222a x a a=−=−，答：抛物线的对称轴为：x a =−；（2）①当0a >时，抛物线开口方向向上，对称轴0x a =−<，在x 轴的负半轴上，所以越靠近对称轴函数值越小， ∴当0t <时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t ∴−<+，∴此时p m n >>与题干m n p >>相矛盾，故舍去， ∴当0t >时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t ∴−<+，∴此时m n <与题干m n p >>相矛盾，故舍去；②当0a <时，抛物线开口方向向下，对称轴0x a =−>，在x 轴的正半轴上，所以越靠近对称轴函数值越大， ∴当0t >时，点M 、N 分别在对称轴同侧时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t ∴−<+， .m n p >>，∴此时02a t <−<−，即20t a −<<，2t ∴>，∴当0t >时，点M 、N 分别在对称轴两侧时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t t ∴−<<+，p m n ∴>>与题干m n p >>相矛盾，故舍去，∴当0t <时，且点M 、N 分别在对称轴两侧时，(2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t t ∴−<<+，n m ∴>与题干m n p >>相矛盾，故舍去，当0t <时，且点M 、N 分别在对称轴同侧时， (2,)M t m −，(2,)N t n +，(,)P t p −在抛物线上，22t t t ∴−<<+，n m ∴>与题干m n p >>相矛盾，故舍去，答：a 的取值范围为20(2)t a t −<<>．7．（2024•张家口一模）某课外小组利用几何画板来研究二次函数的图象，给出二次函数解析式2y x bx c =++，通过输入不同的b ，c 的值，在几何画板的展示区内得到对应的图象．（1）若输入2b =，3c =−，得到如图①所示的图象，求顶点C 的坐标及抛物线与x 轴的交点A ，B 的坐标； （2）已知点(1,10)P −，(4,0)Q ．①若输入b ，c 的值后，得到如图②的图象恰好经过P ，Q 两点，求出b ，c 的值；②淇淇输入b ，嘉嘉输入1c =−，若得到二次函数的图象与线段PQ 有公共点，求淇淇输入b 的取值范围．【分析】（1）将2b =，3c =−，代入函数解析式，进行求解即可； （2）①待定系数法进行求解即可；②将1c =−代入解析式，得到抛物线必过点(0,1)−，求出1x =−和4x =的函数值，根据抛物线与线段PQ 有公共点，列出不等式进行求解即可． 【解答】解：（1）2y x bx c =++，解：当2b =，3c =−时，2223(1)4y x x x =+−=+−， ∴顶点C 的坐标为：(1,4)−−；当0y =时，2230x x +−=，即(3)(1)0x x +−=， 解得：13x =−，21x =， (3,0)A ∴−，(1,0)B ；（2）①抛物线恰好经过P ，Q则：1101640b c b c −+=⎧⎨++=⎩，解得：54b c =−⎧⎨=⎩；②当1c =−时，21y x bx =+−， 当0x =时，1y =−， ∴抛物线过(0,1)−，当1x =−时，11y b b =−−=−，当点(1,)b −−在点P 上方，或与点P 重合时，抛物线与线段PQ 有公共点，即：10b −…， 解得：10b −…；当4x =时，1641415y b b =+−=+，当点(4,154)b +在点Q 上方，或与点Q 重合时，抛物线与线段PQ 有公共点，即：1540b +…，154b ≥−； 综上：10b −…或154b ≥−． 【点评】本题考查二次函数的综合应用．正确的求出函数解析式，熟练掌握二次函数的图象和性质是解题的关键．8．（2024•浙江模拟）设二次函数24(y ax ax c a =−+，c 均为常数，0)a ≠，已知函数值y 和自变量x 的部分对应取值如下表所示：（1）判断m ，n 的大小关系，并说明理由； （2）若328m n −=，求p 的值；（3）若在m ，n ，p 这三个数中，只有一个数是负数，求a 的取值范围．【分析】（1）根据所给函数解析式，可得出抛物线的对称轴为直线2x =，据此可解决问题． （2）根据（1）中发现的关系，可求出m 的值，据此即可解决问题． （3）根据m 和n 相等，所以三个数中的负数只能为p ，据此可解决问题． 【解答】解：（1）m n =．因为二次函数的解析式为24y ax c =+， 所以抛物线的对称轴为直线422ax a−=−=， 又因为1522−+=， 所以点(1,)m −与(5,)n 关于抛物线的对称轴对称， 故m n =．（2）因为m n =，328m n −=， 所以8m =．将(0,3)和(1,8)−代入函数解析式得：348c a a c =⎧⎨++=⎩，解得13a c =⎧⎨=⎩所以二次函数的解析式为243y x x =−+．将2x =代入函数解析式得，224231p =−⨯+=−．（3）由（1）知，m n =， 所以m ，n ，p 中只能p 为负数． 将(0,3)代入函数解析式得，3c =， 所以二次函数解析式为243y ax ax =−+． 将1x =−代入函数解析式得，53m a =+． 将2x =代入函数解析式得，43p a =−+．则430530a a −+<⎧⎨+≥⎩，解得34a >，所以a 的取值范围是34a >． 【点评】本题考查二次函数图象与系数的关系及二次函数图象上点的坐标特征，熟知二次函数的图象和性质是解题的关键．9．（2024•北京模拟）在平面直角坐标系xOy 中，抛物线2(26)1y x m x =+−+经过点1(,)m y −，2(,)m y ，3(2,)m y +．（1）若13y y =，求抛物线的对称轴； （2）若231y y y <<，求m 的取值范围． 【分析】（1）利用对称轴意义即可求解；（2m 的不等式组，解不等式组即可．【解答】解：（1）抛物线2(26)1y x m x =+−+经过点1(,)m y −，2(,)m y ，3(2,)m y +，13y y =， ∴该抛物线的对称轴为：直线22m m x −++=，即直线1x =； （2）当0m >时，可知点1(,)m y −，2(,)m y ，3(2,)m y +从左至右分布， 231y y y <<，∴232232m m m m m m ++⎧−<⎪⎪⎨−++⎪−>⎪⎩，解得12m <<； 当0m <时，3m m m ∴<−<−+，21y y ∴>，不合题意，综上，m 的取值范围是12m <<．【点评】本题考查了二次函数图象上点的坐标特征，二次函数的性质，熟练掌握二次函数的性质是解题的关键．10．（2024•浙江模拟）在平面直角坐标系xOy 中，抛物线2(y ax bx c a =++，b ，c 为常数，且0)a ≠经过(2,4)A −−和(3,1)B 两点．（1）求b 和c 的值（用含a 的代数式表示）；（2）若该抛物线开口向下，且经过(23,)C m n −，(72,)D m n −两点，当33k x k −<<+时，y 随x 的增大而减小，求k 的取值范围；（3）已知点(6,5)M −，(2,5)N ，若该抛物线与线段MN 恰有一个公共点时，结合函数图象，求a 的取值范围．【分析】（1）把(2,4)A −−和(3,1)B 代入2y ax bx c =++，即可求解；（2）先求出对称轴为：直线2x =，结合开口方向和增减性列出不等式即可求解； （3）分0a >时，0a <时，结合图象即可求解．【解答】解：（1）把(2,4)A −−和(3,1)B 代入2y ax bx c =++，得：424931a b c a b c −+=−⎧⎨++=⎩，解得：162b a c a =−⎧⎨=−−⎩；（2）抛物线经过(23,)C m n −，2,)m n −两点， ∴抛物线的对称轴为：直线237222m mx −+−==，抛物线开口向下，当33k x k −<<+时，y 随x 的增大而减小，32k ∴−…，即5k …； （3）①当0a >时，6x =−，5y …，即2(6)(1)(6)625a a a ⨯−+−⨯−−−…， 解得：1336a …，抛物线不经过点N ，如图①，抛物线与线段MN 只有一个交点，结合图象可知：1336a …；②当0a <时，若抛物线的顶点在线段MN 上时，则2244(62)(1)544ac b a a a a a−−−−−==，解得：11a =−，2125a =−， 当11a =−时，111112222(1)a −=−=⨯−， 此时，定点横坐标满足116222a−−……，符合题意； 当11a =−时，如图②，抛物线与线段MN 只有一个交点，如图③，当2125a =−时，11111312222()25a −=−=⨯−，此时顶点横坐标不满足116222a−−……，不符合题意，舍去； 若抛物线与线段MN 有两个交点，且其中一个交点恰好为点N 时，把(2,5)N 代入2(1)62y ax a x a =+−−−，得：252(1)262a a a =⨯+−⨯−−， 解得：54a =−，当54a =−时，如图④，抛物线和线段MN 有两个交点，且其中一个交点恰好为点N ，结合图象可知：54a <−时，抛物线与线段MN 有一个交点，综上所述：a 的取值范围为：1336a …或1a =−或54a <−．【点评】本题考查二次函数的性质和图象，根据题意画出图象，分类讨论是解题的关键．11．（2024•海淀区校级模拟）在平面直角坐标系xOy 中，点(0,3)，1(6,)y 在抛物线2(0)y ax bx c a =++≠上． （1）当13y =时，求抛物线的对称轴；（2）若抛物线2(0)y ax bx c a =++≠经过点(1,1)−−，当自变量x 的值满足12x −……时，y 随x 的增大而增大，求a 的取值范围；（3）当0a >时，点2(4,)m y −，2(,)m y 在抛物线2y ax bx c =++上．若21y y c <<，请直接写出m 的取值范围．【分析】（1）当13y =时，(0,3)，(6,3)为抛物线上的对称点，根据对称性求出对称轴；（2）把(0,3)，(1,1)−−代入抛物线解析式得出a ，b 的关系，然后求出对称轴，再分0a >和0a <，由函数的增减性求出a 的取值范围；（3）先画出函数图象，再根据21y y c <<确定m 的取值范围． 【解答】解：（1）当13y =时，(0,3)，(6,3)为抛物线上的对称点， 0632x +∴==， ∴抛物线的对称轴为直线3x =；（2）2(0)y ax bx c a =++≠过(0,3)，(1,1)−−，3c ∴=，31a b −+=−， 4b a =+，∴对称轴为直线422b a x a a+=−=−，①当0a >时，12x −……时，y 随x 的增大而增大，∴412a a+−−…， 解得4a …，04a ∴<…；②当0a <时，12x −……时，y 随x 的增大而增大，∴422a a+−…， 解得45a −…， ∴405a −<…，综上：a 的取值范围是405a −<… 或04a <…；（3）点(0,3)在抛物线2y ax bx c =++上，3c ∴=，点2(4,)m y −，2(,)m y 在抛物线2y ax bx c =++上， ∴对称轴为直线422m mx m −+==−， ①如图所示：21y y c <<，6m ∴<且06232m +−>=， 56m ∴<<；②如图所示：21y y c <<，46m ∴−>， 10m ∴>，综上所述，m 的取值范围为56m <<或10m >．【点评】本题考查二次函数图象与系数的关系以及二次函数图象上点的坐标特征，关键是利用数形结合和分类讨论的思想进行解答．题型三．待定系数法求二次函数解析式（共3小题）12．（2024•保山一模）如图，抛物线2y ax bx c =++过(2,0)A −，(3,0)B ，(0,6)C 三点；点P 是第一象限内抛物线上的动点，点P 的横坐标是m ，且132m <<． （1）试求抛物线的表达式；（2）过点P 作PN x ⊥轴并交BC 于点N ，作PM y ⊥轴并交抛物线的对称轴于点M ，若12PM PN =，求m 的值．【分析】（1）将A ，B ，C 三点坐标代入函数解析式即可解决问题． （2）用m 表示出PM 和PN ，建立关于m 的方程即可解决问题． 【解答】解：（1）由题知，将A ，B ，C 三点坐标代入函数解析式得，4209306a b c a b c c −+=⎧⎪++=⎨⎪=⎩，解得116a b c =−⎧⎪=⎨⎪=⎩，所以抛物线的表达式为26y x x =−++．（2）将x m =代入抛物线得表达式得，26y m m =−++， 所以点P 的坐标为2(,6)m m m −++． 令直线BC 的函数解析式为y px q =+，则306p q q +=⎧⎨=⎩，解得26p q =−⎧⎨=⎩，所以直线BC 的函数解析式为26y x =−+． 因为132m <<，且抛物线的对称轴为直线12x =，所以12PM m =−． 又因为点N 坐标为(,26)m m −+，所以226(26)3PN m m m m m =−++−−+=−+． 因为12PM PN =， 所以211(3)22m m m −=−+，解得m =， 又因为132m <<，所以m =． 【点评】本题考查待定系数法求二次函数解析式及二次函数的图象和性质，熟知待定系数法及二次函数的图象和性质是解题的关键．13．（2024•东营区校级一模）如图，在平面直角坐标系xOy 中，直线28y x =−+与抛物线2y x bx c =−++交于A ，B 两点，点B 在x 轴上，点A 在y 轴上． （1）求抛物线的函数表达式；（2）点C 是直线AB 上方抛物线上一点，过点C 分别作x 轴，y 轴的平行线，交直线AB 于点D ，E ．当38DE AB =时，求点C 的坐标．【分析】（1）根据一次函数解析式求出A ，B 两点坐标，再将A ，B 两点坐标代入二次函数解析式即可解决问题．（2）根据AOB ECD ∆∆∽得到CD 与OB 的关系，建立方程即可解决问题． 【解答】解：（1）令0x =得，8y =， 所以点A 的坐标为(0,8)； 令0y =得，4x =， 所以点B 的坐标为(4,0)；将A ，B 两点坐标代入二次函数解析式得，81640c b c =⎧⎨−++=⎩，解得28b c =⎧⎨=⎩，所以抛物线的函数表达式为228y x x =−++． （2）因为//CD x 轴，//CE y 轴， 所以AOB ECD ∆∆∽， 则CD DEOB AB=． 因为38DE AB =，4OB =， 所以32CD =． 令点C 坐标为2(,28)m m m −++， 则点D 坐标为21(2m m −，228)m m −++所以2211()222CD m m m m m =−−=−+，则213222m m −+=，解得1m =或3．当1m =时，2289m m −++=； 当3m =时，2285m m −++=； 所以点C 的坐标为(1,9)或(3,5)．【点评】本题考查待定系数法求二次函数解析式及二次函数图象上点的坐标特征，熟知待定系数法及二次函数的图象和性质是解题的关键．14．（2024•南关区校级二模）已知二次函数2y x bx c =++的图象经过点(0,3)A −，(3,0)B ．点P 在抛物线2y x bx c =++上，其横坐标为m ．（1）求抛物线的解析式；（2）当23x −<<时，求y 的取值范围；（3）当抛物线2y x bx c =++上P 、A 两点之间部分的最大值与最小值的差为34时，求m 的值； （4）点M 在抛物线2y x bx c =++上，其横坐标为1m −．过点P 作PQ y ⊥轴于点Q ，过点M 作MN x ⊥轴于点N ，分别连结PM ，PN ，QM ，当PQM ∆与PNM ∆的面积相等时，直接写出m 的值． 【分析】（1）依据题意，将A 、B 两点代入解析式求出b ，c 即可得解；（2）依据题意，结合（1）所求解析式，再配方可得抛物线的最值，进而由23x −<<可以判断得解； （3）依据题意，分类讨论计算可以得解；（4）分别写出P 、Q 、M 、N 的坐标，PQM ∆与PNM ∆的面积相等，所以Q 到PM 的距离等于N 到PM 的距离，可得m 的值．【解答】解：（1）由题意，将(0,3)A −，(3,0)B 代入解析式2y x bx c =++得，3c =−，930b c ++=，2b ∴=−，3c =−，∴抛物线的解析式为223y x x =−−；（2）由题意，抛物线2223(1)4y x x x =−−=−−，∴抛物线223y x x =−−开口向上，当1x =时，y 有最小值为4−，当2x =−时，5y =；当3x =时，0y =， ∴当23x −<<时，45y −<…；（3）由题意得，2(,23)P m m m −−，(0,3)A −，①当0m <时，P 、A 两点之间部分的最大值为223m m −−，最小值为3−， 2323(3)4m m ∴−−−−=，解得：1m =−②当02m ……时，P 、A 两点之间部分的最大值为3−，最小值为223m m −−或4−， 显然最小值是4−时不合题意， ∴最小值为223m m −−， 233(23)4m m ∴−−−−=， 解得：32m =或12m =， 32m =时，P 、A 两点之间部分的最小值为4−，故舍去， ③当2m <时，P 、A 两点之间部分的最大值为223m m −−，最小值为4−， 2323(4)4m m ∴−−−−=，解得：1m =+，12+<，故舍去，综上，满足题意得m 的值为：1或12； （4）由题意得，2(1,4)M m m −−，(1,0)N m −，2(0,23)Q m m −−， 设PM y kx b =+，代入P 、M 两点， 2223(1)4mk b m m m k b m ⎧+=−−⎨−+=−⎩， 解得：1k =−，23b m m =−−，23PM y x m m =−+−−，PQM ∆与PNM ∆的面积相等，Q ∴到23PM y x m m =−+−−的距离与N 到23PM y x m m =−+−−的距离相等，Q 到23PM y x m m =−+−−的距离=，N 到23PMy x m m =−+−−的距离=， 2|||4|m m ∴−=−+，当2m <−时，24m m −=−，解得：m =，当20m −……时，24m m −=−，解得：m =，当02m <…时，24m m =−，解得：m =当2m <时，24m m =−，解得：m =综上，满足题意得m ． 【点评】本题考查了二次函数，关键是注意分类讨论． 题型四．抛物线与x 轴的交点（共14小题）15．（2024•秦淮区校级模拟）已知函数2(2)2(y mx m x m =−−−为常数）． （1）求证：不论m 为何值，该函数的图象与x 轴总有公共点．（2）不论m ． （3）在22x −……的范围中，y 的最大值是2，直接写出m 的值． 【分析】（1）分两种情况讨论，利用判别式证明即可；（2）当1x =时，0y =，当0x =时，2y =−，即可得到定点坐标；（3）利用抛物线过两个定点，得到函数y 随x 增大而增大，代入解析式求出m 值即可． 【解答】解：（1）①当0m =时，函数解析式为22y x =−，此一次函数与x 轴有交点； ②当0m ≠时，函数解析式为2(2)2y mx m x =−−−，令0y =，则有2(2)20mx m x −−−=，△2222(2)4(2)44844(2)0m m m m m m m m =−−⨯−=−++=++=+…． ∴不论m 为何值，该函数的图象与x 轴总有公共点．（2）222(2)222()22y mx m x mx mx x m x x x =−−−=−+−=−+−， 当1x =时，0y =， 当0x =时，2y =−，∴不论m 为何值，该函数的图象经过的定点坐标是(1,0)．(0,2)−故答案为：(1,0)，(0,2)−，（3）若0m =，函数22y x =−，y 随x 增大而增大，当2x =时，2y =，与题干条件符； 当0m ≠时，函数2(2)2y mx m x =−−−是二次函数，①当0m >时，抛物线过(1,0)，(0,2)−两点，当22x −……的范围中时，y 随x 的增大而增大， ∴当2x =时，2y =，即242(2)2m m =−−−，解得0m =（舍去）．②当0m <时，抛物线过(1,0)，(0,2)−两点，其增减性依旧是y 随x 的增大而增大和①相同．综上分析，0m =．【点评】本题考查了二次函数的图象与性质，熟练掌握二次函数的性质是解答本题的关键．16．（2024•柳州模拟）如图，在平面直角坐标系中，二次函数2y x bx c =++的图象与x 轴交于A ，B 两点，B 点的坐标为(3,0)，与y 轴交于点(0,3)C −，点D 为抛物线的顶点． （1）求这个二次函数的解析式； （2）求ABD ∆的面积【分析】（1）利用待定系数法求解即可； （2）先求出点A 和点D 坐标，再根据||2D ABD AB y S ∆⋅=解析求解即可．【解答】解：（1）将(3,0)B ，(0,3)C −代入2y x bx c =++得0933b c c =++⎧⎨=−⎩，解得23b c =−⎧⎨=−⎩，∴二次函数的解析式为：223y x x =−−；（2）将223y x x =−−配方得顶点式2(1)4y x =−−， ∴顶点(1,4)D −，在223y x x =−−中，当2230y x x =−−=时， 解得1x =−或3x =， (1,0)A ∴−，4AB ∴=， ∴||44822D ABD AB y S ∆⋅⨯===． 【点评】本题主要考查了抛物线与x 轴的交点，二次函数的性质，二次函数图象上点的坐标特征，待定系数法求二次函数解析式，熟练掌握二次函数的性质是解答本题的关键．17．（2024•安阳模拟）如图，在平面直角坐标系xOy 中，抛物线2y ax bx c =++与抛物线21y x x =−+−的形状相同，且与x 轴交于点(1,0)−和(4,0)．直线2y kx =+分别与x 轴、y 轴交于点A ，B ，交抛物线2y ax bx c =++于点C ，D （点C 在点D 的左侧）． （1）求抛物线的解析式；（2）点P 是直线2y kx =+上方抛物线上的任意一点，当2k =时，求PCD ∆面积的最大值； （3）若抛物线2y ax bx c =++与线段AB 有公共点，结合函数图象请直接写出k 的取值范围．【分析】（1）根据题意直接求出二次函数解析式即可；（2）求出直线与抛物线的交点C ，D 坐标，过点P 作y 轴的平行线交CD 于点H ，交x 轴于点G ，设点P坐标为(m ，234)(12)m m m −++−<<，则点(,22)H m m +，求出PH ，由三角形的面积公式求出关于m 的函数解析式，再根据函数的性质求最值； （3）分0k >和0k <两种情况讨论即可．【解答】解：（1）抛物线2y ax bx c =++与抛物线21y x x =−+−的形状相同，1a ∴=−，抛物线2y ax bx c =++与x 轴交于点(1,0)−和(4,0)， ∴抛物线的解析式为2(1)(4)34y x x x x =−+−=−++；（2）当2k =时，联立方程组22234y x y x x =+⎧⎨=−++⎩，解得10x y =−⎧⎨=⎩或26x y =⎧⎨=⎩， (1,0)C ∴−，(2,6)D ，过点P 作y 轴的平行线交CD 于点H ，交x 轴于点G ，如图，设点P 坐标为(m ，234)(12)m m m −++−<<， ∴点(,22)H m m +，2234(22)2PH m m m m m ∴=−++−+=−++，221331273(2)()22228PCD S PH m m m ∆∴=⨯=−++=−−+， 302−<，12m −<<， ∴当12m =时，S 有最大值，最大值为278． PCD ∴∆面积的最大值为278； （3）令0x =，则2y =， ∴点B 坐标为(0,2)，令0y =，则20kx +=， 解得2x k=−，∴点A 坐标为2(k−，0)， 若抛物线2y ax bx c =++与线段AB 有公共点， 当0k >时，如图所示，则21k−<−， 解得02k <<； 当0k <时，如图所示：则24k−>， 解得102k −<<；综上所述，k 的取值范围为02k <<或102k −<<．【点评】本题考查抛物线与x 轴的交点，待定系数法求函数解析式，二次函数图象上点的坐标特征，一次函数图象上点的坐标特征，二次函数的最值等知识，关键是对这些知识的掌握和运用．18．（2024•西湖区校级模拟）已知21()y ax a b x b =+++和22()(y bx a b x a a b =+++≠且0)ab ≠是同一直角坐标系中的两条抛物线．（1）当1a =，3b =−时，求抛物线21()y ax a b x b =+++的顶点坐标； （2）判断这两条抛物线与x 轴的交点的总个数，并说明理由；（3）如果对于抛物线21()y ax a b x b =+++上的任意一点(,)P m n 均有22n a b +…．当20y …时，求自变量x 的取值范围．【分析】（1）把a ，b 的值代入配方找顶点即可解题；（2）分别令10y =，20y =，解方程求出方程的解，然后根据条件确定交点的个数即可解题；（3）现根据题意得到0a <，且24()224ab a b a b a−+=+，然后得到30b a =−>，借助图象求出不等式的解集即可．【解答】解：（1）当1a =，3b =−时，2221()23(1)4y ax a b x b x x x =+++=−−=−−， ∴顶点坐标为(1,4)−；（2）3个，理由为：令10y =，则2()0ax a b x b +++=， 即()(1)0ax b x ++=， 解得：1bx a=−，21x =−， 令20y =，则2()0bx a b x a +++=， 即()(1)0bx a x ++=， 解得：1ax b=−，21x =−， 又a b ≠且0ab ≠，∴两条抛物线与x 轴的交点总个数为3个；（3）抛物线21()y ax a b x b =+++上的任意一点(,)P m n 均有22n a b +…，0a ∴<，且24()224ab a b a b a−+=+，整理得：30b a =−>，∴22()y bx a b x a =+++的开口向上，且抛物线与x 轴交点的横坐标为113x =，21x =−， 如图所示，借助图象可知当13x …或1x −…时，20y …．【点评】本题考查二次函数的图象和性质，掌握配方法求顶点坐标，二次函数和一元二次方程的关系是解题的关键．19．（2024•三元区一模）抛物线23y ax bx =++与x 轴相交于点(1,0)A ，(3,0)B ，与y 轴正半轴相交于点C ． （1）求抛物线的解析式；（2）点1(M x ，1)y ，2(N x ，2)y 是抛物线上不同的两点． ①当1x ，2x 满足什么数量关系时，12y y =； ②若12122()x x x x +=−，求12y y −的最小值． 【分析】（1）用待定系数法即可求解；（2）①若12y y =，则M 、N 关于抛物线对称轴对称，即可求解；②22121122121212(43)(43)()()4()y y x x x x x x x x x x −=−+−−+=+−+−，而12122()x x x x +=−，得到12y y −的函数表达式，进而求解．【解答】解：（1）设抛物线的表达式为：12()()y a x x x x =−−， 即2(1)(3)(43)y a x x a x x =−−=−+， 即33a =， 解得：1a =，故抛物线的表达式为：243y x x =−+；（2）如图，。

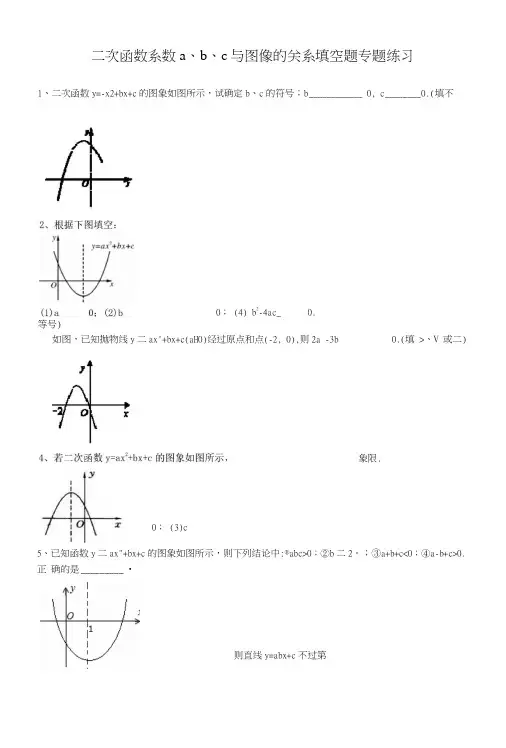
二次函数系数a 、b 、c 与图像的关系填空题专题练习1、二次函数y=-x2+bx+c 的图象如图所示，试确定b 、c 的符号；b ____________ 0, c ________ 0.(填不等号)5、已知函数y 二ax"+bx+c 的图象如图所示，则下列结论中:®abc>0；②b 二2。

；③a+b+c<0；④a-b+c>0.正 确的是 _________ •0； (4) b 2-4ac_ 0.如图，已知抛物线y 二ax'+bx+c(aH0)经过原点和点(-2, 0),则2a -3b0.(填 >、V 或二) 象限.0； (3)c则直线y=abx+c 不过第6、已知如图，抛物线y=ax2+bx+c与x轴交于点A（—1, 0）和点B,化简：如夕★如护的结杲为：①c;②b;③b—a;④a —b + 2c.其中正确的有________________ .7、二次函数y=-x2+bx + c的图象如图，则一次函数y=bx+c的图象不经过第_______________ 象限.8、若二次函数x2+bx+c的图象如图，则ac 0 （“V” “>”或“二”）9、已知二次函数y二ax'+bx+c（aH0）的图象如图所示，则在下列代数式：①ac；②a+b+c；③4a-2b+c；④2a+b；⑤圧-4ac中，值大于0的序号为__________________10、如图是二次函数y=ax2 + bx + c（a^0）的图象的一部分，给出下列命题：①a+b + c二0；②b>2a；③ax2+bx+c=0 的两根分别为一3 和1:④a—2b+c>0.其中正确的命题是 ______________ ・（只要求填写正确命题的序号）有以下结论：①abc>0；②a - b+c<0；③2d二b；④4a+2b+c>0；⑤若点（・2, y（）和（・3, y2）在该图象上，则yi>y2.其中正确的结论是 ______________ （填入正确结论的序号）.12、如图是二次函数ypx'+bx+c 的部分图像,在下列四个结论中正确的是 _________________① 不等式 ax 2+bx+c>0 的解集是-l<x<5；②a-b+c>0；③b 2-4ac>0；④4a+b<0.下列结论：①4a+b 二0；②9a+c>3b ；③8a+7b+2c>0；④当x>・1时，y 的值随x 值的增大而增大.其中正确的结论有 ______________________ （填序号）14>二次函数y=ax^+bx+c （aHO ）的图象如图所示，下列结论：①2a+b 二0；②a+c>b ；③抛物线与 x 轴的另一个交点为（3, 0）；④abc>0.其中正确的结论是 _____________________ （填写序号）.15、如图是二次函数y=ax 2+bx+c 图彖的一部分，图彖过点A （ - 3, 0）,对称轴为直线X 二・1,给 出四个结论:①b 2>4ac ；②2a+b 二0；③a+b+c>0；④若点B （ - 2. 5, yj , C （ - 0. 5, y 2）为函数图象上的两 点，则yi<y2.其中正确结论是 __________________ ・图象过点（-1, 0）,对称轴为直线x=2,16、如图，是二次函数y=ax2+bx+c (aHO)的图象的一部分，给出下列命题：①abc<0；②b>2a；③a+b+c二0④ax'+bx+c二0的两根分别为・3和1；⑤8a+c>0. 其中正确的命题是____________________________ ・17>二次函数y=ax2+bx+c (aHO)的图象如图所示，下列结论:①2a+b>0；②abc<0；③b2 - 4ac>0；④a+b+c<0；⑤la・2b+c<0,其中正确的个数是______________________ .y八18、如图，抛物线y=ax2+bx+c的对称轴是x=-l.且过点(0.5, 0),有下列结论：①abc>0；②a-2b+4c=0；③25a・ 10b+4c=0；④3b+2c>0；⑤a - b^m (am - b)；其中所有正确的结论是___________________ .(填写正确结论的序号)19、己知二次函数y=ax2+bx+c (aHO)的图象如图所示，纟合出以下结论: ®b2>4ac；②abc>0③2a-b=0；④8a+c<0；⑤9a+3b+c<0.其中结论正确的是___________ .(填正确结论的序号)x=l20、在二次函数y=ax2+bx+c的图彖如图所示，下列说法中：①b‘・4ac<0；②2占>0；③abc>0；®a-b-c>0,说法正确的是(填序号).21>已知二次函数y=ax2+bx+c (aHO)的图象如图所示，有下列5个结论：①c二0；②该抛物线的对称轴是直线x二・1；③当x=l时，y=2a；④am2+bm+a>0 (mH - 1)；⑤设A (100, yi) , B (・100, y2)在该抛物线上，则yi>y2.其中正确的结论有・(写出所有正确结论的序号)22、已知二次函数y=ax2+bx+c (aHO)的图象如图所示，则下列结论：①a+b+c<0；②a - b+c<0；③b+2a<0；④abc>0,其屮正确的是_________________ (填编号)23、如图是二次函数y=ax2+bx+c (aHO)图彖的一部分，现有下列结论：①abc<0；②b?・4ac+5> 0；③2a+b<0；④a-b+c<0；⑤抛物线y=ax2+bx+c (a^O)与x轴的另一个点坐标为(・1, 0), 其屮正确的是(把所有正确结论的序号都填在横线上)y八24、己知实数m, n满足m - n2=l,则代数式n/+2n2+4ni - 1的最小值等于_____________ •25、如图所示，己知二次函数y二ax'+bx+c的图象经过（-1, 0）和（0, -1）两点，则化简代数式_ 乎 + 4 + + 乎 _ 4 二 _______________ .\26如图，抛物线y二ax'+bx+c与x轴交于点A （・1, 0）,顶点坐标为（1, n）,与y轴的交点在（0, 2）、（0, 3）之间（包含端点），则下列结论：①当x>3时，y<0；②3a+b>0；③_2④3WnW4中，正确的是_______________27、已知二次函数y二ax'+bx+c的图象如图所示，有以下结论：①a+b+cVO；②a - b+c> 1；③abc>0；④4a - 2b+c<0；其中正确的结论是 ______________28、已知二次函数ypx'+bx+c的图象如图所示，它与x轴的两个交点分别为（-1, 0） , （3, 0）.对于下列命题：①b-2a=0；②abc<0；③a-2b+4c<0；④8a+c>0.其中正确的有___________________________ .29、已知二次函数y=ax2+bx+c (aHO)的图象如图所示，下列结论:①bV0；②4a+2b+c<0； (3)a・b+c>0；④(a+c) 2<b2.其中正确的是___________________ (把所有正确结论的序号都填在横线上).30^己知二次函数y二ax'+bx + c的图象如图所示，则下列结论：①c二2；②b2—4ac<0；③当x=l时，y的最小值为a+b+c中，正确的有___________________31、已知二次函数y=ax'+bx+c(a^O)的图像如图所示，(1)给出三个结论：①『-4眈>0；②c>0；③b>0,其中正确结论的序号是： ___________ ・(2)给出三个结论：①9a+3b+c〈0：②2c>3b；③8a+c>0，其中正确结论的序号是：________________32、已知抛物线y=ax2+bx+c(a^0)经过点(一1, 0),且顶点在第一象限.有下•列三个结论：①a<0；②a+b+c>0；③一2a >0.其中止确的结论有______________ .丄33>如图，抛物线yi=a (x+2) 2 - 3与2 (x・3) ?+1交于点A(l, 3),过点A作x轴的平行线, 分别交两条抛物线于点B, C.则以下结论：①无论x取何值，y2的值总是正数；②沪1；③当x=0 时，y2 - yi=4④2AB=3AC.34、如图，抛物线"曲"窈-3与卩飞“耳+1交于点八（］,3）,过点A作x轴的平行_2线，分别交两条抛物线于点B，C.则以下结论：①无论x収何值，乃的值总是正数；②■亍；③当x二0时，y2-yi二6；④AB+AC二10；⑤刃时乃°,其中正确结论的个数是： ________________ .35>函数y二x'+bx+c与y二x的图象如图所示，有以下结论：①b'-4c>0；②3b+c+6=0；③当lVx< 3时，x2+ （b - 1） x+c<0；④JQ+C? = 3迥.其屮正确的有 _______________ .36、如图抛物线y=ax2+bx+c与只轴的一个交点A在点（-2, 0）和（-1, 0）之间（包括这两个点）, 定点C是矩形DEFG上（包括边界和内部）的一个动点，贝9：（1）_____________ abc 0（填或“〉”；（2）___________________________ 8的取值范围是.1、答案为：V >;2、答案为：(1)> (2)< (3)> (4)>；3、答案为：>；4、答案为：四;5、答案为：①③④.6、答案为：①③④;7、答案为：四；8、答案为：<；9、答案为:10、答案为11、答案为12、答案为13、答案为14、答案为15、答案为16、答案为17、答案为18、答案为19、答案为20、答案为21、答案为22、答案为23、答案为24、答案为25、答案为26、答案为27、答案为28、答案为29、答案为30、答案为31、答案为32、答案为33、答案为34、答案为35、答案为①②⑤；①③；②④.①③；①③；①④.①④.①③④⑤.3.①③⑤.①②⑤；②③④.①②④⑤.②③.②、④.2a；①③.①③.©:①③④.①③；①；①③①②③；①④.①②④⑤,②③④；参考答案36、答案为：<。

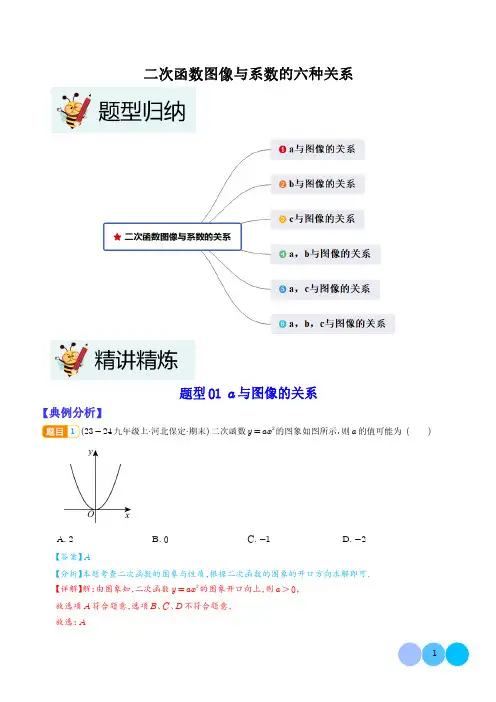
二次函数图像与系数的六种关系题型01a与图像的关系【典例分析】1(23-24九年级上·河北保定·期末)二次函数y=ax2的图象如图所示，则a的值可能为()A.2B.0C.-1D.-2【答案】A【分析】本题考查二次函数的图象与性质，根据二次函数的图象的开口方向求解即可．【详解】解：由图象知，二次函数y=ax2的图象开口向上，则a>0，故选项A符合题意，选项B、C、D不符合题意，故选：A2(2024九年级·全国·专题练习)在同一个平面直角坐标系中，二次函数y1=a1x2，y2=a2x2，y3=a3x2的图象如图所示，则a1，a2，a3的大小关系为．【答案】a3>a2>a1#a1<a2<a3【分析】本题考查了二次函数的性质，抛物线的开口方向和开口大小由a的值决定的，a 越大，开口越小，掌握抛物线的开口方向和开口大小由a的值决定是解题的关键．【详解】解：由抛物线开口方向可知，a1、a2、a3为正数，又由开口大小可得，a3>a2>a1，故答案为：a3>a2>a13(23-24九年级上·福建厦门·阶段练习)已知y=k+2x k2+k-4是二次函数，且当x<0时，y随x的增大而增大．求k的值，并画出它的图象；【答案】k=-3【分析】根据二次函数定义以及当x<0时，y随x的增大而增大．可得出函数解析式，再描点画图即可；【详解】解：由y=k+2x k2+k-4是二次函数，且当x<0时，y随x的增大而增大，得k2+k-4=2，k+2<0解得：k=-3或k=2(舍去)；二次函数的解析式为y=-x2，如图所示：【变式演练】1(23-24九年级上·山东青岛·阶段练习)图中与抛物线y=13x2，y=2x2，y=-13x2，y=-2x2，的图象对应的是()A.①②④③B.②①④③C.①②③④D.②①③④【答案】B【分析】本题考查了二次函数的图象．抛物线的形状与a和a 有关，根据a 的大小即可确定抛物线的开口的宽窄．【详解】解：∵①②开口向上，则a>0，∵②的开口最宽，∴y=13x2是②，y=2x2是①，∵③④开口向下，则a<0，∵④的开口最宽，∴y=-13x2是④，y=-2x2是③，综上，依次②①④③，故选：B2(23-24九年级上·吉林松原·阶段练习)二次函数y=k+2x2的图象如图所示，则k的取值范围是．【答案】k>-2【分析】由图示知，该抛物线的开口方向向上，则系数k+2>0，据此易求k的取值范围．【详解】解：如图，抛物线的开口方向向上，则k+2>0，解得k>-2．故答案为：k>-2．【点睛】本题考查了二次函数的图象．二次函数y=ax2的系数a为正数时，抛物线开口向上；a为负数时，抛物线开口向下；a的绝对值越大，抛物线开口越小3(24-25九年级上·全国·假期作业)已知函数y=(m+3)x m2+3m-2是关于x的二次函数．(1)求m的值；(2)当m为何值时，该函数图像的开口向下？(3)当m为何值时，该函数有最小值？(4)试说明函数的增减性．【答案】(1)m=-4或m=1(2)当m=-4时，该函数图像的开口向下(3)当m=1时，原函数有最小值(4)见解析【分析】(1)由二次函数的定义可得m2+3m-2=2m+3≠0故可求m的值．(2)图像的开口向下，则m+3<0，结合(1)中的结果，即可得m的值；(3)函数有最小值，则m+3>0，结合(1)中的结果，即可得m的值；；(4)根据(1)中求得的m的值，先求出抛物线的解析式，函数的增减性由函数的开口方向及对称轴来确定．【详解】(1)根据题意，得m2+3m-2=2 m+3≠0，解得m1=-4,m2=1 m≠-3，∴当m=-4或m=1时，原函数为二次函数．(2)∵图像开口向下，∴m+3<0，∴m<-3，∴m=-4，∴当m=-4时，该函数图像的开口向下．(3)∵函数有最小值，∴m+3>0，则m>-3，∴m=1，∴当m=1时，原函数有最小值．(4)当m=-4时，此函数为y=-x2，开口向下，对称轴为y轴，当x<0时，y随x的增大而增大；当x>0时，y随x的增大而减小；当m=1时，此函数为y=4x2，开口向上，对称轴为y轴，当x<0时，y随x的增大而减小；当x>0时，y随x的增大而增大．【点睛】本题主要考查二次函数的性质，二次函数的最值，二次函数的增减性．二次函数的最值是顶点的纵坐标，当a>0时，开口向上，顶点最低，此时纵坐标为最小值；当a<0时，开口向下，顶点最高，此时纵坐标为最大值．考虑二次函数的增减性要考虑开口方向和对称轴两方面的因素，因此最好画图观察．题型02b与图像的关系【典例分析】1(21-22九年级上·安徽合肥·开学考试)已知二次函数y=-x2+2m-1x-3，当x>1时，y随x的增大而减小，则m的取值范围是()A.m<32B.m≤32C.m≤12D.m<-12【答案】B【分析】本题主要考查二次函数图象对称轴，增减性，解一元一次不等式的问题，根据题意可得二次函数图象的对称轴为x=2m-22，结合函数图象的增减性可得2m-12≤1，由此即可求解，掌握二次函数图象的性质，解不等式的方法是解题的关键．【详解】解：二次函数y=-x2+2m-3x-3中，a=-1<0，b=2m-1，c=-3，∴图象开口向下，对称轴为x=-2m-12×-1=2m-12，∵当x>1时，y随x的增大而减小，∴2m-12≤1，解得，m≤3 2，故选：B2(2023·九年级上·西藏日喀则·)已知抛物线γ=x²+mx的对称轴为直线x=2．则m的值是() A.-4 B.1 C.4 D.-1【答案】A【分析】本题考查了二次函数y=ax2+bx+c的图象与性质，对于二次函数y=ax2+bx+c，其对称轴为直线x=-b2a，据此即可求解．【详解】解：由题意得：抛物线γ=x²+mx的对称轴为直线：x=-b2a=-m2×1=-m2，∴-m2=2解得：m=-4故选：A3(23-24九年级上·安徽淮北·阶段练习)抛物线y=-x2+2ax+3的对称轴位于y轴的右侧，与x轴交于点A，B(点B在点A的右边)，且AB=4．(1)此抛物线的顶点坐标为．(2)当-1≤x≤m时，-5≤y≤4，则m的值为．【答案】1,44【分析】(1)令y=0，则x2-2ax-3=0．设A x1,0，B x2,0，则x1+x2=2a，x1x2=-3．根据AB=4，得出x2-x1=4，结合完全平方公式得出x2-x12=x1+x22-4x1x2=16，求出a的值，即可求解；(2)根据二次函数的性质可得当x=1时，y取得最大值4．求出当x=-1时，y=0>-5，且-5≤y≤4，得出m>1，则当x=m时，y=-5，即可求解．【详解】解：(1)令y=0，则-x2+2ax+3=0，即x2-2ax-3=0．设A x1,0，B x2,0，则x1+x2=2a，x1x2=-3．∵AB=4，∴x2-x1=4，∴x2-x12=x1+x22-4x1x2=16，∴4a2+12=16，∴a=±1．∵抛物线的对称轴位于y轴的右侧，即a=1，∴y=-x2+2x+3=-x-12+4，∴抛物线的顶点坐标为1,4．(2)∵y=-x2+2x+3=-x-12+4，∴当x=1时，y取得最大值4．∵当x=-1时，y=0>-5，且-5≤y≤4，∴m>1，∴当x=m时，y=-5，∴-m2+2m+3=-5，∴m=4或m=2(舍去)．故答案为：1,4，4．【点睛】本题主要考查了二次函数的图象和性质，解题的关键是掌握二次函数与x轴交点坐标的求法，将二次函数表达式化为顶点式的方法和步骤，以及二次函数的增减性【变式演练】1(22-23九年级上·福建厦门·期中)已知抛物线y=-x2+6-2mx-3的对称轴在y轴的右侧，当x >2时，y的值随着x值的增大而减小，则m的取值范围是()A.m≥1B.m<3C.-3<m≤1D.1≤m<3【答案】D【分析】先得出抛物线对称轴为直线x=3-m，根据抛物线y=-x2+6-2mx-3的对称轴在y轴的右侧，可得m<3，根据当x>2时，y的值随着x值的增大而减小，得出m≥1，即可求解．【详解】解：∵抛物线y=-x2+6-2mx-3的对称轴在y轴的右侧，∴x=-b2a =6-2m2=3-m>0，解得：m<3，又∵a=1<0，抛物线开口向下，当x>2时，y的值随着x值的增大而减小，则3-m≤2，解得：m≥1，综上所述，1≤m<3，故选：D．【点睛】本题考查了二次函数的性质，熟练掌握二次函数的性质是解题的关键2(23-24九年级上·重庆合川·期末)关于x的二次函数y=x2+a-1x-1在y轴的右侧，y随x的增大而增大，且使得关于y的分式方程a-12-y+1y-2=2有非负数解的所有整数a的值之和．【答案】19【分析】本题主要考查了二次函数的性质、分式方程的解以及解一元一次不等式，依据题意，解分式方程可先确定出a的取值范围，再由二次函数的性质可确定出a的范围，从而可确定出a的取值，可求得答案．【详解】解分式方程a-12-y+1y-2=2可得y=6-a2，∵关于y的分式方程a-12-y +1y-2=2有非负数解，∴y=6-a2≥0且y=6-a2≠2，∴a≤6且a≠2，∵y=x2+a-1x-1，∴抛物线开口向上，对称轴为x=1-a2，∴当x>1-a2，时，y随x的增大而增大．∵在x>0时，y随x的增大而增大，≤0，解得a≥1．∴1-a2综上1≤a≤6且a≠2，∴满足条件的整数a的值为1，3，4，5，6．∴所有满足条件的整数a的值之和是1+3+4+5+6=19．故答案为：19．3(23-24九年级上·浙江宁波·期末)如图，已知二次函数y=x2+ax+2的图象经过点E1,5．(1)求a的值和图象的顶点坐标．(2)若点F m,n在该二次函数图象上．①当m=-2时，求n的值．②若n≤2，请根据图象直接写出m的取值范围．【答案】(1)a=2；-1,1(2)①n=2；②-2≤m≤0【分析】本题考查二次函数的图象及性质；熟练掌握二次函数图象上点的特征是解题的关键．(1)把点E(1,5)代入y=x2+ax+2中，即可求出a；(2)①把m=-2代入解析式即可求n的值；②由n≤2，在此范围内求m即可．【详解】(1)把点E(1,5)代入y=x2+ax+2中，∴a=2，∴y=x2+2x+2=(x+1)2+1，∴顶点坐标为(-1,1)；(2)①把m=-2代入n=m2+2m+2=(m+1)2+1，可得：n=2，②∵n≤2，对称轴为x=-1，∴-2≤m≤0．【典例分析】1(23-24九年级上·内蒙古呼和浩特·阶段练习)关于二次函数y=x2-6x+5下列说法中错误的是()A.用配方法可化成y=x-32-4 B.将它的图象向下平移5个单位，会经过原点C.函数有最小值，最小值为5D.当x<3时，y随x的增大而减小【答案】C【分析】本题考查了二次函数的性质，二次函数的图象和几何变换，掌握二次函数的图象与坐标轴交点的求法是解题的关键．运用配方法把一般式化为顶点式，由二次函数的顶点式可判断其开口方向、对称轴、顶点坐标；令x=0可求得与y轴的交点坐标；则可得出答案．【详解】解：y=x2-6x+5=x-32-4，故A正确，不符合题意；2-9+5=x-3∴其对称轴为直线x=3，开口向上，顶点坐标为3，-4，∴函数有最小值，最小值为-4，当x<3时，y随x的增大而减小，故C错误，符合题意，D正确，不符合题意；令x=0可得y=5，∴与y轴的交点坐标为0，5，∴将它的图象向下平移5个单位，会经过原点，故B正确，不符合题意；故选：C2(2023·九年级上·上海杨浦·)将抛物线y=x2-2x+3向下平移m个单位后，它的顶点恰好落在x轴上，那么m=．【答案】2【分析】将抛物线解析式改为顶点式，即可求出平移后的解析式，进而可求出平移后的顶点坐标，最后根据它的顶点恰好落在x轴上，即顶点的纵坐标为0，可求出答案．【详解】解：∵y=x2-2x+3=(x-1)2+2，∴该抛物线向下平移m个单位后的解析式为y=(x-1)2+2-m，∴此时顶点坐标为(1，2-m)．∵此时它的顶点恰好落在x轴上，∴2-m=0，解得：m=2．故答案为：2．【点睛】本题考查二次函数图象的平移，二次函数的图象和性质．掌握二次函数图象的平移规律“上加下减，左加右减”是解题关键3(23-24九年级上·四川泸州·期中)写出抛物线y=-2x2-4x+5的开口方向、对称轴及顶点坐标，并指出抛物线y=-2x2-4x+5可由抛物线y=-2x2怎样平移得到．【答案】抛物线y=-2x2-4x+5开口向下，对称轴为x=-1，顶点坐标为-1,7，抛物线y=-2x2-4x+5可由y=-2x2向上平移7个单位长度，向左平移1个单位长度得到．【分析】本题考查的知识点是二次函数的图像与性质、二次函数图像的平移，解题关键是理解抛物线y=ax2+bx+c的性质及掌握抛物线平移规律．先将抛物线y=-2x2-4x+5经配方转换为y=-2x+12+7，即可直接根据表达式判断抛物线开口方向、对称轴和顶点坐标；另根据抛物线平移规律“上加下减，左加右减”即可得出y=-2x2到y=-2x2-4x+5=-2x+12+7的平移过程．【详解】解：依题得抛物线y=-2x2-4x+5=-2x+12+7，则可根据抛物线性质得：抛物线y=-2x2-4x+5开口向下，对称轴为x=-1，顶点坐标为-1,7，∵根据抛物线平移规律“上加下减，左加右减”，∴y=-2x2-4x+5=-2x+12+7可由y=-2x2向上平移7个单位长度，向左平移1个单位长度得到【变式演练】1(23-24九年级上·安徽合肥·期末)若将抛物线y=ax2(a>0)向右平移h(h>0)个单位，得到抛物线y=ax2+bx+c，则函数y=bx+c的图象可能是()A. B.C. D.【答案】C【分析】本题主要考查了二次函数及一次函数的图象，熟练掌握图象与系数的关系是关键．先根据题意判断 b<0,c>0，再判断经过的象限．【详解】∵将抛物线y=ax2(a>0)向右平移h(h>0)个单位，得到抛物线y=ax2+bx+c，∴y=ax2+bx+c对称轴在y轴的右侧，且交于y轴的正半轴，∴b<0,c>0，∴y=bx+c的图象过第一、二、四象限．故选：C2(22-23九年级上·浙江宁波·期末)将抛物线y=x2+3x-6向上平移m个单位后，得到的图象不经过第四象限，则m的值可能是()A.1B.3C.5D.7【答案】D【分析】根据将抛物线y=x2+3x-6向上平移m个单位后，得到的图象不经过第四象限可知-6+m≥0，即可得出结果．【详解】解：∵将抛物线y=x2+3x-6向上平移m个单位后，得到的图象不经过第四象限，∴-6+m≥0，∴m≥6，∴m的值可能是7，故选：D．【点睛】本题考查了二次函数图象与几何变换，二次函数的性质，熟练掌握二次函数的性质是解题的关键3(21-22九年级上·广东中山·阶段练习)已知二次函数y=x2-2x-3．(1)请写出函数图象顶点坐标和对称轴∶(2)当函数值y为正数时，自变量x的取值范围∶(3)将该函数图象向右平移1个单位，再向上平移4个单位后，求所得图象的函数表达式．【答案】(1)1,-4，直线x=1(2)x<-1或x>3(3)y=x-22【分析】本题考查了二次函数的顶点式，对称轴，平移，不等式解集的确定，熟练掌握二次函数的性质是解题的关键．(1)化成顶点式，确定对称轴和顶点坐标即可．(2)求得x2-2x-3=0的两个根，进而即可求解．(3)根据右减上加的平移规律，即可求解．【详解】(1)∵y=x2-2x-3=x-12-4．∴对称轴为直线x=1，顶点为1,-4．(2)根据题意，得x2-2x-3=0，解得x1=-1,x2=3，∵y=x2-2x-3=x-12-4开口向上，故当x<-1或x>3时，y>0．(3)∵y=x2-2x-3=x-12-4．平移后的解析式为y=x-1-122-4+4即y=x-2题型04a，b与图像的关系【典例分析】1(23-24九年级上·浙江金华·期末)已知二次函数y=-mx2+2mx+4m>0，点经过点A-2,y1 B1,y2，那么y1，y2，y3的大小关系为()，点C3,y3A.y1<y2<y3B.y1<y3<y2C.y2<y3<y1D.y3<y1<y2【答案】B【分析】本题考查利用二次函数性质比较函数值大小，涉及二次函数图像与性质、比较二次函数值大小等知识，根据二次函数图像与性质，利用图像上点到对称轴距离比较函数值大小即可得到答案，熟练掌握利用距离比较二次函数值大小的方法是解决问题的关键．【详解】解：由二次函数y=-mx2+2mx+4m>0可知抛物线开口向下，对称轴为x=-2m-2m=1，∴抛物线上点到对称轴距离越近，函数值y越大，∵二次函数y=-mx2+2mx+4m>0经过点A-2,y1，点B1,y2，点C3,y3，∴三个点A、B、C到对称轴的距离为3、0、2，∴y1<y3<y2，故选：B．2(23-24九年级上·广东广州·期中)若点A-134,y1B-1,y2，C53,y3为二次函数y=-ax2-4ax+5a<0图象上的三个点，则y1，y2，y3的大小关系是．【答案】y3>y1>y2【分析】本题考查了二次函数的图象及性质，根据题意得抛物线开口向上，对称轴为直线x=-2，则点A-134,y1关于直线x=-2的对称点54,y1在抛物线y=-ax2-4ax+5a<0上，根据二次函数的性质即可求解，熟练掌握二次函数的图象及性质是解题的关键．【详解】解：∵y=-ax2-4ax+5a<0，∴-a>0，对称轴为直线x=--4a2×-a=-2，∴抛物线开口向上，∴点A-134,y1关于直线x=-2的对称点54,y1在抛物线y=-ax2-4ax+5a<0上，∵-2<-1<54<53，∴y3>y1>y2，故答案为：y3>y1>y23(23-24九年级上·云南昆明·阶段练习)已知关于x的二次函数y=mx2+3m+1x+3．(1)求证：不论m为任何实数，方程mx2+3m+1x+3=0总有实数根；(2)若抛物线与x轴交于两个不同的整数点，m为正整数，点P x1,y1与Q x1+n,y2在抛物线上(点P, Q不重合)，且y1=y2，求代数式4x21+12x1n+5n2+16n+8的值．【答案】(1)证明见解析；(2)24【分析】本题主要考查了二次函数与一元二次方程的关系以及二次函数的图象与性质等知识；(1)用根的判别式可以直接证明；(2)令y=0，方程可以化为mx+1x+3=0，解得x=-3或x=-1m，又m为正整数，可以求解m的值，进而可求出函数解析式；点P、Q在抛物线上，且y1=y2，可将x1、x1+n代入解析式联立方程，用含n的式子表示出x1，然后带入代数式化简求解即可．【详解】(1)解：由题意可知m≠0，∵Δ=b2-4ac=(3m+1)2-4m×3=(3m-1)2≥0∴此方程总有实数根；综上，不论m为任何实数时，方程总有实数根．(2)解：令y=0，则有mx+1x+3=0解得：x1=-3，x2=-1 m，因为抛物线与x轴交于两个不同的整数点，且m为正整数，所以m=1，所以抛物线为y=x2+4x+3．∵点P、Q在抛物线上，且y1=y2，∴x12+4x1+3=(x1+n)2+2(x1+n)+3∴2x1n+n2+4n=0即：n(2x1+n+4)=0，∵P、Q不重合，∴n≠0，∴2x1=-n-4∴4x12+12x1n+5n2+16n+8=(2x1)2+2x1∙6n+5n2+16n+8=(n+4)2+6n(-n-4)+5n2+16n+8=24所以代数式 4x21+12x1n+5n2+16n+8的值为24【变式演练】1(23-24九年级上·浙江杭州·期末)已知关于x的二次函数y=ax2-4ax a>0．若P m,n和Q5,b是抛物线上的两点，且n>b，则m的取值范围为()A.m<-1B.m>5C.m<-1或m>5D.-1<m<5【答案】C【分析】本题考查了二次函数图象上点的坐标特征，二次函数的性质，由抛物线的解析式可知开口方向和对称轴为直线x=2，根据函数的对称性和增减性即可求解；熟练掌握二次函数的对称性和增减性是解题的关键．【详解】解：∵二次函数y=ax2-4ax a>0．∴抛物线开口向上，对称轴为直线x=--4a2a=2，∵P m,n和Q5,b是抛物线上的两点，∴当n=b时，m=-1，∵抛物线上的点到对称轴的距离越远，函数值越大，∴n>b时，m的取值范围为m<-1或m>5；故选：C．2(23-24九年级上·浙江杭州·期末)已知二次函数y=ax2-4ax+2(a为常数，且a≠0) (1)若函数图象过点1,0，求a的值；(2)当2≤x≤5时，函数的最大值为M，最小值为N，若M-N=18，求a的值．【答案】(1)a=2 3(2)a=±2【分析】本题考查了求二次函数的表达式、二次函数的性质，熟练掌握二次函数的性质是解题的关键．(1)将点1,0的坐标代入表达式求解即可；(2)分类讨论a的正负，结合对称轴和图象的增减性即可得出答案．【详解】(1)解：函数图象过点1,0得a-4a+2=0解得：a=2 3(2)由y=ax2-4ax+2可知对称轴为直线x=2①当a>0时，开口方向向上，当2≤x≤5时当x=2时取最小值，当x=5时取最大值∴M=5a+2，N=-4a+2∵M-N=5a+2--4a+2=9a=18解得a=2，满足题意．②当a<0时，开口方向向下，当2≤x≤5时当x=2时取最大值，当x=5时取最小值∴M=-4a+2，N=5a+2∴M-N=-4a+2-5a+2=-9a=18解得a=-2 满足题意．综上所述：a=±2．3(23-24九年级上·安徽合肥·阶段练习)如图所示，抛物线y=ax2+bx+4(a≠0)经过点A(-1，0)，点B(4，0)，与y轴交于点C，连接AC，BC．点M是线段OB上不与点O、B重合的点，过点M作DM⊥x 轴，交抛物线于点D，交BC于点E．(1)求抛物线的表达式；(2)过点D作DF⊥BC，垂足为点F．设M点的坐标为M(m，0)，请用含m的代数式表示线段DF的长，并求出当m为何值时DF有最大值，最大值是多少？【答案】(1)抛物线的表达式为：y=-x2+3x+4(2)当m=2时，DF有最大值为22【分析】(1)利用待定系数法求函数解析式．(2)先求出B,C所在直线解析式可得∠OBC=∠OCB=45°，通过DF=22DE可表示DF长度的代数式，再配方求解即可．【详解】(1)把点A(-1，0)，点B(4，0)分别代入y=ax2+bx+4a≠0中，得：a-b+4=016a+4b+4=0解得：a=-1 b=3∴抛物线的表达式为：y=-x2+3x+4．(2)把x=0代入y=-x2+3x+4中，得：y=4∴C0,4设BC所在直线解析式为y=kx+b,把B4,0,C0,4代入y=kx+b中，得：0=4k+b 4=b解得k=-1 b=4∴y=-x+4设M m,0,则D(m,-m2+3m+4)，E m,-m+4∴DE=-m2+3m+4+m-4=-m2+4m ∵OB=OC=4,OC⊥OB∴∠OBC=∠OCB=45°∵DM⊥x轴∴∠DEF=∠BEM=45°又∵DF⊥BC∴DF=22DE=22-m2+4m=-22(m-2)2+22∵-22<0∴当m=2时，DF有最大值为22．【点睛】本题考查二次函数与图形的结合，解题关键是掌握待定系数法求函数解析式，掌握配方法求代数式的最值题型05a，c与图像的关系【典例分析】1(23-24九年级上·广东梅州·期末)如图所示是二次函数y=ax2-x+a2-1的图象，则a的值是()A.a=-1B.a=12C.a=1D.a=1或a=-1【答案】C【分析】此题考查了二次函数的图象．由图象得，此二次函数过原点0,0，把点0,0代入函数解析式得a2 -1=0，解得a的值．【详解】解：由图象得，此二次函数过原点0,0，把点0,0代入函数解析式得a2-1=0，解得a=±1；又因为此二次函数的开口向上，所以a>0；所以a=1．故选：C．2(23-24九年级上·浙江丽水·期末)已知二次函数y=ax²+2x+c a≠0的图象如图所示．(1)写出c的值；(2)求出函数的表达式．【答案】(1)3(2)y=-x²+2x+3【分析】本题着重考查了待定系数法求二次函数解析式，综合利用已知条件求出抛物线的解析式是解题的关键．(1)将点0,3即可求出c；代入y=ax²+2x+c a≠0(2)把点A3,0即可求出函数表达式．代入y=ax²+2x+3a≠0【详解】(1)解：∵二次函数y=ax²+2x+c a≠0；的图象经过点0,3∴将点0,3得；代入y=ax²+2x+c a≠0c=3．(2)解：设函数的表达式为y=ax²+2x+3a≠0；∵函数图象经过点A3,0；∴把点A3,0得；代入y=ax²+2x+3a≠0a=-1；∴函数的表达式为：y=-x²+2x+33(23-24九年级上·广东广州·阶段练习)如图，二次函数y=ax2-2x+c的图象与x轴交于点A-3,0和点B，点y轴交于点C0,3．(1)求二次函数的解析式；(2)求B点坐标，并结合图象写出y<0时，x的取值范围；【答案】(1)y=-x2-2x+3；(2)B1,0，x<-3或x>1．【分析】本题主要考查了求二次函数的解析式，二次函数的图象和性质，熟练掌握二次函数的图象和性质，利用数形结合思想解答是解题的关键．(1)利用待定系数解答，即可求解；(2)根据当y=0时，-x2-2x+3=0，求出点B1,0，进而根据图象可得出答案．【详解】(1)解：∵二次函数y=ax2-2x+c的图象经过点A-3,0，C0,3，∴9a+6+c=0 c=3，解得：a=-1 c=3，∴该二次函数的解析式为y=-x2-2x+3；(2)解：由(1)可知，二次函数的解析式为y=-x2-2x+3，当y=0时，-x2-2x+3=0，解得x1=1，x2=-3，∴B1,0，根据图象可知，当y<0时，x的取值范围为x<-3或x>1【变式演练】1(23-24九年级上·广西崇左·期末)已知二次函数y=m+2x2+m2-9有最大值，且图象经过原点，则m的值为()A.±3B.3C.-3D.±4.5【答案】C【分析】本题考查二次函数的基本性质，根据二次函数有最大值得出m<-2，根据二次函数图象经过原点得出m=±3，即可得出答案，掌握二次函数的性质是解题的关键．【详解】解：∵二次函数的解析式为：y=m+2x2+m2-9有最大值，∴m+2<0，∴m<-2，∵二次函数y=m+2x2+m2-9的图象经过原点，∴m2-9=0，∴m=-3或m=3，∵m<-2，∴m=-3．故选：C2(20-21九年级上·全国·单元测试)如图所示，抛物线y=ax2-x+c的图象经过A-1,0、B0,-2两点．1 求此抛物线的解析式；2 求此抛物线的顶点坐标和对称轴；3 观察图象，求出当x取何值时，y>0？【答案】1 y=x2-x-2；2 抛物线的对称轴是直线x=12；顶点坐标是12,-94；3当x取x<-1或x>2时，y>0．【分析】(1)把A点和B点坐标代入y=ax2-x+c得到关于a、c的方程组，然后解方程组求出a、c即可得到抛物线解析式；(2)把一般式配成顶点式，然后根据二次函数的性质求解；(3)先通过解方程x2-x-2=0 得到抛物线y=x2-x-2与x轴的另一个交点的坐标为2,0．然后写出函数图象在x轴上方所对应的自变量的取值范围即可．【详解】1 ∵二次函数y=ax2-x+c的图象经过A-1,0、B0,-2，∴a+1+c=0c=-2，解得a=1c=-2∴此二次函数的解析式是y=x2-x-2；2 ∵y=x2-x-2=x-122-94，∴抛物线的对称轴是直线x=12；顶点坐标是12,-94 ；3 当y=0时，x2-x-2=0，解得x1=-1，x2=2，即抛物线y=x2-x-2与x轴的另一个交点的坐标为2,0．所以当x取x<-1或x>2时，y>0．【点睛】待定系数法求二次函数解析式, 二次函数的性质，二次函数与一元二次方程的关系等，掌握待定系数法求二次函数解析式是解题的关键3(23-24九年级上·江苏扬州·期末)如图，已知二次函数y=ax2+bx+3的图象经过点A1，0，B-2，3(1)求a+b的值；(2)用无刻度直尺画出抛物线的对称轴l；(用虚线表示画图过程，实线表示画图结果)(3)结合图象，直接写出当y≤3时，x的取值范围是．【答案】(1)a+b=-3(2)见解析(3)x≤-2或x≥0【分析】本题考查了待定系数法求二次函数的解析式、二次函数的图象与性质，熟练掌握二次函数的图象与性质，采用数形结合的思想是解此题的关键．(1)利用待定系数法求解即可；(2)根据二次函数图象的对称性可得出抛物线的对称轴；(3)观察函数图象，结合方程，即可得出结论．【详解】(1)解：将A1，0，B-2，3代入二次函数y=ax2+bx+3得：a+b+3=0 4a-2b+3=3，解得：a=-1 b=-2，∴a+b=-1+-2=-3；(2)解：如图，直线l为所求对称轴，，由(1)得二次函数的解析式为y=-x2-2x+3=-x+12+4，∴可以得出顶点坐标为-1，4，对称轴为直线x=-1；(3)解：令y=3，则-x2-2x+3=3，解得：x=0或x=-2，结合图象得：x≤-2或x≥0时，y≤3，故答案为：x≤-2或x≥0题型06a，b，c与图像的关系【典例分析】1(23-24九年级上·山东济南·期末)二次函数y=ax2+bx+c a≠0的图像如图所示，则下列结论中：①abc<0；②2a-b=0；③当-2<x<3时，y<0；④当x≥1时，y随x的增大而减小，正确的个数是()A.1B.2C.3D.4【答案】A【分析】本题考查二次函数图像与系数的关系，二次函数的性质．根据开口方向、对称轴、抛物线与y轴的交点，确定a、b、c的符号，根据对称轴和图像确定y<0时，x的范围，根据二次函数的性质确定增减性．掌握二次函数的图像和性质、灵活运用数形结合思想是解题的关键．【详解】解：①∵二次函数的图像开口向上，∴a>0，∵二次函数图像的对称轴在y轴的右侧，∴-b>0，2a∴b<0，∵抛物线与y轴交于负半轴，∴c<0，∴abc>0，故结论①不正确；②∵a>0，b<0，∴2a-b>0，故结论②不正确；③∵二次函数的图像开口向上，对称轴为：x=1，该图像与x轴的位于对称轴左边的交点的坐标为-2,0，∴该图像与x轴的位于对称轴右边的交点的坐标为4,0，∴当-2<x<4时，y<0，∴当-2<x<3时，y<0，故结论③正确；④∵二次函数的图像开口向上，对称轴为：x=1，∴当x≥1时，y随x的增大而增大，故结论④不正确，∴正确的个数是1个．故选：A2(23-24九年级上·湖北随州·期末)已知二次函数y=ax2+bx+c的图象如图所示抛物线的顶点坐标是1,1在该抛物线上，则am2+bm ，有下列结论①a>0；②b2-4ac>0；③4a+b=1；④若点A m,n+c≥a+b+c．其中正确的结论是．【答案】①③④【分析】本题考查二次函数图象与系数之间的关系，开口方向判断①，与x轴的交点个数，判断②，特殊点判断③，最值判断④．【详解】解：∵抛物线的开口向上，∴a>0；故①正确；∵抛物线与x轴没有交点，∴b2-4ac<0；故②错误；∵顶点坐标为1,1，，图象过3,3∴a+b+c=1,9a+3b+c=3，两式相减，得：8a+2b=2，∴4a+b=1；故③正确；∵当x=1时y=a+b+c=1值最小，∴am2+bm+c≥a+b+c，故④正确；故答案为：①③④3(23-24九年级上·河南洛阳·期末)已知二次函数y=ax2+2ax-m．(1)当a=1时，二次函数y=ax2+2ax-m的图象与x轴有两个交点，求m的取值范围；(2)若二次函数y=ax2+2ax-m的部分图象如图所示，①求二次函数y=ax2+2ax-m图象的对称轴；②求关于x的一元二次方程ax2+2ax-m=0的解．【答案】(1)m>-1(2)①直线x=-1；②x1=1，x2=-3【分析】(1)将a=1代入二次函数y=ax2+2ax-m中，然后根据当a=1时，二次函数y=ax2+2ax-m的图象与x轴有两个交点，可知 22-4×1×-m>0，然后即可求得m的取值范围；(2)①将函数解析式化为顶点式，即可得到该函数的对称轴；②根据图象与x轴的一个交点和二次函数的性质，可以写出该函数图象与x轴的另一个交点，然后即可写出关于x的一元二次方程ax2+2ax-m=0的解；本题考查了抛物线与x轴的交点、二次函数的性质，解题的关键是明确题意，利用数形结合熟练掌握以上知识的应用．【详解】(1)当 a=1时，y=ax2+2ax-m，∵当a=1时，二次函数y=ax²+2ax-m的图象与x轴有两个交点，∴22-4×1×-m>0，解得m>-1；(2)①∵y=ax2+2ax-m=a x+12-a-m，∴二次函数y=ax2+2ax-m的图象的对称轴是直线x=-1；②由图象可知：二次函数y=ax2+2ax-m的图象与x轴交于点(1,0),由①知，该函数的对称轴为直线x=-1，∴该函数与x轴的另一个交点为-3,0，∴关于x的一元二次方程ax2+2ax-m=0的解是x1=1，x2=-3【变式演练】1(23-24九年级上·云南昭通·阶段练习)二次函数y=ax2+bx+c的图象如图所示，下列结论中正确的是()A.b<0B.当x>0时，y>0C.a-3=cD.2a+b=0【答案】D【分析】本题考查抛物线与坐标轴的交点、二次函数的性质．解答本题的关键是明确题意，利用数形结合的思想解答．根据函数图象的开口方向，对称轴，与y轴的交点位置，可以判断各个选项中的说法是否正确，从而可以解答本题．【详解】解：由图象可得，A．该函数图象的开口向下，∴a<0，∵对称轴位于y轴右侧，∴-b>0，2a∴b>0，故此选项不符合题意；B．由图象可得：当x>0时，y不一定大于0，故此选项不符合题意；C．该函数图象与y轴交于正半轴，∴c>0，而a<0，∴a-c<0，∴a-c=3错误，即a-3=c错误；故此选项不符合题意；D．该函数的对称轴为直线x=1，=1，∴x=-b2a∴b=-2a，即2a+b=0，故选项符合题意．故选：D2(23-24九年级上·宁夏吴忠·阶段练习)二次函数y=ax2+bx+c的图象如图所示，则下列结论：①ac<0；②a+b=0；③a+b+c>0；④b2-4ac<0．其中正确的是．(填序号)。

A B CD yOx yO x yO x yO x yO x 一、二次函数图像与系数a 、b 、c 、关系1、二次函数y =ax 2+bx +c （a ≠０）的图象如图2所示，则点c M b a ⎛⎫⎪⎝⎭，在（ ）A 、第一象限B 、第二象限C 、第三象限D 、第四象限 2、如图，若a ＜0，b ＞0，c ＜0，则抛物线y=ax 2＋bx ＋c 的大致图象为（ ）3、二次函数2(0)y ax bx c a =++≠的图象如图所示，则下列说法不正确的是（ ）A 、240b ac ->B 、0a >C 、0c >D 、02ba-< 4、二次函数y =ax 2+bx +c 的图象如图3所示，则下列关于a ，b ，c 间关系的判断正确的是（ ） A 、ab ＜0 B 、bc ＜0 C 、a +b +c ＞0 D 、a -b +c ＜05、 二次函数c bx ax y ++=2，图象如图所示，则反比例函数xab y =的图象的两个分支分别在第 象限。

6、已知反比例函数xky =的图象如图所示，则二次函数222k x kx y +-=的图象大致为( )7、二次函数y=ax 2与一次函数y=ax ＋a 在同一坐标系中的图象大致为（ ）8、函数y=ax 2＋bx ＋c 和y=ax ＋b 在同一坐标系中，如图所示，则正确的是（ ）9、在同一直角坐标系内，二次函数y=ax 2＋（a ＋c ）x ＋c 与一次函数y=ax ＋c 的大致图象，有且只有一个是正确的，正确的是（ ）10、二次函数y=ax 2＋bx ＋c 与一次函数y=ax ＋c 在同一坐标系中的图象大致是图中的（ ）11、在同一坐标系中，函数y=ax 2＋bx 与y=xb的图象大致是图中的（ ）12、已知a ＜0，b ＞0，c ＞0，那么抛物线y =ax 2+bx +c 的顶点在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 13、已知二次函数y =ax 2+bx +c 的图象如图1所示，则a ，b ，c 满足（ ）A ．a ＜0，b ＜0，c ＞0B ．a ＜0，b ＜0，c ＜0C ．a ＜0，b ＞0，c ＞0D ．a ＞0，b ＜0，c ＞014、二次函数y =ax 2+bx +c （a ≠０）的图象如图2所示，则点c M b a ⎛⎫⎪⎝⎭，在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限15、已知二次函数2y ax bx c =++（其中000a b c >><，，），关于这个二次函数的图象有如下说法：①图象的开口一定向上；②图象的顶点一定在第四象限；③图象与x 轴的交点至少有一个在y 轴的右侧．以上说法正确的个数为（ ）A ．0 B ．1 C ．2 D ．3二、⊿的符号的判定例1、下图中⊿0<的是（ ）（A ） （B ） （C ） （D ） （图3）练习：不论x 为何值,函数y=ax 2+bx+c(a ≠0)的值恒大于0的条件是( )A.a>0,△>0;B.a>0, △<0;C.a<0, △<0;D.a<0, △<0 三、含a 、b 的代数式符号的判定例1、抛物线y=x 2+2x-4的对称轴是直线（ ）.A.x=-2B.x=2C.x=-1D.x=1Oy x Oy x y x O y x O ..C A y xOy–1 3 3O xP1 -1O x =1yxy–1 3 3O xP 1 练习：二次函数)1)(3(2-+-=x x y 的图象的对称轴是直线________________．例2、二次函数2(0)y ax bx c a =++≠的图象如图3所示，则①20a b +>②20a b +<③02ba-<④20a b -<⑤20a b ->中正确的有________________________.(请写出序号即可)图4 图5练习：1、二次函数2(0)y ax bx c a =++≠的图象如图4所示，则下列说法不正确的是（ ） A ．240b ac ->B ．0a >C ．0c >D ．02ba-< 例1、如图5，抛物线)0(2>++=a c bx ax y 的对称轴是直线1=x ，且经过点P （3，0），则cb a +-的值为 （ ）A. 0 B. －1 C. 1 D. 2练习：已知a －b ＋c=0 9a ＋3b ＋c=0,则二次函数y=ax 2＋bx ＋c 的图像的顶点可能在（ ） （A ）第一或第二象限； （B ）第三或第四象限；（C ）第一或第四象限； （D ）第二或第三象限例2已知二次函数c bx ax y ++=2的图象如图所示，那么下列判断正确的是（ ）(A)abc ＞0 （B ）ac b 42-＞0(C)2a+b ＞0 （D ）c b a +-24＜0练习：1、已知二次函数2y ax bx c =++（0a ≠）的图象如图所示，有下列4个结论：①0abc >；②b a c <+；③420a b c ++>；④240b ac ->；其中正确的结论有（ ）A ．1个 B ．2个 C ．3个 D ．4个2、抛物线y=ax 2+bx+c 的图象如图6，OA=OC ，则（ ）（A ） ac+1=b; （B ） ab+1=c; （C ）bc+1=a; （D ）以上都不是图4 图5 图6图2y 0 1x-1 图1O xy-11作业：1、若二次函数c bx ax y ++=2中，a ＜0，b ＞0，c ＜0，042>-ac b ，则此二次函数图像不经过（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2、当a>0, b<0,c>0时,下列图象有可能是抛物线y=ax 2+bx+c 的是（ ）3、二次函数c bx ax y ++=2的图象如图1所示，则下列结论中，正确的个数是（ ）①0<++c b a ；②0>+-c b a ；③0>abc ；④a b 2= （A ）4（B ）3（C ）2 （D ）14、已知二次函数c bx ax y ++=2的图象如图2所示，那么下列判断不正确的是（ ） (A)abc ＞0； （B ）ac b 42-＞0；(C)2a+b ＞0； （D ）c b a +-24＜05、二次函数c bx ax y ++=2的图象如图所示，则 abc ，ac b 42-，b a +2，c b a ++这四个式子中， 值为正数的有（ ）A ．4个 B ．3个 C ．2个 D ．1个6、二次函数y =ax 2+bx +c 的图象如图3所示，则下列关于a ，b ，c 间关系的判断正确的是（ ） A ．ab ＜0 B ．bc ＜0 C ．a +b +c ＞0 D ．a -b +c ＜07、(2008年安徽省)如图为二次函数y=ax 2＋bx ＋c 的图象，在下列说法中：① ac ＜0； ②方程ax 2＋bx ＋c=0的根是x 1= －1, x 2= 3 ② a ＋b ＋c ＞0 ④当x ＞1时，y 随x 的增大而增大。

中考数学每日一练：二次函数图象与系数的关系练习题及答案_2020年压轴题版答案答案2020年中考数学：函数_二次函数_二次函数图象与系数的关系练习题~~第1题~~(2019巴中.中考真卷) 如图，抛物线经过x 轴上的点A （1，0）和点B 及y轴上的点C ，经过B 、C 两点的直线为 ．①求抛物线的解析式．②点P 从A 出发，在线段AB 上以每秒1个单位的速度向B 运动，同时点E 从B 出发，在线段BC 上以每秒2个单位的速度向C 运动．当其中一个点到达终点时，另一点也停止运动．设运动时间为t 秒，求t为何值时，△PBE 的面积最大并求出最大值．③过点A 作 于点M ，过抛物线上一动点N （不与点B 、C 重合）作直线AM 的平行线交直线BC 于点Q ．若点A、M 、N 、Q 为顶点的四边形是平行四边形，求点N 的横坐标．考点： 二次函数图象与系数的关系;二次函数的最值;二次函数图象上点的坐标特征;待定系数法求二次函数解析式;二次函数图象与一元二次方程的综合应用;~~第2题~~(2018绍兴.中考模拟) 已知x 轴上有点A （1，0），点B 在y 轴上，点C （m ，0）为x 轴上一动点且m ＜﹣1，连接AB ，BC ，tan ∠ABO= ，以线段BC 为直径作⊙M 交直线AB 于点D ，过点B 作直线l ∥AC ，过A ，B ，C 三点的抛物线为y=ax +bx+c ，直线l 与抛物线和⊙M 的另一个交点分别是E ，F ．（1） 求B 点坐标；（2） 用含m 的式子表示抛物线的对称轴；（3） 线段EF 的长是否为定值？如果是，求出EF 的长；如果不是，说明理由．（4） 是否存在点C （m ，0），使得BD= AB ？若存在，求出此时m 的值；若不存在，说明理由．考点： 二次函数图象与系数的关系;二次函数的实际应用-几何问题;圆周角定理;解直角三角形;~~第3题~~(2017邗江.中考模拟) 如图，点P （x ，y ）与Q （x ，y ）分别是两个函数图象C 与C 上的任一点．当a≤x≤b 时，有﹣1≤y ﹣y ≤1成立，则称这两个函数在a≤x≤b 上是“相邻函数”，否则称它们在a≤x≤b 上是“非相邻函数”．例如，点P （x ，y ）与Q 21212121答案答案答案（x ，y ）分别是两个函数y=3x+1与y=2x ﹣1图象上的任一点，当﹣3≤x≤﹣1时，y ﹣y =（3x+1）﹣（2x ﹣1）=x+2，通过构造函数y=x+2并研究它在﹣3≤x≤﹣1上的性质，得到该函数值的范围是﹣1≤y≤1，所以﹣1≤y ﹣y ≤1成立，因此这两个函数在﹣3≤x≤﹣1上是“相邻函数”．（1） 判断函数y=3x+2与y=2x+1在﹣2≤x≤0上是否为“相邻函数”，并说明理由；（2） 若函数y=x ﹣x 与y=x ﹣a 在0≤x≤2上是“相邻函数”，求a 的取值范围；（3） 若函数y= 与y=﹣2x+4在1≤x≤2上是“相邻函数”，直接写出a 的最大值与最小值．考点： 定义新运算;一次函数的实际应用;反比例函数的实际应用;二次函数图象与系数的关系;二次函数的最值;~~第4题~~(2017祁阳.中考模拟) 将抛物线c ： 沿x轴翻折，得到抛物线c ， 如图1所示．（1）请直接写出抛物线c 的表达式；（2）现将抛物线c 向左平移m 个单位长度，平移后得到新抛物线的顶点为M ，与x 轴的交点从左到右依次为A 、B ；将抛物线c 向右也平移m 个单位长度，平移后得到新抛物线的顶点为N ，与x 轴的交点从左到右依次为D 、E ．①当B 、D 是线段AE 的三等分点时，求m 的值；②在平移过程中，是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形？若存在，请求出此时m 的值；若不存在，请说明理由．考点： 二次函数图象的几何变换;二次函数图象与系数的关系;二次函数的实际应用-几何问题;矩形的判定;轴对称的性质;~~第5题~~(2017越秀.中考模拟) 设二次函数y =a （x ﹣2）+c （a≠0）的图象与y 轴的交点为（0，1），在x 轴上截得的线段长为 ．（1） 求a 、c 的值．（2） 对于任意实数k ，规定：当﹣2≤x≤1时，关于x 的函数y =y ﹣kx 的最小值称为k 的“贡献值”，记作g （k ）．求g （k ）的解析式．（3） 在（2）条件下，当“贡献值”g （k ）=1时，求k 的值．考点： 解二元一次方程组;二次函数图象与系数的关系;二次函数的最值;2020年中考数学：函数_二次函数_二次函数图象与系数的关系练习题答案1.答案：2121221221212212.答案：3.答案：4.答案：5.答案：。

专题训练(二)二次函数y=ax2+bx+c(a≠0)的系数a,b,c与图象的关系知识储备二次函数y=ax2+bx+c的图象与字母系数a,b,c 之间的关系:项目字母字母的符号图象的特征a a>0 开口向上a<0 开口向下bb=0 对称轴为y轴ab>0(b与a同号) 对称轴在y轴左侧ab<0(b与a异号) 对称轴在y轴右侧c c=0 经过原点c>0 与y轴正半轴相交c<0 与y轴负半轴相交b2-4ac b2-4ac=0与x轴有一个交点(顶点)b2-4ac>0 与x轴有两个交点b2-4ac<0 与x轴没有交点特殊关系当x=1时,y=a+b+c;当x=-1时,y=a-b+c当x=2时,y=4a+2b+c;当x=-2时,y=4a-2b+c若a+b+c>0,则当x=1时,y>0若a-b+c>0,则当x=-1时,y>0当对称轴为直线x=1时,2a+b=0;当对称轴为直线x=-1时,2a-b=0;判断2a+b的值大于还是小于0,看对称轴与直线x=1的位置关系;判断2a-b的值大于还是小于0,看对称轴与直线x=-1的位置关系▶类型一利用二次函数图象考查以上表格中的问题1.[2020·宁波江北区期末]二次函数y=ax2+bx+c(a≠0)的图象如图1所示,则下列关系式错误的是()A.a<0B.b>0C.b2-4ac>0D.a+b+c<0图 1 图22.[2020·宁波]如图2,二次函数y=ax2+bx+c(a>0)的图象与x轴交于A,B两点,与y轴正半轴交于点C,它的对称轴为直线x=-1.则下列选项中正确的是A.abc<0 B.4ac-b2>0C.c-a>0D.当x=-n2-2(n为实数)时,y≥c3.在同一平面直角坐标系内,二次函数y=ax2+bx+b(a≠0)与一次函数y=ax+b的图象可能是()图 3▶类型二利用二次函数图象考查ma+nc或mb+nc(m,n为非零整数)与0的关系4.如图4,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1.给出下列结论:①ac<0;②b2-4ac>0;③2a-b=0;④a-b+c=0.其中,正确的结论有()图4A.1个B.2个C.3个D.4个5.[2020·遵义改编]抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=-2,抛物线与x轴的一个交点在点(-4, 0)和点(-3,0)之间,其部分图象如图5所示,下列结论中正确的有()①4a-b=0;②c≤3a;③关于x的方程ax2+bx+c=2有两个不相等的实数根;④b2+2b>4ac.图5A.1个B.2个C.3个D.4个▶类型三利用二次函数图象考查am2+bm+c(a≠0,a,b,c为常数)与a+b+c的关系6.已知二次函数y=ax2+bx+c(a≠0)图象的对称轴为直线x=1,其图象如图6所示,现有下列结论:①abc>0,②b-2a<0,③a-b+c>0,④a+b>n(an+b)(n ≠1),⑤2c<3b.其中正确的是()A.①③B.②⑤C.③④D.④⑤图6 图77.抛物线y=ax2+bx+c(a≠0)的一部分如图7所示,与x轴的一个交点坐标为(4,0),抛物线的对称轴是直线x=1,有下列结论:①abc>0;②2a+b=0;③方程ax2+bx+c=3有两个不相等的实数根;④抛物线与x 轴的另一个交点坐标为(-2,0);⑤若点A(m,n)在该抛物线上,则am2+bm+c≤a+b+c.其中正确的有() A.5个B.4个C.3个D.2个▶类型四利用二次函数图象解一元二次方程或不等式8.若二次函数y=x2+bx的图象的对称轴是经过点(2,0)且平行于y轴的直线,则关于x的方程x2+bx=5的解为()A.x1=0,x2=4B.x1=1,x2=5C.x1=1,x2=-5D.x1=-1,x2=59.二次函数y=ax2+bx+c(a≠0)的图象如图8所示,则关于x的不等式ax2+bx+c>0的解是()图8A.x<-1B.x>3C.-1<x<3D.x<-1或x>3▶类型五利用一次函数、二次函数的图象解一元二次方程或不等式10.如图9所示,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5),B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解为()图9A.-1≤x≤9B.-1≤x<9C.-1<x≤9D.x≤-1或x≥911.二次函数y=ax2+bx+c(a≠0)和正比例函数y=23x的图象如图10所示,则方程ax2+（32b x+c=0的两根之和()图10A.大于0B.等于0C.小于0D.不能确定专题二教师详解详析1.D[解析] 抛物线开口向下,则a<0,所以A选项的关系式正确;抛物线的对称轴在y轴的右侧,a,b异号,则b>0,所以B选项的关系式正确;抛物线与x轴有2个交点,则b2-4ac>0,所以C选项的关系式正确;当x=1时,y>0,则a+b+c>0,所以D选项的关系式错误.故选D.2.D[解析] ∵二次函数图象的对称轴为直线x=-1,∴-b2a=-1,∴b=2a.又∵a>0,∴b>0.∵抛物线与y轴正半轴交于点C,∴c>0,∴abc>0,故A错误;∵抛物线与x轴有两个不同的交点,∴b2-4ac>0,∴4ac-b2<0,故B错误;∵b=2a,∴当x=-1时,y=a-b+c=c-a<0,故C 错误;当x=-n2-2(n为实数)时,y=a(-n2-2)2+b(-n2-2)+c=a(-n2-2)2+2a(-n2-2)+c=a( n2+1)2-a+c.∵n为实数,∴n2≥0,(n2+1)2≥1.又∵a>0,∴a(n2+1)2-a≥0,∴y≥c,故D正确,因此本题选D.3.C4.C[解析] ∵抛物线开口向下,∴a<0.∵抛物线交y轴于正半轴,∴c>0,∴ac<0,故①正确;∵抛物线与x轴有两个交点,∴b2-4ac>0,故②正确;∵抛物线的对称轴为直线x=1,∴-b2a=1,∴-b=2a,∴2a+b=0,故③错误;∵抛物线与x轴的两个交点关于对称轴对称,∴点(3,0)关于直线x=1的对称点为(-1,0),即抛物线经过点(-1,0),∴a-b+c=0,故④正确.综上可知,正确的结论有①②④,共3个.5.C[解析] 由-b2a=-2,得4a-b=0,故①正确;由抛物线与x轴的一个交点在点(-4,0)和点(-3,0)之间,当x≤-2时,y随x的增大而增大,可知当x=-3时,y>0,由抛物线的对称性可知,当x=-1时,y>0,即a-b+c>0.又4a=b,∴a-4a+c>0,即c>3a.故②错误; 由图象得,关于x的方程ax2+bx+c=2有两个不相等的实数根正确; 由4ac-b24a=3,得4ac-b2=12a,∴4ac=12a+b2=3b+b2.易知a<0,b<0,c<0,∴4ac<2b+b2 ,故④正确.故选C.6.D[解析] ①由图象可知:a<0,b>0,c>0,∴abc<0,故此选项错误;②当x=-2时,y=4a-2b+c<0,即b-2a>c2>0,故此选项错误;③当x=-1时,y=a-b+c<0,故此选项错误;④当x=1时,y的值最大,此时,y=a+b+c,而当x=n 时,y=an2+bn+c,所以a+b+c>an2+bn+c(n≠1),故a+b>an2+bn,即a+b>n(an+b)(n≠1),故此选项正确.⑤由抛物线的对称性可知当x=3时函数值小于0,即y=9a+3b+c<0.∵抛物线的对称轴为直线x=-b2a=1,∴a=-b2,代入9a+3b+c<0,得9-b2 +3b+c<0,得2c<3b,故此选项正确;故④⑤正确.因此本题选D.7.B8.D9.D[解析] 根据图象可知,当y=0时,对应的x的值分别为x1=-1,x2=3.当y>0时,函数的图象在x轴的上方,由左边一段图象可知x<-1,由右边一段图象可知x>3.因此,当函数值y>0时,x的取值范围是x<-1或x>3.故选D.10.A[解析] 由图象可以看出:二次函数y2=ax2+bx+c(a≠0)和一次函数y1=kx+n(k≠0)的图象的交点的横坐标分别为-1,9.而当y1≥y2时,对应的图象正好在两交点之间,所以-1≤x≤9.故选A.11.A。

二次函数的各项系数与图象的位置关系一、知识点1．a的正负决定抛物线开口方向，a＞0，开口向上；a＜0，开口向下．2．a的绝对值决定抛物线开口大小，|a|越大，抛物线开口越小．3．a、b同号，对称轴在y轴左侧；a、b在异号，对称轴在y轴右侧；b=0时，对称轴为y轴．4．c＞0时，抛物线与y轴交点在轴上方；c=0时，抛物线过坐标原点；c﹤0时，抛物线与y轴交点在轴下方．5．b2-4ac﹥0，抛物线与轴有两个交点；b2-4ac=0，抛物线与轴有一个交点；b2-4ac﹤0，抛物线与轴无交点．二、例题【例1】二次函数y=a2bc的图象如图26-1所示，则下列结论正确的是（）A．a＞0，b﹤0，c＞0 B．a﹤0，b﹤0，c＞0 C．a﹤0，b＞0，c﹤0 D．a﹤0，b＞0，c＞0【例2】二次函数y=a2bc的图象如图26-2所示，则下列5个代数式：ab，ac，a-bc，b2-4ac，2ab中，值大于0的个数有（）A．5B．4 C．3D．2三、强化练习1．满足a﹤0，b＞0，c=0的函数y=a2bc的图象是图26-3中的（）2．在二次函数y=2bc中，若bc=0，则它的图象一定经过点（）A．（-1，-1）B．（1，-1）C．（-1，1）D．（1，1）3．若ac﹤0，则二次函数y=a2bc的图象与轴交点个数为（）A．2个B．l个C．0个D．无法确定4．已知，图26-4为二次函数y=a2bc的图象，则一次函数y=abc的图象不经过（）A．第一象限B．第二象限C．第三象限D．第四象限5．已知抛物线y=a2bc的图象如图26-5所示，则关于的方程a2bc-3=0的根的情况是（）A．有两个不相等的正实根B．有两个异号实数根C．有两个相等的实数根D．没有实数根6．已知二次函数y=a2bc的图象如图26-6所示，下列结论中：①abc﹥0；②b=2a；③abc＜0；④a-bc＞0．正确的个数是（）A．4个B．3个C．2个D．l 个7．已知一次函数y=ac与二次函数y=a2bc，它们在同一坐标系内的大致图象是图26-7中的（）8．已知反k的图象如图26-8所示，则二次函数y=22-2的图象比例函数y=x大致为图26-9中的（）9c（a﹤c）的图象可能是图．在同一坐标系中，函数y=a2c与y=x26-10中的（）10．在同一坐标系中，函数y=a2与y=a-1（a≠0）的图象可能是图26-11中的（）11．如图26-12，已知二次函数y=a2bc的图象的对称轴是直线=1．下面给出了4个结论：①a﹤0，b＞0；②2ab=0；③abc＞0；④4a2bc=0．正确结论的序号是．四、解答【例1】二次函数y=a2bc的图象如图26-1所示，则下列结论正确的是（）A．a＞0，b﹤0，c＞0 B．a﹤0，b﹤0，c＞0 C．a﹤0，b＞0，c﹤0 D．a﹤0，b＞0，c＞0思维入门指导：由抛物线开口方向，对称轴位置，与y轴交点位置来判断．解：∵抛物线开口向下，∴a﹤0．∵对称轴在y 轴右侧，∴-a b 2＞0．又a ﹤0，∴b＞0． ∵抛物线与y 轴交点在轴上方，∴c＞0．∴选D ．点拨：直接推导a 、b 、c 符号即可．【例2】二次函数y=a 2bc 的图象如图26-2所示，则下列5个代数式：ab ，ac ，a-bc ，b 2-4ac ，2ab 中，值大于0的个数有（）A ．5B ．4C ．3D ．2思维入门指导：当=-1时，y=a-bc ．解：∵抛物线开口向上，∴a＞0．∵对称轴在y 轴左侧，∴a，b 同号．又a ＞0，∴b＞0．∵抛物线与y 轴的交点在轴下方，∴c﹤0．∴ab＞0，ac ﹤0．∵抛物线与轴有两个交点，∴b 2-4ac ＞0．∵对称轴=-a b 2=-1，∴b=2a．∴2ab﹥0 当=-1时，y=a-bc ﹤0．∴选C ．点拨：abc ，a-bc 分别是=l ，=-1时，函数y=a 2bc （a≠0）的函数值．参考答案1．C 点拨：∵a﹤0，b ﹥0，∴对称轴在y 轴右侧．∵c=0，∴抛物线过坐标原点．2．D 点拨：∵bc=0，∴b=-c ，y=a 2-cc ．当=-1时，y=1cc=2c1；当=1时，y=1bc=1．∴过（1，1）点．3．A 点拨：ac ﹤0，∴a≠0，b 2-4ac ﹥0，∴抛物线与轴有两个交点．4．B 点拨：∵抛物线开口向上，∴a﹥0．∵对称轴在y 轴左侧，∴b﹥0．∵与y 轴交点在轴下方，∴c﹤0．∴一次函数y=abc 的图象过一、三、四象限．5．C 点拨：由图象知，抛物线顶点纵坐标为3，∴原图象向下平移3个单位得到y=a 2bc-3．∴方程a 2bc-3=0有两个相等的实数根．6．A 点拨：由图象知，a ﹤0，b ﹤0，c ﹥0．当=1时，y=abc ﹤0；当=-1时，y=a-bc ﹥0．对称轴-a b 2=-1，∴b=2a． 7．C 点拨：由y=ac 过一、二、四象限得a ﹤0，c ﹥0；抛物线y=a 2bc 开口向下，与y 轴交点（0，c ）在轴上方，得a ﹤0，c ﹥0；抛物线与直线交于同一点（0，c ）．8．D 点拨：由y=x k 的图象知，﹤0，∴y=22-2的图象开口向下，对称轴在y 轴左侧，与y 轴交于正半轴．9．A点拨：若抛物线开口向上，即a﹥0，则c﹥0．∴C、D 均错．若抛物线开口向下，即a﹤0．由A、B可知c﹥0，则双曲线只可能在第一、三象限．10．B点拨：若y=a2开口向上，则a﹥0．∴y=a-1过一、三、四象限．若y=a2开口向下，则a﹤0，∴y=a-1过二、三、四象限．11．①②③④。