高频电子线路(知识点整理)

电子行业高频电子线路简介高频电子线路在电子行业中扮演着重要的角色。

它们被广泛应用于无线通信、雷达、卫星通信、医疗诊断设备等领域。

在本文中，将介绍高频电子线路的基础知识、设计原理以及常见应用。

基础知识1.高频信号高频信号是指频率高于1MHz的信号。

在高频电子线路中，频率通常在几十MHz到几百GHz 之间。

高频信号的特点是波长短、频率高、传输能力强。

2.电子线路元件高频电子线路中使用的元件与低频电子线路略有不同。

常见的高频元件包括电感、电容、晶体管、集成电路等。

这些元件在高频电子线路中起到重要的作用，具体将在后文中详细介绍。

设计原理1.传输线理论传输线理论是高频电子线路设计的基础。

传输线是一种将信号从一个点传输到另一个点的导线。

常见的传输线包括微带线、同轴电缆等。

了解传输线理论可以帮助设计师正确地选择传输线的特性阻抗、长度和宽度，以确保信号传输的质量。

2.匹配网络高频信号在传输过程中容易发生反射和衰减。

匹配网络的作用是使信号在传输过程中能够得到最大的功率传输，并尽量避免信号的反射。

匹配网络常用的类型包括L型匹配网络、T型匹配网络等。

3.滤波器滤波器用于过滤高频信号中的噪声和干扰，使得信号在特定频段上得到放大或衰减。

常见的滤波器类型包括低通滤波器、带通滤波器和带阻滤波器。

4.放大器放大器是高频电子线路中常见的元件之一。

放大器的作用是放大输入信号的幅度。

常见的放大器类型包括晶体管放大器、集成电路放大器等。

常见应用1.无线通信高频电子线路在无线通信领域中被广泛应用。

无线通信系统包括手机、无线电和卫星通信系统等。

高频电子线路在这些系统中起到信号调制、放大和解调等重要作用。

2.雷达雷达系统也是高频电子线路的典型应用之一。

雷达系统通过发送和接收无线信号来检测和跟踪目标。

高频电子线路在雷达系统中的作用是发射和接收高频信号，并进行信号处理。

3.医疗诊断设备高频电子线路在医疗诊断设备中也有重要的应用。

例如，X射线机、核磁共振仪等设备使用高频电子线路进行信号放大和处理，以实现准确的诊断结果。

高频电子线路重点内容第一章1.1通信与通信系统1. 信息技术两大重要组成部分——信息传输和信息处理信息传输的要求主要是提高可靠性和有效性。

信息处理的目的就是为了更有效、更可靠地传递信息。

2. 高频的概念所谓“高频”，广义上讲就是适于无线电传播的无线电频率，通常又称为“射频”。

一、基本概念1. 通信：将信息从发送者传到接收者的过程2. 通信系统：实现传送过程的系统3. 通信系统基本组成框图信息源是指需要传送的原始信息，如语言、音乐、图像、文字等，一般是非电物理量。

原始信息经换能器转换成电信号（称为基带信号）后，送入发送设备，将其变成适合于信道传输的信号，然后送入信道。

信道是信号传输的通道，也就是传输媒介。

有线信道，如：架空明线，电缆，波导，光纤等。

无线信道，如：海水，地球表面，自由空间等。

不同信道有不同的传输特性，同一信道对不同频率信号的传输特性也是不同的。

接收设备把有用信号从众多信号和噪声中选取出来，经换能器恢复出原始信息。

4．通信系统的分类按传输的信息的物理特征，可以分为电话、电报、传真通信系统，广播电视通信系统，数据通信系统等；按信道传输的信号传送类型，可以分为模拟和数字通信系统；而按传输媒介（信道）的物理特征，可以分为有线通信系统和无线通信系统。

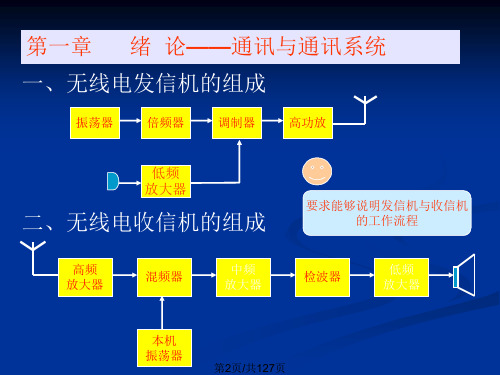
二、无线电发送与接收设备1. 无线通信系统的发射设备（1）振荡器：产生f osc 的高频振荡信号，几十 kHz 以上。

（2）高频放大器：一或多级小信号谐振放大器，放大振荡信号，使频率倍增至f c，并提供足够大的载波功率。

（3）调制信号放大器：多级放大器组成，前几级为小信号放大器，用于放大微音器的电信号；后几级为功放，提供功率足够的调制信号。

（4）振幅调制器：实现调幅功能，将输入的载波信号和调制信号变换为所需的调幅波信号，并加到天线上。

2. 无线通信系统的接收设备（1）高频放大器：由一级或多级小信号谐振放大器组成，放大天线上感生的有用信号；并利用放大器中的谐振系统抑制天线上感生的其它频率的干扰信号。

高频电子线路(知识点整理).doc
高频电子线路是指在射频或超高频范围内工作的电子线路，通常涉及到信号的传输、
处理和放大。

这种电子线路在通信、雷达、卫星通信、无线电等领域中被广泛应用，它有
着复杂的工作原理和设计技术。

下面就是对于高频电子线路的几个知识点整理和介绍。

1.谐振器：谐振器是高频电子线路中经常用到的一个组件，其作用是让电路产生特定
的共振频率，以便信号能够在电路中传输。

谐振器通常由其结构和材料决定，比如管型谐
振器、光纤谐振器、奇异谐振器等。

2.混频器：混频器是将两个输入频率进行混合，产生出一个输出频率的高频电子组件。

混频器主要用于转换信号的频率和增强信号的强度，比如在雷达和无线电通信中，混频器
通常用于将信号从中频转换到基带。

3.射频放大器：射频放大器是一种将低功率信号转化为高功率信号的电子器件，主要
用于放大和传输高频信号。

射频放大器的工作原理是通过对输入信号进行放大使得输出信
号的功率增大，它可以是单通道或多通道的，通常由功率放大器、隔离器等组成。

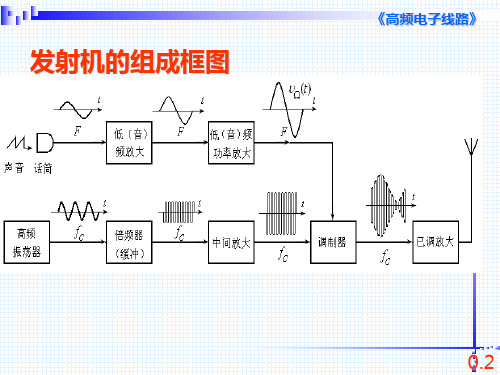
4.发射机：发射机是将信号转换成无线电波并进行发送的高频电子设备。

发射机通常
包括调制器、调谐器、放大器、射频发生器、天线等组件。

它主要将信号转化成无线电波
传输到接收机，以便实现通信或雷达探测等功能。

以上就是对于高频电子线路的几个知识点简要介绍，高频电子线路在通信、雷达、卫
星通信、无线电等领域中轮廓巨大，其涉及到很多的基础理论和设计技术，需要深入钻
研。

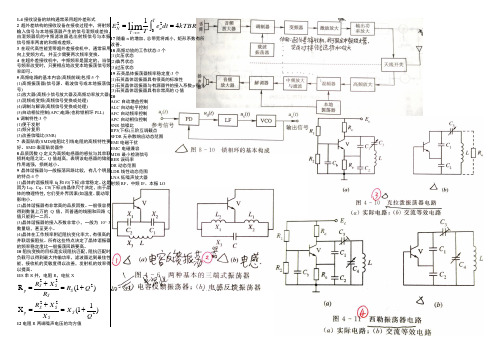
1-4接收设备的结构通常采用超外差形式 2超外差结构的接收设备在接收过程中，将射频输入信号与本地振荡器产生的信号混频或差拍，由混频器后的中频滤波器选出射频信号与本振信号频率两者的和频或差频。

3在现代高性能宽带超外差接收机中，通常采用向上变频方式，并至少需要两次频率变换。

4在超外差接收机中，中频频率是固定的，当信号频率改变时，只要相应地改变本地振荡信号频率即可。

5高频电路的基本内容(高频前端)包括:5个 (1)高频振荡器(信号源、载波信号或本地振荡信号) (2)放大器(高频小信号放大器及高频功率放大器) (3)混频或变频(高频信号变换或处理) (4)调制与解调(高频信号变换或处理) (5)自动相位控制(APC)电路(也称锁相环PLL) 6调制特性:3个 (1)便于发射 (2)频分复用 (3)改善信噪比(SNR) 7表面贴装(SMD)电阻比引线电阻的高频特性要好。

SMD 表面贴装器件 8品质因数Q 定义为高频电感器的感抗与其串联损耗电阻之比。

Q 值越高，表明该电感器的储能作用越强，损耗越小。

9晶体谐振器与一般振荡回路比较，有几个明显的特点:4个 (1)晶体的谐振频率fq 和f0(下标)非常稳定。

这是因为Lq 、Cq 、C0(下标)由晶体尺寸决定，由于晶体的物理特性，它们受外界因素(如温度、震动等)影响小。

(2)晶体谐振器有非常高的品质因数。

一般很容易得到数值上万的Q 值，而普通的线圈和回路Q 值只能到一二百。

(3)晶体谐振器的接入系数非常小，一般为10^-3数量级，甚至更小。

(4)晶体在工作频率附近阻抗变化率大，有很高的并联谐振阻抗。

所有这些特点决定了晶体谐振器的频率稳定度比一般振荡回路要高。

10阻抗变换的目标是实现阻抗匹配，阻抗匹配时负载可以得到最大传输功率，滤波器达到最佳性能，接收机的灵敏度得以改善，发射机的效率得以提高。

11S 串R 并，电阻R ，电抗X )11(X )1(R 222222Q X X X R Q R R X R S S S S p S SS S p +=+=+=+=12电阻R 两端噪声电压的均方值kTBR dt e T E T n T N 41022lim ==⎰∞→ 17随着n 的增加，总带宽将减小，矩形系数有所改善。

127.02ωωω-=∆高频电子线路重点第二章 选频网络一. 基本概念所谓选频（滤波)，就是选出需要的频率分量和滤除不需要的频率分量。

电抗(X ）=容抗（ ）+感抗（wL ） 阻抗=电阻(R ）+j 电抗 阻抗的模把阻抗看成虚数求模 二．串联谐振电路 1。

谐振时,（电抗） ,电容、电感消失了，相角等于0,谐振频率： ，此时|Z ｜最小=R ，电流最大2。

当w<w 0时,电流超前电压，相角小于0，X<0阻抗是容性；当w>w 0时,电压超前电流，相角大于0,X>0阻抗是感性； 3。

回路的品质因素数 （除R ），增大回路电阻，品质因数下降，谐振时,电感和电容两端的电位差大小等于外加电压的Q 倍，相位相反4。

回路电流与谐振时回路电流之比 （幅频),品质因数越高，谐振时的电流越大，比值越大,曲线越尖，选频作用越明显，选择性越好5.失谐△w=w(再加电压的频率）-w 0（回路谐振频率），当w 和w 0很相近时， , ξ=X/R=Q ×2△w/w 0是广义失谐，回路电流与谐振时回路电流之比6。

当外加电压不变,w=w 1=w 2时,其值为1/√2，w 2-w 1为通频带，w 2，w 1为边界频率/半功率点,广义失谐为±17. ，品质因数越高，选择性越好，通频带越窄8.通频带绝对值 通频带相对值 9.相位特性 Q 越大,相位曲线在w 0处越陡峭 10.能量关系电抗元件电感和电容不消耗外加电动势的能量,消耗能量的只有损耗电阻。

回路总瞬时储能 回路一个周期的损耗 ， 表示回路或线圈中的损耗。

就能量关系而言,所谓“谐振"，是指：回路中储存的能量是不变的,只是在电感与电容之间相互转换；外加电动势只提供回路电阻所消耗的能量，以维持回路的等幅振荡，而且谐振回路中电流最大。

11. 电源内阻与负载电阻的影响Q L 三。

并联谐振回路1.一般无特殊说明都考虑wL>>R,Z 反之w p =√[1/LC-(R/L ）2］=1/√RC ·√1—Q 22。

第一章：载波：高频率的电流发射天线：载有载波电流，使电磁能以电磁波形式向空间发射的导体调制分为：连续波调制（调幅、调频、调相），脉冲调制（数字调制、二次调制）脉冲调制：1用信号调制脉冲。

2用已调脉冲对载波进行调制检波：与调制的过程相反调制过程：本地高频震荡→缓冲器→倍频器→中间放大→功率放大器→受调放大器话筒→低频电压放大级→低频功率放大级→调制器↑超外差收音机工作原理：通过混频器将不同的高频信号转化为固定的中频信号，使得收音机的工作选择性和灵敏度提高超外差工作过程：高频小信号放大器→自激式变频器→中频放大→检波→低频放大→输出有线通信媒介：双线对电缆、同轴电缆、光纤。

无线通信媒介：自由空间地波：分为地面波和天波，地面波，电磁波沿地面传播。

空间波，要求天线与接受天线离地面较高，接受点的电磁波由直射波与地面反射波合成天波：是经过电离层反射的电磁波第二章（选频网络）选频网路：1是由电感和电容元件组成的震荡回路（但震荡回路、耦合震荡回路）。

2各种滤波器组成的Q值：Q值越高，谐振曲线越尖锐，对外加电压的选频作用越显著，回路的选择性就越好。

串联谐振（电压谐振）回路适用于低内阻电源，内阻越低，则电路的选择性越好。

并联谐振（电流谐振）回路适用于大内阻的电源串联与并联谐振回路的对偶性：串联谐振回路谐振时回路电阻最小，而并联谐振回路谐振时回路电阻最大纯耦合：只有纯电阻或者是纯电抗复合耦合：有两种或两种以上种类的元件构成第三章（高频小信号放大器）高频放大器与低频放大器的主要区别是：1工作频率范围不同；2频带宽度不同高频放大器是由选频网路组成的谐振或非谐振放大器高频小信号放大器的主要质量指标：1增益（电压、功率）2通频带3选择性（矩形系数、抑制比）4工作稳定性（工作状态、晶体管参数、电路元件参数）5噪声系数等效电路参数：yi/yr/yf/yo晶体管的高频参数：1截至频率：β降为原来的β01/√22特征频率：│β│下降为13最高震荡频率：功率的增益为1时的频率谐振放大器稳定性的破坏原因：存在反馈导纳由反馈导纳产生的自激震荡可以通过1中和法：通过引入外部反馈网络来抵消晶体管内部y fe的反馈作用；2失配法：晶体管输出端负载阻抗不与本级晶体管的输出阻抗匹配第四章（非线性电路、时变参量电路和变频器）无线电元件：1线性元件2非线性元件3时变参量元件非线性电路的分析方法：1幂级数分析法（通过泰勒级数展开，【输入小信号】）2折线分析法（输入大信号）3开关函数分析法（控制信号为大信号，输入信号为小信号）非线性元件的特性：1特性曲线不是直线2变频作用3不满足叠加定理变频器（混频器）：就是把高频信号经过频率变换，变为一个固定的频率变频器的主要质量指标：1变频增益：变频器中频输出电压振幅与高频输入信号电压振幅之比2失真和干扰：频率失真和非线性失真；组合频率、交叉频率与互相调制、阻塞和倒易混频等干扰3选择性：接受有用信号（中频），排除干扰信号的能力取决于中频输出回路的选择性是否良好4噪声系数使用较多的混频器是：输入信号从基极输入，本振电压从发射极输入。

高频电子线路高频电子线路是一种广泛应用于通信、无线电、雷达等领域的电子技术。

它具有传输速度快、信号传输质量高的特点，被广泛应用于各个领域的无线通信系统中。

一、高频电子线路的概述高频电子线路是指频率在兆赫范围（MHz）及以上的电子线路。

相比于低频电子线路，高频电子线路在设计和制造上具有更高的要求，因为在高频范围内，电磁波的行为将产生诸多影响，如传输损耗、信号衰减、干扰等。

因此，高频电子线路的设计需要充分考虑这些因素。

二、高频电子线路的特点1. 传输速度快：高频电子线路传输速度快，可以实现高速数据传输和通信，满足现代通信需求。

2. 信号传输质量高：高频电子线路在频域和时间域上的性能都要求较高，能够保证信号质量的稳定和可靠传输。

3. 抗干扰能力强：高频电子线路需要具备较强的抗干扰能力，能够有效防止外界信号的干扰对系统造成的影响。

4. 体积小：高频电子线路设计中，往往需要将电子元件、线路等尽量紧凑地布局在一个小空间中，以减少传输路径，提高信号传输效率。

三、高频电子线路的应用领域1. 通信领域：在移动通信、卫星通信、光纤通信等领域，高频电子线路被广泛应用于信号的传输和处理。

2. 无线电领域：在无线电通信和广播中，高频电子线路用于收发机、天线等设备的设计和制造。

3. 雷达领域：高频电子线路在雷达系统中扮演重要角色，用于信号的发射、接收和处理。

4. 医疗领域：高频电子线路应用于医学成像设备、医疗监护系统等医疗器械中，用于信号的处理和传输。

四、高频电子线路的设计要点1. 电路板布局：合理的电路板布局是保证高频电子线路性能稳定的重要因素，要避免信号之间的相互干扰和回路耦合。

2. 电子元件的选择：选择高品质的电子元件，如高频电容、电感等，以确保电路的稳定性和可靠性。

3. 噪声控制：对于高频电子线路来说，噪声会严重影响信号的质量，因此需要采取措施控制噪声，如使用屏蔽罩、降噪电路等。

4. 信号损耗：在高频电子线路中，信号损耗是不可避免的，因此需要选择合适的传输介质和降低传输路径，以减少信号损耗。

高频电子线路重点————————————————————————————————作者：————————————————————————————————日期：高频电子线路重点内容第一章1.1通信与通信系统1. 信息技术两大重要组成部分——信息传输和信息处理信息传输的要求主要是提高可靠性和有效性。

信息处理的目的就是为了更有效、更可靠地传递信息。

2. 高频的概念所谓“高频”，广义上讲就是适于无线电传播的无线电频率，通常又称为“射频”。

一、基本概念1. 通信：将信息从发送者传到接收者的过程2. 通信系统：实现传送过程的系统3. 通信系统基本组成框图信息源是指需要传送的原始信息，如语言、音乐、图像、文字等，一般是非电物理量。

原始信息经换能器转换成电信号（称为基带信号）后，送入发送设备，将其变成适合于信道传输的信号，然后送入信道。

信道是信号传输的通道，也就是传输媒介。

有线信道，如：架空明线，电缆，波导，光纤等。

无线信道，如：海水，地球表面，自由空间等。

不同信道有不同的传输特性，同一信道对不同频率信号的传输特性也是不同的。

接收设备把有用信号从众多信号和噪声中选取出来，经换能器恢复出原始信息。

4．通信系统的分类按传输的信息的物理特征，可以分为电话、电报、传真通信系统，广播电视通信系统，数据通信系统等；按信道传输的信号传送类型，可以分为模拟和数字通信系统；而按传输媒介（信道）的物理特征，可以分为有线通信系统和无线通信系统。

二、无线电发送与接收设备1. 无线通信系统的发射设备（1）振荡器：产生f osc 的高频振荡信号，几十 kHz 以上。

（2）高频放大器：一或多级小信号谐振放大器，放大振荡信号，使频率倍增至f c，并提供足够大的载波功率。

（3）调制信号放大器：多级放大器组成，前几级为小信号放大器，用于放大微音器的电信号；后几级为功放，提供功率足够的调制信号。

（4）振幅调制器：实现调幅功能，将输入的载波信号和调制信号变换为所需的调幅波信号，并加到天线上。

大学高频电路知识点总结一、电路基本概念1.1 电路的定义电路是由电学元件(如电阻、电容、电感)和电气源(如电压源、电流源)按一定规律连接而成的结构，通过电学元件传递电流、电压和功率的一种物理结构。

1.2 电路的分类根据不同的连接方式和性质，电路可以分为串联电路、并联电路、混合电路等。

1.3 电路的基本定律基尔霍夫定律(节点电流定律和回路电压定律)和欧姆定律是电路分析和设计中的基本定律。

1.4 电路分析方法电路分析常用的方法包括节点分析法、回路分析法、等效电路分析法等。

二、高频电路的基础知识点2.1 电容和电感电容是存储电荷的器件，电感是存储能量的器件，它们在高频电路中扮演着重要的角色。

2.2 阻抗和复数在高频电路中，我们通常使用复数来描述电路元件的阻抗、电压和电流等。

2.3 传输线传输线是高频电路中的重要组成部分，其特性阻抗、传输功率等对电路性能有重要影响。

2.4 振荡电路振荡电路可以产生稳定的频率信号，是无线通信、射频识别等领域中必不可少的电路。

2.5 放大电路在高频电路中，放大电路能够放大信号，是无线通信、雷达等领域中的核心技术。

三、高频电路的分析和设计3.1 基本分析方法在高频电路中，基尔霍夫定律和欧姆定律依然适用，但在分析中需要考虑元件的频率特性。

3.2 传输线特性传输线的特性参数如特性阻抗、传输时间等需要在设计中进行考虑，影响信号的传输质量。

3.3 滤波器设计滤波器在高频电路中的应用非常广泛，包括低通滤波器、高通滤波器、带通滤波器等。

3.4 放大器设计高频放大器的设计需要考虑稳定性、频率响应、噪声等因素，是高频电路设计中的关键环节。

3.5 振荡器设计振荡器的设计需要考虑频率稳定性、谐波抑制等因素，对振荡器电路中的非线性元件的设计也有很高的要求。

四、高频电路的应用4.1 无线通信系统高频电路在无线通信系统中有着广泛的应用，包括射频放大器、混频器、频率合成器等。

4.2 雷达系统雷达系统是高频电路技术的典型应用，其核心技术包括高频信号的发射、接收、处理等。

高频电子线路知识点高频电子线路在现代通信和无线电技术中起着至关重要的作用。

它们被广泛应用于手机、无线电、卫星通信、雷达等设备中。

理解高频电子线路的基本原理和常见知识点是从事相关领域工作的基础。

本文将介绍一些高频电子线路的重要知识点。

1. 传输线理论传输线是高频电子线路中常用的元件，它用于将信号从发射端传输到接收端。

了解传输线的特性对于设计和分析高频电子线路至关重要。

传输线理论涉及电缆、微带线和同轴电缆等不同类型的传输线。

了解它们的特性阻抗、传播常数和损耗等等是必要的。

2. 双端口网络理论双端口网络是高频电子线路中用于表示电路、分析和设计的重要工具。

双端口网络表示复杂电路的传输特性，如滤波器、功率放大器等。

对双端口网络的理解包括参数矩阵、S参数和Y参数等。

这些参数描述了双端口网络的敏感度和功率传输性能。

3. 高频电源和信号分布在高频电子线路中，电源和信号分布是必不可少的。

了解高频电源的供电要求和电容、电感元件的选择是保证电路功能稳定和性能优异的关键。

同时，信号分布的设计和布线决定了电路中信号的准确传输和最小损耗。

4. 高频放大器设计高频放大器是用于增强电路中信号的电子设备。

设计高频放大器需要考虑信号输入输出的匹配性、增益、稳定性和线性度等因素。

传统的放大器电路设计方法需要和高频电路设计结合起来，通过使用适当的元件和电路结构来提高线路的性能。

5. 射频阻抗匹配在高频电子线路中，阻抗匹配非常重要，以确保信号的能量传输和最小损耗。

对于恒定驻波比的高频线路，正确的阻抗匹配可以使传输更有效。

阻抗匹配的方法包括L型匹配和T型匹配电路等。

6. 射频滤波器设计射频滤波器用于对特定频率范围的信号进行选择性的通过或衰减。

设计和分析射频滤波器需要考虑频率响应、带宽、阻带衰减等参数。

滤波器的类型包括带通滤波器、低通滤波器和高通滤波器等。

7. 射频混频器设计射频混频器是用于将不同频率的信号混合产生新频率的装置。

混频器广泛应用于信号调制和解调、频率合成等领域。

高频电路知识点总结一、高频电路的基本概念高频电路是指工作频率在几百千赫兹至数吉赫兹范围内的电路，它们通常用于射频（射频）系统、通信系统、雷达系统等。

由于高频电路的工作频率很高，因此其特性和设计方法与低频电路有很大不同。

1、高频电路的特点（1）电压和电流的传输速度加快；（2）传输线的长度和电路尺寸相对较小；（3）传输线的电磁波特性需要考虑；（4）电缆损耗增大。

2、高频电路的设计要求（1）降低传输线的损耗；（2）减小串扰和反射；（3）提高电路的灵敏度和抗干扰能力；（4）提高电路的稳定性和可靠性。

二、高频电路的传输线在高频电路中，传输线的特性对系统的性能有着很大的影响，因此设计者需要充分了解和掌握传输线的特性。

1、传输线的特性（1）阻抗：传输线的特性阻抗随着工作频率的增加而改变，这意味着在高频电路中必须考虑传输线的阻抗匹配问题。

（2）传输速度：高频信号在传输线中的传输速度快于低频信号。

（3）色散：高频信号在传输线中会产生色散现象，导致不同频率的信号传播速度不同，需要进行补偿。

（4）损耗：传输线在高频下的损耗较大，特别是在微带线和同轴电缆中。

2、常见的传输线类型（1）同轴电缆：同轴电缆主要用于高频射频信号的传输，具有较好的屏蔽性能和抗干扰能力。

（2）微带线：微带线是常用的高频信号传输线路，其制作工艺简单、成本低廉、尺寸小，适合集成在集成电路板中。

（3）双平行线：双平行线具有低损耗和较高的阻抗稳定性，广泛应用于高频功率放大器和滤波器中。

三、高频电路的元件在高频电路中，元件的性能会影响整个电路的性能，因此需要选择合适的元件进行设计和应用。

1、适用于高频电路的元件（1）电阻器：在高频电路中，电阻器的频率响应特性、串扰和噪声等特性需要特别考虑，因此需要选择适合高频的电阻器进行应用。

（2）电容器：高频电路中常用的电容器包括表面贴装电容器、金属层电容器等，它们具有较小的等效串联电感和等效串联电阻，适合高频电路的应用。