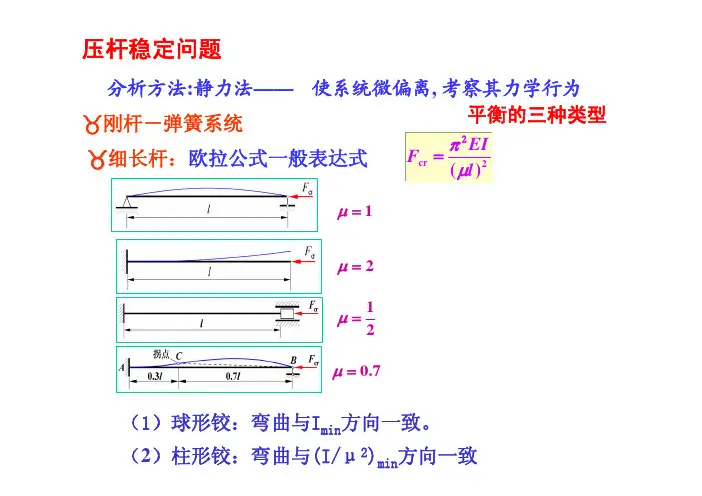
力学竞赛专题能量法静不定
- 格式:ppt
- 大小:2.62 MB
- 文档页数:51





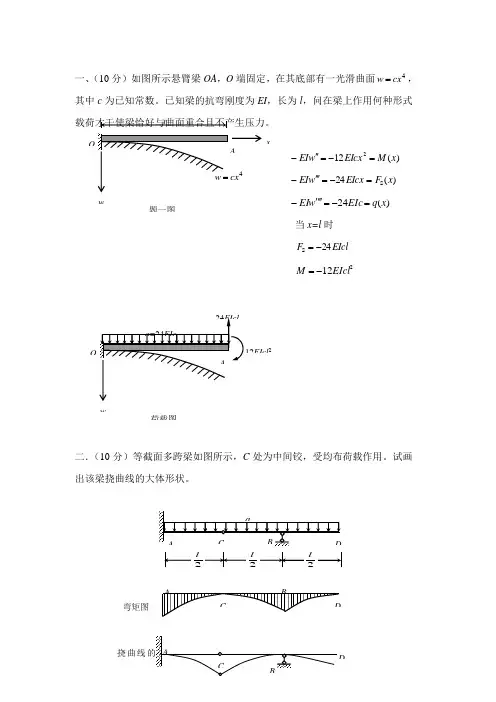
一、(10分)如图所示悬臂梁OA ,O 端固定,在其底部有一光滑曲面4cx w =,其中c 为已知常数。
已知梁的抗弯刚度为EI ,长为l ,问在梁上作用何种形式)(122x M EIcx w EI =-=''-)(24S x F EIcx w EI =-='''-)(24x q EIc w EI =-=''''-当x=l 时 EIcl F 24S -= 212EIcl M -=二.(10分)等截面多跨梁如图所示,C 处为中间铰,受均布荷载作用。
试画出该梁挠曲线的大体形状。
弯矩图挠曲线4cx Ax w 题一图w荷载图EIcl 2三、(10分)图示梁AB 弯曲刚度为EI ,抗弯截面系数为W ,B 端由拉压刚度为EA 的杆BD 连接,已知231Aa I =。
若重量为P 的重物以水平速度v 冲击在梁的中点C 处,求杆BD 和梁AB 内的最大冲击动应力。
EIPa EA aPEI a P 422148)2(33=⋅⋅+=∆st APA P 22st ==杆σWPaW aP 242st =⋅=梁σ 3224gPa EIv g v K =∆=std 杆杆st d d σσK = 梁梁st d d σσK =四.(10分)图示钢筋AD 长度为3a ,总重量为W ,对称地放置于宽为a 的刚性平台上。
试求钢筋与平台间的最大间隙δ。
设EI 为常量。
题三图EI Wa EI aa W EI a a W EI ql EI l M 115219384352166384521634442e =-⨯=-⨯=δ五.(10分)以绕带焊接而成的圆管如图所示,焊缝为螺旋线。
管的内径d =300mm ,壁厚t =1mm ,内压p =0.5MPa 。
求沿焊缝斜面上的正应力和切应力。
焊缝斜面上一点单元体MPa 5.37101410300105.04336=⨯⨯⨯⨯⨯==--t pd x σ MPa 752==tpdy σ,0=xy τ 沿焊缝斜面上的正应力和切应力MPa53)80cos(2755.372755.372sin 2cos 22=⎥⎦⎤⎢⎣⎡--++=--++=ατασσσσσαxy yx yx MPa 5.18)80sin(2755.372cos 2sin 2=⎥⎦⎤⎢⎣⎡--=--=ατασσταxy yxy σ 26a aW 26a aW W q =六.(10分)两根钢轨铆接成组合梁,其连接情况如图所示。