几种插值方法比较与应用2

高中数学中的插值与多项式逼近在高中数学中，插值和多项式逼近是两个重要的概念和技巧。

它们在数学和工程领域中具有广泛的应用，可以用来解决实际问题，提高计算精度和效率。

本文将对插值和多项式逼近进行介绍和探讨。

一、插值的概念和应用1. 插值的概念插值是指通过已知数据点构造一个函数，使得这个函数在已知数据点上与已知函数或数据完全一致。

插值的目的是为了通过已知的离散数据点来估计未知的数据点，从而实现对数据的预测和补充。

2. 插值的应用插值在实际应用中非常广泛，例如地理信息系统中的地图绘制、图像处理中的图像重建、金融领域中的股票价格预测等。

通过插值方法，可以根据已知数据点的特征和规律，推断出未知数据点的值，从而提供更准确的预测和分析。

二、插值方法1. 拉格朗日插值法拉格朗日插值法是一种常用的插值方法，它通过构造一个多项式函数来逼近已知数据点。

这个多项式函数通过已知数据点的横纵坐标来确定，从而实现对未知数据点的估计。

2. 牛顿插值法牛顿插值法是另一种常用的插值方法，它利用差商的概念来构造一个多项式函数。

差商是指已知数据点之间的差值与对应函数值之间的比值，通过差商的递归计算，可以得到一个多项式函数，从而实现对未知数据点的估计。

三、多项式逼近的概念和方法1. 多项式逼近的概念多项式逼近是指通过一个多项式函数来逼近已知函数或数据，使得这个多项式函数在已知数据点上与已知函数或数据最接近。

多项式逼近的目的是为了简化计算和分析，提高计算效率和精度。

2. 最小二乘法最小二乘法是一种常用的多项式逼近方法，它通过最小化已知数据点与多项式函数之间的误差平方和，来确定最优的多项式函数。

最小二乘法可以用来解决数据拟合、曲线拟合等问题，广泛应用于统计学、信号处理等领域。

四、插值与多项式逼近的比较1. 精度比较插值方法可以通过已知数据点完全重构已知函数或数据，因此在已知数据点上的精度非常高。

而多项式逼近方法则是通过一个多项式函数来逼近已知函数或数据，因此在已知数据点上的精度可能会有一定的误差。

几种插值法的对比研究1插值法是一种常用的数据处理方法，特别在数字信号处理和数值计算中广泛应用。

在实际应用中，选择合适的插值方法对数据的良好处理有着重要的作用。

本文将对几种常用的插值方法进行对比研究。

1. 线性插值法线性插值法是最简单也是最常用的插值方法。

它假设函数在两个已知点之间是一条直线，根据该直线与自变量的位置，即可得到插值的函数值。

线性插值法的计算简便，适用于各种连续变化的函数，但是对曲率较大的函数，有时可能会出现较大的误差。

2. 多项式插值法多项式插值法是一种高效的插值方法。

它通过已知的数据点和插值点，构造一个多项式函数。

这个多项式函数与所需求函数一样，在插值点处取相同的函数值。

多项式插值法插值精度较高，但对于高次多项式的构造和计算，不仅容易出现数值不稳定的问题，而且计算量也比较大，往往在实际应用中给计算机带来较大的负担。

样条插值法是一种优秀的插值方法。

样条插值法将整个插值区间划分为若干小区间，每个小区间内部通过一个样条函数连接在一起。

样条函数既可以满足插值的要求，又可以保持函数在区间内的连续性。

这样可以产生较好的插值效果。

相对于线性插值和多项式插值，样条插值法的误差一般较小，满足一定的平滑性要求，而且计算相对简单。

在实际应用中广泛使用。

4. 径向基函数插值法径向基函数插值法是一种数值稳定性较高的方法。

它利用径向基函数的性质，即可以逼近各种连续的函数，将一个函数表示为各个径向基函数的线性组合，建立待插值函数与径向基函数之间的关系。

当插值点趋近于数据点时，径向基函数插值法可以达到较高的精度。

径向基函数插值法的计算方法较为复杂，需要选取合适的径向基函数和其它参数，定位问题更加困难，但是计算结果却更为准确。

综合各种插值方法的优缺点，我们可以根据不同的实际需求选择不同的插值方法。

在插值研究中，需要注意插值方法的数值稳定性、计算效率、精度和平滑性等各个方面的综合考虑，以达到最优的插值效果。

[转载]插值算法（⼀）：各种插值⽅法⽐较原⽂地址：插值算法（⼀）：各种插值⽅法⽐较作者：稻草⼈确定性随机性确定性随机性趋势⾯（⾮精确）回归（⾮精确）泰森（精确）克⾥⾦（精确）密度估算（⾮精确）反距离权重（精确）薄板样条（精确）整体拟合利⽤现有的所有已知点来估算未知点的值。

局部插值使⽤已知点的样本来估算位置点的值。

确定性插值⽅法不提供预测值的误差检验。

随机性插值⽅法则⽤估计变异提供预测误差的评价。

对于某个数据已知的点，精确插值法在该点位置的估算值与该点已知值相同。

也就是，精确插值所⽣成的⾯通过所有控制点，⽽⾮精确插值或叫做近似插值，估算的点值与该点已知值不同。

1、反距离加权法（Inverse Distance Weighted）反距离加权法是⼀种常⽤⽽简单的空间插值⽅法，IDW是基于“地理第⼀定律”的基本假设:即两个物体相似性随他们见的距离增⼤⽽减少。

它以插值点与样本点间的距离为权重进⾏加权平均，离插值点越近的样本赋予的权重越⼤，此种⽅法简单易⾏，直观并且效率⾼，在已知点分布均匀的情况下插值效果好，插值结果在⽤于插值数据的最⼤值和最⼩值之间，但缺点是易受极值的影响。

2、样条插值法（Spline）样条插值是使⽤⼀种数学函数，对⼀些限定的点值，通过控制估计⽅差，利⽤⼀些特征节点，⽤多项式拟合的⽅法来产⽣平滑的插值曲线。

这种⽅法适⽤于逐渐变化的曲⾯，如温度、⾼程、地下⽔位⾼度或污染浓度等。

该⽅法优点是易操作，计算量不⼤，缺点是难以对误差进⾏估计，采样点稀少时效果不好。

样条插值法⼜分为张⼒样条插值法（Spline with Tension）规则样条插值法（Regularized Spline）薄板样条插值法 (Thin-Plate Splin)3、克⾥⾦法（Kriging）克⾥⾦⽅法最早是由法国地理学家Matheron和南⾮矿⼭⼯程师Krige提出的，⽤于矿⼭勘探。

这种⽅法认为在空间连续变化的属性是⾮常不规则的，⽤简单的平滑函数进⾏模拟将出现误差，⽤随机表⾯函数给予描述会⽐较恰当。

各种插值法的对比研究插值法是指通过已知数据点来估计两个数据点之间的未知数值。

在实际生活和科学研究中，经常会遇到需要插值的情况，例如气象预测、金融分析、图像处理等。

本文将对比介绍几种常见的插值方法，包括线性插值、多项式插值、样条插值和逆距离加权插值。

1.线性插值：线性插值是最简单的插值方法，假设两个数据点之间的值变化是线性的。

根据已知数据点的坐标和对应的值，通过线性方程推断两个数据点之间的值。

优点是计算简单快速，但缺点是对数据变化较快的情况下估计效果较差。

2.多项式插值：多项式插值假设两个数据点之间的值变化是一个多项式函数。

通过已知数据点的坐标和对应的值，使用多项式拟合方法求解多项式函数的系数，再根据该多项式求解两个数据点之间的值。

多项式插值可以准确拟合已知数据点，但在插值点较多时容易出现振荡现象，且对数据点分布敏感。

3.样条插值：样条插值是一种平滑的插值方法，通过构建分段连续的多项式函数来逼近整个数据集。

根据已知数据点的坐标和对应的值，通过求解一组多项式函数的系数，使得在相邻区间之间函数值连续，导数连续。

样条插值可以减少振荡现象，对于插值点密集的情况能更好地逼近原始数据。

4.逆距离加权插值：逆距离加权插值是一种基于距离的加权插值方法，根据已知数据点与插值点之间的距离，对每个已知数据点进行加权平均得到插值点的值。

该方法认为距离较近的数据点对插值结果的影响更大。

逆距离加权插值简单易用，对数据点的分布不敏感，但对于距离较远的数据点容易受到较大的干扰。

在实际应用中，选择合适的插值方法需要根据数据的特点和要求来决定。

若数据变化较简单、平滑，可以选择线性插值或多项式插值；若数据变化复杂，存在振荡现象，可以选择样条插值；若数据点分布较稀疏，可以选择逆距离加权插值。

此外，还有一些其他的插值方法，如Kriging插值、径向基函数插值等，它们根据不同的假设和模型进行插值，具有一定的特点和适用范围。

综上所述，对于选择合适的插值方法，需要根据具体问题和数据特点来综合考虑，结合不同方法的优缺点进行比较研究，以得到更准确和可靠的插值结果。

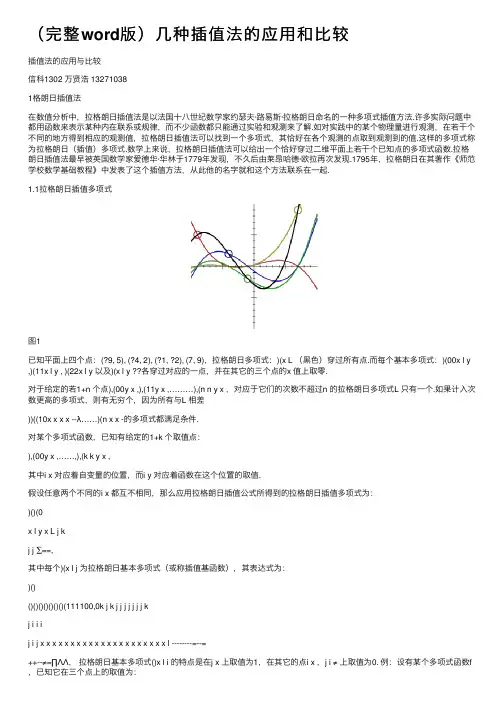
（完整word版）⼏种插值法的应⽤和⽐较插值法的应⽤与⽐较信科1302 万贤浩 132710381格朗⽇插值法在数值分析中，拉格朗⽇插值法是以法国⼗⼋世纪数学家约瑟夫·路易斯·拉格朗⽇命名的⼀种多项式插值⽅法.许多实际问题中都⽤函数来表⽰某种内在联系或规律，⽽不少函数都只能通过实验和观测来了解.如对实践中的某个物理量进⾏观测，在若⼲个不同的地⽅得到相应的观测值，拉格朗⽇插值法可以找到⼀个多项式，其恰好在各个观测的点取到观测到的值.这样的多项式称为拉格朗⽇（插值）多项式.数学上来说，拉格朗⽇插值法可以给出⼀个恰好穿过⼆维平⾯上若⼲个已知点的多项式函数.拉格朗⽇插值法最早被英国数学家爱德华·华林于1779年发现，不久后由莱昂哈德·欧拉再次发现.1795年，拉格朗⽇在其著作《师范学校数学基础教程》中发表了这个插值⽅法，从此他的名字就和这个⽅法联系在⼀起.1.1拉格朗⽇插值多项式图1已知平⾯上四个点：(?9, 5), (?4, 2), (?1, ?2), (7, 9)，拉格朗⽇多项式：)(x L （⿊⾊）穿过所有点.⽽每个基本多项式：)(00x l y ,)(11x l y , )(22x l y 以及)(x l y ??各穿过对应的⼀点，并在其它的三个点的x 值上取零.对于给定的若1+n 个点),(00y x ,),(11y x ,………),(n n y x ，对应于它们的次数不超过n 的拉格朗⽇多项式L 只有⼀个.如果计⼊次数更⾼的多项式，则有⽆穷个，因为所有与L 相差))((10x x x x --λ……)(n x x -的多项式都满⾜条件.对某个多项式函数，已知有给定的1+k 个取值点：),(00y x ,……,),(k k y x ,其中i x 对应着⾃变量的位置，⽽i y 对应着函数在这个位置的取值.假设任意两个不同的i x 都互不相同，那么应⽤拉格朗⽇插值公式所得到的拉格朗⽇插值多项式为：)()(0x l y x L j kj j ∑==，其中每个)(x l j 为拉格朗⽇基本多项式（或称插值基函数），其表达式为：)()()()()()()()()(111100,0k j k j j j j j j j kj i i ij i j x x x x x x x x x x x x x x x x x x x x x l --------=--=++--≠=∏ΛΛ，拉格朗⽇基本多项式()x l i 的特点是在j x 上取值为1，在其它的点i x ，j i ≠ 上取值为0. 例：设有某个多项式函数f ，已知它在三个点上的取值为：10)4(=f ， ? 25.5)5(=f ， ?1)6(=f ，要求)18(f 的值.⾸先写出每个拉格朗⽇基本多项式：())64)(54()6)(5(0----=x x x l ；())65)(45()6)(4(1----=x x x l ；())56)(46()5)(4(2----=x x x l ；然后应⽤拉格朗⽇插值法，就可以得到p 的表达式（p 为函数f 的插值函数）：)()6()()5()()4()(210x l f x l f x l f x p ++=)56)(46()5)(4(1)65)(45()6)(4(25.5)64)(54()6)(5(10----?+----?+----?=x x x x x x)13628(412+-=x x ，此时数值18就可以求出所需之值：11)18()18(-==p f .1.2插值多项式的存在性与唯⼀性存在性对于给定的1+k 个点：),(),,(00k k y x y x K 拉格朗⽇插值法的思路是找到⼀个在⼀点j x 取值为1，⽽在其他点取值都是0的多项式)(x l j .这样，多项式)(x l y j j 在点j x 取值为j y ，⽽在其他点取值都是0.⽽多项式()∑==kj jj x ly x L 0)(就可以满⾜∑==++++==ki j j j i y y x l y x L 0000)()(ΛΛ，在其它点取值为0的多项式容易找到，例如：)())(()(110k j j x x x x x x x x ----+-ΛΛ，它在点j x 取值为：)()()(10k j j j i x x x x x x ---+ΛΛ.由于已经假定i x 两两互不相同，因此上⾯的取值不等于0.于是，将多项式除以这个取值，就得到⼀个满⾜“在j x 取值为1，⽽在其他点取值都是0的多项式”：)()()()()()()()(111100k j k j j j j j j j i j j x x x x x x x x x x x x x x x x x x xx l --------=--=++--∏ΛΛ，这就是拉格朗⽇基本多项式. 唯⼀性次数不超过k 的拉格朗⽇多项式⾄多只有⼀个，因为对任意两个次数不超过k 的拉格朗⽇多项式：1p 和2p ，它们的差21p p -在所有1+k 个点上取值都是0,因此必然是多项式)())((10k x x x x x x ---Λ的倍数.因此，如果这个差21p p -不等于0，次数就⼀定不⼩于1+k .但是21p p -是两个次数不超过k 的多项式之差，它的次数也不超过k ，所以021=-p p 也就是说21p p =.这样就证明了唯⼀性.1.3性质拉格朗⽇插值法中⽤到的拉格朗⽇基本多项式n l l l ,,,10Λ（由某⼀组n x x x <<<Λ10 确定）可以看做是由次数不超过n 的多项式所组成的线性空间：[]X n K 的⼀组基底.⾸先，如果存在⼀组系数：n λλλ,,,10Λ使得，01100=+++=n n l l l P λλλΛ，那么，⼀⽅⾯多项式p 是满⾜n n x P x P x P λλλ===)(,,)(,)(1100Λ的拉格朗⽇插值多项式，另⼀⽅⾯p 是零多项式，所以取值永远是0.所以010====n λλλΛ，这证明了n l l l ,,,10Λ是线性⽆关的.同时它⼀共包含1+n 个多项式，恰好等于[]X n K 的维数.所以n l l l ,,,10Λ构成了[]X n K 的⼀组基底.拉格朗⽇基本多项式作为基底的好处是所有的多项式都是齐次的（都是n 次多项式）.1.4优点与缺点拉格朗⽇插值法的公式结构整齐紧凑，在理论分析中⼗分⽅便，然⽽在计算中，当插值点增加或减少⼀个时，所对应的基本多项式就需要全部重新计算，于是整个公式都会变化，⾮常繁琐.这时可以⽤重⼼拉格朗⽇插值法或⽜顿插值法来代替.此外，当插值点⽐较多的时候，拉格朗⽇插值多项式的次数可能会很⾼，因此具有数值不稳定的特点，也就是说尽管在已知的⼏个点取到给定的数值，但在附近却会和“实际上”的值之间有很⼤的偏差.这类现象也被称为龙格现象，解决的办法是分段⽤较低次数的插值多项式.2 重⼼拉格朗⽇插值法重⼼拉格朗⽇插值法是拉格朗⽇插值法的⼀种改进.在拉格朗⽇插值法中，运⽤多项式)())(()(10k x x x x x x x l ---=Λ，图（2）拉格朗⽇插值法的数值稳定性：如图(2)，⽤于模拟⼀个⼗分平稳的函数时，插值多项式的取值可能会突然出现⼀个⼤的偏差（图中的14⾄15中间）可以将拉格朗⽇基本多项式重新写为：∏≠=--=kji i i j jj x x x x x l x l ,0)(1)()(，定义重⼼权∏≠=-=k ji i i j j x x ,0)(1ω，上⾯的表达式可以简化为：jjj x x x l x l -=ω)()(，于是拉格朗⽇插值多项式变为：j kj jjy xx x l x L ∑=-=0)()(ω，（1）即所谓的重⼼拉格朗⽇插值公式（第⼀型）或改进拉格朗⽇插值公式.它的优点是当插值点的个数增加⼀个时，将每个j ω都除以)(1+-k j x x ，就可以得到新的重⼼权1+k ω，计算复杂度为)(n O ，⽐重新计算每个基本多项式所需要的复杂度)(2n O 降了⼀个量级.将以上的拉格朗⽇插值多项式⽤来对函数1)(≡x g 插值，可以得到：∑=-=?kj jjx x x l x g x 0)()(,ω，因为1)(≡x g 是⼀个多项式. 因此，将)(x L 除以)(x g 后可得到：∑∑==--=k j jjk j jjx x x x x L 00)(ωω，（2）这个公式被称为重⼼拉格朗⽇插值公式（第⼆型）或真正的重⼼拉格朗⽇插值公式.它继承了（1）式容易计算的特点，并且在代⼊x 值计算)(x L 的时候不必计算多项式)(x l 它的另⼀个优点是，结合切⽐雪夫节点进⾏插值的话，可以很好地模拟给定的函数，使得插值点个数趋于⽆穷时，最⼤偏差趋于零.同时，重⼼拉格朗⽇插值结合切⽐雪夫节点进⾏插值可以达到极佳的数值稳定性.第⼀型拉格朗⽇插值是向后稳定的，⽽第⼆型拉格朗⽇插值是向前稳定的，并且勒贝格常数很⼩.3.分段线性插值对于分段线性插值，我们看⼀下下⾯的情况.3.1问题的重诉已知211)(xx g +=,66≤≤-x ⽤分段线性插值法求插值，绘出插值结果图形，并观察插值误差.1.在[-6，6]中平均选取5个点作插值；2.在[-6，6]中平均选取11个点作插值；3.在[-6，6]中平均选取21个点作插值；4.在[-6，6]中平均选取41个点作插值.3.2问题的分析在数值计算中，已知数据通常是离散的，如果要得到这些离散点以外的其他点的函数值，就需要根据这些已知数据进⾏插值.⽽本题只提供了取样点和原函数)(x g .分析问题求解⽅法如下：（1）利⽤已知函数式211)(xx g +=计算取样点X 对应的函数值Y ；将Y X ,作为两个等长的已知向量，分别描述采样点和样本值.因此被插值函数是⼀个单变量函数，可利⽤⼀维插值处理该数据插值问题.⼀维插值采⽤的⽅法通常有拉格朗⽇多项式插值（本题采⽤3次多项式插值），3次样条插值法和分段线性插值.（2）分别利⽤以上插值⽅法求插值.以0.5个单位为步长划分区间[-6，6]，并将每⼀点作为插值函数的取样点.再根据插值函数计算所选取样点的函数值.最后再利⽤所得函数值画出相应的函数图象，并与原函数)(x g 的图象进⾏对⽐.3.3问题的假设为了解决上述分析所提到的问题，本题可以作出如下假设：（1）假设原函数)(x g 仅作为求解取样点对应的样点值的函数关系式.⽽其他各点的函数值都是未知量，叙⽤插值函数计算.（2）为了得到理想的对⽐函数图象，假设)(x g 为已知的标准函数.可以选取0.5个单位为步长划分区间[-6，6]，分别计算插值函数和标准函数)(x g 在该区间的取样点的函数值.画出函数图象进⾏对⽐.3.4分段线性插值原理给定区间[]b a ,, 将其分割成b x x x a n =<<<=Λ10，已知函数)(x f y =在这些插值结点的函数值为),1,0)((n k x f y k k Λ==；求⼀个分段函数)(x I k ,使其满⾜：(1) k k h y x I =)(，),1,0(n k Λ=；(2) 在每个区间[]1,+k k x x 上, )(x I h 是个⼀次函数.易知,)(x I h 是个折线函数, 在每个区间[]1,+k k x x 上,),1,0(n k Λ=1111)(++++--+--=k kk kk k k k k h y x x x x y x x x x x I ,于是, )(x I h 在[]b a ,上是连续的，但其⼀阶导数是不连续的. 于是即可得到如下分段线性插值函数：)()(0x l y x I ni i i n ∑==,其中=≤≤--=≤≤--=+++---.,0;,;0,111111其他时舍去时，且当时舍去时，且当n i x x x x x x x i x x x xx x x l i i i i i i i i ii i3.5问题的求解在MATLAB 中实现分段线性插值，最近点插值，3次多项式插值，3次样条插值的命令为interp 1,其调⽤格式为: Y 1=interp 1(X ,Y ,X 1，’method ’)函数根据X ,Y 的值，计算函数在X 1处的值.X ,Y 是两个等长的已知向量，分别描述采样点和样本值，X 1是⼀个向量或标量，描述欲插值点，Y 1是⼀个与X 1等长的插值结果.method 是插值⽅法，包括：linear ：分段线性插值.它是把与插值点靠近的两个数据点⽤直线连接，然后在直线让选取对应插值点的数.nearest ：近点插值法.根据已知两点间的插值点与这两点间的位置远近插值.当插值点距离前点远时,取前点的值,否则取后点的值.cubic ：3次多项式插值.根据已知数据求出⼀个3次多项式，然后根据多项式进⾏插值. spline ：3次样条插值.在每个分段（⼦区间）内构造⼀个3次多项式，使其插值函数除满⾜插值条件外，还要求个节点处具有光滑条件.再根据已知数据求出样条函数后,按照样条函数插值.运⽤Matlab ⼯具软件编写代码，并分别画出图形如下： (⼀)在[-6，6]中平均选取5个点作插值：-10-5051000.20.40.60.81分段线性插值g(x)y1-10-50510-0.500.513次样条插值g(x)y2-10-5051000.20.40.60.81最近点插值g(x)y3-10-5051000.20.40.60.813次多项式插值g(x)y4（⼆）在[-6，6]中平均选取11个点作插值：-10-5051000.20.40.60.81-10-5051000.20.40.60.81-10-5051000.20.40.60.81最近点插值-10-5051000.20.40.60.813次多项式插值g(x )y1g(x )y2g(x )y3g(x )y4（三）在[-6，6]中平均选取21个点作插值：-10-5051000.20.40.60.81分段线性插值-10-551000.20.40.60.813次样条插值-10-551000.20.40.60.81最近点插值-10-551000.20.40.60.813次多项式插值g(x )y1g(x )y2g(x )y3g(x )y4（四）在[-6，6]中平均选取41个点作插值-10-5051000.20.40.60.81g(x )y1-10-5051000.20.40.60.81g(x )y2-10-5051000.20.40.60.81最近点插值g(x )y3-10-5051000.20.40.60.813次多项式插值g(x )y43.6 分段插值⽅法的优劣性分析从以上对⽐函数图象可以看出，分段线性插值其总体光滑程度不够.在数学上，光滑程度的定量描述是函数(曲线) 的k 阶导数存在且连续，则称该曲线具有k 阶光滑性.⼀般情况下，阶数越⾼光滑程度越好.分段线性插值具有零阶光滑性，也就是不光滑.3次样条插值就是较低次数的多项式⽽达到较⾼阶光滑性的⽅法.总体上分段线性插值具有以下特点：优点: 1.分段线性插值在计算上具有简洁⽅便的特点.2.分段线性插值与3次多项式插值函数在每个⼩区间上相对于原函数都有很强的收敛性，（舍⼊误差影响不⼤），数值稳定性好且容易在计算机上编程实现等优点缺点: 分段线性插值在节点处具有不光滑性的缺点(不能保证节点处插值函数的导数连续)，从⽽不能满⾜某些⼯程技术上的要求.⽽3次样条插值却具有在节点处光滑的特点.。

时序预测中的时间序列插值方法分享在时序预测中，时间序列数据的插值方法是非常重要的一环。

时间序列数据可能会因为各种原因出现缺失值，比如设备故障、数据采集错误等等，这时就需要对缺失值进行插值处理。

本文将分享一些常用的时间序列插值方法，以及它们的优缺点和应用场景。

一、线性插值法线性插值法是一种简单而常用的插值方法。

它的原理是通过已知的数据点之间的线性关系来预测缺失值。

具体来说，就是假设两个已知点之间的数据是线性变化的，然后用这一线性关系来预测缺失值。

线性插值法的优点是简单易用，计算速度快。

但是它也有明显的缺点，比如对数据的变化趋势要求较高，对异常值敏感，不适用于非线性数据。

二、拉格朗日插值法拉格朗日插值法是一种多项式插值法，它通过已知的数据点来构造一个满足插值条件的多项式，从而预测缺失值。

这种方法的优点是可以拟合各种类型的数据，可以达到高阶的插值精度。

然而，拉格朗日插值法也存在一些缺点。

首先，当数据点比较稀疏时，插值多项式可能会出现过拟合的情况。

其次，高阶多项式插值可能会引入振荡和不稳定性，对数据的噪声比较敏感。

三、样条插值法样条插值法是一种光滑插值方法，它通过在相邻数据点处使用不同的低次多项式来拟合数据。

这种方法的优点是能够在保持光滑性的同时拟合数据，也可以避免插值多项式的振荡和不稳定性。

但是样条插值法也有一些限制，比如对于高维数据的计算复杂度较高，需要较多的计算资源。

同时，对于非周期性的数据，样条插值可能会引入不必要的光滑性。

四、基于机器学习的插值方法除了传统的插值方法，近年来基于机器学习的插值方法也逐渐受到关注。

比如使用回归模型、神经网络等方法来学习数据点之间的复杂关系，从而实现时间序列的插值预测。

这种方法的优点是可以适应各种类型的数据，具有很强的灵活性和泛化能力。

但是也需要大量的数据和计算资源来训练模型，对模型的选择和调参要求较高。

五、时间序列插值方法的选择在实际应用中，选择合适的时间序列插值方法是非常重要的。

插值研究1 插值法的应用在函数的近似求解中，插值方法非常的重要。

当我们知道了函数在有限个点处的取值状况后，就可以估算出该函数在其他点处的函数值，进而求解函数的更多相关信息。

插值法除了函数求值的应用之外，其他方面的用法也比较多。

包括：数值微分方法，数值积分方法，数据拟合，以及在图像处理方面的应用。

（1）数值积分法：在进行积分的求解时，经常会遇到被积函数不清楚，即使被积函数已知，然而被积函数的原函数求并不好求，在这种情况下，一般根据)(x f 在积分区间的已知数据，通过构造插值多项式)(x p 替代)(x f ，由于)(x p 为多项式，则)(x f 的积分值就能够比较容易求出。

（2）数值微分方法：通常意义上的数值微分方法，也即是根据距离相等的节点上的插值多项式，求解函数的导数值。

我们知道，两点公式是通过分段线性插值得出的，三点公式是通过分段抛物插值得出的。

然而这两种公式仅仅适合对节点处求导数值。

如果在区间内的其它点求导数值的话，样条插值函数是比较好的选择。

（3）数据拟合：在获得一组测定的离散的数据之后，我们最想获得的就是这些离散数据的数学表达式，探讨这些数据的内在规律。

如果无法求解到精确的数学表达式，尽可能好的去近似得出函数解析式，也会帮助我们获得意想不到的结果。

关于插值法的近似标准是这样规定的：原函数和插值函数在插值点处的误差为零，在实际的应用当中，有些点的误差并不一定为零，只需考虑整体的误差限制即可，因而所求函数并不需要通过所有点，我们所要求的是最好的反应原函数的变化趋势。

通过插值法的求解，便可以求得最优的拟合函数。

（4）图像处理：数字图像的处理涉及到社会生活的很多领域，而图像的放大作为数字图像处理的基本操作，具有很强的重要性。

通过插值法，可以实现图像的放大。

图像处理中，图像之间的转换是通过坐标变换来实现的。

这样做的问题就是目标点的坐标一般不会是常数，因此要解决非整数坐标处的点应该是怎样的。