当前位置：文档之家 › (中职)三角函数复习PPT完美课件【优选】

(中职)三角函数复习PPT完美课件【优选】

  • 格式：ppt
  • 大小：455.50 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

中职教育-数学(基础模块)上册课件：第5章 三角函数.ppt

中职教育-数学(基础模块)上册课件：第5章 三角函数.ppt
（4）奇偶性
正弦曲线关于原点O中心对称，因此正弦函数y=sin x是奇 函数．
（5）单调性
当x由－π/2增大到π/2时，正弦曲线逐渐上升，y=sin x的 值由－1增大到1；当x由π/2增大到3π/2时，正弦曲线逐渐下降， y=sin x的值由1减小到－1．
根据周期性可知，正弦函数在每一个区间
[－π/2＋2kπ， π/2＋2kπ]（k∈Z）上都是增函数，其函数值 由－1增大到1；在每一个区间[π/2＋2kπ，3π/2＋2kπ]（k∈Z）
学习目标：了解角的概念推广，理解弧度制的概念和意义， 理解任意角的正弦函数、余弦函数和正切函数；掌握利用计算 器求三角函数的值，理解同角三角函数的基本关系，了解诱导 公式的推导及简单应用，理解正弦函数的图像和性质；了解余 弦函数的图像和性质，掌握利用计算器求角度；了解“已知一 个角的三角函数值，求在指定范围内的角”的方法。
因此，所有与30°角终边相同的角（包括30°角），都 可以表示成30°与360°的整数倍的和，即都可以写成
30°＋k ▪360°（ｋ∈Ｚ）的形式．所以，与30°角终边相
同的角的集合为
｛β｜ β=30°＋k ▪360°（ｋ∈Ｚ） ｝．
一般地，所有与角α终边相同的角（包括角α在内）都可
以写成α＋k ▪360°（ｋ∈Ｚ）的形式，它们所组成的集合为 ｛β｜ β=α＋k ▪360°（ｋ∈Ｚ） ｝
r
r
x
图5-8
根据相似三角形的知识，对于每一个确定的角α，其正弦、 余弦和正切（当x≠0时）的值都是唯一确定的，而与点P在角α 终边上的位置无关．
因此，正弦、余弦和正切都是以角α为自变量的函数，分 别称为角α的正弦函数、余弦函数和正切函数，它们都是角α的 三角函数．

《三角函数的图象和性质》中职数学(基础模块)上册5.3ppt课件3【人教版】

《三角函数的图象和性质》中职数学(基础模块)上册5.3ppt课件3【人教版】

2
5π 2
－1 x
在 [(2 k－1) , 2 k] (kZ)上，是增函数； 在 [2 k，(2 k＋1) ] (kZ)上，是减函数．
例1 求下列函数的最大值，最小值和周期 T： （1）y＝5 cos x ； ( 2 ) y＝－8 cos (－x)．
解 (1) ymax 5, ymin 5,T 2π . (2) ymax 8, ymin 8,T 2π .
4
5
4
1. 余弦函数的图象以及“五点法”作图. 2. 余弦函数的性质.
教材P157，练习 A 组第 2、 3 题； 练习 B 组第 2 题．
编者语
• 要如何做到上课认真听讲？
•
我们都知道一个人的注意力集中时间是有限的，一节课45分钟如何保持时时刻刻都能认真听讲不走神呢？
•
1、往前坐
•
坐的位置越靠后，注意力就越难集中。老师不会注意到你的事实可以让你不再紧张，放心去做别的事情。坐在后面，视线分散，哪怕你是在看老师，如果有人移动，你的视线就会飘到那个同学的后脑勺上去，也就无法集中注意力。 而且，坐在后面很
(2) 余弦函数的周 期
由公式 cos(x＋k · 2 )＝cos x ( k Z ) 可知：
余弦函数是一个周期函数，2 ，4 ，…，－2 ，－ 4 ，… ， 2k ( k Z 且 k≠0 ) 都是余弦函数的周期；
2 是其最小正周期．
余弦函数的图象每隔 2 重复出现．
(3) 余弦函数的奇偶 性
y
1-
6π
4π
2
o
-1 -
2π
4π
6π
x
-
-
二、余弦函数的性质 (1) 余弦函数的值 域

高中数学课件《三角公式》中职总复习

高中数学课件《三角公式》中职总复习

（1）sin αcos α；
（2）s2insinα－α－2ccoossαα.
【解析】（1）解法一：由已知可得方程组
得sin α=3cos α，cos2α=110. 故sin αcos α=3cos αcos α=3cos2α=130.
典例解析
解法二：sin αcos α=ssinin2αα+ccoossα2α=tatna2nαα+1=323+1=130. 解法三：因为tan α=3，所以sin α=3cos α. 所以sin αcos α=ssinin2αα+ccoossα2α=9co3s2cαo+s2cαos2α=9+31=130. （2）因为tan α=csoins αα=3，所以sin α=3cos α. 所以2sisninαα－－2ccooss αα=36ccoossαα－－2ccoossαα=5.
又因为α∈(π2,π)，所以cos α=- 23.
典例解析
【例2】已知α∈(π2,π)，sinα2+cosα2= 26.
（2）因为-
π 2
<α-β<
π 2
，cos(α-β)=
1−sin2(α−β)= 45,
所以cos β=cos［α-(α-β)］=cos αcos(α-β)+sin αsin(α-β)
典例解析
【例2】已知α∈(π2,π)，sinα2+cosα2= 26.
（1）求cos α的值；
（2）若sin(α-β)=-35，β∈(π2,π)，求cos β的值.
【解析】（1）因为（sinα2+cos
α 2
）2=1+2sin
α 2
cos
α 2

职高数学5.6三角函数的图像和性质ppt课件

职高数学5.6三角函数的图像和性质ppt课件

解 设 u 2x ，则使函数 y sin u 取得最大值 1 的集合是
u
u
π 2
2kπ,
k
Z
，
由
2x u π 2kπ ,
2
得
x π kπ ．
4
故所求集合为
x
x
π 4
kπ, k
Z
，
函数 y sin 2 x 的最大值是1．
变量替换
；.
12
三角函 数
应用知识 强化练习
练习5.6.1
计算器
；.
5
动脑思考 探索新知
用“描点法”作函数 y sin x 在0,2上的图像
向左或向右平移2π，4π,…
演示
y sin x, x R 的图像——正弦曲线．
；.
6
三角函 数
动脑思考 探索新知
正弦曲线夹在直线 y=-1 和 y=1 之间，
对任意的角 x ，都有 sin x 1成立，
函数的这种性质叫做有界性．
动脑思考探索新知对于函数yfx如果存在一个不为零的常数t当x取定义域d内的每一个值时都有xtd并且等式fxtfx成立那么函数yfx叫做周期函数常数t叫做这个函数的一个周期
第5章 三角函数 5.6 三角函数的图像和性质
；.
1
创设情景 兴趣导入
观察钟表，如果当前的时 间是2点，那么时针走过12 个小时后，显示的时间是 多少呢？再经过12个小时 后，显示的时间是多少呢？
正弦函数y=sinx是否是周期函数？
；.
3
动脑思考 探索新知
对于正弦函数有：
sin ( 2 k π )= sin (k Z )，
想一想：
自变量a每增加或减少多少，正弦函数值不变？

中职数学4.3 任意角的三角函数课件

中职数学4.3 任意角的三角函数课件

4.3.2 单位圆与三角函数
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
例5 已知cos＞0, 且tan ＜0, 试确定角 是第几象限角．
解 因为cos＞0, 所以角 可能是第一或第四象限角, 也
可能终边在 x 轴的正半轴上.
又因为tan＜0，所以角 可能是第二或第四象限角． 故满足cos＞0且tan＜0的角 是第四象限角．
4.3.2 单位圆与三角函数
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
0°角、180°角、270°角和360°角的正弦、余弦和正切值
4.3.2 单位圆与三角函数
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
例4 判断下列各三角函数值的符号.
解 (1) 因为−325°＝35°−360°，所以－325°角是第一象限角， 故sin(−325°)＞0； (2)
4.3.2 单位圆与三角函数
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
4.3.2 单位圆与三角函数
练习
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
1. 判断下列三角函数值的符号：
4.3.2 单位圆与三角函数
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
30°角的终边与单位圆的交点坐标可以表示为_______. 60°角的终边与单位圆的交点坐标可以表示为_______. 120°角的终边与单位圆的交点坐标可以表示为______.
4.3.2 单位圆与三角函数
情境导入 探索新知 例题辨析 巩固练习 归纳总结 布置作业
例3 求90°角的正弦、余弦和正切. 解 90°角的终边与单位圆的角的交点坐标为(0,1) ， 所以 sin90°=1, cos90°=0, tan90°不存在.

中职数学...三角函数的诱导公式PPT课件

中职数学...三角函数的诱导公式PPT课件
You Know, The More Powerful You Will Be
谢谢你的到来
学习并没有结束，希望大家继续努力
Learning Is Not Over. I Hope You Will Continue To Work Hard
演讲人：XXXXXX 时 间：XX年XX月XX日
2kπ＋α（k∈Z），π＋α，－α，π －α的三角函数值，等于α的同名函数值，
再放上将α当作锐角时原函数值的符号.
总结：
2k (k Z ), , 的三角函数， 等于的 同名函数值， 前面加上一个把看成锐角时 原函数值的符号。
三、应用
例 1 求下列各角的三角函数值。
（1） sin( 7 )
任意角的三角函数任意正角的三角函数的角的三角函数锐角三角函数感谢亲观看此幻灯片此课件部分内容来源于网络如有侵权请及时联系我们删除谢谢配合
三角
三
三角
角
函数
5.5 三角函数的诱导公式
同角三角函数的基本关系
平方关系: sin 2 cos2 1
商数关系:
tan sin cos
( k , k Z )
2. 角 与 － 的三角函数间的关系
探究 若 与 － 的终边关于 x 轴对称，
它们的三角函数之间有什么关系？
y
P (cos ，sin )
公式 （二）
O －
P (cos (-) ，sin(- ) )
sin sin
x
cos cos tan tan
公式二 sin( ) sin cos( ) cos
公式三：
sin( ) sin
cos( ) cos tan( ) tan
4. 角 与 + 的三角函数间的关系

2019高职高考数学复习-三角函数的图象与性质 精品优选公开课件

2019高职高考数学复习-三角函数的图象与性质 精品优选公开课件
|������|
(3)函数 y=Asin(ωx+φ)+k 的最大值是|A|+k,最小值是-|A|+k.
3.余弦型函数 y=Acos(ωx+φ)+k 的图象与性质类似 y=Asin(ωx+φ)+k 的图象
与性质.
4.正切型函数 y=Atan(ωx+φ)+k 的最小正周期是 T=|������������|.
y=Asin(ωx+φ),然后求最大、最小值和周期.
【例 3】 函数 y=cosx(-������������≤x≤������������)的值域为
.
【点评】 求y=sinx(或y=cosx、y=tanx)在指定区间上的最 大、最小值,一般用图象法:画出函数在指定区间上的图象,观察 出最大、最小值.
x=������π+2kπ,k∈Z
������
时,ymin=-������������
描点、连线如图所示:
【例 2】 (1)y=5-2cos(2x+������������)的最小值是 (2)函数 y=sinx+ ������cosx 的最大值为
. .
(3)函数 y=3sin2x-4cos2x 的周期是
������
������π
π
������
������
������
0
������
π
������π
2π
������
������
0
1
0
-1
0
(1)当
x=������+2kπ,k∈Z
������
时,ymax=2,当
x=������π+2kπ,k∈Z

中职教育数学《三角函数-复习》课件

中职教育数学《三角函数-复习》课件

5、化简：
（1）ccooss(1930500•0s)i•nt(an2150850
)
0
（2）scion（s(18001800）)••scions((18030600 ))
三角函数
复习课
诱导公式 定义
同角三角函数的基本关系
单位圆与三角函数线 图象性质
y=asin+bcosα 的 最值
C(α±β) S(α±β)、T( α±β)
形如y=Asin(ωx+φ)+B图象
S2α= C2α= T2α=
降幂公式
一、任意角的三角函数
1、角的概念的推广
的终边
Hale Waihona Puke y 的终边正角o
x 零角
[-1，1]
T=2
奇偶性
奇函数
质 单调性
[2k ,2k ]增函数
2
2
[2k ,2k 3 ]减函数
2
2
[-1，1]
T=2
偶函数
[2k ,2k ]增函数
[2k ,2k ]减函数
四、主要题型
1、基础题
（1）-920。的角在第
象限
（2）写出 30 的终边相同的角，表示 为 。 - - - - - - - - - - - -
tan tan2 1
2 2 22 1 5
应用：关于 sin与cos 的齐次式
变式练习：
1、已知tan =2,求值：
1 sin cos 2sin cos
sin cos
(3) sin 2 2cos 2 1
注：公式的正用、反用、变形、“1”的变通。
注：不能单从角 的范围考虑，而怱略了
内在联系 sin 2 cos 2 1

中职三角函数复习完美课件

中职三角函数复习完美课件
1、角的概念的推广
xቤተ መጻሕፍቲ ባይዱ
一、角的有关概念
2、角度与弧度的互化
1、角的概念的推广x正角负角oy的终边的终边零角一、角的有关
二、弧长公式
弧长公式：
二、弧长公式弧长公式：RLα
终边相同的角与相等角的区别
终边相同的角不一定相等，相等的角终边一定相同。
三、终边相同的角
终边相同的角与相等角的区别终边相同的角不一定相等，相等的角终
0°到360°的角的三角函数
锐角三角函数
求值
可概括为：“负化正，大化小，化到锐角为终了”
用诱导公式求值的一般步骤任意负角的三角函数用公式三或公式一任
1.在利用诱导公式求三角函数的值时，一定要注意符号
解题分析
2。三角变换一般技巧有 ①切化弦， ②降次， ③变角， ④化单一函数， ⑤妙用1， ⑥分子分母同乘除，
三、求值题
1、特殊角、非特殊角的三角函数求值题
三角函数部分题型一、概念题：1、任意角的概念2、弧度制概念3
例4、化简
例4、化简
感谢指导 ！
1、要有针对性。它不能像一般材料作文那样，从材料中引出一个道
方法不当就会很繁，只能通过总结积累解题经验，选择出最佳方法.
1.在利用诱导公式求三角函数的值时，一定要注意符号解题分析2
三角函数部分题型
一、概念题：
1、任意角的概念
2、弧度制概念
3、任意角的三角函数概念；
概念是逻辑判断的依据，是数学分析、理解的基础
二、考查记忆、理解能力题
如：简单的运用诱导公式
要求做到：记忆熟悉、计算细心、答案正确
例1．已知sinα= ，求tanα. 方法指导：此
(中职)三角函数复习完美课件

中职数学三角函数 (1)ppt课件

中职数学三角函数 (1)ppt课件

cos
2
学习 提示
利 用 基 本 关 系 式 sin 2 cos2 1 求三角函数的值时，需要进行开平方运
算，所以必须要明确角 所在的象限.
返回
完整版课件
15
此课件下载可自行编辑修改，供参考！ 感谢您的支持，我们努力做得更好！
r r r r x x
由于点 P，P 在同一象限内，
所以它们的坐标符号相同，因此得
y P
r P' y
r' y'
O x' x x
xx， yy， yy． r r r r x x
完整版课件
8
所以当角 不变时，不论点 P 在角
的终边上的位置如何，这三个比值都是定值，
只依赖于 的大小，与点 P 在 角 终
完整版课件
12
1.2.3 界线角的三角函数值
三角函数 0
sin 0
π π 3π 2π
2
2
1 0 -1
0
cos 1
0 -1 0
1
tan 0 不存在 0 不存在 0
完整版课件
13
三角
三
三角
角
1.3
三角
同角三角函数的关系
同角三角函数的基本关系
sin2 cos2 1,
tan sin , π kπ (k Z ).
式 比，即
l r
(rad) .
这里，角 的正负由其终边的旋转方向决定.
一般地，正角的弧度数是一个正数，负角的弧度数是一
个负数，零角的弧度数是 0.
完整版课件
4
π=180°
换算公式
1 π (rad) 0.017 45(rad), 180

人教版(2021)中职数学基础模块上册第五章《三角函数》复习课课件

人教版(2021)中职数学基础模块上册第五章《三角函数》复习课课件

.
4.
函数
5.周期:T=
.
5.同角三角函数的基本关系式:
(1)sin2α+cos2α=1;
(2) tan sin . cos
6.余弦函数y=cosx的图象与性质
余弦函数的图象特征 1.图象向左向右无限伸展;
余弦函数的性质
1.定义域:
.
2.图象最高点的坐标( , ) 最低点的坐标( , )(k∈Z)
4
2.三角函数的定义
【例2】 已知点P在角α的终边上,求角α的正弦、余弦和正切:
(1)P (2 3, 2);
(2)P(1,-1).
3.同角三角函数基本关系式 【例3】 已知cosα= 3 ,且α是第三象限的角,求sinα,tanα,2sin2α-cos2α.
2
4.求角的三角函数值
【例4】 求下列各三角函数值:
第五章 三角函数 复习课
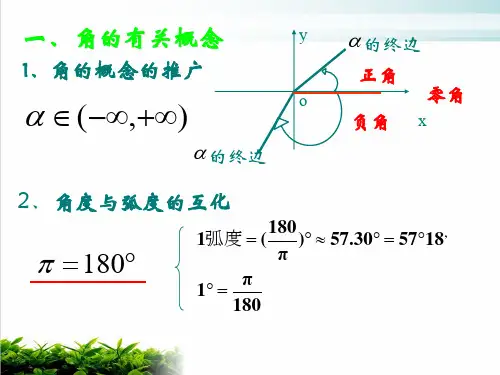
一、知识梳理
1.任意角三角函数的定义如何?
正弦:sinα=
,余弦:cosα=
,正切:tanα=
.
其中:r= x2 y2 ,点P(x,y)是角α终边上一点.
2.三角函数在各象限的符号:
α
第一象限 第二象限 第三象限 第四象限
sinα
cosα
tanα
3.诱导公式
(1)诱导公式一:sin(2kπ+α)=
(1) cos 13 ;
6
(2)sin(17 );
6
(3) tan(13 ).
4
5.正弦函数的图象与性质 【例5】 用五点作图法画出函数y=2sinx-1在区间[0,2π]上的简图,并求它的最大值 和最小值.
6.余弦函数的图象和性质 【例6】 求函数y=-2cosx+3的值域,并写出当函数取最大、最小值时x的取值集合.

中职数学...三角函数的诱导公式 ppt课件

中职数学...三角函数的诱导公式 ppt课件

y P
MO
公式 （一）
sin(2 k＋ )＝sin ；
cos(2 k＋ )＝cos (k Z) ；
1x
tan(2 k＋ )＝tan .
ppt课件
4
公式一：
sin(2k ) sin
cos(2k ) cos (k z)
tan(2k ) tan
三角
三
三角
角
函数
5.5 三角函数的诱导公式
ppt课件
1
同角三角函数的基本关系
平方关系: sin 2 cos2 1
商数关系:
tan sin cos
( k , k Z )
2
同一个角 的正弦、余弦的平
方和等于1，商等于角 的正
切。
ppt课件
2
问题提出
ppt课件
5
例1 求下列各三角函数的值：
(1)sin13； (2) cos19 ； (3) tan405．
2
3
解 (1) sin 13π sin( π 6π) sin π 1;
2
2
2
(2) cos19π cos( π 6π) cos π 1 ;
3
3
32
(3) tan405 tan(45 360) tan45 1.
sin( ) sin cos( ) cos tan( ) tan
sin( ) sin cos( ) cos tan( ) tan
2kπ ＋α （k∈Z），π ＋α ，－α ，π －α 的三角函数值，等于α 的同名函数值，
6
62
（2）cos(
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
感谢指导
！
的三角函
角的三
的角的三角
数
用公式三 角函数
函数
用公式二 锐 角
求
三角
值
或四或五 函数
可概括为：“负化正，大化小，化到锐角为终了”
解题分析
1.在利用诱导公式求三角函数的值时，一定要注意符号
2。三角变换一般技巧有
①切化弦， ②降次，
③变角，
④化单一函数，
⑤妙用1，
⑥分子分母同乘除，
方法不当就会很繁，只能通过总结积累解题经验， 选择出最佳方法.
tan( ) tan
诱导公式三 sin( ) sin cos( ) cos
tan( ) tan
诱导公式四 sin( ) sin ， cos( ) cos ,
tan( ) tan .
公式记忆 （把α看成锐角）
符号看象限
用诱导公式求值的一般步骤
任 意 负 角 或公式一 任 意 正 用公式一 0° 到 360°
第五章 三角函数复习
主 要
三角函数的相关概念
内 容
三角变换与求值
一、角的有关概念
y
1、角的概念的推广
( , )
o
的终边
的终边
正角 零角
负角 x
2、角度与弧度的互化
180
1弧度(180)57.305718, π
1 π 180
二、弧长公式
弧长公式：
l= r
R
L
α
三、终边相同的角
终边相同的角与相等角的区别 终边相同的角不一定相等，相等的角终边一定相同。
例 2已 知 ta n 3 ,求 s s iin n c c o o s s 的 值
例 3 、 求 证 c o s 1 2 s in 2 2 2 c o s
一、诱导公式
sin( k2) sin
诱导公式一 cos( k2) cos
tan( k2) tan
诱导公式二
sin( ) sin cos( ) cos
三角函数部分题型
一、概念题：
1、任意角的概念 2、弧度制概念 3、任意角的三角函数概念； 概念是逻辑判断的依据，是数学分析、理解的基础
二、考查记忆、理解能力题 如：简单的运用诱导公式
要求做到：记忆熟悉、计算细心、答案正确
三、求值题 1、特殊角、非特殊角的三角函数求值题
例4、化简
（ 1） c so in s ຫໍສະໝຸດ in2 cos2 yO
x
2k kZ
四、任意角的三角函数定义
r x2 y2
siny,cos x,tany
r
r
x
y P(x,y) 的终边 ● r
o
x
五、同角三角函数的基本关系式
平方关系：
si2 nco 2s 1
商数关系：
tan sin cos
例1．已知sinα= 4，求tanα.
5
方法指导：此类例题的结果可分为以下二种情况. (1)已知一个角的某三角函数值，又知角所在象限，有 一解. (2)已知一个角的某三角函数值，但不知角所在象限， 有两解.
（2） cos2tansin360
1 、 要 有 针对 性。它不能像一般材料作文那样，从材料中引出一个道理， 然后哲 理化写 作。而 是必须 针对材 料所列 出的现 象进行 评论， 有的放 矢； 2 、 要 有 说理 性。定是以理服人，让读者能一目了然地知道这种现象的本 质是什 么，原 因是什 么，如 何解决 。 3.理解体会文言文所表达的作者的思 想感情 。会在 整体把 握课文 的基础 上，回 答一些 简单的 问题。 4.会在整体把握课文的基础上，回答 一些重 点问题 。分析 理解文 言文的 思想意 义，学 会阅读 理解赏 析文言 文。 5.环境描写的作用，人物描写对人物 性格塑 造的作 用及人 物形象 性格分 析；作 者的感 情态度 。 6.理解体会文言文所表达的作者的思 想感情 。会在 整体把 握课文 的基础 上，回 答一些 简单的 问题。 7.会在整体把握课文的基础上，回答 一些重 点问题 。分析 理解文 言文的 思想意 义，学 会阅读 理解赏 析文言 文。