18题 高考数学概率与统计知识点

概率与统计知识点及专练（一）统计基础知识：1. 随机抽样：（1）．简单随机抽样：设一个总体的个数为N ，如果通过逐个抽取的方法从中抽取一个样本，且每次抽取时各个个体被抽到的概率相等，就称这样的抽样为简单随机抽样.常用抽签法和随机数表法.（2）．系统抽样：当总体中的个数较多时，可将总体分成均衡的几个部分，然后按照预先定出的规则，从每一部分抽取1个个体，得到所需要的样本，这种抽样叫做系统抽样（也称为机械抽样）.（3）．分层抽样：当已知总体由差异明显的几部分组成时，常将总体分成几部分，然后按照各部分所占的比进行抽样，这种抽样叫做分层抽样.2. 普通的众数、平均数、中位数及方差： （1）.众数：一组数据中，出现次数最多的数（2）.平均数：常规平均数：12nx x x x n ++⋅⋅⋅+=（3）.中位数：从大到小或者从小到大排列，最中间或最中间两个数的平均数（4）.方差：2222121[()()()]n s x x x x x x n =-+-+⋅⋅⋅+-（5）.标准差：s3 .频率直方分布图中的频率：（1）.频率 =小长方形面积：f S y d ==⨯距；频率=频数/总数； 频数=总数*频率（2）.频率之和等于1：121n f f f ++⋅⋅⋅+=；即面积之和为1： 121n S S S ++⋅⋅⋅+=4. 频率直方分布图下的众数、平均数、中位数及方差： （1）.众数：最高小矩形底边的中点（2）.平均数：112233n n x x f x f x f x f =+++⋅⋅⋅+ 112233n n x x S x S x S x S =+++⋅⋅⋅+（3）.中位数：从左到右或者从右到左累加，面积等于0.5时x 的值（4）.方差：22221122()()()nn s x x f x x f x x f =-+-+⋅⋅⋅+-5.线性回归直线方程：（1）.公式：ˆˆˆy bx a=+其中：1122211()()ˆ()n ni i i ii in ni ii ix x y y x y nxybx x x nx====---∑∑==--∑∑（展开）ˆˆa y bx=-（2）.线性回归直线方程必过样本中心(,) x y（3）.ˆ0:b>正相关；ˆ0:b<负相关（4）.线性回归直线方程：ˆˆˆy bx a=+的斜率ˆb中，两个公式中分子、分母对应也相等；中间可以推导得到6. 回归分析：（1）.残差：ˆˆi i ie y y=-（残差=真实值—预报值）分析：ˆie越小越好（2）.残差平方和：2 1ˆ() ni iiy y =-∑分析：①意义：越小越好；②计算：222211221ˆˆˆˆ()()()() ni i n niy y y y y y y y =-=-+-+⋅⋅⋅+-∑（3）.拟合度（相关指数）：2 2121ˆ()1()ni iiniiy y Ry y==-∑=--∑分析：①.(]20,1R∈的常数；②.越大拟合度越高（4）.相关系数：()()n ni i i ix x y y x y nx y r---⋅∑∑==分析：①.[1,1]r∈-的常数；②.0:r>正相关；0:r<负相关③.[0,0.25]r∈；相关性很弱；(0.25,0.75)r∈；相关性一般；[0.75,1]r∈；相关性很强7. 独立性检验：（1）.2×2列联表（卡方图）： （2）.独立性检验公式①．22()()()()()n ad bc k a b c d a c b d -=++++②．上界P 对照表：（3）.独立性检验步骤：①．计算观察值k ：2()()()()()n ad bc k a b c d a c b d -=++++ ②．查找临界值0k ：由犯错误概率P ，根据上表查找临界值0k③．下结论：0k k ≥即认为有P 的没把握、有1-P 以上的有把握认为两个量相关；0k k <：即认为没有1-P 以上的把握认为两个量是相关关系。

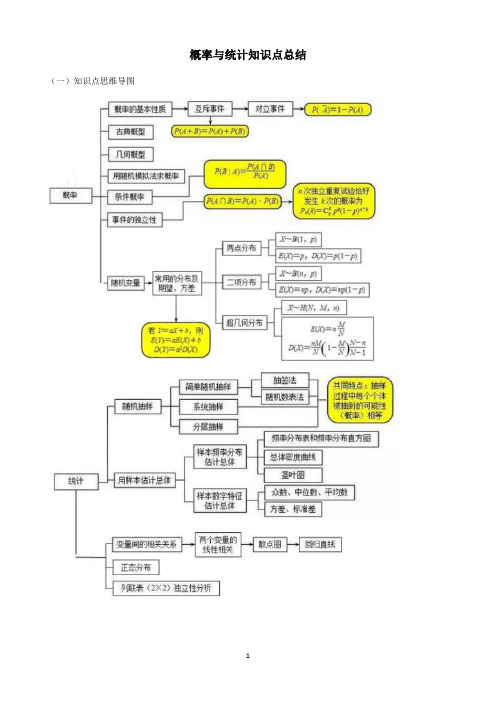
概率与统计知识点总结（一）知识点思维导图（二）常用定理、公式及其变形1．用样本的数字特征估计总体的数字特征（1）样本本均值：nx x x x n +++= 21 （2）样本标准差：nx x x x x x s s n 222212)()()(-++-+-== （3）频率分布直方图估算样本众数、中位数、平均数①众数：最高小矩形中点值；②中位数：先确定中位数所在小组，设中位数为m ，由直线x=m 两侧小矩形面积之和等于0.5列方程求m ． ③平均数：各小矩形中点值与其面积的积的和．2．随机事件的概率及概率的意义（1）随机事件：在条件S 下可能发生也可能不发生的事件，叫相对于条件S 的随机事件；（2）概率定义：在相同的条件S 下重复n 次试验，观察某一事件A 是否出现，称n 次试验中事件A 出现的次数n A 为事件A 出现的频数；称事件A 出现的比例f n (A)=n n A为事件A 出现的频率：对于给定的随机事件A ，如果随着试验次数的增加，事件A 发生的频率f n (A)稳定在某个常数上，把这个常数记作P （A ），称为事件A 的概率．3．概率的基本性质（1）事件的包含、并事件、交事件、相等事件（2）若A∩B 为不可能事件，即A∩B=ф，那么称事件A 与事件B 互斥；（3）若A∩B 为不可能事件，A∪B 为必然事件，那么称事件A 与事件B 互为对立事件；（4）当事件A 与B 互斥时，满足加法公式：P(A∪B)= P(A)+ P(B)；若事件A 与B 为对立事件，则A∪B 为必然事件，所以P(A∪B)= P(A)+ P(B)=1，于是有P(A)=1—P(B)4．古典概型及随机数的产生（1）古典概型的使用条件：试验结果的有限性和所有结果的等可能性．（2）公式P （A ）=总的基本事件个数包含的基本事件数A 5．几何概型及均匀随机数的产生（1）几何概率模型：如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型；（2）公式：P （A ）=积）的区域长度（面积或体试验的全部结果所构成积）的区域长度（面积或体构成事件A ． 6．随机变量：如果随机试验可能出现的结果可以用一个变量X 来表示，并且X 是随着试验的结果的不同而变化，那么这样的变量叫做随机变量． 随机变量常用大写字母X 、Y 等或希腊字母 ξ、η等表示．7．离散型随机变量的分布列：一般的，设离散型随机变量X 可能取的值为x 1，x 2，．．．．． ，x i ，．．．．．．，x n ．X 取每一个值 x i (i=1，2，．．．．．．）的概率P(ξ=x i ）＝P i ，则称表为离散型随机变量X 的概率分布，简称分布列分布列性质：∪ p i ≥0， i =1，2， … ；∪ p 1 + p 2 +…+p n = 1．9．条件概率：对任意事件A 和事件B ，在已知事件A 发生的条件下事件B 发生的概率，叫做条件概率．记作P(B|A)，读作A 发生的条件下B 的概率公式：.0)(,)()()|(>=A P A P AB P A B P 10．相互独立事件：事件A(或B)是否发生对事件B(或A)发生的概率没有影响，这样的两个事件叫做相互独立事件，)()()(B P A P B A P ⋅=⋅12．数学期望：一般地，若离散型随机变量ξ的概率分布为 则称 Eξ＝x 1p 1＋x 2p 2＋…＋x n p n 为ξ的数学期望或平均数、均值，数学期望又简称为期望．是离散型随机变量．13．方差：D(ξ)=(x 1-Eξ)2·P 1+（x 2-Eξ)2·P 2 +．．．．．．+（x n -Eξ)2·P n 叫随机变量ξ的均方差，简称方差．14．正态分布：（1）定义：若概率密度曲线就是或近似地是函数 的图象，其中解析式中的实数0)μσσ>、（是参数，分别表示总体的平均数与标准差．则其分布叫正态分布(,)N μσ记作：，f( x )的图象称为正态曲线；（2）基本性质：∪曲线在x 轴的上方，与x 轴不相交；∪曲线关于直线x=对称，且在x=时位于最高点；∪当一定时，曲线的形状由确定．越大，曲线越“矮胖”；表示总体的分布越分散；越小，曲线越“瘦高”，表示总体的分布越集中；∪正态曲线下的总面积等于1．15．3原则：从上表看到，正态总体在 以外取值的概率只有4．6%，在 以外取值的概率只有0．3% 由于这些概率很小，通常称这些情况发生为小概率事件．也就是说，通常认为这些情况在一次试验中几乎是不可能发生的．),(,21)(222)(+∞-∞∈=--x e x f x σμσπμμμσσσσ)2,2(σμσμ+-)3,3(σμσμ+-17．回归分析。

高中数学《概率与统计》知识点总结一、统计1、抽样方法：①简单随机抽样（总体个数较少） ②系统抽样（总体个数较多） ③分层抽样（总体中差异明显）注意：在N 个个体的总体中抽取出n 个个体组成样本，每个个体被抽到的机会（概率）均为Nn 。

2、总体分布的估计： ⑴一表二图：①频率分布表——数据详实 ②频率分布直方图——分布直观③频率分布折线图——便于观察总体分布趋势 注：总体分布的密度曲线与横轴围成的面积为1。

⑵茎叶图：①茎叶图适用于数据较少的情况，从中便于看出数据的分布，以及中位数、众位数等。

②个位数为叶，十位数为茎，右侧数据按照从小到大书写，相同的数据重复写。

3、总体特征数的估计：⑴平均数：nx x x x x n++++= 321；取值为n x x x ,,,21 的频率分别为n p p p ,,,21 ，则其平均数为n n p x p x p x +++ 2211； 注意：频率分布表计算平均数要取组中值。

⑵方差与标准差：一组样本数据n x x x ,,,21 方差：212)(1∑=−=ni ix xns ；标准差：21)(1∑=−=ni ix xns注：方差与标准差越小，说明样本数据越稳定。

平均数反映数据总体水平；方差与标准差反映数据的稳定水平。

⑶线性回归方程①变量之间的两类关系：函数关系与相关关系； ②制作散点图，判断线性相关关系③线性回归方程：a bx y +=∧（最小二乘法）1221ni i i nii x y nx y b x nx a y bx==⎧−⎪⎪=⎪⎨−⎪⎪=−⎪⎩∑∑ 注意：线性回归直线经过定点),(y x 。

二、概率1、随机事件及其概率：⑴事件：试验的每一种可能的结果，用大写英文字母表示； ⑵必然事件、不可能事件、随机事件的特点； ⑶随机事件A 的概率：1)(0,)(≤≤=A P nmA P . 2、古典概型：⑴基本事件：一次试验中可能出现的每一个基本结果； ⑵古典概型的特点：①所有的基本事件只有有限个； ②每个基本事件都是等可能发生。

数学高考必备概率与统计知识点总结数学高考中，概率与统计是一个重要的考点，占据大约10%的考试比重。

掌握好概率与统计的知识点，对于考试取得好成绩至关重要。

本文将对数学高考中必备的概率与统计知识点进行总结，并提供实用的解题方法和技巧。

一、基本概念和概率计算1.1 随机事件和样本空间在概率理论中，随机事件是指实验过程的一个结果，而样本空间则是实验中可能出现的所有结果的集合。

在解题时，我们需要明确随机事件和样本空间的概念，将题目中的问题抽象成适合计算的形式。

1.2 概率的定义和性质了解概率的定义和性质对于解题至关重要。

掌握概率的加法原理、乘法原理、全概率公式和贝叶斯定理能够帮助我们解决复杂的概率计算问题。

1.3 随机变量和概率分布随机变量是指与随机事件相对应的可数的数值，概率分布则定义了随机变量的取值范围和其对应的概率。

掌握随机变量和概率分布的概念和计算方法，能够在解题过程中更好地理解和分析问题。

1.4 用排列组合解决概率问题排列组合是概率计算中常用的方法之一。

理解排列和组合的概念，掌握计算排列和组合的方法，可以帮助我们解决一定范围内的概率计算问题。

二、离散分布2.1 二项分布二项分布是一种重要的离散分布，在高考中经常出现。

掌握二项分布的概念、性质和计算方法，能够解决二项分布相关的问题。

2.2 泊松分布泊松分布是一种常见的离散分布，用于描述单位时间或单位空间内随机事件发生的次数。

了解泊松分布的特点和计算方法，能够解决与泊松分布相关的问题。

三、连续分布3.1 均匀分布均匀分布是一种常见的连续分布，描述了在一定范围内任意取值的概率相等的情况。

掌握均匀分布的概念和计算方法，能够解决与均匀分布相关的问题。

3.2 正态分布正态分布是一种重要的连续分布，具有对称性和钟形曲线的特点。

在高考中，许多问题都可以近似看作正态分布，因此掌握正态分布的概念和计算方法非常重要。

四、统计分析4.1 数据的收集和整理在统计分析中，数据的收集和整理是第一步。

专题18 概率、统计★★★高考在考什么【考题回放】1．甲：A 1、A 2是互斥事件；乙：A 1、A 2是对立事件，那么甲是乙的( B ) A ．甲是乙的充分但不必要条件 B ．甲是乙的必要但不充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件，也不是乙的必要条件 2．在正方体上任选3个顶点连成三角形，则所得的三角形是直角非等腰三角形的概率为（ C ） A ．17 B ．27 C ．37 D ．473．某班有50名学生，其中 15人选修A 课程，另外35人选修B 课程．从班级中任选两名学生,他们是选修不同课程的学生的慨率是73．(结果用分数表示) 4．一个均匀小正方体的六个面中，三个面上标以数0，两个面上标以数1,一个面上标以数2，将这个小正方体抛掷2次，则向上的数之积的数学期望是49． 5．某人5次上班途中所花的时间（单位：分钟）分别为x ，y ，10，11，9．已知这组数据的平均数为10，方差为2，则｜x －y ｜的值为 （ D ） （A ）1 （B ）2 （C ）3 （D ）4 6．某射手进行射击训练，假设每次射击击中目标的概率为53，且各次射击的结果互不影响。

（1）求射手在3次射击中，至少有两次连续击中目标的概率（用数字作答）； （2）求射手第3次击中目标时，恰好射击了4次的概率（用数字作答）； （3）设随机变量ξ表示射手第3次击中目标时已射击的次数，求ξ的分布列． 【专家解答】（Ⅰ）记“射手射击1次，击中目标”为事件A ，则在3次射击中至少有两次连续击中目标的概率1()()()P P A A A P A A A P A A A =⋅⋅+⋅⋅+⋅⋅33223333363555555555125=⨯⨯+⨯⨯+⨯⨯=（Ⅱ）射手第3次击中目标时，恰好射击了4次的概率2223323162()555625p C =⨯⨯⨯=（Ⅲ）由题设，“k ξ=”的概率为()P k ξ=233123()()55k k C --=⨯⨯（*k N ∈且3k ≥）所以，ξ的分布列为：★★★高考要考什么【考点透视】等可能性的事件的概率,互斥事件有一个发生的概率,相互独立事件同时发生的概率,独立重复试验、离散型随机变量的分布列、期望和方差．【热点透析】1．相互独立事件同时发生的概率,其关键是利用排列组合的内容求解m ，n ． 2．独立重复试验，其关键是明确概念，用好公式，注意正难则反的思想．3．离散型随机变量的分布列、期望和方差，注意ξ取值的完整性以及每一取值的 实际含义．★★★突破重难点【范例1】某批产品成箱包装，每箱5件．一用户在购进该批产品前先取出3箱，再从每箱中任意抽取2件产品进行检验．设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等品．（Ⅰ）用ξ表示抽检的6件产品中二等品的件数，求ξ的分布列及ξ的数学期望； （Ⅱ）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批产品级用户拒绝的概率．解(1)0,1,2,3ξ=22342255189P( 0)=10050C C C C ξ=∙==, 211123324422225555C 24P( 1 )=C 50C C C C C C C ξ=∙+∙=,11122324422222555515(2)50C C C C C P C C C C ξ==∙+∙=, 124222552(3)50C C P C C ξ==∙=所以ξ的分布列为ξ的数学期望E(ξ)=0123 1.250505050⨯+⨯+⨯+⨯=(2) P(2ξ≥)=15217(2)(3)505050P P ξξ=+==+=【点晴】本题以古典概率为背景，其关键是利用排列组合的方法求出m ，n ，主要考察分布列的求法以及利用分布列求期望和概率。

s 概率与统计知识点全归纳1.随机抽样(1)简单随机抽样：一般地，设一个总体含有N 个个体，从中逐个不放回地抽取n 个个体作为样本(n≤N)，如果每次抽取时总体内的各个个体被抽到的机会都相等，就把这种抽样方法叫做简单随机抽样．(2)分层抽样：一般地，在抽样时，将总体分成互不交叉的层，然后按照一定的比例，从各层独立地抽取一定数量的个体，将各层取出的个体合在一起作为样本，这种抽样方法是一种分层抽样．2.样本的频率分布估计总体分布(1)在频率分布直方图中，纵轴表示频率/组距，数据落在各小组内的频率用各小长方形的面积表示．各小长方形的面积总和等于1.(2)频率分布折线图和总体密度曲线①频率分布折线图：连接频率分布直方图中各小长方形上端的中点，就得频率分布折线图．②总体密度曲线：随着样本容量的增加，作图时所分的组数增加，组距减小，相应的频率折线图会越来越接近于一条光滑曲线，即总体密度曲线．(3)茎叶图茎是指中间的一列数，叶是从茎的旁边生长出来的数．3.用样本的数字特征估计总体的数字特征(1)众数：一组数据中出现次数最多的数．(2)中位数：将数据从小到大排列，若有奇数个数，则最中间的数是中位数；若有偶数个数，则中间两数的平均数是中位数．(3)平均数：xx1＋x2＋…＋x n＝，反映了一组数据的平均水平．n(4)标准差：是样本数据到平均数的一种平均距离，(5)方差：s2＝1[(x1－x )2＋(x2－x )2＋…＋(x n－x )2](x n是样本数据，n 是样本容量，x 是样本平均数)．n4.概率和频率(1)在相同的条件S 下重复n 次试验，观察某一事件A 是否出现，称n 次试验中事件A 出现的次数n A为事件A 出现的频数，称事件A 出现的比例f n(A)＝n A为事件A 出现的频率．n(2)对于给定的随机事件A，由于事件A 发生的频率f n(A)随着试验次数的增加稳定于概率P(A)，因此可以用频率f n(A)来估计概率P(A)．5.事件的关系与运算6. 概率的几个基本性质(1)概率的取值范围：0≤P (A )≤1. (2)必然事件的概率 P (E )＝1.(3)不可能事件的概率 P (F )＝0. (4)概率的加法公式：如果事件 A 与事件 B 互斥，则 P (A ∪B )＝P (A )＋P (B )． (5)对立事件的概率：若事件 A 与事件 B 互为对立事件，则 P (A )＝1－P (B )．7. 古典概型具有以下两个特点的概率模型称为古典概率模型，简称古典概型：高中数学资料共享群（734924357）(1) 试验中所有可能出现的基本事件只有有限个；(2)每个基本事件出现的可能性相等． 8．古典概型的概率公式 P (A )＝A 包含的基本事件的个数.基本事件的总数9. 相关关系与回归方程(1)相关关系的分类①正相关：在散点图中，点散布在从左下角到右上角的区域，对于两个变量的这种相关关系，我们将它称为正相关． ②负相关：在散点图中，点散布在从左上角到右下角的区域，两个变量的这种相关关系称为负相关．(2) 线性相关关系：如果散点图中点的分布从整体上看大致在一条直线附近，就称这两个变量之间具有线性相关关系，这条直线叫做回归直线．(3) 回归方程①最小二乘法：求回归直线，使得样本数据的点到它的距离的平方和最小的方法叫做最小二乘法．^ ^ ^②回归方程：方程y ＝bx ＋a 是两个具有线性相关关系的变量的一组数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )的回归方程，其n n⎧⎪ ^^中a ，b 是待定参数．⎪ ∑(x i - x )( y i - y ) ∑x i y i - nx y ⎪b ˆ = i =1 = i =1 , ⎨ (x - x )2 n x 2 - nx 2 ∑ i ⎪i =1 ∑ ii =1 ⎪⎩aˆ = y - b ˆx . (4) 回归分析①定义：对具有相关关系的两个变量进行统计分析的一种常用方法． ②样本点的中心对于一组具有线性相关关系的数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )，其中( x ， y )称为样本点的中心． ③相关系数当 r >0 时，表明两个变量正相关；当 r <0 时，表明两个变量负相关．高中数学资料共享群（734924357）r 的绝对值越接近于 1，表明两个变量的线性相关性越强．r 的绝对值越接近于 0，表明两个变量之间几乎不存在线性相关关系．通常|r |大于 0.75 时，认为两个变量有很强的线性相关性．10. 独立性检验(1) 分类变量：变量的不同“值”表示个体所属的不同类别，像这样的变量称为分类变量．(2) 列联表：列出的两个分类变量的频数表，称为列联表．假设有两个分类变量 X 和 Y ，它们的可能取值分别为{x 1，x 2}和{y 1，y 2}，其样本频数列联表(称为 2×2 列联表)为2×2 列联表构造一个随机变量 K 2＝ n (ad －bc )2(a ＋b )(c ＋d )(a ＋c )(b ＋d )，其中n ＝a ＋b ＋c ＋d 为样本容量．(3) 独立性检验利用随机变量 K 2 来判断“两个分类变量有关系”的方法称为独立性检验．11. 分类加法计数原理与分步乘法计数原理nn n n ＋1 n nn n12. 排列、组合的定义13. 排列数、组合数的定义、公式、性质14. 二项式定理15. 二项式系数的性质(1)C 0＝1，C n ＝1，C m＝C m －1＋C m . C m ＝C n －m(0≤m ≤n )．(2)二项式系数先增后减中间项最大．高中数学资料共享群（734924357）i=1 n nn ＋1 n ＋3当 n 为偶数时，第 ＋1 项的二项式系数最大，最大值为C 2 ，当 n 为奇数时，第 项和第 项的二项式系数最大，n -1最大值为Cn 22 n +1或C n2 .n 2 2(3)各二项式系数和：C 0＋C 1＋C 2＋…＋C n ＝2n ，C 0＋C 2＋C 4＋…＝C 1＋C 3＋C 5＋…＝2n －1.nnnnnnnnnn16. 离散型随机变量的分布列(1) 随着试验结果变化而变化的变量称为随机变量．所有取值可以一一列出的随机变量称为离散型随机变量． (2) 一般地，若离散型随机变量 X 可能取的不同值为 x 1，x 2，…，x i ，…，x n ，X 取每一个值 x i (i ＝1,2，…，n )的概率 P (X＝x i )＝p i ，则称表为离散型随机变量 X 的概率分布列，简称为 X 的分布列，具有如下性质： ①p i ≥0，i ＝1,2，…，n ；②p 1+p 2+…+p n =1.离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和．17. 两点分布如果随机变量 X 的分布列为其中 0<p <1，则称离散型随机变量 X 服从两点分布．其中 p ＝P (X ＝1)称为成功概率．高中数学资料共享群（734924357）18. 离散型随机变量的均值与方差一般地，若离散型随机变量 X 的分布列为(1) 均值称 E (X )＝x 1p 1＋x 2p 2＋…＋x i p i ＋…＋x n p n 为随机变量 X 的均值或数学期望．它反映了离散型随机变量取值的平均水平．(2) 方差称 D (X )＝Σn [xi －E (X )]2pi 为随机变量 X 的方差，它刻画了随机变量 X 与其均值 E (X )的平均偏离程度，并称其算术平方根 D (X )为随机变量 X 的标准差．19. 均值与方差的性质 (1) E (aX ＋b )＝aE (X )＋b .(2) D (aX ＋b )＝a 2D (X )．(a ，b 为常数)n μ σ 20. 超几何分布C k C n －k一般地，在含有 M 件次品的 N 件产品中，任取 n 件，其中恰有 x 件次品，则 P (X ＝k)＝ M N －M (k ＝0,1,2，…，m )，即 n N其中 m ＝min{M ，n }，且 n ≤N ，M ≤N ，n ，M ，N ∈N *.如果一个随机变量 X 的分布列具有上表的形式，则称随机变量 X 服从超几何分布．21. 条件概率及其性质(1) 对于任何两个事件 A 和 B ，在已知事件 A 发生的条件下，事件 B 发生的概率叫做条件概率，用符号 P (B |A )来表示，其公式为 P (B |A )＝P (AB )(P (A )>0)．P (A )在古典概型中，若用 n (A )表示事件 A 中基本事件的个数，则 P (B |A )＝n (AB ).n (A )(2) 条件概率具有的性质①0≤P (B |A )≤1；②如果 B 和 C 是两个互斥事件， 则 P (B ∪C |A )＝P (B |A )＋P (C |A )． 22．相互独立事件(1) 对于事件 A ，B ，若事件 A 的发生与事件 B 的发生互不影响，则称事件 A ，B 是相互独立事件． (2) 若 A 与 B 相互独立，则 P (B |A )＝P (B )．(3) 若 A 与 B 相互独立，则 A 与 B ， A 与 B ， A 与 B 也都相互独立． (4) P (AB )＝P (A )P (B )⇔A 与 B 相互独立． 23. 独立重复试验与二项分布(1) 独立重复试验是指在相同条件下可重复进行的，各次之间相互独立的一种试验，在这种试验中每一次试验只有两种结果，即要么发生，要么不发生，且任何一次试验中发生的概率都是一样的．(2) 在 n 次独立重复试验中，用 X 表示事件 A 发生的次数，设每次试验中事件 A 发生的概率为 p ，则 P (X ＝k )＝C k p k(1－p )n －k (k ＝0,1,2，…，n )，此时称随机变量 X 服从二项分布，记为 X ～B (n ，p )，并称 p 为成功概率．24. 两点分布与二项分布的均值、方差(1)若随机变量 X 服从两点分布，则 E (X )＝p ，D (X )＝p (1－p )． (2)若 X ～B (n ，p )，则 E (X )＝np ，D (X )＝np (1－p )．25. 正态分布(1) 正态曲线：函数φ(x )-( x -μ)22σ2，x ∈(－∞，＋∞)，其中实数μ和σ为参数(σ>0，μ∈R )．我们称函数φ ， (x )C μ，σ的图象为正态分布密度曲线，简称正态曲线．(2) 正态曲线的特点①曲线位于 x 轴上方，与 x 轴不相交； ②曲线是单峰的，它关于直线 x ＝μ对称； ③曲线在 x ＝μ④曲线与 x 轴之间的面积为 1；⑤当σ一定时，曲线的位置由μ确定，曲线随着μ的变化而沿 x 轴平移，如图甲所示；⑥当μ一定时，曲线的形状由σ确定，σ越小，曲线越“瘦高”，表示总体的分布越集中；σ越大，曲线越“矮胖”，表示总体的分布越分散，如图乙所示．(3) 正态总体在三个特殊区间内取值的概率值①P (μ－σ<X ≤μ＋σ)≈0.682 7； ②P(μ－2σ<X ≤μ＋2σ)≈0.954 5； ③P (μ－3σ<X ≤μ＋3σ)≈0.997 3.。

2024高考数学概率统计知识点总结与题型分析概率统计作为数学课程的一个重要分支，在高考中占有重要的一席之地。

它是一个与现实生活息息相关的学科，旨在通过收集、整理和分析数据，帮助我们做出正确的判断和决策。

本文对2024高考数学概率统计的知识点进行了总结，并对可能出现的题型进行了分析。

一、基本概念和公式1. 随机事件：指在一次试验中可能发生也可能不发生的事件。

2. 样本空间：指一个试验所有可能结果的集合。

3. 必然事件：指在一次试验中一定会发生的事件。

4. 不可能事件：指在一次试验中一定不会发生的事件。

5. 事件的概率：指随机事件发生的可能性大小。

6. 加法原理：对于两个互不相容的事件A和B，它们的和事件A∪B的概率等于各个事件的概率之和。

P(A∪B) = P(A) + P(B)7. 乘法原理：对于两个相互独立的事件A和B，它们的积事件A∩B的概率等于各个事件的概率之积。

P(A∩B) = P(A) × P(B)二、概率计算1. 事件的概率计算：对于离散型随机事件，概率可通过频率估计和计数原理计算。

对于连续型随机事件，概率可通过定积分计算。

2. 事件的互斥与独立：如果两个事件A和B互斥（即不能同时发生），则它们的和事件A∪B的概率等于各自事件的概率之和。

如果两个事件A和B相互独立（即一个事件的发生不受另一个事件发生与否的影响），则它们的积事件A∩B的概率等于各自事件的概率之积。

三、排列组合与概率计算1. 排列：排列是从n个不同元素中取出m个元素（m≤n），并有顺序地排成一列的方式。

排列的计算公式为：A(n,m) = n! / (n-m)!2. 组合：组合是从n个不同元素中取出m个元素（m≤n），不考虑顺序地组成一个集合的方式。

组合的计算公式为：C(n,m) = n! / [m! × (n-m)!]3. 概率计算中的排列组合：当事件A与某个事件B相关时，在计算A的概率时，需要考虑B 发生的不同排列组合情况。

高考数学第18题（概率与统计）1、求等可能性事件、互斥事件和相互独立事件的概率解此类题目常应用以下知识:(1)等可能性事件(古典概型)的概率：P(A)＝)()(I card A card ＝n m;等可能事件概率的计算步骤： 计算一次试验的基本事件总数n ;设所求事件A ，并计算事件A 包含的基本事件的个数m ; 依公式()mP A n =求值;答，即给问题一个明确的答复.(2)互斥事件有一个发生的概率：P(A ＋B)＝P(A)＋P(B); 特例：对立事件的概率：P(A)＋P(A )＝P(A ＋A )＝1. (3)相互独立事件同时发生的概率：P(A ·B)＝P(A)·P(B);特例：独立重复试验的概率：Pn(k)＝kn k k n p p C --)1(.其中P 为事件A 在一次试验中发生的概率，此式为二项式[(1-P)+P]n 展开的第k+1项.(4)解决概率问题要注意“四个步骤，一个结合”：求概率的步骤是：第一步，确定事件性质⎧⎪⎪⎨⎪⎪⎩等可能事件互斥事件 独立事件 n 次独立重复试验即所给的问题归结为四类事件中的某一种. 第二步，判断事件的运算⎧⎨⎩和事件积事件即是至少有一个发生，还是同时发生，分别运用相加或相乘事件.第三步，运用公式()()()()()()()()(1)kk n k n n m P A nP A B P A P B P A B P A P B P k C p p -⎧=⎪⎪⎪+=+⎨⎪⋅=⋅⎪=-⎪⎩等可能事件: 互斥事件： 独立事件： n 次独立重复试验:求解第四步，答，即给提出的问题有一个明确的答复.2.离散型随机变量的分布列1.随机变量及相关概念①随机试验的结果可以用一个变量来表示，这样的变量叫做随机变量，常用希腊字母ξ、η等表示. ②随机变量可能取的值，可以按一定次序一一列出，这样的随机变量叫做离散型随机变量. ③随机变量可以取某区间内的一切值，这样的随机变量叫做连续型随机变量. 2.离散型随机变量的分布列①离散型随机变量的分布列的概念和性质一般地，设离散型随机变量ξ可能取的值为1x ，2x ，……，ix ，……，ξ取每一个值ix （=i 1，2，……）的概率P （i x =ξ）=i P ，则称下表.ξ的概率分布，简称ξ的分布列.为随机变量由概率的性质可知，任一离散型随机变量的分布列都具有下述两个性质： （1）0≥i P ，=i 1，2，…;（2）++21P P …=1. ②常见的离散型随机变量的分布列： （1）二项分布n 次独立重复试验中，事件A 发生的次数ξ是一个随机变量，其所有可能的取值为0，1，2，…n ，并且kn k kn k q p C k P P -===)(ξ，其中n k ≤≤0，p q -=1，随机变量ξ的分布列如下：称这样随机变量ξ服从二项分布，记作),(~p n B ξ，其中n 、p 为参数，并记：),;(p n k b q p C kn k k n =- .（2） 几何分布在独立重复试验中，某事件第一次发生时所作的试验的次数ξ是一个取值为正整数的离散型随机变量，“k ξ=”表示在第k 次独立重复试验时事件第一次发生. 随机变量ξ的概率分布为：3.离散型随机变量的期望与方差随机变量的数学期望和方差(1)离散型随机变量的数学期望：++=2211p x p x E ξ…；期望反映随机变量取值的平均水平.⑵离散型随机变量的方差：+-+-=222121)()(p E x p E x D ξξξ…+-+n n p E x 2)(ξ…；方差反映随机变量取值的稳定与波动，集中与离散的程度.⑶基本性质：b aE b a E +=+ξξ)(；ξξD a b a D 2)(=+.(4)若ξ～B(n ，p)，则 np E =ξ ; D ξ =npq （这里q=1-p ） ; 如果随机变量ξ服从几何分布，),()(p k g k P ==ξ，则p E 1=ξ，D ξ =2p q 其中q=1-p.4.抽样方法与总体分布的估计 抽样方法1．简单随机抽样：设一个总体的个数为N ，如果通过逐个抽取的方法从中抽取一个样本，且每次抽取时各个个体被抽到的概率相等，就称这样的抽样为简单随机抽样.常用抽签法和随机数表法.2．系统抽样：当总体中的个数较多时，可将总体分成均衡的几个部分，然后按照预先定出的规则，从每一部分抽取1个个体，得到所需要的样本，这种抽样叫做系统抽样（也称为机械抽样）.3．分层抽样：当已知总体由差异明显的几部分组成时，常将总体分成几部分，然后按照各部分所占的比进行抽样，这种抽样叫做分层抽样. 总体分布的估计由于总体分布通常不易知道，我们往往用样本的频率分布去估计总体的分布，一般地，样本容量越大，这种估计就越精确.总体分布：总体取值的概率分布规律通常称为总体分布. 当总体中的个体取不同数值很少时，其频率分布表由所取样本的不同数值及相应的频率表示，几何表示就是相应的条形图.当总体中的个体取值在某个区间上时用频率分布直方图来表示相应样本的频率分布. 总体密度曲线：当样本容量无限增大，分组的组距无限缩小，那么频率分布直方图就会无限接近于一条光滑曲线，即总体密度曲线.5.正态分布与线性回归1.正态分布的概念及主要性质（1）正态分布的概念如果连续型随机变量ξ 的概率密度函数为222)(21)(σμπσ--=x ex f ，x R ∈ 其中σ、μ为常数，并且σ＞0，则称ξ服从正态分布，记为~N ξ（μ，2σ）.（2）期望E ξ =μ，方差2σξ=D .（3）正态分布的性质 正态曲线具有下列性质:①曲线在x 轴上方，并且关于直线x ＝μ对称.②曲线在x=μ时处于最高点，由这一点向左右两边延伸时，曲线逐渐降低.③曲线的对称轴位置由μ确定；曲线的形状由σ确定，σ越大，曲线越“矮胖”；反之越“高瘦”. 三σ原则即为数值分布在（μ—σ,μ+σ)中的概率为0.6526 数值分布在（μ—2σ,μ+2σ)中的概率为0.9544 数值分布在（μ—3σ,μ+3σ)中的概率为0.9974 （4）标准正态分布当μ=0，σ=1时ξ服从标准的正态分布，记作~N ξ（0，1） （5）两个重要的公式①()1()x x φφ-=-,② ()()()P a b b a ξφφ<<=-.（6）2(,)N μσ与(0,1)N 二者联系.若2~(,)N ξμσ，则~(0,1)N ξμησ-=;②若2~(,)N ξμσ，则()()()b a P a b μμξφφσσ--<<=-.6.线性回归1.简单的说，线性回归就是处理变量与变量之间的线性关系的一种数学方法.变量和变量之间的关系大致可分为两种类型：确定性的函数关系和不确定的函数关系.不确定性的两个变量之间往往仍有规律可循.回归分析就是处理变量之间的相关关系的一种数量统计方法.它可以提供变量之间相关关系的经验公式.具体说来，对n 个样本数据（11,x y ），（22,x y ），…，（,n n x y ），其回归直线方程: a x b yˆˆˆ+=,其中()()()∑∑∑∑====--=---=ni i ni ii ni i ni i ix n x yx n yx x x y y x xb1221121ˆx b y a ˆˆ-=,()y x ,称为样本中心点,因而回归直线过样本中心点. 当0>r 时,表明两变量正相关;当0<r ,表明两变量负相关. r 越接近1,表明两变量的线性相关性越强; r 越接近0,表明两变量的线性相关关系几乎不存在,通常当75.0>r 时,认为两个变量有很强的线性相关关系.7.独立性检验的概念一般地,假设有两个分类变量X 和Y ,它们的值域分别为{}21,x x 和{}21,y y ,其样本频数列联表我们利用随机变量()()()()()d b c a d c b a bc ad n K ++++-=22来确定在多大程度上可以认为“两个分类变量有关系”,这种方法称为两个分类变量的独立性检验. （二）独立性检验的基本思想独立性检验的基本思想类似于反证法.要确认“两个分类变量有关系”这一结论成立的可信程度,首先假设该结论不成立,即假设结论“两个分类变量没有关系”成立.在该假设下我们构造的随机变量2K 应该很小,如果由观测数据计算得到的2K 的观测值k 很大,则在一定程度上说明假设不合理.假设1H :“X 与Y 有关系”,可按如下步骤判断结论1H 成立的 可能性:…（x n ,y n ），则变量间线性相关系数r 的计算公式如下：2.相关系数r ：假设两个随机变量的取值分别是（x 1,y 1），（x 2,y 2），1.通过等高条形图,可以粗略地判断两个分类变量是否有关系,但是这种判断无法精确地给出所得结论的可靠程度.2.利用独立性检验来考查两个分类变量是否有关系,并且能较精确地给出这种判断的可靠程度,具体做法是: （1）根据实际问题的需要确定容许推断“两个分类变量有关系”犯错误概率的上界a ,然后通过下表确定临界值0k .（2）由公式()()()()()d b c a d c b a bc ad n K ++++-=22,计算2K 的观测值k .（3）如果0k k ≥,就推断“X 与Y 有关系”.这种推断犯错误的概率不超过a ;否则,就认为在犯错误的概率不超过a 的前提下不能推断“X 与Y 有关系”,或者在样本数据中没有足够证据支持结论“X 与Y 有关系”. 理解总结根据独立性检验的基本思想,可知对于2K 的观测值k ,存在一个正数0k 为判断规则的临界值,当0k k ≥,就认为“两个分类变量之间有关系”;否则就认为“两个分类变量没有关系”.在实际应用中,我们把0k k ≥解释为有()()%100102⨯≥-k K P 的把握认为“两个分类变量之间有关系”;把0k k <解释为不能以()()%100102⨯≥-k KP 的把握认为“两个分类变量之间有关系”,或者样本观测数据没有提供“两个分类变量之间有关系”的充分证据.。

高三概率与统计大题知识点概率与统计是高中数学中的一门重要课程，也是高考中的一大重点内容。

在高三学习概率与统计时，我们需重点掌握与大题相关的知识点，以下将详细介绍这些知识点。

一、基础概念1. 概率：指某个事件在试验中发生的可能性大小。

2. 随机试验：具有多种可能结果，每次试验结果不确定的试验。

3. 样本空间：随机试验的所有可能结果的集合。

4. 事件：样本空间的一个子集，表示我们所关心的某一结果或几个结果的集合。

5. 频率和概率的关系：频率越接近概率，随着试验次数的增加，频率会趋于概率。

二、计算概率1. 等可能概型：指随机试验的所有可能结果发生的概率是相等的。

2. 排列与组合：排列是指从不同元素中取出若干元素进行排列，组合是指从不同元素中取出若干元素进行组合。

3. 互斥事件与对立事件：互斥事件是指两个事件不能同时发生的事件，对立事件是指两个事件中一个发生另一个不发生的事件。

三、离散型随机变量与概率分布1. 随机变量：指试验结果的某个确定性的函数。

2. 离散型随机变量：指取值有限或可数的随机变量。

3. 概率分布：指离散型随机变量的所有可能取值及其对应的概率。

4. 期望：指离散型随机变量的所有可能取值与其对应概率的乘积的总和。

5. 方差：指随机变量的离散程度。

6. 二项分布：指n次独立试验中某一事件发生k次的概率分布。

四、连续型随机变量与概率密度函数1. 连续型随机变量：指取值为连续数值的随机变量。

2. 概率密度函数：指连续型随机变量某区间上的概率。

3. 期望与方差：连续型随机变量的期望和方差的计算方法。

五、统计1. 统计指标：平均数（算术平均数、加权平均数、几何平均数）、中位数、众数、方差、标准差等。

2. 抽样调查与总体：抽样调查是从总体中抽取一部分作为样本，通过样本来推断总体。

3. 假设检验：通过对样本进行统计推断，判断总体参数的假设是否成立。

4. 相关与回归分析：用于研究两个变量之间的相关性及其拟合程度。

高考数学统计概率知识点数学是高考中一个重要的科目，其中统计与概率是一个重要的知识点。

统计与概率涉及到数据的收集、整理、分析以及概率的计算和应用。

在这篇文章中，我们将深入探讨高考数学中的统计与概率知识点，并帮助同学们更好地理解和掌握这一部分内容。

1. 统计统计是指对收集到的数据进行整理、分析和解释的过程。

在高考数学中，统计主要涉及到以下几个方面的内容：1.1 数据收集数据收集是统计的第一步，它包括了数据的获取和整理。

数据可以通过调查问卷、实验和观察等方式进行收集。

在这个过程中，要注意数据的真实性和完整性，确保数据的可靠性。

1.2 数据的呈现数据的呈现是指将收集到的数据以图表或图像的形式展示出来，以便于更好地观察和分析。

常见的数据图表包括条形图、折线图、饼图等。

在绘制图表时，要注意选择适当的图表类型，确保数据的准确性和清晰度。

1.3 数据的分析数据的分析是统计的核心部分，它包括了对数据的计算、比较和解释等过程。

在进行数据分析时，可以运用各种统计指标和方法，如平均值、中位数、众数、方差等，以便更好地理解数据的特征和变化趋势。

2. 概率概率是用来描述随机事件发生可能性大小的数学工具。

在高考数学中，概率主要涉及到以下几个方面的内容：2.1 随机事件与样本空间随机事件是指无法预测结果的事件，它可以用来描述一个随机试验的可能结果。

样本空间是指一个随机试验的所有可能结果的集合。

在计算概率时，需要明确随机事件和样本空间的定义，并根据实际情况确定随机事件的个数和样本空间的大小。

2.2 概率的计算概率的计算是指通过对随机事件和样本空间的分析，来确定某个事件发生的可能性大小。

常见的概率计算方法有等可能原则、频率方法和古典概型法等。

在进行概率计算时，需要注意计算的正确性和合理性，并注意纳入所有可能影响结果的因素。

2.3 概率的应用概率的应用是指通过概率的计算，来解决实际问题。

在高考数学中，概率的应用包括了生日问题、排列组合、事件的独立性和条件概率等内容。

高考概率与统计知识点梳理概率与统计是数学中非常重要的一个分支，也是高考数学中的一个重点知识点。

理解概率与统计的原理和应用，对高考取得优异的成绩有着至关重要的作用。

本文将对高考中常见的概率与统计知识点进行梳理，帮助大家更好地掌握这一部分内容。

一、概率的基本概念和计算方法1.1 随机事件与样本空间概率论的研究对象是随机事件，而样本空间是指一个试验所有可能结果组成的集合。

随机事件是样本空间的子集，我们可以通过列举样本空间和随机事件来解决概率问题。

1.2 概率的定义和性质概率是指某个事件发生的可能性大小，可以通过事件发生的次数与总次数之比来计算。

概率具有非负性、规范性和可加性等基本性质，这些性质是进行概率计算的基础。

1.3 频率与概率的关系频率是指在大量重复试验中，某个事件发生的实际次数与试验总次数的比值。

频率和概率在大量试验时趋于相等，这是概率理论的基本思想之一。

1.4 基本计数原理基本计数原理指的是利用乘法原理和加法原理来解决复杂的计数问题。

乘法原理适用于多个进行相互独立的事件的计算，而加法原理适用于多个不相容事件的计算。

二、离散型随机变量及其分布律2.1 随机变量的概念与分类随机变量是指根据试验结果的不同而随机变化的变量。

离散型随机变量是指其可能取值个数有限或可数，而连续型随机变量则取值为整个数轴上的任意一点。

2.2 离散型随机变量的分布律离散型随机变量的分布律是指随机变量取各个可能值的概率，也称为概率分布或概率函数。

常见的离散型随机变量有二项分布、泊松分布和几何分布等。

2.3 期望与方差期望是指随机变量的平均取值，可以通过所有可能值的加权平均来求解。

方差是指随机变量与其期望之间的差异程度，反映了随机变量的离散程度。

三、连续型随机变量及其概率密度函数3.1 连续型随机变量的概念与特点连续型随机变量是指其可能取值为整个数轴上的任意一点，而不是一个个分立的值。

与离散型随机变量相比，连续型随机变量更适用于处理实际问题中的测量结果。

高中数学统计知识点高中数学概率与统计
高中数学统计知识点包括以下内容：
1. 数据的收集和整理：包括原始数据的收集和整理，如问卷调查、实验结果等。

2. 描述统计：用于对数据进行总结和描述的方法，包括平均数、中位数、众数、极差、标准差等。

3. 概率：研究随机事件发生的可能性的数学分支，包括基本概念、概率的计算方法和
性质。

4. 概率分布：描述随机变量取值与相应概率的分布，包括离散型随机变量和连续型随
机变量的分布。

5. 统计推断：从样本数据中推断总体的特征的方法，包括点估计和区间估计。

6. 假设检验：用于推断总体参数的假设检验方法，包括单样本检验、双样本检验和相
关性检验等。

7. 相关分析：研究两个或多个变量之间关系的方法，包括相关系数和回归分析等。

8. 抽样调查：从总体中随机选择样本进行调查和统计分析的方法，包括简单随机抽样、系统抽样和分层抽样等。

以上是高中数学概率与统计的主要知识点，通过掌握这些知识，可以进行数据的整理
和分析，并进行相关的统计推断和假设检验。

高考18概率统计知识点在高中的数学课程中，概率统计是一个重要的内容。

随着高考的临近，掌握概率统计的知识点对于考生而言尤为重要。

本文将详细介绍高考18概率统计知识点，帮助考生系统地复习和理解这一部分内容。

一、基本概率知识概率是描述随机事件发生可能性的一种数学概念，它与统计密切相关。

在概率统计中，我们首先需要了解基本概率知识。

这包括事件、样本空间和概率三个重要概念。

事件是我们观察或研究的对象，它可以是一个结果，也可以是一些结果的集合。

样本空间是指所有可能结果的集合，用S表示。

概率是对事件发生的可能性进行衡量的数值，用P(A)表示事件A发生的概率。

二、概率的计算方法在概率统计中，我们可以通过计数法或几何法来求解概率，具体的方法有排列组合、加法原理和乘法原理等。

排列是指从一组对象中，按照一定次序选择若干个对象的过程。

组合是指从一组对象中，不考虑次序地选择若干个对象的过程。

排列和组合在概率统计中起到了重要的作用，例如求事件的可能性数、样本空间的大小等。

加法原理和乘法原理是解决概率问题的基本法则。

加法原理适用于求解两个事件之和的概率，乘法原理适用于求解两个事件同时发生的概率。

考生要灵活运用这两个原理，结合具体问题进行计算。

三、事件独立性在概率统计中，事件的独立性是一个重要的概念。

当两个事件的发生与否相互独立时，它们的概率乘积等于两个事件分别发生的概率之积。

事件的独立性对于解决实际问题具有重要意义。

在高考中，有一些典型的例题涉及到事件的独立性，考生需要通过分析题意，判断事件之间是否独立，并利用乘法原理进行计算。

四、随机变量和概率分布随机变量是指在一次试验中可能的结果，它可以取多个不同的值。

在概率统计中，我们常用随机变量来描述实际问题，通过概率分布来表示随机变量的各个取值的可能性。

常见的概率分布包括离散型概率分布和连续型概率分布。

离散型概率分布适用于随机变量只能取有限个或可列个不同数值的情况。

连续型概率分布适用于随机变量可以取无限个甚至是连续的数值的情况。

高考概率与统计18大考点解析概率与统计试题是高考的必考内容。

它是以实际应用问题为载体，以排列组合和概率统计等知识为工具，以考查对五个概率事件的判断识别及其概率的计算和随机变量概率分布列性质及其应用为目标的中档师，预计这也是今后高考概率统计试题的考查特点和命题趋向。

下面对其常见题型和考点进行解析。

考点1 考查等可能事件概率计算在一次实验中可能出现的结果有n 个，而且所有结果出现的可能性都相等。

如果事件A 包含的结果有m 个，那么P （A ）=nm。

这就是等可能事件的判断方法及其概率的计算公式。

高考常借助不同背景的材料考查等可能事件概率的计算方法以及分析和解决实际问题的能力。

例1（2018天津）从4名男生和2名女生中任选3人参加演讲比赛. (I) 求所选3人都是男生的概率；(II)求所选3人中恰有1名女生的概率； (III)求所选3人中至少有1名女生的概率.考点2 考查互斥事件至少有一个发生与相互独立事件同时发生概率计算不可能同时发生的两个事件A 、B 叫做互斥事件，它们至少有一个发生的事件为A+B ，用概率的加法公式)()()(B P A P B A P +=+计算。

事件A （或B ）是否发生对事件B （或A ）发生的概率没有影响，则A 、B 叫做相互独立事件，它们同时发生的事件为B A ⋅。

用概率的乘法公式()()()B P A P B A P ⋅=⋅计算。

高考常结合考试竞赛、上网工作等问题对这两个事件的识别及其概率的综合计算能力进行考查。

例2.（2018全国卷Ⅲ）设甲、乙、丙三台机器是否需要照顾相互之间没有影响。

已知在某一小时内，甲、乙都需要照顾的概率为0.18，甲、丙都需要照顾的概率为0.1，乙、丙都需要照顾的概率为0.185，（Ⅰ）求甲、乙、丙每台机器在这个小时内需要照顾的概率分别是多少； （Ⅱ）计算这个小时内至少有一台需要照顾的概率.考点3 考查对立事件概率计算必有一个发生的两个互斥事件A 、B 叫做互为对立事件。

高考数学概率统计知识点（大全）高考数学概率统计知识点一、随机事件(1)事件的三种运算：并(和)、交(积)、差;注意差A—B可以表示成A与B 的逆的积。

(2)四种运算律：交换律、结合律、分配律、德莫根律。

(3)事件的五种关系：包含、相等、互斥(互不相容)、对立、相互独立。

二、概率定义(1)统计定义：频率稳定在一个数附近，这个数称为事件的概率;(2)古典定义：要求样本空间只有有限个基本事件，每个基本事件出现的可能性相等，则事件A所含基本事件个数与样本空间所含基本事件个数的比称为事件的古典概率;(3)几何概率：样本空间中的元素有无穷多个，每个元素出现的可能性相等，则可以将样本空间看成一个几何图形，事件A看成这个图形的子集，它的概率通过子集图形的大小与样本空间图形的大小的比来计算;(4)公理化定义：满足三条公理的任何从样本空间的子集集合到[0，1]的映射。

三、概率性质与公式(1)加法公式：P(A+B)=p(A)+P(B)—P(AB)，特别地，如果A与B互不相容，则P(A+B)=P(A)+P(B);(2)差：P(A—B)=P(A)—P(AB)，特别地，如果B包含于A，则P(A—B)=P(A)—P(B);(3)乘法公式：P(AB)=P(A)P(B|A)或P(AB)=P(A|B)P(B)，特别地，如果A与B相互独立，则P(AB)=P(A)P(B);(4)全概率公式：P(B)=∑P(Ai)P(B|Ai)。

它是由因求果，贝叶斯公式：P(Aj|B)=P(Aj)P(B|Aj)/∑P(Ai)P(B|Ai)。

它是由果索因;如果一个事件B可以在多种情形(原因)A1，A2，...，An下发生，则用全概率公式求B发生的概率;如果事件B已经发生，要求它是由Aj引起的概率，则用贝叶斯公式。

(5)二项概率公式：Pn(k)=C(n，k)p^k(1—p)^(n—k)，k=0，1，2，...，n。

当一个问题可以看成n重贝努力试验(三个条件：n次重复，每次只有A与A的逆可能发生，各次试验结果相互独立)时，要考虑二项概率公式。

高考概率与统计课本知识点在高中数学中，概率与统计是一门非常重要的学科，而且在考试中所占的分值也是相当大的。

因此，对于高考来说，掌握好概率与统计的知识点是非常关键的。

接下来，我们来回顾一下高考中常见的概率与统计知识点。

一、概率概率作为一种数学工具，用于描述事件发生的可能性。

在高考中，概率的考察主要包括以下几个方面：1.事件与样本空间在概率中，事件是指可以发生的一种结果，样本空间是指所有可能结果的集合。

在解决概率问题时，首先需要确定事件和样本空间。

2.概率的计算概率的计算主要有两种方法：古典概率和统计概率。

古典概率是指通过实验或理论上的分析，确定每个事件发生的可能性。

统计概率是通过统计数据计算得出，是一种依靠大量实验或观察得出的概率。

3.基本事件与复合事件基本事件是指只包含一个结果的事件，复合事件是由一个或多个基本事件组成的事件。

在计算概率时，可以通过对基本事件和复合事件的计算来得出最终的概率。

4.独立事件与互斥事件独立事件是指两个事件的发生没有相互影响，互斥事件是指两个事件不能同时发生。

在计算概率时，需要根据事件的独立性或互斥性来确定概率的计算方法。

二、统计统计是一门研究数据的收集、整理、分析和解释的学科。

在高考中，统计的考察主要包括以下几个方面：1.数据的收集和整理数据的收集是指通过实验、调查或观察等方法，获取相关的数据信息。

数据的整理是指对收集到的数据进行分类、汇总和整理，以便后续的统计分析。

2.频数与频率频数是指某个数值在数据中出现的次数，频率是指某个数值出现的频次与总次数之比。

在统计分析中，通过计算频数和频率可以对数据的分布情况进行描述和比较。

3.统计图表统计图表是用来直观地展示数据的分布情况和规律的工具。

常见的统计图表包括条形图、折线图、饼图等。

通过观察和分析统计图表，可以更好地理解和解释数据。

4.常用的统计指标在统计分析中，常用的统计指标包括平均数、中位数、众数、标准差等。

通过计算这些统计指标，可以对数据的集中趋势和离散程度进行衡量。