高三第一次质量检测数学试题(附答案)

重庆市高2025届高三第一次质量检测数学试题（答案在最后）2024.9一、单项选择题：本大题共8小题，每小题5分，共计40分.1.不等式()()2110x x +-≥的解集为（）A.1{|2x x ≤-或1}x ≥ B.1{|2x x ≤-或1}x >C.1|12x x ⎧⎫-≤≤⎨⎬⎩⎭D.1|12x x ⎧⎫-<<⎨⎬⎩⎭【答案】A 【解析】【分析】结合一元二次不等式的解法可求不等式的解集.【详解】()()2110x x +-≥的解为12x ≤-或1x ≥，故解集为：1{|2x x ≤-或1}x ≥，故选：A.2.集合{}1,1A a =+，{}0,,5B a a =-+，若A B A ⋂=，则a 为（）A.1B.1-C.4- D.1-或4-【答案】B 【解析】【分析】根据A B A = 可得A B ⊆，故求a 的值.【详解】因为A B A = ，故A B ⊆，故10a +=或1a a +=-，若1a =-，此时{}{}0,1,0,1,4A B ==，满足A B ⊆，若1a a +=-即12a =-，此时1191,,0,,222A B ⎧⎫⎧⎫==⎨⎬⎨⎬⎩⎭⎩⎭，不满足A B ⊆，故选：B.3.命题“()0,,e 20xx ax ∃∈+∞-<”的否定为（）A.(),0,e 20xx ax ∃∈-∞-≥ B.()0,,e 20xx ax ∀∈+∞-≥C.()0,,e 20x x ax ∃∈+∞-> D.()0,,e 20xx ax ∀∈+∞-<【答案】B【解析】【分析】由存在量词命题的否定形式可直接得出结论.【详解】易知命题“()0,,e 20xx ax ∃∈+∞-<”的否定为()0,,e 20xx ax ∀∈+∞-≥.故选：B4.随机变量()2,4N ξ ，13,2B η⎛⎫⎪⎝⎭，则（）A.()()D D ξη=B.()()E E ξη=C.()122P ξ≤=D.()112P η==【答案】C 【解析】【分析】根据二项分布和正态分布的期望和方差公式可判断AB 的正误，根据正态分布的对称性可判断C 的正误，根据二项分布的概率的公式可判断D 的正误.【详解】对于AB ，()()132,322E E ξη==⨯=，故()()E E ξη≠，()()1134,3224D D ξη==⨯⨯=，故()()D D ξη≠，故AB 错误；对于C ，根据正态分布的对称性可得()122P ξ≤=，故C 正确；对于D ，()131131C 248P η==⨯⨯=，故D 错误；故选：C.5.我们可以把365(11%)+看作每天的“进步”率都是1%，一年后是3651.01；而把365(11%)-看作每天的“落后”率都是1%，一年后是3650.99，则一年后“进步”的是“落后”的约（）（参考数据：lg0.990.004,lg1.010.004,lg832 2.92≈-≈≈）A.99倍B.101倍C.292倍D.832倍【答案】D 【解析】【分析】直接计算36536521.010.99lg 2.9≈，根据所给数值求解.【详解】()365365365365l 91.01 1.010.99 1.010.90.99g lg lg 365lg lg =-=-().101365lg lg 29929=-≈，故936536252.108321.010.99=≈.故选：D6.如图，无人机光影秀中，有8架无人机排列成如图所示，每架无人机均可以发出4种不同颜色的光，1至5号的无人机颜色必须相同，6、7号无人机颜色必须相同，8号无人机与其他无人机颜色均不相同，则这8架无人机同时发光时，一共可以有（）种灯光组合.A.48B.12C.18D.36【答案】D 【解析】【分析】对6、7号无人机颜色与1至5号的无人机颜色是否相同进行分类讨论，再由分类加法和分步乘法计数原理计算可得结果.【详解】根据题意可知，1至5号的无人机颜色有4种选择；当6、7号无人机颜色与1至5号的无人机颜色相同时，8号无人机颜色有3种选择；当6、7号无人机颜色与1至5号的无人机颜色不同时，6、7号无人机颜色有3种选择，8号无人机颜色有2种选择；再由分类加法和分步乘法计数原理计算可得共有()4133236⨯⨯+⨯=种.故选：D7.定义在R 上的偶函数()f x 满足()()11f x f x +=-，且当[]0,1x ∈时，()1e xf x =-，若关于x 的方程()()()10f x m x m =+<恰有5个实数解，则实数m 的取值范围为（）A.()0,e 1- B.1e 1e ,56--⎛⎫⎪⎝⎭C.e 1e 1,86--⎛⎫⎪⎝⎭ D.1e 1e ,46--⎛⎫⎪⎝⎭【答案】D 【解析】【分析】根据题意，推得函数()f x 图象关于直线1x =对称，且函数的周期为2，再由题设函数解析式作出函数的图象，再将方程的解的个数转化为两函数的图象交点问题即可解得.【详解】由1+=1−可知函数()f x 的图象关于直线1x =对称，且o2+p =o −p ，因()f x 是偶函数，则()()f x f x -=，故有(2)()f x f x +=，即函数()f x 的周期为2.又当[]0,1x ∈时，()1e xf x =-，故可作出函数()f x 的图象如图.由关于x 的方程()()()10f x m x m =+<恰有5个实数解，可理解为()y f x =与(1)y m x =+恰有5个交点.而这些直线恒过定点(1,0)P -,考虑直线与()f x 相交的两个临界位置(3,1e),(5,1e)A B --,由图知，需使PA PB k m k <<，即1e 1e46m --<<.故选：D .【点睛】思路点睛：本题主要考查函数对称性和周期性的应用以及函数与方程的转化思想，属于难题.解题思路在于通过对抽象等式和奇偶性的理解，推理得到函数对称性和周期性，从而作出函数的简图，接着利用方程的解的个数与两函数的交点个数的对应关系解题.8.已知定义在R 上的函数()()2e x axf x x a -+=∈R ，设()f x 的极大值和极小值分别为,m n ，则mn 的取值范围是（）A.e ,2⎛⎤-∞- ⎥⎝⎦ B.1,2e ⎛⎤-∞-⎥⎝⎦C.e ,02⎡⎫-⎪⎢⎣⎭D.1,02e ⎡⎫-⎪⎢⎣⎭【答案】B 【解析】【分析】求出函数的导数，利用导数求出,m n ，结合韦达定理用a 表示mn ，再求出指数函数的值域得解.【详解】()()()22222e e 21e -+-+-+''=+-++=-+xaxx ax x ax f x x ax x x ax ，令()221g x x ax =-++，显然函数()g x 的图象开口向下，且()01g =，则函数()g x 有两个异号零点12,x x ，不妨设120x x <<，有12121,22+==-a x x x x ，而2e 0xax-+>恒成立，则当1x x <或2x x >时，()0f x '<，当12x x x <<时，()0f x '>，因此函数()f x 在()1,x -∞，()2,x +∞上单调递减，在()12,x x 上单调递增，又当0x <时，()0f x <恒成立，当0x >时，()0f x >恒成立，且()00f =，于是()f x 的最大值()22222e -+==x ax m f x x ，最小值()21111e -+==x ax n f x x ，于是()()()222221212121121241212e12e e--+++-++++===-a x x ax axx x a x x x x mn x x x x ，由a ∈R ，得[)211,4a-∈-+∞，2141e ,e -⎡⎫∈+∞⎪⎢⎣⎭a ，则2141e,212e -⎛⎤∈-∞- ⎥⎝-⎦a ，所以mn 的取值范围是1,2e ⎛⎤-∞- ⎥⎝⎦.故选：B.【点睛】方法点睛：导函数中常用的两种常用的转化方法：一是利用导数研究含参函数的单调性，常化为不等式恒成立问题．注意分类讨论与数形结合思想的应用；二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理．二、多项选择题：本大题共3小题，每小题6分，共计18分.9.若2024220240122024(23)x a a x a x a x -=++++ ，则下列选项正确的有（）A.202402a =B.01220241a a a a +++= C.2024202432024122320241222222a a a a ⎛⎫++++=- ⎪⎝⎭D.1232023202423202320246072a a a a a +++++= 【答案】ACD 【解析】【分析】利用赋值判断AC ，去绝对值后，赋值判断B ，两边求导后，再赋值，判断D.【详解】A.令0x =，得202402a =，故A 正确；B.01220240122024......a a a a a a a a ++++=-+-+，令令展开式中的1x =-，得20240122024 (5)a a a a -+-+=，故B 错误；C.令展开式中的12x =，得2024320241202320241...22222a a a aa ⎛⎫+++++= ⎪⎝⎭，所以2024202432024122320241...222222a a a a⎛⎫++++=- ⎪⎝⎭，故C 正确；D.展开式的两边求导，得()20232202220231232023202432024232320232024x a a x a x a x a x -⨯-=++++，令1x =，得1232023202423...202320246072a a a a a +++++=，故D 正确.故选：ACD10.下列选项正确的有（）A.当()02x ∈，时，函数222y x x -=+的最小值为1B.()1x ∈-∞，，函数31y x x =+-的最大值为-C.函数2y =的最小值为2D.当0a >，0b >时，若2a b ab +=，则2+a b 的最小值为32+【答案】AD 【解析】【分析】利用二次函数的定义域，求函数的最小值，判断A ，根据基本不等式判断BC ，根据“1”的妙用与变形，结合基本不等式，即可判断D.【详解】A.()222211y x x x =-+=-+，()02x ∈，，当1x =时，函数去掉最小值1，故A 正确；B.33111111y x x x x =+=-++≤-=---，当311x x -=-，1x <，得1x =31y x x =+-的最大值为1-，故B 错误；C .22y ==2t =≥，则1y t t =+在区间[)2,+∞单调递增，当2t =时，1y t t =+取得最小值52，所以函数2y =的最小值为52，故C 错误；D.若2a b ab +=，则112a b+=，则()11131231322222222b a a b a b a b a b ⎛⎫⎛⎫+=++=++≥⨯+ ⎪ ⎪⎝⎭⎝⎭当2b aa b=时，即12a +=，24b =时，等号成立，所以2+a b 的最小值为32+，故D 正确.故选：AD11.已知函数()f x 及其导函数()f x '的定义域均为，且满足()()60f x f x +-=，2222233f x f x ''⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭，()31f '=-，()()231g x f x =--，则下列说法中正确的有（）A.函数()f x '的周期为4B.函数()g x '的图象关于点()1,1-对称C.()y f x x =-的图象关于直线=2对称D.数列(){}g n '的前2024项之和为4048-【答案】ACD 【解析】【分析】根据题设条件可得()()60f x f x ''--=、()()42f x f x ''+-=，故可求函数′的周期为4，故可判断A 的正误，利用反证法可判断B 的正误，根据()()42f x f x ''+-=可得()()424f x f x x --=-，故可判断C 的正误，计算出()()()()12348g g g g ''''+++=-后可判断D 的正误.【详解】因为()()60f x f x +-=，所以()()60f x f x ''--=，而2222233f x f x ''⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭，故()()42f x f x ''+-=，故()()462f x f x ''-+-=即()()22f x f x '+'+=，故()()242f x f x ''+++=，故()()4f x f x +'='，故函数′的周期为4，故A 正确；又()()23g x f x ''=--，而()()122g f =-''，而()()222f f ''+=即()21f '=，故()12g '=-，若()g x '关于()1,1-对称，则()11g '=-，矛盾，故B 错误.因为()()42f x f x ''+-=，故()()42f x f x x c --=+，故()()224f f c ''-=+即4c =-，故()()4(4)f x x f x x -=---故()y f x x =-的图象关于直线=2对称，故C 正确.因为′的周期为4，故()g x '的周期也是4，而()()22f x f x '+'+=，故()()022f f ''+=，故()()()()1322204g g f f '''-'+=-=-，因为()31f '=-，故()()0232g f ''=-=，故()42g '=，又()()132f f ''+=，故()13f '=，故()()2216g f ''=-=-，故()()()()12348g g g g ''''+++=-，故数列(){}g n '的前2024项和为()2024840484⨯-=-，故D 正确；故选：ACD.【点睛】思路点睛：根据抽象函数的单调性我们可得到该函数的周期性及导函数的周期性、对称性等，性质讨论的方法是变换的思想.三、填空题：本大题共3小题，每小题5分，共15分.12.已知π1sin 33α⎛⎫+= ⎪⎝⎭，则2πsin 3α⎛⎫-= ⎪⎝⎭_____【答案】13【解析】【分析】根据已知结合诱导公式计算求解即可.【详解】2πππ1sin sin παsin 3333αα⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.故答案为：13.13.若221919C C mm -=，则33345C C C m +++ 的值为______【答案】69【解析】【分析】根据组合数的性质及参数范围得出参数m ，再计算组合数即可.【详解】因为221919C C mm -=，所以22m m =-或2219m m +-=，解得2m =或7m =,因为33345C C C m +++ ，所以3m ≥,可得7m =,所以3333333454567C C C =C C C C 410203569m ++++++=+++= .故答案为：69.14.函数2e 12()e 21x x xh x -=++，不等式()22(2)2h ax h ax -+≤对R x ∀∈恒成立，则实数a 的取值范围是_____【答案】[]2,0-【解析】【分析】由解析式得出()()2h x h x +-=，令()()1f x h x =-，得()f x 为奇函数，再利用导数得出()f x 的单调性，根据奇偶性与单调性求解不等式即可．【详解】因为2e 122()e e e 2121x x xx x xh x --=+=-+++，所以22222()()e e e e 221212121x x x x xx x x x h x h x ---⋅+-=+-++-==++++，令()()1f x h x =-，则()()0f x f x +-=，可得()f x 为奇函数，又因为()()222ln 41ln 4()e e e e e 121e 21222x x x x x xx x x x xf x --'⎛⎫''=+-=+-=+ ⎪+⎝⎭+++，1e 2e x x +≥，当且仅当1e e xx =，即0x =时等号成立；ln 4ln 4ln 2142222xx ≤=++，当且仅当122xx =，即0x =时等号成立；所以()0f x '>，可得()f x 在R 上为增函数，因为()2222(2)2(2)(2)0(2)(2)h ax h ax f ax f ax f ax f ax -+≤⇔-+≤⇔-≤-，所以2220ax ax +-≤在R 上恒成立，当0a =时，显然成立；当0a ≠，需满足2Δ480a a a <⎧⎨=+≤⎩，解得20a -≤<，综上，[]2,0a ∈-，故答案为：[]2,0-．【点睛】关键点点睛：由函数解析式得出()()2h x h x +-=，构造()()1f x h x =-是解题关键．四、解答题：本大题共5小题，共77分.15.已知函数()eln f x x x=+（1）求=op 在()()1,1f 处的切线方程；（2）求=在1,3e⎛⎫ ⎪⎝⎭的最小值.【答案】（1）()1e 2e 1y x =-+-（2）2【解析】【分析】（1）根据导数的几何意义求切线方程；（2）根据导数与函数单调性的关系，判断函数的单调性，再求函数的最小值.【小问1详解】()eln f x x x=+，()1e f ∴=，且()21ef x x x'=-，()11e f '∴=-，切线方程为：()()e 1e 1y x -=--，即()1e 2e 1y x =-+-；【小问2详解】()221e e x f x x x x-'=-=，当1,e e x ⎛⎫∈⎪⎝⎭，()0f x '<，()y f x =在1,e e ⎛⎫⎪⎝⎭上单调递减，当()e,3x ∈，()0f x '>，()y f x =在()e,3上单调递增，()f x \在区间1,3e⎛⎫ ⎪⎝⎭的最小值为()2f =e .16.我国承诺2030年前“碳达峰”，2060年“碳中和”，“碳达峰”是指二氧化碳的排放不再增长，达到峰值之后再慢慢减下去；“碳中和”是指针对排放的二氧化碳要采取植树、节能减排等各种方式全部抵消掉.做好垃圾分类和回收工作可以有效地减少处理废物造成的二氧化碳的排放，助力“碳中和”.重庆十一中某班利用班会课时间组织了垃圾分类知识竞赛活动，竞赛分为初赛、复赛和决赛，只有通过初赛和复赛，才能进入决赛.首先出战的是第一组、第二组、第三组，已知第一组、第二组通过初赛和复赛获胜的概率均为23，第三组通过初赛和复赛的概率分别为p 和43p -，其中304p <≤，三组是否通过初赛和复赛互不影响.（1）求p 取何值时，第三组进入决赛的概率最大；（2）在（1）的条件下，求进入决赛的队伍数X 的分布列和数学期望.【答案】（1）49（2）分布列见解析，43【解析】【分析】（1）根据二次函数的性质可求当23p =时，第三组进入决赛概率最大为49.（2）根据二项分布可求X 的分布列和数学期望.【小问1详解】由题知：第三组通过初赛和复赛的概率2204424()3339p p p p p p ⎛⎫=-=-+=--+ ⎪⎝⎭，又因为3044013p p ⎧<≤⎪⎪⎨⎪≤-≤⎪⎩，所以1334p ≤≤所以，当23p =时，第三组进入决赛概率最大为49.【小问2详解】由（1）知：第一组、第二组、第三组进入决赛的概率均为224339⨯=.因为进入决赛的队伍数43,9X B ⎛⎫~ ⎪⎝⎭，所以()03341250C (19729P X ==⨯-=；()123443001001C (199729243P X ==⨯⨯-==；()22344240802C ()199729243P X ⎛⎫==⨯⨯-== ⎪⎝⎭；()3334643C (9729P X ==⨯=.所以随机变量X 的分布列为:X123P1257291002438024364729()1251008064401237292432437293E X =⨯+⨯+⨯+⨯=.17.四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是正方形，2PA AB ==，点E 是棱PC 上一点.（1）求证：平面PAC ⊥平面BDE ；（2）当E 为PC 中点时，求平面ABE 与平面DBE 所成锐二面角的大小.【答案】（1）证明见解析（2）π3【解析】【分析】（1）根据线面垂直性质以及正方形性质，利用面面垂直判定定理即可得出证明；（2）建立空间直角坐标系，分别求得两平面法向量即可求得结果.【小问1详解】底面ABCD 是正方形，BD AC ∴⊥，PA ⊥ 平面ABCD ，BD ⊂平面ABCD ，PA BD ∴⊥，又BD AC ⊥，PA AC A = ，PA ，AC ⊂平面PAC ，BD ∴⊥平面PAC ，又BD ⊂平面BDE ，∴平面PAC ⊥平面BDE .【小问2详解】PA ⊥ 平面ABCD ，A ，AD ⊂平面ABCD ，所以PA AB ⊥，PA AD ⊥，以A 为坐标原点，A ，A ，AP 所在直线分别为x ，y ，z建立空间直角坐标系,如下图所示：则0,0,0，()2,0,0B ，()0,2,0D ，()2,2,0C ，()0,0,2P ，()1,1,1E ，()()()2,0,0,1,1,1,2,2,0AB BE BD ==-=-，设平面ABE 的法向量为()111,,n x y z =，则1111200n AB x n BE x y z ⎧⋅==⎪⎨⋅=-++=⎪⎩ ，解得10x =，令11y =，得11z =-，故平面ABE 的一个法向量为 =0,1,−1，设平面DBE 的法向量为()222,,m x y z =，则222222200m BD x y m BE x y z ⎧⋅=-+=⎪⎨⋅=-++=⎪⎩ ,解得20z =，令21x =，得21y =，故平面DBE 的一个法向量为()1,1,0m =，设平面ABE 与平面DBE 所成锐二面角为θ，则1cos 2m nm nθ⋅=== ，所以平面ABE 与平面DBE 所成锐二面角的大小为π3.18.椭圆2222:1(0)x y C a b a b +=>>过点23,22⎫-⎪⎝⎭且()0b c c =>.（1）求椭圆C 的标准方程；（2）设C 的左、右焦点分别为1F ，2F ，过点2F 作直线l 与椭圆C 交于,A B 两点，1112AF BF ⋅= ，求1ABF 的面积.【答案】（1）2212x y +=（2）3.【解析】【分析】（1）代入点23,22⎛- ⎝⎭坐标并于b c =联立计算可得222,1a b ==，求出椭圆C 的标准方程；（2）联立直线和椭圆方程并利用向量数量积的坐标表示以及韦达定理即可得出2m =±，再由弦长公式计算可得结果.【小问1详解】将,22⎛- ⎝⎭代入椭圆方程可得2213241a b +=，即2213124a b +=，又因为b c =，所以222a b =，代入上式可得222,1a b ==，故椭圆C 的标准方程为2212x y +=；【小问2详解】由(1)可得()()12121,0,1,0,2F F F F -=，设直线l 的方程为()()11221,,,,x my A x y B x y =+，如下图所示：联立22112x my x y =+⎧⎪⎨+=⎪⎩，得()222210m y my ++-=，所以12122221,22m y y y y m m +=-=-++，则()()1111221,,1,AF x y BF x y =---=---，所以()()1111221212121,1,1AF BF x y x y x x x x y y ⋅=------=++++()()()2221212122222221211142222m m m m y y my my y y m m m m =+++++++=----++++227122m m -==+，解得24m =，即2m =±，所以121221,36y y y y +=±=-，则1ABF 的面积()212121212110423S F F y y y y y y =-=+-=.19.给定两个正整数m ，n ，函数()f x 在=0处的[],m n 阶帕德近似定义为：()0111mm n n a a x a x R x b x b x+++=+++ ，且满足：()()00f R =，()()00f R '='，()()()()()()0000m n m n f R f R ++'='''= .已知()()ln 1f x x =+在=0处的[]1,1阶帕德近似()1a bx R x cx+=+注：()()'''[]f x f x ='，()()'''[]f x f x ''='，()()()4'[]f x f x '''=，()()()()54'[]f x f x =，…（1）求a ，b ，c 的值；（2）比较()11x c f x ⎛⎫+⎪⎝⎭与的大小，并说明理由；（3）求不等式1211(1)e (1)x x x x++<<+的解集，其中e 2.71828=【答案】（1）102a b a c ===，，；（2）()11x c f x ⎛⎫+> ⎪⎝⎭，理由见解析；（3）()0,∞+.【解析】【分析】（1）根据新定义先求导函数，再代入求参即可；（2）先化简换元令11t x+=，再求导函数根据正负得出函数单调性即可证明；（3）结合（2）结论应用单调性解不等式【小问1详解】因为()()()ln 11a bxf x x R x cx+=+=+，，()()()()()''''2232111(1)(1)(1)b ac c b ac f x R x f x R x x cx x cx ---==='-++'=++，，，()()00f R =，则()()000a f R '=='，，则1b ac =-，则1b =，()()()''''100122f R b ac c c =-=--=，，，所以1012a b c ===，，.【小问2详解】()111ln 12x c f x x x ⎛⎫⎛⎫⎛⎫+=++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，令11t x+=，则()()()()11ln 0,11,21t x c f t t x t ∞+⎛⎫+=∈⋃+⎪-⎝⎭，，令()()()()21ln 0,11,1t h t t t t ∞-=-∈⋃++，，ℎ'(p =1−4(r1)2=(K1)2or1)2>0，所以()h t 在()0,1单调递增，在()1,∞+单调递增，()()()0,1,10t h t h ∈<=，即()21ln 1t t t -<+，所以r12(K1)ln >1，∈(1,+∞),ℎ(p >ℎ(1)=0,ln >2(K1)r1，所以r12(K1)ln >1，综上，()11x c f x ⎛⎫+>⎪⎝⎭.【小问3详解】若要使12111e 1xx x x +⎛⎫⎛⎫+<<+ ⎪ ⎪⎝⎭⎝⎭成立，则110x+>，即1x <-或>0，当121e 1xx +⎛⎫<+ ⎪⎝⎭时，即ln 1+r 12>1,ln 1+>1，由（2）知上式成立，所以()(),10,x ∞∞∈--⋃+，当11e xx ⎛⎫+< ⎪⎝⎭等价于1ln 11x x ⎛⎫+< ⎪⎝⎭，当>0时，1ln 11x x ⎛⎫+< ⎪⎝⎭等价于11ln 111x x⎛⎫+<+- ⎪⎝⎭，成立;当1x <-时，1ln 11x x ⎛⎫+< ⎪⎝⎭等价于ln 1>1+1−1，不成立，所以解集为()0,∞+.。

2024—2025学年度上学期普通高中高三第一次联合教学质量检测高三数学试卷解析版满分150分，考试用时120分钟注意事项：1. 答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码贴在答题卡上的指定位置.2. 选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.3. 非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.4. 考试结束后，请将本试卷和答题卡一并上交.一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题所给的四个选项中，只有一项是符合题目要求的）1．若集合{}260M xx x =+−=∣，{}20,N x ax a =+=∈R ∣，且N M ⊆，则a 的取值不可以是（ ）．A ．2B ．23C ．0D ．1−【答案】A【详解】依题意，{3,2}M −，由N M ⊆，得N =∅或{3}N −或{2}N =， 当N =∅时，0a =；当{3}N −时，23a =；当{2}N =时，1a =−， 因此a 的取值不可以是2. 故选：A.2．已知向量()cos ,sin a θθ= ，()2,1b =−，若a b ⊥，则sin cos sin 3cos θθθθ++的值为（ ）A ．13B ．35C ．45D ．23【答案】B【详解】由题设2cos sin 0tan 2θθθ−=⇒=， 而sin cos tan 1213sin 3cos tan 3235θθθθθθ+++===+++.故选：B3．已知等差数列{}n a 和{}n b 的前n 项和分别为n S 、n T ，若342n n S n T n +=+，则62102a b b +（ ） A ．11113B ．3713C ．11126D ．3726【答案】B【详解】因为等差数列{}n a 和{}n b 的前n 项和分别为n S 、n T，满足342n n S n T n +=+， 所以111131143711213S T ×+==+，又11161116111111()211()2a a a Sb b T b +==+，故666210662322371a a a b b b b ===+， 故选：B4．甲、乙、丙、丁、戊共5名同学进行数学建模比赛，决出了第1名到第5名的名次(无并列情况).甲、乙、丙去询问成绩.老师对甲说：“你不是最差的.”对乙说：“很遗憾，你和甲都没有得到冠军.”对丙说：“你不是第2名.”从这三个回答分析，5名同学可能的名次排列情况种数为（ ） A ．44 B ．46 C ．48 D ．54【答案】B【详解】解法一：多重限制的排列问题：甲、乙都不是第一名且甲不是最后一名，且丙不是第二名，即甲的限制最多，故以甲为优先元素分类计数，甲的排位有可能是第二、三、四3种情况：①甲排第二位，乙排第三、四、五位，包含丙的余下3人有33A 种排法，则有3313A 18××=； ②甲排第三、四位，乙排第二位，包含丙的余下3人有33A 种排法，则有3321A 12××=； ③甲排第三、四位，乙不排第一、二位，即有2种排法，丙不排第二位，有2种排法，余下2人有22A 种排法，则有22222A 16×××=； 综上，该5名同学可能的名次排情况种数为18121646++=种. 解法二：间接法：甲不排首尾，有三种情况，再排乙，也有3种情况，包含丙的余下3人有33A 种排法，共有3333A 3332154××=××××=种不同的情况；但如果丙是第二名，则甲有可能是第三、四名2种情况；再排乙，也有2种情况；余下2人有22A 种排法，故共有2222A 22218××=×××=种不同的情况；从而该5名同学可能的名次排情况种数为54846−=种. 故选：B.5．已知直线1:0l x y C ++=与直线2:0l Ax By C ++=均过点()1,1，则原点到直线2l 距离的最大值为（ ） AB ．1 CD ．12【答案】A【详解】因为两直线交于()1,1，则110C ++=，即2C =−， 且0A B C ++=，则2A B +=；由原点到直线2l的距离d=，易知2222(1)11A A A −+=−+≥，则d ≤ 当且仅当1A =时，d 1B =. 即两直线重合时，原点到直线2l 的距离最大. 故选：A.6．已知双曲线22:13x C y −=的右焦点为F ，过点F 的直线交C 于,A B 两点，若3FA FB ⋅= ，则直线AB 的斜率为（ ）ABC ．D ．【答案】D【详解】易知()2,0F ，当直线AB的斜率为零时，得((221FA FB ⋅=×= ，不合题意；当直线AB 的斜率不为零时，设直线AB 的方程为2x my =+， 联立222,1,3x my x y =+ −=得()223410m y my −++=， 设()()1122,,,A x y B x y ，由3FA FB ⋅=得()()()21212122213x x y y m y y −−+=+=， 而12213y y m =−，即22133m m +=−，解得m=k = 故选：D7．已知函数()331f x x x =++，若关于x 的方程()()sin cos 2f x f m x ++=有实数解，则m 的取值范围为（ ）A ． −B ．[]1,1−C ．[]0,1D ．【答案】D【详解】令()()313g x f x x x −+，则()2330g x x ′=+>恒成立，则()g x 在R 上单调递增，且()g x 是奇函数.由()()sin cos 2f x f m x ++=，得()()sin 1cos 1f x f m x −=−+− ，即()()sin cos g x g m x =−−，从而sin cos x m x =−−，即πsin cos 4m x x x=−−+∈ 故选：D【点睛】方法点睛：设()()313g x f x x x −+，可得函数()g x 为奇函数，利用导函数分析函数()g x 的单调性，把()()sin cos 2f x f m x ++=转化成sin cos m x x =−−，再求m 的取值范围. 8．如图，在三棱锥A BCD −中，45ABC ∠=°，点P 在平面BCD 内，过P 作PQ AB ⊥于Q ，当PQ 与面BCD PQ 与平面ABC 所成角的余弦值是（ ）A B C D 【答案】A【详解】过点Q 作AB 的垂面QEF ，交平面ABC 于直线EF ，即,,AB QE AB QF AB EF ⊥⊥⊥， 再过AB 作平面BCD 的垂面ABM ，即平面ABM ⊥平面BCD ， 过O 作QG BM ⊥，垂足为G ，如图所示，设BM EF P = ，则此点即为PQ 与平面BCD 所成角最大时，对应的P 点， 理由如下：因为PQ AB ⊥恒成立，所以P ∈平面QEF ，又因为P ∈平面BCD ，平面QEF 平面BCD EF =，所以P EF ∈，过点Q 作QG BM ⊥，因为平面ABM ⊥平面BCD ，平面ABM ∩平面BCD BM =， 且QG ⊂平面ABM ，所以QG ⊥平面BCD ，所以PQ 与平面BCD 所成角即为QPB ∠，所以sin QGQPB PQ ∠=，因为QG 为定值，所以当PQ 最小时，sin QPB ∠最大，即QPB ∠最大， 又因为EF ⊂平面BCD ，所以QG EF ⊥，因为,AB EF AB QG Q ⊥=，,AB QG ⊂平面ABM ，所以⊥EF 平面ABM ， 则当P 为BM 与EF 交点时，EF PQ ⊥，此时PQ 取得最小值， 所以，当BM EF P = 时，PQ 与平面BCD 所成角最大，即为QPB ∠，所以sin QPB ∠P 作PH QE ⊥，垂足为H ，连接BH ，因为AB ⊥平面QEF ，AB ⊂平面ABC ，所以平面ABC ⊥平面QEF ， 又因为QEF 平面ABC QE =，PH ⊂平面QEF ，所以PH ⊥平面ABC ， 所以EQP ∠即为PQ 与平面ABC 所成角，在直角QPE △中，cos PQEQP QE∠=，因为45ABC ∠= ，且AB QE ⊥，所以BQE △为等腰直角三角形，所以QB QE =， 又因为tan PQQBP OB∠=，所以tan cos QBP EQP ∠=∠，因为sin QPB ∠tan QPB ∠因为π2QBP QPB ∠+∠=，所以1tan tan QBP QPB ∠==∠. 故选：A.二、多项选择题（本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对得6分，部分选对的得部分分，有选错的得0分）9．设1z ，2z 为复数，且120z z ≠，则下列结论正确的是（ ）A ．1212z z z z =B ．1212z z z z +=+C ．若12=z z ，则2212z z = D ．1212z z z z ⋅=⋅【答案】ABD【详解】设1i z a b =+，2i z c d =+(,,,)a b c d ∈R ，对于选项A ，因为12(i)(i)()()i z z a b c d ac bd ad bc =++=−++，所以12z z，所以1212z z z z =，故A 正确；对于选项B ，因为12()()i z z a c b d +=+++，1i z a b =−，2i z c d =−， 则12()()z z a c b d i +=+−+，12()()i z z a c b d +=+−+， 所以1212z z z z +=+，故B 正确；对于选项C ，若12=z z ，例如11i z =+，21i z =−但221(1i)2i z =+=，222(1i)2i z =−=−，即2212z z ≠，故C 错误；对于选项D ，因为21(i)(i)()()i z a b c d ac bd c z ad b ⋅=++=−++，所以21()()i z ac bd a b z d c ⋅−−+2(i)(i)()()i z a b c d ac bd ad bc =−−=−−+， 所以1212z z z z ⋅=⋅，故D 正确. 故选：ABD.10．已知2n >，且*n ∈N ，下列关于二项分布与超几何分布的说法中，错误的有（ ）A ．若1(,)3X B n ，则()22113E X n ++ B ．若1(,)3X B n ，则()4219D X n +=C ．若1(,)3X B n ，则()()11P X P X n ===−D ．当样本总数远大于抽取数目时，可以用二项分布近似估计超几何分布 【答案】BC【详解】对于A ，由1(,)3X B n ，得()13E X n =，则()22113E X n ++，A 正确； 对于B ，由1(,)3X B n ，得()122339D X n n =×=，则()()82149D X D X n +==，B 错误；对于C ，由1(,)3X B n ，得11111221(1)C (),(1)C ()3333n n n n n P X P X n −−−==××=−=××，故(1)(1)P X P X n =≠=−，C 错误； 对于D ，当样本总数远大于抽取数目时，可以用二项分布近似估计超几何分布，D 正确. 故选：BC11．“曼哈顿距离”是十九世纪的赫尔曼·闵可夫斯省所创词汇，用以标明两个点在标准坐标系上的绝对轴距总和，其定义如下：在直角坐标平面上任意两点()()1122,,,A x y B x y 的曼哈顿距离()1212,d A B x x y y =−+−，则下列结论正确的是（ ）A ．若点()()1,3,2,4P Q ，则(),2d P Q =B ．若对于三点,,A BC ，则“()()(),,,d A B d A C d B C +=”当且仅当“点A 在线段BC 上” C ．若点M 在圆224x y +=上，点P 在直线280x y −+=上，则(),d P M 的最小值是8−D ．若点M 在圆224x y +=上，点P 在直线280x y −+=上，则(),d P M 的最小值是4 【答案】AD【详解】对于A 选项：由定义可知(),21432d P Q =−+−=，故A 选项正确； 对于B 选项：设点AA (xx 1,yy 1)，BB (xx 2()33,C x y则()()121313,,d A B d A C x x y x y y +=−+−+−，()2323,d B C x x y y =−+−显然，当点A 在线段BC 上时，121323x x x x x x −+−=−，121323y y y y y y −+−=−，∴()()(),,,d A B d A C d B C +=成立，如图：过点B 作BE y ⊥轴，过点C 作EE x ⊥轴，且相交于点E ，过点A 作AD BE ⊥与D ，过点A 作AF CE ⊥与F ，由图可知121213132323x x y y x x y y BD AD AF CF BE CE x x y y −+−+−+−=+++=+=−+−显然此时点A不在线段BC 上，故B 选项不正确； 对于CD 选项：∵当0,0a b >>a b ≥+≥ ∴想要(),d P M 最小，点M 到直线距离最小时取得，∴过原点O 作OM ⊥直线280x y −+=交圆于M ， 如图：设(),M a b ，则2OM bk a==−∴M设点PP (xx 0,yy 0)，则(0,d P M x =又∵当0ab =，a b +≥①当00x +=时，由00442x y =+=()0,4d P M x =+①当00y =时，由00288x y =−=()0,8d P M x =+−又∵48<−∴(),d P M的最小值为：4.故C 选项错误，D 选项正确. 故选：AD三、填空题（本大题共3小题，每小题5分，共15分）12．已知12,34a b a b ≤−≤≤+≤则93a b +的取值范围为 ．【答案】[]21,30【详解】假设()()93a b a b a b λµ+=−++，则93λµλµ+=−+=，解得36λµ= = ， 因为12a b ≤−≤，所以()336a b ≤−≤； 又因为34a b ≤+≤，所以()18624a b ≤+≤；由上两同向不等式相加得：()()213630a b a b ≤−++≤， 整理得：219330a b ≤+≤ 故答案为：[]21,3013．已知函数()cos 2sin 2sin f x x x x ωωω=−（0ω>）在()0,2π上有最小值没有最大值，则ω的取值范围是 .【答案】11,63【详解】()()()cos 22sin 2sin cos 2cos3f x x x x x x x x ωωωωωωω=−−=+=， 当()0,2πx ∈时，()30,6πx ωω∈，若()f x 在()0,2π上有最小值没有最大值， 则π6π2πω<≤，所以1163ω<≤. 故答案为：11,6314．函数2e 12()e 21x x xh x −=++，不等式()22(2)2h ax h ax −+≤对R x ∀∈恒成立，则实数a 的取值范围是 【答案】[]2,0−【详解】因为2e 122()e ee 2121x x xx x x h x −−=+=−+++， 所以22222()()e e e e 221212121x x x x xxx x x h x h x −−−⋅+−=+−++−=+=++++， 令()()1f x h x =−，则()()0f x f x +−=，可得()f x 为奇函数， 又因为()()222ln 41ln 4()e e e e e 121e 21222x x x x xx x x x x xf x −−′ ′′=+−=+−=+− + +++， 1e 2e x x +≥，当且仅当1e ex x =，即0x =时等号成立；ln 4ln 4ln 2142222x x ≤=++，当且仅当122xx=，即0x =时等号成立；所以()0f x ′>，可得()f x 在R 上为增函数，因为()2222(2)2(2)(2)0(2)(2)h ax h ax f ax f ax f ax f ax −+≤⇔−+≤⇔−≤−，所以2220ax ax +−≤在R 上恒成立， 当0a =时，显然成立；当0a ≠，需满足2Δ480a a a < +≤，解得20a −≤<， 综上，[]2,0a ∈−， 故答案为：[]2,0−．四、解答题（本大题共5小题，共77分.解答应写出必要的文字说明、证明过程或演算步骤）15.（本小题13分）在锐角ABC 中，a ，b ，c 分别为内角A 、B ，C 的对边，且()2sin 2sin a A b c B =−+()2sin c b C −. (1)求A 的大小；(2)求cos 2cos B C +的取值范围. 【答案】(1)π3A =(2) 【详解】（1）由题及正弦定理得：22(2)(2)a b c b c b c =−+−，即222bc b c a =+−，则2221cos 22b c a Abc +−==，∵π0,2A ∈，∴π3A =； （2）由ABC 为锐角三角形知，π022ππ032C C<<<−<，故ππ62C <<，则π3πcos 2cos cos 2cos cos 323B C C C C C C+=−++=+， 有ππ5π236C <+<π3C<+<故cos cos B C +的取值范围为. 16.（本小题15分）已知数列{}n a ，{}n b ，(1)2n n n a =−+，1(0)n n n b a a λλ+=−>，且{}n b 为等比数列. (1)求λ的值； (2)记数列{}2n b n ⋅的前n 项和为nT .若()*2115N i i i T T T i ++⋅=∈，求i 的值.【答案】(1)2 (2)2【详解】（1）因为(1)2n n n a =−+，则11a =，25a =，37a =，417a =. 又1n n n b a a λ+=−，则1215b a a λλ=−=−，23275b a a λλ=−=−，343177b a a λλ=−=−. 因为{bb nn }为等比数列，则2213b b b =⋅，所以2(75)(5)(177)λλλ−=−−， 整理得220λλ−−=，解得1λ=−或2.因为0λ>，故2λ=.当2λ=时，1112(1)22(1)2n n n nn n n b a a +++ =−=−+−−+11(1)(1)22(1)23(1)n n n n n ++=−×−+−×−−=−×−.则113(1)13(1)n n nn b b ++−×−==−−×−，故{bb nn }为等比数列，所以2λ=符合题意. （2）223(1)nn b n n ⋅=−×−⋅，当n 为偶数时，222222223123456(1)n T n n =−×−+−+−+−−−+33(12)(1)2n n n =−×+++=−+ ；当n 为奇数时，221133(1)(1)(2)3(1)(1)22n n n T T b n n n n n n ++=−+=−++++=+. 综上，3(1),21,N 23(1),2,N 2n n n n k k T n n n k k ∗∗ +=−∈ =−+=∈ ， 因为20i i T T +⋅>，又2115i i i T T T ++⋅=， 故10i T +>，所以i 为偶数.所以333(1)(2)(3)15(1)(2)222i i i i i i−+⋅−++=×++ ， 整理得23100i i +−=，解得2i =或5i =−（舍），所以2i =. 17.（本小题15分）如图，棱长为2的正方体1111ABCD A B C D −中，E F ､分别是棱,AB AD 的中点，G 为棱1DD 上的动点.(1)是否存在一点G ，使得1BC ∥面EFG ？若存在，指出点G 位置，并证明你的结论，若不存在，说明理由；(2)若直线EF 与平面CFG ，求三棱锥1G EBC −的体积； (3)求三棱锥1B ACG −的外接球半径的最小值. 【答案】(1)存在点G 为1DD 的中点，证明见解析 (2)13； (3)4−【详解】（1）存在一点G ，当点G 为1DD 的中点，使得1BC ∥面EFG ， 连接1AD ，如图所示：点,F G 分别是1,AD DD 的中点，FG ∴∥1AD ，又AB ∥11D C ，且11AB D C =，∴四边形11ABC D 是平行四边形，1∴AD ∥1,BC FG ∴∥1BC ，又1BC ⊄ 平面EFG ，且FG ⊂平面1,EFG BC ∴∥平面EFG .（2）以D 点为坐标原点，分别以1,,DA DC DD 所在直线为,,x y z 轴，建立空间直角坐标系，如图所示，连接11,,AC AB B C ，则()()()()()112,0,0,2,2,2,0,2,0,2,2,0,0,0,2,(2,1,0),(1,0,0)A B C B D E F ， 设()0,0,G t (02)t ≤≤，(0,2,),(1,2,0)CG t CF =−=− ，(1,1,0)EF =−−，设平面CFG 的一个法向量是(,,)n x y z =，则2020n CG y tz n CF x y ⋅=−+=⋅=−= ，取1y =得2(2,1,)n t = ，因为直线EF 与平面CFG，所以cos ,n EF n EFn EF⋅==1t =（负值舍去）， G 为1DD 中点，取1CC 中点H ，则////GH CD AB ，因此GH 在平面GEB 内，且GEB HEB S S = ，所以1111111112113323G EBC C GEB C HEB E BHC BHC V V V V S EB −−−−====⋅=××××= ； （3）11(0,2,2),(2,2,0),(2,2,2),AB AC BD ==−=−−因为111440,440,AB BD AC BD ⋅=−+=⋅=−=所以111,AB BD AC BD ⊥⊥即111,AB BD AC BD ⊥⊥因为1AB ⊂平面1,AB C AC ⊂平面1AB C ，1AB AC A = ，所以1BD ⊥平面1AB C ，又因为1ABCB B B ==，所以1BD 与平面1ACB 的交点是1ACB 的外心，所以三棱锥1B ACG −的外接球的球心在1BD 上， 设外接球球心为1O ，设()[]112,2,2,0,1BO BD λλλλλ==−−∈，则1O 的坐标为()22,22,2λλλ−−，设()[]()0,0,0,2G m m ∈， 则11O G O A =所以2484m mλ+=+，设[]848,16m t +=∈，则84t m −=， 则22841664648411616t t t t t t tλ−+ −++ +−，而811116t t +−≥=，当且仅当816t t =，即t =[]8,16t ∈，所以11,2λ ∈ ，三棱锥1B ACG −的外接球的半径1r O A ====，因为11,2λ ∈−，所以218124833λ −+∈−，所以r ∈− ， 三棱锥1B ACG −的外接球半径的最小值为4. 18.（本小题17分）已知椭圆C ：()222210x y a b a b+=>>经过点(M −，其右焦点为FF (cc ,0)，下顶点为B ，直线BF 与椭圆C交于另一点D ，且3BF FD =．(1)求椭圆C 的方程；(2)O 为坐标原点，过点M 作x 轴的垂线1l ，垂足为A ，过点A 的直线与C 交于P ，Q 两点，直线OP 与1l 交于点H ．直线OQ 与1l 交于点G ，设APH 的面积为1S ，AQG 的面积为2S ，试探究1212S S S S +是否存在最小值．若存在，求出此时直线PQ 的方程；若不存在，请说明理由．【答案】(1)22184x y +=(2))2y x + 【详解】（1）设()00,D x y ，由(),0F c ，()0,B b −，得(),BF c b = ，()00,FDx c y =−，由3BF FD = ，得()()00,3,c b x c y =−，043x c =，013y b =， 所以2222161991c b a b +=，得2212c a =，所以222212b ac a =−=，将(M −代入椭圆C 的方程得22421a b+=，即22441a a +=，则28a =，所以22142b a ==，故椭圆的方程为22184x y +=.（2）由题意可知()2,0A −，直线PQ 的斜率存在且不为0，设直线PQ 的方程为()2y k x =+，()11,P x y ，()22,Q x y ， 则()221842x y y k x += =+，得()2222128880k x k x k +++−=， 因为点A 在椭圆内，则直线PQ 与椭圆必有两交点，则2122812k x x k +=−+，21228812k x x k −+=+， ()121224412k y y k x x k +=++=+，()()()2221212121224222412k y y k x x k x x x x k =++=+++=− +， 又OP 的方程为11y y x x =，与直线2x =−联立可得1122,y H x−−， 又OQ OP 的方程为22y y x x =，与直线2x =−联立可得2222,y G x−−， 所以111111121222y y S x x x x =×−×+=×+，22222222122y y S x x x x =×−×+=×则()()121212221212112212221122y k y k S S x x S S S S y x y x y y −−+=+=+=+++， 当21k ≥时，()()21212220y k y k k x x −−=≥， 所以()222121212121212122222222212121212121212122222222y y y k y k S S y k y k y y y y y y k k S S y y y y y y y y y y y y y y +−− +−−+++=+=−=−=−−， 又12121y y y y k +=−，22121124k y y k +=−， 所以()222212122221212122111242222y y y y k k k k y y y y y y k k k k ++++ −−=−−−+=−， 所以121222S S k S S k+=+≥22k =时取等号，当201k <<时，()()21212220y k y k k x x −−=<， 所以221212121212222222121212121222222y k y k S S y k y k y y y y k S S y y y y y y y y −− +−−−−=+=−=−， 又知()1212k y y y y −+=， 则1212121236S S y yS S y y +−====>， 综上可知，当22k =时，1212SS S S +存在最小值此时直线PQ 的方程为)2y x +.19.（本小题17分）设()h x ′为()h x 的导函数，若()h x ′在区间D 上单调递减，则称()h x 为D 上的“凸函数”．已知函数()2sin f x x ax ax =−++．(1)若()f x 为π0,2上的“凸函数”，求a 的取值范围；(2)证明：当1a =−时，()()()213ln 22g x f x x x x =++++++有且仅有两个零点． 【答案】(1)1,2−∞−(2)证明见解析【详解】（1）由()2sin f x x ax ax =−++，则()cos 2f x x ax a ′=−++. 由题意可知，()f x 为π0,2上的“凸函数”，则ff ′(xx )在区间π0,2上单调递减，设()()x f x ϕ′=，则()sin 2x x a ϕ′=+，所以sin 20x a +≤在π0,2恒成立， 则2sin a x ≤−在π0,2恒成立，又当π2x =时，函数sin y x =−取最小值，且最小值为1−， 所以有21a ≤−，解得12a ≤−，即a 的取值范围为1,2−∞−.（2）当1a =−时，由2(1)sin(1)(1)(1)f x x x x +=−+−+−+得 22()sin(1)(21)(1)3ln(2)2g x x x x x x x x =−+−++−++++++sin(1)ln(2)x x =−+++. 令()(1)sin ln(1),1H x g x x x x =−=−++>−，其中(0)0H =， 则1()cos 1H x x x ′=−++，其中(0)0H ′=. ①当10x −<<时，则011x <+<，11cos 1x x >≥+， 所以1()cos 01H x x x ′=−+>+，则()H x 在(1,0)−单调递增， 则()(0)0H x H <=恒成立，即()H x 在(1,0)−无零点； ②当π02x <<时，令1()()cos 1G x H x x x ′==−++，其中(0)0G =， 由21()sin (1)G x x x ′=−+在π0,2单调递增， 又ππ(0)10,sin 22G G=−=′′，故存在0π0,2x∈，使得0()0G x ′=，故当00x x <<时，()0G x ′<，()G x 在()00,x 单调递减； 当0π2x x <<时，()0G x ′>，()G x 在0π,2x单调递增； 由ππ11(0)0,cos 0ππ221122G G==−+=>++， 故存在1π0,2x∈ ，使1()0G x =，即1()0H x ′=，故当10x x <<时，()0H x ′<，()H x 在()10,x 单调递减； 当1π2x x <<时，()0H x ′>，()H x 在1π,2x单调递增； 又πππ(0)0,sin ln 11ln e 0222H H==−++<−+=，故当π0,2x ∈ 时，()0H x <，即()H x 在π0,2无零点；③当π22x ≤<时，由1cos 0,01x x −≥>+，则()0H x ′>， 故故()H x 在π,22单调递增，πππsin ln 10222H=−++<，且(2)sin 2ln 3110H =−+>−+=，故由零点存在性定理可知()H x 在π,22有且仅有一个零点；④当2x ≥时，()sin ln(1)1ln 30H x x x =−++≥−+>， 故()H x 在[)2,+∞无零点；综上所述，()H x 有且仅有两个零点，其中(0)0H =，而另一个零点在π,22内.由()(1)H x g x =−，即将()H x 图象向左移1个单位可得()g x 的图象. 故()g x 也有两个零点，一个零点为1−，另一个零点在π1,12 −内.故()()()213ln 22g x f x x x x =++++++有且仅有两个零点，命题得证.。

厦门市2024届高中毕业班第一次质量检测数学试题2024．1准考证号__________姓名__________（在此卷上答题无效）本试卷共4页，22小题，满分150分，考试用时120分钟．注意事项：1．答卷前，考生务必将自己的学校，班级和姓名填在答题卡上，正确粘贴条形码．2．作答选择题时，用2B 铅笔在答题卡上将对应答案的选项涂黑．3．非选择题的答案必须写在答题卡各题目的指定区域内相应位置上，不准使用铅笔和涂改液．4．考试结束后，考生上交答题卡．一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知i 1z z ⋅=+（i 为虚数单位），则||z =（） A.12B.22C.1D.2.设集合{}22M x x =-≤≤，{}21xN y y ==+，则M N ⋃=（）A.[2,)-+∞ B.(1,2]C.[1,2]D.(1,)+∞3.已知直线l 与曲线3y x x =-在原点处相切，则l 的倾斜角为（）A.π6B.π4 C.3π4 D.5π64.已知a ，b 为单位向量，若||||a b a b +=- ，则a b + 与a b - 的夹角为（）A.π3B.π2C.2π3D.3π45.已知()f x 为定义在R 上的奇函数，当0x <时，2()21f x x x =-+，则(2)(0)f f +=（）A.2B.1C.8- D.9-6.已知1a x x=+，e e x x b -=+，sin c x x =，则下列结论错误的为（）A.[1,1]x ∃∈-，a c> B.[1,1]x ∃∈-，b c>C.[1,1]x ∃∈-，a c <D.[1,1]x ∃∈-，b c<7.传说古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，他们根据沙粒或小石子所排列的形状把数分成许多类，如图所示的1，5，12，22被称为五边形数，将所有的五边形数从小到大依次排列，则其第8个数为（）151222A.51B.70C.92D.1178.已知函数()f x 的定义域为R ，x ∀，y ∈R ，(1)(1)()()f x f y f x y f x y ++=+--，若(0)0f ≠，则(2024)f =（）A.2- B.4- C.2D.4二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9.已知函数π()2sin 23f x x ⎛⎫=- ⎪⎝⎭，则（）A.()f x 的最小正周期为π2B.()f x 的图象关于点2π,03⎛⎫⎪⎝⎭成中心对称C.()f x 在区间π0,3⎡⎤⎢⎣⎦上单调递增D.若()f x 的图象关于直线0x x =对称，则01sin 22x =10.已知甲、乙两组数据分别为：20，21，22，23，24，25和a ，23，24，25，26，27，若乙组数据的平均数比甲组数据的平均数大3，则（）A.甲组数据的第70百分位数为23B.甲、乙两组数据的极差相同C.乙组数据的中位数为24.5D.甲、乙两组数据的方差相同11.设椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F ，2F ，过1F 的直线与C 交于A ，B 两点，若122F F =，且2ABF △的周长为8，则（）A.2a = B.C 的离心率为14C.||AB 可以为πD.2BAF ∠可以为直角12.如图所示，在五面体ABCDEF 中，四边形ABCD 是矩形，ABF △和DCE △均是等边三角形，且AB =(0)EF x x =>，则（）A.//EF 平面ABCDB.二面角A EF B --随着x 的减小而减小C.当2BC =时，五面体ABCDEF 的体积(x)V 最大值为272D.当32BC =时，存在x 使得半径为32的球能内含于五面体ABCDEF 三、填空题：本大题共4小题，每小题5分，共20分．13.若π3sin 45α⎛⎫+=- ⎪⎝⎭，则πcos 4α⎛⎫-= ⎪⎝⎭_________．14.《九章算术》、《数书九章》、《周髀算经》是中国古代数学著作，甲、乙、丙三名同学计划每人从中选择一种来阅读，若三人选择的书不全相同，则不同的选法有_________种．15.已知平面α的一个法向量为(1,0,1)n = ，且点(1,2,3)A 在α内，则点(1,1,1)B 到α的距离为_________．16.设ABC 是面积为1的等腰直角三角形，D 是斜边AB 的中点，点P 在ABC 所在的平面内，记PCD与PAB 的面积分别为1S ，2S ，且121S S -=．当||PB =||||PA PB >时，||PA =_________；记PA PB a -=，则实数a 的取值范围为_________．四、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17.已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且2cos cos 2a B ab A c +=．（1）求a ；（2）若2π3A =，且ABC 的周长为2+，求ABC 的面积．18.如图，在四棱锥E ABCD -中，//AD BC ，22AD BC ==，AB =，AB AD ⊥，EA ⊥平面ABCD ，过点B 作平面BD α⊥．（1）证明：平面//α平面EAC ；（2）已知点F 为棱EC 的中点，若2EA =，求直线AD 与平面FBD 所成角的正弦值．19.已知数列{}n a 的前n 项和为n S ，2124a a ==，当*n ∈N ，且2n ≥时，1132n n n S S S +-=-．（1）证明：{}n a 为等比数列；（2）设()()111n n n n a b a a +=--，记数列{}n b 的前n 项和为n T ，若21172m m T -+>⨯，求正整数m 的最小值．20.已知甲、乙两支登山队均有n 名队员，现有新增的4名登山爱好者a b c d ,,,将依次通过摸出小球的颜色来决定其加入哪支登山队，规则如下：在一个不透明的箱中放有红球和黑球各2个，小球除颜色不同之外，其余完全相同先由第一名新增登山爱好者从箱中不放回地摸出1个小球，再另取完全相同的红球和黑球各1个放入箱中；接着由下一名新增登山爱好者摸出1个小球后，再放入完全相同的红球和黑球各1个，如此重复，直至所有新增登山爱好者均摸球和放球完毕．新增登山爱好者若摸出红球，则被分至甲队，否则被分至乙队．（1）求,,a b c 三人均被分至同一队的概率；（2）记甲，乙两队的最终人数分别为1n ，2n ，设随机变量12X n n =-，求()E X ．21.已知函数1()ln 1x f x a x x -=-+有两个极值点1x ，2x ．（1）求实数a 的取值范围；（2）证明：()()2121221f x f x a a x x a -->--．22.在平面直角坐标系xOy 中，点(1,0)P ，点A 为动点，以线段AP 为直径的圆与y 轴相切，记A 的轨迹为Γ，直线AP 交Γ于另一点B ．（1）求Γ的方程；（2）OAB 的外接圆交Γ于点C （不与O ，A ，B 重合），依次连接O ，A ，C ，B 构成凸四边形OACB ，记其面积为S ．（i ）证明：ABC 的重心在定直线上；（ii ）求S 的取值范围．厦门市2024届高中毕业班第一次质量检测数学试题2024．1准考证号__________姓名__________（在此卷上答题无效）本试卷共4页，22小题，满分150分，考试用时120分钟．注意事项：1．答卷前，考生务必将自己的学校，班级和姓名填在答题卡上，正确粘贴条形码．2．作答选择题时，用2B 铅笔在答题卡上将对应答案的选项涂黑．3．非选择题的答案必须写在答题卡各题目的指定区域内相应位置上，不准使用铅笔和涂改液．4．考试结束后，考生上交答题卡．一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知i 1z z ⋅=+（i 为虚数单位），则||z =（） A.12B.22C.1D.【答案】B 【解析】【分析】先求出复数z ，再求||z .【详解】由i 1z z ⋅=+，得()i 11z -=，即()()()i 1111i i 1i 1i 122z --===------，所以||2z ==，故选：B2.设集合{}22M x x =-≤≤，{}21xN y y ==+，则M N ⋃=（）A.[2,)-+∞B.(1,2]C.[1,2]D.(1,)+∞【答案】A 【解析】【分析】由指数函数值域求集合N ，应用集合并运算求结果.【详解】由题设{|1}N y y =>，故M N ⋃={}{}221{|2}x x y y x x -≤≤⋃=≥-.故选：A3.已知直线l 与曲线3y x x =-在原点处相切，则l 的倾斜角为（）A.π6B.π4C.3π4 D.5π6【答案】C 【解析】【分析】利用导数几何意义求直线的斜率，进而确定倾斜角.【详解】由231y x '=-，则0|1x y ='=-，即直线l 的斜率为1-，根据倾斜角与斜率关系及其范围知：l 的倾斜角为3π4.故选：C4.已知a ，b 为单位向量，若||||a b a b +=- ，则a b + 与a b - 的夹角为（）A.π3B.π2C.2π3 D.3π4【答案】B 【解析】【分析】根据已知，应用向量数量积的运算律求()()a b a b +⋅-即可判断夹角大小.【详解】由题意22()()0a b a b a b +⋅-=-= ，则a b + 与a b - 的夹角为π2.故选：B5.已知()f x 为定义在R 上的奇函数，当0x <时，2()21f x x x =-+，则(2)(0)f f +=（）A.2B.1C.8- D.9-【答案】D 【解析】【分析】根据奇函数的定义求解即可.【详解】当0x <时，2()21f x x x =-+，所以()()()2222219f -=--⨯-+=，因为()f x 为定义在R 上的奇函数，所以()()229f f =--=-，且()00f =，所以(2)(0)9f f +=-故选：D6.已知1a xx=+，e e x x b -=+，sin c x x =，则下列结论错误的为（）A.[1,1]x ∃∈-，a c >B.[1,1]x ∃∈-，b c >C.[1,1]x ∃∈-，a c <D.[1,1]x ∃∈-，b c<【答案】D 【解析】【分析】举例即可判断ABC ；再根据基本不等式及三角函数的性质即可判断D.【详解】对于A ，当π6x =时，π63626π64a =+>+=，13222c =+=，此时a c >，所以[1,1]x ∃∈-，a c >，故A 正确；对于B ，当0x =时，2b =，c =b c >，所以[1,1]x ∃∈-，b c >，故B 正确；对于C ，当π6x =-时，π606πa =--<，13122c =-+=，此时a c <，所以[1,1]x ∃∈-，a c <，故C 正确；对于D ，当[]1,1x ∈-时，2e e x x b -=≥=+，当且仅当e e x x-=，即0x =时取等号，πsin 2sin 3c x x x ⎛⎫=+=+ ⎪⎝⎭，由[]1,1x ∈-，得πππ1,1333x ⎡⎤+∈-++⎢⎥⎣⎦，而ππππ1π,012332<+<<-+<，所以当π3x +，即π6x =时，πsin 2sin 23c x x x ⎛⎫=+=+= ⎪⎝⎭，所以2≤c ，当且仅当π6x =时取等号，而π06≠，所以[1,1]x ∀∈-，b c >，故D 错误.故选：D.7.传说古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，他们根据沙粒或小石子所排列的形状把数分成许多类，如图所示的1，5，12，22被称为五边形数，将所有的五边形数从小到大依次排列，则其第8个数为（）151222A.51B.70C.92D.117【答案】C 【解析】【分析】根据题图及前4个五边形数找到规律，即可得第8个数.【详解】由题图及五边形数知：后一个数与前一个数的差依次为4,7,10,13,16,19,22, ，所以五边形数依次为1,5,12,22,35,51,70,92, ，即第8个数为92.故选：C8.已知函数()f x 的定义域为R ，x ∀，y ∈R ，(1)(1)()()f x f y f x y f x y ++=+--，若(0)0f ≠，则(2024)f =（）A.2-B.4- C.2D.4【答案】A 【解析】【分析】利用赋值法对,x y 进行赋值结合函数的周期可得答案.【详解】令0x y ==，得()()()()11000f f f f ⋅=-=，即()10f =，令0x =，得()()()()110f f y f y f y ⋅+=--=，得()()-=f y f y ，所以函数()f x 为偶函数，令1x y ==，得()()()2220ff f =-，令1x y ==-，得()()()()()202020f f f f f =--=-，()()2220f f ∴=，()()20f f ∴=或()()20f f =-，若()()20f f =，解得()00f =与已知()00f ≠矛盾，()()20f f ∴=-，即()()2222f f =，解得()22f =，()02f =-，令1y =，得()()()()1211f x f f x f x +⋅=+--，()()()2111f x f x f x ∴+=+--，()()11f x f x ∴+=--，()()2f x f x ∴+=-，∴()()4f x f x +=，所以函数()f x 的周期为4.()()202402f f ∴==-.故选：A.二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9.已知函数π()2sin 23f x x ⎛⎫=-⎪⎝⎭，则（）A.()f x 的最小正周期为π2B.()f x 的图象关于点2π,03⎛⎫⎪⎝⎭成中心对称C.()f x 在区间π0,3⎡⎤⎢⎣⎦上单调递增D.若()f x 的图象关于直线0x x =对称，则01sin 22x =【答案】BC 【解析】【分析】根据正弦型函数的性质，结合代入法、整体法逐一判断各项正误.【详解】由π()2sin 23f x x ⎛⎫=-⎪⎝⎭，最小正周期2ππ2T ==，A 错；由2π2ππ()2sin 20333f ⎛⎫=⨯-= ⎪⎝⎭，即2π,03⎛⎫⎪⎝⎭是对称中心，B 对；由π0,3x ⎡⎤∈⎢⎥⎣⎦，则πππ2[,]333x -∈-，显然()f x 在区间π0,3⎡⎤⎢⎥⎣⎦上单调递增，C 对；由题意00ππ5π2π2π326x k x k -=+⇒=+，故01sin 22x =±，D 错.故选：BC10.已知甲、乙两组数据分别为：20，21，22，23，24，25和a ，23，24，25，26，27，若乙组数据的平均数比甲组数据的平均数大3，则（）A.甲组数据的第70百分位数为23B.甲、乙两组数据的极差相同C.乙组数据的中位数为24.5D.甲、乙两组数据的方差相同【答案】BD 【解析】【分析】根据已知平均数的关系求得28a =，再由极差、中位数、方差求法判断各项正误即可.【详解】由题设，2021222324252324252627366a ++++++++++=-，所以28a =，甲组数据中670% 4.2⨯=，故第70百分位数为24，A 错；甲乙组数据的极差都为5，B 对；乙组数据从小到大为23,24,25,26,27,28，故其中位数为252625.52+=，C 错；由上易知：甲的平均数为22.5，乙的平均数为25.5，所以甲的方差为2222221(2.5 1.50.50.5 1.5 2.5)6⨯+++++=3512，乙的方差为2222221(2.5 1.50.50.5 1.5 2.5)6⨯+++++=3512，故两组数据的方差相同，D 对.故选：BD11.设椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为1F ，2F ，过1F 的直线与C 交于A ，B 两点，若122F F =，且2ABF △的周长为8，则（）A.2a = B.C 的离心率为14C.||AB 可以为πD.2BAF ∠可以为直角【答案】AC 【解析】【分析】根据已知可得1c =、2a =，进而有12e =，结合椭圆性质求相交弦长的范围及焦点三角形内角的范围判断各项的正误.【详解】由12221F F c c ==⇒=，如下图2ABF △周长为482a a =⇒=，故2223b a c =-=，所以，椭圆离心率为12e =，A 对，B 错；当AB x ⊥轴，即AB 为通径时2min 2||3b AB a==，且||24AB a <=，所以3||4AB ≤<，故||AB 可以为π，C 对；由椭圆性质知：当A 为椭圆上下顶点时2BAF ∠最大，此时222222c 41os 2a a F c a BA +∠-==，且2(0,π)BAF ∈∠，故2max π)3(BAF =∠，即2BAF ∠不可能为直角，D 错.故选：AC12.如图所示，在五面体ABCDEF 中，四边形ABCD 是矩形，ABF △和DCE △均是等边三角形，且23AB =(0)EF x x =>，则（）A.//EF 平面ABCDB.二面角A EF B --随着x 的减小而减小C.当2BC =时，五面体ABCDEF 的体积(x)V 最大值为272D.当32BC =时，存在x 使得半径为32的球能内含于五面体ABCDEF 【答案】ACD 【解析】【分析】A 由线面平行的判定证明；B 设二面角A EF B --的大小为2α，点F 到面ABCD 的距离为h ，则3tan hα=，分析取最小值的对应情况即可判断；C 把五面体ABCDEF 补成直三棱柱FGI EKJ -，取,AB GI 的中点,M H ，设π(0)2FMH θθ∠=<≤，则3cos ,3sin MH FH θθ==，结合()2FGI EKJ F ABIG V x V V --=-并应用导数研究最值；D 先分析特殊情况：ABF △和DCE △所在平面均垂直于面ABCD 时构成正三棱柱ABF DCE -，再借助左视图、正视图研究内切圆半径分析一般情况判断.【详解】A ：由题设//BC AD ，AD ⊂面ADEF ，BC ⊄面ADEF ，则//BC 面ADEF ，由面BCEF 面ADEF EF =，BC ⊂面BCEF ，则//BC EF ，BC ⊂面ABCD ，EF ⊄面ABCD ，则//EF 平面ABCD ，对；B ：设二面角A EF B --的大小为2α，点F 到面ABCD 的距离为h ，则3tan hα=，点F 到面ABCD 的距离，仅在面FAB ⊥面ABCD 时取得最大值，当EF x BC ==时tan α取最小值，即α取最小值，即二面角A EF B --取最小值，所以EF x =∈(0,)+∞，二面角先变小后变大，错；C ：当2BC =，如图，把五面体ABCDEF 补成直三棱柱FGI EKJ -，分别取,AB GI 的中点,M H ，易得FH ⊥面ABCD ，3FM =，设π(02FMH θθ∠=<≤，则3cos ,3sin MH FH θθ==，()2ABCDEFFGI EKJ F ABIG V x V V V --==-=113sin (26cos )23sin 3cos 23θθθθ⨯⨯+-⨯⨯⨯cos θθθ=+，令()cos f θθθθ=+，则()2f θθθ'=+，令2()02cos cos 10f θθθ'=⇒+-=，可得1cos 2θ=或cos 1θ=-（舍），即π3θ=，π03θ<<，()0f θ'>，()f θ递增，ππ32θ<≤，()0f θ'<，()f θ递减，显然π3θ=是()f θ的极大值点，故max 127()2222f θ=+=.所以五面体ABCDEF 的体积(x)V 最大值为272，C 对；D ：当32BC =时，ABF △和DCE △所在平面均垂直于面ABCD 时构成正三棱柱ABF DCE -，此时正三棱柱内最大的求半径342r =<，故半径为2的球不能内含于五面体ABCDEF ，对于一般情形，如下图示，左图为左视图，右图为正视图，由C 分析结果，当五面体ABCDEF 体积最大时，其可内含的球的半径较大，易知，当π3FMH ∠=时，3339,22FH IH IF ===，设FIG 的内切圆半径为1r ，则113313922222r ⨯⨯=⨯⨯，可得12r =>，另外，设等腰梯形EFMN 中圆的半径为2r ，则213π33tan434r r ==>=所以，存在x 使半径为2的球都能内含于五面体ABCDEF ，对.故选：ACD【点睛】关键点点睛：对于C 通过补全几何体为棱柱，设π(02FMH θθ∠=<≤得到五面体ABCDEF 的体积关于θ的函数；对于D 从特殊到一般，结合几何体视图研究内切圆判断最大半径是否大于2为关键.三、填空题：本大题共4小题，每小题5分，共20分．13.若π3sin 45α⎛⎫+=- ⎪⎝⎭，则πcos 4α⎛⎫-= ⎪⎝⎭_________．【答案】35-##0.6-【解析】【分析】应用诱导公式有ππππcos cos[()]sin()4424ααα⎛⎫-=+-=+ ⎪⎝⎭，即可求值.【详解】ππππ3cos cos[()sin()44245ααα⎛⎫-=+-=+=- ⎪⎝⎭.故答案为：35-14.《九章算术》、《数书九章》、《周髀算经》是中国古代数学著作，甲、乙、丙三名同学计划每人从中选择一种来阅读，若三人选择的书不全相同，则不同的选法有_________种．【答案】24【解析】【分析】先求出三人选书没有要求的选法，再排除三人选择的书完全相同的选法即可.【详解】若三人选书没有要求，则有3327=种，若三人选择的书完全相同，则有3种，所以三人选择的书不全相同，不同的选法有27324-=种.故答案为：24.15.已知平面α的一个法向量为(1,0,1)n =，且点(1,2,3)A 在α内，则点(1,1,1)B 到α的距离为_________．【答案】【解析】【分析】由题设得(0,1,2)BA =，应用向量法求点面距离即可.【详解】由题设(0,1,2)BA = ，则点(1,1,1)B 到α的距离为||||BA n n ⋅==16.设ABC 是面积为1的等腰直角三角形，D 是斜边AB 的中点，点P 在ABC 所在的平面内，记PCD与PAB 的面积分别为1S ，2S ，且121S S -=．当||PB =||||PA PB >时，||PA =_________；记PA PB a -=，则实数a 的取值范围为_________．【答案】①.②.(2)5【解析】【分析】以D 为原点，AB为x 轴正方向建立直角坐标系，设00(,)P x y ，根据已知得001||||12y x =-、2200(1)10x y -+=，即可得04x =，0||1y =，应用两点距离公式求||PA ；根据PA PB a -=确定P 的轨迹曲线，并写出方程，利用曲线性质列不等式求参数范围.【详解】以D 为原点，AB为x 轴正方向建立直角坐标系，设00(,)P x y ，则101||2S x =，20||S y =，所以001||||12x y -=，则001||||12y x =-，当||PB =，||||PA PB >时，00x >，即22200||(1)10PB x y =-+=，所以22001(1)(1)102x x -+-=，即200512320x x --=，可得04x =（负值舍），则0||1y =，故||PA ==若0PA PB a -=>，结合双曲线定义知：P 在以,A B 为焦点的双曲线上，但不含顶点，该双曲线为22221()1()22x y a a -=-，即22224414x y a a -=-，双曲线顶点的横坐标的绝对值小于半焦距1，则双曲线与曲线1||||12x y -=有交点，即双曲线的渐近线和曲线1||||12x y -=有交点，则双曲线的渐近线斜率的绝对值小于12，所以221115160424165a a <<⇒<<⇒<<，故4525a <<，所以实数a的取值范围为(,2)5.，(2)5【点睛】关键点点睛：第二空，注意P 在以,A B 为焦点的双曲线上，但不含顶点，将问题化为双曲线的渐近线斜率的绝对值小于12为关键.四、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17.已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且2cos cos 2a B ab A c +=．（1）求a ；（2）若2π3A =，且ABC 的周长为2+，求ABC 的面积．【答案】（1）2a =；（2）4.【解析】【分析】（1）应用正弦边角关系及和角正弦公式有sin()2sin a A B C +=，再由三角形内角性质即可求边长；（2）应用余弦定理及已知得224b c bc ++=且b c +=1bc =，最后应用面积公式求面积.【小问1详解】由题设(cos cos )2a a B b A c +=，由正弦定理有(sin cos sin cos )2sin a A B B A C +=，所以sin()2sin a A B C +=，而πA B C +=-，故sin 2sin a C C =，又sin 0C >，所以2a =.【小问2详解】由（1）及已知，有2222241cos 222b c a b c A bc bc +-+-===-，可得224b c bc ++=，又2a b c ++=+，即b c +=，所以2()541b c bc bc bc +-=-=⇒=，故13sin 24ABC S bc A ==△.18.如图，在四棱锥E ABCD -中，//AD BC ，22AD BC ==，AB =，AB AD ⊥，EA ⊥平面ABCD ，过点B 作平面BD α⊥．（1）证明：平面//α平面EAC ；（2）已知点F 为棱EC 的中点，若2EA =，求直线AD 与平面FBD 所成角的正弦值．【答案】（1）证明见详解（2）277【解析】【分析】（1）利用三角形相似及等量代换得AC BD ⊥，利用线面垂直得EA BD ⊥，进而得BD ⊥平面EAC ，结合已知条件得证；（2）利用空间向量法可求【小问1详解】设AC 与BD 的交点为O ，连接OF ，因为AD BC ∥，且AB AD ⊥，所以AB BC ⊥，因为22AD =，所以1AD =，AB =，AB AD ⊥，且AB =，2BC =，AB BC ⊥，所以ABD BCA ，所以ABD BCA ∠=∠，所以BAC ABD BAC BCA ∠+∠=∠+∠，因为AB BC ⊥，所以90BAC BCA ∠+∠=︒，所以90BAC ABD ∠+∠=︒，即90BAO ABO ∠+∠=︒，所以90AOB ∠=︒，所以AO OB ⊥，即AC BD ⊥，因为EA ⊥平面ABCD ，BD ⊂平面ABCD ，所以EA BD ⊥，因为EA AC A = ，,EA AC ⊂平面EAC ，所以BD ⊥平面EAC ，又因为平面BD α⊥，且B ∉平面EAC ，所以平面//α平面EAC 【小问2详解】因为AB AD ⊥，EA ⊥平面ABCD ，所以,,AB AD EA 两两垂直，如图，以A 为原点，,,AB AD EA 分别为x 轴，y 轴，z 轴，建立空间直角坐标系A xyz -，则()0,0,0A ，()0,1,0D ，()()(),0,0,2,2,0B E C ，所以())())0,1,0,,0,2,0,2AD BD BC BE ====，因为点F 为棱EC 的中点，所以()1,1,122BF BC BE ⎛⎫=+= ⎪ ⎪⎝⎭，设平面FBD 的一个法向量为(),,n x y z =，则00BD n BF n ⎧⋅=⎪⎨⋅=⎪⎩，所以0202y x y z +=++=⎪⎩，取2x =，得y z =-=，所以平面FBD的一个法向量为(2,n =-，记直线AD 与平面FBD 所成角为θ，则27sin cos ,7AD n AD n AD n θ⋅===，所以直线AD 与平面FBD 所成角的正弦值为277．19.已知数列{}n a 的前n 项和为n S ，2124a a ==，当*n ∈N ，且2n ≥时，1132n n n S S S +-=-．（1）证明：{}n a 为等比数列；（2）设()()111n n n n a b a a +=--，记数列{}n b 的前n 项和为n T ，若21172m m T -+>⨯，求正整数m 的最小值．【答案】（1）证明见解析；（2）3.【解析】【分析】（1）由题设112()n n n n S S S S +--=-，结合已知得到12n n a a +=在*n ∈N 上都成立，即可证结论；（2）由（1）得()()122121nn n n b +=--，裂项相消法求n T ，根据不等式关系得221m ->，即可确定正整数m 的最小值.【小问1详解】当2n ≥时，1111322()n n n n n n n S S S S S S S +-+-=-⇒-=-，即12n n a a +=，又2124a a ==，故12n n a a +=在*n ∈N 上都成立，且12a =，所以{}n a 是首项、公比均为2的等比数列.【小问2详解】由（1）知：2n n a =，则()()1121121212121n n n n n n b ++==-----，所以11111111212121211111133712n n n n n n T -++=-+-+--=----+-+- ，则21211117221712m m m m T -+-+=-+>⨯-⨯，即2121722182m m m -+-⨯-⨯<-=，所以221m ->，可得m>2，而*m ∈N ，故3m ≥，正整数m 的最小值为3.20.已知甲、乙两支登山队均有n 名队员，现有新增的4名登山爱好者a b c d ,,,将依次通过摸出小球的颜色来决定其加入哪支登山队，规则如下：在一个不透明的箱中放有红球和黑球各2个，小球除颜色不同之外，其余完全相同先由第一名新增登山爱好者从箱中不放回地摸出1个小球，再另取完全相同的红球和黑球各1个放入箱中；接着由下一名新增登山爱好者摸出1个小球后，再放入完全相同的红球和黑球各1个，如此重复，直至所有新增登山爱好者均摸球和放球完毕．新增登山爱好者若摸出红球，则被分至甲队，否则被分至乙队．（1）求,,a b c 三人均被分至同一队的概率；（2）记甲，乙两队的最终人数分别为1n ，2n ，设随机变量12X n n =-，求()E X ．【答案】（1）215；（2）3835.【解析】【分析】（1）由题意，,,a b c 三人均被分至同一队，即三人同分至甲队或乙队，分别求出a 被分至甲队即a 摸出红球的概率、b 被分至甲队即b 摸出红球的概率、c 被分至甲队即c 摸出红球的概率，再应用条件概率公式及互斥事件加法求,,a b c 三人均被分至同一队的概率；（2）根据题意有X 可能取值为4,2,0，分析X 各对应值的实际含义，并求出对应概率，进而求期望即可.【小问1详解】,,a b c 三人均被分至同一队，即三人同分至甲队或乙队，记事件A =“a 被分至甲队”，事件B =“b 被分至甲队”，事件C =“c 被分至甲队”，当a 即将摸球时，箱中有2个红球和2个黑球，则a 被分至甲队即a 摸出红球的概率为1()2P A =；当a 被分至甲队时，箱中有2个红球和3个黑球，则b 被分至甲队即b 摸出红球的概率为2(|)5P B A =；当,a b 均被分至甲队时，箱中有2个红球和4个黑球，则c 被分至甲队即c 摸出红球的概率为1(|)3P C AB =；所以121()()(|)255P AB P A P B A ==⨯=，则111()()(|)5315P ABC P AB P C AB ==⨯=，同理知：新增登山爱好者,,a b c 均被分至乙队的概率也为115，所以,,a b c 三人均被分至同一队的概率为215.【小问2详解】由题设，X 可能取值为4,2,0，4X =为新增的4名登山爱好者被分至同一队，则22224(4)24567105P X ⨯⨯⨯==⨯=⨯⨯⨯，2X =为新增的4名登山爱好者中有3名均被分至同一队，其余1名被分至另一队，设新增的第(1,2,3,4)k k =名登山爱好者被单独分至甲队或乙队，则123339(1)2456770P P k ⨯⨯⨯===⨯=⨯⨯⨯，223339(2)2456770P P k ⨯⨯⨯===⨯=⨯⨯⨯，322434(3)2456735P P k ⨯⨯⨯===⨯=⨯⨯⨯，422252(4)2456721P P k ⨯⨯⨯===⨯=⨯⨯⨯，所以12347(2)15P X P P P P ==+++=，X 0=为新增的4名登山爱好者中各有2名被分至甲队和乙队，则52(0)1(2)(4)105P X P X P X ==-=-==，所以475238()4201051510535E X =⨯+⨯+⨯=.21.已知函数1()ln 1x f x a x x -=-+有两个极值点1x ，2x ．（1）求实数a 的取值范围；（2）证明：()()2121221f x f x a a x x a -->--．【答案】（1）1(0,2；（2）证明见解析.【解析】【分析】（1）利用导数，结合()f x 的极值点个数，得到0a >且1x ，2x 是22(1)0ax a x a +-+=的两个不同根，列不等式组求参数范围；（2）设1201x x <<<，应用分析法将问题化为证11212211ln 21x x x x x x -<+，令12(0,1)x t x =∈，则证11ln 21t t t -<+，再由12a =对应()f x 单调性即可证结论.【小问1详解】由题设22222(1)()(1)(1)a ax a x a f x x x x x +-+'=-=++且0x >，若0a ≤，则()0f x '<在(0,)+∞上恒成立，即()f x 递增，不可能有两个极值点，不符；故0a >，又()f x 有两个极值点，则1x ，2x 是22(1)0ax a x a +-+=的两个不同正根，所以()()22Δ4144120100a a a a aa ⎧=--=->⎪-⎪->⎨⎪>⎪⎩，可得102a <<，即实数a 的取值范围是1(0,2.【小问2详解】由（1）102a <<且122(1)a x x a-+=，121=x x ，不妨设1201x x <<<，则()()1212f x f x x x -=-1212121211ln ln 11x x a x a x x x x x ----+++-112212122()ln (1)(1)x x x a x x x x x --++=-121212121212ln (ln ln )21x a x a x x a x x x x x x x x -=-=--+++-，要证()()2121221f x f x a a x x a -->--，需证1212ln ln 1211x x a x x a --->--，即1212ln ln 1x x a x x a ->--，只需证121212ln ln 2x x x x x x ->-+，即11212211ln 21x x x x x x -<+，令12(0,1)x t x =∈，则证11ln 21t t t -<+，由（1），12a =时2212(1)(1)02ax a x a x +-+=-≥，即()0f x '≥，所以11()ln 21x f x x x -=-+在(0,)+∞上递增，又01t <<，故()(1)0f t f <=，即11ln 21t t t -<+，综上，()()2121221f x f x a a x x a -->--.【点睛】关键点点睛：第二问，设1201x x <<<，应用分析法将问题转化为证11212211ln 21x x x x x x -<+为关键.22.在平面直角坐标系xOy 中，点(1,0)P ，点A 为动点，以线段AP 为直径的圆与y 轴相切，记A 的轨迹为Γ，直线AP 交Γ于另一点B ．（1）求Γ的方程；（2）OAB 的外接圆交Γ于点C （不与O ，A ，B 重合），依次连接O ，A ，C ，B 构成凸四边形OACB ，记其面积为S ．（i ）证明：ABC 的重心在定直线上；（ii ）求S 的取值范围．【答案】（1）24y x=（2）证明见详解；32,2⎛⎫+∞ ⎪ ⎪⎝⎭【解析】【分析】（1）设(),A x y ，根据已知条件列出方程化简即得；（2）（i ）因为,,,O A B C 四点共圆，设该圆的方程为220x y dx ey +++=，联立22204x y dx ey y x ⎧+++=⎨=⎩，得()42416160y d y ey +++=，结合重心公式可得证；（ii ）记,OAB ABC △△的面积分别为12,S S ，用已知条件分别表示出12,S S ，进而表示出面积为S 的表达式，然后利用导数求最值即得.【小问1详解】设(),A x y ，则线段AP 的中点坐标为1,22x y +⎛⎫ ⎪⎝⎭，因为以线段AP 为直径的圆与y 轴相切，所以1122x AP +==，化简，得24y x =.【小问2详解】（i ）因为,,,O A B C 四点共圆，设该圆的方程为220x y dx ey +++=，联立22204x y dx ey y x⎧+++=⎨=⎩，消去x ，得()42416160y d y ey +++=，即()()3416160y y d y e +++=，所以123,,y y y 即为关于y 的方程()3416160y d y e +++=的3个根，则()()()()312341616y d y e y y y y y y +++=---，因为()()()()()32123123122313123y y y y y y y y y y y y y y y y y y y y y ---=-+++++-，由2y 的系数对应相等得，1230y y y ++=，即()123103y y y ++=，因为ABC 的重心的纵坐标为()12313y y y ++，所以ABC 的重心在定直线0y =上.（ii ）记,OAB ABC △△的面积分别为12,S S ，由已知得直线AB 的斜率不为0设直线AB ：1x my =+，联立241x xy y m =+=⎧⎨⎩，消去x ，得2440y my --=，所以12124,4y y m y y +=⋅=-，所以1121122S OP y y =⋅⋅-==，由（i ）得，()3124y y y m =-+=-，所以()22233114444x y m m ==⨯-=，即()24,4C m m -，因为()212122444AB x x m y y m =++=++=+，点C 到直线AB的距离d =，所以()22211448122S AB d m m =⋅⋅=⋅+=-，所以)221281181S S S m m =+=-=+-不妨设0m >，且A 在第一象限，即120,0y y ><，340y m =-<，依次连接O ，A ，C ，B 构成凸四边形OACB ，所以()3122y y y y =-+<，即122y y -<，又因为124y y ⋅=-，2242y y <，即222y <，即20y <<，所以122244m y y y y =+=->+=，即24m >，即218m >，所以)218116S m m=+-=，设t =，则324t >，令()()2161f t t t =-，则()()()2221611614816f t t t t t '='=-+--，因为324t >，所以()248160f t t -'=>，所以()f t 在区间32,4∞⎛⎫+ ⎪ ⎪⎝⎭上单调递增，所以()323242f t f ⎛⎫>= ⎪ ⎪⎝⎭，所以S 的取值范围为32,2∞⎛⎫+ ⎪ ⎪⎝⎭【点睛】第二问：（i ）关键是把证明ABC 的重心在定直线上转化为方程根的问题，利用韦达定理以及重心公式可得.（ii ）关键是把四边形OACB 拆成两个三角形，然后用相同的变量分别表示两个三角形的面积以及变量的取值范围的确定，进而得到四边形OACB 面积的表达式，然后利用导数求最值即得.。

2023~2024学年福州市高三年级第一次质量检测数学试题（完卷时间120分钟；满分150分）第Ⅰ卷一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知复数z 满足11i z=−，则在复平面内，z 对应的点在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．已知集合{}21A x x=<，{}0B x x =>，则A B = （ ）A ．（0，1）B ．()0,+∞C ．()1,−+∞D ．(),−∞+∞3．已知点()0,2P x 在抛物线C ：24y x =上，则P 到C 的准线的距离为（ ） A ．4B ．3C ．2D ．14．“二十四节气”是中国古代劳动人民伟大的智慧结晶，其划分如图所示．小明打算在网上搜集一些与二十四节气有关的古诗．他准备在春季的6个节气与夏季的6个节气中共选出3个节气，若春季的节气和夏季的节气各至少选出1个，则小明选取节气的不同情况的种数是（ ）A ．90B ．180C ．270D ．3605．一个正四棱台形油槽可以装煤油3190000cm ，其上、下底面边长分别为60cm 和40cm ，则该油槽的深度为（ ） A ．75cm 4B ．25cmC ．50cmD ．75cm6．一个袋子中有大小和质地相同的4个球，其中有2个红球，2个黄球，每次从中随机摸出1个球，摸出的球不再放回，则第二次摸到黄球的条件下，第一次摸到红球的概率为（ ） A ．13B ．12C ．23D ．347．已知1ea =，ln b =，ln c =，则（ ） A ．a b c >> B ．b c a >> C ．a c b >>D ．c a b >>8．若定义在R 上的函数()()sin cos 0f x x x ωωω=+>的图象在区间[]0,π上恰有5条对称轴，则ω的取值范围为（ ） A ．1721,44B ．1725,44C ．1725,44D ．3341,44二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．9．某市抽查一周空气质量指数变化情况，得到一组数据：80，76，73，82，86，75，81．以下关于这组数据判断正确的有（ ） A ．极差为13B ．中位数为82C ．平均数为79D ．方差为12410．已知圆M ：221x y +=，直线l ：(1y k x =−，则（ ）A ．l 恒过定点)1−B ．若l 平分圆周M ，则k =C ．当k =l 与圆M 相切D ．当k <<时，l 与圆M 相交11．已知函数()332f x x ax =−+有两个极值点．则（ ） A ．()f x 的图象关于点()0,2对称 B ．()f x 的极值之和为-4C ．a ∃∈R ，使得()f x 有三个零点D ．当01a <<时，()f x 只有一个零点12．已知正四棱柱1111ABCD A B C D −的底面边长为2，球O 与正四棱柱的上、下底面及侧棱都相切，P 为平面1CDD 上一点，且直线BP 与球O 相切，则（ ） A ．球O 的表面积为4π B ．直线1BD 与BP 夹角等于45°C ．该正四棱柱的侧面积为D ．侧面11ABB A 与球面的交线长为2π第Ⅱ卷注意事项：用0.5毫米黑色签字笔在答题卡上书写作答．在试题卷上作答，答案无效． 三、填空题；本大题共4小题，每小题5分，共20分．13．已知向量()1,2a = ，()1,2b λλ=+−，若a b ⊥ ，则实数λ的值为__________．14．将圆周16等分，设每份圆弧所对的圆心角为θ，则sin cos θθ的值为__________．15．已知定义城为R 的函数()f x 同时具有下列三个性质，则()f x =__________．（写出一个满足条件的函数即可） ①()()()f x y f x f y +=+；②()f x ′是偶函数；③当0x y +>时，()()0f x f y +<．16．已知双曲线C ：()222210,0x y a b a b−=>>的左焦点为F ，两条渐近线分别为1l ，2l ．点A 在1l 上，点B在2l 上，且点A 位于第一象限，原点O 与B 关于直线AF 对称、若2AF b =，则C 的离心率为__________．四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（本小题满分10分）已知等比数列{}n a 的前n 项和为n S ，且12n n a S +=+． （1）求{}n a 的通项公式；（2）若221log n n b a −=，求数列{}n b 的前n 项和n T ． 18．（本小题满分12分）记ABC △的内角A ，B ，C 所对的边分别为a ，b ，c ，已知b =，6B π=．（1）若2c =，求a ；（2）求ABC △面积的最大值． 19．（本小题满分12分）国际上常采用身体质量指数（Body Mass Index ，缩写BMI ）来衡量人体肥瘦程度，其计算公式是()()22kg BMI m=体重单位:身高单位:．为了解某公司员工的身体肥瘦情况，研究人员从该公司员工体检数据中，采用比例分配的分层随机抽样方法抽取了50名男员工、30名女员工的身高和体重数据．计算得到他们的BMI（1）若该公司男员工有1500名，则该公司共有多少名员工？（2）以频率估计概率，分别从该公司男、女员工中各随机抽取2名员工，求抽到的员工中至少有一名是肥胖的概率．20．（本小题满分12分）如图，在底面为菱形的四棱锥M ABCD −中，2AD BD MB ===，MA MD ==（1）求证：平面MAD ⊥平面ABCD ；（2）已知2MN NB =，求直线BN 与平面ACN 所成角的正弦值．21．（本小题满分12分）已知椭圆E ：22143x y +=的右焦点为F ，左、右顶点分别为A ，B ．点C 在E 上，()4,P P y ，()4,Q Q y 分别为直线AC ，BC 上的点． （1）求P Q y y ⋅的值；（2）设直线BP 与E 的另一个交点为D ，求证：直线CD 经过F ．22．（本小题满分12分）已知函数()ln f x x a =−，记曲线()y f x =在点()()11,x f x 处的切线为l ，l 在x 轴上的截距为()220x x >．（1）当1e x =，1a =时，求切线方程； （2）证明：12e e a a x x −≥−．答案一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．【考查意图】本小题以复数为载体，主要考查复数的基本运算、几何意义等基础知识；考查运算求解能力、推理论证能力；考查数学运算、逻辑推理等数学核心素养，体现基础性． 【答案】A ．【解析】由11i z =−得11i1i 2z+==−，应选A ． 2．【考查意图】本小题以不等式为载体，主要考查集合运算等基础知识；考查运算求解能力、推理论证能力；考查数学运算、逻辑推理等核心素养，体现基础性． 【答案】C ． 【解析】{}11A x x =−<<，{}0B x x =>，故()1,A B =−+∞ ，应选C ． 3．【考查意图】本小题以抛物线为载体，主要考查抛物线的图象和性质、直线与抛物线的位置关系等基础知识；考查运算求解能力、推理论证能力；考查数形结合思想、化归与转化思想；考查直观想象、逻辑推理、数学运算等核心素养，体现基础性． 【答案】C ．【解析】抛物线24y x =的准线为1x =−，由P C ∈得01x =，故P 到准线的距离为2，应选C ．4．【考查意图】本小题以二十四节气为载体，主要考查排列与组合等基础知识；考查运算求解能力、推理论证能力和应用意识；考查数学运算、逻辑推理等核心素养，体现基础性和应用性． 【答案】B ．【解析】根据题意可知，小明可以选取1春2夏或2春1夏．其中1春2夏的不同情况有：1266C C 90⋅=种；2春1夏的不同情况有：2166C C 90⋅=种，所以小明选取节气的不同情况有：9090180+=种．应选B ．5．【考查意图】本小题以正四棱台形油槽为载体，主要考查空间几何体的体积等基础知识；考查空间想象能力、推理论证能力、运算求解能力；考查数形结合思想、化归与转化思想；考查直观想象、逻辑推理、数学运算等核心素养，体现基础性和应用性． 【答案】D ．【解析】设正四棱台的高，即深度为cm h ，依题意，得()22190000604060403h=++×，解得75h =，应选D ．6．【考查意图】本小题主要考查条件概率、全概率公式等基础知识；考查推理论证能力、运算求解能力与创新意识；考查化归与转化思想；考查数学建模、逻辑推理、数据分析等核心素养，体现综合性、应用性与创新性． 【答案】C ．【解析】解法一：记第i 次摸到红球为事件i A ，摸到黄球为事件()1,2i B i =，则()()()()()21211211211123232P B P A P B A P B P B B =+=×+×=，()()()12121221433P A B P A P B A ==×=，故()()()1212223P A B P A B P B ==．应选C ． 解法二：记第i 次摸到红球为事件i A ，摸到黄球为事件()1,2i B i =．由抽签的公平性可知()22142P B ==，又()12221433P A B ×==×，所以()()()1212223P A B P A B P B ==．应选C ． 7．【考查意图】本小题以数的大小比较为载体，主要考查函数与导数等基础知识；考查运算求解能力、推理论证能力、应用意识；考查数学建模、数学运算、逻辑推理等核心素养，体现基础性、应用性和综合性． 【答案】A ． 【解答】解法一：1ln e e e a ==，ln 2ln 4ln 24b ==，ln 55c ，令()ln x f x x =，()21ln xf x x−′=，当e x ≥时，()0f x ′≤，故()f x 在区间[)e,+∞上单调递减，所以a b c >>．==>，所以ln ln >b c >．在同一坐标系中作出函数()2xf x =，()2g x x =的图象，如图所示，由图可知，()()e e f g <，即e22e <，所以e22e 2e 2e <，即11e22e <，所以111ln 2ln e 2e e<=，即b a <． （令()ln x f x x=，()21ln xf x x −′=，当0e x <<时，()0f x ′>，故()f x 在区间()0,e 上单调递增，所以1ln e ln 2e e 2a b ==>=．） 综上，a b c >>．应选A ．8．【考查意图】本小题以三角函数为载体，考查三角函数的图象与性质、三角恒等变换等基础知识；考查抽象概括能力、推理论证能力、应用意识；考查数形结合思想；考查直观想象、逻辑推理、数学运算等核心素养，体现基础性和综合性． 【答案】A ．【解析】由已知，()4f x x πω=+，令42x k ππωπ+=+，k ∈Z ，得()414k x πω+=，k ∈Z ，依题意知，有5个整数k 满足()4104k ππω+≤≤，即0414k ω≤+≤，所以0,1,2,3,4k =，则4414451ω×+≤<×+，故172144ω≤<，应选A ． 二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．【考查意图】本小题主要考查极差、中位数、平均数、方差等基础知识；考查推理论证能力、运算求解能力；考查化归与转化思想；考查数据分析等核心素养，体现基础性． 【答案】AC ．10．【考查意图】本小题以直线与圆为载体，考查直线的方程、圆的方程、直线与圆的位置关系等基础知识；考查运算求解能力；考查直观想象、逻辑推理等核心素养；体现基础性和综合性． 【答案】BC ．【解析】依题意，l恒过定点()1−，选项A 错误；若l 平分圆周M ，则l 经过圆M 的圆心()0,0，代入直线方程得k =B 正确； 圆心()0,0O 到l的距离dk =1d r ==，l 与圆M 相切，选项C 正确；若l 与圆M相交，则1d <，即)2211k −<+，即0k <<，故选项D 错误．综上，应选BC ．11．【考查意图】本小题以三次函数为载体，主要考查函数与导数等基础知识；考查运算求解能力、推理论证能力、应用意识；考查数学建模、数学运算、逻辑推理等核心素养，体现基础性、应用性和综合性． 【答案】ACD ．【解答】()f x 的图象可由奇函数()33g x x ax =−的图象向上平移2个单位长度得到，故()f x 的图象关于点()0,2对称，选项A 正确．设()f x 的极值点分别为()1212,x x x x <，则由对称性可知120x x +=，故()()12224f x f x +=×=，即()f x 的极值之和为4，选项B 错误．依题意，方程()2330f x x a ′=−=有两异根，则0a >，1x =2x =，()f x在区间(−∞上单调递增，在区间(上单调递减，在区间)+∞单调递增．由图象可知，当()()120f x f x >>时，()f x 的图象与x 轴有3个交点，即()f x 有3个零点，选项C 正确．当01a <<时，(32210f=−+=−>，此时()f x 只有一个零点，选项D 正确．综上，应选ACD ．12．【考查意图】本小题以正四棱柱为载体，主要考查球、直线与平面的位置关系等基础知识；考查空间想象能力、推理论证能力、运算求解能力；考查化归与转化思想；考查直观想象、逻辑推理等核心素养，体现基础性、应用性和综合性． 【答案】BCD ．【解答】如图，设球O 与下底面相切于点1O ，则1OO ⊥平面ABCD ，连接1O A ，则1OAO ∠为直线OA 与平面ABCD 所成的角．因为球O与正四棱柱的侧棱相切，所以其半径11R OO O A===，所以428S ππ=⋅=表，四棱柱的侧面积为()24××，故选项A 错误，C 正确．依题意，1BB ，BP 均为球O 的切线，1BD 经过球心O ，所以111B BD PBD ∠=∠，又111B D BB =，所以11145PBD B BD ∠=∠=°，选项B 正确．对于选项D ，棱1AA 的中点F ，即球O 与棱1AA 的切点应为交线上的点，故交线应为过F 的圆．截面圆的圆心即为矩形11ABB A 的中心E ，在Rt OEF △中，OFR ==，112OEBC ==，所以截面圆半径1r EF ==，周长为2π，该选项正确．综上，应选BCD ．三、填空题：本大题共4小题，每小题5分，共20分．13．【考查意图】本小题以平面向量为载体，主要考查平面向量的基本运算等基础知识；考查运算求解能力、推理论证能力；考查数学运算、逻辑推理、直观想象等核心素养，体现基础性． 【答案】5．【解析】由a b ⊥得()()1220λλ++−=，解得5λ=． 14．【考查意图】本小题以圆的等分为载体，考查三角恒等变换等基础知识；考查推理论证能力，抽象概括能力；考查逻辑推理等核心素养；体现基础性与应用性．．【解析】依题意，得8πθ=，所以11sin cos sin 2sin 224πθθθ===． 15．【考查意图】本小题以函数的性质为载体，考查函数的奇偶性、函数与导数等基础知识；考查推理论证能力；考查逻辑推理等核心素养；体现基础性、综合性与应用性． 【答案】x −（答案不唯一，()0kx k <均可）．16．【考查意图】本小题以双曲线为载体，主要考查双曲线的离心率、双曲线的图象和性质、直线与双曲线的位置关系等基础知识；考查运算求解能力、推理论证能力；考查数形结合思想、化归与转化思想；考查直观想象、逻辑推理、数学运算等核心素养，体现基础性和综合性． 【答案】2．【解答】依题意，1l 的方程为by x a=，2AF l ⊥，设垂足为P ，则FP b =．因为22AFb FP ==，所以点F ，A 关于直线2l 对称，FOP AOP ∠=∠，又1l ，2l 关于y 轴对称，所以1l 的倾斜角为1180603×°=°，故tan 60ba=°=，所以离心率2e =．四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．【命题意图】本小题主要考查等差数列、等比数列、递推数列及数列求和等基础知识，考查运算求解能力、逻辑推理能力和创新能力等，考查化归与转化思想、分类与整合思想、函数与方程思想、特殊与一般思想等，考查逻辑推理、数学运算等核心素养，体现基础性和综合性．满分10分． 【解答】（1）解法一：由12n n a S +=+得21322,2,a S aS =+ =+设等比数列{}n a 的公比为q ，所以()()12112,12,a q a q q −=−−= 解得12,2,a q == 或12,a q =− = （舍去）．所以2n n a =．（2）212212log log 221n n n b a n −−===−， 故11b =，()()12121122n n b b n n n −−=−−−−=≥ ， 所以{}n b 是首项为1，公差为2的等差数列， 所以()()1212122n n n b b n n T n ++−===．解法二：（1）因为12n n a S +=+，① 所以当2n ≥时，12n n a S −=+，② ①－②得12n n a a +=， 所以等比数列{}n a 的公比12n na qa +==． 由①式得212a a =+，得12a =，所以2n n a =．（2）12n n T b b b =++⋅⋅⋅+2123221log log log n a a a −++⋅⋅⋅+()21321log n a a a −⋅⋅⋅= ()13212log 2n ++⋅⋅⋅+−=()12122log 2n n+− =2n =．18．【命题意图】本小题主要考查正弦定理、余弦定理及三角恒等变换等基础知识，考查逻辑推理能力、运算求解能力等，考查化归与转化思想、函数与方程思想、数形结合思想等，考查数学运算、逻辑推理等核心素养，体现基础性和综合性．满分12分．【解答】解法一：（1）因为b =，2c =，6B π=，根据余弦定理得2222cos b a c ac B =+−，所以22224cos6a a π=+−，即220a −+=，解得1a =．（2）根据余弦定理，得2222cos a b c ac B =+−，所以(222222cos 226a c ac a c ac ac π=+−=+−≥−=，（当且仅当1a c ==时取等号），即(22ac ≤=+，所以ABC △面积(1111sin sin 2222644ABC S ac B ac ac π===≤×△，即ABC △．解法二：（1）因为b =，2c =且6B π=，根据正弦定理，得sin sin b c B C=，2sin C=，即sin C =， 因为c b >，所以C B >，所以566C ππ<<， 所以4C π=或34C π=， 当4C π=时，()1sin sin sin 642A B C ππ =+=+= ， 根据正弦定理，得sin sin a bA B=， 所以sin 1sin b Aa B ==+；当34C π=时，()31sin sin sin 642A B C ππ =+=+=×= ，根据正弦定理，得sin sin a bA B=， 所以sin 1sin b A a B ==； 综上，1a =．（2）略，同解法一．解法三：（1）因为b =，2c =且6B π=， 根据正弦定理，得sin sin b cB C=， 2sin C=，即sin C =， 因为c b >，所以C B >，所以566C ππ<<， 所以4C π=或34C π=，当4C π=时，()76412A B C πππππ =−+=−+= ， 根据正弦定理，得sin sin a b A B=，所以sin sin cos cos sin sin 343434b A a B ππππππ ==+=+ ；sin cos cos sin 13434ππππ ++； 当34C π=时，()36412A B C πππππ =−+=−+= ， 根据正弦定理，得sin sin a b A B =，所以sin sin cos cos sin sin 343434b A a B ππππππ ==−=−sin cos cos sin 13434ππππ −− ；综上，1a =．（2）根据正弦定理，得sin sin sin ac b A C B ===，所以a A =，c C =，即(251sin sin 8sin sin 8sin cos 62aC A C A A A A A π ==−=+21cos 22sin 22sin 22sin 222A A A A A A −=−=+=++14sin 224sin 223A A A π +−+= 因为506A π<<，所以42333A πππ−<−<， 所以当232A ππ−=，即512A π=时，sin 23A π −取得最大值为1，即ac最大值为4+，所以ABC △面积(1111sin sin 422644ABC S ac B ac ac π===≤×+△，即ABC △． 19．【命题意图】本小题主要考查分层抽样、独立事件的概率、互斥事件、对立事件的概率等基础知识；考查数学建模能力，运算求解能力，逻辑推理能力，创新能力以及阅读能力等；考查统计与概率思想、分类与整合思想等；考查数学抽象，数学建模和数学运算等核心素养；体现应用性和创新性．满分12分．【解】（1）设该公司共有x 名员工， 依题意得1500505030x =+， 解得2400x =， 所以该公司共有2400名员工．（2）依题意，事件“抽到一名男员工不为肥胖”的概率为404505=，事件“抽到一名女员工不为肥胖”的概率为2793010=， 由事件的独立性，得抽到的两个男员工都不存在肥胖的概率为44165525×=， 抽到的两个女员工都不存在肥胖的概率为99811010100×=， 设事件M 为“抽到的员工中至少有一名是肥胖”，则事件M 为“抽到的员工都不存在肥胖”， 所以()811632410025625P M =×=， 所以()3243011625625P M =−=， 所以抽到的员工中至少有一名是肥胖的概率为301625． 20．【命题意图】本小题主要考查直线与直线、直线与平面、平面与平面的位置关系，直线与平面所成角等基础知识；考查空间想象能力，逻辑推理能力，运算求解能力等；考查化归与转化思想，数形结合思想，函数与方程思想等；考查直观想象，逻辑推理，数学运算等核心素养；体现基础性和综合性．满分12分．【解答】（1）取AD 的中点为O ，连结OM ，OB ，因为四边形ABCD 是为菱形，且2AD BD ==，所以ABD △为正三角形，所以BO AD ⊥，且BO =．因为MAMD ==，所以MO AD ⊥，所以1MO =，又因为2MB =，所以222MO BO MB +=，所以MO BO ⊥，因为AD BO O ∩=，AD ⊂平面ABCD ，BO ⊂平面ABCD所以MO ⊥平面ABCD ，又因为MO ⊂平面MAD ，所以平面MAD ⊥平面ABCD ．（2）由（1）知，OA ，OB ，OM 两两垂直，故以O 为坐标原点，分别以OA ，OB ，OM 为x ，y ，z 轴的正方向建立如图所示的空间直角坐标系O xyz −．则()1,0,0A，()B，()C −，()0,0,1M，13N ，所以()3,CA =，12,3CN =，()2,0,0CB = ， 设平面ACN 的法向量为(),,n x y z = ， 则0,0,n CA n CN ⋅= ⋅=即30,120,3x x y z = +=取1x =，则()3n − ．因为()0,BM = ，则cos ,BM n BM n BM n⋅=== ， 所以直线BN 与平面ACN21．【命题意图】本小题主要考查椭圆的标准方程及简单几何性质，直线与圆、椭圆的位置关系，平面向量等基础知识；考查运算求解能力，逻辑推理能力，直观想象能力和创新能力等；考查数形结合思想，函数与方程思想，化归与转化思想等；考查直观想象，逻辑推理，数学运算等核心素养；体现基础性，综合性与创新性．满分12分．【解答】（1）依题意，()2,0A −，()2,0B ．设()11,C x y ，则2211143x y +=， 直线AC 方程为()1122y y x x ++，令4x =得1162P y y x =+， 直线BC 方程为()1122y yx x −−，令4x =得1122Q y y x =−， 所以2121124P Q y y y x =− 2121123144x x ×− =− 9=−，即P Q y y ⋅的值为9−．（2）设()22,D x y ，()4,P t ，则直线AP 方程为()26t y x =+，直线BP 的方程为()22t y x =−， 由()222,63412t y x x y =+ +=得()222227441080t x t x t +++−=， 所以2124108227t x t −−=+，即21254227t x t −=+，故()112182627t t y x t=+=+． 由()222,23412t y x x y =− +=得()2222344120t x t x t +−+−=， 所以22241223t x t −=+，即222263t x t −=+，故()2226223t t y x t −=−=+． 所以()()122111x y x y −−−2222222736918273327t t t t t t t t−−−=⋅−⋅++++ ()()()222262733270327t t t t t −−+−=++，又()1,0F ，所以向量()111,FC x y =− ，与()221,FD x y =− 共线，所以直线CD 经过F ． 解法二：（1）依题意，()2,0A −，()2,0B ．设()11,C x y ，则2211143x y +=， 所以111122AC BC y y k k x x ⋅=⋅+− 21214y x =− 21213144x x −−= 34=−． 即B 344242Q P AP Q y y k k −=⋅=⋅+−，故P Q y y 的值为9−． （2）设()11,C x y ，()22,D x y ，()4,P t ．要证直线CD 经过()1,0F ，只需证向量()111,FC x y =− ，与()221,FD x y =− 共线，即证()()122111x y x y −=−．（*） 因为()2222112014343x y −+==+，所以111123246P AC y x y k x y −==−⋅=+， 同理可得222223242P BD y x y k x y +==−⋅=−， 所以()()21122123AC BD x y k k x y −==+，即1221123620x y x y y y −++=，① 同理可得1221123260x y x y y y −+++=，②①－②得12211244440x y x y y y −+−=，即()()122111x y x y −=−．所以（*）式成立，命题得证．22．【命题意图】本小题主要考查导数，函数的单调性、零点、不等式等基础知识；考查逻辑推理能力，直观想象能力，运算求解能力和创新能力等；考查函数与方程思想，化归与转化思想，分类与整合思想等；考查逻辑推理，直观想象，数学运算等核心素养；体现基础性、综合性和创新性．满分12分．【解答】（1）()1f x x′=， 当1e x =，1a =时，()1ln e 10f x =−=，即切点为()e,0， 所以所求切线斜率()1e ek f ′=， 所以所求的切线方程为()1e e y x =−，即11ey x =−． （2）由于()11ln f x x a =−， 所以切线l 的方程为()()1111ln y x a x x x −−=−． 令0y =，得()()1111ln x a x x x −−=−，解得()2111ln x x x x a =−−．（*） 由20x >，得11e a x +<． 构造函数()()ln g x x x x a =−−， 所以()ln g x a x ′=−，所以当0e a x <<时，()0g x ′>，()x 单调递增；当e a x >时，()0g x ′<，()g x 单调递减．故()()max e e a a g x g ==．所以2e a x ≤．若1e a x ≤，由（*）式知12x x ≤，所以12e a x x ≤≤， 故12e e a a x x −≥−．若1e a x >，则()()()121212e e e e 2e a a a a a x x x x x x −−−=−−−=+−， 所以()12111e e 2ln 2e a a a x x x x x a −−−=−−−．构造函数()()()12ln 2e e e aa a x x x x a x ϕ+=−−−<<，所以()()1ln 0x a x ϕ′=+−>，故()x ϕ在区间()1e ,e a a +上单调递增， 所以()()e 0a x ϕϕ>=，所以()1112ln 2e 0a x x x a −−−>，即 所以12e e 0a a x x −−−>，即12e e a a x x −>−． 综上，不等式成立12e e a a x x −≥−成立（当且仅当1e a x =时取等号）．。

2024-2025学年福州市高三年级第一次质量检测数学答案一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的。

有多项符合题目要求。

全部选对的得6分，部分选对的得部分分，有选错的得0分。

15. （13分）已知数列{}n a 满足12a =，132n n a a +=+． （1）证明：数列{}1n a +是等比数列； （2）求{}n a 的前n 项和n S ．【解法一】（1）证明：因为132n n a a +=+，且12a =，所以10n a +≠， ··················································································· 1分 所以1132111n n n n a a a a ++++=++ ········································································ 3分 3(1)31n n a a +==+， ···································································· 5分 又113a +=，所以数列{}1n a +是以3为首项，3为公比的等比数列． ······························· 6分 （2）由（1）得13n n a +=，所以31n n a =−， ············································· 8分 所以()()()2313131n n S =−+−++−()233333n n =++++− ···························································· 10分13313n n +−=−− ············································································ 12分 133.2n n +−=− ············································································ 13分【解法二】（1）证明：因为132n n a a +=+，所以()113331n n n a a a ++=+=+， ····························································· 2分 因为12a =，所以1130a +=≠，所以10n a +≠， ········································ 4分 所以1131n n a a ++=+, 所以数列{}1n a +是以3为首项，3为公比的等比数列． ······························· 6分 （2）略，同解法一． 16. （15分）已知ABC △的内角,,A B C 的对边分别为,,a b c，且2cos cos cos a C C B =⋅． （1）求角C ；（2）若4a =，b =D 为AB 中点，求CD 的长． 【解法一】（1）因为2cos cos cos a C C B =+⋅， 由正弦定理，得2sin cos cos sin A C B C B C =·············································· 2分()B C =+ ·································································· 4分()πA −A =，······································································ 6分 因为0πA <<，则sin 0A ≠，所以cos C =， ·········································· 7分 由于0πC <<，则π6C =； ···································································· 8分 （2）因为D 为AB 中点，故()12CD CA CB =+， ······································ 10分22111πcos 4426CA CB CA CB =++ ············································ 13分 1113164442=⨯+⨯+ 314=，················································································· 14分 所以CD ． ······································································ 15分 【解法二】（1）因为2coscos cos a CC B =⋅，由余弦定理，得2222222cos 22a b c a c b a C ab ac+−+−=··························· 2分 ， ···························································· 4分所以cos C =， ················································································ 6分 由于0πC <<，则π6C =； ···································································· 8分 （2）由（1）知，π6ACB ∠=， 在ABC △中，由余弦定理，得2222cos c a b ab ACB =+−∠··································································· 10分 22424=+−⨯ 7=， ··························································································· 11分 故c =， ······················································································· 12分 因为D 为AB 中点，所以cos cos 0ADC BDC ∠+∠=，故222222022AD CD AC BD CD BC AD CD BD CD +−+−+=⨯⨯⨯⨯， ·········································· 13分22222240CD CD +−+−=，故CD ． ··········································································· 15分 【解法三】（1）略，同解法一或解法二； （2）由（1）知，π6ACB ∠=， 在ABC △中，由余弦定理，得2222cos c a b ab ACB =+−∠··································································· 10分22424=+−⨯ 7=， ··························································································· 11分故c =， ······················································································· 12分 所以222cos 2b c a A bc+−=2224+−==， ············································································· 13分 在ACD △中，由余弦定理， 得2222cos CD AC AD AC AD A =+−⋅222⎛=+− ⎝⎭⎝314=， ······················································································· 14分故CD ． ··········································································· 15分 17. （15分）如图，在四棱锥S ABCD −中，BC ⊥平面SAB ，∥AD BC ，1SA BC ==，SB =，o 45SBA ∠=．（1）求证：SA ⊥平面ABCD ；（2）若12AD =，求平面SCD 与平面SAB 的夹角的余弦值． 【解法一】（1）在△SAB 中， 因为1SA =，o 45SBA ∠=，SB =， 由正弦定理，得sin sin SA SBSBA SAB=∠∠， ········································································· 1分所以1sin 45︒， ······································································ 2分 所以sin 1SAB ∠=，因为0180SAB ︒<∠<︒，所以90SAB ∠=︒，所以SA AB ⊥． ··················································································· 4分 因为BC ⊥平面SAB ，SA ⊂平面SAB ，所以BC SA ⊥， ··················································································· 5分 又BCAB B =，所以SA ⊥平面ABCD ； ········································································· 6分 （2）解：由（1）知SA ⊥平面ABCD ，又,⊂AB AD 平面ABCD ，所以SA AB ⊥，SA AD ⊥，因为BC ⊥平面SAB ， ··········································································· 7分 ⊂AB 平面SAB ，所以BC AB ⊥，因为∥AD BC ，所以AD AB ⊥，所以,,SA AD AB 两两垂直． ··································································· 8分 以点A 为原点，分别以AD ，AB ，AS 所在直线为x 轴，y 轴，z 轴建立如图所示的空间直角坐标系， ················································································ 9分 则1(1,1,0),,0,0,2(0,0,1),D S C ⎛⎫ ⎪⎝⎭所以()1,1,1SC =−，1,0,12SD ⎛⎫=− ⎪⎝⎭，设平面SCD 的法向量为1(,,)x y z =n ，则11,,SC SD ⎧⊥⎪⎨⊥⎪⎩n n 即110,10,2SC x y z SD x z ⎧⋅=+−=⎪⎨⋅=−=⎪⎩n n 取2x =，则()12,1,1=−n ， ·································································· 11分显然平面SAB 的一个法向量()21,0,0=n ， ················································ 12分 所以cos ⋅=⋅121212n n n ,n n n ····································································· 13分==········································································· 14分 所以平面SCD 与平面SAB ． ··································· 15分 【解法二】（1）证明：设AB x =，在△SAB 中， 因为1SA =，o 45SBA ∠=，SB =， 由余弦定理，得2222cos SA SB AB SB S AB BA =∠+−⋅， · (1)分 所以212co 5s 4x =+−︒， (2)分所以221x +−=， 所以2210x x −+=，解得1x =． ························································································ 3分 所以2222SA AB SB +==，所以SA AB ⊥． ················································ 4分 因为BC ⊥平面SAB ，SA ⊂平面SAB ，所以BC SA ⊥， ··················································································· 5分 又BCAB B =，所以SA ⊥平面ABCD ； ········································································· 6分 （2）略，同解法一．【解法三】（1）设AB x =，在△SAB 中， 因为1SA =，o 45SBA ∠=，SB =， 由余弦定理，得2222cos SA SB AB SB S AB BA =∠+−⋅， (1)分所以212co 5s 4x =+−︒， ································································ 2分所以221x+−=，所以2210x x−+=，解得1x=． ························································································3分所以2222SA AB SB+==，所以SA AB⊥．················································4分因为BC⊥平面SAB，BC⊂平面ABCD，所以平面ABCD⊥平面SAB；·································································5分又平面ABCD平面SAB AB=，SA AB⊥，SA⊂平面SAB，所以SA⊥平面ABCD；·········································································6分（2）由（1）知SA⊥平面ABCD，过B作BM SA，则BM⊥平面ABCD，又,AB BC⊂平面ABCD，所以BM AB⊥，BM BC⊥，因为BC⊥平面SAB，···········································································7分又⊂AB平面SAB，所以BC AB⊥，所以,,BM BA BC两两垂直．··································································8分以点B为原点，分别以BA，BC，BM所在直线为x轴，y轴，z轴建立如图所示的空间直角坐标系， ················································································9分则1(0,1,0),1,(,0,21,0,1),CS D⎛⎫⎪⎝⎭所以()1,1,1SC=−−，11,,02CD⎛⎫=−⎪⎝⎭，设平面SCD的法向量为1(,,)x y z=n，则11,,SCCD⎧⊥⎪⎨⊥⎪⎩nn即110,10,2SC x y zCD x y⎧⋅=−+−=⎪⎨⋅=−=⎪⎩nn取2y=，则()11,2,1=n， ···································································· 11分显然平面SAB的一个法向量()20,1,0=n， ··············································· 12分所以cos⋅=⋅121212n nn,nn n····································································· 13分=。

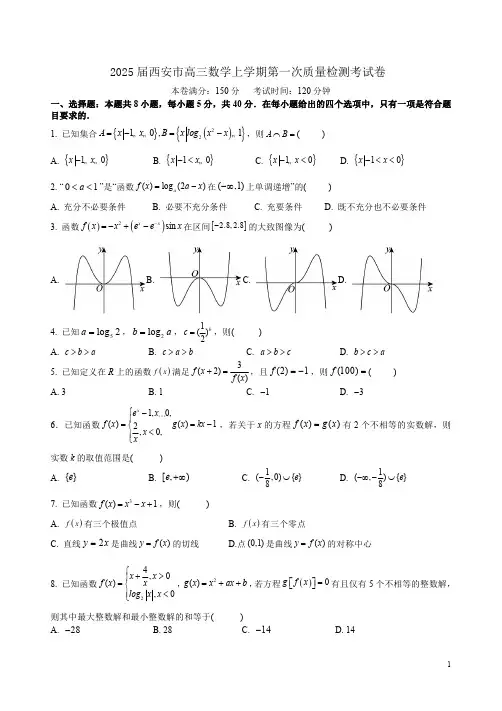
2025届西安市高三数学上学期第一次质量检测考试卷本卷满分：150分考试时间：120分钟一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合{}(){}2210,1=-=-A x x B x log x x ，则A B ⋂=()A.{}10x x - B.{}10x x -< C.{}10x x -< D.{}10x x -<<2.“01a <<”是“函数()log (2)a f x a x =-在(,1)-∞上单调递增”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.函数()()2sin x xf x x e e x-=-+-在区间[]2.8,2.8-的大致图像为()A. B. C. D.4.已知5log 2a =，2log b a =，1()2bc =，则()A.c b a >> B.c a b>> C.a b c>> D.b c a>>5.已知定义在R 上的函数()f x 满足3(2)()f x f x +=，且(2)1f =-，则(100)f =()A.3B.1C.1-D.3-6．已知函数1,0,()()12,0,x e x f x g x kx x x⎧-⎪==-⎨<⎪⎩ ，若关于x 的方程()()f x g x =有2个不相等的实数解，则实数k 的取值范围是()A.{}e B.[,)e +∞ C.1(,0){}8e -⋃ D.1(,){}8e -∞-⋃7.已知函数3()1f x x x =-+，则()A.()f x 有三个极值点B.()f x 有三个零点C.直线2y x =是曲线()y f x =的切线D.点(0,1)是曲线()y f x =的对称中心8.已知函数24,0(),0x x f x x log x x ⎧+>⎪=⎨⎪<⎩，2()g x x ax b =++，若方程()0g f x =⎡⎤⎣⎦有且仅有5个不相等的整数解，则其中最大整数解和最小整数解的和等于()A.28-B.28C.14- D.14二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9.下列导数运算正确的是（）A.211(x x'=- B.()x xe e '--= C.21(tan )x cos x'=D.1(ln ||)x x'=10.甲乙丙等5人的身高互不相同，站成一排进行列队训练，则()A.甲乙不相邻的不同排法有48种B.甲乙中间恰排一个人的不同排法有36种C.甲乙不排在两端的不同排法有36种D.甲乙丙三人从左到右由高到矮的不同排法有20种11.已知0c b a <<<，则()A.ac b bc a+<+ B.333b c a +< C.a c ab c b+<+ D.>三、填空题：本题共3小题，每小题5分，共15分．12.某班的全体学生参加化学测试，成绩的频率分布直方图如图所示，数据的分组依次为[20,40),[40,60),[60,80),[80,100]，则该班学生化学测试成绩的第40百分位数为__________.13.若曲线x y e x =+在点(0,1)处的切线也是曲线ln(1)y x a =++的切线，则a =__________.14.5(1)(2)y x y x-+的展开式中，23x y 的系数为__________.四、解答题：本题共5小题，其中第15题13分，第16,17题15分，第18,19题17分，共77分．解答应写出文字说明、证明过程或演算步骤．15．已知函数3212()2.32a f x x x ax +=-+（1）若1a =，求函数()f x 的极值；（2）讨论函数()f x 的单调性.16．为践行“更快更高更强”的奥林匹克格言，落实全民健身国家战略.某校高三年级发起了“发扬奥林匹克精神，锻炼健康体魄”的年度主题活动，经过一段时间后，学生的身体素质明显提高.为了解活动效果，该年级对开展活动以来近6个月体重超重的人数进行了调查，调查结果统计如图，根据上面的散点图可以认为散点集中在曲线bx a y e +=的附近，请根据下表中的数据求出（1）该年级体重超重人数y 与月份x 之间的经验回归方程(系数a 和b 的最终结果精确到0.01)；（2）预测从开展活动以来第几个月份开始该年级体重超标的人数降至10人以下.月份x 123456体重超标人数y987754483227ln z y= 4.58 4.37 3.98 3.87 3.46 3.29附：经验回归方程：ˆˆˆybx a =+中，1221ˆniii nii x ynx y b xnx ==-⋅=-∑∑，ˆˆay bx =-；参考数据：6123.52i i z ==∑，6177.72i ii x z==∑，62191i i x ==∑，ln10 2.30.≈17.已知函数()log (1)a f x x =+，()2log (2)(a g x x t t =+∈R )，0a >，且 1.a ≠（1）当01a <<且1t =-时，求不等式()()f x g x 的解集；（2）若函数()2()21f x F x a tx t =+-+在区间(1,2]-上有零点，求t 的取值范围．18.某企业对某品牌芯片开发了一条生产线进行试产.其芯片质量按等级划分为五个层级，分别对应如下五组质量指标值：[45,55),[55,65),[65,75),[75,85),[85,95].根据长期检测结果，得到芯片的质量指标值X 服从正态分布2(,)N μσ，并把质量指标值不小于80的产品称为A 等品，其它产品称为B 等品.现从该品牌芯片的生产线中随机抽取100件作为样本，统计得到如图所示的频率分布直方图.（1）根据长期检测结果，该芯片质量指标值的标准差s 的近似值为11，用样本平均数x 作为μ的近似值，用样本标准差s 作为σ的估计值.若从生产线中任取一件芯片，试估计该芯片为A 等品的概率(保留小数点后面两位有效数字);(①同一组中的数据用该组区间的中点值代表;②参考数据：若随机变量ξ服从正态分布2(,)N μσ，则()0.6827P μσξμσ-<<+≈，(22)0.9545P μσξμσ-<<+≈，(33)0.9973.)P μσξμσ-<<+≈（2）（ⅰ）从样本的质量指标值在[45,55)和[85,95]的芯片中随机抽取3件，记其中质量指标值在[85,95]的芯片件数为η，求η的分布列和数学期望；(ⅱ)该企业为节省检测成本，采用随机混装的方式将所有的芯片按100件一箱包装.已知一件A 等品芯片的利润是(124)m m <<元，一件B 等品芯片的利润是ln(25)m -元，根据(1)的计算结果，试求m 的值，使得每箱产品的利润最大.19.已知函数1()ln (1).x f x ae x a x -=+-+（1）当0=a 时，求函数()f x 的单调区间；（2）当1a =时，证明：函数()f x 在(0,)+∞上单调递增；（3）若1x =是函数()f x 的极大值点，求实数a 的取值范围.一.选择题（本题共8小题，每小题5分，共40分）二.选择题（本题共3小题，每小题6分，共18分）三、填空题：(本题共3小题，每小题5分，共15分.)12.6513.ln 214.40三、解答题：(本题共5小题，其中第15题13分，第16,17题15分，第18,19题17分，共77分)15.（本小题满分13分）解：(1)1a =时，3213()2,()(1)(2)32f x x x x f x x x '=-+=--，所以1x <或2x >时，()0f x '>；12x <<时，()0f x '<则()f x 在(1,2)上递减，在(,1),(2,)-∞+∞上递增，所以()f x 的极小值为2(2)3f =，极大值为5(1)6f =...............................5分陕西省西安中学高2025届高三第一次质量检测数学参考答案题号12345678答案CBABDCDA题号91011答案ACDBCDABD3212(2)()232a f x x x ax +=-+，则()()(2)f x x a x '=--，当2a =时，()0f x ' ，所以()f x 在(,)-∞+∞上递增，当2a >时，2x <或x a >时，()0f x '>；2x a <<时，()0f x '<,所以()f x 在(,2),(,)a -∞+∞上递增，在(2,)a 上递减，当2a <时，x a <或2x >时，()0f x '>；2a x <<时，()0f x '<所以()f x 在(,),(2,)a -∞+∞上递增；在(,2)a 上递减................................8分（2）令-+<=≈，所以，解得，由于，所以，所以从第十个月开始，该年级体重超标的人数降至10人以下................................5分17.（本小题满分15分）解：(1)1=- t 时，()()2log 1log 21a a x x +- ，又01a <<，21(21)210x x x ⎧+-∴⎨->⎩，2450151242x x x x ⎧-⎪∴∴<⎨>⎪⎩，∴解集为：15{|}24x x <；...............................6分(2)解法一：()222F x tx x t =+-+，由()0F x =得：22(2x t xx +=-≠-且12)x -< ，22(2)4(2)2x t x x +∴=-+-++，设2U x =+(14U < 且2U ≠，则212424U t U U U U=-=--+-+，令2()U U Uϕ=+， 当1U <<时，()U ϕ4U <<时，()U ϕ单调递增，且9(1)3,(4).2ϕϕϕ===9()2U ϕ∴且() 4.U ϕ≠12402U U∴---< 或2044U U<--- ，t 的取值范围为：2t - 或224t +解法二：()222F x tx x t =+-+，若0t =，则()2F x x =+在(1,2]-上没有零点．下面就0t ≠时分三种情况讨论：①方程()0F x =在(1,2]-上有重根12x x =，则0∆=，解得：24t =，又1212x x t ==-(]1,2,∈-24t +∴=；②()F x 在(1,2]-上只有一个零点，且不是方程的重根，则有()()120F F -<，解得：2t <-或1t >，又经检验：2t =-或1t =时，()F x 在(1,2]-上都有零点；2t ∴- 或 1.t ③方程()0F x =在(1,2]-上有两个相异实根，则有0,01122(1)0(2)0t t F F >∆>⎧⎪⎪-<-<⎪⎨⎪->⎪>⎪⎩或0,01122(1)0(2)0t t F F <∆>⎧⎪⎪-<-<⎪⎨⎪-<⎪<⎪⎩，解得：214t +<<，综上可知：t 的取值范围为2t - 或224t +...............................15分18.（本小题满分17分）(1)(1)由题意，估计从该品牌芯片的生产线中随机抽取100件的平均数为：10(0.01500.025600.04700.015800.0190)69.x =⨯⨯+⨯+⨯+⨯+⨯=即69x μ≈=11s σ≈≈，所以X ∽2(69,11)N ，因为质量指标值X 近似服从正态分布2(69,11)N ，所以1(69116911)1()(80)22P X P X P X μσμσ--<<+--<<+== 10.68270.158650.162-≈=≈，所以从生产线中任取一件芯片，该芯片为A 等品的概率约为0.16................................5分(2)()(0.010.01)1010020i +⨯⨯=，所以所取样本的个数为20件，质量指标值在[85,95]的芯片件数为10件，故η可能取的值为0，1，2，3，相应的概率为：3010103202(0)19C C P C η===，21101032015(1)38C C P C η===，12101032015(2)38C C P C η===，0310103202(3)19C C P C η===，随机变量η的分布列为：η0123P21915381538219所以η的数学期望2151523()0123.193838192E η=⨯+⨯+⨯+⨯=...............................11分()ii 设每箱产品中A 等品有Y 件，则每箱产品中B 等品有(100)Y -件，设每箱产品的利润为Z 元，由题意知：(100)ln(25)(ln(25))100ln(25)Z mY Y m m m Y m =+--=--+-，由(1)知：每箱零件中A 等品的概率为0.16，所以Y ∽(100,0.16)B ，所以()1000.1616E Y =⨯=，所以()[(ln(25))100ln(25)]E Z E m m Y m =--+-(ln(25))()100ln(25)m m E Y m =--+-16(ln(25))100ln(25)m m m =--+-1684ln(25)m m =+-,令()1684ln(25)(124)f x x x x =+-<<84()16025f x x '=-=-得，794x =，又79(1,)4x ∈，()0f x '>，()f x 递增79;(,24)4x ∈，()0f x '<，()f x 递减，所以当79(1,24)4x =∈时，()f x 取得最大值.所以当794m =时，每箱产品利润最大................................17分19.（本小题满分17分）(1)解：当0=a 时，()ln =-f x x x ，且知11()1-'=-=xf x x x，在(0,1)上，()0'>f x >，()f x 在(0,1)上单调递增；在(1,)+∞上，()0'<f x ，()f x 在(1,)+∞上单调递减；所以函数()f x 的单调增区间为(0,1)，单调减区间为(1,)+∞..............................4分(2)证明：因为1a =，所以1()ln 2x f x e x x -=+-，且知11()2x f x e x-'=+-，要证函数()f x 单调递增，即证()0f x ' 在(0,)+∞上恒成立，设11()2x g x ex -=+-，0x >，则121()x g x e x-'=-，注意1x y e -=，21y x=-在(0,)+∞上均为增函数，故()g x '在(0,)+∞上单调递增，且(1)0g '=，于是()g x 在(0,1)上单调递减，在(1,)+∞上单调递增，()(1)0g x g = ，即()0f x ' ，因此函数()f x 在(0,)+∞上单调递增;...............................10分(3)由11()1x f x ae a x -'=+--，有(1)0f '=，令11()1x h x ae a x -=+--，有121()x h x ae x-'=-，①当0a 时，11()0x xh x aex -'=-<在(0,)+∞上恒成立，因此()f x '在(0,)+∞上单调递减，注意到(1)0f '=，故函数()f x 的增区间为(0,1)，减区间为(1,)+∞，此时1x =是函数()f x 的极大值点;②当0a >时，1x y ae -=与21y x=-在(0,)+∞上均为单调增函数，故()h x '在(0,)+∞上单调递增，注意到(1)1h a '=-，若(1)0h '<，即01a <<时，此时存在(1,)n ∈+∞，使()0h n '=，因此()f x '在(0,)n 上单调递减，在(,)n +∞上单调递增，又知(1)0f '=，则()f x 在(0,1)上单调递增，在(1,)n 上单调递减，此时1x =为函数()f x 的极大值点，若(1)0h '>，即1a >时，此时存在(0,1)m ∈，使()0h m '=，因此()f x '在(0,)m 上单调递减.在(,)m +∞上单调递增，又知(1)0f '=，则()f x 在(,1)m 上单调递减，在(1,)+∞上单调递增，此时1x =为函数()f x 的极小值点.当1a =时，由(1)可知()f x 单调递增，因此1x =非极大值点，综上所述，实数a 的取值范围为(,1).-∞..........................17分。

一、选择题1. 答案：D解析：由指数函数的性质可知，当x>0时，y=2^x是增函数，且2^0=1，故选D。

2. 答案：A解析：由函数的性质可知，y=x^3在定义域内单调递增，故选A。

3. 答案：B解析：由二次函数的性质可知，对称轴为x=-b/2a，顶点坐标为(-b/2a, c-b^2/4a)，故选B。

4. 答案：C解析：由数列的性质可知，an+1/an=2an/(an+1-an)，故选C。

5. 答案：A解析：由立体几何的性质可知，正方体的对角线互相垂直，故选A。

二、填空题6. 答案：-1/3解析：由指数函数的性质可知，y=2^x在x=0时，y=1，故2^(-1/3)=1/2^1/3=1/2，故答案为-1/3。

7. 答案：-4解析：由二次函数的性质可知，对称轴为x=-b/2a，顶点坐标为(-b/2a, c-b^2/4a)，故顶点坐标为(-1, -4)。

8. 答案：9解析：由数列的性质可知，an+1/an=2an/(an+1-an)，故an+1=2an(an+1-an)，化简得an+1=2an^2，代入an=1，得an+1=2。

9. 答案：2解析：由立体几何的性质可知，正方体的对角线互相垂直，故正方体的对角线长度为2a，其中a为正方体的边长。

10. 答案：1/2解析：由向量的性质可知，向量a与向量b的数量积等于它们的模长乘以它们的夹角的余弦值，故|a|=1，|b|=2，cosθ=1/2，得θ=60°。

三、解答题11. 解答：（1）由指数函数的性质可知，y=2^x在x=0时，y=1，故2^(-1/3)=1/2^1/3=1/2，得a=1/2。

（2）由二次函数的性质可知，对称轴为x=-b/2a，顶点坐标为(-b/2a, c-b^2/4a)，代入a=1/2，得顶点坐标为(-1, -4)。

12. 解答：（1）由数列的性质可知，an+1/an=2an/(an+1-an)，故an+1=2an(an+1-an)，化简得an+1=2an^2，代入an=1，得an+1=2。

2024届高三第一次学业质量评价(T8联考)数学试题参考答案2024届高三T8第一次联考数学试题2024届高三T8第一次联考数学试题参考答案什么是t8联考秉承发展教育、服务教学宗旨，本着推动进步、共同提高的原则，华中师范大学测量与评价研究中心联合华中师范大学第一附属中学、东北育才学校、福建省福州第一中学、广东实验中学、湖南师范大学附属中学、南京师范大学附属中学、石家庄二中、西南大学附属中学等学校于组成T8联盟。

作为以共同进入第已批高考试点省(市)学校为主的高中名校教育教学联合体，T8联盟以专业的教育评价研究机构作为学术引领和支撑，基于联盟内高中名校多年教育教学实践，以高中学校高考命题研究为切入点，着力服务于高中学校的学业质量检测、学业水平提升、教学管理与教学研究水平的提高，并助推高中教师的专业发展。

八省(市)学业质量评价联考(T8联考)先后于12月、2021年12月、2022年3月及2022年12月成功举办，其具有高度原创性的试题，精准地把握了新高考的方向与特质，引起高中学校和教育研究领域专家的高度关注，赢得师生广泛好评。

T8联考虽然是八省参与，但并不是八省内所有高三生都参加，而是由新高考八省各派出省内重点高中学校进行PK，也是8所名校之间的PK。

高三联考会影响高考吗不影响。

虽然联考只是几所相当的学校，一起出试题，进行考试，并不是真正意义上的高考，所以相对来说，成绩并不会影响什么，只能说，对于高三的学子，多了一种考试的方式，所以并不是很重要。

其实很简单，一旦参与了联考的学生，就能够感受到浓烈的危机意识，毕竟高考在即，要提前适应高三整个学年的高度紧张的学习氛围，从而让学生感受到压力潜意识的去拼搏，为自己博得一个好的人生。

微信搜索关注公众号：得道AI填报温馨提示：看完整版及各省份高考试卷真题，可下载全文查看或微信搜索公众号【得道AI填报】，关注后在对话框回复【高考真题】免费即可获取。

平许济洛2023—2024学年高三第一次质量检测数学（答案在最后）一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一个选项是符合题目要求的。

1.设全集U =R ，集合{}{}22,320x A y y B x x x ===-+<，则()UA B = ð（）A.[)2,+∞ B.()0,∞+ C.(]0,1 D.][()0,12,+∞ 【答案】D 【解析】【分析】根据题意，将集合,A B 化简，结合集合的运算，即可得到结果.【详解】因为{}()20,xA y y ∞===+，{}()23201,2B x xx =-+<=，则(][),12,U B =-∞+∞ ð，所以()U A B = ð][()0,12,+∞ .故选：D 2.复数z 满足()2023i 22i z +=-，则z =（）A.12i -+B.12i+ C.12i-- D.12i-【答案】C 【解析】【分析】由虚数单位的乘方的性质结合除法运算可得12i z =-+，进而可得共轭复数.【详解】因为()505202343i i i i =⋅=-，所以()2023i22i z +=-可化为2i 2iz -=--所以()2i2i i=12i iz +==+-+-，所以12z i =--.故选：C.3.已知椭圆2222:1(0)x y C a b a b +=>>的离心率为121,,2A A 分别为C 的左、右顶点，B 为C 的上顶点．若122BA BA ⋅=-，则椭圆C 的方程为（）A.2211612x y += B.22186x y += C.22143x y += D.222123x y +=【答案】B【解析】【分析】根据离心率及12=2BA BA ⋅-，建立关于22,a b 的等式即可得解.【详解】显然离心率12e a ===，解得2234b a =，即2234b a =，12,A A 分别为C 的左右顶点，B 为上顶点，则()()12,0,,0A a A a -，(0,)B b ，于是12(,),(,)=--=-BA a b BA a b ，而122BA BA ⋅=- ，即222a b -+=-，又2234b a =，因此联立解得228,6a b ==，所以椭圆的方程为22186x y +=.故选：B4.过圆224x y +=内点()1,1P 有若干条弦，它们的长度构成公差为d 的等差数列{}n a ，且11,63d ⎛⎫∈ ⎪⎝⎭，其中1,n a a 分别为过点P 的圆的最短弦长和最长弦长，则n 的取值集合为（）A.{}4,5,6 B.{}5,6,7 C.{}5,6,7,8 D.{}6,7,8,9【答案】C 【解析】【分析】根据圆的性质可得14==n a a ，再结合等差数列运算求解.【详解】由题意可知：圆224x y +=的圆心为()0,0O ，半径2r =，则OP ==，可知124====n a a r ，因为数列{}n a 为等差数列，则1411,1163--⎛⎫==∈ ⎪--⎝⎭n a a d n n ，解得(1325∈--n ，又因为13 4.516,258.032-≈-且*n ∈N ，则{}5,6,7,8n ∈，所以n 的取值集合为{}5,6,7,8.故选：C.5.如图，正方形ABCD 中，2,DE EC P = 是线段BE 上的动点，且(0,0)AP x AB y AD x y =+>>，则11x y+的最小值为（）A.22B.23C.433+ D.4【答案】C 【解析】【分析】根据给定图形，用,AB AE 表示向量AD，再利用共线向量定理的推论，结合“1”的妙用求解即得.【详解】正方形ABCD 中，2DE EC =，则2233AD AE ED AE CD AE AB =+=+=- ，而AP xAB y AD =+ ，则(22)()33A B x AE A x P AB y AB y E y A --=++=，又点,,B P E 共线，于是2()13x y y -+=，即13y x +=，而0,0x y >>，因此313111)(4443()3333x y x y x x y y y x x y x y ++=+=+++≥+⋅，当且仅当3x y y x =，即33332y x -==时取等号，所以当33333,22x y ==时，11x y +取得最小值4233+.故选：C6.定义在R 上的偶函数()f x 满足()()20f x f x -+=，且()f x 在[]2,0-上单调递增．若()()45πtan ,3,log 318a f b f c f ⎛⎫=== ⎪⎝⎭，则（）A.a b c <<B.a c b<< C.c b a<< D.c a b<<【答案】A 【解析】【分析】由(2)()f x f x +=-得(4)()f x f x +=，即函数的周期为4，利用函数的周期性，奇偶性和单调性之间的关系进行判断即可．【详解】由()()20f x f x -+=以及偶函数可得()()()22f x f x f x =--=--，故()()24f x f x -=--，由此可得()()4f x f x =-，即函数的周期是4．偶函数()y f x =在[2-,0]上单调递增，∴函数在[0,2]上单调递减．(3)(34)(1)(1)f f f f =-=-=，40log 31<<,5ππtantan 1184>=,故()()()44π5π5π3>tan 1log 30,tan 13log 331818f f f f ⎛⎫=>>>∴<=< ⎪⎝⎭即a b c <<．故选：A7.2023贺岁档电影精彩纷呈，小明期待去影院观看．小明家附近有甲、乙两家影院，小明第一天去甲、乙两家影院观影的概率分别为25和35．如果他第一天去甲影院，那么第二天去甲影院的概率为35；如果他第一天去乙影院，那么第二天去甲影院的概率为12．若小明第二天去了甲影院，则第一天去乙影院的概率为（）A.2350B.12C.25D.59【答案】D 【解析】【分析】设出事件，根据条件概率公式得到()()63,2510P AB P BC ==，结合全概率公式求出答案.【详解】设小明第一天去甲影院为事件A ，第二天去甲影院为事件B ，小明第一天去乙影院为事件C ，第二天去乙影院为事件D .故()()()()2331,,,5552P A P C P B A P B C ====，由()()()()()()31,52P AB P BC P B A P B C P A P C ====可得()()63,2510P AB P BC ==，故()()()6327251050P B P AB P CB =+=+=，则小明第二天去了甲影院，则第一天去乙影院的概率为()()()351027950P BC P C B P B ===.故选：D8.已知()()()1e ln ln ,1e xf x a x ag x x -=-+=-，当0x >时，()()e f x g x ≥，则a 的取值范围为（）A.1,1e ⎡⎫⎪⎢⎣⎭B.1,e ∞⎡⎫+⎪⎢⎣⎭C.[)1,+∞ D.[)e,+∞【答案】B 【解析】【分析】设()e e xF x x =+，利用同构得到()()ln ln F x a F x +≥，结合()e e xF x x =+的单调性得到ln ln a x x ≥-，构造()ln h x x x =-，求导得到其单调性和最值，得到最大值为()11h =-，故ln 1a ≥-，求出答案.【详解】由题意得，当0x >时，()()()e e eln eln 1e 0xf xg x a x a x -=-+--≥，即()ln ln ee ln eln e eln x ax x a x x x ++++≥+=，0x >，令()e e xF x x =+，则()()ln ln F x a F x +≥，因为()e e 0xF x '=+>恒成立，故()e e xF x x =+在R 上单调递增，故ln ln x a x +≥，即ln ln a x x ≥-，令()ln h x x x =-，则()111x h x x x-'=-=，当()0,1x ∈时，()0h x '>，()ln h x x x =-单调递增，当()1,x ∈+∞时，()0h x '<，()ln h x x x =-单调递减，故()ln h x x x =-在1x =处取得极大值，也是最大值，最大值为()11h =-，故ln 1a ≥-，解得1ea ≥.故选：B【点睛】导函数求解参数取值范围，当函数中同时出现e x 与ln x ，通常使用同构来进行求解，本题难点是将()e eln eln 1e 0xa x a x -+--≥变形得到()ln ln ee ln eln e eln x ax x a x x x ++++≥+=，从而构造()e e x F x x =+进行求解.二、选择题：本题共4小题，每小题5分，共20分。

浙江省台州市2025届高三第一次教学质量评估数学试题本试题卷分选择题和非选择题两部分。

满分150分，考试时间120分钟。

请考生按规定用笔将所有试题的答案涂、写在答题纸上。

选择题部分 (共58分)一、选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知t anα=2, 则c os 2α的值为A. A.255 B. 45C.35D.−352. 椭圆E1:x29+y24=1与椭圆E2:x29−k+y24−k=1(0＜k＜4)的A. 长轴长相等B. 短轴长相等C. 离心率相等D. 焦距相等3.若复数z是方程x²−2x+5=0的一个虚根，则. z+z=A. - 2B. 2C. - 4iD. 4i4.已知集合 A=x|x²+2x＜3,B=x|2ˣ+x＜3,则 “x∈A”是“x∈B”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5.已知变量x与y的成对样本数据具有线性相关关系，由一元线性回归模型根据最小二乘法, 计算得经验回归方程为y=1.6x+a, 若∑=10, y=15, 则a=A. 6.6B. 5C. - 1D. - 146.已知f(x)是定义在R 上的奇函数, 当x∈(0,+∞)时, f(x)=log₃x,则f(-9)=A. - 3B. - 2C. 2D. 37.已知球O的半径为3，P是球O表面上的定点，S是球O表面上的动点，且满足( (2SO+SP)⋅OP=0,则线段OS 轨迹的面积为A. 32πB. 35πC. 62πD. 65π8.台州某校为阳光体育设计了一种课间活动，四位同学(两男两女) 随机地站到4×4的方格场地中(每人站一格，每格至多一人)，则两个男生既不同行也不同列，同时两个女生也既不同行也不同列的概率是A. 2465 B. 1235C. 2165D. 3391二、选择题：本大题共3小题，每小题6分，共18分。

河南省信阳市2023-2024学年高三第一次教学质量检测数学
试题
学校:___________姓名：___________班级：___________考号：___________
一、单选题
二、多选题
．．
．．
．四个实数1-，2，x ，y 按照一定顺序可以构成等比数列，则xy 的可能取值有（
．1
8-
B ．2-16
-D ．．已知0a >，0b >，且a +，则不正确的是（
）
．14
ab ≥
B ．2a 216a b
+≥D ．．函数()f x 及其导函数f '，且()f x 是奇函数，设()4f x x -+，则以下结论正确的有（
．函数()2g x -的图象关于直线．若()g x 的导函数为g ，则()00g '=．()h x 的图象存在对称中心
．设数列{}a 为等差数列，44=，则()()h a h a ++三、填空题
四、解答题
参考答案：
又根据对称性可知()1f x 与12y =
形成的封闭图形的面积为又()()2124f x f x =-，[]4,8x ∈，所以2f 即212a a =，
故以此类推，有12n n a a +=，*n ∈N ，
所以数列{}n a 是以2为首项，2为公比的等比数列，
所以(
)1232122
12
n
n a a a a ⨯-+++⋅⋅⋅⋅⋅⋅+=
=-由8122510511+-=<，91221022511+-=>。

注意事项：1．答卷前，考生务必将自己的班级、姓名、考号填写在答题卡上．2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．写在本试卷上无效．3．回答非选择题时，将答案写在答题卡上．写在本试卷上无效．4四川省绵阳市2024-2025学年高三第一次诊断性考试数学质量检测试题．考试结束后，将答题卡交回．第Ⅰ卷（选择题，共58分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 已知集合{}2,1,0,1,2A =--，(){}211B x x =+≤，则A B = （ ）A. {}2,1--B. {}2,1,0-- C. []2,0- D. []22-,【答案】B 【解析】【分析】先求出集合B ，再根据集合交集运算即可得答案【详解】由()211x +≤，可得20x -≤≤，所以{}20B x x =-≤≤，所以A B = {}{}{}2,1,0,1,2202,1,0x x --⋂-≤≤=--.故选：B2. “22ac bc >”，是“a b >”的（ ）A. 充分不必要条件 B. 必要不充分条件C. 充分必要条件 D. 既不充分也不必要条件【答案】A 【解析】【分析】利用充分条件、必要条件的定义判断即得.【详解】若22ac bc >，则20,0c c ≠>，因此a b >，当a b >，0c =时，220ac bc ==，所以“22ac bc >”，是“a b >”的充分不必要条件.故选：A3. 已知0,0x y >>，且满足3x y xy +=-，则xy 的最小值为（ ）A. 3B. C. 6D. 9【答案】D 【解析】【分析】利用基本不等式化简已知条件，再解不等式求得xy 的范围，从而求得xy 的最小值.详解】3x y xy +=-≥)23310--=+≥，30,9xy -≥≥，当且仅当3x y ==时等号成立，所以xy 的最小值为9.故选：D4. 某公司根据近几年经营经验，得到广告支出与获得利润数据如下：广告支出x /万元258111519利润y /万元334550535864根据表中数据可得利润y 关于广告支出x 的经验回归方程为ˆ 1.6ˆ5yx a =+．据此经验回归方程，若计划利润达到100万元，估计需要支出广告费（ ）A. 30万元 B. 32万元C. 36万元D. 40万元【答案】D 【解析】【分析】先得求数据的中心点()10,50.5，代入ˆ 1.6ˆ5yx a =+得ˆ34a =，再由ˆ100=y 求得40x =即得.【详解】258111519106x +++++==，33455053586450.56y +++++==，因ˆ 1.6ˆ5yx a =+过点()x y ，故ˆ50.5 1.6510a =⨯+，得ˆ34a =，【故当ˆ100=y时，341001.65x +=，得40x =，故选：D5. 下列选项中，既是增函数，也是奇函数的是（ ）A. 2y x -= B. 1y x x=+C. sin y x x =-D. 1ln1x y x -=+【答案】C 【解析】【分析】分别判断函数的奇偶性和单调性即可.【详解】对于A ，令()2f x x -=，0x ≠，()()()22fx x x fx ---=-==，所以2y x -=是偶函数，故A 错误；对于B ，1y x x=+在(),1∞--和()1,+∞上单调递增，在()1,0-和()0,1上单调递减，故B 错误；对于C ，令()sin g x x x =-，R x ∈，()()()()sin sin g x x x x x g x -=---=--=-，所以sin y x x =-是奇函数，又1cos 0y x '=-≥，所以sin y x x =-是R 上的增函数，故C 正确；对于D ，令()1ln1x h x x -=+，()(),11,x ∈-∞-⋃+∞，则()()()11201111x x h x x x x x '+-⎛⎫'=⋅=> ⎪-+-+⎝⎭，所以函数1ln 1x y x -=+在(),1∞--和()1,+∞上单调递增，但在定义域上不单调，故D 错误.故选：C.6. 已知θ为第一象限角，且πtan tan 03θθ⎛⎫++= ⎪⎝⎭，则1cos21cos2θθ-=+（ ）A. 9 B. 3C.13D.19【答案】B 【解析】【分析】根据两角和正切公式结合已知条件可求出tan θ=.【详解】由题意知θ为第一象限角，且πtan tan 03θθ⎛⎫++= ⎪⎝⎭，的故πtan tan3tan 0π1tan tan 3θθθ++=-，解得tan θ=或tan θ=（舍去），则2221cos22sin tan 31cos22cos θθθθθ-===+，故选：B7. 某工厂产生的废气经过滤后排放，过滤过程中废气的污染物含量P （单位：mg/L ）与时间t （单位：h ）间的关系为0ektP P -=（e 是自然对数的底数，0P ，k 为正的常数）．如果前9h 消除了20%的污染物，那么消除60%的污染物需要的时间约为（ ）（参考数据：lg 20.301≈）A. 33h B. 35h C. 37h D. 39h【答案】C 【解析】【分析】根据给定条件，求出常数k ，然后再令0.4P =即可解出t .【详解】依题意，900(120%)ekP P --=，解得1ln 0.89k =-，即900.8t P P =，当0(160%)P P =-时，9000.40.8tP P =，即90.80.4t=，解得9lg 0.49(2lg 21)9(120.301)37lg 0.83lg 21130.301t --⨯==≈≈--⨯，所以污消除60%的污染物需要的时间约为37h .故选：C8. 已知函数()()()()2231,0,e 3,0x x x f x g x mx x x ⎧-+≤⎪==⎨->⎪⎩，若关于x 的不等式()()()0x f x g x -<的整数解有且仅有2个，则实数m 的取值范围是（ ）A. 30,2⎛⎤⎥⎝⎦B. 2e 0,2⎛⎤ ⎥⎝⎦C. (]2e,0- D. ()3,00,2⎛⎤-∞ ⎥⎝⎦【答案】A 【解析】【分析】判断函数的单调性，作出函数图象，结合题意列出相应不等式组，即可求得答案.【详解】令()()2e3,0xh x xx =->，则()()()e 31x h x x x +'=-，当01x <<时，ℎ′(x )<0，则ℎ(x )在(0,1)上单调递减；当1x >时，ℎ′(x )>0，则ℎ(x )在(1,+∞)上单调递增；令()()231,0k x x x =-+≤，则其图象为开口向下，对称轴为1x =-的抛物线；由关于x 的不等式()()()0x f x g x -<，可知0x ≠，当0x >时，()()f x g x <，即有()()h x g x <；当0x <时，()()f x g x >，即有()()k x g x >；作出函数图象如图：要使关于x 的不等式()()()0x f x g x -<的整数解有且仅有2个，显然0m ≤不能满足题意，故需满足()()()()02222m h g k g ⎧>⎪≥⎨⎪-≤-⎩，即20e 232m m m>⎧⎪≥⎨⎪-≤-⎩，解得302m <≤，即m 的取值范围为30,2⎛⎤⎥⎝⎦，故选：A【点睛】关键点睛：解答本题的关键在于作出函数图象，从而列出相应不等式组，求得答案.二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9. 已知数列{a n }的前n 项和为n S ，且116,6n n a a S +==+，则（ ）A. 342S = B. 2n nS a <C. {}n S 是等比数列 D. 存在大于1的整数n ，k ，使得n kS a =【答案】AB 【解析】【分析】通过n a 与n S 的关系，作差得到数列{}n a 是以6为首项，2为公比的等比数列，进而逐项判断即可.【详解】由16n n a S +=+，可得16,2n n a S n -=+≥两式相减可得：12,2n n a a n +=≥，又2211612,2a a S a =+==，所以数列{}n a 是以6为首项，2为公比的等比数列，所以162n n a -=⨯，626nn S =⨯-，所以3362642S =⨯-=，A 正确；262n n a =⨯，所以2n n S a <，B 正确；由626nn S =⨯-，可得1236,18,42S S S ===，显然3212S S S S ≠，可判断{}n S 不是等比数列，C 错误；若n k S a =，即162662n k -⨯-=⨯，也即1221n k --=，显然不存在大于1的整数,n k ，使得等式成立，D 错误；故选：AB10. 已知函数()22sin cos0)222xxxf x ωωωω=-+>在[)0,π上有且仅有4个零点，则（ ）A.1114,33ω⎛⎤∈⎥⎝⎦B. 令()π6g x f x ⎛⎫=+⎪⎝⎭，存在ω，使得()g x '为偶函数C. 函数()f x 在()0,π上可能有3个或4个极值点D. 函数()f x 在ππ,3535⎛⎫- ⎪⎝⎭上单调递增【答案】ABD 【解析】【分析】利用二倍角和辅助角公式化简得到()π2sin 3f x x ω⎛⎫=+⎪⎝⎭，根据()f x 在[)0,π上有且仅有4个零点，可确定πππ,π333x ωω⎡⎫+∈+⎪⎢⎣⎭，进而解得111433ω<≤，再根据其范围结合函数图象和平移知识等逐一判断即可.【详解】()2π2sincossin 2sin (0)2223xxxf x x x x ωωωωωωω⎛⎫=-=+=+> ⎪⎝⎭对于A ， [)0,πx ∈，πππ,π333x ωω⎡⎫+∈+⎪⎢⎣⎭， 因为()f x 在[)0,π上有且仅有4个零点，所以π4ππ5π3ω<+≤，解得111433ω<≤，∴1114,33ω⎛⎤∈ ⎥⎝⎦，故A 正确；对于B ，()π6g x f x ⎛⎫=+⎪⎝⎭ππππ2sin 2sin 6363x x ωωω⎡⎤⎛⎫⎛⎫=++=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，()ππ2cos 63g x x ωωω'⎛⎫=++ ⎪⎝⎭为偶函数，则πππ,63k k ω+=∈Z ，即62,k k ω=-∈Z ，∵0,ω>∴取4ω=，()8cos 4g x x '=-为偶函数,满足题意，故B 正确；对于C ，x ∈(0,π)，πππ,π333x ωω⎛⎫+∈+ ⎪⎝⎭，∵1114,33ω⎛⎤∈⎥⎝⎦，(]ππ4π,5π3ω+∈，∴函数()f x 在()0,π上可能有4个或5个极值点， 故C 不正确；对于D ，若ππ,3535x ⎛⎫∈-⎪⎝⎭，则πππππ,3353353x ωωω⎛⎫+∈-++ ⎪⎝⎭，∵1114,33ω⎛⎤∈⎥⎝⎦，∴ππ7π8πππ46π7π,,,353353535310515ωω⎡⎫⎛⎤-+∈+∈⎪ ⎢⎥⎣⎭⎝⎦，∴函数()f x 在ππ,3535⎛⎫- ⎪⎝⎭上单调递增. 故D 正确；故选：ABD.11. 已知函数()f x 的定义域为R ，()f x 不恒为0，且()()222f x f y x y x y f f ++-⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭，则（ ）A. ()0f 可以等于零 B. ()f x 的解析式可以为：()cos2f x x =C. 曲线f (x−1)为轴对称图形 D. 若()11f =，则201()20k f k ==∑【答案】BCD【解析】【分析】利用赋值法可得()00f =或()01f =，分类讨论可得()01f =，判断A ；.有一只判断出函数的奇偶性，可判断B ；结合B 的分析以及图象的平移可判断C ；判断出(){}f k 是以()11f =为首项，0为公差的等差数列，即可判断D.【详解】令0x y ==，可得()()000000222f f f f ++-⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭，可得()()200f f =，解得()00f =或()01f =，当()00f =时，则可得()()0222f x f x x x x x f f ++-⎛⎫⎛⎫== ⎪⎪⎝⎭⎝⎭，则()0f x =，与()f x 不恒为0矛盾，所以()01f =，故A 错误；令y x =-，可得()()()()()()20,f x f x f f x f x f x +-=∴-=，所以()f x 为偶函数，因为()cos 2f x x =是偶函数，所以()f x 的解析式可以为：()cos2f x x =，故B 正确；因为()f x 为偶函数，所以()f x 的图象关于直线0x =对称，所以()1f x -关于直线1x =对称，所以曲线()1f x -为轴对称图形，故C 正确；令2,x k y k =+=，则可得()()2222222f k f k k f f +++⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭，所以()()()*221,N f k f k f k k ++=+∈，又()()2022222f f f f +⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭，解得()21f =，所以(){}f k 是以()11f =为首项，0为公差的等差数列，所以201()20k f k ==∑，故D 正确.故选：BCD.【点睛】关键点点睛：采用赋值法是解抽象函数的一种有效方法，多领会其思路.第Ⅱ卷（非选择题，共92分）三、填空题：本大题共3小题，每小题5分，共15分．12. 记ABC V 内角A ，B ，C 的对边分别为a ，b ，c ．已知()22,3,cos 3b c B C ==+=-，则a =______．【解析】【分析】结合三角形内角和、诱导公式与余弦定理计算即可得解.【详解】由()()2cos cos πcos 3B C B C A ⎡⎤+=-+=-=-⎣⎦，故2cos 3A =，则22222cos 491253a b c bc A =+-=+-⨯=，故a =..13. 已知函数()|ln|2||f x x m =+-，m 为正的常数，则()f x 的零点之和为________．【答案】8-【解析】【分析】根据给定条件，探讨函数的对称性，再结合零点的意义即可求解得答案.【详解】函数()f x 的定义域为{R |2}x x ∈≠-，由()0f x =，得|ln|2||x m +=，令函数()|ln|2||g x x =+，(4)|ln|42|||ln |2||()g x x x g x --=--+=+=，则函数()y g x =图象关于直线2x =-对称，在同一坐标系内作出直线(0)y m m =>与函数()y g x =的图象，如图，直线(0)y m m =>与函数()y g x =的图象有4个交点，令其横坐标从左到右依次为1234,,,x x x x ，观察图象得14234x x x x +=+=-，所以()f x 的零点之和为8-.故答案为：8-14. 若2x =是函数()()213e 22xf x x a x x ⎛⎫=-+-⎪⎝⎭的极大值点，则实数a 的取值范围为________．【答案】2e a <-【解析】【分析】根据函数的导数，对a 分类讨论，再结合()0f x '=的根，分类讨论，分析函数的极大值点即可得出答案.【详解】()()()()()e222e xx f x x a x x a =-+-=-+'，当0a ≥时，e 0x a +>，当2x <时，f ′(x )<0，当2x >时，f ′(x )>0，所以()f x 在(),2∞-上单调递减，在()2,∞+上单调递增，所以2x =是函数的极小值点，不符合题意；当0a <时，令()0f x '=，可得()122,ln x x a ==-，若()2ln a <-，即2e a <-时，则2x <时，f ′(x )>0，函数()f x 单调递增，()2ln x a <<-时，f ′(x )<0，函数()f x 单调递减，所以2是函数()()213e 22xf x x a x x ⎛⎫=-+- ⎪⎝⎭的极大值点，符合题意；若()2ln a >-即20e a >>-时，则2x >时，f ′(x )>0，函数()f x 单调递增，()ln 2a x -<<时，f ′(x )<0，函数()f x 单调递减，所以2是函数()()213e 22xf x x a x x ⎛⎫=-+-⎪⎝⎭的极小值点，不符合题意；若()2ln a =-即2e a =-时，则R x ∈时，f ′(x )≥0，函数()f x 单调递增，函数()f x 无极值点，不符合题意.综上，当2e a <-时，2是函数()f x 的极大值点.故答案为：2e a <-【点睛】关键点点睛：首先观察导函数，当0a ≥时，分析函数单调性判断2是否为极大值点，当0a <时，根据()0f x '=的两根大小分类，由导数的正负得函数的单调性，再由单调性判断极大值点是否为2.四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15. 近年来，解放军强军兴军的深刻变化，感召了越来越多的高中优秀青年学子献身国防，投身军营.2024年高考，很多高考毕业学生报考了军事类院校．从某地区内学校的高三年级中随机抽取了900名学生，其中男生500人，女生400人，通过调查，有报考军事类院校意向的男生、女生各100名．（1）完成给出的列联表，并分别估计该地区高三男、女学生有报考军事类院校意向的概率；有报考意向无报考意向合计男学生女学生合计（2）根据小概率值0.10α=的独立性检验，能否认为学生有报考军事类院校的意愿与性别有关．参考公式及数据：()()()()()22,n ad bcn a b c da b c d a c b dχ-==+++ ++++．α0.250.150.100.050.0250.0100.0050.001xα1.3232.072 2.7063.841 5.024 6.6357.87910.828【答案】（1）列联表见解析，男生有报考军事类院校意向的概率为15，女生有报考军事类院校意向的概率为1 4（2）能认为学生有报考军事类院校的意愿与性别有关【解析】【分析】（1）先填写22⨯列联表，再根据古典概型概率计算公式求得正确答案.（2）计算2χ的知识，从而作出判断.【小问1详解】根据已知条件，填写22⨯列联表如下：有报考意向无报考意向合计男学生100400500女学生100300400合计200700900男生有报考军事类院校意向的概率为1001 5005=，女生有报考军事类院校意向的概率为1001 4004=.【小问2详解】()22900100300400100 3.214 2.072200700400500χ⨯-⨯=≈>⨯⨯⨯，所以能认为学生有报考军事类院校的意愿与性别有关．16. 记ABC V 的内角A ，B ，C 的对边分别为a ，b ，c ．已知1sin 2a C =，且cos cos 1a C c A +=，（1）求ABC V 的面积；（2）若π4B =，求A ．【答案】（1）14； （2）π8或5π8.【解析】【分析】（1）根据给定条件，利用余弦定理及三角形面积公式求解即得.（2）利用正弦定理，结合和角的正弦公式、二倍角公式求解即得.【小问1详解】在ABC V 中，由余弦定理及cos cos 1a C c A +=，得222222122a b c b c a a c ab bc+-+-⋅+⋅=，整理得1b =，而1sin 2a C =，所以ABC V 的面积11sin 24S ba C ==.【小问2详解】由（1）及正弦定理得1πsin sin sin 4a b A B ===a A =，于1sin 2A C =1sin(2π)4A A +=，12cos )A A A +=，即22sin cos 12sin A A A =-，因此sin 2cos 2A A =，即tan 21A =，由3π04A <<，得3π022A <<，解得π24A =或5π24A =，所以π8A =或5π8A =.17. 已知数列{}{},n n a b 满足()1n n n a nb +=，且1n a +是n b 与1n b +的等比中项．（1）若124a a +=，求1b 的值；（2）若12a =，设数列{}{},n n a b 的前n 项和分别为,n n S T ．（ⅰ）求数列{}{},n n a b 的通项公式；（ⅱ）求n n T S -．【答案】（1）2（2）（ⅰ）()1n a n n =+，()21n b n =+（ⅱ）()32n n n n T S +-=【解析】【分析】（1）先得112b a =，2232b a =，利用1n a +是n b 与1n b +的等比中项可得；（2）（ⅰ）先求得1n n n b a n+=，利用1n a +是n b 与1n b +的等比中项可得12n n n a a n ++=，由累乘法可得()1n a n n =+，进而可得()21n b n =+；（ⅱ）先得1n n n a b -=+，利用等差数列前n 项和公式可得()32n n T S n n +-=.【小问1详解】由()1n n n a nb +=可得112b a =，2232b a =，由题意可知2a 是1b 与2b 的等比中项，故2212a b b =，可得22123a a a =，即213a a =，又因124a a +=，故11a =，故1122b a ==【小问2详解】（ⅰ）由()1n n n a nb +=得1n n n b a n +=，由题意可得1211121n n n n n n n a a a n n b b ++++++==⋅，得12n n n a a n ++=，故12n n a n a n++=，故()1112211321121n n n n n a a a a n n n n a n n a a a ---=⨯⨯⨯⨯+⨯⨯⨯=+--= ，()211n n n b a n n+==+，故()1n a n n =+，()21n b n =+（ⅱ）()()2111n n b n a n n n =+-=-++，()()1212n n n n T b b b a a a S =+++-++-()()()1122n n b a b a b a =-+-++- ()231n =++++ ()212n n++=()32n n +=18. 已知函数()3221f x x ax a x =+--．（1）当5a =-时，则过点()0,2的曲线()f x 的切线有几条?并写出其中一条切线方程；（2）讨论()f x 的单调性；（3）若()f x 有唯一零点，求实数a 的取值范围．【答案】（1）有3条切线，322y x =-+（2）答案见解析 （3）⎛⎫ ⎪ ⎪⎝⎭【解析】【分析】（1）根据导数的几何意义，设出切点得出切线斜率，列方程组分析解得个数即可；（2）求出导函数，对a 分类讨论即可得出函数单调区间；（3）根据函数的单调性，结合当x →+∞时，()f x →+∞，利用极大值建立不等式求解.【小问1详解】当5a =-时，()325251f x x x x =---，()231025f x x x =--'，设切点为()00,x y ，因为切线过点(0,2)，所以切线斜率存在，故可设切线方程为2y kx =+，则3200002002525131025kx x x x k x x ⎧+=---⎨=--⎩，化简可得()2200021330x x x --+=，即()()200012330x x x ---=，由2002330x x --=的判别式9240∆=+>知方程有2个不等实根且不为1，故()()200012330x x x ---=有3个不等的实根，所以切线有3条，其中一条切点横坐标为1，故3102532k =--=-，所以切线方程为322y x =-+.【小问2详解】()()()22323f x x ax a x a x a =+-=-+'，当0a =时，()230f x x ='≥，所以函数R 上单调递增；当0a >时，3a a -<，所以x a <-或3ax <时，f ′(x )>0，()f x 单调递增，当3aa x -<<时，f ′(x )<0，()f x 单调递减；当0a <时，3aa ->，所以x a >-或3a x <时，f ′(x )>0，()f x 单调递增，当3ax a <<-时，f ′(x )<0，()f x 单调递减；综上，0a =时，()f x 在R 上单调递增，无递减区间；当0a >时，()f x 在(),a ∞--和,3a ∞⎛⎫+ ⎪⎝⎭上单调递增，在,3a a ⎛⎫- ⎪⎝⎭上单调递减；当0a <时，()f x 在,3a ∞⎛⎫- ⎪⎝⎭和(),a ∞-+上单调递增，在,3a a ⎛⎫- ⎪⎝⎭上单调递减.【小问3详解】当0a =时，3()1f x x =-，函数仅有1个零点1；当0a >时，由（2）知，()f x 的极大值为()f a -，且当x →+∞时，()f x →+∞，若()f x 有唯一零点，则333()10f a a a a -=-++-<，解得1a <，故()0,1a ∈，当0a <时，由（2）知，()f x 的极大值为3a f ⎛⎫⎪⎝⎭，同理，若()f x 有唯一零点，则3510327a f a ⎛⎫=--< ⎪⎝⎭，解得a >，故a ⎛⎫∈ ⎪ ⎪⎝⎭，综上，实数a的取值范围⎛⎫⎪ ⎪⎝⎭【点睛】关键点点睛：对于含参数的函数，研究单调区间的关键在于对导函数的特点分析，本题导函数为二次函数，所以分析的重点在于导函数零点的关系，在根据函数有唯一零点求参数的时候，利用函数的极大值点建立不等式是解题关键.19. 已知函数()2ln 3f x x x x a =+-+，()f x 在(]0,1上的最大值为3ln24-．在（1）求实数a 的值；（2）若数列{}n a 满足()1231n n n n a a f a a +=+-，且143a =．（ⅰ）当2,n n ≥∈Z 时，比较n a 与1的大小，并说明理由；（ⅱ）求证：1312nii a=-<∑．【答案】（1）a =2（2）(1)1n a >，理由见详解；（2）证明见详解【解析】【分析】（1）利用导数判断()f x 的单调性求出最大值得解；（2）（i ）由已知结合基本不等式可得1ln 12nn na a a +≥+，利用数学归纳法证明1n a >，()2,Z n n ≥∈，（ii ）先构造函数()ln 1x x xϕ+=，并利用导数证明()1x ϕ<，从而得到()11112+-<-n n a a ，将所证明的式子放缩求和证明.【小问1详解】()()()121123x x f x x x x--'=+-=Q ，(]0,1x ∈，当102x <<时，10x -<，210x -<，()0f x '∴>，则()f x 在10,2⎛⎫⎪⎝⎭上单调递增，当112x ≤≤时，10x -≤，210x -≥，()0f x '∴≤，则()f x 在1,12⎡⎤⎢⎥⎣⎦上单调递减，()max 11133ln ln 222424f x f a ⎛⎫∴==+-+=- ⎪⎝⎭，解得2a =所以实数a 的值为2.【小问2详解】（i ）由（1）知，()2ln 32f x x x x =+-+，所以212ln 3231n n n n n n a a a a a a +=+-++-，即21ln 12n n n na a a a +++=，212n n a a +≥Q ，1ln 12nn na a a +∴≥+，.下面用数学归纳法证明1n a >，()2,Z n n ≥∈，当2n =时，143a =，1214lnln 3111823a a a ∴≥+=+>，假设()2,Z n k k k =≥∈时，命题成立，则1k a >，当1n k =+时，有1ln 112kk ka a a +≥+>成立，所以上述命题对2,Z n n ≥∈，均有1n a >成立.（ii ）当1n =时，13112a -=<成立，当2n ≥时，令()ln 1x x x ϕ+=，则()2ln xx x ϕ-'=，当01x <<时，()0x ϕ'>，当1x >时，()0x ϕ'<，所以()x ϕ在()0,1上单调递增，在()1,+∞上单调递减，则()()11x ϕϕ<=，所以()()21ln 11ln 1112222n n n nn n n n n n a a a a a a a a a a ϕ+⎛⎫++++==+=+< ⎪⎝⎭，即11112n n a a +-<-，又由（i ）知1n a >，则()11112+-<-n n a a ，()()()121313111ni n i a a a a =∴-=-+-++-⎡⎤⎣⎦∑L ()121111311222n a -⎡⎤⎛⎫<-++++ ⎪⎢⎥⎝⎭⎣⎦L 111123211322n n -⎛⎫=⨯⨯=- ⎪⎝⎭，102n >Q ，1112n ∴-<，12122n⎛⎫∴-< ⎪⎝⎭，即1312ni i a =-<∑，得证.【点睛】关键点点睛：本题最后小问证明的关键是构造函数()ln 1x x xϕ+=，并利用导数证明()1x ϕ<，从而得到()11112+-<-n n a a .。

高三一诊数学试题及答案一、选择题（本题共10小题，每小题5分，共50分）1. 下列函数中，为奇函数的是：A. y = x^2B. y = |x|C. y = sin(x)D. y = cos(x)答案：B2. 若f(x) = 3x - 5，求f(2)的值：A. -1B. 1C. 4D. 7答案：A3. 已知三角形ABC的面积为12，且AB = 8，AC = 6，求BC的长度：A. 4√2B. 5√2C. 6√2D. 7√2答案：A4. 函数y = x^3 - 2x^2 + 3x - 4的导数为：A. 3x^2 - 4x + 3B. 3x^2 - 4x + 1C. 2x^2 - 4x + 3D. 4x^3 - 8x + 3答案：A5. 已知等差数列的前三项和为12，第二项为5，求该数列的首项和公差：A. 首项为3，公差为2B. 首项为4，公差为1C. 首项为2，公差为3D. 首项为1，公差为4答案：A6. 已知向量\( \vec{a} \)和\( \vec{b} \)的夹角为60°，|\( \vec{a} \)| = 3，| \( \vec{b} \)| = 2，求\( \vec{a} \)和\( \vec{b} \)的点积：A. -1B. 1C. 3D. 6答案：B7. 圆的方程为(x - 2)^2 + (y - 3)^2 = 9，求圆心到直线x + y - 6 = 0的距离：A. √2B. 2√2C. 3√2D. 4√2答案：B8. 已知双曲线x^2/a^2 - y^2/b^2 = 1的焦点在x轴上，且c^2 = a^2 + b^2，求双曲线的离心率：A. √2B. √3C. 2D. 3答案：C9. 抛物线y^2 = 4x的准线方程为：A. x = -1B. x = 1C. y = -1D. y = 1答案：A10. 已知函数f(x) = ln(x) + 2x - 6，求f(x)的单调递增区间：A. (1, ∞)B. (2, ∞)C. (3, ∞)D. (-∞, 1)答案：B二、填空题（本题共5小题，每小题4分，共20分）11. 函数y = sin(2x)的周期为______。

第1页（共4页）岳阳市2024届高三教学质量监测（一）数学试卷本试卷共4页，22道题，满分150分，考试用时120分钟。

注意事项：1．答卷前，考生务必将自己的学校、班级、考号和姓名填写在答题卡指定位置。

2．回答选择题时，选出每小题答案后，用2B 铅笔把答题卡对应的标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

3．非选择题必须用黑色字迹的签字笔作答，答案必须写在答题卡各题目指定区域内；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，只交答题卡。

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{})1ln(|-==x y x A ，{}06|2≤--=x x x B ，则=⋂B A A ．{}21|≤<x x B ．{}31|≤<x x C ．{}32|≤≤-x x D ．{}1|≥x x 2．已知复数z 满足2)1(=+i z ，则=z A ．1B ．2C ．2D ．33．已知数列{}n a 与{}n b 均为等差数列，且252=+b a ，1296=+b a ，则=+74b a A ．5B ．6C ．7D ．84．定义在R 上的函数)(x f 满足：当[)1,0∈x 时，12)(-=xx f ，且对任意实数x ，均有1)1()(=++x f x f ，则)23(f 为A ．23B ．2-C ．21-D ．22-5．自2020年确定针对中国的“融入”政策(和平演变)失败，美国政府开始带领部分西方国家推动“去中国化”的“硬脱钩”政策，技术封锁特别是芯片出口限制就是其中重要一项．为突破围堵，以华为为代表的一批中国高新技术企业不仅着力发展硬件，而且加强了软件技术特别是算法的研发.如我国超级计算机天河一号A 每秒执行2.5×1015条指令，普通计算机每秒执行108条指令．若天河一号A 用“插入排序”法排n 个数需要2n 2条指令，普通计算机用“并归排序”法排n 个数需要50n lg n 条指令．现排1010个数，则超级计算机与普通计算机所花时间的比值为A ．8∶5B ．8∶50000C ．80000∶5D ．8∶5×1086．据统计，我国结核病的感染率约为0.001．在针对结核病的检查中，健康者检测结果显示为阳性的概率为0.05，结核病感染者检测结果显示为阴性的概率为0.01，那么A 同学检测结果为阳性的概率为A ．0.05094B ．0.05001C ．0.001D ．0.05084姓名_____________考号______________第2页（共4页）7．已知F 1，F 2分别为椭圆C ：12222=+by a x (a ＞b ＞0)的左、右焦点，A 为椭圆上顶点，直线AF 2与椭圆C 交于另外一点B ，若∠AF 1F 2＝2∠BF 1F 2，则椭圆离心率e 位于下列哪个区间A ．），（410B ．），（2141C ．），（4321D ．），（1438．已知四棱台的底面为矩形，上底面积为下底面积的41，侧棱长为3．当该四棱台的体积最大时，其外接球的表面积为A ．233πB ．π33C ．257πD ．π57二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．若函数)6,6sin()(≤∈+=+ωωπωN x x f 的图象关于直线6π=x 对称，则A ．21)0(=f B ．)(x f 的图象关于点⎪⎭⎫⎝⎛0,125π对称C ．)(x f 在区间),0(π上有2个极值点D ．)(x f 在区间⎪⎭⎫⎝⎛3,0π上单调递增10．已知正方体ABCD －A 1B 1C 1D 1的棱长为1，下列说法正确的是A ．异面直线A 1D 与B 1D 1所成角为45°B ．若该正方体的所有顶点都在同一个球面上，则该球体的体积为π23C ．A 1C 与平面A 1BD 所成角的正弦值为33D ．若点Q 为正方体ABCD －A 1B 1C 1D 1对角线BD 1上的动点，则∠AQC 的最大值为32π也不能分成7等份，只好先去睡觉，准备第二天再分．夜里1只猴子偷偷爬起来，先吃掉1个桃子，然后将其分成7等份，藏起自己的一份就去睡觉了；第2只猴子又爬起来，吃掉1个桃子后，也将桃子分成7等份，藏起自己的一份睡觉去了；以后的5只猴子都先后照此办理．问最初至少有多少个桃子?最后至少剩下多少个桃子?”．下列说法正确的是A ．若第n 只猴子分得n b 个桃子(不含吃的)，则）（7,6,5,4,3,2,11671=-=-n b b n nB ．若第n 只猴子连吃带分共得到n a 个桃子，则)7,6,5,4,3,2,1}({=n a n 为等比数列C ．若最初有）（677-个桃子，则第7只猴子偷偷办理后还剩得）（767-个桃子D ．若最初有m 个桃子，则m 被7除的余数为1第3页（共4页）三、填空题：本题共4个小题，每小题5分，共20分．13．已知O (0,0)，A (1,2)，B (3,－1)，若向量OA m //，且m 与OB 的夹角为钝角，写出一个满足条件的m 的坐标为______．14．已知曲线x x y ln +=在点），（11处的切线与曲线a x a x y ++++=1)32(2有两个不同的公共点，则a 的取值范围为______．15．过圆22:5O x y +=外一点P 作圆O 的切线，切点分别为A 、B ，若2=AB ，则点P 的轨迹方程为_________．16．正方形ABCD 的边长为1，P 、Q 分别为边AB 、AD 上的点(不包括端点)，且QC 、PC分别为DQP ∠、BPQ ∠的角平分线．则(1)APQ ∆的周长为______；(2)PCQ ∆面积的取值范围为______．四、解答题：本题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17．(本题满分10分)已知正项数列}{n a 的前n 项和为n S ．11=a ，111+--=-n n n S n S n a (n ≥2)．(1)求证：数列}{n S nS nn --为常数列；(2)求数列}{n S 的通项公式，并证明111111433221<++++-nn S S S S S S S S ．18．(本题满分12分)在ABC ∆中，角C B A ,,所对的边分别为c b a ,,且0tan tan 2tan =+-A a A c B a ．(1)求B ；(2)若ABC ∆的面积为3，B ∠的平分线BD 交AC 于点D 且1=BD ，求ac的值．19．(本题满分12分)如图，三棱柱111C B A ABC -中，侧棱ABC AA 平面⊥1，2==BC AC ．E ，F 分别是AB ，11C B 的中点，且11C B EF ⊥．(1)证明：AC BC ⊥；(2)若二面角B EC F --的正切值为22，求直线EF 与平面EC A 1所成角的余弦值．第4页（共4页）20．(本题满分12分)为了进一步深入开展“书香校园”活动，让读书成为每位师生的习惯，让阅读成为学校、家庭、社会的一种良好风气，某校规定每位师生需在学校图书馆借阅一本文学类或理工类书籍．现对该校60名师生的借阅情况进行调查，其中教师与学生的人数之比为1∶2，教师中借阅文学类书籍的占21，学生中借阅文学类书籍的占43，得到如下22⨯列联表：(1)请将22⨯列联表补充完整，并根据小概率值1.0=α的独立性检验，判断老师与学生的借阅情况是否存在差异；(2)若从学校随机抽取m 人，用样本的频率估计总体的概率，若抽取的人中有5人借阅理工类书籍的概率最大，求m 所有可能的取值．附：))()()(()(22d b c a d c b a bc ad n ++++-=χ，其中n a b c d =+++．参考数据：α0.10.050.010.0050.001x α2.7063.8416.6357.87910.82821．(本题满分12分)已知抛物线x y 42=的准线与x 轴相交于点N ，过点N 作抛物线的两条切线，切点分别为A 、B ，其中点A 在第一象限．(1)求直线AB 的方程；(2)过点N 作直线l 交抛物线于C 、D 两点，交直线AB 于点E ，过点E 作AD 的平行直线EH 分别交线段AC 、AN 于点M 、H ．证明：存在实数λ，使得AM AE AH λ=+．22．(本题满分12分)已知函数1)(-=x e xx f ．(1)求函数)(x f 的单调区间；(2)设x x f x g cos )()(-=，(0,2)x π∈，判断()g x 的零点个数，并说明理由．教师学生合计文学类理工类合计岳阳市2024届高三教学质量监测(一)数学参考答案及评分标准一、单项选择题：本题共8小题，每小题5分，共40分．1．B 2．C 3．C 4．D 5．A 6．A7．B8．D二、多项选择题：本题共4小题，每小题5分，共20分．9．ABC 10．BD 11．ACD 12．ABD三、填空题：本题共4个小题，每小题5分，共20分．13．），（21--(满足0),2,1(>--k k 均可)14．),27()27,(+∞⋃--∞15．42522=+y x 16．2(2分)；⎪⎭⎫⎢⎣⎡-2112，(3分)四、解答题：本题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17．(1)由题意，∵111+--=-n n n S n S n a (n ≥2))1(111111--+--=+--=-=∴---n n S n S n S n S n S S a n n n n n n n .......................................................(2分)）（1111----=--∴--n S n S n S n S n n n n ∴数列}{n S nS nn --为常数列........................................................................................................(4分)(2)111==a S ，11111-=--=--∴S S n S n S n n ........................................................................(5分)0)1)(()1(2=+-=---∴n n n n S n S n S n S 又0>n a ，0>∴n S ，n S n =∴..................................................................................................(7分)nn n n S S nn 111)1(111--=-=-........................................................................................................(8分)nn S S S S S S S S n n ⨯-++⨯+⨯=++++∴-)1(132121111111433221 1111113121211<-=-++-+-= ....................................................................................(10分)18．(1)由题意，0cos sin cos sin 2cos sin tan tan 2tan =+-=+-AAa A A c B B aA a A cB a ...............................................(1分)0cos cos 2cos 2=+-∴Aa A ca B ab 又0≠a ，0cos cos 2cos =+-∴A a A cB b ，0cos sin cos sin 2cos sin =+-∴AAA CB B ..................................(3分)0cos sin cos sin 2cos sin =+-∴B A BC A B ,即0cos sin 2sin =-+B C B A ）（即0cos sin 2sin =-B C C 又0sin ≠C ,21cos =∴B ,B 为三角形内角3π=∠∴B ............................................................................................................................................(5分)(2)343sin 21===∆ac B ac S ABC ，4=∴ac ......................................................................(7分)36sin 1216sin 121=⨯⨯+⨯⨯=+=∆∆∆ππc a S S S CBD ABD ABC ，34=+∴c a .......................(9分)1243422==+∴）（）（ac c a ................................................................................................................(10分)整理得01(10(2=+-a c a c ，解得625±=ac............................................................................(12分)19．(1)取BC 的中点Q ,连接FQ ,EQ ，则,//1C C FQ 又,//11C C A A ,//1A A FQ ∴⊥A A 1 平面ABC ABC FQ 平面⊥∴........................................................................(2分),BC FQ ⊥∴BC C B //11 ,,11C B EF ⊥EF BC ⊥∴.........................................................................(3分)F EF FQ =⋂ ，EFQ EQ EFQ BC 平面又平面⊂⊥∴ ,EQ BC ⊥∴..............................(4分)EQ 为ABC ∆的中位线，AC EQ //∴，AC BC ⊥∴............................................................(5分)(2)过Q 作M CE QM 于⊥，连接FM ，由(1)知ABC FQ 平面⊥Q QM FQ EC FQ =⋂⊥∴ ,，FMQ EC 平面⊥∴，FMEC ⊥∴∴二面角B EC F --的平面角为FMQ ∠,22tan ==∠∴QMFQFMQ 又224sin=⋅=πCQ QM ，2=∴FQ ....................................(7分)又1,,CC CB CA 两两垂直，以C 为坐标原点如图建系)2,0,2(),0,0,0(),2,1,0(),0,1,1(1A C F E ，)2,0,1(-=EF )2,0,2(),0,1,1(1==CA CE ...............................................................(8分)设平面EC A 1的法向量为）（z y x n ,,=⎪⎩⎪⎨⎧=⋅=⋅001CA n CE n ,得⎩⎨⎧=+=+00z x y x ，令1=x ，1,1-=-=z y ，）（1,1,1--=∴n ...............................(10分)设直线EF 与平面EC A 1夹角为θ，515cos sin ==n EF θ...............................(11分)∴EF EC A 1510..................................................................................(12分)20．.........................................................................................................(1分)(1)提出零假设0H ：老师与学生的借阅情况不存在差异1.022706.275.340204020)30101010(60x =>=⨯⨯⨯⨯-⨯=χ............................................................................(3分)根据小概率值1.0=α的独立性检验，推断0H 不成立，即认为判断老师与学生的借阅情况是存在差异，此推断犯错误的概率不大于1.0....................................................................................................................(4分)(2)设借阅理工类书籍的概率为p ，则316020==p ............................................................................(5分)设随机抽取m 人中借阅理工类书籍的人数为随机变量X则⎩⎨⎧=≥==≥=)4()5()6()5(X P X P X P X P ，⎪⎪⎩⎪⎪⎨⎧≥≥----444555666555)32(31(32(31()32(31(32(31(m m m m m m m m C C C C .....................................................(8分)⎪⎪⎩⎪⎪⎨⎧≥≥∴（（（）（323131324565m m m m C C C C ，⎪⎪⎩⎪⎪⎨⎧⋅-≥⋅-⋅-≥⋅-∴32)!4(!4!31)!5(!5!31)!6(!6!32)!5(!5!m m m m m m m m 得⎪⎪⎩⎪⎪⎨⎧⋅-≥⋅≥⋅-32411513161325(1m m ）解得1714≤≤m .............................................................................................(11分)又+∈N m m ∴可取17161514，，，.......................................................................................................(12分)21．(1)由题意，其准线为1-=x ，N 点坐标为(01，-)...................................................................(1分)不妨设直线NA 的方程为)1(1+=x k y ，设直线NB 的方程为)1(2+=x k y ，联立⎩⎨⎧+==)1(412x k y xy 得0)42(2121221=+-+k x k x k ，由题知0416164412141=-+-=∆k k k ，得121=k ....................(3分)12242121=-=∴k k x A ，同理1=B x ，故直线AB 的方程为1=x .........................................................(4分)(2)由题可知，若存在实数λ，则0≠λ，AMAE AH λ=+ AM AE AH =+∴λλ11又M E H 、、 在同一条直线上111=+∴λλ，2=∴λ故只需证明M 为H 、E 的中点即可.....................................................................................................(5分)设直线ND 为1-=ty x ，设点C (11,y x )，点D (22,y x )联立⎩⎨⎧-==142ty x x y ，得0442=+-ty y ，4,42121==+y y t y y ...........................................................(6分)教师学生合计文学类103040理工类101020合计204060令1=x 代入直线ND 中得t y E 2=，点E）（t2,12414212222222+=--=--=y y y x y k AD ，同理241+=y k AC tx y y l EH 2)1(24:2+-+=①1:+=x y l AN …②2)1(24:1+-+=x y y l AC ③联立①②得22)1(2122-+--=y y t t x H 联立①③得2121)1(41y y t t x M --+=...................(8分)要证明M 为H ,E 的中点，即证明M E H x x x 2=+,即证明)(18222)1(21121222y y t t y y t t --+=-+--+）（即证明)(1422)1(21222y y t t y y t t --=-+--）（即证明21221422y y t y y -+=-+-）（................................................................................................................(10分)等式右边2121212144414y y y y y y t y y t -++=-+=-+）（，421=y y ，214y y =∴224)2(44442222222222222121-+-=-+=-++=-++y y y y y y y y y y y y y y 故M E H x x x 2=+得证........................................................................................................................(12分)22．(1)由题意，)(x f 的定义域为{}0|≠x x .................................(1分)2')1(11)(---=x x e e x x f ）（，设1)1()(--=xe x x t ...............................................................................(2分)x e x x t )()('-=，若0(),,0('<+∞∈）x t x ，)(x t 在)0(∞+，单调递减，0)0()(=<∴t x t ；若0)(),0,('>-∞∈x t x ，)(x t 在），（0∞-单调递增，0)0()(=<∴t x t .),0()0,(,0)('+∞⋃-∞∈∀<∴x x f )(x f ∴的单调减区间为)0,(-∞和)0(∞+，，无单调增区间........................................................(4分)(2)xe xx x f x g x cos 1cos )()(--=-=①⎥⎦⎤⎢⎣⎡∈23,2ππx 时，0cos ≤x ，01>-x e x ∴0cos 1)(>--=x e x x g x ，∴)(x g 在⎥⎦⎤⎢⎣⎡23,2ππ无零点............................................................(5分)②⎪⎭⎫ ⎝⎛∈ππ2,23x 时，=)('x g x e e x x x sin )1(112+---）（0sin ≤x ，由(1)可知0)1(112<---x x e e x ）（，0)('<∴x g ∴)(x g 在⎪⎭⎫⎝⎛ππ2,23上单调递减，又00123)23(23>--=πππe g ，0112)2(2<--=πππe g ∴)(x g 在⎪⎭⎫⎝⎛ππ2,23存在唯一零点..............................................................................................(7分)③⎪⎭⎫⎝⎛∈2,0πx 时，求)(x g 的零点即求0cos 1)(=--=x e x x g x 的根的个数，即求0cos 1=--x e x x ）（根的个数，设x e x x h x cos 1)(）（--=，即求)(x h 零点的个数0)0(,sin )cos (sin 1)(''=--+=h x x x e x h x ，设x x x e x m x sin )cos (sin 1)(--+=1)0(,cos sin 2)(''-=-=m x x e x m x ，设xx e x n x cos sin 2)(-=∴0sin )cos (sin 2)('>++=x x x e x n x ，⎪⎭⎫⎝⎛∈∀2,0πx ..............................................................(9分)∴)(x n 单调递增，又02)2(,01)0(2>=<-=ππe n n ∴)(x n 在⎪⎭⎫⎝⎛2,0π上存在唯一零点1x ..............................................................................................(10分)∴在)(,0)(,01x m x n x <），（单调递减，在)(,0)(,21x m x n x >），（π单调递增0)2(,0)0(2>==ππe m m ∴)(x m 在⎪⎭⎫ ⎝⎛2,0π上存在唯一零点2x ，且⎪⎭⎫⎝⎛∈2,12πx x ..............(11分)∴在)(,0)(,02x h x m x <），（单调递减，在)(,0)(,22x h x m x >），（π单调递增02)2(,0)0(>==ππh h ∴)(x h 在⎪⎭⎫⎝⎛2,0π上存在唯一零点0x .综上，)(x g 在），（π20内存在两个零点.............................................................................................(12分)。