离散数学第五章集合及其运算习题答案
- 格式:ppt
- 大小:917.04 KB
- 文档页数:51

离散数学课后习题及答案离散数学是计算机科学与数学的重要基础课程之一,它涵盖了很多重要的概念和理论。
为了更好地掌握离散数学的知识,课后习题是必不可少的一部分。
本文将介绍一些常见的离散数学课后习题,并提供相应的答案,希望对读者有所帮助。
一、集合论1. 设A={1,2,3},B={2,3,4},求A∪B和A∩B的结果。
答案:A∪B={1,2,3,4},A∩B={2,3}2. 设A={1,2,3},B={2,3,4},C={3,4,5},求(A∪B)∩C的结果。
答案:(A∪B)∩C={3,4}二、逻辑与命题1. 判断下列命题的真假:a) 若2+2=5,则地球是平的。
b) 若今天下雨,则我会带伞。
c) 若x>0,则x^2>0。
答案:a)假,b)真,c)真。
2. 用真值表验证下列命题的等价性:a) p∧(q∨r) ≡ (p∧q)∨(p∧r)b) p→q ≡ ¬p∨q答案:a)等价,b)等价。
三、关系与函数1. 给定关系R={(1,2),(2,3),(3,4)},求R的逆关系R^-1。
答案:R^-1={(2,1),(3,2),(4,3)}2. 设函数f(x)=x^2,g(x)=2x+1,求复合函数f(g(x))的表达式。
答案:f(g(x))=(2x+1)^2=4x^2+4x+1四、图论1. 给定图G,其邻接矩阵为:0 1 11 0 11 1 0求图G的度数序列。
答案:度数序列为(2,2,2)2. 判断下列图是否为连通图:a) G1的邻接矩阵为:0 1 11 0 01 0 0b) G2的邻接矩阵为:0 1 01 0 10 1 0答案:a)不是连通图,b)是连通图。
五、组合数学1. 从10个不同的球中,任选3个,求共有多少种选法。
答案:C(10,3)=120种选法。
2. 求下列排列的循环节:a) (123)(45)(67)b) (12)(34)(56)(78)答案:a)循环节为(123)(45)(67),b)循环节为(12)(34)(56)(78)。


第5章 习题解答5.1 A:③; B:⑥; C:⑧; D:⑩; E:⑨分析 S 为n 元集,那么有个元素.S 上的一个二元运算就是函数S S ⨯2n .这样的函数有个.因此上的二元运算有个.S S S f →⨯:2n n },{b a 162=n n 下面说明通过运算表判别二元运算性质及求特导元素的方法.1 °交换律 若运算表中元素关于主对角线成对称分布,则该运算满足交换律.2 °幂等律 设运算表表头元素的排列顺序为如果主对角线元,,,21n x x x 素的排列也为 则该运算满足幂等律.,,,21n x x x 其他性质,如结合律或者涉及到两个运算表的分配律和吸收律,在运算表中没有明显的特征,只能针对所有可能的元素等来验证相关的算律是否成立.z y x ,,3 ° 幺元设运算表表头元素的排列顺序为如果元素所在的.e ,,,21n x x x i x 行和列的元素排列顺序也是则为幺元.,,,21n x x x i x 4 ° 零元如果元素所在的行和列的元素都是,则是零元. .θi x i x i x 5 ° 幂等元.设运算表表头元素的排列顺序为如果主对角线上,,,21n x x x 第个元素恰 为那么是幂等元.易见幺元和零元都是幂等元.i },,2,1{n i x i ∈i x 6 ° 可逆元素及其逆元.设为任意元素,如果所在的行和列都有幺元,并i x i x 且这两个幺元关于主对角线成对称分布,比如说第行第列和第行第列的两i j j i 个位置,那么与互为逆元.如果所在的行和列具有共同的幺元,则幺元一j x i x i x 定在主对角线上,那么的逆元就是自己.如果所在的和地或者所在的列没i x i x i x 有幺元,那么不是可逆元素.不难看出幺元一定是可逆元素,且;而零i x e e e =-1元不是可逆元素.θ以本题为例,的运算表是对称分布的,因此,这三个运算是可交换的,321,,f f f而不是可交换的.再看幂等律.四个运算表表头元素排列都是,其中主对角4f b a ,线元素排列为的只有,所以, 遵从幂等律.下面考虑幺元.如果某元素所b a ,4f 4f 在的行和列元素的排列都是,该元素就是幺元.不难看出只有中的a 满足这b a ,2f 一要求,因此,a 是的幺元,其他三个运算都不存在幺元.最后考虑零元.如果a 2f 所在的行和列元素都是a,那么a 就是零元;同样的,若b 所在的行和列元素都是b,那么b 就是零元.检查这四个运算表,中的a 满足要求,是零元,其他运算都没1f 有零元.在的运算表中,尽管a 和b 的列都满足要求,但行不满足要求.因而4f 4f 中也没有零元.5.2 A:①; B:③; C:⑤; D:⑦; E:⑩分析 对于用解析表达式定义的二元运算 °和 *,差别它们是否满足交换律,结合律,幂等律,分配律和吸收律的方法总结如下:任取,根据 °运算的解析表达式验证等式是否成立.如果成y x ,x y y =x 立 °运算就满足交换律.2 ° °运算的地合律任取根据°运算的解析表达式验证等式是否成立. z y x ,,)y (z y)(z x x =如果成立, °运算就是可结合的.3 ° °运算的幂等律任取x,根据 °运算的解析表达式验证等式是否成立.如果成立, °x x x = 运算满足幂等律.4 ° °运算对*运算的分配律任取,根据 °和*运算的解析表达式验证等式z y x ,,和是否成立。

习题5.11.设A=⎨a,b,c⎬,B=⎨1,2,3⎬,试说明下列A到B二元关系,哪些能构成A到B的函数?⑴f1=⎨<a,1>,<a,2>,<b,1>,<c,3>⎬⑵f2=⎨<a,1>,<b,1>,<c,1>⎬⑶f3=⎨<a,2>,<c,3>⎬⑷f4=⎨<a,3>,<b,2>,<c,3>,<b,3>⎬⑸f5=⎨<a,2>,<b,1>,<b,2>⎬解:⑴不能构成函数。
因为<a,1>∈f1且<a,2>∈f1⑵能构成函数⑶不能构成函数。
因为dom f3≠A⑷不能构成函数。
因为<b,2>∈f4且<b,3>∈f4⑸能构成函数。
2.试说明下列A上的二元关系,哪些能构成A到A的函数?⑴A=N(N为自然数集合),f1=⎨<a,b>| a∈A∧b∈A∧a+b<10⎬⑵A=R(R为实数集合),f2=⎨<a,b>| a∈A∧b∈A∧b=a2⎬⑶A=R(R为实数集合),f3=⎨<a,b>| a∈A∧b∈A∧b2=a⎬⑷A=N(N为自然数集合),f4=⎨<a,b>| a∈A∧b∈A∧b为小于a的素数的个数⎬⑸A=Z(Z为整数集合),f5=⎨<a,b>| a∈A∧b∈A∧b=|2a|+1⎬解:⑴不能构成函数。
由于1+1<10且1+2<10,所以<1,1>∈f1且<1,2>∈f1。
⑵能构成函数。
⑶不能构成函数。
由于12=1且(-1)2=1,所以<1,1>∈f3且<1,-1>∈f3。
⑷能构成函数。
⑸能构成函数。
3. 回答下列问题。
⑴设A=⎨a,b⎬,B=⎨1,2,3⎬。
求B A,验证|B A|= |B||A|。

离散数学第五章习题答案题目1: 定义一个关系R在集合A上,如果对于所有的a, b, c属于A,满足以下条件:- 如果(a, b)属于R,则(b, a)属于R。
- 如果(a, b)属于R且(b, c)属于R,则(a, c)属于R。
证明R是传递的。
答案:根据题目给出的条件,R是对称的和传递的。
首先,对称性意味着如果(a, b)属于R,那么(b, a)也必须属于R。
其次,传递性意味着如果(a, b)和(b, c)都属于R,那么(a, c)也必须属于R。
结合这两个性质,我们可以得出结论:对于任意的a, b, c属于A,如果(a, b)和(b, c)都属于R,那么(a, c)也属于R,从而证明了R的传递性。
题目2: 给定一个函数f: A → B,如果对于A中的每个元素a,都有唯一的b属于B使得f(a) = b,那么称f为单射(或一一映射)。
证明如果函数f是单射,那么它的逆函数f^-1也是单射。
答案:要证明f^-1是单射,我们需要证明对于B中的任意两个元素b1和b2,如果f^-1(b1) = f^-1(b2),则b1 = b2。
假设f^-1(b1) = a且f^-1(b2) = a',其中a, a'属于A。
由于f是单射,我们知道f(a) = b1且f(a') = b2。
根据f^-1的定义,我们有b1 = f(a) = f(a') = b2。
因此,如果f^-1(b1) = f^-1(b2),则b1必须等于b2,这证明了f^-1是单射。
题目3: 证明一个函数f: A → B是满射(或到上映射)当且仅当对于B中的每个元素b,都存在A中的元素a使得f(a) = b。
答案:首先,我们证明如果f是满射,那么对于B中的每个元素b,都存在A 中的元素a使得f(a) = b。
假设f是满射,这意味着B中的每个元素都是A中某个元素的像。
因此,对于B中的任意元素b,我们可以找到一个a属于A,使得f(a) = b。


习题答案(P151~P153)1.用枚举法给出下列集合解:(2){-3,2}(4){5,6,7,8,9,10,11,12,13,14,15}2.用抽象法说明下列集合解:(2){x|x为素数,10<x<20}(4){x|x为中国的省会}(6){x|x=2k+1,k∈I}3.判断下列哪些∈关系成立,为什麽?解:根据只有集合中的元素才与该集合有∈关系,故(1)、(4)、(6)、(7)成立,(2)、(3)、(5)、(8)不成立。
4.判断下列哪些集合相等(全集是整数集合I)解:A=G,B=E,C=F6.写出下列集合的幂集解:(2)ρ({1,∅})={∅,{1},{∅},{1,∅}}(4)ρ({∅,{a},{∅}})={∅,{∅},{{a}},{{∅}},{∅,{a}},{∅,{∅}},{{a},{∅}},{∅,{a},{∅}}}7.当把“⊆”插入空位时哪一个为真?解:(1)、(2)、(3)、(6)为真,(4)、(5)为假。
8.设A、B、C分别是集合,若A∈B,B∈C,哪麽A∈C一定成立吗?解:不一定,例如,A={a},B={{a}},C={{{a}}},虽然A∈B,B∈C,但A∈C不成立。
10.设U={1,2,3,4,5},A={1,4},B={1,2,5}和C={2,4}试写出下列集合(8)ρ(A)-ρ(C)解:ρ(A)-ρ(C)={∅,{1},{4},{1,4}}-{∅,{2},{4},{2,4}}={{1},{1,4}}11.证明下列恒等式(1)A-(B⋂C)=(A-B)⋃(A-C)(2)(A-B)⋂B=∅解:(1)A-(B⋂C)= A⋂~(B⋂C)= A⋂(~B⋃~C)=(A⋂~B)⋃(A⋂~C)=(A-B)⋃(A-C)(2)(A-B)⋂B=(A⋂~B)⋂B= A⋂(~B⋂B)= ∅12.设A、B、C是集合,下列等式成立的条件是什么?(1)(A-B)⋃(A-C)=A(2)(A-B)⋃(A-C)= ∅解:(1)因为(A-B)⋃(A-C)= (A⋂~B)⋃(A⋂~C)= A⋂(~B⋃~C)= A⋂~(B⋂C)= A-(B⋂C)所以(A-B)⋃(A-C)=A 当且仅当A-(B⋂C)=A 由-的定义可知A⋂(B⋂C)=∅(2)由(1)可知,(A-B)⋃(A-C)=A-(B⋂C)所以(A-B)⋃(A-C)=∅当且仅当A-(B⋂C)=∅由定理5.11可知A⊆(B⋂C)13. 设A,B是集合(1)A-B=B,问A和B有何关系?(2)A-B=B-A, 问A和B有何关系?解:(1)A=B=φ。

1 集合的概念与运算(一)目标: 1.理解集合、子集的概念,能利用集合中元素的性质解决问题2.理解交集、并集、全集、补集的概念,掌握集合的运算性质,3.能利用数轴或文氏图进行集合的运算,掌握集合问题的常规处理方法.重点: 1.集合中元素的3个性质,集合的3种表示方法,集合语言、集合思想的运用;2.交集、并集、补集的求法,集合语言、集合思想的运用.基本知识点:知识点1、集合的概念(1)集合:某些指定的对象集在一起就形成一个集合(简称集)(2)元素:集合中每个对象叫做这个集合的元素知识点2、常用数集及记法(1)非负整数集(自然数集):全体非负整数的集合记作N ,{} ,2,1,0=N(2)正整数集:非负整数集内排除0的集记作N *或N + {} ,3,2,1*=N(3)整数集:全体整数的集合记作Z , {} ,,,210±±=Z(4)有理数集:全体有理数的集合记作Q , {}整数与分数=Q (5)实数集:全体实数的集合记作R {}数数轴上所有点所对应的=R 注:(1)自然数集与非负整数集是相同的,也就是说,自然数集包括数0(2)非负整数集内排除0的集记作N *或N + Q 、Z 、R 等其它数集内排除0的集,也是这样表示,例如,整数集内排除0的集,表示成Z *知识点3、元素与集合关系(隶属)(1)属于:如果a 是集合A 的元素,就说a 属于A ,记作a ∈A(2)不属于:如果a 不是集合A 的元素,就说a 不属于A ,记作A a ∉注意:“∈”的开口方向,不能把a ∈A 颠倒过来写知识点4、集合中元素的特性(1)确定性:按照明确的判断标准给定一个元素或者在这个集合里, 或者不在,不能模棱两可(2)互异性:集合中的元素没有重复(3)无序性:集合中的元素没有一定的顺序(通常用正常的顺序写出)知识点5、集合与元素的表示:集合通常用大写的拉丁字母表示,如A 、B 、C 、P 、Q ……元素通常用小写的拉丁字母表示,如a 、b 、c 、p 、q ……例题精析1:1、下列各组对象能确定一个集合吗?(1)所有很大的实数 (不确定)(2)好心的人 (不确定)(3)1,2,2,3,4,5.(有重复)2、设a,b 是非零实数,那么b b a a +可能取的值组成集合的元素是_-2,0,2__ 3、由实数x,-x,|x |,332,x x -所组成的集合,最多含( A )(A )2个元素 (B )3个元素 (C )4个元素 (D )5个元素4、设集合G 中的元素是所有形如a +b 2(a ∈Z, b ∈Z )的数,求证:(1) 当x ∈N 时, x ∈G;(2) 若x ∈G ,y ∈G ,则x +y ∈G ,而x1不一定属于集合G 证明(1):在a +b 2(a ∈Z, b ∈Z )中,令a=x ∈N,b=0,则x= x +0*2= a +b 2∈G,即x ∈G证明(2):∵x ∈G ,y ∈G ,∴x= a +b 2(a ∈Z, b ∈Z ),y= c +d 2(c ∈Z, d ∈Z )∴x+y=( a +b 2)+( c +d 2)=(a+c)+(b+d)2∵a ∈Z, b ∈Z,c ∈Z, d ∈Z∴(a+c) ∈Z, (b+d) ∈Z∴x+y =(a+c)+(b+d)2 ∈G ,又∵211b a x +==2222222b a b b a a --+- 且22222,2b a b b a a ---不一定都是整数, ∴211b a x +==2222222b a b b a a --+-不一定属于集合G知识点6、集合的表示方法:(1)列举法:把集合中的元素一一列举出来,写在大括号内表示集合例如,由方程012=-x 的所有解组成的集合,可以表示为{-1,1}注:(1)有些集合亦可如下表示:从51到100的所有整数组成的集合:{51,52,53, (100)所有正奇数组成的集合:{1,3,5,7,…}(2)a 与{a}不同:a 表示一个元素,{a}表示一个集合,该集合只有一个元素(2)描述法:用确定的条件表示某些对象是否属于这个集合,并把这个条件写在大括 号内表示集合的方法格式:{x ∈A| P (x )}含义:在集合A 中满足条件P (x )的x 的集合 例如,不等式23>-x 的解集可以表示为:}23|{>-∈x R x 或}23|{>-x x所有直角三角形的集合可以表示为:}|{是直角三角形x x注:(1)在不致混淆的情况下,可以省去竖线及左边部分如:{直角三角形};{大于104的实数}(2)错误表示法:{实数集};{全体实数}(3)、文氏图:用一条封闭的曲线的内部来表示一个集合的方法思考:何时用列举法?何时用描述法?⑴有些集合的公共属性不明显,难以概括,不便用描述法表示,只能用列举法如:集合},5,23,{2232y x x y x x +-+⑵有些集合的元素不能无遗漏地一一列举出来,或者不便于、不需要一一列举出来,常用描述法如:集合}1|),{(2+=x y y x ;集合{1000以内的质数}例 集合}1|),{(2+=x y y x 与集合}1|{2+=x y y 是同一个集合吗? 答:不是因为集合}1|),{(2+=x y y x 是抛物线12+=x y 上所有的点构成的集合,集合}1|{2+=x y y =}1|{≥y y 是函数12+=x y 的所有函数值构成的数集例题精析2:1、用描述法表示下列集合①{1,4,7,10,13} }5,23|{≤∈-=n N n n x x 且②{-2,-4,-6,-8,-10} }5,2|{≤∈-=n N n n x x 且2、用列举法表示下列集合①{x ∈N|x 是15的约数} {1,3,5,15}②{(x ,y )|x ∈{1,2},y ∈{1,2}}{(1,1),(1,2),(2,1)(2,2)}注:防止把{(1,2)}写成{1,2}或{x=1,y=2}③⎩⎨⎧=-=+}422|),{(y x y x y x )}32,38{(- ④},)1(|{N n x x n ∈-= {-1,1}⑤},,1623|),{(N y N x y x y x ∈∈=+ {(0,8)(2,5),(4,2)}⑥}4,|),{(的正整数约数分别是y x y x{(1,1),(1,2),(1,4)(2,1),(2,2),(2,4),(4,1),(4,2),(4,4)}3、关于x 的方程ax +b=0,当a,b 满足条件____时,解集是有限集;当a,b 满足条件_____时,解集是无限集4、用描述法表示下列集合:(1) { 1, 5, 25, 125, 625 }= ;(2) { 0,±21, ±52, ±103, ±174, ……}= 巩固提升:1、数集{}21,,x x x -中元素x 所满足的条件是 2、已知{}23,21,1A a a a =--+,其中a R ∈, ⑴若3A -∈,求实数a 的值;⑵当a 为何值时,集合A 的表示不正确。

第三章1、用枚举法写出下列集合。
①英语句子“I am a student”中的英文字母;解:{I,a,m,s,t,u,d,e,n}②大于5小于13的所有偶数;解:{6,,8,10,12}③20的所有因数;解:{1,2,4,5,10,20}④小于20的6的正倍数。
解:{6,12,18}2、用描述法写出下列集合。
①全体奇数;解:S={x|x是奇数}②所有实数集上一元二次方程的解组成的集合;解:S={x|x是实数集上一元二次方程的解}③二进制数;解:S={x|x是二进制数}④能被5整除的整数集合。
解:S={x|x是能被5整除的整数}3、求下列集合的基数。
①“proper set”中的英文字母;解:S={p,r,o,e,s,t}所以 cardS=|S|=6②{{1,2},{2,1,1},{2,1,2,1}};解: cardS=|S|=3③{x|x=2或x=3或x=4或x=5};解:cardS=|S|=4④{{1,{2,3}}}。
解:cardS=|S|=14、求下列集合的幂集。
①“power set”中的英文字母;解:S={p,o,w,e,r,s,t}(S)是所有S的子集构成的集合,这里不一一列举了。
②{3,6,9};解:℘(S)={Φ ,{3},{6},{9},{3,6},{3,9},{6,9},{3,6,9}} ③小于20的5的正倍数;解:S={5,10,15} ℘(S)={Φ,{5},{10},{15},{5,10},{5,15},{10,15},{5,10,15}} ④{{1,3}}。
解:℘(S)={Φ,{1,3}}5、设Φ=A ,B=a ,求P(A) ,P(P(A)) ,P(P(P(A))) ,P(B) ,P(P(B)) ,P(P(P(B)))。
解:P(A)={Φ};P(P(A))={Φ,{Φ}};P(P(P(A)))={Φ,{Φ},{{Φ}},{Φ,{Φ}}}P(B)={Φ,a };P(P(B))={Φ,{Φ},{a},{Φ,a}};P(P(P(B)))={Φ,{Φ},{{Φ}},{{a}},{{Φ,a}},{Φ,{Φ}},{Φ,{a}},{Φ,{Φ,a}},{{Φ},{a}},{{Φ},{Φ,a}},{{a},{Φ,a}},{Φ,{Φ},{a}},{Φ,{Φ},{Φ,a}},{Φ,{a},{Φ,a}},{{Φ},{a},{Φ,a}},{{Φ,{Φ},{a},{Φ,a}}}.6、如果集合A 和B 分别满足下列条件,能得出A 和B 之间有什么联系? ①A ∪B=A ; ②A ∩B=A ; ③A -B=A ; ④A ∩B=A -B ; ⑤A -B=B -A ; ⑥A B A =⊕。

离散数学第二版本第五章第四节答案1.3 交集、并集若集合A={x|x是6的倍数},B={x|x是4的倍数},则A与B 有公共元素吗?它们的公共元素能组成一个集合吗?两个集合A与B的公共元素能组成一个集合吗?若能组成一个集合C,则C与A、B的关系如何?基础巩固1.若集合A={0,1,2,3,4},B={1,2,4}则AB=()A.{0,1,2,3,4} B.{1,2,3,4}C.{1,2} D.{0}答案:A2.设S={x||x|3},T={x|3x-51},则ST=()A.B.{x|-33}C.{x|-32} D.{x|23}答案:C3.已知A,B均为集合U={1,3,5,7,9}的子集,且AB={3}, AUB ={9},则A=()A.{1,3} B.{3,7,9}C.{3,5,9} D.{3,9}答案:D4.设A={(x,y)|4x+y=6},B={(x,y)|3x+2y=7},则AB 为()A.{x=1,或y=2} B.{1,2}C.{(1,2)} D.(1,2)解析:AB=x,y4x+y=63x+2y=7={(1,2)}.答案:C5.已知集合A={(x,y)|x,yR且x2+y2=1},B={(x,y)|x,yR且x+y=1,则AB的元素个数为()A.4个B.3个C.2个D.1个解析:由x2+y2=1,x+y=1x=1,y=0或x=0,y=1,即AB={(1,0),(0,1)}.答案:C6.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(UA)B 为()A.{1,2,4} B.{2,3,4}C.{0,2,4} D.{0,2,3,4}答案:C7.已知方程x2-px+15=0与x2-5x+q=0的解分别为M 和S,且MS={3},则pq=________.解析:∵MS={3},3既是方程x2-px+15=0的根,又是x2-5x+q=0的根,从而求出p,q.答案:438.已知全集S=R,A={x|x1},B={x|05},则(SA)B=________.解析:SA={x|x1}.答案:{x|15}9.设集合A={x||x-a|1,xR},B={x|15},若AB=,则a的取值范围是________.解析:∵A={x|a-1a+1},若AB=,则a+11或a-1a0或a6.答案:{a|a0或a6}10.设集合A={0,1,2,3,4,5,7},B={1,3,6,8,9},C={3,7,8},那么集合(AC是________.答案:{1,3,7,8}11.满足条件{1,3}A={1,3,5}的所有集合A的个数是________个.答案:4能力提升12.集合A={x||x|1,xR},B={y|y=x2,xR},则AB为()A.{x|-11} B.{x|x0}C.{x|01} D.解析:∵A={x|-11},B={y|y0}AB={x|01}.答案:C13.若A、B、C为三个集合,且有AB=BC,则一定有()A.AC B.CAC.A D.A=答案:A14.设全集U={a,b,c,d},A={a,b},B={b,c,d},则UAUB=________解析:UA={c,d},UB={a},UAUB={a,c,d}.答案:{a,c,d}15.(2013上海卷)设常数aR,集合A={x|(x-1)(x-a)0},B ={x|xa-1},若AB=R,则a的取值范围为________.解析:当a1时,A={x|x1或xa},要使AB=R,则a1,a-112;当a1时,A={x|xa或x1},要使AB=R,则a1,a-1a1.综上,a答案:{a|a2}16.已知集合A={x||x+2|3,xR},集合B={x|(x-m)(x-2)0},xR},且AB=(-1,n),求m和n的值.解析:|x+2|-3x+2-51,A={x|-51},又∵AB=(-1,n),-1是方程(x-m)(x-2)=0的根,即m=-1,此时B={x|-12},AB=(-1,1),即n=1.17.设集合P={1,2,3,4},求同时满足下列三个条件的集合A:(1)AP;(2)若xA,则2xA;(3)若xPA,则2xPA.解析:∵21=2,22=4,因此1和2不能同时属于A,也不能同时属于UA,同样地,2和4也不能同时属于A和UA,对P的子集进行考查,可知A只能为:{2},{1,4},{2,3}{1,3,4}.18.设集合A={x|x+10或x-40},B={x|2aa+2}.(1)若A,求实数a的取值范围;(2)若AB=B,求实数a的取值范围.解析:(1)A={x|x-1或x4},∵A,2a2+a,a+24或2aa+2,2a-1.a=2或a-12.综上所述,实数a的取值范围为aa-12或a=2.(2)∵AB=B,BA.①B=时,满足BA,则2aa+22,②B时,则2aa+2,a+2-1或2aa+2,2a4.即a-3或a=2.综上所述,实数a的取值范围为{a|a-3或a=2}.。

离散数学第五章答案离散数学第五章答案【篇一:3~离散数学习题解答(第五章)格与布尔代数5】题五(第五章格与布尔代数)1.设〈l,?〉是半序集,?是l上的整除关系。
问当l取下列集合时,〈l,?〉是否是格。
a) l={1,2,3,4,6,12}b) l={1,2,3,4,6,8,12}c) l={1,2,3,4,5,6,8,9,10}[解] a) 〈l,?〉是格,因为l中任两个元素都有上、下确界。
631b) 〈l,?〉不是格。
因为l中存在着两个元素没有上确界。
例如:8?12=lub{8,12}不存在。
12 63 1c) 〈l,?〉不是格。
因为l中存在着两个元素没有上确界。
倒例如:4?6=lub{4,6}不存在。
712.设a,b是两个集合,f是从a到b的映射。
证明:〈s,?〉是〈2b,?〉的子格。
其中s={y|y=f (x),x∈2a}[证] 对于任何b1∈s,存在着a1∈2a,使b1=f(a1),由于f(a1)={y|y∈b∧(?x)(x∈a1∧f (x)=y)}b 所以b1∈2b,故此s?2b;又b0=f (a)∈s (因为a∈2a),所以s非空;对于任何b1,b2∈s,存在着a1,a2∈2a,使得b1=f (a1),b2=f (a2),从而l∪b{b1,b2}=b1∪b2=f (a1)f (a2)=f (a1∪a2) (习题三的8的1))由于a1∪a2?a,即a1∪a2∈2a,因此f (a1∪a2)∈s,即上确界l∪b{b1,b2}存在。
对于任何b1,b2∈s,定义a1=f –1(b1)={x|x∈a∧f (x)∈b1},a2=f-1(b2)={x|x∈a∧f (x)∈b2},则a1,a2∈2a,且显然b1=f (a1),b2=f (a2),于是glb{b1,b2}=b1∩b2=f (a1)∩f (a2)f (a1∩a2) (习题三的8的2))又若y∈b1∩b2,则y∈b,且y∈b2。
由于y∈b1=f(a1)={y|y∈b∧(?x)(x∈a1∧f (x)=y)},于是存在着x∈a1,使f(x)=y,但是 f (x)=y∈b2。

离散数学课后习题答案离散数学课后习题答案离散数学是计算机科学中的一门重要课程,它涵盖了诸多数学概念与技巧,为计算机科学的理论基础打下了坚实的基础。
在学习离散数学的过程中,课后习题是巩固知识、提高能力的重要途径。
然而,有时候我们会遇到一些难以解答的问题,需要参考一些答案来进行思考与学习。
本文将为大家提供一些离散数学课后习题的答案,希望能对大家的学习有所帮助。
一、集合论1. 设A={1,2,3},B={2,3,4},求A∪B和A∩B的结果。
答案:A∪B={1,2,3,4},A∩B={2,3}。
2. 证明:任意集合A和B,有(A-B)∪(B-A)=(A∪B)-(A∩B)。
答案:首先,对于任意元素x,如果x属于(A-B)∪(B-A),那么x属于A-B或者x属于B-A。
如果x属于A-B,那么x属于A∪B,但x不属于A∩B;如果x属于B-A,同样有x属于A∪B,但x不属于A∩B。
所以(A-B)∪(B-A)属于(A∪B)-(A∩B)。
另一方面,对于任意元素x,如果x属于(A∪B)-(A∩B),那么x属于A∪B,但x不属于A∩B。
所以x属于A或者x属于B。
如果x属于A,但x不属于B,那么x属于A-B;如果x属于B,但x不属于A,那么x属于B-A。
所以x属于(A-B)∪(B-A)。
所以(A∪B)-(A∩B)属于(A-B)∪(B-A)。
综上所述,(A-B)∪(B-A)=(A∪B)-(A∩B)。
证毕。
二、逻辑与证明1. 证明:如果p为真命题,那么¬p为假命题。
答案:根据命题的定义,命题要么为真,要么为假,不存在其他情况。
所以如果p为真命题,那么¬p为假命题。
2. 证明:对于任意整数n,如果n^2为偶数,则n为偶数。
答案:假设n为奇数,即n=2k+1(k为整数)。
那么n^2=(2k+1)^2=4k^2+4k+1=2(2k^2+2k)+1。
根据偶数的定义,2(2k^2+2k)为偶数,所以n^2为奇数。

第一章部分课后习题参考答案16 设p、q的真值为0;r、s的真值为1,求下列各命题公式的真值。
(1)p∨(q∧r)⇔ 0∨(0∧1) ⇔0(2)(p?r)∧(﹁q∨s) ⇔(0?1)∧(1∨1) ⇔0∧1⇔0.(3)(⌝p∧⌝q∧r)?(p∧q∧﹁r) ⇔(1∧1∧1) ? (0∧0∧0)⇔0(4)(⌝r∧s)→(p∧⌝q) ⇔(0∧1)→(1∧0) ⇔0→0⇔117.判断下面一段论述是否为真:“π是无理数。
并且,如果3是无理数,则2也是无理数。
另外6能被2整除,6才能被4整除。
”答:p: π是无理数 1q: 3是无理数 0r: 2是无理数 1s: 6能被2整除 1t: 6能被4整除 0命题符号化为: p∧(q→r)∧(t→s)的真值为1,所以这一段的论述为真。
19.用真值表判断下列公式的类型:(4)(p→q) →(⌝q→⌝p)(5)(p∧r) ↔(⌝p∧⌝q)(6)((p→q) ∧(q→r)) →(p→r)答:(4)p q p→q ⌝q ⌝p ⌝q→⌝p (p→q)→(⌝q→⌝p)0 0 1 1 1 1 10 1 1 0 1 1 11 0 0 1 0 0 11 1 1 0 0 1 1所以公式类型为永真式等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出成真赋值.(1) ⌝(p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)答:(2)(p→(p∨q))∨(p→r)⇔(⌝p∨(p∨q))∨(⌝p∨r)⇔⌝p∨p∨q∨r⇔1所以公式类型为永真式(3)P q r p∨q p∧r (p∨q)→(p∧r)0 0 0 0 0 10 0 1 0 0 10 1 0 1 0 00 1 1 1 0 01 0 0 1 0 01 0 1 1 1 11 1 0 1 0 01 1 1 1 1 1所以公式类型为可满足式4.用等值演算法证明下面等值式:(2)(p→q)∧(p→r)⇔(p→(q∧r))(4)(p∧⌝q)∨(⌝p∧q)⇔(p∨q) ∧⌝(p∧q)证明(2)(p→q)∧(p→r)⇔ (⌝p∨q)∧(⌝p∨r)⇔⌝p∨(q∧r))⇔p→(q∧r)(4)(p∧⌝q)∨(⌝p∧q)⇔(p∨(⌝p∧q)) ∧(⌝q∨(⌝p∧q)⇔(p∨⌝p)∧(p∨q)∧(⌝q∨⌝p) ∧(⌝q∨q)⇔1∧(p∨q)∧⌝(p∧q)∧1⇔(p∨q)∧⌝(p∧q)5.求下列公式的主析取范式与主合取范式,并求成真赋值(1)(⌝p→q)→(⌝q∨p)(2)⌝(p→q)∧q∧r(3)(p∨(q∧r))→(p∨q∨r)解:(1)主析取范式(⌝p→q)→(⌝q∨p)⇔⌝(p∨q)∨(⌝q∨p)⇔(⌝p∧⌝q)∨(⌝q∨p)⇔ (⌝p∧⌝q)∨(⌝q∧p)∨(⌝q∧⌝p)∨(p∧q)∨(p∧⌝q)⇔(⌝p∧⌝q)∨(p∧⌝q)∨(p∧q)⇔320m m m ∨∨⇔∑(0,2,3)主合取范式:(⌝p →q)→(⌝q ∨p)⇔⌝(p ∨q)∨(⌝q ∨p)⇔(⌝p ∧⌝q)∨(⌝q ∨p)⇔(⌝p ∨(⌝q ∨p))∧(⌝q ∨(⌝q ∨p))⇔1∧(p ∨⌝q)⇔(p ∨⌝q) ⇔ M 1⇔∏(1)(2) 主合取范式为:⌝(p →q)∧q ∧r ⇔⌝(⌝p ∨q)∧q ∧r⇔(p ∧⌝q)∧q ∧r ⇔0所以该式为矛盾式.主合取范式为∏(0,1,2,3,4,5,6,7)矛盾式的主析取范式为 0(3)主合取范式为:(p ∨(q ∧r))→(p ∨q ∨r)⇔⌝(p ∨(q ∧r))→(p ∨q ∨r)⇔(⌝p ∧(⌝q ∨⌝r))∨(p ∨q ∨r)⇔(⌝p ∨(p ∨q ∨r))∧((⌝q ∨⌝r))∨(p ∨q ∨r))⇔1∧1⇔1所以该式为永真式.永真式的主合取范式为 1主析取范式为∑(0,1,2,3,4,5,6,7)第三章部分课后习题参考答案14. 在自然推理系统P 中构造下面推理的证明:(2)前提:p →q,⌝(q ∧r),r结论:⌝p(4)前提:q→p,q↔s,s↔t,t∧r结论:p∧q证明:(2)①⌝(q∧r) 前提引入②⌝q∨⌝r ①置换③q→⌝r ②蕴含等值式④r 前提引入⑤⌝q ③④拒取式⑥p→q 前提引入⑦¬p ⑤⑥拒取式证明(4):①t∧r 前提引入②t ①化简律③q↔s 前提引入④s↔t 前提引入⑤q↔t ③④等价三段论⑥(q→t)∧(t→q)? ⑤置换⑦(q→t)⑥化简⑧q ②⑥假言推理⑨q→p 前提引入⑩p ⑧⑨假言推理(11)p∧q ⑧⑩合取15在自然推理系统P中用附加前提法证明下面各推理:(1)前提:p→(q→r),s→p,q结论:s→r证明①s 附加前提引入②s→p 前提引入③p ①②假言推理④p→(q→r) 前提引入⑤q→r ③④假言推理⑥q 前提引入⑦r ⑤⑥假言推理16在自然推理系统P中用归谬法证明下面各推理:(1)前提:p→⌝q,⌝r∨q,r∧⌝s结论:⌝p证明:①p 结论的否定引入②p→﹁q 前提引入③﹁q ①②假言推理④¬r∨q 前提引入⑤¬r ④化简律⑥r∧¬s 前提引入⑦r ⑥化简律⑧r∧﹁r ⑤⑦合取由于最后一步r∧﹁r 是矛盾式,所以推理正确.第四章部分课后习题参考答案3. 在一阶逻辑中将下面将下面命题符号化,并分别讨论个体域限制为(a),(b)条件时命题的真值:(1) 对于任意x,均有2=(x+)(x).(2) 存在x,使得x+5=9.其中(a)个体域为自然数集合.(b)个体域为实数集合.解:F(x): 2=(x+)(x).G(x): x+5=9.(1)在两个个体域中都解释为)xF∀,在(a)中为假命题,在(b)中为真命题。

离散数学作业5 ——关系的闭包运算1. 若X 上的关系R 1⊆R 2,则⑴ r(R 1)⊆r(R 2) ⑵ s(R 1)⊆s(R 2) ⑶ t(R 1)⊆t(R 2)分析 : 利用三种闭包的计算公式或者定义证明都可.证明:(1)r(R 1)=I X ∪R 1,r(R 2)=I X ∪R 2,所以r(R 1)⊆r(R 2)。
(2)因为R 1⊆R 2,所以1211--⊆R R 。
因为s(R 1)=111-⋃R R ,s(R 2)=122-⋃R R ,所以s(R 1)⊆s(R 2)。
(3)因为t(R 1)= ⋃⋃211R R ,t(R 2)= ⋃⋃222R R ,,222121R R R R ⊆⊆所以t(R 1)⊆t(R 2)。
2. R 是X 上的关系,⑴ 若R 是自反的,则 s(R)和t(R)也是自反的。
⑵ 若R 是对称的,则 r(R)和t(R)也是对称的。
⑶ 若R 是传递的,则 r(R)也是传递的。
证明:(1)因为s(R)=1-⋃R R ,t(R)= ⋃⋃2R R ,I X ⊆R ,所以 I X ⊆ s(R),I X ⊆ t(R),即s(R)和t(R)也是自反的。
(2)因为R 是对称的,所以1-=R R ,122)(-=R R 。
)()()(111R r R I R I R I R r =⋃=⋃=⋃=--- )()()()(121121R t R R R R R t =⋃⋃=⋃⋃=---- 所以r(R)和t(R)也是对称的。
(3)R 是传递的当且仅当R R ⊆2。
)()()()()(222R r R I R R I R I R I R I R r =⋃⊆⋃⋃=⋃⋃=⋃= 所以r(R)是传递的。
3. 设R 是X 上的关系,则⑴ rs(R)=sr(R); ⑵ rt(R)=tr(R); ⑶st(R)⊆ts(R)。
证明: (1)因为rs(R)=I ∪s(R)=I ∪(R ∪R -1)sr(R)=(I∪R) ∪(I∪R)-1=(I∪R) ∪(I∪R-1)=I(I∪R∪R-1所以rs(R)=sr(R)。


第十四章部分课后习题参考答案5、设无向图G 有10条边,3度与4度顶点各2个,其余顶点的度数均小于3,问G 至少有多少个顶点?在最少顶点的情况下,写出度数列、)()(G G δ、∆。
解:由握手定理图G 的度数之和为:20102=⨯3度与4度顶点各2个,这4个顶点的度数之和为14度。
其余顶点的度数共有6度。
其余顶点的度数均小于3,欲使G 的顶点最少,其余顶点的度数应都取2, 所以,G 至少有7个顶点, 出度数列为3,3,4,4,2,2,2,2)(,4)(==∆G G δ.7、设有向图D 的度数列为2,3,2,3,出度列为1,2,1,1,求D 的入度列,并求)(),(D D δ∆,)(),(D D ++∆δ,)(),(D D --∆δ.解:D 的度数列为2,3,2,3,出度列为1,2,1,1,D 的入度列为1,1,1,2.2)(,3)(==∆D D δ,1)(,2)(==∆++D D δ,1)(,2)(==∆--D D δ8、设无向图中有6条边,3度与5度顶点各1个,其余顶点都是2度点,问该图有多少个顶点?解:由握手定理图G 的度数之和为:1262=⨯设2度点x 个,则1221513=+⨯+⨯x ,2=x ,该图有4个顶点.14、下面给出的两个正整数数列中哪个是可图化的?对可图化的数列,试给出3种非同构的无向图,其中至少有两个时简单图。
(1) 2,2,3,3,4,4,5 (2) 2,2,2,2,3,3,4,4 解:(1) 2+2+3+3+4+4+5=23 是奇数,不可图化; (2) 2+2+2+2+3+3+4+4=16, 是偶数,可图化;18、设有3个4阶4条边的无向简单图G 1、G 2、G 3,证明它们至少有两个是同构的。
证明:4阶4条边的无向简单图的顶点的最大度数为3,度数之和为8,因而度数列为2,2,2,2;3,2,2,1;3,3,1,1。
但3,3,1,1对应的图不是简单图。
所以从同构的观点看,4阶4条边的无向简单图只有两个:所以,G 1、G 2、G 3至少有两个是同构的。
5.1习题参考答案1、阮允准同学提供答案:解:设度数小于3的结点有x个,则有3×4+4×3+2x≥2×16解得:x≥4所以度数小于3的结点至少有4个所以G至少有11个结点2、阮允准同学答案:证明:由题意可知:度数为5的结点数只能是0,2,4,6,8。
若度数为5的结点数为0,2,4个,则度数为6的结点数为9,7,5个结论成立。
若度数为5的结点数为6,8个,结论显然成立。
由上可知,G中至少有5个6度点或至少有6个5度点。
3、晓津证明如下:设简单图有n个结点,某结点的度为最大度,因为简单图任一结点没有平行边,而任一结点的的边必连有另一结点,则其最多有n-1条边与其他结点相连,因此其度数最多只有n-1条,小于结点数n.4 \阮同学给出证明如下:证明:设G中所有结点的度数都小于3,即每个结点度数都小于等于2,则所有结点度数之和小于等于2n,所以G的边数必小于等于n,这和已知G有n+1条边相矛盾。
所以结论成立。
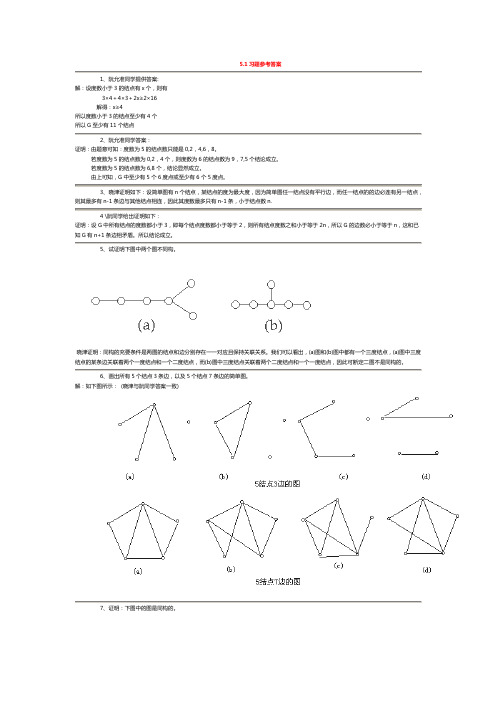
5、试证明下图中两个图不同构。
晓津证明:同构的充要条件是两图的结点和边分别存在一一对应且保持关联关系。
我们可以看出,(a)图和(b)图中都有一个三度结点,(a)图中三度结点的某条边关联着两个一度结点和一个二度结点,而(b)图中三度结点关联着两个二度结点和一个一度结点,因此可断定二图不是同构的。
6、画出所有5个结点3条边,以及5个结点7条边的简单图。
解:如下图所示:(晓津与阮同学答案一致)7、证明:下图中的图是同构的。
证明如下:在两图中我们可以看到有a→e,b→h,c→f,d→g两图中存在结点与边的一一对应关系,并保持关联关系。
8、证明:下面两图是同构的。
阮同学给出证明如下:证明:找出对应关系:a---q, b----r, c-----s, d----t, e-----u,f------v, g-----w, h----x9、证明:三次正则图必有偶数个结点。
阮同学证明如下:由题意可知每个结点度数都是3度,即每个结点均为奇结点,根据有偶数个奇结点可知,三次正则图必有偶数个奇结点。