初二数学 一次函数知识总结及例题解析

初二数学一次函数知识点总结123初二数学习题一次函数知识点深入分析123一次函数总结知识点概括基本概念1、变量：在一个变化过程中可以取每种不同数值的量。

常量：在一个变化过程当中只能取同一并不需要数值的量。

例题：在匀速运动公式svt中,v表示速度,t表示时间,s表示在时间t内所走的路程,则变量是________,常量是_______。

在圆的周长公式C=2πr中，变量是________，常量是_________.2、函数：一般的，在一个变化过程中所，如果有两个变量x和y，并且对于x的每一个确定的系数，y都有唯一确定确定的阈值与其对应，那么我们就把x称为自变量，把y称为因变量，y是x的函数。

*判断Y是否为X的函数，只要看X取值确定的时候，Y是否有唯一确定的值与之近似1-12例题：下列函数（1）y=πx(2)y=2x-1(3)y=(4)y=2-3x(5)y=x-1中，是一次函数的有（）x（A）4个（B）3个（C）2个（D）1个3、定义域：一般的，一个函数的自变量允许取值的定义域范围，特指这个函数的定义域。

（x的取值范围）一次函数1.．自变量x和因变量y有如下关系：y=kx+b（k为任意不为零实数，b为任意实数）则此时称y是x的一次函数。

特别的，当b=0时，y是x的正比例函数。

即：y=kx（k为任意不为零实数）定义域：自变量的取值适用范围，自变量的取值应使函数有意义；要与实际有意义。

2.当x=0时，b为函数在y轴上的截距。

一次函数性质：1在一次函数上的任意一点P（x，y），都满足等式：y=kx+b(k≠0)。

2一次函数与y双轴交点的坐标总是（0，b)，与x轴总是交于（-b/k，0）正比例函数的图像总是过原点。

3．函数不是数，它是指某一变量过程中暧昧关系两个变量之间的关系。

特别地，当b=0时，直线通过原点O（0，0）表示的是正比例函数的对易图像。

这时，当k＞0时，直线只通过一、三象限；当k＜0时，直线只通过二、四象限。

一次函数知识点总结基本概念1、变量：在一个变化过程中可以取不同数值的量。

常量：在一个变化过程中只能取同一数值的量。

例题：在匀速运动公式vt s =中,v 表示速度,t 表示时间,s 表示在时间t 内所走的路程,则变量是________,常量是_______。

在圆的周长公式C=2πr 中，变量是________，常量是_________.2、函数：一般的，在一个变化过程中，如果有两个变量x 和y ，并且对于x 的每一个确定的值，y 都有唯一确定的值与其对应，那么我们就把x 称为自变量，把y 称为因变量，y 是x 的函数。

*判断Y 是否为X 的函数，只要看X 取值确定的时候，Y 是否有唯一确定的值与之对应例题：下列函数（1）y=πx (2)y=2x-1 (3)y=1x(4)y=2-1-3x (5)y=x 2-1中，是一次函数的有（ ） （A ）4个 （B ）3个 （C ）2个 （D ）1个3、定义域：4、确定函数定义域的方法：（1）关系式为整式时，函数定义域为全体实数；（2 （3）关系式含有二次根式时，被开放方数大于等于零；（4（5例题：下列函数中，自变量x 的取值范围是x ≥2的是（ ）A ．．． D ．函数y =x 的取值范围是___________. 已知函数221+-=x y ，当11≤<-x 时，y 的取值范围是 （ ） A.2325≤<-y B.2523<<y C.2523<≤y D.2523≤<y 5、函数的图像一般来说，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象．6、函数解析式：用含有表示自变量的字母的代数式表示因变量的式子叫做解析式。

7、描点法画函数图形的一般步骤第一步：列表（表中给出一些自变量的值及其对应的函数值）；第二步：描点（在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点）；第三步：连线（按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来）。

一次函数一．知识回顾（一）函数1、变量：在一个变化过程中可以取不同数值的量。

常量：在一个变化过程中只能取同一数值的量。

2、函数：一般的，在一个变化过程中，如果有两个变量x 和y ，并且对于x 的每一个确定的值，y 都有唯一确定的值与其对应,那么我们就把x 称为自变量，把y 称为因变量,y 是x 的函数。

*判断Y 是否为X 的函数,只要看X 取值确定的时候，Y 是否有唯一确定的值与之对应3、定义域:一般的，一个函数的自变量允许取值的范围，叫做这个函数的定义域.4、确定函数定义域的方法:（1）关系式为整式时，函数定义域为全体实数； （2）关系式含有分式时，分式的分母不等于零;（3)关系式含有二次根式时,被开放方数大于等于零； （4）关系式中含有指数为零的式子时,底数不等于零;（5）实际问题中，函数定义域还要和实际情况相符合，使之有意义。

5、函数的解析式：用含有表示自变量的字母的代数式表示因变量的式子叫做函数的解析式6、函数的图像一般来说，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象． 7、描点法画函数图形的一般步骤第一步:列表（表中给出一些自变量的值及其对应的函数值）; 第二步：描点（在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标,描出表格中数值对应的各点）；第三步：连线（按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来). 8、函数的表示方法列表法：一目了然，使用起来方便，但列出的对应值是有限的,不易看出自变量与函数之间的对应规律. 解析式法：简单明了，能够准确地反映整个变化过程中自变量与函数之间的相依关系，但有些实际问题中的函数关系，不能用解析式表示。

图象法：形象直观，但只能近似地表达两个变量之间的函数关系。

（二）一次函数 1、一次函数的定义一般地，形如y kx b =+（k ,b 是常数，且0k ≠)的函数,叫做一次函数,其中x 是自变量。

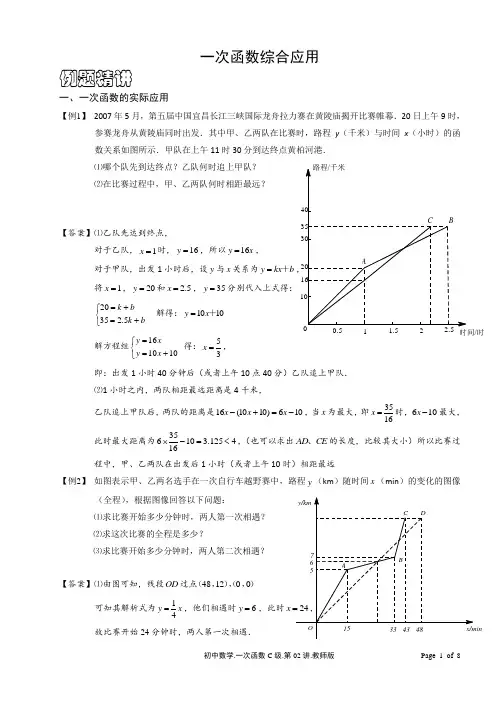
一次函数综合应用例题精讲一、一次函数的实际应用【例1】 2007年5月，第五届中国宜昌长江三峡国际龙舟拉力赛在黄陵庙揭开比赛帷幕．20日上午9时，参赛龙舟从黄陵庙同时出发．其中甲、乙两队在比赛时，路程y （千米）与时间x （小时）的函数关系如图所示．甲队在上午11时30分到达终点黄柏河港． ⑴哪个队先到达终点？乙队何时追上甲队？ ⑵在比赛过程中，甲、乙两队何时相距最远？【答案】⑴乙队先达到终点，对于乙队，1x =时，16y =，所以16y x =，对于甲队，出发1小时后，设y 与x 关系为y kx b =＋将1x =，20y =和 2.5x =，35y =分别代入上式得： 2035 2.5k bk b =+⎧⎨=+⎩解得：1010y x =＋解方程组161010y x y x =⎧⎨=+⎩ 得：53x =，即：出发1小时40分钟后（或者上午10点40分）乙队追上甲队． ⑵1小时之内，两队相距最远距离是4千米，乙队追上甲队后，两队的距离是16(1010)610x x x -+=-，当x 为最大，即3516x =时，610x -最大，此时最大距离为35610 3.125416⨯-=<，（也可以求出AD CE 、的长度，比较其大小）所以比赛过程中，甲、乙两队在出发后1小时（或者上午10时）相距最远【例2】 如图表示甲、乙两名选手在一次自行车越野赛中，路程y （km ）随时间x （min ）的变化的图像（全程），根据图像回答以下问题：⑴求比赛开始多少分钟时，两人第一次相遇？ ⑵求这次比赛的全程是多少？⑶求比赛开始多少分钟时，两人第二次相遇？【答案】⑴由图可知，线段OD 过点481200（，）（，，）可知其解析式为14y x =，他们相遇时6y =，此时x 故比赛开始24分钟时，两人第一次相遇．时间/时⑵由图可知，这次比赛的全程为12km ．⑶点B （33，7）、点C （43，12），故线段BC 的解析式为：()1192y x =-，而线段OD 的解析式为()10484y x =<<，故它们的交点坐标为（38，192），即比赛开始38分钟时，两人第二次相遇． 【例3】 为了保护环境，某企业决定购买10台污水处理设备，现有A B ，两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表：⑴求购买设备的资金y 万元与购买A 型x 台的函数关系，并设计该企业有几种购买方案； ⑵若企业每月产生的污水量为2040吨，利用函数的知识说明，应选择哪种购买方案；⑶在第⑵问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？（注：企业处理污水的费用包括购买设备的资金和消耗费）【答案】⑴购买污水处理设备A 型x 台，则B 型()10x -台，由题意知：()121010y x x =+-，即2100y x =+，2100105y x =+≤，∴ 2.5x ≤ 又∵x 是非负整数，∴x 可取0,1,2 ∴有三种购买方案：①购A 型D 台，B 型10台；②购A 型1台，B 型9台；③购A 型2台，B 型8台； ⑵由题意得()240200102040x x +-≥，解得1x ≥∴x 为1或2，∵由2100y x =+得20k =>，y 随x 的增大而增大． 为了节约资金，应选购A 型1台，B 型9台．⑶10年企业自己处理污水的总资金为：1021010202+⨯=（万元） 若将污水排到污水厂处理，10年所需费用为： 20401210102448000⨯⨯⨯＝（元）244.8=（万元）∵244.820242.8-=（万元），∴能节约资金42.8万元．【例4】 某汽车运输公司根据实际需要计划购买大、中型两种客车共20辆，已知大型客车每辆62万元，中型客车每辆40万元，设购买大型客车x （辆），购车总费用为y （万元）． ⑴求y 与x 的函数关系式（不要求写出自变量x 的取值范围）；⑵若购买中型客车的数量少于大型客车的数量，请你给出一种费用最省的方案，并求出该方案所需费用．【答案】⑴因为购买大型客车x 辆，所以购买中型客车()20x -辆．()62402022800y x x x =+-=+⑵依题意得()20x x -<.解得10x >．∵ 22800y x =+，y 随着x 的增大而增大，x 为整数， ∴ 当11x =时，购车费用最省，为22×11+800=1 042（万元）． 此时需购买大型客车11辆，中型客车9辆．答：购买大型客车11辆，中型客车9辆时，购车费用最省，为1042万元．二、一次函数与几何综合【例5】 已知直线3y x =+的图象与x y 、轴交于A B 、两点，直线l 经过原点，与线段AB 交于点C ，把AOB ∆的面积分为2:1的两部分，求直线l 的解析式。

初二数学一次函数试题答案及解析1.对于函数y=﹣5x+1，下列结论：①它的图象必经过点（﹣1，5）②它的图象经过第一、二、三象限③当x＞1时，y＜0④y的值随x值的增大而增大，其中正确的个数是（）A．0B．1C．2D．3【答案】B．【解析】∵当x=-1时，y=-5×（-1）+1=-6≠5，∴此点不在一次函数的图象上，故①错误；∵k=-5＜0，b=1＞0，∴此函数的图象经过一、二、四象限，故②错误；∵x=1时，y=-5×1+1=-4，又k=-5＜0，∴y随x的增大而减小，∴当x＞1时，y＜-4，则y＜0，故③正确，④错误．综上所述，正确的只有：③故选B．【考点】一次函数的性质．2.某饮料厂开发了A、B两种新型饮料，主要原料均为甲和乙，每瓶饮料中甲、乙的含量如下表所示．现用甲原料和乙原料各2800克进行试生产，计划生产A、B两种饮料共100瓶．设生产A种饮料x瓶，解析下列问题：（1）有几种符合题意的生产方案写出解析过程；（2）如果A种饮料每瓶的成本为2.60元，B种饮料每瓶的成本为2.80元，这两种饮料成本总额为y元，请写出y与x之间的关系式，并说明x取何值会使成本总额最低？【答案】（1）21种．（2）y=-0.2x+280．x=40时成本总额最低．【解析】（1）设生产A种饮料x瓶解出不等式方程组即可．（2）如图可得x与y的关系式，可知道x与y的关系．试题解析：（1）根据题意得：，解这个不等式组，得20≤x≤40．因为其中正整数解共有21个，所以符合题意的生产方案有21种．（2）根据题意，得y=2.6x+2.8（100-x），整理，得y=-0.2x+280．∵k=-0.2＜0，∴y随x的增大而减小．∴当x=40时成本总额最低．【考点】一元一次不等式组的应用．3.关于正比例函数y=-2x,下列说法错误的是( )A．图象经过原点B．图象经过第二,四象限C．y随x增大而增大D．点(2,-4)在函数的图象上【答案】C．【解析】A、正比例函数y=-2x，图象经过原点，正确，不合题意；B、正比例函数y=-2x，图象经过第二，四象限，正确，不合题意；C、正比例函数y=-2x，y随x增大而减小，故此选项错误，不合题意；D、当x=2时，y=-4，故点（2，-4）在函数的图象上正确，不合题意；故选C．【考点】正比例函数的性质．4.已知点A(-5，y1)和B(-4，y2)都在直线y=x-4上,则y1与y2的大小关系是( )A．y1＞y2B．y1=y2C．y1＜y2D．不能确定【答案】C．【解析】∵点A（﹣5，y1）和B（﹣4，y2）都在直线y=x﹣4上，∴y1=﹣5﹣4=﹣9，y2=﹣4﹣4=﹣8，∵﹣9＜﹣8，∴y1＜y2，故选C．【考点】一次函数图象上点的坐标特征．5.一次函数y=kx+b的图象如图所示，当y＞0时，x的取值范围是_________．【答案】x＜2．【解析】由图象可知一次函数y=kx+b的图象经过点（2，0）、（0，3）．∴可列出方程组，解得，∴该一次函数的解析式为y=x+3，∵＜0，∴当y＞0时，x的取值范围是：x＜2．故答案是x＜2．【考点】一次函数的图象．6.已知一次函数y=kx+b的图象如图所示,则k,b的符号是 ( )A．k＞0，b＞0B．k＞0，b＜0C．k＜0，b＞0D．k＜0，b＜0【答案】D.【解析】由一次函数y=kx+b的图象经过二、三、四象限，又有k＜0时，直线必经过二、四象限，故知k＜0，再由图象过三、四象限，即直线与y轴负半轴相交，所以b＜0．故选D．【考点】一次函数图象与系数的关系．7.在一次函数y＝kx＋2中，若y随x的增大而增大，则它的图象不经过第____象限．【答案】四．【解析】∵在一次函数y=kx+2中，y随x的增大而增大，∴k＞0，∵2＞0，∴此函数的图象经过一、二、三象限，不经过第四象限．故答案是四．【考点】一次函数图象与系数的关系．8.如图表示一个正比例函数与一个一次函数的图象，它们交于点A（4，3），一次函数的图象与轴交于点B，且OA=OB，求这两个函数的关系式及两直线与轴围成的三角形的面积.【答案】 3.75【解析】解：如图，过点A作AC⊥轴于点C，则AC=3，OC=4，所以OA=OB=5，故B点坐标为（0，）.设直线AO的关系式为，因为其过点A（4，3），则，解得.所以.设直线AB的关系式为，因为其过点A（4，3）、B（0，），则解得：所以关系式为.令，得，则D点坐标为（2.5，0）.所以两直线与轴围成的三角形AOD的面积为2.5×3÷2=3.75.9.已知一次函数，（1）为何值时，它的图象经过原点；（2）为何值时，它的图象经过点（0，）.【答案】（1）9 （2）10【解析】分析：（1）把点的坐标代入一次函数关系式，并结合一次函数的定义求解即可；（2）把点的坐标代入一次函数关系式即可．解：（1）∵图象经过原点，∴点（0，0）在函数图象上，代入解析式得：，解得：．又∵是一次函数，∴，∴．故符合．（2）∵图象经过点（0，），∴点（0，）满足函数解析式，代入得：，解得：．10.某车间有甲、乙两条生产线．在甲生产线已生产了200吨成品后，乙生产线开始投入生产，甲、乙两条生产线每天分别生产20吨和30吨成品．（1）分别求出甲、乙两条生产线各自总产量（吨）与从乙开始投产以来所用时间（天）之间的函数关系式.（2）作出上述两个函数在如图所示的直角坐标系中的图象，观察图象，分别指出第10天和第30天结束时，哪条生产线的总产量高？【答案】（1）（2）乙生产线的总产量高【解析】解：（1）由题意可得：甲生产线生产时对应的函数关系式是；乙生产线生产时对应的函数关系式为．（2）令，解得，可知在第20天结束时，两条生产线的产量相同，故甲生产线所对应的生产函数图象一定经过点（0，200）和（20，600）；乙生产线所对应的生产函数图象一定经过点（0，0）和（20，600）．作出图象如图所示．由图象可知：第10天结束时，甲生产线的总产量高；第30天结束时，乙生产线的总产量高．11.已知一次函数y=kx+b的图象经过第一、二、三象限，则b的值可以是 ( )A．﹣2B．-1C．0D．2【答案】D．【解析】∵一次函数的图象经过第一、二、三象限，∴b＞0，∴四个选项中只有2符合条件．【考点】一次函数图象与系数的关系12. A、B两码头相距150千米，甲客船顺流由A航行到B，乙客船逆流由B到A，若甲、乙两客船在静水中的速度相同，同时出发，它们航行的路程y（千米）与航行时间x（时）的关系如图所示．（1）求客船在静水中的速度及水流速度；（2）一艘货轮由A码头顺流航行到B码头，货轮比客船早2小时出发，货轮在静水中的速度为10千米/时，在此坐标系中画出货轮航程y（千米）与时间x（时）的关系图象，并求货轮与客船乙相遇时距A码头的路程。

一次函数一．知识回顾（一）函数1、变量：在一个变化过程中可以取不同数值的量。

常量：在一个变化过程中只能取同一数值的量。

2、函数：一般的，在一个变化过程中，如果有两个变量x 和y ，并且对于x 的每一个确定的值，y 都有唯一确定的值与其对应，那么我们就把x称为自变量，把y称为因变量，y是x的函数。

* 判断Y 是否为X 的函数，只要看X 取值确定的时候，Y 是否有唯一确定的值与之对应3、定义域：一般的，一个函数的自变量允许取值的范围，叫做这个函数的定义域。

4、确定函数定义域的方法：（1）关系式为整式时，函数定义域为全体实数；（2）关系式含有分式时，分式的分母不等于零；（3）关系式含有二次根式时，被开放方数大于等于零；（4）关系式中含有指数为零的式子时，底数不等于零；（5）实际问题中，函数定义域还要和实际情况相符合，使之有意义。

5、函数的解析式：用含有表示自变量的字母的代数式表示因变量的式子叫做函数的解析式6、函数的图像一般来说，对于一个函数，如果把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图象．7、描点法画函数图形的一般步骤第一步：列表（表中给出一些自变量的值及其对应的函数值）；第二步：描点（在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点）；第三步：连线（按照横坐标由小到大的顺序把所描出的各点用平滑曲线连接起来）。

8、函数的表示方法列表法：一目了然，使用起来方便，但列出的对应值是有限的，不易看出自变量与函数之间的对应规律。

解析式法：简单明了，能够准确地反映整个变化过程中自变量与函数之间的相依关系，但有些实际问题中的函数关系，不能用解析式表示。

图象法：形象直观，但只能近似地表达两个变量之间的函数关系。

（二）一次函数1、一次函数的定义一般地，形如（，是常数，且）的函数，叫做一次函数，其中x 是自变量。

当时，一次函数，又叫做正比例函数。

北师大版初二数学上册一次函数知识点总结和基础例题解析式法：简单明了，能够准确地反映整个变化过程中自变量与函数之间的相依关系，但有些实际问题中的函数关系，不能用解析式表示。

图象法：形象直观，但只能近似地表达两个变量之间的函数关系。

（二）一次函数1、一次函数的定义一般地，形如y心b（ k，b是常数，且k 0 ）的函数，叫做一次函数，其中是自变量。

当b 0时, 一次函数 y k ，又叫做正比例函数。

⑴一次函数的解析式的形式是y 収b，要判断一个函数是否是一次函数，就是判断是否能化成以上形式．⑵当b 0，k 0时，y k仍是一次函数.⑶当 b 0， k 0时，它不是一次函数．⑷正比例函数是一次函数的特例，一次函数包括正比例函数.2、正比例函数及性质一般地，形如y=k（k是常数，k工0的函数叫做正比例函数，其中 k叫做比例系数.注：正比例函数一般形式 y=k （k不为零）①k不为零②指数为1③ b取零当 k>0 时，直线 y=k 经过三、一象限，从左向右上升，即随的增大 y 也增大；当 k0时，图像经过一、三象限；k0，y随的增大而增大；k0时，向上平移；当b0，图象经过第一、三象限 b>0 ，图象经过第一、二象限直线经过第直线经过第、四象限直线经过第、四象限直线经过第二、三、四象限直线经过第直线经过第、四象限直线经过第、四象限直线经过第二、三、四象限（4）增减性：k>0 , y随的增大而增大；k0时，将直线y=k的图象向上平移b个单位 4、一次函数y=k + b的图象的画法.根据几何知识：经过两点能画出一条直线，并且只能画出一条直线，即两点确定一条直线，所以画一次函数的图象时，只要先描出两点，再连成直线即可 .一般情况下：是先选取它与两坐标轴的交点：（0，b）.?即横坐标或纵坐标为0的点.标轴的交点：（0，b）.b>0b0经过第一、二、三象限经过第一、三、四象限经过第一、三象限图象从左到右上升，y随的增大而增大k0时，向上平移；当b0时，直线经过一、三象限；k 0, b > 0,直线经过第一、二、三象限 k > 0, b v 0直线经过第一、三、四象限 k v 0, b > 0直线经过第一、二、四象限 k v 0, b v 0直线经过第二、三、四象限增减性k>0, y随的增大而增大；（从左向右上升） k0时，将直线y=k的图象向上平移 b个单位；b0M-l/2,解得乞1/2且曲1/2 ,所张分析^p ：根握函数是一一对应的关系，给自娈量一个值，有且只有一个酗值与其对鼠就是酗，如果不是，贝怀是ill数.解答：在兀氐6选项的图上任資取一為做垂直于久的直线，翁现只有一个交点，故正确卜而匚选项、很明显，不止一个交吊不是一对应关凤所以不定函纵错误$故妝侧木在魁的周长公式827T冲，变量罡 F 常量是?料析；根据國数的意冥可知；变量杲改变的壘.常量是不变的量」据此即可确定变量与常量.解在19的周长公式匸二2打孔古「是改变的』7T罡不变的；「?变量罡G J常量是27T?1:骆驼殺称商％漠之舟J它的体温噫吋间的变化而变化.在这—冋題中.目变量是乩沙漠 B.体温u时间D?務菲分析^p ；因为骆驼的体温随时间的变化而变化，符合,#;对于一个变化过程中的两个虽和力对于每一亍疋的值户闹有唯一的值#陀相对应t;的函数定儿自变量是吋间.解答；丁骆驼的体温随时间的变化而变化二自娈量是时间；故迭G例1： (2(6at) T列函数：?y=；y=/4；y=4/；@y=2^lf 其中一茨国埶的个数是( )A? 1 氏 2 C.3 D.4分析^p ：根据一匚殛数的定叉条件遇彳極一分析^p 即可.注嵐一个单项式中厮有字厨的指数的和叫做这个单项式的欢数解昏①归虚一次囲数」②丫=对4是一次過数Fy=4/ ,两边同时乘以得到：待# 是二兄扯不是一次函数；⑥丫曰灯1是—次跚?故选匸.ffi3：下列图象不表示y是的国数的是(>分析^p ：根1S函數的定义可知：对于油任何値崗有喘一的值与之相对应.做垂配轴的直线在左右平穆的过程中与国数图象只会有一个交点.由此很容易就能得出结论。