求证: ∠ABC=∠DCB.
A
D
B
C
【证明】 取AD,BC的中点N,M,
连接BN,CN,MN,则有AN=DN,BM=CM.
A ND
在△ABN和△DCN中,
AN=DN,
∠A= ∠D, AB=CD,
B
C
M
∴ △ABN ≌ △DCN(SAS).∴ ∠ABN = ∠ DCN, NB=NC.
在△NBM和△NCM中,
•
【证明】 ∵CE⊥AD, ∴ ∠AGE=∠AGC=90 °.
在△AGE和△AGC中,
∠AGE=∠AGC, AG=AG, ∠EAG=∠CAG, ∴ △AGE ≌ △AGC(ASA), ∴ GE =GC. 在△DGE和△DGC中,
D
C
EG=CG, ∠ EGD= ∠ CGD=90 °,
DG=DG. ∴ △DGE ≌ △DGC(SAS). ∴ ∠DEG = ∠ DCG.
【证明】 ∵AO平分∠BAC,CD⊥AB于点D,
A
BE⊥AC于点E, ∴OD=OE, ∠ODB=
∠OEC=90 °. 在△BOD和△COE中, ∠ODB= ∠OEC=90 °,
D
E
O
OD=OE, ∠DOB= ∠EOC,
B
C
∴ △BOD ≌ △COE(ASA),∴OB=OC.
专题二 证明角相等
【例2】如图,在△ABC中,AD平分∠BAC,CE⊥AD于点G,交
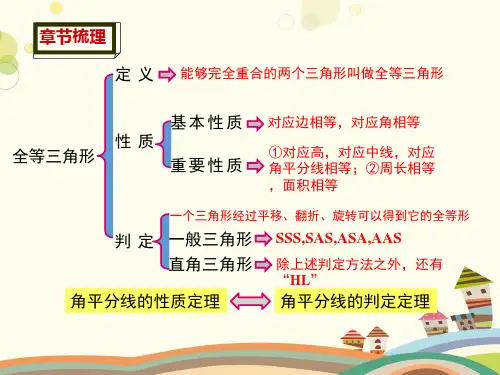
判 定 一般三角形 SSS,SAS,ASA,AAS
直角三角形 除上述判定方法之外,还
有“HL”
角平分线的性质定理
角平分线的判定定理
专题复习
专题一 证明线段相等
【例1】如图,点D、E分别在线段AB、AC上,已知AD=AE, ∠B= ∠C,H为线段BE、CD的交点,求证:BH=CH.