当前位置：文档之家 › 信号与系统(郑君里)第二版 讲义 第二章

信号与系统(郑君里)第二版 讲义 第二章

  • 格式：wps
  • 大小：690.38 KB
  • 文档页数：34

下载文档原格式

  / 34

合集下载

信号与系统课后题解第二章

信号与系统课后题解第二章

⑺
对⑺式求一阶导，有：
de(t ) d 2 i 2 (t ) di (t ) du (t ) =2 +2 2 + c 2 dt dt dt dt de(t ) d 2 i2 (t ) di (t ) =2 + 2 2 + 2i1 (t ) + 2i 2 (t ) 2 dt dt dt
⑻
将⑸式代入⑻式中，有：
λ 2 + 2λ + 1 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1
y h (t ) = C1e −t + C2 te− t
由初始状态为 y (0 ) = 1, y ' (0 ) = 0 ，则有：
C1 = 1 − C 1 + C 2 = 0
由联立方程可得 故系统的零输入响应为：
由联立方程可得 故系统的零输入响应为：
A1 = 2, A2 = −1
y zi (t ) = 2e − t − e −2 t
（2）由原微分方程可得其特征方程为
λ 2 + 2λ + 2 = 0
可解得特征根为 微分方程齐次解为
λ1, 2 = −1 ± i
y h (t ) = e −t (C1 cos t + C2 sin t )
(− 3C1 + 3C2 )δ (t ) + (C1 + C2 )δ ' (t ) − (− 2C1 + C 2 )δ (t ) = δ (t )
(
(
( + C e )δ (t ) + (C e
2 1
)
−2 t
+ C2 e t δ ' (t )

信号与系统(郑君里第二版)讲义第二章 连续时间系统的时域分析

信号与系统(郑君里第二版)讲义第二章 连续时间系统的时域分析

2.1 连续时间系统的数学模型
一、连续时间系统数学模型的建立 原则上，具体问题的数学模型，由具体物理定律列写。 在电学系统中，由电网络结构的约束特性：基尔霍夫第一定律（KCL）和基 尔霍夫第二定律（KVL） ，以及元件的约束特性来建立描述连续时间系统（线性 电路）的数学模型。 电网络结构的约束特性，即各支路电流、电压的关系： KCL： ∑ ± i (t ) = 0
若其特征根均为单根则设零输入响应为zikzi若其特征方程中有一个m阶重根时则设零输入响应为zimzizizi确定个待定常数二零状态响应的定义及其求法1定义不考虑起始时刻系统储能的作用起始状态等于零由系统的外加激励信号所产生的响应称为零状态响应零状态响应满足的微分方程为
第二章
连续时间系统的时域分析
江禹生
⎧原方程的齐次方程 ⎨ (k ) ⎩起始状态r (0 − )
2、全响应 r ( t ) ＝自由响应 rh ( t ) ＋强迫响应 rp ( t ) 微分方程的齐次解就是自由响应，微分方程的特解就是强迫响应。 3、全响应 r ( t ) ＝瞬态响应＋稳态响应 系统响应中随着时间增长而趋于零的部分称为瞬态响应分量， 随着时间增长 而趋于稳定的部分称为稳态响应分量。
rzi (t ) = H [{x(0 − )}]
零输入响应 rzi ( t ) 满足的微分方程为：
dn d n −1 d ( ) r t + a r (t ) + L + a1 rzi (t ) + a 0 rzi (t ) = 0 n −1 n zi n −1 zi dt dt dt
2、零输入响应 rzi ( t ) 的求解步骤 （1）写出特征方程 α n + a n −1α n −1 + L + a1α + a 0 = 0 ， 求出特征根 α 1 ， α 2 ， L ， α n （2）根据特征根的不同形式，写出所对应的齐次解形式。 若其特征根均为单根，则设零输入响应为

郑君里信号与系统讲义

郑君里信号与系统讲义

1, t > 0 u (t ) = 0, t < 0
或
（1-11）
1, = u ( t ) 0, 1 2,
t >0 t<0 t =0
（1-12）
图 1-5 斜升函数 ☻ 符号函数：
图 1-6 单位阶跃函数
4
《信号与系统》讲义
第一章：绪论
1, t > 0 sgn ( t ) = −1, t < 0 或 1, t > 0 sgn ( t ) = −1, t < 0 0, t = 0 ☻ 门函数： G ( t ) = u ( t ) − u ( t − t0 ) , t0 > 0
☻ 采样函数：
= f ( t ) Sa = (t ) sin t t
（1-5）
注意与抽样信号 定义上的差别！
- 0.2122
图 1-3 采样信号 采样函数的性质（三点、三式） ： ♦ 采样函数 Sa ( t ) 为偶函数，在 t 的正、负两方向振幅都逐渐衰减，当
±π , ±2π , , ± nπ 时，信号值为零。 t=
φ ( x)
《信号与系统》讲义
第一章：绪论
=
δ ( x − x0 ) /， f ′ ( x0 )
f ′ ( t0 ) δ ( t − t0 )
−1
φ ( x)
#证毕
即： = δ ( f (t ))
复合冲激函数的直观理解： ① δ ( f ( t ) ) = ∞ 的冲激位置在 f ( t ) =0，即在t 0 点；其余点为 0。 ② δ ( f ( t ) ) 的冲激强度不是 1，而是与 f ( t ) 的陡峭程度成反比。 上述第②条可以通过广义极限逼近的冲激函数来理解：若 f ( t ) 在 t 0 邻域内缓变 （斜率小） ，则 f ( t ) 的取值靠近 0，δ ( f ( t ) ) 的值就大；若 f ( t ) 在t 0 邻域内快变（斜率 大） ，则 f ( t ) 的取值就远离 0， δ ( f ( t ) ) 的值就小；是反比关系。 ☻ 若光滑函数 f ( t ) 满足： f ( t ) |t =t1 , t2 , = 0 ，且 f ′ ( ti ) ≠ 0，∀i = 1, 2,... ，则：

《信号与系统》第二版 (郑君里) 高等教育出版社课件

《信号与系统》第二版 (郑君里) 高等教育出版社课件

第二章连续时间系统的时域分析系统的微分方程及其响应◆系统的微分方程⏹描述LTI 系统的输入-输出特性⏹时域分析法⏹从微分方程出发，在时域中研究输入信号通过系统后响应变化规律的方法⏹建立微分方程的基本依据⏹基尔霍夫定律☐KCL ：☐KVL ：⏹电压-电流关系-VCR ：∑=0)(t i ∑=0)(t u )()(d )(1)(d )(d )(t Ri t u i C t u tt i Lt u L R tC C L L===⎰∞-ττ)()()('21)2....(..........).........()()(')()(d )(d b t g t ay t y t i LRt i L R t i t i t i t t i R L S L L S L L =+=+=+⨯程的一般形式）可以得到一阶微分方）（由（即）有对于图（输入信号的强迫函数系统响应变量(输出)+-)(t u s R )(t u c C+-图(a)+-)(t i s R )(t i L L图(b))1.....().........(1)(1)(')()(d )(d a t u RCt u RC t u t u t u tt u RC S C C S C C =+=+即以列微分方程）为一个一阶系统，可图（tt u C t i t i LCt i LC t i L R t i t t i t i C t u t Ri t u t t i L t Ri t u i C t u t t i Lt u t u t u t u t i t i t i C C S L L L tL s C L C L L R tC C L L R C L L S d )(d )(4)3).....((1)(1)()(12)2........(..........d )]()([1)()1.....(..........).........()(d )(d )()()4........(....................d )(1)(d )(d )(VCR )()()(KVL )5.(..........).........()()(KCL '''C ==++-=-====-=-=⎰⎰∞-∞-）式两边求导得到对（）并求导一次，整理得）带入（将（联立上式得：：：以列微分方程图为一个二阶系统，可ττ系统激励信号(电压源或电流源)系统响应变量(输出)+-)(t u R R)(t u L+-+-)(t i s )(t i L L )(t u c C+-)(t i C )()(...)()()()(...)()(LTI n )()(1)(1)()(3d )(d )()(50'1)1(1)(0'1)1(1)(''''t f b t f b t f b t f b t y a t y a t y a t y a t i LCR t i C t u LC t u L R t u tt u C t i t i m m m m n n n n S S C C C C S L ++++=+++++=++-=----的形式可以写为系统，其微分方程阶因此对于一般的）式得代入（）式得带入（经典法求解微分方程◆设激励信号为e(t)，系统响应为r(t)，则可以用一高阶的微分方程表示◆全解＝齐次解+特解⏹齐次解：满足右端激励e(t)及其各阶导数都为零的齐次方程，即⏹齐次解的形式是形如函数的线性组合，令，代入上式得：)()(...)()()()(...)()()1(1)1(1)(0)1(1)1(1)(0t e E t e E t eE t eE t r C t r C t r C t r C m m m m n n n n ++++=++++----0)()(...)()()1(1)1(1)(0=++++--t r C t r C t r C t r C n n n n atAe at Ae t r =)(0...1110=++++--atn at n at n at n Ae C Aae C e Aa C e Aa C 由初始条件决定，，，其中常数的重根部分的齐次解为阶重根则相对于为如果，则齐次解为称为微分方程的特征根，，，个根对应的特征方程化简得：n i ta ik i ni ta i ta n ta ta h n n n n A A A e tA a a eA eA eA e A t r a a a C a C a C a C i n 21k111121n 211110,)(k )(n 0...121∑∑=-=--=+++==++++)()()(t r t r t r p h +=特解的函数形式与激励函数形式有关，见表2－2，将激励代入微分方程右端，比较系数定出特解。

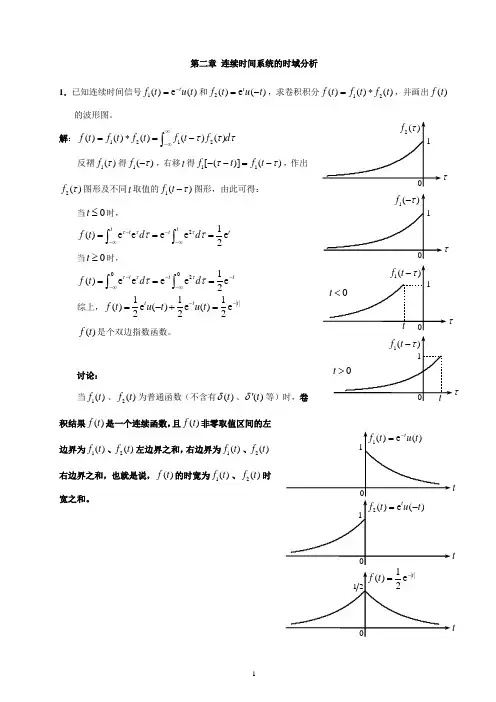
考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解

考研专业课郑君里版《信号与系统》第二章补充习题——附带答案详解

第二章 连续时间系统的时域分析1．已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-，求卷积积分12()()()f t f t f t =*，并画出()f t 的波形图。

解：1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-，右移t 得11[()]()f t f t ττ--=-，作出2()f τ图形及不同t 取值的1()f t τ-图形，由此可得：当0t ≤时，21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时，0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上，||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。

讨论：当1()f t 、2()f t 为普通函数（不含有()t δ、()t δ'等）时，卷积结果()f t 是一个连续函数，且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和，右边界为1()f t 、2()f t 右边界之和，也就是说，()f t 的时宽为1()f t 、2()f t 时宽之和。

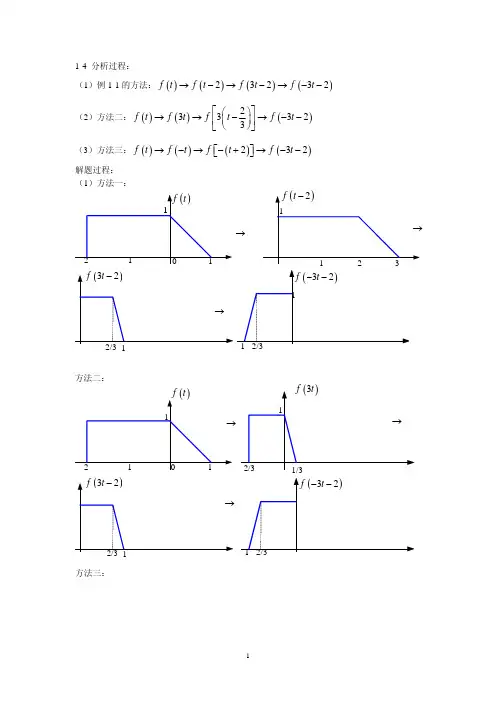
τttt2．计算题图2（a ）所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=，并画出)(t f 的图形。

解法一：图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b)，由此可得： 当10t +≤，即1t ≤-时，()0f t = 当011t ≤+≤，即10t -≤≤时，120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤，即01t ≤≤时，1()21f t d ττ==⎰当011t ≤-≤，即12t ≤≤时，121()21(1)t f t d t ττ-==--⎰当11t -≥，即2t ≥时，()0f t =综上，220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。

信号与系统引论 课件 郑君里 第2章 连续时间系统的时域分析

信号与系统引论 课件 郑君里 第2章 连续时间系统的时域分析

网络拓扑约束：由网络结构决定的电压电流约束关系，
KCL，KVL。
例2-1
电阻 电感 电容
求并联电路的端电压v(t)与激励is(t)间的关系。
1 iR iR t v t R i s t R L 1 t i L t v d L d v t iC t C 元件特性约束 dt
E (常数)
B(常数)
B1t p B2 t p1 B p t B p1
tp e t
cos t sin t
Be t
B1 cos t B2 sin t
t p e t sin t B1t p B2 t p 1 B p t B p 1 e t cos t
2.2 系统数学模型(微分方程)的建立
对于电路系统，主要是根据元件特性约束和网络拓扑
约束列写系统的微分方程。
对于其他物理系统，根据实际系统的物理特性列写系 统的微分方程。 元件特性约束：表征元件特性的关系式。例如二端元
件电阻、电容、电感各自的电压与电流的关系以及
四端元件互感的初、次级电压与电流的关系等等。
等式两端各对应幂次的系数应相等，于是有
3 B1 1 4 B1 3 B2 2 2 B 2 B 3 B 0 2 3 1
联解得到
1 2 10 B1 , B2 , B3 3 9 27
所以，特解为
1 2 2 10 rp t t t 3 9 27
i L (0 ) i L (0 )
例2-6 如图示出RC一阶电路，电路中无储能，起始电
压和电流都为零，激励信号e(t)=u(t)，求t >0系统的响
应——电阻两端电压vR(t)。

信号与系统课件(郑君里版)第二章

信号与系统课件(郑君里版)第二章

e ，t≥0；y(0)=2，y’(0)= 2 t ，t≥0；y(0)= 1， e
t
-1
y’(0)=0时的全解。
解: (1) 特征方程为
2 + 5λ+ 6 = 0
其特征根λ1= – 2，λ2= – 3。 齐次解为
yh (t ) C1e2t C2e2t
由表2-2可知，当f(t) = 2 e t
y fh (t ) C f 1e
2t
C f 2e
t
其特解为常数 3 ， 于是有
y f (t ) C f 1e2t C f 2et 3
C1 1 C 2 4
根据初始值求得:
y f (t ) e2t 4et 3，t 0
四．系统响应划分
自由响应＋强迫响应 (Natural+forced) 暂态响应+稳态响应 (Transient+Steady-state) 零输入响应＋零状态响应 (Zero-input+Zero-state)
零输入响应
2.2 冲激响应和阶跃响应
一．冲激响应 1．定义 系统在单位冲激信号δ(t) 作用下产生的零状态响 应，称为单位冲激响应，简称冲激响应，一般用h(t)表 示。
t
ht
H
[例2.2.1] 描述某系统的微分方程为y”(t)+5y’(t)+6y(t)=f(t)求其 冲激响应h(t)。
相互关系
零输入响应是自由响应的一部分，零状态响应有自由响 应的一部分和强迫响应构成 。
y (t ) e 2t 3 y x (t ) y f (t ) (2e 2t 4e t ) (e 2t 4e t 3)，t 0

信号与系统-课件-郑君里

信号与系统-课件-郑君里
School of Computer Science and Information
1.1 Signals
Signals are functions of independent variables that carry information. The independent variables can be continuous or discrete. The independent variables can be 1-D, 2-D, ••• , n-D. For this course: Focus on a single (1-D) independent variable which we call “time”. Continuous-Time signals: x(t), t-continuous values. Discrete-Time signals: x(n), n-integer values only.
School of Computer Science and Information
Examples
Electrical signals — voltages and currents in a circuit. Acoustic signals — audio or speech signals. Video signals — intensity variations in an image. Biological signals — sequence of bases in a gene.
School of Computer Science and Information
1.3 Types of Signals
1. Certain Signal and Random Signal

郑君里信号与系统第二章

郑君里信号与系统第二章
Pe – t + 5(– Pe – t) + 6Pe – t = 2e – t 解得 P=1 于是特解为 yp(t) = e – t
■ 第 14 页
全解为： y(t) = yh(t) + yp(t) = C1e – 2t + C2e – 3t + e – t 其中 待定常数C1,C2由初始条件确定。
k
yh(t) Cit kieit
n
C jejt
i 1
jk 1
λi是k阶重根,λj是单根。Ci、Cj(常数)由系统初始状态决定。
（3）所有λj为一对共轭复根 j， 则微分方程的齐次解为：
yh (t ) et [C cos t D sin t]
▲
■
第 7页
uC
uS
uC (0 )，uC(0 )
L
uS(t)
R
uC(t)
C
二阶常系数线性微分方程。
抽去具有的物理含义，微分方程写成
a2
d
2
d
y(t) t2

a1
d
y(t) dt

a0
y(t)

f (t)
▲
■
第 2页
2. 离散系统的解析描述
例：某人每月初在银行存入一定数量的款，月息为β元/
月，求第k个月初存折上的款数。
■ 第 20 页
aδ"(t)+bδ'(t)+cδ(t)+r1(t) + 3aδ'(t)+3bδ(t)+3r2(t) + 2aδ(t)+2r3(t)= 2δ"(t) + δ'(t)

《信号与系统》郑君里教学课件讲义

《信号与系统》郑君里教学课件讲义

（４）１９世纪末，人们研究用电磁波传送无线电信号。 赫兹（Ｈ.Hertz）波波夫、马可尼等作出贡献。1901年 马可尼成功地实现了横渡大西洋的无线电通信。
（5）光纤通信 从此，传输电信号的通信方式得到广泛应用和迅速发展。 如今：（１）卫星通信技术为基础“全球定位系统（Global Positioning System, 缩写为GPS）用无线电信号的传输， 测定地球表面和周围空间任意目标的位置，其精度可达 数十米之内。 （２）个人通信技术：无论任何人在任何时候和任何地方 都能够和世界上其他人进行通信。 （３）“全球通信网”是信息网络技术的发展必然趋势。 目前的综合业务数字网（Integrated Services Digital Network,缩写为ISDN),Internet或称因特网，以及其他各 种信息网络技术为全球通信网奠定了基础。
信号与系统
郑君里
教学课件
1、教材：信号与系统 郑君里 杨为理 应启珩编 2、信号与系统 Signals & Systems ALAN V.OPPENHEIM ALANS. WILLSKY 清华大学出版社（英文影印版） （中译本）刘树棠 西安交通大学出版社 3、信号与系统例题分析及习题 乐正友 杨为理 应启珩编 4、信号与系统习题集 西北工业大学
5. 系统的分类
系统可分为物理系统与非物理系统，人工系统以及自 然系统。 物理系统：包括通信系统、电力系统、机械系统等； 非物理系统：政治结构、经济组织、生产管理等； 人工系统：计算机网、交通运输网、水利灌溉网以及 交响乐队等； 自然系统：小至原子核，大如太阳系，可以是无生命 的，也可是有生命的（如动物的神经网络）。
4.信号、电路（网络）与系统的关系
离开了信号，电路与系统将失去意义。

《信号与系统引论》(第二版)郑君里

《信号与系统引论》(第二版)郑君里
波形形状不变。
（3）因果性（Causality）：是指系统在 t0 时刻的响应只与 t = t0 和 t < t0 的时刻有关，与未来
的时刻无关。 满足因果性的系统又称为物理可实现系统。 判断因果性的方法：
① 通过时域关系式： y (t ) = T ⎡⎣x (t )⎤⎦ 判断是否可能有 y (t1 ) = T ⎡⎣x (t2 )⎤⎦ ，t1 < t2 的时刻出
+
e−αtδ
(t)
=
δ
(t)
− α e−αt
8
2-6 解题过程：
（1） e (t ) = u (t ) ， r (0− ) = 1， r' (0− ) = 2
方法一：经典时域法：
①求
rZi
：由已知条件，有
⎪⎪⎨⎧rrZZii
'' '
(t) (0+
+
)
3rZi ' = rZi
(t ) + ' (0− )
1-5 题提醒所有的运算是针对自变量 t 进行的。如果先进行尺度变换或者反转变换，再进行
移位变换，一定要注意移位量和移位的方向。 1-9 解题过程：
（1） f (t ) = (2 − e−t )u (t )
( ) （2） f (t ) = 3e−t + 2e−2t u (t )
2
( ) （3）f (t ) = 5e−t − 5e−2t u (t )
2rZi =2
(
t
)
=
0
⎪⎪⎩rZi' (0+ ) = rZi' (0− ) = 1
特征方程：α 2 + 3α + 2 = 0 特征根为：α1 = −1，α2 = −2

信号与系统(郑君里)ppt

信号与系统(郑君里)ppt

f(t)
O
t
f(n)
O 12
n
4．模拟信号，抽样信号，数字信号
•模拟信号：时间和幅值均为连续
f t
的信号。
抽
样
t
•抽样信号：时间离散的，幅值
O
量
连续的信号。
f n
化
•数字信号：时间和幅值均为离散 O
n
的信号。
f n
主要讨论确定性信号。 n
先连续，后离散；先周期，后非周期。O
时间轴 幅度轴
连续
连续 模拟信号
t
f(t)
t/2
f(t/2)
0
1
0
1
T
2
T
2
时间尺度压缩：t ห้องสมุดไป่ตู้ 2 ,波形扩展
求新坐标
t
f(t/2)
0
1
2T
2
f(t)f(2t)
f t
2 1
O
Tt
宗量相同，函数值相同
t
f(t)
2t
f(2t)
0
1
0
1
T
2
T
2
求新坐标
t
f(2t)
0
1
T/2
2
t2t，时间尺度增加，波形压缩。
比较
f t
2 1
O
Tt
O
t
二．单位阶跃信号
1. 定义
u(t )
0
u(t )
1
t 0 0点无定义或1
t 0
2
2. 有延迟的单位阶跃信号
1
O
t
u(t t0 )
0 u(t t0 ) 1
0 u(t t0 ) 1

《信号与系统》第二版_(郑君里)_高等教育出版社课件

《信号与系统》第二版_(郑君里)_高等教育出版社课件

10
2021/4/2
零输入响应与零状态响应（cont.）
例2 7 设有如图所示的RC电路，电容两端有起始电压u（ C 0），激 励源为e（t），求t 0时系统响应 电容两端电压u（ C t）。 解：列写系统的微分方程为
d dt
uc (t)
1 RC
uc (t)
1 RC
e(t )
根
据微分方
程
的
一般表达式可
t
e RCuc (t) uc (0 )
1 RC
t
e RCe( )d
0-
R
+
+ e(t) uc (0 ) C
-
整
理
得：uc
(t
)＝e
t RC
uc
(0
)
1 RC
t
e
t RC
e(
)d
0-
零输入响应
零状态响应
+
uc (t)
-
smilegs2001@
11
2021/4/2
零输入响应与零状态响应（cont.）
uR (t) RiL (t) 联立上式得
+
is (t)
-
R
iC (t) +
C
uc (t)
-
iL (t)
+
L uL (t)
-
带入（5）式得iL
(t )
iS
(t )
C
duC (t) dt
代入（3）式得
L
diL (t) dt
uC (t)
RiL (t)........................(1)
KVL：
uL

信号与系统考研电子讲义郑君里

信号与系统考研电子讲义郑君里

12§1.2信号的描述，分类和典型示例(续）•指数信号和正弦信号•奇异信号–斜变信号–单位阶跃信号和符号函数–单位冲激和冲激偶信号正交信号•11(k 实指数信号1—(k 和s 都是实数)•若中的为0 , k 为实数βαj k +=β同时•0 , s ωσs +=ω若中的为,为实数j k则为实指数函数stke t x =)(正弦信号1—取周期复指数的实部•欧拉公式sin(cos()(0ωωφω+++=+t t et j •取实部则为正弦信号)()(00φφj =)cos()(0φω+t A t x 81.3§信号的运算（参考网站绪论的内容）Ee whu edu cn用Flash演示的动态过程§1.4阶跃信号与冲激信号一.奇异信号即本身、其导数或其积分有不连续点的函数。

1.斜变信号2.单位阶跃信号3.符号函数4.单位冲激5.冲激偶信号13信号加窗或取单边t t u t u e t t−−=−)]()([)(0f f(t)f()t（1）突然接入的直流电压（）2）突然接通又马上断开电源K负载r(t)r(t 3)r(t 1)r(t 2)r(t-3)-r(t-1)-r(t-2)f(t)1)]2()2()[1()(.101.38−−+−=−t u t u tt f a p 题2....)2()1()()(.+−+−+=t u t u t u t f b )]()([(sin )(.T t u t u t E t f c −−=πT二.单位冲激函数)(t dr )(t du δ=)(t u dt =)(t dt 1.定义:(p17—21))]()([1)(.lim ττδ−−+=t u t u t a 220ττ→)()(t t =δ1=∞dt t limfnn ∞→)(∫∞−fn0=t )(lim ∞→fnn 0≠t 用规则函数脉冲序列的极限来定义)(t Rt ut )(t)(tδtb.Dirac 定义:=)(t δ∫∞=1)(dt t δ00≠t 0=∞t c.利用冲激函数的抽样性∞)()()(00t f dt t t t f =−∫∞δ∞−∫∞−=)0()()(f dt t t f δ∞−)()()(.00t f dt t t t f a =−∫∞−δ1∞)()]([.00t t t t b −=−−δδ)()(.t aat c δδ=)()()()(.000t t t f t t t f d −=−δδt)()(.t dtt u e δ=)()(t u d =∫∞−ττδ+−)(t i c 由于冲激电流的出现，电容两端的电压可以突变；电感电流也可以突变。

郑君里信号与系统 第二章习题解析

郑君里信号与系统 第二章习题解析
第二章 连续时间系统 的时域分析
Copyright © 2012 通信工程
1
知识要点
一、求解系统的响应，就等于求解微分方程。
微分方程的解
= 齐次解+特解
= 自由响应（齐次解，和特征根有关，系数则由起始条件决定） +强迫响应（是特解，和系统的激励端有关） = 零输入响应
（形如齐次解，是齐次解的一部分，由系统储能引起的响应）
Copyright © 2012 通信工程
9
习题解答
2-12 有一系统激励为 e1 t ut 时的完全响应为 r1 t 2et ut ，对激
励为 e2 t t 时的完全响应为 r2 t t 。
（1）求该系统的零输入响应 rzi t ； （2）系统的起始状态保持不变，求其对于激励为 e3 t et ut 的完 全响应 r3 t 。
e (t ) 呈线性性。
（3）零输入线性 当外加激励为零时，系统的零输入响应 rzi (t ) 对于各起始状态 呈线性关系。
Copyright © 2012 通信工程
6
习题解答
2-5 试判断给定系统在起始点是否发生跳变。
Copyright © 2012 通信工程
7
习题解答
2-11 设系统的微分方程表示为
15
习题解答
Copyright © 2012 通信工程
16
习题解答
Copyright © 2012 通信工程
17
习题解答
Copyright © 2012 通信工程
18
习题解答
Copyright © 2012 通信工程
19
习题解答
Copyright © 2012 通信工程

郑君里信号与系统习题解答第二章

郑君里信号与系统习题解答第二章

第二章 连续时间系统的时域分析经典法：双零法卷积积分法：求零状态响应求解系统响应→定初始条件满足换路定则起始点有跳变：求跳变量零输入响应：用经典法求解零状态响应：卷积积分法求解()()()()⎩⎨⎧==-+-+0000L L c c i i u u例题•例题1：连续时间系统求解（经典法，双零法） •例题2：求冲激响应（n >m ） •例题3：求冲激响应（n ＜m ） •例题4：求系统的零状态响应 •例题5：卷积 •例题6：系统互联例2-1分析在求解系统的完全响应时，要用到有关的三个量是： ：起始状态，它决定零输入响应；()()()()()()()()()强迫响应。

状态响应，自由响应，并指出零输入响应，零，求系统的全响应，已知 系统的微分方程为描述某t u t e r r t e t t e t r t t r t t r =='=+=++--,00,206d d 22d d 3d d LTI 22()-0)(k r ⎩⎨⎧状态变量描述法输出描述法—输入建立系统的数学模型：跳变量，它决定零状态响应； ：初始条件，它决定完全响应；这三个量之间的关系是 分别利用 求零状态响应和完全响应，需先确定微分方程的特解。

解：方法一：利用 先来求完全响应，再求零输入响应，零状态响应等于完全响应减去零输入响应。

方法二：用方法一求零输入响应后，利用跳变量 来求零状态响应，零状态响应加上零输入响应等于完全响应。

本题也可以用卷积积分求系统的零状态响应。

方法一1. 完全响应 该完全响应是方程 （1）方程（1）的特征方程为 特征根为 方程（1）的齐次解为因为方程（1）在t >0时，可写为 （2）显然，方程（1）的特解可设为常数D ，把D 代入方程（2）求得 所以方程（1）的解为下面由冲激函数匹配法定初始条件 由冲激函数匹配法定初始条件 据方程（1）可设代入方程（1），得匹配方程两端的 ，及其各阶导数项，得 所以，所以系统的完全响应为()+0)(k zsr ()+0)(k r ()()()+-+=-000)()()(k zs k k r r r ()()++00)()(k k zs r r ，()()代入原方程有将t u t e =()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()++'0,0r r ()()++''0,0zs zs r r ()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()的解且满足00,20='=--r r 0232=++αα2121-=-=αα，()t t e A e A t r 221--+=()()()()t u t r t t r tt r 62d d 3d d 22=++3=D ()3221++=--tt e A e A t r ()()()t u b t a t t r ∆+=δ22d d ()()t u a t t r ∆=d d ()无跳变t r ()()()()()()t u t t r t u a t u b t a 6223+=+∆+∆+δδ2=a ()t δ()()22000=+=+'='-+a r r ()()200==-+r r ()()代入把20,20=='++r r ()3221++=--t t e A e A t r 1,021-==A A 得()0 32≥+-=-t e t r t ()t r zi 再求零输入响应2.求零输入响应 （3）（3）式的特征根为 方程（3）的齐次解即系统的零输入响应为所以，系统的零输入响应为 下面求零状态响应零状态响应=完全响应—零输入响应，即 因为特解为3，所以强迫响应是3，自由响应是方法二（5）以上分析可用下面的数学过程描述 代入（5）式 根据在t =0时刻，微分方程两端的 及其各阶导数应该平衡相等，得 于是t >0时，方程为 齐次解为 ，特解为3，于是有所以，系统的零状态响应为方法一求出系统的零输入响应为()是方程响应因为激励为零，零输入t r zi ()()()02d 3d d 22=++t r dt t r t t r ()()()()()()的解．，且满足 0000 2000='='='===--+--+r r r r r r zi zi zi zi 2121-=-=αα，()t t zi e B e B t r 221--+=()()式解得，代入，由)4(0020='=++zi zi r r 2,421-==B B ()0 242≥-=--t e e t r t t zi ()0 342≥++-=--t e e t r t t zs t t e e 24--+-()是方程零状态响应t r zs ()()()()()t u t t r t t r t t r 622d d 3d d 22+=++δ()()的解且满足000='=--zs zs r r ()项由于上式等号右边有t δ()应含有冲激函数，，故t r zs "()将发生跳变，即从而t r zs '()()-+'≠'00zs zs r r ()处是连续的．在而0=t t r zs ()()()()()t u a t r t t u b t a t r tzs zs∆=+∆+=+d d ,d d 22δ()()()()()()t u t t r t u a t u b t a 6223+=+∆+∆+δδ()t δ2=a ()()()()002000===+'='-+-+zs zs zs zs r r a r r ()()()()t u t r t t r t t r 62d d 3d d 22=++ 221t t e D e D --+()3221++=--t t zi e D e D t r ()()得由初始条件0,200=='++zs zs r r 1,421=-=D D ()0) ( 342≥++-=--t e e t r t t zs ()0 242≥-=--t e e t r t t zi完全响应=零状态响应+零输入响应，即例2-2冲激响应是系统对单位冲激信号激励时的零状态响应。

信号与系统(郑君里)课后答案 第二章习题解答

信号与系统(郑君里)课后答案 第二章习题解答

( p + 5) h(t ) = 1 δ (t ) + 2δ (t )
p +1
3
⇒
h(t) =
1⋅ p+5
1δ p +1
(t ) +
2δ p+5
(t) =
⎛ ⎜ ⎜ ⎜
−1 4+
p+5
1⎞
4 p +1
⎟ ⎟δ ⎟
(t ) +
2δ p+5
(t)
⎝
⎠
⇒
h(t)
=
⎛ ⎜⎝
7 4
e−5t
+
1 4
e−t
⎞ ⎟⎠
卷积的微分与积分；与冲激函数或阶跃函数的卷积）对表达式进一步的化简，甚至直接得到
结果。
解题过程：
（1） f (t ) = u (t ) − u (t −1) = u (t )∗ ⎡⎣δ (t ) − δ (t −1)⎤⎦
∴s (t ) = f (t ) ∗ f (t ) = u (t ) ∗ ⎡⎣δ (t ) −δ (t −1)⎤⎦ ∗u (t )∗ ⎡⎣δ (t ) − δ (t −1)⎤⎦ = ⎡⎣u (t ) ∗u (t )⎤⎦ ∗ ⎡⎣δ (t ) − 2δ (t −1) + δ (t − 2)⎤⎦ = tu (t ) ∗ ⎡⎣δ (t ) − 2δ (t −1) + δ (t − 2)⎤⎦ = tu (t ) − 2(t −1)u (t −1) + (t − 2)u (t − 2)
⎞ ⎟⎠
u
(t)
受迫响应： 3 u (t )
2 综观以上两种方法可发现 p 算子法更简洁，准确性也更高
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二章 连续时间系统的时域分析第一讲 微分方程的建立与求解一、微分方程的建立与求解对电路系统建立微分方程，其各支路的电流、电压将为两种约束所支配： 1.来自连接方式的约束：KVL 和KIL ，与元件的性质无关。

2.来自元件伏安关系的约束：与元件的连接方式无关。

例2-1 如图2-1所示电路，激励信号为，求输出信号。

电路起始电压为零。

图2－1解以输出电压为响应变量，列回路电压方程：所以齐次解为：。

因激励信号为，若，则，将其代入微分方程：所以，从而求得完全解：由于电路起始电压为零并且输入不是冲激信号，所以电容两端电压不会发生跳变，，从而若，则特解为，将其代入微分方程，并利用起始条件求出系数，从而得到：二、起始条件的跳变——从到1.系统的状态(起始与初始状态)(1)系统的状态：系统在某一时刻的状态是一组必须知道的最少量的数据，利用这组数据和系统的模型以及该时刻接入的激励信号，就能够完全确定系统任何时刻的响应。

由于激励信号的接入，系统响应及其各阶导数可能在t=0时刻发生跳变，所以以表示激励接入之前的瞬时，而以表示激励接入以后的瞬时。

(2)起始状态：，它决定了零输入响应，在激励接入之前的瞬时t=系统的状态，它总结了计算未来响应所需要的过去的全部信息。

(3)初始状态：跳变量,它决定了零状态响应，在激励接入之后的瞬时系统的状态。

(4)初始条件：它决定了完全响应。

这三个量的关系是：。

2.初始条件的确定（换路定律）电容电压和电感电流在换路（电路接通、断开、接线突变、电路参数突变、电源突变）瞬间前后不能发生突变，即是连续的。

时不变：时变：例电路如图2-2所示，t=0以前开关位于"1"已进入稳态，t=0时刻，开关自"1"转至"2"。

(1)试从物理概念判断、和、。

(2)写出t>0时间内描述系统的微分方程式,求的完全响应。

图2－2解(1)换路前电路处于稳态电感相当于短路，电感电流，电容相当于开路= 0，= = 0。

开关换到2时，电容两端电压不能突变，== 0，电容相当于短路，可看成电路接入了的电流源。

电感电流不能突变，仍为1A，所以电容支路电流为4A，。

(2)t>0时,电路方程为：特征方程为：，特征根为：。

方程的完全响应为：代入初始条件得：所以零输入响应为零，强迫响应为零；完全响应等于自由响应。

3.初始条件等效为激励源三、零输入响应(z.i.r)和零状态响应(z.s.r)一个系统的完全响应从解微分方程角度来分可分解为通解和特解即自由响应和强迫响应；从因果关系来分可以分解为零输入响应和零状态响应；从系统状态来分可分解为稳态响应和暂态响应，它们之间的联系与区别在第四章详细讨论。

这里仅举例说明。

例2-2如图2-3所示，时刻，同时自位置1转至位置2，求输出电压的完全响应，并指出其零输入、零状态、自由、强迫响应各分量。

(a)(b)图2－3解时的电路如图2-3(b)所示。

根据KCL得齐次解为，特解为，则完全解为因为，所以零输入响应为，零状态响应为；自由响应为，强迫响应为；稳态响应为，暂态响应为。

第二讲冲激响应与阶跃响应用卷积积分的方法求解系统的零状态响应既是本章的重点，也是本章的难点。

卷积积分分析法的步骤有三：首先是将信号在时域表示为冲激函数积分；其次就是求系统的冲激响应；再就是用卷积积分求解系统的零状态响应。

我们首先对第二点进行讨论。

一、冲激响应和阶跃响应1.定义：在初态为零的条件下，若激励是单位冲激函数，系统的零状态响应叫冲激响应；若激励是单位阶跃函数，系统的零状态响应叫阶跃响应。

2.特点：冲激响应有两个特点，一是当时间为负值时，系统响应等于零，这一特点反映了系统的实现性，不能想象在信号加入以前就有输出，系统只能延迟信号，不能提前信号；另一是在经过长时间后，响应函数等于零，这一特点反映了系统的稳定性，无源有耗系统中的有限能量是不可能永远保存的。

因此，冲激响应一般从零值增长到最大值后再逐渐下降为零(如上图所示)。

这两个特点可用如下两式表示：实现性(因果性)：稳定性：3.阶跃响应及与冲激响应的关系由时不变系统特性可知：当输入由原来的输入变为它的积分时，输出也由原来的输出变为它的积分。

4.的求法：将作为一个特殊的零输入响应来处理，思路是单位冲激函数在>0时为零，因此，我们只需要解齐次方程，并求出时的初始条件，用这组初始条件确定齐次方程解的系数，从而得出系统的冲激响应。

这里作两点说明：(1)冲激函数的引入解决了函数在跳变点处导数的存在问题，从而使得一个微分方程在-∞<<∞内都成立。

(2)，匹配就是使方程两端的冲激函数及其导数相匹配。

关键是如何确定时的初始条件。

以一个二阶系统为例，若方程式的左端含有冲激函数，方程式的右端、而且是最高导数项也必须出现冲激函数，这样方程的两端才能匹配。

分析如下：2阶导数项含有冲激，在=0不连续，1阶导数项含有阶跃，在=0不连续，0阶导数项为斜坡，在=0连续，对其取积分：二阶系统需两个条件：下面以RLC串联谐振电路为例来说明如何用这种方法求系统的冲激响应，然后再把它推广到一般情况。

例2-3 已知，输入为冲激函数，求的函数表达式。

解根据KVL，因电路处于零状态，故因t>0时,=0,则齐次微分方程为初始条件为代入上式解得5.结语对于右边只有的情况(1)写出激励和响应关系的微分方程。

(2)<0,=0；>0，是一个特殊的零输入响应。

(3)时的初始条件是由于=0时冲激信号作用的结果。

如果等式右边具有冲激函数及其各阶导数的情况利用算子表示设则，令两边作算子运算，得，交换算子的运算顺序，有，可得。

例写成算子形式，有令，6.冲激函数匹配法(1)原理(a) 对于一个描述系统的微分方程，由于它在整个时间范围内都成立，它在任一特定时刻当然也成立。

在引入冲激函数以前，函数在不连续点(跳变点)的导数不存在。

这样，一个微分方程就不能在整个时间范围内成立。

冲激函数的引入解决了函数在跳变点处导数的存在问题，从而使得微分方程在整个时间范围内成立了。

(b) 因为定义了单位阶跃函数的导数等于单位冲激函数，这表明函数在跳变点处要出现冲激函数项，匹配就是使方程左右两端冲激函数项相等。

(2)归纳(a) 冲激函数只匹配冲激函数及其各阶导数项，使方程两端这些函数项对应相等。

(b) 匹配从方程左端最高项开始，首先使方程右端冲激函数最高阶次项得到匹配。

(c) 每次匹配低阶冲激函数项时，如果方程左端所有同阶次的冲激函数各项系数之和不能和右端匹配，则由左端的最高阶次项中补偿。

(d) 在匹配低阶冲激函数时，已匹配好的高阶次冲激函数项系数不变。

(e) 一般说，冲激函数匹配法不是求微分方程的解，而仅仅是求响应及其各阶导数在激励函数不连续点处的跳变量。

动画演示二、用算子符号表示微分方程1.算符表示法：。

2.算符的某些性质(1) 把微分方程写成代数形式的算子方程。

(2) 由p多项式所组成的运算符号，可以像代数式那样相乘和进行因式分解。

(3) 算子方程的两边公因子不能相消。

3.转移算子(传输算子)对于系统方程的一般形式有：线性方程：算子H(p)完整地建立了描述系统的数学模型，一些有用的系统特性可以通过对H(p)的分析得到如下的结论：(1)求得微分方程的阶数与电路的阶数是一致的。

电路的阶数是指电路中含有独立储能元件的个数。

(2)对于同一电路，无论哪一个变量作为响应变量，描述它们的齐次方程是相同的，这表明同一系统的自由响应是惟一的。

(3)对于同一个电路，有几个响应变量就有几个把响应变量同输入联系起来的传输算子。

第三讲卷积迄今为止，我们已经有三种方式对系统进行具体的描述了，一是用微分方程，二是用系统的传输算子，三是用系统的冲激响应。

一个微分方程代表一个系统，其输入输出由微分方程联系；一个传输算子也代表一个系统，其输出由传输算子对输入作用得出；同样，一个冲激响应函数则可用于表示一般的系统，它可以是由微分方程或传输算子表示的，也可以是不能由微分方程或传输算子表示的。

系统冲激响应表示要一般的多。

上次课讨论过用卷积求解系统的零状态响应有三个步骤，并已讨论了第二个步骤，现对(1)、(3)两个步骤进行分析和推导。

一、卷积1.任意函数表示为冲激函数的积分波形分解可以有许多种方法，其目的是将复杂的信号变为简单信号之和，从而在求系统响应时，通过将各简单信号响应相加得到系统总响应，这是线性系统性质的典型应用(信号的分解→求响应→再叠加)。

时域中最典型的激励就是。

(a)(b)(c)复杂波形(a)分解为序列(b)之和，实际观察起来是不直观的，所以有时用(c)中的脉冲来代替函数。

事实上，如果脉冲单元足够短，并且足够高，那么这种短脉冲的响应与冲激的响应可能难以区分，所以可以用这种脉冲序列近似任意的激励。

基本思想：(1)用一系列脉冲代替激励。

(2)再用一系列冲激代替脉冲。

(3)求一系列冲激在系统中引起的响应之和。

(4)检验(3)的结果与原来激励的真实响应之间有什么差异。

分析的步骤：(a)将分解为一系列相邻的脉冲。

各脉冲宽度为Δt，高度等于左侧所在时间的取值。

(b)用冲激代替每个脉冲，并适当地选取冲激的强度，使得冲激的效果与脉冲相同。

(c)冲激序列之和对于原来函数的近似程度也完全取决于时间间隔的大小。

愈小，冲激序列之和也愈趋近于。

当，对各项的取和也就变成了取积分，这时冲激序列之和也就精确表示。

2.作为叠加积分的卷积积分下图表示单位冲激信号激励系统时，在时域里测定的是系统冲激响应，在频域测定的是系统的频率响应。

由此可以看出，系统的冲激响应和系统的频率响应是由一对傅里叶变换式联系起来的。

卷积有许多应用，所以它也有许多不同的名称，如重叠积分、扫描积分、加权平均等，卷积这一名称来源于它的几何解释。

它应用在不同的学科领域中，如在物理学的测量过程中，我们就常常遇到被测物理量与仪器权函数之间相互作用的卷积。

如下图所示的是物理量测量过程，显示器给出的数据并非待测量物理量本身，而是待测物理量与测试仪表特性二者之综合，若测量仪表是一个线性时不变系统，则之间的关系可用卷积公式来表达。

(1)研究的问题：研究LTI系统对任意信号零状态响应的一种基本运算。

(2)实际意义：求解任意输入下的响应转换为求解系统对一系列冲激函数响应的叠加。

(3)条件或前提：系统必须是线性的(以保证信号的分解有效)系统是时不变的(以保证系统的输出仅与输入有关，而与输入施加的时刻无关。

)初态为零(以保证系统的系统的响应为,而与初始条件无关。

)(4)公式的推导：(a)把激励表示成一系列的冲激函数。

(b)求冲激序列的响应。

因为引起的响应为，所以引起的响应为。

这里应用了时不变特性。

其中代表冲激出现的时刻。

应用线性系统的叠加特性，将总响应近似写成(c)；卷积积分的一个优点是从系统角度来说，如果我们不知道系统的内部结构，因而写不出系统的微分方程时，只要能够通过实验的方法，获得系统的冲激响应曲线的波形或实验数据，仍可求出系统对任意激励的零状态响应。