核心解释变量为0 1变量的门限回归
- 格式:docx
- 大小:28.45 KB
- 文档页数:2

Beta回归模型基于EM算法的变量选择方法王玲;赵为华【摘要】本文针对响应变量取值为(0,1)区间上的比例数据研究Beta回归模型的贝叶斯变量选择方法.首先通过选取合适的先验分布,基于贝叶斯随机搜索和EM方法提出了参数的估计算法;然后根据回归系数相应的指示变量后验分布提出了重要变量选择的门限准则,所提方法具有易实施、快速计算等特点;最后通过研究中国上市公司股息率实际数据的影响因素以说明所提方法的有效性.【期刊名称】《安徽师范大学学报(自然科学版)》【年(卷),期】2019(042)001【总页数】6页(P16-21)【关键词】Beta回归模型;EM算法;贝叶斯变量选择【作者】王玲;赵为华【作者单位】南通大学理学院,江苏南通226019;南通大学理学院,江苏南通226019【正文语种】中文【中图分类】O212引言在对众多领域的实际问题进行统计分析时,取值在(0,1)区间上的比例数据是很常见的,比如股息率、考试通过率、工作效率、次品率以及资本比率等。
对于(0,1)上的连续分布,最简单明确的方法是线性回归建模,并用普通最小二乘法估计回归系数。
然而线性回归并不能保证拟合值或预测值完全落在区间(0,1)内,这使得结果很难解释,还会产生异方差问题。
因此对分数响应变量建模时,直接线性回归是不合适的。
为此,Ferrari 和CribariNeto(2004)针对这样的响应变量提出了Beta 回归模型,对Beta分布的密度函数进行参数重变换后,y~Beta(μ,φ),即其中0<μ<1,φ>0,通过链接函数建立了Beta均值回归模型(1)其中β=(β0,β1,…,βk)T是一个未知回归参数向量,x1,…,xk是k个解释变量。
由于Beta分布是一个双参数的分布,因此利用Beta回归刻画比例数据具有很好的灵活性。
在初始回归建模时通常引入许多解释变量去拟合响应变量。
然而,这些潜在的解释变量中通常只有一小部分对响应变量有影响,而大部分解释变量的影响都是非常小甚至为零的。

Stata门限模型的操作和结果详细解读一、门限面板模型概览如果你不愿意看下面一堆堆的文字,更不想看计量模型的估计和检验原理,那就去《数量经济技术经济研究》上,找一篇标题带有“双门槛(或者双门限)”的文章,浏览一遍,看看文章计量部分列示的统计量和检验结果。
这样,在软件操作时,你就知道每一步得到的结果有什么意义,怎么解释了,起码心里会有点印象。
Hanen于1996年在《Econometrica》上发表文章《Inferencewhenanuianceparameterinotidentifiedunderthenullhypoth ei》,提出了时间序列门限自回归模型(TAR)的估计和检验。
之后,他在门限模型上连续追踪,发表了几篇经典文章,尤其是1999年的《Threholdeffectinnon-dynamicpanel:Etimation,tetingandinference》,2000年的《Sampleplittingandthreholdetimation》和2004年与他人合作的《IntrumentalVariableEtimationofaThreholdModel》。
在这些文章中,Hanen介绍了包含个体固定效应的静态平衡面板数据门限回归模型,阐述了计量分析方法。
方法方面,首先要通过减去时间均值方程,消除个体固定效应,然后再利用OLS(最小二乘法)进行系数估计。
如果样本数量有限,那么可以使用自举法(Boottrap)重复抽取样本,提高门限效应的显著性检验效率。
在Hanen(1999)的模型中,解释变量中不能包含内生解释变量,无法扩展应用领域。
Caner和Hanen在2004年解决了这个问题。
他们研究了带有内生变量和一个外生门限变量的面板门限模型。
与静态面板数据门限回归模型有所不同,在含有内生解释变量的面板数据门限回归模型中,需要利用简化型对内生变量进行一定的处理,然后用2SLS(两阶段最小二乘法)或者GMM(广义矩估计)对参数进行估计。

门槛回归是一种用于分析门槛效应的统计模型,通常用于处理因变量受某个或某些自变量影响而发生门槛式变化的情况。
在进行门槛回归之前,对数据进行适当的预处理是至关重要的。
下面是对门槛回归数据预处理的讨论。
1. 数据清洗:首先,需要检查数据的质量,并进行必要的清洗。
这可能包括删除缺失值、异常值和重复值。
对于缺失值,可以考虑使用插补或删除含有缺失值的观察对象。
异常值可能包括极端值或明显偏离正常分布的数据点,可以通过删除或使用适当的统计方法进行处理。
2. 变量转换:为了使门槛效应更加明显,可能需要将某些变量进行转换。
例如,如果因变量是连续的,可以考虑将其转换为二元或有序数据。
此外,如果自变量之间存在相关性,可以考虑进行多重共线性处理,例如使用主成分分析或逐步回归等方法。
3. 缺失值处理:对于门槛回归,某些自变量可能包含缺失值。
对于这种情况,可以考虑使用插补方法填充缺失值,如均值插补、回归插补等。
如果无法找到合适的插补方法,也可以考虑删除含有缺失值的观察对象。
4. 数据平衡性检查:门槛效应通常在数据平衡的情况下更易观察到。
因此,需要检查数据是否平衡,如果不平衡,可以通过删除不平衡的数据集或使用适当的平衡方法进行处理。
5. 数据标准化:为了使门槛效应在不同自变量之间具有可比性,需要对数据进行标准化处理。
可以使用Z-score或T-score等方法对数据进行标准化,使其具有相同的尺度。
6. 分类变量处理:对于分类变量,需要将其转换为数值型数据。
可以使用哑变量、卡方检验等方法进行处理。
7. 构建虚拟变量:对于门槛效应可能起作用的特定因素,可以将其视为虚拟变量进行处理。
即创建多个不同的水平组合(即“条件”),并根据不同的组合预测结果的变化趋势来检验是否存在门槛效应。
总之,在进行门槛回归之前,进行适当的预处理可以提高结果的可靠性和解释性。
具体而言,需要考虑数据清洗、变量转换、缺失值处理、平衡性检查、数据标准化和分类变量的处理等步骤。
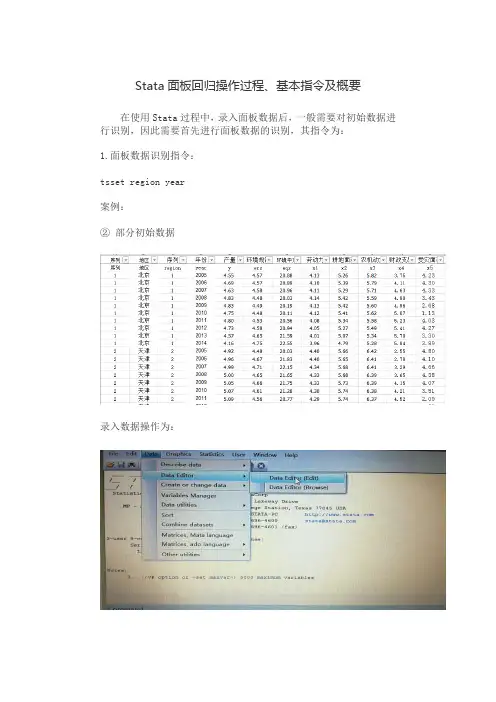
Stata面板回归操作过程、基本指令及概要在使用Stata过程中,录入面板数据后,一般需要对初始数据进行识别,因此需要首先进行面板数据的识别,其指令为:1.面板数据识别指令:tsset region year案例:②部分初始数据录入数据操作为:②将上述初始数据录入stata后(注意:录入数据及首行只能是英文字母或者数字,不能有汉字),显示如下:③输入指令tsset region year,显示如下结果. tsset region yearpanel variable: region (strongly balanced)time variable: year, 2005 to 2014delta: 1 unit2.面板数据固定效应回归指令:xtreg y ers eqs x1 x2 x3 x4 x5,fe案例:录入数据,并进行面板数据识别之后,输入以上指令:xtreg y ers eqs x1 x2 x3 x4 x5,fe其中,xtreg为面板回归指令,y为选取的因变量,ers、eqs、x1、x2、x3、x4、x5为自变量,末尾加fe表示为固定效应,如果末尾加re则是随机效应。
上述回归结果显示如下:3.面板数据随机效应回归指令:xtreg y ers eqs x1 x2 x3 x4 x5,re4.hausman 检验指令:Hausman检验是固定效应或者随机效应回归之后,需要加入的一个检验,具体指令如下:qui xtreg y ers eqs x1 x2 x3 x4 x5,feest store fequi xtreg y ers eqs x1 x2 x3 x4 x5,feest store rehausman fe re5.门限回归指令使用门限(或者门槛)回归模型的,只需要在录入数据后,使用以下指令进行回归即可,xthreg为门限回归指令,y eqs x1 x2 x3 x4 x5分别为自变量和因变量,rx和qx括号中的分别为核心解释变量与门限变量,可以一致也可以不一致。


重磅!门限回归总结(Eviews版本)2018-01-2221:01来源|计量经济学服务中心综合整理转载请联系今日,由计量经济学服务中心举办的高级计量经济学及Eviews应用研讨班圆满落幕,此次课程,首次讲解了用Eviews软件处理门限回归等最新内容。
据悉,此次课程于2018年1月20日至1月20日举办,主要讲解了时间序列专题、面板数据专题等内容,涉及面板数据的平稳性、协整、格兰杰以及VAR、SVAR、GARCH等模型,而今日对因子分析和门限回归进行了学习,下面就跟着小编一起来回顾下今天的内容吧!一、Threshold Regression Estimation阈值回归模型描述了一种简单的非线性回归模型。
TR规范很受欢迎,因为它们很容易。
估计和解释,并能产生有趣的非线性和丰富的动力学。
在TR的应用中,有样品分裂,多重平衡。
非常流行的阈值自回归(TAR)和自激励阈值自回归(SETAR)(Hansen1999,2011;波特2003)。
在功能强大的特性中,Eviews有选择最佳阈值TR模型选择工具。
能够从候选列表中,并且能够指定两种状态的变化和非变化的变量。
例如,您可以轻松地指定两种模式的门限模型并允许EViews估计最优变量和参数、阈值、系数和协方差。
并对变化和回归参数的估计。
二、Smooth Threshold Regression EstimationEViews10为它的计量经济和统计特性提供了令人兴奋的新添加和改进。
详情可以阅读重磅首发|Eviews10.0新增的十大功能变化(一)Eviews10.0新版本主要在Eviews软件界面、数据处理(现场数据展示、与R兼容性、与UN、欧盟、BLS等数据接口)、新命令、图形表格和计算等方面均有更新。
新功能:Smooth Threshold Regression EstimationSmooth Transition Autoregressive(STAR)modeling(Teräsvirta,1994)is an extremely popular approach for nonlinear time series analysis.STAR models,which are a special case of Smooth Transition Regression(STR) models,embed regime-dependent linear auto-regression specifications in a smooth transition nonlinear regression framework.EViews tools for estimation of two-regime STR models with unknown parameters for the shape and location of the smooth threshold.EViews estimation supports several different transition functions,provides model selection tools for selecting the best threshold variable from a candidate list,and offers the ability to specify regime varying and non-varying variables and variables that appear in only one regime. To estimate a smooth transition model,Quick/Estimate Equation...from the main EViews menu,select THRESHOLD-Threshold Regression from the main Method dropdown menu near the bottom of the dialog, and click on the Smooth radio button in the Threshold type setting.The options page allows you specify the transition function,covariance estimation method(including various robust estimators),and optimization settings.Following estimation,EViews offers specialized views for the transition function and weights along with support for tests for linearity against STR alternatives and tests of no remaining nonlinearity and parameter constancy,alongside conventional tests for heteroskedasticity and serial correlation.三、Eviews门限回归总结笔记门限回归模型是一种重要的结构变化模型,当观测变量通过未知门限时,函数模型具有分段线性的特征,并且区制发生变化。

回归单因子二次-概述说明以及解释1.引言1.1 概述概述部分的内容可以从以下几个方面进行描述:首先,我们可以介绍回归分析的背景和意义。
回归分析作为一种常用的统计分析方法,在许多领域都有着广泛的应用。
它可以帮助我们建立并探索变量之间的关系,为解决实际问题提供有力的支持。
而在具体的回归分析中,单因子回归和二次回归是两个重要的方法。
本文将重点探讨单因子二次回归分析,从理论到实际应用进行深入研究。
其次,我们可以简要介绍单因子回归和二次回归的基本概念。
单因子回归分析是指通过建立一个因变量与一个自变量之间的线性关系模型来分析它们之间的关系。
而二次回归则是在单因子回归的基础上,将自变量引入到一个二次方程中,以更好地拟合实际数据。
这两种分析方法在数据分析中具有广泛的应用场景和重要性。
接下来,我们可以简要说明单因子二次回归分析的特点和优势。
相比于单因子回归和二次回归分析,单因子二次回归分析将线性与非线性因素结合在一起,被认为是一种更加灵活和准确的分析方法。
它能够更好地适应实际数据的分布情况,并能够更全面地描述因变量与自变量之间的关系。
因此,对于一些复杂的数据模型,单因子二次回归分析具有一定的优势和应用价值。
最后,我们可以提出本文的研究目标和意义。
本文旨在探索单因子二次回归分析的理论基础和实际应用,深入研究其模型评估与解释方法,以及对结果的分析和总结。
通过本文的研究,可以为相关领域的学者和研究人员提供参考和借鉴,同时也为实际问题的解决提供有力的支持。
综上所述,本文的引言部分概述了回归分析的意义和背景,介绍了单因子回归和二次回归的基本概念,重点强调了单因子二次回归分析的特点和优势,并指出本文的研究目标和意义。
通过本文的研究,可以为读者提供关于单因子二次回归分析的详细理论和实践知识,以及对相关问题的深入理解和解决方法。
1.2 文章结构文章结构部分的内容应包括以下内容:文章结构部分旨在介绍本篇长文的整体结构和各个部分的内容安排。

⾯板门限回归有两个命令的使⽤⽅法——⼈⼤论坛(shenciyou作者)stata学习笔记:hello,guys!很⾼兴⼜和⼤家见⾯了,由于很多同学在⾯板门限回归实证处理上存在着⼀些困难,今天我们这⾥来统⼀解析⼀下⾯板门限回归的相关命令。
⽬前⾯板门限回归有两个命令。
⼀个是xtptm(stata 12.0),⼀个是xthreg(stata 14.0),这两个程序都是王群勇⽼师开发的,其中xthreg 使⽤⾼版本进⾏编译,⽆法在低版本的环境下运⾏(即低于13.0就⽆法执⾏)。
【代码⽰例】use thresholddata,clearSTATA12.0:xtptm pollution population urbanization_level industrialization_level, rx(pgdp) thrvar(fdi) regime(1) iters(300) trim(0.01) grid(100)STATA14.0:xthreg pollution population urbanization_level industrialization_level, rx(pgdp) qx(fdi) thnum(1) bs(300) trim(0.01) grid(100)【命令区别】两个命令⾥的rx都代表受门限变量影响的核⼼解释变量;xthreg命令⾥的qx代表门限变量,⽽xtptm命令⾥的thrvar代表门限变量(有⼀些旧版的xtptm也是以qx代表门限变量);xthreg命令⾥的thnum代表门限数量,⽽xtptm命令⾥的regime代表门限数量(有⼀些旧版的xtptm也是以thnum代表门限数量);xthreg命令⾥的bs代表⾃举抽样次数,⽽xtptm命令⾥的iters代表⾃举抽样次数;两个命令⾥的trim都代表每个门限分组内异常值去除的⽐例;两个命令⾥的grid代表样本⽹格计算的⽹格数(不设的话该值为0,设置这个option可以减少运算时间,提⾼运算效率)。

门限分位数自回归模型及在股市收益自相关分析中的应用摘要:门限分位数自然回归模型是一种非限行分位数回归模型,其可以应用讨论系统之中的门限效应。
并且在该模型之中,自然回归阶数以及门限值的确定等都将会为模型的分析效果带来直接的影响。
本文主要对门限分位数自然回归模型以及其在股市收益中的相关应用做出分析,希望能够给予同行业的工作人员提供一定参考价值。
关键词:门限分位数;回归模型;股市收益;分析股市收益的自相关性是金融市场研究中的一个重要问题,研究人员针对于理性预定理论提出了有效的市场假说,奠定了传统的金融学基础。
有效的市场假说理论认为在一个有效的市场之中,股市的价格或者收益直接地反映了所有可能会获得的信息,过去的收益以及未来的收益并不相关,股市的收益则是不可以预测的,反而言之如果股市的收益在时间上是自相关的,那么历史收益是可以影响当前的收益的,这也直接表明了有效市场假说是难以成立的,可以采取序列自相关分析的方法,对其有效市场假说做出相应验证。
一、门限分位数自然回归模型的分析1. 模型的表示分析主要是记{ yt }作为其1 维响应的变量,然而x =(1,yt -1,yy-2,…,yt -p)T 主要是为p+1为向量组成的解释变量,然而{ yt }则是为1维门限的白能量,其自然回归模型之中的门限变量通常情况下是需要相应变量{ yt }的滞后项,而γ则表示为门限,其模型如下所示:和均值自激励门限自然回归的模型进行对比,门限分位数自回归模型存在着下述的优点:一是信息刻画更加全面,回归系数估计在不同的分位点可能存在着不同的表型,同时不同阶段的变量之间关系更加细致。
二是具有比较强的稳健性,和均值自激励门限自回归模型要求误差项服从特定分布的不同,其允许误差项服从一般的非对称的分布。
2. 模型的定阶在门限分位数自然回归之中,最优滞后阶数p的选择是十分重要的,可以通过AIC的准确去进行实现,然而定义AIC的准则则是如下所示:可以看出,AIC主要由两个部分所组成,一是可以反映出模型的拟合程度,主要是为前半段进行表示。

stata门槛回归指令-回复Stata是一种统计软件,广泛应用于数据分析和建模。
在Stata中,门槛回归是一项强大的工具,可用于解决传统OLS回归中存在的一些问题,例如异方差性、高度相关的解释变量和模型误设定。
本文将一步一步回答关于Stata门槛回归指令的相关问题。
首先,我们需要理解什么是门槛回归。
门槛回归是一种非线性回归方法,它将数据集分成两个或多个子集,并在每个子集上估计不同的回归方程。
这些子集根据自变量的特定阈值进行划分,其中的观测值高于或低于阈值将遵循不同的回归方程。
在Stata中,进行门槛回归的命令是"thresholdreg"。
我们可以使用这个命令来估计两个子集的门槛值,并在每个子集上拟合不同的线性回归模型。
下面我们将一步一步解释如何使用该命令。
第一步是安装Stata软件,并确保已正确加载数据。
在Stata界面上,我们可以在命令窗口输入数据加载语句,如"use datasetname",其中"datasetname"是我们要加载的数据文件名。
第二步是检查数据集中的变量是否适用于门槛回归。
门槛回归通常适用于连续解释变量和连续或二进制因变量。
如果我们的数据集满足这些条件,我们可以继续下一步。
第三步是使用命令"thresholdreg"来估计门槛值和回归模型参数。
语法如下:thresholdreg dependent_var independent_var, [options]其中,"dependent_var"是因变量的名称,"independent_var"是解释变量的名称。
在方括号内,我们可以提供一些可选选项,用于改变回归模型的估计方法和性质。
第四步是解读门槛回归的结果。
使用"thresholdreg"命令后,Stata会报告估计的门槛值和每个子集上的回归系数。

logistic回归取值范围-回复Logistic回归是一种常用的分类算法,它可以根据特征变量的取值来预测一个事件发生的概率。
但是,对于某些人来说,理解Logistic回归的取值范围可能会有些困惑。
在本文中,我将一步一步回答关于Logistic回归取值范围的问题,希望能够帮助读者更好地理解这个概念。
首先,我们需要了解Logistic回归的基本原理。
Logistic回归是通过将线性回归的结果映射到[0,1]范围内来解决二分类问题的。
这是通过使用逻辑函数或称为sigmoid函数来实现的。
逻辑函数的定义如下:sigmoid(z) = 1 / (1 + exp(-z))其中,z是线性回归的结果,表示待预测变量的线性组合,可以写成如下形式:z = w1*x1 + w2*x2 + ... + wn*xn + b回归系数(w)是Logistic回归模型的参数,决定了每个特征变量(x)的重要性。
截距项(b)表示当所有特征变量取值为0时的预测概率。
逻辑函数的取值范围在[0,1]之间,因为分子为1,分母不可能为0,所以除法会得到0到1之间的结果。
逻辑函数的图形是一个S形曲线,它的特点是在z的取值趋近于正无穷时,函数的值趋近于1,而在z的取值趋近于负无穷时,函数的值趋近于0。
回到Logistic回归模型,当我们预测一个事件发生的概率时,我们需要找到使得逻辑函数的值接近0或1的那个z值。
当z的值非常大时,逻辑函数的值趋近于1,这意味着事件发生的概率很高。
当z的值非常小时,逻辑函数的值趋近于0,这意味着事件发生的概率很低。
然而,我们需要注意的是,Logistic回归的输出并不是一个离散的事件,而是一个概率值。
在一些应用中,我们可以根据设定一个阈值来对输出进行二分类,例如,当概率大于0.5时,我们将其分类为正类,否则分类为负类。
但是,这个阈值是可调整的,具体取决于模型的应用场景和需要。
另外需要提醒的是,Logistic回归模型的输出并不是严格在[0,1]范围内的数值,它可以大于1或小于0。
0-1变量决策模型相关知识在0-1变量决策模型中,变量只能取0或1两个值,其中0表示不选择某个选项,1表示选择某个选项。
这种限制使得模型更加简化和易于处理,同时也使得模型的应用范围有所限制。
下面我们将从模型的基本原理、应用案例和解决方法三个方面对0-1变量决策模型进行详细介绍。
让我们来了解一下0-1变量决策模型的基本原理。
在这种模型中,决策问题被抽象成一个决策变量的集合,每个决策变量只能取0或1两个值。
通过对决策变量的取值进行组合,可以得到不同的决策方案。
模型的目标是找到最优的决策方案,使得满足一定的约束条件的同时,达到最大的效益或最小的成本。
接下来,我们将通过一个应用案例来说明0-1变量决策模型的具体应用。
假设我们是某个公司的采购经理,需要在多个供应商中选择一个供应商进行合作。
我们需要考虑的因素包括供应商的价格、质量、交货时间等。
我们可以将每个供应商表示为一个决策变量,取值为0表示不选择该供应商,取值为1表示选择该供应商。
通过对各个供应商决策变量的取值进行组合,我们可以得到不同的供应商选择方案。
通过建立0-1变量决策模型,我们可以确定最优的供应商选择方案,使得在满足各种约束条件的前提下,获得最大的采购效益。
我们来介绍一下解决0-1变量决策模型的方法。
常用的解决方法包括整数规划、线性规划、动态规划等。
其中,整数规划是一种将线性规划与整数变量约束相结合的方法,可以有效地解决0-1变量决策模型。
动态规划则是一种将问题分解成子问题并逐步求解的方法,适用于具有重叠子问题结构的问题。
通过运用这些解决方法,我们可以有效地求解0-1变量决策模型,得到最优的决策方案。
总结起来,0-1变量决策模型是一种常用的决策模型,它在实际应用中具有广泛的应用价值。
通过建立0-1变量决策模型,我们可以在满足一定约束条件的前提下,找到最优的决策方案,从而获得最大的效益或最小的成本。
在实际应用中,我们可以通过整数规划、线性规划、动态规划等方法来解决0-1变量决策模型。
门槛回归解释变量、门槛变量、控制变量文章标题:解析门槛回归中的变量类型及其作用导言门槛回归,在统计学和经济学中是一种常用的回归分析方法,它能够更准确地描述变量之间的非线性关系。
在门槛回归分析中,我们需要对门槛回归中涉及的变量类型有一个清晰的认识,包括门槛变量、解释变量和控制变量。
本文将从浅入深地解析这些变量类型,帮助读者更好地理解门槛回归分析的原理及应用。
一、门槛变量的定义及作用1. 门槛变量的概念门槛变量是指在门槛回归分析中起到划分样本群体的作用的变量。
在门槛回归中,我们通常会设定一个阈值,当某一变量的取值超过或不足这个阈值时,就会引发截然不同的影响。
这个具有影响力的变量就是门槛变量。
2. 门槛变量的作用门槛变量的作用在于帮助我们更准确地描述变量之间的非线性关系。
通过设定门槛变量,我们能够将样本分成不同的群体,分别对其进行回归分析,从而得到更加精确的模型拟合结果。
二、解释变量的作用及重要性1. 解释变量的概念解释变量是用来解释因变量变化的原因或影响因素的变量。
在门槛回归分析中,解释变量对于解释门槛变量产生的不同效应至关重要。
2. 解释变量的作用解释变量的作用在于帮助我们理解门槛变量产生的不同效应。
通过引入解释变量,我们能够更清晰地探究门槛变量与因变量之间的关系,深入理解门槛回归模型的内在机制。
三、控制变量的重要性及影响1. 控制变量的概念控制变量是在门槛回归分析中用来控制其他干扰因素的变量。
在门槛回归中,我们需要尽可能地控制其他可能影响因变量的变量,以确保门槛变量和解释变量之间的关系是准确和可靠的。
2. 控制变量的重要性控制变量的重要性在于确保回归模型的准确性和可靠性。
通过控制其他干扰因素,我们能够更加清晰地揭示门槛变量和解释变量对因变量的影响,提高模型的解释力和预测能力。
结论门槛回归分析中的门槛变量、解释变量和控制变量都是不可或缺的重要元素。
它们共同构成了门槛回归模型的基本框架,帮助我们更准确地描述变量之间的非线性关系,并揭示影响因变量变化的内在机制。
门槛变量与核心解释变量的概念与作用在实证研究中,门槛变量和核心解释变量是用来探究因果关系的重要工具。
门槛变量用于筛选样本,帮助我们更准确地解释核心解释变量与因变量之间的关系。
门槛变量的定义和作用门槛变量是指在研究主题中起到筛选作用的一个或多个变量。
通常,门槛变量与核心解释变量有一定的相关性,但与因变量的相关性较弱。
门槛变量可以帮助研究者在样本中选取特定子集,以便更好地研究核心解释变量与因变量之间的关系。
门槛变量的作用有三个方面:1.控制混淆因素:门槛变量可以用来控制影响因变量的混淆因素,以减少伪关联的可能性。
通过选择与核心解释变量相关但与因变量不相关的门槛变量,可以减少某些潜在的混淆因素对结果的干扰。
2.增加研究的可解释性:门槛变量提供了一种更全面地解释核心解释变量与因变量之间关系的方式。
通过将门槛变量引入模型中,我们可以更细致地分析核心解释变量的影响是否存在条件依赖。
3.确定子群效应:门槛变量有助于确定核心解释变量在样本的不同子群中是否具有不同的效应。
通过对门槛变量进行子群分析,我们可以发现在不同背景条件下,核心解释变量对因变量的影响是否存在差异。
核心解释变量的定义和作用核心解释变量是研究中最关注的自变量,也是需要解释的主要变量。
通过对核心解释变量的研究,我们可以更好地理解它与因变量之间的因果关系。
核心解释变量的作用有三个方面:1.提供关键信息:核心解释变量是研究中最关键的变量,通过研究核心解释变量的取值与因变量之间的关系,我们可以获得有关因果关系的重要信息。
核心解释变量对因变量的变化趋势和强度提供了直接的度量。
2.量化因果关系:核心解释变量在研究中往往代表真正感兴趣的解释因素,通过对其进行定量分析,可以帮助我们了解它与因变量之间的因果关系。
通过建立回归模型等统计方法,可以量化核心解释变量对因变量的影响。
3.解释机制:核心解释变量可以作为对因变量影响机制的解释,帮助我们理解为什么核心解释变量会对因变量产生影响。
门限回归方法门限回归方法是一种统计分析方法,主要用于研究两个变量之间的关系,并确定门限值。
门限值是一个非常重要的参数,可以用来确定变量之间的非线性关系,并确定变量之间的阈值。
门限回归方法在机器学习、数据挖掘、医学、生物学等领域都有广泛的应用。
门限回归方法是一种非参数方法,其基本思想是将自变量分为两个或多个组,并对每个组进行线性回归分析。
然后,根据每个组的回归方程和统计检验结果,确定门限值。
门限值可以是一个具体的数值,也可以是一个变量的范围。
通常,门限值表示数据分布的变化点,也可以解释为数据进入一个新的状态。
门限回归方法的基本步骤如下:1.将自变量分为两个或多个组。
2.对每个组进行线性回归分析。
3.根据每个组的回归方程和统计检验结果,确定门限值。
4.根据门限值给出变量之间的非线性关系。
门限回归方法的具体应用比较广泛,下面介绍一些典型的应用场景。
1.风险控制门限回归方法可以用于风险控制领域。
例如,在股票交易中,门限回归模型可以用来确定买入和卖出的时机。
根据股票的历史数据,可以确定股票价格和时间的门限值,并根据门限值进行预测和决策。
2.医学研究门限回归方法可以用于医学研究中。
例如,根据患者的症状和治疗结果,可以确定治疗时间和治疗剂量的门限值,并根据门限值调整治疗方案。
门限回归方法可以用于生物学研究中。
例如,在研究基因表达时,可以根据基因表达水平和相关的生物学特征,确定基因表达的门限值,并进一步研究基因表达和生物学特征之间的关系。
4.机器学习门限回归方法可以用于机器学习领域。
例如,在图像处理中,可以根据像素值和像素位置,确定图像处理的门限值,并实现图像分类和图像特征提取。
门槛变量为核心解释变量stata代码
本文介绍如何使用Stata软件中的门槛变量来解释和分析变量
的影响。
门槛变量是指在某个阈值点上,变量的效应发生了显著变化。
例如,在某个收入水平上,一个政策对收入的影响可能会从正向变成负向。
本文将介绍如何使用门槛回归模型来识别和分析门槛变量,并展示如何使用Stata代码进行分析。
首先,我们需要利用Stata中的门槛回归模型来识别门槛变量。
门槛回归模型可以通过stcrreg命令来实现。
例如,我们可以使用以下命令来拟合一个简单的门槛回归模型:
stcrreg y x, cut1(0.5)
这个命令将y作为因变量,x作为自变量,并设置了一个门槛点为0.5。
在这个门槛点上,x的效应将会发生显著变化。
我们还可以使用cut2选项来设置第二个门槛点。
接下来,我们可以使用Stata中的margins命令来计算门槛变量的影响。
例如,我们可以使用以下命令来计算在门槛点上x的影响: margins, at(x=0.5)
这个命令将会计算在门槛点0.5上,x对y的影响。
我们还可以使用Stata中的marginsplot命令来绘制门槛变量的影响图。
例如,我们可以使用以下命令来绘制x在门槛点上的影响图: marginsplot, at(x=0.5)
这个命令将会绘制出在门槛点0.5上,x对y的影响图。
综上所述,使用Stata软件中的门槛回归模型和相关命令可以帮
助我们识别和解释变量的门槛变量,并进一步分析其影响。
核心解释变量为0 1变量的门限回归
门限回归模型是一种回归分析方法,用于处理自变量和因变量之
间具有非线性关系的情况。
其中,门限回归模型是一种特殊的回归模型,用于处理自变量为0-1变量的情况。
在门限回归中,自变量被分为两个子集,分别对应于因变量取1
和0的情况。
这种分割通常由一个门限变量来实现,门限变量将观测
值分为两个组。
门限变量将自变量的取值映射到一个门限值,当自变
量大于门限值时,因变量的取值为1,否则为0。
举例来说,假设我们研究一个关于人们是否购买某种产品的回归
模型。
自变量可以是性别、年龄、收入等,而因变量是一个0-1变量,表示是否购买该产品。
我们可以假设在某个收入水平以上,人们更有
可能购买该产品,那么我们可以将收入设为门限变量,当收入大于门
限值时,因变量为1,否则为0。
这样,我们就可以建立门限回归模型,来研究这个关系。
门限回归模型的估计过程通常使用最大似然估计方法。
最大似然
估计方法用于找到最能解释已观测数据的模型参数,使得观测数据出
现的概率最大化。
在门限回归模型中,最大似然估计方法用于找到最
能解释已观测数据的门限变量的值,并建立最拟合数据的模型。
门限回归模型的优点是可以处理自变量为0-1变量的情况,适用
于研究存在门限效应的情况。
门限效应指的是自变量对因变量的影响
不是线性的,而是存在一个阈值或门限,当自变量的取值超过门限值时,因变量的取值发生变化。
门限回归模型在许多领域都有应用,比如经济学、金融学、社会
科学等。
在经济学中,门限回归模型被用于研究收入对消费的影响,
研究劳动力供给的决策等。
在金融学中,门限回归模型被用于研究市
场波动对投资者行为的影响等。
在社会科学中,门限回归模型被用于
研究教育对工资的影响,研究健康对生活满意度的影响等。
总之,门限回归模型是一种处理自变量为0-1变量的回归模型。
它通过将观测值分为两个组,建立两个子集的回归模型,来研究自变
量和因变量之间的关系。
门限回归模型在很多领域都具有广泛的应用,并且可以处理一些线性回归模型无法处理的问题。