傅立叶光学第一章总结

L1
O
F S+1
A B
S0
C
S-1
阿贝成象原理
I’
1
C’
通过衍射屏的光发生夫
琅禾费衍射，在透镜后
B’
焦平面上得到傅里叶频
A’
2
谱 (S+1, S0, S-1)
虚物
2 频谱图上各发光点发出的球面波在象平面上相干叠
加而形成象A’，B’，C’ 。
第一步是信息分解 第二步是信息合成
频 ❖ 第一步夫琅禾费衍射起分频作用将各 谱 语 种空间频率的平面波分开在L后焦面上形 言 成频谱 描 述 ❖ 第二步干涉起综合作用
傅里叶光学的应用
（1）光学信息处理的特点
✓ 高速 处理 并行传输 并行处理 响应 光开关 10-15s 光传输速度 3×108 m/s 电开关 10-9s 电传输速度 105 m/s
✓ 抗干扰能力强 ✓ 大容量 传输容量大 光纤
存储容量大 全息存储
（2）信息光学的应用
✓ 新型成像系统
✓ 图像处理、图像识别
傅里叶变换+线性系统理论
➢空间频率
照片的二维平面 上光振幅有一定 的强弱分布
➢空间频率
空间频率：单位长度光振幅变化的次数。 反映了光强分布随空间变量作周期性变化的频繁程 度，它同光振动本身的时间频率完全是两回事。时 间是一维的，空间可以是一维、二维、三维。
➢ 数学上的傅立叶变换
数学上可以将一个复杂的周期性函数作 傅立叶级数展开，这一点在光学中体现 为：一幅复杂的图像可以被分解为一系 列不同空间频率的单频信息的合成，即， 一个复杂的图像可以看作是一系列不同 频率不同取向的余弦光栅之和。
✓透镜的发明 ✓望远镜、显微镜的发明 ✓Snell折射定律、费马原理 ✓微粒说、波动说

u 两者的区别在于，电信理论处理的是电信号，是时间的 一维函数，频率是时间频率，只涉及时间的一维函数的傅 里叶变换；在光学领域，处理的是光信号，它是空间的三 维函数，不同方向传播的光用空间频率来表征，需用空间 的三维函数的傅里叶变换。
傅里叶光学（信息光学，变换光学）的含义 信息光学＝数学工具（级数、积分）＋经典光学 （光波的传播、干涉、衍射、成像、光学信息的记 录与再现、光学信号的处理）
①将光波看成光信号的载波: 空间复振幅分布E（x，y），空间光场分布 I (x, y) ②将光学系统看成是信息的收集与处理系统
题记：从惠更斯菲涅耳原理看衍射现象
对衍射不同深度的认识： 光在传播过程中遇到障碍物时偏离直线传播，或更广泛 一点，偏离几何光学的传播规律。 当将波的传播规律已由HFK( Huygens Fresnel Kirchhoff )理 论应用到圆孔、圆盘、单缝、多缝问题时：衍射的发生 是由于光在传播过程中波面受到了某种抑制，亦即自由 波面发生破损。我们要说：在光的传播过程中，由于种 种原因而改变了波前的复振幅分布（振幅和相位），后 场不再是自由传播时的光波场，这便是衍射。用较为数 学化的语言：无源空间的边值定解问题。 ikr " % i e cos( n , r ) − cos( n , l ) ! ( P ) = − ∫∫ E ! (l ) E $ 'dσ λ Σ r # 2 &
等位相线的方程为
x cos α + y cos β = C
dx =
λ
cos α
dy =
λ
cos β
x λ dx dy y
Ø 在两个方向上的空间周期 和空间频率分别为
ux =
cos α
λ

因位置不同而引起的位相色散
x , y
z z
菲涅耳衍射可视为函数
U
0
(
x0
,
y0 ) exp[
j
k 2z
( x0 2
y
0
2
)]
的傅里叶变换在处的值
（3）频域（角谱）表达式： A(u,v) A0 (u,v)exp( jkz)exp[ jz(u2 v2 )]
A(u, v) A0 , • H , H(u,v) exp( jkz)exp[ jz(u2 v2 )] A(u, v) 衍射场角谱 A0 , 孔径后角谱
3、脉冲响应是孔径的傅里叶变换或夫朗和费衍射图样，中心在（-Mx0, -My0）点。 8. 衍射受限系统, 阿贝成像理论；
所谓衍射受限 是指仅仅考虑系统的衍射限制， 不考虑系统的几何像差。
在衍射受限系统中，光的衍射仅受到系统孔径光阑尺寸的限制，因此在考察衍射受限系统时，实际上主要考察
孔径光阑的衍射作用。如果入（出）射光瞳无限大，则光的衍射不受系统的限制，点物应该成理想的点像。然而，
δ 函数的性质：①偶函数性质： （- x) （x) ②坐标缩放性质： (ax) 1 (x)
a
③筛选性质： f (x) (x x0 )dx f (x0 )
④乘积性质： f x• x x0 f x0 • x x0
⑤卷积性质： f x x f x
f x x x0 f x x0
成像过程包含了两次衍射过程：由物面到后焦面，物体衍射光波分解为各种频率的角谱分量，即不同方向传播
的平面波分量，在后焦面上得到物体的频谱。这是一次傅里叶变换过程。由后焦面到像面，各角谱分量又合成为
像，这是一次傅里叶变换逆过程。
9. 相干成像系统的点扩展函数, 相干传递函数； 相干照明系统中，脉冲响应是点物产生的衍射斑的振幅分布。

考点一：矩形函数
1()20a x x rect a other ⎧≤⎪=⎨⎪⎩
（1）讨论特殊情况：
11()02x rect ξ⎧--=⎨⎩
性质：中心点是 –(x-1) ，宽度是2，高度是1，左端是x-1-1，右端是x-1+1。

（2）二维矩形函数可以表示成两个一维函数的乘积 如图：(,)()()x y f x y rect rect a b
=
考点二：什么叫卷积、卷积的四个步骤。

估计会考课件上的卷积计算！！！
考点三：有关傅里叶变换的计算题
考点四：证明傅里叶变换的反比性。

反比性即其频谱的有效宽度与原函数的有效宽度之间存在一定的反比关系1x f
∆⋅∆=。

其
物理意义是原函数越窄，则其频谱函数就越宽
考点五：证明卷积定理[(,)(,)](,)(,)x y x y F g x y h x y G f f H f f *=
考点六：设一实函数h(x)，其频谱为H(f)，即()[()]()()i f a F h x H f H f e φ==
证明其与余弦函数的卷积为：0000()cos 2()cos[2()]a h x f x H f f x f ππφ*=⋅+ 考点七：菲
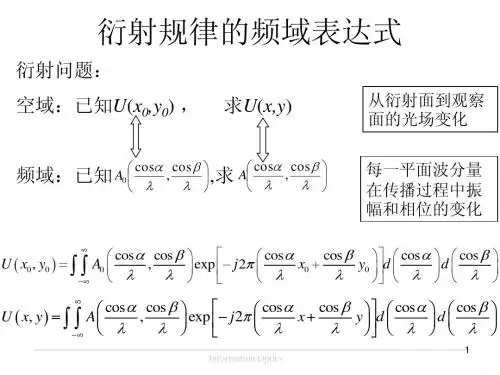
涅尔衍射积分公式的表达式221101111()()exp()(,)(,)exp 2x x y y jkz U x y U x y jk dx dy j z z λ∞-∞⎡⎤-+-=⎢⎥⎣⎦
⎰⎰ 考点七：问答：用菲涅耳衍射公式可以计算的情况：会聚球面波照明衍射屏，衍射花样是屏函数的傅里叶变换。

（详细计算见ppt ）。

考点八：空间频率的定义（两种定义方式）。

考点九：阐述傅里叶光学，*计算题为课件上讲的，证明题为重点。

Q’ Q’’
(无焦)望远镜
Lo

物体很远，近似平行光线
Fo' FE
-y1 -’
LE
y y1 s fo fo ' M fE
y1 ' fE
负号表示成倒立像 物镜和目镜的直径之比越大， 望远镜的视角放大倍数越大。
fo Do f E DE
结构光路
折射系统 refracting telescopes 反射系统 reflecting telescopes
同心光束 同心光束 （几何光学）
L(QM1 N1Q ') L(QM 2 N 2Q ') L(QM i NiQ ')
球面波 球面波 等相位面-等光程 （波动光学）
单球面成像
u
M
h O n’ C s’ Q’
Q
s
n
n n' n' n s s' r
n 物方焦距和像方焦距： f ,
阿贝正弦条件
nysin u n ' y 'sin u '
在轴上已消除球差的前提下，傍轴物 点能以大孔径光束成像的充分必要条件。 阿贝正弦条件可以不要求光线满足傍 轴条件。齐明点满足阿贝正弦条件。
Q
油浸物镜：Q调到齐明点，宽光束成像于共轭
点Q1，弯月透镜的前折射面的中心位于Q1,并使 Q1成为后折射面的齐明点，则前面不折射，后面 成像于Q2。像逐级放大，孔径角逐级减小。
2
2
— 折射率仅沿空间某一方向(y)变化时的光线方程。
d y 1 2 2 2 dx 2n0 sin 0
2
d n2 dy
梯度折射率光纤中光线经迹

屏
1 0 -1 -3
λ
G
光 栅
f′
对于光栅我们可以用透过率函数′（x）来描 来描 对于光栅我们可以用透过率函数 一维透射光栅的透过率函数是一矩形波函数. 述,一维透射光栅的透过率函数是一矩形波函数 一维透射光栅的透过率函数是一矩形波函数 为了讨论问题方便, 设光栅狭缝总数N无限大 无限大. 为了讨论问题方便 设光栅狭缝总数 无限大d s源自n θ = mλ,在近轴条件下
(m = 0, ±1, ± 2,L )
= mp0λ,
sin θ ≈
ξ
f′
=m
λ
d
因此透镜后焦面上频率为
ξ p = mp0 = , ′ fλ
上面的讨论可以说明, 上面的讨论可以说明 理想夫琅和费衍射系统 起到空间频率分析器的作用.这就是现代光学对夫 起到空间频率分析器的作用 这就是现代光学对夫 琅和费衍射的新认识。 琅和费衍射的新认识。 当单色光波入射到待分析的图象上时,通过夫琅 当单色光波入射到待分析的图象上时 通过夫琅 和费衍射,一定空间频率的信息就被一定特定方向 和费衍射 一定空间频率的信息就被一定特定方向 的平面衍射波输送出来. 的平面衍射波输送出来 这些衍射波在近场彼此 交织在一起,到了远场它们彼此分开 到了远场它们彼此分开,从而达到分 交织在一起 到了远场它们彼此分开 从而达到分 频的目的. 频的目的
1 1 i2π p0x i2π p0x 1 i2π 3p0x i2π 3 p0x f (x) = + (e +e +e ) ) (e 2 π 3π 1 i2π 5 p0x i2π 5 p0x + (e +e )L L 5π
在光学中,负的空间频率也可以被赋予物理意义 在光学 在光学中 负的空间频率也可以被赋予物理意义.在光学 负的空间频率也可以被赋予物理意义 用复数表示更方便,更合理 中,用复数表示更方便 更合理 用复数表示更方便

1
菲涅耳衍射
e jkz U ( x, y ) j z
U( x


0
, y0 )e
j
k x xo 2 y yo 2 2z


dx0 dy0
k 衍射场是透射函数 j x 2 y2 e jkz U 0 ( x, y ) e 2z 和球面波的卷积 j z k 2 2 j x0 y0 e jkz j 2kz x 2 y 2 e F uin ( x0 , y0 )e 2 z j z
1，夫琅和费衍射-圆孔衍射
0
的夫琅和费衍射场的复振幅分布为（利用傅里叶-贝塞尔变换）：
2 J kar kr 1 ka z U r exp jkz exp j kar j2z 2 z z 中央亮斑（爱里斑）的半径为：
2 2


强度分布为：
r 0.61
m z m z z d d L
光栅的分辨本领为（m为光栅级次，N为光栅缝数）：
若光栅的大小限制为边长为L的正方形，则其透过率为：
x 1 x x y t x0 rect 0 * comb 0 rect 0 rect 0 a d d L L
cos cos cos cos A , exp j 2 x
Information Optics

cos cos y d d
x y t ( x0 , y0 ) rect 0 rect 0 e jkz jk x y a b e 2 z ab sin cafx sin cbf y 求夫琅和费衍射观察面光场

x 3 的图形： 1. 选出函数 f ( x) rect 2
(a)
-7 -6 -5
f ( x)
f ( x)
(b)
x
0 0 2 3 4
x
x x )rect tri(x) 3. 画出函数的图形： h( x) rect exp(j 5 3
Gaus(x)
x
0
二维情形:
Gaus(x)Gaus(y)=exp[- (x2+y2)] 可代表单模激光束的光强分布
§0-1 常用函数 (续)
七、圆域函数 Circular Function
1, 2 2 定义: circ(r) = circ( x y ) 0,
circ函数是不可分离变量的二元函数
1 0
d ( x)
x
d (x,y)
0
1
y
x
§0-2
d -函数
二、性质
1. 筛选性质 sifting (由定义3直接可证) 设f(x)在x0点连续, 则 f ( x)d ( x x0 )dx f ( x0 )

通过此积分,可从f(x)中筛选出单一的f(x0)值.
1 2. 缩放性质 scaling d (ax) d ( x) a 证明思路:二者对检验函数 在积分中的作用相同.(练习) 推论: d (x)是偶函数
x2 y 2 1 其它
描述无穷大不透明屏上半径为1的圆孔的透过率
1 y
0
x
a 0
x2 y2 circ a
注意
以上定义的函数,其宗量均无量纲. 在处理 实际问题时,要根据所取的单位采用适当的 缩放因子. 例: 以 rect(x) 代表单缝. 若x单位为cm, 则 rect(x) 代表宽度为1cm 的单缝.若x单位 为mm,则 rect(x/10) 代表宽度为1cm 的单缝.

输入
1 x x g ( x) = comb rect ∗ Λ ( x) 3 50 3
间隔为3的 脉冲阵列, 基频为1/3 g(x) 1 在有限空间 区域不为零, |x|<25 三角波, 底宽为2
......
-25 -3 0 3
......
x 25
光栅由无穷多狭缝构成,每条狭缝的宽度均为a, 相邻缝的中心矩(光栅常数)为d(d›a),且光栅被 限制在边长为L的正方形内,求光栅频谱
+∞ −∞ +∞ −∞
f (ξ )h( x − ξ )d ξ
f (ξ − x0 )h( x − ξ )dξ
设ξ − x0 = ξ ′, 则ξ = x0 + ξ ′, d ξ = d ξ ′ 则f ( x − x0 ) * h( x) = ∫ =∫
+∞ −∞ +∞ −∞
f (ξ ′)h( x − ( x0 + ξ ′))d ξ
−∞
exp[ −i 2π ( f xα + f y β )]dαdβ
H ( fx, f y )
= ∫ ∫ H ( f x , f y ) g (α , β ) exp[ −i 2π ( f xα + f y β )]dαdβ
= H ( f x , f y ) ⋅ G( f x , f y ) = G ⋅ H
{1}= δ (fx,fy);
{δ (fx,fy)}= 1
1 与δ 函数互为F.T.
{comb(x)}= comb(f) x 1 comb( ) = comb(τ f) τ τ
{rect(x)}= sinc(f); {sinc(x)}= rect(f) {exp(j2πfax)}= δ (fx-fa) {δ (x-a)}= exp(-j2πfxa)

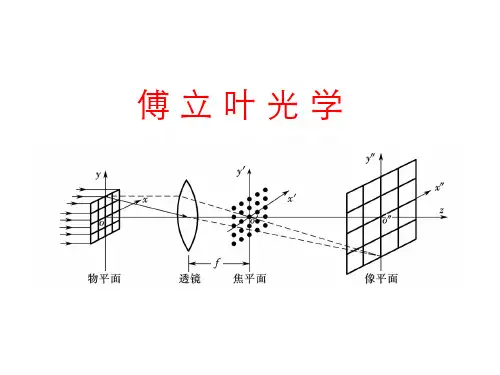
补充读物傅里叶光学和数字图象处理光学与电通讯和电信息理论相互结合，逐渐形成了傅里叶光学。

傅里叶光学的数学基础是傅里叶变换，它的物理基础是光的衍射理论。

一、空间频率和复振幅设一维简谐波以相速度u 沿x 轴正方向传播，)(cos ),(0ϕωξ+−=x k t A t x简谐振动的时间周期性：时间周期T ，时间频率ν，时间角频率ω .简谐波还具有空间周期性？波速u ：(单位时间内振动状态的传播距离称为波速，相速)πλωλνλ2===T u . 空间周期性：空间周期：波长λ (表示振动在一个周期T 内所传播的距离，两个相邻的振动相位相同的点之间距离。

)空间频率：1/λ空间角频率：波数2π/λ若两个单色波沿其传播方向有不同的空间频率，意味着它们有不同的波长。

时间周期性和空间周期性的联系(对单色光)：λ ＝ uT 沿空间任意k 方向传播的单色平面波，复振幅 )(i 00e )(~ϕ−⋅=r k r A E ])cos cos cos ([i 0e ϕγβα−++=z y x k A ,其中α , β 和γ 为传播矢量k 的方位角。

在多数情况下，若不考虑光波随时间的变化，可以只用复振幅表示光波以简化计算。

二、空间频率概念的推广（二维）通常，要处理一个二维的复振幅分布或光强分布，如分析平面上的衍射花样，这时要推广空间频率。

沿k 方向传播的单色平面波，0z z =平面的复振幅分布为 γcos i 000e ),(~z k A y x E =)cos cos (i e βαy x k +对于沿一定方向传播的平面波，γcos i 0e z k ＝常数，则A y x E =),(~0)cos cos (i e βαy x k +x, y 平面上各点复振幅的差别仅来源于不同的(x, y )处有不同的相位差。

x y 平面上的相位分布？k 方向传播的平面波的波面如上图示，0z z =平面与任一波面的交线(虚线)上，各点的位相＝该波面的相位值；交线族 ＝ 等相位线族，其方程为 =+)cos cos (2βαλπy x 常数 故，0z z =平面上复振幅分布的特点：等位相线是一组平行线, 呈周期分布(周期为π2)。

光学
2014年9月
光
学
第一章 光 的 干 涉
第六节 薄膜干涉
上一节的干涉属于分波阵面干 涉，薄膜干涉是属于分振幅干涉
P
P
光
学
第一章 第六节 薄膜干涉
光的干涉
1、薄膜干涉的概况
薄膜干涉的与特点 一束光入射到透明媒质薄膜上，薄膜的上下两个表面对光的振幅分
解，两个表面的反射光在空间相遇时将发生干涉；两个表面的透射光相 遇时也同样会发生干涉。
2、牛顿圈及其应用
j 级暗纹半径透镜半径的关系：
rk Rj
R rk 2
j
j 0, 1, 2K
R j 级暗纹半径与j +N级暗纹半径关系为：
r2 jN
rj 2
(
j
N)R
jR
NR
R
r2 jN
rj 2
N
D
P
h
O
r
有什么应用？两个 R 的表达式有什么不同？
光
学
第一章 光 的 干 涉
第七节 等厚干涉的实现和应用
2、牛顿圈及其应用 牛顿圈实验装置
光
学
第一章 光 的 干 涉
第七节 等厚干涉的实现和应用
2、牛顿圈及其应用
牛顿圈主要用于透镜的曲率半径的检测
牛顿圈移动演示（frmv.m, nt）
当工件表面有不规则起伏时牛顿圈演示（frmv.m, bnt）
光
学
第一章 光 的 干 涉
第七节 等厚干涉的实现和应用
2、薄膜的颜色
P点的空气隙厚度与R及r的关系为：
r2 R2 (R h)2 2Rh h2 2Rh
垂直入射时的光程差 n=1，cosi2=1 2nh r2

傅里叶光学导论
读书笔记
01 思维导图
03 精彩摘录 05 目录分析
目录
02 内容摘要 04 阅读感受 06 作者简介
思维导图
本书关键字分析思维导图
傅里叶
应用
基本概念
论
光学
傅里叶 领域
重点
光学
成像
相干
变换
教材
包括
光电
内容摘要
内容摘要
《傅里叶光学导论》是一本全面介绍傅里叶光学基本概念和应用的教材。该书的重点是介绍傅里 叶光学的基本原理和应用，以及其在图像处理、光学系统设计、光学仪器、光学测量等领域中的 应用。 全书共分为12章，第一章是引言，介绍了傅里叶光学的背景和基本概念。第二章至第四章重点介 绍了傅里叶变换的基本原理和应用，包括离散和连续的傅里叶变换，以及其在光学领域中的应用。 第五章至第七章介绍了光学成像系统的基本概念和特性，包括透镜的成像特性、相干和非相干成 像系统的比较等。 第八章至第十章重点介绍了傅里叶变换在光学成像系统中的应用，包括光学系统的传递函数、相 干成像系统的像差、光学系统的设计等。第十一章和第十二章则分别介绍了傅里叶变换在光学仪 器和光学测量中的应用，包括光学仪器的分辨率、光学测量的基本原理和方法等。
《傅里叶光学导论》是一本全面介绍傅里叶光学的经典教材，由著名物理学 家和光学专家John W. Goodman所著。该书系统地介绍了傅里叶光学的核心概念、 基本原理以及在各种领域中的应用，如图像处理、光学通信、光谱学等。
通过对《傅里叶光学导论》这本书的目录进行详细分析，我们可以将其分为 以下几个主要部分：
这一章主要介绍了傅里叶变换光谱学的基本原理和应用，包括干涉仪、光探 测器等关键部件的设计和应用。同时，还介绍了傅里叶变换光谱学在化学、材料 科学等领域的应用。

光在垂直入射（i =0）或者掠入射（i =90°）的情况下，如果光是从光疏媒 质传向光密媒质，在其分界面上反射时将发生半波损失。 折射波无半波损失
n1 n2
n2 n1 或者 n2 n1 有半波损失
n1
n1 n2
nn13
n2 n2
或者
nn13
n2 n2
有半波损失
n3
n3 n2 n1 或者 n3 n2 n1
两个同振动方向同频率的振动叠加
E1 A1 cos(t-k1r1 1) E2 A2 cos(t-k2r2 2 )
1 = k1r1 1 2 = k2r2 2
干涉相长
2
1
k1r1
k2r2 =
2 0
n1r1
2 0
n2r2
2
j
( j 0,1, 2L )
光程差
n1r1
n2r2
2
j
0
2
( j 0,1, 2L )
干涉相消
2
1
k1r1
k2r2 =
2 0
n1r1
2 0
n2r2
（2
j+1）
( j 0,1, 2L )
光程差
n1r1
n2r2
（.2
j +1）0
2
( j 0,1, 2L ) 1
等倾干涉
n2 n1
1
L 2
P
i1 D
3
M1 n1 n2
Ai 2 i
C
d
M2 n1
2
B
E
45
光程差
0 2d0
n22 n12 sin2 2d0n2 cos i2
等倾干涉 .
等厚干涉 6

更具意义的是：衍射斑的光学特征反映了余弦光栅作为一种典型结构 的特征。
▲特征表
余弦光栅的组合 （1） 平行密接 组合 G 1 · G 2 ：
共有9 个衍射斑，分布于x′轴上，方向角分别为
（2） 正交密 接
组合 G 1 · G 2 ：
(3) 复合光栅 设某光栅其屏函数含有两种频率成分：
屏函数曲线图
在光学领域，处理的是光信号，它是空间的三维函数， 不同方向传播的光用空间频率来表征，需用空间的三维函 数的傅里叶变换。
6.1 衍射系统 波前变换
光源：脉冲光源：发光短暂，激发一个波包而在空间传播。 连续光源：稳定地持续发光。激发一个长波列而在空间推移。
波场中的各点以与光源同样的时间特性稳定地持续 发生扰动，且扰动的基本形式是简谐式振荡。
)
z(1
2w04 2 z 2
)
1 2
有效 z 半 o ,w (0 ) 径 w 0 达 ； 到 腰 最 粗 小
曲率半径：各等相面的曲率中心不重合于一点，是 随光束的传播而移动。
（ 1 ） 知 腰 位 w 0 置 w (z)r,(、 z) U ~ 腰 (x,y,z)粗 （ 2 ） 知w 某 、 r 一 w 0 、 z处 的
波前相因子分析法：根据波前函数的相因子，来判断其波场的 类型、分析其衍射场的主要特性。
两类典型相因子函数：
1.波前函数的相因子：平面波前与球面波前（系可供选择的两种基元成分）
（1）平面波 U ~ (x ,y ) A e i( ks 1 x i s n i2 n y ) 1
其空间角频率为
其空间频率为
特点：振幅A 为常数 ，与场点坐标无关。
位相因子是场点直角坐标的线性函数——线性相因子。
2. 单色球面波复振幅:

§7 傅里叶光学简介
１．光栅衍射和空间频率
２．阿贝成像原理 3. 空间滤波和光学信息处理 (1) 阿贝-波特空间实验 (2) 网格实验 (3) 调制实验
数学中的傅里叶分析,应用到通信理论中, 将电信号的特征在频率域中讨论; 傅里叶分 析与光学中的衍射理论结合起来,形成傅里叶 光学. 傅里叶光学,是在频率域中讨论图象信 息.通信理论中涉及的是一维时间函数,傅立 叶光学中讨论的是二维空间的信号.
１．光栅衍射和空间频率
波长为的单色平面波垂直入射到平面 光栅G上．设光栅d/a=2, N很大,会聚透镜后 的焦平面上得到各级干涉极大，且偶数干涉 极大缺级.
x
0

3

1 -1
屏
0 -3

G光 栅
f
对于光栅我们可以用透过率函数（x） 来描述,一维透射光栅的透过率函数是一矩形 波函数.
为了讨论问题方便, 设光栅狭缝总数N无限大.
像
倾斜方向的频谱通过
像
灰网 尘格 粘 上 的
过只 让 网 格 的 频 谱 通
失网 格 的 像 灰 尘 消
(3)
调制实验
用白光照明透明物体,物体的不同部分是 由不同取向的透射光栅片组成.频谱面上(除 零级外)干涉主极大呈彩色.物面上不同的部 分的频谱在不同方向上. 将一个方向的频谱, 只保留一种颜色,滤掉其余的颜色,其对应的 象面上,就显示出该频率的颜色来.
5 p0
p
透射光栅的空间频率和功率谱
上图是矩形波在频率域中的表示,横坐标是 空间频率p, 纵坐标分别表示振幅A和功率A2. 周期性函数的频谱都是分立的谱,各谱线的 频率为基频整数倍.在p=0处有直流分量. 再回到光栅装置.由光栅方程,
d sin m ,

傅里叶光学实验报告摘要：本实验通过光学元件的调整，利用干涉仪实现了傅里叶光学实验。

实验结果表明，在合适的条件下，可以实现光场的物理变换，为光学信号的处理和传输提供了新的思路。

引言：傅里叶光学是基于傅里叶变换的原理，研究光场在透镜、衍射及干涉等传输过程中的变换规律。

傅里叶光学理论的应用，不仅可以为光学领域提供新的方法和实现技术，而且对于信息科学、通信技术等领域也具有重要的意义。

本次实验旨在掌握傅里叶光学实验的原理和方法，以及掌握干涉仪的基本操作技术。

实验原理：在光学传输过程中，各种光学元件会对光场进行各种变换，如缩放、旋转、平移等。

傅里叶光学理论认为，任何复杂的光学变换都可以分解为一系列基本变换的乘积，这些基本变换因形式各异而具有不同的物理意义。

例如，平移变换对应了频率空间中的相移，旋转变换对应了频率空间中的相位，缩放变换对应了频率空间中的尺度变换等。

傅里叶光学实验利用了干涉仪的干涉效应，实现了光场的物理变换，并通过干涉图案的记录和分析，得到了相关的光学信息。

在干涉仪中，可以通过调整反射镜、透镜等光学元件的位置和角度，实现不同的光学变换效果。

例如，在Fourier变换的情况下，通过调整透镜的位置或反射镜的角度，可以实现平移变换、缩放变换等操作。

实验结果：本次实验中，我们通过调整干涉仪的各个光学元件，实现了物理变换效果，并得到了相应的干涉图案。

通过对干涉图案的分析，实验结果表明，在适当的条件下，我们可以通过傅里叶光学实验，实现光学信号的物理变换、建模、分析和传输。

结论：傅里叶光学是一种重要的光学变换技术和分析手段，利用其可以实现光学信号的稳定传输和处理。

本次实验通过干涉仪实现了傅里叶光学实验，对傅里叶光学基本原理和实现方法有了更深入的了解，对后续的光学研究和应用具有良好的指导意义。

傅里叶光学实验报告原理引言傅里叶光学是一种研究光的传播、变换和调制的重要实验方法。

通过傅里叶光学实验，人们可以深入了解光的波动性质，并应用于许多科学技术领域，如光学通信、光谱分析和图像处理等。

本实验旨在通过获取光信号的频谱和波形信息，介绍傅里叶光学的基本原理和方法。

实验原理傅里叶光学实验的基本原理是将光信号在频域上进行分析和合成。

根据傅里叶级数展开的理论基础，任意周期函数都可以表示为一系列正弦和余弦函数的叠加，即傅里叶级数。

对于连续光信号而言，可以将其频谱分解为一系列连续的频率分量。

而在实际应用中，常使用离散傅里叶变换（DFT）对光信号进行数字处理。

傅里叶光学实验通常包括以下几个关键步骤：1. 发光源：实验中需要使用一种稳定而强亮度的发光源，常见的有激光器、白炽灯等。

2. 空间滤波：为了使实验的结果更加清晰，可以使用光阑等光学元件对入射光进行空间滤波，以去除噪声和杂散光。

3. 波像记录：通过使用适当的光学元件（如透镜或光栅）对光信号进行处理，并将光场信息转化为一个空间上的二维图像。

4. 光信号检测：使用光电探测器或像敏元件将光信号转化为电信号，进一步进行数字处理和分析。

5. 数据处理：利用数学方法对光信号的频谱进行计算和分析，如进行傅里叶变换、滤波和谱线提取等。

实验设备- 一台激光器- 一块光栅- 一组准直透镜- 一个光电探测器- 一个光电转换器- 一台示波器- 一台计算机实验步骤1. 将激光器与准直透镜对准，使激光的光斑尽量小且清晰。

2. 将光栅放在准直激光的路径上，调整角度使激光通过光栅后形成干涉条纹。

3. 放置光电探测器，将光栅产生的干涉条纹转化为电信号。

4. 将光电转换器与光电探测器连接，转化电信号为适当的电压信号。

5. 使用示波器对电压信号进行测量和分析，获取干涉条纹的波形信息。

6. 将示波器与计算机相连，将数据导入计算机进行进一步处理和分析，如进行傅里叶变换并提取频谱信息。

实验结果与分析在实验中，我们成功地观察到了干涉条纹的形成，并通过光电探测器将其转化为电信号。