分派问题的回溯算法(整理版)

算法设计中的分治与回溯策略算法设计中的分治与回溯策略是两种常用的问题解决方法，它们在解决复杂问题时具有重要的作用。

本文将介绍分治与回溯策略的基本概念和应用场景，并通过实例详细探讨它们的具体应用。

一、分治策略分治策略是一种将问题划分为更小的子问题，并通过在子问题上递归地应用相同的方法来解决原问题的方法。

它包含以下三个基本步骤：1. 分解（Divide）：将原问题分解为若干个规模较小且相互独立的子问题。

2. 解决（Conquer）：递归地解决每个子问题，如果子问题的规模足够小，则直接求解。

3. 合并（Combine）：将子问题的解合并为原问题的解。

分治策略的经典应用是归并排序和快速排序。

以归并排序为例，其思想是将待排序的序列划分为若干个子序列，分别进行排序，然后将排好序的子序列合并成最终有序序列。

这个过程中，分解步骤是通过将序列划分为两个子序列，解决步骤是递归地对子序列进行排序，合并步骤是将排好序的子序列合并。

二、回溯策略回溯策略是一种通过穷举所有可能的解并逐步构建可行解的方法。

它通常用于求解组合优化问题、排列问题和搜索问题。

回溯法的基本思想如下：1. 选择（Choose）：在每一步选择中，我们都有多个选择可以进行尝试。

2. 约束（Constraint）：对选择进行约束条件的限制，以排除不满足要求的选择。

3. 撤销（Un-choose）：如果发现当前选择并不是正确的解，可以撤销上一步或几步的选择，进行其他尝试。

回溯策略经常使用递归来实现，其关键是正确地定义选择、约束和撤销的操作。

回溯法可以通过剪枝操作来减少搜索空间，提高求解效率。

回溯策略的一个典型应用是八皇后问题。

八皇后问题是要求在一个8×8的棋盘上放置8个皇后，使得任意两个皇后都不能相互攻击。

回溯法通过逐行放置皇后，并检查每个位置是否满足约束条件，如果满足则进入下一行继续放置，如果不满足则进行回溯，尝试其他选择。

结语分治策略和回溯策略都是算法设计中常用的解决复杂问题的方法。

回溯算法（一）第一部分回溯寻找问题的解的一种可靠的方法是首先列出所有候选解，然后依次检查每一个，在检查完所有或部分候选解后，即可找到所需要的解。

理论上，当候选解数量有限并且通过检查所有或部分候选解能够得到所需解时，上述方法是可行的。

不过，在实际应用中，很少使用这种方法，因为候选解的数量通常都非常大（比如指数级，甚至是大数阶乘），即便采用最快的计算机也只能解决规模很小的问题。

对候选解进行系统检查的方法有多种，其中回溯和分枝定界法是比较常用的两种方法。

按照这两种方法对候选解进行系统检查通常会使问题的求解时间大大减少（无论对于最坏情形还是对于一般情形）。

事实上，这些方法可以使我们避免对很大的候选解集合进行检查，同时能够保证算法运行结束时可以找到所需要的解。

因此，这些方法通常能够用来求解规模很大的问题。

一、回溯的概念从问题的某种可能情况出发，搜索所有能到达的可能情况，然后以其中一种可能的情况为新的出发点，继续向下探索，当所有可能情况都探索过且都无法到达目标的时候，再回退到上一个出发点，继续探索另一个可能情况，这种不断回头寻找目标的方法称为“回溯法”。

回溯算法是一种系统的搜索问题答案的方法，是一种能避免不必要搜索的穷举式的搜索算法，其基本思想就是穷举搜索。

常用于查找问题的解集或符合某些限制条件的最佳解集。

回溯算法常被用来解决自然数排列问题、皇后问题、迷宫问题、数的拆分、0/1背包问题、旅行商问题、货船装箱问题和图形覆盖问题等。

我们先来看一个老鼠走迷宫的演示，体会一下在回溯法中是如何回溯的。

二、回溯的一般描述可用回溯法求解的问题P，通常要能表达为：对于已知的由n元组（x1，x2，…，xn）组成的一个状态空间E={（x1，x2，…，xn）∣xi∈Si ，i=1，2，…，n}，给定关于n元组中的一个分量的一个约束集D，要求E中满足D的全部约束条件的所有n元组。

其中Si是分量xi的定义域，且|Si| 有限，i=1，2，…，n。

回溯算法1、概念回溯算法实际上⼀个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满⾜求解条件时，就“回溯”返回，尝试别的路径。

回溯法是⼀种选优搜索法，按选优条件向前搜索，以达到⽬标。

但当探索到某⼀步时，发现原先选择并不优或达不到⽬标，就退回⼀步重新选择，这种⾛不通就退回再⾛的技术为回溯法，⽽满⾜回溯条件的某个状态的点称为“回溯点”。

回溯法（英语：backtracking）也称试探法，回溯法有“通⽤的解题⽅法”之称。

它可以系统的搜索⼀个问题的所有解或者任意解。

回溯法是⼀个既带有系统性⼜带有跳跃性的的搜索算法。

它在包含问题的所有解的解空间树中，按照深度优先的策略，从根结点出发搜索解空间树。

算法搜索⾄解空间树的任⼀结点时，总是先判断该结点是否肯定不包含问题的解。

如果肯定不包含，则跳过对以该结点为根的⼦树的系统搜索，逐层向其祖先结点回溯。

否则，进⼊该⼦树，继续按深度优先的策略进⾏搜索。

回溯法在⽤来求问题的所有解时，要回溯到根，且根结点的所有⼦树都已被搜索遍才结束。

⽽回溯法在⽤来求问题的任⼀解时，只要搜索到问题的⼀个解就可以结束。

这种以深度优先的⽅式系统地搜索问题的解的算法称为回溯法，它适⽤于解⼀些组合数较⼤的问题.回溯法通常⽤最简单的递归⽅法来实现，在反复重复上述的步骤后可能出现两种情况：1 .找到⼀个可能存在的正确的答案。

2. 在尝试了所有可能的分步⽅法后宣告该问题没有答案。

在最坏的情况下，回溯法会导致⼀次复杂度为指数时间的计算。

2、适⽤范围在包含问题的所有解的解空间树中，按照深度优先搜索的策略，从根结点出发深度探索解空间树。

适⽤范围：1，问题的解⽤向量表⽰X = (x1, x2, ..., xn)2，需要搜索⼀个或⼀组解3，满⾜约束条件的最优解等回溯法的基本思想对于⽤回溯法求解的问题，⾸先要将问题进⾏适当的转化，得出状态空间树。

这棵树的每条完整路径都代表了⼀种解的可能。

通过深度优先搜索这棵树，枚举每种可能的解的情况；从⽽得出结果。

回溯算法详解
回溯算法是一种经典问题求解方法，通常被应用于在候选解的搜索空间中，通过深度优先搜索的方式找到所有可行解的问题。

回溯算法的本质是对一棵树的深度优先遍历，因此也被称为树形搜索算法。

回溯算法的基本思想是逐步构建候选解，并试图将其扩展为一个完整的解。

当无法继续扩展解时，则回溯到上一步并尝试其他的扩展，直到找到所有可行的解为止。

在回溯算法中，通常会维护一个状态向量，用于记录当前已经构建的解的情况。

通常情况下，状态向量的长度等于问题的规模。

在搜索过程中，我们尝试在状态向量中改变一个或多个元素，并检查修改后的状态是否合法。

如果合法，则继续搜索；如果不合法，则放弃当前修改并回溯到上一步。

在实际应用中，回溯算法通常用来解决以下类型的问题：
1. 组合问题：从n个元素中选取k个元素的所有组合；
2. 排列问题：从n个元素中选择k个元素，并按照一定顺序排列的所有可能；
3. 子集问题：从n个元素中选择所有可能的子集；
4. 棋盘问题：在一个给定的n x n棋盘上放置n个皇后，并满足彼此之间不会互相攻击的要求。

回溯算法的时间复杂度取决于候选解的规模以及搜索空间中的剪枝效果。

在最坏情况下，回溯算法的时间复杂度与候选解的数量成指数级增长，因此通常会使用剪枝算法来尽可能减少搜索空间的规模，从而提高算法的效率。

总之，回溯算法是一种非常有用的问题求解方法，在实际应用中被广泛使用。

同时，由于其时间复杂度较高，对于大规模的问题，需要慎重考虑是否使用回溯算法以及如何优化算法。

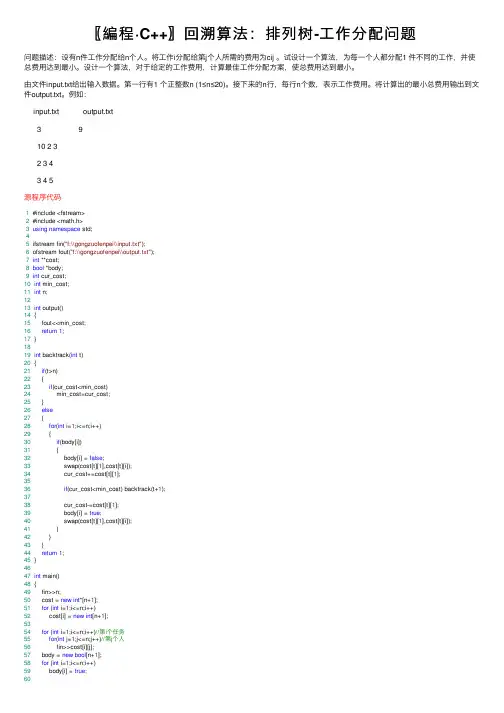
〖編程·C++〗回溯算法：排列树-⼯作分配问题问题描述：设有n件⼯作分配给n个⼈。

将⼯作i分配给第j个⼈所需的费⽤为cij 。

试设计⼀个算法，为每⼀个⼈都分配1 件不同的⼯作，并使总费⽤达到最⼩。

设计⼀个算法，对于给定的⼯作费⽤，计算最佳⼯作分配⽅案，使总费⽤达到最⼩。

由⽂件input.txt给出输⼊数据。

第⼀⾏有1 个正整数n (1≤n≤20)。

接下来的n⾏，每⾏n个数，表⽰⼯作费⽤。

将计算出的最⼩总费⽤输出到⽂件output.txt。

例如：input.txt output.txt3 910 2 32 3 43 4 5源程序代码1 #include <fstream>2 #include <math.h>3using namespace std;45 ifstream fin("f:\\gongzuofenpei\\input.txt");6 ofstream fout("f:\\gongzuofenpei\\output.txt");7int **cost;8bool *body;9int cur_cost;10int min_cost;11int n;1213int output()14 {15 fout<<min_cost;16return1;17 }1819int backtrack(int t)20 {21if(t>n)22 {23if(cur_cost<min_cost)24 min_cost=cur_cost;25 }26else27 {28for(int i=1;i<=n;i++)29 {30if(body[i])31 {32 body[i] = false;33 swap(cost[t][1],cost[t][i]);34 cur_cost+=cost[t][1];3536if(cur_cost<min_cost) backtrack(t+1);3738 cur_cost-=cost[t][1];39 body[i] = true;40 swap(cost[t][1],cost[t][i]);41 }42 }43 }44return1;45 }4647int main()48 {49 fin>>n;50 cost = new int*[n+1];51for (int i=1;i<=n;i++)52 cost[i] = new int[n+1];5354for (int i=1;i<=n;i++)//第i个任务55for(int j=1;j<=n;j++)//第j个⼈56 fin>>cost[i][j];57 body = new bool[n+1];58for (int i=1;i<=n;i++)59 body[i] = true;61//分配min_cost初值，为第i个任务分配给第i个⼈的总花费62 min_cost = 0;63for(int i=1;i<=n;i++)64 min_cost += cost[i][i];65 cur_cost=0;6667 backtrack(1);6869 output();7071for(int i=1;i<=n;i++)72 delete cost[i];73 delete cost,body;7475 fin.close();76 fout.close();7778return1;79 }增加输出⼀种分配⽅法的代码如下：改进的代码1 #include <fstream>2 #include <math.h>3using namespace std;45 ifstream fin("f:\\gongzuofenpei\\input.txt");6 ofstream fout("f:\\gongzuofenpei\\output.txt");7int **cost;8bool *body;9int *best;10int *test;11int cur_cost;12int min_cost;13int n;1415int output()16 {17 fout<<"最低花费为："<<min_cost<<endl;18for(int i=1;i<=n;i++)19 fout<<"第"<<i<<"任务由"<<"第"<<best[i]<<"个⼈做，花费为"<<cost[i][best[i]]<<";"<<endl; 20return1;21 }2223int backtrack(int t)24 {25if(t>n)26 {27if(cur_cost<min_cost)28 min_cost=cur_cost;29for(int i=1;i<=n;i++)30 best[i] = test[i];3132 }33else34 {35for(int i=1;i<=n;i++)36 {37if(body[i])38 {39 body[i] = false;40 swap(cost[t][1],cost[t][i]);41 cur_cost+=cost[t][1];42 test[t]=i;43if(cur_cost<min_cost) backtrack(t+1);4445 cur_cost-=cost[t][1];46 body[i] = true;47 swap(cost[t][1],cost[t][i]);48 }49 }50 }51return1;52 }5354int main()56 fin>>n;57 cost = new int*[n+1];58for (int i=1;i<=n;i++)59 cost[i] = new int[n+1];6061for (int i=1;i<=n;i++)//第i个任务62for(int j=1;j<=n;j++)//第j个⼈63 fin>>cost[i][j];64 body = new bool[n+1];65for (int i=1;i<=n;i++)66 body[i] = true;67686970//分配min_cost初值，为第i个任务分配给第i个⼈的总花费71 min_cost = 0;72for(int i=1;i<=n;i++)73 min_cost += cost[i][i];74 cur_cost=0;75 best = new int[n+1];76for(int i=1;i<=n;i++)77 best[i] = i;78 test = new int[n+1];79for(int i=1;i<=n;i++)80 test[i] = 0;81 backtrack(1);8283 output();8485for(int i=1;i<=n;i++)86 delete cost[i];87 delete cost,body,test,best;8889 fin.close();90 fout.close();9192return1;93 }。

五大常用算法回溯算法一、回溯算法的概述回溯算法是一种常用的解决问题的算法，通常用于解决组合优化问题，如排列、组合、子集等问题。

回溯算法通过不断地尝试可能的解，直到找到问题的解或者确定不存在解为止。

它的核心思想是通过递归实现穷举，然后进行剪枝，以提高效率。

回溯算法主要包含以下五个步骤：1.选择：在每一步中，可以根据条件选择一个或多个可能的路径。

2.约束：根据问题的约束条件，限制可选择的路径。

3.：以递归的方式进行，尝试所有可能的解。

4.判断：在的过程中，判断当前路径是否符合问题的要求，如果符合则接受，否则进行回溯。

5.取消选择：在判断出当前路径不符合要求时，撤销当前选择，回到上一步继续尝试其他可能的选择。

回溯算法的优缺点：优点：1.简单直观：回溯算法的思路清晰，易于理解和实现。

2.灵活性高：回溯算法适用于各种问题，没有固定的限制条件，可以根据具体问题进行调整。

3.扩展性好：回溯算法可以通过剪枝策略提高效率，并且可以和其他算法结合使用。

缺点：1.效率低：回溯算法通常需要穷举所有的可能解，因此在处理大规模问题时效率较低。

2.可能的重复计算：由于回溯算法会尝试所有可能的解，所以有可能会产生重复计算的问题。

二、回溯算法的应用回溯算法在许多实际问题中都有应用，包括但不限于以下几个领域：1.组合求解：回溯算法可以用来求解排列、组合、子集等问题。

例如，在给定一组数字的情况下，找到所有可能的组合，使其和等于给定的目标值。

2.图的：回溯算法可以用来解决图的遍历问题，如深度优先、广度优先等。

例如，在给定一张无向图的情况下，找到从起点到终点的路径。

3.数独游戏：回溯算法可以用来解决数独游戏。

数独是一种逻辑类的游戏，在一个9×9的网格中填入1-9的数字，要求每行、每列、每个3×3的子网格都包含1-9的数字，且不能重复。

4.八皇后问题：回溯算法可以用来解决八皇后问题。

八皇后问题是在一个8×8的棋盘上放置八个皇后，要求每行、每列、每个对角线上都不能有两个皇后。

分派问题的回缩解法一． 考查题目给n 个人分派n 件工作, 把工作j 分派给第i 个人的成本为cost(i, j), 设计、编程、测试回溯算法, 在给每个人分派一件不同工作的情况下使得总成本最小。

二． 问题的解决方案 1.分派问题的解决方案1）设计的状态空间树：图中是用静态树表示分派问题的状态空间树，本实验使用n=4，图中x1,x2,x3,x4表示不同的人。

树中的节点是求解过程的一个状态，树中的边是标示 x i 的一个可能被分配到的一个任务。

由根节点到任意叶节点的路径定义为解向量。

由根节点到所有叶节点的路径定义为解空间。

2）阐述用回溯法求解的基本思想：1）先设计一个成本最小值summin ，如果有一组解的成本之和sum 小于summin ，则sum 就覆盖summin ，如果在搜索过程中发现已有解的成本大于summin ，那么就没有必要再搜索下去了。

在搜索过程中，每生成一个新结点都要将成本sum 与summin 进行比较以此来判断是否要沿着此结点遍历下去。

2）规范函数int place(int cont,int sum) //判断第cout 个人能否做工作X[cont] {int i;for(i=0;i<cont;i++) if(X[i]==X[cont]) //判断X[cont] 在前面是否有人做 return false;if(sum>summin) //如果此时的sum 已经大于summin 时4567391011128141516171322021222319252627282430313233291836373839354142434440464748494534525354555157585960566263646561501x 1x 2x 3x 41234234134124123342423341413241412231312434232434131424121323121return true;}3）主要的搜索流程图：先设Summin=100,部分搜索如下4）主要数据类型与变量int sum; /* 成本总和*/int summin /* 最小的成本总和*/int cont /* 第cont个人*/X[cont] /*X[cont]来保存任务的分配方案*/A[i][j] /* 表示i个人做第j号任务的成本*/5）算法或程序模块int place(int cont,int sum)功能: 判断第cont个人能否做第X[cont]号任务void huisuo(int cont,int sum)功能: 遍历每种情况，比较每种情况下的的成本，得出最小成本summin 各函数的伪C语言代码：int place(int cont,int sum){int i;for(i=0;i<cont;i++)if(X[i]==X[cont]) //判断此问题在以前是否有人做if(sum>summin) //现在sum大于summin时return false;elsereturn true;}void huisuo(int cont,int sum){int k,i;if(cont==N) //当所有人都分配任务时{if(sum<summin) //判断此任务分配方案是否比前面的分配方案更优{summin=sum; //将sum覆盖summinfor(i=0;i<N;i++)Q[i]=X[i]; //将更优的分配方案放到Q[N]中}}else //所有人还没有分到任务时即任务还没有分配完{for(k=0;k<N;k++) //用k表示第几号任务{X[cont]=k; //第cont号人做第k号任务if(place(cont,sum)) //判断是否合理{sum=A[cont][k]+sum; //可以分配时，增加sum值huisuo(cont+1,sum); //给下一个人分配分配任务sum=sum-A[cont][k];}}cont=cont-1; //返回到上一个人}}2. 测试a)方案测试数据1 2 3 43 3 2 16 4 1 89 1 2 5行表示1,2,3,4号人，列表示1 2 3 4号任务b)结果三．总结与讨论本实验是用回缩递归方法求解分派问题，设计时我们采用N皇后问题的思路，在设计place 函数时，我们不仅使用了同一任务不能同时两个人做这一约束条件，还增加了增加了sum要小于summin这一约束条件，这样可以避免一些不要的搜索，提高了程序运行的效率。

回溯算法详解
回溯算法是一种常用的解决问题的方法，它的目的是在一个大的问题空间中寻找到一个解决方案。

回溯算法的基本思想是穷举所有可能的解决方案，直到找到符合条件的解决方案为止。

回溯算法的实现通常包括两个部分：状态表示和状态转移。

状态表示是指将问题的解答空间表示为一个状态树，每个节点表示一个状态，状态转移是指从一个节点转移到另一个节点的过程。

回溯算法的实现过程通常包括三个步骤：选择、回溯和剪枝。

选择是指从当前状态节点选择一个扩展节点作为下一步的状态，回溯是指从一个状态节点返回到它的父节点，剪枝是指在搜索过程中对一些不可能达到目标的状态进行剪枝。

回溯算法常常用于求解组合、排列、子集、划分等问题。

由于回溯算法的时间复杂度很高，因此在实际应用中往往需要结合其他优化算法来提高效率。

总的来说，回溯算法是一种通用的算法，它可以解决许多不同类型的问题。

只要能够将问题的解答空间表示为一个状态树，并且能够找到一种回溯的方法来搜索这个状态树，就可以使用回溯算法来求解问题。

- 1 -。

回溯算法-算法介绍回溯法1、有许多问题，当需要找出它的解集或者要求回答什么解是满⾜某些约束条件的最佳解时，往往要使⽤回溯法。

2、回溯法的基本做法是搜索，或是⼀种组织得井井有条的，能避免不必要搜索的穷举式搜索法。

这种⽅法适⽤于解⼀些组合数相当⼤的问题。

3、回溯法在问题的解空间树中，按深度优先策略，从根结点出发搜索解空间树。

算法搜索⾄解空间树的任意⼀点时，先判断该结点是否包含问题的解。

如果肯定不包含（剪枝过程），则跳过对该结点为根的⼦树的搜索，逐层向其祖先结点回溯；否则，进⼊该⼦树，继续按深度优先策略搜索。

问题的解空间问题的解向量：回溯法希望⼀个问题的解能够表⽰成⼀个n元式(x1,x2,…,xn)的形式。

显约束：对分量xi的取值限定。

隐约束：为满⾜问题的解⽽对不同分量之间施加的约束。

解空间：对于问题的⼀个实例，解向量满⾜显式约束条件的所有多元组，构成了该实例的⼀个解空间。

注意：同⼀个问题可以有多种表⽰，有些表⽰⽅法更简单，所需表⽰的状态空间更⼩（存储量少，搜索⽅法简单）。

下⾯是n=3时的0-1背包问题⽤完全⼆叉树表⽰的解空间：⽣成问题状态的基本⽅法扩展结点:⼀个正在产⽣⼉⼦的结点称为扩展结点活结点:⼀个⾃⾝已⽣成但其⼉⼦还没有全部⽣成的节点称做活结点死结点:⼀个所有⼉⼦已经产⽣的结点称做死结点深度优先的问题状态⽣成法：如果对⼀个扩展结点R，⼀旦产⽣了它的⼀个⼉⼦C，就把C当做新的扩展结点。

在完成对⼦树C（以C为根的⼦树）的穷尽搜索之后，将R重新变成扩展结点，继续⽣成R的下⼀个⼉⼦（如果存在）宽度优先的问题状态⽣成法：在⼀个扩展结点变成死结点之前，它⼀直是扩展结点回溯法：为了避免⽣成那些不可能产⽣最佳解的问题状态，要不断地利⽤限界函数(bounding function)来处死(剪枝)那些实际上不可能产⽣所需解的活结点，以减少问题的计算量。

具有限界函数的深度优先⽣成法称为回溯法。

（回溯法 = 穷举 + 剪枝）回溯法的基本思想(1)针对所给问题，定义问题的解空间；(2)确定易于搜索的解空间结构；(3)以深度优先⽅式搜索解空间，并在搜索过程中⽤剪枝函数避免⽆效搜索。

排列组合中的分组分配问题的有效解法
排列组合中的分组分配问题是一类常见的组合优化问题，其目标是将一组对象分配到不同的组中，并满足一定的条件或限制。

在实际应用中，这类问题常常涉及到资源分配、任务调度、人员安排等方面。

1. 贪心算法：贪心算法是一种简单而常用的解法，它根据问题的特点每次选择当前最优的解决方案，并逐步构建最终的解。

在分组分配问题中，贪心算法可以从初始状态开始，每次选择满足一定条件的对象，并将其分配到符合要求的组中，直到所有对象都被分配完毕或达到某种终止条件。

2. 动态规划：动态规划是一种使用备忘录或状态转移方程的方法，通过将原问题分解为若干个子问题，并记录子问题的解，最终通过子问题的解构造出原问题的解。

在分组分配问题中，可以使用动态规划求解最优解。

具体方法是定义一个状态转移方程来描述每个子问题的最优解，然后采用自底向上的方式逐步计算出最终解。

3. 回溯算法：回溯算法是一种逐步试探的算法，通过不断尝试所有可能的解，并及时剪枝来找到最优解。

在分组分配问题中，回溯算法可以通过递归的方式遍历所有可能的分组分配方案，并通过剪枝操作来减少搜索空间。

具体方法是定义一个递归函数，在每一步选择一个对象并加入到某个组中，直到所有对象被分配完成或达到某个终止条件。

4. 蚁群算法：蚁群算法是一种模拟蚂蚁觅食行为的启发式算法，通过模拟蚂蚁找到食物的行为，来寻找问题的最优解。

在分组分配问题中，蚁群算法可以通过定义蚂蚁的移动规则、信息素的更新规则等，来模拟蚂蚁在不同组中选择对象的过程，并通过信息素的增强来引导蚂蚁选择更优的解。

经典回溯算法：集合划分问题读完本⽂，你不仅学会了算法套路，还可以顺便去 LeetCode 上拿下如下题⽬：-----------之前说过回溯算法是笔试中最好⽤的算法，只要你没什么思路，就⽤回溯算法暴⼒求解，即便不能通过所有测试⽤例，多少能过⼀点。

回溯算法的技巧也不难，前⽂说过，回溯算法就是穷举⼀棵决策树的过程，只要在递归之前「做选择」，在递归之后「撤销选择」就⾏了。

但是，就算暴⼒穷举，不同的思路也有优劣之分。

本⽂就来看⼀道⾮常经典的回溯算法问题，⼒扣第 698 题「划分为k个相等的⼦集」。

这道题可以帮你更深刻理解回溯算法的思维，得⼼应⼿地写出回溯函数。

题⽬⾮常简单：给你输⼊⼀个数组nums和⼀个正整数k，请你判断nums是否能够被平分为元素和相同的k个⼦集。

函数签名如下：boolean canPartitionKSubsets(int[] nums, int k);我们之前写过⼀次⼦集划分问题，不过那道题只需要我们把集合划分成两个相等的集合，可以转化成背包问题⽤动态规划技巧解决。

但是如果划分成多个相等的集合，解法⼀般只能通过暴⼒穷举，时间复杂度爆表，是练习回溯算法和递归思维的好机会。

⼀、思路分析⾸先，我们回顾⼀下以前学过的排列组合知识：1、P(n, k)（也有很多书写成A(n, k)）表⽰从n个不同元素中拿出k个元素的排列（Permutation/Arrangement）；C(n, k)表⽰从n个不同元素中拿出k个元素的组合（Combination）总数。

2、「排列」和「组合」的主要区别在于是否考虑顺序的差异。

3、排列、组合总数的计算公式：好，现在我问⼀个问题，这个排列公式P(n, k)是如何推导出来的？为了搞清楚这个问题，我需要讲⼀点组合数学的知识。

排列组合问题的各种变体都可以抽象成「球盒模型」，P(n, k)就可以抽象成下⾯这个场景：即，将n个标记了不同序号的球（标号为了体现顺序的差异），放⼊k个标记了不同序号的盒⼦中（其中n >= k，每个盒⼦最终都装有恰好⼀个球），共有P(n, k)种不同的⽅法。

回溯算法（DFS：深度优先）1. ⼋皇后问题⼋皇后问题，是⼀个古⽼⽽著名的问题，是回溯算法的典型案例。

该问题是国际西洋棋棋⼿马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放⼋个皇后，使其不能互相攻击，即任意两个皇后都不能处于同⼀⾏、同⼀列或同⼀斜线上，问有多少种摆法。

思路：使⽤⼀个数组gEightQueen存储第i⾏的皇后摆在第gEightQueen[i]列的位置上步骤⼀：对于第0⾏，⼀共有⼋个位置可以选择，逐⼀选择步骤⼆：对于以后的每⼀⾏，⼀共有⼋个位置可以选择，确定位置后需要判断该位置放置元素是否与前⾯的⾏冲突，如果冲突，继续在剩余的位置中选择测试。

如果不冲突，则继续向下递归，递归结束后应当将改⾏的元素置0。

步骤三：当递归到第7⾏，选择位置不冲突则找到了⼀种情况，将总的情况统计数加1。

#include<iostream>using namespace std;static int gEightQueen[8] = { 0 }, gCount = 0;void print()//输出每⼀种情况下棋盘中皇后的摆放情况{for (int i = 0; i < 8; i++){int inner;for (inner = 0; inner < gEightQueen[i]; inner++)cout << "0";cout <<"#";for (inner = gEightQueen[i] + 1; inner < 8; inner++)cout << "0";cout << endl;}cout << "==========================\n";}int check_pos_valid(int loop, int value)//检查是否存在有多个皇后在同⼀⾏/列/对⾓线的情况{int index;int data;for (index = 0; index < loop; index++){data = gEightQueen[index];if (value == data)return0;if ((index + data) == (loop + value))return0;if ((index - data) == (loop - value))return0;}return1;}void eight_queen(int index){int loop;for (loop = 0; loop < 8; loop++){if (check_pos_valid(index, loop)){gEightQueen[index] = loop;if (7 == index){gCount++, print();gEightQueen[index] = 0;return;}eight_queen(index + 1);gEightQueen[index] = 0;}}}int main(int argc, char*argv[]){eight_queen(0);cout << "total=" << gCount << endl;return0;}2. 数独问题解法：只需要求出⼀个解，solve()返回布尔类型对于判断是否完成解⼗分有⽤步骤⼀：依此遍历数独中所有的元素，如果不存在'.'，说明已经获得了解，如果存在'.'，说明需要继续向下求解。

指派问题回溯法
指派问题回溯法是一种解决任务分配问题的数学算法。

该方法在实际生活中被广泛应用，如人力资源管理、航空调度、医院排班等领域。

指派问题是一个典型的优化问题，通常可以用线性规划、贪心算法、遗传算法等多种方法求解。

而指派问题回溯法则是其中一种比较简单但有效的算法。

其基本思想是从一个初始解开始，逐步调整已分配的任务或者重新分配未完成的任务，直到找到最优解。

在此过程中，需要注意一些约束条件，如每个任务只能被一个人完成，每个人只能完成一个任务等。

具体来说，指派问题回溯法可以通过以下步骤进行：
1. 初始化：确定初始任务分配方案，并计算当前方案的成本。

2. 变换：对当前方案进行变换，包括交换任务的分配、增加或减少任务等。

3. 评估：计算新方案的成本，并与当前方案进行比较。

4. 更新：如果新方案优于当前方案，则更新任务分配方案，否则保留原方案并返回上一步。

5. 终止：当满足一定条件时，停止迭代并输出最优解。

虽然指派问题回溯法可能不是最优解决方案，但它的优点在于简单易懂，可以快速得到可行解。

因此，在实际应用中，可以根据具体情况选择合适的算法来解决任务分配问题。

第二讲回溯
回溯算法可以很方便的解决“循环层数不确定”的题目，由于题目适应性强，很受竞赛选手的喜爱，尤其在初高中竞赛中。

从其外形表现上来看，回溯算法更像生成一个一维数组，这个一维数组里面的数字所表达的含义符合我们的题目要求，那么就是其中的一组解。

这个一维数组中数字的个数，就是通常意义上的循环层数。

下面我们通过几个循序渐进的例子来看这些情况：
1.输入n，m，请用回溯的方法生成从n个中取m个的全排列和组合
组合程序
回溯算法规律：
2.整数拆分：任何一个自然数n，总可以拆分成若干个自然数的和，且拆分的方法有很多
种【数字相同，顺序不同，被认为是同一种】，如n=3,则有：
1 1 1
1 2
3
N=5则有
1 1 1 1 1
1 1 1 2
1 1 3
1 2 2
1 4
2 3
5
请编写程序完成，输入n 输出n的所有拆分方法；
如果为乘积形式的拆分应该如何完成。

3.素数环【需要理清很多条件】
输入n 将1，2，3，……n，这n个数字排成一排，使得相邻的两数字之和为一个素数，且首尾两数字之和也为一个素数，如，n=4: 则有：
1 2 3 4
2 3 4 1
3 2 1 4
等
编写程序输出所有的解( n<=20 )
4.骑士巡游
在边长为n方格棋盘上，设想有一位骑士，按照马行走的规则从棋盘的某一个位置出发走n*n-1步，不重复的踏遍整个棋盘，在没有计算机时这个问题非常的麻烦，但在计算机出现后，就可以很方便的解决这个问题。

算法——回溯法回溯法回溯法有“通⽤的解题法”之称。

⽤它可以系统地搜索⼀个问题的所有解或任⼀解。

回溯法是⼀种即带有系统性⼜带有跳跃性的搜索算法。

它在问题的解空间树中，按深度优先策略，从根节点出发搜索解空间树。

算法搜索⾄解空间树的任⼀结点时，先判断该节点是否包含问题的解。

如果不包含，则跳过对以该节点为根的⼦树的搜索，逐层向其它祖先节点回溯。

否则，进⼊该⼦树，继续按照深度优先策略搜索。

回溯法求问题的所有解时，要回溯到根，且根节点的所有⼦树都已被搜索遍才结束。

回溯法求问题的⼀个解时，只要搜索到问题的⼀个解就可结束。

这种以深度优先⽅式系统搜索问题的算法称为回溯法，它是⽤于解组合数⼤的问题。

问题的解空间⽤回溯法解问题时，应明确定义问题的解空间。

问题的解空间⾄少包含问题的⼀个（最优）解。

例如对于有n种可选择物品的0-1背包问题，其解空间由长度为n的0-1向量组成。

该解空间包含对变量的所有可能的0-1赋值。

例如n=3时，其解空间是{(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0),(1,0,1),(1,1,0),(1,1,1)}定义了问题的解空间后，还应该将解空间很好地组织起来，使得能⽤回溯法⽅便地搜索整个解空间。

通常将解空间组织成树或者图的形式。

例如，对于n=3时的0-1背包问题，可⽤⼀颗完全的⼆叉树表⽰其解空间，如下图。

解空间树的第i层到第i+1层边上的标号给出了变量的值。

从树根到叶⼦的任⼀路径表⽰解空间中的⼀个元素。

例如，从根节点到节点H的路径相当与解空间中的元素(1,1,1)。

回溯法的基本思想确定了解空间的组织结构后，回溯法从根节点出发，以深度优先搜索⽅式搜索整个解空间。

回溯法以这种⼯作⽅式递归地在解空间中搜索，直到找到所要求的解或解空间所有解都被遍历过为⽌。

回溯法搜索解空间树时，通常采⽤两种策略避免⽆效搜索，提⾼回溯法的搜索效率。

其⼀是⽤约束函数在当前节点（扩展节点）处剪去不满⾜约束的⼦树；其⼆是⽤限界函数剪去得不到最优解的⼦树。