常微分方程数值解法

高斯-赛德尔迭代法
松弛法
通过迭代更新函数值并逐步放松约束 条件来逼近解，适用于刚性和非刚性 问题。
利用线性组合迭代函数值来逼近解， 具有更高的收敛速度和稳定性。
03
数值解法的稳定性分析
数值解法的稳定性定义
数值解法的稳定性是指当微分方程的初值有微小的扰动时， 其数值解的近似值的变化情况。如果数值解在微小扰动下变 化较小，则称该数值方法是稳定的。
更高的精度和稳定性。
数值逼近法
泰勒级数法
将微分方程的解展开为泰勒级数，通过截断级数来逼 近解。
多项式逼近法
利用多项式来逼近微分方程的解，通过选取合适的基 函数和系数来提高逼近精度。
样条插值法
利用样条函数来逼近微分方程的解，具有更好的光滑 性和连续性。
迭代法
雅可比迭代法
通过迭代更新函数值来逼近微分方程 的解，具有简单易行的优点。
初值和边界条件的处理
根据实际问题，合理设定初值和边界 条件，以获得更准确的数值解。
收敛性和误差分析
对数值解进行收敛性和误差分析，评 估解的精度和稳定性。
数值解法的应用案例分析
人口增长模型
通过数值解法求解人口增长模型，预测未来人口数量，为政策制 定提供依据。
化学反应动力学
利用数值解法研究化学反应的动力学过程，模拟反应过程和结果。
数值分析第九章常微分方 程数值解法
• 引言 • 常微分方程数值解法的基本思想 • 数值解法的稳定性分析 • 数值解法的收敛性和误差分析 • 数值解法的实现和应用案例
01
引言
常微分方程的应用背景
自然科学
描述物理、化学、生物等自然 现象的变化规律。
工程领域
控制系统设计、航天器轨道计 算等。

7
第8页/共105页
➢ 数值积分方法(Euler公式)
设将方程 y=f (x, y)的两端从 xn 到xn+1 求积分, 得
y( xn1) y( xn )
xn1 f ( x, y( x))dx :
xn
xn1 F ( x)dx
xn
用不同的数值积分方法近似上式右端积分, 可以得到计算 y(xn+1)的不同的差分格 式.
h2 2
y''( )
Rn1
:
y( xn1)
yn1
h2 2
y''( )
h2 2
y''( xn ) O(h3 ).
局部截断误差主项
19
第20页/共105页
➢ 向后Euler法的局部截断误差
向后Euler法的计算公式
yn1 yn hf ( xn1, yn1 ), n 0, 1, 2,
定义其局部截断误差为
y 计算 的n递1 推公式，此类计算格式统称为差分格式.
3
第4页/共105页
数值求解一阶常微分方程初值问题
y' f ( x, y), a x b,
y(a)
y0
难点: 如何离散 y ?
➢ 常见离散方法
差商近似导数 数值积分方法 Taylor展开方法
4
第5页/共105页
➢ 差商近似导数(Euler公式)
(0 x 1)
y(0) 1.
解 计算公式为
yn1
yn
hfn
yn
h( yn
2xn ), yn
y0 1.0
n 0, 1, 2,
取步长h=0.1, 计算结果见下表
13

常微分方程的数值解法及其应用研究引言：常微分方程是数学中的重要分支，广泛应用于自然科学、工程技术和社会经济等领域。

常微分方程的解析解往往难以获得，因此数值解法的研究成为解决实际问题的有效手段。

本文将介绍常微分方程的数值解法以及其在各个领域的应用。

一、常微分方程的数值解法1. 欧拉方法欧拉方法是最基本的数值解法之一，通过将微分方程中的函数进行逐步的线性近似，得到方程的递推关系，并根据该关系逼近解析解。

欧拉方法具有简单、易于实现的优点，但在稳定性和精度方面存在一定的局限性。

2. 改进的欧拉方法改进的欧拉方法通过使用中点梯形公式，对欧拉方法的误差进行修正，提高了数值解的准确性。

改进的欧拉方法在简单性和准确性方面取得了一定的平衡。

3. 4阶龙格-库塔法4阶龙格-库塔法是一类常用的数值解法，通过计算多个近似解，并按照一定的权重进行加权平均，得到更高精度的数值解。

4阶龙格-库塔法具有高精度和较好的稳定性，被广泛应用于各个领域。

4. 多步法多步法是一类基于历史步长的数值解法，利用之前计算的步长来估计下一个步长的近似值。

常见的多步法包括亚当斯方法和预报校正方法等。

多步法在一定程度上提高了数值解的稳定性和准确性。

5. 常微分方程的辛方法辛方法是一类特殊的数值解法，能够保持微分方程的守恒性质。

辛方法在长时间积分和保持能量守恒方面具有优势，被广泛应用于天体力学和分子动力学等领域。

二、常微分方程数值解法的应用1. 物理科学中的应用常微分方程的数值解法在物理学中有广泛的应用，如天体力学中的行星轨道计算、量子力学中的薛定谔方程求解等。

数值解法处理了复杂的物理现象，为物理学研究提供了可行的途径。

2. 工程技术中的应用常微分方程的数值解法在工程技术中被广泛应用，如电路分析、结构力学、流体力学等。

通过数值解法，可以模拟和分析复杂的工程问题，提供设计和优化方案。

3. 经济学中的应用经济学中的许多问题可以转化为常微分方程的形式，如经济增长模型、市场供需关系等。

h2 h3 y ( xi 1 ) y ( xi h) y ( xi ) hy '( xi ) y ''( xi ) y '''( xi ) 2! 3!
丢掉高阶项，有
y( xi 1 ) y( xi h) y( xi ) hy '( xi ) yi hf ( xi , yi )
| f ( x, y1 ) f ( x, y2 ) | L | y1 y2 | ,
那么模型问题在 [ a, b] 存在唯一解。
Lipschitz 连续： | f ( x, y1 ) f ( x, y2 ) | L | y1 y2 | .
(1) 比连续性强: y1 y2 可推出 f ( x, y1 ) f ( x, y2 ) ; (2) 比连续的 1 阶导弱：具有连续的 1 阶导，则
f | f ( x, y1 ) f ( x, y2 ) || ( ) || y1 y2 | L | y1 y2 | . y
常微分方程数值解法
目标：计算出解析解 y ( x) 在一系列节点 a x0 x1 xn1 xn b 处的近似值 yi y( xi ) ，即所谓的数值解。节点间距 hi xi 1 xi ，一般 取为等距节点。
常微分方程初值问题的数值解法一般分为两大类： (1)单步法：在计算 yn 1 时，只用到前一步的值，即用到 xn1 , xn , yn ，则给定初
值之后，就可逐步计算。例如 Euler 法、向后欧拉法、梯形公式、龙格-库塔法；
(2) 多步法： 这 类 方 法 在 计算 yn 1 时 ， 除 了 用 到 xn1 , xn , yn 外 ， 还 要 用到

介绍常微分方程数值解法常微分方程（ordinary differential equations，ODE）可用于描述许多日常存在的物理系统。

处理ODE问题常常被称为数值求解法，这指的是找到概括ODE或者其他适用于数学模型的解决方案来模括这些ODE。

这种解决方案可能在一系列不同方案中发挥重要作用，以此来提供更好的解释和预测。

常微分方程与几何图形更为相关，它利用二维或者三维空间中曲线的绘制以及分析。

通过引入一些不同的方法，可以对不同的常微分方程中的量进行描述，使得可以通过数值方法的解析来进行研究。

数值解法可能是时间消耗较多的，但有助于验证几何图形中的某些过程，以此帮助揭示数学模型。

四种常见的常微分方程数值解法四种常见的常微分方程数值解法是：前向差分法、向后差分法、中点法和全分方法。

•前向差分法：前向差分法的基本概念是利用ODE的特定解来表达时间步的影响。

这是一种基本的数值法，可以在ODE中确定任意位置的点作为终点。

在这里，任何这样的点都可以表示为ODE右边的时间步。

•向后差分法：它是反过来基于前向差分法。

它要求对ODE中的时间步进行逆向推导，以获得某一特定点的解。

向后差分法要求推导反向解中点，以便可以从每一步中获取该点的解。

•中点法：这是一种非常基本的数值解法，可以用来求解ODE中的某一步的解，但不具有直观的方法解释。

主要的思想是在每一次时间步中通过求出ODE的中点来寻找解。

•全分方法：这是一种更复杂的数值解法，它要求将ODE中的每一步解细分并解决。

与前面提到的三种解法不同，它首先要求将ODE分解成若干离散区间，然后计算每一段区间中的点。

这种解法可以更准确地进行处理，但时间消耗较多，因此比较少被使用。

优化方案在需要解决常微分方程时，为了得到最佳的结果，有必要考虑一些优化措施。

•首先，应考虑将一个复杂的ODE拆分成一些更易解决的问题。

这样做的结果是，预见到解决此ODR的总耗时将会降低。

•其次，为了加快计算速度，可以考虑使用预解算法。

常微分方程的数值解法1. 引言常微分方程是自变量只有一个的微分方程，广泛应用于自然科学、工程技术和社会科学等领域。

由于常微分方程的解析解不易得到或难以求得，数值解法成为解决常微分方程问题的重要手段之一。

本文将介绍几种常用的常微分方程的数值解法。

2. 欧拉方法欧拉方法是最简单的一种数值解法，其具体步骤如下：- 将自变量的区间等分为n个子区间；- 在每个子区间上假设解函数为线性函数，即通过给定的初始条件在每个子区间上构造切线；- 使用切线的斜率（即导数）逼近每个子区间上的解函数，并将其作为下一个子区间的初始条件；- 重复上述过程直至达到所需的精度。

3. 改进的欧拉方法改进的欧拉方法是对欧拉方法的一种改进，主要思想是利用两个切线的斜率的平均值来逼近每个子区间上的解函数。

具体步骤如下： - 将自变量的区间等分为n个子区间；- 在每个子区间上构造两个切线，分别通过给定的初始条件和通过欧拉方法得到的下一个初始条件；- 取两个切线的斜率的平均值，将其作为该子区间上解函数的斜率，并计算下一个子区间的初始条件；- 重复上述过程直至达到所需的精度。

4. 二阶龙格-库塔方法二阶龙格-库塔方法是一种更为精确的数值解法，其基本思想是通过近似计算解函数在每个子区间上的平均斜率。

具体步骤如下： - 将自变量的区间等分为n个子区间；- 在每个子区间上计算解函数的斜率，并以该斜率的平均值近似表示该子区间上解函数的斜率；- 利用该斜率近似值计算下一个子区间的初始条件，并进一步逼近解函数；- 重复上述过程直至达到所需的精度。

5. 龙格-库塔法（四阶）龙格-库塔法是目前常用的数值解法之一，其精度较高。

四阶龙格-库塔法是其中较为常用的一种，其具体步骤如下：- 将自变量的区间等分为n个子区间；- 在每个子区间上进行多次迭代计算，得到该子区间上解函数的近似值；- 利用近似值计算每个子区间上的斜率，并以其加权平均值逼近解函数的斜率；- 计算下一个子区间的初始条件，并进一步逼近解函数；- 重复上述过程直至达到所需的精度。

n

h
2
所以,只要令
2
f
xn
f n f yn O ( h )
3
1+2=1, 2=1/2, 2=1/2
(7.4)
若取=1,则得1=2=1/2,=1,此时公式(8.3)就是改进的 Euler公式; 若取1=0,则得2=1,==1/2,公式(8.3)为
y n 1 y n hK 2 K 1 f (xn , yn ) K f ( x 1 h, y 2 n n 2
……
……
f ( x n P h, y n h
i 1
p 1
pi
Ki)
其中i,i,ij为待定参数. 若此公式的局部截断误差为
O(h3),称此公式为p阶Runge-kutta方法,简称p阶R-K方法.
对于p=2的情形, 应有
K 1 f (xn , yn ) K f ( x h , y hK ) n n 1 2
显式表示出来,称这类差分公式为显式公式,而梯形公式中,
需要更多的计算量,但其计算稳定性较好.
§2 改进的Euler方法和Taylor展开方法
§2.1 改进的Euler方法 从数值积分的角度来看,梯形公式
y0
y n 1 y n h 2 , n 0 ,1, 2 , N 1 [ f ( x n , y n ) f ( x n 1 , y n 1 )]
2
1
分别取步长h=0.2 ,0.1 ,0.05,计算结果如下
h
h=0.2
h=0.1
h=0.05
xn 0.00 0.40 0.80 1.20 1.60 2.00 0.00 0.40 0.80 1.20 1.60 2.00 0.00 0.40 0.80 1.20 1.60 2.00

ρ ρ
n+1 n
≤1
三、梯形公式
由 分 径 y ( xn+1) = y ( xn) + 积 途 ： xn+1
∫
f ( x, y)dt
（
积分 梯形 式 且令：yn+1 = y( xn+1), yn = y( xn) 用 公 ， h 则 yn+1 = yn + ( f (xn , yn) + f (xn+1 , yn+1)) 得： 2
第九章 常微分方程数值解法
§1 、引言
一 常 分 程 初 问 : 阶 微 方 的 值 题 dy dx = f (x, y) y( x0) = y0
'
a ≤ x ≤b
2 y 例 : 方 程 xy -2 y = 4 x ⇒ y = + 4 x 2 y 令 ：f ( x , y ) = + 4 且 给 出 初 值 y (1 )= -3 x 就 得 到 一 阶 常 微 分 方 程 的 初 值 问 题 ： 2 y dy = f (x, y) = + 4 dx x y(1) = − 3
n n n n n 2 // n n+1
~
y
n+1
= yn + hf ( xn, yn ) = y(xn) + hf
n+1
~
y
n+1
( x , y( x ))
n n
则 T = y( x ) − = h y (ξ ) x y 2 ~
// n+1 n+1
2
n
< ξ < xn+1
令

2hyxn
2h3 3!
y
yxn1
yxn1 2hyxn
h3 3
y ②
将①、②两式相减：
y
xn1
h3 yn1 3
y
——两步法局部截断误差
18
第19页/共24页
2024年8月7日
（2）梯形公式
yn1
yn
h 2
f
xn , yn
f
xn1 , yn1
yxn
hf
2
xn ,
yn1 yxn1 2hyxn ①
2024年8月7日
17
第18页/共24页
2024年8月7日
将函数用泰勒级数展开：（ h 较小， 相差不大）
yxn1
yxn
h 1!
yxn
h2 2!
yxn
h3 3!
y
yxn1
yxn
h
1!
yxn
h2
2!
yxn
h3
3!
y
yxn1
yxn1
yxn
f
xn1 , yxn1
yn1
yxn
h 2
y
xn
yxn1 ①
将函数用泰勒级数展开：
yxn1
yxn
h 1!
yxn
h2 2!
yxn
h3 3!
y ②
yxn1
yxn
h 1!
yxn
h2 2!
y ③
（ h 较小， 相差不大）
19
第20页/共24页
2024年8月7日
①、②两式相减，并代入③式：
（图示表示梯形法计算结果）

常微分方程组数值解法一、引言常微分方程组是数学中的一个重要分支，它在物理、工程、生物等领域都有广泛应用。

对于一些复杂的常微分方程组，往往难以通过解析方法求解，这时候数值解法就显得尤为重要。

本文将介绍常微分方程组数值解法的相关内容。

二、数值解法的基本思想1.欧拉法欧拉法是最基础的数值解法之一，它的思想是将时间连续化，将微分方程转化为差分方程。

对于一个一阶常微分方程y'=f(x,y)，其欧拉公式为：y_{n+1}=y_n+hf(x_n,y_n)其中h为步长，x_n和y_n为第n个时间点上x和y的取值。

2.改进欧拉法改进欧拉法是对欧拉法的改良，其公式如下：y_{n+1}=y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},y_n+hf(x_n,y_n))] 3.四阶龙格-库塔方法四阶龙格-库塔方法是目前最常用的数值解法之一。

其公式如下：k_1=f(x_n,y_n)k_2=f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_1)k_3=f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_2)k_4=f(x_n+h,y_n+hk_3)y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)其中，k_i为中间变量。

三、常微分方程组的数值解法1.欧拉法对于一个二阶常微分方程组：\begin{cases} y'_1=f_1(x,y_1,y_2) \\ y'_2=f_2(x,y_1,y_2)\end{cases}其欧拉公式为：\begin{cases} y_{n+1,1}=y_{n,1}+hf_1(x_n,y_{n,1},y_{n,2}) \\y_{n+1,2}=y_{n,2}+hf_2(x_n,y_{n,1},y_{n,2}) \end{cases}其中，x_n和y_{n,i}(i=1, 2)为第n个时间点上x和y_i的取值。

欧拉方法
总结词
欧拉方法是常微分方程数值解法中最基础的方法之一，其基本思想是通过离散化时间点上的函数值来 逼近微分方程的解。
详细描述
欧拉方法基于微分方程的局部线性化，通过在时间点上逐步逼近微分方程的解，得到一系列离散点上 的近似值。该方法简单易行，但精度较低，适用于求解初值问题。
龙格-库塔方法
总结词
影响
数值解法的稳定性对计算结果的精度和可靠 性有重要影响。
判断方法
通过分析数值解法的迭代公式或离散化方法， 判断其是否具有稳定性和收敛性。
数值解法的收敛性
定义
数值解法的收敛性是指随着迭代次数的增加， 数值解逐渐接近于真实解的性质。
影响
数值解法的收敛性决定了计算结果的精度和 计算效率。
分类
根据收敛速度的快慢，可以分为线性收敛和 超线性收敛等。
判断方法
通过分析数值解法的迭代公式或离散化方法， 判断其是否具有收敛性。
误差分析
定义
误差分析是指对数值解法计算过程中 产生的误差进行定量分析和估计的过 程。
分类
误差可以分为舍入误差、截断误差和 初始误差等。
影响
误差分析对于提高计算精度和改进数 值解法具有重要意义。
分析方法
通过建立误差传递公式或误差估计公 式，对误差进行定量分析和估计。
生物学
生态学、生物种群动态和流行病传播 等问题可以通过常微分方程进行建模
和求解。
化学工程
化学反应动力学、化学工程流程模拟 等领域的问题可以通过常微分方程进 行描述和求解。
经济学
经济系统动态、金融市场模拟和预测 等问题可以通过常微分方程进行建模 和求解。
02 常微分方程的基本概念
常微分方程的定义

用分段的折线逼近函数,此为 “折线法”而非“切线法”， 除第一个点是曲线上的切线，
其它都不是。
2、Euler方法的误差估计
1)局部截断误差。 在一步中产生的误差而非累积误差：
~
T x y y

n1
n1
n1
其中
~
y
是当
y
n

y(
x
)
n
（精确解！）时
n1
由Euler法求出的值，即y 无误差！ n
T x y h y 则
y
n1
~
2

n1
n1 2
//
x x
n
n1
令 M 2 max y// (x) , y(x) 充分光滑，则： a xb
T M h h n 1
2
O 2 22
3、 总体方法误差(1)
递推方法：从任意两相邻步的总体误差关系
第九章 常微分方程数值解法
§1 、引言
一阶常微分方程的初值问题:
dy

dx

f (x, y)
a xb

y
(
x
)
0

y 0
例: 方程 xy' -2y=4x y' = 2 y 4 x
令：f(x,y)= 2 y 4 且给出初值 y(1)=-3 x
就得到一阶常微分方程的初值问题：
n
n
n1
y y x y hf ( , ) n 0, 1, 2,
n1
n
n
n
Taylor展开法不仅可得到求数值解的公式，且容易估计
截断误差。
§2 尤拉（Eular)方法

常微分方程的数值解法常微分方程是研究变量的变化率与其当前状态之间的关系的数学分支。

它在物理、工程、经济等领域有着广泛的应用。

解常微分方程的精确解往往十分困难甚至不可得，因此数值解法在实际问题中起到了重要的作用。

本文将介绍常见的常微分方程的数值解法，并比较其优缺点。

1. 欧拉方法欧拉方法是最简单的数值解法之一。

它基于近似替代的思想，将微分方程中的导数用差商近似表示。

具体步骤如下：（1）确定初始条件，即问题的初值。

（2）选择相应的步长h。

（3）根据微分方程的定义使用近似来计算下一个点的值。

欧拉方法的计算简单，但是由于误差累积，精度较低。

2. 改进欧拉方法为了提高欧拉方法的精度，改进欧拉方法应运而生。

改进欧拉方法通过使用两个点的斜率的平均值来计算下一个点的值。

具体步骤如下：（1）确定初始条件，即问题的初值。

（2）选择相应的步长h。

（3）根据微分方程的定义使用近似来计算下一个点的值。

改进欧拉方法相较于欧拉方法而言，精度更高。

3. 龙格-库塔法龙格-库塔法（Runge-Kutta）是常微分方程数值解法中最常用的方法之一。

它通过迭代逼近精确解，并在每一步中计算出多个斜率的加权平均值。

具体步骤如下：（1）确定初始条件，即问题的初值。

（2）选择相应的步长h。

（3）计算各阶导数的导数值。

（4）根据权重系数计算下一个点的值。

与欧拉方法和改进欧拉方法相比，龙格-库塔法的精度更高，但计算量也更大。

4. 亚当斯法亚当斯法（Adams）是一种多步法，它利用之前的解来近似下一个点的值。

具体步骤如下：（1）确定初始条件，即问题的初值。

（2）选择相应的步长h。

（3）通过隐式或显式的方式计算下一个点的值。

亚当斯法可以提高精度，并且比龙格-库塔法更加高效。

5. 多步法和多级法除了亚当斯法，还有其他的多步法和多级法可以用于解常微分方程。

多步法通过利用多个点的值来逼近解，从而提高精度。

而多级法则将步长进行分割，分别计算每个子问题的解，再进行组合得到整体解。

第8章常微分方程的数值解法8.4单步法的收敛性与稳定性8.4.1相容性与收敛性上面所介绍的方法都是用离散化的方法，将微分方程初值问题化为差分方程初值问题求解的.这些转化是否合理？即当h →∞时，差分方程是否能无限逼近微分方程，差分方程的解n y 是否能无限逼近微分方程初值问题的准确解()n y x ，这就是相容性与收敛性问题.用单步法(8.3.14)求解初值问题(8.1.1)，即用差分方程初值问题100(,,)()n n n n y y h x y h y x y ϕ+=+⎧⎨=⎩(8.4.1)的解作为问题(8.1.1)的近似解，如果近似是合理的，则应有()()(,(),)0 (0)y x h y x x y x h h hϕ+--→→(8.4.2)其中()y x 为问题(8.1.1)的精确解.因为0()()lim ()(,)h y x h y x y x f x y h→+-'==故由(8.4.2)得lim (,,)(,)h x y h f x y ϕ→=如果增量函数(,(),)x y x h ϕ关于h 连续，则有(,,0)(,)x y f x y ϕ=(8.4.3)定义8.3如果单步法的增量函数(,,)x y h ϕ满足条件(8.4.3)，则称单步法(8.3.14)与初值问题(8.1.1)相容.通常称(8.4.3)为单步法的相容条件.满足相容条件(8.4.3)是可以用单步法求解初值问题(8.1.1)的必要条件.容易验证欧拉法和改进欧拉法均满足相容性条件.一般地，如果单步法有p 阶精度（1p ≥），则其局部截断误差为[]1()()(,(),)()p y x h y x h x y x h O h ϕ++-+=上式两端同除以h ，得()()(,,)()p y x h y x x y h O h hϕ+--=令0h →，如果(,(),)x y x h ϕ连续，则有()(,,0)0y x x y ϕ'-=所以1p ≥的单步法均与问题(8.1.1)相容.由此即得各阶龙格－库塔法与初值问题(8.1.1)相容.定义8.4一种数值方法称为是收敛的，如果对于任意初值0y 及任意固定的(,]x a b ∈，都有lim () ()n h y y x x a nh →==+其中()y x 为初值问题(8.1.1)的精确解.如果我们取消局部化假定，使用某单步法公式，从0x 出发，一步一步地推算到1n x +处的近似值1n y +.若不计各步的舍入误差，而每一步都有局部截断误差，这些局部截断误差的积累就是整体截断误差.定义8.5称111()n n n e y x y +++=-为某数值方法的整体截断误差.其中()y x 为初值问题(8.1.1)的精确解，1n y +为不计舍入误差时用某数值方法从0x 开始，逐步得到的在1n x +处的近似值（不考虑舍入误差的情况下，局部截断误差的积累）.定理8.1设单步法(8.3.14)具有p 阶精度，其增量函数(,,)x y h ϕ关于y 满足利普希茨条件，问题(8.1.1)的初值是精确的，即00()y x y =，则单步法的整体截断误差为111()()p n n n e y x y O h +++=-=证明由已知，(,,)x y h ϕ关于y 满足利普希茨条件，故存在0L >，使得对任意的12,y y 及[,]x a b ∈，00h h <≤，都有1212(,,)(,,)x y h x y h L y y ϕϕ-≤-记1()(,(),)n n n n y y x h x y x h ϕ+=+，因为单步法具有p 阶精度，故存在0M >，使得1111()p n n n R y x y Mh ++++=-≤从而有111111111()()()(,(),)(,,)()(,(),)(,,)n n n n n n n p n n n n n n p n n n n n n e y x y y x y y y Mh y x h x y x h y h x y h Mh y x y h x y x h x y h ϕϕϕϕ+++++++++=-≤-+-≤++--≤+-+-1(1)p nMh hL e +≤++反复递推得11111101110(1)(1)1(1)(1)(1)(1)1(1)p p n n n p n n p n e Mh hL Mh hL e hL hL Mh hL e hL Mh hL e hL+++-+++++⎡⎤≤++++⎣⎦⎡⎤≤+++++++⎣⎦+-≤++因为00()y x y =，即00e =，又(1)n h b a +≤-，于是ln(1)1()(1)(1)b a b a hL n L b a h h hL hL e e --++-+≤+=≤所以()11()p L b a p n M e h e O h L -+⎡⎤≤-=⎣⎦推论设单步法具有p (1p ≥)阶精度，增量函数(,,)x y h ϕ在区域G ：, , 0a x b y h h ≤≤-∞<<+∞≤≤上连续，且关于y 满足利普希茨条件，则单步法是收敛的.当(,)f x y 在区域:,D a x b y ≤≤-∞<<+∞上连续，且关于y 满足利普希茨条件时，改进欧拉法，各阶龙格－库塔法的增量函数(,,)x y h ϕ在区域G 上连续，且关于y 满足利普希茨条件，因而它们都是收敛的.关于单步法收敛的一般结果是：定理8.2设增量函数(,,)x y h ϕ在区域G 上连续，且关于y 满足利普希茨条件，则单步法收敛的充分必要条件是相容性条件(8.4.3).8.4.2稳定性稳定性与收敛性是两个不同的概念，收敛性是在假定每一步计算都准确的前提下，讨论当步长0h →时，方法的整体截断误差是否趋于零的问题.而稳定性则是讨论舍入误差的积累能否对计算结果有严重影响的问题.定义8.6若一种数值方法在节点值n y 上有一个大小为δ的扰动，于以后各节点()m y m n >上产生的偏差均不超过δ，则称该方法是稳定的.我们以欧拉法为例进行讨论.假设由于舍入误差，实际得到的不是n y 而是n n n y y δ=+，其中n δ是误差.由此再计算一步，得到1(,)n n n n y y hf x y +=+把它与不考虑舍入误差的欧拉公式相减，并记111n n n y y δ+++=-，就有[]1(,)(,)1(,)n n n n n n y n nh f x y f x y hf x δδηδ+⎡⎤=+-=+⎣⎦其中y f f y∂=∂.如果满足条件1(,)1y n hf x η+≤，(8.4.4)则从n y 到1n y +的计算，误差是不增的，可以认为计算是稳定的.如果条件(8.4.4)不满足，则每步误差将增大.当0y f >时，显然条件(8.4.4)不可能满足，我们认为问题本身具有先天的不稳定性.当0y f <时，为了满足稳定性要求(8.4.4)，有时h 要很小.一般的，稳定性与方法有关，也与步长h 的大小有关，当然也与方程中的(,)f x y 有关.为简单起见，通常只考虑数值方法用于求解模型方程的稳定性，模型方程为y y λ'=(8.4.5)其中λ为复数.一般的方程可以通过局部线性化转化为模型方程，例如在(,)x y 的邻域(,)(,)(,)()(,)()x y y f x y f x y f x y x x f x y y y '==+-+-+略去高阶项，再作变量替换就得到u u λ'=的形式.对于模型方程(8.4.5)，若Re 0λ>，类似以上分析，可以认为方程是不稳定的.所以我们只考虑Re 0λ<的情形，这时不同的数值方法可能是数值稳定的或者是数值不稳定的.当一个单步法用于试验方程y y λ'=，从n y 计算一步得到1()n n y E h y λ+=(8.4.6)其中()E h λ依赖于所选的方法.因为通过点(,)n n x y 试验方程的解曲线（它满足,()n n y y y x y λ'==）为[]exp ()n n y y x x λ=-，而一个p 阶单步法的局部截断误差在()n n y x y =时有1111()()p n n n T y x y O h ++++=-=，所以有1exp()()()p n n y h E h y O h λλ+-=(8.4.7)这样可以看出()E h λ是h e λ的一个近似值.由(8.4.6)可以看到，若n y 计算中有误差ε，则计算1n y +时将产生误差()E h λε，所以有下面定义.定义8.7如果(8.4.6)式中，()1E h λ<，则称单步法(8.3.14)是绝对稳定的.在复平面上复变量h λ满足()1E h λ<的区域，称为方法(8.3.14)的绝对稳定区域，它与实轴的交称为绝对稳定区间.在上述定义中，规定严格不等式成立，是为了和线性多步法的绝对稳定性定义一致.事实上，()1E h λ=时也可以认为误差不增长.(1)欧拉法的稳定性欧拉法用于模型方程(8.4.5)，得1(1)n n y h y λ+=+，所以有()1E h h λλ=+.所以绝对稳定条件是11h λ+<，它的绝对稳定区域是h λ复平面上以(1,0)-为中心的单位圆，见图8.3.而λ为实数时，绝对稳定区间是(2,0)-.Im()h λRe()h λ2-1-O 图8.3欧拉法的绝对稳定区域(2)梯形公式的稳定性对模型方程，梯形公式的具体表达式为11()2n n n n h y y y y λλ++=++，即11212n nh y y h λλ++=-，所以梯形公式的绝对稳定区域为12112h h λλ+<-.化简得Re()0h λ<，因此梯形公式的绝对稳定区域为h λ平面的左半平面，见图8.4.特别地，当λ为负实数时，对任意的0h >，梯形公式都是稳定的.Im()h λRe()h λO 图8.4梯形公式的绝对稳定区域(3)龙格－库塔法的稳定性与前面的讨论相仿，将龙格－库塔法用于模型方程(8.4.5)，可得二、三、四阶龙格－库塔法的绝对稳定区域分别为211()12h h λλ++<23111()()126h h h λλλ+++<2341111()()()12624h h h h λλλλ++++<当λ为实数时，二、三、四阶显式龙格－库塔法的绝对稳定区域分别为20h λ-<<、2.510h λ-<<、 2.780h λ-<<.例8.5设有初值问题21010101(0)0xy y x x y ⎧'=-≤≤⎪+⎨⎪=⎩用四阶经典龙格－库塔公式求解时，从绝对稳定性考虑，对步长h 有何限制？解对于所给的微分方程有2100,(010)1f x x y xλ∂==-<≤≤∂+在区间[0,10]上，有201010max ||max51t x x λ<<==+由于四阶经典龙格－库塔公式的绝对稳定区间为 2.7850h λ-<<，则步长h 应满足00.557h <<.。

数值分析第九章常微分方程数值解法常微分方程数值解法是数值分析中非常重要的一部分内容。

常微分方程是描述自然现象中动态变化规律的数学模型，解常微分方程可以揭示系统的变化趋势和规律。

然而，大多数常微分方程是无法通过解析方法求出解的，因此需要借助计算机进行数值计算。

数值解常微分方程方法主要包括：Euler方法、改进的Euler方法、四阶Runge-Kutta方法和龙格-库塔方法。

Euler方法是最简单的方法之一，它采用的是一阶Taylor展开式。

将待求的函数值与函数的一阶导数值代入Taylor展开式中，可以得到函数值在下一个时间步长上的近似值。

Euler方法的优点是简单易于实现，但其精度不够高，容易积累误差。

改进的Euler方法是对Euler方法的改进，它通过使用中间点上的导数值来减小误差。

改进的Euler方法的精度相比Euler方法要高一些，但仍然不够高。

四阶Runge-Kutta方法是目前使用较为广泛的数值解常微分方程的方法之一、它通过计算不同时间点上的斜率来估计函数值，在多个时间点上计算斜率的平均值来提高精度。

四阶Runge-Kutta方法的精度比Euler方法和改进的Euler方法要高，但计算量也相对较大。

龙格-库塔方法是数值解常微分方程中最常用的方法之一、它是四阶Runge-Kutta方法的延伸，通过计算不同时间点上的斜率来估计函数值，然后利用这些估计值计算更准确的斜率，在不同步长上进行迭代计算，直到满足所需精度。

龙格-库塔方法的精度比四阶Runge-Kutta方法要高，但计算量也相对较大。

除了以上几种方法外，还有一些其他数值解常微分方程的方法，如Adams法、Gear法等。

这些方法在不同场景下有着不同的适用性和优劣势。

总结起来，数值解常微分方程方法是研究常微分方程数值计算中的重要内容。

不同的方法有着不同的精度和计算量，可以根据具体问题的特点选择合适的方法进行数值计算。

然而，需要注意的是，数值解只是在给定的步长下对函数的近似值，可能会引入误差。

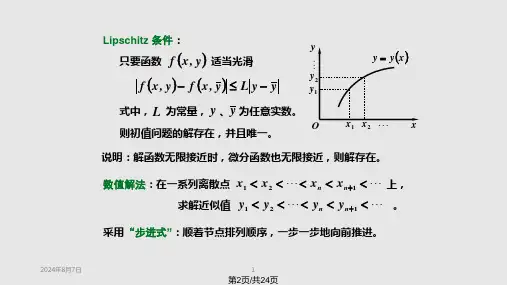
第八章 常微分方程的数值解法一．内容要点考虑一阶常微分方程初值问题:⎪⎩⎪⎨⎧==00)(),(y x y y x f dx dy微分方程的数值解：设微分方程的解y (x )的存在区间是[a,b ]，在[a,b ]内取一系列节点a= x 0< x 1<…< x n =b ,其中h k =x k+1-x k ；(一般采用等距节点，h=(b-a)/n 称为步长)。

在每个节点x k 求解函数y(x)的近似值:y k ≈y(x k )，这样y 0 , y 1 ,...,y n 称为微分方程的数值解。

用数值方法，求得f(x k )的近似值y k ，再用插值或拟合方法就求得y(x)的近似函数。

(一)常微分方程处置问题解得存在唯一性定理对于常微分方程初值问题:⎪⎩⎪⎨⎧==00)(),(y x y y x f dx dy如果：(1) 在B y y A x x 00≤-≤≤,的矩形内),(y x f 是一个二元连续函数。

(2) ),(y x f 对于y 满足利普希茨条件，即2121y y L y x f y x f -≤-),(),(则在C x x 0≤≤上方程⎪⎩⎪⎨⎧==00)(),(y x y y x f dxdy的解存在且唯一，这里C=min((A-x 0),x 0+B/L),L 是利普希茨常数。

定义：任何一个一步方法可以写为),,(h y x h y y k k k 1k Φ+=+，其中),,(h y x k k Φ称为算法的增量函数。

收敛性定理：若一步方法满足： (1)是p 解的.(2) 增量函数),,(h y x k k Φ对于y 满足利普希茨条件.(3) 初始值y 0是精确的。

则),()()(p h O x y kh y =-kh =x -x 0,也就是有0x y y lim k x x kh 0h 0=--=→)((一)、主要算法 1．局部截断误差局部截断误差：当y(x k )是精确解时，由y(x k )按照数值方法计算出来的1~+k y 的误差y (x k+1)- 1~+k y 称为局部截断误差。

常微分方程数值解法常微分方程是研究函数的导数与自变量之间的关系的数学分支，广泛应用于物理、工程、生物等领域的建模与分析。

在实际问题中，我们常常遇到无法通过解析方法求得精确解的常微分方程，因此需要利用数值解法进行求解。

本文将介绍几种常用的常微分方程数值解法。

一、欧拉方法(Euler's Method)欧拉方法是最基本的数值解法之一。

它的思想是将微分方程转化为差分方程，通过逐步逼近解的方式求得数值解。

具体步骤如下：1. 将微分方程转化为差分方程：根据微分方程的定义，可以得到差分方程形式。

2. 选择步长：将自变量范围进行离散化，确定步长h。

3. 迭代计算：根据差分方程递推公式，利用前一步的数值解计算后一步的数值解。

二、改进的欧拉方法(Improved Euler's Method)改进的欧拉方法通过使用欧拉方法中的斜率来进行更准确的数值计算。

具体步骤如下：1. 计算欧拉方法的斜率：根据当前节点的数值解计算斜率。

2. 根据斜率计算改进的数值解：将得到的斜率代入欧拉方法的递推公式中，计算改进的数值解。

三、龙格-库塔方法(Runge-Kutta Method)龙格-库塔方法是一类常微分方程数值解法，其中最著名的是四阶龙格-库塔方法。

它通过计算各阶导数的加权平均值来逼近解，在精度和稳定性方面相对较高。

具体步骤如下：1. 计算每一步的斜率：根据当前节点的数值解计算每一步的斜率。

2. 计算权重：根据斜率计算各个权重。

3. 计算下一步的数值解：根据计算得到的权重，将其代入龙格-库塔方法的递推公式中，计算下一步的数值解。

四、多步法(多步差分法)多步法是需要利用多个前面节点的数值解来计算当前节点的数值解的数值方法。

常见的多步法有Adams-Bashforth法和Adams-Moulton法。

具体步骤如下：1. 选择初始值：根据差分方程的初始条件，确定初始值。

2. 迭代计算：根据递推公式，利用前面节点的数值解计算当前节点的数值解。