离散数学 群与环习题及解答
- 格式:doc
- 大小:66.50 KB
- 文档页数:10

离散数学课后习题及答案离散数学是计算机科学与数学的重要基础课程之一,它涵盖了很多重要的概念和理论。
为了更好地掌握离散数学的知识,课后习题是必不可少的一部分。
本文将介绍一些常见的离散数学课后习题,并提供相应的答案,希望对读者有所帮助。
一、集合论1. 设A={1,2,3},B={2,3,4},求A∪B和A∩B的结果。
答案:A∪B={1,2,3,4},A∩B={2,3}2. 设A={1,2,3},B={2,3,4},C={3,4,5},求(A∪B)∩C的结果。
答案:(A∪B)∩C={3,4}二、逻辑与命题1. 判断下列命题的真假:a) 若2+2=5,则地球是平的。
b) 若今天下雨,则我会带伞。
c) 若x>0,则x^2>0。
答案:a)假,b)真,c)真。
2. 用真值表验证下列命题的等价性:a) p∧(q∨r) ≡ (p∧q)∨(p∧r)b) p→q ≡ ¬p∨q答案:a)等价,b)等价。
三、关系与函数1. 给定关系R={(1,2),(2,3),(3,4)},求R的逆关系R^-1。
答案:R^-1={(2,1),(3,2),(4,3)}2. 设函数f(x)=x^2,g(x)=2x+1,求复合函数f(g(x))的表达式。
答案:f(g(x))=(2x+1)^2=4x^2+4x+1四、图论1. 给定图G,其邻接矩阵为:0 1 11 0 11 1 0求图G的度数序列。
答案:度数序列为(2,2,2)2. 判断下列图是否为连通图:a) G1的邻接矩阵为:0 1 11 0 01 0 0b) G2的邻接矩阵为:0 1 01 0 10 1 0答案:a)不是连通图,b)是连通图。
五、组合数学1. 从10个不同的球中,任选3个,求共有多少种选法。
答案:C(10,3)=120种选法。
2. 求下列排列的循环节:a) (123)(45)(67)b) (12)(34)(56)(78)答案:a)循环节为(123)(45)(67),b)循环节为(12)(34)(56)(78)。

离散数学习题答案习题一1、利用逻辑联结词把下列命题翻译成符号逻辑形式(1)他既是本片的编剧,又是导演--- P∧ Q(2)银行利率一降低,股价随之上扬--- P→ Q(3)尽管银行利率降低,股价却没有上扬--- P∧ Q(4)占据空间的、有质量而且不断变化的对象称为物质--- M ←→<S∧P∧T> (5)他今天不是乘火车去北京,就是随旅行团去了九寨沟 --- P▽ Q(6)小张身体单薄,但是极少生病,并且头脑好使--- P∧ Q ∧ R(7)不识庐山真面目,只缘身在此山中--- P→ Q〔解释:因为身在此山中,所以不识庐山真面目(8)两个三角形相似,当且仅当他们的对应角相等或者对应边成比例--- S ←→<E∨T>(9)如果一个整数能被6整除,那么它就能被2和3整除。
如果一个整数能被3整除,那么它的各位数字之和也能被3整除解:设 P –一个整数能被6整除Q –一个整数能被2整除 R –一个整数能被3整除S –一个整数各位数字之和能被3整除翻译为:〔P→〔Q ∧ R∧〔R→ S2、判别下面各语句是否命题,如果是命题,说出它的真值〔1BASIC语言是最完美的程序设计语言--- Y,T/F〔2这件事大概是小王干的--- N〔3x2 = 64 --- N〔4可导的实函数都是连续函数--- Y,T/F〔5我们要发扬连续作战的作风,再接再厉,争取更大的胜利--- N〔6客观规律是不以人们意志为转移的--- Y,T〔7到2020年,中国的国民生产总值将赶上和超过美国--- Y,N/A〔8凡事都有例外--- Y,F3、构造下列公式的真值表,并由此判别哪些公式是永真式、矛盾式或可满足式〔1〔P∨〔~P∧ Q→ Q〔2~〔4表略:〔2可满足式、〔3永真式、〔4可满足式4、利用真值表方法验证下列各式为永真式〔1~〔8略5、证明下列各等价式〔3P→〔Q∨ R⇔〔P→ Q∨〔P→ R证明:左式⇔~P∨Q∨ R⇔~P∨Q∨~P∨ R⇔〔~P∨Q∨〔~P∨ R⇔〔P→ Q∨〔P→ R⇔右式〔4〔P∧ Q∨〔R∧ Q∨〔R∧ P⇔〔P∨ Q∧〔R∨ Q∧〔R∨ P证明:左式⇔<〔P∨R∧ Q∨〔R∧ P⇔<〔P∨R∨R>>∧<〔P∨R∨P>>∧〔Q∨R∧〔Q∨P⇔〔P∨ Q∧〔R∨ Q∧〔R∨ P⇔右式6、如果P∨ Q ⇔ Q∨R,能否断定 P ⇔ R ?如果P∧ Q ⇔ Q∧R,能否断定 P ⇔ R?如果~P ⇔~R,能否断定 P ⇔ R?解:〔1如果P∨ Q ⇔ Q∨R,不能判断P ⇔ R,因为如果 Q = P∨ R, 那么P∨ Q⇔P ∨P∨ R ⇔ Q∨R,但P可以不等价于R.〔2如果P∧ Q ⇔ Q∧R,不能判断P ⇔ R,因为如果 Q = P∧ R, 那么P∧ Q⇔P ∧P∧ R ⇔ Q∧R,但P可以不等价于R.〔3如果~P ⇔~R,那么有P ⇔ R,因为~P ⇔~R,则~P <-> ~R为永真式,及有P <-> R为永真式,所以P ⇔ R.8、把下列各式用↑等价表示出来〔1<P∧Q>∨~P解:原式⇔ <<P↑Q>↑<P↑Q>>∨<P↑P>⇔ <<<P↑Q>↑<P↑Q>>↑<<P↑Q>↑<P↑Q>>>↑<<P↑P>↑<P↑P>>9、证明:{ ~→}是最小功能完备集合证明: 因为{~,∨}是最小功能完备集合,所以,如果{ ~→}能表示出∨,则其是功能完备集合。

离散数学--第⼗章群,环,域群基本定义设V=<S, ∘ >是代数系统,∘为⼆元运算,如果∘运算是可结合的,则称V为半群(代数系统的前提不要忘,详情可看第九章)如果半群中有单位元==> 含⼳半群|独异点含⼳半群还有逆元==>群通常记作G群中的⼆元运算可交换==>交换群|阿贝尔群Klein四元群特征:1. 满⾜交换律2. 每个元素都是⾃⼰的逆元3. a, b, c中任何两个元素运算结果都等于剩下的第三个元素平凡群只有单位元有限群群中元素有限⼦群如果把群看成集合,⼦群就是⼦集中能满⾜群定义的⼀个集合(可以有多个集合)群是代数系统,最基本要满⾜封闭性!真⼦群就类似真⼦集⼦群判定定理:设G为群,H是G的⾮空⼦集. H是G的⼦群当且仅当∀a,b∈H 有ab−1∈H(感觉很懵逼)证必要性显然. 只证充分性. 因为H⾮空,必存在a∈H. 根据给定条件得aa−1∈H,即e∈H. 任取a∈H, 由e,a∈H 得 ea−1∈H,即a−1∈H. 任取a,b∈H,知b−1∈H. 再利⽤给定条件得a(b−1)−1∈H,即 ab∈H. 综合上述,可知H是G的⼦群.⽣成⼦群:设G为群,a∈G,令H={a k| k∈Z},则H是G的⼦群,称为由 a ⽣成的⼦群,记作<a>例如:Klein四元群 G = {e,a,b,c}的所有⽣成⼦群是:<e>={e}, <a>={e,a}, <b>={e,b}, <c>={e,c}.则偏序集< L(G), ⊆ >称为G的⼦群格就相当于⼦群先变成偏序集然后就满⾜了格的定义?因为是⼦群所以叫⼦群格?右(左)陪集设H是G的⼦群,a∈G.令Ha={ha | h∈H}称Ha是⼦群H在G中的右陪集. 称a为Ha的代表元素.相当于右(左)乘a所得的集合?循环群设G是群,若在G中存在⼀个元素a,使得G中的任意元素都是a的幂,则称该群为循环群,元素a为循环群G的⽣成元。

离散数学练习题(含答案)题目1. 对于集合 $A={1,2,3,...,10}$ 和 $B={n|n是偶数,2<n<8}$,求 $A \cap B$ 的元素。
2. 存在三个可识别的状态A,B,C。
置换群 $S_3$ 作用在状态集上。
定义四个动作:$α: A → C, β: A → B, γ: C→ A, δ: B→ C$。
确定式子,描述 $\{α,β,γ,δ\}$ 的乘法表。
3. 证明 $\forall n \in \mathbb{N}$,合数的个数不小于$n$。
4. 给定一个无向带权图,图中每个节点编号分别是$1,2,...,n$,证明下列结论:a. 如果从节点$i$到$j$只有一条权值最小的路径,则这条路径的任意子路径都是最短路径。
b. 如果从节点$i$到$j$有两条或两条以上权值相等的路径,则从$i$到$j$的最短路径可能不唯一。
答案1. $A \cap B = \{2,4,6\}$。
2. 乘法表:3. 对于任意$n$,我们可以选择$n+1$个连续的自然数$k+1,k+2,...,k+n,k+n+1$中的$n$个数,其中$k \in \mathbb{Z}$。
这$n$个数构成的$n$个正整数均为合数,因为它们都至少有一个小于它自身的因子,所以不是质数。
所以合数的个数不小于任意$n$。
4.a. 根据题意,从$i$到$j$只有一条权值最小的路径,即这条最短路径已被确定。
如果从这条路径中任意取出一段子路径,假设这段子路径不是这个节点到$j$的最短路径,那么存在其他从$i$到$j$的路径比这段子路径更优,又因为这条路径是最短路径,所以这段子路径也一定不优于最短路径,矛盾。
所以从这条路径中任意取出的子路径都是最短路径。
b. 如果从节点$i$到$j$有多条权值相等的路径,则这些路径权值都是最短路径的权值。
因为所有最短路径的权值相等,所以这些路径的权值就是最短路径的权值。
所以从$i$到$j$的最短路径可能不唯一。

【半群】G非空,·为G上的二元代数运算,满足结合律。
【群】(非空,封闭,结合律,单位元,逆元)恰有一个元素1适合1·a=a·1=a,恰有一个元素a-1适合a·a-1=a-1·a=1。
【Abel群/交换群】·适合交换律。
可能不只有两个元素适合x2=1【置换】n元置换的全体作成的集合Sn对置换的乘法作成n 次对称群。
【子群】按照G中的乘法运算·,子集H仍是一个群。
单位子群{1}和G称为平凡子群。
【循环群】G可以由它的某元素a生成,即G=(a)。
a所有幂的集合an,n=0,±1,±2,…做成G的一个子群,由a生成的子群。
若G的元数是一个质数,则G必是循环群。
n元循环群(a)中,元素ak是(a)的生成元的充要条件是(n,k)=1。
共有ϕ(n)个。
【三次对称群】{I(12)(13)(23)(123)(132)}【陪集】a,b∈G,若有h∈H,使得a =bh,则称a合同于b(右模H),a≡b(右mod H)。
H有限,则H的任意右陪集aH的元数皆等于H的元数。
任意两个右陪集aH和bH或者相等或者不相交。
求右陪集:H本身是一个;任取a∉H而求aH又得到一个;任取b∉H∪aH而求bH又一个。
G=H∪aH∪bH∪…【正规子群】G中任意g,gH=Hg。
(H=gHg-1对任意g∈G都成立)Lagrange定理G为有限群,则任意子群H的元数整除群G的元数。
1有限群G的元数除以H的元数所得的商,记为(G:H),叫做H在G中的指数,H的指数也就是H的右(左)陪集的个数。
2设G为有限群,元数为n,对任意a∈G,有an=1。
3若H在G中的指数是2,则H必然是G的正规子群。
证明:此时对H的左陪集aH,右陪集Ha,都是G中元去掉H的所余部分。
故Ha=aH。
4G的任意多个子群的交集是G的子群。
并且,G的任意多个正规子群的交集仍是G的正规子群。
5 H是G的子群。

习题二谓词逻辑一、选择题1、下列哪个式子不是谓词演算的合式公式( )A. (x)(A(x,2)∧B(y))B. (x)(A(x)∧B(x,y))C. ((x)∧(y))→(A(x,y)∧B(x,y))D. (x)(A(x)→B(y))2、设个体域是整数集,则下列命题的真值为真的是()A.∀x∃y (xy=1)B. ∃x∀y(x+y=y)C.∃x∀y(x+y=x)D. ∀x∃y(y=2x)3、设B是不含变元x的公式,谓词公式(x)(A(x)→B)等价于( )A.(x)A(x)→BB. (x)A(x)→BC. A(x)→BD.(x)A(x)→(x)B4、谓词公式(x)(P(x)∨(y)R(y))→Q(x)中的x( ).A.只是约束变元B.只是自由变元C.既非约束变元又非自由变元D.既是约束变元又是自由变元5、谓词公式(x)P(x,y)∧(x)(Q(x,z)→(x)(y)R(x,y,z))中量词x的辖域是().A.(x)Q(x,z)→(x)(y)R(x,y,z))B.Q(x,z)→(y)R(x,y,z)C.Q(x,z)→(x)(y)R(x,y,z)D.Q(x,z)6、在论域D={a,b}中与公式()A(x)等价的不含存在量词的公式是()A. B.C. D.7、设M(x):x是人;F(x):x要吃饭.用谓词公式表达下述命题:所有的人都要吃饭,其中错误的表达式是().A.B.C.D.8、设个体域A={a,b},公式xP(x)∧xS(x)在A中消去量词后应为().A.P(x)∧S(x) B.P(a)∧P(b)∧(S(a)∨S(b))C.P(a)∧S(b) D.P(a)∧P(b)∧S(a)∨S(b)9、按照约束变元的改名规则,∀xP(x) →∃yR(x,y)不可改写成(). A.∀mP(m) →∃yR(x,y) B.∀xP(x) →∃zR(x,z)C.∀xP(x) →∃xR(x,x) D.∀xP(x) →∃nR(x,n)10、∀ x∀y(P(x,y)∧Q(y,z))∧(∃x)p(x,y),下面的描述中错误的是()A.(∀ x)的辖域是(∀ y)(P(x,y)∧Q(y,z))B.z是该谓词公式的约束变元C.(∃ x)的辖域是P(x,y)D. x是该谓词公式的约束变元二、填空题1、设P(x):x非常聪明;Q(x):x非常能干;a:小李;则命题“小李非常聪明和能干”的为谓词表达式为_______.2、使公式(x)( y)(A(x)∧B(y))(x)A(x)∧(y)B(y)成立的条件是______不含有y,______不含有x.3、公式(x)A(x)→B(y)的前束范式为______.4、公式x(P(x)→Q(x,y)∨zR(y, z))→S(x)中的自由变元为________________,约束变元为________________.5、令R(x):x是实数,Q(x):x是有理数。


《离散数学》题库及答案一、选择或填空(数理逻辑部分)1、下列哪些公式为永真蕴含式?()(1)Q=>Q→P(2)Q=>P→Q(3)P=>P→Q(4)P(PQ)=>P答:(1),(4)2、下列公式中哪些是永真式?()(1)(┐PQ)→(Q→R)(2)P→(Q→Q)(3)(PQ)→P(4)P→(PQ)答:(2),(3),(4)3、设有下列公式,请问哪几个是永真蕴涵式()(1)P=>PQ(2)PQ=>P(3)PQ=>PQ(4)P(P→Q)=>Q(5)(P→Q)=>P(6)P(PQ)=>P答:(2),(3),(4),(5),(6)4、公式某((A(某)B(y,某))zC(y,z))D(某)中,自由变元是(变元是()。
答:某,y,某,z5、判断下列语句是不是命题。
若是,给出命题的真值。
((1)北京是中华人民共和国的首都。
(2)陕西师大是一座工厂。
),约束)(3)你喜欢唱歌吗?(4)若7+8>18,则三角形有4条边。
(5)前进!(6)给我一杯水吧!答:(1)是,T(2)是,F(3)不是(4)是,T(5)不是(6)不是6、命题“存在一些人是大学生”的否定是(),而命题“所有的人都是要死的”的否定是()。
答:所有人都不是大学生,有些人不会死7、设P:我生病,Q:我去学校,则下列命题可符号化为()。
(1)只有在生病时,我才不去学校(2)若我生病,则我不去学校(3)当且仅当我生病时,我才不去学校(4)若我不生病,则我一定去学校答:(1)QP(2)PQ(3)PQ(4)PQ8、设个体域为整数集,则下列公式的意义是()。
(1)某y(某+y=0)(2)y某(某+y=0)答:(1)对任一整数某存在整数y满足某+y=0(2)存在整数y对任一整数某满足某+y=09、设全体域D是正整数集合,确定下列命题的真值:(1)某y(某y=y)()(2)某y(某+y=y)()(3)某y(某+y=某)()(4)某y(y=2某)()答:(1)F(2)F(3)F(4)T10、设谓词P(某):某是奇数,Q(某):某是偶数,谓词公式某(P(某)Q(某))在哪个个体域中为真()2(1)自然数(2)实数(3)复数(4)(1)--(3)均成立答:(1)11、命题“2是偶数或-3是负数”的否定是()。
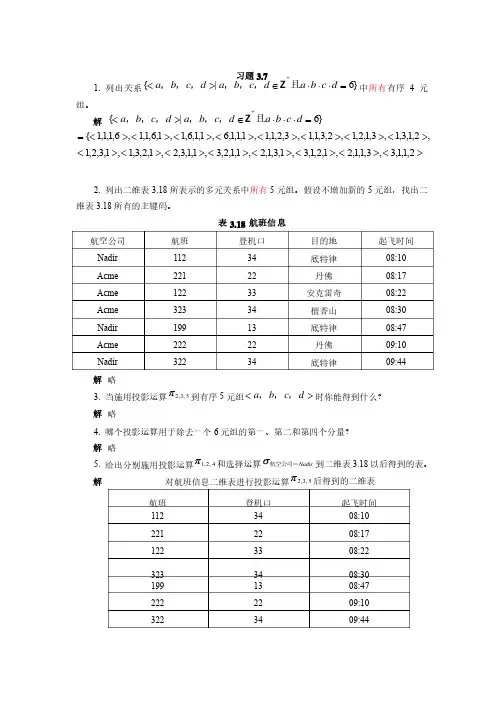
习题3.71. 列出关系}6|{=×××Î><+d c b a d c b a d c b a 且,,,,,,Z 中所有有序4元组。
组。
解}6|{=×××Î><+d c b a d c b a d c b a 且,,,,,,Z ,2,1,3,1,3,1,2,1,2,3,1,1,3,2,1,1,1,1,1,6,1,1,6,1,1,6,1,1,6,1,1,1{><><><><><><><><=><><><><><><><><2,1,1,3,3,1,1,2,1,2,1,3,1,3,1,2,1,1,2,3,1,1,3,2,1,2,3,1,1,3,2,12. 列出二维表3.18所表示的多元关系中所表示的多元关系中所有所有5元组。
假设不增加新的5元组,找出二维表3.18所有的主键码。
所有的主键码。
表3.18 航班信息航空公司航空公司 航班航班 登机口登机口 目的地目的地 起飞时间起飞时间 Nadir 112 34 底特律底特律 08:10 Acme 221 22 丹佛丹佛 08:17 Acme 122 33 安克雷奇安克雷奇 08:22 Acme 323 34 檀香山檀香山 08:30 Nadir 199 13 底特律底特律 08:47 Acme 222 22 丹佛丹佛 09:10 Nadir 32234底特律底特律09:44解 略3. 当施用投影运算5,3,2p 到有序5元组><d c b a ,,,时你能得到什么?时你能得到什么? 解 略4. 哪个投影运算用于除去一个6元组的第一、第二和第四个分量?元组的第一、第二和第四个分量? 解 略5. 给出分别施用投影运算4,2,1p 和选择运算Nadir 航空公司=s 到二维表3.18以后得到的表。
离散数学课后习题答案1. 第一章习题答案1.1 习题一答案1.1.1 习题一.1 答案根据题意,设集合A和B如下:Set A and BSet A and B在此情况下,我们可以得出以下结论:•A的幂集为{ {}, {a}, {b}, {a, b} };•B的幂集为{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} };•A和B的笛卡尔积为{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) }。
因此,习题一.1的答案为:•A的幂集为{ {}, {a}, {b}, {a, b} };•B的幂集为{ {}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3} };•A和B的笛卡尔积为{ (a, 1), (a, 2), (a, 3), (b, 1), (b,2), (b, 3) }。
1.1.2 习题一.2 答案根据题意,集合A和B如下所示:Set A and BSet A and B根据集合的定义,习题一.2要求我们判断以下命题的真假性:a)$A \\cap B = \\{ 2, 3 \\}$b)$\\emptyset \\in B$c)$A \\times B = \\{ (a, 2), (b, 1), (b, 3) \\}$d)$B \\subseteq A$接下来,我们来逐个判断这些命题的真假性。
a)首先计算集合A和B的交集:$A \\cap B = \\{ x\\,|\\, x \\in A \\, \\text{且} \\, x \\in B \\} = \\{ 2, 3 \\}$。
因此,命题a)为真。
b)大家都知道,空集合是任意集合的子集,因此空集合一定属于任意集合的幂集。
根据题意,$\\emptyset \\in B$,因此命题b)为真。
c)计算集合A和B的笛卡尔积:$A \\times B = \\{ (x, y) \\,|\\, x \\in A \\, \\text{且} \\, y \\in B \\} = \\{ (a, 1), (a, 2), (a, 3), (b, 1), (b, 2), (b, 3) \\}$。
离散数学课后习题答案离散数学课后习题答案离散数学是计算机科学中的一门重要课程,它涵盖了诸多数学概念与技巧,为计算机科学的理论基础打下了坚实的基础。
在学习离散数学的过程中,课后习题是巩固知识、提高能力的重要途径。
然而,有时候我们会遇到一些难以解答的问题,需要参考一些答案来进行思考与学习。
本文将为大家提供一些离散数学课后习题的答案,希望能对大家的学习有所帮助。
一、集合论1. 设A={1,2,3},B={2,3,4},求A∪B和A∩B的结果。
答案:A∪B={1,2,3,4},A∩B={2,3}。
2. 证明:任意集合A和B,有(A-B)∪(B-A)=(A∪B)-(A∩B)。
答案:首先,对于任意元素x,如果x属于(A-B)∪(B-A),那么x属于A-B或者x属于B-A。
如果x属于A-B,那么x属于A∪B,但x不属于A∩B;如果x属于B-A,同样有x属于A∪B,但x不属于A∩B。
所以(A-B)∪(B-A)属于(A∪B)-(A∩B)。
另一方面,对于任意元素x,如果x属于(A∪B)-(A∩B),那么x属于A∪B,但x不属于A∩B。
所以x属于A或者x属于B。
如果x属于A,但x不属于B,那么x属于A-B;如果x属于B,但x不属于A,那么x属于B-A。
所以x属于(A-B)∪(B-A)。
所以(A∪B)-(A∩B)属于(A-B)∪(B-A)。
综上所述,(A-B)∪(B-A)=(A∪B)-(A∩B)。
证毕。
二、逻辑与证明1. 证明:如果p为真命题,那么¬p为假命题。
答案:根据命题的定义,命题要么为真,要么为假,不存在其他情况。
所以如果p为真命题,那么¬p为假命题。
2. 证明:对于任意整数n,如果n^2为偶数,则n为偶数。
答案:假设n为奇数,即n=2k+1(k为整数)。
那么n^2=(2k+1)^2=4k^2+4k+1=2(2k^2+2k)+1。
根据偶数的定义,2(2k^2+2k)为偶数,所以n^2为奇数。
§4.6 环与域习题4.61.设。
证明关于复数地加法与乘法构成环,称为高斯整数环。
证明:(1) A 任意二个元素a+bi 与 c+di,都有(a+bi )+(c+di )=a+c +(b+d ) i 仍属于A,满足封闭性要求。
(2)+满足结合律。
(3)有单位元0。
(4)每个元素a+bi 都有逆元-a-bi(5)+满足交换律。
所以<A,+>是交换群。
(6)(a+bi )×(c+di )=ac-bd +(ad+bc ) i 仍属于A((a+bi )×(c+di ))×(w+ti )=( ac-bd )w-(ad+bc )t+(( ac-bd )t+(ad+bc )w) i= acw -bdw -adt-bc t+(act-bd t+adw+bc w) i而(a+bi )×((c+di ))×(w+ti )=(a+bi )×(cw-dt+(ct+dw)i )= acw -bdw -adt-bc t+(act-bd t+adw+bc w) i所以<A, ×>是半群。
(7)二个运算满足分配律。
综上所述,关于复数地加法与乘法构成环。
2.设为实数,称为实数域上地次多项式,令。
证明关于多项式地加法与乘法构成环,称为实数域上地多项式环。
证明:(1) 任意地二个多项式(a 0+a 1x+a 2x 2+….+a n x n )+(b 0+b 1x+b 2x 2+….+b n x n ) = a 0+ b 0+( a 1+ b 1)x+….+ ( a m + b m )x m +….+ a n x n 仍然属于A,满足封闭性要求。
(2) 加法满足结合律与交换律。
(3) 有单位无0。
}1|{2-=∈+=i Z b a bi a A ,,A A n n n a a a x a x a x a a x f ,,,, 212210)(++++=)(x f n })(|)({N n x f x f A n ∈=,次多项式为实数域上的A(4) 每个多顶式a 0+a 1x+a 2x 2+….+a n x n 都有逆元-a 0-a 1x-a 2x 2-….-a n x n 所以关于多项式地加法是交换群。
第六章群与环1. S={2n | n N},加法是S上的二元代数运算吗?乘法呢?解:加法不是S上的二元代数运算,乘法是。
2. 自然数集N 上的二元代数运算* 定义为x * y = x y,* 是否满足结合律?是否满足交换律?解:都不满足。
3. 设* 是集合S上的二元代数运算,且满足结合律,设x,y是S中任意元素,如果x * y = y * x,则x = y。
试证明* 满足等幂律。
证明:由于对S中任意的x,y和z,有x*(y*z)=(x*y)*z,故x*(x*x)=(x*x)*x,于是有x*x=x。
4. 设(G,·)是代数系统,则(G×G,*)是代数系统,这里G×G的运算“*”规定如下:(a,b)*(c,d)=(a·c,b·d),其中,a,b,c,d为G中任意元素。
证明:当(G,·)是半群时,(G×G,*)是半群;当(G,·)有单位元素时,(G×G,*)有单位元素;当(G,·)是群时,(G×G,*)是群;证明:设(G,·)是半群,a,b,c,d,e,f为G中任意元素,若有(a,b),(c,d),(e,f)属于G×G,则有(a,b)*((c,d)*(e,f))=(a,b)*(c·e,d·f)=(a·(c·e),b·(d·f))=((a·c)·e,(b·d)·f))=((a·c),(b·d))*(e,f)=((a,b)*(c,d))*(e,f),这就证明了当(G,·)是半群时,(G×G,*)是半群。
设(G,·)有单位元素1,(a,b)是(G×G,*)中任意元素,则有(a,b)=(a·1,b·1)=(a,b)*(1,1)且(a,b)=(1·a,1·b)=(1,1)*(a,b),故(1,1)就是(G×G,*)的单位元素。
设(G,·)是群,1是群(G,·)的单位元素,则由前面的证明知(1,1)就是(G×G,*)的1且(G×G,*)是半群。
我们来证明(G×G,*)中的任意元素(a,b)有逆元素。
(1,1)=(a·a’,b·b’)=(a,b)*(a’,b’),其中a’和b’分别是a和b在群(G,·)中的逆元素。
同样有(1,1)=(a’·a,b’·b )=(a’,b’ )*(a,b ),这就证明了(a’,b’ )是(a,b)的逆元素,从而说明(G×G,*)是群。
5. 举例说明不要求可除条件而要求消去条件,即要求由aχ=ay可推出χ=y,由χ·a=y·a可推出χ=y,则G不见得是一个群,若G有限怎么样?解:例如,全体自然数在普通乘法下,适合消去律,但不是群。
若G={a1,a2,…a n},用a右乘G中各元素得a1a,a2a,…,a n a必不相同,否则若a i a=a j a (i≠j) ,由消去条件有a i=a j,矛盾。
对任意b∈G,必有a i,使a i a=b,因之方程xa=b有解。
同理可知ay=b 有解。
故G是群。
6. 举例说明定理6.2.2中的(1)ˊ和(2)ˊ分别改成:(1)ˊG中有一个元素1适合1·a=a,(2)ˊ对于任意a有一个a-1适合a·a-1=1,则G不见得是一个群。
解:例如,a bG= a,b是实数。
001 0 a-1 0有左1= 右逆:,但G不是群0 0 0 0因当b≠0时a b 1 0 a 0 a b= ≠。
0 0 0 0 0 0 0 0而不难知道G中无1。
7. 设集合G={a,b,c}上的二元运算表如下:则(G,·)是否为半群?是否为群?为什么?解:由于G非空且对任意的a,b属于G,有a·b 属于G,故(G,·)是代数系统。
又由于·运算满足结合律,故(G,·)是半群,但(G,·)不是群,因为元素c没有逆元素。
8. 计算(1 2 3)(2 3 4)(1 4)(2 3)。
解:(1 2 3)(2 3 4)(1 4)(2 3)=(1 3)(2 4)。
9. 用1,2,…,n代表M中元素。
求证M的任意置换可以表为(1 2),(1 3),…,(1 n)的乘积。
又可表为(1 2),(2 3),…,(n-1 n)的乘积。
解:M的任意置换都可分为对换之乘积,又注意到:(a r a s)=(1 a r)(1 a s)(1 a r),(a r,a s 1),而(1 a r)=(1 2)(2 3)…(a r-2 a r-1)(a r-1 a r)(a r-2 a r-1)…(2 3)(1 2)。
10. 设σ,τ是两个置换。
把τ表示为不相杂的轮换的乘积。
求证στσ-1只要用σ变换τ中文字。
例如σ=(1 2 3)。
τ=(1 2)(3 4)则στσ-1=(2 3)(1 4)。
即按照σ的变法把τ中之1换成2,2换成3,3换成1,即得στσ-1。
证明:若τ=(a 11 a 12 …a 1r )(a 21… a 2s )…(a m1…a mt )a 11 …a 1r a 21…a 2s …a m1…a mt而σ=b 11 …b 1r b 21…b 2s …b m1…b mt取典型元素b jk ,我们有111++−→−−→−−→−-jk jk jk jk b a a b στσ 所以在στσ-1下,b jk →b jk+1。
11. 试证明n 个元素的所有置换作成一个群(通常叫做n 次对称群)。
证明n 个元素的所有偶置换作成群(叫做n 次交代群)。
写出四次交代群中的元素。
n 次交代群的元数为何?证明:只需验证满足群的各条件,略。
注意到偶置换×偶置换=偶置换。
易知偶置换成群。
A 4:(1),(1 2 3),(1 3 2),(1 2 4),(1 4 2),(1 3 4),(1 4 3),(2 3 4),(2 4 3),(1 2)(3 4),(1 3)(2 4),(1 4)(2 3),21n!。
12. (1),(1 2)(3 4),(1 3)(2 4),(1 2)(2 3)四个置换作成一个群叫klein四元群,求证klein四元群是四次对称群的正规子群。
证明:用H记Klein四元群,对任σ∈S4,τ∈H,στσ-1只须用σ变τ中文字,不变轮换长度,结果仍是二对换之积,而这种乘积全在H中,故στσ-1∈H,故σHσ-1⊆H。
13. 写出三次对称群的所有子群。
解:{(1),(1 2),(1 3),(2 3),(1 2 3),(1 3 2)},{(1),(1 2 3),(1 3 2)},{(1),(1 2)},{(1),(1 3)},{(1),(2 3)},{(1)}。
14. 求证G的任意多个子群的交集是G 的子群。
并且,G的任意多个正规子群的交集仍是G的正规子群。
证明:设G的任意多个子群的交为H。
显然1∈H。
故H非空。
若a,b∈H,则a,b∈各子群,故ab-1∈各子群。
ab-1∈H。
从而H是群。
设任意多个正规子群的交为H。
对任g∈G,h∈H,h∈每个正规子群,故ghg-1∈每个正规子群。
ghg-1∈H,所以gHg-1⊆H。
15. 设H是G的子群。
N是G的正规子群。
命HN为H的元素乘N的元素所得的所有元素的集合。
求证HN是G的子群。
证明:显然1∈HN,NH非空。
对任a,b∈HN,可以有:a=h1n1,b= h2n2ab-1=h1n1(h2n2)-1=h1n1n2-1h2-1=h1n1h2'n2'=h1h2'n1'n2'∈HN由此推知HN是G的子群。
16. 求证循环群的子群仍是循环群。
证明:若循环群G由其中元a生成。
H 是G的子群,但不是单位元群。
则H中必含有幂m>0的元a m。
因为若m<0,a m的逆元a-m也在H内,而-m>0。
假定a m是H中的最小正幂,显然H包含a m的任意乘幂。
假如又有H中任意元a S,由S=tm+r。
0≤r<m 知a r=a S-tm=(a S)·(a m)-t是H中元,但m最小。
而0≤r<m,故r=0,因此有a S=(a m)t这表明H中任意元a S也是a m的乘幂,而知H为a m 生成的循环群。
17. 求证若G的元数是一个质数,则G 必是循环群。
证明:设G的元数为质数P,任取G中非单位元a,则(a)是G的一个循环子群,设a的周期为r,则(a)的元数为r,因此r|P。
但P是质数。
显然r≠1,故r=P,所以G=(a),即G是由a生成的循环群。
18. 设G是6元循环群,试找出G的所有生成元,并找出G的所有子群。
解:设G={1,a,a2,a3,a4,a5},容易证明a和a5是G的生成元,因为由第16题知循环群的子群仍是循环群,故用G的每个元素去生成群,即得G的子群,它们是{1},(a3)={1,a3},(a2)={1,a2,a4},以及G本身。
19. 设K和H都是群G的子群,试证明:若H·K是G的子群,则K·H = H·K。
证明:对任意的k·h∈K·H,(k·h)-1=h-1·k-1∈H·K,由于H·K是G的子群,所以((k·h)-1)-1∈H·K,因此K·H⊆H·K。
同样,对于任意的h·k∈H·K,(h·k)-1∈H·K,即存在h1∈H,k1∈K使得(h·k)-1=h1·k1,所以h·k=(h1·k1)-1=k1·h1∈K·H,因此H·K⊆K·H。
由集合论知识知K·H = H·K。