3-模拟退火算法工具箱及应用解析

模拟退火算法解决优化问题模拟退火算法（Simulated Annealing，SA）是一种基于模拟固体退火过程的全局优化算法，被广泛应用于解决各种优化问题。

它的基本思想源于固体退火过程中的原子热运动，通过模拟原子在退火过程中的状态变化，寻找全局最优解。

本文将介绍模拟退火算法的基本原理、算法流程以及在解决优化问题中的应用。

一、模拟退火算法的基本原理模拟退火算法的基本原理来自于固体物理学中的固体退火过程。

在固体退火过程中，固体在高温下加热后逐渐冷却，原子会随着温度的降低而逐渐趋于稳定状态。

类比到优化问题中，算法在搜索过程中允许一定概率接受比当前解更差的解，以避免陷入局部最优解，最终达到全局最优解。

二、模拟退火算法的基本步骤1. 初始化：随机生成初始解，并设定初始温度和终止条件。

2. 选择邻域解：根据当前解生成邻域解。

3. 接受准则：根据一定概率接受邻域解，更新当前解。

4. 降温策略：根据降温策略逐渐降低温度。

5. 终止条件：达到终止条件时停止搜索，输出最优解。

三、模拟退火算法的应用模拟退火算法在解决各种优化问题中都有广泛的应用，包括组合优化、函数优化、图像处理等领域。

下面以组合优化问题为例，介绍模拟退火算法的具体应用。

1. 旅行商问题（TSP）：旅行商问题是一个经典的组合优化问题，目标是找到一条最短路径经过所有城市并回到起点。

模拟退火算法可以通过不断调整路径来寻找最优解。

2. 排课问题：在学校排课过程中，需要合理安排老师和班级的上课时间，避免冲突和空闲时间过长。

模拟退火算法可以优化排课方案，使得课程安排更加合理。

3. 装箱问题：在物流领域中，需要将不同大小的物品合理装箱，使得装箱空间利用率最大化。

模拟退火算法可以帮助优化装箱方案，减少空间浪费。

四、总结模拟退火算法作为一种全局优化算法，具有较好的全局搜索能力和收敛性。

通过模拟退火算法，可以有效解决各种优化问题，得到较优的解决方案。

在实际应用中，可以根据具体问题的特点调整算法参数和策略，进一步提高算法的效率和准确性。

一、概论1.1 问题概述在自然科学以及大多数科学当中和社会生活里经常出现最大或最小的问题，我们从小学开始学习大小比较，一直到高中大学时的最优解问题，都是一种名为最优化问题.最优化问题在大多是领域中都有重要的地位，例如管理科学、计算机科学、图像处理等等需要大量数据的学科中都存在着需要解决的组合优化问题。

用我们比较容易理解的说法就是已知一组固定的函数，令这组函数所对应的函数到达最大或最小值.而我们所想到的最简单的方法便是穷举法，然而这种方式存在这大量的数据计算穷举的缺点。

优化组合问题中的NP问题是一个很麻烦的问题，它解得规模会随着问题的规模增大而增大，求解所需的时间也会随问题的规模增大而成指数级增长，而当规模过大时就会因为时间的限制而失去了可行性。

旅行商问题（TSP）是优化组合问题中最为著名的一个问题，它的特点是容易描述却难于求解.这是一个经典的图论问题，假设有n个城市，用表示.城市之间距离为，i，j=1，2，3，···，n，假设所有城市之间两两连通，要求从一个城市出发，把所有城市都走一遍，而TSP问题就是恰好所有城市都走一遍，而所走路径形成回路且路径最短.将这个问题对应在一个n个顶点的完全图上，假设图为对称图，则要从个可能的解当中找到最小的解，需要的对比则要进行次，当的数值增大时，那么需要的次数也会随之以几何数倍增长，例如每秒运算一亿次的计算机，当需要的时间也只是0.0018秒，当需要的时间却是17年，可当时所需的时间却猛增到年，这个结果是我们所不想看到的。

优化组合问题的目标函数是从组合优化问题的可行解集当中求出最优解。

组合优化问题有三个基本要素：变量，约束和目标函数，在求解过程中选定的基本参数成为标量，对于变量的取值的所有限制称之为约束，表示可行的方案的标准的函数称之为目标函数。

随着问题种类的不同以及问题规模的扩大，要找到一种能够已有限代价来求解最优化问题的通用方法一直都是一个难题，建立用最大的可能性求解全局解一直是一个重要问题。

【文章】matlab带约束模拟退火算法深入探讨和分析matlab带约束模拟退火算法在现代科学和工程领域，优化问题是十分常见的。

而其中，约束优化问题更是一种常见的形式。

为了解决这类问题，人们经过长时间的探索，提出了许多方法，其中模拟退火算法便是一种被广泛应用的优化算法之一。

而在matlab中，带约束的模拟退火算法更是得到了丰富的实现和应用。

本文将从简单到复杂，由浅入深地介绍matlab带约束模拟退火算法，以帮助读者更好地理解和掌握这一优化方法。

1. 什么是模拟退火算法？模拟退火算法是一种基于模拟退火过程的全局优化算法。

它模拟了金属在高温下退火时的物理过程，通过不断降低系统的温度来寻找全局最优解。

在matlab中，模拟退火算法通常通过设置初始温度、终止温度、温度下降率等参数来实现。

2. 为什么需要约束？在实际问题中，许多优化问题都存在着一定的约束条件。

比如工程设计中的材料强度、生产计划中的资源限制等。

如何在求解优化问题时满足这些约束条件便成为了一个重要的问题。

3. matlab带约束模拟退火算法是如何工作的？在matlab中，带约束的模拟退火算法通过引入罚函数、拉格朗日乘子等方法来处理约束条件。

它不仅要寻找全局最优解，还要确保解满足一定的约束条件。

这就需要在温度下降的过程中，不断调整解的位置，以在搜索最优解的同时满足约束条件。

4. 代码实现及应用在matlab中，带约束的模拟退火算法通常通过调用现成的优化工具箱来实现。

我们可以通过设置目标函数、约束条件等参数，来对不同的优化问题进行求解。

可以用该算法来求解工程设计中的优化问题、生产计划中的调度优化问题等。

总结回顾通过本文的介绍，我们对matlab带约束模拟退火算法有了一个较为全面的了解。

我们知道了模拟退火算法是如何工作的，以及在matlab中如何处理带约束的优化问题。

在实际应用中，我们可以根据具体的问题，合理地设置参数和约束条件，来求解复杂的优化问题。

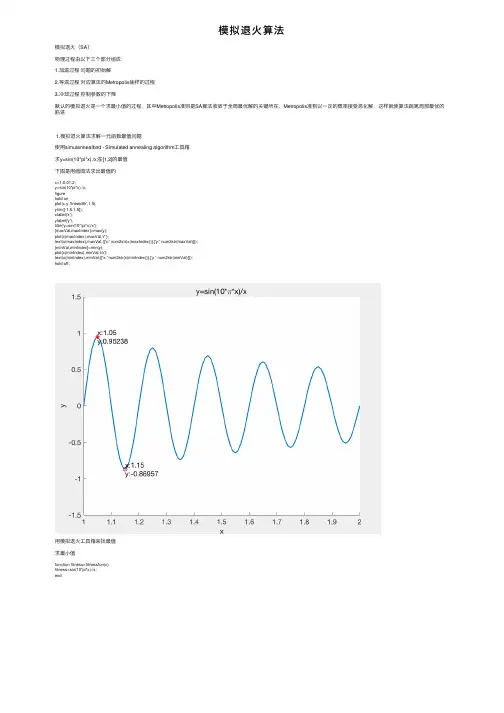
模拟退⽕算法模拟退⽕（SA）物理过程由以下三个部分组成1.加温过程问题的初始解2.等温过程对应算法的Metropolis抽样的过程3.冷却过程控制参数的下降默认的模拟退⽕是⼀个求最⼩值的过程，其中Metropolis准则是SA算法收敛于全局最优解的关键所在，Metropolis准则以⼀定的概率接受恶化解，这样就使算法跳离局部最优的陷进1.模拟退⽕算法求解⼀元函数最值问题使⽤simulannealbnd - Simulated annealing algorithm⼯具箱求y=sin(10*pi*x)./x;在[1,2]的最值下图是⽤画图法求出最值的x=1:0.01:2;y=sin(10*pi*x)./x;figurehold onplot(x,y,'linewidth',1.5);ylim([-1.5,1.5]);xlabel('x');ylabel('y');title('y=sin(10*\pi*x)/x');[maxVal,maxIndex]=max(y);plot(x(maxIndex),maxVal,'r*');text(x(maxIndex),maxVal,{['x:' num2str(x(maxIndex))],['y:' num2str(maxVal)]});[minVal,minIndex]=min(y);plot(x(minIndex),minVal,'ro');text(x(minIndex),minVal,{['x:' num2str(x(minIndex))],['y:' num2str(minVal)]});hold off;⽤模拟退⽕⼯具箱来找最值求最⼩值function fitness=fitnessfun(x)fitness=sin(10*pi*x)./x;end求最⼤值function fitness=fitnessfun(x)fitness=-sin(10*pi*x)./x;endOptimization running.Objective function value: -0.9527670052175917Maximum number of iterations exceeded: increase options.MaxIterations.⽤⼯具箱求得的最⼤值为0.95276700521759172.⼆元函数优化[x,y]=meshgrid(-5:0.1:5,-5:0.1:5);z=x.^2+y.^2-10*cos(2*pi*x)-10*cos(2*pi*y)+20;figuremesh(x,y,z);hold onxlabel('x');ylabel('y');zlabel('z');title('z=x^2+y^2-10*cos(2*\pi*x)-10*cos(2*\pi*y)+20');maxVal=max(z(:));[maxIndexX,maxIndexY]=find(z==maxVal);%返回z==maxVal时，x和y的索引for i=1:length(maxIndexX)plot3(x(maxIndexX(i),maxIndexY(i)),y(maxIndexX(i),maxIndexY(i)),maxVal,'r*');text(x(maxIndexX(i),maxIndexY(i)),y(maxIndexX(i),maxIndexY(i)),maxVal,{['x:' num2str(x(maxIndexX(i)))] ['y:' num2str(y(maxIndexY(i)))] ['z:' num2str(maxVal)] }); endhold off;function fitness=fitnessfun(x)fitness=-(x(1).^2+x(2).^2-10*cos(2*pi*x(1))-10*cos(2*pi*x(2))+20);endOptimization running.Objective function value: -80.50038894455415Maximum number of iterations exceeded: increase options.MaxIterations.找到的最⼤值：80.500388944554153.解TSP问题（⽤的数据和前⼏天⽤遗传算法写TSP问题的数据⼀致，但是结果⽐遗传算法算出来效果差很多，不知道是不是我写错了，怀疑⼈⽣_(:з」∠)_中。

模拟退⽕算法及其应⽤摘要⽣活中存在许多需要使⽤优化的情况，⽽为了解决这种情况便出现了很多的优化算法.模拟退⽕算法就是多种优化组合算法中的⼀种，它⼀直以来都是⼀个优化领域的热点，收到⼴⼤研究者的关注.作为优化组合算法中的佼佼者，它拥有相较于早期其他优化算法更便于计算，使⽤灵活适⽤于并⾏运算的优点，解决了部分传统算法⽆法规避⼤规模问题的不可⾏因素.模拟退⽕算法来源于模拟退⽕的过程，在1953年被Metropofis提出这种先进的思想，⽽后被Kirkpatrick等⼈于1983年引⼊到优化组合领域中，从此模拟退⽕算法就成为了许多优化算法中的⼀种.当然对于这种优越的算法并不仅仅是⽤于简单的优化问题中，它可⽤于的领域包括着⼯程科学在内的多种领域中.(删掉,摘要⾥不需要写这些)模拟退⽕算法虽然在各个领域中有着⼗分的成就，但它在组合优化上还是占有着⾮常重要的地位.本⽂中将会对于模拟退⽕算法的背景做出简述，并对模拟退⽕算法的原理内容做出介绍.为了更加清楚的了解模拟退⽕算法的性能，本⽂中对其举出例⼦来演⽰其在优化问题中的表现.在组合优化领域中NP(NP-Hard)问题⼀直都是⼀个⿇烦的问题，尤其其中著名的旅⾏商问题有着简单、⿇烦的特点.简单是指它的问题描述最为简化时，就是在⼏个点中找出最为短的路径；⿇烦却是当⼏个点增长到⼀定程度是就很难得出⼀个准确的解.⽽模拟退⽕算法却在这种难题中有着不俗的表现.关键词：模拟退⽕算法；组合优化问题；TSP问题AbstractMany require the use of optimization condition exists in life, and in order to resolve this situation occurs many optimization algorithm. Simulation is a combination of several optimization algorithm of simulated annealing algorithm, it is always a hot one optimization field, received the majority of researchers. As a leader in combination optimization algorithm, it has compared to other early optimization algorithm more easy to calculate, the use of flexible advantages of parallel computing, solve the infeasible factor part of traditional algorithm cannot avoid large-scale problems. Simulated annealing algorithm derived from the simulated annealing process, in 1953 Metropofis proposed the advanced ideas, and then by Kirkpatrick et al in 1983 into the optimization in the field, then the simulated annealing algorithm is one of many in the optimization algorithm. Of course, this algorithm is not only superior to simple optimization problems in various fields, which can be used in fields including engineering science in. Simulated annealing algorithm is very success in every field, but it is in the combinatorial optimization and occupies a very important position. This paper will make a brief for the simulated annealing algorithm to make the background, principle and content of the simulated annealing algorithm. In order to more clearly understand the performance of simulated annealing, to demonstrate the optimization problem in the performance for the examples in this article.In the field of combinatorial optimization problem in NP is always a difficult problem, especially the well-known traveling salesman problem which has the characteristics of simple, trouble. Simple refers to the description of the problem is the most simple, is at several points out the most short path; the trouble is when several points up to a certain extent is hardly an accurate solution. The simulated annealing algorithm has a good performance in this problem.Key words: the simulated annealing algorithm; combinatorial optimization;TSP⽬录第1章引⾔ ........................................... 错误！未定义书签。

模拟退火算法模拟退火算法3.5 模拟退火算法模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

根据Metropolis准则，粒子在温度T时趋于平衡的概率为e-ΔE/(kT)，其中E为温度T时的内能，ΔE为其改变量，k为Boltzmann常数。

用固体退火模拟组合优化问题，将内能E模拟为目标函数值f，温度T演化成控制参数t，即得到解组合优化问题的模拟退火算法：由初始解i和控制参数初值t开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步衰减t 值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。

退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。

3.5.1 模拟退火算法的模型模拟退火算法可以分解为解空间、目标函数和初始解三部分。

模拟退火的基本思想:(1) 初始化：初始温度T(充分大)，初始解状态S(是算法迭代的起点)，每个T值的迭代次数L(2) 对k=1，……，L做第(3)至第6步：(3) 产生新解S′(4) 计算增量Δt′=C(S′)-C(S)，其中C(S)为评价函数(5) 若Δt′<0则接受S′作为新的当前解，否则以概率exp(-Δt′/T)接受S′作为新的当前解.(6) 如果满足终止条件则输出当前解作为最优解，结束程序。

终止条件通常取为连续若干个新解都没有被接受时终止算法。

(7) T逐渐减少，且T->0，然后转第2步。

算法对应动态演示图：模拟退火算法新解的产生和接受可分为如下四个步骤：第一步是由一个产生函数从当前解产生一个位于解空间的新解；为便于后续的计算和接受，减少算法耗时，通常选择由当前新解经过简单地变换即可产生新解的方法，如对构成新解的全部或部分元素进行置换、互换等，注意到产生新解的变换方法决定了当前新解的邻域结构，因而对冷却进度表的选取有一定的影响。

旅⾏商问题——模拟退⽕算法实现1.问题描述旅⾏商问题（Travelling Salesman Problem, 简记TSP，亦称货郎担问题)：设有n个城市和距离矩阵D=[d ij]，其中d ij表⽰城市i到城市j的距离（i，j=1，2 … n），则问题是要找出遍访每个城市恰好⼀次的⼀条回路并使其路径长度为最短。

2.算法设计对原问题进⾏分析，TSP的⼀个解可表述为⼀个循环排列：Π= (Π1，Π2，Π3… Πn），即Π1→Π2→ … →Πn→Π1有（n-1）！/2 种不同⽅案，若使⽤穷举法，当n很⼤时计算量是不可接受的。

旅⾏商问题综合了⼀⼤类组合优化问题的典型特征，属于NP 难题，不能在多项式时间内进⾏检验。

若使⽤动态规划的⽅法时间复杂性和空间复杂性都保持为n的指数函数。

本次实验利⽤模拟退⽕算法（Simulated Annealing）求解TSP问题。

模拟退⽕算法最早由N.Metropolis等⼈于1953年提出，基于物理中固体物质的退⽕过程与⼀般组合优化问题之间的相似性。

该算法从某⼀较⾼初温出发，伴随温度参数的不断下降，结合概率突跳特性在解空间随机寻找全局最优解。

退⽕是将固体加热到⾜够⾼的温度，使分⼦呈随机排列态，然后逐步降温冷却，最后分⼦以低能状态排列，得到稳定状态的固体。

退⽕的过程有：（1）加温过程：增强粒⼦运动，消除系统原本可能存在的⾮均匀态；（2）等温过程：对于与环境换热⽽温度不变的封闭系统，系统状态的⾃发变化总是朝向⾃由能减少的⽅向进⾏，当⾃由能达到最⼩时，系统平衡；（3）冷却过程：使粒⼦热运动减弱并逐渐趋于有序，系统能量逐渐下降，从⽽得到低能的晶体结构。

其中，固体在恒温下达到热平衡的过程采⽤Metropolis⽅法进⾏模拟：温度恒定为T时，当前状态i转为新状态j，如果j状态的能量⼩于i，则接受状态j为当前状态；否则，如果概率p=exp{-(E j-E i)/(k*T)}⼤于[0,1)区间的随机数，则仍接受状态j为当前状态；若不成⽴则保留状态i为当前状态。

如何在Matlab中进行模拟退火算法的优化模拟退火算法是一种用于求解复杂问题的全局优化算法。

在Matlab中，我们可以利用其强大的数值计算和优化工具箱来实现模拟退火算法的优化。

本文将介绍如何在Matlab中进行模拟退火算法的优化，并通过一个实际的案例来演示其应用。

一、模拟退火算法简介模拟退火算法是一种启发式的全局优化算法，模拟了固体物体在退火过程中的特性。

其基本原理是通过模拟固体退火过程，逐渐降低系统能量，从而找到全局最优解。

在模拟退火算法中，由于退火过程中存在较高的温度，使算法有机会跳出局部极小值点，因此能够在搜索空间中全面地寻找最优解。

二、Matlab中的模拟退火算法优化函数Matlab提供了优化工具箱，在其中包含了一系列优化函数，其中包括模拟退火算法。

我们可以使用"simulannealbnd"函数来在Matlab中实现模拟退火算法的优化。

三、案例演示：函数最优化假设我们要求解以下函数的最小值：f(x) = x^2 + sin(5x)我们可以使用Matlab中的模拟退火算法优化函数来找到该函数的全局最小值。

1. 定义目标函数首先，我们需要在Matlab中定义目标函数：function y = myfunc(x)y = x.^2 + sin(5*x);2. 编写优化代码接下来，我们可以编写优化代码，利用"simulannealbnd"函数进行模拟退火算法的优化：options = saoptimset('Display','iter','TolFun',1e-6);[x,fval] = simulannealbnd(@myfunc, [-10,10],[],[],options);在上述代码中，"options"用于设置优化选项，"@myfunc"是要优化的目标函数，[-10,10]为变量的取值范围，[]表示无约束条件。

模拟退火算法及其在最优化中的应用随着计算机科学的不断发展，求解模型的最优解已成为一项重要课题。

而对于许多实际问题来说，求解最优解是一个 NP 难问题。

因此，人们常常使用各种算法来解决这些问题。

模拟退火算法作为一种求解 NP 难问题的启发式算法，越来越受到学术界和工业界的关注。

一、模拟退火算法的原理模拟退火算法源于统计物理学中的模拟物理过程。

它的核心思想是以一定的概率接受比当前状态差的解，为了避免陷入局部最优解，随着时间的推移逐渐减小概率。

在求解问题时，模拟退火算法首先会随机选择一个初始解，然后根据一定的规则来生成邻域解。

接下来，算法会计算这个邻域解与当前最优解之间的差距，如果邻域解更优，那么它就成为新的最优解；否则，按照一定的概率接受它，以避免陷入局部最优解。

这个概率与当前的温度有关。

在初始阶段，温度非常高，此时概率极大，那么算法就更有可能接受一个比最优解差的解。

但随着时间的推移，温度越来越低，概率就越来越小，这时算法的行为就趋向于贪心算法，只会接受更优的解。

二、模拟退火在最优化中的应用模拟退火算法广泛应用于组合优化问题，如图形着色、旅行商问题、背包问题等。

它也可以用于解决连续优化问题，如函数最大值或最小值的求解。

在实践过程中，模拟退火算法已经被证明是一种有效、高效的求解方法。

下面我们以图形着色问题为例来说明模拟退火算法的应用。

给定一个图 $G=(V,E)$，要求每个顶点 $v_i \in V$ 都染上一种颜色，使得相邻的两个点不会被染上相同的颜色。

这就是图形着色问题，也是一个 NP 难问题。

对于这个问题，我们可以用模拟退火算法来求解。

首先我们随机给每个顶点染上一种颜色，然后计算与当前方案不同的解，每次取这些解中最优的一个。

如果这个解比当前最优的解更优，那么它成为新的最优解。

否则，以一定的概率接受新的解，以避免陷入局部最优解。

在实际应用中，我们通常将温度初始值设为一个稍大于 1 的常数，然后进行一定的迭代次数，直到温度降到一个极小值。

Matlab技术模拟退火算法随着科学技术的进步和应用领域的扩展，我们对问题的求解和优化的需求也越来越高。

而在这个过程中，模拟退火算法就显得格外重要。

本文将介绍Matlab技术中的模拟退火算法，以及其原理和应用。

一、模拟退火算法简介模拟退火算法（simulated annealing）是一种全局优化算法，它模拟物质从高温状态慢慢冷却至低温状态的过程，通过跳出局部极值，寻找全局最优解。

其基本思路是在搜索空间中随机生成一个解并逐渐改进，以一定的概率接受差解，以避免陷入局部最优解而无法找到全局最优解。

二、模拟退火算法原理模拟退火算法的基本原理源自于固体退火过程。

在固体的退火过程中，随着温度的逐渐下降，原子的运动趋于平稳，达到了最低能量态。

根据固体退火过程的原理，模拟退火算法将其应用在问题的求解过程中。

模拟退火算法主要由三个元素组成：初始温度、降温策略和能量函数。

初始温度决定了搜索空间的范围，温度越高，搜索范围越广。

降温策略决定了温度的降低速度，常见的降温策略有线性降温、指数降温和对数降温等。

能量函数用于评估解的质量，根据问题的性质和目标确定不同的能量函数。

算法的基本流程是：首先，随机生成一个初始解，并将其作为当前解。

随后，通过交换解中的元素、改变解的部分值等操作，产生新的解。

如果新解优于当前解，则接受新解作为当前解；如果新解不优于当前解，则以一定的概率接受差解，以避免陷入局部最优。

重复上述步骤，直到满足终止条件。

三、模拟退火算法在Matlab中的应用Matlab作为一种强大的数学计算工具，提供了丰富的优化算法库。

在Matlab中使用模拟退火算法解决问题，可以通过调用相应的函数实现。

首先，在Matlab中创建一个目标函数，该函数用于评估解的质量。

可以根据不同的问题需求，自定义目标函数。

然后，使用Matlab中的SA函数进行模拟退火算法的实现。

SA函数的参数包括目标函数、初始温度、降温率等。

下面以一个简单的例子来说明模拟退火算法在Matlab中的使用。

第二章模拟退火算法（Simulated Annealing）搜索问题描述搜索问题描述搜索算法盲目搜索还是启发式搜索？按照预定的控制策略实行搜索，在搜索过程中获取的中间信息不用来改进控制策略，称为盲目搜索，反之，称为启发式搜索。

关于“启发式”，可有两种看法：1)任何有助于找到问题的解，但不能保证找到解的方法均是启发式方法；2)有助于加速求解过程和找到较优解的方法是启发式方法。

搜索算法盲目搜索深度优先、广度优先、代价优先、向前、向后、双向。

启发式搜索爬山法、模拟退火算法、遗传算法、粒子群算法、蚁群算法。

贪心算法1.随机选定一个初始解x 0；2.Do while （中止条件不满足）1.在某个邻域函数所定义的邻域范围内，按照某个（随机）扰动Δ产生策略，得到一个新解x i ’；2.对新解进行评估，得f (x i ’)；3.如果f (x i ’) > f (x i )（或者f (x i ’) < f (x i )），即新解比老解好，则令x i ＋1＝x i ’；4.否则，x i ＋1＝x i 。

3.End Do爬山法1.随机选定一个初始解x 0；2.Do while （中止条件不满足）1.在某个邻域函数所定义的邻域范围内，按照某个（随机）扰动Δ产生策略，得到多个新解X new ={x i 1, x i2,…, x i k }；2.对这组新解进行评估，得{f (x i 1), f (x i 2), …, f (x i k )}；3.x i ＋1＝x i ’,x i ’∈X new ,∀x i j , (i =1,2,…,n; j =1,2,…,k ), f (x i ’) > f (x i )且f(x i ’) > f (x i j )（或者f (x i ’) < f (x i )且f (x i ’) < f (x i j )），即新的当前解比老解好，并且是所有新解中最好的一个；4.如果，∀x i j , (i =1,2,…,n; j =1,2,…,k ), f(x i ) > f (x i j )（或者f (x i ) <f (x i j )），则x i ＋1＝x i 。

模拟退火算法一、模拟退火算法概念模拟退火算法来源于固体退火原理，将固体加温至充分高，再让其徐徐冷却，加温时，固体内部粒子随温升变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小。

根据Metropolis准则，粒子在温度T 时趋于平衡的概率为e-ΔE/(kT)，其中E为温度T时的内能，ΔE为其改变量，k为Boltzmann 常数。

用固体退火模拟组合优化问题，将内能E模拟为目标函数值f，温度T演化成控制参数t，即得到解组合优化问题的模拟退火算法：由初始解i和控制参数初值t开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步衰减t值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。

退火过程由冷却进度表(Cooling Schedule)控制，包括控制参数的初值t及其衰减因子Δt、每个t值时的迭代次数L和停止条件S。

二、模拟退火算法的模型模拟退火算法可以分解为解空间、目标函数和初始解三部分。

模拟退火的基本思想:(1) 初始化：初始温度T(充分大)，初始解状态S(是算法迭代的起点)，每个T值的迭代次数L(2) 对k=1，……，L做第(3)至第6步：(3) 产生新解S′(4) 计算增量Δt′=C(S′)-C(S)，其中C(S)为评价函数(5) 若Δt′<0则接受S′作为新的当前解，否则以概率exp(-Δt′/T)接受S′作为新的当前解.(6) 如果满足终止条件则输出当前解作为最优解，结束程序。

终止条件通常取为连续若干个新解都没有被接受时终止算法。

(7) T逐渐减少，且T->0，然后转第2步。

算法对应动态演示图：模拟退火算法新解的产生和接受可分为如下四个步骤：第一步是由一个产生函数从当前解产生一个位于解空间的新解；为便于后续的计算和接受，减少算法耗时，通常选择由当前新解经过简单地变换即可产生新解的方法，如对构成新解的全部或部分元素进行置换、互换等，注意到产生新解的变换方法决定了当前新解的邻域结构，因而对冷却进度表的选取有一定的影响。

matlab模拟退火算法工具箱原理概述及解释说明1. 引言1.1 概述模拟退火算法是一种元启发式算法，用于在优化问题中寻找全局最优解。

该算法受到自然界中固体物体冷却过程的启发，通过随机搜索和接受次优解的方式，在搜索空间中逐渐降低温度来达到寻找最优解的目标。

Matlab模拟退火算法工具箱是一个集成了多种模拟退火算法的算法库，旨在帮助研究者和工程师解决各种优化问题。

本文将对Matlab模拟退火算法工具箱进行原理概述，并详细解释其功能和使用方法，以及应用场景和技巧。

1.2 文章结构本文将分为五个部分进行阐述。

首先是引言部分，介绍文章的背景和整体结构。

其次是Matlab模拟退火算法工具箱原理部分，包括对模拟退火算法概述、算法原理解析以及工具箱功能的介绍。

第三部分是Matlab模拟退火算法工具箱的应用场景，包括解决优化问题、参数调优与搜索空间探索等方面。

接着是Matlab 模拟退火算法工具箱的使用方法与技巧，详细说明安装与设置环境、建立模型与参数设定以及运行与结果分析等方面。

最后是结论与展望部分，对全文进行总结并展望未来的研究方向。

1.3 目的本文旨在向读者全面介绍Matlab模拟退火算法工具箱的原理和功能，使其能够理解和应用该工具箱来解决各类优化问题。

通过对应用场景的举例和使用方法与技巧的详细说明，希望读者能够掌握该工具箱的使用，并在实际问题中提取更准确、更高效的优化解。

最后，为了推进该领域的研究，还将提出一些可能的研究方向和展望。

2. Matlab模拟退火算法工具箱原理2.1 模拟退火算法概述模拟退火算法（Simulated Annealing）是一种基于统计物理学中固体退火原理的全局优化算法。

它模拟金属在高温下冷却过程中的晶格结构演变，通过随机搜索和接受恶化解以避免陷入局部最优解，并最终找到全局最优解。

2.2 算法原理解析模拟退火算法的主要原理是通过引入一个控制参数“温度”来控制搜索过程。

在初始阶段，温度较高，搜索范围较广，能够灵活地跳出局部最优解。

模拟退火算法在路径规划中的应用路径规划是指在给定起点和终点的情况下，找到一条最优路径的问题。

这个问题出现在很多应用场景中，比如机器人导航、物流配送等。

而模拟退火算法，则是一种优化算法，用于寻找全局最优解。

将这两个算法结合起来，可以解决路径规划问题，并得到全局最优解。

1. 路径规划问题简介路径规划问题是在给定起点和终点情况下，找到可以连接起点和终点的一条路径的问题。

这个问题在现实生活中非常普遍，比如在城市中寻找最短的驾车路线，或者在电子地图中寻找最短的步行路线。

随着智能制造和自动化技术的普及，路径规划也成为了机器人导航、物流配送等领域中的重要问题。

2. 模拟退火算法简介模拟退火算法是一种全局优化算法，也称为辅助函数优化法。

它最初由Kirkpatrick et.al提出，是一种模拟金属退火过程的一种优化算法。

这个算法通过随机选取搜索方向，通过一定的能量函数计算来判断搜索的方向是否可行；然后以某个概率接受不可行的搜索方向，并进行下一次搜索，最终找到最优解。

3. 在路径规划问题中，模拟退火算法可以通过随机生成起点和终点的位置，然后以起点到终点之间的路径长度作为能量函数，搜索能量函数最小的路径。

在搜索过程中，模拟退火算法不会像贪心算法一样，一直选择局部最优解。

相反，模拟退火算法有概率接受劣解并继续搜索，从而避免陷入局部最优解。

4. 模拟退火算法的优缺点模拟退火算法具有以下优点：- 可以搜索全局最优解。

- 在早期搜索过程中，可以接受一定的次优解，从而可以避免陷入局部最优解。

- 搜索过程可以进行多次，以找到最佳结果。

然而，模拟退火算法也有以下缺点：- 算法的时间和空间复杂度较高。

- 算法的表现受到初始温度和退火速度等参数的影响。

- 由于模拟退火算法的随机性，算法可能会在搜索过程中陷入循环。

5. 模拟退火算法的应用领域模拟退火算法具有广泛的应用领域，包括：- 金融投资中的组合优化问题。

- 机器学习中的参数优化问题。