下载文档原格式
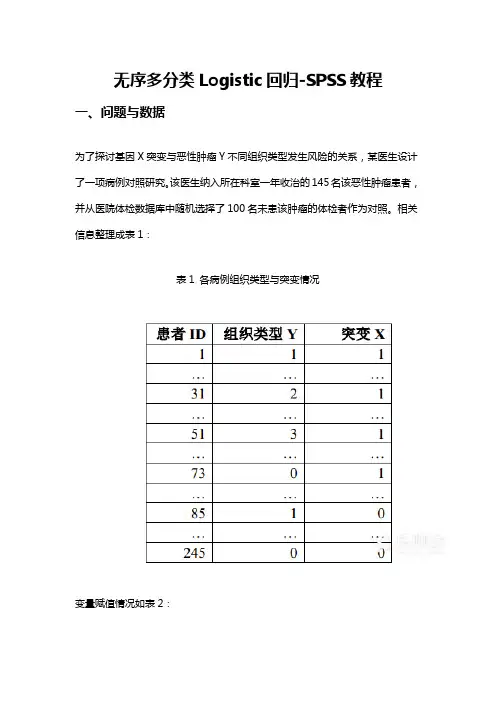
无序多分类Logistic回归-SPSS教程一、问题与数据为了探讨基因X突变与恶性肿瘤Y不同组织类型发生风险的关系，某医生设计了一项病例对照研究。
该医生纳入所在科室一年收治的145名该恶性肿瘤患者，并从医院体检数据库中随机选择了100名未患该肿瘤的体检者作为对照。
相关信息整理成表1：表1 各病例组织类型与突变情况变量赋值情况如表2：表2 变量及变量赋值情况二、对问题分析该研究中，“病例”与“对照”的关系不再是简单的“患病”与“不患病”，而是病例分为四类（本例中包含对照组共四类），且各类别无次序关系。
或者说，因变量Y不再是二分类的，而是无序多分类的。
通过无序多分类的Logistic回归分析可以将三种不同组织类型的病例分别与对照组进行对比，分别得到基因X 突变与三种肿瘤组织类型的暴露-风险关系。
三、SPSS操作A. 数据录入SPSS若数据格式如表1所示，则首先在SPSS变量视图（Variable View）中新建三个变量：ID代表患者编号，Y代表组织类型，X代表是否突变，赋值参考表2.然后在数据视图（Data View）中录入数据。
B. 选择Analyze →Regression →Multinomial LogisticC. 选项设置将变量Y选入因变量（Dependent）位置，变量X选入因子（Factors）位置。
如果自变量中还有连续型变量，则需要放入协变量（Covariate）位置。
由于因变量Y有多个分类，而无序多分类Logistic回归的原理是先指定一个类别为参考类别，然后将其他类别分别与参考类别对比。
故需点击Reference Category 设置参考类别（本例中作为参考类别的为对照组）。
SPSS默认选择因变量赋值中按升序排列后最后类别（即赋值最大者）为参考类别（即对照组），而本研究中参考类别Y赋值为0，故可以点击First Category 或直接在Custom中输入0，点击Continue。
《医学统计学》课程教学大纲（Medical Statistics）一、课程基本信息课程编号：14232080课程类别：专业必修课适用专业：医学检验技术学分：理论教学学分：2学分，实验学分：0.5学分总学时：40学时（其中讲授学时：24学时；实验(上机)学时：16学时）先修课程：医学基础课程后续课程：医学检验、预防医学选用教材：李康主编：医学统计学(第6版)[M].北京：人民卫生出版社，2013必读书目：[1]方积乾主编.医学统计学(第7版)[M].北京：人民卫生出版社，2013[2]袁兆康.医学统计学[M].北京：人民军医出版社.2013[3]张文彤主编.SPSS统计分析基础教程(第2版)[M].北京：高等教育出版社，2011选读书目：[1] 颜虹, 医学统计学[M]. 北京：人民卫生出版社，2005[2] 康晓平，实用卫生统计学 [M].北京：北京大学医学出版社，2002[3] Belinda Barton，Medical Statistics: A Guide to SPSS, Data Analysis and Critical Appraisal [M].美国：WILEY Blackwell，2014二、课程教学目标通过本门课程的学习，要使学生学会人群健康研究的统计学方法，学会数值变量和分类变量资料的分析，配对资料的分析，直线相关和直线回归，非参数统计方法，病例随访资料分析。
其目的使大家具备新的推理思维，结合专业问题合理设计试验，科学获取资料，提高科研素质。
本课程教学的主要方法有理论讲授、课堂讨论、实验实习、课堂演算、统计软件SPSS上机等。
通过实验实习，使学生加深对理论的理解。
三、课程教学内容与教学要求1．绪论教学要求：掌握：同质与变异，总体、个体和样本，变量的分类，统计量与参数，抽样误差，频率与概率等基本概念。
理解：统计工作的基本步骤，医学统计学的主要内容。
了解：学习统计学的目的和要求。
Kendall's W检验-SPSS教程一、问题与数据某研究者拟分析5位放射科医生对疾病严重程度诊断的一致性。
现搜集50位研究对象的MRI检查结果，并要求放射科医生分别针对每份MRI检查给予Grade I（最轻）到Grade V（最重）五个等级的临床诊断，Grade I、Grade II、GradeIII、Grade IV和Grade V赋值分别为1、2、3、4和5，部分数据如图1。
图1 部分数据二、对问题分析在本研究中，研究者拟探讨5位放射科医生对疾病严重程度（5分类）诊断的一致性。
对于这种存在3位及以上观察者，观测变量为连续变量或有序分类变量的一致性检验，我们推荐使用Kendall’s W检验。
一般来说，采用Kendall’s W 检验的研究设计需要满足以下3项假设：假设1：观察者不少于3人，判定结果是连续变量或有序分类变量。
如本研究中需要判断5位放射科医生诊断结果的一致性，且观测变量是Grade I到Grade V 五个等级，属于有序分类变量。
假设2：要求判定结果配对，即不同观测者判定的对象相同。
如本研究中，5位放射科医生诊断的是同一组研究对象的MRI，编号统一。
假设3：观察者之间相互独立。
这要求不同观测者独立完成结果判定，相互不干扰。
根据研究设计，我们认为本研究符合Kendall’s W 检验的3项假设，可以采用该方法进行一致性评价。
三、SPSS操作在主界面点击Analyze→NonparametricTests→Related Samples，确认What is your objective?栏中点选了Automatically compare observed data to hypothesized，如图2。
图2 NonparametricTests: Two or More Related Samples点击Fields→Use custom field assignments，并将50个观测变量P1到P50放入Test Fields栏。
正态分布的检验数据的正态分布是通过Analyze -> Descriptive Statistics -> Explore来实现的，同时该命令也可以检查异常值和极值，和进行方差齐性检验（方差齐性，本节不介绍）。
打开文件data0201-protein.sav，如下图，50种树叶中粗蛋白占干重的比例，如果检验变量protein的正态性，按Analyze -> Descriptive Statistics -> Explore打开如下对话框，把要检验的变量送入Dependent List框（可同时检验多个变量），Factor List框是分组变量（本例中无分组变量），Label Cases by框指定一个变量作为标识变量（可忽略），Display栏指定要输出的是统计量或统计图，或同时输出。
点击Statistics按钮，打开如下左对话框，选择要输出的统计量，选项Descriptives：描述统计量，选项M-estimators：集中趋势最大似然比（可忽略），选项outliers：5个最大值和最小值，选项Percentiles：第5、10、25、50、75、90、95百分位数，点击continue回到Explore对话框，点击Plots，打开如上右对话框，Boxplots框选择箱状图的格式，选项None：不输出箱状图，选项Factor levels together：变量按分组生成箱状图，并列输出（本例未分组），选项Dependents together：在一个图形中生成所有变量箱状图（本例只有一个变量），Descriptive框选择输出图形的类型；选项stem-and-leaf：茎叶图，选项Histogram：直方图；Normality plots with tests栏，输出正态概率和无趋势概率图，以及统计检验结果；Spread vs Level with Levene Test栏各选项与方差齐性检验有关，本节不介绍（只有选择分组变量时，才被激活）。
SPSS统计与分析统计要与大量的数据打交道，涉及繁杂的计算和图表绘制。
现代的数据分析工作如果离开统计软件几乎是无法正常开展。
在准确理解和掌握了各种统计方法原理之后，再来掌握几种统计分析软件的实际操作，是十分必要的。
常见的统计软件有SAS，SPSS，MINITAB，EXCEL等。
这些统计软件的功能和作用大同小异，各自有所侧重。
其中的SAS和SPSS是目前在大型企业、各类院校以及科研机构中较为流行的两种统计软件。
特别是SPSS，其界面友好、功能强大、易学、易用，包含了几乎全部尖端的统计分析方法，具备完善的数据定义、操作管理和开放的数据接口以及灵活而美观的统计图表制作。
SPSS在各类院校以及科研机构中更为流行。
SPSS（Statistical Product and Service Solutions,意为统计产品与服务解决方案）。
自20世纪60年代SPSS诞生以来，为适应各种操作系统平台的要求经历了多次版本更新，各种版本的SPSS for Windows大同小异，在本试验课程中我们选择PASW Statistics 18.0作为统计分析应用试验活动的工具。
1．SPSS的运行模式SPSS主要有三种运行模式：（1） 批处理模式这种模式把已编写好的程序（语句程序）存为一个文件，提交给[开始]菜单上[SPSS for Windows]→[Production Mode Facility]程序运行。
（2） 完全窗口菜单运行模式这种模式通过选择窗口菜单和对话框完成各种操作。
用户无须学会编程，简单易用。
（3） 程序运行模式这种模式是在语句（Syntax）窗口中直接运行编写好的程序或者在脚本（script）窗口中运行脚本程序的一种运行方式。
这种模式要求掌握SPSS的语句或脚本语言。
本试验指导手册为初学者提供入门试验教程，采用“完全窗口菜单运行模式”。
2．SPSS的启动（1） 在windows[开始]→[程序]→[PASW]，在它的次级菜单中单击“SPSS 12.0 for Windows”即可启动SPSS软件，进入SPSS for Windows对话框，如图1.1，图1.2所示。
第12章时间序列分析社会经济现象随着时间的推移在不断地发生着变化，关于社会经济现象的统计指标也是在不同的时间进行观察记录的，从而形成了统计指标的时间序列。
时间序列是一种基于随机过程理论和数理统计学方法的动态数据处理的一种统计方法，包括一般统计分析和统计模型的建立与推断，以及关于时间序列的最优预测、控制和滤波等内容。
而随着计算机的普及和相关软件的开发，时间序列分析已越来越被研究者所重视。
在本章中，将以SPSS软件进行时间序列分析为基线，详细介绍时间序列分析的基础理论，以及指数平滑和季节分析等模型的使用技巧。
本章学习目标：时间序列分析概述时间序列数据的预处理指数平滑模型ARIMA模型季节分析模型时间序列又称为动态数列或时间数列，主要反映了不同时间内的社会经济现象的统计指标值，并将这些统计指标值按照时间的先后顺序加以排列后形成分析数列。
在本小节中，将详细介绍时间序列分析的基本原理。
时间序列分析在统计分析学中具有非常重要的地位，其具有了解和分析社会经济现象的发展过程、发展变化的规律性和预测现象的未来发展趋势等目的。
另外，时间序列按照其指标的性质，可分为总量指标、相对指标和平均指标。
其中，总量指标时间序列又称为绝对数时间序列，而相对指标和平均指标则是在总量指标时间序列上派生出来的。
1．总量指标时间序列总量指标时间序列反映了社会经济现象的绝对水平情况。
根据社会经济现象性质而定，总量指标又分为时期指标和时点指标时间序列，其中：“ 时期指标 时期指标具有可加性特点，即将不同时期的总量指标相加，从而获得长时期的指标值。
另外，指标值的大小和所属时间的长度有着直接的关系，以及其指标值必须采用连续统计的方法来获取。
“ 时点指标 时点指标和时期指标具有一定的相反性，时点指标具有不可加性特点，即不同时点的总量指标不能相加在一起。
另外，指标数值的大小和时点间隔的长短不存在相关性，以及其指标值必须采用间断统计的方法来获取。
2．相对指标和平均指标相对指标和平均指标主要反映了社会经济现象达到的相对水平或平均水平，并将一系列相对指标和平均指标值，按照时间先后顺序排列起来所形成的时间分析序列。
如何用spss做一般（含虚拟变量）多元线性回归回归一直是个很重要的主题。
因为在数据分析的领域里边，模型重要的也是主要的作用包括两个方面，一是发现，一是预测。
而很多时候我们就要通过回归来进行预测。
关于回归的知识点也许不一定比参数检验，非参数检验多，但是复杂度却绝对在其上。
回归主要包括线性回归，非线性回归以及分类回归。
本文主要讨论多元线性回归（包括一般多元回归，含有虚拟变量的多元回归，以及一点广义差分的知识）。
请大家不要觉得本人偷奸耍滑，居然只有一个主题，两个半知识点。
相信我，内容会很充实的。
对于线性回归的定义主要是这样的：线性回归，是基于最小二乘法原理产生古典统计假设下的最优线性无偏估计。
是研究一个或多个自变量与一个因变量之间是否存在某种线性关系的统计学方法。
这个什么叫线性回归，什么叫最小二乘法，在在高中数学课本里边就有涉及。
我就不重复了嘿嘿。
本质上讲一元线性回归是多元线性回归的一个特例，因此我们就直接讨论多元线性回归了哈。
为了便于叙述，我们先举个例子，假设我们想研究年龄，体重，身高，和血压的线性回归关系。
打开菜单分析——回归——线性，打开主对话框。
很容易可以知道在本例中因变量选择血压，自变量选择年龄，身高，体重。
然后注意，在因变量那个框框下边还有一个写着方法的下拉的单选菜单。
这个方法指的是建立多元线性方程的方法，也就是自变量进入分析的方法。
一共包括五种，进入，逐步，删除，向后，向前。
进入是最简单的一种，就是强迫指定选中的自变量都进入方程。
其余四个方法比较复杂，系统会依照不同的规则自动的帮助你剔除不合格的自变量，以此保证方程的可靠性。
下边的选择变量框框是用来指定分析个案的选择规则，这个一般大家是所有的个案都利用，所以不用管它。
再下边的个案标签变量，是用来在图形中标注值得，也不是重点。
最下边的WLS权重，是在加权最小二乘法里边使用的，这里不管它。
介绍完主面板以后我们来看统计量选项卡。
这张选项卡比较小，一般勾选的主要有估计，模型拟合度，共线性诊断，DW检验统计量。
SPSS详细操作：配对卡⽅检验（McNemar’stest）⼀、问题与数据某研究者想要观察戒烟⼲预的效果，招募了50名研究对象，其中吸烟者和不吸烟者各25名。
所有研究对象均观看吸烟导致癌症的视频。
两周后，研究者询问研究对象是否还在吸烟。
研究者收集了所有研究对象的⼲预前吸烟状态（before）和⼲预后吸烟状态（after）。
两个变量均为⼆分类变量，即不吸烟与吸烟（分别赋值为1和2），部分数据如下图。
其中，Individual scores for each paticipant列出了每⼀个研究对象的情况，⽽Total count data (frequencies)则是对相同情况研究对象的数据进⾏了汇总。
⼆、对问题的分析研究者想了解同⼀⼈群⼲预前后的吸烟状态，且吸烟状态为⼆分类变量。
针对这种情况，可以使⽤McNemar’s检验，但需要先满⾜2项假设。
假设1：变量为⼆分类，且两类之间互斥。
假设2：所有研究对象均有前后两次测量数据。
这2项假设均与研究设计和数据类型有关。
三、SPSS操作1. 数据加权如果数据是汇总格式（如上图中的Total count data），则在进⾏卡⽅检验之前，需要先对数据加权。
如果数据是个案格式（如上图中的Individual scores for each paticipant），则可以跳过“数据加权”步骤，直接进⾏SPSS操作。
数据加权的步骤如下：在主界⾯点击Data→Weight Cases，弹出Weight Cases对话框后，点击Weight cases by，激活Frequency Variable窗⼝。
将freq变量放⼊Frequency Variable栏，点击OK。
2. McNemar’s检验在主界⾯点击Analyze→Nonparametric Tests→Related Samples。
出现Nonparametric Tests：Two or More Related Samples对话框。
