当前位置：文档之家 › 要领悟世界上最常用传递函数详解

要领悟世界上最常用传递函数详解

  • 格式：ppt
  • 大小：823.50 KB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

自动控制原理传递函数知识点总结

自动控制原理传递函数知识点总结

自动控制原理传递函数知识点总结自动控制原理是研究自动控制系统中信号传递、处理、转换等基本理论和方法的学科。

传递函数是描述线性时不变系统的数学模型，它对于分析和设计控制系统起着重要的作用。

下面将对自动控制原理中关于传递函数的知识点进行总结。

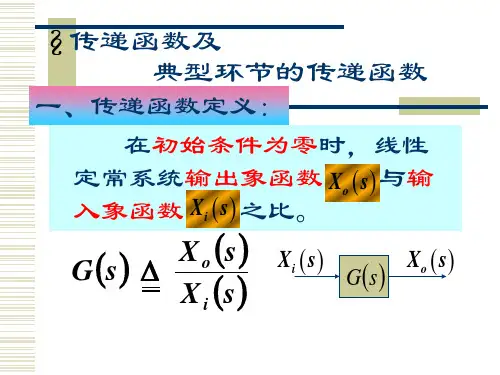
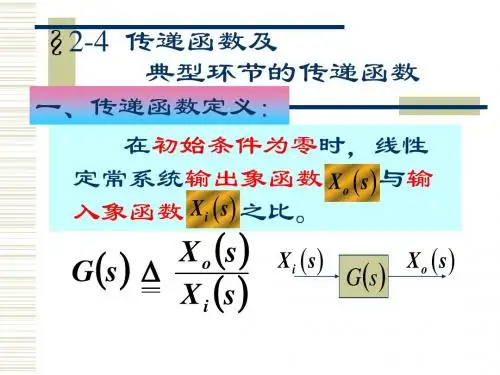
一、传递函数的定义传递函数是用来描述线性时不变系统输入-输出关系的数学函数。

对于连续时间系统，传递函数可以表示为：G(s) = Y(s) / X(s)其中，G(s)为传递函数，Y(s)为系统的输出信号，X(s)为系统的输入信号，s为复变量。

对于离散时间系统，传递函数可以表示为：G(z) = Y(z) / X(z)其中，G(z)为传递函数，Y(z)为系统的输出信号，X(z)为系统的输入信号，z为复变量。

二、传递函数的性质1. 时域特性：传递函数可以通过拉氏变换将时域的微分、积分方程转换为频域的代数方程，从而简化系统的分析和设计。

2. 稳定性：传递函数的稳定性与其极点位置有关。

当所有极点均位于左半平面时，传递函数是稳定的；当存在极点位于右半平面时，传递函数是不稳定的。

3. 零点和极点：传递函数的零点是使得传递函数为零的点，极点是使得传递函数无穷大的点。

零点和极点的位置对系统的动态性能和稳定性有重要影响。

4. 频率响应：传递函数的频率响应是指系统对不同频率输入信号的响应特性。

频率响应可以通过传递函数的频域分析获得，包括幅频特性和相频特性。

三、传递函数的常见形式1. 一阶系统传递函数：一阶系统的传递函数形式为：G(s) = K / (s + a)其中，K为传递函数的增益，a为系统的时间常数。

2. 二阶系统传递函数：二阶系统的传递函数形式为：G(s) = K / (s^2 + 2ζω_ns + ω_n^2)其中，K为传递函数的增益，ζ为阻尼比，ω_n为自然频率。

3. 传递函数的因果性：因果系统的传递函数在复平面上的极点全部位于左半平面，即Re(s) < 0。

非因果系统的传递函数在复平面上的极点存在于右半平面，即Re(s) > 0。

第03讲 传递函数

第03讲 传递函数
在零初始条件下，线性定常系统输出量的 拉普拉斯变换与输入量的拉普拉斯变换之比， 定义为线性定常系统的传递函数。 即，
2020/7/27
第3讲 传递函数
3
若已知线性定常系统的微分方程为
式中c(t)为输出量，r(t)为输入量 。
设c(t)和r(t)及其各阶导数初始值均为零，对式) 取拉氏变换，得
2020/7/27
（2）极点的位置决定模态的敛散性，即决定稳定 性、快速性。
2020/7/27
第3讲 传递函数
13
（3）零点决定各运动模态的比重。其本身并不形 成自由运动的模态，但它们却影响各模态在响应 中所占的比重。
➢零点距极点的距离越远，该极点所产生的模态所 占比重越大 ➢零点距极点的距离越近，该极点所产生的模态所 占比重越小 ➢如果零极点重合－该极点所产生的模态为零，因 为分子分母相互抵消。
其传递函数为
式中 T—— 惯性环节的时间常数 K—— 惯性环节的增益或放大系数
2020/7/27
第3讲 传递函数
20
当输入为单位阶跃函数时，其单位阶跃响应为 单位阶跃响应曲线
1)(is 1)
1)(Tjs 1)
式中，分子和分母中的一次因子对应于实数零点和极点；二次 因式对应于共轭的复数零点和极点；τi和Tj称为时间常数；K为 系统的传递系数或称静态增益；ξ或ζ为阻尼比。
由该表达式可以看出：系统可以分解为一些比较典型的环节。
2020/7/27
第3讲 传递函数
16
传递系数
前面介绍了两种传递系数K和Kg： 其中： Kg=b0/a0为分子与分母多项式中最高次项系
2020/7/27
第3讲 传递函数
8
6.传递函数分母多项式称为特征多项式，记为

传递函数

传递函数
传递函数
求助编辑百科名片
传递函数 transfer function 零初始条件下线性系统响应（即输出）量的拉普拉斯变换（或z变换）与激励（即输入）量的拉普拉斯变换之比。记作G（s）=Y（s）/U（s），其中Y（s）、U（s)分别为输出量和输入量的拉普拉斯变换。传递函数是描述线性系统动态特性的基本数学工具之一，经典控制理论的主要研究方法——频率响应法和根轨迹法——都是建立在传递函数的基础之上。
4. 如果系统的传递函数已知，则可以针对各种不同形式的输入量研究系统的输出或响应，以便掌握系统的性质；
5. 如果不知道系统的传递函数，则可通过引入已知输入量并研究系统输出量的实验方法，确定系统的传递函数.系统的传递函数一旦被确定，就能对系统的动态特性进行充分描述，它不同于对系统的物理描述；
6. 用传递函数表示的常用连续系统有两种比较常用的数学模型。
编辑本段
应用
传递函数主要应用在三个方面。
1、 确定系统的输出响应。对于传递函数G(s)已知的系统，在输入作用u(s)给定后，系统的输出响应y(s)可直接由G(s)U(s)运用拉普拉斯反变换方法来定出。
2、分析系统参数变化对输出响应的影响。对于闭环控制系统，运用根轨迹法可方便地分析系统开环增益的变化对闭环传递函数极点、零点位置的影响，从而可进一步估计对输出响应的影响。
3、用于控制系统的设计。直接由系统开环传递函数进行设计时，采用根轨迹法。根据频率响应来设计时，采用频率响应法。
编辑本段
局限性
1960年以来关于能控性和能观测性的研究表明，传递函数只是对系统内部结构的一种不完全的描述，只能表征其中直接或间接地由输入可控制和从输出中可观测到的那一部分。引入状态空间描述（见状态空间法），可弥补这种缺陷。

自动控制原理第四次课—传递函数及结构图简化

自动控制原理第四次课—传递函数及结构图简化

Mm(s)=CmIa(s)
Eb(s)=Kbsm(s)
J s2 m (s)=M m fsm (s)
c(s) = 1i m(s)
r (s)
e (s) Ks Us(s)
K Ua(s) a
1 Las Ra
c (s)
Eb(s)
Ia(s)
Cm Mm(s)
精选2021版课件
26
系统各元部件的动态结构图(6)
式的连接称为并联连接。
精选2021版课件
17
3. 反馈连接
R(s)
－
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后，得 到的输出再返回到这个方框的输入端，构成输 入信号的一部分。这种连接形式称为反馈连接。
精选2021版课件
18
三、系统动态结构图的构成
• 构成原则：
按照动态结构图的基本连接形式，构 成系统的各个环节，连接成系统的动 态结构图。
31
1. 串联结构的等效变换（２）
• 等效变换证明推导
R(s)
U(s)
G1(s)
G2(s) C(s)
U (s)= G 1 (s)R C ( (s s ) )= G 2 (s)U (s)
精选2021版课件
32
1. 串联结构的等效变换（３）
• 等效变换证明推导
R(s)
U(s)
C(s)
G1(s)
G2(s)
Ua(s)=KaUs(s) Ua(s)=RaIa(s)LasIa(s)
Eb(s)
Eb(s)=Kbsm(s)
J s2 m (s)=M m fsm (s)
c(s) = 1i m(s)
r (s)
e (s) K s Us(s) c (s)

第三节 系统的传递函数

第三节 系统的传递函数
输出量与输入量的积分成比例的环节，称为积 分环节。其显著特点是输出量取决输入量对时间的 积累过程。输入量作用一段时间后，即使输入量消 失为零，输出量仍将保持在已达到的数值，故积分 环节有记忆功能。
x(t )
xi (t)
1
xo (t)
O
t0
t
其运动微分方程为：x0 t
1 T1
xi t dt
其传递函数为：G s 1
2 n
m
Bx
式中 n
k; m
B。 2 km
由式 2-6 已知RLC电路的微分方程式为
LC d 2u0 t dt 2
RC du0 t dt
u0 t
ui t
通过拉氏变换求得其传递函数为
G s U0 s
1
Ui s LCs2 RCs 1
2
= s2
n
2 ns
2 n
R
L
式中
n
1; LC
R 。 ui(t) 2 L/C
与微分环节一样，一阶微分环节和二阶微分环 节在物理系统中也不会单独出现，在其组成中必然 包含有惯性环节或振荡环节。系统中引入一阶微分 环节和二阶微分环节主要是用于改善系统的动态品 质。
例2-16 如图2-16所示的无源RC电路，根据基尔霍夫定律 和欧姆定律可求得其传递函数为:
ui (t)
R1
C R2
二、典型环节及其传递函数
自动控制系统种类很多，构成环节的类型就其物 理本质可能差别很大。但从数学分析的观点看， 任何一个复杂的系统都仅有有限的几个典型环节 组成。这些典型环节是：比例环节、惯性环节、 积分环节、微分环节、振荡环节和延时环节。因 此，在研究系统动态特性时，熟悉和掌握各种典 型环节，有助于我们对复杂的系统进行分析研究。

要领悟世界上最常用传递函数详解

要领悟世界上最常用传递函数详解

例
如图所示弹簧-阻尼系统。
Xi(t)
kx i (t ) x 0 (t ) D
dx0 (t ) dt
Xo(t)
kX i (s) X o (s) DsXo (s)
D s 1X o (s) X i (s) k
X (s) 1 G (s) 0 X i (s) D s 1 k
其中
n
1 ； LC
R 2
C 。 L
（6）延时环节
输入xi (t )与输出xo (t )之间的关系 xo (t ) xi (t ) X o ( s ) e - s X i ( s ) X o ( s) G ( s) e - s X i ( s)
特点：延时环节也是线性环节，有输入信号后，在τ时间内没有任何输出， 到τ时间后，不失真地反映输入。 延时常作为一个特性，与其他环节共同存在，而不单独存在。
例 如图所示无源滤波电路，
1 u ( t ) i ( t ) R i( t )dt i C u ( t ) 1 i( t )dt 0 C
k
m
c
略去质量的阻尼—弹簧系统
Ui(t)
R
i(t)
Uo(t) C
已知


拉氏变换后得 消去I(s)，得
1 U ( s ) I ( s ) R I(s) i Cs U (s) 1 I(s) 0 Cs
数学模型 o (t ) ui (t ) RCu
uo(t)
RCsUo (s) U i (s)
U o ( s) 1 K G( s) U i ( s) RCs s
5
二阶振荡环节
G (s)

传递函数h(s)

传递函数h(s)

传递函数h(s)传递函数h(s)是控制工程中的一个重要概念，它能够描述一个系统的输入、输出之间的关系，被广泛地用于系统建模和控制器设计中。

本文将从以下几个方面介绍传递函数h(s)的相关内容。

1. 什么是传递函数h(s)传递函数h(s)被定义为系统输出与输入之间的比值，其中s表示Laplace变换的复频域变量。

传递函数h(s)通常表示成以下形式：h(s)=Y(s)/X(s)其中Y(s)为系统输出的Laplace变换，X(s)为系统输入的Laplace变换。

2. 传递函数h(s)的意义传递函数h(s)描述了输入信号在系统内传输和处理的方式，可以揭示系统的动态特性和频率响应特性。

其中，系统的动态特性包括零极点分布、系统阶数等内容；频率响应特性包括截止频率、幅频特性、相频特性等内容。

3. 传递函数h(s)的性质传递函数h(s)具有多种性质，下面介绍其中几个重要性质。

（1）时域特性：传递函数h(s)的逆Laplace变换可以得到系统的时间响应，这个响应包括系统的稳态响应和暂态响应。

（2）稳定性：当传递函数h(s)的所有极点均位于s平面的左半面时，系统是稳定的，否则系统是不稳定的。

（3）因果性：当传递函数h(s)是因果传递函数时，系统是因果的，否则系统是非因果的。

4. 传递函数h(s)的应用传递函数h(s)广泛应用于系统建模和控制器设计中。

在系统建模中，传递函数h(s)可以用来描述电路、机械系统、化学反应等各种物理系统；在控制器设计中，传递函数h(s)可以用来设计比例-积分-微分（PID）控制器、模型预测控制器、自适应控制器等各种控制器。

总之，传递函数h(s)是控制工程中不可或缺的重要概念，理解和掌握传递函数h(s)的相关内容，对于系统建模和控制器设计具有重大的意义。

传递函数介绍

传递函数介绍

第一节传递函数一、传递函数的概念为了描述控制系统中每一个部分或整个系统的输入变量与输出变量之间的关系，最常用的就是传递函数。

控制系统中的任意一个部分理论上讲都可以有多个输入变量和输出变量，如图2－l所示。

当只考虑一个输入量与一个输出量之间的关系时，就简化为图2－2。

如果描述该系统的微分方程已知为（2-1）对方程（2－l）进行拉普拉斯变换（设初始条件为零），得aOs2Y（s）＋a1sY（s）＋a2Y（s）=b0sX（s）＋blX（s）整理得（2-2）方程2－2中的G（S）就叫做方程2－l描述的系统的输入变量x与输出变量y之间的传递函数。

传递函数的使用，使得控制系统的分析非常方便。

二、拉普拉斯变换拉普拉斯变换将t域（时域）的函数变换为S域（复域）的函数，以带来运算和分析的方便。

这里不做严格的数学方法介绍，完全从实用的角度介绍一些结论和常用函数在t域和S域之间的对应关系。

所幸运的是，能在实际中产生的信号总有相对应的拉普拉斯函数。

设：①f（t）为实域函数，且当t＜0时f（t）=0；②s为复变量，F（s）为复域函数；③为拉普拉斯（算子）变换的运算符号。

定义f（t）的拉普拉斯变换为（2-3）1、常用函数的拉普拉斯变换（l）阶跃函数设函数f（t）为符合如下条件的阶跃函数：f（t）＝0 （t＜0＝（2－4）f（t）=A=常数（t ≥0）该函数的拉普拉斯变换用〔f（t）〕表示，得（2-5）当A=l时，称阶跃函数为单位阶跃函数，记为u（t），此时的拉普拉斯变换为（2-6）（2）斜坡函数没函数f（t）为符合下列条件的斜坡函数：f（t）＝0 （t＜0 （2-7）f（t）=At （t≥0）斜坡函数的拉普拉斯变换为（2-8）（3）指数函数设有符合如下条件的指数函数：f（t）=0 （t＜0＝f（t）＝Ae-αt （t≥0）式中，A和α为常数，指数函数的拉普拉斯变换为（2-10）（4）脉冲函数设有符合如下条件的脉冲函数：(0＜t＜t0＝(2-11)f（t）＝0 （t＜0,t＞t。

2-2 传递函数及方块图

2-2 传递函数及方块图

1 R1C1s 1
1 R2C2s 1
C (s)
R1C2 s
(b)
13
2－3
方块图
（C） 消除主反馈回路
R(s) 1 R1C1R2C2 s 2 ( R1C1 R2C2 R1C2 ) s 1 C (s)
可以看出：方块图的化简方法不是唯一 的，人们应充分地利用各种变换技巧，选择最 简捷的路径，以达到省力省时的目。
B
C + A BC
2
比较点分解
A
+
A BC
A +
-
+
B
+ AG B
A +
-
AG B G
1 G
3
比较点前移
A
G
B
AG BG
B
A 4 比较点后移 + B A AG BG
A B
G
G
+ -
G
5
分支点前移
G
AG
AG
A
G G
AG AG
10
6
分支点后移
A
G
AG
A
AG
G
1 G
A
B
A
A B
方块图
C N (s) G 2 (s) N(s) 1 G 1 (s)G 2 (s)H(s)
G1(s)H(s) 1
当 此时扰动的影响可被抑制 。 设扰动信号N（s）=0
R (s)
时，
C N (s) 0 N(s)
C R (s) G 1 (s)G 2 (s) R(s) 1 G 1 (s)G 2 (s)H(s)
21
4

传递函数及方块图

传递函数及方块图
± Bs Hs
反馈系统如图所 示，我们先熟悉几个
X o s 概念。
前向通路：输入 到输 出的一条线。
Xi s G s Xo s
反馈通路:输出到比较 点的曲线。
反馈回路 ：由前向通路和反馈通路 组成，终点与起点重合，是封闭的曲线。
X i s ×Es G1 s
± Bs Hs
X o s
Xi s+ E sG1
G7 s
X i s
G1 sG2 sG3 sG4 s
X o s
1G2 sG3 sG5 s G3 sG4 sG6 s G1 sG2 sG3 sG4 sG7 s
G
s
1
G2
s
G3
s
G5
s
G1 sG2 sG3 sG4 G3 sG4 sG6 s G1
s s
G2
s
G3
s
G4
s
G7
s
例：求下图所示系统的传递函数。
H3(s)
Xo(s)
5、消去H3(s) 反馈回路
Xi(s)
G1(s)G2 (s)G3 (s)
Xo(s)
1 G1(s)G2 (s)H1(s) G2 (s)G3 (s)H2 (s) G1(s)G2 (s)G3 (s)H3 (s)
G(s)
G1(s)G2 (s)G3(s)
1 G1(s)G2 (s)H1(s) G2 (s)G3(s)H2 (s) G1(s)G2 (s)G3(s)H3(s)
法一
G5 s
X i s ×
-
G1 s
×- G2 s × G3 s G4 s X o s
-
1
2
G6 s
步骤1） 比较点2 前移 G7 s

2.3传递函数及方块图

2.3传递函数及方块图

5 二阶振荡环节
对应时域方程： 拉氏变换：
1 G s = 2 2 T s + 2ζTs + 1
其中 0 < ζ < 1
T 2 xo t 2 Txo t xo t xi t T s X o s 2 TsX o s X o s X i s
1
G3
2
+
G2
A S
-
G1
+ H
Xo(s)
Xi(S)
-
A S
G1

G3 +
+ G2
Xo(s)
H
Xi(S)
1
G3 G1
2
+
G2
+ H
Xo(s)
步骤1） 比较点2 前移
G3/G1 Xi(S)
1
-
2 +
+
G1
H
G2
Xo(s)
步骤2） 比较点1、2交换位置
G3/G1
2
Xi(S)
+
1
+ -
G1 H
G2
Xo(s)
a n 1 s a n X o s


则系统传递函数为：
m m 1 Xo s b0 s b1 s bm 1 s bm G s n n 1 X i s a 0 s a 1 s a n 1 s a n
X i s
× G1 s × G2 s × G3 s 2 1
G7 s
-
G4 s
X o s
G6 s
X i s

五、传递函数

五、传递函数
LCs 2U o ( s ) RCsU o ( s ) U o ( s ) U i ( s )
Uo ( s) 1 G( s) U i ( s ) LCs 2 RCs 1
3
几点结论
传递函数是复数s域中的系统数学模型， 其参数仅取决于系统本身的结构及参数， 与系统的输入形式无关。 若输入给定，则系统输出特性完全由传递函 数G(s) 决定，即传递函数表征了系统内在的 固有动态特性。 传递函数通过系统输入量与输出量之间的关 系来描述系统的固有特性。即以系统外部的 输入－输出特性来描述系统的内部特性。
10
惯性环节
凡运动方程为一阶微分方程：
d T xo (t ) xo (t ) Kxi (t ) dt
形式的环节称为惯性环节。其传递函数为：
X o ( s) K G( s) X i ( s ) Ts 1
式中，K—环节增益（放大系数）； T—时间常数，表征环节的惯性，和 环节结构参数有关
式中，M(s)=b0(s-z1)(s-z2)…(s-zm)=0的根s=zi (i=1, 2, …, m)，称为传递函数的零点； 影响瞬态响应曲线的形状，不影响系统稳定性 N(s)=a0(s-p1)(s-p2)…(s-pn)=0的根s=pj (j=1, 2, …, n)，称为传递函数的极点； 决定系统瞬态响应曲线的收敛性，即稳定性
传递函数为：
G( s)
式中，T—积分环节的时间常数。
15
积分环节特点： 输出量取决于输入量对时间的积累过程。 且具有记忆功能； 具有明显的滞后作用。
如当输入量为常值 A 时，由于：
1 t 1 xo (t ) 0 Adt At T T
输出量须经过时间T才能达到输入量在t = 0 时的值A。 积分环节常用来改善系统的稳态性能。

第二章传递函数讲解ppt课件

第二章传递函数讲解ppt课件
求指数函数e-αt的象函数。
解:
F(s)L[eat] eaet stdt e(sa)tdt
0
0
1 e(sa)t
s
|0s1
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
常用函数的拉氏变换对照表
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
②定义： 设函数f(t)满足 ①t<0时 f(t)=0 ②t>0时，f(t)连续，则f(t)的拉氏变换存在，表示为：
F(s)L [f(t)]f(t)esdt 0
拉氏变换函数 （象函数）
原函数
衰减因子，其中： τ-时间常数 s = -σ+jω为拉氏变换算
子，其中： σ-衰减系数 ω-振荡频率（rad/s）
篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
建立控制系统数学模型的方法:
分析法(又称机理建模法)是根据组成系统各元 件工作过程中所遵循的物理定理来进行。例如： 电路中的基尔霍夫电路定理，力学中的牛顿定 理，热力学中的热力学定理等。对于系统结构 以知的常用此法。
④ 性质： 篮球比赛是根据运动队在规定的比赛 时间里 得分多 少来决 定胜负 的，因 此，篮 球比赛 的计时 计分系 统是一 种得分 类型的 系统
1) 叠加定理：两个函数代数和的拉氏变换等 于两个函数拉氏变换的代数和。 即
L[f1(t)f2(t) ]L[f1(t) ]L[f2(t) ]
dt

传 递 函 数

传 递 函 数
控制系统的传递函数主要具有以下性质。
（1）传递函数只适用于线性定常系统。由于传递函数是基于拉氏变换将原来的线 性常系数微分方程从时域变换至复频域而得到的，故仅用于描述线性定常系统。
（2）传递函数是在零初始条件下定义的，因此它表示了在系统内部没有任何能量 储存条件下的系统描述。如果系统内部有能量储存，传递函数中将会出现系统在
1.1 传递函数的定义
传递函数的概念是在用拉氏变换求解线性微分方程的基础上提出的，它是
经典控制理论中应用最广泛的一种动态数学模型。
设描述n阶线性定常系统的微分方程为
dnc(t) dn1c(t)
dc(t)
a0 dtn a1 dtn1 an1 dt anc(t)
b0
d m r (t ) dt m
记作
G(s)
C(s) R(s)
b0 s m a0 s n
b1sm1 a1sn1
bm1s bm an1s an
(n
m)
G(s) 反映了系统输出与输入之间的关系，描述了系统的特性，即为线性定
常系统的传递函数。
【定义 2-1】 线性定常系统中，在零初始条件下，系统输出量拉氏变换与输入
R(s) L (t) 1
所以，系统在单位脉冲输入信号 (t)作用下输出量的拉氏变换为 C(s) G(s)
故有：
g(t) L1 C(s) L1 G(s)
可见，传递函数 G(s) 的拉氏反变换是系统在单位脉冲输入信号 (t) 作
用下的输出量，它完全描述了系统的动态特性，所以是系统的数学模型，通常 也称为脉冲响应函数。
b1
d m 1r (t ) dt m1
bm1
dr(t) dt
bm r (t )
式中 c(t) ——系统输出量；

自动控制原理--传递函数相关知识

自动控制原理--传递函数相关知识

26.5
1
s 17.25
17.25
26.5
s (s 17.25)2 (26.5)2 (s 17.25)2 (26.5)2
所以
y(t)
1 e17.25t
cos 26.5t 17.25 e17.25t 26.5
sin 26.5t
1 e17.25t
cos
26.5t
17.25 26.5
sin
26.5t
D(s) a0sn a1sn1 an1s an D(s) 0即是系统的特征方程。
G(s) N (s) b0 (s z1)(s z2 ) (s zm ) D(s) a0 (s p1)(s p2 ) (s pn )
s zi (i 1, 2 m)是N (s) 0的根，称为传递 函数的零点，s pi (i 1, 2 n)是D(s) 0的根 是传递函数的极点。
因为组成系统的元部件或多或少存在惯 性，所以G(s)的分母阶次大于等于分子阶 次，即 n,是m有理真分式，若 ,我们m 就 n 说这是物理不可实现的系统。
二、传递函数的性质
(1)传递函数是一种数学模型，是对微分方程在零初始条件 下进行拉氏变换得到的；
(2)传递函数与微分方程一一对应；
(3)传递函数描述了系统的外部特性。不反映系统的内部物 理结构的有关信息；
R(s)
式中 ——环节的时间常数。
特点：输出量正比输入量变化的速度，能预示输 入信号的变化趋势。
实例：测速发电机输出电压与输入角度间的传递 函数即为微分环节。
5）振荡环节：其输出量和输入量的关系，由下面的 二阶微分方程式来表示。
T2
d 2 y(t) dt 2
2 T
dy (t ) dt

《控制工程》传递函数解析PPT课件

《控制工程》传递函数解析PPT课件

m
.. y(t
)
+
c
. y(t
)
+
k
y
(t)
f (t)
令初始条件均为零， 方程两边取拉氏变换
k c
第二章 传递函数
y(t)
m
f(t)
(ms 2 + cs + k ) Y( s ) F( s )
∴
G(s)
Y(s) F(s)
ms2
1 + cs
+
k
-
图2-5
例2 ： L、R、C 电路系统
R
L
u1(t)
则该系统的传递函数 G(S) 为：
G(s)
X0 (s) Xi (s)
bms m ansn
+ bm1s m1 + L + s0 + an1s n1 + L + a0
-
（n≥m）
传递函数方框图：
Xi(s) G（s）
X0(s)
第二章 传递函数
求传递函数的步骤：
1）列出系统微分方程（非线性方程需线性化） 2）假设全部初始条件均为零，对微分方程进行拉氏变换
系统综合设计的基础，因此，十分重要。
-
一、定义
第二章 传递函数
定义：对于单输入、单输出线性定常系统，当输入 输出的初始条件为零时，其输出量的拉氏变
换与输入量的拉氏变换之比。
设线性定常系统的微分方程为：
an x(0n)( t) + an1x(0n1)( t) + L + a0 x0( t)
bm x(i m)( t)
第二章 传递函数
第二章 传递函数

矿产

矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

矿产

矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

矿产

矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

则
G (s)
X 0 (s) 1 2 2 X i (s) T s 2Ts 1
特点:在一定条件下，具有振荡可能，取决于系统本身的固有特性， 这是因为有两个储能元件，有能量交换，这种能量交换在一定条件下 以振荡方式存在。 y 0 (t) f (t)
i
例 如图所示质量-弹簧-阻尼系统， 0 (t ) ky0 (t ) M 0 (t ) y 列方程 f i (t ) Dy 2 F ( s ) DsY ( s ) kY ( s ) Ms Y0 (s) i 0 0 经拉氏变换得 则传递函数为
由运算放大器构成的比例环节
R2 uo (t ) ui (t ) Kui (t ) R1 拉氏变换 U o ( s ) KU i ( s ) G ( s )
如图所示齿轮传动副，
i2 (t )
i1 (t )
u i (t )
+
K
0
u o (t )
R1
U o (s) K U i (s)
其中
n
1 ； LC
R 2
C 。 L
（6）延时环节
输入xi (t )与输出xo (t )之间的关系 xo (t ) xi (t ) X o ( s ) e - s X i ( s ) X o ( s) G ( s) e - s X i ( s)
特点：延时环节也是线性环节，有输入信号后，在τ时间内没有任何输出， 到τ时间后，不失真地反映输入。 延时常作为一个特性，与其他环节共同存在，而不单独存在。
典型环节的传递函数
（ 1）比例环节 由比例环节的数学模型 xo (t ) Kxi (t ) X o ( s ) KX i ( s ) 传递函数 X o (s) G( s) K X i (s)
特点：输出量与输入量成正比，输出不失真也不延迟，而 是按比例反映输入，即线性变化。
R2
(2)一阶惯性环节 凡运动方程为下面一阶微分方程
T d xo (t ) xo (t ) Kxi (t ) dt
形式的环节称为一阶惯性环节。其传递函数为：
G( s) X o ( s) K X i ( s ) Ts 1
式中，K—环节增益（放大系数）； T—时间常数，表征环节的惯性，和 环节结构参数有关
U i (s) (RCs 1)U o (s)
则
G (s )
U 0 (s ) 1 , 图 无源滤波电路 U i (s) RCs 1
其中，ui(t) ——输入电压； uo(t) ——输出电压； R为电阻；C为电容。
R
求低通滤波器的传递函数
u i (t )
i (t )
C
u o (t )
F s kX s
k
阻尼器
D
x(t)
t f t Dx
F s DsX s
Ds
质量
M
x(t)
t f t M x
F s Ms 2 X s
Ms 2
等效复阻抗
xi (t )
x0 (t )
k
数学模型为 o cx o kxo kxi m x (m s cs k ) X o ( s) kX i ( s)
i (t)
对于相同量纲的理想微分环节物理上是难以实现的， 电路中常遇到下述的近似微分环节。 2 近似微分环节
u i (t)
i (t ) ——输入转角； 其中， u0(t) ——输出电压。
图 永磁式直流测速机
G(s)
kTs Ts 1
1 u ( t ) i(t )dt i(t )R 已知 i C u 0 (t ) i(t )R
j 1 k 1 i 1 d 1 e b c

例7 图2-14所示的无源微分电路
C
i( t )
图 无源微分网络
1 U i (s) I(s) RI(s) 拉氏变换得 Cs u 0 (t) U 0 (s) RI(s) 其中， RCs 1 ui(t) ——输入电压 化简得 U i (s) R U 0 (s) u0(t) ——输出电压 RCs RC=T U ( s ) RCs R——电阻； G (s) 0 K=1 则 C——电容。 U i (s) RCs 1
2
m
c
质量 - 阻尼 - 弹簧系统
其传递函数为 X o (s) k G ( s) 2 X i ( s) m s cs k k/m 2 s (c / m) s k / m
振荡环节传递函数的一般表达式
2 n G ( s) 2 2 s 2n s n
k c 其中,n ， m 2 mk
式中，T—振荡环节的时间常数 ζ—阻尼比，对于振荡环节，0<ζ<1 K—比例系数
特点:在一定条件下，具有振荡可能，取决于系统本身的固有特性， 这是因为有两个储能元件，有能量交换，这种能量交换在一定条件下 以振荡方式存在。
等效弹性刚度
等效弹簧 刚度
力学模型
时域方程
拉氏变换式
弹簧
k
x(t)
f t kxt
传递函数
延迟环节与惯性环节的区别： 惯性环节从输入开始时刻起就已有输出，仅 由于惯性，输出要滞后一段时间才接近所要 求的输出值； 延迟环节从输入开始之初，在0 ~ 时间内, 没有输出，但t=之后，输出等于之前时刻 的 输入。
系统的传递函数可以写成：
K ( i s 1) ( 2 s 2 2 s 1) s v (T j s 1) (Tk2 s 2 2 kTk s 1)
(t )
r
x(t )
数学模型 x(t ) r (t )dt
0
t
X (s)
r X (s) r ( s) G ( s) s ( s) s
齿轮——齿条传动
ห้องสมุดไป่ตู้
积分环节传递函数的一般形式 : K G ( s) s
i2(t) ui(t)
i1(t)
R a +
C
例 如图所示无源滤波电路，
1 u ( t ) i ( t ) R i( t )dt i C u ( t ) 1 i( t )dt 0 C
k
m
c
略去质量的阻尼—弹簧系统
Ui(t)
R
i(t)
Uo(t) C
已知


拉氏变换后得 消去I(s)，得
1 U ( s ) I ( s ) R I(s) i Cs U (s) 1 I(s) 0 Cs
Y (s) 1 G (s) 0 Fi (s) Ms 2 Ds k 1/ k 2 M D M s2 2 s 1 k k 2 Mk 1/ k T 2s 2 , T 2Ts 1 M D , k 2 Mk
M k
D
f i (t) ——输入外力； 其中， y 0 ( t ) ——输出位移； M——质量； k——弹簧刚度； D——拈行阻尼系数。 图 质量-弹簧-阻尼系统
返回
5 二阶振荡环节
含有两个独立的储能元件，且所存储的能量能够相互 转换，从而导致输出带有振荡的性质，运动方程为：
2 d d T 2 2 xo (t ) 2 T xo (t ) xo (t ) Kxi (t ), 0 1 dt dt X o ( s) K G ( s ) 传递函数： X i ( s) T 2 s 2 2 Ts 1
电感 L 上的电压降 V L Li 电阻上的电压降 VR iR
L
i (t )
R
u i (t )
振荡电路
C
u o (t )
i Cuo VL LCuo ,VR CRuo
由电压平衡方程 ui (t ) VL VR uo (t ) 可得此网络的数学模型
数学模型 传递函数
其中，xi(t) ——输入位移； x0(t) ——输出位移 K——弹簧刚度； D——粘性阻尼系统。
图 弹簧-阻尼系统
（3）微分环节
输出量正比于输入量的微分。
i (t ) 微分环节的数学模型 xo (t ) T x X o ( s) X o ( s) TsX i ( s) 传递函数 G( s) Ts X i ( s)
LCuo (t ) RCuo (t ) uo (t ) ui (t ) ( LCs 2 RCs 1)U o ( s ) U i ( s )
U o (s) 1 G (s) 2 U i ( s ) LCs RCs 1
2 n 1/( LC ) 2 2 2 s ( R / L) s 1/( LC ) s 2n s n
z1 ni(t) z2
z1 z2
n 0 (t ) z 2 n i (t ) z1
N 0 (s) z 2 N i (s) z 1 G (s) N 0 (s) z 1 , N i (s) z2
k
n0(t)
其中，ni(t) ——输入轴转速； n0(t) ——输出轴速； Z1，Z2——齿轮齿数。
例
如图所示弹簧-阻尼系统。
Xi(t)
kx i (t ) x 0 (t ) D
dx0 (t ) dt
Xo(t)
kX i (s) X o (s) DsXo (s)
D s 1X o (s) X i (s) k
X (s) 1 G (s) 0 X i (s) D s 1 k
数学模型 o (t ) ui (t ) RCu
uo(t)
RCsUo (s) U i (s)