下载文档原格式
玉林市暴雨强度公式及计算图表广西壮族自治区气象服务中心2017年11月说 明1.本计算公式和图表是根据玉林国家气象站30年（1987-2016年）的连续自记雨量记录为基础，采用“年最大值法”对暴雨样本资料进行选样，由皮尔逊—Ⅲ型分布曲线拟合数据，得到P-i-t 关系表，再由最小二乘法求解公式参数得到。
2.以重现期2、3、5、10、20、30、50、100（年）相应的单一重现期暴雨强度公式制表。
设计暴雨强度可按选定设计重现期直接查用表列数值（单一重现期暴雨强度公式见表二）。
3.若采用其它重现期，设计暴雨强度可用重现期区间参数公式计算：n b t Aq )(167+=式中：q —设计暴雨强度[升/（秒·公顷）]，t —降雨历时（分钟），A —雨力，b 、n —地方常数（A 、b 、n 按重现期区间参数公式计算，公式见表三）。
4.考虑到绘制全国城市暴雨强度公式等值线图，列出包含重现期在内的暴雨强度总公式：457.0)16.065()lg 672.01(3544.319++=t P q 因总公式精度不及重现期区间参数公式，故建议推求其它重现期设计暴雨强度时使用区间参数公式。
5.本计算公式和图表适用的时间范围是1~200分钟，重现期范围是2~100年，空间范围是玉林市玉州区（含玉东新区）和福绵区。
应用重现期区间参数公式计算暴雨强度实例：求P=25年，t=50分钟的暴雨强度q 。
从重现期区间参数公式II ，得：)7.842ln(030.00.729--=P n =0.72047（取0.720） )842.7ln(334.014.169-+=P b =15.39979（取15.400） )870.2ln(4.18823.890-+=P A =36.85996（取36.860） 配得P=25年的暴雨强度计算公式如下：0.720)15.400(36.860167+⨯=t q 可按上式计算1～200分钟中任何时段的暴雨强度。
暴雨强度公式推求研究近年来由于气候的变暖和城镇化进程的加快,极端降雨事件频现,由此往往会导致排水系统排水不畅,甚至造成“内涝”的发生。
这就对城镇排水系统提出了更加严格的要求。
暴雨强度公式是城镇雨水排水系统设计的依据,直接影响着工程的投资和城市的安全。
然而,我国许多大城市所用暴雨强度公式多为上世纪80年代所编,在实际运用时存在诸多问题,更广泛的中小城市(镇)根本就没有编制过暴雨强度公式,只能套用邻近大城市的暴雨强度公式,这种做法显然不稳妥。
吴堡县的情况属于后者,因此迫切需要编制反映吴堡县暴雨规律的暴雨强度公式,以指导排水系统的规划和设计。
本文以吴堡县气象局提供的1995～2014年的原始降雨资料为基础,通过年最大值法和非年最大值法选样对比分析、三种频率曲线对原始降雨样本资料的频率调整,获得3组i-t-P数据表,然后运用4种求解非线性参数方程的方法推求出12组暴雨强度公式,以各种方法拟合的均方根误差结合计算值与实际值的差率为衡量标准,比选出最优的频率分布线型和最佳的吴堡县暴雨强度总公式和分公式。
对比分析两种选样方法得出,年最大值法较非年最大值法有选样简单、资料易得、独立性好、高重现期雨强合理、应用范围广等诸多优点,因此本文采用年最大值法选样。
以年最大值法选出的样本,分别采用三种频率曲线对样本资料进行频率调整,通过比较拟合误差得出皮尔逊III型分布曲线拟合效果最好、耿贝尔分布曲线次之、指数分布曲线拟合效果最差。
由三种频率曲线调整的3组i-t-P数据表为源数据,采用4种求参方法优化出12组暴雨强度公式,拟合结果表明：在同一分布曲线下4种优化算法的优劣顺序依次为麦夸尔特法、高斯牛顿法、黄金分割法、最小二乘法；在同一求参方法下3种分布曲线的优劣顺序依次为耿贝尔分布曲线、指数分布曲线、皮尔逊III 型分布曲线,这与频率调整结果不一致。
因此,在优选暴雨强度公式的最佳频率调整模型时应综合考虑原始降雨资料的规律特征、频率调整以及推求公式的拟合误差等诸多因素。
暴雨强度公式引言暴雨是一种极端降雨过程，通常伴随着强烈的降雨、大风和雷电等天气现象。
了解暴雨的强度对于城市防洪、农田排水等方面具有重要意义。
而暴雨强度公式是用来计算暴雨强度的数学模型，通过该公式可以预测暴雨的降雨强度，从而指导相关工程设计和防灾减灾工作。
背景在过去的几十年里，研究人员尝试利用不同的方法来推导暴雨强度公式。
根据降雨形成机理的不同，暴雨强度公式可以分为物理公式和经验公式两种类型。
物理公式是通过建立数学模型，考虑大气层中水汽的输送和降落过程等因素，推导出的暴雨强度公式。
这类公式具有较强的理论依据，但由于大气复杂性和参数难以精确确定等原因，物理公式的应用范围较窄。
经验公式则是通过统计分析历史降雨资料，结合观测数据推导出来的。
这类公式应用广泛，但其推导过程主要基于经验法则，对特定地区和特定时间范围内的数据拟合效果较好，但在其他地区和时间上的适用性有一定限制。
暴雨强度公式的常用形式针对不同的应用场景和需求，研究人员提出了多种暴雨强度公式。
以下是一些常用的形式：1.雷雨暴雨强度公式：•这类公式主要用于预测较短时段（通常小于1小时）的强降雨。
•典型的公式形式为：–$I = C \\times T^{-a}$–其中，I代表暴雨强度（单位为毫米/小时），I代表降雨的持续时间（单位为小时），I和I是经验系数。
•不同地区的经验系数可能有所不同，需要根据实际情况进行调整。
2.设计暴雨强度公式：•这类公式主要用于城市排水系统和防洪设施的设计。
•典型的公式形式为：–$I = \\frac{P}{T_m} \\times K$–其中，I代表暴雨强度（单位为毫米/小时），I代表设计降雨量（单位为毫米），I I代表设计降雨持续时间（单位为小时），I是经验修正系数。
•不同国家和地区有不同的设计暴雨强度公式，需要根据当地的设计标准进行选择和使用。
暴雨强度公式的应用根据实际需要，暴雨强度公式可以应用于以下方面：1.工程设计和规划：•防洪设施、城市排水系统、行道路和桥梁等工程的设计和规划过程中，需要预测暴雨强度，以确定相应的设计参数。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
暴雨强度公式的简便推求方法邓卫东 李萍 李艺 曹志农 徐浩宇（北京市市政工程设计研究总院，北京 100082）摘 要 利用计算机快速、循环计算的特点，对暴雨强度公式（总公式）的4个参数循环计算，以平均绝对均方差为计算目标，优选出各个参数的值。
此方法数学原理简单，计算过程便捷。
关键词 暴雨强度公式 简便计算方法0引言暴雨强度公式，是利用数学公式来拟合实测暴雨数据频率分析的结果P-i-t （重现期-降雨强度-降雨历时）关系值。
我国的暴雨强度公式（总公式）形式为：nb t P C A i )()lg 1(++=《室外排水设计规范》中提到用解析法、图解与计算结合法或图解法等方法求得A 、C 、b 、n 各个参数，此类方法求解单一公式（如2y 重现期、降雨历时5~120min ）或小范围（如重现期0.25~10y 、降雨历时5~120min ）总公式的精度基本能满足规范要求。
但是要推求大范围（如重现期2~100y 、降雨历时5~1440min ）总公式的精度很难满足要求。
本次介绍的暴雨强度公式寻优计算方法（Optimization calculation 以下简称OC 法），利用计算机程序对公式参数A 、C 、b 、n 在一定范围内循环计算，以平均绝对方差为计算目标，优选出各个参数的值。
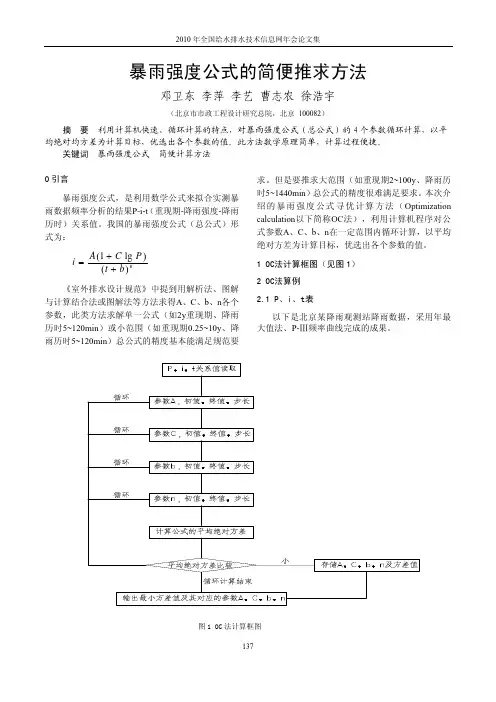
1 OC法计算框图（见图1） 2 OC法算例 2.1 P、i、t表以下是北京某降雨观测站降雨数据，采用年最大值法、P-Ⅲ频率曲线完成的成果。
图1 OC 法计算框图表1 P-i-t 表(单位：mm/min)2.2计算过程简介根据我国暴雨强度公式参数的特点，参数A 值的范围一般在5~50，参数C 值的范围一般在0.5~1.5，参数b 值的范围一般在5~20，参数n 值的范围一般在0.5~0.9。
计算过程中掌握好各个参数初值、终值和步长的关系，首先选用的初值、终值范围要大，步长也相应的大，根据计算结果，逐步缩小初值、终值范围及步长，这样可以节省计算时间。
收稿日期:2006-03-07基金项目:辽宁省自然基金项目(20072005)作者简介:傅金祥(1955-),男,教授,博士后,主要从事水处理理论与技术研究.
文章编号:1671-2021(2006)06-0959-03曲面搜索法推求暴雨强度公式参数傅金祥1,林 齐1,王俊凯2(1.沈阳建筑大学市政与环境工程学院,辽宁沈阳110168; 2.大连理工大学数学系,辽宁大连116023)摘 要:目的为解决暴雨强度公式参数在传统推求方法中所存在的非线性函数拟合的问题.方法应用黄金分割法将参数b和n的值固定,即将非线性函数进行线性化,并在由这两个参数所确定的曲面上,通过计算机的特性来搜索参数A1和C的最优
值.结果通过对线性函数的拟合,可以依次得到4个参数的值,近而推得暴雨强度公式.结论经过对多个城市的暴雨强度公式推求与比较,曲面搜索法能够快速、精确地得出计算结果,有效地解决了传统推求方法存在的诸多弊端,计算误差远远小于国家规范要求.
关键词:暴雨强度公式;曲面搜索法;黄金分割;最小二乘法中图分类号:X143 文献标识码:A
目前我国各城市应用的暴雨强度公式为超定非线性方程[1],参数的求解过程属于非线性函数
的优化问题.传统推求公式的方法一般存在着难以直接优化,或计算较为烦琐、拟合误差较大等诸多问题.现将曲面搜索法应用到暴雨强度公式的推求中.此法可以有效地对方程进行拟合并解得最优值,在对传统推求方法改进的基础上,大大提高了公式推求的速度和精度.使用VisualBasic610计算机语言编制了曲面搜索法推求暴雨强度公式参数的程序,计算机程序的应用大大提高了参数推求的速度,并且可以避免人为的计算错误,其推求结果远远小于国家规范所要求的0105mm#min-1的绝对误差和5%的相对误差[2].
1 曲面搜索法基本原理
曲面搜索法是在由已知参数所确定的二维曲面上,将曲面无限网格化,并对未知参数进行全局搜索,根据误差最小原则,得出参数的最优值.暴雨强度公式为四参数超定非线性方程,对未知参数进行拟合,可将参数A1和C分别看作是参数
b、n的函数,并分别表示为fA1(b,n)和fC(b,
n).则暴雨强度公式变为线性函数[3]i=f(A1,C,b,n)=fA1(b,n)(1+fC(b,n)lgP)(t+b)n=
g(b,n)(1)式中:降雨强度i、重现期P以及降雨历时t均为已知参数.A1为重现期1年的设计降雨的雨力,C为雨力变动参数,b为历时附加参数,n历时参数函数g(b,n)即为参数b、n构成的二维曲面函数,使用计算机程序,根据拟合式
EF=6mk=1[g(b,n)-ik]2(2)在曲面上对参数进行全局搜索,便可以将参数b、n的最优值解出.式中m为降雨历时的个数.在搜索过程中,还使用了黄金分割法,不断的大范围压缩搜索空间,以达到使未知参数快速接近最优值的目的.拟合得最优参数值后,便可以通过最小二乘法分别计算求得参数A1和C的值[4].
由于传统的曲面最小二乘法所使用的推导基础曲面,是由重现期P和降雨历时t所构成的二元空间曲面[5],所以这种方法只能推导出暴雨强
2006年11月第22卷第6期 沈阳建筑大学学报(自然科学版)JournalofShenyangJianzhuUniversity(NaturalScience) Nov. 2006Vol122,No16度公式的总公式.如果所提供的重现期只有一个,则公式推导过程中就会出现计算错误.而在曲面搜索法中,寻优基础是由降雨历时修正参数b和降雨衰减指数n所构成的曲面,这种方法不但可以推导出总公式,还可以推导出分公式[6].2 曲面搜索法推求步骤为了提高推求速度和计算精度,笔者使用计算机VisualBasic610语言编制了曲面搜索法推求暴雨强度公式的程序.现就其推求步骤进行说明.第一步:使用计算机程序导入降雨强度值i、降雨历时t和重现期P,即已知的i-t-P表.第二步:用黄金分割法在区间[0,20]内搜索降雨历时修正参数b的值;在区间[0,2]内搜索降雨衰减指数n的值[7].第三步:使用公式推求出雨力变动参数C的值.C=6lgP6i(t+b)n-m6ilgP(t+b)n6lgP6ilgP(t+b)n-6lgP26i(t+b)n第四步:使用公式推出重现期为一年的设计降雨的雨力参数A1的值.A1=6i(1+ClgP)(t+b)n6i(1+ClgP)2(t+b)2n第五步:计算公式的拟合误差EFEF=6mk=1[g(b,n)-ik]2第六步:比较误差的大小;如果符合要求,则返回参数的值;否则返回第二步,直到满足误差要求.至此,便得到了使用曲面搜索法推求出的暴雨强度公式的4个参数值.曲面搜索法推求暴雨强度公式程序流程图如图1所示.
图1 曲面搜索法推求暴雨强度公式程序流程图3 应用与分析
分别使用曲面搜索法和传统使用的最小二乘法推求4个城市的暴雨强度公式,并计算出公式的绝对误差R绝和相对误差R相并在表1中(4个城市分别定义为A、B、C、D)进行对比.其中,R绝
=6(i表-A1(1+ClgP)(t+b)n)2/m,R相=R绝/i表,式中的i表为所收集的降雨强度值[8].
表1 曲面搜索法和最小二乘法计算误差比较计算法A市R绝R相B市R绝R相C市R绝R相D市R绝R相
最小二乘法0106254169010461316101032421390102672143
曲面搜索法0103932195010343216901023811750101641149 注:表1中绝对均方差R绝的单位为mm#min-1;相对均方差R相的单位为%.
从表1中可以看到,曲面搜索法相对于最小二乘法在推求暴雨强度公式时,无论是绝对误差还是相对误差都有明显地下降[9].4个城市的误差最大下降了3816%,最小下降了2516%,平均下降26195%.可见,曲面法在推求暴雨强度公式时,计算精
960 沈阳建筑大学学报(自然科学版)第22卷度得到了显著地提高.此外,在计算速度,即搜索速度方面也有很大地提高.
4 结 论
(1)曲面搜索法将超定非线性式化为关于未知参数b、n的线性函数,利用计算机快速的全局搜索能力,在二维空间上寻得最优值[10].所解得
的值对目标值具有良好的拟合性,其计算速度相对于传统推求方法也有显著提高.(2)曲面搜索法可以作为一种新的方法来推求暴雨强度公式的参数,经过大量实际计算与应用,其计算速度与精度均高于其他方法,计算误差远远小于国家规范标准.(3)使用VisualBasic610语言编制的计算机程序,能够快速准确地计算出结果,可以节省大量烦琐的推求计算过程,并能避免人工推求出现的错误.可广泛的应用于暴雨强度公式参数的推求中.
参考文献:[1] 陈芸.GBJ14-87室外排水设计规范[S].北京:中
国建筑工业出版社,1998.[2] 周玉文,赵洪宾.排水管网理论与计算[M].北京:中国建筑工业出版社,2000.[3] LorenteJ.Relationbetweenmaximalrainfallratesfordifferenttimeintervalsinthecourseofastorm[J].AtmosRes,1991(7):61-66.[4] 金光淡.水文统计原理与方法[M].北京:中国工业出版社,1994.[5] GuestPG.Numericalmethodsofcurvefitting[M].Camb:CambridgeUniversityPress,1999.[6] 刘钧哲,马兴冠,傅金祥,等.皮尔逊III型分布曲线的快速简便算法[J].沈阳建筑工程学院学报,2004,20(1):60-62.[7] SrinivasM,PatnaikLM.Adaptiveprobabilitiesofcrossoverandmutationingeneticalgorithm[J].IEEETransactiononSystems,ManandCybernetics,1994,24(4):28-32.[8] HollandJH.GeneticAlgorithm[J].ScientificAmer2ican,1992(4):44-50.[9] 王小平.遗传算法理论、应用与软件实现[M].西安:西安交通大学出版社,2002.[10] AmrnellV.Reviewofrainfalldataapplicationforde2signandanalysis[J].WaterScienseandTechnology,1994(16):8-9.
CalculatingRainfallIntensityFormulaThroughtheMethodofSearchinginCurvedFace
FUJinxiang1,LINQi1,WANGJunkai2(1.SchoolofMunicipalandEnvironmentalEngineering,ShenyangJianzhuUniversity,Shenyang110168,China; 2.Depart2mentofMathematics,DalianUniversityofTechnology,Dalian116023,China)
Abstract:Toresolvetheproblemofnon2linearfunctionduringtheprocessoftraditionalcalculatingrainfallintensityformula.Wesuggestthemethodofsearchingincurvedface.Itfixesuptheparametersbandn,inanotherwords,itletthenon2linearfunctionbethelinearone.Onthefaceofparametersbandn,searchthebestanswersofparametersA1andC.Bycalculatingthelinearfunction,wecangetthefourparametersor2derlyandtherainfallintensityformula.Bycalculatingandcomparingseveralcitiescrainfallintensityformu2la,themethodofsearchingincurvedfacecouldgottheanswersfleetlyandaccurately,anditcouldresolvethedisadvantageoftraditionalcalculatingmethods.Theerrorisfarlessthanthecriterionrequest.KeyWords:rainfallintensityformula;methodofsearchingincurvedface;goldsegmentation;leasttwicemultiplication
