哈工程船舶流体力学答案六章

哈尔滨工程大学考研真题一、简要说明下列各种力产生的原因、求解思路及表达式1、 沿程阻力2、形状阻力3、惯性阻力4、机翼升力5、湍流应力二、图示水箱1中的水经光滑无阻力的圆孔口水平射出，冲到一平板上。

平板封盖着另一水箱2的孔口，水箱1中水位高度为1h ，水箱2 的水位高度为2h ，两孔口中心重合，而且直径12d d /2=。

若射流的形状时对称的，冲击到平板后转向平行于平板的方向，并向四周均匀流出。

假定流动是无粘性不可压缩定常的，平板和水质量力不计。

当已知1h 和水的密度ρ时，求保持平板封盖住水箱2的孔口时2h 的最大值。

三、工程中常用文丘里管测量管路中水的流量。

管路和收缩管段截面积分别为1S 、2S ，水的密度和U 型测压计中液体的密度分别为ρ、m ρ，且m ρρ〈。

若不计水的粘性，试导出倾斜管路中水的流量Q 与测压计中液体的高度差读数h 之间的关系式。

四、设在平面直角域中点A （a ，b ）处放着一个强度为Q 的平面点源，0,0x y ==是半无限固体壁面，远方压力为ρ∞。

试求： 1. 平面流动复势W(z)； 2. 壁面上流体的速度分布；3. 壁面0x =上流体的压力分布。

五、两块无限长二维平行平板如图所示，其间充满两种密度和粘性系数分别为12,ρρ和12,μμ的液体，高度分别为1h ，2h 。

已知下板静止，上板以速度U 向右运动，全流场应力相同，不计重力，流体运动为层流。

试求流场中的速度分布。

六、圆球在静水中释放后上浮，圆球的半径为a ，水和圆球的密度分别为,w m ρρ。

忽略水的粘性，试求圆球上浮运动之距离随时间的变化规律。

标准答案 一、（分析）考察学生对流体力学中出现的专业中常用的有关力的掌握程度。

1、沿程阻力：管道壁面粘性摩擦和粗糙度引起的阻力。

表达为圆管沿程阻力系数，2f l Vh d gλ∆= 2、形状阻力：由于粘性和流动分离产生的压力沿流动方向投影的合力。

求得压力后积分或试验测得，20cos 12p n D sD D p ds C U A αρ==⎰⎰或3、惯性阻力：非定常运动改变流体的惯性引起的阻力。

船舶与海洋工程结构物强度智慧树知到课后章节答案2023年下哈尔滨工程大学哈尔滨工程大学第一章测试1.不同类型的海洋平台的载荷工况都一样（）答案:错2.军船和民船的装载工况是相同的。

（）答案:错3.海洋平台结构的破坏模式主要是屈服破坏和疲劳破坏。

（）答案:错4.强度分析主要包括外载荷计算、内力分析、强度校核标准。

（）答案:对5.长方形梁截面的惯性矩与（）无关。

答案:粱的长度6.以下为全船性的外力的是（）。

答案:波浪压力;船体结构重量7.载荷随时间的变化性质分类有（）。

答案:动变载荷;静变载荷;冲击载荷;不变载荷8.虽然海洋平台的结构形式较多，但其总强度的模型主要有（）。

答案:三维空间模型;三维空间梁模型9.海洋平台受到的间接自然环境载荷包括以下（）答案:系泊力;惯性力10.造成海损事故的原因主要有（）。

答案:人为因素;恶劣海况;强度不足;意外事故第二章测试1.静置在波浪上的船体载荷曲线有两条性质，分别是：沿着船长分布的整个载荷曲线与轴线之间所包含的面积之和为0；上述面积对轴上任意一点的静力矩之和为零。

（）答案:对2.波长远大于船长或者远小于船长的情况下，浮力的分布与在静水中的浮力分布相差很小（）。

答案:对3.船体结构的响应分析是指（）。

答案:确定结构剖面中的应力或变形4.静置法中，船与波的相对速度为（）。

答案:=05.船舶静置在波浪上的总纵弯矩等于船舶在静水中的弯矩和船舶静置在波浪上的波浪附加弯矩之（）。

答案:和6.船舶在中垂状态下，（）在船中，此时船中浮力较（）。

答案:波谷；小7.进行平衡水线调整时，需要满足以下（）条件。

答案:重力和浮力的力矩相等;船体的排水体积不变;重力和浮力相等8.绘制船体重量曲线时，需要遵循以下（）原则。

答案:重量的重心位置不变;重量的大小不变;重量的分布范围大体一致9.船舶静置在波浪上的波浪附加弯矩，其值的大小与下列（）因素有关。

答案:波浪要素;船与波的相对位置10.下列图中为涌浪的是（）。

船舶流体力学测验第六章1.求解势流问题，首先要在一定边界条件和初始条件下求解（A）。

A.拉普拉斯方程B.欧拉方程C.拉格朗日方程D.伯努利方程2.理想流体的无旋流动称为（D）。

A.定常流动B.均匀流动C.不可压缩流动D.势流3.关于势流问题，下列错误的是（B）。

A.势流为无旋流B.基本方程为伯努利方程C.势函数满足拉普拉斯方程D.波浪问题可以用势流理论求解4.流体由平面上各个方向流过来汇聚于一点，这种流动称为（B）。

A.源B.汇C.偶极子D.点涡5.关于偶极子流，说法错误的是（B）。

A.是一种极限流动B.有大小，没有方向C.是一对特殊状态下的源、汇D.大小用偶极矩来表达6.流场中坐标原点处有一根无穷长的直涡线，强度为，方向垂直于图平面，则该涡线与图平面的交点即为一个点涡。

（对）7.绕圆柱体有环量流动中，单位长圆柱体所受升力大小与（D）无关。

A.来流密度B.来流速度C.环量D.圆柱体长度8.流体由平面上坐标原点流出，流向各个方向，这种流动称为（A）。

A.源B.汇C.偶极子D.点涡9.平面无环量圆柱绕流可以视为下列哪种流动的叠加（D）。

A.点源+点汇B.点源+均匀流C.点汇+均匀流D.偶极子+均匀流10.下列哪项不是流场中达朗贝尔缪理成立的条件（C）。

A.理想流体B.物体周围流场是无边际的C.物体做变速直线运动D.物体表面上没有分离11.绕圆柱体有环量流动可由下列（ABD）叠加得到。

A.均匀流B.点涡C.点汇D.偶极子12.物体在静止流体中做加速运动引起的附加质量，比在非定常流体中固定物体的绕流流动所引起的附加质量小，因而所受的流体作用力也小。

（对）13.在非匀速运动中，物体和流体存在相互作用。

流体会使物体产生附加惯性力的作用。

它是流体对物体的一种反作用力，表现为附加质量。

（对）。

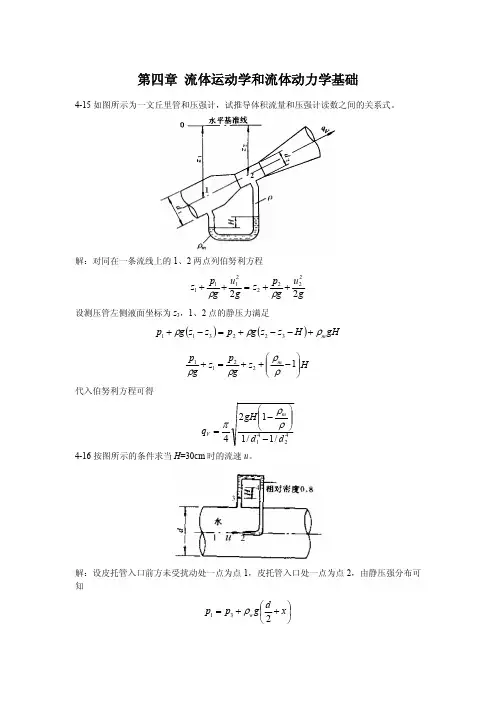
第四章 流体运动学和流体动力学基础4-15如图所示为一文丘里管和压强计，试推导体积流量和压强计读数之间的关系式。

解：对同在一条流线上的1、2两点列伯努利方程gu g p z g u g p z 2222222111 设测压管左侧液面坐标为z 3，1、2点的静压力满足gH H z z g p z z g p m 322311H z g p z g p m12211 代入伯努利方程可得4241/1/1124d d gH q m V4-16按图所示的条件求当H =30cm 时的流速u 。

解：设皮托管入口前方未受扰动处一点为点1，皮托管入口处一点为点2，由静压强分布可知x d g p p w 231x d H g p p w 242 gH p p w 8.043由以上三式，可得gH p p w 2.012由于1，2两点处于同一条流线上，对其列伯努利方程gp g u g p w w 2212 可得s m gH gp p g u w /084.13.08.94.04.0212 4-22如图所示，离心式水泵借一内径d =150mm 的吸水管以q V =60m 3/h 的流量从一敞口水槽中吸水，并将水送至压力水箱。

设装在水泵与吸水管接头上的真空计指示出负压值为39997Pa 。

水力损失不计，试求水泵的吸水高度H s 。

解：（1）取敞口水槽的自由液面与水泵出口之间的流体为控制体，令动能修正系数 1= 2=1，列伯努利方程gV g p H s 202222 吸水管内的平均流速为s m d q V V /943.015.03600/6044222可得 m g V g p H s 036.48.92943.08.910399972232224-29如图所示，一股射流以速度 0水平射到倾斜光滑平板上，体积流量为q V 0。

求沿板面向两侧的分流流量q V 1和q V 2的表达式，以及流体对板面的作用力。

忽略流体撞击的损失和重力影响，射流的压强分布在分流前后都没有变化。

第六章流体节流与缝隙流动(了解各种节流及缝隙流动现象，理解影响流量的因素，理解偏心状缝。

掌握气蚀现象。

) §6.1 流体的节流节流：管道内流体流经断面突然缩小的截面后，又进入和以前一样断面的管道，致使压力下降的现象，称为节流。

一、气体节流气体节流后各参数的变化规律，表6－1进行简要分析二、液体节流缝隙中油液产生运动的原因：1）缝隙两端存在压力差；1）组成缝隙的壁面存在相对运动；3）缝隙大小的变化。

缝隙中油液的运动大都呈稳定层流：1）缝隙高度与其长度宽度相比很小，液体在缝隙中流动时受固体壁面的影响；2）油液具有一定的粘度，Re一般很小。

§6.2 液体在小孔中的流动通道截面为圆孔型（分为薄壁小孔型和细长小孔型）。

l d≤。

薄壁小孔：当横隔板壁厚L与孔口直径d之比小于0.5，即/0.5l d>。

液压和润滑系统中的导油管。

细长小孔：小孔的长径比/4§6.3 液体流经平面缝隙平面缝隙：由两平行平面夹成的缝隙。

齿轮泵齿顶与泵壳之间的油液运动，柴油机中滑块与导板之间的油液流动。

结论：1）缝隙中液体流速按抛物线规律分布的；2）流经平面缝隙的流量与缝隙厚度δ的三次方成正比，和动力粘度μ成反比。

§6.4 液体流经同心环状缝隙同心环状缝隙：由内外两个同心圆柱面所围成的缝隙。

结论：流经平面缝隙的流量与缝隙厚度δ的三次方成正比。

§6.5 液体流经偏心环状缝隙偏心环状缝隙：在船舶机械中的环状缝隙，当运动部件装配不当或工作受力不均时，同心环状缝隙就变成偏心环状缝隙。

结论：流经偏心环状缝隙的流量与偏心距成正比，偏心距最大时，泄漏量为同心环状缝隙的2.5倍。

§6.6 液体流经具有相对运动的平行面缝隙喷油泵中的柱塞泵。

类型：（1、2、3）1）平行剪切流动∆=p，由于液体粘滞性，通过平行板的运动液体运动。

2）压差流动液体的运动，在缝隙两端的压差作用下实现。

3）压差与剪切流动的合成液体的运动，在缝隙两端的压差和平行剪切力的作用下共同实现。

工程流体力学水力学实验报告实验一流体静力学实验实验原理在重力作用下不可压缩流体静力学基本方程或(1.1)式中：z被测点在基准面的相对位置高度；p被测点的静水压强，用相对压强表示，以下同；p0水箱中液面的表面压强；γ液体容重；h被测点的液体深度。

另对装有水油（图1.2及图1.3）U型测管，应用等压面可得油的比重S0有下列关系：(1.2)据此可用仪器（不用另外尺）直接测得S0。

实验分析与讨论1.同一静止液体内的测管水头线是根什么线？测压管水头指，即静水力学实验仪显示的测管液面至基准面的垂直高度。

测压管水头线指测压管液面的连线。

实验直接观察可知，同一静止液面的测压管水头线是一根水平线。

<0时，试根据记录数据，确定水箱内的真空区域。

2.当PB，相应容器的真空区域包括以下三部分：(1)过测压管2液面作一水平面，由等压面原理知，相对测压管2及水箱内的水体而言，该水平面为等压面，均为大气压强，故该平面以上由密封的水、气所占的空间区域，均为真空区域。

(2)同理，过箱顶小水杯的液面作一水平面，测压管4中，该平面以上的水体亦为真空区域。

(3)在测压管5中，自水面向下深度某一段水柱亦为真空区。

这段高度与测压管2液面低于水箱液面的高度相等，亦与测压管4液面高于小水杯液面高度相等。

3.若再备一根直尺，试采用另外最简便的方法测定γ最简单的方法，是用直尺分别测量水箱内通大气情况下，管5油水界面至水面和油水界面至油面的垂直高度h和h0，由式，从而求得γ0。

4.如测压管太细，对测压管液面的读数将有何影响？设被测液体为水，测压管太细，测压管液面因毛细现象而升高，造成测量误差，毛细高度由下式计算式中，为表面张力系数；为液体的容量；d为测压管的内径；h为毛细升高。

常温(t=20℃)的水，=7.28dyn/mm，=0.98dyn/mm。

水与玻璃的浸润角很小，可认为cosθ=1.0。

于是有(h、d单位为mm)一般来说，当玻璃测压管的内径大于10mm时，毛细影响可略而不计。

6-1 求波长为145m 的海洋波传播速度和波动周期，假定海洋是无限深的。

解 考虑海洋波为平面进行波 当h →∞时， C=λαπλ25.1≈gm145=λ ⇒c=15m/sλπλτ8.02≈=gs 6.9=τ6-2 海洋波以10m/s 移动，试求这些波的波长和周期。

解 考虑海洋波为平面进行波 当h →∞时， C=λπλ25.12≈g ⇒225.1⎪⎭⎫ ⎝⎛=c λ=m 6425.1102=⎪⎭⎫⎝⎛λπλτ8.02≈=g⇒ s4.6648.0==τ6-3证明()()t iH A z w Ω-+=ξλπ2cos 为水深为H 的进行波的复势，其中iy x +=ξ为复变数，y 轴垂直向上，原点在静水面上。

并证明λπλπHth222=Ω(提示：xshy i xchy iy x sin cos )cos(-=+）证明： 由P134页 平面进行波速度势为)sin()(t kx chkhh z chk ag ωωϕ-+=（坐标轴为XOZ ，z 轴垂直向上）当上式速度势叠加1个相位=+-+=)2sin()(πωωϕt kx chkh h z chk ag )cos()(t kx chkhh y chk ag ωωϕ-+=（且坐标轴为XOY ，y 轴垂直向上） k ag x x∙-=∂∂=ωϕν )sin()(t kx chkHH y chk ω-+ =y v y ∂∂ϕ=)cos()(t kx chkHH y shk k ag ωω-+∙ 流出的ϕ与速度的关系：x∂∂ϕ=yv -=-=⇒⎰dx v y ϕ)sin()(t kx chkHH y shk ag ωω-+-y∂∂ϕ=xv则复势为：()[])()sin()cos()(1'H y chk wt kx i wt kx H y chk chkhagi z w +---+=+=ωφϕ因为()()t iH A z w Ω-+=ξλπ2cosk=λπ2iyx +=ξ⇒()()t iH iy x k A z w Ω-++=cos()())]()cos[()(cos H y ik t k kx A H y i t x k A z w ++Ω-=++Ω-=因为xshy i xchy iy x sin cos )cos(-=+ 则())]()sin()()[cos()]()cos[(H y shk t k kx i H y chk t k kx A H y ik t k kx A z w +∙Ω--+∙Ω-=++Ω-=令w k chkH agA =Ω⋅=1ω⇒)()('z w z w =因λπ22==k gkthkHw ⇒gkthkH k =Ω22⇒λπαπλH th g thkH k g 22⋅==Ω6-4 在水深为d 的水平底部（即d z -=处）用压力船热器记录到沿X 方向传播的进行波的压力为)(t P ，设)(t P 的最大高度（相对平衡状态来说）为H ，试确定所对应的自由面波的懂得圆频率，振幅。

习题二2.1 设质量力222222f ()()()y yz z z zx x x xy y =++++++++i j k 在此力场中，正压流体和斜压流体是否可以保持静止？说明原因。

解：22(22)(22)()0f y z i z x j x xy y k ∇⨯=-+-+++≠333333()2222220f f y z z x x y ⋅∇⨯=-+-+-=固正压流体不能保持静止，斜压流体可以保持静止。

2.2 在自由面以下10m 深处，水的绝对压力和表压分别是多少？假定水的密度为1000kg 3m -,大气压为101kpa 。

解： 表压为：10p p p gh ρ=-==1000*9.81=98100pa. 绝对压力为：10p p p =+=98100+101000=199100pa.2.3 正立方体水箱内空间每边长0.6m,水箱上面装有一根长30m 的垂直水管，内径为25mm,水管下端与水箱内部上表面齐平，箱底是水平的。

若水箱和管装满水（密度为1000kg 3m -），试计算：（1）作用在箱底的静水压力；（2）作用在承箱台面上的力。

解： （1）p gh ρ==1000*9.8*（30+0.6）=300186pa (2) F gv ρ==1000*9.8*(0.216+0.015)=2264N.2.4 如题图2.4所示，大气压力为a p =100kN 2m -,底部A 点出绝对压力为130kN 2m -,问压力计B 和压力计C 所显示的表压各是多少？解：C 表显示：1c A p p gh ρ=-=130-9.81*1=120.43kN 2m -B 表显示：2B A p p gh ρ=-=100+9.81*1*3=139.43kN 2m -2.5 倾斜式微压计由贮液杯和倾斜管组成，如题图2.5所示，贮液杯内自由面上的压力为大气压力a p ，斜管接待测压力p(<a p ),若p=a p 时斜管中液柱读数为0a ，试证明 00()(1)sin sin a sp p g a a s ραα-=-+式中，a 为测压时斜管中液柱的读数；s 为斜管的横截面积；0s 为贮液杯的横截面积；α为斜管的倾斜角。