模块综合评价

格式：docx
大小：322.53 KB
文档页数：13

下载文档原格式

/ 13

【学分】高中新课程学科模块学分认定的依据及认定表

高中新课程学科模块学分认定的依据学分认定的依据是学校已经开设、学生已经选修且经过考试（考核）已经达到课程标准要求的课程（模块）。

学生修习的课程（模块）达到的课程标准要求的条件是：1、学生修习时间要至少达到课程标准要求修习时间的4/5以上；2、学分认定考试（考核）成绩合格；学分认定考试科目：语文、数学、英语、政治、历史、地理、物理、化学、生物、信息技术。

学分认定考试难度为课程标准要求的基础知识和基本技能，每个模块学习结束后由学校统一组织命题和考试。

学分认定考核科目：音乐、美术、体育与健康、通用技术、研究性学习活动、社区活动、社会实践及学校课程。

考核科目由任课教师制定考核方案并报学分认定委员会审查后，对学生进行综合评价。

3、模块综合评价合格。

模块综合评价采用对学生学习量和学习过程表现及结果进行综合评价的办法（1）.考试科目模块综合评价成绩=学习过程表现成绩（40分）+考试成绩（60分）学习过程表现成绩（40分）=出勤分（满分10分）+课堂表现分（满分10分）+作业（满分10分）+平时测验分（满分10分）。

出勤分：迟到、早退扣0.5分/次，请假扣1分/节，旷课扣2分/节，扣完为止。

课堂表现分：优秀9-10分、良好7-9分、一般5-7分、差0-5分。

作业分：优秀9-10分、良好7-9分、一般5-7分、差0-5分。

平时测验分：平时测验平均分×10%。

出勤和作业情况由任课教师做好详细记录，经与班主任核实后，将原始表格交教导处存档保管。

考试成绩=学分认定考试卷面成绩×60%（2）.考核科目模块综合评价成绩=学习过程表现成绩（60分）+考核成绩（40分）学习过程表现成绩=出勤分（20分）+课堂表现分（40分）出勤：迟到、早退扣1分/次，请假扣2分/节，旷课扣4分/节，扣完为止。

课堂表现：优秀36-40分、良好28-36分、一般20-28分、差0-20分。

课堂表现优秀：指学习认真，勤于思考，敢于发表自己的见解，积极进行小组合作学习，课堂知识检查掌握情况好。

综合评价项目设计怎么写范文

综合评价项目设计怎么写范文综合评价项目设计范文：项目名称：综合评价系统设计1.项目背景介绍：随着教育的改革和发展，综合评价越来越受到重视。

在传统的教育模式中，只注重学生的考试成绩，忽视了其他方面的培养。

为了全面评估学生的能力和潜力，需要设计一个综合评价系统。

2.项目目标：设计一个综合评价系统，通过多个维度、多种方式对学生进行评价，提供全面的能力评估。

3.功能模块：（1）用户管理模块：管理员可以添加学生、教师和家长的信息，管理用户账号。

（2）评价指标设置模块：管理员可以设置评价指标，包括学科成绩、综合素质、课堂表现等。

（3）学生自评模块：学生可以在系统中进行自我评价，反思自己的学习和成长。

（4）教师评价模块：教师可以对学生进行评价，包括学习态度、课堂表现、作业完成情况等。

（5）家长评价模块：家长可以对学生进行评价，包括学习习惯、社交能力、与老师、同学的相处情况等。

（6）综合评价报告生成模块：系统可以根据各个评价指标的权重，生成综合评价报告，提供给教师、家长和学生查看。

4.项目实施计划：（1）需求分析和系统设计：2021年1月（2）系统开发和测试：2021年2月-2021年5月（3）系统上线和试运行：2021年6月（4）用户培训和反馈收集：2021年7月（5）项目总结和验收：2021年8月5.项目预期成果：（1）提供全面的学生评价，不仅考虑学科成绩，还包括综合素质、课堂表现等方面。

（2）激发学生的自主学习和反思能力，帮助他们全面发展。

（3）加强家校沟通，增进家长对学生发展的了解和参与。

6.项目风险分析和对策：（1）技术风险：可以提前进行系统开发和测试，确保系统的稳定性和安全性。

（2）用户接受度风险：可以提供用户培训和技术支持，帮助用户熟悉和使用系统。

（3）数据安全性风险：可以加强系统的数据安全保护措施，防止数据泄露和滥用。

7.项目评估和改进：在项目实施过程中，可以通过收集用户反馈和评估系统的使用效果，及时进行改进和优化，提高系统的稳定性和用户满意度。

2019年春八年级英语下册 Module 5 Cartoons模块自我综合评价五练习 (新版)外研版

模块自我综合评价五[测试范围：Module 5 时间：40分钟分值：100分] Ⅰ. 单项填空(20分)1．—Hurry up! It's time ________ class.—I'm coming.A．have B．have to C．to have D．having2．Mary expects ________ pets, but she finds them difficult ________．A．to have; to teach B．having; teachingC．to have; teaching D．having; to teach3．—________ your son ________ a camera?—No. He ________ one this summer vacation.A．Has; bought; will buyB．Did; buy; boughtC．Does; buy; boughtD．Does; buy; will buy4．About ________ of the students in our school were born in the________．A．three five; 2000 B．three fifths; 2000sC．third fifth; 2000 D．third fifths; 2000s5．Ultraman(奥特曼) can fly ________ the sky and fight ________ monsters(怪物)．A．over; with B．through; forC．in; for D．through; against6．The girl couldn't help ________ when her brother ate her apple.A．cried B．cries C．crying D．to cry7．I want to see how much he has changed ________ I saw him last time.A．since B．when C．as D．while8．—What a ________！ You must tidy up your room at once.—Sorry, Mum. I'll do it now.A．pity B．mess C．lie D．day9．—Which magazine do you like better, Crazy Reading or Teen's Space?—I like ________ of them, because they are useful for English learning.A．neither B．both C．all D．none10．—Would you mind ________ soccer here?—Sorry. We'll go and play on the playground.A．playing B．not playingC．not to play D．not playⅡ.完形填空(20分)I'm interested in __11__ cartoon movies a lot.My favourite cartoon character is Tintin who has lots of exciting experiences.Tintin has been popular __12__ more than 80 years, ever since the artist Hergé invented the character in 1929.Tintin is a reporter who has red hair and a small white dog.He looks very lovely and handsome.__13__ a reporter, he has fun in travelling all over the world and __14__ photos.He has travelled to the jungles, the backstreets of Shanghai and many places of interest.__15__ my surprise, he has even been to the surface of the moon.Tintinis not only clever but also helpful.He is always ready __16__ those who are in trouble.Tintin has won the __17__ of children as well as adults, so we can see him everywhere.__18__ a word, Tintin is the most excellent cartoon character that I've ever seen.In my opinion, we should learn __19__ Tintin and we should understand that __20__ is difficult if we put the heart into it.11．A.watch B．watched C．watching D．watches12．A.with B．for C．in D．on13．A.To B．As C．For D．With14．A.take B．took C．takes D．taking15．A.To B．For C．At D．As16．A.help B．helping C．to help D．helped17．A.head B．hearts C．hear D．heard18．A.As B．To C．In D．For19．A.in B．about C．from D．with20．A.everything B．something C．nothing D．anythingⅢ.阅读理解(20分)A．Mariah Carey.B．Colleen Madden.C．Kathy Duval.D．Gerry Turley.22．It's Dec. 8th. Mr Black wanted to give his little daughter a book as Christmas present, he'd better buy ________.A．All I Want for Christmas Is YouB．A Bear's YearC．The Only ChildD．The Perfect Dog23．What does the underlined word “hibernation” mean?A．物品 B．冬眠 C．运动 D．迁移24．The Only Child is mainly about ________.A．a young girl's Christmas wishB．the only girl in a familyC．a girl lost her way in a cityD．a lost girl lived in the forest25．We can find the information in ________．A．a clothes store B．a bookstoreC．a movie theatre D．a school libraryⅣ.选词填空(20分)根据短文内容，从方框中选择适当的单词填空，使短文意思完整。

雷达模块化效益综合评价研究

ＲｅｅｒｈＯｍｐｅｅｓｖａｕｔｏｆｓａｃｎＣｏｒｈｎｉｅＥｖｌａｉｎｏ
Ｒａａ０ｕａｉａｉｎＢｅｅｉｄｒＭｄｌｒｚｔ０ｎｆｔ
ＣＨＥＮＨｕｕｉｙｎ，ＨＵＡｎ —ａ，ＺＨＥＮＧｎ — ｈｎＸｉｇｌｉＬｏｇｓቤተ መጻሕፍቲ ባይዱｅｇ，ＰＡＮｎｌｎＸｉ —ｏｇ
（军雷达学院，湖北武汉４０１）空３０９
摘要：针对雷达模块化效益涉及众多方面因素的特点，定量研究雷达模块化效益，先对雷达模为首
块化效益的概念进行了界定，析了效益特点，立了构建评价指标体系的原则。其次针对科研、产、分确生使
用和维修保障四个部门，过分解与综合的方法，立了１通建５个分别属于军事效益、济效益、术效益和环经技
保效益四种不同形态的效益指标体系，后根据雷达模块化效益和指标体系的特点，择灰色层次评价模最选
型进行综合评价，用具体例子予以论证。并
关键词：雷达；块化；效益；综合评价；色层次分析模灰
中图分类号：ＴＮ９６５文献标识码：Ａ文章编号：６２２３（０００５３０１７ — ３７２１）６００ — ７

九年级英语上册 module 7 great books自我综合评价七课件

第二十页，共三十六页。
模块自我(zìwǒ)综合评价七
“What is it？” whispered Huck, going white with fright. “Keep quiet! There's someone downstairs.” The boys lay down, looking through the holes in the wooden floor. There were two men downstairs. One was an old Spaniard in a wide sombrero hat and the other was dirty and unpleasantlooking.
D．the best
【解析】“one of＋the＋形容词的最高级＋名词(míng cí)复数”表示
“……中最……之一”。
C 17．A.listen B．Speak C．listening D．speaking
B 18．A.in
B．at
C．for
D．to
C 19．A.write B．wrote C．to write D 20．A.writers B．drivers C．singers
A．in turn
B．in reward
C．in return
D．in honour
11．—Why don't you go to Lao She Teahouse tonight?
—_____D___．
A．It doesn't matter
B．Thank you
C．Sorry to hear that D．Sounds great
第十九页，共三十六页。

外研版九年级英语下册Module6模块自我综合评价

第1页/共15页模块自我综合评价六 [测试范围：Module 6 时间：45分钟分值：100分] Ⅰ.单项选择(15分) ( )1.—How to keep the children safe is a problem at the zoo. —Ask them just to do ________ the rules say. A．as B．with C．by D．for ( )2.Don't get angry. You needn't be ________ for such small things. A．pleased B．strict C．cross D．borrowed ( )3.This machine is used ________ car wheels. A．by making B．for make C．to making D．for making ( )4.Here are some fish and chicken. Help ________， children. A．yourself B．you C．your D．yourselves ( )5.There will be a sale at the clothing store. Some clothes at half price will be ________. A．served B．played C．taken D．carried ( )6.Bill didn't play computer games ________． A．any more B．no more 第2页/共15页

C．any longer D．no longer ( )7.Books are made ________ paper and paper is made ________ wood. So, saving paper is protecting the environment. A．from; from B．of; from C．from; of D．of; of ( )8.—Has Jane done the washing yet? —You can't ________ her to do such a thing. A．want B．hope C．expect D．wish ( )9.According to the school ________， our schoolleavers' party falls on May 30th. A．event B．experience C．calendar D．note ( )10.Hurry up! Once the concert starts, nobody________ to enter the concert hall. A．allows B．allowed C．is allowed D．is allowing ( )11.A lot of money will be spent________ poor people live better lives. A．to help B．helping C．helped D．help ( )12.Finger food is the food that you can eat________ your fingers. 第3页/共15页

八年级英语下册Module5Cartoons模块自我综合评价五练习(新版)外研版

浙江综合素质评价评价系统(学生版)

学生操作手册
第一步：账号登录
模块成绩确认的综合素质评价网址https:///index.action ，（可百度搜索“浙江省普通高中学生综合素质评价信息管理平台”）
附：平台技术中心提示，新系统建议使用谷歌浏览器，其他浏览器无法全面支持新系统）用户名：学生本人的身份证号码
密码：身份证后8位（进入后要修改密码，密码要设为“强”强度密码）
第二步：进行模块成绩，选修课成绩，获奖和综合素养情况的确认高一学生需要确认高一上、高一下两学期的模块成绩、选修课成绩，获奖情况和综合素养情况。

高二学生需要确认高一上、高一下、高二上、高二下两学期的模块成绩、选修课成绩，高二上、高二下两学期获奖情况和综合素养情况。

①点左侧的，出现
学生对自己所获得的模块成绩，选修课成绩没有异议的点击右侧的“确认”，如成绩有明显出入的可以点击“申诉”按钮向责任教师提出申诉(同时电话联系责任教师回应申诉，否则老师没及时看到将导致原始成绩生效而无法更改)。

②点击左侧的，如果有获奖情况的就会有显示，没有的就会显示“无符合条件的信息”，对自己的获奖情况没有意义的点击右侧的“确认”。

③点左侧的，
会出现
如果对自己的综合素养情况没有异议的点击右侧的“确认”。

（确认与申诉、责任教师回应申诉必须在7月31号之前完成）。

浙江省普通高中综合素质评价系统

浙江省普通高中综合素质评价系统篇一：浙江综合素质评价评价系统(学生版)学生操作手册第一步：账号登录模块成绩确认的综合素质评价网址https:///index.action，（可百度搜索“浙江省普通高中学生综合素质评价信息管理平台”）附：平台技术中心提示，新系统建议使用谷歌浏览器，其他浏览器无法全面支持新系统）用户名：学生本人的身份证号码密码：身份证后8位（进入后要修改密码，密码要设为“强”强度密码）第二步：进行模块成绩，选修课成绩，获奖和综合素养情况的确认高一学生需要确认高一上、高一下两学期的模块成绩、选修课成绩，获奖情况和综合素养情况。

高二学生需要确认高一上、高一下、高二上、高二下两学期的模块成绩、选修课成绩，高二上、高二下两学期获奖情况和综合素养情况。

①点左侧的，出现学生对自己所获得的模块成绩，选修课成绩没有异议的点击右侧的“确认”，如成绩有明显出入的可以点击“申诉”按钮向责任教师提出申诉(同时电话联系责任教师回应申诉，否则老师没及时看到将导致原始成绩生效而无法更改)。

②点击左侧的，如果有获奖情况的就会有显示，没有的就会显示“无符合条件的信息”，对自己的获奖情况没有意义的点击右侧的“确认”。

③点左侧的，会出现如果对自己的综合素养情况没有异议的点击右侧的“确认”。

（确认与申诉、责任教师回应申诉必须在7月31号之前完成）篇二：浙江省普通高中学生综合素质评价浙江省普通高中学生综合素质评价实施指导意见各市、县（市、区）教育局：普通高中学生综合素质评价工作是课程改革的重要内容。

为加强指导，积极推进普通高中学生综合素质评价工作，现将普通高中学生综合素质评价的有关指导意见印发给你们，并就有关事项通知如下：一、各地根据本指导意见的要求，结合当地实际，可制定具体的实施方案。

各地在制定具体实施方案时，要努力体现高中新课程改革精神，反映高中新课程实施方案的要求。

要通过基础教育评价体系的改革和评价结果的合理使用，给普通高中的教育以正确的导向，促进全面实施素质教育。

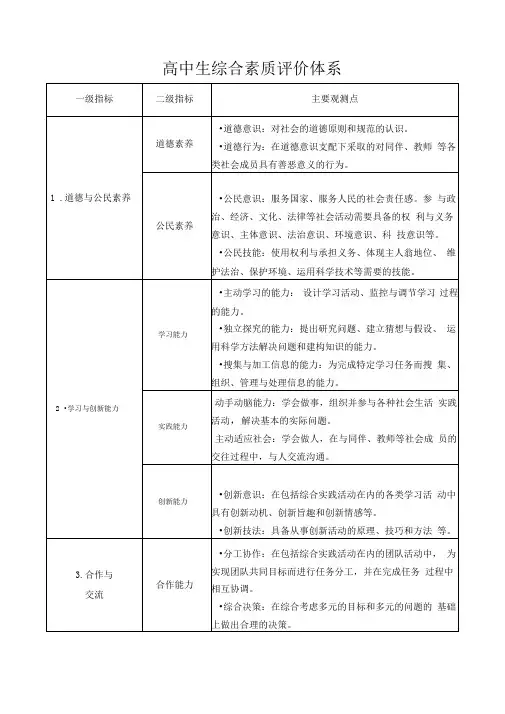
高中生综合素质评价体系

高中生综合素质评价体系
普通高中学生综合素质评价表
（年级第学期）
普通高中毕业生综合素质评价报告单
高中学生综合素质评价表
高级中学学生综合素质评价表
填写说明
（1）A1分值在11分及以上、A2分值在7分及以上、A4分值在11分及以上者，评价结果为合格。

受到学校记过处分的， A1、A2、A4被评为不合格。

（2）A3：
阶段性考试成绩班级前90涉，该项目评价为A（36分及以上）；
经常不交作业；考试有舞弊行为的为 D级（低于24分）；
32分到35分（包括32分、35分）为B级；
24分到31分（包括24分、31分）为C级。

（3）A5:以体育老师提供的成绩为等级评价标准。

这里相应的A级为9、10分；
7、8分为B级；
6分为C级；
5以及以下为D级。

（4）A6:
以艺术老师提供的成绩为等级评价标准。

这里相应的 A级为9、10分；
7、8分为B级；
6分为C级；
5以及以下为D级。

（5）优秀学生评选的基本条件：3合格1A2B总分在85分以上（含85分）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

模块综合评价 (时间：120分钟满分：150分) 一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的) 1.如图所示，已知AB∥A′B′，BC∥B′C′，那么下列比例式成立的是( )

A.OA′OA＝OCOC′ B.A′B′AB＝B′C′BC C.A′C′AC＝OCOC′ D.ABA′B′＝OCCC′ 解析：因为AB∥A′B′，所以OA′OA＝OB′OB.同理OC′OC＝OB′OB. 所以OA′OA＝OC′OC，所以A不成立． A′B′AB＝OB′OB＝B′C′BC，所以A′B′AB＝B′C′BC，

所以B成立．由于OA′OA＝OC′OC.所以AC∥A′C′. 所以A′C′AC＝OC′OC，所以C不成立． ABA′B′＝OBOB′＝OCOC′，所以D不成立．答案：B 2．在Rt△ABC中，CD是斜边上的高线，AC∶BC＝3∶1，则S△ABC∶S△

ACD为( )

A．4∶3 B．9∶1 C．10∶1 D．10∶9 解析：因为AC∶BC＝3∶1，所以S△ACD∶S△CBD＝9∶1，所以S△ABC∶S△ACD＝10∶9. 答案：D 3.如图所示，在正方形ABCD中，E为AB中点，BF⊥CE于F，那么S△BFC∶S正方形ABCD＝( )

A．1∶3 B．1∶4 C．1∶5 D．1∶6 解析：因为S△BEC∶S正方形ABCD＝1∶4，又S△BEF∶S△BCF＝(BE∶BC)2＝1∶4，所以S△BFC∶S正方形ABCD＝1∶5. 答案：C 4.如图所示，在△ABC中，EE1∥FF1∥MM1∥BC，若AE＝EF＝FM＝MB

，则∶∶∶为( )

A．1∶2∶3∶4 B．2∶3∶4∶5 C．1∶3∶5∶7 D．3∶5∶7∶9 解析：因为∶＝1∶4，所以∶＝1∶3，又因为∶＝1∶9，所以∶＝1∶5，又因为∶S△ABC＝1∶16，所以∶＝1∶7. 答案：C 5．如图所示，⊙O中弧AB的度数为60°，AC是⊙O的直径，那么∠BOC＝( )

A．150°B．130°C．120°D．60° 解析：由条件可知，∠AOB＝60°，所以∠BOC＝120°. 答案：C 6．圆内接四边形ABCD中，∠A，∠B，∠C的度数比是2∶3∶6，则∠D＝( ) A．67.5° B．135° C．112.5° D．110° 解析：因为∠A＋∠C＝∠B＋∠D＝180°，∠A∶∠B∶∠C＝2∶3∶6，所

以∠B∶∠D＝3∶5，所以∠D的度数为58×180°＝112.5°. 答案：C 7.如图所示，在△ABC中，∠C＝90°，CD⊥AB，D为垂足，若CD＝6 cm，AC∶BC＝1∶2，则AD的值是( ) A．6 cm B．32 cm C．18 cm D．36 cm 解析：因为AC∶BC＝1∶2，AC2＝AD·AB， BC2＝BD·AB，所以AD∶DB＝1∶2，所以可设AD＝t，DB＝2t，又因为CD2＝AD·DB，所以36＝t·2t，所以2t2＝36，所以t＝32(cm)，即AD＝32 cm. 答案：B 8.如图所示，用与底面成30°角的平面截圆柱得一椭圆截线，则该椭圆的离心率为( )

A.12 B.33 C.32 D．非上述结论解析：用平面截圆柱，椭圆截线的短轴长为圆柱截面圆的直径，且椭圆所在平面与底面成30°角，

则离心率e＝cos 60°＝12. 答案：A 9.如图所示，AB，AC为⊙O的切线，B和C是切点，延长OB到D，使BD＝OB，连接AD.如果∠DAC＝78°，那么∠ADO等于( )

A．70° B．64° C．62° D．51° 解析：如图所示，连接OC.

由AB为切线，有OB⊥AB.因为OB＝BD，所以∠AOB＝∠D，∠OAB＝∠DAB，而∠CAO＝∠OAB，

所以∠OAB＝13∠CAD＝13×78°＝26°. 所以∠AOD＝∠ADO＝64°. 答案：B 10.如图所示，AB是⊙O的直径，BC，CD，DA是⊙O的弦，且BC＝CD＝DA，则∠BCD＝( )

A．100° B．110° C．120° D．135°

解析：因为AB是⊙O的直径，所以ACB︵的度数是180°，因为BC＝CD＝DA，所以BC︵＝CD︵＝DA︵，所以∠BCD＝12(180°＋60°)＝120°. 答案：C 11.如图所示，⊙

O是△ABC的外接圆，AD是⊙O的直径，连接CD，若⊙O的半径r＝32，AC＝2，则cos B的值是( )

A.32 B.53 C.52 D.23 解析：cos B＝cos D，又因为AD为直径，所以cos D＝DCAD＝32－223＝53. 答案：B 12．如图所示，AB＝2，BC＝2，CD＝1，∠ABC＝45°，则四边形ABCD的面积为( )

A.3＋33 B.3＋224 C.3＋222 D.3＋34 解析：如图所示，连接AC，OD，则△ABC为等腰直角三角形，AC＝2，S△ABC＝12×2×2＝1.又因为OD＝OC＝CD，所以△OCD为等边三角形，所以∠OCD＝60°，所以∠ACD＝60°－45°＝15°，

S△ADC＝12·AC·DCsin 15°＝3－14，因此四边形ABCD的面积为3＋34. 答案：D 二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上) 13．如图所示，点E、F分别在AD、BC上，已知CD＝2，EF＝3，AB＝5

，若EF∥CD∥AB，则CFFB等于________．

解析：如图所示，过点C作CH∥DA交EF于点G，交AB于点H，则EG＝AH＝DC＝2，

GF＝1，BH＝3. 因为GF∥HB，

所以CFCB＝GFHB＝13，所以CFFB＝12. 答案：12 14.如图所示，AB是半圆O的直径，点C在半圆上，CD⊥AB于点D，且AD＝3DB，设∠COD＝θ，则tan2θ2＝__．解析：设半径为r，则AD＝32r， BD＝12r，由CD2＝AD·BD得CD＝32r，从而θ＝π3，故tan2θ2＝13. 答案：13 15.如图所示，PA与圆O相切于点A，不过圆心O的割线PCB与直径AE相交于D点．已知∠BPA＝30°，AD＝2，PC＝1，则圆O的半径等于________．

解析：因为PA为切线，所以AE垂直于PA，又因为∠BPA＝ 30°，且AD＝2，所以PD＝4，由切割线定理得PA2＝PC·PB，所以(23)2＝1×PB⇒PB＝12，所以CD＝3，BD＝8，所以CD·DB＝AD·DE⇒3×8＝2×DE，所以DE＝12，所以圆的直径为14，所以圆的半径为7. 答案：7 16．如图所示，AC为⊙O的直径，OB⊥AC，弦BN交AC于点M.若OC＝3，OM＝1，则MN的长为________．答案：1 三、解答题(本大题共6小题，共70分．解答时应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)如图所示，在△ABC中，AD为BC边上的中线，F为AB上任意一点，CF交AD于点E，求证：AE·BF＝2DE·AF.

证明：如图所示，过D作DG∥AB，交CF于点G，所以△AEF∽△DEG，△CDG∽△CBF，

所以AEAF＝DEDG，DGBF＝CDCB. 因为D为BC的中点，CD＝12CB， DGBF＝12，DG＝12BF，AEAF＝2DEBF，

即AE·BF＝2DE·AF 18.(本小题满分12分)如图所示，⊙O与⊙O′相交于A、B两点，过A引直线CD，EF分别交两圆于点C、D、E、F，EC与DF的延长线相交于点P，求证：∠P＋∠CBD＝180°.

证明：如图所示，连接AB，因为∠E与∠CBA是圆O中AC︵所对的圆周角，所以∠E＝∠CBA. 又四边形ABDF内接于⊙O′，所以∠PFA＝∠ABD，所以∠E＋∠PFE＝ ∠CBA＋∠ABD＝∠CBD. 又因为∠E＋∠P＋∠PFE＝180°，所以∠P＋∠CBD＝180°. 19.(本小题满分12分)如图所示，在⊙O中，相交于点E的两弦AB，CD的中点分别是M，N，直线MO与直线CD相交于点F.

证明：(1)∠MEN＋∠NOM＝180°； (2)FE·FN＝FM·FO. 证明：(1)如图所示，

因为M，N分别是弦AB，CD的中点，所以OM⊥AB， ON⊥CD，即∠OME＝90°，∠ENO＝90°，因此∠OME＋∠ENO＝180°. 又四边形的内角和等于360°，故∠MEN＋∠NOM＝180°. (2)由(1)知，O，M，E，N四点共圆，故由割线定理即得 FE·FN＝FM·FO. 20.(本小题满分12分)如图所示，AB和BC分别与圆O相切于点D，C，AC经过圆心O，且BC＝2OC.求证：AC＝2AD.

证明：如图所示，连接OD. 因为AB和BC分别与圆O相切于点D，C，所以∠ADO＝∠ACB＝90°. 又因为∠A＝∠A，所以Rt△ADO∽Rt△ACB.

所以BCOD＝ACAD. 又BC＝2OC＝2OD，故AC＝2AD. 21．(本小题满分12分)如图所示，AB为⊙O的直径，直线CD与⊙O相切于E，AD垂直CD于D，BC垂直CD于C，EF垂直AB于F，连接AE，BE. 证明：(1)∠FEB＝∠CEB； (2)EF2＝AD·BC.