2018年中考常见几何模型分析

2018-2019学年九年级数学初中常见几何模型汇总（图片版）第一篇：2018-2019学年九年级数学初中常见几何模型汇总(图片版) 初中常见几何模型汇总全等变换平移：平行等线段（平行四边形）对称：角平分线或垂直或半角旋转：相邻等线段绕公共顶点旋转对称全等模型说明：以角平分线为轴在角两边进行截长补短或者作边的垂线，形成对称全等。

两边进行边或者角的等量代换，产生联系。

垂直也可以做为轴进行对称全等。

对称半角模型说明：上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称（翻折），翻折成正方形或者等腰直角三角形、等边三角形、对称全等。

旋转全等模型半角：有一个角含1/2角及相邻线段自旋转：有一对相邻等线段，需要构造旋转全等共旋转：有两对相邻等线段，直接寻找旋转全等中点旋转：倍长中点相关线段转换成旋转全等问题旋转半角模型说明：旋转半角的特征是相邻等线段所成角含一个二分之一角，通过旋转将另外两个和为二分之一的角拼接在一起，成对称全等。

自旋转模型构造方法：遇60度旋60度，造等边三角形遇90度旋90度，造等腰直角遇等腰旋顶点，造旋转全等遇中点旋180度，造中心对称共旋转模型说明：旋转中所成的全等三角形，第三边所成的角是一个经常考察的内容。

通过“8”字模型可以证明。

模型变换说明：模型变形主要是两个正多边形或者等腰三角形的夹角的变化，另外是等腰直角三角形与正方形的混用。

当遇到复杂图形找不到旋转全等时，先找两个正多边形或者等腰三角形的公共顶点，围绕公共顶点找到两组相邻等线段，分组组成三角形证全等。

中点旋转：说明：两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点，证明另外两个顶点与中点所成图形为等腰直角三角形。

证明方法是倍长所要证等腰直角三角形的一直角边，转化成要证明的等腰直角三角形和已知的等腰直角三角形（或者正方形）公旋转顶点，通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。

中考专题复习——几何题用旋转构造“手拉手”模型一、教学目标：1.了解并熟悉“手拉手模型”，归纳掌握其基本特征．2.借助“手拉手模型”，利用旋转构造全等解决相关问题．3.举一反三，解决求定值，定角，最值等一类问题． 二、教学重难点：1.挖掘和构造“手拉手模型”，学会用旋转构造全等．2.用旋转构造全等的解题方法最优化选择． 三、教学过程： 1.复习旧知师：如图，△ABD ，△BCE 为等边三角形，从中你能得出哪些结论？生：（1）△ABE ≌△DBC （2）△ABG ≌△DBF （3）△CFB ≌△EGB （4）△BFG 为等边三角形（5）△AGB ∽△DGH （6）∠DHA ＝60°（7）H ，G ，F ，B 四点共圆 （8）BH 平分∠AHC …… 师：我们再来重点研究△ABE 与△DBC ，这两个全等的三角形除了对应边相等，对应角相等外，还有什么共同特征呢？生：它们有同一个字母B ，即同一个顶点B ．师：我们也可以把△DBC 看作由△ABE 经过怎样的图形运动得到？ 生：绕点B 逆时针旋转60°得到．2.引入新课师：其实我们可以给这两个全等的三角形赋予一个模型，叫“手拉手模型”，谁可以将这个模型的特征再做进一步的简化归纳呢？ 生：对应边相等．师：我们可以称之为“等线段”． 生：有同一个顶点．师：我们可以称之为“共顶点”．师：等线段，共顶点的两个全等三角形，我们一般可以考虑哪一种图形运动？ 生：旋转．师： “手拉手模型”可以归纳为：等线段，共顶点，一般用旋转．H GFEDC B A3.小题热身图1 图2 图31．如图1，△BAD中，∠BAD＝45°，AB＝AD，AE⊥BD于E，BC⊥AD于C，则AF＝____BE．2．如图2，△ABC和△BED均为等边三角形，ADE三点共线，若BE＝2，CE＝4，则AE＝______．3．如图3，正方形ABCD中，∠EAF＝45°，BE＝3，DF＝5，则EF＝_______．师：我们来看第1，第2题，这里面有“手拉手模型”吗？请你找出其中的“等线段，共顶点”．生：题1中，等线段是AC，BC，共顶点是C，△ACF绕点C逆时针旋转90°得△BCD．题2中，等线段是AB，BC，共顶点是B，△ABD绕点D顺时针旋转60°得△CBE．师：我们再来看第3题，这里有“手拉手模型”吗？生：没有．师：那其中有没有“等线段，共顶点”呢？生：等线段是AD，AB，共顶点是A．师：我们可否利用旋转来构造“手拉手模型”呢？生：将AE旋转，绕点A逆时针旋转90°．师：为什么是逆时针旋转90°，你是如何思考的？生：我准备构造一个和△ABE全等的三角形，AB绕点A逆时针旋转90°即为AD，那么将AE逆时针旋转90°可得AG，连接GD，证明全等．师：说的不错，谁能再来归纳一下，借助“手拉手模型”，用旋转构造全等的方法吗？生：先找有没有“等线段，共顶点”，再找其中一条“共顶点”的线段，将其旋转．师：旋转角度如何确定，方向怎么选择？生：选择其中一个三角形，将“共顶点”的线段旋转．旋转角为两条“等线段”间的夹角．方向应与所选择的起始“等线段”旋转到另一条“等线段”时的方向一致．师：非常棒，可以说，你已经掌握了这节课的精髓．但是，很多题目中只是隐含了“手拉手模型”的一些条件，剩余的需要我们自己去构造，可以如何构造呢？步骤1：先找有没有“等线段，共顶点”．步骤2：选择其中一个三角形，将其中经过“共顶点”的线段旋转．步骤3：旋转方向与这个三角形的“等线段”旋转到另一条“等线段”的方向一致，旋转角为“等线段”间的夹角．师：这道题还有一个要注意的地方，你发现了吗？生：连接GD后，要证明G，D，F三点共线．4.例题精讲例1：等边△ABC中，AD＝4，DC＝3，BD＝5，求∠ADC度数．师：这里有没有隐含的“手拉手模型”？要构造全等，该怎样旋转？生：将△ADC绕点A顺时针旋转60°．师：你是怎么想的，还有其他做法吗？生：我发现AB＝AC，A为“共顶点”，我选择的旋转线段是AD，因为AC绕点A顺时针旋转60°到AB，所以△ADC也要绕点A顺时针旋转60°．也可将△ADB绕点A逆时针旋转60°．【解答】将AD绕点A顺时针旋转60°到AE，连接BE，DE．则△ADE也为等边三角形．易证△AEB≌△ADC，∴BE＝DC＝4，根据勾股定理逆定理，可证∠BED＝90°，则∠AEB＝∠ADC＝150°例2：如图，△ABO和△CDO均为等腰直角三角形，AOB ＝COD ＝．若△BOC的面积为1，试求以AD、BC、OC＋OD的长度为三边长的三角形的面积．师：由于线段分散，如何通过图形变换，使这些线段能构成一个三角形？生：将OD绕点O逆时针旋转90°至OE，即可使OC，OD共线，再通过证明确定△BCE即是以AD、BC、OC＋OD的长度为三边长的三角形．【解答】如图，将OD绕点O逆时针旋转90°至OE，连接BE．易证△OAD≌△OBE，AD＝BE，∴△BCE即是以AD、BC、OC＋OD长度为三边长的三角形．又∵OC＝OE，∴S△BCE＝2S△BOC＝2．EAOBCDDC BOABBDCBA5.自主练习1．如图，在四边形ABCD 中，AD ＝4，CD ＝3，∠ABC ＝∠ACB ＝∠ADC ＝45°，则BD 的长为 _________．师：请找出隐含的“手拉手模型”，并写出解决方法．生：“等线段”是CA 和BA ，“共顶点”是A ．方法是将AD 绕点A 顺时针旋转90°．2．如图，在△ABC 中，BC ＝2，AB ＝2，以AC 为边，向外做正方形ACDE ，连接BE ，则BE 最大值为_________．师：请找出隐含的“手拉手模型”，并写出解决方法． 生：“等线段”是CA 和EA ，“共顶点”是A ． 方法是将AB 绕点A 逆时针旋转90°．师：你为何要逆时针旋转，你准备旋转哪个三角形？生：△ABC ，因为AC 是逆时针旋转90°到AE ，所以AB 也绕点A 逆时针旋转90°． 3．如图，点A 在⊙B 上，AB ＝1，BC ＝2，△ACD 是等边三角形，求△BCD 面积的最大值．师：请找出隐含的“手拉手模型”，并写出解决方法． 生：“等线段”是CA 和CD ，“共顶点”是C ． 方法是将CA 绕点C 逆时针旋转60°．附：自主练习解答1． 如图，将AD 绕点A 顺时针旋转90°至AE ，易证△EAC ≌△DAB ，可得CE ＝BD ，又∵∠EDA ＝45°，∴∠CDE ＝90°，CD ＝3，DE ＝42，则Rt △CDE 中，CE 2＝CD 2＋DE 2＝32＋ (42)2＝41 ∴CE ＝41，∴DB ＝412.如图，将AB 绕点A 逆时针旋转90°至AF ，易证△EAF ≌△CAB ，可得EF ＝BC ＝2．Rt △BAF 中，AF ＝AB ＝2，∴BF ＝2．由三角形三边关系易知，BE ≤EF ＋BF ，∴BE 最小值为4.3.如图，将CB 绕点C 逆时针旋转60°至CE ，连接DE ，过点E 作EF ⊥CBEDCBAADC BDG EFABCDFEBCDA于F ，过点D 作DG ⊥CB 于G ．易证△CBA ≌CED ， 则DE ＝1，EF ＝3，过E 作DG 边上的高，可证DG ＜DE ＋EF ．当D ，E ，F 三点共线时，DG ＝DE ＋EF ．即高的最大值为1＋3， S △BCDmax ＝12×2×（1＋3）＝1＋3FED CBA。

2018年中考常见几何模型分析(总19页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除中考直通车·数学广州分册第八章专题拓展第24讲常见几何模型【考点解读】A常见几何模型是广州市中考的压轴题常考题型，主要以考察选择、填空最后一题和几何压轴题为主。

几何模型类型较多，综合性强，属于中考中重点但同样是难点的一个考点。

【考点分析】2011年 考查三角形全等和三角形中位线性质，标准的手拉手模型。

2014年 考查三角形全等的判断和性质，根据手拉手模型找出全等三角形，再应用其性质2016年 本年度模型思想明显，分值占比大，主要考查三角形全等的判定及其性质、图像的旋转，利用模型思想作为解题突破口顺利完成辅助线。

【模型介绍】 手拉手模型：1、 【条件】 如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，【结论】（1）DBC ABE ∆≅∆（2）DC AE =（3）AE 与DC 之间的夹角为︒60（4）AE 与DC 的交点设为H , BH 平分AHC ∠2、 【条件】如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H 。

【结论】 （1）CDE ADG ∆≅∆是否成立？（2）AG =CE（3）AG 与CE 之间的夹角为 90（4）HD 是否平分AHE ∠旋转模型：一、邻角相等对角互补模型【条件】如图，四边形ABCD 中，AB =AD ，90BAD BCD ︒∠=∠= 【结论】452ACB ACD BC CD AC︒∠=∠=+=① ②FECDBA二、角含半角模型：全等角含半角要旋转：构造两次全等FED CBAG FED CBAABC D E ABCD E F【条件】：如图，点E F 、分别是正方形ABCD 的边BC CD 、上的点，45EAF ∠=︒，连接EF ；【结论】（1）AFE AGE △△≅ （2）EF BE FD =+ ；一线三等角模型:【条件】 一条直线同一侧三个相等的角（如图）； 【结论】CDE ABC ∽△△1、锐角形一线三等角2、直角形一线三等角3、钝角形一线三等角【真题拾遗】1．（2014•广州）如图，四边形ABCD、CEFG都是正方形，点G在线段CD上，连接BG、DE，DE和FG相交于点O，设AB=a，CG=b（a＞b）．下列结论：①△BCG≌△DCE；②BG⊥DE；③=；④（a﹣b）2•S△EFO=b2•S△DGO．其中结论正确的个数是（）A．4个B．3个C．2个D．1个2．（2016•广州）如图，正方形ABCD的边长为1，AC，BD是对角线．将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．则下列结论：①四边形AEGF是菱形②△AED≌△GED ③∠DFG=°④BC+FG=其中正确的结论是．三、解答题3．（2011广州中考）如图1，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角三角形DCE中∠DCE是直角，点D在线段AC上．（1）证明：B、C、E三点共线；（2）若M是线段BE的中点，N是线段AD的中点，证明：MN=OM；（3）将△DCE绕点C逆时针旋转α（0°＜α＜90°）后，记为△D1CE1（图2），若M1是线段BE1的中点，N1是线段AD1的中点，M1N1=OM1是否成立？若是，请证明；若不是，说明理由．4．（2016广州中考）如图，点C为△ABD的外接圆上的一动点（点C不在上，且不与点B，D重合），∠ACB=∠ABD=45°（1）求证：BD是该外接圆的直径；（2）连结CD，求证： AC=BC+CD；（3）若△ABC关于直线AB的对称图形为△ABM，连接DM，试探究DM2，AM2，BM2三者之间满足的等量关系，并证明你的结论．参考答案一、选择题1、C考点：相似三角形的判定与性质；全等三角形的判定与性质；正方形的性质．分析：由四边形ABCD和四边形CEFG是正方形，根据正方形的性质，即可得BC=DC，CG=CE，∠BCD=∠ECG=90°，则可根据SAS证得①△BCG≌△DCE；然后根据全等三角形的对应角相等，求得∠CDE+∠DGH=90°，则可得②BH⊥DE．由△DGF与△DCE相似即可判定③错误，由△GOD与△FOE相似即可求得④．解答：证明：①∵四边形ABCD和四边形CEFG是正方形，∴BC=DC，CG=CE，∠BCD=∠ECG=90°，∴∠BCG=∠DCE，在△BCG和△DCE中，，∴△BCG≌△DCE（SAS），②∵△BCG≌△DCE，∴∠CBG=∠CDE，又∠CBG+∠BGC=90°，∴∠CDE+∠DGH=90°，∴∠DHG=90°，∴BH⊥DE；③∵四边形GCEF是正方形，∴GF∥CE，∴=，∴=是错误的．④∵DC∥EF，∴∠GDO=∠OEF，∵∠GOD=∠FOE，∴△OGD∽△OFE，∴=（）2=（）2=，∴（a﹣b）2•S△EFO=b2•S△DGO．故应选B点评：此题考查了正方形的性质，全等三角形的判定与性质，相似三角形的判定和性质，直角三角形的判定和性质．二、填空题2、①②③考点：三角形全等、三角形内角和、菱形分析：首先证明△ADE≌△GDE，再求出∠AEF、∠AFE、∠GEF、∠GFE的度数，推出AE=EG=FG=AF，由此可以一一判断．解答：证明：∵四边形ABCD是正方形，∴AD=DC=BC=AB，∠DAB=∠ADC=∠DCB=∠ABC=90°，∠ADB=∠BDC=∠CAD=∠CAB=45°，∵△DHG是由△DBC旋转得到，∴DG=DC=AD，∠DGE=∠DCB=∠DAE=90°，在RT△ADE和RT△GDE中，，∴AED≌△GED，故②正确，∴∠ADE=∠EDG=°，AE=EG，∴∠AED=∠AFE=°，∴AE=AF，同理EG=GF，∴AE=EG=GF=FA，∴四边形AEGF是菱形，故①正确，∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=°，故③正确．∵AE=FG=EG=BG，BE=AE，∴BE＞AE，∴AE＜，∴CB+FG＜，故④错误故答案为①②③．点评：本题考查正方形的性质、全等三角形的判定和性质、菱形的判定和性质、等腰直角三角形的性质等知识，解题的关键是通过计算发现角相等，学会这种证明角相等的方法，属于中考常考题型．三、解答题3、考点：（1）三点共线（2）中位线、全等三角形（手拉手性质）（3）同（2）分析：（1）根据直径所对的圆周角为直角得到∠BCA=90°，∠DCE是直角，即可得到∠BCA+∠DCE=90°+90°=180°；（2）连接BD，AE，ON，延长BD交AE于F，先证明Rt△BCD≌Rt△ACE，得到BD=AE，∠EBD=∠CAE，则∠CAE+∠ADF=∠CBD+∠BDC=90°，即BD⊥AE，再利用三角形的中位线的性质得到ON=BD，OM=AE，ON∥BD，AE∥OM，于是有ON=OM，ON⊥OM，即△ONM为等腰直角三角形，即可得到结论；（3）证明的方法和（2）一样．解答：（1）证明：∵AB是直径，∴∠BCA=90°，而等腰直角三角形DCE中∠DCE是直角，∴∠BCA+∠DCE=90°+90°=180°，∴B、C、E三点共线；（2）连接BD，AE，ON，延长BD交AE于F，如图1，∵CB=CA，CD=CE，∴Rt△BCD≌Rt△ACE，∴BD=AE，∠EBD=∠CAE，∴∠CAE+∠ADF=∠CBD+∠BDC=90°，即BF⊥AE，又∵M是线段BE的中点，N是线段AD的中点，而O为AB的中点，∴BD21=ON，AE21=OM，ON∥BD，AE∥OM；∴ON=OM，ON⊥OM，即△ONM为等腰直角三角形，∴MN=OM；（3）成立．理由如下：如图2，连接BD1，AE1，ON1，∵∠ACB﹣∠ACD1=∠D1CE1﹣∠ACD1，∴∠BCD1=∠ACE1，又∵CB=CA，CD1=CE1，∴△BCD1≌△ACE1，与（2）同理可证BD1⊥AE1，△ON1M1为等腰直角三角形，从而有M1N1=OM1．点评：本题考查主要三角形全等的判定和中位线的性质，熟练掌握手拉手模型，作为本题切入点，可以非常顺利的解决本题。

专题05 一线三等角（K 型图）模型（从全等到相似） 全等三角形与相似三角形在中考数学几何模块中占据着重要地位。

相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。

如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了．本专题就一线三等角模型进行梳理及对应试题分析，方便掌握。

模型1.一线三等角（K 型图）模型（全等模型）【模型解读】在某条直线上有三个角相等，利用平角为180°与三角形内角和为180°，证得两个三角形全等。

【常见模型及证法】同侧型一线三等角（常见）：锐角一线三等角 直角一线三等角（“K 型图”） 钝角一线三等角条件：A CED B ∠=∠=∠+ CE=DE证明思路：,A B C BED ∠=∠∠=∠+任一边相等BED ACE ⇒≅异侧型一线三等角：锐角一线三等角 直角一线三等角 钝角一线三等角条件：FAC ABD CED ∠=∠=∠+ 任意一边相等证明思路：,A B C BED ∠=∠∠=∠+任一边相等BED ACE ⇒≅1．（2022·湖南湘潭·中考真题）在ABC 中，90BAC ∠=︒，AB AC =，直线l 经过点A ，过点B 、C 分别作l 的垂线，垂足分别为点D 、E ．(1)特例体验：如图①，若直线l BC ∥，AB AC ==分别求出线段BD 、CE 和DE 的长；(2)规律探究：①如图②，若直线l 从图①状态开始绕点A 旋转()045αα<<︒，请探究线段BD 、CE 和DE 的数量关系并说明理由；②如图③，若直线l 从图①状态开始绕点A 顺时针旋转()4590αα︒<<︒，与线段BC 相交于点H ，请再探线段BD 、CE 和DE 的数量关系并说明理由；(3)尝试应用：在图③中，延长线段BD 交线段AC 于点F ，若3CE =，1DE =，求BFC S △．【答案】(1)BD =1；CE =1；DE =2(2)①DE =CE +BD ；理由见解析；②BD =CE +DE ；理由见解析 (3)258BFC S ∆=【分析】（1）先根据得出90452ABC ACB ︒∠=∠==︒，根据l BC ∥，得出45DAB ABC ∠=∠=︒，45EAC ACE ∠=∠=︒，再根据90BDA CEA ∠=∠=︒，求出45ABD ∠=︒，45ACE ∠=︒， 即可得出45DAB ABD EAC ACE ∠=∠=∠=∠=︒，最后根据三角函数得出1AD BD ==，1AE CE ==，即可求出2DE AD AE =+=；（2）①DE =CE +BD “AAS”证明ABD CAE ∆∆≌，得出AD =CE ，BD =AE ，即可得出结论；②BD =CE +DE ；根据题意，利用“AAS”证明ABD CAE ∆∆≌，得出AD =CE ，BD =AE ，即可得出结论；（3）在Rt△AEC 中，根据勾股定理求出5AC =，根据DF CE ∥，得出AD AF AE CF =，代入数据求出AF ，根据AC =5，算出CF ，即可求出三角形的面积．(1)解：△90BAC ∠=︒，AB AC =，△90452ABC ACB ︒∠=∠==︒， △l BC ∥，△45DAB ABC ∠=∠=︒，45EAC ACE ∠=∠=︒，△BD △AE ，CE △DE ，△90BDA CEA ∠=∠=︒，△904545ABD ∠=︒-︒=︒，904545ACE ∠=-=︒︒︒，△45DAB ABD EAC ACE ∠=∠=∠=∠=︒，△sin 1AD BD AB DAB ==⨯∠==，sin 1AE CE AC EAC ==⨯∠==，△2DE AD AE =+=． (2)①DE =CE +BD ；理由如下：△BD △AE ，CE △DE ，△90BDA CEA ∠=∠=︒，△90DAB DBA ∠+∠=︒，△90BAC ∠=︒，△90DAB CAE ∠+∠=︒，△DBA CAE ∠=∠，△AB =AC ，△ABD CAE ∆∆≌，△AD =CE ，BD =AE ，△DE =AD +AE =CE +BD ，即DE =CE +BD ；②BD =CE +DE ，理由如下：△BD △AE ，CE △DE ，△90BDA CEA ∠=∠=︒，△90DAB DBA ∠+∠=︒，△90BAC ∠=︒，△90DAB CAE ∠+∠=︒，△DBA CAE ∠=∠，△AB =AC ，△ABD CAE ∆∆≌，△AD =CE ，BD =AE ，△BD =AE =AD +DE =CE +DE ，即BD =CE +DE ．(3)根据解析（2）可知，AD =CE=3，△314AE AD DE =+=+=，在Rt△AEC 中，根据勾股定理可得：5AC =，△BD △AE ，CE △AE ，△DF CE ∥，△AD AF AE CF =，即345AF =，解得：154=AF ， △155544CF AC AF =-=-=，△AB =AC =5，△1152552248BFC S CF AB ∆=⨯=⨯⨯=． 【点睛】本题主要考查了三角形全等的判定和性质，等腰三角形的判定和性质，勾股定理，平行线的性质，解直角三角形，根据题意证明ABD CAE ∆∆≌，是解题的关键．2．（2022·黑龙江·九年级期末）（1）如图（1），已知：在△ABC 中，△BAC ＝90°，AB =AC ，直线m 经过点A ，BD △直线m ， CE △直线m ，垂足分别为点D 、E ．证明△DE =BD +CE ．（2）如图（2），将（1）中的条件改为：在△ABC 中，AB =AC ，D 、A 、E 三点都在直线m 上，并且有△BDA =△AEC =△BAC =α，其中α为任意锐角或钝角．请问结论DE =BD +CE 是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D 、E 是D 、A 、E 三点所在直线m 上的两动点（D 、A 、E 三点互不重合），点F 为△BAC 平分线上的一点，且△ABF 和△ACF 均为等边三角形，连接BD 、CE ，若△BDA =△AEC =△BAC ，试判断△DEF 的形状．【答案】（1）见解析（2）成立，证明见解析（3）△DEF 为等边三角形，证明见解析【分析】（1）因为DE=DA+AE，故由全等三角形的判定AAS证△ADB△△CEA，得出DA=EC，AE=BD，从而证得DE=BD+CE；（2）成立，仍然通过证明△ADB△△CEA，得出BD=AE，AD=CE，所以DE=DA+AE=EC+BD；（3）由△ADB△△CEA得BD=AE，△DBA =△CAE，由△ABF和△ACF均等边三角形，得△ABF=△CAF=60°，FB=F A，所以△DBA+△ABF=△CAE+△CAF，即△DBF=△F AE，所以△DBF△△EAF，所以FD=FE，△BFD=△AFE，再根据△DFE=△DF A+△AFE=△DF A+△BFD=600得到△DEF是等边三角形．【详解】解：（1）证明：△BD△直线m，CE△直线m，△△BDA＝△CEA=90°．△△BAC＝90°，△△BAD+△CAE=90°．△△BAD+△ABD=90°，△△CAE=△ABD．又AB=AC，△△ADB△△CEA（AAS）．△AE=BD，AD=CE．△DE=AE+AD=BD+CE；（2）成立．证明如下：△△BDA =△BAC=α，△△DBA+△BAD=△BAD +△CAE=180°-α．△△DBA=△CAE．△△BDA=△AEC=α，AB=AC，△△ADB△△CEA（AAS）．△AE=BD，AD=CE．△DE=AE+AD=BD+CE；（3）△DEF为等边三角形．理由如下：由（2）知，△ADB△△CEA，BD=AE，△DBA =△CAE，△△ABF和△ACF均为等边三角形，△△ABF=△CAF=60°．△△DBA+△ABF=△CAE+△CAF．△△DBF=△F AE．△BF=AF，△△DBF△△EAF（SAS）．△DF=EF，△BFD=△AFE．△△DFE=△DF A+△AFE=△DF A+△BFD=60°．△△DEF为等边三角形．【点睛】此题考查了全等三角形的性质和判定、等边三角形的性质和判定，解题的关键是熟练掌握全等三角形的性质和判定，等边三角形的性质和判定．3．（2022·江苏·九年级专题练习）【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一，请根据以下问题，把你的感知填写出来：①如图1，ABC 是等腰直角三角形，90C ∠=︒，AE =BD ，则AED ≌_______； ②如图2，ABC 为正三角形，,60BD CF EDF =∠=︒，则BDE ≌________；③如图3，正方形ABCD 的顶点B 在直线l 上，分别过点A 、C 作AE l ⊥于E ，CF l ⊥于F ．若1AE =，2CF =，则EF 的长为________．【模型应用】（2）如图4，将正方形OABC 放在平面直角坐标系中，点O 为原点，点A 的坐标为(，则点C 的坐标为________．【模型变式】（3）如图5所示，在ABC 中，90ACB ∠=︒，AC BC =，BE CE ⊥于E ，AD △CE 于D ，4cm DE =，6cm AD =，求BE 的长．△四边形OABC是正方形△△AOC=90゜，AO=OC模型2.一线三等角模型（相似模型）【模型解读与图示】“一线三等角”型的图形，因为一条直线上有三个相等的角，一般就会有两个三角形的“一对角相等”，再利用平角为180°，三角形的内角和为180°，就可以得到两个三角形的另外一对角也相等，从而得到两个三角形相似．1．（2022·四川·一模）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形：（1）如图1，已知：在△ABC 中，AB AC =，D 、A 、E 三点都在直线m 上，并且有BDA AEC BAC α∠=∠=∠=．试猜想DE 、BD 、CE 有怎样的数量关系，请证明你的结论； （2）老师鼓励学习小组继续探索相似的情形．于是，学习小组又研究以下问题：如图2，△ABC 中，(060)B C αα∠=∠=<<︒．将一把三角尺中30°角顶点P 放在BC 边上，当P 在BC 边上移动时，三角尺中30°角的一条边始终过点A ，另一条边交AC 边于点Q ，P 、Q 不与三角形顶点重合．设CPQ β∠=．当β在许可范围内变化时，α取何值总有△ABP △△PCQ ？当α在许可范围内变化时，β取何值总有△ABP △△QCP ？（3）试探索有无可能使△ABP 、△QPC 、△ABC 两两相似？若可能，写出所有α、β的值（不写过程）；若不可能，请说明理由．【答案】（1）DE AE AD BD CE =+=+；证明见解析；（2）30α=︒；75β=︒；（3）可能；30α=︒，30β=︒或52.5α=︒，75β=︒．【分析】（1）证明△ADB △△CEA （AAS ），由全等三角形的性质得出AE =BD ，AD =CE ，则可得出结论；（2）由β=△2或△1=△CQP ，即△2=30°+β-α=β，解得α=30°，即可求解；由β=△1或△2=△CQP ，同理可得：β=75°，即可求解；（3）①当α=30°，β=30°时，则△2=△B =α=30°，即可求解；②当β=75°，α=52.5°时，同理可解．【详解】解：（1）如图1，△BDA BAC α∠=∠=，△180DBA BAD BAD CAE ∠∠∠∠α+=+=︒-，△DBA CAE ∠=∠，在△ADB 和△CEA 中，DBA EAC BDA AEC BA AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，△△ADB △△CEA （AAS ），△AE BD =，AD CE =， △DE AE AD BD CE =+=+；（2）在△ABP 中，2230APC B αβ∠=∠+∠=+∠=︒+，△1150β∠=︒-，同理可得：230βα∠=︒+-；由2β=∠或1CQP ∠=∠，即230βαβ∠=︒+-=，解得30α=︒，则△ABP △△PCQ ；△当β在许可范围内变化时，30α=︒时，总有△ABP △△PCQ ；由1β=∠或2CQP ∠=∠，同理可得：75β=︒．△当α在许可范围内变化时，75β=︒总有△ABP △△QCP ；（3）可能．①当30α=︒，30β=︒时，则230B α∠=∠==︒，则△ABP △△PCQ △△BCA ； ②当75β=︒，52.5α=︒时，同理可得：115075ββ∠=︒-=︒=，23052.5βαα∠=︒+-=︒=，△△ABP △△CQP △△BCA ．【点睛】本题是相似形综合题，主要考查了全等三角形的判定和性质，相似三角形的判定和性质，熟练掌握相似三角形的性质是解本题的关键．2．（2022·河南新乡·二模）如图，△ABC 和△ADE 是有公共顶点A 的两个等腰直角三角形，△DAE ＝△BAC ＝90°，AD ＝AE ，AB ＝AC ＝6，D 在线段BC 上，从B 到C 运动，点M 和点N 分别是边BC ，DE 的中点．(1)【问题发现】若点D 是BC 边的中点时，BD MN＝ ，直线BD 与MN 相交所成的锐角的度数为 （请直接写出结果）(2)【解决问题]若点D 是BC 边上任意一点时，上述结论是否成立，请说明理由．(3)【拓展探究】在整个运动过程中，请直接写出N 点运动的路径长，及CN 的最小值．当点D 是BC 的中点时，△AB =AC ，△AD △BC ，AD 平分△BAC ，如图1，在四边形ABCD 中，点P 为AB 上一点，当90DPC A B ∠=∠=∠=︒时，求证：AD BC AP BP ⋅=⋅．（2）探究：若将90°角改为锐角或钝角（如图2），其他条件不变，上述结论还成立吗？说明理由．（3）应用：如图3，在ABC 中，AB =45B ∠=︒，以点A 为直角顶点作等腰Rt ADE △．点D 在BC 上，点E 在AC 上，点F 在BC 上，且45EFD ∠=︒，若CE =CD 的长．）结论仍然成立，理由如下，BPD ∠=又BPD ∠=DPC BPC +∠DPC ∠=∠α，BPC ∴∠ADP ∴∽△△，△AD ⋅BC）∠ABD DFE ∴∽，AB DF ∴ADE 是等腰直角三角形，，2AB =，4DF ∴=，45EFD ∠=135DEC =︒，EFC DEC ∴∽，FC EC ∴5EC =,()45FC CD FC FC ⋅=⋅+=，1FC ∴= 【点睛】本题考查相似三角形的综合题，三角形的相似；能够通过构造45°角将问题转化为一线三角是解题的关键．模型3.一线三直角模型（相似模型）【模型解读与图示】“一线三直角”模型的图形，实则是“一线三等角”型的图形的特例，因为这种图形在正方形和矩形中出现的比较多，对它做一专门研究，这样的图形，因为有三个角是直角，就有两个角相等，再根据“等角的余角相等”可以得到另外一对角相等，从而判定两个三角形相似．1．（2022·湖南郴州·中考真题）如图1，在矩形ABCD 中，4AB =，6BC =．点E 是线段AD 上的动点（点E 不与点A ，D 重合），连接CE ，过点E 作EF CE ⊥，交AB 于点F ．(1)求证：AEF DCE ∽；(2)如图2，连接CF ，过点B 作BG CF ⊥，垂足为G ，连接AG ．点M 是线段BC 的中点，连接GM ．①求AG GM +的最小值；②当AG GM +取最小值时，求线段DE 的长．【答案】(1)见解析(2)①5；②3DE =3DE =【分析】（1）证明出DCE AEF ∠=∠即可求解；（2）①连接AM ．先证明132BM CM GM BC ====．确定出点G 在以点M 为圆心，3为半径的圆上．当A ，G ，M 三点共线时，AG GM AM +=．此时，AG GM +取最小值．在Rt ABM 中利用勾股定理即可求出AM ，则问题得解．②先求出AF ，求AF 的第一种方法：过点M 作∥MN AB 交FC 于点N ，即有CMN CBF ∽△△，进而有12MN CM BF CB ==．设AF x =，则4BF x =-，()142MN x =-．再根据∥MN AB ，得到AFG MNG ∽△△，得到AF AG MN GM =，则有()21342xx =-，解方程即可求出AF ；求AF 的第二种方法：过点G 作GH AB ∥交BC于点H ．即有MHG MBA ∽△△．则有GM GH MH AM AB MB ==，根据5AM =，可得3543GH MH ==，进而求出125GH =，95MH =．由GH AB ∥得CHG CBF ∽△△，即可求出AF ．求出AF 之后，由（1）的结论可得AF AE DE DC．设DE y =，则6AE y =-，即有164y y -=，解得解方程即可求出DE ．(1)证明：如图1，△四边形ABCD 是矩形，△90A D ∠=∠=︒，△90CED DCE ∠+∠=︒．△EF CE ⊥，△90CED AEF ∠+∠=︒，△DCE AEF ∠=∠，△AEF DCE ∽；(2)①解：如图2-1，连接AM ．△BG CF ⊥，△BGC 是直角二角形．△132BM CM GM BC ====． △点G 在以点M 为圆心，3为半径的圆上．当A ，G ，M 三点不共线时，由三角形两边之和大于箒三边得：AG GM AM +>， 当A ，G ，M 三点共线时，AG GM AM +=．此时，AG GM +取最小值．在Rt ABM中，5AM ==．△AG GM+的最小值为5．②（求AF 的方法一）如图2-2，过点M 作∥MN AB 交FC 于点N ，△CMN CBF ∽△△．△12MN CM BF CB ==． 设AF x =，则4BF x =-，△()11422MN BF x ==-． △∥MN AB ，△AFG MNG ∽△△，△AF AG MN GM =， 由①知AG GM +的最小值为5、即5AM =，又△3GM =，△2AG =．△()21342xx =-，解得1x =，即1AF =．（求AF 的方法二）如图2-3，过点G 作GH AB ∥交BC 于点H ．△MHG MBA ∽△△．△GM GH MH AM AB MB==， 由①知AG GM +的最小值为5，即5=，又△3GM =，△3543GH MH ==．△125GH =，95MH =． 由GH AB ∥得CHG CBF ∽△△，△GH CH FB CB =，即1293556FB +=，解得3FB =． △1AF AB FB =-=．由（1）的结论可得AF AE DE DC ． 设DE y =，则6AE y =-，△164y y -=，解得3y =3△036<，036<<，△3DE =+或3DE =【点睛】本题主要考查了相似三角形的判定与性质、平行的性质、勾股定理以及一元二次方程的应用等知识，掌握相似三角形的判定与性质是解答本题的关键．2．（2022·山东济宁·二模）情境观察:将含45°角的三角板的直角顶点R 放在直线l 上，分别过两锐角的顶点M ，N 作l 的垂线，垂足分别为P ， Q ，（1）如图1.观察图1可知：与NQ 相等的线段是______________，与NRQ ∠相等的角是_____(2)问题探究直角ABC 中，90B ∠=︒，在AB 边上任取一点D ，连接CD ，分别以AC ，DC 为边作正方形ACEF 和正方形CDGH ，如图2，过E ，H 分别作BC 所在直线的垂线，垂足分别为K ，L .试探究EK 与HL 之间的数量关系，并证明你的结论.(3)拓展延伸：直角ABC 中，90B ∠=︒，在AB 边上任取一点D ，连接CD ，分别以AC ，DC 为边作矩形ACEF 和矩形CDGH ，连接EH 交BC 所在的直线于点T ，如图3.如果AC kCE =，CD kCH =，试探究TE 与TH 之间的数量关系，并证明你的结论.【答案】(1)PR ，PMR ∠，(2)EK LH =，证明见解析；(3)ET HT=，证明见解析．【分析】（1）根据等腰直角三角形的性质得到，=MR RN ，90MRN ∠=︒，根据余角性质得到PMR NRQ ∠=∠，再证明MPR NRQ ≌△△，即可得到QN PR =，NRQ PMR ∠=∠；（2）证明ABC CEK ≌△△，得到EK BC =，再证明DCB CHL ≌△△，得到BC HL =，可得到EK LH =；（3）证明ACB ECM ∽△△，得到BC kEM =，证明BCD NHC ∽△△，得到BC kHN =，得到EM HN =，证明NHT EMT ≌△△即可得到ET HT =． （1）解：△MRN △是等腰直角三角形，△=MR RN ，90MRN ∠=︒，△MP PQ ⊥，NQ PQ ⊥，△90MPR NQR ∠=∠=︒，△90PMR MRP MRP NRQ ∠+∠=∠+∠=︒，△PMR NRQ ∠=∠，在MPR △和NRQ △中，PMR NRQ MPR NRQ MR NR ∠=∠⎧⎪∠=∠⎨⎪=⎩△MPR NRQ ≌△△，△QN PR =，NRQ PMR ∠=∠，故答案为：PR ，PMR ∠；（2）解：△四边形ACEF 是正方形，△AC CE =，90ACE ∠=︒，△EK BK ⊥△90B EKC ∠=∠=︒，△90BAC ACB ACB ECK ∠+∠=∠+∠=︒，△BAC ECK ∠=∠，在ABC 和CEK △中，BAC KCE B EKCAC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩△ABC CEK ≌△△，△EK BC =， △四边形CDGH 是正方形，△CD CH =，90DCH ∠=︒在DCB和△3）解：过△四边形ACEF是矩形，△90ACE∠=︒，△90BAC ACB ACB ECM∠+∠=∠+∠=︒，顶点，过另外两个顶点分别向该直线作垂线，即可得三垂直模型”如图①：在△ABC中，△ACB ＝90°，AC＝BC，分别过A、B向经过点C直线作垂线，垂足分别为D、E，我们很容易发现结论：△ADC△△CEB．(1)探究问题：如果AC≠BC，其他条件不变，如图②，可得到结论；△ADC△△CEB．请你说明理由．(2)学以致用：如图③，在平面直角坐标系中，直线y＝12x与直线CD交于点M（2，1），且两直线夹角为α，且tanα＝32，请你求出直线CD的解析式．(3)拓展应用：如图④，在矩形ABCD中，AB＝4，BC＝5，点E为BC边上一个动点，连接AE，将线段AE绕点E顺时针旋转90°，点A落在点P处，当点P在矩形ABCD外部时，连接PC，PD．若△DPC为直角三角形时，请你探究并直接写出BE的长．由（1）可得：△NFO△△OEM，△NF OF NO==，△点M（2，1），△OE＝2，ME＝1，OE ME MONF OF33ON33课后专项训练：1．（2022·贵州铜仁·三模）（1）探索发现：如图1，已知Rt ABC 中，90ACB ∠=︒，AC BC =，直线l 过点C ，过点A 作AD l ⊥，过点B 作BE l ⊥，垂足分别为D 、E ．求证：CD BE =． （2）迁移应用：如图2，将一块等腰直角的三角板MON 放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O 重合，另两个顶点均落在第一象限内，已知点N 的坐标为()4,2，求点M 的坐标．（3）拓展应用：如图3，在平面直角坐标系内，已知直线44y x =-+与y 轴交于点P ，与x 轴交于点Q ，将直线PQ 绕P 点沿逆时针方向旋转45︒后，所得的直线交x 轴于点R ．求点R 的坐标．20由已知得OM＝ON，且△OMN＝90°，△由（1）得△OFM△△MGN，＝35x+4．【点睛】本题是一次函数综合题，主要考查了待定系数法，全等三角形的判定和性质，汕头市潮阳区教师发展中心教学研究室一模）直角三角形ABC中，△ACB=90°，CB=CA，直线ED经过点C，过A作AD△ED于D，过B作BE△ED于E．求证：△BEC△△CDA；（2）模型应用：①已知直线AB与y轴交于A点，与x轴交于B点，sin△ABO=35，OB=4，将线段AB绕点B逆时针旋转90度，得到线段BC，过点A，C作直线，求直线AC的解析式；②如图3，矩形ABCO，O为坐标原点，B的坐标为（8，6），A，C分别在坐标轴上，P是线段BC上动点，已知点D在第一象限，且是直线y=2x-5上的一点，若△APD是以D为直角顶点的等腰直角三角形，请求出所有符合条件的点D的坐标．和CDA中⎧⎪⎨⎪⎩①如图，过点中sin△ABO ，AB=5m，）可证得CDB∆当D在AB的下方时，过D作DE△y轴于E，交BC于F,，在ABC中，MN经过点C，且AD MN⊥于D，BE MN⊥于E．(1)由图1，证明：DE AD BE=+；(2)当直线MN绕点C旋转到图2的位置时，请猜想出DE，AD，BE的等量关系并说明理由；(3)当直线MN绕点C旋转到图3的位置时，试问DE，AD，BE又具有怎样的等量关系？请直接写出这个等量关系（不必说明理由）．【答案】(1)证明见解析；(2)DE AD BE =-，证明过程见解析；(3)DE BE AD =-，证明过程见解析【分析】(1)先证明△ADC △△CEB ，得到AD=CE ，DC=BE ，进而得到DE=CE+DC=AD+BE 即可；(2)同(1)中思路，证明△ADC △△CEB ，进而得到DE=CE -DC=AD -BE 即可；(3)同(1)中思路，证明△ADC △△CEB ，进而得到DE=DC -CE=BE -AD 即可．【详解】解：(1)证明：在ABC 中，△90ACB ∠=︒，△90ACD BCE ∠+∠=︒，△AD MN ⊥，△90ACD CAD ∠+∠=︒，△BCE =∠∠CAD ，又△AC BC =，90ADC CEB ∠=∠=，△()≌ADC CEB AAS ，△AD CE =，DC BE =， △直线MN 经过点C ，△DE CE DC AD BE =+=+；(2)DE ，AD ，BE 的等量关系为：DE AD BE =-，理由如下：△AD MN ⊥于D ，BE MN ⊥于E △90ADC BEC ACB ∠=∠=∠=︒，△90CAD ACD ∠+∠=︒，90ACD BCE ∠+∠=︒，△CAD BCE ∠=∠，在ADC 和CEB △中90CAD BCE ADC BEC AC CB ∠=∠⎧⎪∠=∠=⎨⎪=⎩，△()ADC CEB AAS △≌△△CE AD =，CD BE =，△DE CE CD AD BE =-=-；(3)当MN 旋转到图3的位置时，DE 、AD 、BE 所满足的等量关系是DE BE AD =-，理由如下：△AD MN ⊥于D ，BE MN ⊥于E △90ADC BEC ACB ∠=∠=∠=︒，△90CAD ACD ∠+∠=︒，90ACD BCE ∠+∠=︒，△CAD BCE ∠=∠，在ADC 和CEB △中90CAD BCE ADC BEC AC CB ∠=∠⎧⎪∠=∠=⎨⎪=⎩，△()ADC CEB AAS △≌△△CE AD =，CD BE =，△DE CD CE BE AD =-=-.【点睛】本题考查了全等三角形的判定方法、等腰直角三角形的性质及等角的余角相等等知识点，熟练掌握三角形全等的判定方法是求解的关键．4．（2022·山东·九年级课时练习）（1）课本习题回放：“如图①，90ACB ∠=︒，AC BC =，AD CE ⊥，BE CE ⊥，垂足分别为D ，E ， 2.5cm AD =， 1.7cm DE =．求BE 的长”，请直接写出此题答案：BE 的长为________．（2）探索证明：如图②，点B ，C 在MAN ∠的边AM 、AN 上，AB AC =，点E ，F 在MAN∠内部的射线AD 上，且BED CFD BAC ∠=∠=∠．求证：ABE CAF ∆∆≌．（3）拓展应用：如图③，在ABC ∆中，AB AC =，AB BC >．点D 在边BC 上，2CD BD =，点E 、F 在线段AD 上，BED CFD BAC ∠=∠=∠．若ABC ∆的面积为15，则ACF ∆与BDE ∆的面积之和为________．（直接填写结果，不需要写解答过程）【答案】（1）0.8cm ；（2）见解析（3）5【分析】（1）利用AAS 定理证明△CEB △△ADC ，根据全等三角形的性质解答即可； （2）由条件可得△BEA ＝△AFC ，△4＝△ABE ，根据AAS 可证明△ABE △△CAF ；（3）先证明△ABE △△CAF ，得到ACF ∆与BDE ∆的面积之和为△ABD 的面积，再根据2CD BD =故可求解．【详解】解：（1）△BE △CE ，AD △CE ，△△E ＝△ADC ＝90°，△△EBC ＋△BCE ＝90°．△△BCE ＋△ACD ＝90°，△△EBC ＝△DCA ．在△CEB 和△ADC 中，E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△CEB △△ADC （AAS ），△BE ＝DC ，CE ＝AD ＝2.5cm ．△DC ＝CE −DE ，DE ＝1.7cm ，△DC ＝2.5−1.7＝0.8cm ，△BE ＝0.8cm 故答案为：0.8cm ； （2）证明：△△1＝△2，△△BEA ＝△AFC ．△△1＝△ABE ＋△3，△3＋△4＝△BAC ，△1＝△BAC ，△△BAC ＝△ABE ＋△3，△△4＝△ABE ．△△AEB ＝△AFC ，△ABE ＝△4，AB ＝AC ，△△ABE △△CAF （AAS ）．（3）△BED CFD BAC ∠=∠=∠△△ABE +△BAE =△F AC +△BAE =△F AC +△ACF△△ABE =△CAF ，△BAE =△ACF又AB AC =△△ABE △△CAF ，△ABE CAF S S =△ACF ∆与BDE ∆的面积之和等于ABE ∆与BDE ∆的面积之和，即为△ABD 的面积，△2CD BD =，△ABD 与△ACD 的高相同则13ABD ABC S S =△△=5 故ACF ∆与BDE ∆的面积之和为5故答案为：5．【点睛】本题考查的是全等三角形的判定和性质、三角形内角和定理，掌握全等三角形的判定定理和性质定理是解题的关键．5．（2022·无锡市九年级月考）（1）如图1，直线m 经过等腰直角△ABC 的直角顶点A ，过点B 、C 分别作BD ⊥m ，CE ⊥m D 、E ．求证：BD ＋CE ＝DE ；（2）如图2，直线m 经过△ABC 的顶点A ，AB ＝AC ，在直线m 上取两点 D 、E ，使∠ADB ＝∠AEC ＝α，补充∠BAC ＝ （用α表示），线段BD 、CE 与DE 之间满足BD ＋CE ＝DE ，补充条件后并证明；（3）在（2）的条件中，将直线m 绕着点A 逆时针方向旋转一个角度到如图3的位置，并改变条件∠ADB ＝∠AEC ＝ （用α表示）．通过观察或测量，猜想线段BD 、CE 与DE 之间满足的数量关系，并予以证明．【答案】（1）证明见详解，（2）∠BAC=α，证法见详解，（3）180º-α，DE=EC-BD，证明见详解．【分析】（1）根据已知首先证明∠DAB=∠ECA，再利用AAS即可得出△ADB≌△CEA；（2）补充∠BAC=α．利用△ADB≌△CAE，即可得出三角形对应边之间的关系，即可得出答案；（3）180º-α，DE=CE-BD，根据已知首先证明∠DAB=∠ECA，再利用AAS即可得出△ADB≌△CEA，即可得出三角形对应边之间的关系，即可得出答案．【详解】证明：（1）∵BD⊥m，CE⊥m，∠ABC=90°，AC=BC，∴△ADB和△AEC都是直角三角形，∴∠DBA+∠DAB=90°，∴∠ECA+∠EAC=90°，∵∠BAC=90°，∠DAB+∠EAC=90º，∴∠DAB=∠ECA，又∵∠ADB=∠CEA=90°，AB=BC，所以△ADB≌△CEA（AAS），BD=AE，DA=EC，DE=DA+AE=EC+BD，BD＋CE＝DE．（2）∵等腰△ABC中，AC=CB，∠ADB=∠BAC=∠CEA=α，∴∠DAB+∠EAC=180°-α，∠ECA+∠CAE=180º-α，∴∠DAB=∠ECA，∵∠ADB=∠CEA=α，AC=CB，∴△ADB≌△CEA（AAS），∴CE=AD，BD=AE，∴AD+BE=CE+CD，所以BD+CE=DE．（3）180º-α，数量关系为DE=CE-BD，∵∠ADB＝∠AEC＝180º-α，∠BAC=α，∴∠ABD+∠BAD=α，∠BAD+∠EAC=α，∴∠ABD=∠CAE，∵AB=AC，∴△BAD≌△ACE（AAS），∴AD=CE，BD=AE，∴DE=AD-AE=EC-BD．【点睛】点评：此题主要考查了三角形全等的证明，根据已知得出∠DAB=∠ECA，再利用全等三角形的判定方法得出是解决问题的关键．6．（2022·河南新乡·九年级期中）某学习小组在探究三角形相似时，发现了下面这种典型的基本图形．（1）如图1，在ABC中，△BAC＝90°，ABAC＝k，直线l经过点A，BD△直线I，CE上直线l，垂足分别为D、E．求证：BDAE＝k．（2）组员小刘想，如果三个角都不是直角，那么结论是否仍然成立呢？如图2，将（1）中的条件做以下修改：在ABC中，ABAC＝k，D、A、E三点都在直线l上，并且有△BDA＝△AEC＝△BAC＝α，其中α为任意锐角或钝角．请问（1）中的结论还成立吗？若成立，请你给出证明；若不成立，请说明理由．（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，在ABC中，沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG，ABAE＝ACAG＝12，AH是BC边上的高，延长HA交EG于点I．①求证：I是EG的中点．②直接写出线段BC与AI 之间的数量关系：．【答案】（1）见解析（2）结论还成立，证明见解析（3）①见解析②BC=AI【分析】（1）由条件可证明△ABD△△CAE，可得BDAE=ABAC＝k；（2）由条件可知△BAD＋△CAE＝180°−α，且△DBA＋△BAD＝180°−α，可得△DBA＝△CAE，结合条件可证明△ABD△△CAE，同（1）可得出结论；（3）①过点G作GM∥AE交AI的延长线于点M，连接EM，证明△ABC△△GMA，再得到四边形AGME是平行四边形，故可求解；②由①得到BC=12AM，再根据四边形AGME是平行四边形得到BC=AI，故可求解．【详解】（1）如图1，△BD△直线l，CE△直线l，△△BDA＝△CEA＝90°，△△BAC＝90°，△△BAD＋△CAE＝90°△△BAD＋△ABD＝90°，△△CAE＝△ABD△△ABD＝△CAE，△BDA＝△CEA，△△ADB△△CEA，△BDAE =ABAC＝k；（2）成立，证明如下：如图2，△△BDA＝△BAC＝α，△△DBA＋△BAD＝△BAD＋△CAE＝180°−α，△△DBA＝△CAE，△△ABD＝△CAE，△BDA＝△CEA△△ADB△△CEA，△BDAE =ABAC＝k；（3）①过点G作GM∥AE交AI的延长线于点M，连接EM △四边形AGFC是矩形，△△GAC=90°又AH△BC△△AHC=90° △△5+△CAH=△4+△CAH=90°△△5=△4△△BDE=△AHB=90°△△2+△BAH=△1+△BAH=90°△△2=△1又GM∥AE△△3=△2△△3=△1△△ABC△△GMA【点睛】此题主要考查相似三角形的判断与性质综合，解题的关键是根据题意找到相似三角，ABC 是等腰直角三角形，直线l 过点C ，AM l ⊥，BN l ⊥，垂足分别为M ，N ．求证：AMC CNB △≌△；[尝试应用]（2）如图2，AC BC =，90ACB ∠=︒，N ，B ，E 三点共线，CN NE ⊥，45E ∠=︒，1CN =，2BN =．求AE 的长；[拓展创新]（3）如图3，在DCE 中，45CDE ∠=︒，点A ，B 分别在DE ，CE 上，AC BC =，90ACB ∠=︒，若1tan 2DCA ∠=，直接写出AE AD 的值为 ．在AMC和△△()AMC CNB AAS≌2）如图2AM NH⊥于M，由（1）可知：BCN CAM△≌△，△2CM BN==，1CN AM==，）可知：AMC BNC≌，45DAM DFN=∠=∠=a，△32AF a=，BCN BFH∽△，等腰直角三角形的性质等知识，添加恰当辅助线构造全等三角形或相似三角形是本题的关键．8．（2022·黑龙江齐齐哈尔·三模）数学实践课堂上，张老师带领学生们从一道题入手，开始研究，并对此题做适当变式，尝试举一反三，开阔学生思维．(1)原型题：如图1，AB BD ⊥于点B ，CD BD ⊥于点D ，P 是BD 上一点，AP PC =，AP PC ⊥，则ABP △≌△________，请你说明理由．(2)利用结论，直接应用：①如图2，四边形ABCD 、EFGH 、NHMC 都是正方形，边长分别为a 、b 、c ，A 、B 、N 、E ，F 五点在同一条直线上，则CBN △≌△________，c =________（用含a 、b 的式子表示）．②如图3，四边形ABCD 中，AB DC ，AB BC ⊥，2AB =，4CD =，以BC 上一点O 为圆心的圆经过A 、D 两点，且90AOD ∠=︒，则圆心O 到弦AD 的距离为________．(3)弱化条件，变化引申：如图4，M 为线段AB 的中点，AE 与BD 交于点C ，45DME A B ∠=∠=∠=︒，且DM 交AC 于点F ，ME 交BC 于点G ，连接FG ，则AMF 与BGM 的关系为：________，若AB =3AF =，则FG =________．5即可证明∽AMF BGM ，即可求出△AB DC ∥，AB BC ⊥△90B C ∠=∠=︒ △90AOD ∠=︒△90AOB DOC +=︒∠∠在AOB 和△Rt AOB 中，Rt AOD △中，12AD OE ⨯⨯=10=△圆心解：AMF 与BGM 的关系为：相似，45︒△AMD AFM +∠∠△∽AMF BGM △AM BG 45︒△90ACB ∠=︒△AC 84433=-=△FG FC =本题考查了全等三角形的判定和性质、x 轴上，C 、D 、E 分别是AB 、OB 、OA 上的动点，且满足BD ＝2AC ，DE ∥AB ，连接CD 、CE ，当点E 坐标为 时，△CDE 与△ACE 相似．【分析】因为DE ∥AB 得到∠DEC ＝∠ACE ，所以△CDE 与△ACE 相似分两种情况分类讨论．【解答】解：∵DE ∥AB ，∴∠DEC ACE ，△ODE ∽△OBA ，∴△ODE 也是等边三角形，则OD ＝OE ＝DE ，设E （a ，0），则OE ＝OD ＝DE ＝a ，BD ＝AE ＝4﹣a ．∵△CDE 与△ACE 相似，分两种情况讨论：①当△CDE ∽△EAC 时，则∠DCE ＝∠CEA ，∴CD ∥AE ，∴四边形AEDC 是平行四边形，∴AC ＝a ，，∵BD ＝2AC ，∴4﹣a ＝2a ，∴a ＝．∴E ；②当△CDE ∽△AEC 时，∠DCE ＝∠EAC ＝60°＝∠B ，∴∠BCD +∠ECA ＝180°﹣60°＝120°，又∵∠BDC +∠BCD ＝180°﹣∠B ＝120°，∴∠BCD +∠ECA ＝∠BDC +∠BCD ， ∴∠ECA ＝∠BDC ，∴△BDC ∽△ACE ，∴，∴BC ＝2AE ＝2（4﹣a ）＝8﹣2a ， ∴8﹣2a +2＝4，∴a ＝．∴．综上所述，点E 的坐标为或．【点评】本题主要考查相似三角形，考虑分类讨论是本题的关键．10．（2022•广东中考模拟）（1）模型探究：如图1，D 、E 、F 分别为ABC ∆三边BC 、AB 、AC 上的点，且B C EDF α∠=∠=∠=，BDE ∆与CFD ∆相似吗？请说明理由.（2）模型应用：ABC ∆为等边三角形，其边长为8，E 为边AB 上一点，F 为射线AC 上一点，将AEF ∆沿EF 翻折，使点A 落在射线CB 上的点D 处，且2BD =.①如图2，当点D 在线段BC 上时，求AE AF的值； ②如图3，当点D 落在线段CB 的延长线上时，求BDE ∆与CFD ∆的周长之比.【答案】（1）~∆∆BDE CFD ，见解析；（2）①57AE AF =；②BDE ∆与CFD ∆的周长之比为13. 【分析】（1）根据三角形的内角和得到BED CDF ∠=∠，即可证明；（2）①设AE x =，AF y =，根据等边三角形的性质与折叠可知DE AE x ==，DF AF y ==，60EDF A ∠=∠=，根据三角形的内角和定理得BED CDF ∠=∠，即可证明~∆∆BDE CFD ，故BD BE DE CF CD FD ==，再根据比例关系求出AE AF的值； ②同理可证~∆∆BDE CFD ，得BD BE DE CF CD FD ==，得28810x x y y -==-，再得到13x y =，再根据相似三角形的性质即可求解.【详解】解（1）~∆∆BDE CFD ，理由：B C EDF α∠=∠=∠=，在BDE ∆中，180B BDE BED ∠+∠+∠=，180180BDE BED B α∴∠+∠=-∠=-，180BDE EDF CDF ∠+∠+∠=，180180BDE CDF EDF α∴∠+∠=-∠=-，BED CDF ∴∠=∠，B C ∠=∠，~BDE CFD ∴∆∆；（2）①设AE x =，AF y =，ABC ∆是等边三角形，60A B C ∴∠=∠=∠=，8AB BC AC ===，由折叠知，DE AE x ==，DF AF y ==，60EDF A ∠=∠=，在BDE ∆中，180B BDE BED ∠+∠+∠=，180120BDE BED B ∴∠+∠=-∠=， 180120BDE BED B ∠+∠=-∠=，180BDE EDF CDF ∠+∠+∠=，180120BDE CDF EDF ∴∠+∠=-∠=，BED CDF ∴∠=∠，60B C ∠=∠=，~BDE CFD ∴∆∆，BD BE DE CF CD FD∴==， 8BE AB AE x =-=-，8CF AC AF y =-=-，6CD BC BD =-=2886x x y y -∴==-，()()2868y x y x y x ⎧=-⎪∴⎨=-⎪⎩，105147x y ∴==，57AE AF ∴=； ②设AE x =，AF y =，ABC ∆是等边三角形， 60A ABC ACB ∴∠=∠=∠=，8AB BC AC ===，由折叠知，DE AE x ==，DF AF y ==，60EDF A ∠=∠=，在BDE ∆中，180ABC BDE BED ∠+∠+∠=，180120BDE BED ABC ∴∠+∠=-∠=， 180BDE EDF CDF ∠+∠+∠=，180120BDE CDF EDF ∴∠+∠=-∠=，BED CDF ∴∠=∠，60ABC ACB ∠=∠=，120DBE DCF ∴∠=∠=，~BDE CFD ∴∆∆，BD BE DE CF CD FD ∴== 8BE AB AE x =-=-，8CF AF AC y =-=-，10CD BC BD =+=，28810x x y y -∴==-，2(8)10(8y x y x y x =-⎧∴⎨=-⎩，13x y ∴=. ~BDE CFD ∆∆.BDE ∴∆与CFD ∆的周长之比为13DE x DF y ==. 【点睛】此题主要考查相似三角形的判定与性质，解题的关键是熟知等边三角形的性质及相似三角形的判定与性质.11．（2022·山西晋中·一模）阅读材料：我们知道：一条直线经过等腰直角三角形的直角顶点，过另外两个顶点分别向该直线作垂线，即可得三垂直模型”如图①，在ABC 中，90ACB ∠=︒，AC BC =，分别过A 、B 向经过点C 直线作垂线，垂足分别为D 、E ，我们很容易发现结论：ADC CEB △≌△．（1）探究问题：如果AC BC ≠，其他条件不变，如图②，可得到结论；ADC CEB △∽△．请你说明理由．（2）学以致用：如图③，在平面直角坐标系中，直线12y x =与直线CD 交于点()2,1M ，且两直线夹角为α，且3tan 2α=，请你求出直线CD 的解析式．（3）拓展应用：如图④，在矩形ABCD中，3AB=，5BC=，点E为BC边上—个动点，连接AE，将线段AE绕点E顺时针旋转90︒，点A落在点P处，当点P在矩形ABCD外部时，连接PC，PD．若DPC△为直角三角形时，请你探究并直接写出BE的长．415NF OF NO△△ADC=90°，△△ADC+△PDC=180°，△A 、D 、P 共线，90△△ABE△△EFP12．（2022·山东青岛·九年级期中）【模型引入】我们在全等学习中所总结的“一线三等角、K型全等”这一基本图形，可以使得我们在观察新问题的时候很迅速地联想，从而借助已有经验，迅速解决问题．【模型探究】如图，正方形ABCD中，E是对角线BD上一点，连接AE，过点E作EF△AE，交直线CB于点F．（1）如图1，若点F在线段BC上，写出EA与EF的数量关系并加以证明；（2）如图2，若点F在线段CB的延长线上，请直接写出线段BC，BE和BF的数量关系．【模型应用】（3）如图3，正方形ABCD中，AB＝4，E为CD上一动点，连接AE交BD于F，过F作FH△AE于F，过H作HG△BD于G．则下列结论：①AF＝FH；②△HAE＝45°；③BD＝2FG；④△CEH的周长为8．正确的结论有个．（4）如图4，点E是正方形ABCD对角线BD上一点，连接AE，过点E作EF△AE，交线段BC于点F，交线段AC于点M，连接AF交线段BD于点H．给出下列四个结论，①AE＝EF；＝CF；③S△AEM＝S△MCF；④BE＝DE；正确的结论有个．【模型变式】（5）如图5，在平面直角坐标系中，四边形OBCD是正方形，且D（0，2），点E是线段OB延长线上一点，M是线段OB上一动点（不包括点O、B），作MN△DM，垂足为M，交△CBE的平分线与点N，求证：MD＝MN（6）如图6，在上一问的条件下，连接DN交BC于点F，连接FM，则△FMN和△NMB之间有怎样的数量关系？请给出证明．【拓展延伸】（7）已知△MON＝90°，点A是射线ON上的一个定点，点B是射线OM上的一个动点，且满足OB＞OA．点C在线段OA的延长线上，且AC＝OB．如图7，在线段BO 上截取BE，使BE＝OA，连接CE．若△OBA+△OCE＝β，当点B在射线OM上运动时，β的大小是否会发生变化？如果不变，请求出这个定值；如果变化，请说明理由．（8）如图8，正方形ABCD中，AD＝6，点E是对角线AC上一点，连接DE，过点E作EF△ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF 于点N，若点F是AB边的中点，则△EDM的面积是．。

专题01 全等模型--倍长中线与截长补短全等三角形在中考数学几何模块中占据着重要地位，也是学生必须掌握的一块内容，本专题就全等三角形中的重要模型（倍长中线模型、截长补短模型）进行梳理及对应试题分析，方便掌握。

模型1.倍长中线模型【模型解读】中线是三角形中的重要线段之一，在利用中线解决几何问题时，常常采用“倍长中线法”添加辅助线．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，从而运用全等三角形的有关知识来解决问题的方法．（注：一般都是原题已经有中线时用，不太会有自己画中线的时候）。

【常见模型及证法】1、基本型：如图1，在三角形ABC 中，AD 为BC 边上的中线.证明思路：延长AD 至点E ，使得AD =DE . 若连结BE ，则BDE CDA ∆≅∆；若连结EC ，则ABD ECD ∆≅∆；2、中点型:如图2，C 为AB 的中点.证明思路：若延长EC 至点F ，使得CF EC =，连结AF ，则BCE ACF ∆≅∆; 若延长DC 至点G ，使得CG DC =，连结BG ，则ACD BCG ∆≅∆. 3、中点+平行线型：如图3, //AB CD ，点E 为线段AD 的中点.证明思路：延长CE 交AB 于点F (或交BA 延长线于点F )，则EDC EAF ∆≅∆.1．（2022·山东烟台·一模）（1）方法呈现：如图①：在ABC 中，若6AB =，4AC =，点D 为BC 边的中点，求BC 边上的中线AD 的取值范围．解决此问题可以用如下方法：延长AD 到点E 使DE AD =，再连接BE ，可证ACD EBD △≌△，从而把AB 、AC ，2AD 集中在ABE △中，利用三角形三边的关系即可判断中线AD 的取值范围是_______________，这种解决问题的方法我们称为倍长中线法；（2）探究应用：如图②，在ABC 中，点D 是BC 的中点，DE DF ⊥于点D ，DE 交AB 于点E ，DF 交AC 于点F ，连接EF ，判断BE CF +与EF 的大小关系并证明；（3）问题拓展：如图③，在四边形ABCD 中，//AB CD ，AF 与DC 的延长线交于点F 、点E 是BC 的中点，若AE 是BAF ∠的角平分线．试探究线段AB ，AF ，CF 之间的数量关系，并加以证明．【答案】（1）1＜AD ＜5，（2）BE +CF＞EF ，证明见解析；（3）AF +CF ＝AB ，证明见解析．【分析】（1）由已知得出AC ﹣CE ＜AE ＜AC +CE ，即5﹣4＜AE ＜5+3，据此可得答案；（2）延长FD 至点M ，使DM ＝DF ，连接BM 、EM ，同（1）得△BMD △△CFD ，得出BM ＝CF ，由线段垂直平分线的性质得出EM ＝EF ，在△BME 中，由三角形的三边关系得出BE +BM ＞EM 即可得出结论；（3）如图③，延长AE ，DF 交于点G ，根据平行和角平分线可证AF ＝FG ，易证△ABE △△GEC ，据此知AB ＝CG ，继而得出答案．【详解】解：（1）延长AD 至E ，使DE ＝AD ，连接BE ，如图①所示，△AD 是BC 边上的中线，△BD ＝CD ，在△BDE 和△CDA 中，△BD CD BDE CDA DE AD =⎧⎪∠=∠⎨⎪=⎩，△△BDE △△CDA （SAS ），△BE ＝AC ＝4，在△ABE 中，由三角形的三边关系得：AB ﹣BE ＜AE ＜AB +BE ，△6﹣4＜AE ＜6+4，即2＜AE ＜10，△1＜AD ＜5；故答案为：1＜AD ＜5，（2）BE +CF ＞EF ；证明：延长FD 至点M ，使DM ＝DF ，连接BM 、EM ，如图②所示． 同（1）得：△BMD △△CFD （SAS ），△BM ＝CF ，△DE △DF ，DM ＝DF ，△EM ＝EF ，（3）AF +CF ＝AB ．如图③，延长AE ，DF 交于点G ，【点睛】此题是三角形综合题，主要考查了三角形的三边关系、全等三角形的判定与性质、分内容：如图，在ABC 中，D 是边BC 的中点，过点C 画直线CE ，使//CE AB ，交AD 的延长线于点E ，求证：AD ED =证明△//CE AB （已知）△ABD ECD ∠=∠，BAD CED ∠=∠（两直线平行，内错角相等）．在ABD △与ECD 中，△ABD ECD ∠=∠，BAD CED ∠=∠（已证），BD CD =（已知），△()A.A.S ABD ECD △△≌，△AD ED =（全等三角形的对应边相等）．（1）【方法应用】如图①，在ABC 中，6AB =，4AC =，则BC 边上的中线AD 长度的取值范围是______．（2）【猜想证明】如图②，在四边形ABCD 中，//AB CD ，点E 是BC 的中点，若AE 是BAD ∠的平分线，试猜想线段AB 、AD 、DC 之间的数量关系，并证明你的猜想；（3）【拓展延伸】如图③，已知//AB CF ，点E 是BC 的中点，点D 在线段AE 上，EDF BAE ∠=∠，若5AB =，2CF =，求出线段DF 的长．【答案】（1）1＜AD ＜5；（2）AD =AB +DC ．理由见解析；（3）DF =3．【分析】（1）延长AD 到E ，使AD =DE ，连接BE ，证△ADC △△EDB ，推出AC =BE =4，在△ABE 中，根据三角形三边关系定理得出AB -BE ＜AE ＜AB +BE ，代入求出即可；（2）结论：AD =AB +DC ．延长AE ，DC 交于点F ，证明△ABE △△FEC （AAS ），推出AB =CF ，再证明DA =DF 即可解决问题；（3）如图③，延长AE 交CF 的延长线于点G ，证明AB =DF +CF ，可得结论．【详解】解：（1）延长AD 到E ，使AD =DE ，连接BE ，△AD 是BC 边上的中线，△BD =CD ，在△ADC 和△EDB 中，AD DE ADC EDB DC DB =⎧⎪∠=∠⎨⎪=⎩，△△ADC △△EDB （SAS ），△AC =BE =4， 在△ABE 中，AB -BE ＜AE ＜AB +BE ，△6-4＜2AD ＜6+4，△1＜AD ＜5，故答案为：1＜AD ＜5；（2）结论：AD =AB +DC ．理由：如图②中，延长AE ，DC 交于点F ，△AB △CD ，△△BAF =△F ，在△ABE 和△FCE 中，AEB FEC BAE F BE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，△△ABE △△FCE （AAS ），△CF =AB ， △AE 是△BAD 的平分线，△△BAF =△F AD ，△△F AD =△F ，△AD =DF ，△DC +CF =DF ，△DC +AB =AD ；（3）如图③，延长AE 交CF 的延长线于点G ，△E 是BC 的中点，△CE =BE ，△AB △CF ，△△BAE =△G ，在△AEB 和△GEC 中，BAE G AEB GEC BE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩，△△AEB △△GEC （AAS ），△AB =GC ， △△EDF =△BAE ，△△FDG =△G ，△FD =FG ，△AB =DF +CF ，△AB =5，CF =2，△DF =AB -CF =3．【点睛】本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、角平分线的性质、三角形三边关系等知识点，解题的关键是学会添加常用辅助线，构造全等三角形解决问题． 3．（2022·河北·中考模拟）倍长中线的思想在丁倍长某条线段（被延长的线段a 要满足两个条件：①线段a 一个端点是图中一条线段b 的中点；②线段a 与这条线段b 不共线)，然后进行连接，构造三角形全等，再进一步将某些线段进行等量代换，再证明全等或其他的结论，从而解决问题．【应用举例】如图（1），已知：AD 为ABC ∆的中线，求证：2AB AC AD +>．简证：如图（2），延长AD到E，使得DE AD=，连接CE，易证ABD ECD∆≅∆，得AB=，在ACE∆中，AC CE+>，2AB AC AD+>．【问题解决】（1）如图（3），在ABC∆中，AD是BC边上的中线，E是AD上一点，且BE AC=，延长BE交AC于F，求证：AF EF=．（2）如图（4），在ABC∆中，90,A D∠=︒是BC边的中点，E F、分别在边AB AC、上，DE DF⊥，若3,4BE CF==，求EF的长．（3）如图（5），AD是ABC∆的中线，,AB AE AC AF==，且90BAE FAC∠=∠=︒，请直接写出AD与EF的数量关系_ 及位置关系_ ．【答案】,CE AE；（1）详见解析；（2）5；（3）2EF AD=，EF AD⊥【分析】【应用举例】由全等的性质可得AB=EC，由三角形三边关系可得AC+CE>AE，即AB+AC>2AD；故答案为EC，AE；【问题解决】（1）由题意不难得到,ACD GBD∆≅∆所以△BGD=△BED=△AEF=△DAC，△有AF=EF；（2）延长ED 到G ，使DG=ED ，连结CG 、FG ，不难得到EF=FG ，另同（1）有△BDE△△CDG ，所以△FCG=△FCD+△GCD=△FCD+△EBD=90°，CG=BE=3，由勾股定理可得FG 即EF 的长；（3）由全等三角形的性质可以得到解答．【详解】【应用举例】,CE AE【问题解决】()1如图()1延长AD 到G ，使得,DG AD =连接,BG 易证,ACD GBD ∆≅∆得,BG AC G DAC =∠=∠，,BE AC =,BE BG ∴=,G BEG ∴∠=∠,BEG AEF ∠=∠,AEF EAC ∴∠=∠AF EF ∴=．()2如图()2，延长ED 到G ，使得,DG ED =连接,CG FG 、易证,BDE CDG ∆≅∆得,,CG BE ED GD B DCG ==∠=∠，,DE DF ⊥DF ∴垂直平分,EG ,FE FG ∴=90,A ∠=︒90,B ACB ∴∠+∠=︒90,DCG ACB ∴∠+∠=︒即90,FCG ∠=︒在Rt FCG ∆中，3,4CG BE CF ===，5,FG ∴=5,EF ∴=()32EF AD EF AD =⊥，，理由如下：如图3，延长AD 到G ，使AD=DG ，延长DA 交EF 于P ，连结BG ，则不难得到△BGD△△CAD ， △BG=AC ，△GBD=△ACD ，△DGB=△DAC ，又AF=AC ，△BG=AF ，△△ABG=△ABD+△GBD=△ABD+△ACD=180°-△ BAC=△EAF ，△在△ABG 和△EAF 中，AB AE ABG EAF BG AF =⎧⎪∠=∠⎨⎪=⎩，△△ABG△△EAF ，△EF=AG=2AD ，△EFA=△DGB=△DAC ，△△DAC+△PAF=180°-△FAC=180°-90°=90°，△△EFA+△PAF=90°，△△APF=90°，△EF△AD ．【点睛】本题考查全等三角形的综合运用，熟练掌握全等三角形的判定和性质是解题关键 ．模型2.截长补短模型【模型解读】截长补短的方法适用于求证线段的和差倍分关系。

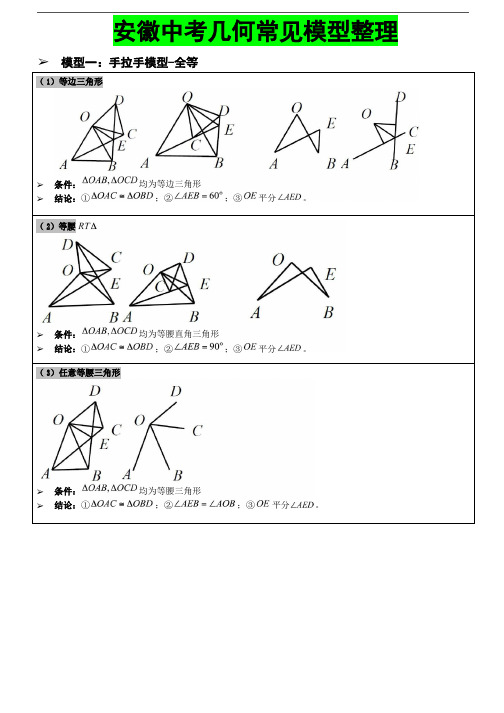
安徽中考几何常见模型整理➢模型一：手拉手模型-全等（1 ）等边三角形➢条件：均为等边三角形➢结论：①；②；③平分。

（2 ）等腰➢条件：均为等腰直角三角形➢结论：①；②；③平分。

（3 ）任意等腰三角形➢条件：均为等腰三角形➢结论：①；②；③平分。

➢模型二：手拉手模型-相似（1 ）一般情况➢条件：，将旋转至右图位置➢结论：右图中①；②延长AC交BD于点E，必有（2 ）特殊情况➢条件：，，将旋转至右图位置➢结论：右图中①；②延长AC交BD于点E，必有；③；④；⑤ 连接AD、BC，必有；⑥（对角线互相垂直的四边形）➢➢模型三：对角互补模型（1）全等型-90°➢条件：①；②OC平分➢结论：①CD=CE;②；③➢证明提示：①作垂直，如图，证明；②过点C作,如上图（右），证明；➢当的一边交AO的延长线于点D时：以上三个结论：①CD=CE（不变）；②；③此结论证明方法与前一种情况一致，可自行尝试。

（2）全等型-120°➢条件：①；②平分；➢结论：①；②；③➢证明提示：①可参考“全等型-90°”证法一；②如图：在OB上取一点F，使OF=OC，证明为等边三角形。

➢当的一边交AO的延长线于点D时（如上图右）：原结论变成：①；②；③；可参考上述第②种方法进行证明。

第4页（3）全等型-任意角➢条件：①；②；➢结论：①平分；②；③. ➢当的一边交AO的延长线于点D时（如右上图）：原结论变成：①；②；③；可参考上述第②种方法进行证明。

◇请思考初始条件的变化对模型的影响。

➢。

中考数学几何模型大汇总下面是中考几何模型的大汇总：1、平面直角坐标系模型平面直角坐标系模型中，我们可以使用坐标系来描述平面上图形和点的位置关系。

这个模型常用于图形的平移、旋转、对称等问题。

2、矩形模型矩形模型用于讨论四边形的性质、面积、周长等问题。

在这个模型中，我们将四边形近似为一个矩形，从而使问题更易解决。

3、三角形模型三角形模型是中考中最常见的模型之一、它可以用于计算三角形的面积、周长，讨论三角形的性质。

在这个模型中，我们通常使用海伦公式、正弦定理、余弦定理等方法来求解。

4、圆形模型圆形模型用于讨论圆、弧、扇形等问题。

在这个模型中，我们通常使用圆的周长、面积公式，以及角度与弧长的关系来进行计算。

5、球体模型球体模型用于讨论球体的体积、表面积以及球冠、球缺等问题。

在这个模型中，我们通常使用球的体积、表面积公式，以及球冠、球缺的体积和表面积公式来求解。

6、棱锥模型棱锥模型用于讨论棱锥的体积、表面积、正棱锥、锥台等问题。

在这个模型中，我们通常使用棱锥的体积、表面积公式，以及正棱锥、锥台的体积和表面积公式来求解。

7、棱柱模型棱柱模型用于讨论棱柱的体积、表面积、正棱柱、柱台等问题。

在这个模型中，我们通常使用棱柱的体积、表面积公式，以及正棱柱、柱台的体积和表面积公式来求解。

8、立体几何模型立体几何模型用于讨论正方体、长方体、正六面体等立体图形的体积、表面积、对角线等问题。

在这个模型中，我们通常使用立体图形的体积、表面积公式，以及对角线长的求法来计算。

总之，几何模型是中考数学中重要的一环，通过利用这些模型，我们可以更好地理解几何知识，更好地应对考试。

一、常见的八大类几何模型在解决几何题目时，我们经常会遇到一些常见的几何模型。

这些模型包括但不限于：直角三角形、等腰三角形、等边三角形、直接相似三角形、等腰梯形、菱形、正方形和矩形。

1. 直角三角形直角三角形是一个内角为90度的三角形。

在求解直角三角形题目时，可以运用勾股定理、正弦定理、余弦定理等方法。

2. 等腰三角形等腰三角形是指两边相等的三角形。

在解决等腰三角形问题时，可以利用等角定理、等边角定理等。

3. 等边三角形等边三角形是指三边相等的三角形。

解决等边三角形问题时，可以利用等边三角形的性质，如高、中线等。

4. 直接相似三角形直接相似三角形是指对应角相等的两个三角形。

在对直接相似三角形进行解题时，可以利用相似三角形的性质，如边比例定理等。

5. 等腰梯形等腰梯形是指有两对对边相等的梯形。

解决等腰梯形问题时，可以运用梯形的性质以及各边的关系。

6. 菱形菱形是指四条边都相等的四边形。

在解决菱形问题时，可以利用菱形的性质，如对角线垂直平分、对角相等等。

7. 正方形正方形是指四条边相等且四个角均为直角的四边形。

解决正方形问题时，可以利用正方形的性质，如对角线相等、对角线垂直等。

8. 矩形矩形是指四边均为直角的四边形。

在解决矩形问题时，可以利用矩形的性质，如对角线相等、邻边互相垂直等。

二、60种解题技巧在解决几何题目时，我们还可以运用一些解题技巧来更快更准确地得出答案。

下面列举了60种解题技巧，以供参考。

1. 勾股定理2. 余弦定理3. 正弦定理4. 度角关系5. 弧度制下的两点间弧长相关关系6. 三角恒等变形7. 各角平分线8. 高度定理9. 中线定理10. 角平分线定理11. 等角定理12. 外角定理13. 内角定理14. 中位线定理15. 等腰三角形的性质16. 等边三角形的性质17. 相似三角形的三边对应比例关系18. 相似三角形的高度关系19. 相似三角形的边对应比例关系20. 相似三角形的面积关系21. 三角形高到底关系22. 三角形高乘底除以2的面积公式23. 三角形内切圆24. 三角形外接圆25. 正方形的性质26. 矩形的对角线关系27. 矩形的邻边互相垂直关系28. 长方形的面积公式29. 长方形的周长公式30. 菱形的性质31. 菱形对角线垂直平分32. 平行四边形的性质33. 平行四边形的对角线相等关系34. 平行四边形的对角互补35. 梯形的中位线关系36. 梯形的对角线垂直关系37. 梯形的高关系38. 圆的性质39. 圆周角的关系40. 圆心角的关系41. 切线关系42. 切线长定理43. 余弦定理的推广44. 余角关系45. 同位角关系46. 交叉线定理47. 锐角三角函数的关系48. 平行线夹角关系49. 余切函数的关系50. 同义形的面积公式51. 直角三角形斜边上的高52. 各角平分线角度关系53. 三角形中位线长度关系54. 三角形中位线平行长的关系55. 等角三角形三角函数的关系56. 三角形半周长乘外切圆内切圆面积关系57. 圆相关不等式58. 反证法59. 斜率性质60. 坐标系下平移关系解决几何问题时，首先要熟练掌握常见的八大类几何模型，然后灵活运用各种解题技巧，以便更加高效地解决问题。

专题05 一线三等角（K 型图）模型（从全等到相似） 全等三角形与相似三角形在中考数学几何模块中占据着重要地位。

相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。

如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了．本专题就一线三等角模型进行梳理及对应试题分析，方便掌握。

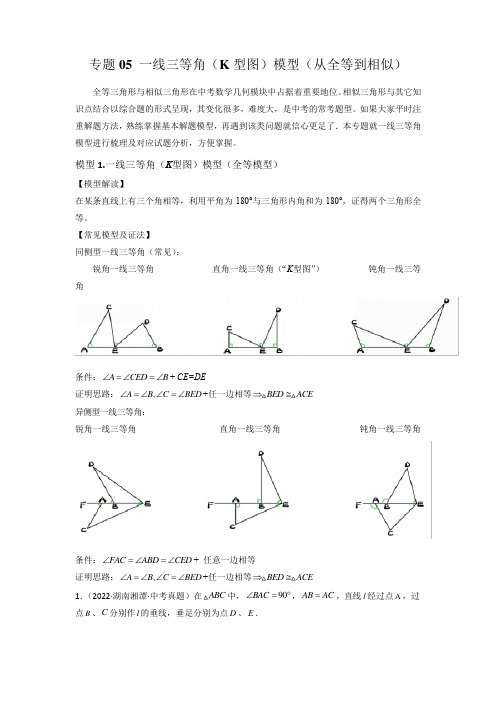
模型1.一线三等角（K 型图）模型（全等模型）【模型解读】在某条直线上有三个角相等，利用平角为180°与三角形内角和为180°，证得两个三角形全等。

【常见模型及证法】同侧型一线三等角（常见）：锐角一线三等角 直角一线三等角（“K 型图”） 钝角一线三等角条件：A CED B ∠=∠=∠+ CE=DE证明思路：,A B C BED ∠=∠∠=∠+任一边相等BED ACE ⇒≅异侧型一线三等角：锐角一线三等角 直角一线三等角 钝角一线三等角条件：FAC ABD CED ∠=∠=∠+ 任意一边相等证明思路：,A B C BED ∠=∠∠=∠+任一边相等BED ACE ⇒≅1．（2022·湖南湘潭·中考真题）在ABC 中，90BAC ∠=︒，AB AC =，直线l 经过点A ，过点B 、C 分别作l 的垂线，垂足分别为点D 、E ．(1)特例体验：如图①，若直线l BC ∥，2AB AC ==，分别求出线段BD 、CE 和DE 的长；(2)规律探究：①如图②，若直线l 从图①状态开始绕点A 旋转()045αα<<︒，请探究线段BD 、CE 和DE 的数量关系并说明理由；②如图③，若直线l 从图①状态开始绕点A 顺时针旋转()4590αα︒<<︒，与线段BC 相交于点H ，请再探线段BD 、CE 和DE 的数量关系并说明理由；(3)尝试应用：在图③中，延长线段BD 交线段AC 于点F ，若3CE =，1DE =，求BFCS △． 【答案】(1)BD =1；CE =1；DE =2(2)①DE =CE +BD ；理由见解析；②BD =CE +DE ；理由见解析 (3)258BFC S ∆= 【分析】（1）先根据得出90452ABC ACB ︒∠=∠==︒，根据l BC ∥，得出45DAB ABC ∠=∠=︒，45EAC ACE ∠=∠=︒，再根据90BDA CEA ∠=∠=︒，求出45ABD ∠=︒，45ACE ∠=︒， 即可得出45DAB ABD EAC ACE ∠=∠=∠=∠=︒，最后根据三角函数得出1AD BD ==，1AE CE ==，即可求出2DE AD AE =+=；（2）①DE =CE +BD ；根据题意，利用“AAS”证明ABD CAE ∆∆≌，得出AD =CE ，BD =AE ，即可得出结论；②BD =CE +DE ；根据题意，利用“AAS”证明ABD CAE ∆∆≌，得出AD =CE ，BD =AE ，即可得出结论；（3）在Rt△AEC 中，根据勾股定理求出225AC AE CE =+=，根据DF CE ∥，得出AD AF AE CF=，代入数据求出AF ，根据AC =5，算出CF ，即可求出三角形的面积．(1)解：△90BAC ∠=︒，AB AC =，△90452ABC ACB ︒∠=∠==︒， △l BC ∥，△45DAB ABC ∠=∠=︒，45EAC ACE ∠=∠=︒，△BD △AE ，CE △DE ，△90BDA CEA ∠=∠=︒，△904545ABD ∠=︒-︒=︒，904545ACE ∠=-=︒︒︒，△45DAB ABD EAC ACE ∠=∠=∠=∠=︒，△2sin 212AD BD AB DAB ==⨯∠=⨯=，2sin 212AE CE AC EAC ==⨯∠=⨯=，△2DE AD AE =+=． (2)①DE =CE +BD ；理由如下：△BD △AE ，CE △DE ，△90BDA CEA ∠=∠=︒，△90DAB DBA ∠+∠=︒，△90BAC ∠=︒，△90DAB CAE ∠+∠=︒，△DBA CAE ∠=∠，△AB =AC ，△ABD CAE ∆∆≌，△AD =CE ，BD =AE ，△DE =AD +AE =CE +BD ，即DE =CE +BD ；②BD =CE +DE ，理由如下：△BD △AE ，CE △DE ，△90BDA CEA ∠=∠=︒，△90DAB DBA ∠+∠=︒，△90BAC ∠=︒，△90DAB CAE ∠+∠=︒，△DBA CAE ∠=∠，△AB =AC ，△ABD CAE ∆∆≌，△AD =CE ，BD =AE ，△BD =AE =AD +DE =CE +DE ，即BD =CE +DE ．(3)根据解析（2）可知，AD =CE=3，△314AE AD DE =+=+=，在Rt△AEC 中，根据勾股定理可得：225AC AE CE =+=，△BD △AE ，CE △AE ，△DF CE ∥，△AD AF AE CF =，即345AF =，解得：154=AF ， △155544CF AC AF =-=-=，△AB =AC =5，△1152552248BFC S CF AB ∆=⨯=⨯⨯=． 【点睛】本题主要考查了三角形全等的判定和性质，等腰三角形的判定和性质，勾股定理，平行线的性质，解直角三角形，根据题意证明ABD CAE ∆∆≌，是解题的关键．2．（2022·黑龙江·九年级期末）（1）如图（1），已知：在△ABC 中，△BAC ＝90°，AB =AC ，直线m 经过点A ，BD △直线m ， CE △直线m ，垂足分别为点D 、E ．证明△DE =BD +CE ．（2）如图（2），将（1）中的条件改为：在△ABC 中，AB =AC ，D 、A 、E 三点都在直线m 上，并且有△BDA =△AEC =△BAC =α，其中α为任意锐角或钝角．请问结论DE =BD +CE 是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D 、E 是D 、A 、E 三点所在直线m 上的两动点（D 、A 、E 三点互不重合），点F 为△BAC 平分线上的一点，且△ABF 和△ACF 均为等边三角形，连接BD 、CE ，若△BDA =△AEC =△BAC ，试判断△DEF 的形状．【答案】（1）见解析（2）成立，证明见解析（3）△DEF为等边三角形，证明见解析【分析】（1）因为DE=DA+AE，故由全等三角形的判定AAS证△ADB△△CEA，得出DA=EC，AE=BD，从而证得DE=BD+CE；（2）成立，仍然通过证明△ADB△△CEA，得出BD=AE，AD=CE，所以DE=DA+AE=EC+BD；（3）由△ADB△△CEA得BD=AE，△DBA =△CAE，由△ABF和△ACF均等边三角形，得△ABF=△CAF=60°，FB=F A，所以△DBA+△ABF=△CAE+△CAF，即△DBF=△F AE，所以△DBF△△EAF，所以FD=FE，△BFD=△AFE，再根据△DFE=△DF A+△AFE=△DF A+△BFD=600得到△DEF是等边三角形．【详解】解：（1）证明：△BD△直线m，CE△直线m，△△BDA＝△CEA=90°．△△BAC＝90°，△△BAD+△CAE=90°．△△BAD+△ABD=90°，△△CAE=△ABD．又AB=AC，△△ADB△△CEA（AAS）．△AE=BD，AD=CE．△DE=AE+AD=BD+CE；（2）成立．证明如下：△△BDA =△BAC=α，△△DBA+△BAD=△BAD +△CAE=180°-α．△△DBA=△CAE．△△BDA=△AEC=α，AB=AC，△△ADB△△CEA（AAS）．△AE=BD，AD=CE．△DE=AE+AD=BD+CE；（3）△DEF为等边三角形．理由如下：由（2）知，△ADB△△CEA，BD=AE，△DBA =△CAE，△△ABF和△ACF均为等边三角形，△△ABF=△CAF=60°．△△DBA+△ABF=△CAE+△CAF．△△DBF=△F AE．△BF=AF，△△DBF△△EAF（SAS）．△DF=EF，△BFD=△AFE．△△DFE=△DF A+△AFE=△DF A+△BFD=60°．△△DEF为等边三角形．【点睛】此题考查了全等三角形的性质和判定、等边三角形的性质和判定，解题的关键是熟练掌握全等三角形的性质和判定，等边三角形的性质和判定．3．（2022·江苏·九年级专题练习）【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一，请根据以下问题，把你的感知填写出来：①如图1，ABC 是等腰直角三角形，90C ∠=︒，AE =BD ，则AED ≌_______； ②如图2，ABC 为正三角形，,60BD CF EDF =∠=︒，则BDE ≌________；③如图3，正方形ABCD 的顶点B 在直线l 上，分别过点A 、C 作AE l ⊥于E ，CF l ⊥于F ．若1AE =，2CF =，则EF 的长为________．【模型应用】（2）如图4，将正方形OABC 放在平面直角坐标系中，点O 为原点，点A 的坐标为()1,3，则点C 的坐标为________．【模型变式】（3）如图5所示，在ABC 中，90ACB ∠=︒，AC BC =，BE CE ⊥于E ，AD △CE 于D ，4cm DE =，6cm AD =，求BE 的长．【答案】①△BDF ；②△CFD ；③3；（2）(31)-，（3）2cm【分析】①根据等腰直角三角形的性质及和角关系，可得△AED △△BDF ；②根据等边三角形的性质及和角关系，可得△BDE △△CFD ；③根据正方形的性质及和角关系，可得△ABE △△BCF ，由全等三角形的性质即可求得EF 的长；（2）分别过A 、C 作x 轴的垂线，垂足分别为点D 、E ，根据正方形的性质及和角关系，可得△COE △△OAD ，从而可求得OE 、CE 的长，进而得到点C 的坐标；（3）由三个垂直及等腰直角三角形可证明△BCE △△CAD ，由全等三角形的性质即可求得BE 的长．【详解】①△△ABC 是等腰直角三角形，△C =90゜△△A =△B =45゜△△BDF +△BFD =180゜−△B =135゜△△EDF =45゜△△ADE +△BDF =180゜−△EDF =135゜△△ADE =△BFD在△AED 和△BDF 中A B ADE BFD AEBD ∠=∠⎧⎪∠=∠⎨⎪=⎩△△AED △△BDF (AAS ) 答案为：△BDF ； ②△△ABC 是等边三角形△△B =△C =60゜△△BDE +△BED =180゜−△B =120゜△△EDF =60゜△△BDE +△CDF =180゜−△EDF =120゜△△BED =△CDF在△BDE 和△CFD 中B C BED CDF BD CF ∠=∠⎧⎪∠=∠⎨⎪=⎩△△BDE △△CFD (AAS )故答案为：△CFD ； ③△四边形ABCD 是正方形△△ABC =90゜，AB =BC△△ABE +△CBF =180゜−△ABC =90゜△AE △l ，CF △l △△AEB =△CFB =90゜△△ABE +△EAB =90゜△△EAB =△CBF在△ABE 和△BCF 中AEB CFB EAB CBF AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△ABE △△BCF (AAS ) △AE =BF =1，BE =CF =2△EF =BE +BF =2+1=3 故答案为：3；（2）分别过A 、C 作x 轴的垂线，垂足分别为点D 、E ，如图所示△四边形OABC 是正方形△△AOC =90゜，AO =OC△△COE +△AOD =180゜−△ACO =90゜△AD △x 轴，CE △x 轴△△CEO =△ADO =90゜△△ECO +△COE =90゜△△ECO =△AOD在△COE 和△OAD 中CEO ADO ECO AOD OC AO ∠=∠⎧⎪∠=∠⎨⎪=⎩△△COE △△OAD (AAS )△CE =OD ，OE =AD △(1,3)A △OD =1，3AD =△CE =1，3OE =△点C 在第二象限△点C 的坐标为(31)-，故答案为：(31)-，； （3）△△ACB =90゜△△BCE +△ACD =90゜△BE △CE ，AD △CE △△CEB =△ADC =90゜△△BCE +△CBE =90゜ △△CBE =△ACD在△BCE 和△CAD 中CBE ACD CEB ADC BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△BCE △△CAD (AAS ) △BE =CD ，CE =AD =6cm △BE =CD =CE －DE =6－4=2(cm)【点睛】本题是三角形全等的综合，考查了全等三角形的判定与性质，掌握全等三角形的判定方法是关键．模型2.一线三等角模型（相似模型）【模型解读与图示】“一线三等角”型的图形，因为一条直线上有三个相等的角，一般就会有两个三角形的“一对角相等”，再利用平角为180°，三角形的内角和为180°，就可以得到两个三角形的另外一对角也相等，从而得到两个三角形相似．1．（2022·四川·一模）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形：（1）如图1，已知：在△ABC 中，AB AC =，D 、A 、E 三点都在直线m 上，并且有BDA AEC BAC α∠=∠=∠=．试猜想DE 、BD 、CE 有怎样的数量关系，请证明你的结论； （2）老师鼓励学习小组继续探索相似的情形．于是，学习小组又研究以下问题：如图2，△ABC 中，(060)B C αα∠=∠=<<︒．将一把三角尺中30°角顶点P 放在BC 边上，当P 在BC 边上移动时，三角尺中30°角的一条边始终过点A ，另一条边交AC 边于点Q ，P 、Q 不与三角形顶点重合．设CPQ β∠=．当β在许可范围内变化时，α取何值总有△ABP △△PCQ ？当α在许可范围内变化时，β取何值总有△ABP △△QCP ？（3）试探索有无可能使△ABP 、△QPC 、△ABC 两两相似？若可能，写出所有α、β的值（不写过程）；若不可能，请说明理由．【答案】（1）DE AE AD BD CE =+=+；证明见解析；（2）30α=︒；75β=︒；（3）可能；30α=︒，30β=︒或52.5α=︒，75β=︒．【分析】（1）证明△ADB △△CEA （AAS ），由全等三角形的性质得出AE =BD ，AD =CE ，则可得出结论；（2）由β=△2或△1=△CQP ，即△2=30°+β-α=β，解得α=30°，即可求解；由β=△1或△2=△CQP ，同理可得：β=75°，即可求解；（3）①当α=30°，β=30°时，则△2=△B =α=30°，即可求解；②当β=75°，α=52.5°时，同理可解．【详解】解：（1）如图1，△BDA BAC α∠=∠=，△180DBA BAD BAD CAE ∠∠∠∠α+=+=︒-，△DBA CAE ∠=∠，在△ADB 和△CEA 中，DBA EAC BDA AEC BA AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，△△ADB △△CEA （AAS ），△AE BD =，AD CE =， △DE AE AD BD CE =+=+；（2）在△ABP 中，2230APC B αβ∠=∠+∠=+∠=︒+，△1150β∠=︒-，同理可得：230βα∠=︒+-；由2β=∠或1CQP ∠=∠，即230βαβ∠=︒+-=，解得30α=︒，则△ABP △△PCQ ；△当β在许可范围内变化时，30α=︒时，总有△ABP △△PCQ ；由1β=∠或2CQP ∠=∠，同理可得：75β=︒．△当α在许可范围内变化时，75β=︒总有△ABP △△QCP ；（3）可能．①当30α=︒，30β=︒时，则230B α∠=∠==︒，则△ABP △△PCQ △△BCA ； ②当75β=︒，52.5α=︒时，同理可得：115075ββ∠=︒-=︒=，23052.5βαα∠=︒+-=︒=，△△ABP △△CQP △△BCA ．【点睛】本题是相似形综合题，主要考查了全等三角形的判定和性质，相似三角形的判定和性质，熟练掌握相似三角形的性质是解本题的关键．2．（2022·河南新乡·二模）如图，△ABC 和△ADE 是有公共顶点A 的两个等腰直角三角形，△DAE ＝△BAC ＝90°，AD ＝AE ，AB ＝AC ＝6，D 在线段BC 上，从B 到C 运动，点M 和点N 分别是边BC ，DE 的中点．(1)【问题发现】若点D 是BC 边的中点时，BD MN＝ ，直线BD 与MN 相交所成的锐角的度数为 （请直接写出结果）(2)【解决问题]若点D 是BC 边上任意一点时，上述结论是否成立，请说明理由．(3)【拓展探究】在整个运动过程中，请直接写出N 点运动的路径长，及CN 的最小值．【答案】(1)2，45° (2)成立，理由见解析(3)N 点运动的路径长为6，CN 的最小值为3【分析】（1）证明△AMN 是等腰直角三角形，可得结论．（2）结论不变．连接AM ，AN ，证明△BAD △△MAN ，可得结论．（3）利用三角形中位线定理，垂线段最短解决问题即可．(1)解：如图1中，当点D 是BC 的中点时，△AB =AC ，△AD △BC ，AD 平分△BAC ，△△CAD =△ADE =45°，△AC △DE ，△AC 平分DE ，△点N 落在AC 上，△BM =AM =2MN ，△NMC =45°，△BD MN=2，故答案为：2，45°． (2)解：如图2中，连接AM ，AN ．△AB =AC ，△BAC =90°，BM =CM ，△AM △MC ，AM =BM =CM ，△AB =2AM ，同法可证AD =2AN ，△△BAM =△DAN =45°，△△BAD =△MAN ，△AB AM =AD AN ，△△BAD △△MAN ，△BD MN =AB AM=2，△ABD =△AMN =45°．(3)解：如图3中，当D 在线段BC 上，从B 运动到C 时，由（2）问可知，△AMN =45°，所以点N 的运动路径是图3中的线段MN ，MN =12BE =6．当CN △MN 时，CN 的值最小，最小值=12AC =3．【点睛】本题属于三角形综合题，考查了等腰直角三角形的性质，相似三角形的判定和性质，三角形中位线定理，垂线段最短等知识，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，属于中考压轴题．3．（2022·山东菏泽·三模）（1）问题：如图1，在四边形ABCD 中，点P 为AB 上一点，当90DPC A B ∠=∠=∠=︒时，求证：AD BC AP BP ⋅=⋅．（2）探究：若将90°角改为锐角或钝角（如图2），其他条件不变，上述结论还成立吗？说明理由．（3）应用：如图3，在ABC 中，22AB =，45B ∠=︒，以点A 为直角顶点作等腰Rt ADE △．点D 在BC 上，点E 在AC 上，点F 在BC 上，且45EFD ∠=︒，若5CE =，求CD 的长．【答案】（1）见解析；（2）成立，理由见解析；（3）5CD =【分析】（1）由△DPC =△A =B =90°，可得△ADP ＝△BPC ，即可证到△ADP ∽△BPC ，然后运用相似三角形的性质即可解决问题；（2）由△DPC ＝△A ＝△B ＝α，可得△ADP =△BPC ，即可证到△ADP∽△BPC ，然后运用相似三角形的性质即可解决问题；（3）先证△ABD ∽△DFE ，求出DF =4，再证△EFC ∽△DEC ，可求FC ＝1，进而解答即可．【详解】（1）证明：如题图1，△△DPC =△A =△B =90°，△△ADP ＋△APD =90°，△BPC ＋△APD = 90°，△△ADP = △BPC ，△△ADP ∽△BPC ，AD AP BP BC∴=，△AD ⋅BC = AP ⋅BP ， （2）结论仍然成立，理由如下，BPD DPC BPC ∠=∠+∠，又BPD A ADP ∠=∠+∠，DPC BPC A ADP ∴∠+∠=∠+∠，DPC A ∠=∠，设DPC A α∠=∠=，BPC ADP ∴∠=∠，ADP BPC ∴∽△△，AD AP BP BC ∴=，△AD ⋅BC = AP ⋅BP ，（3）45EFD ∠=︒，45B ADE ∴∠=∠=︒，BAD EDF ∴∠=∠，ABD DFE ∴∽，AB AD DF DE∴=，ADE 是等腰直角三角形，2DE AD ∴=，22AB =，4DF ∴=，45,45EFD ADE ∠=︒∠=︒，135EFC DEC ∴∠=∠=︒，EFC DEC ∴∽，FC EC EC CD ∴=， 5EC =,4CD DF FC FC =+=+，()245EC FC CD FC FC ∴=⋅=⋅+=，1FC ∴=，5CD ∴=． 【点睛】本题考查相似三角形的综合题，三角形的相似；能够通过构造45°角将问题转化为一线三角是解题的关键．模型3.一线三直角模型（相似模型）【模型解读与图示】“一线三直角”模型的图形，实则是“一线三等角”型的图形的特例，因为这种图形在正方形和矩形中出现的比较多，对它做一专门研究，这样的图形，因为有三个角是直角，就有两个角相等，再根据“等角的余角相等”可以得到另外一对角相等，从而判定两个三角形相似．1．（2022·湖南郴州·中考真题）如图1，在矩形ABCD 中，4AB =，6BC =．点E 是线段AD 上的动点（点E 不与点A ，D 重合），连接CE ，过点E 作EF CE ⊥，交AB 于点F ．(1)求证：AEF DCE ∽；(2)如图2，连接CF ，过点B 作BG CF ⊥，垂足为G ，连接AG ．点M 是线段BC 的中点，连接GM ．①求AG GM +的最小值；②当AG GM +取最小值时，求线段DE 的长．【答案】(1)见解析(2)①5；②35DE =+或35DE =-【分析】（1）证明出DCE AEF ∠=∠即可求解；（2）①连接AM ．先证明132BM CM GM BC ====．确定出点G 在以点M 为圆心，3为半径的圆上．当A ，G ，M 三点共线时，AG GM AM +=．此时，AG GM +取最小值．在Rt ABM 中利用勾股定理即可求出AM ，则问题得解．②先求出AF ，求AF 的第一种方法：过点M 作∥MN AB 交FC 于点N ，即有CMN CBF ∽△△，进而有12MN CM BF CB ==．设AF x =，则4BF x =-，()142MN x =-．再根据∥MN AB ，得到AFG MNG ∽△△，得到AF AG MN GM =，则有()21342xx =-，解方程即可求出AF ；求AF 的第二种方法：过点G 作GH AB ∥交BC 于点H ．即有MHG MBA ∽△△．则有GM GH MH AM AB MB ==，根据5AM =，可得3543GH MH ==，进而求出125GH =，95MH =．由GH AB ∥得CHG CBF ∽△△，即可求出AF ．求出AF 之后，由（1）的结论可得AF AE DE DC．设DE y =，则6AE y =-，即有164y y -=，解得解方程即可求出DE ．(1)证明：如图1，△四边形ABCD 是矩形，△90A D ∠=∠=︒，△90CED DCE ∠+∠=︒．△EF CE ⊥，△90CED AEF ∠+∠=︒，△DCE AEF ∠=∠，△AEF DCE ∽；(2)①解：如图2-1，连接AM ．△BG CF ⊥，△BGC 是直角二角形．△132BM CM GM BC ====． △点G 在以点M 为圆心，3为半径的圆上．当A ，G ，M 三点不共线时，由三角形两边之和大于箒三边得：AG GM AM +>， 当A ，G ，M 三点共线时，AG GM AM +=．此时，AG GM +取最小值．在Rt ABM 中，225AM AB BM =+=．△AGGM+的最小值为5．②（求AF 的方法一）如图2-2，过点M 作∥MN AB 交FC 于点N ，△CMN CBF ∽△△．△12MN CM BF CB ==． 设AF x =，则4BF x =-，△()11422MN BF x ==-． △∥MN AB ，△AFG MNG ∽△△，△AF AG MN GM=， 由①知AG GM +的最小值为5、即5AM =，又△3GM =，△2AG =．△()21342xx =-，解得1x =，即1AF =． （求AF 的方法二）如图2-3，过点G 作GH AB ∥交BC 于点H ．△MHG MBA ∽△△．△GM GH MH AM AB MB ==， 由①知AG GM +的最小值为5，即5AM =，又△3GM =，△3543GH MH ==．△125GH =，95MH =． 由GH AB ∥得CHG CBF ∽△△，△GH CH FB CB =，即1293556FB +=，解得3FB =． △1AF AB FB =-=．由（1）的结论可得AF AE DE DC． 设DE y =，则6AE y =-，△164y y -=，解得35y =+或35-． △0356<+<，0356<-<，△35DE =+或35DE =-．【点睛】本题主要考查了相似三角形的判定与性质、平行的性质、勾股定理以及一元二次方程的应用等知识，掌握相似三角形的判定与性质是解答本题的关键．2．（2022·山东济宁·二模）情境观察:将含45°角的三角板的直角顶点R 放在直线l 上，分别过两锐角的顶点M ，N 作l 的垂线，垂足分别为P ， Q ，（1）如图1.观察图1可知：与NQ 相等的线段是______________，与NRQ∠相等的角是_____(2)问题探究直角ABC 中，90B ∠=︒，在AB 边上任取一点D ，连接CD ，分别以AC ，DC 为边作正方形ACEF 和正方形CDGH ，如图2，过E ，H 分别作BC 所在直线的垂线，垂足分别为K ，L .试探究EK 与HL 之间的数量关系，并证明你的结论.(3)拓展延伸：直角ABC 中，90B ∠=︒，在AB 边上任取一点D ，连接CD ，分别以AC ，DC 为边作矩形ACEF 和矩形CDGH ，连接EH 交BC 所在的直线于点T ，如图3.如果AC kCE =，CD kCH =，试探究TE 与TH 之间的数量关系，并证明你的结论.【答案】(1)PR ，PMR ∠，(2)EK LH =，证明见解析；(3)ET HT=，证明见解析．【分析】（1）根据等腰直角三角形的性质得到，=MR RN ，90MRN ∠=︒，根据余角性质得到PMR NRQ ∠=∠，再证明MPR NRQ ≌△△，即可得到QN PR =，NRQ PMR ∠=∠；（2）证明ABC CEK ≌△△，得到EK BC =，再证明DCB CHL ≌△△，得到BC HL =，可得到EK LH =；（3）证明ACB ECM ∽△△，得到BC kEM =，证明BCD NHC ∽△△，得到BC kHN =，得到EM HN =，证明NHT EMT ≌△△即可得到ET HT =．（1）解：△MRN △是等腰直角三角形，△=MR RN ，90MRN ∠=︒，△MP PQ ⊥，NQ PQ ⊥，△90MPR NQR ∠=∠=︒，△90PMR MRP MRP NRQ ∠+∠=∠+∠=︒，△PMR NRQ ∠=∠，在MPR △和NRQ △中，PMR NRQ MPR NRQ MR NR ∠=∠⎧⎪∠=∠⎨⎪=⎩△MPR NRQ ≌△△，△QN PR =，NRQ PMR ∠=∠，故答案为：PR ，PMR ∠；（2）解：△四边形ACEF 是正方形，△AC CE =，90ACE ∠=︒，△EK BK ⊥△90B EKC ∠=∠=︒，△90BAC ACB ACB ECK ∠+∠=∠+∠=︒，△BAC ECK ∠=∠，在ABC 和CEK △中，BAC KCE B EKCAC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩△ABC CEK ≌△△，△EK BC =， △四边形CDGH 是正方形，△CD CH =，90DCH ∠=︒△HL BC ⊥，△90B CLH ∠=∠=︒，△90DCB LCK LCK CHL ∠+∠=∠+∠=︒，△DCB CHL ∠=∠，在DCB 和CHL △中，B CLH BCD CHL CD CH ∠=∠⎧⎪∠=∠⎨⎪=⎩△DCB CHL ≌△△，△BC HL =，EK LH =， （3）解：过E 作EM BC ⊥与M ，过H 作HN BC ⊥与N ，△四边形ACEF 是矩形，△90ACE ∠=︒，△90BAC ACB ACB ECM ∠+∠=∠+∠=︒，△BAC ECM ∠=∠，△ACB ECM ∽△△，△BC AC k EM CE==，△BC kEM =， 同理：BCD NHC ∽△△，△BC CD k HN CH==，△BC kHN =，△EM HN =， 在NHT △和EMT △中，HNT EMT NTH MTE HN EM ∠=∠⎧⎪∠=∠⎨⎪=⎩△NHT EMT ≌△△，△ET HT =． 【点睛】本题考查全等三角形的判定及性质，相似三角形的判定及性质，正方形的性质，矩形的性质，余角的性质，（3）证明ACB ECM ∽△△，BCD NHC ∽△△是解题的关键．3.（2022·浙江·嘉兴一中一模）阅读材料：我们知道：一条直线经过等腰直角三角形的直角顶点，过另外两个顶点分别向该直线作垂线，即可得三垂直模型”如图①：在△ABC 中，△ACB ＝90°，AC ＝BC ，分别过A 、B 向经过点C 直线作垂线，垂足分别为D 、E ，我们很容易发现结论：△ADC △△CEB ．(1)探究问题：如果AC ≠BC ，其他条件不变，如图②，可得到结论；△ADC △△CEB ．请你说明理由．(2)学以致用：如图③，在平面直角坐标系中，直线y ＝12x 与直线CD 交于点M （2，1），且两直线夹角为α，且tanα＝32，请你求出直线CD 的解析式．(3)拓展应用：如图④，在矩形ABCD 中，AB ＝4，BC ＝5，点E 为BC 边上一个动点，连接AE ，将线段AE 绕点E 顺时针旋转90°，点A 落在点P 处，当点P 在矩形ABCD 外部时，连接PC ，PD ．若△DPC 为直角三角形时，请你探究并直接写出BE 的长．【答案】(1)见解析(2)41577y x =-+(3)4或372+ 【分析】（1）由同角的余角相等可得△BCE =△DAC ，且△ADC =△BEC =90°，可得结论；（2）过点O 作ON △OM 交直线CD 于点N ，分别过M 、N 作ME △x 轴NF △x 轴，由（1）的结论可得： △NFO △△OEM ，可得NF OF NO OE ME MO== ，可求点N 坐标，利用待定系数法可求解析式；（3）分两种情况讨论，由全等三角形的性质和相似三角形的性质可求解．(1)解：理由如下，△△ACB ＝90°，△△ACD +△BCE ＝90°，又△△ADC ＝90°，△△ACD +△DAC ＝90°，△△BCE ＝△DAC ，且△ADC ＝△BEC ＝90°，△△ADC △△CEB ；(2)解：如图，过点O 作ON △OM 交直线CD 于点N ，分别过M 、N 作ME △x 轴，NF △x 轴，由（1）可得：△NFO △△OEM ，△NF OF NO OE ME MO==，△点M （2，1），△OE ＝2，ME ＝1， △tanα＝ON OM ＝32，△3212NF OF ==，△NF ＝3，OF ＝32 ，△点N （32-，3）， △设直线CD 表达式：y ＝kx +b ，△12332k b k b =+⎧⎪⎨=-+⎪⎩△47157k b ⎧=-⎪⎪⎨⎪=⎪⎩△直线CD 的解析式为：y ＝-47x +157； (3)解：当△CDP ＝90°时，如图，过点P 作PH △BC ，交BC 延长线于点H ，△△ADC +△CDP ＝180°，△点A ，点D ，点P 三点共线，△△BAP ＝△B ＝△H ＝90°，△四边形ABHP 是矩形，△AB ＝PH ＝4，△将线段AE 绕点E 顺时针旋转90°，△AE ＝EP ，△AEP ＝90°，△△AEB +△PEH ＝90°，且△BAE +△AEB ＝90°，△△BAE ＝△PEH ，且△B ＝△H ＝90°，AE ＝EP ，△△ABE △△EHP （AAS ），△BE ＝PH ＝4，当△CPD ＝90°时，如图，过点P 作PH △BC ，交BC 延长线于点H ，延长HP 交AD 的延长线于N ，则四边形CDNH 是矩形，△CD ＝NH ＝4，DN ＝CH ，设BE ＝x ，则EC ＝5-x ，△将线段AE 绕点E 顺时针旋转90°，△AE ＝EP ，△AEP ＝90°，△△AEB +△PEH ＝90°，且△BAE +△AEB ＝90°，△△BAE ＝△PEH ，且△B ＝△EHP ＝90°，AE ＝EP ，△△ABE △△EHP （AAS ），△PH ＝BE ＝x ，AB ＝EH ＝4，△PN ＝4-x ，CH ＝4-（5-x ）＝x -1＝DN ，△△DPC ＝90°，△△DPN +△CPH ＝90°，且△CPH +△PCH ＝90°，△△PCH ＝△DPN ，且△N ＝△CHP ＝90°，△△CPH △△PDN ，△DN NP PH CH =，△1x x -=41x x --△x ＝372± △点P 在矩形ABCD 外部，△x ＝372+，△BE ＝372+， 综上所述：当BE 的长为4或372+时，△DPC 为直角三角形． 【点睛】本题是考查了待定系数法求解析式，相似三角形的判定和性质，全等三角形的判定和性质，矩形的判定和性质等知识，添加恰当辅助线构造相似三角形是本题的关键．课后专项训练：1．（2022·贵州铜仁·三模）（1）探索发现：如图1，已知Rt ABC 中，90ACB ∠=︒，AC BC =，直线l 过点C ，过点A 作AD l ⊥，过点B 作BE l ⊥，垂足分别为D 、E ．求证：CD BE =． （2）迁移应用：如图2，将一块等腰直角的三角板MON 放在平面直角坐标系内，三角板的一个锐角的顶点与坐标原点O 重合，另两个顶点均落在第一象限内，已知点N 的坐标为()4,2，求点M 的坐标．（3）拓展应用：如图3，在平面直角坐标系内，已知直线44y x =-+与y 轴交于点P ，与x 轴交于点Q ，将直线PQ 绕P 点沿逆时针方向旋转45︒后，所得的直线交x 轴于点R ．求点R 的坐标．【答案】（1）见详解；（2）点M的坐标为（1，3）；（3）R（203，0）【分析】（1）先判断出△ACB=△ADC，再判断出△CAD=△BCE，进而判断出△ACD△△CBE，即可得出结论；（2）过点M作MF△y轴，垂足为F，过点N作NG△MF，判断出MF=NG，OF=MG，设M（m，n）列方程组求解，即可得出结论；（3）过点Q作QS△PQ，交PR于S，过点S 作SH△x轴于H，先求出OP=4，由y=0得x=1，进而得出Q（1，0），OQ=1，再判断出PQ=SQ，即可判断出OH=5，SH=OQ=1，进而求出直线PR的解析式，即可得出结论．【详解】（1）证明：△△ACB＝90°，AD△l，△△ACB＝△ADC．△△ACE＝△ADC+△CAD，△ACE＝△ACB+△BCE，△△CAD＝△BCE，△△ADC＝△CEB＝90°，AC＝BC．△△ACD△△CBE，△CD＝BE，（2）解：如图2，过点M作MF△y轴，垂足为F，过点N作NG△MF，交FM的延长线于G，由已知得OM＝ON，且△OMN＝90°，△由（1）得△OFM△△MGN，△MF＝NG，OF＝MG，设M（m，n），△MF＝m，OF＝n，△MG＝n，NG＝m，△点N的坐标为（4，2）△42m n n m +=⎧⎨-=⎩解得13m n =⎧⎨=⎩△点M 的坐标为（1，3）； （3）如图3，过点Q 作QS △PQ ，交PR 于S ，过点S 作SH △x 轴于H ，对于直线y ＝﹣4x +4，由x ＝0得y ＝4，△P （0，4），△OP ＝4，由y ＝0得x ＝1，△Q （1，0），OQ ＝1，△△QPR ＝45°，△△PSQ ＝45°＝△QPS ．△PQ ＝SQ ．△由（1）得SH ＝OQ ，QH ＝OP ． △OH ＝OQ+QH ＝OQ+OP ＝4+1＝5，SH ＝OQ ＝1．△S （5，1），设直线PR 为y ＝kx+b ，则451b k b =⎧⎨+=⎩，解得435b k =⎧⎪⎨=-⎪⎩．△直线PR 为y ＝35x +4．由y ＝0得，x ＝203，△R （203，0）． 【点睛】本题是一次函数综合题，主要考查了待定系数法，全等三角形的判定和性质，构造出全等三角形是解本题的关键．2．（2022·广东·汕头市潮阳区教师发展中心教学研究室一模）（1）模型建立，如图1，等腰直角三角形ABC 中，△ACB =90°，CB =CA ，直线ED 经过点C ，过A 作AD △ED 于D ，过B 作BE △ED 于E ．求证：△BEC △△CDA ；（2）模型应用：①已知直线AB 与y 轴交于A 点，与x 轴交于B 点，sin△ABO =35，OB =4，将线段AB 绕点B 逆时针旋转90度，得到线段BC ，过点A ，C 作直线，求直线AC 的解析式；②如图3，矩形ABCO ，O 为坐标原点，B 的坐标为（8，6），A ，C 分别在坐标轴上，P 是线段BC 上动点，已知点D 在第一象限，且是直线y =2x -5上的一点，若△APD 是以D 为直角顶点的等腰直角三角形，请求出所有符合条件的点D 的坐标．【答案】（1）见解析；（2）①137y x =-+；②D （3，1）或1923,33D ⎛⎫ ⎪⎝⎭【详解】（1）解：由题意可得， 90ACB ADC BEC ∠∠∠===︒ ，△90EBC BCE BCE ACD ∠+∠=∠+∠=︒ ，△EBC ACD ∠=∠ ，在BEC △和CDA 中EBC ACD E D BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩，△BEC CDAAAS ∆∆≌（） ， （2）解：①如图，过点C 作 CD x ⊥ 轴于点D ，在Rt △ABO 中 sin△ABO 35=，OB =4， △设AO =3m ，AB =5m ，△OB =4m =4，△m =1，△AO =3，同（1）可证得CDB BOA ∆∆≌，△4CD BO == ，3BD AO ==，△437OD =+=，△74C -（，），△03A （，），设直线AC 解析式为 3y kx =+ ，把C 点坐标代入可得734k -+=，解得 17k =- ， △直线AC 解析式为137y x =-+； ②设D 坐标为（x ，2x -5）,当D 在AB 的下方时，过D 作DE △y 轴于E ，交BC 于F ,同（1）可证得△ADE △△DPF ，△DF =AE =6-（2x -5）=11-2x ，DE =x,△11-2x +x =8,△x =3，△D （3，1），当D 在AB 的上方时，如图，过D 作DE △y 轴于E ，交BC 的延长线于F , 同（1）可证得ADE DPF △△≌，△DF =AE =（2x -5）-6=2x -11，DE =x ，△2x -11+x =8，△193x =，△1923,33D ⎛⎫ ⎪⎝⎭，综上述D （3，1）或1923,33D ⎛⎫ ⎪⎝⎭． 【点睛】本题考查了全等三角形的判定和性质、待定系数法一次函数的解析式、正弦的定义、勾股定理、等腰三角形的判定和性质及方程思想，作辅助线构造模型是解本题的关键． 3．（2022·黑龙江·桦南县九年级期中）如图1，在ABC 中，90ACB ∠=︒，AC BC =，直线MN 经过点C ，且AD MN ⊥于D ，BE MN ⊥于E ．(1)由图1，证明：DE AD BE =+；(2)当直线MN 绕点C 旋转到图2的位置时，请猜想出DE ，AD ，BE 的等量关系并说明理由；(3)当直线MN 绕点C 旋转到图3的位置时，试问DE ，AD ，BE 又具有怎样的等量关系？请直接写出这个等量关系（不必说明理由）．【答案】(1)证明见解析；(2)DE AD BE =-，证明过程见解析；(3)DE BE AD =-，证明过程见解析【分析】(1)先证明△ADC △△CEB ，得到AD=CE ，DC=BE ，进而得到DE=CE+DC=AD+BE 即可；(2)同(1)中思路，证明△ADC △△CEB ，进而得到DE=CE -DC=AD -BE 即可；(3)同(1)中思路，证明△ADC △△CEB ，进而得到DE=DC -CE=BE -AD 即可．【详解】解：(1)证明：在ABC 中，△90ACB ∠=︒，△90ACD BCE ∠+∠=︒，△AD MN ⊥，△90ACD CAD ∠+∠=︒，△BCE =∠∠CAD ，又△AC BC =，90ADC CEB ∠=∠=，△()≌ADC CEB AAS ，△AD CE =，DC BE =， △直线MN 经过点C ，△DE CE DC AD BE =+=+；(2)DE ，AD ，BE 的等量关系为：DE AD BE =-，理由如下：△AD MN ⊥于D ，BE MN ⊥于E △90ADC BEC ACB ∠=∠=∠=︒，△90CAD ACD ∠+∠=︒，90ACD BCE ∠+∠=︒，△CAD BCE ∠=∠， 在ADC 和CEB △中90CAD BCE ADC BEC AC CB ∠=∠⎧⎪∠=∠=⎨⎪=⎩，△()ADC CEB AAS △≌△ △CE AD =，CD BE =，△DE CE CD AD BE =-=-；(3)当MN 旋转到图3的位置时，DE 、AD 、BE 所满足的等量关系是DE BE AD =-，理由如下：△AD MN ⊥于D ，BE MN ⊥于E △90ADC BEC ACB ∠=∠=∠=︒，△90CAD ACD ∠+∠=︒，90ACD BCE ∠+∠=︒，△CAD BCE ∠=∠， 在ADC 和CEB △中90CAD BCE ADC BEC AC CB ∠=∠⎧⎪∠=∠=⎨⎪=⎩，△()ADC CEB AAS △≌△ △CE AD =，CD BE =，△DE CD CE BE AD =-=-.【点睛】本题考查了全等三角形的判定方法、等腰直角三角形的性质及等角的余角相等等知识点，熟练掌握三角形全等的判定方法是求解的关键．4．（2022·山东·九年级课时练习）（1）课本习题回放：“如图①，90ACB ∠=︒，AC BC =，AD CE ⊥，BE CE ⊥，垂足分别为D ，E ， 2.5cm AD =， 1.7cm DE =．求BE 的长”，请直接写出此题答案：BE 的长为________．（2）探索证明：如图②，点B ，C 在MAN ∠的边AM 、AN 上，AB AC =，点E ，F 在MAN∠内部的射线AD 上，且BED CFD BAC ∠=∠=∠．求证：ABE CAF ∆∆≌．（3）拓展应用：如图③，在ABC ∆中，AB AC =，AB BC >．点D 在边BC 上，2CD BD =，点E 、F 在线段AD 上，BED CFD BAC ∠=∠=∠．若ABC ∆的面积为15，则ACF ∆与BDE ∆的面积之和为________．（直接填写结果，不需要写解答过程）【答案】（1）0.8cm ；（2）见解析（3）5【分析】（1）利用AAS 定理证明△CEB △△ADC ，根据全等三角形的性质解答即可； （2）由条件可得△BEA ＝△AFC ，△4＝△ABE ，根据AAS 可证明△ABE △△CAF ；（3）先证明△ABE △△CAF ，得到ACF ∆与BDE ∆的面积之和为△ABD 的面积，再根据2CD BD =故可求解．【详解】解：（1）△BE △CE ，AD △CE ，△△E ＝△ADC ＝90°，△△EBC ＋△BCE ＝90°．△△BCE ＋△ACD ＝90°，△△EBC ＝△DCA ．在△CEB 和△ADC 中，E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩△△CEB △△ADC （AAS ），△BE ＝DC ，CE ＝AD ＝2.5cm ．△DC ＝CE −DE ，DE ＝1.7cm ，△DC ＝2.5−1.7＝0.8cm ，△BE ＝0.8cm 故答案为：0.8cm ； （2）证明：△△1＝△2，△△BEA ＝△AFC ．△△1＝△ABE ＋△3，△3＋△4＝△BAC ，△1＝△BAC ，△△BAC ＝△ABE ＋△3，△△4＝△ABE ．△△AEB ＝△AFC ，△ABE ＝△4，AB ＝AC ，△△ABE △△CAF （AAS ）．（3）△BED CFD BAC ∠=∠=∠△△ABE +△BAE =△F AC +△BAE =△F AC +△ACF△△ABE =△CAF ，△BAE =△ACF又AB AC =△△ABE △△CAF ，△ABE CAF S S =△ACF ∆与BDE ∆的面积之和等于ABE ∆与BDE ∆的面积之和，即为△ABD 的面积， △2CD BD =，△ABD 与△ACD 的高相同则13ABD ABC S S =△△=5 故ACF ∆与BDE ∆的面积之和为5故答案为：5．【点睛】本题考查的是全等三角形的判定和性质、三角形内角和定理，掌握全等三角形的判定定理和性质定理是解题的关键．5．（2022·无锡市九年级月考）（1）如图1，直线m 经过等腰直角△ABC 的直角顶点A ，过点B 、C 分别作BD ⊥m ，CE ⊥m ，垂足分别是D 、E ．求证：BD ＋CE ＝DE ；（2）如图2，直线m 经过△ABC 的顶点A ，AB ＝AC ，在直线m 上取两点 D 、E ，使∠ADB ＝∠AEC ＝α，补充∠BAC ＝ （用α表示），线段BD 、CE 与DE 之间满足BD ＋CE ＝DE ，补充条件后并证明；（3）在（2）的条件中，将直线m 绕着点A 逆时针方向旋转一个角度到如图3的位置，并改变条件∠ADB ＝∠AEC ＝ （用α表示）．通过观察或测量，猜想线段BD 、CE 与DE 之间满足的数量关系，并予以证明．【答案】（1）证明见详解，（2）∠BAC=α，证法见详解，（3）180º-α，DE=EC-BD，证明见详解．【分析】（1）根据已知首先证明∠DAB=∠ECA，再利用AAS即可得出△ADB≌△CEA；（2）补充∠BAC=α．利用△ADB≌△CAE，即可得出三角形对应边之间的关系，即可得出答案；（3）180º-α，DE=CE-BD，根据已知首先证明∠DAB=∠ECA，再利用AAS即可得出△ADB≌△CEA，即可得出三角形对应边之间的关系，即可得出答案．【详解】证明：（1）∵BD⊥m，CE⊥m，∠ABC=90°，AC=BC，∴△ADB和△AEC都是直角三角形，∴∠DBA+∠DAB=90°，∴∠ECA+∠EAC=90°，∵∠BAC=90°，∠DAB+∠EAC=90º，∴∠DAB=∠ECA，又∵∠ADB=∠CEA=90°，AB=BC，所以△ADB≌△CEA（AAS），BD=AE，DA=EC，DE=DA+AE=EC+BD，BD＋CE＝DE．（2）∵等腰△ABC中，AC=CB，∠ADB=∠BAC=∠CEA=α，∴∠DAB+∠EAC=180°-α，∠ECA+∠CAE=180º-α，∴∠DAB=∠ECA，∵∠ADB=∠CEA=α，AC=CB，∴△ADB≌△CEA（AAS），∴CE=AD，BD=AE，∴AD+BE=CE+CD，所以BD+CE=DE．（3）180º-α，数量关系为DE=CE-BD，∵∠ADB＝∠AEC＝ 180º-α，∠BAC=α，∴∠ABD+∠BAD=α，∠BAD+∠EAC=α，∴∠ABD=∠CAE，∵AB=AC，∴△BAD≌△ACE（AAS），∴AD=CE，BD=AE，∴DE=AD-AE=EC-BD．【点睛】点评：此题主要考查了三角形全等的证明，根据已知得出∠DAB=∠ECA，再利用全等三角形的判定方法得出是解决问题的关键．6．（2022·河南新乡·九年级期中）某学习小组在探究三角形相似时，发现了下面这种典型的基本图形．（1）如图1，在ABC中，△BAC＝90°，ABAC＝k，直线l经过点A，BD△直线I，CE上直线l，垂足分别为D、E．求证：BDAE＝k．（2）组员小刘想，如果三个角都不是直角，那么结论是否仍然成立呢？如图2，将（1）中的条件做以下修改：在ABC中，ABAC＝k，D、A、E三点都在直线l上，并且有△BDA＝△AEC＝△BAC＝α，其中α为任意锐角或钝角．请问（1）中的结论还成立吗？若成立，请你给出证明；若不成立，请说明理由．（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，在。

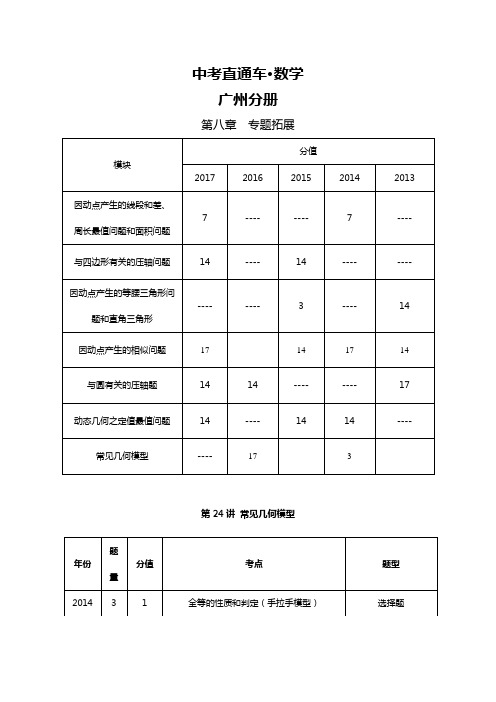
中考直通车·数学广州分册第八章专题拓展第24讲常见几何模型【考点解读】常见几何模型是广州市中考的压轴题常考题型，主要以考察选择、填空最后一题和几何压轴题为主。

几何模型类型较多，综合性强，属于中考中重点但同样是难点的一个考点。

【考点分析】2011年 考查三角形全等和三角形中位线性质，标准的手拉手模型。

2014年 考查三角形全等的判断和性质，根据手拉手模型找出全等三角形，再应用其性质 2016年 本年度模型思想明显，分值占比大，主要考查三角形全等的判定及其性质、图像的旋转，利用模型思想作为解题突破口顺利完成辅助线。

【模型介绍】 手拉手模型：1、 【条件】 如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，【结论】（1）DBC ABE ∆≅∆（2）DC AE =（3）AE 与DC 之间的夹角为︒60 （4）AE 与DC 的交点设为H ,BH 平分AHC ∠CDABFECD2、 【条件】如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H 。

【结论】 （1）CDE ADG ∆≅∆是否成立？（2）AG =CE（3）AG 与CE 之间的夹角为 90 （4）HD 是否平分AHE ∠？旋转模型：一、邻角相等对角互补模型【条件】如图，四边形ABCD 中，AB =AD ，90BAD BCD ︒∠=∠=【结论】45ACB ACD BC CD ︒∠=∠=+=① ②二、角含半角模型：全等 角含半角要旋转：构造两次全等FED CBAG FED CBA AC D E ACD EF【条件】：如图，点分别是正方形的边上的点，，连接；【结论】（1）AFE AGE △△≅ （2） ；一线三等角模型:【条件】 一条直线同一侧三个相等的角（如图）； 【结论】CDE ABC ∽△△1、锐角形一线三等角2、直角形一线三等角3、钝角形一线三等角【真题拾遗】1．（2014•广州）如图，四边形ABCD 、CEFG 都是正方形，点G 在线段CD 上，连接BG 、DE ，DE 和FG 相交于点O ，设AB=a ，CG=b （a ＞b ）．下列结论：①△BCG ≌△DCE ；②BG ⊥DE ；③=；④（a ﹣b ）2•S △EFO =b 2•S △DGO ．其中结论正确的个数是（ ）E F 、ABCD BC CD 、45EAF ∠=︒EFEF BE FD =+A．4个B．3个C．2个D．1个2．（2016•广州）如图，正方形ABCD的边长为1，AC，BD是对角线．将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．则下列结论：①四边形AEGF是菱形②△AED≌△GED ③∠DFG=112.5°④BC+FG=1.5其中正确的结论是．三、解答题3．（2011广州中考）如图1，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角三角形DCE中∠DCE是直角，点D在线段AC上．（1）证明：B、C、E三点共线；（2）若M是线段BE的中点，N是线段AD的中点，证明：MN=OM；（3）将△DCE绕点C逆时针旋转α（0°＜α＜90°）后，记为△D1CE1（图2），若M1是线段BE1的中点，N1是线段AD1的中点，M1N1=OM1是否成立？若是，请证明；若不是，说明理由．4．（2016广州中考）如图，点C为△ABD的外接圆上的一动点（点C不在上，且不与点B，D重合），∠ACB=∠ABD=45°（1）求证：BD是该外接圆的直径；（2）连结CD，求证：AC=BC+CD；（3）若△ABC关于直线AB的对称图形为△ABM，连接DM，试探究DM2，AM2，BM2三者之间满足的等量关系，并证明你的结论．参考答案一、选择题1、C考点：相似三角形的判定与性质；全等三角形的判定与性质；正方形的性质．分析：由四边形ABCD和四边形CEFG是正方形，根据正方形的性质，即可得BC=DC，CG=CE，∠BCD=∠ECG=90°，则可根据SAS证得①△BCG≌△DCE；然后根据全等三角形的对应角相等，求得∠CDE+∠DGH=90°，则可得②BH⊥DE．由△DGF与△DCE 相似即可判定③错误，由△GOD与△FOE相似即可求得④．解答：证明：①∵四边形ABCD和四边形CEFG是正方形，∴BC=DC，CG=CE，∠BCD=∠ECG=90°，∴∠BCG=∠DCE，在△BCG和△DCE中，，∴△BCG≌△DCE（SAS），②∵△BCG≌△DCE，∴∠CBG=∠CDE，又∠CBG+∠BGC=90°，∴∠CDE+∠DGH=90°，∴∠DHG=90°，∴BH⊥DE；③∵四边形GCEF是正方形，∴GF∥CE，∴=，∴=是错误的．④∵DC∥EF，∴∠GDO=∠OEF，∵∠GOD=∠FOE，∴△OGD∽△OFE，∴=（）2=（）2=，∴（a﹣b）2•S△EFO=b2•S△DGO．故应选B点评：此题考查了正方形的性质，全等三角形的判定与性质，相似三角形的判定和性质，直角三角形的判定和性质．二、填空题2、①②③考点：三角形全等、三角形内角和、菱形分析：首先证明△ADE≌△GDE，再求出∠AEF、∠AFE、∠GEF、∠GFE的度数，推出AE=EG=FG=AF，由此可以一一判断．解答：证明：∵四边形ABCD是正方形，∴AD=DC=BC=AB，∠DAB=∠ADC=∠DCB=∠ABC=90°，∠ADB=∠BDC=∠CAD=∠CAB=45°，∵△DHG是由△DBC旋转得到，∴DG=DC=AD，∠DGE=∠DCB=∠DAE=90°，在RT△ADE和RT△GDE中，，∴AED≌△GED，故②正确，∴∠ADE=∠EDG=22.5°，AE=EG，∴∠AED=∠AFE=67.5°，∴AE=AF，同理EG=GF，∴AE=EG=GF=FA，∴四边形AEGF是菱形，故①正确，∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°，故③正确．∵AE=FG=EG=BG，BE=AE，∴BE＞AE，∴AE＜，∴CB+FG＜1.5，故④错误故答案为①②③．点评：本题考查正方形的性质、全等三角形的判定和性质、菱形的判定和性质、等腰直角三角形的性质等知识，解题的关键是通过计算发现角相等，学会这种证明角相等的方法，属于中考常考题型．三、解答题3、考点：（1）三点共线（2）中位线、全等三角形（手拉手性质）（3）同（2）分析：（1）根据直径所对的圆周角为直角得到∠BCA=90°，∠DCE是直角，即可得到∠BCA+∠DCE=90°+90°=180°；（2）连接BD，AE，ON，延长BD交AE于F，先证明Rt△BCD≌Rt△ACE，得到BD=AE，∠EBD=∠CAE，则∠CAE+∠ADF=∠CBD+∠BDC=90°，即BD⊥AE，再利用三角形的中位线的性质得到ON=BD，OM=AE，ON∥BD，AE∥OM，于是有ON=OM，ON⊥OM，即△ONM为等腰直角三角形，即可得到结论；（3）证明的方法和（2）一样．解答：（1）证明：∵AB是直径，∴∠BCA=90°，而等腰直角三角形DCE中∠DCE是直角，∴∠BCA+∠DCE=90°+90°=180°，∴B、C、E三点共线；（2）连接BD ，AE ，ON ，延长BD 交AE 于F ，如图1，∵CB=CA ，CD=CE ，∴Rt △BCD ≌Rt △ACE ，∴BD=AE ，∠EBD=∠CAE ， ∴∠CAE+∠ADF=∠CBD+∠BDC=90°，即BF ⊥AE ，又∵M 是线段BE 的中点，N 是线段AD 的中点，而O 为AB 的中点， ∴BD 21 =ON ，AE 21=OM ，ON ∥BD ，AE ∥OM ； ∴ON=OM ，ON ⊥OM ，即△ONM 为等腰直角三角形， ∴MN=OM ；（3）成立．理由如下：如图2，连接BD1，AE1，ON1，∵∠ACB ﹣∠ACD1=∠D1CE1﹣∠ACD1， ∴∠BCD1=∠ACE1，又∵CB=CA ，CD1=CE1，∴△BCD1≌△ACE1， 与（2）同理可证BD1⊥AE1，△ON1M1为等腰直角三角形， 从而有M1N1=OM1．点评：本题考查主要三角形全等的判定和中位线的性质，熟练掌握手拉手模型，作为本题切入点，可以非常顺利的解决本题。

中考数学常见的11种几何模型一、三角形的不等关系模型：A字型、K字型、X字型1. 三角形两边之和大于第三边；2. 三角形两边之差小于第三边；3. 直角三角形斜边上的中线等于斜边的一半；4. 直角三角形中30度所对的直角边等于斜边的一半；5. 三角形三个内角之和等于180度。

二、全等、相似模型模型：A字型全等、A字型相似、8字型全等、8字型相似、蝴蝶型全等、蝴蝶型相似、平行型全等、平行型相似、等积模型等。

三、平行四边形模型模型：平行四边形ABCD中，E为AB中点，则：AC、DE互相平分；模型：平行四边形ABCD中，AC、BD交于O，则：AO=CO，BO=DO；模型：平行四边形ABCD中，AC平分角BAD，则：四边形ABCD为菱形。

四、梯形模型模型：梯形ABCD中，E为AD中点，则：延长BE交DC延长线于F，则：BE=FE；模型：梯形ABCD中，A、B在直线EF上，则：延长DC交AB延长线于F，则：梯形ABCD面积等于三角形面积的2倍；模型：梯形ABCD中，E为AD中点，则：延长BE交DC延长线于F，则：EF=FC。

五、矩形模型模型：矩形ABCD中，E为BC中点，则：AE平分角BAD；模型：矩形ABCD中，E为AD中点，则：AF平分角ABC；模型：矩形ABCD中，AC平分角BAD，则：四边形ABCD为菱形。

六、多边形模型模型：任意多边形ABCD中，E为AD中点，则：延长BE交DC延长线于F，则：BF=FE；模型：任意多边形ABCD中，E为AD中点，延长BE交DC延长线于F，则：EF=FC。

七、燕尾模型模型：在三角形ABC中，BD平分角ABC，CE平分角ACB，则：点D、E在BC同旁，则：三角形ADE的面积等于三角形ABC面积的一半。

八、风筝模型模型：在三角形ABC中，点D、E在BC上，且AD平分角BAE，则：三角形ABC与三角形ADE的面积相等。

九、铅笔模型模型：在矩形ABCD中，点E、F分别在AB、CD上，则：EF平行于AD，则：矩形ABFE与矩形EFCD相似。

2018年中考常见几何模型分析中考直通车·数学广州分册第八章专题拓展第24讲常见几何模型【考点解读】常见几何模型是广州市中考的压轴题常考题型，主要以考察选择、填空最后一题和几何压轴题为主。

几何模型类型较多，综合性强，属于中考中重点但同样是难点的一个考点。

【考点分析】2011年 考查三角形全等和三角形中位线性质，标准的手拉手模型。

2014年 考查三角形全等的判断和性质，根据手拉手模型找出全等三角形，再应用其性质2016年 本年度模型思想明显，分值占比大，主要考查三角形全等的判定及其性质、图像的旋转，利用模型思想作为解题突破口顺利完成辅助线。

【模型介绍】 手拉手模型：1、 【条件】 如图两个等边三角形ABD ∆与BCE ∆，连结AE 与CD ，【结论】（1）DBC ABE ∆≅∆（2）DC AE =（3）AE 与DC 之间的夹角为︒60 （4）AE 与DC 的交点设为H ,BH 平分AHC ∠CDABEFECDBA2、 【条件】如图两个等腰直角三角形ADC 与EDG ，连结CE AG ,,二者相交于点H 。

【结论】 （1）CDE ADG ∆≅∆是否成立？（2）AG =CE（3）AG 与CE 之间的夹角为 90（4）HD 是否平分AHE ∠？旋转模型：一、邻角相等对角互补模型【条件】如图，四边形ABCD 中，AB =AD ，90BAD BCD ︒∠=∠= 【结论】452ACB ACD BC CD AC ︒∠=∠=+=① ②二、角含半角模型：全等 角含半角要旋转：构造两次全等FED CBAG FED CBAAB CD EAB CD EF【条件】：如图，点E F、分别是正方形ABCD的边BC CD、上的点，45EAF∠=︒，连接EF；【结论】（1）AFEAGE△△≅（2）EF BE FD=+；一线三等角模型:【条件】一条直线同一侧三个相等的角（如图）；【结论】CDEABC∽△△1、锐角形一线三等角2、直角形一线三等角3、钝角形一线三等角【真题拾遗】1．（2014•广州）如图，四边形ABCD、CEFG都是正方形，点G在线段CD上，连接BG、DE，DE和FG相交于点O，设AB=a，CG=b（a＞b）．下列结论：①△BCG≌△DCE；②BG⊥DE；③=；④（a﹣b）2•S△EFO=b2•S△DGO．其中结论正确的个数是（）A．4个B．3个C．2个D．1个2．（2016•广州）如图，正方形ABCD的边长为1，AC，BD是对角线．将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．则下列结论：①四边形AEGF是菱形②△AED≌△GED ③∠DFG=112.5°④BC+FG=1.5其中正确的结论是．三、解答题3．（2011广州中考）如图1，⊙O中AB是直径，C是⊙O上一点，∠ABC=45°，等腰直角三角形DCE中∠DCE是直角，点D在线段AC上．（1）证明：B、C、E三点共线；（2）若M是线段BE的中点，N是线段AD的中点，证明：MN=OM；（3）将△DCE绕点C逆时针旋转α（0°＜α＜90°）后，记为△D1CE1（图2），若M1是线段BE1的中点，N1是线段AD1的中点，M1N1=OM1是否成立？若是，请证明；若不是，说明理由．4．（2016广州中考）如图，点C为△ABD的外接圆上的一动点（点C不在上，且不与点B，D重合），∠ACB=∠ABD=45°（1）求证：BD是该外接圆的直径；（2）连结CD，求证： AC=BC+CD；（3）若△ABC关于直线AB的对称图形为△ABM，连接DM，试探究DM2，AM2，BM2三者之间满足的等量关系，并证明你的结论．参考答案一、选择题1、C考点：相似三角形的判定与性质；全等三角形的判定与性质；正方形的性质．分析：由四边形ABCD和四边形CEFG是正方形，根据正方形的性质，即可得BC=DC，CG=CE，∠BCD=∠ECG=90°，则可根据SAS证得①△BCG≌△DCE；然后根据全等三角形的对应角相等，求得∠CDE+∠DGH=90°，则可得②BH⊥DE．由△DGF与△DCE相似即可判定③错误，由△GOD与△FOE相似即可求得④．解答：证明：①∵四边形ABCD和四边形CEFG是正方形，∴BC=DC，CG=CE，∠BCD=∠ECG=90°，∴∠BCG=∠DCE，在△BCG和△DCE中，，∴△BCG≌△DCE（SAS），②∵△BCG≌△DCE，∴∠CBG=∠CDE，又∠CBG+∠BGC=90°，∴∠CDE+∠DGH=90°，∴∠DHG=90°，∴BH⊥DE；③∵四边形GCEF是正方形，∴GF∥CE，∴=，∴=是错误的．④∵DC∥EF，∴∠GDO=∠OEF，∵∠GOD=∠FOE，∴△OGD∽△OFE，∴=（）2=（）2=，∴（a﹣b）2•S△EFO=b2•S△DGO．故应选B点评：此题考查了正方形的性质，全等三角形的判定与性质，相似三角形的判定和性质，直角三角形的判定和性质．二、填空题2、①②③考点：三角形全等、三角形内角和、菱形分析：首先证明△ADE≌△GDE，再求出∠AEF、∠AFE、∠GEF、∠GFE的度数，推出AE=EG=FG=AF，由此可以一一判断．解答：证明：∵四边形ABCD是正方形，∴AD=DC=BC=AB，∠DAB=∠ADC=∠DCB=∠ABC=90°，∠ADB=∠BDC=∠CAD=∠CAB=45°，∵△DHG是由△DBC旋转得到，∴DG=DC=AD，∠DGE=∠DCB=∠DAE=90°，在RT△ADE和RT△GDE中，，∴AED≌△GED，故②正确，∴∠ADE=∠EDG=22.5°，AE=EG，∴∠AED=∠AFE=67.5°，∴AE=AF，同理EG=GF，∴AE=EG=GF=FA，∴四边形AEGF是菱形，故①正确，∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°，故③正确．∵AE=FG=EG=BG，BE=AE，∴BE＞AE，∴AE＜，∴CB+FG＜1.5，故④错误故答案为①②③．点评：本题考查正方形的性质、全等三角形的判定和性质、菱形的判定和性质、等腰直角三角形的性质等知识，解题的关键是通过计算发现角相等，学会这种证明角相等的方法，属于中考常考题型．三、解答题3、考点：（1）三点共线（2）中位线、全等三角形（手拉手性质）（3）同（2）分析：（1）根据直径所对的圆周角为直角得到∠BCA=90°，∠DCE是直角，即可得到∠BCA+∠DCE=90°+90°=180°；（2）连接BD，AE，ON，延长BD交AE于F，先证明Rt△BCD≌Rt△ACE，得到BD=AE，∠EBD=∠CAE，则∠CAE+∠ADF=∠CBD+∠BDC=90°，即BD⊥AE，再利用三角形的中位线的性质得到ON=BD，OM=AE，ON∥BD，AE∥OM，于是有ON=OM，ON⊥OM，即△ONM为等腰直角三角形，即可得到结论；（3）证明的方法和（2）一样．解答：（1）证明：∵AB是直径，∴∠BCA=90°，而等腰直角三角形DCE中∠DCE是直角，∴∠BCA+∠DCE=90°+90°=180°，∴B、C、E三点共线；（2）连接BD，AE，ON，延长BD交AE于F，如图1，∵CB=CA，CD=CE，∴Rt△BCD≌Rt△ACE，∴BD=AE，∠EBD=∠CAE，∴∠CAE+∠ADF=∠CBD+∠BDC=90°，即BF⊥AE，又∵M是线段BE的中点，N是线段AD的中点，而O为AB的中点，∴BD21=ON，AE21=OM，ON∥BD，AE∥OM；∴ON=OM，ON⊥OM，即△ONM为等腰直角三角形，∴MN=OM；（3）成立．理由如下：如图2，连接BD1，AE1，ON1，∵∠ACB﹣∠ACD1=∠D1CE1﹣∠ACD1，∴∠BCD1=∠ACE1，又∵CB=CA，CD1=CE1，∴△BCD1≌△ACE1，与（2）同理可证BD1⊥AE1，△ON1M1为等腰直角三角形，从而有M1N1=OM1．点本题考查主要三角形全等的判定和中位线的性质，熟练掌握手拉手模型，作为本题评：切入点，可以非常顺利的解决本题。

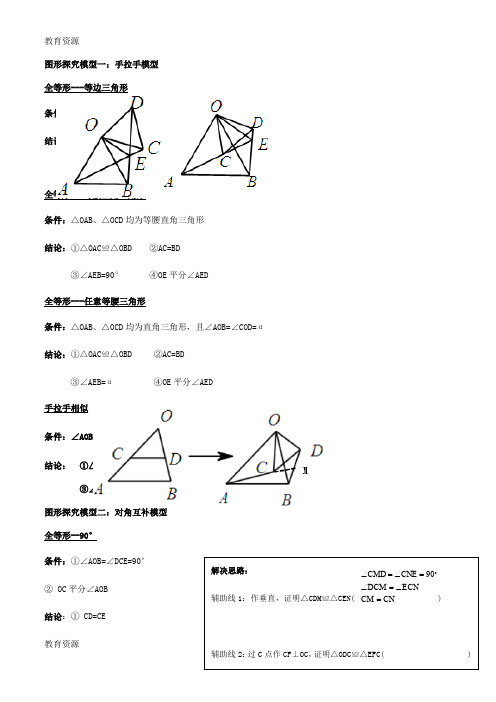
图形探究模型一：手拉手模型 全等形---等边三角形条件：△OAB 、△OCD 均为等边三角形 结论：①△OAC ≌△OBD ②AC=BD ③∠AEB=60° ④OE 平分∠AED 全等形---等腰直角三角形条件：△OAB 、△OCD 均为等腰直角三角形 结论：①△OAC ≌△OBD ②AC=BD ③∠AEB=90° ④OE 平分∠AED全等形---任意等腰三角形条件：△OAB 、△OCD 均为直角三角形，且∠AOB=∠COD=α 结论：①△OAC ≌△OBD ②AC=BD ③∠AEB=α ④OE 平分∠AED 手拉手相似条件：∠AOB=∠COD= α k ODOCOB OA == 结论： ①△AOC ∽△BOD ③∠AMB=α图形探究模型二：对角互补模型 全等形--90°条件：①∠AOB=∠DCE=90°② OC 平分∠AOB 结论：① CD=CE② OD+OE=2OC③ S 四边形ODCE =S △OCE +S △OCD =21OC 2变式一：当∠DCE 一边交AO 的延长线上于D 点时 条件：①∠AOB=∠DCE=90° ② OC 平分∠AOB 结论：① CD=CE(不变）② OE-OD=2OC （重点）③S △OCE -S △OCD =21OC 2（难点） 变式二：细节变化：若将条件“OC 平分∠AOB ”与结论“CD=CE ”互换 条件：①∠AOB=∠DCE=90° ②CD=CE结论：①OC 平分∠AOB② OD+OE=2OC （ OE-OD=2OC ）③ S 四边形ODCE =S △OCE +S △OCD =21OC 2（S △OCE -S △OCD =21OC 2） 变式三：对角互补模型（相似型）条件：∠AOB=∠DCE=90° ∠COB=α结论：①CE=CD ·tan α②(OD ·tan α+OE)cos α=OCCFCO EFC DOC ECF DCO ==∠=∠∠=∠ 45CCC③S △OCD ·tan 2α+S △OCe =21OC 2·tan α 全等形--120°条件：①∠AOB=2∠DCE=120° ② OC 平分∠AOB 结论：① CD=CE② OD+OE=OC③ S 四边形ODCE =S △OCE +S △OCD =43OC 2变式一：当∠DCE 一边交AO 的延长线上于D 点时 结论：① CD=CE （不变） ② OE-OD=OC(重点）③S △OCE +S △OCD =43OC 2（难点） 全等形--任意角α条件：①∠AOB=2α，∠DCE=180°-2α ②CD=CE结论：①OC 平分∠AOB ② OD+OE=2OC ·cos α③ S 四边形ODCE =S △OCE +S △OCD =OC 2·sin α·cos α 变式一：当∠DCE 一边交AO 的延长线上于D 点时 条件：①∠AOB=2α，∠DCE=180°-2α结论：① CD=CE （不变） ② OE-OD=2OC ·cos α(重点）③S △OCE -S △OCD =OC 2·sin α·cos α（难点）变式二：细节变化：若将条件“OC 平分∠AOB ”与结论“CD=CE ”互换 条件：①∠AOB=∠DCE=90° ②CD=CE结论：①OC 平分∠AOB② OD+OE=2OC ·cos α(OE-OD=2OC ·cos α)③S 四边形ODCE =S △OCE +S △OCD =OC 2·sin α·cos α（S △OCE -S △OCD =OC 2·sin α·cos α） 图形探究模型三：角含半角模型 正方形--90°条件：①正方形；②∠EAF=45° 结论：①EF=DF+BE②△CEF 周长为正方形周长一半 变式一：条件：①正方形；②EF=DF+BE 结论：①∠EAF=45°②△CEF 周长为正方形周长一半变式二：当∠EAF 的两边交边CB 和DC 的延长线于E 、F 条件：①正方形；②∠EAF=45° 结论：①EF=DF-BE②△CEF 周长为正方形周长一半 ABCD ABCD ABCD ABCD ABCDABCD条件：①正方形；②∠EAF=45° 结论：①EF=DF+BE ; EF=BE-DF②△CEF 周长为正方形周长一半③△AHE 为等腰直角三角形（延伸） 等腰直角三角形--90°条件：①等腰直角△ABC ；②∠DAE=45° 结论：BD 2+CE 2=DE 2变式：若∠DAE 旋转到△ABC 外部时条件：①等腰直角△ABC ；②∠DAE=45°结论：BD 2+CE 2=DE 2（不变)120°条件：①四边形ABCD,AB=AD,∠BAD=α∠ABC+∠ADC=180° 结论：EF=DF+BE变式：当∠EAF 的两边交边CB 和DC 的延长线于E 、F ED C B AFAB CDEFEDCBAABCDEDA ACAH AE=条件：①四边形ABCD,AB=AD,∠BAD=α∠ABC+∠ADC=180°；图形探究模型四：倍长中线模型条件：①矩形ABCD ②BD=BE③DF=EF结论：AF⊥CF条件：①平行四边形ABCD ②BC=2AB③AM=DM ④CE⊥CD结论：∠EMD=3∠MEA。

2018中考数学几何部分考点分析2018中考数学几何部分考点分析一、线与角1.两点之间，线段最短。

2.经过两点有一条直线，并且只有一条直线。

3.等角的补角相等，等角的余角相等。

4.对顶角相等5.经过直线外或直线上一点，有且只有一条直线与已知直线垂直。

6.(1)经过已知直线外一点，有且只有一条直线与已知直线平行。

(2)如果两条直线都和第三条直线平行，那么这两条直线也平行.7.连接直线外一点与直线上各点的所有线段中，垂线段最短。

8.平行线的判定：(1)同位角相等，两直线平行;(2)内错角相等，两直线平行;(3)同旁内角互补，两直线平行;(4)垂直于同一条直线的两条的直线互相平行.9.平行线的特征：(1)两直线平行，同位角相等。

(2)两直线平行，内错角相等。

(3)两直线平行，同旁内角互补。

10.角平分线的性质：角平分线上的点到这个角的两边的距离相等.角平分线的判定：到一个角的两边距离相等的点在这个角的平分线上.11.线段垂直平分线的性质：线段的垂直平分线上的点到这条线段的两个端点的距离相等.线段垂直平分线的判定：到一条线段的两个端点的距离相等的点，在这条线段的垂直平分线上.二、三角形、多边形12.三角形中的有关公理、定理：(1)三角形外角的性质：①三角形的一个外角等于与它不相邻的两个内角的和;②三角形的一个外角大于任何一个与它不相邻的内角;③三角形的外角和等于360.(2)三角形内角和定理：三角形的内角和等于180.(3)三角形的任何两边的和大于第三边(4)三角形中位线定理:三角形的中位线平行于第三边，并且等于第三边的一半.13.多边形中的有关公理、定理：(1)多边形的内角和定理：n边形的内角和等于(n-2)180.(2)多边形的外角和定理：任意多边形的外角和都为360.14.(1)如果图形关于某一直线对称，那么连结对应点的线段被对称轴垂直平分.(2)轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线。

中考几何48个模型及题型中考几何常见的48个模型及题型主要包括以下几类：
1. 直线与角。

a. 直线与角的性质，如同位角、对顶角等。

b. 直线间的夹角关系，如邻补角、对顶角等。

2. 三角形。

a. 三角形的性质，如三角形内角和为180度、三角形的外角性质等。

b. 三角形的全等与相似，如全等三角形的判定条件、相似三角形的性质等。

c. 三角形的高、中线、角平分线等线段的性质。

3. 四边形。

a. 平行四边形的性质，如对角线互相平分、对角线长度关系等。

b. 矩形、菱形、正方形和长方形的性质，如对角线长度关系、边长关系等。

c. 梯形的性质，如梯形的中位线、高的性质等。

4. 圆。

a. 圆的性质，如圆心角、弧、切线等。

b. 圆的相交关系，如相交弦定理、相交弧的性质等。

5. 相似。

a. 图形的相似性质，如相似三角形的判定条件、相似多边形的性质等。

b. 相似三角形的应用，如相似三角形的边比例定理、高线定理等。

6. 地理中的几何。

a. 地图的比例尺计算。

b. 方位角的计算。

c. 测量角度、距离等。

以上是中考几何常见的48个模型及题型，涵盖了直线与角、三角形、四边形、圆、相似和地理中的几何等多个方面。

希望这些信息能够帮助到你。

2018年初中数学突破中考压轴题几何模型之相似三角形中的一线三等角模型(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018年初中数学突破中考压轴题几何模型之相似三角形中的一线三等角模型(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018年初中数学突破中考压轴题几何模型之相似三角形中的一线三等角模型(word版可编辑修改)的全部内容。

相似三角形判定的基本模型A字型 X字型反A字型反8字型母子型旋转型双垂直三垂直相似三角形判定的变化模型CB EDA一线三等角型相似三角形三等角型相似三角形是以等腰三角形（等腰梯形)或者等边三角形为背景，一个与等腰三角形的底角相等的顶点在底边所在的直线上，角的两边分别与等腰三角形的两边相交如图所示:等角的顶点在底边上的位置不同得到的相似三角形的结论也不同,当顶点移动到底边的延长线时,形成变式图形，图形虽然变化但是求证的方法不变。

此规律需通过认真做题，细细体会。

（1）连接AP、AQ、PQ，试判断△APQ的形状，并说明理由.(2）当t=1秒时,连接AC，与PQ相交于点K。

求AK的长.（3）当t=2秒时，连接AP、PQ,将∠APQ逆时针旋转,使角的两边与AB、AD、AC分别交于点E、N、F，连接EF。

若AN=1,求S△EPF。

AB C DP Q KAB CDPQDCBA【应用】1.如图,在平面直角坐标中，四边形OABC是等腰梯形，CB∥OA，OA=7,BC=1,AB=5，点P为x轴上的一个动点，点P不与点0、点A重合．连接CP，过点P作PD交AB 于点D．（1)直接写出点B的坐标．（2）当点P在线段OA上运动时，使得∠CPD=∠OAB,且BD: AD=3：2 ，求点P的坐标．2、已知在梯形ABCD中，AD∥BC,AD＜BC，且BC =6，AB=DC=4,点E是AB的中点．（1)如图，P为BC上的一点，且BP=2．求证：△BEP∽△CPD；一线三等角。

2018年中考数学压轴学霸提分秘籍之因面积产生的动点问
题六大模型
面积是平面几何中一个重要的概念，关联着平面图形中的重要元素边与角，由动点而生成的面积问题，是抛物线与直线形结合的觉形式，常见的面积问题有规则的图形的面积(如直角三角形、平行四边形、菱形、矩形的面积计算问题)以及不规则的图形的面积计算，解决不规则的图形的面积问题是中考压轴题常考的题型，此类问题计算量较大。

有时也要根据题目的动点问题产生解的不确定性或多样性。

解决这类问题常用到以下与面积相关的知识:图形的割补、等积变形、等比转化等数学方法.面积的存在性问题常见的题型和解题策略有两类:一是先根据几何法确定存在性，再列方程求解，后检验方程的根.二是先假设关系存在，再列方程，后根据方程的解验证假设是否正确.解决动点产生的面积问题，常用到的知识和方法，如下:如图1，如果三角形的某一条边与坐标轴平行，计算这样“规则”的三角形的面积，直接用面积公式.如图2，图3，三角形的三条边没有与坐标轴平行的，计算这样“不规则”的三角形的面积，用“割”或“补”的方法.图1图2图3计算面积长用到的策略还有:如图4，同底等高三角形的面积相等.平行线间的距离处处相等.如图5，同底三角形的面积比等于高的比.如图6，同高三角形的面积比
等于底的比.图4图5图6【典题突破】。