三角函数与反三角函数公式大全

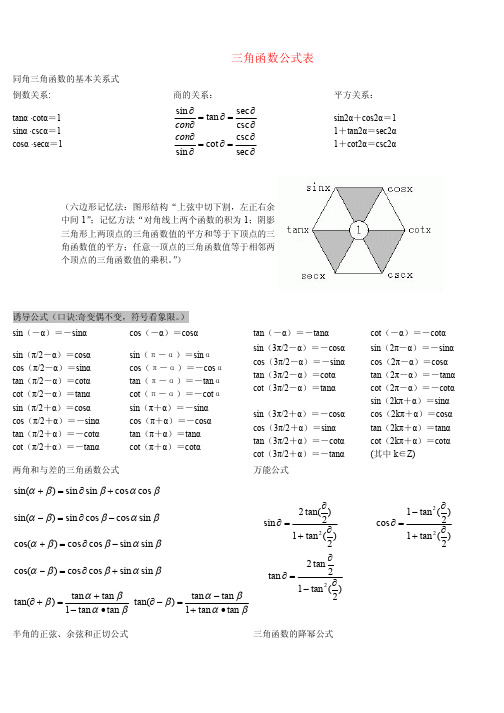
三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA?CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=AA cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 诱导公式s in(-a) = -sina c os(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosasin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aa cos sin 万能公式 sina=2)2(tan 12tan2a a + cosa= 22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a - 其它公式 a?sina+b?cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a?sin(a)-b?cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数 csc(a) =a sin 1 sec(a) =acos 1 双曲函数 sinh(a)=2e -e -a a cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）= sinα cos （2kπ＋α）= cosαtan （2kπ＋α）= tanα cot （2kπ＋α）= cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin （π＋α）= -sinα cos （π＋α）= -cosαtan （π＋α）= tanα cot （π＋α）= cotα公式三：任意角α与 -α的三角函数值之间的关系：sin （-α）= -sinα cos （-α）= cosαtan （-α）= -tanα cot （-α）= -cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin （π-α）= sinα cos （π-α）= -cosαtan （π-α）= -tanα cot （π-α）= -cotα公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin （2π-α）= -sinα cos （2π-α）= cosαtan （2π-α）= -tanα cot （2π-α）= -cotα公式六：2π±α及23π±α与α的三角函数值之间的关系： sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosα cos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k ∈Z)正弦定理 a/sinA=b/sinB=c/sinC=2R 注： 其中 R 表示三角形的外接圆半径 余弦定理 b2=a2+c2-2accosB 注：角B 是边a 和边c 的夹角正切定理 [(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]} 正切函数sin tan cos x x x =；余切函数cos cot sin x x x=； 正割函数1sec cos x x =；余割函数1csc sin x x = 三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|三角形中的一些结论(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)????(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1????(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC????(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1反三角函数： a r c s i n a r c c o s 2x x π+= a r c t a n a r c c o t 2x x π+= arcsin x ：定义域[1,1]-，值域[,]22ππ-；arccos x ：定义域[1,1]-，值域[0,]π； arctan x ：定义域(,)-∞+∞，值域(,)22ππ-；arccot x ：定义域(,)-∞+∞，值域(0,)π式中n 为任意整数. arc sin x =arc cos x = arc tan x = arc cot x =。

三角函数与反三角函数的关系公式
三角函数与反三角函数的关系公式：sin(A+B)=sinAcosB+cosAsinBsin(A-B)。

反三角函数是一种基本初等函数。

它是反正弦arcsinx，反余弦arccosx，反正切arctanx，反余切arccotx，反正割arcsecx，反余割arccscx这些函数的统称，各自表示其反正弦、反余弦、反正切、反余切，反正割，反余割为x的角。

三角函数是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

也可以等价地用与单位圆有关的各种线段的长度来定义。

三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。

在数学分析中，三角函数也被定义为无穷级数或特定微分方程的解，允许它们的取值扩展到任意实数值，甚至是复数值。

三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+ 倍角公式 tan2A =Atan 12tanA 2- Sin2A=2SinA?CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=AA cos 1cos 1+- cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cosb = 2cos 2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2b a - tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)] sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 诱导公式s in(-a) = -sina c os(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosasin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aa cos sin 万能公式 sina=2)2(tan 12tan2a a + cosa= 22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a - 其它公式 a?sina+b?cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a?sin(a)-b?cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2 其他非重点三角函数 csc(a) =a sin 1 sec(a) =acos 1 双曲函数 sinh(a)=2e -e -a a cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一：设α为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）= sinα cos （2kπ＋α）= cosαtan （2kπ＋α）= tanα cot （2kπ＋α）= cotα公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系：sin （π＋α）= -sinα cos （π＋α）= -cosαtan （π＋α）= tanα cot （π＋α）= cotα公式三：任意角α与 -α的三角函数值之间的关系：sin （-α）= -sinα cos （-α）= cosαtan （-α）= -tanα cot （-α）= -cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin （π-α）= sinα cos （π-α）= -cosαtan （π-α）= -tanα cot （π-α）= -cotα公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin （2π-α）= -sinα cos （2π-α）= cosαtan （2π-α）= -tanα cot （2π-α）= -cotα公式六：2π±α及23π±α与α的三角函数值之间的关系： sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosα cos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k ∈Z)正弦定理 a/sinA=b/sinB=c/sinC=2R 注： 其中 R 表示三角形的外接圆半径 余弦定理 b2=a2+c2-2accosB 注：角B 是边a 和边c 的夹角正切定理 [(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]} 正切函数sin tan cos x x x =；余切函数cos cot sin x x x=； 正割函数1sec cos x x =；余割函数1csc sin x x = 三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b|a-b|≥|a|-|b| -|a|≤a≤|a|三角形中的一些结论(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)????(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1????(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC????(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1反三角函数： a r c s i n a r c c o s 2x x π+= a r c t a n a r c c o t 2x x π+= arcsin x ：定义域[1,1]-，值域[,]22ππ-；arccos x ：定义域[1,1]-，值域[0,]π； arctan x ：定义域(,)-∞+∞，值域(,)22ππ-；arccot x ：定义域(,)-∞+∞，值域(0,)π式中n 为任意整数. arc sin x =arc cos x = arc tan x = arc cot x =。

三角函数-反三角函数公式大全tan （π＋α）= tanα cot （π＋α）= cotα 公式三：任意角α与 -α的三角函数值之间的关系： sin （-α）= -sinα cos （-α）= cosα tan （-α）= -tanα cot （-α）= -cotα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin （π-α）= sinα cos （π-α）= -cosα tan （π-α）= -tanα cot （π-α）= -cotα 公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系： sin （2π-α）= -sinα cos （2π-α）= cosα tan （2π-α）= -tanα cot （2π-α）= -cotα 公式六：2π±α及23π±α与α的三角函数值之间的关系：sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosα cos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A正切函数sin tan cos x x x =；余切函数cos cot sin xx x =； 正割函数1sec cos x x =；余割函数1csc sin x x= 三角函数奇偶、周期性sin x ，tan x ，cot x 奇函数；cos x 偶函数；sin x，cos x 周期2π；sin()t ωϕ+ 周期2πω；tan x ，cot x 周期π常用三角函数公式：22cos sin 1x x += 22cos sin cos2x x x -=2s i n c o ssx x x = 21cos 22sin x x -= 21c o s 22c o sx x +=22211tan sec cos x x x+== 22211cotcsc sin x x x +==1sin sin [cos()cos()]2x y x y x y =-+-- 1c o sc o s[c o s ()c o s ()]2x y x y x y =++-1sin cos [sin()sin()]2x y x y x y =++-反三角函数：a r c s i na r c c o s 2x x π+=a r c t a na r c c o t2x x π+=arcsin x：定义域[1,1]-，值域[,]22ππ-；arccos x ：定义域[1,1]-，值域[0,]π；arctan x：定义域(,)-∞+∞，值域(,)22ππ-；arccot x ：定义域(,)-∞+∞，值域(0,)π式中n为任意整数.arc sin x = arc cos x = arc tan x = arc cot x =。

三角函数反三角函数公式大全
三角函数与反三角函数的关系公式：sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cos AcosB+sinAsinBtan(A+B)。

反三角函数是一种基本初等函数。

它是反正弦arcsinx，反余弦arccosx，反正切arctanx，反余切arccotx，反正割arcsecx，反余割arccscx这些函数的统称，各自表示其反正弦、反余弦、反正切、反余切，反正割，反余割为x的角。

三角函数的反函数是个多值函数，因为它并不满足一个自变量对应一个函数值的要求，其图像与其原函数关于函数y=x对称。

欧拉提出反三角函数的概念，并且首先使用了“arc+函数名”的形式表示反三角函数。

三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+倍角公式 tan2A =Atan 12tanA2- Sin2A=2SinA•CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=AAcos 1sin +和差化积 sina+sinb=2sin2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cosb = 2cos2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2ba - tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB积化和差 sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 诱导公式s in(-a) = -sina c os(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2a a + cosa= 22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan2aa- 其它公式a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin2a -cos 2a )2 其他非重点三角函数 csc(a) =a sin 1 sec(a) =acos 1 公式一：设α为任意角，终边相同的角的同一三角函数的值相等： sin （2kπ＋α）= sinα cos （2kπ＋α）= cosα tan （2kπ＋α）= tanα cot （2kπ＋α）= cotα 公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin （π＋α）= -sinα cos （π＋α）= -cosαtan （π＋α）= tanα cot （π＋α）= co tα 公式三：任意角α与 -α的三角函数值之间的关系： sin （-α）= -sinα cos （-α）= cosα tan （-α）= -tanα cot （-α）= -cotα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin （π-α）= sinα cos （π-α）= -cosα tan （π-α）= -tanα cot （π-α）= -cotα 公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系： sin （2π-α）= -sinα cos （2π-α）= cosα tan （2π-α）= -tanα cot （2π-α）= -cotα 公式六：2π±α及23π±α与α的三角函数值之间的关系： sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosα cos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A正切函数sin tan cos x x x =；余切函数cos cot sin xx x =； 正割函数1sec cos x x =；余割函数1csc sin x x= 三角函数奇偶、周期性sin x ，tan x ，cot x 奇函数；cos x 偶函数；sin x ，cos x 周期2π；sin()t ωϕ+ 周期2πω；tan x ，cot x 周期π常用三角函数公式：22cos sin 1x x += 22cos sin cos 2x x x -= 2s i n c o s s i n x x x= 21cos22sin x x -= 21c o s 22c o sx x += 22211tan sec cos x x x+== 22211cot csc sin x x x +== 1sin sin [cos()cos()]2x y x y x y =-+-- 1c o s c o s [c o s ()c o s ()]2x y x y x y =++- 1sin cos [sin()sin()]2x y x y x y =++-反三角函数： a r c s i na r c c o s 2x x π+= a r c t a na r c c o t 2x x π+=arcsin x ：定义域[1,1]-，值域[,]22ππ-；arccos x ：定义域[1,1]-，值域[0,]π； arctan x ：定义域(,)-∞+∞，值域(,)22ππ-；arccot x ：定义域(,)-∞+∞，值域(0,)π式中n为任意整数.arc sin x = arc cos x = arc tan x = arc cot x =。

三角-反三角函数公式大全sin （2π-α）= -sinα cos （2π-α）= cosα tan （2π-α）= -tanα cot （2π-α）= -cotα 公式六： 2π±α及23π±α与α的三角函数值之间的关系： sin （2π+α）= cosα cos （2π+α）= -sinαtan （2π+α）= -cotα cot （2π+α）= -tanαsin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanαsin （23π+α）= -cosα cos （23π+α）= sinαtan （23π+α）= -cotα cot （23π+α）= -tanαsin （23π-α）= -cosα cos （23π-α）= -sinαtan （23π-α）= cotα cot （23π-α）= tanα(以上k ∈Z)正弦定理 a/sinA=b/sinB=c/sinC=2R 注： 其中 R 表示三角形的外接圆半径 余弦定理 b2=a2+c2-2accosB 注：角B 是边a 和边c 的夹角 正切定理 [(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}正切函数sin tan cos x x x =；余切函数cos cot sin xx x =； 正割函数1sec cos x x =；余割函数1csc sin x x= 三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b |a-b|≥|a|-|b| -|a|≤a≤|a| 三角形中的一些结论(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1 (4)sin2A+sin2B+sin2C=4sinA·sinB·sinC (5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1反三角函数：a r c s i na r c c o s 2x x π+=a r c t a na r c c o t2x x π+=arcsin x：定义域[1,1]-，值域[,]22ππ-；arccos x ：定义域[1,1]-，值域[0,]π；arctan x：定义域(,)-∞+∞，值域(,)22ππ-；arccot x ：定义域(,)-∞+∞，值域(0,)π式中n为任意整数.arc sin x = arc cot x =。

三角函数与反三角函数公式大全1. 正弦函数（sine function）的公式：- 基本关系式：sinθ = 对边/斜边- 余角关系式：sin(90°-θ) = cosθ- 二倍角关系式：sin2θ = 2sinθcosθ- 半角关系式：sin(θ/2) = ±√[(1-cosθ)/2]- 三倍角关系式：sin3θ = 3sinθ - 4sin^3θ- 和差关系式：sin(α±β) = sinαcosβ ± cosαsinβ2. 余弦函数（cosine function）的公式：- 基本关系式：cosθ = 邻边/斜边- 余角关系式：cos(90°-θ) = sinθ- 二倍角关系式：cos2θ = cos^2θ - sin^2θ- 半角关系式：cos(θ/2) = ±√[(1+cosθ)/2]- 三倍角关系式：cos3θ = 4cos^3θ - 3cosθ- 和差关系式：cos(α±β) = cosαcosβ ∓ sinαsinβ3. 正切函数（tangent function）的公式：- 基本关系式：tanθ = 对边/邻边= sinθ/cosθ- 余角关系式：t an(90°-θ) = 1/tanθ- 二倍角关系式：tan2θ = (2tanθ)/(1-tan^2θ)- 半角关系式：tan(θ/2) = ±√[(1-cosθ)/(1+cosθ)]- 三倍角关系式：tan3θ = (3tanθ-tan^3θ)/(1-3tan^2θ)- 和差关系式：tan(α±β) = (tanα±tanβ)/(1∓tanαtanβ) 4. 余切函数（cotangent function）的公式：- 基本关系式：cotθ = 邻边/对边= 1/tanθ- 余角关系式：co t(90°-θ) = tanθ- 二倍角关系式：cot2θ = (cot^2θ-1)/(2cotθ)- 半角关系式：cot(θ/2) = ±√[(1+cosθ)/(1-cosθ)]- 三倍角关系式：cot3θ = (3cotθ-cot^3θ)/(1-3cot^2θ)- 和差关系式：cot(α±β) = (cotαcotβ-1)/(cotβ±cotα) 1. 反正弦函数（arcsine function）的公式：- 基本关系式：sinθ = arcsin(x)- 余角关系式：arcsin(x) = 90° - arccos(x)- 二倍角关系式：arcsin(2x√(1-x^2)) = 2arcsin(x)- 和差关系式：arcsin(x ± y) ≠ arcsin(x) ± arcsin(y) 2. 反余弦函数（arccosine function）的公式：- 基本关系式：cosθ = arccos(x)- 余角关系式：arccos(x) = 90° - arcsin(x)- 二倍角关系式：arccos(2x^2 - 1) = 2arccos(x)- 和差关系式：arccos(x ± y) ≠ arccos(x) ± arccos(y) 3. 反正切函数（arctangent function）的公式：- 基本关系式：tanθ = arctan(x)- 余角关系式：arctan(x) = 90° - arctan(1/x)- 二倍角关系式：arctan(2x/(1-x^2)) = 2arctan(x)- 和差关系式：arctan(x ± y) ≠ arctan(x) ± arctan(y)。

三角函数和反三角函数的运算公式标题：三角函数与反三角函数——视角下的数学之美导语：在数学的世界里，有着一组神奇的函数，它们被称作三角函数和反三角函数。

它们不仅在数学中发挥着重要的作用，还与我们的生活息息相关。

本文将以人类的视角，以生动的语言，为您揭示三角函数和反三角函数的运算公式及其美妙之处。

一、三角函数的运算公式1. 正弦函数（sin）正弦函数是三角函数中最为常见的函数之一，它描述了一个角度对应的直角三角形中，斜边与对边之比。

可以简单地表示为sinθ。

正弦函数的运算公式如下：- 任意角θ的正弦值等于对边与斜边的比值：sinθ = 对边 / 斜边。

- 正弦函数具有周期性，即sin(θ + 2π) = sinθ。

2. 余弦函数（cos）余弦函数也是三角函数中常见的函数之一，它描述了一个角度对应的直角三角形中，邻边与斜边之比。

可以简单地表示为cosθ。

余弦函数的运算公式如下：- 任意角θ的余弦值等于邻边与斜边的比值：cosθ = 邻边 / 斜边。

- 余弦函数同样具有周期性，即cos(θ + 2π) = cosθ。

3. 正切函数（tan）正切函数是三角函数中的另一个重要函数，它描述了一个角度对应的直角三角形中，对边与邻边之比。

可以简单地表示为tanθ。

正切函数的运算公式如下：- 任意角θ的正切值等于对边与邻边的比值：tanθ = 对边 / 邻边。

- 正切函数也具有周期性，即tan(θ + π) = tanθ。

二、反三角函数的运算公式1. 反正弦函数（arcsin）反正弦函数是三角函数的逆函数，它描述了一个比值对应的角度，即根据给定的对边与斜边的比值，求出相应的角度。

可以简单地表示为arcsin(x)。

反正弦函数的运算公式如下：- 给定一个比值x，反正弦函数返回对应的角度θ：arcsin(x) = θ。

2. 反余弦函数（arccos）反余弦函数是三角函数的逆函数，它描述了一个比值对应的角度，即根据给定的邻边与斜边的比值，求出相应的角度。

三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tan(A-B) =tanAtanB -1tanB tanA +tanAtanB1tanBtanA +-cot(A+B) = cot(A-B) =cotA cotB 1-cotAcotB +cotAcotB 1cotAcotB -+倍角公式tan2A =Sin2A=2SinA•CosA Atan 12tanA2-Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(+a)·tan(-a)3π3π半角公式sin()= cos()= tan()= cot()=2A 2cos 1A -2A 2cos 1A +2A A A cos 1cos 1+-2Atan()==A A cos 1cos 1-+2A A A sin cos 1-AAcos 1sin +和差化积 sina+sinb=2sincos sina-sinb=2cos sin 2b a +2b a -2b a +2ba -cosa+cosb = 2coscos cosa-cosb = -2sin sin 2b a +2b a -2b a +2ba -tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB积化和差 sinasinb = -[cos(a+b)-cos(a-b)] cosacosb = [cos(a+b)+cos(a-b)]2121sinacosb = [sin(a+b)+sin(a-b)] cosasinb = [sin(a+b)-sin(a-b)]2121诱导公式s in(-a) = -sina c os(-a) = cosa sin(-a) = cosa cos(-a) = sina2π2πsin(+a) = cosa cos(+a) = -sina sin(π-a) = sina cos(π-a) = -cosa2π2πsin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aacos sin 万能公式sina=cosa= tana=2)2(tan 12tan2a a +22)2(tan 1)2(tan 1aa+-2)2(tan 12tan2aa-其它公式a•sina+b•cosa=×sin(a+c) [其中tanc=])b (a 22+ab a•sin(a)-b•cos(a) = ×cos(a-c) [其中tan(c)=])b (a 22+ba 1+sin(a) =(sin+cos )22a 2a 1-sin(a) = (sin-cos )22a 2a 其他非重点三角函数csc(a) =sec(a) =a sin 1acos 1公式一：设α为任意角，终边相同的角的同一三角函数的值相等： sin （2kπ＋α）= sinα cos （2kπ＋α）= cosα tan （2kπ＋α）= tanα cot （2kπ＋α）= cotα 公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin （π＋α）= -sinα cos （π＋α）= -cosαtan （π＋α）= tanα cot （π＋α）= cotα 公式三：任意角α与 -α的三角函数值之间的关系： sin （-α）= -sinα cos （-α）= cosα tan （-α）= -tanα cot （-α）= -cotα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin （π-α）= sinα cos （π-α）= -cosα tan （π-α）= -tanα cot （π-α）= -cotα 公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系： sin （2π-α）= -sinα cos （2π-α）= cosα tan （2π-α）= -tanα cot （2π-α）= -cotα 公式六：±α及±α与α的三角函数值之间的关系： 2π23πsin （+α）= cosα cos （+α）= -sinα2π2πtan （+α）= -cotα cot （+α）= -tanα2π2πsin （-α）= cosα cos （-α）= sinα tan （-α）= cotα cot （-α）=2π2π2π2πtanα sin （+α）= -cosα cos （+α）= sinα 23π23πtan （+α）= -cotα cot （+α）= -tanα 23π23πsin （-α）= -cosα cos （-α）= -sinα 23π23πtan （-α）= cotα cot （-α）= tanα 23π23π(以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A•sin(ωt+θ)+ B•sin(ωt+φ) =×sin)cos(222ϕθ⋅++AB B A )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A 正切函数；余切函数；sin tan cos x x x =cos cot sin xx x=正割函数；余割函数1sec cos x x =1csc sin x x=三角函数奇偶、周期性，， 奇函数； 偶函数； sin x tan x cot x cos x ， 周期； 周期；，周期sin x cos x 2πsin()t ωϕ+2πωtan x cot x π常用三角函数公式：22cos sin 1x x +=22cos sin cos 2x x x -=2sin cos sin 2x x x = 21cos 22sin x x -=21cos 22cos x x += 22211tan sec cos x x x +==22211cot csc sin x x x+== 1sin sin [cos()cos()]2x y x y x y =-+--1cos cos [cos()cos()]2x y x y x y =++-1sin cos [sin()sin()]2x y x y x y =++-反三角函数：arcsin arccos 2x x π+=arctan arccot 2x x π+=：定义域，值域；：定义域，值域；arcsin x [1,1]-[,22ππ-arccos x [1,1]-[0,]π：定义域，值域；：定义域，值域arctan x (,)-∞+∞(,)22ππ-arc cot x (,)-∞+∞(0,)πe i r b e i n g a re go o式中n 为任意整数.arc sin x =arc cos x =arc tan x =arc cot x =。

三角函数反三角函数公式大全Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotAcotB 1cotAcotB -+倍角公式 tan2A =Atan 12tanA2- Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3π-a) 半角公式 sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+ tan(2A )=A A sin cos 1-=A Acos 1sin +和差化积 sina+sinb=2sin2b a +cos 2b a - sina-sinb=2cos 2b a +sin 2b a - cosa+cosb = 2cos2b a +cos 2b a - cosa-cosb = -2sin 2b a +sin 2ba -tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)] cosasinb = 21[sin(a+b)-sin(a-b)] 诱导公式s in(-a) = -sina c os(-a) = cosa sin(2π-a) = cosa cos(2π-a) = sina sin(2π+a) = cosa cos(2π+a) = -sina sin(π-a) = sina cos(π-a) = -cosasin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2a a + cosa= 22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan2aa- 其它公式a?sina+b?cosa=)b (a 22+×sin(a+c) [其中tanc=ab]a?sin(a)-b?cos(a) = )b (a 22 ×cos(a-c) [其中tan(c)=ba ]1+sin(a) =(sin 2a +cos 2a )21-sin(a) = (sin 2a -cos 2a )2其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1公式一：设α为任意角，终边相同的角的同一三角函数的值相等： sin （2kπ＋α）= sinα cos （2kπ＋α）= cosα tan （2kπ＋α）= tanα cot （2kπ＋α）= cotα 公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin （π＋α）= -sinα cos （π＋α）= -cosα tan （π＋α）= tanα cot （π＋α）= cotα 公式三：任意角α与 -α的三角函数值之间的关系： sin （-α）= -sinα cos （-α）= cosα tan （-α）= -tanα cot （-α）= -cotα 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系： sin （π-α）= sinα cos （π-α）= -cosαtan （π-α）= -tanα cot （π-α）= -cotα 公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系： sin （2π-α）= -sinα cos （2π-α）= cosα tan （2π-α）= -tanα cot （2π-α）= -cotα 公式六：2π±α及23π±α与α的三角函数值之间的关系：sin （2π+α）= cosα cos （2π+α）= -sinα tan （2π+α）= -cotα cot （2π+α）= -tanα sin （2π-α）= cosα cos （2π-α）= sinα tan （2π-α）= cotα cot （2π-α）= tanα sin （23π+α）= -cosα cos （23π+α）= sinα tan （23π+α）= -cotα cot （23π+α）= -tanα sin （23π-α）= -cosα cos （23π-α）= -sinα tan （23π-α）= cotα cot （23π-α）= tanα (以上k∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A?sin(ωt+θ)+ B?sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin)cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A正切函数sin tan cos x x x =；余切函数cos cot sin xx x =； 正割函数1sec cos x x =；余割函数1csc sin x x= 三角函数奇偶、周期性sin x ，tan x ，cot x 奇函数；cos x 偶函数； sin x ，cos x 周期2π；sin()t ωϕ+ 周期2πω；tan x ，cot x 周期π常用三角函数公式：22cos sin 1x x += 22cos sin cos2x x x -= 2sin cos sin 2x x x = 21cos 22sin x x -= 21cos 22cos x x += 22211tan sec cos x x x +== 22211cot csc sin x x x+== 1sin sin [cos()cos()]2x y x y x y =-+-- 1cos cos [cos()cos()]2x y x y x y =++-1sin cos [sin()sin()]2x y x y x y =++-反三角函数： arcsin arccos 2x x π+=arctan arccot 2x x π+=arcsin x ：定义域[1,1]-，值域[,]22ππ-；arccos x ：定义域[1,1]-，值域[0,]π；arctan x ：定义域(,)-∞+∞，值域(,)22ππ-；arccot x ：定义域(,)-∞+∞，值域(0,)π式中n 为任意整数.arc sin x = arc tan x = arc cot x =。

三角函数与反三角函数第一部分三角函数公式·两角和与差的三角函数cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+ta nβ)/(1-tanα·tanβ) tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)·半角公式：sin(α/2)=±√((1-cosα)/2)cos(α/2)=±√((1+cosα)/2)tan(α/2)=±√((1-cosα)/(1+cosα))=sinα/(1+cosα)=(1-cosα)/sinα cot(α/2)=±√((1+cosα)/(1-cosα))=(1+cosα)/sinα=sinα/(1-cosα)sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2se cα/(secα-1))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))·辅助角公式：Asinα+Bcosα=√(A^2+B^2)sin(α+φ）（tanφ=B/A）Asinα+Bcosα=√(A^2+B^2)cos(α-φ）（tanφ=A/B）·万能公式sin(a)= (2tan(a/2))/(1+tan^2(a/2)) cos(a)= (1-tan^2(a/2))/(1+tan^2(a/2))tan(a)= (2tan(a/2))/(1-tan^2(a/2))·降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·和差化积公式：sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2] cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgB=sin(A+B)/sinAsinB -ctgA+ctgB=sin(A+B)/sinAsinB·积化和差公式：sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·倍角公式：sin(2α)=2sinα·cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2tan(2α)=2tanα/(1-tan^2α) co t(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα·cscα·三倍角公式：sin(3α) = 3sinα-4sin^3α = 4sinα·sin(60°+α)sin(60°-α)cos(3α) = 4cos^3α-3cosα = 4cosα·cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) =tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)·n倍角公式：sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α-…·三角和的三角函数：sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tanγ-tanγ·tanα)·其它公式1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^csc(a)=1/sin(a) sec(a)=1/cos( a)·推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α 1-cos2α=2sin^2α1+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)。