2013年重点中学自主招生数学模拟试题 一
- 格式:doc
- 大小:246.00 KB
- 文档页数:4

2024年重点中学自主招生模拟试卷(1)数学参考答案一.选择题(共10小题)1.(2024春•礼县校级月考)已知a﹣2+b=0(a>0,b>0),则等于()A.B.C.D.【分析】由已知可得()2=0,则,代入原式计算即可.【解答】解:由已知可得()2=0,则,即a=b,原式==.故选:D.2.(2024•九龙坡区自主招生)在数轴上,若点M、N分别表示数m、n,则|m|表示点M到原点的距离,|m﹣n|表示M、N两点间的距离.以下说法正确的有()①若|m﹣2|+|n+3|=0,则m﹣2n=8;②若|m﹣2|=|m+3|,则;③若,则;④函数y=|x2+6|﹣|x2﹣6|与函数y=x有三个交点.A.1个B.2个C.3个D.4个【分析】利用非负数的性质得出m=2,n=﹣3,代入m﹣2n即可判断①;解绝对值方程求得m的值即可判断②;由可知a<0,b <0,c>0,得到ab>0,bc<0,ac<0即可判断③;作出函数y=|x2+6|﹣|x2﹣6|与函数y=x的图象,根据函数的图象即可判断④.【解答】解:①∵|m﹣2|+|n+3|=0,∴m﹣2=0,n+3=0,∴m=2,n=﹣3,∴m﹣2n=8,故①正确;②∵|m﹣2|=|m+3|,∴m﹣2=﹣m﹣3,∴m=﹣,故②错误;③若,则a<0,b<0,c>0,∴ab>0,bc<0,ac<0,∴,故③正确;④当x2﹣6≤0时,即﹣≤x≤,y=|x2+6|﹣|x2﹣6|=2x2;当x2﹣6>0时,即x<﹣或x>,y=|x2+6|﹣|x2﹣6|=12;作出函数的图象如图:由图象可知,函数y=|x2+6|﹣|x2﹣6|与函数y=x有三个交点,故④正确.故选:C.3.(2023•南安市校级模拟)如图,矩形ABCD由3×4个小正方形组成,此图中不是正方形的矩形有()A.34个B.36个C.38个D.40个【分析】解答此题要从矩形的两边长进行分类分析,在由3×4个小正方形组成矩形ABCD中,不是正方形的矩形的两边长存在以下几种情况:2、1;3、1;4、1;3、2;3、4;4、2.【解答】解:在由3×4个小正方形组成矩形ABCD中,共有矩形60个,是正方形的有20个,其中,边长为1的12个,边长为2的6个,边长为3的2个;不是正方形的矩形有40个,其中,两边长分别为2和1的有17个;两边长分别为3和1的有10个;两边长分别为4和1的有3个;两边长分别为3和2的有7个;两边长分别为3和4的有1个;两边长分别为4和2的有2个;故选:D.4.(2023•惠城区校级开学)已知x,y为实数,且满足x2﹣xy+4y2=4,记u=x2+xy+4y2的最大值为M,最小值为m,则M+m=()A.B.C.D.【分析】本题先将u转化为2xy+4,然后根据x2﹣xy+4y2=4进行配方,确定xy的范围,从而求出u的范围,得到M,m的大小即可得解.【解答】解:方法一:∵x2﹣xy+4y2=4,∴x2+4y2=xy+4,∴u=x2+xy+4y2=2xy+4,∵5xy=4xy+(x2+4y2﹣4)=(x+2y)2﹣4≥﹣4,当且仅当x=﹣2y,即,,或,时等号成立.∴xy的最小值为,u=x2+xy+4y2=2xy+4的最小值为,即.∵3xy=4xy﹣(x2+4y2﹣4)=4﹣(x﹣2y)2≤4,当且仅当x=2y,即,或,时等号成立.∴xy的最大值为,u=x2+xy+4y2=2xy+4的最大值为,即.∴.方法二:由x2﹣xy+4y2=4,得x2+4y2=xy+4,u=x2+xy+4y2=2xy+4.设xy=t,若x=0,则u=4;x≠0时,,将代入x2﹣xy+4y2=4,得,即x4﹣(t+4)x2+4t2=0,…①由△=(t+4)2﹣16t2≥0,解得.将代入方程①,解得,;代入方程①,解得,.∴xy的最大值为,最小值为.因此,,,,故选:C.方法三:由题意得,①﹣②,得2xy=u﹣4,u=2xy+4,把②两边加5xy,得(x+2y)2=4+5xy⩾0,解得:,把②两边减3xy,得(x﹣2y)2=4﹣3xy⩾0,解得:xy≤,∴,,因此,,,,故选:C.5.(2024•碑林区校级自主招生)在一种扑克牌游戏中,玩家可以利用“牌值”来预估还没有发出的牌的点数大小,“牌值”的计算方式为:没有发牌时,“牌值”为0;发出的牌点数为2至9时,表示发出点数小的牌,则“牌值”加1;发出的牌点数为10、J、Q、K、A、大王、小王时,表示发出点数大的牌,则“牌值”减1.若一副完整的扑克牌已发出34张,且此时的“牌值”为10,则随机发出的下一张牌的可能性判断正确的是()A.点数小的牌可能性大B.点数大的牌可能性大C.两者可能性一样大D.无法判断【分析】利用方程组的思想求得已发出的34张牌中的点数大的张数与点数小的张数,从而得到剩余的牌中点数大的张数与点数小的张数,再利用计算概率的方法解答即可.【解答】解:设一副完整的扑克牌已发出的34张牌中点数小的张数为x张,点数大的张数为y张,∴.解得:,∴已发出的34张牌中点数小的张数为22张,点数大的张数为12张,∴剩余的20张牌中点数大的张数为5×4+2﹣12=10张,点数小的张数为8×4﹣22=10张,∵剩下的牌中每一张牌被发出的机会皆相等,∴下一张发出的牌是点数大的牌的几率是,下一张发出的牌是点数小的牌的几率是,∴两者可能性一样大,故选:C.6.(2021•龙岗区校级自主招生)如图,点A是函数y=的图象上的点,点B,C的坐标分别为B(﹣,﹣),C(,).试利用性质:“函数y=的图象上任意一点A都满足|AB﹣AC|=2”求解下面问题:作∠BAC的角平分线AE,过B作AE的垂线交AE于F,已知当点A在函数y=的图象上运动时,点F总在一条曲线上运动,则这条曲线为()A.直线B.抛物线C.圆D.反比例函数的曲线【分析】如图:延长AC交BF的延长线于G,连接OF.只要证明OF是△BCG的中位线,可得OF=CG=,即可解决问题.【解答】解:如图:延长AC交BF的延长线于G,连接OF.∵AF⊥BG,∴∠AFB=∠AFG=90°,∴∠BAF+∠ABF=90°,∠G+∠GAF=90°,∵AE为∠BAG的平分线,∴∠BAF=∠FAG,∴∠ABF=∠G,∴AB=AG,∵AF⊥BG,∴BF=FG,∵B(﹣,﹣),C(,),∴OB=OC,∴OF=CG,∵AC=AG﹣CG,AB=AG,∴AB﹣AC=CG,∵|AB﹣AC|=2,∴CG=2,∴OF=,∴点F在以O为圆心为半径的圆上运动.故选:C.7.(2013•宁波自主招生)正方形ABCD中,点P,Q分别是边AB,AD上的点,连接PQ、PC、QC,下列说法:①若∠PCQ=45°,则PB+QD=PQ;②若AP=AQ=,∠PCQ=36°,则;③若△PQC是正三角形,若PB=1,则AP=.其中正确的说法有()A.3个B.2个C.1个D.0个【分析】(1)延长AB至点E,使BE=DQ,连接EC,AC,首先通过求证△BEC和△DQC全等推出等量关系,求出∠ECP=45°,然后再求证△PCE≌△PCQ,通过等量代换即可推出结论,(2)过点Q作∠PQC的角平分线,交PC于点E,首先根据题意推出△PBC 和△QDC全等,推出有关的等量关系,推出△PQC为等腰三角形,然后,通过顶角为36°角的等腰三角形的特殊性质,推出PQ2=PE•PC,PE=PC﹣2,解方程组即可推出结论,(3)取PC的中点E,连接BE,做BM⊥PC于点M,首先根据题意推出Rt △PBC和Rt△QDC全等,然后根据其性质推出相关角的度数和PB=QD,再通过直角三角形斜边上的中线的性质,和解直角三角形,推出4BM=PC,PC =AP,即得,4BM=AP,然后通过求证△PBM∽△PCB,推出BP:PC =BM:BC,最后通过等量代换,求关于AP的方程即可.注意不合适的值要舍去.【解答】(1)证明:延长AB至点E,使BE=DQ,连接EC,AC,∵正方形ABCD,∴∠BCA=∠DCA=45°,CD=DA=AB=BC,∠D=∠EBC=90°,∴在△BEC和△DQC中,,∴△BEC≌△DQC(SAS),∴CE=CQ,∠BCE=∠DCQ,∵∠PCQ=45°,∴∠DCQ+∠PCB=45°,∴∠BCE+∠PCB=45°,即∠ECP=45°,∵在△PCE和△PCQ中,,∴△PCE≌△PCQ(SAS),∴PE=PQ,∵PE=PB+BE=PB+QD,∴PQ=PB+QD,(2)过点Q作∠PQC的角平分线,交PC于点E,∵正方形ABCD,∴∠A=∠D=∠B=90°,AD=AB=BC=CD,∵∠PCQ=36°,AP=AQ=,∴PQ=2,PB=QD,∴PE=PC﹣2,∵在△PBC和△QDC中,,∴△PBC≌△QDC(SAS),∴QC=PC,∴∠CPQ=∠CQP=72°,∴∠PQE=∠EQC=36°,∴QE=QP=EC=2,∵△QPE∽△CQP,∴PQ:QC=PE:PQ,即PQ2=PE•PC,∵PQ=2,∴PE•PC=4,∵PE=PC﹣2,∴PC2﹣2PC﹣4=0,解得:PC1=1﹣<0(舍去),PC2=1+,∴PC=+1,(3)取PC的中点E,连接BE,做BM⊥PC于点M,∵正方形ABCD,∴BC=CD=AB=AD,∠D=∠B=∠A=∠BCD=90°,∵△PCQ为正三角形,∴QC=PQ=PC,∠QCP=60°,∵在Rt△PBC和Rt△QDC中,,∴Rt△PBC≌Rt△QDC(HL),∴∠BCP=∠DCQ=,PB=QD,∵E为PC的中点,∴BE=EC=PE=,∴∠BEM=30°,∴2BM=BE,∴4BM=PC,∵PC=AP,∴4BM=AP,∵BM⊥PC,∠BCP=15°,∴∠PBM=15°,∴△PBM∽△PCB,∴BP:PC=BM:BC,∵PB=1,∴BC=AB=AP+1,∴,∴AP2﹣AP﹣1=0,解得:AP1=1+,AP2=1﹣<0(舍去),∴AP=+1,∴其中说法正确的共3个,故选:A.8.(2021•龙岗区校级自主招生)如图,直线AB:y=﹣x+9交y轴于A,交x轴于B,x轴上一点C(﹣1,0),D为y轴上一动点,把线段BD绕B点逆时针旋转120°得到线段BE,连接CE,CD,则当CE长度最小时,线段CD 的长为()A.B.C.2D.5【分析】如图,设D(0,m).在BD的下方作等边三角形△BDQ,延长DQ 到M,使得QM=DQ,连接BM,DE,DE交BQ于点N,作MH⊥x轴于H.想办法求出点E的坐标,构建二次函数,利用二次函数的性质求出m的值即可解决问题;【解答】解:如图,设D(0,m).由题意:B(5,0).在BD的下方作等边三角形△BDQ,延长DQ到M,使得QM=DQ,连接BM,DE,DE交BQ于点N,作MH⊥x轴于H.∵△BDQ是等边三角形,∴∠DQB=∠DBQ=60°,∵QM=BQ,∴∠QMB=∠QBM,∵∠DQB=∠QMB+∠BQM,∴∠QMB=∠QBM=30°,∴∠DBM=90°,∴BM=BD,∵∠DBO+∠ODB=90°,∠DBO+∠MBH=90°,∴∠MBH=∠BDO,∵∠DOB=∠MHB=90°,∴△DOB∽△BHM,∴===,∵OD=m,OB=5,∴BH=m,MH=5,∴M(5﹣m,﹣5),∵MQ=DQ,∴Q(,),∵∠DBE=120°,∴∠DBN=∠EBN=60°,∴DE⊥BQ,DN=NE,QN=BN,∴N(,),E(,),∴CE2=()2+()2=m2﹣6m+91,∴当m=﹣=3时,CE的值最小,此时D(0,3),∴CD==2,方法二:如图,将线段OB绕点B逆时针旋转120°得到线段BP,直线EP交x轴于G,作CM⊥PE于M.易证△BOD≌△BPE,BG=2BP=10,∴点E的运动轨迹是直线PE,当点E与M重合时,CE的值最小,此时PM=OD=3,∴CD===2.故选:C.9.(2022秋•高邑县期中)已知实数a,b,c满足a+b+c=0,abc=6,那么++的值()A.是正数B.是零C.是负数D.正、负不能确定【分析】根据abc=6,可以将所求式子化简,然后再根据a+b+c=0,可以得到bc+ac+ab的正负情况,从而可以判断所求式子的正负情况,本题得以解决.【解答】解:∵abc=6,∴++==,∵bc+ac+ab=[(a+b+c)2﹣(a2+b2+c2)],a+b+c=0,∴bc+ac+ab=﹣(a2+b2+c2),∵a、b、c均不为0,∴bc+ac+ab<0,∴<0,即++的值是负数,故选:C.10.(2022•温州)如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,连结CF,作GM⊥CF于点M,BJ⊥GM于点J,AK⊥BJ于点K,交CF于点L.若正方形ABGF与正方形JKLM的面积之比为5,CE=+,则CH的长为()A.B.C.2D.【分析】设CF交AB于点P,过C作CN⊥AB于点N,设正方形JKLM边长为m,根据正方形ABGF与正方形JKLM的面积之比为5,得AF=AB=m,证明△AFL≌△FGM(AAS),可得AL=FM,设AL=FM=x,在Rt△AFL中,x2+(x+m)2=(m)2,可解得x=m,有AL=FM=m,FL=2m,从而可得AP=,FP=m,BP=,即知P为AB中点,CP=AP=BP=,由△CPN∽△FPA,得CN=m,PN=m,即得AN=m,而tan∠BAC===,又△AEC∽△BCH,得=,即=,故CH=2.【解答】解:设CF交AB于点P,过C作CN⊥AB于点N,如图:设正方形JKLM边长为m,∴正方形JKLM面积为m2,∵正方形ABGF与正方形JKLM的面积之比为5,∴正方形ABGF的面积为5m2,∴AF=AB=m,由已知可得:∠AFL=90°﹣∠MFG=∠MGF,∠ALF=90°=∠FMG,AF =GF,∴△AFL≌△FGM(AAS),∴AL=FM,设AL=FM=x,则FL=FM+ML=x+m,在Rt△AFL中,AL2+FL2=AF2,∴x2+(x+m)2=(m)2,解得x=m或x=﹣2m(舍去),∴AL=FM=m,FL=2m,∵tan∠AFL====,∴=,∴AP=,∴FP===m,BP=AB﹣AP=m﹣=,∴AP=BP,即P为AB中点,∵∠ACB=90°,∴CP=AP=BP=,∵∠CPN=∠APF,∠CNP=90°=∠FAP,∴△CPN∽△FPA,∴==,即==,∴CN=m,PN=m,∴AN=AP+PN=m,∴tan∠BAC====,∵△AEC和△BCH是等腰直角三角形,∴△AEC∽△BCH,∴=,∵CE=+,∴=,∴CH=2,故选:C.二.填空题(共6小题)11.(2023秋•长治月考)如图平行四边形ABCD,F为BC中点,延长AD至E,使DE:AD=1:3,连接EF交DC于点G,则△DEG与五边形DABFG的面积比值是.【分析】连接BG,先由平行四边形的性质得AD∥BC,AD=BC及∠E=∠CFG;再由F为BC中点及DE:AD=1:3得DE:CF的比值;然后由∠E=∠CFG,∠DGE=∠CGF证得△DGE∽CGF,最后由相似三角形的面积比等于相似比的平方及△CFG和△BGC之间的关系,可得答案.【解答】解:如图,连接BG,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴∠E=∠CFG,∵F为BC中点,∴FC=BC=AD,∵DE:AD=1:3,∴DE:BC=1:3,∴DE:CF=2:3,∵∠E=∠CFG,∠DGE=∠CGF,∴△DGE∽CGF,∴DG:CG=DE:CF=2:3,设△DEG的面积为a∴SDEG:S△CFG=4:9=a:S△CFG,△∴SCFG=,△取AD的中点Q,连接FQ,∴FQ∥DG,∴△EDG∽△EQF,∴DE:EQ=1:2.5=2:5,∴SDEG:S△QEF=4:25=a:S△EQF,△∴SEQF=,△∴SDQFG=a﹣a=a,四边形∴SABFQ=S四边形DQFG+S△CFG=,四边形∴SDABFG=.五边形∴△DEG与五边形DABFG的面积比值是.故答案为:.12.(2022•温江区校级自主招生)若关于x的方程(1﹣m2)x2+2mx﹣1=0的所有根都是比1小的正实数,则实数m的取值范围是m=1或m>2.【分析】分1﹣m2=0,1﹣m2≠0两种情况先求出原方程的实数根,再根据两个实数根都是比1小的正实数,列出不等式,求出m的取值范围.【解答】解:当1﹣m2=0时,m=±1.当m=1时,可得2x﹣1=0,x=,符合题意;当m=﹣1时,可得﹣2x﹣1=0,x=﹣,不符合题意;当1﹣m2≠0时,(1﹣m2)x2+2mx﹣1=0,[(1+m)x﹣1][(1﹣m)x+1]=0,∴x1=,x2=.∵关于x的方程(1﹣m2)x2+2mx﹣1=0的所有根都是比1小的正实数,∴0<<1,解得m>0,0<<1,解得m>2.综上可得,实数m的取值范围是m=1或m>2.故答案为:m=1或m>2.13.(2022•宁波)如图,四边形OABC为矩形,点A在第二象限,点A关于OB的对称点为点D,点B,D都在函数y=(x>0)的图象上,BE⊥x轴于点E.若DC的延长线交x轴于点F,当矩形OABC的面积为9时,的值为,点F的坐标为(,0).【分析】连接OD,作DG⊥x轴,设点B(b,),D(a,),根据矩形的面积得出三角形BOD的面积,将三角形BOD的面积转化为梯形BEGD 的面积,从而得出a,b的等式,将其分解因式,从而得出a,b的关系,进而在直角三角形BOD中,根据勾股定理列出方程,进而求得B,D的坐标,进一步可求得结果.【解答】解:如图,方法一:作DG⊥x轴于G,连接OD,设BC和OD交于I,设点B(b,),D(a,),由对称性可得:△BOD≌△BOA≌△OBC,∴∠OBC=∠BOD,BC=OD,∴OI=BI,∴DI=CI,∴=,∵∠CID=∠BIO,∴△CDI∽△BOI,∴∠CDI=∠BOI,∴CD∥OB,∴SBOD=S△AOB=S矩形AOCB=,△∵SBOE=S△DOG==3,S四边形BOGD=S△BOD+S△DOG=S梯形BEGD+S△BOE,△∴SBEGD=S△BOD=,梯形∴•(a﹣b)=,∴2a2﹣3ab﹣2b2=0,∴(a﹣2b)•(2a+b)=0,∴a=2b,a=﹣(舍去),∴D(2b,),即:(2b,),在Rt△BOD中,由勾股定理得,OD2+BD2=OB2,∴[(2b)2+()2]+[(2b﹣b)2+(﹣)2]=b2+()2,∴b=,∴B(,2),D(2,),∵直线OB的解析式为:y=2x,∴直线DF的解析式为:y=2x﹣3,当y=0时,2﹣3=0,∴x=,∴F(,0),∵OE=,OF=,∴EF=OF﹣OE=,∴=,方法二:如图,连接OD,连接BF,BD,作DG⊥x轴于G,直线BD交x轴于H,由上知:DF∥OB,∴SBOF=S△BOD=,△∵SBOE=|k|=3,△∴==,设EF=a,FG=b,则OE=2a,∴BE=,OG=3a+b,DG=,∵△BOE∽△DFG,∴=,∴=,∴a=b,a=﹣(舍去),∴D(4a,),∵B(2a,),∴==,∴GH=EG=2a,∵∠ODH=90°,DG⊥OH,∴△ODG∽△DHG,∴,∴,∴a=,∴3a=,∴F(,0)故答案为:,(,0).14.(2020•黄州区校级模拟)若方程x2+2(1+a)x+3a2+4ab+4b2+2=0有实根,则=﹣.【分析】由二次方程有实根,得到△≥0,即Δ=4(1+a)2﹣4(3a2+4ab+4b2+2)≥0,通过代数式变形可得两个非负数的和小于或等于0,从而得到a,b的方程组,解方程组即可求出它们的比.【解答】解:∵方程有实根,∴△≥0,即Δ=4(1+a)2﹣4(3a2+4ab+4b2+2)≥0,化简得:2a2+4ab+4b2﹣2a+1≤0,∴(a+2b)2+(a﹣1)2≤0,而(a+2b)2+(a﹣1)2≥0,∴a+2b=0,a﹣1=0,解得a=1,b=﹣,所以=﹣.故答案为﹣.15.(2022•成都自主招生)如图,面积为4的平行四边形ABCD中,AB=4,过点B作CD边的垂线,垂足为点E,点E正好是CD的中点,点M、点N分别是AB、AC.上的动点,MN的延长线交线段DE于点P,若点P是唯一使得∠MPB=45°的点,则线段BM长x的取值范围是x=2﹣2或<x≤.【分析】根据点P是唯一使得∠MPB=45°的点,可看成弦MB所对的圆周角∠MPB=45°,设△MBP外接圆的圆心为O,分三种情况画图,列出方程即可得结果.【解答】解:∵平行四边形ABCD的面积为4,AB=4,BE⊥CD,∴BE=1,∵点P是唯一使得∠MPB=45°的点,则可看成弦MB所对的圆周角∠MPB=45°,设△MBP外接圆的圆心为O,则∠MOB=90°,∴,∵CD与AB之间的距离为1,当⊙O经过点D时,即点P在点D处时,(x)2=(2﹣x)2+(1﹣x)2解得x=;当四边形PEBM是正方形时,圆与DE有两个交点,此时BM=BE=1;∴1<x≤;当△PMB 的外接圆经过D 时,算的x =,只有当x >时才成立,要让有且只有一个点,D 点应该在外接圆内.∴<x ≤4;当圆与DE 相切时,如图,x +x =1,解得x =2﹣2.综上所述:线段BM 长x 的取值范围是x =2﹣2或<x ≤4.但是由题意:“MN 的延长线交线段DE 于点P ,若点P 是唯一使得线段∠MPB =45°的点”,也就是说点P 只能在线段DE 上,如果x 大于了,那么P 点就在线段EC 上了,与题意不符,因此答案应该是:2倍根号2﹣2或者1<x ≤(x =时,P 与D 重合,P也在线段DE 上).故答案为:x =2﹣2或1<x ≤.16.(2022秋•长沙月考)已知a ,b ,c ,d ,x ,y ,z ,w 是互不相等的非零实数,且==,则的值为2.【分析】可设===,则====k ,即=,=,=k ,设==k 1,==k 2,由=k 可得k =,由+=得k1+k2=k,代入计算即可求解.【解答】解:设===,则====k,整理得+=+=+==k,∴=,=,=k,设==k1,==k2,由=k得k=,由+=得k1+k2=k,∴原式=2×+2×==2.故答案为:2.三.解答题(共9小题)17.解方程:(1);(2)|x2+4x﹣5|=2﹣2x.【分析】(1)设=t,则原方程可化为t2﹣t﹣6=0,再解整式方程得到当=3或当t==﹣2,然后分别解两个无方程;(2)利用绝对值的意义,当x2+4x﹣5≥0时,解得x≤﹣5或x≥1,则x2+4x ﹣5=2﹣2x;当x2+4x﹣5<0时,解得﹣5<x<1,则x2+4x﹣5=﹣(2﹣2x),然后分别解两个一元二次方程,最后进行检验确定原方程的解.【解答】解:(1)设=t,则原方程可化为t2﹣t﹣6=0,解得t1=3,t2=﹣2,当t=3时,=3,x2﹣3x+5=9,解得x1=4,x2=﹣1,当t=﹣2时,=﹣2,此方程无解所以经检验原方程的解为x1=4,x2=﹣1;(2)当x2+4x﹣5≥0时,x≤﹣5或x≥1,所以x2+4x﹣5=2﹣2x,整理得x2+6x﹣7=0,解得x1=1,x2=﹣7,当x2+4x﹣5<0时,﹣5<x<1,所以x2+4x﹣5=﹣(2﹣2x),整理得x2+2x﹣3=0,解得x1=1(舍去),x2=﹣3,综上所述,原方程的解为x1=1,x2=﹣7,x3=﹣3.18.(2022•镜湖区校级自主招生)对a>b>c>0,作二次方程x2﹣(a+b+c)x+ab+bc+ca=0.(1)若方程有实根,求证:a,b,c不能成为一个三角形的三条边长;(2)若方程有实根x0,求证:a>x0>b+c;(3)当方程有实根6,9时,求正整数a,b,c.【分析】(1)若一元二次方程有实根,则根的判别式Δ=b2﹣4ac≥0,建立a、b、c的关系,则能证明.(2)设f(x)=x2﹣(a+b+c)x+ab+bc+ca,由二次函数性质可证.(3)由根与系数关系可得a、b、c的关系,进而解得a、b、c的值.【解答】解:(1)由方程有实根得,Δ=(a+b+c)2﹣4(ab+bc+ca)≥0即0≤a2+b2+c2﹣2ab﹣2bc﹣2ca=a(a﹣b﹣c)﹣b(a+c﹣b)﹣c(a+b﹣c)<a(a﹣b﹣c),由a>0,得a﹣b﹣c>0,即a>b+c.所以,a,b,c不能成为一个三角形的三边.(4分)(2)设f(x)=x2﹣(a+b+c)x+ab+bc+ca,则f(b+c)=bc>0,f(a)=bc>0,且f()=<0由(1)知b+c<<a,所以二次方程的实根x0都在b+c与a之间,即a>x0>b+c.(7分)(3)由根与系数关系有a+b+c=15,ab+bc+ca=54,得a2+b2+c2=(a+b+c)2﹣2(ab+bc+ca)=225﹣108=117<112.由(2)知a>9,故得92<a2<112,∴a=10.∴b+c=5,bc=4,由b>c,解得b=4,c=1,∴a=10,b=4,c=1.(10分)19.(2022•相城区校级自主招生)阅读材料:对于正数a、b,有(﹣)2≥0,所以a+b﹣2≥0,即a+b≥2(当且仅当a=b时取“=”).特别地:a+≥2=2(当且仅当a=1时取“=”).因此,当a>0时,a+有最小值2,此时a=1.简单应用:(1)函数y=2﹣x﹣(x>0)的最大值为﹣2.(2)求函数y=9x+(x>1),当x=时,最小值为5.解决问题:(3)已知P(﹣2,3)是反比例函数y=图象上的点,Q是双曲线在第四象限这一分支上的动点,过点Q作直线,使其与双曲线y=只有一个公共点,且与x轴、y轴分别交于点A、B.另一直线y=x+6与x轴、y轴分别交于点C、D,求四边形ABCD面积的最小值.【分析】(1)求得x+≥4,进而求得结果;(2)变形y=9x+=9(x﹣1)++9,进一步求得结果;(3)设点A(a,0),B(0,b),求出AB的解析式和反比例函数的解析式,进而联立得出一元二次方程,由根的判别式为0,求得a,b的关系,进而表示出四边形ABCD的面积,进一步得出结果.【解答】解:(1)∵x+≥2=4,=2﹣4=﹣2,∴y最大故答案为:﹣2;(2)y=9x+=9(x﹣1)++9≥2+9=15,当9(x﹣1)=时,=15,即:当x=时,y最小故答案为:,15;(3)把x=﹣2,y=3代入y=得,3=,∴k=﹣6,∴y=﹣,设点A(a,0),B(0,b),(a>0,b<0),∴直线AB的解析式为:y=﹣x+b,由﹣=﹣+b得,bx2﹣abx﹣6a=0,∵直线AB与双曲线y=只有一个公共点,∴Δ=(ab)2+24ab=0,∴b=﹣,由y=+6得:D(0,6),C(﹣4,0),∴AC=a+4,BD=6﹣b=6+,∴SABCD===3(a+)+24≥3×2+24四边形=48,∴当a=,即:a=4时,四边形ABCD的面积最小值为:48.20.(2020•汉阳区校级自主招生)如图1,平面直角坐标系xOy中,A(﹣4,3),反比例函数y=(k<0)的图象分别交矩形ABOC的两边AC,BC于E,F (E,F不与A重合),沿着EF将矩形ABOC折叠使A,D重合.(1)①如图2,当点D恰好在矩形ABOC的对角线BC上时,求CE的长;②若折叠后点D落在矩形ABOC内(不包括边界),求线段CE长度的取值范围.(2)若折叠后,△ABD是等腰三角形,请直接写出此时点D的坐标.【分析】(1)①如图2中,连接AD交EF于H.想办法证明△AEF∽△ACB,推出EF∥BC,再利用平行线分线段成比例定理证明AE=EC=2即可.②如图3中,当点D落在OB上时,连接AD交EF于H.求出CE的长即可判断.(2)由△ABD是等腰三角形,F与B不重合,推出AB≠BD.分两种情形:①如图4中,当AD=BD时,②如图5中,当AD=AB时,分别求解即可.【解答】解:(1)①如图2中,连接AD交EF于H.∵四边形ABOC是矩形,A(﹣4,3),∴∠A=90°,OB=AC=4,AB=OC=3,∵E,F在y=时,∴可以假设E(,3),F(﹣4,),∴AE=4+,AF=3+,∴AE:AF=4:3,∵AC:BC=4:3,∴=,∵∠EAF=∠CAB,∴△EAF∽△CAB,∴∠AEF=∠ACB,∴EF∥BC,∵A,D关于EF对称,点D落在BC上,∴EF垂直平分线段AD,∴AH=DH,∵EF∥BC,∴=,∴AE=EC=2.②如图3中,当点D落在OB上时,连接AD交EF于H.∵∠EAF=∠ABD=90°,∠AEF=∠BAD,∴△AEF∽△BAD,∴=,则==,∴BD=AB÷=,设AF=x,则FB=3﹣x,FD=AF=x在Rt△BDF中,∵FB2+BD2=DF2,∴(3﹣x)2+()2=x2,解得x=,∴AF=,∴AE=AF=,∴EC=4﹣AE=4﹣=,∴<CE<4时,折叠后点D落在矩形ABOC内(不包括边界),线段CE长度的取值范围为:<CE<4.(2)∵△ABD是等腰三角形,F与B不重合,∴AB≠BD.①如图4中,当AD=BD时,∠BAD=∠ABD,由(1)可知∠BAD=∠AEF,∴∠ABD=∠AEF.作DM∥OB交AB于M,交OC于N.则DM⊥AB,MN=AC=4,∴∠BMD=∠EAF=90°,BM=AB=,∴△AEF∽△MBD,∴=,则==,∴MD=BM÷=,∴DN=MN﹣MD=4﹣=,∴D(﹣,).②如图5中,当AD=AB时,作DM∥OB交AB于M,交OC于N.则DM⊥AB,MN=AC=4,∴∠AMD=∠EAF=90°,由(1)可得∠BAD=∠AEF,∴△AEF∽△MAD,∴=,则==,设AM=4a,则MD=3a,在Rt△MAD中,∵AM2+DM2=AD2,∴(4a)2+(3a)2=32,∴a=,∴AM=,MD=,∴BM=AB=AM=3﹣=,DN=MN﹣MD=4﹣=,∴D(﹣,).综上所述,满足条件的点D的坐标为(﹣,)或(﹣,).21.(2020春•禹会区校级月考)当m为整数时,关于x的方程(2m﹣1)x2﹣(2m+1)x+1=0是否有有理根?如果有,求出m的值;如果没有,请说明理由.【分析】先计算出△并且设Δ=(2m+1)2﹣4(2m﹣1)=4m2﹣4m+5=(2m ﹣1)2+4=n2(n为整数),整系数方程有有理根的条件是△为完全平方数.解不定方程,讨论m的存在性.变形为(2m﹣1)2﹣n2=4,(2m﹣1﹣n)(2m ﹣1+n)=﹣4,利用m,n都为整数进行讨论即可.【解答】解:当m为整数时,关于x的方程(2m﹣1)x2﹣(2m+1)x+1=0没有有理根.理由如下:①当m为整数时,假设关于x的方程(2m﹣1)x2﹣(2m+1)x+1=0有有理根,则要Δ=b2﹣4ac为完全平方数,而Δ=(2m+1)2﹣4(2m﹣1)=4m2﹣4m+5=(2m﹣1)2+4,设Δ=n2(n为整数),即(2m﹣1)2+4=n2(n为整数),所以有(2m﹣1﹣n)(2m﹣1+n)=﹣4,∵2m﹣1与n的奇偶性相同,并且m、n都是整数,所以或,解得m=,②2m﹣1=0时,m=(不合题意舍去).所以当m为整数时,关于x的方程(2m﹣1)x2﹣(2m+1)x+1=0没有有理根.22.(2011•浙江校级自主招生)请你利用直角坐标平面上任意两点(x1,y1)、(x2,y2)间的距离公式解答下列问题:已知:反比例函数与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(﹣2,﹣2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1﹣PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).【分析】由和y=x组成的方程组可得A、B两点的坐标分别为(,)、(,),利用两点间的距离公式可求出线段AB的长度,由P为反比例函数y=上一点可得出x0与y0的关系式,利用两点间的距离公式可得出PF1、PF2的长,代入d=|PF1﹣PF2|即可得到x0的表达式,再根据x0的取值范围即可求出d的长,进而得出结论.【解答】解:解由和y=x组成的方程组可得A、B两点的坐标分别为,(,)、(,),线段AB的长度=4(2分)∵点P(x0,y0)是反比例函数图象上一点,∴y0=∴PF1===||,PF2===||,∴d=|PF1﹣PF2|=|||﹣|||,当x0>0时,d=4;当x0<0时,d=4.因此,无论点P的位置如何,线段AB的长度与d一定相等.由此可知:到两个定点的距离之差(取正值)是定值的点的集合(轨迹)是双曲线.23.(2023春•宜丰县校级月考)已知x=,y=,且19x2+123xy+19y2=1985.试求正整数n.【分析】首先化简x与y,可得:x=()2=2n+1﹣2,y =2n+1+2,所以x+y=4n+2,xy=1;将所得结果看作整体代入方程,化简即可求得.【解答】解:化简x与y得:x==2n+1﹣2,y==2n+1+2,∴x+y=4n+2,xy==[(+)(﹣)]2=1,∴将xy=1代入方程,化简得:x2+y2=98,∴(x+y)2=x2+y2+2xy=98+2×1=100,∴x+y=10.∴4n+2=10,解得n=2.24.(淳安县自主招生)如图正方形ABCD中,E为AD边上的中点,过A作AF⊥BE,交CD边于F,M是AD边上一点,且有BM=DM+CD.(1)求证:点F是CD边的中点;(2)求证:∠MBC=2∠ABE.【分析】(1)由正方形得到AD=DC=AB=BC,∠C=∠D=∠BAD=90°,AB∥CD,根据AF⊥BE,求出∠AEB=∠AFD,推出△BAE≌△ADF,即可证出点F是CD边的中点;(2)延长AD到G使BM=MG,得到DG=BC=DC,证△FDG≌△FCB,求出B,F,G共线,再证△ABE≌△CBF,得到∠ABE=∠CBF,根据三角形的外角性质即可求出结论.【解答】(1)证明:∵正方形ABCD,∴AD=DC=AB=BC,∠C=∠D=∠BAD=90°,AB∥CD,∵AF⊥BE,∴∠AOE=90°,∴∠EAF+∠AEB=90°,∠EAF+∠BAF=90°,∴∠AEB=∠BAF,∵AB∥CD,∴∠BAF=∠AFD,∴∠AEB=∠AFD,∵∠BAD=∠D,AB=AD,∴△BAE≌△ADF,∴AE=DF,∵E为AD边上的中点,∴点F是CD边的中点;(2)证明:延长AD到G.使MG=MB.连接FG,FB,∵BM=DM+CD,∴DG=DC=BC,∵∠GDF=∠C=90°,DF=CF,∴△FDG≌△FCB(SAS),∴∠DFG=∠CFB,∴B,F,G共线,∵E为AD边上的中点,点F是CD边的中点,AD=CD ∴AE=CF,∵AB=BC,∠C=∠BAD=90°,AE=CF,∴△ABE≌△CBF,∴∠ABE=∠CBF,∵AG∥BC,∴∠AGB=∠CBF=∠ABE,∴∠MBC=∠AMB=2∠AGB=2∠GBC=2∠ABE,∴∠MBC=2∠ABE.。

2013年全国高校自主招生数学模拟试卷三一、选择题(36分)1.函数254()2x x f x x-+=-在(,2)-∞上的最小值是 ( )A .0B .1C .2D .32.设[2,4)A =-,2{40}B x x ax =--≤,若B A ⊆,则实数a 的取值范围为 ( ) A .[1,2)- B .[1,2]- C .[0,3] D .[0,3)3.甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为23,乙在每局中获胜的概率为13,且各局胜负相互独立,则比赛停止时已打局数ξ的期望E ξ为 () A.24181 B. 26681 C. 27481D. 670243 4.若三个棱长均为整数(单位:cm )的正方体的表面积之和为564 cm 2,则这三个正方体的体积之和为 ( ) A. 764 cm 3或586 cm 3B. 764 cm 3C. 586 cm 3或564 cm 3D. 586 cm 35.方程组0,0,0x y z xyz z xy yz xz y ++=⎧⎪+=⎨⎪+++=⎩的有理数解(,,)x y z 的个数为 ( ) A. 1 B. 2 C. 3 D. 4 6.设ABC ∆的内角A B C ,,所对的边,,a b c 成等比数列,则sin cot cos sin cot cos A C AB C B++的取值范围是( )A. (0,)+∞B.C.D. )+∞二、填空题(54分,每小题9分)7.设()f x ax b =+,其中,a b 为实数,1()()f x f x =,1()(())n n f x f f x +=,1,2,3,n = ,若7()128381f x x =+,则a b += .8.设()cos 22(1cos )f x x a x =-+的最小值为12-,则a =.题15图9.将24个志愿者名额分配给3个学校,则每校至少有一个名额且各校名额互不相同的分配方法共有 种.10.设数列{}n a 的前n 项和n S 满足:1(1)n n n S a n n -+=+,1,2,n = ,则通项n a =.11.设()f x 是定义在R 上的函数,若(0)2008f = ,且对任意x ∈R ,满足 (2)()32x f x f x +-≤⋅,(6)()632x f x f x +-≥⋅,则)2008(f =.12.一个半径为1的小球在一个内壁棱长为则该小球永远不可能接触到的容器内壁的面积是. 12.一个半径为1的小球在一个内壁棱长为则该小球永远不可能接触到的容器内壁的面积是. 14.解不等式121086422log (3531)1log (1)x x x x x ++++<++.15.如题15图,P 是抛物线22y x =上的动点,点B C ,在y 轴上,圆22(1)1x y -+=内切于PBC ∆,求PBC ∆面积的最小值.2013年全国高校自主招生数学模拟试卷三参考答案1[解]当2x <时,20x ->,因此21(44)1()(2)22x x f x x x x +-+==+---2≥2=,当且仅当122x x=--时上式取等号.而此方程有解1(,2)x =∈-∞,因此()f x 在(,2)-∞上的最小值为2.[解法一] 因240x ax --=有两个实根12a x =22a x =故B A ⊆等价于12x ≥-且24x <,即22a -且42a , 解之得03a ≤<.[解法二](特殊值验证法)令3,[1,4],a B B A ==-⊄,排除C ,令171,]a B =-=,B A ⊄排除A 、B ,故选D 。


四川省绵阳市绵阳中学2013年自主招生数学试题一.选择题:(本大题共12个小题,每个4分,共48分,将所选答案填涂在机读卡上) 1、下列因式分解中,结果正确的是( )A.2322()x y y y x y -=-B.424(2)(x x x x -=+C.211(1)x x x x x--=--D.21(2)(1)(3)a a a --=--2、“已知二次函数2y ax bx c =++的图像如图所示,试判断a b c ++与 0的大小.”一同学是这样回答的:“由图像可知:当1x =时0y <, 所以0a b c ++<.”他这种说明问题的方式体现的数学思想方法叫 做( )A.换元法B.配方法C.数形结合法D.分类讨论法 3、已知实数x 满足22114x x x x ++-=,则1x x-的值是( )A.-2B.1C.-1或2D.-2或14、若直线21y x =-与反比例函数k y x =的图像交于点(2,)P a ,则反比例函数ky x=的图像还必过点( )A. (-1,6)B.(1,-6)C.(-2,-3)D.(2,12)5、现规定一种新的运算:“*”:*()m nm n m n -=+,那么51*22=( )A.54B.5C.3D.96、一副三角板,如图所示叠放在一起,则AOB COD ∠+∠=( )A.180°B.150°C.160°D.170°7、某中学对2005年、2006年、2007年该校住校人数统计时发现,2006年比2005年增加20%,2007年比2006年减少20%,那么2007年比2005年( )A.不增不减B.增加4%C.减少4%D.减少2%8、一半径为8的圆中,圆心角θ为锐角,且θ=,则角θ所对的弦长等于( )A.8B.10C. D.169、一支长为13cm 的金属筷子(粗细忽略不计),放入一个长、宽、高分别是4cm 、3cm 、16cm 的长方体水槽中,那么水槽至少要放进( )深的水才能完全淹没筷子。


第 1 页 共 4 页22018年高中自主招生考试数学模拟试题(满分:120 分时间:120 分钟)一、选择题。
(每小题 4 分,共 24 分)1. 若正方形的外接圆半径为 2,则其内切圆半径为( )A. B.2 C. 2 2D.1 2. 如图,在△ABC 中,AC ⊥BC ,∠ABC =30°,点 D 是 CB 延长线上的一点,且 BD =BA ,则tan ∠DAC 的值为( )A.2+B.2C.3+D.3 A MPONB第 2 题图第 3 题图第 5 题图3. 如图,正方形 ABCD 中,E 为 CD 的中点,EF ⊥AE ,交 BC 于点 F ,则∠1 与∠2 的大小关系 为 ( )A.∠1>∠2B.∠1<∠2C.∠1=∠2D.无法确定4. 若点 M (-7,m )、N (-8,n )都是函数 y =-(k 2+2k +4)x +1(k 为常数)的图象上,则 m 和n 的大小关系是( )A.m >nB.m <nC.m =nD.不能确定5. 如图,点 P 为定角∠AOB 的平分线上的一个定点,且∠MPN 与∠AOB 互补.若∠MPN 在绕点 P 旋转的过程中,其两边分别与 OA ,OB 相交于 M 、N 两点,则以下结论:(1)PM =PN 恒成立,(2)OM +ON 的值不变,(3)四边形 PMON 的面积不变,(4)MN 的长不变,其中正确的 个 数 为 ( )A.4B.3C.2D.16. 在平面直角坐标系内,直线 AB 垂直于 x 轴于点 C (点 C 在原点的右侧),并分别与直线 y =23333第 2 页 共 4 页2 3 2 x 和双曲线 y = 1x相交于点 A 、B ,且 AC +BC =4,则△OAB 的面积为()A.2 +3 或 2 -3B. +1 或 -1C.2 -3D. -1二、填空题。
(每小题 4 分,共 24 分)7. 一个人把四根绳子紧握在手中,仅在两端露出它们的头和尾,然后随机地把一端的四个头中的某两个相接,另两个相接,把另一端的四个尾中的某两个相接,另两个相接,则放开手后四根 绳子恰好连成一个圈的概率是.8. 有 4 张看上去无差别的卡片,上面分别写着 2,3,4,6,小红随机抽取 1 张后,放回并混在一起,再随机抽取 1 张,则小红第二次取出的数字能够整除第一次取出的数字的概率为.9. 如图,在直角三角形 ABC 中,AB =3,BC =4,∠ABC =90°,过 B 作 BA 1⊥AC ,过 A 1 作 A 1B 1⊥BC ,得阴影直角三角形 A 1B 1B ;再过 B 1 作 B 1A 2⊥AC ,过 A 2 作 A 2B 2⊥BC ,得阴影直角三角形 A 2B 2B 1;…,如此无限下去,请猜测这样得到的所有阴影三角形的面积之和为.AHDE GBFCQ第 9 题图 第 10 题图第 11 题图10. 如图,四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是 13,小正方形的面积是 1,直角三角形的两条直角边长分别为 a ,b ,则(a +b )2 的值是 .11. 如图,将矩形 ABCD 沿 GH 对折,点 C 落在 Q 处,点 D 落在 AB 边上的 E 处,EQ 与 BC相交于点 F .若 AD =8,AB =6,AE =4,则△EBF 周长的大小为 .12. 观察下列各式: 2 = 1 - 1 , 2 = 1 - 1 2 = 1 - 1 ……请利用你所得结论,化简 1⨯ 3 1 3 2 ⨯ 4 2 4 , 3 ⨯ 5 3 5 ,代 数 式 21⨯ 3+ 2 2 ⨯ 4 + 2 3 ⨯ 5 +…+ 2 n (n + 2) (n ≥3 且为整数),其结果为.三、解答题。

6.如图,点A 在函数=y x6-)0(<x 的图象上,过点A 作AE 垂直x 轴,垂足为E ,过点A 作AF 垂直y 轴,垂足为F ,则矩形AEOF 的面积是……( A.2 B.3C.6D.不能确定7.用大小和形状完全相同的小正方体木块搭成 一个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小 正方体木块的个数为………………( ) A.22个 B.19个C.16个D.13个8.用半径为cm 6、圆心角为︒120的扇形做成一个圆锥的侧面, 则这个圆锥的底面半径是……………………………………………………………………( ) A.2cm B.3cm C.4cm D.6cm 9.若n 为整数,则能使11-+n n 也为整数的n 的个数有 ……………………( ) A.1个 B.2个 C.3个 D.4个10.已知a 为实数,则代数式221227a a +-的最小值为………………( ) A.0 B.3 C.33 D.9 14.如图,正方形ABCD 的边长为4cm ,正方形AEFG 的边长为1cm .如果正方形AEFG 绕点A 旋转,那么C 、F 两点之间的最小距离为 cm .15.若规定:①{} m 表示大于m 的最小整数,例如:{}4 3 =,{}2 4.2-=-;②[] m 表示不大于m 的最大整数,例如:[]5 5 =,[]4 6.3-=-.则使等式{}[]4 2=-x x 成立的整数..=x . 16.如图,E 、F ABCD 的边AB 、CD 上 的点,AF 与DE 相交于点P ,BF 与CE 相交于 点Q ,若S △APD 15=2cm ,S △BQC 25=2cm , 则阴影部分的面积为 2cm . . (第6题图) (正视图) (俯视图) (第7题图)(第16题图)19.将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌面上. (1)从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率; (2)先从中随机抽取一张卡片(不放回...),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.20.为配合我市“创卫”工作,某中学选派部分学生到若干处公共场所参加义务劳动.若每处安排10人,则还剩15人;若每处安排14人,则有一处的人数不足14人,但不少于10人.求这所学校选派学生的人数和学生所参加义务劳动的公共场所个数.21.如图,四边形ABCD 是正方形,点N 是CD 的中点,M 是AD 边上不同于点A 、D 的点,若1010sin =∠ABM ,求证:MBC NMB ∠=∠.(第21题图)N22.如图,抛物线的顶点坐标是⎪⎭⎫ ⎝⎛8925,-,且经过点) 14 , 8 (A .(1)求该抛物线的解析式;(2)设该抛物线与y 轴相交于点B ,与x 轴相交于C 、D 两点(点C 在点D 的左边), 试求点B 、C 、D 的坐标;(3)设点P 是x 轴上的任意一点,分别连结AC 、BC . 试判断:PB PA +与BC AC +的大小关系,并说明理由.23.如图,AB 是⊙O 的直径,过点B 作⊙O 的切线BM ,点P 在右半圆上移动点P 与点A 、B 不重合),过点P 作PC ⊥AB ,垂足为C ;点Q 在射线BM 上移动(点M 在点B 的右边),且在移动过程中保持OQ ∥AP .(1)若PC 、QO 的延长线相交于点E ,判断是否存在点P ,使得点E 恰好在⊙O 上? 若存在,求出APC ∠的大小;若不存在,请说明理由; (2)连结AQ 交PC 于点F ,设PC PFk =,试问:k 的值是否随点P 的移动而变化?证明你的结论.(第22题图) Q ABC EFPO(第23题图).1、若匀速行驶的汽车速度提高40%,则行车时间可节省( )%(精确至1%) A 、6 0 B 、40 C 、 29 D 、252、如图,一个正方形被5条平行于一组对边的直线和3条平行于另一组对边的直线分成24个(形状不一定相同的)长方形,如果这24个长方形的周长的和为24,则原正方形的面积为( ).A 、1B 、9/4C 、4D 、36/25 3、已知:2)3(3322=+-+x x xx ,x 2+3x 为( ) A 、1 B 、-3和1 C 、3 D 、-1或34、四边形ABCD 的对角线AC 、BD 交于点O ,且S △AOB =4,S △COD =9,则四边形A B CD 面积有( )A 、最小值12B 、最大值12C 、.最小值25D 、最大值255、二个天平的盘中,形状相同的物体质尊相等,如图(1)图(2)所示的两个天平处于平街状态,要使第三个天平也保持平衡,则需在它的右盘中放置( )A 、 3个球B 、4个球C 、5个球D 、6个球 5、9人分24张票,每人至少1张,则( )A 、至少有3人票数相等B 、至少有4人票数无异C 、不会有5人票数一致D 、不会有6人票数同样2、半径为10的圆0内有一点P ,OP=8,过点P 所有的弦中长是整数的弦有 条。

绝密☆启用前试卷类型:A2013年枣庄市实验中学自主招生考试数 学 试 题 2013.5注意事项:1.本试卷共6页,满分100分,考试用时90分钟。
考试结束时,将本试卷一并交回。
2.答题前,考生务必将自己的姓名、准考证号等信息写在试卷密封线内。
3.必须用黑色签字笔或蓝黑色钢笔作答(作图除外),答案必须写在答题纸各题目指定区域相应的位置,不按要求作答的答案无效。
第Ⅰ卷 选择题(共30分)一、选择题:本大题共10小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一 个均计零分. 1.在实数π,2,0,3.14,2-,tan45°,3.1415926,71,1.010010001……(每两个1之 间0的个数依次加1)中,无理数的个数是 ( )A . 2个 B. 3个 C. 4个 D. 5个2.某品牌商品,按标价九折出售,仍可获得20%的利润.若该商品标价为28元,则商品的进价为( )A .21元B .19.8元C . 22.4元D . 25.2元 3.已知a >b ,c ≠0,则下列关系一定成立的是( )A .c +a >c +bB .a bc c> C .c -a >c -b D . ac >bc4.在围棋盒中有x 颗白色棋子和y 颗黑色棋子,从盒中随机取出一颗棋子,取得白色棋子的概率是2 5 .如果再往盒中放进6颗黑色棋子,取得白色棋子的概率是14 ,则原来盒中有黑色棋子( )A .8颗B .6颗C .4颗D .2颗5.已知一个菱形的周长是20cm ,两条对角线的比是4∶3,则这个菱形的面积是A .12cm 2B .96cm 2C .48cm 2D .24cm 26.函数1ky x-=的图象与直线y x =没有交点,那么k 的取值范围是( ) A .1k > B .1k < C .1k >- D .1k <-区市 学校 姓名 准考证号 ——————密————————————————封——————————————————线——————————7.函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是( )8.如图,矩形纸片ABCD 中,已知AD=8,折叠纸片使AB 边与对角线AC 重合,点B 落在点F 处,折痕为AE ,且EF=3,则AB 的长为( ) A .3 B .4 C .5 D .69.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm 2,则该半圆的半径为( ) A. (45)+ cm B. 9 cm C. 45cm D. 62cm(第9题图)10.如图,AB 是O ⊙的直径,O ⊙交BC 的中点于D ,DE AC ⊥于E ,连接AD ,则下列结论正确的个数是( ) AD BC ⊥① EDA B ∠=∠② 12OA AC =③ ④DE 是O ⊙的切线 A .1个 B .2个 C .3个 D .4个(第8题图) F ED C BA CDBAE O(第10题图)第Ⅱ卷 非选择题 (共70分)二、填空题:本大题共7小题,满分21分.只要求填写最后结果,每题填对得3分. 11.平面上一点P 到⊙O 上一点的距离最长6cm ,最短为2cm ,则⊙O 的半径为 _____ 12.已知关于x 的不等式组0521x a x -⎧⎨->⎩≥,只有四个整数解,则a 的取值范围是13.右图是一个食品包装盒的侧面展开图,根据图中所标的尺寸,求这个多面体的全面积(侧面积与两个底面体之和)_____14.已知等腰△ABC 中,AD 是BC 边上的高,点D 是垂足,且AD=21BC , 则△ABC 底角的度数为_____。

2013华师一附中自主招生考试数学模拟试卷(二)本卷满分150分 考试时间90分钟一、选择题(每题5分,共30分)1.如图,边长为1的菱形ABCD 绕点A 旋转,当B 、C 两点恰好 落在扇形AEF 的弧EF 上时,弧BC 的长度等于( )A .6π B.4π C.3π D.2π 2.二次函数的图象如何移动就得到的图象( )A .向左移动1个单位,向上移动3个单位. B. 向左移动1个单位,向下移动3个单位. C. 向右移动1个单位,向上移动3个单位. D. 向右移动1个单位,向下移动3个单位.3.已知a 、b 、c 为正实数,且满足b +c a=a +b c =a +cb =k ,则一次函数y kx k =+A .第一、二、三象限B .第一、二、四象限C .第一、三、四象限D. 第二、三、四象限4.某学校要召开学生代表大会,规定各班每10人推选一名代表,当各班人数除以10的余数大于7时再增选一名代表.那么,各班可推选代表人数y 与该班人数x 之间的函数关系用取整函数y =[x ]([x ]表示不大于x 的最大整数)可以表示为( ) A .y =[110x +] B. y =[210x +] C. y =[310x +] D. y =[410x +] 5.正实数,x y 满足1xy =,那么44119x y +的最小值为() A .23B.54C.1 6.如图,点P 为弦AB 上一点,连结OP ,过P 作,PC 交于点C ,若AP=4,PB=2,则PC 的长为()A .2 B. 3D.二、填空题(本大题共6个小题,每小题7分,共42分)7. 二次函数y =a x 2+(a -b )x —b 的图象如图所示,那么化简的结果是______________.8.随机掷三枚硬币,落地后恰有两枚正面朝上的概率是 .9.设x1、x 2 是一元二次方程x 2+4x -3=0的两个根,2x 1(2x 22+5x 2-6)+a =2,则a =.10.已知三角形的三边a 、b 、c 都是整数,且满足abc+bc+ca+ab+a+b+c=7,则此三角形的面积等于. 11.已知方程在实数范围内恒有解,并且恰有一个解大于1小于2,则的取值范围是.12.如图,AB 是半圆O 的直径,四边形CDMN 和DEFG 都是正方形,其中C,D,E 在1422++-=x x y 22x y -=PC OP ⊥O ||b a()0332=+-+x a x aAB 上,F,N 在半圆上.若AB=10,则正方形CDMN 的面积与正方形DEFG 的面积之和是. 三、解答题:(本大题共6小题,计78分,写出必要的推算或演算步骤.) 13.(12分)已知二次函数222(1)22y x m x m =--+-(1)证明:不论m 为何值,二次函数图象的顶点均在某一函数图象上,并求出此图象的函数解析式; (2)若二次函数图象在x轴上截得的线段长为14.(10分)如图所示,△ABC 中AB=2,∠A=∠BCD=45°,求BC 的长及△BDC 的面积。
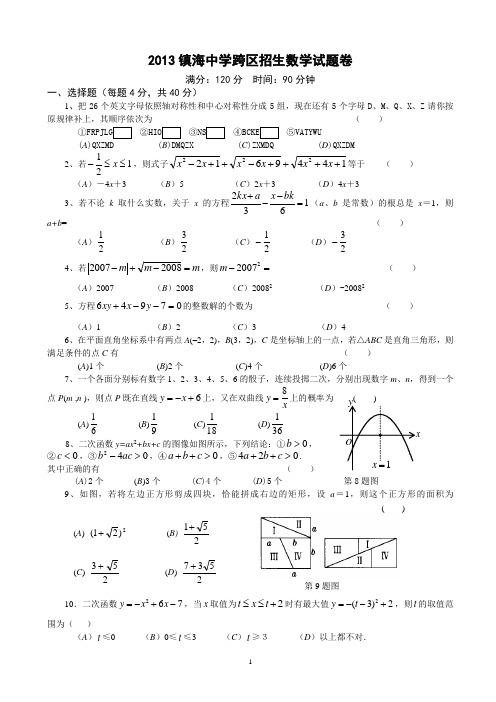
2013镇海中学跨区招生数学试题卷满分:120分 时间:90分钟一、选择题(每题4分,共40分)1、把26个英文字母依照轴对称性和中心对称性分成5组,现在还有5个字母D 、M 、Q 、X 、Z 请你按原规律补上,其顺序依次为 -------------------------------------------------------------------( )⑤VATYWU (A )QXZMD (B )DMQZX (C )ZXMDQ (D )QXZDM2、若121≤≤-x ,则式子1449612222++++-++-x x x x x x 等于------( ) (A )-4x +3(B )5(C )2x +3(D )4x +33、若不论k 取什么实数,关于x 的方程1632=--+bkx a kx (a 、b 是常数)的根总是x =1,则a+b =---------------------------------------------------------------------------------------------------------( )(A )21(B )23 (C )21-(D )23- 4、若m m m =-+-20082007,则=-22007m ---------------------------------------( ) (A )2007 (B )2008 (C )20082 (D )-200825、方程07946=--+y x xy 的整数解的个数为 -------------------------------------------( ) (A )1 (B )2 (C )3 (D )46、在平面直角坐标系中有两点A (–2,2),B (3,2),C 是坐标轴上的一点,若△ABC 是直角三角形,则满足条件的点C 有----------------------------------------------------------------------------( )(A )1个 (B )2个 (C )4个 (D )6个7、一个各面分别标有数字1、2、3、4、5、6的骰子,连续投掷二次,分别出现数字m 、n ,得到一个点P (m ,n ),则点P 既在直线6+-=x y 上,又在双曲线xy 8=上的概率为------ ( ) (A )61 (B )91 (C )181 (D )3618、二次函数y=ax 2+bx+c 的图像如图所示,下列结论:①0>b ,②0<c ,③042>-ac b ,④0>++c b a ,⑤024>++c b a .其中正确的有---------------------------------------------------------------( )(A )2个 (B )3个 (C )4个 (D )5个 第8题图9、如图,若将左边正方形剪成四块,恰能拼成右边的矩形,设a =1,则这个正方形的面积为------------------------------------------------------------------------------------------------------------------ ( )(A ) 2)21(+ (B)251+ (C )253+ (D ) 2537+10.二次函数267y x x =-+-,当x 取值为2t x t ≤≤+时有最大值2(3)2y t =--+,则t 的取值范围为( )(A )t ≤0 (B )0≤t ≤3 (C )t ≥3 (D )以上都不对.第9题图二、填空题(每题 6分,共30分)11、已知关于x 的不等式mx -2≤0的负整数解只有-1,-2,则m 的取值范围是 _____ . 12、用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面.已知正 多边形的边数为x 、y 、z ,则zy x 111++的值为_______________. 13、如图,△OAP 、△ABQ 是等腰直角三角形,点P 、Q 在双曲线)0(4>=x y 上,直角顶点A 、B 均在x 轴上,则点Q 的坐标为_______________.第11题图 14、若关于x 、y 的方程组⎩⎨⎧=+=+222111c y b x a c y b x a 的解为⎩⎨⎧==65y x ,则方程组⎩⎨⎧=+=+222111435435c y b x a c y b x a 的解为____________.15、如图,墙角处有若干大小相同的小正方体堆成如图所示的立体图形,如果你搬走其中部分小正方体,但希望搬完后从正面、从上面、从右面用平行光线照射时,在墙面及地面上的影子不变,那么你最多可以搬走 __ ____ 个小正方体.三、解答题(共50分)16、(本题满分6分)如图,ABCD 是矩形纸片,E 是AB 上一点,且BE :EA =5:3,EC =155,把△BCE 沿折痕EC 向上翻折,若点B 恰好落在AD 边上,设这个点为F ,求AB 、BC 的长.17、(本题满分8分) 如图,已知四边形ABCD 内接于一圆,AB =BD ,BM ⊥AC 于M ,求证:AM =DC +CM(图1)(图2)OM N QPHK FEDCBAyx18、(本题满分13分)某种电缆在空中架设时,两端挂起的电缆下垂都近似成抛物线21001x y =的形状,现按操作要求,电缆最低点离水平地面不得小于6米.⑴ 如图1,若水平距离间隔80米建造一个电缆塔柱,求此电缆塔柱用于固定电缆的位置离地面至少应有多少米的高度?⑵ 如图2,若在一个坡度为1:5的斜坡上,按水平距离间隔50米架设两固定电缆的位置离地面高度为20米的塔柱。

[选取日期]2013年全国高校自主招生数学模拟试卷一一、选择题(本题满分36分,每小题6分)1. 如图,在正四棱锥P −ABCD 中,∠APC =60°,则二面角A −PB −C 的平面角的余弦值为( ) A.71 B. 71-C.21 D. 21-2. 设实数a 使得不等式|2x −a |+|3x −2a |≥a 2对任意实数x 恒成立,则满足条件的a 所组成的集合是( ) A. ]31,31[-B. ]21,21[-C. ]31,41[- D. [−3,3]3. 将号码分别为1、2、…、9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同。
甲从袋中摸出一个球,其号码为a ,放回后,乙从此袋中再摸出一个球,其号码为b 。
则使不等式a −2b +10>0成立的事件发生的概率等于( ) A.8152 B.8159 C.8160 D.8161 4. 设函数f (x )=3sin x +2cos x +1。
若实数a 、b 、c 使得af (x )+bf (x −c )=1对任意实数x 恒成立,则acb cos 的值等于( ) A. 21-B.21 C. −1 D. 15. 设圆O 1和圆O 2是两个定圆,动圆P 与这两个定圆都相切,则圆P 的圆心轨迹不可能是( )6. 已知A 与B 是集合{1,2,3,…,100}的两个子集,满足:A 与B 的元素个数相同,且为A ∩B 空集。
若n ∈A 时总有2n +2∈B ,则集合A ∪B 的元素个数最多为( ) A. 62 B. 66 C. 68 D. 74二、填空题(本题满分54分,每小题9分)7. 在平面直角坐标系内,有四个定点A (−3,0),B (1,−1),C (0,3),D (−1,3)及一个动点P ,则|PA |+|PB |+|PC |+|PD |的最小值为__________。
8. 在△ABC 和△AEF 中,B 是EF 的中点,AB =EF =1,BC =6,33=CA ,若2=⋅+⋅,则与的夹角的余弦值等于________。


2012年重点中学自主招生模拟试题(试题卷)时间:90分钟 满分:120分 一、选择题(每小题4分,共40分)1.如果关于x 的方程2230x ax a -+-=至少有一个正根,则实数a 的取值范围是( )A 、22<<-aB 、23≤<aC 、23≤<-a D 、23≤≤-a2.如图,在△ABC 中,︒=∠∠=∠90,21DAC B C,AB=5.1cm,BC=12cm,则BD 的长为( )A .1.2B .1.6C . 1.8D .23.一组互不相等的数据,它的中位数为80,小于中位数的数的平均数为70,大于中位数的数的平均数为96,设这组数据的平均数为x ,则x =( )。
A .82B .83C .80≤x ≤82D .82≤x <834.如图,在直角三角形ABC 中(∠C=900),放置边长分别3,4,x 的三个正方形,则x 的值为( ) A. 5 B. 6 C. 7 D. 125.若)如331155,(==nn a a ,1x >,0y >,且满足3y yx xy x xy==,,则x y +的值为( ) A .1 B .2 C .92D .1126. 已知二次函数2y ax bx c =++(,,a b c 均为实数且0a ≠)满足条件:对任意实数x 都有2y x ≥;且当02x <<时,总有21(1)2y x ≤+成立,则a b c ++的值为( )A .1B .2C .1.5D .2.57.图1是用钢丝制作的一个几何探究工具,其中△ABC 内接于⊙G ,AB 是⊙G 的直径,AB=6,AC=2.现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A 在射线OX 上由点O 开始向右滑动,点B 在射线OY 上也随之向点O 滑动(如图3),当点B 滑动至与点O 重合时运动结束. 在整个运动过程中,点C 运动的路程是( )A .4B .6C .4 2 -2D .10-4 28.如图所示,在ABC ∆中,AC AB =,N M 、分别是AC AB 、的中点,E D 、为BC 上的点,连接EM DN 、,若cm DE cm BC cm AB 8,16,10===,则图中阴影部分的面积为( )A. 42cmB. 62cmC. 82cmD. 122cm9.数x a y =与a x y +=的图像恰有两个公共点,则实数a 的取值范围是( ) A .a >1 B .-1<a <1 C .a ≥1或a ≤-1 D .a >1或a <-1 10.将四个编号为2,3,4,5的小球随机放入4个编号为1,2,3,4的盒子中。

2013年北约自主招生数学试题与答案2013-03-16(时间90分钟,满分120分)(1(7)(232(630g a b c d e a b c d a b c =-+----+++++702320a b c d e a b c d +---=⎧⇒⎨+++=⎩即方程组:420(1)20(2)70(3)2320(4)630(5)a c e b d a b c d e a b c d a b c ++=⎧⎪+=⎪⎪+---=⎨⎪+++=⎪++=⎪⎩,有非0有理数解.由(1)+(3)得:110a b c d ++-= (6) 由(6)+(2)得:1130a b c ++= (7) 由(6)+(4)得:13430a b c ++= (8) 由(7)-(5)得:0a =,代入(7)、(8)得:0b c ==,代入(1)、(2)知:0d e ==.于是知0a b c d e =====,与,,,,abcd e不全为0矛盾.所以不存在一个次数不超过4的有理系数多项式()g x和11为两根的有理系数多项式的次数最小为5.2.在66⨯的表中停放3辆完全相同的红色车和3辆完全相同的黑色车,每一行每一列只有一辆车,每辆车占一格,共有几种停放方法?A. 720B. 20C. 518400D. 14400解析:先从6行中选取3行停放红色车,有36C 种选择.最上面一行的红色车位置有6种选择;最上面一行的红色车位置选定后,中间一行的红色车位置有5种选择;上面两行的红色车位置选定后,最下面一行的红色车位置有4种选择。
三辆红色车的位置选定后,黑色车的位置有3!=6种选择。
所以共有36654614400C ⨯⨯⨯⨯=种停放汽车的方法. 3.已知2225,25x y y x =+=+,求32232x x y y -+的值. A. 10 B. 12 C. 14 D. 16 解析:根据条件知:32232(25)2(25)(25)(25)x x y y x y y x y x -+=+-++++1515450x y xy =---由2225,25x y y x =+=+两式相减得()()22x y x y y x -+=-故y x =或2x y +=-①若x y =则225x x =+,解得1x =±于是知1x y ==+1x y ==当1x y ==+3223222415()50430504(25)3870x x y y xy x y x x x x x -+=-++-=---=-----3870108x =--=--.当1x y ==-3223222415()50430504(25)3870x x y y xy x y x x x x -+=--+-=---=-+---22(25)(25)2()2x y y x y x x y +=+-+=-⇒+=-3870108x =--=-+.(2)若x y ≠,则根据条件知:22(25)(25)2()2x y y x y x x y +=+-+=-⇒+=-,于是22(25)(25)2()106x y y x x y +=+-+=++=,进而知222()()12x y x y xy +-+==-. 于是知:32232415()5016x x y y xy x y -+=-+-=-.综上所述知,32232x x y y -+的值为108-±或16-.4.数列{}n a 满足11a =,前n 项和为1,42n n n S S a +=+,求2013a . A. 3019⨯22012B. 3019⨯22013C. 3018⨯22012D.无法确定解析:根据条件知:1221221424244n n n n n n n n n a S a S a a a a a ++++++++==+=++⇒=-.又根据条件知:1212121,425a S a a a a ==+=+⇒=.所以数列{}1221:1,5,44n n n n a a a a a a ++===-.又212114422(2)n n n n n n n a a a a a a a +++++=-⇔-=-.令12n n n b a a +=-, 则11212,23n n b b b a a +==-=,所以132n n b -=⋅.即11232n n n a a -+-=⋅.对11232n n n a a -+-=⋅,两边同除以12n +,有113224n n n n a a ++-=,即113224n n n n a a ++=+.令2n nn a c =,则134n n c c +=+,11122a c ==,于是知1331(1)244n n c n -=+-=.所以231,2(31)24nn n n a n --==-⋅.于是知:201120122013(320131)230192a =⨯-⋅=⋅.5.如图,ABC ∆中,AD 为BC 边上中线,,DM DN 分别,ADB ADC ∠∠的角平分线,试比较BM CN +与MN 的大小关系,并说明理由. A. BM+CN>MNB. MN +CN <MNC. BM+CN =MND.无法确定解析:如图,延长ND 到E ,使得DE DN =,连接BE ME 、.易知BDE CDN ∆≅∆,所以CN BE =.又因为,DM DN 分别为,ADB ADC ∠∠的角平分线,所以90MDN ∠=︒,知MD 为线段EN 的垂直平分线,所以MN ME =.所以B M C N B M B E +=+>=.6.模长为1的复数A B C 、、,满足0A B C ++≠,求AB BC CAA B C++++的模长.A. -1/2B. 1C. 2D.无法确定解析:根据公式z =1,1,1A A B B C C ⋅=⋅=⋅=.于是知:AB BC CAA B C ++=++=1==.所以AB BC CAA B C++++的模长为1.7.最多能取多少个两两不等的正整数,使得其中任意三个数之和都为素数. 解析:所有正整数按取模3可分为三类:3k 型、31k +型、32k +型.首先,我们可以证明,所取的数最多只能取到两类.否则,若三类数都有取到,设所取3k 型数为3a ,31k +型数为31b +,32k +型数为32c +,则3(31)(32)3(1)a b c a b c ++++=+++,不可能为素数.所以三类数中,最多能取到两类.其次,我们容易知道,每类数最多只能取两个.否则,若某一类3(012)k r r +=、、型的数至少取到三个,设其中三个分别为333a r b r c r +++、、,则(3)(3)(3)3()a r b r c r a b c r +++++=+++,不可能为素数.所以每类数最多只能取两个.结合上述两条,我们知道最多只能取224⨯=个数,才有可能满足题设条件. 另一方面,设所取的四个数为1、7、5、11,即满足题设条件. 综上所述,若要满足题设条件,最多能取四个两两不同的正整数.8.已知1232a a a a R ∈ 、、、、,满足12320130a a a a ++++= ,且122334201220132013122222a a a a a a a aa a -=-=-==-=- ,求证:12320130a a a a ===== .解析:根据条件知:122334************(2)(2)(2)(2)()0a a a a a a a a a a a a -+-+-++-=-++++= ,(1)另一方面,令12233421312222a a a a a a a a m -=-=-==-= ,则1223342222a a a a a a a a ---- 、、、、中每个数或为m ,或为m -.设其中有k 个m ,(2013)k -个m -,则:12233420131(2)(2)(2)(2)(2013)()(22013)a a a a a a a a k m k m k m-+-+-++-=⨯+-⨯-=- (2)由(1)、(2)知:(22013)0k m -= (3)而22013k -为奇数,不可能为0,所以0m =.于是知:12233420122013201312,2,2,,2,2a a a a a a a a a a ===== .从而知:2013112a a =⋅,即得10a =.同理可知:2320130a a a ==== .命题得证.9.对任意的θ,求632cos cos66cos 415cos 2θθθθ---的值. 解析:根据二倍角和三倍角公式知:632cos cos66cos 415cos 2θθθθ---622232cos (2cos 31)6(2cos 21)15(2cos 1)θθθθ=------63222232cos 2(4cos 3cos )162(2cos 1)115(2cos 1)θθθθθ⎡⎤⎡⎤=--------⎣⎦⎣⎦664242232cos (32cos 48cos 18cos 1)(48cos 48cos 6)(30cos 15)θθθθθθθ=--+---+--10=.10.已知有mn 个实数,排列成m n ⨯阶数阵,记作{}mxnija ,使得数阵中的每一行从左到右都是递增的,即对任意的123i m = 、、、、,当12j j <时,都有12ij ij a a ≤.现将{}mxnija 的每一列原有的各数按照从上到下递增的顺序排列,形成一个新的m n ⨯阶数阵,记作{}mxnija ',即对任意的123j n = 、、、、,当12i i <时,都有12i j i j a a ''≤.试判断{}mxnija '中每一行的n 个数的大小关系,并说明理由.解析:数阵{}mxnija '中每一行的n 个数从左到右都是递增的,理由如下:显然,我们要证数阵{}mxnija '中每一行的n 个数从左到右都是递增的,我们只需证明,对于任意123i m = 、、、、,都有(1)iji j a a +''≤,其中1231j n =- 、、、、. 若存在一组(1p qp qa a +''>.令(1)(1)k k q i q a a ++'=,其中123k m = 、、、、,{}{}123,,,,1,2,3,,m i i i i m = .则当t p ≤时,都有(1)(1)(1)tti q i q t q p q pq a a a a a +++'''≤=≤<.也即在(123iq a i = 、、、、m)中,至少有p 个数小于pq a ',也即pq a '在数阵{}mxnij a '的第q 列中,至少排在第1p +行,与pq a '排在第p 行矛盾.所以对于任意123i m = 、、、、,都有(1)iji j a a +''≤,即数阵{}mxnij a '中每一行的n 个数从左到右都是递增的.。



2013年重点中学自主招生数学模拟试题一答题时注意:1试卷满分150分;考试时间:120分钟.2、试卷共三大题,计 16道题。
考试结束后,将本卷及演算的草稿纸一并上交。
一、选择题(共5小题,每题6分,共30分.以下每小题均给出了代号为 A,B,C,D 的四个选项,其中有且只有一个选项是正确的.请将正确选项的代号填入题后 的括号内•不填、多填或错填均不得分)2 21、如果关于x 的方程x -ax a -3=0至少有一个正根,贝U 实数a 的取值范围是( )A 、 - 2 ■: a 2B 、3 ■- a — 2 C > - ■. 3 ■■■ a —2 D 、 3 — a — 22、如图,已知:点 交CE 于点G 、H E 、F 分别是正方形 ,若正方形ABCDABCD 的边AB 、BC 的中点,BD 、DF 分别 的面积是240,则四边形BFHG 的面积等 于 ................ ( ) A 、 26 B 、 28 C 、24D 、303、设x 、y 、z 是两两不等的实数,且满足下列等式:6.x 3(y -x)3 - 6. x 3(z -x)3 =6 y - x - Q .x -z ,则代数式 x 3 y 3 z 3-3xyz 的值是 ............................. ()C 、3D 、条件不足,无法计算4、如图,四边形 BDCE 内接于以BC 为直径的O A ,已知:3BC =10,cos BCD , BCE =30,则线段 DE 的长5是 ................ ( )A 、89 B 、7 - 3 C 、4+3 .3D 、3+4、35、某学校共有3125名学生,一次活动中全体学生被排成 一个n排的等腰梯形阵,且这 n 排学生数按每排都比前一排 多一人的规律排列,则当n 取到最大值时,排在这等腰梯形阵最外面的一周的学生总人数是 ................ ( ) A 、296B 、221C 、225D 、641二、填空题:(共5小题,每题6分,共30分)6、已知:实常数 a 、b 、c 、d 同时满足下列两个等式:⑴ a sinv - bcosv - c = 0 ; ⑵a cos bsinv d =0 (其中'为任意锐角),则a 、b 、c 、d 之间的关系式是:7、函数 y = x —1 +2x —2 +3x —3+4x —4 的最小值是 ___________________________ 8已知一个三角形的周长和面积分别是84、210,一个单位圆在它的内部沿着三边匀速无摩擦地滚动一周后回到原来的位置(如图),则这个三角形的内部以及边界没有被单位圆滚过的部分的面积是 ____________________________________ 。

2013年高中自主招生数学模拟试卷(一)参考答案与试题解析一、选择题(本大题共有10小题,每小题4分,单项选择)(.=是最简二次根式,错误.2.(4分)如图,点A在数轴上表示的实数为a,则|a﹣2|等于()3.(4分)甲、乙两名运动员在10次的百米跑练习中,平均成绩分别为=10.7秒,=10.7秒,方差分别为S甲2=0.054,S乙2=0.103,那么在这次百米跑练习中,甲、乙两名运动员成绩较为稳定的4.(4分)如图,A,B,C,D是直线L上顺次四点,M,N分别是AB,CD的中点,且MN=6cm,BC=1cm,则AD的长等于()(6.(4分)如图,点A在函数(x<0)的图象上,过点A作AE垂直X轴,垂足为E,过点A作AF垂直y轴,垂足为F,则矩形AEOF的面积是()中7.(4分)用大小和形状完全相同的小正方体木块搭成一个几何体,使得它的正视图和俯视图如图所示,则搭成这样的一个几何体至少需要小正方体木块的个数为()r=9.(4分)若n为整数,则能使也为整数的n的个数有()=1+10.(4分)已知a为实数,则代数式的最小值为()的值最小,为二、填空题(本大题共有6小题,每小题4分,共24分.请将正确的答案直接填写在答题卷中相应的横线上)11.(4分)函数中,自变量x的取值范围是x≥﹣2且x≠1.解:根据题意得:12.(4分)分解因式:﹣3x3y+27xy=﹣3xy(x+3)(x﹣3).13.(4分)把2007个边长为1的正方形排成如图所示的图形,则这个图形的周长是4016.14.(4分)如图,正方形ABCD的边长为4cm,正方形AEFG的边长为1cm.如果正方形AEFG 绕点A旋转,那么C、F两点之间的最小距离为3cm.﹣=315.(4分)若规定:①{m}表示大于m的最小整数,例如:{3}=4,{﹣2.4}=﹣2;②[m]表示不大于m的最大整数,例如:[5]=5,[﹣3.6]=﹣4,则使等式2{x}﹣[x]=4成立的整数x=2.16.(4分)如图,E、F分别是平行四边形ABCD的边AB、CD上的点,AF与DE相交于点P,BF 与CE相交于点Q,若S△APD=15cm2,S△BQC=25cm2,则阴影部分的面积为40cm2.三、解答题(本大题共有7小题,共86分.其中第17题8分,第18、19题各10分,第20题12分,第21题14分,第22、23题各16分.请将解答过程写在答题卷的相应位置上)17.(8分)计算:.|×﹣(﹣18.(10分)先化简,再求值:÷,其中.19.(12分)(2007•兰州)将背面相同,正面分别标有数字1,2,3,4的四张卡片洗匀后,背面朝上放在桌面上.(1)从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率;(2)先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.==20.(12分)为配合我市“创卫”工作,某中学选派部分学生到若干处公共场所参加义务劳动.若每处安排10人,则还剩15人;若每处安排14人,则有一处的人数不足14人,但不少于10人.求这所学校选派学生的人数和学生所参加义务劳动的公共场所个数.依题意得:321.(14分)如图,四边形ABCD是正方形,点N是CD的中点,M是AD边上不同于点A、D的点,若sin∠ABM=,求证:∠NMB=∠MBC.,由,所以,中,,22.(14分)如图,抛物线的顶点坐标是,且经过点A(8,14).(1)求该抛物线的解析式;(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;(3)设点P是x轴上的任意一点,分别连接AC、BC.试判断:PA+PB与AC+BC的大小关系,并说明理由.﹣﹣﹣,()(或得﹣23.(16分)如图,AB是⊙O的直径,过点B作⊙O的切线BM,点P在右半圆上移动(点P与点A,B不重合),过点P作PC⊥AB,垂足为C;点Q在射线BM上移动(点M在点B的右边),且在移动过程中保持OQ∥AP.(1)若PC,QO的延长线相交于点E,判断是否存在点P,使得点E恰好在⊙O上?若存在,求出∠APC的大小;若不存在,请说明理由;(2)连接AQ交PC于点F,设,试问:k的值是否随点P的移动而变化?证明你的结论.中,由正弦的概念知得到,可知,则,所以有====,.。
F
2013年重点中学自主招生数学模拟试题一
答题时注意:
1、试卷满分150分;考试时间:120分钟.
2、试卷共三大题,计16道题。
考试结束后,将本卷及演算的草稿纸一并上交。
一、选择题(共5小题,每题6分,共30分.以下每小题均给出了代号为A,B,C,D的四个选项,其中有且只有一个选项是正确的.请将正确选项的代号填入题后的括号内.不填、多填或错填均不得分)
1、如果关于x的方程2230
x ax a
-+-=至少有一个正根,则实数a的取值范围是()
A、2
2<
<
-a B、2
3≤
<a C、2
3≤
<
-a D、2
3≤
≤
-a
2、如图,已知:点E、F分别是正方形ABCD的边BC
AB、的中点,DF
BD、分别交CE于点H
G、,若正方形ABCD的面积是240,则四边形BFHG的面积等于……………………()A、26 B、28
第2题第4题第8题
3、设z
y
x、
、是两两不等的实数,且满足下列等式:6
6
63
3
63
3)
(
)
(z
x
x
y
x
z
x
x
y
x-
-
-
=
-
+
-,则代数式xyz
z
y
x3
3
3
3-
+
+的值是…………………()
A、0
B、1
C、3
D、条件不足,无法计算
4、如图,四边形BDCE内接于以BC为直径的⊙A,已知:︒
=
∠
=
∠
=30
,
5
3
cos
,
10BCE
BCD
BC,则线段DE的长是…………………()
A、89
B、73
C、4+33
D、3+43
5、某学校共有3125名学生,一次活动中全体学生被排成一个n排的等腰梯形阵,且这n排学生数按每排都比前一排多一人的规律排列,则当n取到最大值时,排在这等腰梯形阵最外面的一周的学生总人数是…………………()
A、296
B、221
C、225
D、641
二、填空题:(共5小题,每题6分,共30分)
6、已知:实常数d
c
b
a、
、
、同时满足下列两个等式:⑴0
cos
sin=
-
+c
b
aθ
θ;⑵0
s i n
c o s=
+
-d
b
aθ
θ(其中θ为任意锐角),则d
c
b
a、
、
、之间的关系式是:。
7、函数4
4
3
3
2
2
1-
+
-
+
-
+
-
=x
x
x
x
y的最小值是。
8、已知一个三角形的周长和面积分别是84、210,一个单位圆在它的内部沿着三边匀速无摩擦地滚动一周后回到原来的位置(如图),则这个三角形的内部以及边界没有被单位圆滚过的部分的面积是。
9、已知:2
53+=
x ,则2可用含x 的 有理系数三次多项式来表示为:2= 。
10、设p 、q 、r 为素数,则方程 2
2
2
3
r q p p ++= 的所有可能的解p 、q 、r 组成的三元数组( p , q , r )是
三、解答题(共6题,共90分)
11、(本题满分12分)
赵岩,徐婷婷,韩磊不但是同班同学,而且是非常要好的朋友,三个人的学习成绩不相伯仲,且在整个年级中都遥遥领先,高中毕业后三个人都如愿的考入自己心慕以久的大学.后来三个人应母校邀请给全校学生作一次报告.报告后三个人还出了一道数学题:有一种密码把英文按字母分解,英文中的26a b c z ,,,,个字母(不论大小写)依次用12326 ,,,,这26个自然数表示,并给出如下一个
变换公式:⎪⎩⎪⎨⎧+++=的正偶数)是不超过其中的正奇数)
是不超过其中26(13]2
1[26(1]2[x x x x
y ;已知对于任意的实数x ,记号[x ]表示
不超过x 的最大整数;将英文字母转化成密码,如1713]2
1
8[8=++→,即q h 变成 ,再如
61]2
11
[11=+→,即f k 变成。
他们给出下列一组密码:etwcvcjw ej ncjw
wcabqcv ,把它翻译出来就是一句很好的临别赠言。
现在就请你把它翻译出来,并简单地写出翻译过
程。
12、(本题满分15分)
如果有理数m 可以表示成2
2
562y xy x +-(其中y x 、是任意有理数)的形式,我们就称m 为“世博数”。
⑴ 个“世博数”b a 、之积也是“世博数”吗?为什么?
⑵ 证明:两个“世博数”b a 、(0≠b )之商也是“世博数”。
D
如图,在四边形ABCD 中,已知△ABC 、△BCD 、△ACD 的面积之比是3∶1∶4,点E 在边AD
上,CE 交BD 于G ,设k EA DE
GD BG ==。
⑴求32207+k 的值; ⑵若点H 分线段BE 成2=HE
BH
的两段,且2222p DH BH AH =++,试用含p 的代数式表示△
ABD 三边长的平方和。
14、(本题满分16分)
观察下列各个等式: ,304321,14321,521,112
2
2
2
2
2
2
2
2
2
=+++=++=+=。
⑴你能从中推导出计算2
22224321n +++++ 的公式吗?请写出你的推导过程; ⑵请你用⑴中推导出的公式来解决下列问题:
已知:如图,抛物线322
++-=x x y 与x 、y 轴的正半轴分别交于点B A 、,将线段OA
n 等分,分点从左到右依次为1654321-n A A A A A A A 、、
、、、、、 ,分别过这1-n 个点作x 轴的垂线依次交抛物线于点1654321-n B B B B B B B 、、
、、、、、 ,设△1OBA 、 △211A B A 、△322A B A 、△433A B A 、…、△A B A n n 11--的面积依次为n S S S S S 、、
、、、 4321 。
①当2010n =时,求123452010S S S S S S ++++++ 的值;
②试探究:当n 取到无穷无尽时,题中所有三角形的面积和将是什么值?为什么?
N
Y 有如图所示的五种塑料薄板(厚度不计):①两直角边分别为3、4的直角三角形ABC ; ②腰长为4、顶角为︒36的等腰三角形JKL ; ③腰长为5、顶角为︒120的等腰三角形OMN ;
④两对角线和一边长都是4且另三边长相等的凸四边形PQRS ;
⑤长为4且宽(小于长)与长的比是黄金分割比的黄金矩形WXYZ 。
它们都不能折叠,现在将它们一一穿过一个内、外径分别为2.4、2.7的铁圆环。
我们规定:如果塑料板能穿过铁环内圈,则称为此板“可操作”;否则,便称为“不可操作”。
⑴证明:第④种塑料板“可操作”;
⑵求:从这五种塑料板中任意取两种至少有一种“不可操作”的概率。
16、(本题满分16分)
定义:和三角形一边和另两边的延长线同时相切的圆叫做三角形这边上的旁切圆。
如图所示,已知:⊙I 是△ABC 的BC 边上的旁切圆,F E 、分别是切点,IC AD ⊥于点D 。
⑴试探究:F E D 、、三点是否同在一条直线上?证明你的结论。
⑵设,6,5===BC AC AB 如果△DIE 和△AEF 的面积之比等于m ,
n EF
DE
=,试作出分别以m
n
n m 、为两根且二次项系数为6。