数学北师大版九下2.3《刹车距离与二次函数》导学案3

2.3 刹车距离与二次函数 导学案【学习目标】1、 会作出y=ax 2和y=ax 2＋c 的图象，并能比较它们与y=x 2的异同，理解a 与c 对二次函数图象的影响2、 能说出y=ax 2和y=ax 2＋c 的图象开口方向、对称轴和顶点坐标【学习重点】二次函数y=ax 2、y=ax 2＋c 的图象和性质【学习难点】由函数图象概括出y=ax 2、y=ax 2＋c 的性质． 【课前自学】1、 二次函数y= x 2 与y=- x 2的性质： 2、在同一坐标系中作二次函数y=x 2和y=2x 2的图象 (2)在直角坐标系（表一）中描点：(3)用光滑的曲线连接各点，便得到函数y ＝x 2和y=2x 2的图象．相同点：不同点：归纳：二次函数y=ax 2图象的开口大小与 有关，若|a|越大，函数图象开口越 ，函数值的增长速度越 。

【新课学习】 探究：认识和理解二次函数y=2x 2、y=2x 2+1和y=2x 2-1的性质X1、在同一平面内画出函数y=2x2、y=2x 2+1和y=2x 2-1的图象。

(2)在直角坐标系（表二）中描点：(3)用光滑的曲线连接各点， 便得到函数y=2x 2、y=2x 2+1和y=2x 2-1的图象．2222归纳：当c ＞0时，把y=ax 2（a ≠0）的图象向 平移 个单位得到y=ax 2＋c （a ≠0，c ≠0）的图象，它的顶点坐标是 。

当c ＜0时，把y=ax 2（a ≠0）的图象向 平移 个单位得到y=ax 2＋c （a ≠0，c ≠0）的图象，它的顶点坐标是 。

【巩固练习】1、y=2x 2-3的图象可以看成函数y=2x 2的图象向 平移 个单位2、函数y=- x 2+2开口向 ，顶点坐标是 , 当x= 时，y 有最 值，y=4、把y ＝x 2的图象向下平移2个单位得到的图象是函数y= 的图象。

5、将y=-2x 2+1的图像向下平移1个单位，将得到函数y= 的图象 【课堂小结】这节课你学到了什么? 【课后作业】同步伴读Ｐ1012.3 刹车距离与二次函数 当堂训练1、下列各组函数中，开口方向、对称轴和顶点坐标都相同的是（ ） A 、y=2x 2和y=-2x 2B 、y=2x 2和y=x 2C 、y=2x 2 和y=-21x 2 D 、y=2x 2 和y=x 2+1 2、对于二次函数y=-x 2+1,开口向 ，顶点坐标是 。

《刹车距离与二次函数》说课稿宁夏银川市回民中学 杨子鸣尊敬的各位专家、各位老师：下午好！我说课的内容是北师大版九年级下册第二章《二次函数》的第三节《刹车距离与二次函数》我分背景分析、教学目标设计、教学媒体设计、课堂结构设计、教学过程设计、教学评价设计六个方面进行说课。

一、背景分析（我从学习任务、学生情况两个方面进行背景分析）1、学习任务分析本节课主要研究二次函数c ax y ax y +==22,的图象和性质，安排为1课时教学。

二次函数是现实中有着广泛应用的基本初等函数，对它的的研究，将为学生进一步学习其他函数，体会函数思想奠定基础，积累经验。

教材对二次函数图象的研究经历的是从简单到复杂，从特殊到一般的过程，对函数性质采用的是利用图象的、直观的、非形式化的研究方式。

本节课是在研究了2x y =和2x y -=的图象和性质的基础上，探究二次函数c ax y ax y +==22,的图象和性质，通过让学生经历作图、联系、对比、概括与反思等探究活动，达到对抛物线自身特点的认识和对其性质的理解，进一步获得将表格、表达式、图象三者联系起来的经验，初步建立二次函数表达式与图象之间的联系，渗透数形结合思想，进一步发展识图、抽象概括以及利用表达式或图象解决问题的能力。

本节课在探索方式、总结规律、解决问题等方面，都为探究二次函数c bx ax y k h x a y h x a y ++=++=+=222,)(,)(的图象和性质起到铺垫和引领作用，因此，本节课具有承上启下的作用。

根据本节课的学习任务和后续学习的需要，确定本节课的教学重点是： 能作出二次函数c ax y ax y +==22,的图象，能说出它们的图象的开口方向、对称轴和顶点坐标。

2、学生情况分析学生在此之前，已系统研究过一次函数和反比例函数，积累了一些研究函数图象和性质的经验。

对本节课内容的学习，知道抛物线的有关概念，具备用描点法画函数图象的基本技能，有一定的数形结合研究函数的能力。

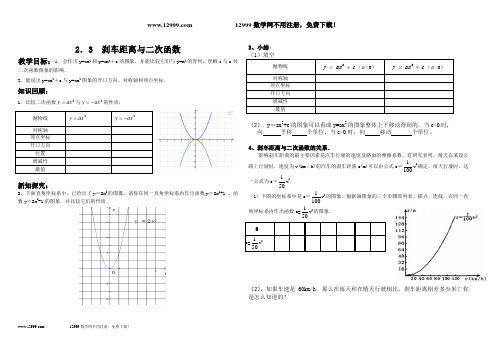
2．3 刹车距离与二次函数教学目标：1．会作出y=ax 2和y=ax 2＋c 的图象，并能比较它们与y=x 2的异同，理解a 与c 对二次函数图象的影响．2．能说出y=ax 2＋c 与y=ax 2图象的开口方向、对称轴和顶点坐标．知识回顾：1．比较二次函数2ax y =与2ax y -=的性质：新知探究：2、下面直角坐标系中，已给出了y ＝2x 2的图像，请你在同一直角坐标系内作出函数y ＝2x 2+1 、函数y ＝2x 2-1的图象．并比较它们的性质．3、小结：（2）. y ＝ax 2+c 的图象可以看成y=ax 2的图象整体上下移动得到的，当c>0时, 向 平移 个单位，当c<0时，向 移动 个单位。

4、刹车距离与二次函数的关系．影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数．有研究表明，晴天在某段公路上行驶时，速度为v(km ／h)的汽车的刹车距离s(m)可以由公式s ＝1001v 2确定，雨天行驶时，这一公式为s ＝501v 2． （1）下图的坐标系中是s ＝1001v 2的图象，根据画图象的三个步骤即列表、描点、连线，在同一直角坐标系内作出函数s=501v 2的图象．（2）、如果车速是60km/h ，那么在雨天和在晴天行驶相比，刹车距离相差多少米？你是怎么知道的？课后反馈一、填空题：1. 二次函数y = ax 2的图象是 ，对称轴是 ，顶点坐标是 ，当a<0时，在对称轴 侧，y 随x 的增大而减小；2、二次函数y=5x 2的图像是 ，它的开口方向 、对称轴 ，顶点坐标 ,最值 ，增减性：在对称抽左侧 ，在对称轴右侧 。

3、二次函数y=-5x 2-5的图像是 ，它的开口方向 、对称轴 ，顶点坐标最值 ，增减性：在对称抽左侧 ，在对称轴右侧 。

4. 若点P （m ，4）是抛物线y = 12x 2上的一点，则m = ； 5. 抛物线y=-3x 2+2可以看成是由抛物线y=-3x 2-4向 平移 个单位得到的. 6. 抛物线y=－4x 2－4，当x= 时，y 有最 值，此时y= ．7. 将函数y=2x 2+4的图象沿x 轴对折,得到图象的函数解析式为 .8、写出两个开口向上，对称轴是y 轴，最值是y=-8的二次函数关系式 。

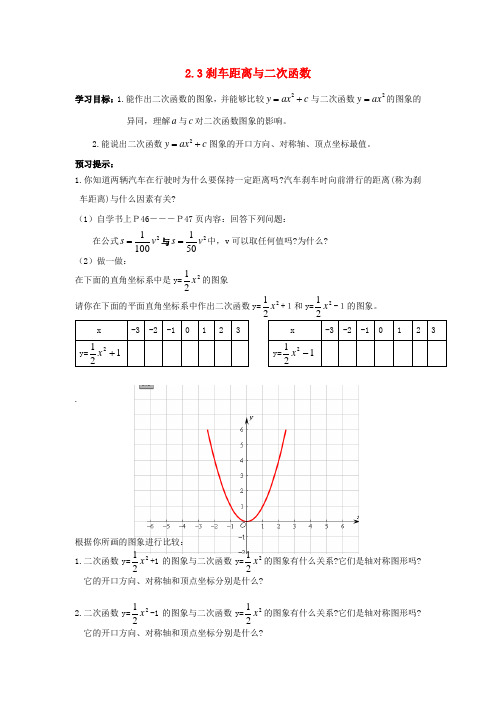
2.3刹车距离与二次函数学习目标：1.能作出二次函数的图象，并能够比较2y ax c =+与二次函数2y ax =的图象的异同，理解a 与c 对二次函数图象的影响。

2.能说出二次函数2y ax c =+图象的开口方向、对称轴、顶点坐标最值。

预习提示：1.你知道两辆汽车在行驶时为什么要保持一定距离吗?汽车刹车时向前滑行的距离(称为刹车距离)与什么因素有关?（1）自学书上Ｐ46―――Ｐ47页内容：回答下列问题：在公式21001v s =与2150s v =中，v 可以取任何值吗?为什么? （2）做一做：在下面的直角坐标系中是y=221x 的图象 请你在下面的平面直角坐标系中作出二次函数y=21x +１和y=21x -１的图象。

.根据你所画的图象进行比较： 1.二次函数y=221x +1的图象与二次函数y=221x 的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?2.二次函数y=221x -1的图象与二次函数y=221x 的图象有什么关系?它们是轴对称图形吗?它的开口方向、对称轴和顶点坐标分别是什么?归纳：1.二次函数y=ax 2＋c 图象的对称轴为 ，顶点坐标为 ，①当a ＞0时，它的开口方向向 ，当x= 时,y 有最 值＝ ，当x ﹤0时，（对称轴左侧），y 随x 的增大而 ，当x ﹥0时，（对称轴右侧），y 随x 的增大而 ；②当a ＜0时，它的开口方向向 ，当x= 时,y 有最 值＝ . 当x ﹤0时，（对称轴左侧），y 随x 的增大而 ，当x ﹥0时，（对称轴右侧），y 随x 的增大而 ； 2. 二次函数y=ax 2＋c 的图象与y=ax 2的图象形状相同，即开口大小方向一致，但在坐标系中的 不同，二次函数y=ax 2＋c 的顶点为 ．如果c ＞0，y=ax 2＋c ，可以由y=ax 2沿y 轴向 平移个单位长度得到．如果c ＜0，y=a x 2＋c 可以由y=ax2沿y 轴向 平移 个单位得到． 预习检测：1抛物线y=－4x 2－4的开口向 ，当x= 时，y 有最 值，y= ．2.当m= 时，y=（m －1）x mm +2－3m 是关于x 的二次函数．3.抛物线y=－3x 2上两点A （x ，－27），B （2，y ），则x= ，y= ．4.当m= 时，抛物线y=（m ＋1）xmm +2＋9开口向下，对称轴是 ．在对称轴左侧，y 随x 的增大而 ；在对称轴右侧，y 随x 的增大而 ．5.已知抛物线的顶点在原点，对称轴为y 轴，且经过点（－1，－2），则抛物线的表达式 .6. 抛物线，y=4x 2，y=－2x 2的图象，开口最大的是（ ）A ．y=41x 2B ．y=4x 2C ．y=－2x 2D ．无法确定7.在同一坐标系中，图象与y=2x 2的图象关于x 轴对称的是（ ）A ．y=21x 2B ．y=－21x 2C ．y=－2x 2D ．y=－x 2说说你的收获及存在的问题：2.53.05mlxyO小甸子中学九数下 2.3刹车距离与二次函数 展示学案预习反馈：通过预习你有什么收获及存在的问题？ 达标测试： 1.抛物线y=291x -－1的顶点坐标是 ，对称轴是，开口方向是若点（m ，－2）在其图象上，则m 的值是．2.抛物线y=3x 2-1的对称轴是_____，顶点坐标为______，它是由抛物线y=3x 2•向_____平移______个单位得到的．3.把抛物线y=2x 2向上平移1个单位，得到抛物线_______，把抛物线y=-2x 2•向下平移3 个单位，得到抛物线________．4.二次函数24y x =+的最小值是 ．5.将抛物线23y x =-向上平移一个单位后，得到的抛物线解析式是 ．6.在平面直角坐标系中，抛物线21y x =-与x 轴的交点的个数是（ ）A ．3B ．2C ．1D ．07.直线y=x 与抛物线y=x 2－2的两个交点的坐标分别是（ ）A ．（2，2），（1，1）B ．（2，2），（－1，－1）C ．（－2，－2），（1，1）D ．（－2，－2），（－1，－１） 8.函数y=x 2－4的图象与y 轴的交点坐标是（ ）A ．（2，0）B ．（－2，0）C ．（0，4）D ．（0，－4）9.如图，小芳在某次投篮中，球的运动路线是抛物线y ＝－15x 2＋3.5的一部分，若命中篮圈中心，则他与篮底的距离l 是（ ）A ．3.5mB ．4mC ．4.5mD ．4.6m第9题图10.如图，在同一直角坐标系中，一次函数y =ax +c 和二次函数y =ax 2+c 的图象大致为( )AyByC1:11000AB=5cm ，拱高OC=0.9cm ，线段DE 表示大桥拱内桥长，DE//AB ，如左图所示；在比例图上，以直线AB 为x 轴，抛物线的对称轴为y 轴，以1cm 作为数轴的单位长度，建立平面直角坐标系，如右图所示．(1）求出右图x 轴以上这一部分抛物线为图像的函数解析式.(2）如果DE 与AB 的距离OM=0.45cm 1.4，计算结果精确到lm).能力拓展：12.一座拱桥的轮廓是抛物线型（如图16所示），拱高6m ，跨度20m ，相邻两支柱间的距离均为5m ．（1）将抛物线放在所给的直角坐标系中（如图17所示），求抛物线的解析式； （2）求支柱EF 的长度；（3）拱桥下地平面是双向行车道（正中间是一条宽2m 的隔离带），其中的一条行车道能否并排行驶宽2m 、高3mx图16。

北师版初三数学刹车距离与二次函数
第九课时
§2.3刹车距离与二次函数●教学目标
1、能作出y=ax2 和y=ax2+c 的图象．并研究它们的性质。

2、比较y=ax2 和y＝ax2+c 的图象与y=x2 的异同．理解a 与c 对二次函数图象的影响。

3、经历探索二次函数y=ax2 和y=ax2+c 的图象的作法和性质的过程，进一步获得将表格、表达式、图象三者联系起来的经验。

4、通过比较y＝ax2，y=ax2+c 与y=x2 的图象和性质的比较．培养学生的比较、鉴别能力。

●教学重点
1、能作出y＝ax2 和y=ax2+c 的图象，并能够比较它们与y＝x2 的异同，理解a 与c 对二次函数图象的影响。

2、能说出y＝ax2 和y=ax2+c 图象的开口方向；对称轴和顶点坐标。

●教学难点
能作出函数y＝ax2 和y=ax2+c 的图象，并总结其性质，还能和y=x2 作比较。

●教学方法
类比学习法．
●教学过程
Ⅰ、创设问题情境，引入新课
在前两节课我们学习了二次函数的定义，会画函数y＝x2 与y=-x2 的图
象，知道它们的图象是抛物线，并且还研究了抛物线的有关性质．如图象x。

3.刹车距离与二次函数教学目标 知识与技能1.能作出二次函数2y ax =和2y ax c =+的图象，并能够比较它们与二次函数2y ax =的图象的异同，理解a 与c 对二次函数图象的影响。

2.能说出二次函数2y ax =和2y ax c =+图象的开口方向、对称轴、顶点坐标。

过程与方法经历探索二次函数2y ax =和2y ax c =+的图象的作法和性质的过程，进一步获得将表格、表达式、图象三者联系起来的经验。

情感态度与价值观体会二次函数是某些实际问题的数学模型，由有趣的实际问题，使学生能积极参与数学学习活动，对数学有好奇心和求知欲。

教学重点：2y ax =和2y ax c =+图象的作法和性质教学难点：能够比较2y ax =、2y ax =和2y ax c =+的图象的异同，理解a 与c 对二次函数图象的影响。

教学过程“第一环节 情境创设（5分钟）1.二次函数y ＝x 2与y=-x 2的图象一样吗？它们有什么相同点？不同点？ 2.二次函数是否只有y ＝x 2与y ＝-x 2这两种呢?有没有其他形式的二次函数？以问题串的形式引导学生逐步深入的思考，在复习的同时，开门见山的引出新课内容。

第二环节 新课讲解（10分钟）1. 给出s ＝1001v 2的图象，在同一直角坐标系内作出函数s=501v 2的图象； 2. 比较s=1001v 2和s ＝501v 2的图象。

可以利用描点法作出s=501v 2的图象，体会二次函数表达式、表格、图象三者之间的联系，也为比较s=1001v 2和s ＝501v 2的图象做好准备。

1.相同点：(1)它们都是抛物线的一部分；(2)二者都位于s 轴的左侧；(3)函数值都随v 值的增大而增大。

2.不同点：(1)s=501v 2的图象在s=1001v 2的图象的内侧； (2)s=501v 2的s 比s ＝1001 v 2中的s 增长速度快。

第三环节 做一做（10分钟）1.在同一坐标系中作二次函数y=x 2和y=2x 2的图象． (1)完成下表：9(2)分别作出二次函数y=x 2和y=2x 2的图象．(3)二次函数y ＝2x 2的图象是什么形状?它与二次函数y=x 2的图象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么? 第四环节 议一议（10分钟）1.在同一直角坐标系内作出函数y ＝2x 2与y ＝2x 2+1的图象，并比较它们的性质． 2.在同一直角坐标系内作出函数y ＝3x 2与y ＝3x 2-1的图象，并比较它们的性质． 第五环节 课堂小结（5分钟）师生互相交流总结：1.作二次函数图象的步骤：列表、描点、连线。

2019-2020学年九年级数学下册《2.3 刹车距离与二次函数》导学案北师大版【学习目标】1．理解抛物线2ax y =的开口大小与a 的关系，以及二次函数c ax y +=2与2ax y =的图象之间的移动规律；2．二次函数c ax y +=2与2ax y =的图象和性质及运用。

【媒体使用】【学习过程】【探究1】抛物线的开口与a的关系1．在同一直角坐标系中画出二次函数2x y =与221xy =的图象（1）列表：（2）描点：在平面直角坐标系中分别描出各点；（3）连线：用平滑的曲线描出函数的图象(注意要体现图象的延伸趋势)。

2．请再画出二次函数22x y =的图象，观察3条抛物线，有何发现？3．对于抛物线2x y -=、221x y -=、22x y -=呢？有何发现？【发现与归纳】抛物线的开口大小由a 决定，a越大，抛物线开口就________；反之，a越小，抛物线开口就________【自我巩固】1．下列二次函数中，其图象开口向下，且开口最小的是( )A ．221x y -=B ．23x y -=C ．2x y -=D ．25x y =【探究2】二次函数c ax y +=2与2ax y =的图象之间的关系x … … 2x y = … … 221x y =……在同一坐标系中分别画出二次函数221x y=与2212+=xy、2212-=xy的图象【发现与归纳】（1）二次函数221xy=与2212+=xy、2212-=xy的图象的形状____________，原因是______________，但它们的_______不同；（2）抛物线221xy=的顶点坐标是________；抛物线2212+=xy的顶点坐标是_________；抛物线2212-=xy的顶点坐标是_________；（3）抛物线2212+=xy可由抛物线221xy=向______平移______单位得到；抛物线2212-=xy可由抛物线221xy=向______平移______单位得到；（4）抛物线caxy+=2与2axy=的形状_______（因为_____相等）；抛物线caxy+=2可由抛物线2axy=向_______平移(当c______时)或向_____平移(当c______时)_____个单位得到。

2.3《刹车距离与二次函数》（1）学习目标1、经历探索二次函数y=ax2和y=ax2＋c的图象的作法和性质的过程2、会作出y=ax2和y=ax2＋c的图象，并能比较它们与y=x2的异同，理解a与c对二次函数图象的影响3、能说出y=ax2＋c与y=ax2图象的开口方向、对称轴和顶点坐标．学习重点：二次函数y=ax2、y=ax2＋c的图象和性质学习难点：由函数图象概括出y=ax2、y=ax2＋c的性质知识回顾二次函数y=x2 与y=-x2的性质：抛物线y=x2 y=-x2对称轴顶点坐标开口方向增减性最值知识探究一、自主探究：1、完成课本P47；2.在同一平面内画出函数y=2x2与y=2x2+1的图象。

3.在同一平面内画出函数y=3x2与y=3x2-1的图象。

比较它们的性质，你可以得到什么结论？二、自主探究：在同一坐标系中，作出函数①y=－3x2，②y=3x2，③y= x2，④y=－ x2的图象，并根据图象回答问题：（1）当x=2时，y= x2比y=3x2大还是小？（2）当x=－2时，y=－ x2比y=－3x2大还是小？三、例题讲解;1、已知抛物线y=（m＋1）x 开口向下，求m的值．2、已知直线y=－2x＋3与抛物线y=ax2相交于A、B两点，且A点坐标为（－3，m）．（1）求a、m的值；（2）求抛物线的表达式及其对称轴和顶点坐标；（3）x取何值时，二次函数y=ax2中的y随x的增大而减小；（4）求A、B两点及二次函数y=ax2的顶点构成的三角形的面积．知识反馈基础题：1、抛物线y=－4x2－4的开口向，当x= 时，y 有最值，y= ．2．当m= 时，y=（m－1）x －3m是关于x的二次函数．3．抛物线y=－3x2上两点A（x，－27），B（2，y），则x= ，y= ．4．当m= 时，抛物线y=（m＋1）x ＋9开口向下，对称轴是．在对称轴左侧，y随x的增大而；在对称轴右侧，y随x的增大而．提高题：1 抛物线y=3x2与直线y=kx＋3的交点为（2，b），则k= ，b= ．2、已知抛物线的顶点在原点，对称轴为y轴，且经过点（－1，－2），则抛物线的表达式为．3、抛物线，y=4x2，y=－2x2的图象，开口最大的是（）A．y= x2 B．y=4x2 C．y=－2x2 D．无法确定创新题：如图，直线ι经过A（3，0），B（0，3）两点，且与二次函数y=x2＋1的图象在第一象限内相交于点C．求：（1）△AOC的面积；（2）二次函数图象顶点D与点A、B组成的三角形的面积．知识小结说出y=ax2与y=ax2＋c图象的开口方向、对称轴和顶点坐标．课后反思。

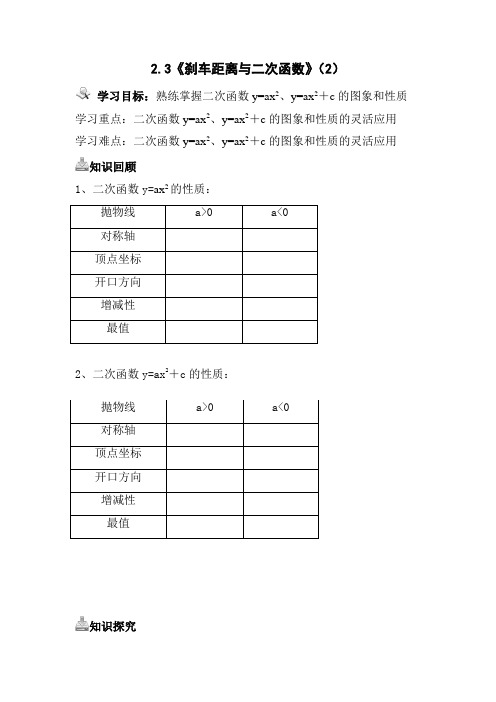
2.3《刹车距离与二次函数》（2）学习目标：熟练掌握二次函数y=ax2、y=ax2＋c的图象和性质学习重点：二次函数y=ax2、y=ax2＋c的图象和性质的灵活应用学习难点：二次函数y=ax2、y=ax2＋c的图象和性质的灵活应用知识回顾1、二次函数y=ax2的性质：抛物线a>0 a<0对称轴顶点坐标开口方向增减性最值2、二次函数y=ax2＋c的性质：抛物线a>0 a<0对称轴顶点坐标开口方向增减性最值知识探究例题1：有一座抛物线型拱桥，桥下面在正常水位AB 时宽20m ．水位上升3m ，就达到警戒线CD ，这时，水面宽度为10m ．（1）在如图2-3-9所示的坐标系中求抛物线的表达式； （2）若洪水到来时，水位以每小时0．2m 的速度上升，从警戒线开始，再持续多少小时才能到拱桥顶？例题2：已知函数：221x y -=， 3212+-=x y 和1212--=x y 。

（1）分别画出它们的图象；（2）说出各个图象的开口方向，对称轴和顶点坐标；（3）说出函数6212+-=x y 的图象的开口方向、对称轴和顶点坐标； （4）试说明函数3212+-=x y 、1212--=x y 、6212+-=x y 的图象分别有抛物线221x y -=作怎样的平移才能得到知识反馈基础题：1、二次函数y=ax 2与一次函数y=ax ＋a 在同一坐标系中的图象大致为（）2、将抛物线231x y =向下平移2个单位得到的抛物线的解析式为,再向上平移3个单位得到的抛物线的解析式为,并分别写出这两个函数的顶点坐标、。

提高题：1任给一些不同的实数k ，得到不同的抛物线k x y +=2，当k 取0，1±时，关于这些抛物线有以下判断：①开口方向都相同；②对称轴都相同；③形状相同；④都有最低点。

其中判断正确的是。

2、将抛物线122-=x y 向上平移4个单位后，所得的抛物线是，当x=时，该抛物线有最（填大或小）值，是。

2019-2020学年九年级数学下册《2.3 刹车距离与二次函数》学案 北师大版学习目标：1．能作出2ax y =和c ax y +=2的图象．并研究它们的性质．2．比较2ax y =和c ax y +=2的图象与2y x =的异同．理解a 与c 对二次函数图象的影响． 3．通过比2ax y =，c ax y +=2与2y x =的图象和性质的比较，培养比较、鉴别能力． 学习重点：1．能作出2ax y =和c ax y +=2的图象，并能够比较它们与2y x =的异同，理解a 与c 对二次函数图象的影响．2．能说出2ax y =和c ax y +=2图象的开口方向、对称轴和顶点坐标． 学习难点：能作出函数2ax y =和c ax y +=2的图象，并总结其性质，还能和2y x =作比较. 知识回顾比较二次函数2y x =与2y x =-的性质：2y x =2y x =-开口方向 对称轴 顶点坐标 最值 增减性学习过程问题引入：刹车距离与二次函数的关系．你知道两辆汽车在行驶时为什么要保持一定距离吗？ 刹车距离与什么因素有关？影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数．有研究表明，晴天在某段公路上行驶时，速度为v(km ／h)的汽车的刹车距离s(m)可以由公式21001v s =确定，雨天行驶时，这一公式为2501v s =．（想一想，在21001v s =和2501v s =中，v 可以取任何值吗？为什么？）下图是21001v s =的图象,在同一直角坐标系内作出函数2501v s =的图象． 1、完成下表：v/(km/h) 0 20 40 60 80 100 120 s/m(潮湿路面)xy2、在图中作出2501v s =的图象. 3、比较21001v s =和2501v s =的图象．相同点：不同点：4、如果行车速度是60 km ／h ，那么在雨天行驶和在晴天行驶相比，刹车距离相差多少米?做一做作二次函数22x y =的图象． (1)完成下表：x22x(2)在下图中作 出22x y =的图象．次函数22x y =的图象是什么形状?它与二次函数2y x =的图(3)二象有什么相同和不同?它的开口方向、对称轴和顶点坐标分别是什么?议一议(1)二次函数122+=x y 的图象与二次函数22x y =的图像有什么关系？它是轴对称图形吗？它的开口方向、对称轴和顶点坐标分别是什么？做图看一看.(2)二次函数132-=x y 的图象与二次函数23x y =的图象有什么关系？并比较它们的性质．当堂检测1、下列函数的开口方向、对称轴、顶点坐标、最值各是什么？23x y =2212+-=x y 322-=x y开口方向 对称轴 顶点坐标 最值2、函数332-=x y 的图象，由23x y =的图象向________平移_________个单位得到.函数332+=x y 的图象，可由23x y =的图象向________平移________个单位得到.3、如果抛物线y = ax 2的开口比抛物线y = 3x –2的开口大，且开口向下，那么a 的取值范围是 .4、把函数232+=x y 的图象沿x 轴对折，得到的图象的函数解析式为_________________. 小结对于二次函数2ax y =和c ax y +=2的图象，当a >0时，抛物线的开口方向向上，当a <0时，抛物线的开口方向向下；开口的大小与a 的绝对值的大小有关：a 的绝对值越小，开口方向越大；图象的顶点坐标和最值与c 的取值有关. 课后作业1、已知抛物线y=（m ＋1）xmm +2开口向下，则m =__________.2、在同一坐标系中，图象与22x y =的图象关于x 轴对称的是（ ）A ．221x y =B ．221x y -=C ．22x y -=D ．2x y -=y 03、若122-+=k x y 的顶点位于x 轴上方，则k 的取值范围是___________________. 4、抛物线241x y =，24x y =，22x y -=的图象，开口最大的是（ ） A ．241x y =B ．24x y =C ．22x y -=D ．无法确定5、(考点链接) 已知直线32+-=x y 与抛物线2ax y =相交于A 、B 两点，且A 点坐标为（－3，m ）． （1）求a 、m 的值；（2）求抛物线的表达式及其对称轴和顶点坐标；（3）x 取何值时，二次函数2ax y =中的y 随x 的增大而减小； （4）求A 、B 两点及二次函数2ax y =的顶点构成的三角形的面积．。