小学五年级奥数 等积变形
- 格式:doc
- 大小:282.00 KB
- 文档页数:8

小学奥数精讲:等积变形求面积“三角形的面积等于底与高的积的一半”这个结论是大家熟知的,据此我们立刻就可以知道: 等底等高的两个三角形面积相等. 这就是说两个三角形的形状可以不同,但只要底与高分别相等,它们的面积就相等,当然这个问题不能反过来说成是“面积相等的两个三角形底与高一定分别相等”.另一类是两个三角形有一条公共的底边,而这条底边上的高相等,即这条底边的所对的顶点在一条与底边平行的直线上,如右图中的三角形A 1BC 与A 2BC 、A 3BC 的面积都相等。
图形割补是求图形面积的重要方法,利用割补可以把—些形状不规则的图形转换成与之面积相等但形状规则的图形,或把不易求面积的图形转换成易求面积的图形.利用添平行线或添垂线的办法,常常是进行面积割补的有效方法,利用等底等高的三角形面积相等这个性质则是面积割补的重要依据,抓住具体的图形的特点进行分析以确定正确的割补方法则是面积割补的关键.进行图形切拼时,应该有意识地进行计算,算好了再动手寻找切拼的方案.不要盲目地乱动手.本讲中.的几个例子都是经过仔细计算才切拼成功的。
例1、已知三角形ABC 的面积为1,BE = 2AB ,BC =CD ,求三角形BDE 的面积?例2、如下图,A 为△CDE 的DE 边上中点,BC=31 CD ,若△ABC(阴影部分)面积为5平方厘米,求△ABD 及△ACE 的面积.例3、 2002年在北京召开了国际数学家大会,大会会标如下图所示,它是由四个相同的直角基本概念例题分析三角形拼成(直角边长为2和3),问:大正方形面积是多少?例4、下图中,三角形ABC和DEF是两个完全相同的直角边长等于9厘米的等腰直角三角形,求阴影部分的面积.练习提高1、如图,已知平行四边形ABCD的面积是60平方分米,E、F分别是AB、AD边上的中点,图中阴影部分的面积是多少平方分米?2、右图中的长方形ABCD的长是20厘米,宽是12厘米,AF=BE,图中阴影部分的面积是多少平方厘米?3、如图,四边形ABCD 是平行四边形,DC =CE ,如果△BCE 的面积是15平方厘米,那么梯形ABED 的面积是多少平方厘米?4、正方形ABCD 的边长是12厘米,已知DE 是EC 长度的2倍,三角形DEF 的面积是多少平方厘米?CF 长多少厘米?5、如图,在平行四边形ABCD 中,AE =ED ,BF =FC ,CG =GD ,平行四边形ABCD 的面积是阴影三角形EFG 的多少倍?(4)6、一个长方形被两条直线分成四个长方形,其中三个面积分别是20平方米,25平方米和30平方米,阴影部分的面积是多少平方米?7、如右图,平行四边形ABCD 的面积是240平方厘米,如果平行四边形内任取一点0,连接AO 、BO 、CO 、DO ,三角形AOD 与三角形BOC 的面积和的21,加上三角形AOB 与三角形DOC 的面积和的31,结果是多少?8、图8-17中,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的2倍,求三角形CDE的面积.9、如图,正方形的边长为10厘米,用一根铁丝弯成直角,把这根铁丝放到正方形上,使直角顶点与正方形的中心O重合,问正方形在直角内部的部分有多大面积?答案:【例题分析】例1. 4例2.三角形ABD=10平方厘米三角形ACE=15平方厘米例3. 13例4. 27【练习提高】1. 22.52. 1203. 454. 三角形DEF=24平方厘米 CF=6厘米5. 4倍6. 37.57. 1008. 59. 25。

奥数拓展:等积变形(一)故事导入:有一个富翁留了一块三角形的土地给两个儿子,两个儿子要求平分这块地,这可伤透了他们的脑筋,因为他们不知道怎样去测量、平分。
同学们,你们能想出多少种方法将这块土地平分成2个面积相等的三角形吗?根据这个问题,你能得出什么结论?结论一:。
(二)即学即练:2.如图,把△ABC的底边BC四等分,那么甲、乙两个三角形的面积谁大,为什么?如图.三角形ABC中.D是AB的中点.点E、F.G、H把BC平均分成五份.阴影部分的面积占三角形ABC面积的几分之几?AB£FG H C三)思维探索:(平行线间的等积变形)如下图,AACD和厶BCD夹在一组平行线之间,且有公共底边,那么△ACD和厶BCD的面积关系是怎样的?为什么?四)即学即练:1.如图,在梯形ABCD中共有8个三角形,其中面积相等的三角形有哪几对?2.如下圏,在梯形ABCP中,梯形舫CD的面釈是ZIABC的面視是1也AAKD的面秩是瘗少?(五)结论总结:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化。
同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状。
为便于实际问题的研究,我们还会常常用到以下结论:(1)等底等高的两个三角形面积相等;(2)底在同一条直线上并且相等,该底所对的角的的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等;(3)若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
(六)例题梳理【例1】等积变形的等分点应用1.如图,在直角三角形ABC中,D、E分别是AB、AC的中点,如果△AED的面积是30平方厘米.求AABC2.如图,A为三角形DE边上的中点,BF为CD边上的三等分点,如果三角形ABC的面积为5,求三角形ABD和三角形ACE的面积。
3.在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若三角形ADE的面积是1,求三角形BEF的面积。
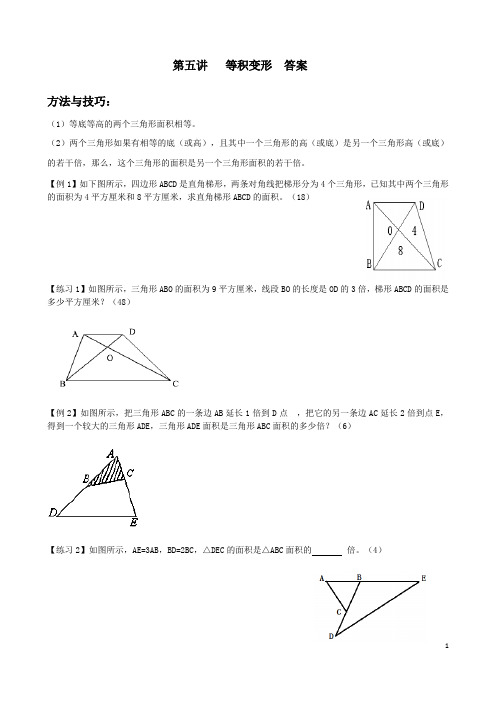
第五讲等积变形答案方法与技巧:(1)等底等高的两个三角形面积相等。
(2)两个三角形如果有相等的底(或高),且其中一个三角形的高(或底)是另一个三角形高(或底)的若干倍,那么,这个三角形的面积是另一个三角形面积的若干倍。
【例1】如下图所示,四边形ABCD是直角梯形,两条对角线把梯形分为4个三角形,已知其中两个三角形的面积为4平方厘米和8平方厘米,求直角梯形ABCD的面积。
(18)【练习1】如图所示,三角形ABO的面积为9平方厘米,线段BO的长度是OD的3倍,梯形ABCD的面积是多少平方厘米?(48)【例2】如图所示,把三角形ABC的一条边AB延长1倍到D点,把它的另一条边AC延长2倍到点E,得到一个较大的三角形ADE,三角形ADE面积是三角形ABC面积的多少倍?(6)【练习2】如图所示,AE=3AB,BD=2BC,△DEC的面积是△ABC面积的倍。
(4)【例3】已知三角形ABC面积为56平方厘米,是平行四边形DEFC的2倍,则阴影部分的面积是多少平方厘米?(14)【例4】如图所示,矩形ABCD的面积为24平方厘米,三角形ADM与三角形BCN的面积和为7.8平方厘米,则四边形PMON的面积是多少平方厘米?(1.8)【例5】如图所示,点M、N、P、Q分别在平行四边形ABCD的边AB、BC、CD、DA上,且PE//GM//CB,HN//QF//AB。
若平行四边形ABCD的面积为600平方厘米、阴影部分的面积为80平方厘米。
请问四边形MNPQ的面积为多少平方厘米?(340)【例6】如图所示,在正方形ABCD的BC边上取一动点E,以DE为边作矩形DEFG,且FG边通过点A。
在点E从点B移动到点C过程中,矩形DEFG的面积()(E)(A)一直变大。
(B)一直变小。
(C)先变小后变大。
(D)先变大后变小。
(E)保持不变。
【练习1】如左下图,△ABC中,D、E分别为边BC、AB的中点。
若图中阴影部分面积为1,则△ABC的面积为多少?(4)【练习2】如右上图所示,图中阴影部分的面积为多少平方厘米?(24)【练习3】如图,六角形的6个顶点恰好是一个正六边形的6个顶点。

小学五年级数学思维专题训练—等积变形例1.长方形ABCD的面积是40平方厘米,E、F、G、H分别为AD、AH、DH、BC的中点,三角形EFG的面积是平方厘米例 2.梯形ABCD中,AE与DC平行,S ABE∆=15,S BCF∆= .例3。
如下图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD= 15.四边EFGO 的面积为。
例4.如下图所示,在平行四边形ABCD中,已知三角形ABP.BPC的面积分别是73、100,求三角形BPD的面积.例5.如下图所示,BD是平行四边形ABCD的对角线,EF平行于BD,如果三角形ABE的面积是12平方厘米,那么三角形AFD的面积是平方厘米。
例6.如下图所示,已知AE=EC,CD=DB,S ABC =60,求四边形FDCE的面积.例7.如右图所示,正方形ABC D和正方形ECGF并排放置,BF与CD相交于点H,已知AB=6厘米,则阴影部分的面积是平方厘米.例8.如下图所示,E、F、G、H分别是四边形ABCD各边的中点,EG与FH交于点O,S1、S2、S3及S4分别表示4个小四边形的面积.试比较S1+S3与S2+S4的大小.例9.将长15厘米、宽9厘米的长方形的长和宽都分成三等份,长方形内任意一点与分点及顶点连结,如右图所示,则阴影部分的面积是 平方厘米.例10.右图所示ABCD 是个直角梯形(∠DAB=∠ABC= 900),以 , AD 为一边向外作长方形ADEF ,其面积为6.36平方厘米,连接BE 交AD 于P ,再连接PC .则图中阴影部分的面积是 平方厘米。
A.6.36B.3.18C.2.12D.1.59例11.如下图所示,平行四边形内有两个大小一样的正六边形,那么阴影部分的面积占平行四边形面积的 。
A .21B .32C .52D .125例12.如下图所示,矩形ABCD 的面积是24平方厘米,三角形ADM 与三角形BCN 的面积之和是7.8平方厘米,则四边形PMON 的面积是 平方厘米.例13.一个矩形分成4个不同的三角形(如下图),绿色三角形面积占矩形面积的15%,黄色三角形的面积是21平方厘米.问:矩形的面积是多少平方厘米?例14.如下图所示,正方形每条边上的三个点(端点除外)都是这条边的四等分点,则阴影部分的面积是正方形面积的。

学科培优数学等积变换、切割、平移、旋转学生姓名授课日期教师姓名授课时长知识定位本讲是几何知识体系中的一个基石同时也是一个升华,等积变换试平面几何的基础,解决三角形问题几乎无处不在,切割、平移、旋转是解决个性问题的个性思想,在几何中举足轻重,能使复杂的问题巧妙化解。
所以本讲是非常重要的一讲,也是竞赛常考的知识板块。
重点难点:1. 等积变换中等地等高三角形的寻找。
2.化未知图形为已知图形。
3. 合理做辅助线4. 平移、旋转、切割等知识的适用范围主要考点:1. 面积和边的比例关系2. 利用平移、旋转解复杂问题知识梳理常见图形面积的解题方法我们已经知道三角形面积的计算公式:三角形面积=底×高÷2从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小);如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的1/3,则三角形面积与原来的一样。
这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: 1、等底等高的两个三角形面积相等.2、若两个三角形的高相等,其中一个三角形的底是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.若两个三角形的底相等,其中一个三角形的高是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍. 3、夹在一组平行线之间的等积变形,如下图,和夹在一组平行线之间,且有公共底边那么;反之,如果,则可知直线平行于。
4、把未知图形转化为三角形、长方形、正方形来求解。

五年级奥数三角形等积变形姓名:探究必备:三角形的面积=底×高÷2,这个公式虽然简单,但有很多“妙”用。
(1)底和高不变,那么它的面积就不变。
例如:下图中三角形Ⅰ和Ⅱ面积相等。
(2)高不变,底扩大(或缩小)多少倍,面积就扩大(或缩小)多少倍。
例如:下图中的两个三角形,高都是h,大三角形Ⅰ的底是小三角形Ⅱ的底的5倍,那么Ⅰ的面积=Ⅱ的面积的5倍(3)底不变,高扩大(或缩小)多少倍,面积就扩大(或缩小)多少倍。
例如:下图中的两个三角形,底都是a,大三角形Ⅰ的高是小三角形Ⅱ的高的4倍,那么Ⅰ的面积=Ⅱ的面积的4倍尝试练习:1、如图,是三条互相平行的直线,并且AB=CD,求证:图中的四边形的面积和三角形的面积相等。
2、用三种不同的方法把任意三角形分成5个面积相等的小三角形。
3、如果下图三角形的面积是20平方厘米,想办法把它分成三部分,使三部分的面积分别是10平方厘米、6平方厘米、4平方厘米。
4、如图,ABCD是一个长为6,宽为4的矩形,EF∥AB,求阴影部分的面积。
5、如图,在三角形ABC的三边BC、CA、AB上分别有三点D、E、F,且BC=4CD,AC=5AE,BA=6BF。
求:△ABC的面积是△DEF面积的几倍?6、如图,证明:梯形ABCD中,三角形AOB的面积与三角形DOC的面积相等。
7、如图,ABCD是一个长为9、宽为6的矩形,E在BC上,F在CD上,并且三角形ABE、三角形ADF、四边形AECF的面积彼此相等,求三角形AEF的面积。
8、如图,ABCD是平行四边形,直线CF与AB交于E,求证:△ADE与△BEF面积相等。
9、如图,四边形ABCD两对角线交于E,延长CA到F,使AF=CE;延长DB到G使BG=DE。
求证:四边形ABCD 的面积等于三角形EFG的面积。
10、如图,△ABC的面积为1。
延长AB到E,使BE=2AB;延长BC到D,使CD=BC。
求△BED的面积。
11、如图,AB=AD,BE=2BC,CF=3CA,△ABC的面积为1,求△DEF的面积。

奥数拓展:等积变形2【例1】重叠面积中的等积变形1.如图是有两个相同的直角梯形重叠而成(单位:厘米),阴影部分的面积是()平方厘米.2.如图,两个完全一样的直角三角形重叠一部分,图中阴影部分面积是()平方厘米.A.90 B.75 C.52 D.30【例2】等积变形的灵活运用1.如图,长方形ABCD的面积是56平方厘米,点E、F、G分别是长方形ABCD边上的中点,H为AD 边上的任意一点,求阴影部分的面积.HGEDCBA2.将三角形ABC的BA边延长1倍到D;CB边延长2倍到E,AC边延长3倍到F,如果三角形ABC的面积等于2,那么三角形DEF的面积是_____。
备用图1 备用图23.如图直角三角形中的空白部分是正方形,正方形的一个顶点将这个直角三角形的斜边分成两部分,阴影部分的面积是6 平方厘米,DB长厘米.三.出门考1. 一个等腰三角形的两条边长分别是51米和21米,这个三角形的周长是( )米。
2. 如下图,ABCD 为平行四边形,E 、F 分别为AD 、DC 的中点,如果△BFC 的面积为4平方厘米,则△AEB 的面积是( )平方厘米.3. 如图是由两个相同的直角梯形重叠而成的,图中只标出三个数据(单位:厘米),图中阴影部分的面积是多少平方厘米?4*.如图,两个正方形摆放在一起,其中大正方形边长为12,那么阴影部分面积是多少?(圆周率取3.14)四.课后作业1. 计算,能简算的要简算。
435177-- 4847157+- 74512712⎛⎫-- ⎪⎝⎭ 4357910910+++ 41327373-+-2. 一根长2米的绳子,先用去41米,又用去21米,这根绳子短了多少米?3. 光明小学拥有一块 公顷的菜地,其中青菜占菜地的,黄瓜占菜地的.剩下的种西红柿,西红柿占菜地的几分之几?4. 光明小学拥有一块公顷的菜地,其中种青菜的有公顷,种黄瓜的有公顷.剩下的种西红柿,西红柿有多少公顷?5. 如图将△ABC 的AB 边延长到D ,BC 边延长到E ,CA 边延长到F ,使DB=AB ,EC=2BC ,FA=2AC ,如果三角形ABC 的面积是5平方厘米,那么三角形DEF 的面积是平方厘米.6. 探索规律并计算=-4131 =-5131 =-6151 =-8151 =+4131 =+5131 =+6151 =+8151 我发现我会计算:4213012011216121+++++ 每日一练第一天:周天(5月20日)1. 三根电线共长87米,第一根和第二根共长43米,第二根和第三根共长31米。
等积变形(上)
例1
(★★)
⑴图中每个小正方形面积都是1平方厘米,那么下面的三角形面积各是多少?
⑵图中每个小正方形面积都是1平方厘米,那么下面的三角形面积各是多少?
⑶图中每个小正方形面积都是1平方厘米,那么下面的三角形面积各是多少?
例2
(★★★)
如图,在梯形ABCD中,共有八个三角形,其中面积相等的三角形共有哪几对?
例3
(★★★)
正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中阴影面积为多少平方厘米?
例4
(★★★)
下图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC的面积。
例5
(★★★★)
如图,有三个正方形的顶点D、G、K恰好在同一条直线上,其中正方形GFEB的边长为10厘米,求阴影部分的面积。
例6
(★★★)
在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积。
例7
(★★★★)
如图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米。
求三角形CDF的面积。
⑴夹在一组平行线之间的等积变形,如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边CD,反之,如果S△ACD=S△BCD,且A、B在CD同侧,则可知直线AB平行于CD。
⑵平行线藏在哪里?
——并列正方形的同方向对角线
【先睹为快】
(★★★★)
如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=BC;延长CA至F,使AF=2AC,求三角形DEF的面积。

第3讲等积变形一、知识点等积变形一般指三角形的等积变形,就是三角形面积相等的变化,经常用到的结论有:1.等底等高的两个三角形面积相等;2.两个三角形的底在同一条直线上而且相等,底所对的角顶点是同一个,则面积相等;3.如果两个三角形的底(高)相等,一个三角形的高(底)是另一个三角形的几倍,则这个三角形的面积也是另一个三角形面积的几倍;4.几个三角形的底相等,都在两条平行线的同一条直线上,且同样长度底边所对的顶点在两条平行线的另一条上,则这几个三角形的面积相等.二、例题精讲例1 两条对角线将梯形分成四个小三角形,已知图中两个三角形的面积,则另外两个三角形的面积分别为多少?例2 如图,三角形ABC中D、E分别为各边中点.若阴影部分面积为1,则三角形ABC的面积为__________.例3 如图,把三角形ABC的一条边AB延长1倍到D,把它的另一边AC延长2倍到E,得到一个较大的三角形ADE,三角形ADE的面积是三角形ABC面积的________倍.例4 如图,在三角形ABC中,BC=8厘米,AD=6厘米,E、F分别为AB和AC的中点,三角形EBF的面积是____________平方厘米.例5 如图,已知三角形ABC的面积为56平方厘米,是平行四边形DEFC面积的2倍,则阴影部分的面积是______________平方厘米.例6 如图,长方形ABCD中,AB=24厘米,BC=36厘米,E是BC的中点,F、G分别是AB、CD的四等分点,H为AD上任意一点,求阴影部分的面积.例7 在梯形ABCD中,若AB=8,DC=10,三角形AMD的面积是10,三角形BCM的面积是15,则梯形ABCD的面积是_____________.例8 如图,三角形ABC的面积为10平方厘米,AE=ED,BD=2CD,则图中阴影部分的面积是________平方厘米.三、水平测试1、如图,梯形的下底长10厘米,高6厘米,则阴影部分的面积是________平方厘米.2、如图,AE=3AB,BD=2BC,三角形DBE的面积是三角形ABC面积的_______倍.3、如图,讲三角形ABC的AB边延长1倍,将BC边延长2倍,得三角形ADE,则三角形ADE 的面积是三角形ABC的_________倍.4、如图,平行四边形ABCD中,DO=2BO,AE和BO垂直,直角三角形AOB的面积为16平方厘米,则四边形OECD的面积是_____________.5、如图,BE=EC,CA=FA,三角形BDE的面积为5平方厘米,则三角形ADF的面积是_____平方厘米.6、矩形ABCD中三条线段长度如图所示,M 线段DE的中点,求阴影部分的面积.。

等积变形题目五年级等积变形是指图形在形状发生改变的过程中,其面积大小保持不变的一种变形。
例如,一个四边形可以变成正方形、长方形、梯形或不规则的其他几边形,只要其面积大小保持不变,就是等积变形。
1.问题:有一个长方体,它的长、宽、高分别是a、b、c(a>b>c),现在进行等积变形,把长方体的长变成d,宽和高保持不变。
请问变形后的长方体与原长方体的体积相比,是变大还是变小?解析:因为等积变形不改变物体的体积,所以原长方体和变形后的长方体的体积是相等的。
2.问题:有一个正方体,边长为a,现在进行等积变形,把正方体的边长变成d,请问变形后的正方体与原正方体的体积相比,是变大还是变小?解析:因为等积变形不改变物体的体积,所以原正方体和变形后的正方体的体积是相等的。
3.问题:有一个三角形,它的底边为a,高为h,现在进行等积变形,把三角形的底边变成d,高保持不变。
请问变形后的三角形与原三角形的面积相比,是变大还是变小?解析:因为等积变形不改变三角形的面积,所以原三角形和变形后的三角形的面积是相等的。
4.问题:有一个正方形,边长为a,现在进行等积变形,把正方形的边长变成d,请问变形后的正方形与原正方形的面积相比,是变大还是变小?解析:因为等积变形不改变正方形的面积,所以原正方形和变形后的正方形的面积是相等的。
5.问题:有一个长方形,长为a,宽为b,现在进行等积变形,把长方形的长变成d,宽保持不变。
请问变形后的长方形与原长方形的面积相比,是变大还是变小?解析:因为等积变形不改变长方形的面积,所以原长方形和变形后的长方形的面积是相等的。

苏教版五上同步奥数培优第三讲多边形的面积(等积变形)【知识概述】三角形面积的公式是底×高÷2,两个三角形只要是底和高分别相等,它们的面积就相等,而这两个三角形的形状不一定完全相同,例如,下面的两个三角形面积就是相等的。
在解答一些平面图形的面积4时,我们可以巧用等底等高两个三角形面积相等的方法来解答。
例题1:四边形ABCD中,M为AB的中点,N为CD的中点,如果四边形ABCD的面积是80平方厘米,求阴影部分BNDM的面积是多少平方厘米。
练习一:1.如图,六边形ABCDEF的面积是16平方厘米,M,N,P,Q分别是AB,CD,DE,AF的中点。
求图中阴影部分的面积。
2.如图,平行四边形的面积为50平方厘米,P是其中任意一点,求阴影部分面积。
3.如图,正方形的边长是6厘米,E,H是所在边的二等分点,F, G,L,M是所在边的三等分点,求阴影部分的面积和。
例2:如下图,三角形ABC为等边三角形,D为AB边上的中点。
已知三角形BDE的面积为5平方厘米。
求等边三角形ABC的面积。
练习二: 1.如图,平行四边形ABCD中,AE=EF=FB,AG=2CG,三角形GEF的面积是6平方厘米,平行四边形的面积是多少平方厘米?2.如图,已知长方形ABCD,三角形ABG的面积为20平方厘米,三角形CDQ的面积为35平方厘米,求阴影部分的面积是多少平方厘米。
3.如图,在一个等边三角形中任意取一点P,连接PA,PB,PC,过P点作三角形三边的垂线,E,F,G分别为垂足。
三角形ABC被分成6个三角形。
已知三角形ABC的面积为40平方厘米,求图中阴影部分的面积。
例3:下图中正方形ABCD的边长是4厘米,长方形DEFG的长DG=5厘米,问长方形的宽DE为多少厘米?练习三:1.如图,两个相同的直角三角形叠放在一起,求阴影部分的面积。
(单位:分米)2.如图,ABCD为长方形,AB=10厘米,BC=6厘米,E,F分别为AB,AD的中点,且FG=2CGE。

第九次课 等积变形(一)内容概述我们已经知道三角形面积的计算公式:三角形面积=底⨯高2÷从这个公式我们可以发现:三角形面积的大小,取决于三角形底和高的乘积. 如果三角形的底不变,高越大(小),三角形面积也就越大(小); 如果三角形的高不变,底越大(小),三角形面积也就越大(小);这说明当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来的3倍,底变为原来的13,则三角形面积与原来的一样.这就是说:一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.在实际问题的研究中,我们还会常常用到以下结论: ①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如左图12::S S a b =③夹在一组平行线之间的等积变形,如右上图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);DC BA⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.例题精讲1. 下图中,矩形ABCD 的面积是60平方厘米,F 是BC 的中点,E 是AD 上任意一点,求阴影部分的面积2. 如图,BD 长12厘米,DC 长4厘米,B 、C 、D 在同一条直线上.⑴ 求三角形ABD 的面积是三角形ADC 面积的多少倍? ⑵ 求三角形ABC 的面积是三角形ACD 面积的多少倍?3. 如图,AD 垂直BC ,12AD =厘米,3DE =厘米.求三角形ABC 的面积是三角形EBC面积的几倍?如果D 是BC 中点,那么三角形ABC 面积是三角形EDC 面积的几倍?CDBAEDCBA4. 如图,在三角形ABC 中,D 是BC 中点,E 是AD 中点,连结BE 、CE ,那么与三角形ABE 等积的三角形一共有哪几个三角形?5. 如图,在平行四边形ABCD 中,EF 平行AC ,连结BE 、AE 、CF 、BF 那么与三角形BEC等积的三角形一共有哪几个三角形?6. 如图,直角三角形ABC 中,AB=10CM ,BC=8CM ,E 和D 分别是AB 、AC 中点,求三角形CDE 的面积。

学生课程讲义课程名称五年级奥数上课时间任课老师沈老师第05 讲,本讲课题:等积变形内容概要熟知各种规则图形的面积求法,结合等积变形来求出不规则图形面积。
两个平面图形面积相等,称为这两个图形等积.解决平面图形面积问题的主要渠道是将欲求的图形的面积转化为已经学过的基本图形的面积问题.其中三角形的等积变形的技巧是各种等积变形的核心,都要运用到“等(同)底、等(同)高的两个三角形面积相等”这个基本规则,并由此衍生出因题而宜的种种精巧的等积变形的技巧。
【例1】计算:如图,5-1,ABCD是直角梯形,两条对角线把梯形分为4个三角形,已知其中两个三角形的面积为3平方厘米和6平方厘米,求直角梯形ABCD的面积。
随堂练习1如图5-2,三角形ABO的面积为9平方厘米,线段BO的长度是OD的3倍,梯形ABCD的面积是多少平方厘米?【例2】如图5-3,把三角形ABC的一条边AB延长1倍到D,把它的另一边AC延长2倍到E,得到一个较大的三角形ADE,三角形ADE的面积是三角形ABC面积的多少倍?随堂练习2如图5-5,AE=3AB,BD=2BC,△DBE面积是△ABC面积的多少倍?【例3】如图5-6,已知三角形ABC的面积为56平方厘米,是平行四边形DEFC的2倍,阴影部分的面积是多少平方厘米?随堂练习3如图5-8,△ABC面积=24平方厘米,M为AB中点,E 为AM上任意一点,MD与EC平行,求EBD的面积。
【例4】如图5-9所示,矩形ABCD的面积为24平方厘米,三角形ADM 与三角形BCN的面积之和为7.8平方厘米,则四边形PMON的面积是多少平方厘米。
随堂练习4如图5-10,平行四边形ABCD中BF=2DF.E是BC中点。
三角形BEF的面积等于8平方厘米,求平行四边形ABCD的面积。
【例5】如图5-11,梯形ABCD的面积是45平方厘米,高6厘米,AD∥BC,三角形AED的面积是5平方厘米,BC=10厘米。
求三角形BCE的面积。

小学五年级奥数精讲等积变形求面积(含答案)小学奥数精讲:等积变形求面积基本概念“三角形的面积等于底与高的积的一半”这个结论是大家熟知的,据此我们立刻就可以知道:等底等高的两个三角形面积相等.这就是说两个三角形的形状可以不同,但只要底与高分别相等,它们的面积就相等,当然这个问题不能反过来说成是“面积相等的两个三角形底与高一定分别相等”.另一类是两个三角形有一条公共的底边,而这条底边上的高相等,即这条底边的所对的顶点在一条与底边平行的直线上,如右图中的三角形A1BC与A2BC、A3BC的面积都相等。
图形割补是求图形面积的重要方法,利用割补可以把—些形状不规则的图形转换成与之面积相等但形状规则的图形,或把不易求面积的图形转换成易求面积的图形.利用添平行线或添垂线的办法,常常是进行面积割补的有效方法,利用等底等高的三角形面积相等这个性质则是面积割补的重要依据,抓住具体的图形的特点进行分析以确定正确的割补方法则是面积割补的关键.进行图形切拼时,应该有意识地进行计算,算好了再动手寻找切拼的方案.不要盲目地乱动手.本讲中.的几个例子都是经过仔细计算才切拼成功的。
例题分析例1、已知三角形ABC的面积为1,BE=2AB,BC=CD,求三角形BDE 的面积1例2、如下图,A为△CDE的DE边上中点,BC=CD,若△ABC(阴影部分)面积为5平方厘米,3求△ABD及△ACE的面积.例3、2002年在北京召开了国际数学家大会,大会会标如下图所示,它是由四个相同的直角三角形拼成(直角边长为2和3),问:大正方形面积是多少例4、下图中,三角形ABC和DEF是两个完全相同的直角边长等于9厘米的等腰直角三角形,求阴影部分的面积.练习提高1、如图,已知平行四边形ABCD的面积是60平方分米,E、F分别是AB、AD边上的中点,图中阴影部分的面积是多少平方分米2、右图中的长方形ABCD的长是20厘米,宽是12厘米,AF=BE,图中阴影部分的面积是多少平方厘米?23、如图,四边形ABCD是平行四边形,DC=CE,如果△BCE的面积是15平方厘米,那么梯形ABED的面积是多少平方厘米?4、正方形ABCD的边长是12厘米,已知DE是EC长度的2倍,三角形DEF的面积是多少平方厘米?CF长多少厘米?5、如图,在平行四边形ABCD中,AE=ED,BF=FC,CG=GD,平行四边形ABCD的面积是阴影三角形EFG的多少倍?(4)6、一个长方形被两条直线分成四个长方形,其中三个面积分别是20平方米,25平方米和30平方米,阴影部分的面积是多少平方米?7、如右图,平行四边形ABCD的面积是240平方厘米,如果平行四边形内任取一点0,连接1AO、BO、CO、DO,三角形AOD与三角形BOC的面积和的,加上三角形AOB与三角形DOC21的面积和的,结果是多少33。

【例1】计学生课程讲义课程名称五年级奥数上课时间任课老师沈老师第05讲,本讲课题:等积变形内容概要熟知各种规则图形的面积求法,结合等积变形来求出不规则图形面积。
两个平面图形面积相等,称为这两个图形等积•解决平面图形面积问题的主要渠道是将欲求的图形的面积转化为已经学过的基本图形的面积问题•其中三角形的等积变形的技巧是各种等积变形的核心,都要运用到“等(同)底、等(同)高的两个三角形面积相等”这个基本规则, 并由此衍生出因题而宜的种种精巧的等积变形的技巧。
如图,5-1,ABCD是直角梯形,两条对角线把梯形分为4个三角形,已知其中两个三角形的面积为3平方厘米和6平方厘米求直角梯形ABCD的面积。
◎I 多少平方厘米?A 界C梦想从这里起飞【例2】如图5-3,把三角形ABC 的一条边 少平方厘米?AB 延长1倍到D,把它的 另一边AC 延长2倍到E, 得到一个较大的三角形ADE ,三角形ADE 的面积是三角形ABC 面积的多少【例3】如图5-6,已知三角形ABC 的面积为56平方厘米,是平行四边形DEFC 的2倍,阴影部分的面积是多倍?随堂练习3随堂练习2 如图5-5,AE=3AB BD=2BC,ADBE 面积是△ ABC 面积的多少倍? 如图5-8,^ABC 面积=24平方厘米,M 为AB 中点,E 为AM 上任意一点,MD 与EC 平行,求EBD 的面积。
as-sE和为7.8平方厘米,则1'■只—9四边形PMON的面积是BC=10厘米。
求三角形BCE的面积。
【例4】如图5-9所示, 矩形ABCD的面积为24 平方厘米,三角形ADM 与三角形BCN的面积之【例5】如图5-11,梯形ABCD的面积是45平方厘米,高6厘米,AD〃BC,三角形AED的面积是5平方厘米,多少平方厘米。
随堂练习4如图5-10,平行四边形ABCD中BF=2DF.E是BC中点。
三角形BEF的面积等于8平方厘米,求平行四边形ABCD的面积。

第五讲长方体、正方体的表面积和体积等积变形例一、一个装有水的长方体水槽,底面积为80平方厘米,水深8厘米。
现将一个底面积为16平方厘米的长方体铁块竖放入水底,仍有部分铁块露在外面,现在水深多少厘米?分析:根据题意可知,水槽中的水的体积在放入铁块后没有变化,依然是80×8=640(立方厘米),这时底面积为80-16=64(平方厘米)。
根据体积=底面积×高,再求出现在的水深。
80×8÷(80-16)=640÷64=10(厘米)答:现在水深是10厘米。
巩固练习1(1)一个底面积为360平方厘米的水槽内,水深12厘米,现将一个底面积为72平方厘米的长方体铁块竖放入水槽底部,仍有部分铁块露在外面,现在水深多少厘米?(2)在一个长5分米、宽4分米、高6分米的水箱中,水深4分米,现将一个底面边长20厘米、高10分米的的长方体铁块,竖放入水底,现在水面距离水箱口多少分米?(3)一个底面积为1200平方厘米、深为30厘米的水槽内,水深10厘米,现将一个底面边长为20厘米的长方体铁块竖放入水底,这时铁块仍高于水面,现在水面高是多少厘米?例二、有一个长方体水槽,它的底面是边长是边长为20厘米的正方形,有一段横截面积是80平方厘米的长方形钢材浸没在其中,当钢材从水槽中取出以后,水槽的水面下降了3厘米,求这段钢材的长。
分析:根据题意可知,钢材的体积相当于水槽内下降部分的体积,即20×20×3=1200(立方厘米),再根据横截面面积×长=体积,求出这段钢材的长。
20×20×3÷8=1200÷80=15(厘米)答:这段钢材的长是15厘米。
巩固练习2(1)在一个棱长是24厘米的正方体容器中注入水。
有一根横截面积是192平方厘米的长方形铁棒浸没在水中,当把铁棒从容器中取出后,容器中的水面下降了5厘米,求这根铁棒的长度。
奥数拓展:等积变形
(一)故事导入:
有一个富翁留了一块三角形的土地给两个儿子,两个儿子要求平分这块地,这可伤透了他们的脑筋,因为他们不知道怎样去测量、平分。
同学们,你们能想出多少种方法将这块土地平分成2个面积相等的三角形吗
根据这个问题,你能得出什么结论
结论一:。
(二)即学即练:
1.你有什么方法将任意一个三角形分成3个面积相等的三角形
2.如图,把△ABC的底边BC四等分,那么甲、乙两个三角形的面积谁大,为什么
如图.三角形ABC中.D是AB的中点.点E、F.G、H把BC平均分成五份.阴影部分的面积占三角形ABC面积的几分之几?
(三)思维探索:
(平行线间的等积变形)如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边,那么△ACD和△BCD的面积关系是怎样的为什么
(四)即学即练:
1.如图,在梯形ABCD中共有8个三角形,其中面积相等的三角形有哪几对
(五)结论总结:
一个三角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化。
同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状。
为便于实际问题的研究,我们还会常常用到以下结论:
(1)等底等高的两个三角形面积相等;
(2)底在同一条直线上并且相等,该底所对的角的的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等;
(3)若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
(六)例题梳理
【例
1】等积变形的等分点应用
1.如图,在直角三角形ABC中,D、E分别是AB、AC的中点,如果△AED的面积是30平方厘米.求△ABC的面积
结论2:夹在间的一组同底三角形面积相等
2.如图,A为三角形DE边上的中点,BF为CD边上的三等分点,如果三角形ABC的面积为5,求三角形ABD和三角形ACE的面积。
3.在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若三角形ADE的面积是1,求三角形BEF 的面积。
【例2】平行线中的等积变形
1.下图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC的面积。
2.已知四边形ABCD和CEFG都是正方形,且正方形ABCD的边长为10厘米,那么图中阴影三角形BFD 的面积为多少平方厘米
3.如图,有三个正方形ABCD,BEFG和CHIJ,其中正方形ABCD的边长是10,正方形BEFG的边长是6,那么三角形DFI的面积是______.
4.
三.出门考
1. 如右图,已知在△ABC 中,BE=3AE ,CD=2AD .若△ADE 的面积为1平方厘米.求三角形ABC 的面积.
2.如图,是大小两个正方形组成的图形,大正方形边长是8厘米,小正方形边长为6厘米,求阴影部分的面积.
1. 如图,A 、B 分别是长方形长和宽的中点,那么四边形ABCD 面积占长方形面积的几分之几
四.课后作业
1.选择
(1)两根长1米的绳子,第一根剪去31,第二根剪去3
1米,剩下的( ) A. 第一根长 B.第二根长 C.一样长
(2)把8
7的分子加上7,要使分数大小不变,分母应加上( )。
(3)把一根绳子分成两段,第一段长95米,第二段占全长的95,比较这两段绳子的长度( )
A .第一段长
B .第二段长
C .一样长
D .无法比较
(4)如果一个圆的直径增加1厘米,那么它的周长就增加多少厘米( )
A .厘米
B .厘米
C .厘米
(5)有若干张长6厘米,宽4厘米的长方形纸,要拼成一个正方形,且没有剩余.最少需要( )张这样的长方形纸。
A .12个
B .15个
C .9个
D .6个
(6)一个半圆形花坛的直径是4米,则这个花坛的周长是( )米.
A .
B .
C . 2.74
的分子加上28以后,要使分数的大小不,分母应加( )。
3.一个分数,分子、分母之和是30,如果在分子上加8,这个分数就等于1。
这个分数是多少
4.一个分数,分子和分母的和是35,约分后的分数是43
,这个分数原来是多少
5.
他们俩谁跑得快一些
6*.有一个分数,分子加上1可约简为41,分母减去1可约简为51,这个分数是多少 每日一练
第一天:周天(5月13日)
1.如图,在三角形ABC 中,D 是AB 边上的三等分点,E 是AC 边上的四等分点,三角形ABC 的面积是24平方厘米,求三角形ADE 的面积.
2.直线CF 与平行四边形ABCD 的AB 边相交于E 点,如果三角形BEF 的面积为6平方厘米,求三角形ADE 的面积是 平方厘米。
第二天:周一(5月14日)
1. 图中有三个正方形,大正方形ABCD 的边长是10cm ,中正方形BEFG 的边长是8cm ,求如图图形阴影部分的面积.
2.如图,在三角形ABC中,D是BC的中点,AF=FE=EC,已知三角形CDE的面积是3平方厘米,三角形ABC的面积是多少平方厘米?
3.
第三天:周三(5月15日)
1.如图,ABCD和CEFG是两个小正方形.已知小正方形边长4厘米,求△AGE的面积.
2.正方形ABCD、正方形BEFG和正方形RKPF的位置如图所示,点G在线段DK上,正方形BEFG的边长为4,则△DEK的面积为()
A.10 B.12 C.14 D.16
3.如下图,每个小正方形的边长都是1厘米,阴影部分的面积是大长方形面积的几分之几
第四天:周四(5月16日)
1.如图由大小两个正方形组成,已知大正方形的边长是12厘米,求阴影部分面积.
2. 如图,已知D是BC的中点,E是CD的中点,F是AC的中点。
已知三角形DEF的面积是6平方厘米,那么三角形ABC的面积是多少平方厘米
:。