六年级 圆的周长与面积 竞赛题(择校专题)

《圆的周长、面积》练习题一.选择题(共10题，共20分)1.把一个圆的半径按n：1的比放大，放大后与放大前圆的面积比是（）。

A.n：1B.2n：1C.：1 D.：22.圆的面积与它半径成（）比例。

A.正B.反C.不成3.强强要在方格纸上画一个圆，要求点（1，4）、（3，2）、（3，6）恰好在圆周上（如图），这个圆的圆心应该在（）上。

A.（3，5）B.（4，4）C.（3，4）D.（5，4）4.圆的周长是它的半径的（）倍。

A.πB.2πC.3.14D.6.285.画圆时，圆的周长为15.7cm，那么圆规两脚间的距离为（）。

A.2.5cmB.5cmC.15.7cm6.一个圆的直径与一个正方形的边长相等，比较它们的面积（）。

A.相等B.圆面积大C.正方形面积大D.不能确定7.如图。

以大圆的半径为直径画一小圆。

大圆的周长是小圆周长的（）倍。

A.2B.4C.68.一个直径为2厘米的半圆面，它的周长是（）厘米。

A.6.28B.3.14C.4.14D.5.149.在同圆或等圆中,扇形的大小和（）有关。

A.直径B.半径C.圆心角10.一个圆的半径扩大2倍，那么面积和周长（）。

A.面积和周长扩大2倍B.面积扩大4倍，周长扩大2倍 C.周长扩大4倍，面积扩大2倍二.判断题(共10题，共20分)1.如果圆的半径扩大2倍，那么它的周长扩大6倍，它的面积扩大9倍。

（）2.把一张圆形纸片从不同方向折叠，折痕都经过圆心。

（）3.任何一个圆的周长都是它直径长度的π倍。

（）4.圆周率π=3.14。

（）5.有两个面积相等的圆，他们的周长也一定相等。

（）6.通过圆心的线段是半径。

（）7.在一个圆内，剪去一个扇形后，剩下的部分仍是扇形。

（）8.半圆的面积是圆面积的一半，半圆的周长也是圆周长的一半。

（）9.量角器是把半圆分成180份制成的。

（）10.周长相等的长方形正方形和圆，正方形的面积最大。

（）三.填空题(共10题，共17分)1.把一个圆平均分成若干（偶数）等份，剪开后可以拼成一个近似的（），这个长方形的长相当于圆的（），宽相当于圆的（）。

六年级数学圆的周长与面积试题1.把一个面积是28.26cm2的圆的半径缩小到原来的，现在圆的面积是（）cm2．A．18.84B．9.42C．4.71D．3.14【答案】D【解析】半径缩小到原来的，变化后的面积缩小到原来的×=，依此列式计算即可求解．．解：28.26×（×）=28.26×=3.14（cm2）．答：现在圆的面积是3.14cm2．故选：D．【点评】本题考查了圆的面积公式，在公式中：圆的面积和半径的平方成正比．2.将圆分成若干等分，拼成一个近似的长方形，如果长方形的周长是82.8厘米，那么圆的面积是多少平方厘米？【答案】314平方厘米．【解析】拼成的长方形的周长等于圆的周长加上圆的2个半径的长度，长方形的周长已知，于是可以求出求出圆的半径，进而求出圆的面积．解：设圆的半径为r厘米，则2×3.14×r+2r=82.88.28r=82.8r=103.14×102=314（平方厘米）；答：圆的面积是314平方厘米．【点评】依据推导过程求出圆的半径，是解答本题的关键．3.甲乙两人分别绕如图的内圆（半径30米）和外圆（半径50米）跑步．（1）两人各跑一圈相差多少米？（2）求图中阴影部分的面积？【答案】相差125.6米；面积是5024平方米．【解析】（1）两人各跑一圈相差多少米，就是求出这两个圆的周长相差多少米，据此利用圆的周长公式计算即可解答问题；（2）圆环的面积=π（R2﹣r2），据此代入数据即可解答．解：（1）3.14×50×2﹣3.14×30×2=314﹣188.4=125.6（米）答：两人各跑一圈相差125.6米．（2）3.14×（502﹣302）=3.14×（2500﹣900）=3.14×1600=5024（平方米）答：阴影部分的面积是5024平方米．【点评】此题主要考查圆的周长公式与圆环的面积公式的计算应用．4.把周长为12.56厘米的圆平均分成两个半圆，每个半圆的周长是厘米．【答案】10.28．【解析】由题干“把周长为12.56厘米的圆平均分成两个半圆”可知每个半圆的周长=圆周长的一半+直径，根据圆周长公式求出圆的直径，将直径代入上式即可得出每个半圆的周长．解：已知C=12.56厘米，d=C÷π圆的直径：12.56÷3.14=4（厘米）；半圆的周长：12.56÷2+4，=6.28+4，=10.28（厘米）；答：每个半圆的周长是10.28厘米．故填：10.28．【点评】此题主要考查的是圆周长公式的使用．5.圆的半径是2米，它的直径是米，周长是米，面积是平方米．【答案】4，12.56，12.56．【解析】圆的直径是半径的2倍，所以其直径为2×2=4（米）．圆的周长公式为：C=2πr，面积公式为：S=πr2，已知半径，周长、面积据公式求出即可．解：（1）直径为：2×2=4（米）；（2）周长为：2×2×3.14=12.56（米）；（3）面积为：3.13×22=12.56（平方米）．故答案为：4，12.56，12.56．【点评】本题主要考查了圆的面积及周长的求法．6.在长为8厘米，宽为6厘米的长方形中画一个最大的圆，这个圆的面积是平方厘米，周长是厘米．【答案】28.26，18.84．【解析】根据题意可知：所画的最大圆的直径等于长方形的宽，根据圆的面积公式：s=πr2，圆的周长公式：c=πd，把数据分别代入公式解答．解：3.14×（）2，=3.14×9，=28.26（平方厘米），3.14×6=18.84（厘米），答：这个圆的面积是28.26平方厘米，周长是18.84平方厘米．故答案为：28.26，18.84．【点评】此题主要考查圆的面积公式、周长公式的灵活运用．7.填表半径/cm直径/cm周长/cm面积/cm2【答案】【解析】根据圆的直径d=2r、圆的周长C=2πr、圆的面积S=πr2代入数据计算即可．解：（1）半径为：10÷2=5（cm），周长为：3.14×10=31.4cm，面积为：3.14×52=3.14×25=78.5（cm2）；（2）半径为：61.8÷3.14÷2≈9.84（cm），直径为：9.84×2=19.68（cm），面积为：3.14×9.842=3.14×96.8256≈304.03（cm2）；（3）直径为：3×2=6（cm），周长为：3.14×6=18.84（cm），面积为：3.14×33=3.14×9=28.26（cm2）；（4）当半径为2cm时，面积为；3.14×22=3.14×4=12.56（cm2），所以半径为2cm；直径为：2×2=4（cm），周长为：3.14×4=12.56（cm）．故答案为：【点评】本题主要考查了圆的直径、周长和面积的计算方法，熟记灵活应用公式是关键．8.把一个直径是6厘米的圆分成若干等份，然后把它剪开，照图的样子拼起来，拼成的图形的周长比原来圆的周长增加厘米．【答案】6【解析】由圆的面积推导过程可知：将圆拼成近似的长方形后，长方形的长就等于圆的周长的一半，宽就等于圆的半径，从而可知，这个长方形的周长比原来圆的周长多出了两个半径的长度，据此即可求解．解：因为将圆拼成近似的长方形后，长方形的长就等于圆的周长的一半，宽就等于圆的半径，所以这个长方形的周长比原来圆的周长多出了两个半径的长度，即多出了一个直径的长度，也就是6厘米．故答案为：6．【点评】解答此题的主要依据是圆的面积推导过程．9.有大、小两个圆，大圆半径是5厘米，小圆半径是4厘米，小圆面积是大圆面积的（）A． B． C．倍【答案】B【解析】根据题意，由圆的面积公式，求出大小圆的面积，列式解答即可．解：由圆的面积公式得：大圆的面积：π×52=25π，小圆的面积：π×42=16π，小圆面积是大圆面积的几分之几：16π÷（25π）==．故选：B．【点评】根据题意，分别求出大小圆的面积，就可以求出结果．10.一年用塑料薄膜覆盖的蔬菜大棚，长20米，横截面是一个半径2米的半圆．（1）大棚内的空间大约有多大？（2）如果每平方米能产蔬菜20千克，这个大棚能产蔬菜多少千克？【答案】125.6立方米；1600千克【解析】（1）大棚的空间是所在圆柱体积的一半，圆柱的底面半径是2米，高是20米，根据圆柱的体积公式V=sh解答即可；（2）根据题干，这个大棚的种植面积就是这个长20米，宽2×2=4米的长方形的面积，根据长方形的面积公式：S=ab求出面积，再乘20即可．据此解答．解：（1）3.14×22×20÷2=251.2÷2=125.6（立方米）答：大棚的空间大约是125.6立方米．（2）20×2×2×20=80×20=1600（千克）答：这个大棚能产蔬菜1600千克．【点评】解答此题主要分清所求物体的形状，转化为求有关图形的体积或面积的问题，把实际问题转化为数学问题，再运用数学知识解决．。

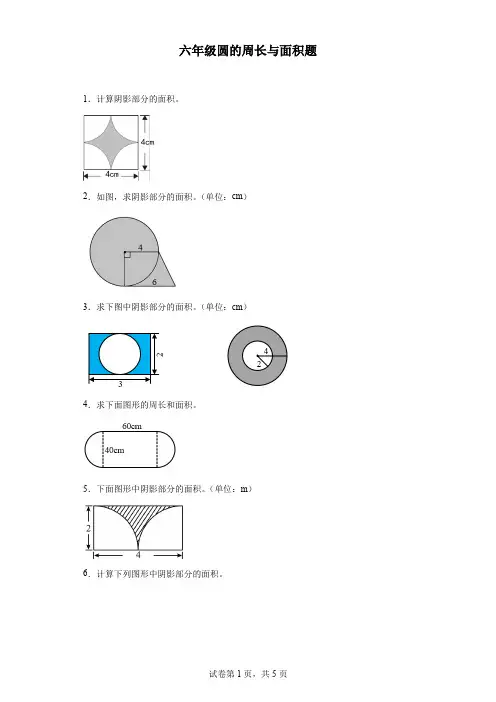
六年级圆的周长和面积常考题型讲解和练习及答案一、圆包正，正包圆题型。

圆包正阴影面积：S内正方形=d*d÷2、πr2___S内正正包圆阴影面积:正方形边长=圆的直径、S正—S圆=边长*边长—π*（边长/2)2练习1图①正方形的周长是80cm，图二圆的直径是80cm,求图①和图②的阴影面积。

二、环形C=C大圆+C小圆S=π*（R2__r2）练习2：求环形面积和周长。

三、羊圈绳子=半径练习3 ：羊能吃多大面积的草？四、操场或者跑道组合图形练习四：一条跑道，宽是7.2m，这条跑道最内侧和最外侧的周长差是多少？这条跑道的面积是多少平方米？五．半圆C=πr+2rS=πr2/2练习五：求图形的周长和面积。

六、花瓣题C=3.14*d*2S=d*d+3.14*(d/2)2*2练习6 学校植物园的门是一个花瓣状门洞，它是由4个直径相等的半圆组成的。

这个门洞的周长和面积分别是多少？七、已知几种相同周长的图形，求面积。

练习7：有三根长62.8m的绳子，小东、小西、小方分别用一根绳子在操场上围出一块地，性状如下图，谁围的面积最大？为什么？练习1答案练习二答案：内圆半径：10—4=6cm 3.14*(102—62)=200.96 cm2练习三答案：π*3*3=28.26 平方米练习四答案：练习五答案：周长3.14*2.4/2+2.4=6.168 cm 面积3.14*（2.4/2）2/2=2.2608 cm2练习6答案：周长1.2*3.14*2=7.536 m 面积：1.2/2=0.6 m 0.6*0.6*3.14*2=2.2608 m21.2*1.2=1.44 m2 1.44+2.2608=2.7008 m2练习7答案：小东62.8/4=15.7m 15.7*15.7=246.49 m2 小西62.8/(3.14/2)=10m 10*10*3.14=314 m2小方62.8/2—10=21.4 m 21.4*10=214 m2 小西围成的圆面积最大。

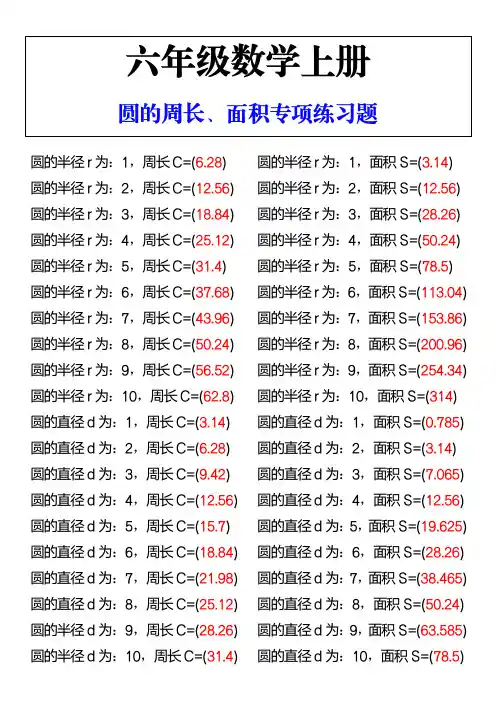
圆的半径r为：1，周长C=(6.28)圆的半径r为：2，周长C=(12.56)圆的半径r为：3，周长C=(18.84)圆的半径r为：4，周长C=(25.12)圆的半径r为：5，周长C=(31.4)圆的半径r为：6，周长C=(37.68)圆的半径r为：7，周长C=(43.96)圆的半径r为：8，周长C=(50.24)圆的半径r为：9，周长C=(56.52)圆的半径r为：10，周长C=(62.8) 圆的直径d为：1，周长C=(3.14)圆的直径d为：2，周长C=(6.28)圆的直径d为：3，周长C=(9.42)圆的直径d为：4，周长C=(12.56)圆的直径d为：5，周长C=(15.7)圆的直径d为：6，周长C=(18.84)圆的直径d为：7，周长C=(21.98)圆的直径d为：8，周长C=(25.12)圆的半径d为：9，周长C=(28.26) 圆的半径d为：10，周长C=(31.4) 圆的半径r为：1，面积S=(3.14)圆的半径r为：2，面积S=(12.56)圆的半径r为：3，面积S=(28.26)圆的半径r为：4，面积S=(50.24)圆的半径r为：5，面积S=(78.5)圆的半径r为：6，面积S=(113.04)圆的半径r为：7，面积S=(153.86)圆的半径r为：8，面积S=(200.96)圆的半径r为：9，面积S=(254.34)圆的半径r为：10，面积S=(314) 圆的直径d为：1，面积S=(0.785)圆的直径d为：2，面积S=(3.14)圆的直径d为：3，面积S=(7.065)圆的直径d为：4，面积S=(12.56)圆的直径d为：5，面积S=(19.625)圆的直径d为：6，面积S=(28.26)圆的直径d为：7，面积S=(38.465)圆的直径d为：8，面积S=(50.24)圆的直径d为：9，面积S=(63.585) 圆的直径d为：10，面积S=(78.5)。

六年级上圆的周长和面积试题一、试卷整体说明这是一份专门针对六年级上册圆的周长和面积知识的测试题哦，满分100分呢。

咱们就开开心心地来一场关于圆的知识小挑战吧。

二、试题部分1. 填空题（每题5分，共30分）圆的周长公式是（）。

一个圆的半径是3厘米，它的面积是（）平方厘米。

（π取3.14）一个圆的直径是8分米，它的周长是（）分米。

（π取3.14）把一个圆平均分成若干等份，可以拼成一个近似的（）形。

圆的半径扩大3倍，它的周长扩大（）倍，面积扩大（）倍。

在同一个圆里，有（）条半径，有（）条直径。

2. 判断题（每题4分，共20分）圆的周长总是它直径的π倍。

（）半径是2厘米的圆，它的周长和面积相等。

（）半圆的周长就是圆周长的一半。

（）直径是圆内最长的线段。

（）一个圆的半径增加1厘米，它的周长就增加2π厘米。

（）3. 选择题（每题4分，共20分）圆的半径是r，它的周长是（）。

A. πrB. 2πrC. πr²一个圆的直径是10厘米，它的面积是（）平方厘米。

（π取3.14）A. 31.4 B. 78.5 C. 15.7要画一个周长是18.84厘米的圆，圆规两脚间的距离应是（）厘米。

（π取3.14）A. 3B. 6C. 9一个环形，内圆半径是2厘米，外圆半径是3厘米，这个环形的面积是（）平方厘米。

（π取3.14）A. 15.7B. 3.14C. 28.26下列图形中，对称轴最多的是（）。

A. 长方形B. 正方形C. 圆4. 应用题（每题10分，共30分）一个圆形花坛的直径是8米，现在要在花坛周围铺一条宽1米的石子路，求这条石子路的面积是多少平方米？（π取3.14）一个圆的周长是31.4分米，这个圆的面积是多少平方分米？（π取3.14）一个车轮的半径是0.3米，车轮滚动一周前进多少米？如果要前进18.84米，车轮要滚动多少周？（π取3.14）三、答案和解析1. 填空题答案圆的周长公式是（C = 2πr或C = πd）。

六年级数学圆的周长和面积专项练习题一、细心填写：１、圆是平面上的一种（）图形 , 围成圆的（）的长叫做圆的周长。

在大大小小的圆中 , 它们的周长总是各自圆直径的（）倍多一些 , 我们把这个固定的数叫做（） , 用字母（）表示 , 它是一个（）小数 , 在（）和（）之间 , 在计算时 , 一般只取它的近似值（）。

2 、一个圆的直径扩大 2 倍 , 它的半径扩大（）倍 , 它的周长扩大（）倍。

3 、两个圆的半径的比是2:3, 它们直径的比是（）, 周长的比是（）。

二、求圆的周长：d＝ 5 厘米 d ＝ 2.4 分米 d ＝ 3 米r ＝ 2 米r ＝ 4 分米 r ＝ 1 厘米3 米12厘米三、解决问题：六年级数学圆的周长3、在一块半径 20 米的圆形花坛周围围一圈篱笆。

篱笆长多少米？和面积专项练习题4、一种自行车轮胎的外直径60 厘米 ,小红骑车车轮每分钟转动100 周。

她骑车每分钟行使多少米？2、一捆电线绕了9 圈 , 每圈直径都是48厘米 , 这捆电线长多少米？5、两个小圆的周长的和与大圆的周长相比, 哪个长？ ( 单位：厘米 )610六年级数学圆的周长和面积专项练习题一、判断是否：1、圆的周长是这个圆的直径的 3.14 倍。

2、小圆的圆周率比大圆的圆周率小。

3、把一张圆形纸片对折若干次, 所有折痕相交于圆心。

4、圆的半径扩大 3 倍 , 它的直径就扩大 6 倍。

5、半圆的周长等于圆周长的一半。

二、填表：半径（分米） 2 8 直径（分米） 3 12周长（分米）18.84 62.8三、解决问题：1、一个圆形花坛的直径是2.2 米 , 它的周长多少米？2、一个圆形水池的半径 6 米。

小明沿着水池边走了 5 圈 , 一共走了多少米？3、小红家圆桌的直径 1.2 米 , 买铝合金条把桌边包起来, 要买多少米铝合金条？4、一辆汽车从甲地去乙地, 已行了全程的2,这时距中点还有15千米。

已行了多少5千米？5、建造一座污水处理厂, 实际投资是计划的9,比计划节约 1.8万元。

一、填空题。

(1)把一个圆分成若干等份，剪开拼成一个近似的长方形。

这个长方形的长相当于( )，长方形的宽就是圆的( )。

因为长方形的面积是( )，所以圆的面积是( )。

(2)圆的直径是6厘米，它的周长是( )，面积是( )。

(3)圆的周长是25.12分米，它的面积是( )。

(4)甲圆半径是乙圆半径的`3倍，甲圆的周长是乙圆周长的( )，甲圆面积是乙圆面积的( )。

(5)一个圆的半径是8厘米，这个圆面积的3/4 是( )平方厘米。

(6)周长相等的长方形、正方形、圆，( )面积最大。

(7)圆的半径由6厘米增加到9厘米，圆的面积增加了( )平方厘米。

(8)要在一个边长为10厘米的正方形纸板里剪出一个最大的圆，剩下的面积是( )。

(9)要在底面半径是12厘米的圆柱形水桶外面打上一个铁丝箍，接头部分是8厘米，需用铁丝( )厘米。

(10)用圆规画一个圆，如果圆规两脚之间的距离是7厘米，画出的这个圆的周长是( )厘米。

这个圆的面积是( )平方厘米。

(11)有大小两个圆，大圆直径是小圆半径的4倍，小圆与大圆周长的比是( )，小圆与大圆面积的比是( )。

(12)一个半圆半径是r，它的周长是( )。

二、应用题。

(1)有一只羊栓在草地的木桩上，绳子的长度是4米，这只羊最多可以吃到多少平方米的草?(2)一种手榴弹爆炸后，有效杀伤范围的半径是8米，有效杀伤面积是多少平方米?(3)一种铝制面盆是用直径30厘米的圆形铝板冲压而成的，要做1000个这样的面盆至少需要多少平方米的铝板?(4)一张长30厘米，宽20厘米的长方形纸，在纸上剪一个最大的圆。

还剩下多少平方厘米的纸没用?(5)一个圆形喷水池的周长是62.8米，绕着这个水池修一条宽2米的水泥路。

求路面的面积。

(6)一个半圆形养鱼池，直径是4米，这个养鱼池的周长是多少米?占地面积是多少平方米?(7)在一个直径是16米的圆心花坛周围，有一条宽为2米的小路围绕，小路的面积是多少平方米?。

圆的竞赛试题及答案1. 已知圆的半径为5cm，求圆的周长。

答案：圆的周长公式为C = 2πr，其中r为半径。

将半径r=5cm代入公式，得C = 2 × 3.14 × 5 = 31.4cm。

2. 若一个圆的直径为10cm，求圆的面积。

答案：圆的面积公式为A = πr²，其中r为半径。

直径为10cm，则半径r=5cm。

代入公式得A = 3.14 × 5² = 78.5cm²。

3. 一个圆的周长为62.8cm，求圆的半径。

答案：根据周长公式C = 2πr，可得半径r = C ÷ (2π)。

将周长C=62.8cm代入公式，得r = 62.8 ÷ (2 × 3.14) = 10cm。

4. 已知圆的面积为78.5cm²，求圆的半径。

答案：根据面积公式A = πr²，可得半径r = √(A ÷ π)。

将面积A=78.5cm²代入公式，得r = √(78.5 ÷ 3.14) = 5cm。

5. 圆的半径增加2cm后，面积增加了多少？答案：设原圆半径为r，则增加后的半径为r+2。

原圆面积为πr²，新圆面积为π(r+2)²。

面积增加量为新圆面积减去原圆面积，即π(r+2)² - πr² = 4πr + 4π。

6. 一个圆的直径是另一个圆的直径的两倍，求这两个圆的面积比。

答案：设小圆的直径为d，则大圆的直径为2d，半径分别为r和小圆半径的两倍。

小圆面积为πr²，大圆面积为4πr²。

因此，面积比为4πr² : πr² = 4 : 1。

7. 圆的周长与直径的比值是一个常数，这个常数是多少？答案：圆的周长与直径的比值是π，即π = C ÷ d，其中C为周长，d为直径。

8. 已知一个圆的半径是另一个圆的半径的3倍，求这两个圆的周长比。

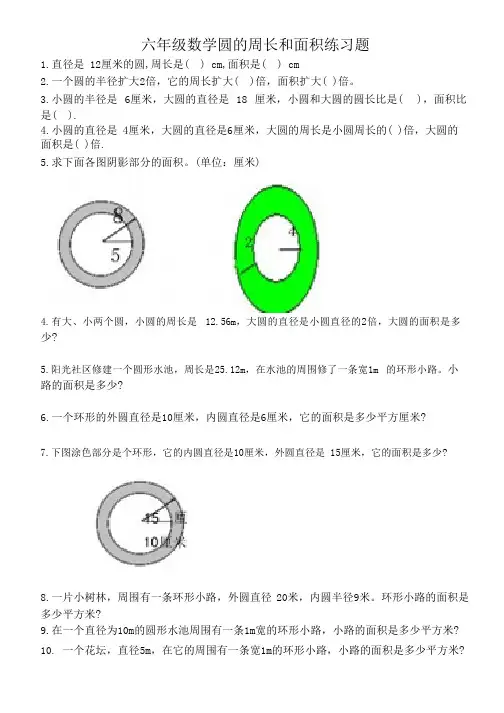
六年级数学圆的周长和面积练习题
1.直径是 12厘米的圆,周长是( ) cm,面积是( ) cm
2.一个圆的半径扩大2倍，它的周长扩大( )倍，面积扩大( )倍。

3.小圆的半径是6厘米，大圆的直径是18 厘米，小圆和大圆的圆长比是( )，面积比是( ).
4.小圆的直径是 4厘米，大圆的直径是6厘米，大圆的周长是小圆周长的( )倍，大圆的面积是( )倍.
5.求下面各图阴影部分的面积。

(单位：厘米)
4.有大、小两个圆，小圆的周长是12.56m，大圆的直径是小圆直径的2倍，大圆的面积是多少?
5.阳光社区修建一个圆形水池，周长是25.12m，在水池的周围修了一条宽1m 的环形小路。

小路的面积是多少?
6.一个环形的外圆直径是10厘米，内圆直径是6厘米，它的面积是多少平方厘米?
7.下图涂色部分是个环形，它的内圆直径是10厘米，外圆直径是 15厘米，它的面积是多少?
8.一片小树林，周围有一条环形小路，外圆直径 20米，内圆半径9米。

环形小路的面积是多少平方米?
9.在一个直径为10m的圆形水池周围有一条1m宽的环形小路，小路的面积是多少平方米?
10. 一个花坛，直径5m，在它的周围有一条宽1m的环形小路，小路的面积是多少平方米?。