双代号网络计算实例

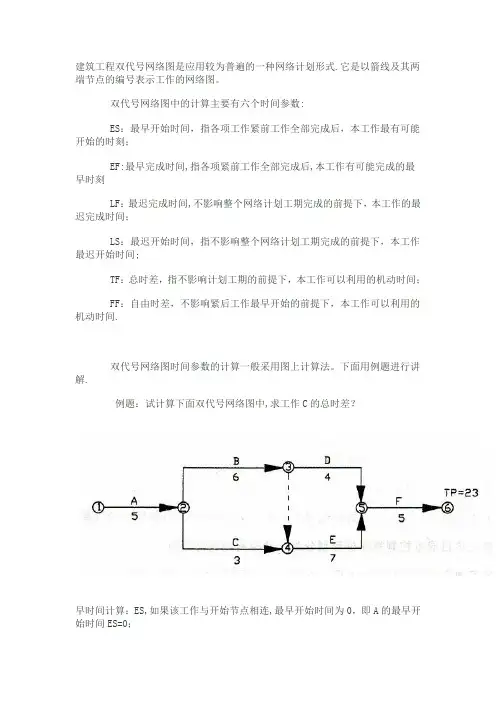
建筑工程双代号网络图是应用较为普遍的一种网络计划形式.它是以箭线及其两端节点的编号表示工作的网络图。

双代号网络图中的计算主要有六个时间参数:ES：最早开始时间，指各项工作紧前工作全部完成后，本工作最有可能开始的时刻；EF:最早完成时间,指各项紧前工作全部完成后,本工作有可能完成的最早时刻LF：最迟完成时间,不影响整个网络计划工期完成的前提下，本工作的最迟完成时间；LS：最迟开始时间，指不影响整个网络计划工期完成的前提下，本工作最迟开始时间;TF：总时差，指不影响计划工期的前提下，本工作可以利用的机动时间；FF：自由时差，不影响紧后工作最早开始的前提下，本工作可以利用的机动时间.双代号网络图时间参数的计算一般采用图上计算法。

下面用例题进行讲解.例题：试计算下面双代号网络图中,求工作C的总时差？早时间计算：ES,如果该工作与开始节点相连,最早开始时间为0，即A的最早开始时间ES=0；EF，最早结束时间等于该工作的最早开始+持续时间，即A的最早结束EF为0+5=5；如果工作有紧前工作的时候,最早开始等于紧前工作的最早结束取大值，即B的最早开始FS=5，同理最早结束EF为5+6=11，而E工作的最早开始ES为B、C工作最早结束（11、8)取大值为11。

最迟完成时间计算：LF,从最后节点开始算起也就是自右向左。

如果该工作与结束节点相连,最迟完成时间为计算工期23,即F的最迟结束时间LF=23；中间工作最迟完成时间等于紧后工作的最迟完成时间减去紧后工作的持续时间.如果工作有紧后工作，最迟完成时间等于紧后工作最迟开始时间取小值.LS，最迟开始时间等于最迟结束时间减去持续时间，即LS=LF—D；时差计算: FF，自由时差=（紧后工作的ES—本工作的EF);TF，总时差=（紧后工作的LS—本工作的ES）或者=（紧后工作的LF-本工作的EF)。

该题解析:则C工作的总时差为3。

双代号网络图简明计算技术（修）参看《建设工程项目管理》教材137 页：图1Z203033-2〔全国一级建造师执业资格考试用书，2007-3 月建工版，2009 年5 月第四次印刷〕的网络图计算实例归纳。

六个时间参数：最早开始时间ES，最早完成时间EF，最迟开始时间LS，最迟完成时间LF，总时差TF，自由时差FF。

标注参数图：ES LS TFEF LF FF这些参数的相互关系是：若设D 为本工作持续时间，则有：ES+D=EF，这个等式是最早时间参数的计算顺箭头方向使用的，从参数图的左上向下运算。

LF-D=LS，这个等式是最迟时间参数的计算逆箭头方向使用的，从参数图的中下向上运算。

TF=LS-ES，从参数图的上部的右方向左方运算。

FF=紧后ES-EF一、计算各项工作的最早开始时间（ES）和最早完成时间（EF），或最早时间参数的计算：从起点节点①开始顺着箭线方向依次逐项计算到终点节点⒂。

1、规定（一）：以网络计划起点节点①为开始节点的各项工作的最早开始时间为零。

工作1-2 的最早开始时间ES1-2 =0。

2、而只要知道了工作1-2 的最早开始时间，已知工作1-2 的持续时间D，那么工作1-2 的最早完成时间就是：最早完成时间（EF）=本工作的最早开始时间ES+本工作的持续时间D。

即：ES+D=EF。

而本工作的持续时间D 就标注在网络图箭线的下方，是已知的数据。

3、而本工作的最早完成时间，就是紧后工作的最早开始时间。

4、所有虚工作的最早开始时间等于它的最早完成时间。

在双代号网络图上，以虚线表示的工作如3-5、4-5、6-8、6-7、9-10、13-14，都是如此，因为他们无持续时间。

注意，一定要顺着箭线方向，才能区分紧前工作是哪些。

5、但是，：当某项工作有两项以上的紧前工作时，应选择其中最早完成时间较大或最大的来做紧后工作的最早开始时间。

例如：工作5-6 有两项紧前工作：工作3-5 与工作4-5。

而EF3-5=5；EF4-5=4；所以，选择其中较大的一项5，得：ES5-6=EF3-5 =5。

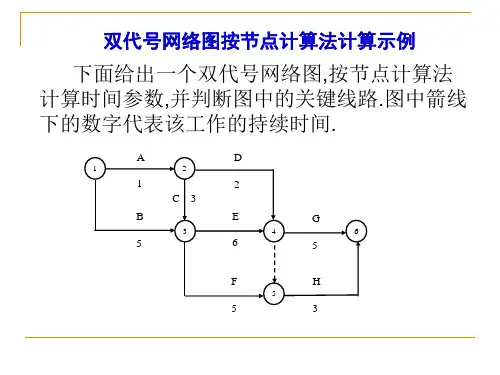
一、双代号网络图6个时间参数的计算方法（图上计算法）从左向右累加，多个紧前取大，计算最早开始结束；从右到左累减，多个紧后取小，计算最迟结束开始。

紧后左上-自己右下=自由时差。

上方之差或下方之差是总时差。

计算某工作总时差的简单方法：①找出关键线路，计算总工期；②找出经过该工作的所有线路，求出最长的时间③该工作总时差=总工期-②二、双代号时标网络图双代号时标网络计划是以时间坐标为尺度编制的网络计划，以实箭线表示工作，以虚箭线表示虚工作，以波形线表示工作的自由时差。

双代号时标网络图1、关键线路在时标双代号网络图上逆方向看，没有出现波形线的线路为关键线路（包括虚工作）。

如图中①→②→⑥→⑧2、时差计算1）自由时差双代号时标网络图自由时差的计算很简单，就是该工作箭线上波形线的长度。

如A工作的FF=0，B工作的FF=1但是有一种特殊情况，很容易忽略。

如上图，E工作的箭线上没有波形线，但是E工作与其紧后工作之间都有时间间隔，此时E工作的自由时差=E与其紧后工作时间间隔的最小值，即E的自由时差为1。

2）总时差。

总时差的简单计算方法：计算哪个工作的总时差，就以哪个工作为起点工作（一定要注意，即不是从头算，也不是从该工作的紧后算，而是从该工作开始算），寻找通过该工作的所有线路，然后计算各条线路的波形线的长度和，该工作的总时差=波形线长度和的最小值。

还是以上面的网络图为例，计算E工作的总时差：以E工作为起点工作，通过E工作的线路有EH和EJ，两条线路的波形线的和都是2，所以此时E的总时差就是2。

再比如，计算C工作的总时差：通过C工作的线路有三条，CEH，波形线的和为4；CEJ，波形线的和为4；CGJ，波形线的和为1，那么C的总时差就是1。

双代号网络图经典例题引言双代号网络图是一种图形表示方法，用于描述一系列活动之间的关系。

通过双代号网络图，可以清晰地表示出活动的先后顺序、重要性以及活动之间的关系，从而有助于优化和管理项目进度。

本文将介绍双代号网络图的经典例题，并通过Markdown文本格式输出。

双代号网络图的基本概念在介绍双代号网络图的经典例题之前，我们先来了解一些基本概念。

活动（Activity）：指项目中的一项任务或工作。

活动可以是一个简单的任务，也可以是一个复杂的工作流程。

节点（Node）：用于表示活动的圆形图形，通常用字母来标识。

弧（Arc）：用于表示活动之间的关系，通常用箭头表示。

箭头的方向表示活动的先后顺序，箭头的长度表示活动的持续时间。

关键路径（Critical Path）：指项目中由一系列关键活动组成的路径，如果关键路径上的任何一个活动延迟，整个项目的进度都会受到影响。

经典例题下面我们将介绍一个经典的双代号网络图例题。

例题描述假设有一个软件开发项目，需要完成以下五个活动：A、B、C、D和E。

这些活动之间存在一些限制条件，它们之间的关系如下：1.活动A必须在活动B完成之前开始；2.活动B必须在活动C完成之前开始；3.活动C必须在活动D完成之前开始；4.活动D必须在活动E完成之前开始。

同时，给出了这些活动的预计持续时间（以天为单位）：A（3天）、B（4天）、C（2天）、D（5天）和E（3天）。

构建双代号网络图根据以上描述，我们可以构建双代号网络图来表示活动之间的关系和持续时间。

A(3) --> B(4) --> C(2) --> D(5) --> E(3)计算关键路径在双代号网络图中，关键路径表示项目中的关键活动，任何一个关键活动的延迟都会延迟整个项目的进度。

为了找到关键路径，我们需要计算每个活动的最早开始时间（ES）和最晚开始时间（LS），以及项目的最早完成时间（EF）和最晚完成时间（LF）。

双代号网络计划案例
假设我们要盖一个超级酷炫的树屋，这里面有好多工序呢。

工序B是把挑选好的木材按照设计尺寸切割好，这个得等工序A完成了才能做，工序B要3天时间。

这时候在双代号网络计划图里，工序A的箭头就指向工序B的节点。

然后是工序C，它是给切割好的木材打磨光滑，工序C需要依赖工序B的成果，而且它得干4天。

那我们就把工序B的箭头连到工序C的节点上。

还有工序D，是组装这个树屋的框架，这个工序要等工序C完成后才能开始，它花费5天时间。

在图里就形成了从工序C到工序D的箭头连接。

最后工序E，是给树屋盖上屋顶并且进行内部装饰，工序E要在工序D完成之后做，这个工序大概需要6天。

这样一个简单的盖树屋的双代号网络计划就形成了。

从这个计划图里，我们可以很清楚地看到每个工序之间的先后顺序，就像看一场接力比赛一样，一个工序完成了，下一个工序才能接过“接力棒”开始跑。

而且还能算出整个盖树屋工程大概需要多长时间呢。

从工序A开始到工序E结束，总共需要2 + 3+ 4 + 5+ 6 = 20天（这里是假设各工序严格按顺序依次进行，没有并行工序的情况哦）。

怎么样，是不是感觉这个双代号网络计划还挺好玩的？。

双代号网络计划案例
那我开始讲一个双代号网络计划的案例啦。

就说咱们要盖一个小房子，这事儿就像一个双代号网络计划里的项目。

咱们先得打地基，这就是一个任务，咱们把它叫做任务A。

从开始盖房子到打完地基，假设需要5天的时间，那这个任务A就有个开始时间和结束时间，开始时间就是第1天，结束时间就是第5天。

然后呢，打完地基后咱们要砌墙，这是任务B。

不过呢，墙必须得等地基打完了才能砌，所以任务B得紧挨着任务A，任务B从第6天开始，要是砌墙需要8天，那就在第13天结束。

在砌墙的过程中呢，咱们还有个小任务，就是安装水电管，这个是任务C。

水电管可以在墙砌到一半的时候就开始安装，不用等墙完全砌好。

假设墙砌到第4天的时候（也就是从开始砌墙后的第4天，整个项目的第10天）开始安装水电管，安装水电管需要6天，那就在第15天结束。

这里面就有个关系啦，任务C和任务B有一部分时间是同时进行的。

墙砌好了，水电管也装好了，咱们就盖屋顶，这是任务D。

任务D得等墙砌好（第13天）和水电管安装好（第15天）才能开始，那就取最晚的那个时间，第15天开始，要是盖屋顶需要7天，那就在第21天结束。

在这个双代号网络计划图里呢，任务A、B、C、D就是那些节点，然后它们之间的连线就表示先后顺序和相互关系。

比如说从任务A到任务B的连线就表示先打地基才能砌墙。

而且每个任务都有自己的代号，就像A、B、C、D这样，这样我们一看这个图就能清楚地知道整个盖房子这个项目每个步骤的顺序和时间安排啦。

这样是不是就很好理解双代号网络计划这个事儿了呢？。

双代号网络图计算方法是每年建造师考试中的必考题，小到选择题、大到案例分析题，笔者在此总结2种计算方法，并附实例，供大家参考学习，互相交流，考出好成绩。

双代号网络图计算方法一一、要点：任何一个工作总时差≥自由时差自由时差等于各时间间隔的最小值（这点对六时参数的计算非常用用）关键线路上相邻工作的时间间隔为零，且自由时差=总时差最迟开始时间—最早开始时间（最小）关键工作：总时差最小的工作最迟完成时间—最早完成时间（最小）在网络计划中，计算工期是根据终点节点的最早完成时间的最大值二、双代号网络图六时参数我总结的计算步骤（比书上简单得多）①②t过程做题次序： 1 4 5 ES LS TF2 3 6 FS LF FF步骤一：1、A 上再做A 下23、起点的A 上=0，下一个的A 上=A 上 4、A 下=A 上+t 过程（时间）步骤二：1、 B 下再做B 上2、 做的方向从结束点往开始点3、 结束点B 下=T （需要的总时间=结束工作节点中最大的A 下）结束点B 上=T-t 过程（时间）4、B 下=前一个的B 上（这里的前一个是从终点起算的） 遇到多指出去的时，取数值小的B 上B 上=B 下—t 过程（时间）步骤三：总时差=B 上—A 上=B 下—A 下 如果不相等，你就是算错了步骤四：自由时差=紧后工作A 上（取最小的）—本工作A 下=紧后工作的最早开始时间—本工作的最迟开始时间 （有多个紧后工作的取最小值） 例：双代号网络图计算方法二一、双代号网络图6个时间参数的计算方法（图上计算法）从左向右累加，多个紧前取大，计算最早开始结束；从右到左累减，多个紧后取小，计算最迟结束开始。

紧后左上-自己右下=自由时差。

上方之差或下方之差是总时差。

计算某工作总时差的简单方法：①找出关键线路，计算总工期；②找出经过该工作的所有线路，求出最长的时间③该工作总时差=总工期-②二、双代号时标网络图双代号时标网络计划是以时间坐标为尺度编制的网络计划，以实箭线表示工作，以虚箭线表示虚工作，以波形线表示工作的自由时差。

双代号网络计划工作计算法例题在双代号网络计划中，工作的最早开始时间（ESi-j）是指：A. 工作i-j的开始时间B. 各紧前工作全部完成后，工作i-j可能开始的最早时刻C. 工作i-j的完成时间D. 工作i-j的持续时间在双代号网络计划中，工作的最早完成时间（EFi-j）与以下哪个参数有关？A. 最早开始时间（ESi-j）B. 最迟开始时间（LSi-j）C. 工作的持续时间（Di-j）D. 工作的自由时差（FFi-j）双代号网络计划中，工作的最迟完成时间（LFi-j）是指：A. 工作i-j的完成时间B. 工作i-j的开始时间C. 在不影响整个任务按期完成的前提下，工作i-j必须完成的最迟时刻D. 工作i-j的总时差在双代号网络计划中，工作的总时差（TFi-j）是指：A. 工作i-j的开始时间与完成时间之差B. 工作i-j的最早开始时间与最迟开始时间之差C. 在不影响总工期的前提下，工作i-j可以利用的机动时间D. 工作i-j的自由时差计算工作的最早开始时间和最早完成时间时，应首先考虑以下哪个因素？A. 工作的持续时间B. 工作的紧后工作C. 工作的紧前工作D. 工作的自由时差在网络计划的计划工期（Tp）未特别说明时，一般情况下，Tp等于：A. 计算工期（Tc）B. 要求工期（Tr）C. 关键线路上的最长工作时间D. 最早完成时间的最大值双代号网络计划中，工作的自由时差（FFi-j）是指：A. 在不影响整个任务按期完成的前提下，工作i-j可以利用的机动时间B. 在不影响其紧后工作最早开始的前提下，工作i-j可以利用的机动时间C. 工作i-j的最早开始时间与最迟开始时间之差D. 工作i-j的最早完成时间与最迟完成时间之差在双代号网络计划中，确定关键工作和关键线路时，应关注以下哪个参数？A. 工作的最早开始时间B. 工作的最早完成时间C. 工作的总时差D. 工作的自由时差。

二建网络计划双代号计算及例题
二、双代号网络计划时间参数计算
工作的持续时间(D)；(类似于流水节拍)
工序时间参数：
最早开始时间
ES T ，最早完成时间EF T ，最迟开始时间
LS T ，最迟完成时间LF T ，总时差T F ，自由时差
F F 。

（总时差T F
：在不影响计划工期的前提下，本工作可以利用的机动时间。

即：T F =LS T -ES T =LF T -EF T ）
（自由时差
F F ：是在不影响紧后工作最早开始时间的条件下，本工作可以利用的机动时间。

即:F j i F =ES
k j T -EF
j i T ）
（英文单词：Time;Early;Starting;Late;Finish;Total;Free;Float
）帮助大家理解总时差和自由时差的小例子
假设有上午上课（A 工作）3小时，A 工作最早8:00开始，吃午饭（B 工作）预留1小时（B 工作最早12:00开始），吃午饭最短20分钟，下午1点必须上课（或者说A 、B
工作必须在13:00结束）。

求A 工作的总时差和自由时差。

A 的自由时差是1小时（12:00-11:00）；
A 的总时差是100分钟（12:40-11:00）。

计算方法：
1.公式计算法
2.表格计算法
3.图上计算法**图上计算法**
例题：
某装饰工程有吊顶、内墙面刷涂料和地面铺装3项分部工程，划
分为3个施工段，
各分部工程在每一个施工段的施工持续时间分别为：吊顶4d 、内墙面刷涂料2d 、地面铺装3d 。

双代号网络图参数计算的简易方法
一、非常有用的要点：
任何一个工作总时差≥自由时差
自由时差等于各时间间隔的最小值（这点对六时参数的计算非常用用）
关键线路上相邻工作的时间间隔为零，且自由时差=总时差
在网络计划中，计算工期是根据终点节点的最早完成时间的最大值
二、双代号网络图六时参数
最早开始时间ES 最迟开始时间LS 总时差
最早完成时间EF 最迟完成时间LF 自由时差
①②
t过程
做题次序： 1 4 5
2 3 6
步骤一：
1、A上再做A下
2、的方向从起始工作往结束工作方向；
3、起点的A上=0，下一个的A上=前一个的A下；
当遇到多指向时，要取数值大的A
下
4、A下=A上+t过程（时间）
步骤二：
1、
B下再做B上
2、做的方向从结束点往开始点
3、结束点B下=T（需要的总时间=结束工作节点中最大的A下）
结束点B
上=
T-t过程（时间）
4、B下=前一个的B上（这里的前一个是从终点起算的）
遇到多指出去的时，取数值小的B上
B上=B下—t过程（时间）
步骤三：
总时差=B
上—A
上
=B
下
—A
下
如果不相等，你就是算错了步骤四：
自由时差=紧后工作A
上（取最小的）—本工作A
下
例：。