高一数学平面向量知识点及典型例题解析

高一平面向量的知识点归纳总结平面向量是高中数学中一个重要的概念，也是数学建模中常用的工具。

在高一阶段，学生首次接触平面向量，并需要掌握其相关的计算方法和性质。

本文将对高一平面向量的知识点进行归纳总结，以帮助学生更好地理解和掌握这一概念。

一、平面向量的定义与表示方法平面向量是有大小和方向的量，可以用有向线段表示，用一个点与另一个点之间的坐标差表示。

一般用字母加箭头表示，如AB→表示从点A指向点B的向量。

二、平面向量的运算1. 平面向量的相加减：向量的相加是指将一个向量的终点与另一个向量的起点相连，并以此线段为新向量的长度和方向。

向量的相减可以转换为向量的相加：A - B = A + (-B)。

2. 向量的数量乘法：向量的数量乘法是指将向量的长度与一个实数相乘，得到一个新的向量，其方向与原向量相同（若实数为正）或相反（若实数为负）。

3. 向量的数量积：向量的数量积等于向量的长度乘积与两向量夹角的余弦值的乘积。

数量积具有交换律和分配律。

三、平面向量的基本性质1. 平移性质：可以将一个向量平移至另一个点，其大小和方向不变。

2. 平面向量的共线性：如果两个向量的方向相同或相反，那么它们是共线的；如果两个向量的方向互相垂直，那么它们是互相垂直的；如果两个向量不共线且不垂直，那么它们是不共线也不垂直的。

3. 向量共点性质：三个向量共点的充分必要条件是其中一个向量等于另外两个向量的和。

四、平面向量的几何应用平面向量在几何中具有广泛的应用。

其中，平面向量的模表示向量的长度，平面向量的方向角表示向量与坐标轴的夹角，平面向量的端点坐标可以确定向量在平面直角坐标系中的位置。

通过对平面向量的几何运算，可以解决平面上的定位、距离和角度等问题。

五、平面向量的坐标表示在平面直角坐标系中，一个向量可以用其横坐标和纵坐标来表示。

具体地说，如果向量的起点在原点O(0, 0)，终点在A(x₁, y₁)，那么这个向量可以用[x₁, y₁]来表示。

新高一平面向量知识点汇总高一学生开始接触平面向量，平面向量是数学中的一个基本概念。

它不仅在数学中有重要应用，也在物理学和工程学等领域有广泛应用。

本文将汇总新高一平面向量的知识点，帮助同学们系统学习和理解这一概念。

一、平面向量的定义和表示方式平面向量是有大小和方向的量。

通常用有向线段来表示，其中线段的长度表示向量的大小，箭头表示向量的方向。

平面向量可以用字母加箭头（如a→）来表示，或者用坐标表示（如(a, b)）。

二、平面向量的运算1. 平面向量的加法：平面向量的加法是将两个向量的对应分量相加得到一个新的向量。

例如，向量a→ = (a₁, a₂) 和向量b→ = (b₁, b₂) 的和为a→ + b→ = (a₁ + b₁, a₂ + b₂)。

2. 平面向量的数乘：平面向量的数乘是将向量的每个分量与一个数相乘得到一个新的向量。

例如，向量a→ = (a₁, a₂) 乘以数k的结果为k·a→ = (k·a₁, k·a₂)。

3. 平面向量的减法：平面向量的减法可以利用向量的加法和数乘来表示。

例如，向量a→ 和向量b→ 的差为a→ - b→ = a→ + (-b→)。

4. 平面向量的数量积：平面向量的数量积（内积）是将两个向量的对应分量相乘，并将结果相加得到一个数。

数量积可以用以下公式表示：a→ · b→ = a₁b₁ + a₂b₂。

三、平面向量的性质1. 平面向量的相等性：两个平面向量相等，当且仅当它们的对应分量相等。

即，a→ = b→ 当且仅当 a₁ = b₁且 a₂ = b₂。

2. 平面向量的数量积性质：平面向量的数量积有以下性质：- 交换律：a→ · b→ = b→ · a→- 结合律：(k·a→) · b→ = k·(a→ · b→)，其中k是一个数- 分配律：(a→ + b→) · c→ = a→ · c→ + b→ · c→- 数乘结合律：(k·a→) · b→ = k·(a→ · b→)- 单位向量性质：一个向量与其自身的数量积等于它的大小的平方：a→ · a→ = ||a→||²四、平面向量的应用平面向量在几何学和物理学中有广泛的应用。

平面向量高一数学知识点在高中数学中，平面向量是一个重要的概念。

它不仅在几何学中有着广泛的应用，也在其他学科中发挥着重要的作用。

本文将重点介绍平面向量的定义、性质以及相关定理。

一、平面向量的定义和运算平面向量可以用有序数对表示，也可以用箭头表示。

设点A和点B是平面上的两个点，用A和B表示它们对应的平面向量。

平面向量有两个重要的运算：加法和数乘。

1. 加法：设有平面向量OA和平面向量OB，它们的和记作OA + OB。

根据平行四边形法则，我们可以通过将OA和OB的起点放在同一个点，然后连接它们的终点，得到一个新的平面向量，即OA + OB。

加法满足交换律、结合律和平移律。

2. 数乘：设有平面向量OA和实数k，它们的数乘记作kOA。

根据数乘的定义，kOA的模长是|k|乘以OA的模长，并且kOA与OA的方向相同（当k>0）或相反（当k<0）。

二、平面向量的性质平面向量有多个重要的性质，下面我们来介绍其中的一些。

1. 零向量：零向量是一个特殊的平面向量，记作O，它的模长为0，方向任意。

对于任意平面向量OA，都有OA + O = OA。

2. 相等条件：平面向量OA和平面向量OB相等的充分必要条件是它们的模长相等并且方向相同。

3. 负向量：平面向量OA的负向量记作-OA，它的模长与OA 相等，方向相反。

4. 平面向量的基本性质：设A、B、C是平面上的三个点，对应的平面向量分别为OA、OB、OC。

有以下基本性质： - OA + O = OA- OA + OA = O- OA + (-OA) = O- OA - OA = O- k(OA + OB) = kOA + kOB (数乘的分配律)- (k + m)OA = kOA + mOA (数乘的分配律)三、平面向量的定理平面向量的定理是高中数学中一些重要的定理。

1. 平行定理：设有两个平面向量OA和OB，当且仅当它们的方向相同或相反时，即OA = kOB（k为非零实数），则表示向量OA和向量OB平行。

高一数学平面向量知识点6在高中数学的学习过程中，平面向量是一个非常重要的知识点。

它不仅仅是数学的一部分，还可以应用于物理、几何等领域。

在高一的数学课程中，学生会接触到平面向量的各种知识点，其中包括平面向量的加法、减法、数量积以及向量的共线与垂直等。

本文将重点介绍高一数学平面向量知识点6，帮助学生更好地理解和掌握这一知识。

知识点6：向量的数量积向量的数量积，也叫点乘或内积，是平面向量的一种运算。

它可以用来计算两个向量的夹角、向量的模长及向量之间的关系等。

向量的数量积的公式如下：A·B = |A||B|cosθ其中，A·B代表向量A与向量B的数量积，|A|和|B|分别代表向量A和向量B的模长，θ代表两个向量之间的夹角。

通过这个公式，我们可以计算两个向量之间的夹角。

当向量A与向量B夹角为0度时，cos0度等于1，所以向量的数量积等于两个向量的模长之积。

当向量A与向量B夹角为90度时，cos90度等于0，所以向量的数量积等于0。

当夹角为其他角度时，通过计算cosθ可以得到向量的数量积。

除了可以计算夹角外，向量的数量积还可以用来判断两个向量之间的关系。

当向量的数量积为正数时，表示两个向量的方向相近，当向量的数量积为负数时，表示两个向量的方向相反，当向量的数量积为0时，表示两个向量垂直。

在实际应用中，向量的数量积也有着广泛的运用。

比如，在力学中，向量的数量积可以用来计算力的分解和合成。

在几何中，向量的数量积可以用来判断两条直线的关系，比如判断两条直线是否平行、垂直等。

总结一下，向量的数量积是平面向量的一种运算，可以用来计算两个向量的夹角、向量的模长及向量之间的关系等。

通过向量的数量积，我们可以更好地理解和应用向量的知识。

在高一的数学学习中，学生应该多做相关的练习题，提高自己对向量的数量积的理解和应用能力。

此外，学生还可以阅读相关数学书籍或参考资料，加深对这一知识点的了解和掌握。

希望本文对高一数学平面向量知识点6的学习有所帮助。

）））））））第五章 平面向量【考纲说明】1、理解平面向量的概念和几何表示，理解两个向量相等及共线的含义，掌握向量的加、减、数乘运算及其几何意义，会用坐标表示。

2、了解平面向量的基本定理，掌握平面向量的坐标运算。

3、掌握数量积的坐标表达式，会进行平面向量数量积的运算，会用向量方法解决简单的平面几何问题、力学问题与其他一些实际问题。

【知识梳理】一、 向量的基本概念与线性运算 1 向量的概念：（1）向量：既有大小又有方向的量，记作AB ；向量的大小即向量的模（长度），记作|AB | 向量不能比较大小，但向量的模可以比较大小．（2）零向量：长度为0的向量，记为0 ，其方向是任意的，0与任意向量平行（3）单位向量：模为1个单位长度的向量常用e 表示．（4）平行向量（共线向量）：方向相同或相反的非零向量，记作a ∥b平行向量也称为共线向量（5）相等向量：长度相等且方向相同的向量相等向量经过平移后总可以重合，记为b a= 大小相等，方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x（6）相反向量：与a 长度相等、方向相反的向量，叫做a的相反向量记作a-,零向量的相反向量仍是零向量若a 、b是互为相反向量，则a =b -,b =a -,a +b =2 向量的线性运算：（1）向量的加法：求两个向量和的运算叫做向量的加法 向量加法满足交换律与结合律；向量加法有“三角形法则”与“平行四边形法则” ．（2）向量的减法 ：求向量a 加上b 的相反向量的运算叫做a 与b的差．向量的减法有三角形法则，b a -可以表示为从b 的终点指向a 的终点的向量（a 、b有共同起点）（3）向量的数乘运算：求实数λ与向量a 的积的运算，记作λa．①a a⋅=λλ；②当0>λ时，λa 的方向与a 的方向相同；当0<λ时，λa 的方向与a的方向相反； 当0=λ时，0 =a λ，方向是任意的③数乘向量满足交换律、结合律与分配律3. 两个向量共线定理：向量b 与非零向量a共线⇔有且只有一个实数λ，使得b =λ向量b 与非零向量a共线⇔有两个均不是零的实数λ、μ，使得0a b λμ+=．二、平面向量的基本定理与坐标表示 1 平面向量的基本定理：如果21,e e 是一个平面内的两个不共线向量，那么对这一平面内的任一向量a，有且只有一对实数21,λλ使：2211e e a λλ+=，其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底2. 平面向量的坐标表示：（1）在直角坐标系中，分别取与x 轴、y 轴方向相同的两个单位向量,i j 作为基底 由平面向量的基本定理知，该平面内的任一向量a 可表示成a xi yj =+，由于a 与数对(x,y)是一一对应的，因此把(x,y)叫做向量a 的坐标，记作a =(x,y)，其中x 叫作a 在x 轴上的坐标，y 叫做在y 轴上的坐标显然0=（0,0），(1,0)i =，(0,1)j =． （2）设OA xi y j =+.则向量OA 的坐标(x,y)就是终点A 的坐标，即若OA =(x,y)，则A 点的坐标为(x,y)，反之亦成立（O 是坐标原点）． 3 平面向量的坐标运算：（1）若()()1122,,,a x y b x y ==，则()1212,a b x x y y ±=±±． （2）若()()2211,,,y x B y x A ，则()2121,AB x x y y =--，1(AB x =（3）若a =(x,y)，则λa =(λx,λy)．（4）若()()1122,,,a x y b x y ==，则1221//0a b x y x y ⇔-=． （5）若()()1122,,,a x y b x y ==，则1212a b x x y y ⋅=⋅+⋅． 三、平面向量的数量积 1 两个向量的数量积：已知两个非零向量a 与b ，它们的夹角为θ，a ·b 等于a 的长度与b 在a 方向上的投影的乘积叫做a 与b 的数量积（或内积），即a ·b =︱a ︱·︱b ︱cos θ，规定00a ⋅=2 向量的投影：︱b ︱cos θ=||a ba ⋅∈R ，称为向量b 在a 方向上的投影 投影的绝对值称为射影 3 向量的模与平方的关系：22||a a a a ⋅==4 乘法公式成立：()()2222a b a b a b a b +⋅-=-=-； ()2222a b a a b b±=±⋅+222a a b b =±⋅+．5 平面向量数量积的运算律：①交换律成立：a b b a ⋅=⋅．②对实数的结合律成立：()()()()a b a b a b R λλλλ⋅=⋅=⋅∈．③分配律成立：()a b c a c b c ±⋅=⋅±⋅()c a b =⋅±； 特别注意：①结合律不成立：()()a b c a b c ⋅⋅≠⋅⋅．②消去律不成立a b a c⋅=⋅不能得到b c =．③a b ⋅=0不能得到a =0或b =06 两个向量的数量积的坐标运算：已知两个向量1122(,),(,)a x y b x y ==，则a ·b =1212x x y y + 7 向量的夹角：已知两个非零向量a 与b ，作OA =a , OB =b ,则∠AOB=θ （001800≤≤θ）叫做向量a 与b 的夹角cos θ=cos ,a b a b a b⋅<>=⋅=当且仅当两个非零向量a 与b 同方向时，θ=00，当且仅当a 与b 反方向时θ=1800，同时0与其它任何非零向量之间不谈夹角这一问题8 垂直：如果a 与b 的夹角为900则称a 与b 垂直，记作a ⊥ba ⊥b ⇔a ·b＝O ⇔2121=+y y x x【经典例题】【例1】（2010全国Ⅱ，8）△ABC 中，点D 在边AB 上，CD 平分∠ACB ，若CB a =，ECBA CA b =，1,2a b ==，则CD = （ ）（A ）1233a b + （B ）2133a b + （C ）3455a b + （D ）4355a b + 【答案】B ．【解析】由角平分线的性质得2AD DB =,即有22()()33AD CB CA a b =-=-．从而221()333CD CA AD b a b a b =+=+-=+．故选B ．【例2】（2009北京，2）已知向量a 、b 不共线，c k =a +b (k ∈R ),d =a -b ,如果c //d ， 那么 （ ） A ．1k =且c 与d 同向 B ．1k =且c 与d 反向 C ．1k =-且c 与d 同向 D ．1k =-且c 与d 反向 【答案】D ．【解析】取a ()1,0=，b ()0,1=，若1k =，则c =a +b ()1,1=，d =a -b ()1,1=-， 显然，a 与b 不平行，排除A 、B ．若1k =-，则c =-a +b ()1,1=-，d =-a +b ()1,1=--， 即c //d 且c 与d 反向，排除C ，故选D ．【例3】（2009湖南卷文）如图，D ，E ，F 分别是∆ABC 的边AB ，BC ，CA 的中点，则( ) A ．0AD BE CF ++= B ．0BD CF DF -+=C ．0AD CE CF +-= D ．0BD BE FC --= 【答案】A ． 【解析】,,AD DB AD BE DB BE DE FC =∴+=+==得0AD BE CF ++=．或0AD BE CF AD DF CF AF CF ++=++=+=．【例4】（2009宁夏海南卷文）已知()()3,2,1,0a b =-=-，向量a b λ+与2a b -垂直，则实数λ的值为( )A.17-B.17C.16-D.16【答案】A ．【解析】向量a b λ+＝（－3λ－1，2λ），2a b -＝（－1,2），因为两个向量垂直，故有（－3λ－1，2λ）×（－1,2）＝0，即3λ＋1＋4λ＝0，解得：λ＝17-，故选A ． 【例5】（2009全国卷Ⅰ文）设非零向量a 、b 、c 满足c b a c b a =+==|,|||||，则>=<b a , （ ）A ．150° B.120° C.60° D.30° 【答案】B ．【解析】由向量加法的平行四边形法则，知a 、b 可构成菱形的两条相邻边，且a 、b 为起点处的对角线长等于菱形的边长，故选择B ．【例6】（2009安徽卷文）在平行四边形ABCD 中，E 和F 分别是边CD 和BC 的中点，或=+，其中，R ，则+= _________．【答案】43． 【解析】设BC b =、BA a =则12AF b a =- ,12AE b a =- ,AC b a =- 代入条件得2433u u λλ==∴+=． 【例7】（2009辽宁卷文）在平面直角坐标系xoy 中，四边形ABCD 的边AB ∥DC,AD ∥BC,已知点A(－2，0)，B （6，8），C(8,6),则D 点的坐标为___________． 【答案】(0,－2)．【解析】平行四边形ABCD 中,OB OD OA OC +=+ ∴OD OA OC OB =+-＝(－2,0)＋(8,6)－(6,8)＝(0,－2) 即D 点坐标为(0,－2)．【例8】（2012江苏）如图,在矩形ABCD 中,22AB BC ==，，点E 为 BC 的中点，点F 在边CD 上,若2AB AF =,则AE BF 的值是___．【答案】2．【解析】由2AB AF =,得cos 2ABAF FAB ∠=,由矩形的性质,得cos =AF FAB DF ∠．∵2AB =，∴22DF ⋅=，∴1DF =∴21CF =-．记AE BF 和之间的夹角为,AEB FBC θαβ∠=∠=，，则θαβ=+． 又∵2BC =，点E 为BC 的中点，∴1BE =． ∴()()=cos =cos =cos cos sin sin AE BF AEBF AEBF AE BF θαβαβαβ+-()=cos cos sin sin =122212AE BF AE BF BE BC AB CF αβαβ--=⨯--=.本题也可建立以, AB AD 为坐标轴的直角坐标系,求出各点坐标后求解．【例9】(2009湖南卷理)在ABC ∆，已知2233AB AC AB AC BC ⋅=⋅=，求角A ，B ，C 的大小． 【答案】2,,663A B C πππ===． 【解析】解：设,,BC a AC b AB c ===由23AB AC AB AC ⋅=⋅得2cos 3bc A bc =，所以3cos 2A = 又(0,),A π∈因此6A π=由233AB AC BC ⋅=得23bc a =，于是23sin sin 3sin 4C B A ⋅=-所以53sin sin()64C C π⋅-=，133sin (cos sin )224C C C ⋅+=，因此 22sin cos 23sin 3,sin 23cos 20C C C C C ⋅+=-=，既sin(2)03C π-=由A=6π知506C π<<，所以3π-，4233C ππ-<，从而20,3C π-=或2,3C ππ-=，既,6C π=或2,3C π=故2,,,636A B C πππ===或2,,663A B C πππ===． 【课堂练习】一、选择题1.（2012辽宁理）已知两个非零向量a ,b 满足|a +b |=|a -b |,则下面结论正确的是（ ）A ．a ∥bB ．a ⊥bC ．{0,1,3}D ．a +b =a -b2. (2009年广东卷文)已知平面向量a =,1x （），b =2,x x （－），则向量+a b ( )A. 平行于x 轴B. 平行于第一、三象限的角平分线C. 平行于y 轴D. 平行于第二、四象限的角平分线3.（2012天津文）在ABC ∆中,90A ∠=︒,1AB =,AC=2,设点,P Q 满足,(1),AP AB AQ AC R λλλ==-∈.若2BQ CP ⋅=-,则λ=( )（ ）A ．13 B ．23C ．43D ．2 4.（2009浙江卷理）设向量a ，b 满足：||3=a ，||4=b ，0⋅=a b ．以a ，b ，-a b 的模为边长构成三角形，则它的边与半径为1的圆的公共点个数最多为 ( )A ．3 B.4 C ．5D ．65.（2012重庆理）设,x y ∈R,向量()()()4,2,,1,1,-===c y b x a ,且c b c a //,⊥,则a b += （）A B C ．D ．106. （2009浙江卷文）已知向量(1,2)=a ，(2,3)=-b ．若向量c 满足()//+c a b ，()⊥+c a b ，则c =（ ）A ．77(,)93B ．77(,)39--C ．77(,)39D ．77(,)93--7．（2012浙江理）设a ,b 是两个非零向量.（ ）A ．若|a +b |=|a |-|b |,则a ⊥bB ．若a ⊥b ,则|a +b |=|a |-|b |C ．若|a +b |=|a |-|b |,则存在实数λ,使得a =λbD ．若存在实数λ,使得a =λb ,则|a +b |=|a |-|b |8.（2009全国卷Ⅰ理）设a 、b 、c 是单位向量，且a ·b ＝0，则()()a c b c -•-的最 小值为( )A.2- 2C.1-D.19.（2012天津理）已知△ABC 为等边三角形,=2AB ,设点P,Q 满足=AP AB λ,=(1)AQ AC λ-,R λ∈,若3=2BQ CP ⋅-,则=λ （ ）A ．12 B ．12± C ．12± D ．32-±10.（2009全国卷Ⅱ理）已知向量()2,1,10,||a a b a b =⋅=+=||b =( )A.B. C. 5 D. 2511.（2012大纲理）ABC ∆中,AB 边上的高为CD ,若,,0,||1,||2CB a CA b a b a b ==⋅===,则AD =（ ）A ．1133a b -B ．2233a b - C ．3355a b - D ．4455a b - 12.（2008湖南）设D 、E 、F 分别是△ABC 的三边BC 、CA 、AB 上的点，且2,DC BD =2,CE EA =2,AF FB =则AD BE CF ++与BC( )A. 反向平行B. 同向平行C. 互相垂直D. 既不平行也不垂直13.（2008广东）在平行四边形ABCD 中，AC 与BD 交于点O E ，是线段OD 的中点，AE 的延长线与CD 交于点F ．若AC =a ，BD =b ，则AF =（ ）A ．1142+a b B ．2133+a b C ．1124+a bD ．1233+a b 14.（2007湖北）设(43)=，a ，a 在b 上的投影为522，b 在x 轴上的投影为2，且||14≤b ，则b 为（ ）A ．(214)，B ．227⎛⎫- ⎪⎝⎭，C ．227⎛⎫- ⎪⎝⎭，D ．(28)，15.（2012安徽理）在平面直角坐标系中,(0,0),(6,8)O P ,将向量OP 按逆时针旋转34π后,得向量OQ 则点Q 的坐标是 （ ） A ．(72,2)-- B ．(72,2)- C ．(46,2)-- D ．(46,2)-二、填空题16.（2012浙江文）在△ABC 中,M 是BC 的中点,AM=3,BC=10,则AB AC ⋅=________.17.（2009安徽卷理）给定两个长度为1的平面向量OA 和OB ，它们的夹角为120o.如图所示，点C 在以O 为圆心的圆弧AB 上变动. 若,OC xOA yOB =+其中,x y R ∈,则x y + 的最大值是________.18.（2012上海文）在知形ABCD 中,边AB 、AD 的长分别为2、1. 若M 、N 分别是边BC 、CD 上的点,且满足||||||||CD CN BC BM =,则AN AM ⋅的取值范围是_________ .19.（2012课标文）已知向量a ,b 夹角为045,且|a |=1,|2-a b |=10,则|b |=_______. 20.（2012湖南文）如图4,在平行四边形ABCD 中 ,AP ⊥BD,垂足为P,3AP =且APAC = _____.A DBCP21.（2012湖北文）已知向量(1,0),(1,1)a b ==,则(Ⅰ)与2a b +同向的单位向量的坐标表示为____________; (Ⅱ)向量3b a -与向量a 夹角的余弦值为____________.22.（2012北京文）已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE CB ⋅的值为________. 23.（2012安徽文）设向量(1,2),(1,1),(2,)a m b m c m ==+=,若()a c +⊥b ,则a =_____.24.（2012江苏）如图,在矩形ABCD 中,22AB BC ==，，点E 为BC 的中点,点F 在边CD上,若2AB AF =,则AE BF 的值是___.25.（2012安徽理）若平面向量,a b 满足:23a b -≤;则a b 的最小值是_____三、解答题26. (2009年广东卷文)（已知向量)2,(sin -=θa 与)cos ,1(θ=b 互相垂直，其中)2,0(πθ∈（1）求θsin 和θcos 的值（2）若ϕϕθcos 53)cos(5=-，<<ϕ02π,求ϕcos 的值 27.（2009上海卷文）已知ΔABC 的角A 、B 、C 所对的边分别是a 、b 、c ，设向量(,)m a b =， (sin ,sin )n B A =，(2,2)p b a =-- .（1） 若m //n ，求证：ΔABC 为等腰三角形； （2） 若m ⊥p ，边长c = 2，角C =3π，求ΔABC 的面积 . 28. 已知A 、B 、C 分别为ABC △的三边a 、b 、c 所对的角，向量)sin ,(sin B A m =，)cos ,(cos A B n =，且C n m 2sin =⋅.（Ⅰ）求角C 的大小；（Ⅱ）若A sin ，C sin ，B sin 成等差数列，且18)(=-⋅AC AB CA ，求边c 的长.【课后作业】一、选择题1.（2009辽宁卷理）平面向量a 与b 的夹角为060，(2,0)a =，1b = 则2a b +=( )A.B. C. 4 D. 22.（2009宁夏海南卷理）已知O ，N ，P 在ABC ∆所在平面内，且,0OA OB OC NA NB NC ==++=，且PA PB PB PC PC PA •=•=•，则点O ，N ，P 依次是ABC ∆的( )A. 重心 外心 垂心B. 重心 外心 内心C. 外心 重心 垂心D. 外心 重心 内心3.（2008安徽）在平行四边形ABCD 中，AC 为一条对角线，若(2,4)AB =，(1,3)AC =,则BD =（ ）A ． （－2，－4）B ．（－3，－5）C ．（3，5）D ．（2，4）4.（2008浙江）已知a ，b 是平面内两个互相垂直的单位向量，若向量c 满足0)()(=-⋅-c b c a ,则c 的最大值是( )A. 1B. 2C.2 D.225.（2007海南、宁夏）已知平面向量(11)(11)==-，，，a b ，则向量1322-=a b（ ） A ．(21)--， B ．(21)-，C ．(10)-，D ．(12)，6.（2007湖南）设，a b 是非零向量，若函数()()()f x x x =+-a b a b 的图象是一条直线，则必有（ ）A ．⊥a bB ．∥a bC ．||||=a bD ．||||≠a b7. （2007天津）设两个向量22(2cos )λλα=+-，a 和sin 2m m α⎛⎫=+ ⎪⎝⎭，b ，其中mλα，，为实数．若2=a b ，则mλ的取值范围是 （ ） A ．[-6，1]B ．[48]，C ．（-6，1]D ．[-1，6]8. 在ABC BC AB ABC ∆︒︒=︒︒=∆则已知向量中),27cos 2,63cos 2(),72cos ,18(cos ,的面积等于（ ） A ．22 B ．42 C ．23 D ．29. 已知平面向量(3,1),(,3),//,a b x a b x ==-则等于 （ ）A ．9B ．1C ．－1D ．－910. 已知a 、b 是不共线的AB a b λ=+AC a b μ=+(,)R λμ∈，则A 、B 、C 三点共线的充要条件是：（ ）A ．1λμ+=B ．1λμ-=C ．1λμ=-D ．1λμ=二、填空题11. 设向量2,3,19,AB AC AB AC CAB ==+=∠=则_________.12. 若向量,2,2,()a b a b a b a ==-⊥ 满足，则向量b a 与的夹角等于 .13. 已知平面上的向量PA 、PB 满足224PA PB +=,2AB =，设向量2PC PA PB =+，则PC 的最小值是 .14.（2008江苏）a ，b 的夹角为120︒，1a =，3b = 则5a b -= ． 15. （2007安徽）在四面体O ABC -中，OA OB OC D ===，，，a b c 为BC 的中点，E 为AD 的中点，则OE = （用，，a b c 表示）．16.（2007北京）已知向量2411()()，，，a =b =．若向量()λ⊥b a +b ，则实数λ的值是 .17. 已知向量(cos15,sin15)a =，(sin15,cos15)b =--，则a b |+|的值为 .18.（2007广东）若向量a 、b 满足b a b a 与,1==的夹角为120°，则b a b a ··+＝ .三、解答题19.（2009湖南卷文）已知向量(sin ,cos 2sin ),(1,2).a b θθθ=-=（1）若//a b ，求tan θ的值；（2）若||||,0,a b θπ=<<求θ的值。

高一数学平面向量的概念试题答案及解析1.已知向量表示“向东航行1km”，向量表示“向南航行1km”，则向量表示（）A．向东南航行km B．向东南航行2kmC．向东北航行km D．向东北航行2km【答案】A【解析】根据题意由于向量表示“向东航行1km”，向量表示“向南航行1km”，那么可知向量表示向东南航行km ，故选A.【考点】向量的物理意义点评：主要是考查了向量的物理意义的运用，属于基础题。

2.在平行四边形ABCD中, + +等于（）A．B．C．D．【答案】A【解析】结合图形，+ += + += ，故选A。

【考点】本题主要考查平面向量的线性运算。

点评：简单题，在平行四边形中，由平行四边形法则。

注意相等向量及相反向量。

3.已知点，向量，且，则点的坐标为。

【答案】【解析】设点的坐标为（x,y）,则由得，（x-2,y-4）=2(3,4),所以x-2=6,y-4=8，所以x=8,y=12，即点的坐标为。

【考点】本题主要考查平面向量的概念及其坐标运算。

点评：简单题，注意若A（a,b）,B(c,d),则。

4.作用于原点的两个力F1 ="(1,1)" ,F2 ="(2,3)" ,为使得它们平衡，需加力F3=【答案】(-3,-4)【解析】F3=-(F1+F2)=-(3,4)=(-3,-4).5.下列判断正确的是 ( )A．若向量与是共线向量，则A,B,C,D四点共线；B．单位向量都相等；C．共线的向量，若起点不同，则终点一定不同；D．模为0的向量的方向是不确定的。

【答案】D【解析】解：因为A.若向量与是共线向量，则A,B,C,D四点共线；可能构成四边形。

B.单位向量都相等；方向不一样。

C.共线的向量，若起点不同，则终点一定不同；不一定。

D.模为0的向量的方向是不确定的，成立6.下列命题中正确的是（）A．若两个向量相等,则它们的起点和终点分别重合.B．模相等的两个平行向量是相等向量.C．若和都是单位向量,则.D．两个相等向量的模相等.【答案】D【解析】根据向量相等的定义易知两个相等向量的模相等，故选D相等向量只需要模相同，方向相同，所以（1）错；模相等的平行向量有可能方向相反，所以（2）错；都是单位向量，向量的模不一定相同，所以两个向量不一定相等，所以（3）错；相等向量是模相同，方向相同的向量，所以（4）对．解：对于（1），相等向量只需要模相同，方向相同，所以（1）错；对于（2）模相等的平行向量有可能方向相反，所以（2）错；对于（3），都是单位向量，向量的模不一定相同，所以两个向量不一定相等，所以（3）错；对于（4），相等向量是模相同，方向相同的向量，所以（4）对．故选C7.给出下列命题：①向量与是共线向量，则A、B、C、D四点必在一直线上；②两个单位向量是相等向量；③若, ,则；④若一个向量的模为0，则该向量的方向不确定；⑤若,则。

高一数学 第八章 平面向量第一讲 向量的概念与线性运算 一．【要点精讲】 1．向量的概念①向量：既有大小又有方向的量。

几何表示法AB ，a ；坐标表示法),(y x j y i x a =+= 。

向量的模（长度），记作|AB |.即向量的大小，记作｜a|。

向量不能比较大小，但向量的模可以比较大小.②零向量：长度为0的向量，记为0，其方向是任意的，规定0平行于任何向量。

（与0的区别） ③单位向量｜a｜＝1。

④平行向量（共线向量）方向相同或相反的非零向量，记作a ∥b⑤相等向量记为b a=。

大小相等，方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x 2．向量的运算（1）向量加法：求两个向量和的运算叫做向量的加法.如图，已知向量a ，b ，在平面内任取一点A ，作AB =a ，BC =b ，则向量叫做a 与b的和，记作a+b ，即 a+b AB BC AC =+=特殊情况：(1)BBabba +AABC C)2()3(向量加法的三角形法则可推广至多个向量相加：AB BC CD PQ QR AR +++++=，但这时必须“首尾相连”。

②向量减法： 同一个图中画出a b a b +-、要点:向量加法的“三角形法则”与“平行四边形法则”（1）用平行四边形法则时，两个已知向量是要共始点的，和向量是始点与已知向量的始点重合的那条对角线，而差向量是另一条对角线，方向是从减向量指向被减向量。

（2） 三角形法则的特点是“首尾相接”，由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和；差向量是从减向量的终点指向被减向量的终点. （3）实数与向量的积3．两个向量共线定理：向量b 与非零向量a共线⇔有且只有一个实数λ，使得b =a λ。

二．【典例解析】题型一： 向量及与向量相关的基本概念概念 例1判断下列各命题是否正确(1)零向量没有方向 (2)ba ==则 (3)单位向量都相等 (4) 向量就是有向线段(5)两相等向量若共起点,则终点也相同 (6)若b a =，c b =，则c a =；(7)若b a //，c b //，则c a// (8) b a =的充要条件是||||b a =且b a //；(9) 若四边形ABCD 是平行四边形,则DA BC CD B ==,A练习. (四川省成都市一诊)在四边形ABCD 中，“AB →＝2DC →”是“四边形ABCD 为梯形”的 A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件题型二: 考查加法、减法运算及相关运算律 例2 化简)()(BD AC CD AB ---=练习1.下列命题中正确的是 A ．OA OB AB -= B ．0AB BA +=C ．00AB ⋅=D ．AB BC CD AD ++=2.化简AC -BD +CD -AB 得 A ．AB B ．DA C ． D ．03．如图，D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点，则( )A.AD →＋BE →＋CF →＝0B.BD →－CF →＋DF →＝0C.AD →＋CE →－CF →＝0D.BD →－BE →－FC →＝0题型三: 结合图型考查向量加、减法例3在ABC ∆所在的平面上有一点P ，满足PA PB PC AB ++=，则PBC ∆与ABC ∆的面积之比是( )A ．13B ．12C ．23D ．34例4重心、垂心、外心性质练习: 1．如图，在ΔABC 中，D 、E 为边AB 的两个三等分点，CA →=3a ，CB → =2b ，求CD → ，CE → ． 2已知a b a b+-=求证a b ⊥3若O 为ABC ∆的内心，且满足()(2)0OB OC OB OC OA -⋅+-=，则ABC ∆的形状为（ ）A.等腰三角形B.正三角形C.直角三角形D.钝角三角形4．已知O 、A 、B 是平面上的三个点，直线AB 上有一点C ，满足2AC →＋CB →＝0，则OC →＝( ) A ．2OA →－OB → B ．－OA →＋2OB →C.23OA →－13OB → D ．－13OA →＋23OB → 5．已知平面上不共线的四点O ，A ，B ，C .若OA →－3OB →＋2OC →＝0，则|AB →||BC →|等于________．6．已知平面内有一点P 及一个△ABC ，若PA →＋PB →＋PC →＝AB →，则( )A ．点P 在△ABC 外部B ．点P 在线段AB 上C ．点P 在线段BC 上D ．点P 在线段AC 上ABDE7．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ等于( ) A.23 B.13 C ．－13 D ．－23 题型四: 三点共线问题例 4 设21,e e 是不共线的向量,已知向量2121212,3,2e e e e e k e -=+=+=,若A,B,D 三点共线,求k 的值例5已知A 、B 、C 、P 为平面内四点， A 、B 、C 三点在一条直线上 PC → =mPA → +nPB →，求证： m+n=1．练习：1．已知：2121212 ,B),(3e e e +=-=+=，则下列关系一定成立的是（ ）A 、A ，B ，C 三点共线 B 、A ，B ，D 三点共线 C 、C ，A ，D 三点共线 D 、B ，C ，D 三点共线2．(原创题)设a ，b 是两个不共线的向量，若AB →＝2a ＋k b ，CB →＝a ＋b ，CD →＝2a －b ，且A ，B ，D 三点共线，则实数k 的值等于________．第2讲 平面向量的基本定理与坐标表示 一．【要点精讲】1．平面向量的基本定理如果21,e e 是一个平面内的两个不共线向量，那么对这一平面内的任一向量a ，有且只有一对实数21,λλ使：2211e e a λλ+=其中不共线的向量21,e e 叫做表示这一平面内所有向量的一组基底. 2．平面向量的坐标表示如图，在直角坐标系内，我们分别取与x 轴、y 轴方向相同的_单位向量_ i 、j 作为基底a ，有且只有一对实数x 、y ，BC AOM D使得a xi yj =+…………○1，把),(y x 叫做向量a 的（直角）坐标，记作(,)a x y =…………○2其中x 叫做a 在x 轴上的坐标，y 叫做a 在y 轴上的坐标，○2式叫做向量的坐标表示与a 相等的向量的坐标也为,(y x 特别地，(1,0)i =，(0,1)j =，0(0,0)=特别提醒：设yj xi +=，则向量的坐标),(y x 就是点A 的坐标；反过来，点A 的坐标),(y x 也就是向量的坐标在平面直角坐标系内，每一个平面向量都是可以用一对实数唯一表示3．平面向量的坐标运算（1）若11(,)a x y =，22(,)b x y =，则a b +=1212(,)x x y y ++，a b -= 1212(,)x x y y --（2） 若),(11y x A ，),(22y x B ，则AB = （3）若(,)a x y =和实数λ，则a λ=(,)x y λλ4．向量平行的充要条件的坐标表示：设a=(x 1, y 1) ，b =(x 2, y 2) 其中b ≠aa ∥b (b≠)的充要条件是12210x y x y -=二．【典例解析】题型一. 利用一组基底表示平面内的任一向量[例1] 在△OAB 中，21,41==，AD 与BC 交于点M ，设OA =a ，OB =b ，用a ,b 表示OM .练习:1．若已知1e 、2e 是平面上的一组基底，则下列各组向量中不能作为基底的一组是 ( ) A ．1e 与—2e B ．31e 与22e C ．1e ＋2e 与1e —2e D ．1e 与21e 2．在平行四边形ABCD 中，E 和F 分别是边CD 和BC 的中点，若AC →＝λAE →＋μAF →，其中λ、μ∈R ，则λ＋μ＝________.题型二: 向量加、减、数乘的坐标运算 例 3 已知A （—2,4）、B （3,—1）、C （—3,—4）且3=,2=,求点M 、N 的坐标及向量的坐标.练习:1. (2008年高考辽宁卷)已知四边形ABCD 的三个顶点A (0,2)，B (－1，－2)，C (3,1)，且BC →＝2AD →，则顶点D 的坐标为( )A ．(2，72)B ．(2，－12) C ．(3,2) D ．(1,3)2．若M(3, -2) N(-5, -1) 且 12MP =MN , 求P 点的坐标；3．若M(3, -2) N(-5, -1)，点P 在MN 的延长线上，且 12MP MN =,求P 点的坐标；4.(2009年广东卷文)已知平面向量a =,1x （） ，b =2,x x （－）， 则向量+a b ( )A 平行于x 轴B.平行于第一、三象限的角平分线C.平行于y 轴D.平行于第二、四象限的角平分线5．在三角形ABC 中，已知A (2,3)，B (8，－4)，点G (2，－1)在中线AD 上，且AG →＝2GD →， 则点C 的坐标是( )A ．(－4,2)B ．(－4，－2)C ．(4，－2)D ．(4,2)6．设向量a ＝(1，－3)，b ＝(－2,4)，c ＝(－1，－2)，若表示向量4a 、4b －2c 、2(a －c )、d 的有向线段首尾相接能构成四边形，则向量d 为( )A ．(2,6)B ．(－2,6)C ．(2，－6)D ．(－2，－6)7．已知A (7,1)、B (1,4)，直线y ＝12ax 与线段AB 交于C ，且AC →＝2CB →，则实数a 等于( ) A ．2 B ．1 C.45 D.53 题型三: 平行、共线问题例4已知向量(1sin ,1)θ=-a ，1(,1sin )2θ=+b ，若a ∥b ，则锐角θ等于（ ）A ．30︒B ． 45︒C ．60︒D ．75︒例5．（2009北京卷文）已知向量(1,0),(0,1),(),a b c ka b k R d a b ===+∈=-， 如果//c d 那么( )A ．1k =且c 与d 同向B ．1k =且c 与d 反向C ．1k =-且c 与d 同向D ．1k =-且c 与d 反向练习：1．若向量a=(-1,x)与b =(-x, 2)共线且方向相同，求x2．已知点O(0，0)，A(1，2)，B(4，5)及AB t OA OP +=，求(1)t 为何值时，P 在x 轴上？P 在y 轴上？P 在第二象限。

高一平面向量知识点及典例平面向量是高一数学学习中的重要内容，它不仅在数学中有着广泛的应用，还在物理、工程等领域发挥着重要作用。

本文将介绍高一平面向量的基本概念、性质和典型例题，希望能帮助同学们更好地理解和应用平面向量。

一、平面向量的概念平面向量是由大小和方向共同确定的有向线段，通常用大写字母表示。

平面向量AB可以记作→AB，其中A称为起点，B称为终点。

平面向量还可以用坐标表示，例如向量→AB可以表示为AB的坐标 (x, y)。

二、平面向量的性质1. 平面向量的加法与减法给定两个平面向量→AB和→CD，可以进行向量的加法和减法运算。

向量加法的结果是一个新的向量→EF，满足→EF = →AB +→CD；向量减法的结果是一个新的向量→GH，满足→GH =→AB - →CD。

2. 平面向量的数量积平面向量→AB和→CD的数量积记作→AB·→CD，表示两个向量的数量积等于向量→AB的模长乘以向量→CD在→AB上的投影长度。

若→AB·→CD = 0，则称向量→AB与→CD垂直。

3. 平面向量的数量积性质平面向量的数量积具有以下性质：交换律（→AB·→CD =→CD·→AB）、分配律（→AB·(→CD +→EF) = →AB·→CD +→AB·→EF）以及数量积与平移无关等。

三、平面向量的典型例题1. 例题一已知向量→AB = (3, 4)，→CD = (5, -2)，求→AB +→CD的坐标。

解：向量→AB +→CD的坐标为(3+5, 4+(-2)) = (8, 2)。

2. 例题二设向量→AB = (2, -3)，→CD = (4, 1)，求→AB·→CD的值。

解：→AB·→CD = (2*4)+(-3*1) = 5。

3. 例题三如图所示，在△ABC中，向量→AB = (2, 3)，向量→BC = (4, 1)，求向量→AC的坐标。

高一平面向量的知识点归纳总结一、向量的概念和表示法在平面几何中，向量是具有大小和方向的量，可以用有序数对表示。

表示为AB或→AB，其中A为向量的起点，B为终点。

二、向量的运算1. 向量加法向量加法满足交换律和结合律。

设有向量→AB和→CD，则→AB+→CD=→AC。

2. 向量减法向量减法的定义：→AB-→AC=→CB。

3. 数乘数乘的定义：k→AB=(k, k)×→AB，其中k为实数。

三、向量的性质1. 零向量零向量的定义：→0=→AB-→AB，其大小为0。

2. 向量共线向量共线的定义：若存在实数k，使得k→AB=→CD，则→AB与→CD共线。

3. 向量相等向量相等的定义：两个向量→AB和→CD相等，当且仅当它们的起点和终点坐标相等。

四、向量的数量积1. 数量积的定义向量数量积的定义：→AB·→CD=|→AB|·|→CD|·cosθ，其中θ为两个向量的夹角。

2. 数量积的性质（1）交换律：→AB·→CD=→CD·→AB（2）分配律：→AB·(→CD+→EF)=→AB·→CD+→AB·→EF（3）数量积与夹角的关系：若θ为两个向量的夹角，则→AB·→CD=|→AB|·|→CD|·cosθ五、平面向量的坐标表示1. 平面直角坐标系平面直角坐标系在平面上确定了一个原点O和两个互相垂直的单位向量i和j。

2. 平面向量的坐标表示平面向量的坐标表示：→AB=(x2-x1, y2-y1)，其中A(x1, y1)为向量的起点，B(x2, y2)为终点。

3. 向量共线的判断向量共线的判断：若两个向量→AB和→CD的坐标之比相等，则→AB与→CD共线。

六、向量的线性运算1. 向量的线性组合向量的线性组合：若有向量→AB和→CD，则k→AB+l→CD为向量的线性组合，其中k和l为实数。

2. 向量的线性相关与线性无关（1）若存在不全为0的实数k和l，使得k→AB + l→CD = →0，则称→AB和→CD线性相关。

高一数学平面向量的知识点引言高一数学中，平面向量是一个重要的概念。

它不仅在数学中有广泛的应用，还在物理、工程等领域中扮演着重要的角色。

掌握好平面向量的知识点，对于学生的整体数学素养的提升是至关重要的。

本文将从平面向量的定义、表示和运算等几个方面进行讲解。

一. 平面向量的定义平面向量是指具有大小和方向的量，用箭头表示。

平面向量通常用大写字母表示，例如A，A。

这个箭头的长度表示向量的大小，箭头的指向表示向量的方向。

平面向量的大小通常用模表示，记作|A|。

二. 平面向量的表示平面向量可以用坐标表示，也可以用点表示。

用坐标表示时，一个向量分别由x和y方向的分量表示。

例如，向量A的坐标表示为(AA,AA)或A=AA+AA，其中A和A分别是该向量在x和y方向上的分量。

用点表示时，可以用起点和终点表示一个向量。

例如，向量A的点表示为AA。

三. 平面向量的运算1. 向量的加法和减法向量的加法和减法都遵循平行四边形法则。

加法表示两个向量的合成，减法表示两个向量的分解。

2. 向量的数乘向量的数乘是指一个向量与一个实数相乘。

数乘的结果是一个新的向量，它的大小是原向量大小的绝对值倍，方向与原向量相同（如果实数为正）或相反（如果实数为负）。

3. 向量的数量积向量的数量积又称为内积或点积，用符号·表示。

数量积的结果是一个实数。

数量积满足交换律和分配律，并且与夹角的余弦有密切的关系，即A·A=|A||A|cosθ，其中θ为两个向量之间的夹角。

四. 平面向量的应用平面向量在几何、物理等领域有着广泛的应用。

以下是一些典型的应用：1. 几何定理证明平面向量在几何中的应用主要体现在定理证明中。

例如，可以用平面向量证明中点四边形对角线平分定理等。

2. 向量的分解向量的分解是平面向量的重要应用之一。

通过将一个向量分解成若干个平行于坐标轴的分量，使得计算变得简单而直观。

3. 力的合成与分解在物理学中，力的合成与分解是平面向量的重要应用之一。

环 球 雅 思 教 育 学 科 教 师 讲 义讲义编号： ______________ 副校长/组长签字： 签字日期：【考纲说明】1、理解平面向量的概念和几何表示，掌握向量的加、减、数乘运算及其几何意义，会用坐标表示.2、了解平面向量的基本定理，掌握平面向量的坐标运算.3、本部分在高考中占5分.【趣味链接】1、向量最初被应用于物理学，被称之为矢量。

很多物理量，如力、速度、位移、电场强度、磁场强度等都是向量.2、大约公元前350年，古希腊著名学者亚里士多德就知道了力可以表示为向量，向量一词来自力学、解析几何中的有向线段.3、大陆与台湾在2008年12月25日开通了直航，在此之前乘飞机要先从台北到香港，再从香港到上海，这里发生了两次位移.【知识梳理】一、 向量的基本概念与线性运算 1、向量的概念（1）向量：既有大小又有方向的量，记作AB ；向量的大小即向量的模（长度），记作|AB|，向量不能比较大小，但向量的模可以比较大小．（2）零向量：长度为0的向量，记为0 ，其方向是任意的，0与任意向量平行.（3）单位向量：模为1个单位长度的向量，常用e 表示．（4）平行向量（共线向量）：方向相同或相反的非零向量，记作a ∥b，平行向量也称为共线向量（5）相等向量：长度相等且方向相同的向量，相等向量经过平移后总可以重合，记为b a=，大小相等，方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x .（6）相反向量：与a 长度相等、方向相反的向量，叫做a 的相反向量.记作a-,零向量的相反向量仍是零向量.若a 、b是互为相反向量，则a =b -,b =a -,a +b =0 .2、向量的线性运算（1）向量的加法：求两个向量和的运算叫做向量的加法.向量加法满足交换律与结合律；向量加法有“三角形法则”与“平行四边形法则”.（2）向量的减法 ：求向量a 加上b 的相反向量的运算叫做a 与b的差．向量的减法有三角形法则，b a -可以表示为从b 的终点指向a 的终点的向量（a 、b有共同起点）.（3）向量的数乘运算：求实数λ与向量a 的积的运算，记作λa．①a a ⋅=λλ；②当0>λ时，λa 的方向与a 的方向相同；当0<λ时，λa 的方向与a的方向相反； 当0=λ时，0 =a λ，方向是任意的.③数乘向量满足交换律、结合律与分配律. 二、平面向量的基本定理与坐标表示 1、平面向量的基本定理如果21,e e 是一个平面内的两个不共线向量，那么对这一平面内的任一向量a，有且只有一对实数21,λλ使：2211e e a λλ+=，其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底.2、平面向量的坐标表示（1）在直角坐标系中，分别取与x 轴、y 轴方向相同的两个单位向量,i j作为基底. 由平面向量的基本定理知，该平面内的任一向量a 可表示成a xi yj =+ ，由于a 与数对(x,y)是一一对应的，因此把(x,y)叫做向量a的坐标，记作a =(x,y)，其中x 叫作a在x 轴上的坐标，y 叫做在y 轴上的坐标.显然0 =（0,0），(1,0)i = ，(0,1)j =．（2）设OA xi y j =+.则向量OA 的坐标(x,y)就是终点A 的坐标，即若OA =(x,y)，则A 点的坐标为(x,y)，反之亦成立ECBA（O 是坐标原点）． 3、平面向量的坐标运算（1）若()()1122,,,a x y b x y == ，则()1212,a b x x y y ±=±±．（2）若()()2211,,,y x B y x A ，则()2121,AB x x y y =-- ，AB =（3）若a =(x,y)，则λa=(λx, λy)．（4）若()()1122,,,a x y b x y == ，则1221//0a b x y x y ⇔-=． （5）若()()1122,,,a x y b x y == ，则1212a b x x y y ⋅=⋅+⋅．【经典例题】【例1】（2010全国）△ABC 中，点D 在边AB 上，CD 平分∠ACB ，若CB a =，CA b =，1,2a b ==，则CD =（ ） A.1233a b +B.2133a b +C.3455a b +D.4355a b + 【例2】（2009湖南）如图，D ，E ，F 分别是∆ABC 的边AB ，BC ，CA 的中点，则( )A ．0AD BE CF ++=B ．0BD CF DF -+=C ．0AD CE CF +-= D ．0BD BE FC --=【例3】（2009全国）设非零向量a 、b 、c 满足c b a c b a =+==|,|||||，则>=<b a , （ ）A ．150° B.120° C.60° D.30°【例4】（2012辽宁）已知两个非零向量a ,b 满足|a +b |=|a -b |,则下面结论正确的是（ ） A ．a ∥b B ．a ⊥b C ．{0,1,3} D ．a +b =a -b【例5】(2009广东)已知平面向量a =,1x （），b =2,x x （－），则向量+a b ( )A. 平行于x 轴B. 平行于第一、三象限的角平分线C. 平行于y 轴D. 平行于第二、四象限的角平分线【例6】（2012浙江）设a ,b 是两个非零向量，以下说法正确的是（ ）A ．若|a +b |=|a |-|b |,则a ⊥bB ．若a ⊥b ,则|a +b |=|a |-|b |C ．若|a +b |=|a |-|b |,则存在实数λ,使得a =λbD ．若存在实数λ,使得a =λb ,则|a +b |=|a |-|b |【例7】若向量,2,()a b a b a b a ==-⊥满足，则向量b a 与的夹角等于 .【例8】已知平面上的向量PA 、PB满足224PA PB += ,2AB = ，设向量2PC PA PB =+ ，则PC 的最小值是 .【例9】（2009湖南）已知向量(sin ,cos 2sin ),(1,2).a b θθθ=-=（1）若//a b ，求tan θ的值；（2）若||||,0,a b θπ=<< 求θ的值。

高一知识点总结平面向量高一知识点总结：平面向量引言：高一是学习数学的一个重要阶段，学生们会接触到许多新的数学概念。

其中一个重要的概念是平面向量。

平面向量既有理论性的意义，又具有广泛的应用价值。

本文将总结高一阶段学习的关于平面向量的知识点。

一、平面向量的定义和表示方式1.1 平面向量的定义平面向量是具有大小和方向的量，可以用有向线段表示。

它由起点和终点确定，起点表示向量的起点，终点表示向量的方向和大小。

1.2 平面向量的表示方式平面向量可以用坐标表示，也可以用字母表示。

以字母表示时，通常用大写字母表示向量，如A、B，用小写字母表示向量的坐标，如a、b。

二、平面向量的运算2.1 平面向量的加法平面向量的加法满足平行四边形法则。

即把一个向量的起点与另一个向量的终点相连，新向量的起点为第一个向量的起点，终点为第二个向量的终点。

2.2 平面向量的数乘平面向量的数乘就是将向量的模长与一个实数相乘。

三、平面向量的性质3.1 平行向量若两个向量的方向相同或相反，且模长成比例，则它们为平行向量。

3.2 垂直向量若两个向量的数量积为零，则它们为垂直向量。

3.3 向量的模长向量的模长即向量的长度，可以通过勾股定理计算。

四、平面向量的坐标表示4.1 向量的坐标表示向量的坐标表示是通过向量的终点坐标减去起点坐标得出的差值。

4.2 向量相等的条件两个向量相等的充要条件是它们的起点和终点坐标分别相等。

五、平面向量的应用5.1 向量的平移通过平移向量可以将一个向量的起点变为另一个点，且起点、终点、大小和方向不变。

5.2 向量的投影当一个向量与另一个向量垂直时，可以通过计算数量积得到向量在另一个向量上的投影。

5.3 向量的共线与共面若两个向量共线，则它们可以表示同一直线上的不同点。

若三个向量共面，则它们可以表示同一个平面上的不同点。

结论：平面向量是高一数学中一个重要的概念，掌握平面向量的定义、表示方式以及运算法则是解决平面向量相关问题的基础。

平面向量一. 向量的根本看法与根本运算1向量的看法：①向量：既有大小又有方向的量向量一般用 a, b ,c 来表示，或用有向线段的起点与终uuur uuuryj ( x, y) 向点的大写字母表示，如： AB几何表示法AB ，a；坐标表示法 a xiuuur即向量的大小，记作｜ a ｜量的大小即向量的模〔长度〕，记作 | AB |向量不能够比较大小，但向量的模能够比较大小．②零向量：长度为0 的向量，记为0，其方向是任意的，0与任意向量平行零向量 a ＝0r r｜ a ｜＝0由于 0的方向是任意的，且规定0 平行于任何向量，故在有关向量平行〔共线〕的问题中务必看清楚可否有“非零向量〞这个条件．〔注意与 0 的差异〕③单位向量：模为 1 个单位长度的向量向量a0为单位向量｜a0｜＝ 1④平行向量〔共线向量〕：方向相同或相反的非零向量任意一组平行向量都能够移到同素来线上方向相同或相反的向量，称为平行向量记作 a ∥ b 由于向量能够进行任意的平移( 即自由向量 ) ，平行向量总能够平移到同素来线上，故平行向量也称为共线向量⑤相等向量：长度相等且方向相同的向量相等向量经过平移后总能够重合，记为a b 大小相等，方向相同 (x1 , y1 ) (x2 , y2 )x1x2 y1y22向量加法求两个向量和的运算叫做向量的加法uuur r uuur r r uuur uuur uuur设 AB a, BC b ，那么a+b=AB BC=AC〔1〕0 a a 0 a ；〔2〕向量加法满足交换律与结合律；向量加法有“三角形法那么〞与“平行四边形法那么〞：（1〕用平行四边形法那么时，两个向量是要共始点的，和向量是始点与向量的始点重合的那条对角线，而差向量是另一条对角线，方向是从减向量指向被减向量（2〕三角形法那么的特点是“首尾相接〞，由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和；差向量是从减向量的终点指向被减向量的终点当两个向量的起点公共时，用平行四边形法那么；当两向量是首尾连接时，用三角形法那么．向量加法的三角形法那么可实行至多个向量相加：1uuur uuur uuurL uuur uuur uuurAB BC CD PQ QR AR ，但这时必定“首尾相连〞．3 向量的减法①相反向量：与 a 长度相等、方向相反的向量，叫做 a 的相反向量记作 a ,零向量的相反向量仍是零向量关于相反向量有：〔 i 〕( a) = a； (ii) a +( a )=( a )+ a = 0 ；(iii) 假设a、b是互为相反向量，那么a = b , b = a , a + b = 0②向量减法：向量 a 加上b的相反向量叫做 a 与b的差，记作： a b a ( b) 求两个向量差的运算，叫做向量的减法③作图法： a b 能够表示为从 b 的终点指向a的终点的向量〔 a 、b有共同起点〕4实数与向量的积：①实数λ与向量 a 的积是一个向量，记作λ a ，它的长度与方向规定以下：〔Ⅰ〕a a ；〔Ⅱ〕当0 时，λa的方向与a的方向相同；当0 时，λa的方向与a的方向相反；当0 时， a 0，方向是任意的②数乘向量满足交换律、结合律与分配律5两个向量共线定理：向量 b 与非零向量a共线有且只有一个实数，使得b= a6平面向量的根本定理：若是 e1 , e2是一个平面内的两个不共线向量，那么对这一平面内的任向来量 a ，有且只有一对实数1 , 2 使：a1e1 2 e2，其中不共线的向量e1 , e2叫做表示这一平面内所有向量的一组基底7特别注意 :（1〕向量的加法与减法是互逆运算（2〕相等向量与平行向量有差异，向量平行是向量相等的必要条件（3〕向量平行与直线平行有差异，直线平行不包括共线〔即重合〕，而向量平行那么包括共线〔重合〕的情况（4〕向量的坐标与表示该向量的有向线条的始点、终点的详尽地址没关，只与其相对地址有关2二. 平面向量的坐标表示1 平面向量的坐标表示：在直角坐标系中，分别取与r rx 轴、 y 轴方向相同的两个单位向量 i , j 作为基底 由平面向量的根本定理知，该平面内的任向来量r r r rr 是一一 a 可表示成 a xi yj ，由于 a 与数对 (x,y) r r r对应的，因此把 (x,y) 叫做向量 a 的坐标，记作 a =(x,y) ，其中 x 叫作 a 在 x 轴上的坐标， y叫做在 y 轴上的坐标(1) 相等的向量坐标相同，坐标相同的向量是相等的向量(2) 向量的坐标与表示该向量的有向线段的始点、终点的详尽地址没关，只与其相对位置有关2 平面向量的坐标运算：(1) r x 1, y 1 rx 2 , y 2 r rx 1 x 2 , y 1 y 2 假设 a,b ，那么a b 假设 A x 1 ,y 1, B x 2 , y 2 uuur (2) ，那么 AB x 2 x 1, y 2 y 1 (3) r =(x,y) ，那么 r x, y)假设aa =((4) rx 1, y 1 rx 2 , y 2 r rx 1 y 2 x 2 y 1 0假设 a,b，那么 a // b(5) rx 1, y 1 r x 2 , y 2 r rx 1 x 2y 1 y 2假设 a,b ，那么 a brry 1 y 2 0假设a b ，那么 x 1 x 23 向量的运算向量的加减法，数与向量的乘积，向量的数量〔内积〕及其各运算的坐标表示和性质运 算 几何方法坐标方法 运算性质种类向 1 平行四边形法那么 r ra b b a量2 三角形法那么a b (x 1 x 2, y 1 y 2)的 (a b) c a (b c)加法uuur uuur uuurAB BC AC向 三角形法那么rra b a ( b )量a b (x 1 x 2,y 1 y 2)的 uuur uuur 减AB BA法uuur uuur uuurOB OA AB 3向a 是一个向量 ,a( x, y)( a)()a 量 满足 :的>0 时 ,a 与 a 同()aaa 乘 向 ;法<0 时 ,a 与 a 异( ab )ab向 ;=0 时,a = 0a ∥b a b向 a ?b 是一个数rrx 1x 2 y 1 y 2 a ? bb ? a量 a?b的a0 或 b 0时 ,???数( a) b a ( b)(a b)量 a?b =0 (ab) ?c a?cb ?c积a0 且 b 0 时 ,a 2 | a |2 , | a | x 2 y 2a?b | || |cos ,| a ? b | | a || b |a b a b三．平面向量的数量积1 两个向量的数量积：两个非零向量 rrr rr rrra 与b ，它们的夹角为，那么 a · b =︱ a ︱·︱ b ︱cos叫做 a 与 b 的数量积〔或内积〕r r规定 0 arr rr r2=a b向量的投影： ︱ b ︱ cosr∈ R ，称为向量 b 在 a 方向上的投影投影的绝对值称| a |为射影3r r r r r数量积的几何意义： a · b 等于 a 的长度与 b 在 a 方向上的投影的乘积4 向量的模与平方的关系：r r r 2 r 2a a a | a |5 乘法公式成立：r r r r r 2 r 2r 2 r 2a b a b a b ab ；r r 2 r 2 r r r 2 r 2r r r 2ab a2a b ba 2a bb6 平面向量数量积的运算律：4①交换律成立： r rr r a bb a②对实数的结合律成立：r r r r r r Ra ba b a b③分配律成立：r r r r r r r rr r a b ca cb c ca b特别注意：〔 1〕结合律不成立：r r r r r r；a b ca b cr r r rr r〔2〕消去律不成立 a b a c 不能够获取b cr rr r r r 〔3〕 a b =0 不能够获取 a =0 或 b=07 两个向量的数量积的坐标运算：rrr ry 1 y 2两个向量 a( x 1 , y 1 ), b( x 2 , y 2 ) ，那么 a · b =x 1 x 28 向量的夹角：r r uuur r uuur r已 知 两 个 非 零 向 量 a 与 b ， 作 OA = a , OB = b , 那么 ∠AOB=〔 0 01800〕叫做向量 r ra 与b 的夹角r rr r x 1x 2 y 1 y 2cos = cosa ?ba,b r r = 22x 2 22a ? bx 1 y 1 y 2当且仅当两个非零向量rr 0 r r 0ra 与b 同方向时， θ=0 ，当且仅当 a 与 b 反方向时θ =180 ，同时 0与其他任何非零向量之间不谈夹角这一问题rrr r r r9 垂直：若是 a 与 b 的夹角为 90 那么称 a 与b 垂直，记作 a ⊥ b10 两个非零向量垂直的充要条件 ：a ⊥ba·b＝ Ox 1x 2y 1 y 2 0 平面向量数量积的性质题型 1. 根本看法判断正误 ：（ 1〕共线向量就是在同一条直线上的向量.（ 2〕假设两个向量不相等，那么它们的终点不能能是同一点.（ 3〕与向量共线的单位向量是唯一的.〔4〕四边形 ABCD 是平行四边形的条件是uuur uuurAB CD .uuur uuur〔5〕假设 AB CD ，那么 A 、 B 、 C 、 D 四点构成平行四边形 .〔6 〕由于向量就是有向线段，因此数轴是向量.〔7 r rr r r r〕假设 a 与 b 共b 与 c 共线，那么 a 与 c 共线 .线，〔8r r r r〕假设 mamb ，那么a b .5rr n .〔9〕假设mana ，那么mr rr r〔10〕假设 a 与 b 不共线，那么a 与b 都不是零向量 . r r r r r r〔11〕假设 a b | a | | b | ，那么 a / /b .r r r r r r〔12〕假设 |a b | | a b | ，那么 a b .题型 2. 向量的加减运算1. rrr r.设 a 表示“向东走 8km 〞 ,b 表示“向北走 6km 〞 , 那么 |ab |2.uuur uuur uuur uuur uuuur. 化简 (AB MB ) (BO BC ) OMuuur uuur3 uuur3. |OA|5, |OB|, 那么 | AB |的最大值和最小值分别为、 .4.uuur uuur uuuruuur r uuurr uuuruuurAC 为 AB 与 AD 的和向量，且 AC a, BDb ，那么 AB， AD5.uuur3 uuur uuuruuuruuuruuur点 C 在线段 AB 上，且 ACAB ,那么ACBC ， ABBC .5题型 3. 向量的数乘运算1.r r r rr r rrr 计算：〔 1〕 3(a b) 2( a b)〔 2〕 2(2 a 5b 3c)3( 2a3b2.rr3,8) ，那么 r1r.a (1, 4),b (3ab题型 4.2作图法球向量的和r rr 1 rr3r向量 a,b ，如以以下图，请做出向量3a2 b 和2ab .r2arb题型 5. 依照图形由向量求未知向量1. 在 ABC 中， D 是 BC 的中点，请用向量uuur uuur uuurAB ，AC 表示 AD . 2.uuur r uuurr uuur uuur 在平行四边形 ABCD 中， ACa, BD b ，求 AB 和 AD ..r2c )题型 6. 向量的坐标运算uuur (4,5) A(2,3) ，那么点 B 的坐标是1. AB， .uuur( 3, 5) ， P(3,7) ，那么点 Q 的坐标是2. PQ.r r r4) , 那么合力的坐标为.3. 假设物体受三个力 F 1 (1,2) , F 2 ( 2,3),F 3 ( 1,6rr(5, 2) r r r r r r4. a( 3,4) ， b，求 a b ， a b ， 3a 2b .ruuur5. A(1,2), B(3,2) , 向量2, x 3y 2) 与 AB 相等，求 x, y 的值 .a (x6. uuur uuur uuur (uuur . AB (2,3) ， BC (m, n) ， CD 1,4) ，那么DA7. O 是坐标原点， A(2,1),B( 4,8)uuur uuur r uuur，且 AB 3BC 0 ，求 OC 的坐标 .题型 7. 判断两个向量可否作为一组基底ur uur1. e 1 ,e 2 是平面内的一组基底，判断以下每组向量可否能构成一组基底：ur uur ur uur uruuruurururuuruururuur uur urA.e 1 e 2和e 1e 2B.3e 1 2e 2 和4e 2 6e 1 C.e 1 3e 2和e 23e 1 D.e 2和e 2e 12.r(3,4) ，能与 r〕aa 构成基底的是〔A. (3,4)B.(4,3) C.(3,4)D. (1,4)5 55 5553题型 8. 结合三角函数求向量坐标uuur1. O 是坐标原点，点uuur2 ， xOAA 在第二象限， | OA | 150o ，求 OA 的坐标 . 2.uuur 4 3 xOA uuurO 是原点，点 A 在第一象限， | OA | ， 60o ，求 OA 的坐标 .题型 9. 求数量积rr 4 r r 的夹角为 60 or rr r r 1. | a | 3,| b | ，且 a 与 b ，求〔 1〕 a b ，〔 2〕 a ( a b) ，r 1 r r r r r r〔3〕 ( a 2 b) b ，〔 4〕 (2 a b ) (a 3b ) .r(2, r ( 8,10) r r r rrr r2. a 6), b ，求〔 1〕 | a |,| b | ，〔2〕 a b ，〔 3〕 a (2 a b ) ，r r r r〔4〕 (2 a b ) (a 3b ) .题型 10. 求向量的夹角71. rrr r12 r r | a |8,| b | 3 ， a b ，求 a 与 b 的夹角 .2. rr( 2 3, 2) r r a( 3,1), b ，求 a 与 b 的夹角 .3. A(1,0) ， B(0,1) ， C (2,5)，求 cos BAC .题型 11. 求向量的模rrr r or r r r 1. | a |3,| b | 4 ，且 a 与 b 的夹角为 60 ，求〔 1〕 | a b | ，〔 2〕 | 2a 3b |.rr( 8,10) r r r r r 1 r2. a(2, 6), b，求〔 1〕 | a |,| b | ，〔5〕 | a b | ，〔 6〕 | a 2 b |.r r2 r r3 rr3. | a | 1，|b | ， | 3a 2b |，求 | 3a b | .r r r 题型 12. 求单位向量a【与 a 平行的单位向量： e r】| a |1. r(12,5) 平行的单位向量是.与 a2. r1) 平行的单位向量是.与 m( 1,2题型 13. 向量的平行与垂直rr1. rrr r a(6,2) ， b (3,m) ，当 m 为何值时，〔 1〕 a / /b ？〔 2〕 a b ？rrr r r r垂直？2. a (1,2) ， b( 3,2) ，〔 1〕 k 为何值时，向量 ka b 与 a 3b 〔2〕 k 为何值时，向量 r r r rka b 与 a 3b 平行？rr r r r rr r rr3. a 是非零向量，a b a c ，且 bc ，求证： a (b c) .题型 14. 三点共线问题 1. A(0,2) ， B(2, 2) ， C (3, 4) ，求证： A, B,C 三点共线 .8uuur2r r uuur r r uuur r r2.设AB2(a5b), BC2a8b,CD3(a b) ，求证：A、B、D三点共线.3.uuur r r uuur r r uuur r r. AB a2b, BC5a6b, CD7a2b ，那么必然共线的三点是4. A(1,3)， B(8,1) ，假设点 C (2a1,a2) 在直线 AB 上，求 a 的值.5.已知四个点的坐标 O(0,0) ， A(3, 4) ， B( 1,2) ， C (1,1) ，是否存在常数 t ，使uuur uuur uuurOA tOB OC 成立？题型 15. 判断多边形的形状1.uuur r uuur r uuur uuur.假设AB3e， CD5e ，且| AD | | BC |,那么四边形的形状是2. A(1,0) ， B(4,3)， C(2,4) ， D (0, 2) ，证明四边形ABCD 是梯形.3. A( 2,1)，B(6,3) ， C (0,5) ，求证：ABC 是直角三角形.4.在平面直角坐标系内，三角形 . uuur uuur uuur(1,3) ,求证：ABC 是等腰直角OA( 1,8), OB( 4,1),OC题型 16. 平面向量的综合应用1.r r r r r ra(1,0) ， b(2,1) ，当k为何值时，向量ka b 与 a3b 平行？2.r( 3,r r r ra5) ，且a b ，| b | 2 ，求b的坐标.3.r r r r r ra与 b 同向， b(1,2) ，那么ab10，求 a 的坐标.3.r r(3,1)r(5,4)r r r a(1,2) ， b， c，那么 c a b .9rr(3,4) r(5,0) ，请将用向量 rrr4. a(5,10) ， b ， ca, b 表示向量 c .rrrrm 的范围；5. a(m,3) ， b(2, 1) ，〔 1〕假设 a 与 b 的夹角为钝角，求rr（ 2〕假设 a 与 b 的夹角为锐角，求 m 的范围 .rr( 3,m) r r r r6. a(6,2) ， b，当 m 为何值时，〔 1〕 a 与 b 的夹角为钝角？〔 2〕 a 与 b的夹角为锐角？7. 梯形ABCD 的极点坐标分别为 A( 1,2) ， B(3, 4) ， D (2,1) ，且 AB / / DC ，AB 2CD ，求点 C 的坐标 .8. 平行四边形ABCD 的三个极点的坐标分别为A(2,1) ， B( 1,3) ，C (3, 4) ，求第四个极点 D 的坐标.9. 一航船以 5km/h 的速度向垂直于对岸方向行驶，航船实质航行方向与水流方向成 30o 角，求水流速度与船的实质速度 .10. ABC 三个极点的坐标分别为A(3, 4) ， B(0,0) ， C (c,0) ，uuur uuur〔1〕假设 AB AC 0 ，求 c 的值；〔 2〕假设 c5 ，求 sin A 的值 .【备用】1. rr r r r r r r | a |3,| b | 4,| a b | 5，求 | a b |和向量 a, b 的夹角 .2. rr r ur r r r rr r r urx a b ， y 2a b ，且 | a | | b | 1， ab ，求 x, y 的夹角的余弦 .1. rr2,r r r r.a(1,3),b (1) ，那么 (3a 2b) (2a 5b)rr (2, r r r r4. 两向量 a(3, 4), b 1) ，求当 a xb 与 a b 垂直时的 x 的值 . 5.rr (2, r r的范围 .两向量 a(1,3), b ) ， a 与b 的夹角 为锐角，求10rr r r的取值范围 .变式： 假设a( , 2), b ( 3,5) ， a 与 b 的夹角 为钝角，求选择、填空题的特别方法：1. 代入考据法r r(1, r( 1, 2) r例：向量 a (1,1),b1),c ，那么c 〔〕A.1 r3 r1 r3 rC.3 r1rD.3 r1 rab B.a bab ab222222 222. 消除法uuur例： M 是 ABC 的重心，那么以下向量与AB 共线的是〔〕uuuur uuur uuur uuuur uuur uuur uuur uuur uuuur uuuur uuuur A. AM MB BC B. 3AM AC C. AB BC AC D. AM BM CM11。

高一数学 第八章 平面向量第一讲 向量的概念与线性运算 一．【要点精讲】 1．向量的概念①向量：既有大小又有方向的量。

几何表示法AB ，a ；坐标表示法),(y x j y i x a =+= 。

向量的模（长度），记作|AB |.即向量的大小，记作｜a|。

向量不能比较大小，但向量的模可以比较大小.②零向量：长度为0的向量，记为0，其方向是任意的，规定0平行于任何向量。

（与0的区别） ③单位向量｜a｜＝1。

④平行向量（共线向量）方向相同或相反的非零向量，记作a ∥b⑤相等向量记为b a=。

大小相等，方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x 2．向量的运算（1）向量加法：求两个向量和的运算叫做向量的加法.如图，已知向量a ，b ，在平面内任取一点A ，作AB =a ，BC =b ，则向量叫做a 与b的和，记作a+b ，即 a+b AB BC AC =+=特殊情况：(1)BBabba +AABC C)2()3(向量加法的三角形法则可推广至多个向量相加：AB BC CD PQ QR AR +++++=，但这时必须“首尾相连”。

②向量减法： 同一个图中画出a b a b +-、要点:向量加法的“三角形法则”与“平行四边形法则”（1）用平行四边形法则时，两个已知向量是要共始点的，和向量是始点与已知向量的始点重合的那条对角线，而差向量是另一条对角线，方向是从减向量指向被减向量。

（2） 三角形法则的特点是“首尾相接”，由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和；差向量是从减向量的终点指向被减向量的终点. （3）实数与向量的积3．两个向量共线定理：向量b 与非零向量a共线⇔有且只有一个实数λ，使得b =a λ。

二．【典例解析】题型一： 向量及与向量相关的基本概念概念 例1判断下列各命题是否正确(1)零向量没有方向 (2)==则 (3)单位向量都相等 (4) 向量就是有向线段(5)两相等向量若共起点,则终点也相同 (6)若b a =，c b =，则c a =；(7)若b a //，c b //，则c a // (8) b a =的充要条件是||||b a =且b a //；(9) 若四边形ABCD 是平行四边形,则DA BC CD B ==,A练习. (四川省成都市一诊)在四边形ABCD 中，“AB →＝2DC →”是“四边形ABCD 为梯形”的 A 、充分不必要条件 B 、必要不充分条件 C 、充要条件 D 、既不充分也不必要条件题型二: 考查加法、减法运算及相关运算律 例2 化简)()(---=练习1.下列命题中正确的是 A ．OA OB AB -= B ．0AB BA +=C ．00AB ⋅=D ．AB BC CD AD ++=2.化简AC -BD +CD -AB 得A ．AB B ．C ．D ．3．如图，D 、E 、F 分别是△ABC 的边AB 、BC 、CA 的中点，则( ) A.AD →＋BE →＋CF →＝0 B.BD →－CF →＋DF →＝0 C.AD →＋CE →－CF →＝0 D.BD →－BE →－FC →＝0题型三: 结合图型考查向量加、减法例3在ABC ∆所在的平面上有一点P ，满足PA PB PC AB ++=，则PBC ∆与ABC ∆的面积之比是( )A ．13B ．12C ．23D ．34例4重心、垂心、外心性质练习: 1．如图，在ΔABC 中，D 、E 为边AB 的两个三等分点，CA →=3a ，CB → =2b ，求CD → ，CE → ． 2已知a b a b+-=求证a b ⊥3若O 为ABC ∆的内心，且满足()(2)0OB OC OB OC OA -⋅+-=，则ABC ∆的形状为（ ）A.等腰三角形B.正三角形C.直角三角形D.钝角三角形4．已知O 、A 、B 是平面上的三个点，直线AB 上有一点C ，满足2AC →＋CB →＝0，则OC →＝( ) A ．2OA →－OB → B ．－OA →＋2OB →C.23OA →－13OB → D ．－13OA →＋23OB →ABDE5．已知平面上不共线的四点O ，A ，B ，C .若OA →－3OB →＋2OC →＝0，则|AB →||BC →|等于________．6．已知平面内有一点P 及一个△ABC ，若PA →＋PB →＋PC →＝AB →，则( )A ．点P 在△ABC 外部B ．点P 在线段AB 上C ．点P 在线段BC 上D ．点P 在线段AC 上7．在△ABC 中，已知D 是AB 边上一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ等于( )A.23B.13 C ．－13 D ．－23 题型四: 三点共线问题例 4 设21,e e 是不共线的向量,已知向量2121212,3,2e e e e e k e -=+=+=,若A,B,D 三点共线,求k 的值例5已知A 、B 、C 、P 为平面内四点， A 、B 、C 三点在一条直线上 PC → =mPA → +nPB → ，求证： m+n=1．练习：1．已知：2121212 ,B),(3e e e +=-=+=，则下列关系一定成立的是（ ）A 、A ，B ，C 三点共线 B 、A ，B ，D 三点共线 C 、C ，A ，D 三点共线 D 、B ，C ，D 三点共线2．(原创题)设a ，b 是两个不共线的向量，若AB →＝2a ＋k b ，CB →＝a ＋b ，CD →＝2a －b ，且A ，B ，D 三点共线，则实数k 的值等于________．第2讲 平面向量的基本定理与坐标表示 一．【要点精讲】1．平面向量的基本定理如果21,e e 是一个平面内的两个不共线向量，那么对这一平面内的任一向量a ，有且只有一对BC AOM D实数21,λλ使：2211e e a λλ+=其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底.2．平面向量的坐标表示如图，在直角坐标系内，我们分别取与x 轴、y 轴方向相同的_单位向量_ i 、j 作为基底任作一个向量a ，有且只有一对实数x 、y ，使得a xi yj =+…………○1，把),(y x 叫做向量a 的（直角）坐标，记作(,)a x y =…………○2其中x 叫做a 在x 轴上的坐标，y 叫做a 在y 轴上的坐标，○2式叫做向量的坐标表示与a 相等的向量的坐标也为,(y x 特别地，(1,0)i =，(0,1)j =，0(0,0)=特别提醒：设yj xi +=，则向量的坐标),(y x 就是点A 的坐标；反过来，点A 的坐标),(y x 也就是向量的坐标因此，在平面直角坐标系内，每一个平面向量都是可以用一对实数唯一表示3．平面向量的坐标运算（1）若11(,)a x y =，22(,)b x y =，则a b +=1212(,)x x y y ++，a b -= 1212(,)x x y y --（2） 若),(11y x A ，),(22y x B ，则AB = （3）若(,)a x y =和实数λ，则a λ=(,)x y λλ4．向量平行的充要条件的坐标表示：设a=(x 1, y 1) ，b =(x 2, y 2) 其中b ≠aa ∥b (b≠)的充要条件是12210x y x y -=二．【典例解析】题型一. 利用一组基底表示平面内的任一向量[例1] 在△OAB 中，21,41==，AD 与BC 交于点M ，设OA =a ，OB =b ，用a ,b 表示OM .练习:1．若已知1e 、2e 是平面上的一组基底，则下列各组向量中不能作为基底的一组是 ( )A ．1e 与—2eB ．31e 与22eC ．1e ＋2e 与1e —2eD ．1e 与21e 2．在平行四边形ABCD 中，E 和F 分别是边CD 和BC 的中点，若AC →＝λAE →＋μAF →，其中λ、μ∈R ，则λ＋μ＝________.题型二: 向量加、减、数乘的坐标运算 例 3 已知A （—2,4）、B （3,—1）、C （—3,—4）且CA CM 3=,CB CN 2=,求点M 、N 的坐标及向量MN 的坐标.练习:1. (2008年高考辽宁卷)已知四边形ABCD 的三个顶点A (0,2)，B (－1，－2)，C (3,1)，且BC →＝2AD →，则顶点D 的坐标为( )A ．(2，72)B ．(2，－12) C ．(3,2) D ．(1,3)2．若M(3, -2) N(-5, -1) 且 12MP =MN , 求P 点的坐标；3．若M(3, -2) N(-5, -1)，点P 在MN 的延长线上，且 12MP MN =,求P 点的坐标；4.(2009年广东卷文)已知平面向量a =,1x （） ，b =2,x x （－）， 则向量+a b ( )A 平行于x 轴B.平行于第一、三象限的角平分线C.平行于y 轴D.平行于第二、四象限的角平分线5．在三角形ABC 中，已知A (2,3)，B (8，－4)，点G (2，－1)在中线AD 上，且AG →＝2GD →， 则点C 的坐标是( )A ．(－4,2)B ．(－4，－2)C ．(4，－2)D ．(4,2)6．设向量a ＝(1，－3)，b ＝(－2,4)，c ＝(－1，－2)，若表示向量4a 、4b －2c 、2(a －c )、d 的有向线段首尾相接能构成四边形，则向量d 为( )A ．(2,6)B ．(－2,6)C ．(2，－6)D ．(－2，－6)7．已知A (7,1)、B (1,4)，直线y ＝12ax 与线段AB 交于C ，且AC →＝2CB →，则实数a 等于( )A ．2B ．1 C.45 D.53题型三: 平行、共线问题例4已知向量(1sin ,1)θ=-a ，1(,1sin )2θ=+b ，若a ∥b ，则锐角θ等于（ ）A ．30︒B ． 45︒C ．60︒D ．75︒例5．（2009北京卷文）已知向量(1,0),(0,1),(),a b c ka b k R d a b ===+∈=-， 如果//c d 那么( )A ．1k =且c 与d 同向B ．1k =且c 与d 反向C ．1k =-且c 与d 同向D ．1k =-且c 与d 反向练习：1．若向量a=(-1,x)与b =(-x, 2)共线且方向相同，求x2．已知点O(0，0)，A(1，2)，B(4，5)及AB t OA OP +=，求(1)t 为何值时，P 在x 轴上？P 在y 轴上？P 在第二象限。

高一的平面向量知识点归纳总结平面向量是数学中的一种重要概念，它具有方向和大小。

在高一数学学习中，平面向量是一个重要的知识点。

在这篇文章中，我将对高一平面向量的相关知识进行归纳总结，以帮助大家更好地理解和应用平面向量的概念。

一、平面向量的定义和表示方法平面向量是由有序的数对表示的。

我们通常用大写的字母加箭头表示平面向量，如AB→表示从点A到点B的平面向量。

平面向量的表示方法有坐标表示、单位向量表示和分解表示。

1. 坐标表示：假设A和B两点的坐标分别为A(x₁, y₁)和B(x₂, y₂)，则向量AB→的坐标表示为(Δx, Δy)，其中Δx = x₂ - x₁，Δy = y₂ - y₁。

2. 单位向量表示：单位向量是长度为1的向量，表示方向而不考虑大小。

我们可以通过求出向量AB→的模长，然后将向量AB→除以它的模长，得到单位向量。

3. 分解表示：平面向量可以分解为两个分量，即横坐标和纵坐标的分量。

假设向量AB→的坐标表示为(Δx, Δy)，则向量AB→可以表示为AB→ = Δx * i + Δy * j，其中i和j分别表示x轴和y轴的单位向量。

二、平面向量的运算法则平面向量有加法、减法和数量乘法三种运算法则，这些法则可以帮助我们对平面向量进行运算和求解。

1. 向量的加法：向量的加法是指将两个向量相加，得到一个新的向量。

假设向量A→和向量B→的坐标表示分别为(Δx₁, Δy₁)和(Δx₂, Δy₂)，则向量A→ + B→的坐标表示为(Δx₁ + Δx₂, Δy₁+ Δy₂)。

2. 向量的减法：向量的减法是指将一个向量减去另一个向量，得到一个新的向量。

假设向量A→和向量B→的坐标表示分别为(Δx₁, Δy₁)和(Δx₂, Δy₂)，则向量A→ - B→的坐标表示为(Δx₁ - Δx₂, Δy₁ - Δy₂)。

3. 数量乘法：数量乘法是指将一个向量乘以一个实数，得到一个新的向量。

假设向量A→的坐标表示为(Δx, Δy)，实数k，则数量乘积kA→的坐标表示为(kΔx, kΔy)。

1．平面向量基本定理如果e 1、e 2是同一平面内两个不共线的向量，那么对于这一平面内的任一向量a ，有且只有一对实数λ1、λ2，使a ＝λ1e 1＋λ2e 2.其中，不共线的向量e 1、e 2叫做表示这一平面内所有向量的一组基底． 2．平面向量的坐标运算(1)向量加法、减法、数乘及向量的模 设a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ＋b ＝(x 1＋x 2，y 1＋y 2)，a －b ＝(x 1－x 2，y 1－y 2)，λa ＝(λx 1，λy 1)，|a |＝x 21＋y 21. (2)向量坐标的求法①若向量的起点是坐标原点，则终点坐标即为向量的坐标．②设A (x 1，y 1)，B (x 2，y 2)，则AB →＝(x 2－x 1，y 2－y 1)，|AB →|＝(x 2－x 1)2＋(y 2－y 1)2. 3．平面向量共线的坐标表示设向量a ＝(x 1，y 1)，b ＝(x 2，y 2) (a ≠0)，如果a ∥b ，那么x 1y 2－x 2y 1＝0；反过来，如果x 1y 2－x 2y 1＝0，那么a ∥b . 【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”) (1)平面内的任何两个向量都可以作为一组基底．( × )(2)若a ，b 不共线，且λ1a ＋μ1b ＝λ2a ＋μ2b ，则λ1＝λ2，μ1＝μ2.( √ )(3)平面向量的基底不唯一，只要基底确定后，平面内的任何一个向量都可被这组基底唯一表示．( √ )(4)若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b 的充要条件可表示成x 1x 2＝y 1y 2.( × )(5)当向量的起点在坐标原点时，向量的坐标就是向量终点的坐标．( √ )1．设e 1，e 2是平面内一组基底，那么下列说法正确的是________(填序号)． ①若实数λ1，λ2使λ1e 1＋λ2e 2＝0，则λ1＝λ2＝0；②空间内任一向量a 可以表示为a ＝λ1e 1＋λ2e 2(λ1，λ2为实数)； ③对实数λ1，λ2，λ1e 1＋λ2e 2不一定在该平面内；④对平面内任一向量a ，使a ＝λ1e 1＋λ2e 2的实数λ1，λ2有无数对． 答案 ①2．在△ABC 中，点D 在BC 边上，且CD →＝2DB →，CD →＝rAB →＋sAC →，则r ＋s ＝________. 答案 0解析 因为CD →＝2DB →，所以CD →＝23CB →＝23(AB →－AC →)＝23AB →－23AC →，则r ＋s ＝23＋⎝⎛⎭⎫－23＝0. 3．在▱ABCD 中，AC 为一条对角线，AB →＝(2,4)，AC →＝(1,3)，则向量BD →的坐标为__________． 答案 (－3，－5)解析 ∵AB →＋BC →＝AC →，∴BC →＝AC →－AB →＝(－1，－1)， ∴BD →＝AD →－AB →＝BC →－AB →＝(－3，－5)．4．设0＜θ＜π2，向量a ＝(sin 2θ，cos θ)，b ＝(cos θ，1)，若a ∥b ，则tan θ＝________.答案 12解析 ∵a ∥b ，∴sin 2θ×1－cos 2 θ＝0， ∴2sin θcos θ－cos 2 θ＝0，∵0＜θ＜π2，∴cos θ＞0，∴2sin θ＝cos θ，∴tan θ＝12.5．(教材改编)已知▱ABCD 的顶点A (－1，－2)，B (3，－1)，C (5,6)，则顶点D 的坐标为________． 答案 (1,5)解析 设D (x ，y )，则由AB →＝DC →，得(4,1)＝(5－x,6－y )，即⎩⎪⎨⎪⎧ 4＝5－x ，1＝6－y ，解得⎩⎪⎨⎪⎧x ＝1，y ＝5.题型一 平面向量基本定理的应用例1 (1)在梯形ABCD 中，AB ∥CD ，AB ＝2CD ，M ，N 分别为CD ，BC 的中点，若AB →＝λAM →＋μAN →，则λ＋μ＝________.(2)如图，在△ABC 中，AN →＝13NC →，P 是BN 上的一点，若AP →＝mAB →＋211AC →，则实数m 的值为________． 答案 (1)45 (2)311解析 (1)因为AB →＝AN →＋NB →＝AN →＋CN →＝AN →＋(CA →＋AN →)＝2AN →＋CM →＋MA →＝2AN →－14AB →－AM →，所以AB →＝85AN →－45AM →，所以λ＋μ＝45.(2)设BP →＝kBN →，k ∈R . 因为AP →＝AB →＋BP →＝AB →＋kBN → ＝AB →＋k (AN →－AB →)＝AB →＋k (14AC →－AB →)＝(1－k )AB →＋k 4AC →，且AP →＝mAB →＋211AC →，所以1－k ＝m ，k 4＝211，解得k ＝811，m ＝311.思维升华 (1)应用平面向量基本定理表示向量的实质是利用平行四边形法则或三角形法则进行向量的加、减或数乘运算．(2)用向量基本定理解决问题的一般思路是先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决．(1)在平行四边形ABCD 中，AB →＝e 1，AC →＝e 2，NC →＝14AC →，BM →＝12MC →，则MN →＝________.(用e 1，e 2表示)(2)如图，已知点G 是△ABC 的重心，过G 作直线与AB ，AC 两边分别交于M ，N 两点，且AM →＝xAB →，AN →＝yAC →，则xy x ＋y的值为________．答案 (1)－23e 1＋512e 2 (2)13解析 (1)如图，MN →＝CN →－CM →＝CN →＋2BM →＝CN →＋23BC →＝－14AC →＋23(AC →－AB →)＝－14e 2＋23(e 2－e 1)＝－23e 1＋512e 2.(2)易知AG →＝13AB →＋13AC →，MN →＝－xAB →＋yAC →，故MG →＝⎝⎛⎭⎫13－x AB →＋13AC →.由于MG →与MN →共线，所以⎝⎛⎭⎫13－x y ＝－13x ， 即xy ＝13(x ＋y )，因此xy x ＋y ＝13.题型二 平面向量的坐标运算例2 (1)已知a ＝(5，－2)，b ＝(－4，－3)，若a －2b ＋3c ＝0，则c ＝________. (2)已知点A (1,3)，B (4，－1)，则与向量A B →同方向的单位向量为__________． 答案 (1)⎝⎛⎭⎫－133，－43 (2)⎝⎛⎭⎫35，－45 解析 (1)由已知3c ＝－a ＋2b ＝(－5,2)＋(－8，－6)＝(－13，－4)．所以c ＝⎝⎛⎭⎫－133，－43. (2)A B →＝O B →－O A →＝(4，－1)－(1,3)＝(3，－4)， ∴与A B →同方向的单位向量为A B→|A B →|＝⎝⎛⎭⎫35，－45. 思维升华 向量的坐标运算主要是利用加、减、数乘运算法则进行计算．若已知有向线段两端点的坐标，则应先求出向量的坐标，解题过程中要注意方程思想的运用及正确使用运算法则．(1)已知点A (－1,5)和向量a ＝(2,3)，若AB →＝3a ，则点B 的坐标为__________．(2)在△ABC 中，点P 在BC 上，且BP →＝2PC →，点Q 是AC 的中点，若P A →＝(4,3)，PQ →＝(1,5)，则BC →＝________.答案 (1)(5,14) (2)(－6,21)解析 (1)设点B 的坐标为(x ，y )，则AB →＝(x ＋1，y －5)．由AB →＝3a ，得⎩⎪⎨⎪⎧ x ＋1＝6，y －5＝9，解得⎩⎪⎨⎪⎧x ＝5，y ＝14.(2)BC →＝3PC →＝3(2PQ →－P A →)＝6PQ →－3P A →＝(6,30)－(12,9)＝(－6,21)．题型三 向量共线的坐标表示命题点1 利用向量共线求向量或点的坐标例3 (1)已知平面向量a ＝(1,2)，b ＝(－2，m )，且a ∥b ，则2a ＋3b ＝________.(2)已知梯形ABCD ，其中AB ∥CD ，且DC ＝2AB ，三个顶点A (1,2)，B (2,1)，C (4,2)，则点D 的坐标为________． 答案 (1)(－4，－8) (2)(2,4)解析 (1)由a ＝(1,2)，b ＝(－2，m )，且a ∥b ， 得1×m ＝2×(－2)，即m ＝－4. 从而b ＝(－2，－4)，那么2a ＋3b ＝2(1,2)＋3(－2，－4)＝(－4，－8)． (2)∵在梯形ABCD 中，AB ∥CD ，DC ＝2AB ， ∴DC →＝2AB →.设点D 的坐标为(x ，y )，则DC →＝(4,2)－(x ，y )＝(4－x,2－y )， AB →＝(2,1)－(1,2)＝(1，－1)，∴(4－x,2－y )＝2(1，－1)，即(4－x,2－y )＝(2，－2)，∴⎩⎪⎨⎪⎧ 4－x ＝2，2－y ＝－2，解得⎩⎪⎨⎪⎧x ＝2，y ＝4，故点D 的坐标为(2,4)． 命题点2 利用向量共线求参数例4 若三点A (1，－5)，B (a ，－2)，C (－2，－1)共线，则实数a 的值为________． 答案 －54解析 AB →＝(a －1,3)，AC →＝(－3,4)，根据题意AB →∥AC →，∴4(a －1)＝3×(－3)，即4a ＝－5， ∴a ＝－54.命题点3 求交点坐标例5 已知点A (4,0)，B (4,4)，C (2,6)，则AC 与OB 的交点P 的坐标为________． 答案 (3,3)解析 方法一 由O ，P ，B 三点共线，可设OP →＝λOB →＝(4λ，4λ)，则AP →＝OP →－OA →＝(4λ－4,4λ)． 又AC →＝OC →－OA →＝(－2,6)，由AP →与AC →共线，得(4λ－4)×6－4λ×(－2)＝0，解得λ＝34，所以OP→＝34OB →＝(3,3)，所以点P 的坐标为(3,3)． 方法二 设点P (x ，y )，则OP →＝(x ，y )，因为OB →＝(4,4)，且OP →与OB →共线，所以x 4＝y 4，即x ＝y .又AP →＝(x －4，y )，AC →＝(－2,6)，且AP →与AC →共线， 所以(x －4)×6－y ×(－2)＝0，解得x ＝y ＝3， 所以点P 的坐标为(3,3)．思维升华 平面向量共线的坐标表示问题的常见类型及解题策略(1)利用两向量共线求参数．如果已知两向量共线，求某些参数的取值时，利用“若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b 的充要条件是x 1y 2＝x 2y 1”解题比较方便．(2)利用两向量共线的条件求向量坐标．一般地，在求与一个已知向量a 共线的向量时，可设所求向量为λa (λ∈R )，然后结合其他条件列出关于λ的方程，求出λ的值后代入λa 即可得到所求的向量．(3)三点共线问题．A ，B ，C 三点共线等价于AB →与AC →共线．设OA →＝(－2,4)，OB →＝(－a,2)，OC →＝(b,0)，a >0，b >0，O 为坐标原点，若A ，B ，C 三点共线，则1a ＋1b 的最小值为________．答案3＋222解析 由题意得AB →＝(－a ＋2，－2)，AC →＝(b ＋2，－4)， 又AB →∥AC →，所以(－a ＋2，－2)＝λ(b ＋2，－4)，即⎩⎪⎨⎪⎧－a ＋2＝λ(b ＋2)，－2＝－4λ，整理得2a ＋b ＝2， 所以1a ＋1b ＝12(2a ＋b )(1a ＋1b )＝12(3＋2a b ＋b a )≥12(3＋22a b ·b a )＝3＋222(当且仅当b ＝2a 时，等号成立)．11．解析法(坐标法)在向量中的应用典例 (14分)给定两个长度为1的平面向量OA →和OB →，它们的夹角为2π3.如图所示，点C 在以O 为圆心的AB 上运动．若OC →＝xOA →＋yOB →，其中x ，y ∈R ，求x ＋y 的最大值．思维点拨 可以建立平面直角坐标系，将向量坐标化，求出点A ，B 的坐标，用三角函数表示出点C 的坐标，最后转化为三角函数求最值． 规范解答解 以O 为坐标原点，OA →所在的直线为x 轴建立平面直角坐标系，如图所示，则A (1,0)，B (－12，32)．[4分]设∠AOC ＝α(α∈[0，2π3])，则C (cos α，sin α)，由OC →＝xOA →＋yOB →，得⎩⎨⎧cos α＝x －12y ，sin α＝32y ，所以x ＝cos α＋33sin α，y ＝233sin α，[8分] 所以x ＋y ＝cos α＋3sin α＝2sin(α＋π6)，[11分]又α∈[0，2π3]，所以当α＝π3时，x ＋y 取得最大值2.[14分]温馨提醒 本题首先通过建立平面直角坐标系，引入向量的坐标运算，然后用三角函数的知识求出x ＋y 的最大值．引入向量的坐标运算使得本题比较容易解决，体现了解析法(坐标法)解决问题的优势，凸显出了向量的代数特征，为用代数的方法研究向量问题奠定了基础．[方法与技巧]1．平面向量基本定理的本质是运用向量加法的平行四边形法则，将向量进行分解． 向量的坐标表示的本质是向量的代数表示，其中坐标运算法则是运算的关键． 2．根据向量共线可以证明点共线；利用两向量共线也可以求点的坐标或参数值． [失误与防范]1．要区分点的坐标和向量的坐标，向量坐标中包含向量大小和方向两种信息；两个向量共线有方向相同、相反两种情况．2．若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b 的充要条件不能表示成x 1x 2＝y 1y 2，因为x 2，y 2有可能等于0，所以应表示为x 1y 2－x 2y 1＝0.A 组 专项基础训练 (时间：40分钟)1.如图，设O 是平行四边形ABCD 两对角线的交点，给出下列向量组： ①AD →与AB →；②DA →与BC →；③CA →与DC →；④OD →与OB →.其中可作为该平面内其他向量的基底的是________． 答案 ①③解析 ①中AD →，AB →不共线；③中CA →，DC →不共线．2．已知平面向量a ＝(1,1)，b ＝(1，－1)，则向量12a －32b ＝________.答案 (－1,2)解析 12a ＝(12，12)，32b ＝(32，－32)，故12a －32b ＝(－1,2)． 3．已知a ＝(1,1)，b ＝(1，－1)，c ＝(－1,2)，则c ＝________. 答案 12a －32b解析 设c ＝λa ＋μb ，∴(－1,2)＝λ(1,1)＋μ(1，－1)，∴⎩⎪⎨⎪⎧－1＝λ＋μ，2＝λ－μ，∴⎩⎨⎧λ＝12，μ＝－32，∴c ＝12a －32b .4．已知向量a ＝(1,2)，b ＝(1,0)，c ＝(3,4)．若λ为实数，(a ＋λb )∥c ，则λ＝________. 答案 12解析 ∵a ＋λb ＝(1＋λ，2)，c ＝(3,4)， 且(a ＋λb )∥c ，∴1＋λ3＝24，∴λ＝12.5．已知|OA →|＝1，|OB →|＝3，OA →·OB →＝0，点C 在∠AOB 内，且OC →与OA →的夹角为30°，设OC →＝mOA →＋nOB →(m ，n ∈R )，则m n 的值为________．答案 3解析 ∵OA →·OB →＝0，∴OA →⊥OB →，以OA 为x 轴，OB 为y 轴建立直角坐标系，OA →＝(1,0)，OB →＝(0，3)，OC →＝mOA →＋nOB →＝(m ，3n )．∵tan 30°＝3n m ＝33，∴m ＝3n ，即mn＝3. 6．已知A (7,1)，B (1,4)，直线y ＝12ax 与线段AB 交于点C ，且AC →＝2CB →，则实数a ＝________.答案 2解析 设C (x ，y )，则AC →＝(x －7，y －1)，CB →＝(1－x,4－y )，∵AC →＝2CB →，∴⎩⎪⎨⎪⎧ x －7＝2(1－x )，y －1＝2(4－y )，解得⎩⎪⎨⎪⎧x ＝3，y ＝3.∴C (3,3)．又∵C 在直线y ＝12ax 上，∴3＝12a ·3，∴a ＝2.7．已知点A (－1,2)，B (2,8)，AC →＝13AB →，DA →＝－13BA →，则CD →的坐标为________．答案 (－2，－4)解析 设点C ，D 的坐标分别为(x 1，y 1)，(x 2，y 2)． 由题意得AC →＝(x 1＋1，y 1－2)，AB →＝(3,6)， DA →＝(－1－x 2,2－y 2)，BA →＝(－3，－6)． 因为AC →＝13AB →，DA →＝－13BA →，所以有⎩⎪⎨⎪⎧ x 1＋1＝1，y 1－2＝2和⎩⎪⎨⎪⎧－1－x 2＝1，2－y 2＝2.解得⎩⎪⎨⎪⎧ x 1＝0，y 1＝4和⎩⎪⎨⎪⎧x 2＝－2，y 2＝0.所以点C ，D 的坐标分别为(0,4)，(－2,0)， 从而CD →＝(－2，－4)．8．已知向量OA →＝(3，－4)，OB →＝(0，－3)，OC →＝(5－m ，－3－m )，若点A ，B ，C 能构成三角形，则实数m 满足的条件是________． 答案 m ≠54解析 由题意得AB →＝(－3,1)，AC →＝(2－m,1－m )，若A ，B ，C 能构成三角形，则AB →，AC →不共线，则－3×(1－m )≠1×(2－m )，解得m ≠54. 9．已知A (1,1)，B (3，－1)，C (a ，b )．(1)若A ，B ，C 三点共线，求a ，b 的关系式；(2)若AC →＝2AB →，求点C 的坐标．解 (1)由已知得AB →＝(2，－2)，AC →＝(a －1，b －1)，∵A ，B ，C 三点共线，∴AB →∥AC →.∴2(b －1)＋2(a －1)＝0，即a ＋b ＝2.(2)∵AC →＝2AB →，∴(a －1，b －1)＝2(2，－2)．∴⎩⎪⎨⎪⎧ a －1＝4，b －1＝－4，解得⎩⎪⎨⎪⎧a ＝5，b ＝－3.∴点C 的坐标为(5，－3)．10．已知点O 为坐标原点，A (0,2)，B (4,6)，OM →＝t 1OA →＋t 2AB →.(1)求点M 在第二或第三象限的充要条件；(2)求证：当t 1＝1时，不论t 2为何实数，A ，B ，M 三点共线．(1)解 OM →＝t 1OA →＋t 2AB →＝t 1(0,2)＋t 2(4,4)＝(4t 2,2t 1＋4t 2)． 当点M 在第二或第三象限时，有⎩⎪⎨⎪⎧4t 2＜0，2t 1＋4t 2≠0， 故所求的充要条件为t 2＜0且t 1＋2t 2≠0.(2)证明 当t 1＝1时，由(1)知OM →＝(4t 2,4t 2＋2)．∵AB →＝OB →－OA →＝(4,4)，AM →＝OM →－OA →＝(4t 2,4t 2)＝t 2(4,4)＝t 2AB →，∴AM →与AB →共线，又有公共点A ，∴A ，B ，M 三点共线．B 组 专项能力提升(时间：15分钟)11．在△ABC 中，点P 是AB 上的一点，且CP →＝23CA →＋13CB →，Q 是BC 的中点，AQ 与CP 的交点为M ，又CM →＝tCP →，则t 的值为________．答案 34解析 ∵CP →＝23CA →＋13CB →， ∴3CP →＝2CA →＋CB →，即2CP →－2CA →＝CB →－CP →.∴2AP →＝PB →，因此P 为AB 的一个三等分点．∵A ，M ，Q 三点共线，∴CM →＝xCQ →＋(1－x )CA →＝x 2CB →＋(x －1)AC → (0<x <1)． ∵CB →＝AB →－AC →，∴CM →＝x 2AB →＋⎝⎛⎭⎫x 2－1AC →. ∵CP →＝CA →－P A →＝－AC →＋13AB →， 且CM →＝tCP →(0<t <1)，∴x 2AB →＋⎝⎛⎭⎫x 2－1AC →＝t ⎝⎛⎭⎫－AC →＋13AB →. ∴x 2＝t 3且x 2－1＝－t ，解得t ＝34. 12．已知向量a ＝(1,2)，b ＝(0,1)，设u ＝a ＋k b ，v ＝2a －b ，若u ∥v ，则实数k 的值为________．答案 －12解析 ∵u ＝(1,2)＋k (0,1)＝(1,2＋k )，v ＝(2,4)－(0,1)＝(2,3)，又u ∥v ，∴1×3＝2(2＋k )，得k ＝－12. 13．已知向量a ＝(1,1)，b ＝(1，－1)，c ＝(2cos α，2sin α)(α∈R )，实数m ，n 满足m a ＋n b ＝c ，则(m －3)2＋n 2的最大值为________．答案 16解析 由m a ＋n b ＝c ，可得⎩⎪⎨⎪⎧m ＋n ＝2cos α，m －n ＝2sin α，故(m ＋n )2＋(m －n )2＝2，即m 2＋n 2＝1，故点M (m ，n )在单位圆上，则点P (3,0)到点M 的距离的最大值为OP ＋1＝3＋1＝4，故(m －3)2＋n 2的最大值为42＝16.14．已知△ABC 和点M 满足MA →＋MB →＋MC →＝0.若存在实数m ，使得AB →＋AC →＝mAM →成立，则m ＝________.答案 3解析 ∵MA →＋MB →＋MC →＝0，∴M 为△ABC 的重心．如图所示，连结AM 并延长交BC 于D ，则D 为BC 的中点．∴AM →＝23AD →. 又AD →＝12(AB →＋AC →)， ∴AM →＝13(AB →＋AC →)， 即AB →＋AC →＝3AM →，∴m ＝3.15．如图所示，A ，B ，C 是圆O 上的三点，线段CO 的延长线与BA 的延长线交于圆O 外的一点D ，若OC →＝mOA →＋nOB →，则m ＋n 的取值范围是________．答案 (－1,0)解析 由题意得，OC →＝kOD →(k ＜0)，又|k |＝|OC →||OD →|＜1，∴－1＜k ＜0. 又∵B ，A ，D 三点共线，∴OD →＝λOA →＋(1－λ)OB →，∴mOA →＋nOB →＝kλOA →＋k (1－λ)OB →，∴m ＝kλ，n ＝k (1－λ)，∴m ＋n ＝k ，从而m ＋n ∈(－1,0)．。

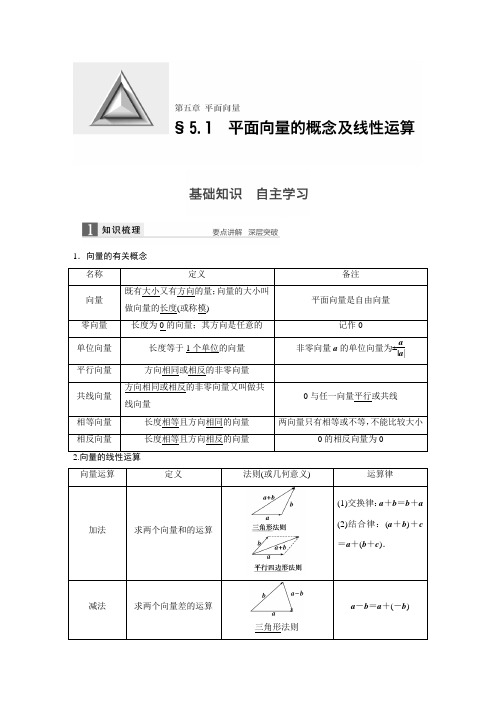
1．向量的有关概念 名称 定义备注向量 既有大小又有方向的量；向量的大小叫做向量的长度(或称模)平面向量是自由向量零向量 长度为0的向量；其方向是任意的记作0单位向量 长度等于1个单位的向量 非零向量a 的单位向量为±a|a |平行向量 方向相同或相反的非零向量共线向量 方向相同或相反的非零向量又叫做共线向量0与任一向量平行或共线 相等向量 长度相等且方向相同的向量 两向量只有相等或不等，不能比较大小相反向量 长度相等且方向相反的向量0的相反向量为02.向量的线性运算 向量运算定义法则(或几何意义)运算律加法求两个向量和的运算(1)交换律：a ＋b ＝b ＋a(2)结合律：(a ＋b )＋c ＝a ＋(b ＋c )．减法 求两个向量差的运算三角形法则a －b ＝a ＋(－b )数乘求实数λ与向量a 的积的运算(1)|λa |＝|λ||a |；(2)当λ>0时，λa 的方向与a 的方向相同；当λ<0时，λa 的方向与a 的方向相反；当λ＝0时，λa＝0(1)λ(μa )＝(λμ)a ；(2)(λ＋μ)a ＝λa ＋μa ； (3)λ(a ＋b )＝λa ＋λb3.共线向量定理对空间任意两个向量a ，b (a ≠0)，a 与b 共线的充要条件是存在实数λ，使得b ＝λa . 【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”)(1)向量与有向线段是一样的，因此可以用有向线段来表示向量．( × ) (2)|a |与|b |是否相等与a ，b 的方向无关．( √ ) (3)若a ∥b ，b ∥c ，则a ∥c .( × )(4)向量AB →与向量CD →是共线向量，则A ，B ，C ，D 四点在一条直线上．( × ) (5)当两个非零向量a ，b 共线时，一定有b ＝λa ，反之成立．( √ ) (6)△ABC 中，D 是BC 中点，则AD →＝12(AC →＋AB →)．( √ )1．给出下列命题：①零向量的长度为零，方向是任意的；②若a ，b 都是单位向量，则a ＝b ；③向量AB →与BA →相等 .则所有正确命题的序号是________． 答案 ①解析 根据零向量的定义可知①正确；根据单位向量的定义可知，单位向量的模相等，但方向不一定相同，故两个单位向量不一定相等，故②错误；向量AB →与BA →互为相反向量，故③错误．2．如图所示，向量a －b ＝________(用e 1，e 2表示)．答案 e 1－3e 2解析 由题图可得a －b ＝BA →＝e 1－3e 2.3．(2015·课标全国Ⅰ改编)设D 为△ABC 所在平面内一点，BC →＝3CD →，则AD →＝______________(用AB →，AC →表示)． 答案 －13AB →＋43AC →解析 ∵BC →＝3CD →，∴AC →－AB →＝3(AD →－AC →)， 即4AC →－AB →＝3AD →，∴AD →＝－13AB →＋43AC →.4．(教材改编)已知▱ABCD 的对角线AC 和BD 相交于O ，且OA →＝a ，OB →＝b ，则DC →＝________，BC →＝________(用a ，b 表示)． 答案 b －a －a －b解析 如图，DC →＝AB →＝OB →－OA →＝b －a ，BC →＝OC →－OB →＝－OA →－OB →＝－a －b .5．已知a 与b 是两个不共线向量，且向量a ＋λb 与－(b －3a )共线，则λ＝________. 答案 －13解析 由已知得a ＋λb ＝－k (b －3a )，∴⎩⎪⎨⎪⎧λ＝－k ，3k ＝1.解得⎩⎨⎧λ＝－13，k ＝13.题型一 平面向量的概念例1 下列命题中，正确的是________．(填序号) ①有向线段就是向量，向量就是有向线段；②向量a 与向量b 平行，则a 与b 的方向相同或相反； ③向量AB →与向量CD →共线，则A 、B 、C 、D 四点共线； ④两个向量不能比较大小，但它们的模能比较大小．答案 ④解析 ①不正确，向量可以用有向线段表示，但向量不是有向线段，有向线段也不是向量； ②不正确，若a 与b 中有一个为零向量，零向量的方向是不确定的，故两向量方向不一定相同或相反；③不正确，共线向量所在的直线可以重合，也可以平行；④正确，向量既有大小，又有方向，不能比较大小；向量的模均为实数，可以比较大小． 思维升华 (1)相等向量具有传递性，非零向量的平行也具有传递性．(2)共线向量即为平行向量，它们均与起点无关．(3)向量可以平移，平移后的向量与原向量是相等向量．解题时，不要把它与函数图象的移动混为一谈．(4)非零向量a 与a |a |的关系：a|a |是与a 同方向的单位向量．设a 0为单位向量，①若a 为平面内的某个向量，则a ＝|a |a 0；②若a 与a 0平行，则a ＝|a |a 0；③若a 与a 0平行且|a |＝1，则a ＝a 0.上述命题中，假命题的个数是________． 答案 3解析 向量是既有大小又有方向的量，a 与|a |a 0的模相同，但方向不一定相同，故①是假命题；若a 与a 0平行，则a 与a 0的方向有两种情况：一是同向，二是反向，反向时a ＝－|a |a 0，故②③也是假命题．综上所述，假命题的个数是3.题型二 平面向量的线性运算命题点1 向量的线性运算例2 (1)设D ，E ，F 分别为△ABC 的三边BC ，CA ，AB 的中点，则EB →＋FC →＝________. (2)在△ABC 中，AB →＝c ，AC →＝b ，若点D 满足BD →＝2DC →，则AD →＝______________(用b ，c 表示)．答案 (1)AD →(2)23b ＋13c解析 (1)EB →＋FC →＝12(AB →＋CB →)＋12(AC →＋BC →)＝12(AB →＋AC →)＝AD →. (2)∵BD →＝2DC →，∴AD →－AB →＝BD →＝2DC →＝2(AC →－AD →)， ∴3AD →＝2AC →＋AB →，∴AD →＝23AC →＋13AB →＝23b ＋13c .命题点2 根据向量线性运算求参数例3 (1)在△ABC 中，已知D 是AB 边上的一点，若AD →＝2DB →，CD →＝13CA →＋λCB →，则λ＝____________.(2)在△ABC 中，点D 在线段BC 的延长线上，且BC →＝3CD →，点O 在线段CD 上(与点C ，D 不重合)，若AO →＝xAB →＋(1－x )AC →，则x 的取值范围是______________． 答案 (1)23(2)⎝⎛⎭⎫－13，0 解析 (1)∵AD →＝2DB →，即CD →－CA →＝2(CB →－CD →)， ∴CD →＝13CA →＋23CB →，∴λ＝23.(2)设CO →＝yBC →， ∵AO →＝AC →＋CO →＝AC →＋yBC →＝AC →＋y (AC →－AB →) ＝－yAB →＋(1＋y )AC →.∵BC →＝3CD →，点O 在线段CD 上(与点C ，D 不重合)， ∴y ∈⎝⎛⎭⎫0，13， ∵AO →＝xAB →＋(1－x )AC →， ∴x ＝－y ，∴x ∈⎝⎛⎭⎫－13，0. 思维升华 平面向量线性运算问题的常见类型及解题策略(1)向量加法或减法的几何意义．向量加法和减法均适合三角形法则．(2)求已知向量的和．一般共起点的向量求和用平行四边形法则；求差用三角形法则；求首尾相连向量的和用三角形法则．(3)求参数问题可以通过研究向量间的关系，通过向量的运算将向量表示出来，进行比较求参数的值．如图，一直线EF 与平行四边形ABCD 的两边AB ，AD 分别交于E ，F 两点，且交对角线AC 于K ，其中，AE →＝25AB →，AF →＝12AD →，AK →＝λAC →，则λ的值为________． 答案 29解析 ∵AE →＝25AB →，AF →＝12AD →，∴AB →＝52AE →，AD →＝2AF →.由向量加法的平行四边形法则可知， AC →＝AB →＋AD →， ∴AK →＝λAC →＝λ(AB →＋AD →) ＝λ⎝⎛⎭⎫52AE →＋2AF → ＝52λAE →＋2λAF →， 由E ，F ，K 三点共线，可得λ＝29.题型三 共线定理的应用例4 设两个非零向量a 与b 不共线，(1)若AB →＝a ＋b ，BC →＝2a ＋8b ，CD →＝3(a －b )，求证：A 、B 、D 三点共线； (2)试确定实数k ，使k a ＋b 和a ＋k b 共线．(1)证明 ∵AB →＝a ＋b ，BC →＝2a ＋8b ，CD →＝3(a －b )， ∴BD →＝BC →＋CD →＝2a ＋8b ＋3(a －b ) ＝2a ＋8b ＋3a －3b ＝5(a ＋b )＝5AB →. ∴AB →、BD →共线，又∵它们有公共点B ， ∴A 、B 、D 三点共线． (2)解 ∵k a ＋b 和a ＋k b 共线， ∴存在实数λ，使k a ＋b ＝λ(a ＋k b )， 即k a ＋b ＝λa ＋λk b .∴(k －λ)a ＝(λk －1)b . ∵a 、b 是两个不共线的非零向量，∴k －λ＝λk －1＝0，∴k 2－1＝0.∴k ＝±1.思维升华 (1)证明三点共线问题，可用向量共线解决，但应注意向量共线与三点共线的区别与联系．当两向量共线且有公共点时，才能得出三点共线．(2)向量a 、b 共线是指存在不全为零的实数λ1，λ2，使λ1a ＋λ2b ＝0成立，若λ1a ＋λ2b ＝0，当且仅当λ1＝λ2＝0时成立，则向量a 、b 不共线．设D ，E 分别是△ABC 的边AB ，BC 上的点，AD ＝12AB ，BE ＝23BC .若DE →＝λ1AB→＋λ2AC →(λ1，λ2为实数)，则λ1＋λ2的值为________． 答案 12解析 DE →＝DB →＋BE →＝12AB →＋23BC →＝12AB →＋23(AC →－AB →) ＝－16AB →＋23AC →，∵DE →＝λ1AB →＋λ2AC →，∴λ1＝－16，λ2＝23，故λ1＋λ2＝12.10．方程思想在平面向量线性运算中的应用典例 (14分)如图所示，在△ABO 中，OC →＝14OA →，OD →＝12OB →，AD 与BC 相交于点M ，设OA →＝a ，OB →＝b .试用a 和b 表示向量OM →.思维点拨 (1)用已知向量来表示另外一些向量是用向量解题的基本要领，要尽可能地转化到平行四边形或三角形中去求解．(2)既然OM →能用a 、b 表示，那我们不妨设出OM →＝m a ＋n b . (3)利用向量共线建立方程，用方程的思想求解． 规范解答解 设OM →＝m a ＋n b ，则AM →＝OM →－OA →＝m a ＋n b －a ＝(m －1)a ＋n b .AD →＝OD →－OA →＝12OB →－OA →＝－a ＋12b .[3分]又∵A 、M 、D 三点共线，∴AM →与AD →共线． ∴存在实数t ，使得AM →＝tAD →， 即(m －1)a ＋n b ＝t ⎝⎛⎭⎫－a ＋12b .[5分] ∴(m －1)a ＋n b ＝－t a ＋12t b .∴⎩⎪⎨⎪⎧m －1＝－t ，n ＝t 2，消去t 得，m －1＝－2n ， 即m ＋2n ＝1.① [8分]又∵CM →＝OM →－OC →＝m a ＋n b －14a ＝⎝⎛⎭⎫m －14a ＋n b ， CB →＝OB →－OC →＝b －14a ＝－14a ＋b .又∵C 、M 、B 三点共线，∴CM →与CB →共线．[11分] ∴存在实数t 1，使得CM →＝t 1CB →， ∴⎝⎛⎭⎫m －14a ＋n b ＝t 1⎝⎛⎭⎫－14a ＋b ， ∴⎩⎪⎨⎪⎧m －14＝－14t 1，n ＝t 1. 消去t 1得，4m ＋n ＝1. ②由①②得m ＝17，n ＝37，∴OM →＝17a ＋37b .[14分]温馨提醒 (1)本题考查了向量的线性运算，知识要点清楚，但解题过程复杂，有一定的难度．(2)易错点是找不到问题的切入口，想不到利用待定系数法求解．(3)数形结合思想是向量加法、减法运算的核心，向量是一个几何量，是有“形”的量，因此在解决向量有关问题时，多数习题要结合图形进行分析、判断、求解，这是研究平面向量最重要的方法与技巧．如本题易忽视A 、M 、D 三点共线和B 、M 、C 三点共线这个几何特征．(4)方程思想是解决本题的关键，要注意体会．[方法与技巧]1．向量的线性运算要满足三角形法则和平行四边形法则，做题时，要注意三角形法则与平行四边形法则的要素．向量加法的三角形法则要素是“首尾相接，指向终点”；向量减法的三角形法则要素是“起点重合，指向被减向量”；平行四边形法则要素是“起点重合”． 2．证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得出三点共线．3．对于三点共线有以下结论：对于平面上的任一点O ，OA →，OB →不共线，满足OP →＝xOA →＋yOB →(x ，y ∈R )，则P ，A ，B 共线⇔x ＋y ＝1. [失误与防范]1．解决向量的概念问题要注意两点：一是不仅要考虑向量的大小，更重要的是要考虑向量的方向；二是考虑零向量是否也满足条件．要特别注意零向量的特殊性．2．在利用向量减法时，易弄错两向量的顺序，从而求得所求向量的相反向量，导致错误．A 组 专项基础训练 (时间：40分钟)1．给出下列四个命题，其中所有正确命题的序号是___________________．①a 与b 共线，b 与c 共线，则a 与c 也共线；②任意两个相等的非零向量的始点与终点是一个平行四边形的四顶点；③向量a 与b 不共线，则a 与b 都是非零向量；④有相同起点的两个非零向量不平行． 答案 ③解析 由于零向量与任一向量都共线，所以命题①中的b 可能为零向量，从而不正确；由于数学中研究的向量是自由向量，所以两个相等的非零向量可以在同一直线上，而此时就构不成四边形，更不可能是一个平行四边形的四个顶点，所以命题②不正确；向量的平行只要方向相同或相反即可，与起点是否相同无关，所以命题④不正确；对于命题③，其条件以否定形式给出，所以可从其逆否命题入手考虑，假若a 与b 不都是非零向量，即a 与b 至少有一个是零向量，而由零向量与任一向量都共线，可有a 与b 共线，其逆否命题正确，故命题③正确．综上所述，正确命题的序号是③.2．在△ABC 中，CA →＝a ，CB →＝b ，M 是CB 的中点，N 是AB 的中点，且CN 、AM 交于点P ，则AP →可用a 、b 表示为______________． 答案 －23a ＋13b解析 如图所示，AP →＝AC →＋CP →＝－CA →＋23CN →＝－CA →＋23×12(CA →＋CB →)＝－CA →＋13CA →＋13CB →＝－23CA →＋13CB →＝－23a ＋13b . 3.如图，在四边形ABCD 中，AB ∥CD ，AB ＝3DC ，E 为BC 的中点，则AE →＝________(用AB →，AD →表示)． 答案 23AB →＋12AD →解析 BC →＝BA →＋AD →＋DC →＝－23AB →＋AD →，AE →＝AB →＋BE →＝AB →＋12BC →＝AB →＋12⎝⎛⎭⎫AD →－23AB → ＝23AB →＋12AD →. 4．已知平面内一点P 及△ABC ，若P A →＋PB →＋PC →＝AB →，则有关点P 与△ABC 的位置关系判断正确的是________(填序号)．①点P 在线段AB 上； ②点P 在线段BC 上； ③点P 在线段AC 上； ④点P 在△ABC 外部． 答案 ③解析 由P A →＋PB →＋PC →＝AB →得P A →＋PC →＝AB →－PB →＝AP →，即PC →＝AP →－P A →＝2AP →，所以点P 在线段AC 上．5．已知点O 为△ABC 外接圆的圆心，且OA →＋OB →＋OC →＝0，则△ABC 的内角A 等于________． 答案 60°解析 由OA →＋OB →＋OC →＝0，知点O 为△ABC 的重心，又∵O 为△ABC 外接圆的圆心，∴△ABC 为等边三角形，A ＝60°.6．已知O 为四边形ABCD 所在平面内一点，且向量OA →，OB →，OC →，OD →满足等式OA →＋OC →＝OB →＋OD →，则四边形ABCD 的形状为________． 答案 平行四边形解析 由OA →＋OC →＝OB →＋OD →得OA →－OB →＝OD →－OC →，所以BA →＝CD →.所以四边形ABCD 为平行四边形．7．设点M 是线段BC 的中点，点A 在直线BC 外，BC →2＝16，|AB →＋AC →|＝|AB →－AC →|，则|AM →|＝________.答案 2解析 由|AB →＋AC →|＝|AB →－AC →|可知，AB →⊥AC →，则AM 为Rt △ABC 斜边BC 上的中线，因此，|AM →|＝12|BC →|＝2. 8．(2015·北京)在△ABC 中，点M ，N 满足AM →＝2MC →，BN →＝NC →.若MN →＝xAB →＋yAC →，则x ＝________；y ＝________.答案 12 －16解析 如图，MN →＝MC →＋CN →＝13AC →＋12CB → ＝13AC →＋12(AB →－AC →) ＝12AB →－16AC →，∴x ＝12，y ＝－16. 9.如图，在△ABC 中，D 、E 分别为BC 、AC 边上的中点，G 为BE 上一点，且GB ＝2GE ，设AB →＝a ，AC →＝b ，试用a ，b 表示AD →，AG →.解 AD →＝12(AB →＋AC →)＝12a ＋12b . AG →＝AB →＋BG →＝AB →＋23BE →＝AB →＋13(BA →＋BC →) ＝23AB →＋13(AC →－AB →)＝13AB →＋13AC →＝13a ＋13b . 10．设两个非零向量e 1和e 2不共线．(1)如果AB →＝e 1－e 2，BC →＝3e 1＋2e 2，CD →＝－8e 1－2e 2，求证：A 、C 、D 三点共线；(2)如果AB →＝e 1＋e 2，BC →＝2e 1－3e 2，CD →＝2e 1－k e 2，且A 、C 、D 三点共线，求k 的值．(1)证明 ∵AB →＝e 1－e 2，BC →＝3e 1＋2e 2，CD →＝－8e 1－2e 2，∴AC →＝AB →＋BC →＝4e 1＋e 2＝－12(－8e 1－2e 2)＝－12CD →，∴AC →与CD →共线． 又∵AC →与CD →有公共点C ，∴A 、C 、D 三点共线．(2)解 AC →＝AB →＋BC →＝(e 1＋e 2)＋(2e 1－3e 2)＝3e 1－2e 2，∵A 、C 、D 三点共线，∴AC →与CD →共线，从而存在实数λ使得AC →＝λCD →，即3e 1－2e 2＝λ(2e 1－k e 2)，得⎩⎪⎨⎪⎧3＝2λ，－2＝－λk ，解得λ＝32，k ＝43. B 组 专项能力提升(时间：15分钟)11．设a ，b 不共线，AB →＝2a ＋p b ，BC →＝a ＋b ，CD →＝a －2b ，若A ，B ，D 三点共线，则实数p 的值是________．答案 －1解析 ∵BC →＝a ＋b ，CD →＝a －2b ，∴BD →＝BC →＋CD →＝2a －b .又∵A ，B ，D 三点共线，∴AB →，BD →共线．设AB →＝λBD →，∴2a ＋p b ＝λ(2a －b )，∴2＝2λ，p ＝－λ，∴λ＝1，p ＝－1.12．如图，已知AB 是圆O 的直径，点C ，D 是半圆弧的两个三等分点，AB →＝a ，AC →＝b ，则AD →＝____________(用a ，b 表示)．答案 12a ＋b 解析 连结CD ，由点C ，D 是半圆弧的三等分点，得CD ∥AB 且CD →＝12AB →＝12a ，所以AD →＝AC →＋CD →＝b ＋12a . 13．设G 为△ABC 的重心，且sin A ·GA →＋sin B ·GB →＋sin C ·GC →＝0，则B 的大小为________．答案 60°解析 ∵G 是△ABC 的重心，∴GA →＋GB →＋GC →＝0，GA →＝－(GB →＋GC →)，将其代入sin A ·GA →＋sin B ·GB →＋sin C ·GC →＝0，得(sin B －sin A )GB →＋(sin C －sin A )GC →＝0.又GB →，GC →不共线，∴sin B －sin A ＝0，sin C －sin A ＝0，则sin B ＝sin A ＝sin C ．根据正弦定理知b ＝a ＝c ， ∴△ABC 是等边三角形，则角B ＝60°.14．在▱ABCD 中，AB →＝a ，AD →＝b ，AN →＝3NC →，M 为BC 的中点，则MN →＝____________.(用a ，b 表示)答案 －14a ＋14b 解析 由AN →＝3NC →得AN →＝34AC →＝34(a ＋b )， AM →＝a ＋12b ，所以MN →＝AN →－AM → ＝34(a ＋b )－⎝⎛⎭⎫a ＋12b ＝－14a ＋14b . 15．如图，经过△OAB 的重心G 的直线与OA ，OB 分别交于点P ，Q ，设OP →＝mOA →，OQ →＝nOB →，m ，n ∈R ，则1n ＋1m的值为________． 答案 3解析 设OA →＝a ，OB →＝b ，由题意知OG →＝23×12(OA →＋OB →)＝13(a ＋b )，PQ →＝OQ →－OP →＝n b －m a ，PG →＝OG →－OP →＝⎝⎛⎭⎫13－m a ＋13b ，由P ，G ，Q 三点共线得，存在实数λ，使得PQ →＝λPG →，即n b －m a ＝λ⎝⎛⎭⎫13－m a ＋13λb ， 从而⎩⎨⎧ －m ＝λ⎝⎛⎭⎫13－m ，n ＝13λ，消去λ得1n ＋1m ＝3.。

平面向量知识点回顾一、 向量的概念（1）向量的基本要素：大小和方向.（2）向量的表示：几何表示法AB ；字母表示：a ；坐标表示法(,)x i y j x y α→→=⋅+⋅=. （3）向量的长度：即向量的大小，记作2a x y =+（4）特殊的向量：零向量a ＝O｜a ｜＝O . 单位向量a 为单位向量｜a ｜＝1.（5）相等的向量：大小相等，方向相同12112212(,)(,)x x x y x y y y =⎧=⇔⎨=⎩（6） 相反向量：0a b b a a b =−⇔=−⇔+=（7）平行向量(共线向量)：方向相同或相反的向量，称为平行向量.记作a ∥b .平行向量也称为共线向量.二、向量的运算法则（1）加法a b b a +=+()()a b c a b c ++=++AB BC AC +=注：向量的加法口诀：首尾相连，首连尾，方向指向末向量。

（2）减法()a b a b −=+− （减法可以变成加法来计算，因此加法的相关运算法则减法也适用）AB BA =− OB OA AB −=注：向量的减法口诀：首首相连，尾连尾，方向指向被减向量。

（3）数乘()()a a λμλμ=()a a a λμλμ+=+()a b a b λλλ+=+//a b a b λ⇔=注：1.a λ是一个向量,满足:a a λλ=；2.λ>0时, a λ与a 同向; λ<0时, a λ与a 异向; λ=0时,0a λ=.（4）数量积a b b a ⋅=⋅()()()a b a b a b λλλ⋅=⋅=⋅()a b c a c b c +⋅=⋅+⋅()22a a =a b a b ⋅≤注：1.a b ⋅是一个数；2.00a b ==或时，0a b ⋅=；3. 00a b ≠≠且时，()cos ,,a b a b a b θθ⋅=是之间的夹角三、向量的直角坐标系运算法则 ()11,a x y =，()22,b x y =（1） 加法()1212,a b x x y y +=++（2） 减法()1212,a b x x y y −=−−（3） 数乘()11,a x y λλλ=（4） 数量积1212a b x x y y ⋅=+21a x y =+四、重要的定理以及公式（应用）（1）平面向量基本定理1e ，2e 是同一平面内两个不共线的向量，那么，对于这个平面内任一向量，有且仅有一对实数12,λλ，使112a e e λλ=+.注：1.我们把不是共线的1e ，2e 叫做表示这一平面内所有向量的一组基底；2.基底不是唯一的，关键是不是共线；3.由定理可以将平面内任一a 在给出基底1e ，2e 的条件下进行分解；4.基底给定时，分解形式是唯一的，12,λλ是被a 、1e ，2e 唯一确定的数量。

第2讲 平面向量（知识点串讲）知识整合1．向量的有关概念(1)向量：既有大小又有方向的量叫做向量，向量的大小叫做向量的长度(或模). (2)零向量：长度为0的向量，其方向是任意的． (3)单位向量：长度等于1个单位的向量．(4)平行向量：方向相同或相反的非零向量．平行向量又叫共线向量.规定：0与任一向量平行. (5)相等向量：长度相等且方向相同的向量． (6)相反向量：长度相等且方向相反的向量．例1、判断下列结论的正误(正确的打“√”，错误的打“×”) (1)向量不能比较大小，但向量的模可以比较大小．( ) (2)BA →＝OA →－OB →.( )(3)向量AB →与向量CD →是共线向量，则A ，B ，C ，D 四点在一条直线上．( )(4)已知a ，b 是两个非零向量，当a ，b 共线时，一定有b ＝λa (λ为常数)，反之也成立．( ) 【答案】 (1)√ (2)√ (3)× (4)√ [跟踪训练]1、有下列命题：①两个相等向量，它们的起点相同，终点也相同；②若|a |＝|b |，则a ＝b ；③若|AB →|＝|DC →|，则四边形ABCD 是平行四边形；④若m ＝n ，n ＝k ，则m ＝k ；⑤若a ∥b ，b ∥c ，则a ∥c ；⑥有向线段就是向量，向量就是有向线段．其中，假命题的个数是( )A ．2B ．3C ．4D ．5【答案】C [对于①，两个相等向量，它们的起点相同，终点也相同，①正确；对于②，若|a |＝|b |，方向不确定，则a ，b 不一定相等，∴②错误；对于③，若|AB →|＝|DC →|，AB →，DC →不一定相等，∴四边形ABCD 不一定是平行四边形，③错误；对于④，若m ＝n ，n ＝k ，则m ＝k ，④正确；对于⑤，若a ∥b ，b ∥c ，当b ＝0时，a ∥c 不一定成立，∴⑤错误；对于⑥，有向线段不是向量，向量可以用有向线段表示，∴⑥错误．综上，假命题是②③⑤⑥，共4个．] 知识整合2．向量的线性运算如果e 1，e 2是同一平面内的两个不共线向量，那么对于这一平面内的任意向量a ，有且只有一对实数λ1，λ2，使a ＝λ1e 1＋λ2e 2.其中，不共线的向量e 1，e 2叫做表示这一平面内所有向量的一组基底.例2、(2019·山东东营检测)如图所示，BC →＝3CD →，O 在线段CD 上，且O 不与端点C ，D 重合，若AO →＝mAB →＋(1－m )AC →，则实数m 的取值范围为________.【答案】⎝⎛⎭⎫－13，0 [设CO →＝kBC →，则k ∈⎝⎛⎭⎫0，13， ∴AO →＝AC →＋CO →＝AC →＋kBC →＝AC →＋k (AC →－AB →)＝(1＋k )AC →－kAB →. 又AO →＝mAB →＋(1－m )AC →，∴m ＝－k . ∵k ∈⎝⎛⎭⎫0，13，∴m ∈⎝⎛⎭⎫－13，0.] [跟踪训练]2、(2019·山东潍坊调研)如图，在平行四边形ABCD 中，AC ，BD 相交于点O ，E 为线段AO 的中点．若BE →＝λBA →＋μBD →(λ，μ∈R )，则λ＋μ等于( )A ．1B ．34C ．23D ．12【答案】B [∵E 为线段AO 的中点，∴BE →＝12BA →＋12BO →＝12BA →＋12⎝⎛⎭⎫12BD →＝12BA →＋14BD →＝λBA →＋μBD →，∴λ＋μ＝12＋14＝34.] 知识整合4．共线向量定理向量a (a ≠0)与b 共线，当且仅当有唯一一个实数λ，使b ＝λa .(1)一般地，首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量，即A 1A 2→＋A 2A 3→＋A 3A 4→＋…＋A n －1A n ＝A 1A n →，特别地，一个封闭图形，首尾连接而成的向量和为零向量．(2)若P 为线段AB 的中点，O 为平面内任一点，则OP →＝12(OA →＋OB →)．(3)OA →＝λOB →＋μOC →(λ，μ为实数)，若点A ，B ，C 共线，则λ＋μ＝1.例3、(2019·山东青州月考)已知O 为△ABC 内一点，且2AO →＝OB →＋OC →，AD →＝tAC →，若B ，O ，D 三点共线，则t 的值为( )A ．14B ．13C ．12D ．23【答案】B [设线段BC 的中点为M ， 则OB →＋OC →＝2OM →.因为2AO →＝OB →＋OC →，所以AO →＝OM →， 则AO →＝12AM →＝14(AB →＋AC →)＝14⎝⎛⎭⎫AB →＋1t AD →＝14AB →＋14tAD →. 由B ，O ，D 三点共线，得14＋14t ＝1，解得t ＝13.][跟踪训练]3、设两个非零向量a 与b 不共线．(1)若AB →＝a ＋b ，BC →＝2a ＋8b ，CD →＝3(a －b )， 求证：A ，B ，D 三点共线；(2)试确定实数k ，使k a ＋b 和a ＋k b 共线．【答案】(1)证明 ∵AB →＝a ＋b ，BC →＝2a ＋8b ，CD →＝3(a －b )， ∴BD →＝BC →＋CD →＝2a ＋8b ＋3(a －b ) ＝2a ＋8b ＋3a －3b ＝5(a ＋b )＝5AB →，∴AB →，BD →共线．又∵它们有公共点B ，∴A ，B ，D 三点共线． (2)解 假设k a ＋b 与a ＋k b 共线， 则存在实数λ，使k a ＋b ＝λ(a ＋k b )， 即(k －λ)a ＝(λk －1)b .又a ，b 是两个不共线的非零向量， ∴k －λ＝λk －1＝0.消去λ，得k 2－1＝0，∴k ＝±1. 知识整合5．平面向量的坐标运算(1)向量的加法、减法、数乘向量及向量的模： 设a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ＋b ＝(x 1＋x 2，y 1＋y 2)，a －b ＝(x 1－x 2，y 1－y 2)，λa ＝(λx 1，λy 1)，|a |＝x 21＋y 21. (2)向量坐标的求法：①若向量的起点是坐标原点，则终点坐标即为向量的坐标． ②设A (x 1，y 1)，B (x 2，y 2)，则AB →＝(x 2－x 1，y 2－y 1)， |AB →|＝x 2－x 12y 2－y 12.6．平面向量共线的坐标表示设a ＝(x 1，y 1)，b ＝(x 2，y 2)，其中b ≠0，则a ∥b ⇔x 1x 2＝y 1y 2.⇔x 1y 2－x 2y 1＝0.例4、(2019·山东潍坊检测)如图，正方形ABCD 中，E 为DC 的中点，若AE →＝λAB →＋μAC →，则λ＋μ的值为( )A ． 12B ．－12C ．1D ．－1【答案】A [法一：由题意得AE →＝AD →＋12AB →＝BC →＋AB →－12AB →＝AC →－12AB →，∴λ＝－12，μ＝1，∴λ＋μ＝12.法二：利用坐标法，以A 为坐标原点，AB 、AD 所在直线分别为x 轴，y 轴建立平面直角坐标系(图略)， 设正方形的边长为1，则A (0,0)，B (1,0)，C (1,1)，E ⎝⎛⎭⎫12， 1，∴AE →＝⎝⎛⎭⎫12， 1，AB →＝(1,0)，AC →＝(1,1)，则⎝⎛⎭⎫12， 1＝λ(1,0)＋μ(1,1)，∴λ＋μ＝12.][跟踪训练]4、(2019·山东青岛调研)已知向量a ＝(－1,1)，b ＝(3，m )，若a ∥(a ＋b )，则m ＝( ) A ．－2 B ．2 C ．3D ．－3【答案】D [向量a ＝(－1,1)，b ＝(3，m )，则a ＋b ＝(2，m ＋1)，a ∥(a ＋b )，则－(m ＋1)＝2，解得m ＝－3.] 知识整合7．向量的夹角已知两个非零向量a 和b ，作OA →＝a ，OB →＝b ，则∠AOB 就是向量a 与b 的夹角，向量夹角的范围是：[0，π].8．平面向量的数量积9．①交换律：a ·b ＝b ·a ；②数乘结合律：(λa )·b ＝λ(a ·b )＝a ·(λb )； ③分配律：a ·(b ＋c )＝a ·b ＋a ·c . (2)平面向量数量积运算的常用公式①(a ＋b )·(a －b )＝a 2－b 2. ②(a ＋b )2＝a 2＋2a ·b ＋b 2. ③(a －b )2＝a 2－2a ·b ＋b 2. 10．平面向量数量积的性质及其坐标表示设非零向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，θ＝〈a ，b 〉.注：两个向量a ，b 的夹角为锐角⇔a ·b >0且a ，b 不共线；两个向量a ，b 的夹角为钝角⇔a ·b <0且a ，b 不共线．例5、(2018·天津卷)如图，在平面四边形ABCD 中，AB ⊥BC ，AD ⊥CD ，∠BAD ＝120°，AB ＝AD ＝1.若点E 为边CD 上的动点，则AE →·BE →的最小值为( )A ．2116B ．32C ．2516D ．3【答案】A [如图，以D 为坐标原点建立直角坐标系．连接AC ，由题意知∠CAD ＝∠CAB ＝60°，∠ACD ＝∠ACB ＝30°，则D (0,0)，A (1,0)，B ⎝⎛⎭⎫32，32，C (0，3)．设E (0，y )(0≤y ≤3)，则AE →＝(－1，y )，BE →＝⎝⎛⎭⎫－32，y －32，∴AE →·BE →＝32＋y 2－32y ＝⎝⎛⎭⎫y －342＋2116，∴当y ＝34时，AE →·BE →有最小值2116.] [跟踪训练]5、(2018·天津卷)在如图所示的平面图形中，已知OM ＝1，ON ＝2，∠MON ＝120°，BM →＝2MA →，CN →＝2NA →，则BC →·OM →的值为( )A ．－15B ．－9C ．－6D ．0【答案】C [如图，连接MN .∵BM →＝2MA →，CN →＝2NA →，∴AM AB ＝13＝AN AC ，∴MN ∥BC ，且MN BC ＝13，∴BC →＝3MN →＝3(ON →－OM →)， ∴BC →·OM →＝3(ON →·OM →－OM →2) ＝3(2×1×cos 120°－12)＝－6.]。