圆的总结归纳

初中数学圆知识点总结归纳一、圆的基本性质圆的定义：平面内到定点距离等于定长的所有点组成的图形叫做圆。

其中定点称为圆心，定长称为半径。

圆的基本性质：(1)圆是中心对称图形，对称中心为圆心。

(2)圆是轴对称图形，对称轴为经过圆心的任意一条直线。

(3)垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧。

(4)圆心角定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等。

(5)弦心距定理：在同圆或等圆中，弦心距等于所对弧的半径的一半。

二、圆的几何表示圆的方程：在平面直角坐标系中，以圆心为坐标原点，以半径为r的圆的方程为x^2 + y^2 = r^2。

圆的标准方程：以圆心为坐标原点，以半径为r，且经过点P(x0, y0)的圆的方程为(x - x0)^2 + (y - y0)^2 = r^2。

圆的参数方程：以x为参数，描述圆的方程为x = x0 + rcos(θ)，y = y0 + rsin(θ)，其中θ为参数。

三、与圆相关的定理和性质切线判定定理：经过半径的外端点并且垂直于这条半径的直线是圆的切线。

切线性质定理：圆的切线上的任一点到圆心的距离等于半径。

切线长定理：经过圆外一点引两条切线，它们的切线长相等。

相交弦定理：经过圆内一点引两条弦，它们的交点与该点的距离乘积等于常数。

切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。

割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的乘积相等。

圆幂定理：对于同圆或等圆中的两个相等的非零实数，有：(ab)(cd) = (ac)(bd) - (ad)(b*c)。

弦中点定理：经过弦的两个端点的直径垂直于这条弦。

相交弦定理：两弦交于圆内一点，各弦被这点所平分。

余弦定理：对于任何三角形ABC，有c^2 = a^2 + b^2 - 2ab*cos(C)。

正弦定理：对于任何三角形ABC，有a/sin(A) = b/sin(B) = c/sin(C)。

圆的知识点总结大全
圆是平面几何中最简单、最常见的图像之一，它与其他几何体如正方形、长方形等形
状不同，被称为“以无穷多条直线为边缘的无边形”。

圆的定义：圆是一种对称的几何形状，由一条椭圆的弧度组成，上部的点和下部的点
都通过一条半径来连接，中心点叫圆心。

一、圆半径：
圆半径是圆心到任意点的距离，也叫做圆的直径，是描述圆的重要参数。

可以以圆心
为原点，将同等距离的点放在X轴上，圆心点就是半径。

二、圆周长：
圆周长是指圆上某一点离圆心点沿着圆弧一圈行走所经过的距离，也叫圆的弧长。

圆
周长的计算公式：C=2πr。

三、圆面积：
圆面积是指圆心到任意点的空间面积，也即圆的表面积。

圆面积的计算公式：S=πr2。

四、圆的结构形式：
1、圆有两种结构形式：实心圆和空心圆。

实心圆就是内部是完整的，空心圆外面有
一个边框，但内部是空着的。

2、圆的结构形式也分为两种：圆环和楔形圆，圆环就是在实心圆上面扣一个空心圆，楔形圆就是只有一个弧度，但是有两个相不相等的半径。

五、圆的关系特点：
1、圆的半径、圆周长以及圆面积成正比，也即圆的半径越大，其圆周长和圆面积也
越大；反之，圆的半径越小，其圆周长和圆面积也越小。

2、不同半径的圆之间的关系称为“半径比”，有两种关系：1）一个圆的半径是另一
个圆半径的“半径倍数”；2）两个圆的半径和比值为“半径比”。

以上就是圆的知识点总结大全的全部内容，圆的定义、特性、特点及其特殊的关系可
以用来解决很多几何问题，可以为我们更好的理解几何形状提供帮助。

圆有关的知识点总结公式一、圆的定义圆的定义是平面上到一个定点距离恒定的点的集合。

这个定点称为圆心，到圆心的距离称为半径。

圆的边界称为圆周。

圆可以用圆心和半径来描述，也可以用圆周上的点的坐标来描述。

圆的定义在数学中是基础性的概念之一。

二、圆的性质1. 圆的直径是圆周上任意两点之间的最长线段，它恰好等于圆周的两倍。

圆的半径是圆心到圆周上任意一点的距离。

2. 圆的周长公式为：C=2πr，其中C表示圆的周长，r表示圆的半径，π是一个数学常数，约等于3.14159。

3. 圆的面积公式为：A=πr²，其中A表示圆的面积。

4. 圆的内切和外切问题：一个图形是否能内切于圆，或外切于一个圆，是几何中一个重要的问题。

5. 圆的相关角度问题：圆周角、圆心角等概念与性质。

三、圆的公式1. 圆的周长公式：C=2πr这个公式表示了圆的周长与半径之间的关系，即周长等于半径的两倍乘以π。

2. 圆的面积公式：A=πr²这个公式表示了圆的面积与半径之间的关系，即面积等于半径的平方乘以π。

3. 圆的弧长公式：L=θr这个公式表示了圆的弧长与圆心角的大小以及半径的关系，即弧长等于圆心角的大小乘以半径。

4. 圆的扇形面积公式：A=1/2θr²这个公式表示了圆的扇形面积与圆心角的大小以及半径的关系，即扇形面积等于圆心角的大小乘以半径的平方再除以2。

5. 圆的相似性公式：S₁/S₂=r₁/r₂这个公式表示了两个相似圆的面积与半径的关系，即两个相似圆的面积之比等于它们半径的平方之比。

四、圆的应用圆在生活和工作中有许多应用，其中包括但不限于以下几个方面：1. 圆的几何学应用：圆的几何性质是几何学中的重要内容，它们在建筑、绘图、地理等领域都有广泛的应用。

2. 圆的工程应用：在工程中，圆形轮胎、圆形齿轮、圆形管道等都是圆的应用场景。

3. 圆的数学模型应用：在数学建模中，圆常常被用来描述一些现实中的问题，如行星轨道、电子轨道等。

数学圆知识点总结在学习中，大家对知识点应该都不陌生吧？知识点也可以通俗的理解为重要的内容。

掌握知识点有助于大家更好的学习。

下面是小编整理的数学圆知识点总结，欢迎大家借鉴与参考，希望对大家有所帮助。

数学圆知识点总结11、圆是定点的距离等于定长的点的集合2、圆的内部可以看作是圆心的距离小于半径的点的集合3、圆的外部可以看作是圆心的距离大于半径的点的集合4、同圆或等圆的半径相等5、到定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半径的圆6、和已知线段两个端点的距离相等的点的轨迹，是这条线段的垂直平分线7、到已知角的两边距离相等的点的轨迹，是这个角的平分线8、到两条平行线距离相等的点的轨迹，是和这两条平行线平行且距离相等的一条直线9、定理不在同一直线上的三点确定一个圆。

10、垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧11、推论1：①平分弦(不是直径)的直径垂直于弦，并且平分弦所对的两条弧②弦的垂直平分线经过圆心，并且平分弦所对的两条弧③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。

12、推论2：圆的两条平行弦所夹的弧相等13、圆是以圆心为对称中心的中心对称图形14、定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等15、推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等16、定理：一条弧所对的圆周角等于它所对的圆心角的一半17、推论：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等18、推论：半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径19、推论：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形20、定理：圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角21、①直线L和⊙O相交d﹤r②直线L和⊙O相切d=r③直线L和⊙O相离d﹥r22、切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线23、切线的性质定理：圆的切线垂直于经过切点的半径24、推论：经过圆心且垂直于切线的直线必经过切点25、推论：经过切点且垂直于切线的直线必经过圆心26、切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角27、圆的外切四边形的两组对边的和相等28、弦切角定理：弦切角等于它所夹的弧对的圆周角29、推论：如果两个弦切角所夹的弧相等，那么这两个弦切角也相等30、相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等31、推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项32、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项33、推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等34、如果两个圆相切，那么切点一定在连心线上35、①两圆外离d﹥R+r②两圆外切d=R+r③两圆相交R-r﹤d﹤R+r(R﹥r)④两圆内切d=R-r(R﹥r)⑤两圆内含d﹤R-r(R﹥r)36、定理：相交两圆的连心线垂直平分两圆的公共弦37、定理：把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形38、定理：任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆39、正n边形的每个内角都等于(n-2)×180°/n40、定理：正n边形的半径和边心距把正n边形分成2n个全等的直角三角形41、正n边形的面积Sn=pr/2p表示正n边形的周长，r为边心距42、正三角形面积√3a2/4a表示边长43、如果在一个顶点周围有k个正n边形的角，由于这些角的和应为360°，因此k(n-2)180°/n=360°化为(n-2)(k-2)=444、弧长计算公式：L=n兀R/18045、扇形面积公式：S扇形=n兀R2/360=LR/2外公切线长=d-(R+r)数学学习中常见问题分析大部分学生在学习中或多或少的都会积累一些问题，这些问题平时我们可能不是很在意，那么到了初二后就会突显出来。

圆的概念知识点总结一、基本概念1. 圆的定义圆是一个平面上的一个点到另一个点距离相等的所有点的集合。

这个距离被称为圆的半径。

2. 圆的元素圆的元素有两个，一个是圆心，一个是半径。

圆心是圆的中心点，而半径是从圆心到圆上的任意一点的距离。

3. 圆的属性圆的属性有几个重要的特点，比如圆半径、圆心、圆直径、圆周长、圆面积等。

二、圆的相关公式1. 圆的周长圆的周长是指圆的边界长度，它可以通过公式2πr来计算，其中r表示圆的半径，π表示圆周率，它的值约为3.14。

2. 圆的面积圆的面积是指圆内部的部分，它可以通过公式πr^2来计算，其中r表示圆的半径。

3. 圆的直径圆的直径是指圆的两个相对的边界之间的距离，它可以通过圆的半径乘以2来计算。

4. 圆的弧长圆的弧长是指圆周上的一部分长度，它可以通过圆的半径乘以弧度来计算。

5. 圆的扇形面积圆的扇形面积是指圆的一部分面积，它可以通过圆的半径乘以弧长除以2来计算。

6. 圆的切线圆的切线是指与圆相切的一条直线，在接触点处与圆相切且与圆的半径垂直。

三、圆的相关定理1. 圆的同位角定理同位角是指平行线与一条直线相交时所成的对应角，对应角相等，角的度数相等。

2. 圆的相交角定理相交角是指两个相交直线所成的四个角，相邻角相等。

3. 圆的正切定理圆内一点的切线长度等于这个点到圆心的距离乘以切点到切线之间的夹角的正切值。

4. 圆的切线定理切于圆上的直线与半径的夹角等于直线与半径的切线夹角的一半。

5. 圆的弦切定理圆内一点的切线长的平方等于这个点到圆心的距离的平方减去弦长的平方。

四、圆的相关性质1. 圆的切线垂直定理相切于同一个圆的两条切线相互垂直。

2. 圆心角和弦定理圆心角是指以圆心为端点的两条半径所成的角，它的度数等于其所对的圆周弧所对的圆心角。

3. 圆的切线与半径定理切于圆的切线和该圆上的半径垂直。

4. 圆的内切定理在一个三角形中，内切圆的半径等于周长与半周长之差。

以上就是关于圆的基本概念、公式、定理和性质的一些知识点总结，希望对大家有所帮助。

九年级圆的知识点总结圆是九年级数学中的一个重要内容，它具有独特的性质和广泛的应用。

下面我们来对九年级圆的知识点进行一个全面的总结。

一、圆的定义圆是平面内到定点的距离等于定长的点的集合。

这个定点称为圆心，定长称为半径。

圆的标准方程为$（x a)＾2 ＋（y b)＾2 ＝ r^2$，其中$（a, b)＄为圆心坐标，＄r$为半径。

二、圆的相关概念1、弦：连接圆上任意两点的线段叫做弦。

2、直径：经过圆心的弦叫做直径，直径是圆中最长的弦。

3、弧：圆上任意两点间的部分叫做弧。

弧分为优弧（大于半圆的弧）、劣弧（小于半圆的弧）。

4、半圆：圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆。

5、等圆：能够重合的两个圆叫做等圆。

6、等弧：在同圆或等圆中，能够互相重合的弧叫做等弧。

三、圆的性质1、圆的对称性圆是轴对称图形，其对称轴是任意一条通过圆心的直线。

圆是中心对称图形，其对称中心是圆心。

2、垂径定理垂直于弦的直径平分弦且平分弦所对的两条弧。

推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧。

弦的垂直平分线经过圆心，并且平分弦所对的两条弧。

平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。

3、圆心角、弧、弦之间的关系在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等。

推论：在同圆或等圆中，如果两条弧相等，那么它们所对的圆心角相等，所对的弦相等。

在同圆或等圆中，如果两条弦相等，那么它们所对的圆心角相等，所对的弧相等。

4、圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半。

推论：同弧或等弧所对的圆周角相等。

半圆（或直径）所对的圆周角是直角，＄90^｛＼circ}＄的圆周角所对的弦是直径。

四、圆的位置关系1、点与圆的位置关系设点$P$到圆心的距离为$d$，圆的半径为$r$，则有：点$P$在圆外＄＼Leftrightarrow$ ＄d ＞ r$点$P$在圆上＄＼Leftrightarrow$ ＄d ＝ r$点$P$在圆内＄＼Leftrightarrow$ ＄d ＜ r$2、直线与圆的位置关系设圆心到直线的距离为$d$，圆的半径为$r$，则有：直线与圆相离＄＼Leftrightarrow$ ＄d ＞ r$，此时直线与圆没有公共点。

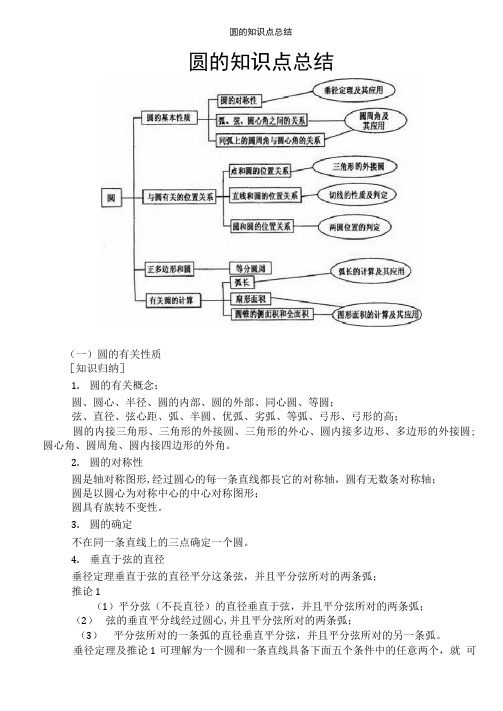
圆的知识点总结（一）圆的有关性质［知识归纳］1.圆的有关概念：圆、圆心、半径、圆的内部、圆的外部、同心圆、等圆；弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧、弓形、弓形的高；圆的内接三角形、三角形的外接圆、三角形的外心、圆内接多边形、多边形的外接圆; 圆心角、圆周角、圆内接四边形的外角。

2.圆的对称性圆是轴对称图形,经过圆心的每一条直线都長它的对称轴，圆有无数条对称轴；圆是以圆心为对称中心的中心对称图形；圆具有族转不变性。

3.圆的确定不在同一条直线上的三点确定一个圆。

4.垂直于弦的直径垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧；推论1（1）平分弦（不長直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心,并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。

垂径定理及推论1可理解为一个圆和一条直线具备下面五个条件中的任意两个，就可推出另外三个:①过圆心；②垂直于弦;③平分弦（不長直径）;④平分弦所对的优弧；⑤平分弦所对的劣弧。

推论2圆的两条平行弦所夹的弧相等。

5.圆心角、弧、弦.弦心距之间的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等；所对的弦的弦心距相等。

推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。

此定理和推论可以理解成:在同圆或等圆中，满足下面四个条件中的任何一个就能推出另外三个:①两个圆心角相等；②两个圆心角所对的弧相等;③两个圆心角或两条弧所对的弦相等;④两条弦的弦心距相等。

圆心角的度数等于它所对的弧的度数。

6.圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半；推论1同弧或等弧所对的圆周角相等;在同圆或等圆中，相等的圆周角所对的弧也相等;推论2半圆(或直径)所对的圆周角是直角；90。

的圆周角所对的弦是直径；推论3如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

圆的知识点总结（一）圆的有关性质［知识归纳］1. 圆的有关概念：圆、圆心、半径、圆的内部、圆的外部、同心圆、等圆；弦、直径、弦心距、弧、半圆、优弧、劣弧、等弧、弓形、弓形的高；圆的内接三角形、三角形的外接圆、三角形的外心、圆内接多边形、多边形的外接圆；圆心角、圆周角、圆内接四边形的外角。

2. 圆的对称性圆是轴对称图形，经过圆心的每一条直线都是它的对称轴，圆有无数条对称轴；圆是以圆心为对称中心的中心对称图形；圆具有旋转不变性。

3. 圆的确定不在同一条直线上的三点确定一个圆。

4. 垂直于弦的直径垂径定理垂直于弦的直径平分这条弦，并且平分弦所对的两条弧；推论1（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧；（3）平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。

垂径定理及推论1 可理解为一个圆和一条直线具备下面五个条件中的任意两个，就可推出另外三个：①过圆心；②垂直于弦；③平分弦（不是直径）；④平分弦所对的优弧；⑤平分弦所对的劣弧。

1推论2圆的两条平行弦所夹的弧相等。

5. 圆心角、弧、弦、弦心距之间的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等；所对的弦的弦心距相等。

推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等，那么它们所对应的其余各组量都分别相等。

此定理和推论可以理解成：在同圆或等圆中，满足下面四个条件中的任何一个就能推出另外三个：①两个圆心角相等；②两个圆心角所对的弧相等；③两个圆心角或两条弧所对的弦相等；④两条弦的弦心距相等。

圆心角的度数等于它所对的弧的度数。

6. 圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半；推论1同弧或等弧所对的圆周角相等；在同圆或等圆中，相等的圆周角所对的弧也相等；推论2半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径；推论3如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

圆的高考知识点总结一、圆的性质1. 圆的定义：平面上到定点距离等于定长的点的轨迹叫做圆。

2. 圆的标准方程：圆的标准方程为（x-a）^2 + (y-b)^2 = r^2，其中（a，b）是圆心坐标，r为半径。

3. 圆的性质：圆的性质包括圆心、半径、直径、弧、圆周长和面积。

4. 圆的弧长：弧长公式为S=rθ，其中S为弧长，r为半径，θ为圆心角的弧度数。

5. 圆的面积：圆的面积公式为A=πr^2，其中A为面积，r为半径，π≈3.14。

二、圆的相关概念1. 圆的切线：与圆相切的直线叫做圆的切线，切线与半径的夹角为90度。

2. 圆的切点：切线与圆的交点叫做圆的切点。

3. 关于圆的几何变换：包括平移、旋转、对称等几何变换。

4. 圆锥曲线的定义：平面上一个点到两定点的距离之比等于一个定值的轨迹称为圆锥曲线。

三、圆的相关性质1. 直径定理：直径等于周长的一半，即d=2r。

2. 平行切线定理：平行切线所切的弦长相等。

3. 关于弧和角的关系：圆心角、弧、半径、正切线之间有一定的关系。

4. 圆的几何关系：包括圆与圆的位置关系，圆与直线的位置关系等。

四、相关题型解析1. 圆的证明题：包括通过已知条件证明圆的性质等。

2. 圆的计算题：包括计算圆的周长、面积、半径、直径等。

3. 圆的几何问题：包括求解关于圆的几何问题，包括切线问题、相切问题等。

4. 圆的几何变换：包括求解通过平移、旋转、对称等几何变换后的圆的性质等。

五、应试技巧1. 熟练掌握圆的相关定理和性质，灵活运用解题。

2. 多做圆的计算题和几何问题，提高解题能力。

3. 善于分析题目，归纳规律，合理运用几何知识解决问题。

4. 必要时候灵活使用代数方法解题，提高解题效率。

总结：圆是高考数学中重要的几何知识点，掌握圆的相关定理、性质以及解题技巧对于高考数学至关重要。

在备考过程中，要多练习相关题型，理解圆的性质和运用方法，提高解题能力。

同时要善于发现圆与其他几何图形之间的联系，提高综合解题能力。

圆的认识（一）知识点北师大版1、圆是由曲线围成的平面图形（或封闭图形）。

2、围成圆的曲线叫圆周（或圆上），曲线以内的区域叫圆内，曲线以外的区域叫圆外。

3、画圆的方法有：实物画圆法，手指画圆法，系（jì）绳画圆法，圆规画圆法。

最常用的是圆规画圆法。

4、圆中心的一点叫做圆心，用字母o表示。

连接圆心和圆上任意一点的线段叫做半径，通常用字母r表示。

通过圆心并且两端都在圆上的线段叫做直径，通常用字母d表示。

5、圆心到圆上任意一点的距离都相等。

6、圆规两脚间的距离是圆的半径。

7、在同一个圆中，圆有无数条半径和无数条直径。

8、在同圆或等圆中，所有的半径都相等，所有的直径也都相等。

并且直径的长度是半径的2倍，半径的长度是直径的1/2 。

用字母表示是d=2r或r= 1/2d。

9、同圆是一个圆，指圆心相同，半径相等。

等圆是两个相等的圆，指圆心不同，但半径相等。

10、圆心决定圆的位置，半径（直径）决定圆的大小。

11、圆形车轮轴心到地面的距离为半径，所以圆形车轮轴心到地面的距离处处相等。

12、车轴一定要装在圆心的位置，才能使车身平稳。

13、圆是由曲线围成的封闭图形；三角形、长方形、平行四边形、梯形等图形是由线段首尾相连的封闭图形。

圆的认识（二）知识点北师大版1、圆是轴对称图形，并且任何一个圆都有无数条对称轴，直径所在的直线就是圆的对称轴。

2、圆的对称轴是一条直线。

3、圆的任意两条直径的交点是圆心，由圆的两条直径可以确定圆心。

4、圆与正多边形组成的组合图形（圆心与正多边形的中心点重合。

）的对称轴是经过圆心的正多边形的对称轴。

5、直径是圆中最长的线段。

圆的知识点高中归纳总结圆是几何学中的基本概念之一，具有许多特殊的性质和定理。

本文将从圆的定义、圆的元素、圆的性质和定理等方面进行归纳总结。

一、圆的定义圆是平面上一点到另一点距离不变的轨迹。

其中，到圆心的距离称为半径，半径的两倍称为直径。

二、圆的元素1. 圆心：圆上任意两点与圆心连线的线段称为半径，圆心是圆上所有点的中心。

2. 半径：连接圆心和圆上任意一点的线段称为半径，圆的半径相等。

3. 直径：通过圆心的两个点并且在圆上的线段称为直径，直径是圆的最长线段，直径的长度是半径的两倍。

4. 弦：在圆上两点之间的线段称为弦，直径也是一条特殊的弦，其长度等于圆的直径。

5. 弧：在圆上两个点之间的部分称为弧，直径对应的弧称为直径弧。

6. 扇形：以圆心为顶点的角和所对应的弧组成的图形称为扇形。

7. 弓形：以弧为界的两个扇形组成的图形称为弓形。

三、圆的性质1. 圆的半径相等，圆的直径是半径的两倍。

2. 圆的弧长与其所对应的圆心角成正比，即弧长等于圆心角的弧度数乘以半径。

3. 圆的面积与其半径的平方成正比，即面积等于π乘以半径的平方。

4. 圆的外切圆和内切圆的圆心在同一条直线上，且内切圆的半径小于圆的半径，外切圆的半径大于圆的半径。

5. 切线与半径的关系：切线与半径的交点处的切线垂直于半径。

6. 圆的切线和半径的夹角等于切线所对应的弧的一半的角度。

四、圆的定理1. 相交弦定理：两条相交弦所夹的弧所对应的圆心角相等。

2. 弦切定理：切线与弦的交点外切弧所对应的圆心角相等。

3. 弦角定理：弦所对应的弧所对应的圆心角等于弦上两个角的和。

4. 切线定理：切线与半径的夹角等于切线所对应的弧的一半的角度。

5. 弧角定理：两个相交弧所对应的圆心角等于它们所夹的弧的角度之和。

圆是平面上一点到另一点距离不变的轨迹，具有许多特殊的性质和定理。

通过对圆的定义、圆的元素、圆的性质和定理的归纳总结，我们可以更好地理解和应用圆的知识点，进一步拓展几何学的相关内容。

圆的知识点总结六年级大全一、圆的定义圆是平面上到一个点的距离等于定长的点的集合。

其中，到这个点的距离称为半径，定长称为圆的半径，这个点称为圆心。

圆的中心位置叫做圆心，定长叫做半径。

由此可见，圆是一个平面上到一个点的距离等于定长的点的集合。

二、圆的性质1. 圆的直径：过圆心，且与圆的边界相切的直线段叫做圆的直径，直径的长度是圆半径的两倍。

2. 圆的周长：围绕圆心一周的距离叫做圆的周长，它等于圆的直径乘以3.14，或者等于圆的半径的两倍乘以3.14。

3. 圆的面积：圆的内部区域叫做圆的面积，圆的面积等于圆的半径的平方再乘以3.14。

4. 弧长和扇形的面积：圆是由无数个弧线组成的，每一个弧线的长度叫做弧长，而每一段弧线所围成的区域叫做扇形。

扇形的面积等于扇形的弧长乘以圆的半径再除以2。

5. 圆的相交：两个圆如果相交，那么它们相交的地方叫做交点，并且形成四个交点。

6. 圆的圆心角：如果圆上的两个点与圆心连接起来构成一个角，这样的角称为圆心角。

7. 圆的切线：通过圆与圆相切的直线叫做切线，切线与半径的夹角为90度。

以上是圆的一些基本性质，我们可以通过这些性质来解决各种与圆相关的问题。

三、圆的公式1. 圆的直径公式：圆的直径是圆的半径的两倍，所以圆的直径D=2R。

2. 圆的周长公式：圆的周长等于圆的直径乘以3.14，C=πD。

3. 圆的面积公式：圆的面积等于圆的半径的平方再乘以3.14，A=πR^2。

4. 圆的弧长公式：圆的弧长等于圆的半径乘以圆心角的弧度数，L=∮R。

5. 圆的扇形面积公式：圆的扇形面积等于扇形的弧长乘以圆的半径再除以2。

圆的公式是我们解决与圆相关问题的重要依据，我们通过这些公式可以计算出圆的周长、面积、弧长等数据。

四、圆的相关定理1. 等腰三角形的内切圆：一个等腰三角形内切圆的半径是等腰三角形底边的一半。

2. 等边三角形的内切圆：一个等边三角形内切圆的半径等于等边三角形边长的三分之一。

3. 直角三角形的内切圆：一个直角三角形内切圆的半径等于直角三角形的斜边减去直角边之和再除以2。

圆的单元知识点总结一、圆的基本概念1. 圆的定义：平面上距离给定点一定距离的点的集合称为圆，给定点称为圆心，给定距离称为半径。

2. 直径：圆的直径是通过圆心的两个点之间的线段，且与圆的两个点相切。

3. 弧长和弧度：圆的周长称为圆周，圆周上任意两点之间的弧长称为圆弧。

角度的单位通常使用弧度来表示，弧度的大小等于半径长的圆弧所对的圆心角的大小。

4. 圆心角：以圆心为顶点的角称为圆心角，其对应的圆弧称为圆心角所对应的圆弧。

5. 圆扇形和圆面积：以圆心为顶点的两条射线和圆上的弧所围成的图形称为圆扇形，其面积的计算公式为：S = 1/2r²θ（其中r为半径，θ为圆心角的弧度）。

二、圆的性质1. 圆的对称性：圆具有无数个对称轴，其中最重要的是与直径有关的对称性2. 圆的切线和切点：圆上的每一点都有且只有一条切线与之相切，这条切线始终垂直于半径，并且切点处的切线为水平。

3. 圆的不等式：对于任意两条不同的弦，它们所对应的圆心角的大小是不同的4. 圆的相交特性：两个圆相交于两个互异的点，这两个点称为交点。

三、圆的基本定理1. 圆的三要素：圆由圆心、半径和圆周组成。

2. 圆的唯一性：通过圆上任意两点可以唯一确定一个圆。

3. 圆的定位：圆可以在平面内任意一个点作为圆心，任意一段正数作为半径。

四、圆的相关公式和定理1. 圆的面积：圆的面积公式为：S=πr²，其中π≈3.14，r为半径长度。

2. 圆的周长：圆的周长公式为：C=2πr，其中C为周长，r为半径长度。

3. 圆的三角函数关系：三角函数与单位圆的关系，圆的三角函数包括正弦函数、余弦函数和正切函数。

4. 圆的角度关系：圆心角、圆周角和相交弦的角度关系，圆的角度关系在解决实际问题时具有重要的应用价值。

五、圆的相关实际应用1. 圆的测量与绘制：在实际应用中，圆的测量和绘制是非常重要的，例如在建筑、制图和工程设计中经常会用到圆的测量和绘制技术。

2. 圆的运动学问题：在物理学和工程学中，圆的运动学问题是研究物体在圆周运动和旋转运动中的相关规律和特点。

高中圆知识点总结高中圆知识点总结一、基本概念1. 圆：由平面内的一点到另一点距离等于定长的所有点的集合。

2. 圆心：圆所在平面内到圆内任意点的距离相等的点。

3. 半径：圆心到圆上任意点的距离。

4. 直径：通过圆心的线段，且两端点都在圆上。

5. 弦：圆上两点之间的线段。

6. 弧：圆上两点之间的部分。

7. 圆周：圆的周长。

8. 圆内切：一个圆恰好与另一个圆内部相切。

9. 圆外切：一个圆恰好与另一个圆外部相切。

二、圆的性质1. 圆心角的度数等于其所对的弧的度数。

2. 弧对应的圆心角具有相等的度数。

3. 同弧的两个圆心角互为补角。

4. 相等的圆心角所对应的弧长相等。

5. 同弧的两个弧所对应的圆心角互为补角。

6. 切线与半径垂直相交。

7. 切线与弦的交角等于其所对的弧所对应的圆心角的一半。

8. 直径是弧上的非常量弦中长度最长的。

9. 圆的直径是半径的2倍。

10. 同弧所对应的弧长与圆周的比例等于圆心角的比例。

三、圆的方程1. 标准方程：(x - a)² + (y - b)² = r²，其中(a, b)为圆心坐标，r为半径长度。

2. 一般方程：x² + y² + Dx + Ey + F = 0，其中D、E、F为实数。

四、圆的相关定理1. 必要条件：如果两条弦相交于圆内或圆上一点，则这两条弦所对的圆心角互为补角。

2. 若两弦相交于圆上一点，则这两条弦的交点、两端点以及圆心所成的角的度数相等。

3. 切线与半径的垂直性质：过切点的切线垂直于过切点的半径。

4. 弦切角定理：切线与弦的交角等于其所对的弧所对应的圆心角的一半。

5. 切线分割弦定理：切点到圆心的距离与切点分割的弦的两部分的积相等。

6. 弧切角定理：相等的弧所对应的圆心角相等。

7. 弦切角定理：相等的弦所对应的圆心角相等。

五、圆与三角形的关系1. 内切圆：一个圆与三角形的内部相切。

2. 外切圆：一个圆与三角形的外部相切。

圆的知识点归纳总结大全一、圆的定义.1、以定点为圆心，定长为半径的点组成的图形。

2、在同一平面内，到一个定点的距离都相等的点组成的图形。

二、圆的各元素。

1、半径：圆上一点与圆心的连线段.2、直径：连接圆上两点有经过圆心的线段。

3、弦:连接圆上两点线段(直径也是弦）。

4、弧：圆上两点之间的曲线部分。

半圆周也是弧.（1)劣弧：小于半圆周的弧。

(2）优弧：大于半圆周的弧.5、圆心角：以圆心为顶点,半径为角的边。

6、圆周角：顶点在圆周上，圆周角的两边是弦。

7、弦心距：圆心到弦的垂线段的长.三、圆的基本性质。

1、圆的对称性.（1）圆是轴对称图形，它的对称轴是直径所在的直线。

（2）圆是中心对称图形,它的对称中心是圆心。

（3）圆是旋转对称图形。

2、垂径定理。

（1）垂直于弦的直径平分这条弦，且平分这条弦所对的两条弧。

（2)推论:➢平分弦（非直径）的直径,垂直于弦且平分弦所对的两条弧.➢平分弧的直径，垂直平分弧所对的弦.3、圆心角的度数等于它所对弧的度数。

圆周角的度数等于它所对弧度数的一半。

（1)同弧所对的圆周角相等.(2）直径所对的圆周角是直角;圆周角为直角,它所对的弦是直径。

4、在同圆或等圆中，两条弦、两条弧、两个圆周角、两个圆心角、两条弦心距五对量中只要有一对量相等,其余四对量也分别相等。

5、夹在平行线间的两条弧相等. 6、设⊙O 的半径为r ，OP=d 。

7、（1)（2个点的距离相等。

（直角三角形的外心就是斜边的中点。

）8、直线与圆的位置关系。

d 表示圆心到直线的距离，r 表示圆的半径。

直线与圆有两个交点,直线与圆相交；直线与圆只有一个交点，直线与圆相切； 直线与圆没有交点,直线与圆相离. 29,A(x 1，y 1)、B （x 2,y 2）。

则AB=10、圆的切线判定。

(1）d=r 时，直线是圆的切线。

切点不明确：画垂直,证半径。

（2)经过半径的外端且与半径垂直的直线是圆的切线。

切点明确：连半径，证垂直。