习题作业-第十一章 快速傅里叶变换

⽂中内容均为个⼈理解，如有错误请指出，不胜感激前⾔先解释⼏个⽐较容易混淆的缩写吧FMT 快速莫⽐乌斯变化—>感谢stump提供多项式复数在介绍复数之前，⾸先介绍⼀些可能会⽤到的东西(好像画的不是很标准。

)定义设a ,b 为实数，i 2=−1，形如a +bi 的数叫复数，其中i 被称为虚数单位，复数域是⽬前已知最⼤的域在复平⾯中，x 代表实数，y 轴（除原点外的点）代表虚数，从原点(0,0)到(a ,b )的向量表⽰复数a +bi模长：从原点(0,0)到点(a ,b )的距离，即√a 2+b 2幅⾓：假设以逆时针为正⽅向，从x 轴正半轴到已知向量的转⾓的有向⾓叫做幅⾓运算法则加法：因为在复平⾯中，复数可以被表⽰为向量，因此复数的加法与向量的加法相同，都满⾜平⾏四边形定则（就是上⾯那个）乘法：⼏何定义：复数相乘，模长相乘，幅⾓相加代数定义：(a +bi )∗(c +di )=ac +adi +bci +bdi 2=ac +adi +bci −bd=(ac −bd )+(bc +ad )i单位根下⽂中，默认n 为2的正整数次幂在复平⾯上，以原点为圆⼼，1为半径作圆，所得的圆叫单位圆。

以圆点为起点，圆的n 等分点为终点，做n 个向量，设幅⾓为正且最⼩的向量对应的复数为ωn ，称为n 次单位根。

根据复数乘法的运算法则，其余n −1个复数为ω2n ,ω3n ,…,ωn n 注意ω0n =ωn n =1（对应复平⾯上以x 轴为正⽅向的向量）那么如何计算它们的值呢？这个问题可以由欧拉公式解决ωk n =cos k ∗2πn +i sin k ∗2πn例如图中向量AB 表⽰的复数为8次单位根单位根的幅⾓为周⾓的1n在代数中，若z n =1，我们把z 称为n 次单位根单位根的性质ωk n =cos k2πn +i sin k 2πn （即上⾯的公式）ω2k 2n =ωk n证明：ω2k 2n =cos2k ∗2π2n +i sin2k ∗2π2n =ωk nωk +n2n =−ωk n ωn2n =cos n 2∗2πn +i sin n 2∗2πn =cos π+i sin π=−1ω0n =ωn n =1讲了这么多，貌似跟我们的正题没啥关系啊。

第一章1.连续图像中，图像为一个二维平面，(x,y)图像中的任意一点，f（x,y）为图像于(x,y)于处的值。

连续图像中，(x,y)的取值是连续的，f(x,y)也是连续的数字图像中，图像为一个由有限行有限列组成的二维平面，（i,j)为平面中的任意一点，g（i,j)则为图像在（i,j)处的灰度值，数字图像中，（i,j) 的取值是不连续的，只能取整数，对应第i行j列,g（i,j) 也是不连续的，表示图像i行j列处图像灰度值。

联系：数字图像g(i,j)是对连续图像f(x,y)经过采样和量化这两个步骤得到的。

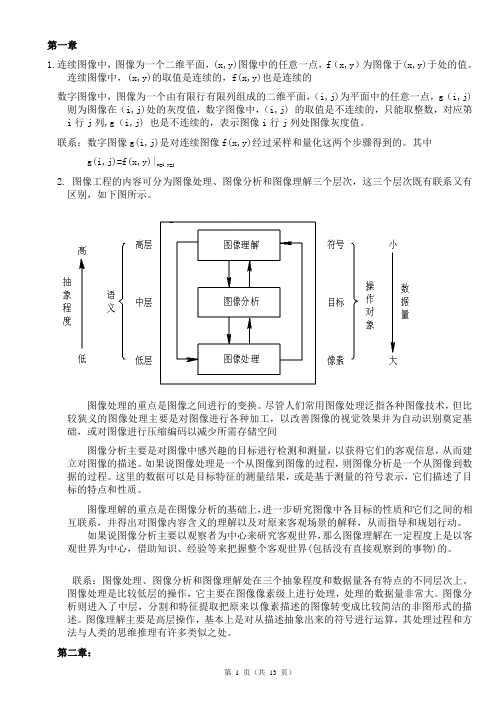
其中g(i,j)=f(x,y)|x=i,y=j2. 图像工程的内容可分为图像处理、图像分析和图像理解三个层次，这三个层次既有联系又有区别，如下图所示。

图像处理的重点是图像之间进行的变换。

尽管人们常用图像处理泛指各种图像技术，但比较狭义的图像处理主要是对图像进行各种加工，以改善图像的视觉效果并为自动识别奠定基础，或对图像进行压缩编码以减少所需存储空间图像分析主要是对图像中感兴趣的目标进行检测和测量，以获得它们的客观信息，从而建立对图像的描述。

如果说图像处理是一个从图像到图像的过程，则图像分析是一个从图像到数据的过程。

这里的数据可以是目标特征的测量结果，或是基于测量的符号表示，它们描述了目标的特点和性质。

图像理解的重点是在图像分析的基础上，进一步研究图像中各目标的性质和它们之间的相互联系，并得出对图像内容含义的理解以及对原来客观场景的解释，从而指导和规划行动。

如果说图像分析主要以观察者为中心来研究客观世界，那么图像理解在一定程度上是以客观世界为中心，借助知识、经验等来把握整个客观世界(包括没有直接观察到的事物)的。

联系：图像处理、图像分析和图像理解处在三个抽象程度和数据量各有特点的不同层次上。

图像处理是比较低层的操作，它主要在图像像素级上进行处理，处理的数据量非常大。

图像分析则进入了中层，分割和特征提取把原来以像素描述的图像转变成比较简洁的非图形式的描述。

傅里叶变换方程练习题在信号与系统学科中，傅里叶变换是一种非常重要的数学工具，用于将一个函数从时域（时间域）转换为频域（频率域）表示。

傅里叶变换方程是进行这种转换的数学表达式。

在本文中，我们将通过一些练习题来巩固对傅里叶变换方程的理解与应用。

练习一：考虑一个实值函数f(t)，其傅里叶变换F(ω)表示为：F(ω) = ∫[从负无穷到正无穷] f(t) * e^(-iωt) dt1. 当f(t)为一个矩形脉冲函数时，求它的频域表示F(ω)。

2. 当f(t)为一个正弦函数时，求它的频域表示F(ω)。

3. 当f(t)为一个指数衰减函数时，求它的频域表示F(ω)。

练习二：考虑一个信号g(t)和一个信号h(t)，它们的傅里叶变换分别为G(ω)和H(ω)。

求以下函数的傅里叶变换：1. f(t) = g(t) + h(t)2. f(t) = g(t - a), 其中a为常数3. f(t) = g(at), 其中a为常数4. f(t) = g(-t)练习三：考虑一个实值函数f(t)，其傅里叶变换F(ω)表示为：F(ω) = ∫[从负无穷到正无穷] f(t) * e^(-iωt) dt1. 当f(t)为偶函数时，证明它的傅里叶变换F(ω)也为偶函数。

2. 当f(t)为奇函数时，证明它的傅里叶变换F(ω)也为奇函数。

3. 当f(t)为实值函数时，证明它的傅里叶变换F(ω)的共轭和实部为偶函数，虚部为奇函数。

练习四：考虑一个实值函数f(t)，其傅里叶变换F(ω)表示为：F(ω) = ∫[从负无穷到正无穷] f(t) * e^(-iωt) dt1. 当f(t)是一个无限长的周期函数时，证明它的傅里叶变换F(ω)也是一个周期函数。

2. 当f(t)是一个有限长的周期函数时，证明它的傅里叶变换F(ω)也是一个有限长的周期函数。

练习五：考虑一个离散时间信号序列x[n]，其傅里叶变换表示为X(e^(jω))，其中e^(jω)表示复指数函数。

快速傅⾥叶变换快速傅⾥叶变换快速傅⾥叶变换（FFT ）是根据计算量的最⼩化原理来设计和实施离散傅⾥叶变换(DFT)计算的⽅法。

1965年，库利（T.W.Cooley ）和图基（J.W.tukey ）发表了著名的《计算机计算傅⾥叶级数的⼀种算法》论⽂。

从此掀起了快速傅⾥叶变换计算⽅法研究的热潮。

快速傅⾥叶变换（FFT ）的出现，实现了快速、⾼效的信号分析和信号处理，为离散傅⾥叶变换(DFT)的⼴泛应⽤奠定了基础。

1.1离散傅⾥叶变换(DFT)的计算设x(n)是⼀个长度为M 的有限长序列，则定义x(n)的N 点离散傅⾥叶变换为∑-===10)()]([)(N n kn NW n x n x DFT k X 其中由于计算⼀个X(k)值需要N 次复乘法和(N-1)次复数加法，因⽽计算N 个X(k)值，共需N2次复乘法和N(N-1)次复加法。

每次复乘法包括4次实数乘法和2次实数加法，每次复加法包括2次实数加法，因此计算N 点的DFT 共需要4N2次实数乘法和(2N2+2N ·(N-1))次实数加法。

当N 很⼤时，这是⼀个⾮常⼤的计算量。

1.2减少DFT 计算量的⽅法减少DFT 的计算量的主要途径是利⽤k N W 的性质和计算表达式的组合使⽤，其本质是减少DFT 计算的点数N 以便减少DFT 的计算量。

k N W 的性质：（1）对称性： (2)周期性： (3) 可约性： (4) 特殊点：选择其中⼀个证明N N j k N j N k N j N k N e e e W 222)2(22πππ--+-+==ππj k N j e e --=2k N j e π2--=k N W -=FFT 算法是基于可以将⼀个长度为N 的序列的离散傅⾥叶变换逐次分解为较短的离散傅⾥叶变换来计算这⼀基本原理的。

这⼀原理产⽣了许多不同的算法，但它们在计算速度上均取得了⼤致相当的改善。

0,1,,1k N =-()*nk nk N N W W -=()()nk N n k n N k N N NW W W ++==nk mnk N mN W W =//nk nk m N N mW W =01N W =/21N N W =-(/2)k N k N NW W +=-在这⾥讨论两类基本的FFT 算法。

【知识总结】快速傅⾥叶变换（FFT ）这可能是我第五次学FFT 了……菜哭qwq 先给出⼀些个⼈认为⾮常优秀的参考资料：快速傅⾥叶变换（FFT ）⽤于计算两个n 次多项式相乘，能把复杂度从朴素的O (n 2)优化到O (nlog 2n )。

⼀个常见的应⽤是计算⼤整数相乘。

本⽂中所有多项式默认x 为变量，其他字母均为常数。

所有⾓均为弧度制。

⼀、多项式的两种表⽰⽅法我们平时常⽤的表⽰⽅法称为“系数表⽰法”，即A (x )=n∑i =0a i x i上⾯那个式⼦也可以看作⼀个以x 为⾃变量的n 次函数。

⽤n +1个点可以确定⼀个n 次函数（⾃⾏脑补初中学习的⼆次函数）。

所以，给定n +1组x 和对应的A (x )，就可以求出原多项式。

⽤n +1个点表⽰⼀个n 次多项式的⽅式称为“点值表⽰法”。

在“点值表⽰法”中，两个多项式相乘是O (n )的。

因为对于同⼀个x ，把它代⼊A 和B 求值的结果之积就是把它带⼊多项式A ×B 求值的结果（这是多项式乘法的意义）。

所以把点值表⽰法下的两个多项式的n +1个点的值相乘即可求出两多项式之积的点值表⽰。

线性复杂度点值表⽰好哇好但是，把系数表⽰法转换成点值表⽰法需要对n +1个点求值，⽽每次求值是O (n )的，所以复杂度是O (n 2)。

把点值表⽰法转换成系数表⽰法据说也是O (n 2)的（然⽽我只会O (n 3)的⾼斯消元qwq ）。

所以暴⼒取点然后算还不如直接朴素算法相乘……但是有⼀种神奇的算法，通过取⼀些具有特殊性质的点可以把复杂度降到O (nlog 2n )。

⼆、单位根从现在开始，所有n 都默认是2的⾮负整数次幂，多项式次数为n −1。

应⽤时如果多项式次数不是2的⾮负整数次幂减1，可以加系数为0的项补齐。

先看⼀些预备知识：复数a +bi 可以看作平⾯直⾓坐标系上的点(a ,b )。

这个点到原点的距离称为模长，即√a 2+b 2；原点与(a ,b )所连的直线与实轴正半轴的夹⾓称为辐⾓，即sin −1ba 。

快速傅里叶变换快速傅里叶变换在信号处理等领域有着广泛的应用。

在竞赛中，TTF 主要用途是求两个多项式的乘积，即给定两个阶小于n 的多项式∑-==1)(n k kk xa x A ，∑-==1)(n k kk xb x B ，需要求解)()()(220x B x A x C x C n k k k==∑-=。

注意)(x C 的阶是不超过n 2，而不是n 。

朴素算法依次计算)(x C 的各个系数∑=-=ki ik i k ba C 0，复杂度为)(2n O ，而通过FFT 可以做到)log (n n O 。

在FFT 中需要应用到一些复数的知识。

方程1=nx 在复数域上一共有n 个不同的解，可以表示为nk i n k ππ2sin 2cos+或是等价的)1..0(/2-=n k e ni k π。

记n i e /2π为n ω，则这n 个解也可以表示成1...-n n n ωω。

n ω被称为单位根。

从几何的角度来看，这n 个解对应到的是复平面上单位圆的n 等分点。

对于一个小于n 阶的多项式，如果给出它在n 个不同位置的取值，则该多项式的系数是唯一确定的 。

例如若已知一个小于3阶的多项式)(x F 满足1)0(=F 、3)1(=F 、1)1(=-F ，则可以知道1)(2++=x x x F 。

如果已知一个小于n 阶多项式的系数，则可以在)(2n O 的时间内求得它在任意n 个不同位置上的取值。

如果已知一个小于n 阶的多项式在n 个不同位置上的取值，则可以通过拉格朗日插值公式（)(2n O 的复杂度）或是求解线性方程组()(3n O 的复杂度）得到它的系数。

若n 为偶数，则kn k n 2/2ωω=。

FFT 基本思路是通过计算)(x A 在n 2个不同位置上的取值以及)(x B 同样在这n 2个位置上的取值之后，将这两组取值按位置相乘，就得到了)(x C 在这n 2个位置上去取值。

最后再将)(x C 的系数推出来。

快速傅里叶变换fast Fourier transform计算离散傅里叶变换的一种快速算法,简称FFT。

快速傅里叶变换是1965年由J.W.库利和T.W.图基提出的。

采用这种算法能使计算机计算离散傅里叶变换所需要的乘法次数大为减少,特别是被变换的抽样点数N越多,FFT算法计算量的节省就越显著。

当用数字计算机计算信号序列x(n)的离散傅里叶变换时，它的正变换(1)反变换(IDFT)是(2)式中、x(n)和X(k)可以是实数或复数。

由上式可见,要计算一个抽样序列就需要做N次复数乘法运算及N-1次复数加法运算。

计算离散傅里叶变换的快速方法，有按时间抽取的FFT算法和按频率抽取的FFT算法。

前者是将时域信号序列按偶奇分排,后者是将频域信号序列按偶奇分排。

它们都借助于的两个特点:一是的周期性；另一是的对称性，这里符号*代表其共轭。

这样,便可以把离散傅里叶变换的计算分成若干步进行，计算效率大为提高。

时间抽取算法令信号序列的长度为N＝2M,其中M是正整数，可以将时域信号序列x(n)分解成两部分，一是偶数部分x（2n），另一是奇数部分x（2n+1），其中。

于是信号序列x(n)的离散傅里叶变换可以用两个 N/2抽样点的离散傅里叶变换来表示和计算。

考虑到和离散傅里叶变换的周期性,式(1)可以写成(3)其中(4a)(4b)由此可见，式(4)是两个只含有N/2个点的离散傅里叶变换，G(k)仅包括原信号序列中的偶数点序列，H(k)则仅包括它的奇数点序列。

虽然k=0，1，2，…，N-1，但是G(k)和H(k)的周期都是N/2,它们的数值以N/2周期重复。

因为于是由式(3)和式(4)得到(5a)(5b)因此,一个抽样点数为N 的信号序列 x(n)的离散傅里叶变换，可以由两个 N/2抽样点序列的离散傅里叶变换求出。

依此类推，这种按时间抽取算法是将输入信号序列分成越来越小的子序列进行离散傅里叶变换计算，最后合成为N点的离散傅里叶变换。

傅里叶变换练习题及答案傅里叶变换练习题及答案傅里叶变换是一种在信号处理和数学分析领域中广泛应用的重要工具。

它可以将一个函数在时域（时间域）中的表达转换为频域（频率域）中的表达，从而揭示出信号中的频率成分和振幅信息。

在学习和掌握傅里叶变换的过程中，练习题是必不可少的一部分，通过解答练习题可以帮助我们更好地理解和运用傅里叶变换。

下面是一些傅里叶变换的练习题及其答案，供大家参考和练习：1. 计算函数 f(t) = e^(-2πit) 的傅里叶变换F(ω)。

解答：根据傅里叶变换的定义，F(ω) = ∫[e^(-2πit)] * e^(-iωt) dt。

将函数代入计算，得到F(ω) = ∫[e^(-2πit)] * e^(-iωt) dt = δ(ω + 2π)。

2. 计算函数f(t) = cos(2πt) 的傅里叶变换F(ω)。

解答：同样地，根据傅里叶变换的定义，F(ω) = ∫[cos(2πt)] * e^(-iωt) dt。

将函数代入计算，得到F(ω) = ∫[cos(2πt)] * e^(-iωt) dt = 1/2 * [δ(ω + 1) + δ(ω - 1)]。

3. 计算函数 f(t) = e^(-|t|) 的傅里叶变换F(ω)。

解答：同样地，根据傅里叶变换的定义，F(ω) = ∫[e^(-|t|)] * e^(-iωt) dt。

将函数代入计算，得到F(ω) = ∫[e^(-|t|)] * e^(-iωt) dt = 2/(1 + ω^2)。

通过解答以上练习题，我们可以发现傅里叶变换可以将复杂的函数转换为简洁的频域表达式，从而更好地描述信号的频率特性。

在实际应用中，傅里叶变换被广泛应用于信号处理、图像处理、通信系统等领域。

掌握傅里叶变换的原理和技巧，对于理解和应用这些领域的相关知识非常重要。

总之，通过练习傅里叶变换的题目，我们可以更好地理解和掌握傅里叶变换的原理和应用。

希望以上练习题及答案能够对大家的学习和实践有所帮助，同时也希望大家能够进一步深入学习和探索傅里叶变换的更多知识和应用。

习题作业-第十一章快速傅里叶变换第十一章快速傅里叶变换习题例题：1.试计算下属序列的DFT ：(a) (13,17,19,23)(b) (2,1,3,7,5,4,0,6)2.试计算下述序列的逆DFT ：(a) ( 16, -0.76 + 8.66i , -6+6i, -9.25+2.66i, 0, -9.25-2.66i, -6-6i, -0.76-8.66i )(b) ( 4-i, 2+i, 2+i, -i 4-i, 2+i, 2+i, -i, )3.参照算法11.1,设计一个单处理机上时间为((nlogn)的离散傅氏逆变换算法;并以n = 8为例。

画出其逆变换蝶氏计算流图。

4.Cormen 曾给了另一种形式的FFT 递归算法：(a) 试分析此算法的执行过程；(b) 它和算法11.2有何区别？(c) 按此算法画出n = 8的FFT 蝶氏计算流图。

算法11.7 SISD 上Cormen 计算FFT 算法输入：a 0 , a 1 , ... , a n-1输出：b 0 , b 1 ... , b n-1Begi nif n = 1 then return aelse(1) w = e 2πi/n(2) z=1(3) a [0] = (a 0 , a 2 , ... , a n-2)(4) a [1] = (a 1 , a 3 , ... , a n-1)(5) b [0] = RECURSIVEFFT(a [0])(6) b [1] = RECURSIVEFFT(a [1])(7) for k=0 to n/2 -1 do(i) b k = b [0]k + zb [1]k(ii) b k + n/2 = b [0]k - zb [1]k(iii) z = z·wendfor(8) return bendifend5.根据算法11.2，逐步计算n –8的FFT ，并画出其蝶氏计算流图。

6.令n = 8 = 2k ，在蝶式网络上，按照exp(r,i) = j (0≤i≤n-1,0≤r≤k)的计算方法，试计算分布在蝶形网络中的8点FFT 的系数矩阵元素w j 。

快速傅⾥叶变换FFT试题第⼀章快速傅⾥叶变换（FFT ）4.1 填空题（1）如果序列)(n x 是⼀长度为64点的有限长序列)630(≤≤n ，序列)(n h 是⼀长度为128点的有限长序列)1270(≤≤n ，记)()()(n h n x n y *=（线性卷积），则)(n y 为点的序列，如果采⽤基FFT 2算法以快速卷积的⽅式实现线性卷积，则FFT 的点数⾄少为点。

解：64+128-1＝191点; 256(2)如果⼀台通⽤机算计的速度为：平均每次复乘需100s µ，每次复加需20s µ，今⽤来计算N=1024点的DFT )]([n x 。

问直接运算需（）时间，⽤FFT 运算需要（）时间。

解：①直接运算：需复数乘法2N 次，复数加法）（1-N N 次。

直接运算所⽤计算时间1T 为s s N N N T 80864.12512580864020110021==?-+?=µ）（②基2FFT 运算：需复数乘法N N2log 2次，复数加法N N 2log 次。

⽤FFT 计算1024点DTF 所需计算时间2T 为s s N N N NT 7168.071680020log 100log 2222==?+?=µ。

(3)快速傅⾥叶变换是基于对离散傅⾥叶变换和利⽤旋转因⼦k Nj e π2-的来减少计算量，其特点是 _______、_________和__________。

解：长度逐次变短；周期性；蝶形计算、原位计算、码位倒置（4）N 点的FFT 的运算量为复乘、复加。

解：N NL N mF 2log 22==；N N NL aF 2log ==4.2 选择题1．在基2DIT —FFT 运算中通过不断地将长序列的DFT 分解成短序列的DFT ，最后达到2点DFT 来降低运算量。

若有⼀个64点的序列进⾏基2DIT —FFT 运算，需要分解次，⽅能完成运算。

A.32 B.6 C.16 D. 8 解：B2．在基2 DIT —FFT 运算时，需要对输⼊序列进⾏倒序，若进⾏计算的序列点数N=16，倒序前信号点序号为8，则倒序后该信号点的序号为。

快速傅⾥叶变换（FFT）略解前⾔如果我们能⽤⼀种时间上⽐ \(O(n^2)\) 更优秀的⽅法来计算⼤整数（函数）的乘法，那就好了。

快速傅⾥叶变换（FFT）可以帮我们在 \ (O(n\log n)\) 的时间内解决问题。

函数乘积计算两个⼤整数之积时，我们发现\[(2x+3)(4x+5)=8x^2+22x+15\quad...(*)\\ 23\times45=1035\]⽽如果我们把 \((*)\) 式右边的每⼀位的系数看做⼀个数每位上的数码，正好得到了 \(1035\)。

事实上，对于所有的多项式乘法，以上规律同样成⽴。

证明：（提⽰）考虑竖式乘法的过程，和多项式乘法的过程，它们的本质都是⼀样的。

这样，我们就把问题转换为：计算两个已知函数之积的函数的解析式。

复平⾯、单位圆考虑 \(\sqrt{-9}\) 的值。

\[\begin{aligned}\sqrt{-9}&=\sqrt{-1}\times\sqrt9=3\sqrt{-1}.\end{aligned} \]类似地，\(\forall N\in \Z_-\) 我们都可以⽤类似的⽅法得到 $$\sqrt{N}=\sqrt{-N}\times\sqrt{-1}$$引⼊虚数单位 \(\text{i}\)，使 \(\text{i}^2=-1.\) 这样我们就重新认识了数的范围，从实数扩充到复数。

⼀复数 \(a+b\text{i}\) 中的 \(a,b\in\R\)，\(a\) 是它的实数部分，\(b\text{i}\) 是虚数部分。

若 \(b=0\)，则它是实数。

复数服从实数的⼤部分运算法则。

若两个复数，它们的实数部分相等，虚数部分之和为 \(0\)，我们称它们互为共轭复数。

我们知道，数轴上的每个点与每个实数⼀⼀对应。

类似地，我们可以使⽤复平⾯上的点表⽰复数。

复平⾯与平⾯直⾓坐标系类似，它的 \ (x\) 轴单位长度为 \(1\)，\(y\) 轴单位长度为 \(\text{i}\)。

快速Fourier变换()()()()10210,1,2,,Four 1,ie 1r 2jk i N N j ex k X j k N i N -===-=-∑π离散逆变换：()()()()()()()()2100,1,2,,Fourier 0,1,2,,1,111N n nj i N ex x x x N X j x n j N i -⎛⎫⎪⎝⎭=- -==-=-∑π离散变换给号序列::定信FFT-Fast Fourier Transform Fourie FFT FFT ,r FFT.逆变换的形式与完全相同结论平行地用到逆（）：快速变换优化()()()()()()()()()()()1111000001010000112222()()1nji N mn j mn j nj n n mj j N N n j n j n j n j n j m N N N N N e W W a W W W b W W W π+-+===⇓⇓=-010101012,,0,1,,10,1,,1,0,10,12,0,1,,1N m j n j n N j m j mj j j n n n n n m ==-=-⎧=+⎨=⎩=⎧=+⎨=-⎩设将和分别改写成22221(3)1,i m N m i m i N m N N N N N W e W W e W W eW ---====-===πππ记则计算复杂度降低！()()()()()()()()()()()100010101101001001100000111000,2,1,0,1,0,1;0,1,6271m n j n j N m n n j n m n j m n z n j W x n n W X j j z n j n j j m x n n W 对原信号偶数和奇数序列信号傅里叶变换-=-==⎧=+⎪⎪⎪⎪⎨⎪⎪=-⎪⎪===-⎩+∑∑∑()()()()()()()()()()()()()()0010000110010101121101011001110000100,2141Fourie 5r ,22nj N i N n m n j n j n j m N n n m n j n j N n n m j n j m X j X j j x n ex n n W W j j n n n W x n n W --=-=-======+=+=+⎡⎤+⎢⎦-⎥=⎣-∑∑∑∑∑π根据离散变换公式：进行一次分解快速Fourier 变换()()()()()()()()()()()()()()0010110101101010010011110011000010012,2221,1,,0,1,0,1;0,16,1m n j n j N m n m m n j n j m m n n n j n z n j W x n n W x n W x n W X j j z n j n j j m X j X j -=--====++===-===-∑∑∑∑快速Fourier 变换()()()()()()()()()001101001001001100006,2*,17,m n n n j n j N m j n z n j x n n X j j z n W W j -==⎧=+⎪⎪⎨⎪=-⎪⎩∑∑()(){}(){}()()()()()()()()()()()001000002200.601:,:111111:1,:17.66222n j N n j n j N N n j m W Wa n m m m m m m n m m m m m mb W N W N m N 因子和都是事先算好存储在计算机内的复杂度分奇偶项分析：时，次复数乘法，次复数加法乘法加法时，次复数乘法，次复数加法乘法加法复，，实际处理数据与计算复杂度杂度分析：2复数加法分析一次优化：总共需要做次复数乘法和次复数加法==+-⨯⨯-=+-⨯+⨯-≠0100,1,0,10,1,1n j j m ===-快速Fourier变换进行一次分解3N 为例分析FFT计算过程：232N =为例分析FFT计算过程：41+22+141242+24+1824⨯⨯⨯⨯⨯⨯FFT 计算量:=次复数乘法,=次复数加法2iN N W e 离散傅里叶逆变换:8个信号序列的离散傅里叶逆变换其中π=2iNN W e 离散傅里叶逆变换:8个信号序列的离散傅里叶逆变换其中π=()22=2,2FFT 1log 22log k N k kN N N kN N N==复执行一个以为底的完整数乘法：复数加法：的计算复杂度次优化：2log 0,N N N由于→→∞210FFT ,.,=2=1024()FFT 200!N N 与离散傅立叶变换需要次运算的在数量级上有了重大改进节省的工作量相当惊人比如对对实际问题来讲,这仅是一个很小的数字原算法的复数乘法次数就超过的倍()()()FFT 322FFT 21FFT ,)kk m N N ===计算直到为止的过程称为以为底的变换信号个数信号个数任何一个大于的自然数都可以作为变换的底在同一计算过程中还可以混合使用以3为底的换多个底数变()()()()()()()()()00101010100100110000010,2*,1,0,1,0,1;0,9,811m n j n j N m n n j n z n j W x n n W X j j z n j n j j m -==⎧=+⎪⎪⎪⎪=-⎨⎪⎪===-⎪⎪⎩∑∑James W. Cooley John W. Tukey 美国普林斯顿大学教授IBM 研究员James W. Cooley,John W. Tukey.An Algorithm for the Machine Calculation of Complex Fourier Series. Math. Comp.19(1965), 297-301.。