(完整版)基本初等函数图像及其性质表

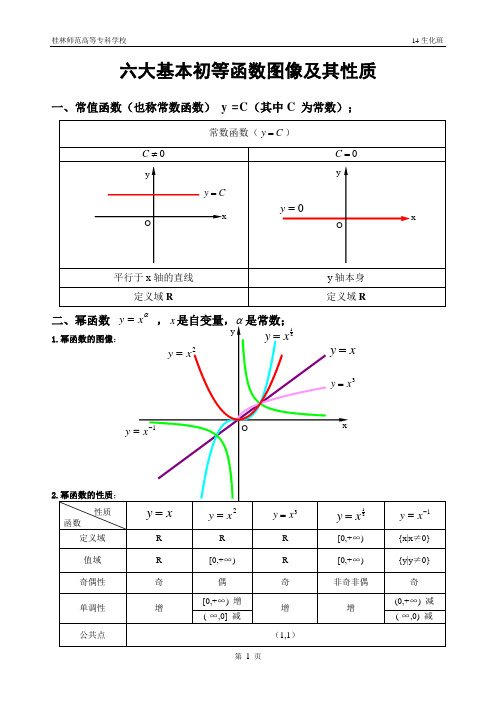
六大基本初等函数图像及其性质一、常值函数（也称常数函数）y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。

b.1.当1>a 时，a 值越大，xa y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，x a y =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。

一、一次函数与二次函数 （一）一次函数一次k kxb k 0函数k ， bk 0k符号b 0b 0b 0b 0b 0b 0y y y y y y图象OxOxOx性质y 随 x 的增大而增大（二）二次函数（1）二次函数分析式的三种形式 O xOxOxy 随 x 的增大而减小①一般式： f ( x) ax 2 bx c(a0) ②极点式： f (x)a( x h) 2 k (a 0)③两根式： f ( x) a( x x 1)( x x 2 )(a 0)（ 2）求二次函数分析式的方法①已知三个点坐标时，宜用一般式．②已知抛物线的极点坐标或与对称轴相关或与最大（小）值相关时，常使用极点式．③若已知抛物线与x 轴有两个交点，且横线坐标已知时，采用两根式求 f (x) 更方便．（3）二次函数图象的性质f xax 2 bx c a0 a 0 a 0图像xbxb2 a2 a定义域,对称轴xb2a极点坐标b 4 ac b 22 a,4 a值域4 ac b 2,,4 acb 24 a4 a, b 递减, b递加2a 单一区间2 ab递加 b, 递减,2 a2 a①. 二次函数f ( x) ax2 bx c(a 0) 的图象是一条抛物线，对称轴方程为 x b , 极点坐标2a是 ( b , 4ac b2 )2a 4a②当 a 0 时，抛物线张口向上，函数在( , b] 上递减，在 [ b , ) 上递加，当 x b 2a 2a 2a4ac b20 时，抛物线张口向下，函数在( b] 上递加，在 [b)时， f min ( x) ；当 a , , 4a 2a 2a上递减，当x4ac b2b时， f max (x)4a．2a二、幂函数（1）幂函数的定义一般地，函数y x 叫做幂函数，此中x 为自变量，是常数．（2）幂函数的图象过定点：全部的幂函数在(0,) 都有定义，而且图象都经过点(1,1)．三、指数函数（1）根式的观点：假如 x na, a R, x R, n 1，且 n N ，那么 x 叫做 a 的 n 次方根．（2）分数指数幂的观点mna m (a①正数的 正分数指数幂 的意义是： a n 0, m, n N , 且 n 1) ．0 的正分数指数幂等于 0．m m1)m (a 0, m, n②正数的 负分数指数幂 的意义是： an(1)nn (N , 且 n 1) ．0 的负aa分数指数幂没存心义． （3）运算性质①a ra sa r s(a 0, , )r sa rs(a 0, r , s R)r s R ② ( a )③ (ab )rrb r( a 0, b 0, r )a R（4）指数函数函数名称指数函数定义函数 y a x( a且 a 1) 叫做指数函数a 10 a 1yy a xya xy图象y 1y 1(0,1)(0,1)OxOx定义域 R值域(0, )过定点图象过定点(0,1) ，即当 x 0 时， y 1．奇偶性非奇非偶单一性在 R 上是增函数 在 R 上是减函数a x1 ( x 0) a x 1 ( x 0) 函数值的 a x 1 ( x 0)a x1 ( x 0) 变化状况a xa x1 (x 0)1 ( x 0)a 变化对图象的影响 在第一象限内， a 越大图象越高；在第二象限内， a 越大图象越低．四、对数函数（1）对数的定义： ① 若a xN (a0, 且a1)，则 x 叫做以 a为底 N的对数，记作 x log a N ，此中 a 叫做底数， N 叫做真数．② 负数和零没有对数．③ 对数式与指数式的互化：x log a Na xN (a 0, a 1, N0) ．（2）几个重要的对数恒等式：log a 1 0 ， log a a 1， log a a bb ．（3）常用对数与自然对数常用对数： lg N ，即 log 10 N ；自然对数： ln N ，即 log e N （此中 ）． （4）对数的运算性质假如 a 0, a 1, M 0, N 0 ，那么①加法： log a M log a Nlog a (MN )②减法： log a M log a Nlog a MN③数乘： n log a M log a M n(n R)④alog aNN⑤ log bMnnlog a M ( b 0, n)⑥换底公式： loga logb N0, 且 b 1)abRN(blog b a（5）对数函数函数名称对数函数定义函数 y log a x( a 0 且 a 1) 叫做对数函数a 10 a 1yx 1yx 1y log a xy log a x图象(1,0)O (1,0)xOx定义域 (0, ) 值域R过定点 图象过定点 (1,0) ，即当 x1 时， y0 ．奇偶性非奇非偶单一性在 定义域 上是增函数 在 定义域 上是减函数log a x 0 ( x 1)log a x 0 ( x 1) 函数值的 log a x 0 ( x 1)log a x 0 ( x 1) 变化状况log a x 0 (0x 1)log a x0 (0 x 1)五、反函数 （1）反函数的观点设函数 yf (x) 的定义域为 A ，值域为 C ，从式子 yf ( x) 中解出 x ，得式子 x ( y) ．假如对于 y 在 C 中的任何一个值，经过式子x( y) ， x 在 A 中都有独一确立的值和它对应，那么式子 x( y) 表示 x 是 y 的函数， 函数 x( y) 叫做函数 y f (x) 的反函数， 记作 x f1( y) ，习惯上改写成 yf 1 ( x) ．（ 2）反函数的求法①确立反函数的定义域，即原函数的值域；②从原函数式 y f ( x) 中反解出 xf 1 ( y) ；③将 x f1( y) 改写成 y f 1 (x) ，并注明反函数的定义域．（3）反函数的性质①原函数 yf ( x) 与反函数 y f1( x)的图象对于直线y x对称．②函数 yf (x) 的定义域、值域分别是其反函数 y f 1(x) 的值域、定义域．③若 P(a,b) 在原函数 y f ( x) 的图象上，则 P ' (b, a) 在反函数 y f1( x) 的图象上．④一般地，函数 yf ( x) 要有反函数则它一定为单一函数．六、三角函数的图像和性质 （一）正弦与余函数的图像与性质函数y cosxy sin x图像定域义 RR值域1,11,1最值x2k 时 ,y 最大 ， k Zx2k 时, y 最大，k Z112x2k 时, y 最小， Zx2k 时, y 最小 ，Z1 k1k2单一性在每个 [2 k, 2k ] 上递加 22在每个 [2k,32 k ] 上递减在每个 [ 2k ,2 k ]上递加在每个 [2 k ,2k ] 上递减奇偶性 奇函数偶函数周期性 是周期函数， 2 为最小正周期 是周期函数， 2 为最小正周期 对称性对称中心 (k ,0)，对称中心 (k ,0) ，2对称轴 : xk ,( k Z )对称轴 : x k ,( kZ )22. 正切与余切函数的图像与性质函数 图像y tan x y cot x定域义{ x | x R 且 xk ,k Z} { x | x R 且xk ,k Z}2值域 RR单一性在每个 (k ,k )上递加 在每个 ( k ,k )上递减2 2k Zk Z奇偶性 奇函数奇函数周期性 是周期函数， 为最小正周期是周期函数， 为最小正周期对称性对称中心 (k,0)对称中心 (k,0)2 2七、反三角函数的图像与性质1.反正弦与反余函数的图像与性质反正弦函数yarcsin x 反余弦函数 y arccosx函数是y cos x， x 0, 的反函数ysin x ， x ,2是 2 的反函数图像定域义1,1 1,1值域,2 0,2单一性在[ 1, 1]上递加在[ 1, 1]上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心(0,0) 对称中心 (0, )2 2.反正切与反余切函数的图像与性质函数arctan x 反余切函数 y arccot x反正切函数 y是y tan x， x ( , ) 的反函数是y cot x， x 0,的反函数2 2图像定域义( , , ) ( , , )值域2 2 0,,单一性在 ( , , )上递加在( , , )上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心（ 0， 0）对称中心（0，π /2）。

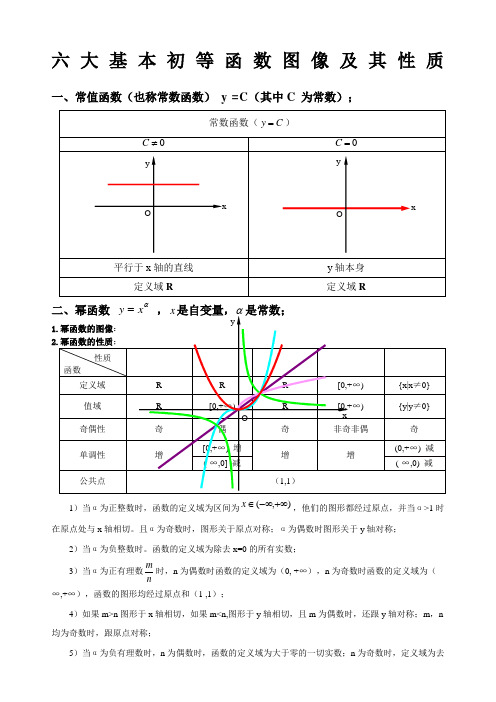
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫⎝⎛=1)(的函数图像关于y 轴对称。

b.2. 4.a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) nm n m a a a +=⋅(2)nm n m aa a -=÷b.y(1)()a a nn= ； (2)当n 为奇数时，a a nn=当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2xy =3x y =21xy =1-=x y定义域 R RR [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xyOxy =2x y =3x y =1-=x y 21xy =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性 非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性 在），（∞+∞-是增函数在），（∞+∞-是减函数1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2xy =3x y =21xy =1-=x y定义域 R RR [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xyOxy =2x y =3x y =1-=x y 21xy =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性 非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性 在），（∞+∞-是增函数在），（∞+∞-是减函数1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

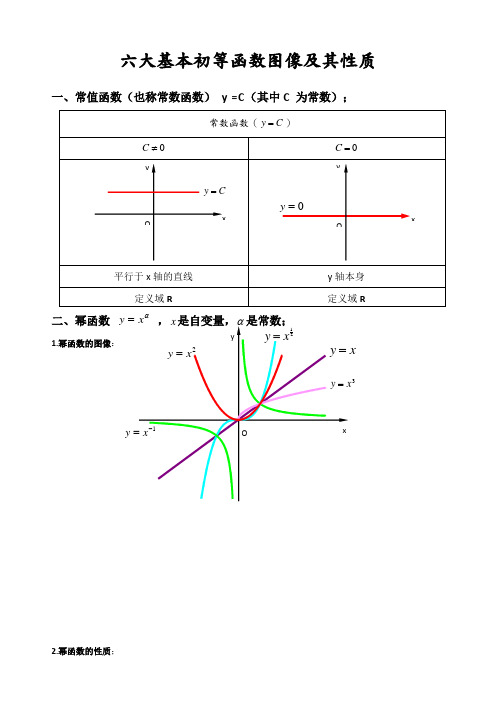
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；二、幂函数 αy =1.幂函数的图像：2.幂函数的性质；3y1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：1(2.指数函数的性质；1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。

.当1>a 时，a 值越大，x a y =的图像越靠近y 轴；xf x.当10<<a 时，a 值越大，xa y =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅ (2)n m n m a a a -=÷(3) ()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质；(1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。

b.1.当1>a 时，a 值越大，xa y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，x a y =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。

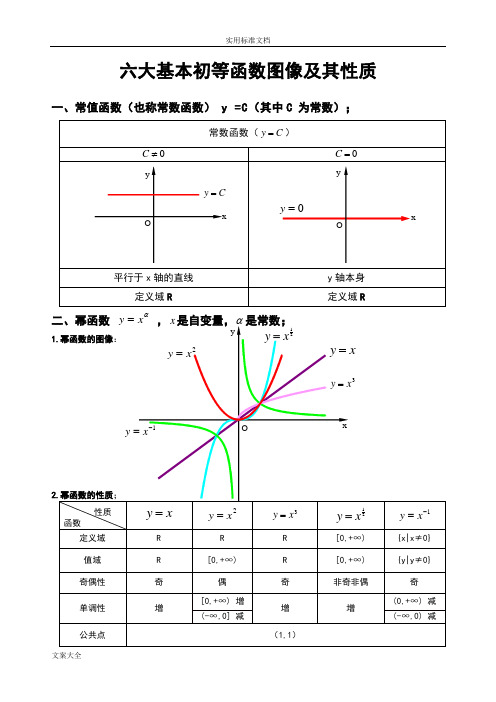
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性 非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数 在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

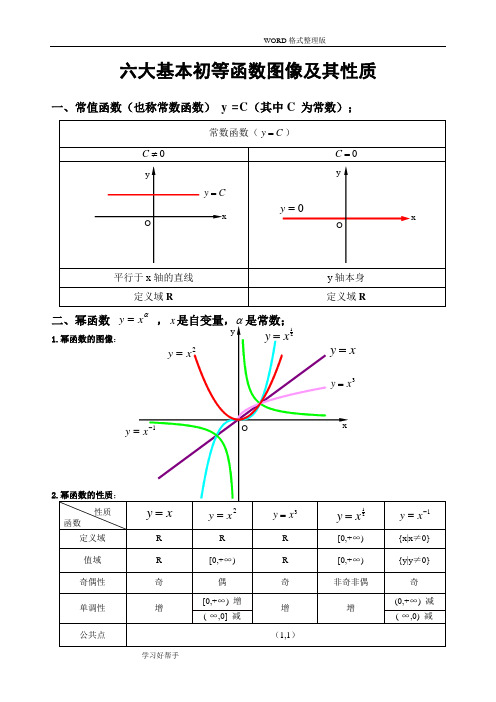
六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）0≠C0=C平行于x 轴的直线y 轴本身 定义域R定义域R二、幂函数 αx y = ，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数x y =2x y =3x y =21xy =1-=x y定义域 R R R [0,+∞) {x|x ≠0} 值域 R [0,+∞) R [0,+∞) {y|y ≠0} 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增[0,+∞) 增 增 增(0,+∞) 减 (-∞,0] 减(-∞,0) 减公共点（1,1）xyOxy =2x y =3x y =1-=xy 21xy =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.指数函数的性质；性质函数x a y =)1(>ax a y =)10(<<a定义域 R 值域(0，+∞) 奇偶性 非奇非偶公共点过点(0，1)，即0=x 时，1=y单调性在），（∞+∞-是增函数 在），（∞+∞-是减函数 1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

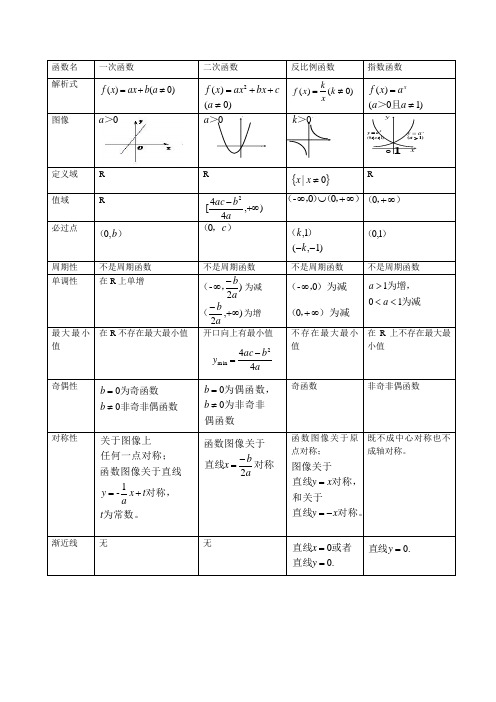
函数名 一次函数 二次函数 反比例函数 指数函数 解析式)0()(≠+=a b ax x f)0()(≠=k xkx f图像定义域 R R {}0|≠x xR值域 R），（∞+0 必过点）（b ,0），（c 0 )1,(1,--k k ）（）（1,0 周期性 不是周期函数 不是周期函数 不是周期函数不是周期函数单调性在R 上单增)2-a b-∞，（为减),2+∞-ab （为增 ）为减，（0-∞）为减，（∞+0为减为增，101<<>a a最大最小值在R 不存在最大最小值开口向上有最小值ab ac y 442min-=不存在最大最小值在R 上不存在最大最小值奇偶性非奇非偶函数为奇函数00≠=b b偶函数为非奇非为偶函数，00≠=b b 奇函数 非奇非偶函数对称性为常数。

对称，函数图像关于直线任何一点对称；关于图像上t t x a y +=1-对称直线函数图像关于abx 2-= 函数图像关于原点对称； 对称。

直线和关于对称，直线图像关于x y x y -==既不成中心对称也不成轴对称。

渐近线 无 无.00==y x 直线或者直线.0=y 直线)0()(2≠++=a cbx ax x f )10()(≠=a a a x f x且＞0＞a＞a 0＞k ),44[2+∞-ab ac ），（），（∞+⋃∞00-a y =)10(<<a xa y =)1(>a xyO1函数名 对数函数 幂函数的一个例子 双钩函数含绝对值函数解析式)10(log ≠>=a a y xa且)0(≥=x xyba b x a x y <-+-=设为了研究方便 图像O 1yx)10(log <<=a y xa)1(log >=a y xaOyxxy =11定义域 ()∞+，0[)∞+，00}x |{x ≠R值域R[)∞+，0(][)∞+∞，，ab ab 22--[)+∞-,a b必过点）（0,1()1,1)2,(2,ab abab ab--）（),(,a b b a b a --）（周期性 不是周期函数 不是周期函数 不是周期函数 不是周期函数单调性单调递减。

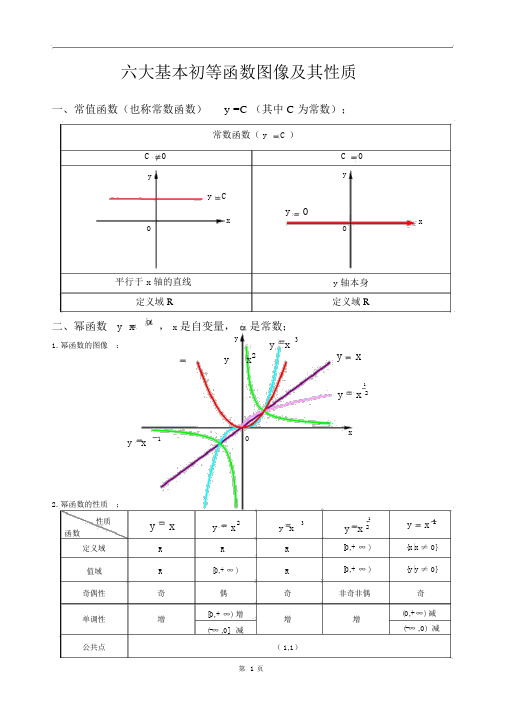
六大基本初等函数图像及其性质一、常值函数（也称常数函数）y =C （其中 C 为常数）；常数函数（ y C ）C 0yy Cy 0xO平行于 x 轴的直线定义域 R二、幂函数 y x， x 是自变量，是常数；1. 幂函数的图像：y y x3y x2y x1O2.幂函数的性质；性质y x y x2y x3函数定义域R R R值域R[0,+ ∞ )R奇偶性奇偶奇单调性增[0,+ ∞) 增增(-∞ ,0]减公共点（ 1,1）C 0yOy轴本身定义域 Ry x1y x 2x1y x 2[0,+ ∞ )[0,+ ∞ )非奇非偶增xy x 1{x|x ≠ 0}{y|y ≠ 0}奇(0,+∞) 减(-∞ ,0) 减第 1 页1）当 α 为正整数时，函数的定义域为区间为x ( ,)，他们的图形都经过原点，并当α >1 时在原点处与 x 轴相切。

且 α为奇数时，图形关于原点对称；α 为偶数时图形关于 y 轴对称；2）当 α 为负整数时。

函数的定义域为除去 x=0 的所有实数；3）当 α 为正有理数m时， n 为偶数时函数的定义域为（0, +∞）， n 为奇数时函数的定义域为（ -n∞ ,+∞），函数的图形均经过原点和（ 1 ,1）；4）如果 m>n 图形于 x 轴相切，如果m<n,图形于 y 轴相切，且 m 为偶数时，还跟y 轴对称； m ， n均为奇数时，跟原点对称；5）当 α 为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数ya x(x 是自变量,a 是常数且a0 ， a1 )，定义域是R ；[ 无界函数 ]1. 指数函数的图象 ：yaxyyy ax(a 1)(0 a1)(0,1)y 1(0,1)y 1OxOx2. 指数函数的性质 ；性质y a x(a 1)y a x(0 a 1)函数定义域 R值域(0，+∞)奇偶性非奇非偶公共点过点 (0，1)，即 x 0 时， y1单调性 在（， ）是增函数 （， ）在是减函数1 ） 当 a1时 函 数 为 单 调 增 , 当 0 a 1时函数为单调减；2 ） 不 论 x 为 何 值 , y 总 是 正 的 , 图 形 在 x 轴 上 方 ；3 ） 当 x 0 时 , y1,所以它的图形通过(0,1)点 。

标准实用文案大全六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C （其中C 为常数）；常数函数（C y =）≠C 0=C 平行于x 轴的直线y 轴本身定义域R 定义域R二、幂函数αx y=，x 是自变量，α是常数；1.幂函数的图像：2.幂函数的性质；性质函数xy =2xy =3xy =21x y =1-=xy 定义域R R R [0,+[0,+∞∞) {x|x {x|x≠≠0} 值域R [0,+[0,+∞∞) R [0,+[0,+∞∞) {y|y {y|y≠≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+[0,+∞∞) ) 增增增增(0,+(0,+∞∞) ) 减减(-(-∞∞,0] ,0] 减减(-(-∞∞,0) ,0) 减减公共点（1,11,1））xyOxy =2x y =3x y =1-=x y 21x y =O=y xCy =Oxyy1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α，他们的图形都经过原点，并当α>1>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm 时，时，n n 为偶数时函数的定义域为（为偶数时函数的定义域为（0, +0, +0, +∞），∞），∞），n n 为奇数时函数的定义域为（为奇数时函数的定义域为（--∞,+,+∞），函数的图形均经过原点和（∞），函数的图形均经过原点和（∞），函数的图形均经过原点和（1 ,11 ,11 ,1）；）；4）如果m>n 图形于x 轴相切，如果m<n,m<n,图形于图形于y 轴相切，且m 为偶数时，还跟y 轴对称；轴对称；m m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，）当α为负有理数时，n n 为偶数时，函数的定义域为大于零的一切实数；为偶数时，函数的定义域为大于零的一切实数；n n 为奇数时，定义域为去除x=0以外的一切实数。

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。

b.1.当1>a 时，a 值越大，xa y =的图像越靠近y 轴；b.2.当10<<a 时，a 值越大，x a y =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m a a a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。

1、一次函数与二次函数（一）一次函数（二）二次函数①一般式：2()(0)f x ax bx c a =++≠ ②顶点式：2()()(0)f x a x h k a =-+≠③两根式：12()()()(0)f x a x x x x a =--≠（2）求二次函数解析式的方法①已知三个点坐标时，宜用一般式．②已知抛物线的顶点坐标或与对称轴有关或与最大（小）值有关时，常使用顶点式．③若已知抛物线与x 轴有两个交点，且横线坐标已知时，选用两根式求()f x 更方便．①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线，对称轴方程为,2bx a=-顶点坐标是24(,24b ac b a a--②当0a >时，抛物线开口向上，函数在(,]2b a -∞-上递减，在[,)2ba-+∞上递增，当2b x a =-时，2min 4()4ac b f x a -=；当0a <时，抛物线开口向下，函数在(,]2b a -∞-上递增，在[,)2b a -+∞上递减，当2b x a =-时，2max 4()4ac b f x a-=．二、幂函数过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)．三、指数函数（1）根式的概念：如果,,,1nx a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．①正数的正分数指数幂的意义是：0,,,m na a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是：1(0,,,m m nn a a m n N a -+==>∈且1)n >．0的负分数指数幂没有意义．（3）运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)rrrab a b a b r R =>>∈（4）指数函数函数名称指数函数四、对数函数（1）对数的定义： ①若(0,1)x a N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数． ②负数和零没有对数．③对数式与指数式的互化： log (0,1,0)x a x N a N a a N =⇔=>≠>．常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）．①加法：log log log ()a a a M N MN += ②减法：log log log a a aMM N N-=③数乘：log log ()naan M M n R =∈ ④log a Na N=⑤log log (0,)b n a a nM M b n R b =≠∈⑥换底公式：log log (0,1)log b a b N N b b a =>≠且（5）对数函数五、反函数设函数()y f x =的定义域为A ，值域为C ，从式子()y f x =中解出x ，得式子()x y ϕ=．如果对于y 在C 中的任何一个值，通过式子()x y ϕ=，x 在A 中都有唯一确定的值和它对应，那么式子()x y ϕ=表示x 是y 的函数，函数()x y ϕ=叫做函数()y f x =的反函数，记作1()x f y -=，习惯上改写成1()y f x -=．①确定反函数的定义域，即原函数的值域；②从原函数式()y f x =中反解出1()x f y -=；③将1()x fy -=改写成1()y f x -=，并注明反函数的定义域．①原函数()y f x =与反函数1()y fx -=的图象关于直线y x =对称．②函数()y f x =的定义域、值域分别是其反函数1()y fx -=的值域、定义域．③若(,)P a b 在原函数()y f x =的图象上，则'(,)P b a 在反函数1()y f x -=的图象上．④一般地，函数()y f x =要有反函数则它必须为单调函数．六、三角函数的图像和性质（一）正弦与余函数的图像与性质函数xy sin =xy cos =图像定域义R R值域[]1,1-[]1,1-最值2,1 22,1 2x k y k Zx k y k Zππππ=+=∈=-+=-∈最大最小时，时，2, 1 2,1x k y k Zx k y k Z πππ==∈=+=-∈最大最小时，时，单调性[2,2]223[2,2]22Zk k k k k ππππππππ-++++∈在每个上递增在每个上递减[2,2][2,2]Zk k k k k ππππππ-++∈在每个上递增在每个上递减奇偶性奇函数偶函数周期性是周期函数，2为最小正周期π是周期函数，2为最小正周期π对称性对称中心(,0)k π，:,()2x k k Z ππ=+∈对称轴对称中心(,0)2k ππ+，:,()x k k Z π=∈对称轴2. 正切与余切函数的图像与性质函数x y tan =xy cot =图像定域义{|,}2x x R x k k Z ππ∈≠+∈且{|,}x x R x k k Z ππ∈≠+∈且值域RR单调性(,)22Zk k k ππππ-++∈在每个上递增(,)Zk k k πππ+∈在每个上递减奇偶性奇函数奇函数周期性是周期函数，为最小正周期π是周期函数，为最小正周期π对称性对称中心(,0)2k π对称中心(,0)2k π七、反三角函数的图像与性质1. 反正弦与反余函数的图像与性质函数反正弦函数arcsin y x =是sin ,22y x x ππ⎡⎤=∈-⎢⎥⎣⎦，的反函数反余弦函数arccos y x=是[]cos 0,y x x π=∈，的反函数图像定域义[]1,1-[]1,1-值域,22ππ⎡⎤-⎢⎥⎣⎦[]0,π单调性[1,1]-+在上递增[1,1]-+在上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心(0,0)对称中心(0,)2π2. 反正切与反余切函数的图像与性质函数反正切函数arctan y x =是tan (,)22y x x ππ=∈-，的反函数反余切函数arccot y x =是()cot 0,y x x π=∈，的反函数图像定域义(,,)-∞+∞(,,)-∞+∞值域,22ππ⎛⎫- ⎪⎝⎭()0,π单调性(,,)-∞+∞在上递增(,,)-∞+∞在上递减奇偶性奇函数非奇非偶周期性无无对称性对称中心（0，0）对称中心（0，π/2）11。

六大基本初等函数图像及其性质一、常值函数（也称常数函数） y =C（其中C 为常数）；α1）当α为正整数时，函数的定义域为区间为),(+∞-∞∈x ，他们的图形都经过原点，并当α>1时在原点处与x 轴相切。

且α为奇数时，图形关于原点对称；α为偶数时图形关于y 轴对称；2）当α为负整数时。

函数的定义域为除去x=0的所有实数； 3）当α为正有理数nm时，n 为偶数时函数的定义域为（0, +∞），n 为奇数时函数的定义域为（-∞,+∞），函数的图形均经过原点和（1 ,1）；4）如果m>n 图形于x 轴相切，如果m<n,图形于y 轴相切，且m 为偶数时，还跟y 轴对称；m ，n 均为奇数时，跟原点对称；5）当α为负有理数时，n 为偶数时，函数的定义域为大于零的一切实数；n 为奇数时，定义域为去除x=0以外的一切实数。

三、指数函数xa y =(x 是自变量,a 是常数且0>a ，1≠a )，定义域是R ；[无界函数]1.指数函数的图象：2.1）当1>a 时函数为单调增,当10<<a 时函数为单调减； 2）不论x 为何值,y 总是正的,图形在x 轴上方； 3）当0=x 时,1=y ,所以它的图形通过(0,1)点。

1(3.（选，补充）指数函数值的大小比较*N ∈a ；a.底数互为倒数的两个指数函数x a x f =)(，xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。

.当1>a 时，a 值越大，x a y =的图像越靠近y 轴；.当10<<a 时，a 值越大，xa y =的图像越远离y 轴。

4.指数的运算法则（公式）；a.整数指数幂的运算性质),,0(Q n m a ∈≥；(1) nm n m aa a +=⋅(2)nm nmaa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质； (1)()a a nn= ； (2)当n 为奇数时，a a nn =当n 为偶数时，⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂；(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a )，定义域),0(+∞∈x [无界]1.对数的概念：如果a(a ＞0，a ≠1)的b 次幂等于N ，就是 N a b=，那么数b 叫做以a 为底N 的对数，记作b N a =log ,其中a 叫做对数的底数，N 叫做真数，式子N a log 叫做对数式。