信息论编码 田宝玉chapter11-1

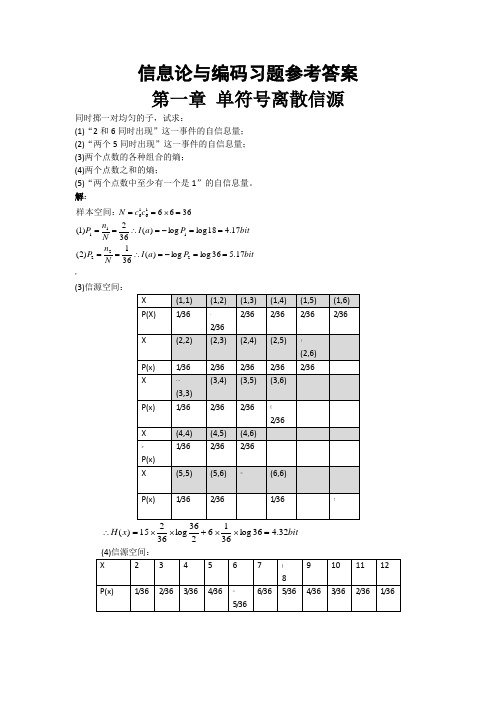
信息论与编码习题参考答案第一章 单符号离散信源同时掷一对均匀的子，试求：(1)“2和6同时出现”这一事件的自信息量； (2)“两个5同时出现”这一事件的自信息量； (3)两个点数的各种组合的熵； (4)两个点数之和的熵；(5)“两个点数中至少有一个是1”的自信息量。

解：bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间：* (3)信源空间：bit x H 32.436log 3616236log 36215)(=⨯⨯+⨯⨯=∴bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴＋＋ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==?如有6行、8列的棋型方格，若有两个质点A 和B ，分别以等概落入任一方格内，且它们的坐标分别为（Xa ，Ya ）, （Xb ，Yb ）,但A ，B 不能同时落入同一方格内。

（1） 若仅有质点A ，求A 落入任一方格的平均信息量； （2） 若已知A 已落入，求B 落入的平均信息量； （3） 若A ，B 是可辨认的，求A ，B 落入的平均信息量。

解： ！bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率bitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知 bitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为%.如果你问一位男士：“你是否是红绿色盲”他的回答可能是：“是”，也可能“不是”。

信息论与编码第二版答案《信息论与编码（第二版）》是Claude Elwood Shannon所撰写的经典著作，该书于1948年首次出版，至今被广泛认可为信息论领域的权威指南。

本书通过数学模型和理论阐述了信息的量化、传输、存储以及编码等相关概念和原理。

深入浅出的阐述方式使得本书具备了普适性和可读性，成为信息论领域学习者和研究者的必备参考。

信息论是研究信息的传输、处理和应用的科学，其最初来源于通信工程领域。

而编码作为信息论的一个重要分支，旨在寻求一种有效的方式将信息转化为符号或信号，以便能够高效地传输和存储。

编码的主要目标是通过减少冗余或利用统计特征来压缩信息，并提高信号传输过程中的容错性。

在信息论中，最重要的概念之一是“信息熵”。

信息熵是信息的不确定性度量，也可以看作是信息的平均编码长度。

当一个事件出现的可能性均匀时，信息熵达到最大值，表示信息的不确定度最高；而当事件的概率趋于一个时，信息熵达到最小值，表示事件的确定性最高。

例如，抛一枚公正的硬币，其正反面出现的概率均为0.5，那么信息熵将达到最大值，即1比特。

如果硬币是正面朝上或者反面朝上，那么信息熵将达到最小值，即0比特。

除了信息熵，信息论中还有许多重要的概念，如条件熵、相对熵和互信息等。

其中，条件熵表示给定某些信息后的不确定性，相对熵则用于比较两个概率分布之间的差异，而互信息则度量了两个随机变量之间的相关性。

编码是信息论中的关键技术之一，其目的是将信息通过某种规则进行转换，使其适于传输或存储。

常见的编码方法有哈夫曼编码、香农-费诺编码和算术编码等。

其中，哈夫曼编码常用于无损压缩，通过根据字符频率设计不等长的编码，使得频率高的字符用较短的编码表示，而频率低的字符用较长的编码表示，从而达到压缩的效果。

算术编码则通过将整个信息序列映射为一个实数，从而实现更高的压缩比。

信息论与编码的研究对众多领域都具有重要意义。

在通信领域中，信息论的结果对于提高信道容量和降低误差率具有指导意义。

信息论与编码课后习题答案信息论与编码课后习题答案[信息论与编码]课后习题答案1、在认识论层次上研究信息的时候，必须同时考虑到形式、含义和效用三个方面的因素。

2、1948年，美国数学家香农发表了题为“通信的数学理论”的长篇论文，从而创立了信息论。

3、按照信息的性质，可以把信息分为语法信息、语义信息和语用信息。

4、按照信息的地位，可以把信息分成客观信息和主观信息。

5、人们研究信息论的目的就是为了高效率、可信、安全地互换和利用各种各样的信息。

6、信息的是建立信息论的基础。

8、就是香农信息论最基本最重要的概念。

9、事物的不确定度是用时间统计发生概率的对数来描述的。

10、单符号线性信源通常用随机变量叙述，而多符号线性信源通常用随机矢量叙述。

11、一个随机事件发生某一结果后所带来的信息量称为自信息量，定义为其发生概率对数的负值。

12、自信息量的单位通常存有比特、奈特和哈特。

13、必然事件的自信息是。

14、不可能将事件的自信息量就是15、两个相互独立的随机变量的联合自信息量等于两个自信息量之和。

16、数据处理定理：当消息经过多级处置后，随着处理器数目的激增，输出消息与输入消息之间的平均值互信息量趋向变大。

17、离散平稳无记忆信源x的n次扩展信源的熵等于离散信源x的熵的。

limh(xn/x1x2xn1)h n18、线性稳定存有记忆信源的音速熵，。

19、对于n元m阶马尔可夫信源，其状态空间共有m个不同的状态。

20、一维已连续随即变量x在[a，b]。

1log22ep21、平均功率为p的高斯分布的已连续信源，其信源熵，hc（x）=2。

22、对于限峰值功率的n维连续信源，当概率密度均匀分布时连续信源熵具有最大值。

23、对于减半平均功率的一维已连续信源，当概率密度24、对于均值为0，平均功率受限的连续信源，信源的冗余度决定于平均功率的限定值p和信源的熵功率p25、若一线性并无记忆信源的信源熵h（x）等同于2.5，对信源展开相切的并无杂讯二进制编码，则编码长度至少为。

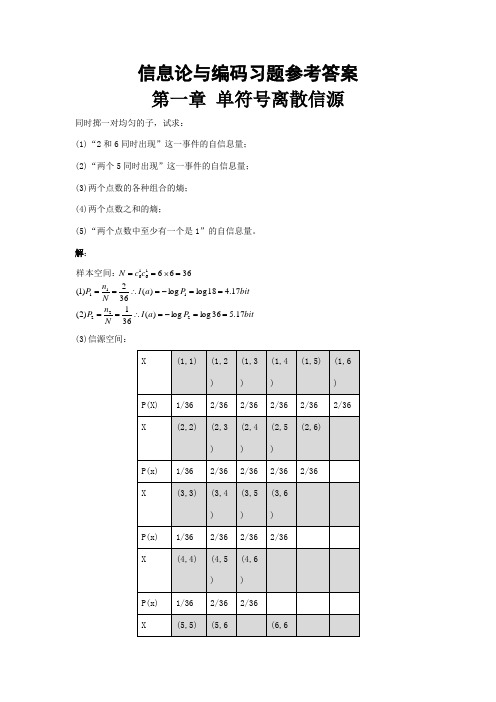
信息论与编码习题参考答案 第一章 单符号离散信源同时掷一对均匀的子，试求：(1)“2和6同时出现”这一事件的自信息量； (2)“两个5同时出现”这一事件的自信息量； (3)两个点数的各种组合的熵； (4)两个点数之和的熵；(5)“两个点数中至少有一个是1”的自信息量。

解：bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间：(3)信源空间：bit x H 32.436log 3616236log 36215)(=⨯⨯+⨯⨯=∴ (4)信源空间：bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴＋＋ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==如有6行、8列的棋型方格，若有两个质点A 和B ，分别以等概落入任一方格内，且它们的坐标分别为（Xa ，Ya ）, （Xb ，Yb ）,但A ，B 不能同时落入同一方格内。

（1） 若仅有质点A ，求A 落入任一方格的平均信息量； （2） 若已知A 已落入，求B 落入的平均信息量； （3） 若A ，B 是可辨认的，求A ，B 落入的平均信息量。

解：bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率bitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知bitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为%.如果你问一位男士：“你是否是红绿色盲”他的回答可能是：“是”，也可能“不是”。

《信息论、编码与密码学》课后习题答案第1章信源编码1.1 考虑一个信源概率为｛0.30 , 0.25 , 0.20 , 0.15 , 0.10｝的DMS求信源嫡H (X)。

5解：信源嫡H(X) = -£P k log 2( P k)H(X)=-[0.30*(-1.737)+0.25*(-2)+0.2*(-2.322)+0.15*(-2.737)+0.1*(-3.322)]=[0.521+0.5+0.464+0.411+0.332]=2.228(bit)故得其信源嫡H(X)为2.228bit1.2 证明一个离散信源在它的输出符号等概率的情况下其嫡达到最大值。

解：若二元离散信源的统计特性为P+Q=1 H(X)=-[P*log(P)+(1-P)*log(1-P)]对H(X)求导求极值，由dH(X)/d(P)=0可得log可知当概率P=Q=1/2时,有信源嫡H (X)max = 1(bit)对丁三元离散信源，当概率R = P2 = P3 = 1/3时，信源嫡H (X )m a=x1 .5 8 (5bit ),此结论可以推广到N元的离散信源。

1.3证明不等式lnx^x—1。

画出曲线y〔=lnx和y2 = x — 1的平■面图以表明上述不等式的正确性。

证明：f (x) = ln x 「x 1(x - 0) f(x)=【x令f(x)，=0, x =1 又有x 0. 0 ：. x < 1 时f(x) 0 此时 f(x) fx =0 也即 In x _x -1当x _1时同理可得此时Inx _x -1综上可得lnx 笑x -1证毕 绘制图形说明如下 可以很明确说明上述 不等式的正确性。

1.4证明I(X;Y)芝0。

在什么条件下等号成立?n mI(X ； V =' ' P(x,y j )i(x, y j )i 目j 目n m =' P(x,y j )logi 注j T 当和相互独立时等号成立。

信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子，试求：(1)“2和6同时出现”这一事件的自信息量； (2)“两个5同时出现”这一事件的自信息量； (3)两个点数的各种组合的熵； (4)两个点数之和的熵；(5)“两个点数中至少有一个是1”的自信息量。

解：bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间：(3)信源空间：bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴＋＋ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格，若有两个质点A 和B ，分别以等概落入任一方格，且它们的坐标分别为（Xa ，Ya ）, （Xb ，Yb ）,但A ，B 不能同时落入同一方格。

（1） 若仅有质点A ，求A 落入任一方格的平均信息量； （2） 若已知A 已落入，求B 落入的平均信息量； （3） 若A ，B 是可辨认的，求A ，B 落入的平均信息量。

解：bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士：“你是否是红绿色盲？”他的回答可能是：“是”，也可能“不是”。