偏微分方程数值解期末试题及标准答案

一．填空（1553=⨯分）1．若步长趋于零时，差分方程的截断误差0→lmR ，则差分方程的解lm U 趋近于微分方程的解lm u . 此结论_______（错或对）； 2．一阶Sobolev 空间{})(,,),()(21Ω∈''=ΩL f f f y x f H y x关于内积=1),(g f _____________________是Hilbert 空间；3．对非线性（变系数）差分格式，常用 _______系数法讨论差分格式的_______稳定性； 4．写出3x y =在区间]2,1[上的两个一阶广义导数：_________________________________， ________________________________________；5．隐式差分格式关于初值是无条件稳定的. 此结论_______（错或对）。

二．（13分）设有椭圆型方程边值问题用1.0=h 作正方形网格剖分 。

（1）用五点菱形差分格式将微分方程在内点离散化； （2）用截断误差为)(2h O 的差分法将第三边界条件离散化； （3）整理后的差分方程组为 三．（12）给定初值问题xut u ∂∂=∂∂ ， ()10,+=x x u 取时间步长1.0=τ，空间步长2.0=h 。

试合理选用一阶偏心差分格式（最简显格式）, 并以此格式求出解函数),(t x u 在2.0,2.0=-=t x 处的近似值。

1．所选用的差分格式是： 2．计算所求近似值：四．（12分）试讨论差分方程()ha h a r u u r u u k l k l k l k l ττ+-=-+=++++11,1111逼近微分方程0=∂∂+∂∂xu a t u 的截断误差阶R 。

思路一：将r 带入到原式，展开后可得格式是在点（l+1/2,k+1/2）展开的。

思路二：差分格式的用到的四个点刚好是矩形区域的四个顶点，可由此构造中心点的差分格式。

数学偏微分方程的数值解法当然可以。

这里是根据标题“数学偏微分方程的数值解法”出的20道试题，包括选择题和填空题，每道题目都有详细的序号介绍：1. 选择题：偏微分方程的数值解法主要适用于哪类方程？A. 常微分方程B. 偏微分方程C. 代数方程D. 差分方程2.填空题：数值解法中常用的一种基础方法是______________。

3.选择题：有限差分法是一种适用于哪种类型的偏微分方程的数值解法？A. 椭圆型B. 抛物型C. 双曲型D. 超越型4.填空题：偏微分方程的数值解法通常要求将空间区域离散化为___ ___________。

5. 选择题：哪种方法适合处理偏微分方程的初始值问题？A. 有限元法B. 有限差分法C. 傅里叶变换法D. 辛普森法则6.填空题：数值解法中，常用的稳定性分析方法包括_____________ _。

7.选择题：对于偏微分方程的边值问题，常用的数值方法是_______ _______。

A. 有限体积法B. 辛普森法则C. 椭圆积分法D. 有限元法8.填空题：描述一种常见的数值解法的收敛性条件______________。

9.选择题：哪种方法在处理时间依赖性偏微分方程时特别有效？A. 隐式方法B. 显式方法C. 中心差分法D. 前进差分法10.填空题：数值解法中的矩阵求解通常利用______________方法。

11.选择题：在有限元法中，通常要对空间区域进行如何划分？A. 正交分解B. 三角剖分C. 曲面划分D. 直角分割12.填空题：有限差分法的精度通常与______________相关。

13.选择题：哪种方法适合处理非线性偏微分方程的数值解？A. 变分法B. 有限元法C. 辛普森法则D. 显式方法14.填空题：对于稳定性的要求，常用的数值方法需要满足_________ _____条件。

15.选择题：哪种方法可以有效地处理多维偏微分方程的数值解？A. 傅里叶变换法B. 辛普森法则C. 多重网格法D. 变分法16.填空题：在求解偏微分方程数值解时，通常需要考虑___________ ___问题。

偏微分⽅程数值习题解答李微分⽅程数值解习题解答 1-1 如果0)0('=?，则称0x 是)(x J 的驻点（或稳定点）.矩阵A 对称（不必正定），求证0x 是)(x J 的驻点的充要条件是：0x 是⽅程组 b Ax =的解证明:由)(λ?的定义与内积的性线性性质,得),()),((21)()(0000x x b x x x x A x x J λλλλλ?+-++=+=),(2),()(200x Ax x b Ax x J λλ+-+=),(),()(0'x Ax x b Ax λλ?+-=必要性:由0)0('=?,得,对于任何n R x ∈,有0),(0=-x b Ax ,由线性代数结论知,b Ax b Ax ==-00,0充分性: 由b Ax =0,对于任何n R x ∈,0|),(),()0(00'=+-==λλ?x Ax x b Ax即0x 是)(x J 的驻点. §1-2补充: 证明)(x f 的不同的⼴义导数⼏乎处处相等.证明:设)(2I L f ∈,)(,221I L g g ∈为)(x f 的⼴义导数,由⼴义导数的定义可知,对于任意)()(0I C x ∞∈?,有-=ba ba dx x x f dx x x g )()()()('1?? ??-=ba ba dx x x f dx x x g )()()()('2?? 两式相减,得到)(0)()(021I C x g g ba ∞∈?=- 由变分基本引理,21g g -⼏乎处处为零,即21,g g ⼏乎处处相等.补充:证明),(v u a 的连续性条件(1.2.21) 证明: 设'|)(|,|)(|M x q M x p ≤≤,由Schwarz 不等式||||.||||||||.|||||)(||),(|'''''v u M v u M dx quv v pu v u a ba +≤+=?11*||||.||||2v u M ≤,其中},max{'*M M M =习题:1 设)('x f 为)(x f 的⼀阶⼴义导数,试⽤类似的⽅法定义)(x f 的k 阶导数,...2,1(=k ) 解:⼀阶⼴义导数的定义,主要是从经典导数经过分部积分得到的关系式来定义,因此可得到如下定义:对于)()(2I L x f ∈,若有)()(2I L x g ∈,使得对于任意的)(0I C ∞∈?,有 ?-=bak kba dx x x f dx x x g )()()1()()()(??则称)(x f 有k 阶⼴义导数,)(x g 称为)(x f 的k 阶⼴义导数,并记kk dxfd x g =)(注:⾼阶⼴义导数不是通过递推定义的,可能有⾼阶导数⽽没有低阶导数.2.利⽤)(2I L 的完全性证明))()((1I H I H m 是Hilbert 空间.证明:只证)(1I H 的完全性.设}{n f 为)(1I H 的基本列,即0||||||||||||0''01→-+-=-m n m n m n f f f f f f因此知}{},{'n n f f 都是)(2I L 中的基本列(按)(2I L 的范数).由)(2I L 的完全性,存在)(,2I L g f ∈,使0||||,0||||0'0→-→-g f f f n n ,以下证明0||||1→-f f n (关键证明dxdfg =)由Schwarz 不等式,有00||||.|||||)())()((|??f f x x f x f n ba n -≤-?00'''|||||||||)())()((|??f f dx x x g x f n ba n -≤-?对于任意的)()(0I C x ∞∈?,成⽴=∞a ba n n dx x x f dx x x f )()()()(lim ??=∞→ba b a nn dx x x g dx x x f )()()()(lim '??由?-=ba n ba ndx x x f dx x x f )()()()(''??取极限得到dx x x f dx x x g ba ba ??-=)()()()('??即')(f x g =,即)(1I H f ∈,且0||||||||||||0''01→-+-=-f f f f f f n n n故)(1I H 中的基本列是收敛的,)(1I H 是完全的. 3.证明⾮齐次两点边值问题证明:边界条件齐次化令)()(0a x x u -+=βα,则0u u w -=满⾜齐次边界条件.w 满⾜的⽅程为00Lu f Lu Lu Lw -=-=,即w 对应的边值问题为==-=0)(,0)('b w a w Lu f Lw (P) 由定理知,问题P 与下列变分问题等价求)(min )(,**12*1w J w J H C w Ew E ∈=∈其中),(),(21)(0*w Lu f w w a w J --=.⽽Cu u a u Lu u J u u Lu f u u u u a w J +-+=-----=),(),()(~),(),(21)(000000*⽽200)()(),(),(C b u b p u u a u Lu +-=-β从⽽**)()()(~)(C b u b p u Jw J +-=β则关于w 的变分问题P 等价于:求α=∈)(,12*a u H C u使得)(min )()(*1u J u J a u H u α=∈=其中)()(),(),(21)(b u b p u f u u a u J β--=4就边值问题（1.2.28）建⽴虚功原理解:令)(0a x u -+=βα,0u u w -=,则w 满⾜)(,0)('00==-=-=b w a w Lu f Lu Lu Lw等价于:1E H v ∈?0),(),(0=--v Lu f v Lw应⽤分部积分,+-=-=-b a b a b a dx dx dv dx dw p v dx dw p vdx dx du p dx d v dx dw p dx d |)()),((还原u ,)()(),(),(),(),(),(),(),(),(000b v b p v f v u a v u a v Lu v f v u a v Lu f v w a β--=-+-=--于是,边值问题等价于:求α=∈)(,1a u H u ,使得1E H v ∈?,成⽴0)()(),(),(=--b v b p v f v u a β注:形式上与⽤v 去乘⽅程两端,应⽤分部积分得到的相同. 5试建⽴与边值问题等价的变分问题.解:取解函数空间为)(20I H ,对于任意)(20I H v ∈⽤v 乘⽅程两端,应⽤分部积分,得到0),(),(44=-+=-v f u dx ud v f Lu⽽??-==b a b a b a dx dxdvdx u d v dx u d vdx dx u d v dx u d .|),(33334444 dx dxv d dx u d dx dx vd dx u d dx dv dx u d b a b a b a ??=+-=2222222222| 上式为),(][2222v f dx uv dx vd dx u d b a =+?定义dx uv dxvd dx u d v u a ba ][),(2222+=?,为双线性形式.变分问题为:求)(20I H u ∈,)(20I H v ∈?),(),(v f v u a =1-41.⽤Galerkin Ritz -⽅法求边值问题==<<=+-1)1(,0)0(102"u u x x u u 的第n 次近似)(x u n ,基函数n i x i x i ,...,2,1),sin()(==π?解:(1)边界条件齐次化:令x u =0,0u u w -=,则w 满⾜齐次边界条件,且)1(,0)0(20==-=-=w w x x Lu Lu Lw第n 次近似n w 取为∑==n i i i n c w 1,其中),...2,1(n i c i =满⾜的Galerkin Ritz -⽅程为n j x x c a j ni i j i ,...,2,1),(),(21=-=∑= ⼜xd jx ix ij dx x j x i dxx j x i ij dx a j i jij i ?-=+=+=ππππππππ)cos()cos(2)sin()sin()cos()cos()(),(1010210''-+πππjx ix sin sin 21由三⾓函数的正交性,得到≠=+=j i j i i a j i ,0,212),(22π??⽽]1)1[()(2)sin()1(),(3102--=-=-?jj j dx x j x x x x ππ? 于是得到+-=-=为偶数为奇数j j j j a x x c j j j j 0 )1()(8),(),(2232ππ最后得到∑+=-+---+=]21[1233])12(1[)12(])12sin[(8)(n k n k k x k x x u ππ 2.在题1中,⽤0)1(=u 代替右边值条件,)(x u n 是⽤Galerkin Ritz -⽅法求解相应问题的第n 次近似,证明)(x u n 按)1,0(2L 收敛到)(x u ,并估计误差.证明:n u 对应的级数绝对收敛,由}{sin x i π的完全性知极限就是解)(x u ,其误差估计为338nR n π≤3.就边值问题(1.2.28)和基函数),...,2,1()()(n i a x x i i =-=?,写出Galerkin Ritz -⽅程解:边界条件齐次化,取)(0a x u -+=βα,0u u w -=, w 对应的微分⽅程为)(,0)('00==-=-=b w a w Lu f Lu Lu Lw对应的变分⽅程为0),(),(0=--v Lu f v w a)]([)(000a x q dx dpqu dx du p dx d Lu -++-=+-=βαβ+-=-ba b a dx x pv b v b p v dxdp )()()(' 变分⽅程为dx v qu x pv b v b p v f v w a ba ?--+=])([)()(),(),(0'ββ取n i a x x i i ,...,2,1,)()(=-=?,则Galerkin -Ritz ⽅程为∑-++--+=-=ba i ba i i nj j jidxa x x q dx a x i x pb b p fc a )]()[()()()()(),(),(11βαβ?β??+=ba j i j i j i dx q p a ][),(''取1,0,1===f q p ,具体计算1=n , )(1),(11a b dx a ba -==221)(21)()()(21a b a b a b a b d -=---+-=ββ, )(211a b c -=,即解)(2101a x u u -+= 2=n :22111)()(2),(),(),(a b dx a x a a b a ba -=-=-=3222)(34)(4),(a b dx a x a ba -=-=3223222)(31)()()(31)(2)()(a b a b a b a b dxa x ab dx a x d ba b a -=---+-=---+-=??ββββ得到⽅程组为 --=----3221322)(31)(21c )(34)()(a b a b c a b a b a b a b特别取1,0==b a ,有= 31213411121c c求解得到1,21,6131122=-=-=c c c其解为202)(21)(a x a x u u ---+=C h2 椭圆与抛物型⽅程有限元法§1.1 ⽤线性元求下列边值问题的数值解: 10,2sin242"<<=+-x x y y ππ0)1(,0)0('==y y此题改为4/1,0)1()0(,1"====+-h y y y y解: 取2/1=h ,)2,1,0(==j jh x j ,21,y y 为未知数. Galerkin 形式的变分⽅程为),(),(v f v Lu =,其中+-=10210"4),(uvdx vdx u v Lu π,?=1)(2sin 2),(dx x xv v f π⼜dx v u dx v u v u vdx u =+-=-10''10''10'10"|因此dx uv v u v u a )4(),(12''?+=π在单元],[1i i i x x I -=中,应⽤仿射变换(局部坐标)hx x i 1--=ξ节点基函数为)3,2,1(,0,,,1)(111=≤≤-=≤≤-=-=--+i other x x x h x x x x x h x x x i i i i i i i ξξξξ?-+++=++=1022210222222'111)1(41]41[]4[),(1021ξξπξξπ?πd h d hh dxa x x x x取2/1=h ,则计算得124),(211π??+=a122)1(41[),(210221πξξξπ??+-=-+-=?d h h a-+++=10101)1)(2121(2sin )0(2sin [2),(ξξξπξξξπ?d d h h f ??-++=1010)1(4)1(sin 2sin ξξξπξξξπd d hξξξπ?d h f ?+=102)2121(2sin 2),(代数⽅程组为= ),(),(),(),(),(),(212122212111f f y y a a a a 代如求值.取4/1=h ,未知节点值为4321,,,u u u u ,⽅程为4,3,2,1),(),(41==∑=j f ua j i iji应⽤局部坐标ξ表⽰,-+++=10221022])1(41[)41(),(ξξπξξπ??d hh d h h a j j248]88[21022πξξπ+=+=?dξξξπ??d hh a j j ])1(41[),(1021?-+-=++964)1(164212πξξξπ+-=-+-=?d 964),(21π??+-=-j j a系数矩阵为}964,248,964{222πππ+-++-=diag A取1=f ,41)1(),(1010=-+=??ξξξξ?d h d h f j-+++=+10110)1)]((2sin[2)](2sin[2),(ξξξπξξξπd h x h d h x h f j j j -++++=1010)1)](4 41(2sin[21)]44(2sin[42ξξξπξξξπd j d j++?=+++++-+=100110|)]8)1([cos(821]8)1(sin[21]8)1(sin[]8)(sin[21ξππξξπξξξπξπj d j d j j+2.就⾮齐次第三边值条件22'11')()(,)()(βαβα=+=+b u b u a u a u导出有限元⽅程.解:设⽅程为f qu pu Lu =+-='')( 则由),()]()[()()]()[()(),(|),)((''1122'''''v pu a u a v a p b u b v b p v pu v pu v pu b a----=-=αβαβ变分形式为:),(1b a H v ∈?)()()()(),()()()()()()(),(),(1212''a v a p b v b p v f a v a u a p b v b u b p v qu v pu ββαα-+=-++)(),(0b u u a u u N ==记)()()()(),()()()()()()()(),(),(),(1212''a v a p b v b p v f v F a v a u a p b v b u b p v qu v pu v u A ββαα-+=-++=则上述变分形式可表⽰为)(),(v F v u A =设节点基函数为),...,2,1,0)((N j x j =? 则有限元⽅程为),...,1,0()(),(0N j F u A j Ni i j i ==∑=具体计算使⽤标准坐标ξ.。

偏微分⽅程数值解法期末考试题答案期末考试试题答案及评分标准学年学期：专业：数学与应⽤数学班级：数学课程：偏微分⽅程数值解法教学⼤纲：《偏微分⽅程数值解法》教学⼤纲（⾃编，2006）使⽤教材：《偏微分⽅程数值解法》教材作者：陆⾦甫、关治出版社：清华⼤学出版社⼀、判断题（每⼩题1分，共10分） 1、（O ） 2、（O ） 3、（X ） 4、（X ） 5、（O ） 6、（O ） 7、（O ） 8、（X ）9、（X ） 10、（O ）⼆、选择题（每⼩题2分，共10分） 11、（D ） 12、（A ） 13、（C ） 14、（B ）15、（C ）三、填空题（每⼩题2分，共20分）16、22222212nx x x +++ 17、A=[4 5 9;23 5 17;11 23 1] 18、y=exp(-t/3)*sin(3*t) 19、help 20、zeros(m,n) 21、inva(A)*b 或者A/b 22、A=sym('[cos(x-y),sin(x+y);exp(x-y),(x-1)^3]')23、22221[()]2()()[()]0a s b s s c s '''-+= 24()i xv e d λλλ+∞-∞25、1(,)(,)j n j n u x t u x t τ+-四、计算题：（每⼩题12分，共36分）26、写成对流⽅程0u ua t x+=（,0x R t ∈>）的有限差分⽅程（两层显⽰格式，⽤第n 层计算第n+1层），并把有限差分⽅程改写为便于计算的迭代格式/h λτ=为⽹格⽐。

解：在点(,)j n x t 处，差分⽅程为110n n n nj jj ju u u u ahτ++--+=（0,1,2,j =±±，0,1,2,n =）（8分）便于计算的形式为11()n n n n j j j j u u a u u λ++=--，/h λτ= （4分）27、写出扩散⽅程22u ua t x=的有限差分⽅程（中⼼差分格式，⽤第n 层计算第n+1层），并把有限差分⽅程改写为便于计算的迭代格式，2/h µτ=为⽹格⽐。

L试讨论逼近对蘇程詈+若。

的差分沁1)2)q1 二：行口匚1）解：设点为（X ? ，/曲）屮则町=讥心厶）=班勺厶+J + °（工心）（Y ）+0（F ）.ot所以截断误差为：3E=丄 ------ + ---- 「 T h 啰_喟+竺护一 o （F ）T= 0（T + 力”2）解：设点为：（X y ，/林1 ） 3则町=讥勺,_）=以E ，_+1）+ （Y ） +o （巧卩 ot “；：；=班心+1 厶+i ）=叽厶+i ）+滋（ h ）+ * 臥工心）（为 2）+o ox (X)d心;=班心亠心）=班心，/+1）+敕:;D （一力）+ 3 役;D（血 2）+0（亥2）«截断误差为：2舟A 1 ” E= ------------ + ------------ — （―+ _） T h dt dx叭：=班％厶+i ）+敗？心）（_勿+0 @2）〜dx-(史+空八dt dx 呼1_吋】+竺丛Q —O （X ）-(叱 3 +dtdx 22・试用积分插值法推导知铁。

逼近的差分裕式班勺厶叙）一班勺，乩i）+ ——-——£）dtTq2 “-” *\ | (— 4- —)dxdt = | (un t 4- un x)ds = 0* dt & \得-U] /J+U2 r+x^ A-u4 r = 0+JE (j-l? n)F (j,n)G (j^n+l)H (j-l,n+l)^% ~ 的=旳=竹“4 = W/-lMf MTh=h T-T-ll"h + LL r H + ll：4h —LL：N =Op第二章第三章第四章第五章第六章P781.如果①'（0）二0,则称工。

是』（0）的驻点（或稳定:点）-设矩阵A对称（不必正定），求证忑是』（工）的驻点.的充要条件是1心是方程加二&的解B 42・ 试用积分插值法推导知铁。

逼近的差分裕式证： 充分性：①⑻二J 缶)+ 乂(加° -b t ^+—(Ax r x)①'(Ji) = (Ax c - A, x) + A{Ax r x) aEff))S 宀沪若①0)二Q,即(山° 一氛对=0 心怎宀A X Q -h = ()目卩 Ax-b^则帀是方程Ax^b 的解卩 必要性*若心是芳程A^ = b^\解则 Ax a —h - 0 (J 4X 0 — Z?,x) = 0+^◎ (0)=(吐命-b t x) - 0+J所以町是』0)的驻点dpg%3：证明非齐次两点边值间题心現(&)二 e it (E)二 Qu与T 7面的变分间题等价：求血EH 】，认@) = G 使 J(w t ) = min J(y)其中心SiuHU (2)-d』(#) =壬仗站)-(7» —芒⑹戲(D) +而久込叭如(2.13)(提示；先把边值条件齐衩化)+d dxO 字)+梓二/ ax13页证明：令 = w(x) + v(x)其中 w(x) = Q + (x-a)0 w(a) = a yv @) = “v(a) = 0 v(^>) = 0®所以2S = 瞥+qu = j DX DX Pd r /w 血、《, 乂 、 f"丁〔P(T + ：F)]+Q(W + V )" ax dx ax* 丫 d z dv. 产 / d dw 、 豪 令 = - — O —) +(?v = /-(- —^> — +^w) = y;^ ax ax dx ax 所以(1)的等价的形式2厶” =一?0 字)= 卩ax axu(a) = a u\b) = 0a其中久=/-(-£■去字+0W )"ax ax 则由定理22知，讥是辺值间题（2）的解的充要条件是 且满定变分方程"ogf)-C/i 小 0 Vve^Pr (Zv> 一 /j )tdx + p @»： (b)f @) ① W = J(u) = J(u.+^)^— a （u^ + 兔，以.+ 无）一（/,功・ +加）［以・（E ）+加@）］ 2 □2=J(认)+ N[a@・,f)-(/,£)-+乙agd-Qfm 沁卜• Q dx dx 「（加•一/）加x +卩@加：（砂@）-卩@）戊@） Ja（3） => （4）所以可证得• 3必要性：若如 是边值间题（1）的解。

课程名称：偏微分方程数值解法 课程编号：24014110 适用专业（班级）：数学 共1页 命题人：潘晓丽 教研室主任： 第1页一、（15分）写出三类典型泛定方程并分别说明其名称和特点.二、（10分）求一维波动方程()()()()()22222,,0,0,,0t u u a x t t x u x x u x x ϕψ⎧∂∂=-∞<<+∞>⎪∂∂⎨⎪==⎩的通解. 三、（15分）写出达朗贝尔公式并利用公式求解()()()2,0,,0sin ,0cos tt xx t u a u t x u x xu x x ⎧=>-∞<<+∞⎪=⎨⎪=⎩ 四、（10分）计算积分()32x J x dx -⎰. 五、（15分）设1,1≥≥n m ，证明()()()dx x p x m dx x p x n m n m n m ⎰⎰--=++11111六、（15分）用分离变量法求解()()()()()20,0,0,00,,00,0,,0tt xx t u a u x l t u x u x xu t u l t ⎧-=<<>⎪==⎨⎪==⎩ 七、（10分）解固有值问题()()()''0,''0y y l x l y l y l λ+=-<<⎧⎪⎨-==⎪⎩ 八、（10分）叙述斯图模-刘维尔定理.课程名称：偏微分方程数值解法 课程编号：24014110 适用专业（班级）：数学 共1页 命题人：潘晓丽 教研室主任： 第1页一、解：波动方程：()222,u a u f t x t∂=∆+∂热传导方程：()2,ua u f t x t∂=∆+∂ 位势方程：()u f x ∆= ……………………….5分 其中()12,,,n x x x x =，a 为常数，(),f t x 及()f x 为已知函数，在波动方程及热传导方程中，未知函数u 是时间变量t 和空间坐标变量()12,,,n x x x x =的函数，在位势方程中，未知函数u 是空间坐标变量()12,,,n x x x x =的函数，而与时间t 无关，三类典型方程均为二阶线性偏微分方程。

《偏微分方程数值解》试卷参考答案与评分标准专业班级信息与计算科学开课系室考试日期 2006.4.14命题教师王子亭偏微分方程数值解试题(06A)参考答案与评分标准信息与计算科学专业一（10分）、设矩阵A 对称正定，定义)(),(),(21)(n R x x b x Ax x J ∈-=，证明下列两个问题等价：(1)求n R x ∈0使 )(min )(0x J x J nRx ∈=;(2)求下列方程组的解：b Ax =解: 设n R x ∈0是)(x J 的最小值点,对于任意的n R x ∈,令),(2),()()()(2000x Ax x b Ax x J x x J λλλλϕ+-+=+=, (3分)因此0=λ是)(λϕ的极小值点,0)0('=ϕ,即对于任意的n R x ∈,0),(0=-x b Ax ,特别取b Ax x -=0,则有0||||),(2000=-=--b Ax b Ax b Ax ,得到b Ax =0. (3分) 反之,若nR x ∈0满足bAx =0,则对于任意的x ,)(),(21)0()1()(00x J x Ax x x J >+==+ϕϕ,因此0x 是)(x J 的最小值点. (4分)评分标准:)(λϕ的表示式3分, 每问3分,推理逻辑性1分二（10分）、 对于两点边值问题：⎪⎩⎪⎨⎧==∈=+-=0)(,0)(),()(b u a u b a x f qu dxdu p dx d Lu 其中]),([,0]),,([,0)(min )(]),,([0min ],[1b a H f q b a C q p x p x p b a C p b a x ∈≥∈>=≥∈∈建立与上述两点边值问题等价的变分问题的两种形式：求泛函极小的Ritz 形式和Galerkin 形式的变分方程。

解: 设}0)()(),,(|{110==∈=b u a u b a H u u H 为求解函数空间,检验函数空间.取),(10b a H v ∈,乘方程两端,积分应用分部积分得到 (3分))().(),(v f fvdx dx quv dxdv dx du pv u a b a ba ==+=⎰⎰,),(10b a H v ∈∀ 即变分问题的Galerkin 形式. (3分)令⎰-+=-=b a dx fu qu dxdup u f u u a u J ])([21),(),(21)(22,则变分问题的Ritz 形式为求),(10*b a H u ∈,使)(min )(1*u J u J H u ∈= (4分)评分标准:空间描述与积分步骤3分,变分方程3分,极小函数及其变分问题4分,三（20分）、对于边值问题⎪⎩⎪⎨⎧=⨯=∈-=∂∂+∂∂∂0|)1,0()1,0(),(,12222G u G y x yux u （1）建立该边值问题的五点差分格式（五点棱形格式又称正五点格式），推导截断误差的阶。

2014—2015学年第二学期研究生期末考试试卷学 院： 数信学院 考试对象：2014级计算数学专业硕士研究生课程名称： 偏微分方程数值解法 课程类型： 学位专业课考试方式： 开 卷 考试时间： 120 分钟答题要求：请把答案写在答题纸上，写在试卷上无效。

本卷共5题，每题20分。

一． (40分) 对求解抛物型方程的初边值问题0,(0,2),0,(,)(2,),(,0)sin(),(0,2),t xx u u x t u x t u x t u x x x πππ-=∈>⎧⎪=+⎨⎪=∈⎩的常用的差分方法进行归纳总结，分析它们各自的优缺点，算出其精确解，用前面的数值方法模拟此问题，验证得到的有关结论的正确性。

二．（20分） 设12[0,][0,]l l Ω=⨯，,u v 为确定在12h h I I Ω=⨯上的网函数，且在满足齐次边界条件，h -Λ表示Laplace 差分算子h u u u Λ=--，λ为h Λ的特征值，求证：(i) 算子h Λ是自共轭的，(,)(,)h h u v u v Λ=Λ。

(ii) 算子h Λ是正定的，2(,)h u u u εΛ=，其中1min 022288l l ελε=≥+=。

(iii) 有下列估计式22(,),h u u u u εμ≤Λ≤ 其中1max 022244l l μλμ=≤+=。

三．（20分） 用Fourier 分析方法证明四阶抛物型方程的周期初值问题00,(0,),0,(,)(,),(,0)(),(0,),t xxxx u u x L t u x t u x L t u x u x x L +=∈>⎧⎪=+⎨⎪=∈⎩ 的差分格式， （其中222221(2)nn n n x j j j j u u u u h δ-+=-+）， 是绝对稳定的，其截断误差为222(())O h hττ++。

四．(20分) 用能量不等式方法讨论变系数对流方程的初值问题 (,)0,,0,(,0)(),,t x u a x t u x R t T u x g x x R +=∈<≤⎧⎨=∈⎩(,)0a x t ≥， 的差分格式11100,(),n n n n j j j j n j j j u u a h u g x ϕϕτ++-⎧--+=⎪⎨⎪=⎩ 的稳定性。

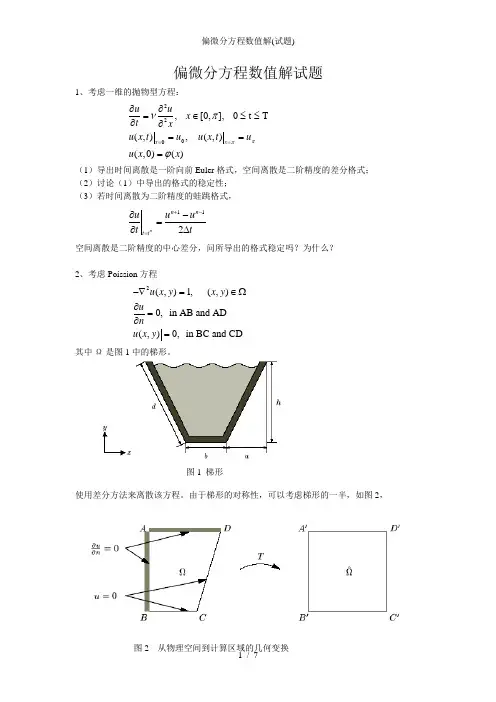
偏微分方程数值解试题1、考虑一维的抛物型方程：2200, [0,], 0t T (,), (,)(,0)()x x u ux t xu x t u u x t u u x x ππνπϕ==∂∂=∈≤≤∂∂=== （1）导出时间离散是一阶向前Euler 格式，空间离散是二阶精度的差分格式；（2）讨论（1）中导出的格式的稳定性； （3）若时间离散为二阶精度的蛙跳格式，112n n n t t u u u t t+-=∂-=∂∆ 空间离散是二阶精度的中心差分，问所导出的格式稳定吗？为什么？2、考虑Poission 方程2(,)1, (,)0, in AB and AD (,)0, in BC and CDu x y x y unu x y -∇=∈Ω∂=∂= 其中Ω是图1中的梯形。

使用差分方法来离散该方程。

由于梯形的对称性，可以考虑梯形的一半，如图2，图1 梯形为了求解本问题，采用如下方法：将Ω的一半投影到正方形区域ˆΩ，然后在ˆΩ上使用差分方法来离散该方程。

在计算区域ˆΩ上用N N ⨯个网格点，空间步长为1/(1)N ξη∆=∆=-。

（1）引入一个映射T 将原区域Ω（带有坐标,x y ）变换到单位正方形ˆΩ（带有坐标,ξη）。

同时导出在新区域上的方程和边界条件。

（2）在变换区域，使用泰勒展开导出各导数项在区域内部和边界点上的差分格式。

3、对线性对流方程0 constant >0u u a a t x∂∂+=∂∂，其一阶迎风有限体积法离散格式为 1ˆn j u +=ˆnj u a t x∆-∆（ˆn j u 1ˆn j u --）（1）写出0a <时的一阶迎风有限体积法的离散格式；（2）写出a 为任意符号的常数的一阶迎风有限体积法的守恒形式。

（3）使用0 u uu t x∂∂+=∂∂说明一阶迎风有限体积法不是熵保持的格式。

4、对一维Poission 方程, (0,1)(0)(1)0x xx u xe x u u ⎧-=∈⎨==⎩ 将[]01，分成(1)n +等分，写出用中心差分离散上述方程的差分格式，并问： （1）该差分格式与原微分方程相容吗？为什么？ （2）该差分格式稳定吗？为什么？（3）该差分格式是否收敛到原微分方程的解？为什么？ （4）取(1)6n +=，写出该差分格式的矩阵表示。

李微分方程数值解习题解答1-1如果（P（0）= 0 ,则称X。

是丿（X）的驻点（或稳走点）•矩阵A对称（不必正走）, 求证兀0是丿（兀）的驻点的充要条件是：兀0是方程组= b的解证明:由恥）的走义与内积的性线性性质，得必要性:由0 （0） = 0,得，对于任何X w R",有（Ax Q-b,x） = 0r由线性代数结论知，充分性：由Ax0 = b,对于任何'G R",即兀是丿0）的驻点.§1-2补充：证明广（劝的不同的广义导数几乎处处相等. 证明:设f e L2（Z）,碍e E⑴为/（x）的广义导数，由广义导数的定义可知，对于任意0（劝《：（/）,有两式相减，得到由变分基本引理胡-&几乎处处为零间g理几乎处处相等•补充证明血巧的连续性条件（证明：设I p(x) \<M.\q{x) \<M ,^Sch warz不等式I tz(w,v) 1=1 ^\puv + quv)dx \< M II u II .11 v II II w II .11 v II< 2M*II u II, .11 v II*其中W = max{ M,M }习题:1设fg为/g的一阶广义导数,试用类似的方法走义f⑴的k阶导数伙=1,2,...）解:一阶广义导数的定义，主要是从经典导数经过分部积分得到的关系式来走义，因此可得到如下走义:对于/⑴e厶S若有g（x） e皿）,使得对于任意的^eC；（Z）f有则称/（X）有k阶广义导数,g（x）称为/（X）的k阶广义导数，并记gd）卑dx注:高阶广义导数不是通过递推走义的，可能有高阶导数而没有低阶导数.2.利用必）的完全性证明是Hilbert空间• 证明:只证刃⑴的完全性•设｛/“｝为刃⑴的基本列间因此知｛九｝,｛/；｝都是厶（/）中的基本列（按厂（/）的范数）•由从/）的完全性，存在f,g € %）,使II f n -门0,11 f n - g ll°T 0,以下证明皿-门TO（关键证明防孚）ax由Schwarz不等式f有对于任意的0(兀)e C；(/)f成立由 f fn (x)(p(x)dx = -£ f n (x)(p (x)dx 取极限得到［g(x)0(x)Jx = -^f(x)(p(x)dx 即g(x) = f \即仔H'(D且故H (/)中的基本列是收敛的,H (/)是完全的.3•证明非齐次两点边值问题证明:边界条件齐次化令u0(x) = a + p(x — d)f则w = u—如满足齐次边界条件亠满足的方程为5 =Lu — Lu(} = f - Lu{} f即w对应的边值问题为f Lw = f-Lu0⑹[w(d) = 0, vv (/?) = 0由走理知，问题p与下列变分问题等价求哄cm；, J(w.) = rninJ\w) 其中丿(w) = |a(w,w)-(y- Lu0,w)・而而(Lu Q,u)-a(u Q9u) = -p(b)j3u(b) + C2从而J*(w) = 7(w)- p(b)陋b) + C则关于w的变分问题p等价于：求仏 e C2C\H l,u(a) = a使得其中丿(u) = - p(b)陋b)4就边值问题(解:令％ =& + J3(x-a)t w = u- u()t则"满足等价于:Vve/7；应用分部积分，还原"，于是，边值问题等价于:求"e H',u(a) = 使得VveH；,成立注:形式上与用i去乘方程两端，应用分部积分得到的相同.5试建立与边值问题 等价的变分问题.解:取解函数空间为比(D 对于任意「e 比(/)用v 乘方程两端,应用分部积分，得到rjz ,d 4u 、 z d'u - dhi lh c h u M 而加小【乔皿二乔以T 冇 上式为+ uv ^dx =(/' v)走义a(",y) = f ［丫 : : : +他］必, 为双线性形式. Ja dx- dx^变分问题为:求u e /7j(/)f Vv e &(/)1-41.•用Ritz - Galerkin 方法求边值问题(p t (x) = sin(iTZX ),/ = 1,2,…屮3 -bd u dv 1 2 •——dx ]il dx dx 次近似色(%) f 基解：(1)边界条件齐次化:令如=x,w = u-u0,则W 满足齐次边界条件，且第n次近似W”取为W” = £c,0 , M中 c.(z = l,2,...n)满足的叭 - Galerkin方程为由三角函数的正交性得到2而八®十（_ 25）心丙［―于是得到最后得到2•在题1中專（1）=0代替右边值条件川3是用Ritz - Galerkin方法求解相应问题的第斤次近似"证明色（兀）按厂（0,1）收敛至U叭x），并估计误差• 证明:他对应的级数绝对收敛，由｛血沁｝的完全性知极限就是解畑直误差估计为3•就边值问题（(p.(x) = (x-ay(i = 1,2,•・；)，写出Ritz - Galerkin方程解：边界条件齐次化，取竝=CC p(X _ 6Z)，W = U _ U() 9 W对应的微分方程为对应的变分方程为变分方程为d(w,y) = (/,*) + /3p(b)v(b)— £[/^?v(x) —qu^lx取0(x) = (x-ay9i= 1,2,…，心则Ritz ・GaleTkin方程为取P = 1,纟=0, / = 1，具体计算〃=1，d(0], 0]) = f \dx = (b _ a)£ =丄(b - a)2 + 0(b - a) - 0(b — a) = L (b - a)，，2 2C[ =q(b —%即解络=%0 + —(x — a)n = 2：d(%,0)= (b_a), Q(0,輕)=^2(x-a)dx = (b-a)2得到方程组为特别取a=oe=i z有求解得到* *=-詁=1其解为均=况（）+（X 一Cl）（X 一Q）~Ch2椭圆与抛物型方程有限元法§1.1用线性元求下列边值问题的数值解：此题改为一y + y = 1, y(0) = y(l) = 0/ = 1/4 解：取/i = l/2,x y. = = 0,1,2)』,儿为未知数.Galerkin形式的变分方程为(Lu.v) = (/», 其中龙2(Lu,v) = vdx + — ^uvdx,(/,v) = £2sin —xv{x)dx又一vdx = -uv Ijj ^uvdx =9因此a（u.v） = £（wv -^-—uv）dx在单元/. = [x,,兀]中，应用仿射变换侷部坐标）Eh节点基函数为取/7 = 1 / 2,则计算得G ®, %) = 4 +咅丄厶代数方程组为代如求值・取力= 1/4,未知节点值为坷上2，均，弘4方程为应用局部坐标f表示，系数矩阵为A =他{—4 + £ ,8 +壬,_4 + £} 取/=1, (/ ®)=町:磁+皿(1—§)込占2.就非齐次第三边值条件导出有限元方程.解:设方程为厶“ = -(pu) +qu=f则由变分形式为:V「记I IA(u,v) = (pu ) + (qu°) + a2p(b)u(b)v(b) - a l p(a)u(a)v(a) F(v) = (/» + p(b)/32v(b) — p(a)^v(a)则上述变分形式可表示为4仏巧= F(v)设节点基函数为03(丿=0,1,2, (7V)则有限元方程为具体计算使用标准坐标二。

偏微分方程习题及答案【篇一：偏微分方程数值解法期末考试题答案】题答案及评分标准学年学期：专业：班级：课程：教学大纲：使用教材：教材作者：出版社：数学与应用数学数学偏微分方程数值解法《偏微分方程数值解法》教学大纲（自编，2006）《偏微分方程数值解法》陆金甫、关治清华大学出版社一、判断题（每小题1分，共10分）1、（o）2、（o）3、（x）4、（x）5、（o）6、（o）7、（o）8、（x）9、（x） 10、（o）二、选择题（每小题2分，共10分） 11、（d） 12、（a） 13、（c） 14、（b）15、（c）三、填空题（每小题2分，共20分）?2?216、2?2??x1?x2?2?2 17、a=[4 5 9;23 5 17;11 23 1] 18、y=exp(-t/3)*sin(3*t) ?xn19、help 20、zeros(m,n)21、inva(a)*b或者a/b22、a=sym([cos(x-y),sin(x+y);exp(x-y),(x-1)^3])?(s)?1?(s)?c[??(s)]2?023、a[?2(s)]2?2b?224????v(?)ed? 25、i?xu(xj,tn?1)?u(xj,tn)?四、计算题：（每小题12分，共36分）?u?u?0（x?r,t?0）的有限差分方程（两层显示26、写成对流方程?a?t?x格式，用第n层计算第n+1层），并把有限差分方程改写为便于计算的迭代格式???/h为网格比。

解：在点(xj,tn)处，差分方程为?1un?unjj??anunj?1?ujh?0（j?0,?1,?2,，n?0,1,2,）（8分）便于计算的形式为?1nnn???/h （4分） un?u?a?(u?ujjj?1j)，?u?2u?a2的有限差分方程（中心差分格式，用第n层27、写出扩散方程?t?x计算第n+1层），并把有限差分方程改写为便于计算的迭代格式，???/h2为网格比。

偏微分方程数值解期末试题及参考答案Ａ卷2005—2006学年第2学期《偏微分方程数值解》试卷参考答案与评分标准专业班级信息与计算科学开课系室考试日期命题教师王子亭题号一二三四五六七八总分得分阅卷人偏微分方程数值解试题(06A) 参考答案与评分标准信息与计算科学专业1一、设矩阵A对称正定，定义J(x)?(Ax,x)?(b,x)(x?Rn)，证明下2J(x);(2)求下列方程组的解：列两个问题等价：(1)求x0?Rn使J(x0)?minnx?RAx?b 解: 设x0?Rn 是J(x)的最小值点,对于任意的x?Rn,令?(?)?J(x0??x)?J(x0)??(Ax0?b,x)?? 22(Ax,x),(3分) 因此??0是?(?)的极小值点,?’(0)?0,即对于任意的x?Rn,(Ax0?b,x)?0,特别取x?Ax0?b,则有(Ax0?b,Ax0?b)?||Ax0?b||2?0,得到Ax0?b. (3分)反之,若x0?Rn满足Ax0?b,则对于任意的1x,J(x0?x)??(1)??(0)?(Ax,x)?J(x0),因此x0是J(x)的最小值点. (4分) 2评分标准:?(?)的表示式3分, 每问3分,推理逻辑性1分ddu??Lu??(p)?qu?fx?(a,b)二、对于两点边值问题：? dxdx??u(a)?0,u(b)?0其中p?C1([a,b]),p(x)?minp(x)?pmin?0,q?C([a, b]),q?0,f?H0([a,b]) x?[a,b]建立与上述两点边值问题等价的变分问题的两种形式：求泛函极小的Ritz形式和Galerkin形式的变分方程。

1解: 设H0?{u|u?H1(a,b),u(a)?u(b)?0}为求解函数空间,检验函数空间.取1v?H0(a,b),乘方程两端,积分应用分部积分得到(3分) bdudv1.?quv)dx??fvdx?f(v),?v?H0(a,b) aadxdx即变分问题的Galerkin形式. (3分) 11bdu 令J(u)?a(u,u)?(f,u)??[p()2?qu2?fu]dx,则变分问题的Ritz形式22adx a(u,v)??(pb1J(u)(4分) 为求u*?H0(a,b),使J(u*)?min1u?H0评分标准:空间描述与积分步骤3分,变分方程3分,极小函数及其变分问题4分, 三、对于边值问题??2u?2u?2?2??1,(x,y)?G?(0,1)?(0 ,1) ??x?y??u|?G?0建立该边值问题的五点差分格式，推导截断误差的阶。

偏微分方程数值解一（10分）、设矩阵A 对称正定，定义)(),(),(21)(n R x x b x Ax x J ∈-=，证明下列两个问题等价：(1)求n R x ∈0使)(min )(0x J x J n Rx ∈=;(2)求下列方程组的解：b Ax = 解: 设n R x ∈0是)(x J 的最小值点,对于任意的n R x ∈,令),(2),()()()(2000x Ax x b Ax x J x x J λλλλϕ+-+=+=, (3分)因此0=λ是)(λϕ的极小值点,0)0('=ϕ,即对于任意的n R x ∈,0),(0=-x b Ax ,特别取b Ax x -=0,则有0||||),(2000=-=--b Ax b Ax b Ax ,得到b Ax =0. (3分) 反之,若nR x ∈0满足bAx =0,则对于任意的x ,)(),(21)0()1()(00x J x Ax x x J >+==+ϕϕ,因此0x 是)(x J 的最小值点. (4分)评分标准:)(λϕ的表示式3分, 每问3分,推理逻辑性1分二（10分）、对于两点边值问题：⎪⎩⎪⎨⎧==∈=+-=0)(,0)(),()(b u a u b a x f qu dxdu p dx d Lu 其中]),([,0]),,([,0)(min )(]),,([0min ],[1b a H f q b a C q p x p x p b a C p b a x ∈≥∈>=≥∈∈建立与上述两点边值问题等价的变分问题的两种形式：求泛函极小的Ritz 形式和Galerkin 形式的变分方程。

解: 设}0)()(),,(|{11==∈=b u a u b a H u u H 为求解函数空间,检验函数空间.取),(10b a H v ∈,乘方程两端,积分应用分部积分得到 (3分))().(),(v f fvdx dx quv dxdv dx du p v u a b a ba ==+=⎰⎰,),(1b a H v ∈∀ 即变分问题的Galerkin 形式. (3分)令⎰-+=-=b a dx fu qu dxdup u f u u a u J ])([21),(),(21)(22,则变分问题的Ritz 形式为求),(1*b a H u ∈,使)(m in )(10*u J u J H u ∈= (4分) 评分标准:空间描述与积分步骤3分,变分方程3分,极小函数及其变分问题4分,三（20分）、对于边值问题⎪⎩⎪⎨⎧=⨯=∈-=∂∂+∂∂∂0|)1,0()1,0(),(,12222G u G y x yux u （1）建立该边值问题的五点差分格式（五点棱形格式又称正五点格式），推导截断误差的阶。