速算与巧算

第一章速算与巧算知识要点在速算与巧算中，主要是运算定律、性质和一些技巧方法的运用。

1.加法巧算。

(1)加法交换律：两个数相加，交换加数的位置，它们的和不变。

字母表示：a＋b＝b＋a(2)加法结合律；三个数相加，先把前两个数相加，再加上第三个数，或者先把后两个数相加，再同第一个数相加，它们的和不变。

字母表示：a＋b＋c＝(a＋b)＋c＝a＋(b＋c)交换律和结合律通常是在一起使用。

如果多个数相加，任意交换加数的位置，它们的和不变，或者先把其中的几个数结合成一组相加，再把所得的和同其他剩下的数相加，它们的和仍然不变。

字母表示：a＋b＋c＋d＋e＝d＋(b＋d＋e)＋c2.减法巧算。

(1)减法的运算性质(有时可以将减法的运算性质理解成填括号或去括号的性质)：一个数减去几个数的和，等于从这个数里依次减去和中的每一个加数。

字母表示：a－(b＋c＋d)＝a－b－c－d(2)一个数连续减去几个数，等于从这个数中减去这几个数的和。

字母表示：a－b－c－d＝a－(b＋c＋d)3.乘法巧算。

(1)乘法交换律：两个数相乘，交换因数的位置，积不变。

字母表示：a×b＝b×a(2)乘法结合律：三个数相乘，可以先把前两个数结合起来相乘，再和第三个数相乘；也可以先把后两个数结合起来先乘，再和第一个数相乘，它们的积不变。

字母表示：a×b×c＝(a×b)×c＝a×(b×c)交换律和结合律通常是在一起使用。

如果多个数相乘，任意交换因数的位置，它们的积不变；可以选择两个因数相乘，得出便于运算的整十、整百、整千……的积，再将这个积与其他的因数相乘；有时可以把一个因数用几个因数相乘的形式表示，使其中一个因数与算式中其他的某个因数的积成为便于运算的数，然后再与其他的因数相乘，使计算快捷准确。

(3)积不变的规律：如果一个因数扩大若干倍，另一个因数缩小同样的倍数，那么它们的积不变。

速算与巧算(后附答案)一【要点提示】1、简便运算是计算中的一个非常重要的组成部分，掌握一些简便算法，有助于提高我的计算能力和思维能力。

而简便算法往往要根据一定的运算定律和运算性质通过对算式进行“有的放矢”从而使计算简便。

2、在巧算的方法里，蕴含着重要的解决问题的策略：转化法。

即把所给的算式，根据运算定律和运算性质，或改变它的运算顺序，或凑整，从而变成一个易于算出结果的算式。

3、运算定律和运算性质：如交换律、结合律、乘法分配律、添括号、拆分法。

除法的性质：如4、在分解因数凑整相乘时，记住一些特殊的积有益于速算，如25=10 25258=200 1258=1000 6258=5000等等。

但是，凑整法需要灵活运用，要想算的快又准，最根本的是抓住题目特点，灵活运用乘、除法运算定律进行计算。

二【经典题型】例1计算（1）9+99+999 （2）479+478+477+476+481+482（3）326+289+74-189 (4)354+(146-78)(5) 735-(335-287) (6)735-487+187【模仿提升】第1页共 5 页1、99999+9999+999+99+92、9+98+997+9996+999953、80+81+82+83+84+854、998+999+1000+1001+10025、1306-889-3066、2426-589+74+8897、564-（212-236） 8、639+（410-239）9、632-385+185 10、458-889+188911、12345+23451+34512+45123+51234第2页共 5 页【奥数训练营】速算与巧算速算与巧算是在运算过程中，根据数的特点与数之间的特殊关系，恰当，准确，灵活地运用定律，性质及和、差、积、商的变化规律，进行一种简便、迅速的计算。

++++例1. 计算889899899989999例2. 计算：20191817161514134321…+--++--+++--⨯例3. 44425⨯+⨯例4. 375480625048⨯例5. 计算：333333333333第3页共 5 页第 4 页 共 5 页例6. 计算：343535353434⨯-⨯【模拟试题】（答题时间：40分钟）1. 用简便方法计算（1）678354322++()（2）283147171653+++ （3）38437184-+()（4）29041327173-- （5）653197-（6）12517125⨯-（7）23599⨯（8）()130052013-÷ （ 9）672118218579⨯+⨯+⨯（10）222222999999⨯ （11）399999399993999399393+++++第 5 页 共 5 页（12）201918174321-+-++-+-… （13）8888125⨯ (14) 34534515015÷。

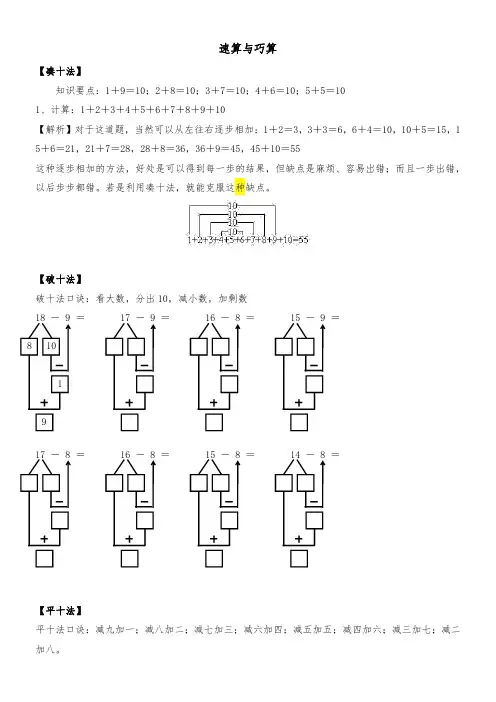
速算与巧算【凑十法】知识要点：1＋9＝10；2＋8＝10；3＋7＝10；4＋6＝10；5＋5＝101、计算：1＋2＋3＋4＋5＋6＋7＋8＋9＋10【解析】对于这道题，当然可以从左往右逐步相加：1＋2＝3，3＋3＝6，6＋4＝10，10＋5＝15，1 5＋6＝21，21＋7＝28，28＋8＝36，36＋9＝45，45＋10＝55这种逐歩相加的方法，好处是可以得到每一歩的结果，但缺点是麻烦、容易岀错；而且一歩出错，以后歩步都错。

若是利用凑十法，就能克服这种缺点。

【破十法】破十法口诀：看大数，分出10，减小数，加剩数18－9＝17－9＝16－8＝15－9＝8101917－8＝16－8＝15－8＝14－8＝【平十法】平十法口诀：减九加一；减八加二；减七加三；减六加四；减五加五；减四加六；减三加七；减二加八。

18－9＝17－9＝16－9＝15－9＝8110917－8＝16－8＝15－8＝14－8＝【退十加补法】18－9＝17－9＝16－9＝15－9＝1018917－8＝16－8＝15－8＝14－8＝【凑整法】同学们还知道，有些数相加之和是整十、整百的数，如：1＋19＝20；11＋19＝30；2＋18＝20；12＋28＝40；3＋17＝20；13＋37＝504＋16＝20；14＋46＝60；5＋15＝20；15＋55＝70；6＋14＝20；16＋64＝807＋13＝20；17＋73＝90；8＋12＝20；18＋82＝100；9＋11＝20又如：15＋85＝100；14＋86＝100；25＋75＝100；24＋76＝10035＋65＝100；34＋66＝100；45＋55＝100；44＋56＝100等等巧用这些结果，可以使那些较大的数相加又快又准。

像10、20、30、40、50、60、70、80、90、1 00等等这些整十、整百的数就是凑整的目标。

【用已知求未知】利用己经获得较简单的知识来解决面临的更复杂的难题这是人们认识事物的一般过程，凑十法、凑整法的实质就是这个道理，可见把这种认识规律用于计算方面，可使计算更快更准。

第一讲速算和巧算例1 计算：18+21+23+20+19+15例2 计算：199999+19999+1999+199+19例3 计算：2541－1998例4 计算：1991+8119+8009+1881例5 计算：25×19×64×125例6 计算：（1）125×34＋125×66（2）43×11＋43×36＋43×52＋43例7 计算：（1）68×62（2）85×85例8 计算：26×11例9 计算：358×11练习1. 计算：78＋76＋81＋82＋77＋80＋79＋832. 计算：998＋1413＋99893. 计算：19+299+3999+499995. 计算：673+（528－373）6. 计算：829+（571－629）7. 计算：（1）1164×25 （2）1730÷58. 计算：3600－785+534－2159. 计算：9+99+999+9999+…+99999个11. 计算：26×8612. 计算：548－164－23613. 计算：（1）54－36+64+36 （2）54×36×64÷3614. 计算：28÷3×54×15÷54÷1415. 速算下面各题：（1）2×31×5 （2）72×125×3（3）125×64＋125×36 （4）21×73＋26×21＋2116. 先观察下列各题有什么特点再计算：（1）23×27 （2）46×44 （3）55×55 （4）353×11 （5）638×9 （6）38×999四年级第一讲速算与巧算（一）例题例1 计算：1966+1976+1986+1996+2006例2 计算：125×25×32例3 计算：（1）567×422＋567＋577×567 （2）5328×9999 例4 计算：99999×22222＋33333×33334例5 计算：1991×199219921992－1992×199119911991例6 计算：1234+3142+4321+2413练习一1. 计算：1+2＋3＋4＋5＋6＋7＋8＋9＋10＋11＋…＋1002. 计算：3600000÷125÷32÷253. 计算：5×96×125×254. 计算：899998+89998+8998+8985. 计算：3456×9986. 计算：37×18＋27×427. 计算：38×82＋17×38＋388. 计算：347×69＋653×31＋306×199. 计算：3983993433333个个10. 计算：111111×999999＋999999×77777711. 计算：123+234+345+456+567+67812. 计算：（2+4+6+…+1998+2000）－（1+3+5+…+1997+1999）13. 计算：99999×77778＋33333×6666614. 计算：12345+23451+34512+45123+5123415. 计算：19961997×19971996－19961996×19971997第二讲 速算与巧算（二）例19199291992919929991999999个个个+⨯的末尾有多少个零？例2 计算：98＋97－96－95＋94＋93－92－91＋90＋89－…－4－3＋2＋1例3 计算：98989898×99999999÷1010101÷11111111例4 计算：7+77+777+7777+77777例5 计算：9÷(9÷8)÷(8÷7)÷(7÷6)÷(6÷5)÷(5÷4)÷(4÷3) 例6 计算：11111×11111练习二1. 计算：999999999×999999999+19999999992. 计算：1－2＋3－4＋5－6＋…＋97－98＋99＋1003. 计算：76000÷98010000020001个个4. 计算：[1－1×﹙0＋1﹚＋1÷1] ÷﹙1000－999﹚5. 计算：3+33+333+…+39333个6. 计算：1＋2－3－4＋5＋6－7－8＋9＋10－…＋19907. 计算：1＋2－3＋4＋5－6＋7＋8－9＋…＋97＋98－1008. 计算：99＋198＋297＋396＋495＋594＋693＋792＋891＋9909. 计算：（1）11111111×11111111（2）1111111111×111111111110. 计算：1÷(2÷3) ÷(3÷4) ÷(4÷5) ÷(5÷6) ÷(6÷7) ÷(7÷8)11. 计算：36×12004111个＋412. 计算：22222×2222213. 计算：61996619976766666个个14. 计算：123456789×987654321－123456788×987654322。

小学数学速算与巧算方法例解【转】速算与巧算在小学数学中，关于整数、小数、分数的四则运算，怎么样才能算得既快又准确呢？这就需要我们熟练地掌握计算法则和运算顺序，根据题目本身的特点，综合应用各种运算定律和性质，或利用和、差、积、商变化规律及有关运算公式，选用合理、灵活的计算方法。

速算和巧算不仅能简便运算过程，化繁为简，化难为易，同时又会算得又快又准确。

一、“凑整”先算1.计算：（1）24+44+56（2）53+36+47解：（1）24+44+56=24+（44+56）=24+100=124这样想：因为44+56=100是个整百的数，所以先把它们的和算出来.（2）53+36+47=53+47+36=（53+47）+36=100+36=136这样想：因为53+47=100是个整百的数，所以先把+47带着符号搬家，搬到+36前面；然后再把53+47的和算出来.2.计算：（1）96+15（2）52+69解：（1）96+15=96+（4+11）=（96+4）+11=100+11=111这样想：把15分拆成15=4+11，这是因为96+4=100，可凑整先算.（2）52+69=（21+31）+69=21+（31+69）=21+100=121这样想：因为69+31=100，所以把52分拆成21与31之和，再把31+69=100凑整先算.3.计算：（1）63+18+19（2）28+28+28解：（1）63+18+19=60+2+1+18+19=60+（2+18）+（1+19）=60+20+20=100这样想：将63分拆成63=60+2+1就是因为2+18和1+19可以凑整先算.（2）28+28+28=（28+2）+（28+2）+（28+2）-6=30+30+30-6=90-6=84这样想：因为28+2=30可凑整，但最后要把多加的三个2减去.二、改变运算顺序：在只有“+”、“-”号的混合算式中，运算顺序可改变计算：（1）45-18+19（2）45+18-19解：（1）45-18+19=45+19-18=45+（19-18）=45+1=46这样想：把+19带着符号搬家，搬到-18的前面.然后先算19-18=1.（2）45+18-19=45+（18-19）=45-1=44这样想：加18减19的结果就等于减1.三、计算等差连续数的和相邻的两个数的差都相等的一串数就叫等差连续数，又叫等差数列，如：1，2，3，4，5，6，7，8，91，3，5，7，92，4，6，8，103，6，9，12，154，8，12，16，20等等都是等差连续数.1. 等差连续数的个数是奇数时，它们的和等于中间数乘以个数，简记成：（1）计算：1+2+3+4+5+6+7+8+9=5×9 中间数是5=45 共9个数（2）计算：1+3+5+7+9=5×5 中间数是5=25 共有5个数（3）计算：2+4+6+8+10=6×5 中间数是6=30 共有5个数（4）计算：3+6+9+12+15=9×5 中间数是9=45 共有5个数（5）计算：4+8+12+16+20=12×5 中间数是12=60 共有5个数2. 等差连续数的个数是偶数时，它们的和等于首数与末数之和乘以个数的一半，简记成：（1）计算：1+2+3+4+5+6+7+8+9+10=（1+10）×5=11×5=55共10个数，个数的一半是5，首数是1，末数是10.（2）计算：3+5+7+9+11+13+15+17=（3+17）×4=20×4=80共8个数，个数的一半是4，首数是3，末数是17.（3）计算：2+4+6+8+10+12+14+16+18+20=（2+20）×5=110共10个数，个数的一半是5，首数是2，末数是20.四、基准数法（1）计算：23+20+19+22+18+21解：仔细观察，各个加数的大小都接近20，所以可以把每个加数先按20相加，然后再把少算的加上，把多算的减去.23+20+19+22+18+21=20×6+3+0-1+2-2+1=120+3=1236个加数都按20相加，其和=20×6=120.23按20计算就少加了“3”，所以再加上“3”；19按20计算多加了“1”，所以再减去“1”，以此类推.（2）计算：102+100+99+101+98解：方法1：仔细观察，可知各个加数都接近100，所以选100为基准数，采用基准数法进行巧算.102+100+99+101+98=100×5+2+0-1+1-2=500方法2：仔细观察，可将5个数重新排列如下：（实际上就是把有的加数带有符号搬家）102+100+99+101+98=98+99+100+101+102=100×5=500可发现这是一个等差连续数的求和问题，中间数是100，个数是5.加法中的巧算1.什么叫“补数”？两个数相加，若能恰好凑成整十、整百、整千、整万…，就把其中的一个数叫做另一个数的“补数”。

速算与巧算速算与巧算（⼀）加减法中的巧算⽅法：1、运⽤运算律和运算性质；2、凑整；3、拆⼩补⼤；4、找准基数；5、数列求和等等。

练习：1、147＋369＋353＋631 32＋81＋157＋19＋682、852－39－153－161 5613－（613+261）－2393、656－289＋144－111 745＋(672－525)－5724、537－（543－163）－57 756－576＋376＋2445、659＋427－727－159 1256＋125＋875－2566、9998＋3＋99＋998＋3＋9 9＋99＋999＋9999＋999997、75＋86＋83＋72＋78＋80＋81＋79＋878、1＋2＋3＋…＋9＋10＋9＋…＋3＋2＋1速算与巧算⼆乘除法的巧算主要靠乘法的运算律和除法的运算性质，并进⾏适当的扩展，使计算更灵活、合理；做到算得快、准。

练习：1、125×25×8×4 125×16×52、36×98 56×2013、4400÷25÷4÷11 236＋1800÷（9×25）4、720－198×25÷99×4 12000÷125＋325÷255、56×165÷7÷11 123×456÷789÷456×789÷1237、9999×2222＋3333×3334 54＋99×99＋458、1÷（2÷3）÷（3÷4）÷（4÷5）÷（5÷6）和差问题1、和差问题基本模式：已知两个数的和与差，求两个数。

2、和差问题的基本关系式：（和＋差）÷2=较⼤数（和－差）÷2=较⼩数3、解题的关键要找准两个数的和与差。

第一讲 速算与巧算一、 知识点：1. 要认真观察算式中数的特点，算式中运算符号的特点。

2. 掌握基本的运算定律：乘法交换律、乘法结合律、乘法分配律。

3. 掌握速算与巧算的方法：如等差数列求知、凑整、拆数等等。

二、典例剖析：例（1） 19199199919999199999++++分析：运用凑整法来解十分方便，也不容易出错误。

解：原式()()()() =(201)+2001+20001+200001+2000001 -----=20+200+2000+20000+2000005 =2222205 =222215--练一练：898998999899998999998+++++=答案：1111098例（2）10099989796321+-+-++-+分析：暂不看头尾两个数，就会发现中间都是先加后减，并且加数与减数相差1，所以就算这题可以先把中间部分分组凑成若干个1，再与其余部分进行计算。

解：原式100(9998)(9796)(32)1=+-+-++-+ 100491=++150=练一练：989796959493929190894321+--++--++---++答案：99例（3） 1111111111⨯分析：111,1111121,11111112321⨯=⨯=⨯= 解：1111111111123454321⨯=练一练：2222222222⨯答案：493817284例（4） 1234314243212413+++分析：数字1、2、3、4，在个位、十位、百位、千位上均各出现一次。

解：原式1111222233334444=+++ 1111(1234)=⨯+++ 111110=⨯ 11110=练一练：5678967895789568956795678++++答案：388885例（5） 339340341342343344345++++++分析：这七个数均差1，且个数为7个，所以中间数就是七个数的中位数。

常用的巧算和速算方法【顺逆相加】用"顺逆相加〞算式可求出假设干个连续数的和。

例如著名的大数学家高斯〔德国〕小时候就做过的"百数求和〞题，可以计算为1 +2 + ……+ 99 + 100所以，1＋2＋3＋4＋……＋99＋100=101×100÷2=5050。

"3+5+7+………＋97+99=？3+5＋7＋……＋97+99=〔99＋3〕×49÷2= 2499。

这种算法的思路，见于书籍中最早的是我国古代的"张丘建算经"。

张丘建利用这一思路巧妙地解答了"有女不善织〞这一名题："今有女子不善织，日减功，迟。

初日织五尺，末日织一尺，今三十日织讫。

问织几何？〞题目的意思是：有位妇女不善于织布，她每天织的布都比上一天减少一些，并且减少的数量都相等。

她第一天织了5 尺布，最后一天织了1 尺，一共织了30 天。

问她一共织了多少布？张丘建在"算经"上给出的解法是："并初末日织尺数，半之，余以乘织讫日数，即得。

〞"答曰：二匹一丈〞。

这一解法，用现代的算式表达，就是1 匹=4 丈，1 丈=10 尺，90 尺=9 丈=2 匹1 丈。

〔答略〕张丘建这一解法的思路，据推测为：如果把这妇女从第一天直到第30 天所织的布都加起来，算式就是5＋…………＋1在这一算式中，每一个往后加的加数，都会比它前一个紧挨着它的加数，要递减一个一样的数，而这一递减的数不会是个整数。

假设把这个式子反过来，则算式便是1+………………＋5此时，每一个往后的加数，就都会比它前一个紧挨着它的加数，要递增一个一样的数。

同样，这一递增的一样的数，也不是一个整数。

假假设把上面这两个式子相加，并在相加时，利用"对应的数相加和会相等〞这一特点，则，就会出现下面的式子：所以，加得的结果是6×30=180〔尺〕但这妇女用30 天织的布没有180 尺，而只有180 尺布的一半。

一、速算与巧算之凑整先算【点拨】：加法、减法的简便计算中，基本思路是“凑整”，根据加法（乘法）的交换律、结合律以及减法的性质，其中若有能够凑整的，可以变更算式，使能凑整的数结成一对好朋友，进行凑整计算，能使计算简便。

例：298+304+196+502【分析】：本题可以运用加法交换律和结合律，把能够凑成整十、整百、整千……的数先加起来，可以使计算简便。

【解答】：原式=（298+502）+（304+196）=800+500=1300二、速算与巧算之带符号搬家【点拨】：在加减混合，乘除混合同级运算中，可以根据运算的需要以及题目的特点，交换数字的位置，可以使计算变得简便。

特别提醒的是：交换数字的位置，要注意运算符号也随之换位置。

例：464-545＋836-455【分析】：观察例题我们会发现，如果按照惯例应该从左往右计算，464减545根本就不够减，在小学阶段，学生没办法做，所以要想做这道题，学生必须先观察数字特点，进行简便计算。

【解答】原式=464+836-545-455=1300-（545+455）=300思考：4.75÷0.25-4.75能带符号搬家吗？什么情况下才能带符号搬家？带符号搬家需要注意什么？三、速算与巧算之拆数凑整【点拨】：根据运算定律和数字特点，常常灵活地把算式中的数拆分，重新组合，分别凑成整十、整百、整千。

例：998+1413+9989【分析】：给998添上2能凑成1000，给9989添上11凑成10000，所以就把1413分成1400、2与11三个数的和。

【解答】原式==（998+2）+1400+（11+9989）=1000+1400+10000=12400 例：73.15×9.9【分析】把9.9看作10减0.1的差，然后用乘法分配率可简化运算。

【解答】原式=73.15×（10-0.1）=73.15×10-73.15×0.1=731.5-7.315=724.185四、速算与巧算之基准数法【点拨】：许多数相加，如果这些数都接近某一个数，可以把这个数确定为一个基准数，将其他的数与这个数比较，在基准数的倍数上加上多余的部分，减去不足的，这样可以使计算简便。