因果矩阵表

如何制作因果矩阵表（CEMatrix）？
在测量（MEASURE)阶段，过程图（Process Map）设别出很多输入变量（Input Variable），因果矩阵（C&E Matrix）是其后变量筛选的重要工具。

因果矩阵（C&E Matrix）适用范围：适用定性地筛选变量，非定量，比较主观。

因果矩阵（C&E Matrix）制作步骤：
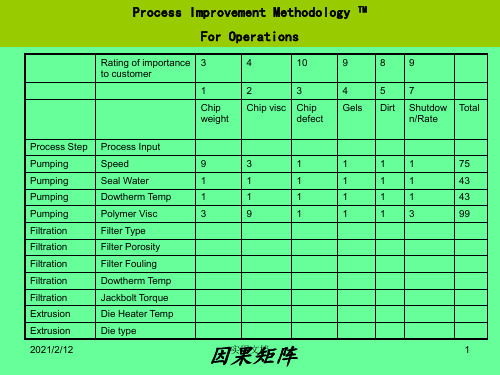
将过程的关键输出变量（KPOV）或项目的目标（Y）放在因果矩阵的表头, 表头变量一般3-5个;
根据项目要解决的问题（Y-目标）团队决定各个输出变量的权重（1-10分），越重要分一般越高；
将过程图中步骤（Process Step）和输入变量（Input）放在因果矩阵表的纵列；
根据各个输入变量和表头输出变量的关系紧密程度进行关系评分，一般是0-1-3-9，分越高，代表输入变量对表头输出变量影响越大；反之亦然。

实际评分时是一个变量一个变量去评（按行）；
计算总分，每个分值乘以权重再分别加和；
按总分由高到底排序，在明显断差的地方取关键输入变量（KPIV），一般不超过8个。

因果矩阵（C&E Matrix）制作注意事项：
因果矩阵是项目团队工作，与项目过程相关的团队成员都应该参加;
表头输出变量衡量某类属性的只能放一个变量；
团队打分不能投票或平均；
各个输出变量或输入变量评分前要定义清楚，确保团队理解不会有歧义，打分标准一致。

六西格玛之因果矩阵图引言在现代管理和生产体系中，六西格玛（Six Sigma）是一种以数据驱动的方法和工具，旨在提高质量和效率，减少变异性和缺陷率。

六西格玛采用了一系列统计分析和管理策略，帮助组织识别并解决问题，从而实现持续的改善。

因果矩阵图（Cause and Effect Matrix Diagram），也称为鱼骨图（Fishbone Diagram）或石墨盘（Ishikawa Diagram），是六西格玛中常用的工具之一。

它可以帮助团队全面理解问题的根本原因，并找出相关的因素。

本文将介绍因果矩阵图的定义、使用场景、绘制方法以及应用实例，以帮助读者更好地理解和应用这一工具。

定义因果矩阵图是一种用于分析和解决问题的图形工具，它通过将问题链接到可能的原因，帮助识别问题的根本原因和相关因素。

这种图形工具形状类似于鱼骨，因此也常常被称为鱼骨图。

使用场景因果矩阵图可以在各种领域和场景中使用，例如生产制造、服务行业、软件开发等。

它可以帮助团队快速分析和解决问题，并促进团队合作和沟通。

以下是一些适用于因果矩阵图的使用场景：1.产品质量问题：当产品出现质量问题时，团队可以使用因果矩阵图来确定可能的原因，从而采取相应的改进措施。

2.流程优化：对于复杂的流程或业务流程，团队可以使用因果矩阵图来分析并改进关键因素，以提高效率。

3.项目计划：在项目计划阶段，团队可以使用因果矩阵图来确定可能影响项目成功的因素，并制定相应的应对策略。

4.服务问题解决：当客户投诉或问题发生时，团队可以使用因果矩阵图来追踪可能的因素，并采取适当的措施来解决问题。

绘制方法绘制因果矩阵图需要以下步骤：1.定义问题：首先，团队需要明确定义问题，并确保所有成员对问题的定义达成共识。

2.确定主要因素：接下来，团队需要确定可能与问题有关的主要因素。

这些因素通常可以分为六个类别，即人员（People）、方法（Methods）、材料（Materials）、机器（Machines）、测量（Measurements）和环境（Environment）。

因果关系矩阵(C&E matrix)又名：C&E矩阵(C8E matrix)概述因果关系矩阵将过程的每一步与顾客需求紧密相连。

划分需求的重要度等级以及过程的每个步骤与需求的相关程度等级对理解过程的哪些方面在满足顾客需求时最为重要是有帮助的。

适用场合·利用质量功能展开( QFD)或关键质量特性(CTQ)树定义出关键质量特性后；·确定过程的哪些方面对顾客的需求影响最大时；·确定改善的焦点时。

实施步骤1得到一张关键过程输出变量列表，通常是顾客需求。

这些也被称作关键质量特性(CTQ)，可以使用质量屋或关键质量特性树确定。

对CTQ的描述需具体，便于分析。

将输出变量写在L 型矩阵的第一行中作为标题。

2根据对顾客的重要程度为每个输出变量分配一个权重，将其写在对应的输出变量旁边。

3得到一张关键过程输入变量列表，可以从宏观流程图过程的步骤中找到。

对输入变量的描述同样需要具体，便于分析。

将输入变量写在矩阵的第一列中作为标示。

4评价每个输入变量与输出变量的相互关系。

试问：“如果改变这个变量，是否会导致结果的改变？”使用一个等级量表来表示变量之间的相关程度。

较低的分值表示结果改变很小或没有改变，中间分值表示结果有一些改变，较高的分值表示结果改变很大。

通常给这种相关程度赋值为1，2，3或1，3，5或l，4，9。

将相关程度的分值填在矩阵中。

5将每一单元的相关程度的分值乘以该列对应输出变量的权重，然后将每一行的乘积加起来。

总分最高的行对应的输入变量就是对输出变量影响最大的变量。

6作为检查，将步骤5中每个单元按列求和。

这些总分应该反应出输出变量的相对重要程度。

如果不是，则说明在评分时可能有错误、丢失了输入变量、输出变量不受过程的影响，或者没有很好的识别过程的联系。

示例Ben-Hur比萨店为扩大经营业务，打算增加送货上门服务。

他们通过对现有和潜在的顾客进行调查，试图确定顾客购买他们的比萨、而非其他竞争者或是其他种类的食品的原因。

对客户的重要
性排序
1
2
3
4
5
6
7
8
9
10
11
12
13
需求
需求
需求
需求
需求
需求
需求
需求
需求
需求
需求
需求需求
过程步骤
过程输入
1234567891011121314151617181920
合计
规格下限目标规格上限
因果矩阵
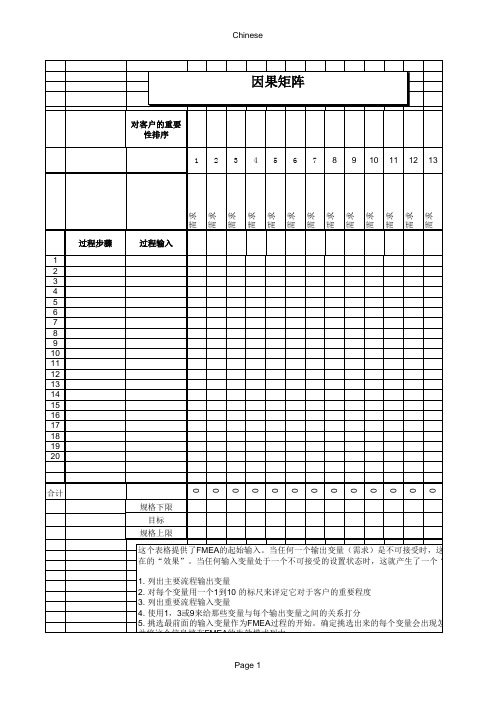
这个表格提供了FMEA 的起始输入。

当任何一个输出变量（需求）是不可接受时，这代在的“效果”。

当任何输入变量处于一个不可接受的设置状态时，这就产生了一个“失1. 列出主要流程输出变量
2. 对每个变量用一个1到10 的标尺来评定它对于客户的重要程度
3. 列出重要流程输入变量
4. 使用1，3或9来给那些变量与每个输出变量之间的关系打分
5. 挑选最前面的输入变量作为FMEA 过程的开始。

确定挑选出来的每个变量会出现怎样的并将这个信息填在FMEA 的失效模式列中。

并将这个信息填在FMEA的失效模式列中。

1415
需求
需求
总和
000000000000000000000
，这代表了一个潜个“失效模式”。

怎样的“问题”，。

因果矩阵表权重在决策过程中，我们常常需要对不同的因素进行权重的评估，以便更好地进行决策。

而因果矩阵是一种常用的工具，可以帮助我们对不同因素进行权重分配，从而更好地进行决策。

在因果矩阵中，我们可以列出我们需要评估的各个因素，并对它们进行排列。

然后，我们可以对每个因素进行评分，以反映其在决策中的重要性。

这些评分可以基于主观的判断，也可以基于客观的数据。

评分越高，表示该因素对决策的影响越大。

在进行权重评估时，我们需要考虑多个方面。

首先，我们需要考虑各个因素之间的相关性。

如果两个因素之间存在较强的相关性，那么它们的权重可能会相互影响。

其次，我们还需要考虑因素的可行性和可操作性。

如果某个因素很难实现或者无法控制，那么它的权重可能会相应降低。

在进行权重评估时，我们可以使用不同的方法。

一种常用的方法是专家评估法，即请相关领域的专家对各个因素进行评分。

另一种方法是统计分析法，即通过对历史数据进行分析，得出各个因素的权重。

无论使用哪种方法，我们都需要保证评估过程的客观性和准确性。

我们需要避免主观偏见，并尽量使用可靠的数据和信息进行评估。

在进行权重评估后，我们可以根据各个因素的权重来进行决策。

具有较高权重的因素，我们可以给予更多的关注和重视，以确保决策的有效性和成功性。

因果矩阵可以帮助我们对不同因素进行权重评估，从而更好地进行决策。

在进行权重评估时，我们需要考虑多个因素，并使用准确可靠的方法进行评估。

通过合理地分配权重，我们可以更好地进行决策，并取得更好的结果。

在决策过程中，我们需要保证客观性和准确性，以确保决策的有效性。