山西省晋中市和诚高中高二数学周练试题(5.18)文(无答案)

和诚中学2020-2021学年度高二9月周练理数试题（二）考试时间：65分钟 满分：100分一、选择题(共15题，每题3分，共45分)1.下图为某几何体的三视图，则该几何体的表面积是（ ） A.246+ B.244+ C.326+ D.324+2.已知 为球 的球面上的三个点，⊙ 为 的外接圆，若⊙的面积为 ， ，则球 的表面积为（ ）A. B. C. D.3.已知各顶点都在一个球面上的正四棱锥的高3，体积为6，则 球的半径为( )A. 2 B C. D. 34.在正方体ABCD -A 1B 1C 1D 1中，三棱锥D 1-AB 1C 的表面积与正方体的表面积的比为( )A. 1∶1B. 1∶C. 1∶D. 1∶25.如图，将无盖正方体纸盒展开，直线AB 、CD 在原正方体中的位置关系是( )A. 平行B. 相交且垂直C. 异面D. 相交成60°6、在空间四边形ABCD 中，AB 、BC 、CD 的中点分别为P 、Q 、R ，且AC =4，BD =2 ，PR =3，则AC 和BD 所成角的大小为( )A. 90°B. 60°C. 45°D. 30°7.下列命题中①如果一个角的两边与另一个角的两边分别平行，那么这两个角相等；②如果两条相交直线和另两条直线分别平行，那么这两组直线所成的锐角(或直角)相等；③如果一个角的两边和另一个角的两边分别垂直，那么这两个角相等或互补；④如果两条直线同时平行于第三条直线，那么这两条直线平行.正确的结论有( )A. 1个B.2个C. 3个D. 4个8.下列命题中，是假命题的为( )A. 平行于同一直线的两个平面平行B. 平行于同一平面的两个平面平行C.垂直于同一平面的两条直线平行D. 垂直于同一直线的两个平面平行9.如图，已知正方体ABCD-A1B1C1D1，则直线EF是平面ACD1与下列哪个平面的交线?( )A. 平面BDB1B. 平面BDC1C. 平面ACB1D. 平面ACC110.在四面体A-BCD中，E是CD的中点，M、N分别是EA、EB上的点，且则四面体A-BCD的四个表面中所有与MN平行的是()A. 平面ABDB. 平面BCDC. 平面ABCD. 平面ABD与平面ABC11.如图，P为平行四边形ABCD所在平面外一点，Q为PA的中点，O为AC与BD 的交点，下面说法错误的是( ) A. OQ∥平面PCDB. PC∥平面BDQC. AQ∥平面PCDD. CD∥平面PAB12.如图，E，F，G分别是四面体ABCD的棱BC、CD、DA的中点，则此四面体中与过点E、F、G的截面平行的棱的条数是( )A. 0B. 1C. 2D. 3二、填空题（20分）13.如图是正方体的平面展开图，在这个正方体中，①BM∥平面DE；②CN∥平面AF；③平面BDM∥平面AFN；④平面BDE∥平面NCF.以上四个命题中，正确命题的序号是.14.如图，在正方体ABCD-A1B1C1D1中，AB=2，点E为AD的中点，点F在CD上.若EF∥平面AB1C，则线段EF的长度等于.14题图15题图15.如图，四棱锥PABCD的底面是直角梯形，AB∥CD，BA⊥AD，CD＝2AB，PA⊥底面ABCD，E为PC的中点，则BE与平面PAD的位置关系为．16.在长方体中，，，则直线与平面所成角的正弦值为．三、解答题（20分，18题4分）17.如图所示，在△ABC中，∠ABC=90°，SA⊥平面ABC，过点A向SC和SB引垂线，垂足分别是P、Q.求证：(1)AQ⊥平面SBC；(2)PQ⊥SC.18.如图所示，在底面为直角梯形的四棱锥P-ABCD中，AC与BD相交于点E，AD∥BC，∠ABC=90°，PA⊥平面ABCD，AD=2，AB=2 ，BC=6.求证：BD⊥平面PAC.19.如图，在斜三棱柱中，底面是边长为的正三角形，为棱的中点，，，.（Ⅰ）求证：平面；（Ⅱ）求斜三棱柱的体积.试卷答案1、C根据三视图特征，在正方体中截取出符合题意的立体图形，求出每个面的面积，即可求得其表面积.解：根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：根据勾股定理可得：是边长为的等边三角形根据三角形面积公式可得：该几何体的表面积是： .故选：C.2、A设圆半径为，球的半径为，依题意，得，由正弦定理可得，，根据圆截面性质平面，，球的表面积 .故选：A3、A本题考查四棱锥的外接球问题.设正四棱锥的底面边长为a，由V= a2×3=a2=6，得a= .由题意知球心在正四棱锥的高上，设球的半径为r，则(3-r)2+( )2=r2，解得r=2.4、C本题考查棱锥的表面积.设正方体ABCD-A1B1C1D1的棱长为a，则正方体ABCD-A1B1C1D1的表面积为S2=6a2，且三棱锥D1-AB1C为各棱长均为a的正四面体，其中一个面的面积为S=a×a=a2，所以三棱锥D1-AB1C的表面积为S1=4S=4×a2=2a2，所以三棱锥D1-AB1C的体积与正方体ABCD-A1B1C1D1的表面积之比为S1∶S 2=1∶.5、D本题考查折叠问题与异面直线的关系的判断.将展开图还原为正方体，如图所示，则△ABC是等边三角形，所以直线AB、CD在原正方体中的位置关系是相交成60°.6、A本题考查异面直线的夹角.如图，P、Q、R分别为AB、BC、CD中点，∴PQ∥AC，QR∥BD，∴∠PQR为AC和BD所成角.又∵PQ= AC=2，QR= BD= ，RP=3，∴PR2=PQ2+QR2，∴∠PQR=90°，即AC和BD所成角的大小为90°，故选A项.7、B本题考查空间中直线的关系.对于①，这两个角也可能互补，故①错；对于②，正确；对于③，不正确，举反例：如图所示，BC⊥PB，AC⊥PA，∠ACB的两条边分别垂直于∠APB的两条边，但这两个角既不一定相等，也不一定互补；对于④，由公理4可知正确.故②④正确，所以正确的结论有2个.8、A本题考查两平面间的位置关系.对于A，平行于同一直线的两个平面，其位置关系是相交或平行，故A错误；B，C ，D都是真命题.9、B本题考查直线与平面相交.连接BC1.因为E∈DC1，F∈BD，所以EF⊂平面BDC1，故EF=平面ACD1∩平面BDC1 .10、D如图，因为，所以MN∥AB.因为AB⊂平面ABD，MN⊄平面ABD，所以MN∥平面ABD，因为AB⊂平面ABC，MN⊄平面ABC，所以MN∥平面ABC.11、C本题考查线面平行的判定.因为O为▱ABCD对角线的交点，所以AO=OC，又Q为PA的中点，所以QO∥PC. 由线面平行的判定定理，可知选项A、B正确，又四边形ABCD为平行四边形，所以AB∥CD，故CD∥平面PAB，D选项正确.12、C本题考查线面平行的判断.只有AC，BD与此平面平行.13、①②③④本题考查线面及面面平行的判定.以ABCD为下底面还原正方体，如图，则易判定四个命题都是正确的.14、本题考查线面平行的性质.∵在正方体ABCD—A1B1C1D1中，AB=2，∴AC=2 .又∵E为AD的中点，EF∥平面AB1 C，EF⊂平面ADC，平面ADC∩平面AB1C=AC，∴EF∥AC，∴F为DC的中点，∴E F= AC= .15、平行取PD的中点F，连接EF，AF，在△PCD中，EF綊CD.又因为AB∥CD且CD＝2AB，所以EF綊AB，所以四边形ABEF是平行四边形，所以EB∥AF.又因为EB⊄平面PAD，AF⊂平面PAD，所以BE∥平面PAD.答案：平行16、分析：过作，垂足为，则平面，则即为所求平面角，从而可得结果.详解：依题意，画出图形，如图，过作，垂足为，由平面，可得，所以平面，则即为所求平面角，因为，，所以，故答案为.点睛：本题考查长方体的性质，以及直线与平面所成的角，属于中档题.求直线与平面所成的角由两种方法：一是传统法，证明线面垂直找到直线与平面所成的角，利用平面几何知识解答；二是利用空间向量，求出直线的方向向量以及平面的方向向量，利用空间向量夹角余弦公式求解即可.17、见解析本题考查线面垂直的证明.(1)∵SA⊥平面ABC，BC⊂平面ABC，∴SA⊥BC.又∵BC⊥AB，SA∩AB=A，∴BC⊥平面SAB.又∵AQ⊂平面SAB，∴BC⊥AQ.又∵AQ⊥SB，BC∩SB=B，∴AQ⊥平面SBC.(2)∵AQ⊥平面SBC，SC⊂平面SBC，∴AQ⊥SC.又∵AP⊥SC，AQ∩AP=A，∴SC⊥平面APQ.∵PQ⊂平面APQ，∴PQ⊥SC.18、见解析本题考查线面垂直的证明.∵PA⊥平面ABCD，BD⊂平面ABCD，∴BD⊥P A.∵∠BAD=∠ABC=90°，∴tan∠ABD= ，tan∠BAC= ，∴∠ABD=30°，∠BAC=60°，∴∠AEB=90°，即BD⊥AC，又PA∩AC=A，∴BD⊥平面PAC.19、(1)见解析;(2)（Ⅰ）根据底面为正三角形，易得；由各边长度，结合余弦定理，可求得的值，再根据勾股定理逆定理可得，可证平面。

山西省晋中市和诚高中2021届上学期高三年级周练数学试卷（文科）时间（65分钟）总分100一、选择题（共125=60）1．已知集合A＝{|||＜3，∈Z}，B＝{|||＞1，∈Z}，则A∩B＝（）A．∅ B．{﹣3，﹣2，2，3} C．{﹣2，0，2} D．{﹣2，2}2．已知集合A＝{（，y）|y≤2，，y∈N}，则A中元素的个数为（）A．1 B．5 C．6 D．无数个3．设∈R，则“0＜＜5”是“|﹣1|＜1”的（）A．充分而不必要条件 B．必要而不充分条件C．充要条件 D．既不充分也不必要条件4．已知命题＞a”是“函数的图象不过第三象限”的必要不充分条件，则实数a的取值范围是（）A． B． C． D．二、填空题（共45=20）13．f（）＝，则不等式2•f（）﹣2≤0解集是．14．已知全集U＝R，集合M＝{|﹣1＜﹣2＜1}和N＝{|＝2，＝1，2，…}的关系如图所示，则阴影部分所示的集合的元素有．15．若定义在（﹣∞，1）∪（1，∞）上的函数f（）满足f（）2f（）＝2017﹣，则f（2019）＝．16．已知函数f（）＝e||2（e为自然对数的底数），且f（3a﹣2）＞f（a﹣1），则实数a的取值范围为．三、解答题（共2小题,每小题10分）17．求函数f（）＝的值域．18．已知a＞0，设命题﹣≥﹣1，解得m≥﹣．∵“m＞a”是“函数的图象不过第三象限”的必要不充分条件，∴a＜﹣．则实数a的取值范围是．故选：D．13．{|＜2}【解析】当≥2时，原不等式可化为2﹣2≤0解可得，﹣2≤≤1此时不存在当＜2时，原不等式可化为﹣2﹣2≤0即2﹣2≥0解不等式可得∈R此时＜2综上可得，原不等式的解集为{|＜2}故答案为：{|＜2}14．1个【解析】阴影部分所示的集合为M∩N∵M＝{|﹣1＜﹣2＜1}＝{|1＜＜3}N＝{|＝2，＝1，2，…}＝{2，4，6，8，…}∴M∩N＝{2}即阴影部分所示的集合的元素有1个故答案为：1个15．1344【解析】f（）2f（）＝2017﹣，当＝2时，f（2）2f（2019）＝2015，①当＝2019：f（2019）2f（2）＝﹣2，②，①×2﹣②可得3f（2019）＝4032，∴f（2019）＝1344．故答案为：134416．（﹣∞，）∪（，∞）【解析】∵函数f（）＝e||2（e为自然对数的底数），∴f（﹣）＝f（）＝f（||），且在（0，∞）单调递增，∵f（3a﹣2）＞f（a﹣1），∴|3a﹣2|＞|a﹣1|，即8a2﹣10a3＞0，实数a的取值范围为a或a，故答案为：（﹣∞，）∪（，∞）三、解答题（共2小题）17．解：变形可得f（）＝＝＝＝1，令1＝t，则y＝t，由“对号函数”的性质可得y∈（﹣∞，﹣2]∪∪[2，∞）18．解：∵y＝a在R上单调递增，∴a＞1；又a＞0，不等式a2a1＞0对∀∈R恒成立，∴△＜0，即a2﹣4a＜0，∴0＜a＜4，∴q：0＜a＜4．而命题p且q为假，p或q为真，那么p、q中有且只有一个为真，一个为假．①若p真，q假，则a≥4；②若p假，q真，则0＜a≤1．所以a的取值范围为（0，1]∪[4，∞）．。

和诚中学2018-2019学年度高二理科数学知识清单易错题目训练考试时间：60分钟 满分：100分一、选择题（本题共8小题，每小题7分，共56分．） 1、下列四个命题正确的是（ ）①线性相关系数r 越大，两个变量的线性相关性越强；反之，线性相关性越小；②残差平方和越小的模型，拟合的效果越好；③用相关指数2R 来刻画回归效果，2R 越小，说明模型的拟合效果越好； ④随机误差e 是衡量预报精确度的一个量，它的平均值为0． A ． ①②③ B ． ②④ C ．②③④ D ．①②④ 2、在回归分析中，残差图中的纵坐标为（ ）A ．残差B ． 样本编号C ．随机误差D ．i yˆ的估计值 3、在画两个变量的散点图时，下面叙述正确的是（ ） A 预报变量在x 轴上，解释变量在y 轴上 B 解释变量在x 轴上，预报变量在y 轴上 C 可以选择两个变量中的任意一个变量在x 轴上 D 可以选择两个变量中的任意一个变量在y 轴上4.两个变量y 与x 的回归模型中，分别选择了4个不同模型，它们的相关指数R 2如下，其中拟合效果最好的模型是( ) A.模型1的相关指数R 2为0.98 B.模型2的相关指数R 2为0.80 C.模型3的相关指数R 2为0.50 D.模型4的相关指数R 2为0.255、为了考察两个变量y x ,之间的线性相关性，甲乙两位同学各自独立地做了10次和15次试验，并且利用线性回归方法求得回归直线21,l l ，已知两人在试验中发现对变量x 的观测数据的平均值都是s ，对变量y 的观测数据的平均值都是t ，那么下列说法正确的是( ) A ．21,l l 必定平行 B ．21,l l 必定重合C ．21,l l 有交点()t s ,D ．21,l l 相交，但交点不一定是()t s ,6、已知有5组数据()()()()()12,10,10,3,5,4,4,2,3,1E D C B A ，去掉哪一组数据后，剩下4组数据的线性相关系数最大（）A．E B．D C．B D．A 7、通过随机询问110名不同的大学生是否爱好某项运动，得到如下的列联表：则得到的正确结论是（）A．有99%以上的把握认为“爱好该项运动与性别有关”B．有99%以上的把握认为“爱好该项运动与性别无关”C．在犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别有关”D．在犯错误的概率不超过0．1%的前提下，认为“爱好该项运动与性别无关”8.为了解某社区居民的家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：根据上表可得回归直线方程y＝b x＋a，其中b＝0.76，a＝y－b x，据此估计，该社区一户年收入为15万元家庭的年支出为( )A.11.4万元B.11.8万元C.12.0万元D.12.2万元二、填空题（本题共3小题，每小题8分，共24分）9..若8名学生的身高和体重数据如下表：第3名学生的体重漏填，但线性回归方程是y＝0.849x－85.712，则第3名学生的体重估计为________.10.(2017·广州模拟)为了判断高中三年级学生选修文理科是否与性别有关，现随机抽取50名学生，得到2×2列联表如下：已知P (K 2≥3.841根据表中数据，得到K 2＝50×（13×20－10×7）223×27×20×30≈4.844，则认为选修文理科与性别有关系出错的可能性约为________.11.某单位为了了解用电量y (度)与气温x (℃)之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：由表中数据得回归直线方程y ＝b x ＋a 中的b ＝－2，预测当气温为－4 ℃时，用电量约为________度.三、解答题（共2小题，每题10，共20分）12..( 2016·全国Ⅲ)下图是我国2008年至2014年生活垃圾无害化处理量(单位：亿吨)的折线图.注：年份代码1－7分别对应年份2008－2014.(1)由折线图看出，可用线性回归模型拟合y 与t 的关系，请用相关系数加以说明； (2)建立y 关于t 的回归方程(系数精确到0.01)，预测2016年我国生活垃圾无害化处理量.附注： 参考数据：7719.32,40.17,ii i i yt y ===∑∑i=12.646=≈，()()niit t y y --∑回归方程y ^＝a ^＋b ^t 中斜率和截距的最小二乘估计公式分别为：b ^＝121()(),.()niii ni i t t y y a y bt t t ==--=--∑∑13. 某公司生产部门经调研发现，该公司第二、三季度的用电量与月份相关，数据统计如下：(1)核对电费时发现一组数据统计有误，请指出哪组数据有误，并说明理由；(2)在排除有误数据后，求用电量与月份之间的回归直线方程y ^＝b ^x ＋a ^，并计算出统计有误的月份的正确用电量．。

和诚中学2019-2020年高二11月周练数学试卷（文）考试时间：60min 分值：100分一、单选题（60分）1．若坐标原点在圆22222240x y mx my m +-++-=的内部，则实数m 的取值范围是（ ）A ．()1,1-B ．,22⎛- ⎝⎭C ．(D ．( 2．一根细金属丝下端挂着一个半径为1cm 的金属球，将它浸没底面半径为2cm 的圆柱形容器内的水中，现将金属丝向上提升，当金属球被拉出水面时，容器内的水面下降（） A ．43cm B ．316cm C ．34cm D ．13cm3．圆22420x y x y c +-++=与直线340x y -=相交于,A B 两点，圆心为P ，若90APB ∠=︒，则c 的值为（ ）A ．8B ．C ．-3D ．3 4．圆心为点()4,7C ，并且截直线3410x y -+=所得的弦长为8的圆的方程为（ ） A ．()()22475x y -+-=B ．()()224725x y -+-= C ．()()22745x y -+-= D ．()()227425x y -+-=5．已知点,A B 分别在圆()2211x y +-=与圆()()22259x y -+-=上，则,A B 两点之间的最短距离为（ ）A ．B ．2-C ．4D ．26．已知圆22:230C x y x ay +++-=（a 为实数）上任意一点关于直线:20l x y -+=的对称点都在圆C 上，则a =（ ）A ．1B ．2C ．1-D ．2-7．直线1y kx =+与圆2210x y kx y ++--=的两个交点恰好关于y 轴对称，则k 等于（ ）A ．0B ．1C ．2D ．38．与圆22:(2)(2)1C x y ++-=关于直线10x y -+=对称的圆的方程为（ ）A.22(1)(1)1x y -++=B.22(1)(1)1x y +++=C.22(1)(1)1x y -+-=D.22(1)(1)1x y ++-= 9．已知圆()()221 221:C x y ++-=，圆 ()()222 2516:C x y -+-= ，则圆1C 与圆2 C 的位置关系是（ ）A.相离B.相交C.外切D.内切10．设m ，n 是两条不同的直线，α，β，γ是三个不同的平面，给出下列命题： ①若//m α，//n β，//αβ，则//m n ；②若//αγ，//βγ，则//αβ；③若m α⊥，n β⊥，//αβ，则//m n ；④若αγ⊥，βγ⊥，则//αβ其中正确命题的序号是（ ）A.①③B.①④C.②③D.②④11．下列四个命题中，其中错误的个数是（）①经过球面上任意两点，可以作且只可以作一个大圆；②经过球直径的三等分点，作垂直于该直径的两个平面，则这两个平面把球面分成三部分的面积相等；③球的面积是它大圆面积的四倍；④球面上两点的球面距离，是这两点所在截面圆上，以这两点为端点的劣弧的长． A ．0 B ．1 C ．2 D ．312．定义1分的地球球心角所对的地球大圆弧长为1海里．在北纬45°圈上有甲、乙两地，甲地位于东经120°，乙位于西经150°，则甲乙两地在球面上的最短距离为（）A ．5400海里B ．2700海里C ．4800海里D ．3600海里二、填空题（20分）13．直线()12230a x y --+=与直线320x y a ++=垂直，则实数a 的值为__________． 14．若()4,2A -，()6,4B -，()12,6C ，()2,12D ．给出下列结论：①//AB CD ；②AB AD ⊥；③AC BD ⊥；④CD CB ⊥．其中正确的结论是________．15．已知点()1,1A ，()1,3B -，()0,0O ，则ABO V 的面积为________．16．若x ，y ，z 满足约束条件4802400x y x y y --≤⎧⎪-+≥⎨⎪≤⎩，则z =__________．三、解答题（20分）17．已知直线1:2(1)40l x m y +++=与2:360l mx y +-=平行.（1）求实数m 的值：（2）设直线l 过点()1,2，它被直线1l ，2l 所截的线段的中点在直线3:20l x y -+=上，求l 的方程.18．已知圆22:2430C x y x y ++-+=.(1)已知不过原点的直线l 与圆C 相切，且在x 轴，y 轴上的截距相等，求直线l 的方程；(2)求经过原点且被圆C 截得的线段长为2的直线方程.参考答案1．D【解析】【分析】将原点坐标代入圆的方程得到不等式，解不等式得到结果.【详解】把原点坐标代入圆的方程得:222002020240m m m +-⨯+⨯+-<解得：m 本题正确选项：D【点睛】本题考查点与圆的位置关系的问题，属于基础题.2．D【解析】【分析】利用等体积法求水面下降高度。

和诚中学2018-2019学年度高二8月月考数学试题考试时间：120分钟 满分：150分 命题人：一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A ＝{x |x 2－x －2<0，x ∈R }，B ＝{x |x 2－1≥0，x ∈R }，则A ∩B 等于( ) A ．{x |－1<x <2} B ．{x |x ≤－1或1≤x <2} C ．{x |1<x <2} D ．{x |1≤x <2} 2．若a ＜1，b ＞1，那么下列不等式中正确的是( ) A.1a ＞1b B ．b a＞1 C ．a 2＜b 2D ．ab ＜a ＋b3．若f (x )＝－x 2＋mx －1的函数值有正值，则m 的取值范围是( ) A ．m <－2或m >2 B ．－2<m <2 C ．m ≠±2 D ．1<m <34．已知z ＝2x ＋y ，x ，y 满足⎩⎪⎨⎪⎧y ≥x ，x ＋y ≤2，x ≥a ，且z 的最大值是最小值的4倍，则实数a 的值是( )A.13 B ．14 C.15 D ．165．若log a 5<log a 2，则不等式(a －x )⎝⎛⎭⎪⎫x －1a >0的解集为( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪a <x <1a B ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1a <x <a C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >1a 或x <a D ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <1a 或x >a 6．不等式组⎩⎪⎨⎪⎧－2（x －3）＞10，x 2＋7x ＋12≤0的解集为( )A ．[－4，－3]B ．[－4，－2]C ．[－3，－2]D ．∅7．在坐标平面上，不等式组⎩⎪⎨⎪⎧y ≥x －1，y ≤－3|x |＋1所表示的平面区域的面积为( )A. 2 B ．32 C.322D ．28．已知x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ≥0x ＋y －4≤0，y ≥1则z ＝－2x ＋y 的最大值是( )A ．－1B ．－2C ．－5D ．19．已知x ＞0，y ＞0.若2y x ＋8x y＞m 2＋2m 恒成立，则实数m 的取值范围是( )A ．m ≥4或m ≤－2B ．m ≥2或m ≤－4C ．－2＜m ＜4D ．－4＜m ＜210．已知－1≤x ＋y ≤4，且2≤x －y ≤3，则z ＝2x －3y 的取值范围是( ) A ．[3，8] B ．[3，6] C ．[6，7] D ．[4，5]11．若x ，y 满足条件⎩⎪⎨⎪⎧3x －5y ＋6≥0，2x ＋3y －15≤0，y ≥0，当且仅当x ＝y ＝3时，z ＝ax ＋y 取得最大值，则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫－23，35B.⎝ ⎛⎭⎪⎫－∞，－35∪⎝ ⎛⎭⎪⎫23，＋∞C.⎝ ⎛⎭⎪⎫－35，23D.⎝ ⎛⎭⎪⎫－∞，－23∪⎝ ⎛⎭⎪⎫35，＋∞12．若不等式x 2＋ax ＋1≥0对一切x ∈⎝ ⎛⎦⎥⎤0，12恒成立，则实数a 的最小值为( )A ．0B ．－2C ．－52 D ．－3二、填空题：本题共4小题，每小题5分．13．设x ，y ∈R ，且xy ≠0，则(x 2＋1y 2)(1x2＋4y 2)的最小值为________．14.若a ＞0，b ＞0，a ＋b ＝2，则下列不等式对一切满足条件的a ，b 恒成立的是________(写出所有正确不等式的编号)．①ab ≤1；②a ＋b ≤2；③a 2＋b 2≥2；④1a ＋1b≥2.15．函数y ＝2－x －4x(x ＞0)的值域为________．16．设x ＞5，P ＝x －4－x －5，Q ＝x －2－x －3，则P 与Q 的大小关系是__________． 三、解答题：解答应写出文字说明、证明过程或演算步骤．17．(本小题满分10分)已知函数f (x )＝x 2＋2x，解不等式f (x )－f (x －1)＞2x －1.18．(本小题满分10分)已知方程ax 2＋bx ＋2＝0的两根为－12和2.解不等式ax 2＋bx －1>0.19．(本小题满分12分)正数x ，y 满足1x ＋9y＝1.(1)求xy的最小值；(2)求x＋2y的最小值．20．(本小题满分12分)已知函数f(x)＝log3(x2－4x＋m)的图像过点(0，1)．解不等式：f(x)≤1.21.(本小题满分12分)已知函数f(x)＝x2－2x－8，g(x)＝2x2－4x－16.(1)求不等式g(x)<0的解集；(2)若对一切x>2，均有f(x)≥(m＋2)x－m－15恒成立，求实数m的取值范围．22．(本小题满分12分)某蔬菜基地种植甲、乙两种无公害蔬菜．生产一吨甲种蔬菜需用电力9千瓦时，耗肥4吨，3个工时；生产一吨乙种蔬菜需用电力5千瓦时，耗肥5吨，10个工时，现该基地仅有电力360千瓦时，肥200吨，工时300个．已知生产一吨甲种蔬菜获利700元，生产一吨乙种蔬菜获利1 200元，在上述电力、肥、工时的限制下，问如何安排甲、乙两种蔬菜种植，才能使利润最大？最大利润是多少？和诚中学2018-2019学年度高二8月月考数学试题答案考试时间：120分钟 满分：150分一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是 符合题目要求的．1．已知集合A ＝{x |x 2－x －2<0，x ∈R }，B ＝{x |x 2－1≥0，x ∈R }，则A ∩B 等于( ) A ．{x |－1<x <2} B ．{x |x ≤－1或1≤x <2} C ．{x |1<x <2} D ．{x |1≤x <2}解析：选D.因为A ＝{x |－1<x <2}，B ＝{x |x ≥1或x ≤－1}，所以A ∩B ＝{x |1≤x <2}．2．若a ＜1，b ＞1，那么下列不等式中正确的是( ) A.1a ＞1bB ．b a＞1 C ．a 2＜b 2D ．ab ＜a ＋b解析：选D.利用特值法，令a ＝－2，b ＝2，则1a ＜1b ，A 错；b a＜0，B 错；a 2＝b 2，C 错．3．若f (x )＝－x 2＋mx －1的函数值有正值，则m 的取值范围是( ) A ．m <－2或m >2 B ．－2<m <2 C ．m ≠±2D ．1<m <3解析：选A.因为f (x )＝－x 2＋mx －1有正值， 所以Δ＝m 2－4>0，所以m >2或m <－2.4．已知z ＝2x ＋y ，x ，y 满足⎩⎪⎨⎪⎧y ≥x ，x ＋y ≤2，x ≥a ，且z 的最大值是最小值的4倍，则实数a 的值是( )A.13 B ．14 C.15D ．16解析：选B.在坐标平面内画出题中的不等式组表示的平面区域及直线2x ＋y ＝0，平移该直线，当相应直线分别经过该平面区域内的点(a ，a )与(1，1)时，相应直线在x 轴上的截距达到最小与最大，此时z ＝2x ＋y 取得最小值与最大值，于是有2×1＋1＝4(2a ＋a )，a ＝14.5．若log a 5<log a 2，则不等式(a －x )⎝⎛⎭⎪⎫x －1a >0的解集为( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪a <x <1a B ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪1a <x <a C.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x >1a或x <a D ．⎩⎨⎧⎭⎬⎫x ⎪⎪⎪x <1a或x >a 解析：选A.由log a 5<log a 2知0<a <1，所以a <1a；不等式(a －x )⎝⎛⎭⎪⎫x －1a >0⇔(x －a )⎝ ⎛⎭⎪⎫x －1a <0，解得a <x <1a.6．不等式组⎩⎪⎨⎪⎧－2（x －3）＞10，x 2＋7x ＋12≤0的解集为( )A ．[－4，－3]B ．[－4，－2]C ．[－3，－2]D ．∅解析：选A.⎩⎪⎨⎪⎧－2（x －3）＞10，x 2＋7x ＋12≤0⇒⎩⎪⎨⎪⎧x －3＜－5，（x ＋3）（x ＋4）≤0 ⇒⎩⎪⎨⎪⎧x ＜－2，－4≤x ≤－3⇒－4≤x ≤－3. 7．在坐标平面上，不等式组⎩⎪⎨⎪⎧y ≥x －1，y ≤－3|x |＋1所表示的平面区域的面积为( )A. 2 B ．32 C.322D ．2解析：选B.由题意得，图中阴影部分面积即为所求．B 、C 两点横坐标分别为－1、12，A 、D 两点纵坐标分别为1，－1.所以S △ABC ＝12×2×⎪⎪⎪⎪⎪⎪12－（－1）＝32.8．已知x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ≥0x ＋y －4≤0，y ≥1则z ＝－2x ＋y 的最大值是( )A ．－1B ．－2C ．－5D ．1解析：选A.作出可行域，如图中阴影部分所示，易知在点A (1，1)处，z 取得最大值，故z max ＝－2×1＋1＝－1.9．已知x ＞0，y ＞0.若2y x ＋8x y＞m 2＋2m 恒成立，则实数m 的取值范围是( )A ．m ≥4或m ≤－2B ．m ≥2或m ≤－4C ．－2＜m ＜4D ．－4＜m ＜2解析：选D.因为x ＞0，y ＞0，所以2y x ＋8x y ≥8(当且仅当2y x ＝8xy时取“＝”)．若2y x ＋8x y＞m 2＋2m 恒成立，则m 2＋2m ＜8，解之得－4＜m ＜2.10．已知－1≤x ＋y ≤4，且2≤x －y ≤3，则z ＝2x －3y 的取值范围是( ) A ．[3，8] B ．[3，6] C ．[6，7]D ．[4，5]解析：选A.设2x －3y ＝λ(x ＋y )＋μ(x －y )， 则(λ＋μ)x ＋(λ－μ)y ＝2x －3y ， 所以⎩⎪⎨⎪⎧λ＋μ＝2，λ－μ＝－3，解得⎩⎪⎨⎪⎧λ＝－12，μ＝52， 所以z ＝－12(x ＋y )＋52(x －y )．因为－1≤x ＋y ≤4， 所以－2≤－12(x ＋y )≤12.①因为2≤x －y ≤3，所以5≤52(x －y )≤152.②①＋②得，3≤－12(x ＋y )＋52(x －y )≤8，所以z 的取值范围是[3，8]．11．若x ，y 满足条件⎩⎪⎨⎪⎧3x －5y ＋6≥0，2x ＋3y －15≤0，y ≥0，当且仅当x ＝y ＝3时，z ＝ax ＋y 取得最大值，则实数a 的取值范围是( )A.⎝ ⎛⎭⎪⎫－23，35B.⎝ ⎛⎭⎪⎫－∞，－35∪⎝ ⎛⎭⎪⎫23，＋∞ C.⎝ ⎛⎭⎪⎫－35，23D.⎝ ⎛⎭⎪⎫－∞，－23∪⎝ ⎛⎭⎪⎫35，＋∞ 解析：选C.直线3x －5y ＋6＝0和直线2x ＋3y －15＝0的斜率分别为k 1＝35，k 2＝－23，且两直线的交点坐标为(3，3)，作出可行域如图所示，当且仅当直线z ＝ax ＋y 经过点 (3，3)时，z 取得最大值，则直线z ＝ax ＋y 的斜率－a 满足－23<－a <35，解得－35<a <23，故选C.12．若不等式x 2＋ax ＋1≥0对一切x ∈⎝ ⎛⎦⎥⎤0，12恒成立，则实数a 的最小值为( )A ．0B ．－2C ．－52D ．－3解析：选C.因为不等式x 2＋ax ＋1≥0对一切x ∈⎝ ⎛⎦⎥⎤0，12恒成立，所以对一切x ∈⎝ ⎛⎦⎥⎤0，12，ax ≥－x 2－1，即a ≥－x 2＋1x恒成立．令g (x )＝－x 2＋1x ＝－⎝ ⎛⎭⎪⎫x ＋1x .易知g (x )＝－⎝ ⎛⎭⎪⎫x ＋1x 在⎝ ⎛⎦⎥⎤0，12内为增函数．所以当x ＝12时，g (x )max ＝－52，所以a 的取值 范围是⎣⎢⎡⎭⎪⎫－52，＋∞，即a 的最小值是－52.故选C.二、填空题：本题共4小题，每小题5分．13．设x ，y ∈R ，且xy ≠0，则(x 2＋1y 2)(1x2＋4y 2)的最小值为________．解析：⎝ ⎛⎭⎪⎫x 2＋1y 2⎝ ⎛⎭⎪⎫1x 2＋4y 2＝1＋4＋4x 2y 2＋1x 2y 2≥1＋4＋24x 2y 2·1x 2y2＝9，当且仅当4x 2y 2＝1x 2y 2，即|xy |＝22时等号成立． 答案：914.若a ＞0，b ＞0，a ＋b ＝2，则下列不等式对一切满足条件的a ，b 恒成立的是________ (写出所有正确不等式的编号)．ab ≤1；②a ＋b ≤2；③a 2＋b 2≥2；④1a ＋1b≥2.解析：两个正数，和为定值，积有最大值，即ab ≤（a ＋b ）24＝1，当且仅当a ＝b 时取等号，故①正确；(a ＋b )2＝a ＋b ＋2ab ＝2＋2ab ≤4，当且仅当a ＝b 时取等号，得a ＋b ≤2，故②错误；由于a 2＋b 22≥（a ＋b ）24＝1，故a 2＋b 2≥2成立，故③正确；1a ＋1b ＝⎝ ⎛⎭⎪⎫1a ＋1b a ＋b 2＝1＋a 2b ＋b2a ≥1＋1＝2，当且仅当a ＝b 时取等号，故④正确． 答案：①③④ 答案：315．函数y ＝2－x －4x(x ＞0)的值域为________．解析：当x ＞0时，y ＝2－⎝⎛⎭⎪⎫x ＋4x ≤2－2x ×4x ＝－2.当且仅当x ＝4x，x ＝2时取等号．答案：(－∞，－2]16．设x ＞5，P ＝x －4－x －5，Q ＝x －2－x －3，则P 与Q 的大小关系是__________． 解析：P ＝x －4－x －5＝1x －4＋x －5，Q ＝x －2－x －3＝1x －2＋x －3，而0＜x －4＋x －5＜x －2＋x －3，所以必有P ＞Q ．三、解答题：解答应写出文字说明、证明过程或演算步骤．17．(本小题满分1 0分)已知函数f (x )＝x 2＋2x，解不等式f (x )－f (x －1)＞2x －1.解：由题意可得x 2＋2x －(x －1)2－2x －1＞2x －1，化简得2x （x －1）＜0，即x (x －1)＜0，解得0＜x ＜1.所以原不等式的解集为{x |0＜x ＜1}．18．(本小题满分10分)已知方程ax 2＋bx ＋2＝0的两根为－12和2.解不等式ax 2＋bx －1>0.解：因为方程ax 2＋bx ＋2＝0的两根为－12和2.由根与系数的关系，得⎩⎪⎨⎪⎧－12＋2＝－b a，－12×2＝2a ，解得a ＝－2，b ＝3.可知ax 2＋bx －1>0，即2x 2－3x ＋1<0，解得12<x <1.所以不等式ax 2＋bx －1>0的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪12<x <1. 19．(本小题满分12分)正数x ，y 满足1x ＋9y＝1.(1)求xy 的最小值； (2)求x ＋2y 的最小值． 解：(1)由1＝1x ＋9y≥21x ·9y 得xy ≥36，当且仅当1x ＝9y，即y ＝9x ＝18时取等号，故xy 的最小值为36.(2)由题意可得x ＋2y ＝(x ＋2y )·⎝ ⎛⎭⎪⎫1x ＋9y ＝19＋2y x ＋9x y≥19＋22y x ·9xy＝19＋62，当且仅当2y x ＝9x y，即9x 2＝2y 2时取等号，故x ＋2y 的最小值为19＋6 2.20．(本小题满分12分)已知函数f (x )＝log 3(x 2－4x ＋m )的图像过点(0，1)． 解不等式：f (x )≤1.解：由已知有f (0)＝log 3m ＝1，所以m ＝3.f (x )＝log 3(x 2－4x ＋3)．由x 2－4x ＋3＞0，得x ＜1或x ＞3，所以函数的定义域为(－∞，1)∪(3，＋∞)． 因为log 3(x 2－4x ＋3)≤1且y ＝log 3x 为增函数， 所以0＜x 2－4x ＋3≤3， 所以0≤x ＜1或3＜x ≤4，所以不等式的解集为{x |0≤x ＜1或3＜x ≤4}．21.(本小题满分12分)已知函数f (x )＝x 2－2x －8，g (x )＝2x 2－4x －16. (1)求不等式g (x )<0的解集；(2)若对一切x >2，均有f (x )≥(m ＋2)x －m －15恒成立，求实数m 的取值范围． 解：(1)g (x )＝2x 2－4x －16<0， 所以(2x ＋4)(x －4)<0，所以－2<x <4， 所以不等式g (x )<0的解集为{x |－2<x <4}． (2)因为f (x )＝x 2－2x －8.当x >2时，f (x )≥(m ＋2)x －m －15恒成立， 所以x 2－2x －8≥(m ＋2)x －m －15， 则x 2－4x ＋7≥m (x －1)．所以对一切x >2，均有不等式x 2－4x ＋7x －1≥m 成立．又x 2－4x ＋7x －1＝(x －1)＋4x －1－2≥2（x －1）×4x －1－2＝2(当x ＝3时等号成立)． 所以实数m 的取值范围是(－∞，2]．22．(本小题满分12分)某蔬菜基地种植甲、乙两种无公害蔬菜．生产一吨甲种蔬菜需 用电力9千瓦时，耗肥4吨，3个工时；生产一吨乙种蔬菜需用电力5千瓦时，耗肥 5吨，10个工时，现该基地仅有电力360千瓦时，肥200吨，工时300个．已知生产 一吨甲种蔬菜获利700元，生产一吨乙种蔬菜获利1 200元，在上述电力、肥、工时 的限制下，问如何安排甲、乙两种蔬菜种植，才能使利润最大？最大利润是多少？解：设种植甲种蔬菜x 吨，乙种蔬菜y 吨，利润为z 元，根据题意可得⎩⎪⎨⎪⎧9x ＋5y ≤360，4x ＋5y ≤200，3x ＋10y ≤300，x ≥0，y ≥0，目标函数为：z ＝700x ＋1 200y ，作出二元一次不等式组表示的平面区域，即可行域，如图，作直线：700x ＋1 200y ＝0， 即7x ＋12y ＝0，平移直线，当直线过A 点时目标函数取最大值．解方程组⎩⎪⎨⎪⎧4x ＋5y ＝200，3x ＋10y ＝300，得x ＝20，y ＝24. 所以点A 的坐标为(20，24)．所以z max ＝700×20＋1 200×24＝42 800.即种植甲种蔬菜20吨，乙种蔬菜24吨，才能使利润最大，最大利润为42 800元．。

山西省晋中市和诚高中2018-2019学年高二数学上学期周练8编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（山西省晋中市和诚高中2018-2019学年高二数学上学期周练8）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为山西省晋中市和诚高中2018-2019学年高二数学上学期周练8的全部内容。

山西省晋中市和诚高中2018—2019学年高二数学上学期周练8(时间：60分钟，满分：100分 命题人：)一、选择题：本题共6小题，每小题9分，在每小题给出的四个选项中，只有一项是符合题目要求的．1． 已知m ，n 为异面直线，m ⊥平面α，n ⊥平面β.直线l 满足l ⊥m ，l ⊥n ,l α，l β,则( )．A ．α∥β且l ∥αB ．α⊥β且l ⊥βC ．α与β相交，且交线垂直于lD ．α与β相交，且交线平行于l2．已知正四棱柱ABCD －A 1B 1C 1D 1中，AB ＝2，122CC =，E 为CC 1的中点，则直线AC 1与平面BED 的距离为（ )A ．2B ．3C ．2D ．13．过球的一条半径的中点,作垂直于该半径的平面，则所得截面的面积与球的表面积的比为A.163 B.169C 。

83 D 。

3294．如图,平面α⊥平面β,A ∈α,B ∈β，AB 与两平面α,β所成的角分别为4π和6π.过A ，B 分别作两平面交线的垂线,垂足为A ′,B ′,则AB ∶A ′B ′等于A.2∶1B 。

3∶1C 。

3∶2D 。

4∶35．设三棱柱ABC-A 1B 1C 1的体积为V ，P 、Q 分别是侧棱AA 1、CC 1上的点，且PA=QC 1,则四棱锥B-APQC 的体积为（ ）A ．16V B ．14VC ．13VD ．12V6．正方体1111ABCD A B C D -中，P 、Q 、R 分别是AB 、AD 、11B C 的中点．那么，正方体的过P 、Q 、R 的截面图形是（ )(A) 三角形（B ） 四边形 （C) 五边形 （D ） 六边形二、填空题：本题共2小题，每小题9分．7．已知矩形ABCD的顶点都在半径为4的球O的球面上，且AB＝6，BC＝O.ABCD 的体积为__________．8．α，β是两个平面，m，n是两条直线，有下列四个命题:①如果m⊥n，m⊥α，n∥β,那么α⊥β。

山西省晋中市和诚高中2018-2019学年高二数学周练试题（5.18）文（无答案）一选择题（本题共8小题，每小题7分，共56分．）1．(2018·广东汕头一模)函数f (x )＝11－x＋lg (1＋x )的定义域为 ( ) A ．(－∞，－1) B ．(1，＋∞)C ．(－1，1)∪(1，＋∞) D．(－∞，＋∞)2．(2018·河北保定一模)若f (x )是定义在R 上的函数，则“f (0)＝0”是“函数f (x )为奇函数”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．若f (x )是幂函数，且满足f f ＝3，则f ⎝ ⎛⎭⎪⎫12＝( ) A ．3 B ．－3 C.13 D ．－134．(2018·大连测试)下列函数中，与函数y ＝－3|x |的奇偶性相同，且在(－∞，0)上单调性也相同的是( )A ．y ＝－1xB ．y ＝log 2|x |C ．y ＝1－x 2D ．y ＝x 3－1 5．已知集合M ＝{－1，1，2，4}，N ＝{1，2，4}，给出下列四个对应关系：①y ＝x 2，②y ＝x ＋1，③y ＝x －1，④y ＝|x |，其中能构成从M 到N 的函数的是( )A ．①B ．②C ．③D ．④6．(2018·山东济宁一中月考)某产品的总成本y (万元)与产量x (台)之间的函数关系式是y ＝3000＋20x －0.1x 2(0<x <240，x ∈N *)．若每台产品的售价为25万元，则生产者不亏本(销售收入不少于总成本)时的最低产量是( )A ．100台B ．120台C ．150台D ．180台7．已知定义在区间[0，2]上的函数y ＝f (x )的图象如图所示，则y ＝－f (2－x )的图象为( )8．(2018·安庆二模)定义在R 上的函数f (x )满足f (－x )＝－f (x )，f (x －2)＝f (x ＋2)且x ∈(－1，0)时，f (x )＝2x ＋15，则f (log 220)＝( ) A ．1 B.45 C ．－1 D ．－45二、填空题（本题共3小题，每小题8分，共24分）9．(2018·济南模拟)已知函数y ＝5a x －2＋3恒过点A (m ，n )，则log m n ＝________.10．若函数y ＝f (x )的定义域为[0，2]，则函数g (x )＝f (x ＋1)－f (x －1)的定义域为________．11．(2018·广东广州测试)已知函数f (x )＝ln x ＋1x 2＋3在(1，4)处的切线与g (x )＝ax 2－2x 的图象相切，则a ＝________.三、解答题（共2小题，每题10分，共20分）12．函数f (x )＝1a －1x(a >0，x >0)． (1)判断函数f (x )在(0，＋∞)上的单调性；(2)若函数f (x )在⎣⎢⎡⎦⎥⎤12，2上的值域是⎣⎢⎡⎦⎥⎤12，m ，求a ，m 的值．18．已知函数f (x )是(－∞，＋∞)上的奇函数，且f (x )的图象关于x ＝1对称，当x ∈[0，1]时，f (x )＝2x －1.(1)当x ∈[1，2]时，求f (x )的解析式；(2)计算f (0)＋f (1)＋f (2)＋…＋f (2018)的值．。

和诚中学2018-2019学年高二数学周练试题一、选择题：本题共6小题，每小题9分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．若x ≠－2且y ≠1，则M ＝x 2＋y 2＋4x －2y 的值与－5的大小关系是( )A ．M >－5B ．M <－5C ．M ≥－5D ．M ≤－52．设x ，y >0，且x ＋2y ＝3，则1x ＋1y的最小值为( ) A ．2B.32 C ．1＋223 D ．3＋2 23．若不等式ax 2＋bx ＋c >0的解集是(－4,1)，则不等式b (x 2－1)＋a (x ＋3)＋c >0 的解集为 ( ) A.⎝ ⎛⎭⎪⎫－43，1 B ．(－∞，1)∪⎝ ⎛⎭⎪⎫43，＋∞ C ．(－1,4) D ．(－∞，－2)∪(1，＋∞)4．已知实数x ，y 满足x 2＋y 2＝1，则(1－xy )(1＋xy )有( )A ．最小值12和最大值1B ．最小值34和最大值1C ．最小值12和最大值34D ．最小值15．【2015高考湖北，文6】函数256()lg 3x x f x x -+=+-的定义域为（ ）A ．(2,3)B ．(2,4]C ．(2,3)(3,4] D ．(1,3)(3,6]-6．设10()2,0x x f x x ⎧≥⎪=⎨<⎪⎩，则((2))f f -=（ ） A ．1- B ．14 C ．12 D ．32二、填空题：本题共2小题，每小题9分．7．若a ＝ln 22，b ＝ln 33，c ＝ln 55，则a ，b ， c 的大小关系是________(由小到大排列)．8．函数125x y x -=+的值域是___________三、解答题：9．(本小题满分14分) 求函数12++=x x y 的值域.10．(本小题14分) 求函数1212xx y -=+的值域。

和诚中学高二数学知识清单定时训练不等式、函数答案 2018、8、26(时间：60分钟，满分：100分)一、选择题：本题共6小题，每小题9分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．若x ≠－2且y ≠1，则M ＝x 2＋y 2＋4x －2y 的值与－5的大小关系是( )A ．M >－5B ．M <－5C ．M ≥－5D ．M ≤－5 解析：M －(－5)＝x 2＋y 2＋4x －2y ＋5＝(x ＋2)2＋(y －1)2，∵x ≠－2，y ≠1，∴(x ＋2)2>0，(y －1)2>0，因此(x ＋2)2＋(y －1)2>0.故M >－5. 答案：A2．设x ，y >0，且x ＋2y ＝3，则1x ＋1y的最小值为( ) A ．2 B.32 C ．1＋223 D ．3＋2 2解析：1x ＋1y ＝13(3x ＋3y )＝13(x ＋2y x ＋x ＋2y y )＝13(2y x ＋x y ＋3)≥13(22＋3)＝232＋1， 当且仅当2y x ＝x y ，即x ＝32－3，y ＝3－322时取等号．答案：C 3．若不等式ax 2＋bx ＋c >0的解集是(－4,1)，则不等式b (x 2－1)＋a (x ＋3)＋c >0 的解集为 ( ) A.⎝ ⎛⎭⎪⎫－43，1 B ．(－∞，1)∪⎝ ⎛⎭⎪⎫43，＋∞ C ．(－1,4) D ．(－∞，－2)∪(1，＋∞)答案：A4．已知实数x ，y 满足x 2＋y 2＝1，则(1－xy )(1＋xy )有( )A ．最小值12和最大值1B ．最小值34和最大值1C ．最小值12和最大值34D ．最小值1 解析：选B. 因为x 2y 2≤⎝ ⎛⎭⎪⎫x 2＋y 222＝14，当且仅当x 2＝y 2＝12时，等号成立，所以 (1－xy )(1＋xy )＝1－x 2y 2≥34.因为x 2y 2≥0，所以34≤1－x 2y 2≤1.5．【2015高考湖北，文6】函数256()lg 3x x f x x -+=+-的定义域为（ ） A ．(2,3)B ．(2,4]C ．(2,3)(3,4]D ．(1,3)(3,6]-【解析】由函数()y f x =的表达式可知，函数()f x 的定义域应满足条件：2564||0,03x x x x -+-≥>-，解之得22,2,3x x x -≤≤>≠，即函数()f x 的定义域为(2,3)(3,4]，故应选C .6．设10()2,0x x f x x ⎧≥⎪=⎨<⎪⎩，则((2))f f -=（ ）A ．1-B ．14 C ．12 D ．32【答案】C 【解析】因为21(2)24f --==，所以111((2))()11422f f f -===-=， 二、填空题：本题共2小题，每小题9分．7．若a ＝ln 22，b ＝ln 33，c ＝ln 55，则a ，b ，c 的大小关系是________(由小到大排列)． 解析：因为a －b ＝3ln 2－2ln 36＝ln 8－ln 96<0，所以a <b . 因为a －c ＝5ln 2－2ln 510＝ln 32－ln 2510>0，所以a >c . 所以c <a <b . 答案：c <a <b8．函数125x y x -=+的值域是___________ 解：∵177(25)112222525225x x y x x x -++-===-++++， ∵72025x ≠+，∴12y ≠-， ∴函数125x y x -=+的值域为1{|}2y y ≠-。

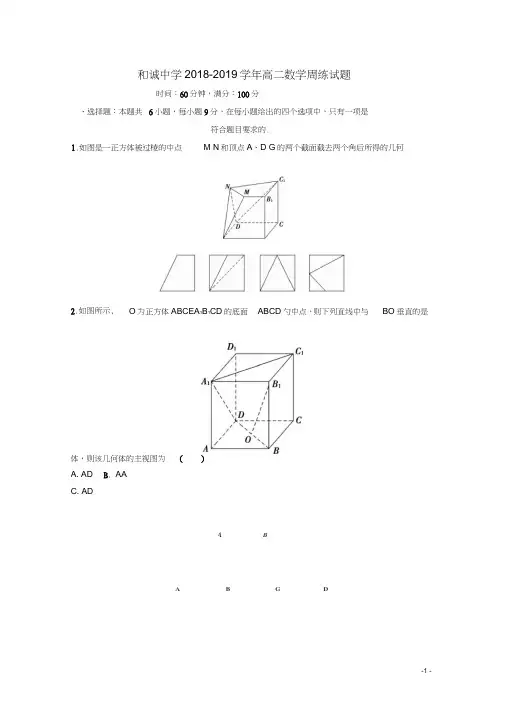
和诚中学2018-2019学年高二数学周练试题时间：60分钟，满分：100分6小题，每小题9分，在每小题给出的四个选项中，只有一项是符合题目要求的.M N 和顶点A 、D G 的两个截面截去两个角后所得的几何体，则该几何体的主视图为 （ ）B . AA、选择题：本题共 1.如图是一正方体被过棱的中点2.如图所示,O 为正方体ABCEA 1B 1CD 的底面 ABCD 勺中点，则下列直线中与 BO 垂直的是A. ADC. ADA BA B G DD. AQ3•在如图所示的四个正方体中，能得出ABL CD的是（）则（）A. a // 3 且 I 〃aB. a 丄3且I 丄3C. a 与3相交，且交线垂直于ID. a 与3相交，且交线平行于l5.将图1中的等腰直角三角形 ABC 沿斜边BC 的中线折起得到空间四面体 ABCD 如图 在空间四面体 ABCDK AD 与 BC 的位置关系是（）4.已知m n 为异面直线, mL 平面 a , n 丄平面 3 .直线l 满足I 丄m l 丄n , l ? a ,l ? 3，2），则A.相交且垂直B. 相交但不垂直C.异面且垂直D.异面但不垂直6 .已知三棱锥S - ABO 的所有顶点都在球 0的球面上，△ ABC 是边长为1的正三角形,SC 为球B0的直径，且SC= 2，则此棱锥的体积为（）A. C.二、填空题：本题共 2小题，每小题9分.7.如图，在正方体 ABCDABCD 中，点P 是上底面 ABQD 内一动点，则三棱锥 PABC 勺正视 图与侧视图的面积的比值为 _______________ .& 如图，矩形 O A B' C'是水平放置的一个平面图形的直观图，其中O A'= 6 ,O C = 2,则原图形 OABC 勺面积为 ____________ .三、解答题：9.（本小题满分14分）10 •如图，四棱锥 P-ABC ［中，底面ABC ［是平行四边形,若Q 是PC 的中点，求证：PA//平面BDQ 10.（本小题14分）在如图所示的正方体“V 中，■分别棱是。

(时间：60分钟，满分：100分命题人：)BED 的距离为(4.如图,平面a 丄平面卩，A € a , B€卩,AB 与两平面a ,卩所成的角分别为一和一•过A B 4 6 分别作两平面交线的垂线，垂足为A , B',则AB ： A B'等于A.2 : 1B.3 : 1C.3 : 2D.4 : 35.设三棱柱 ABC-A 1B 1C 1的体积为V, P 、Q 分别是侧棱 AA 、CC 上的点，且PA=QC 则四棱锥B- APQC 勺体积为()A . 1V6B. *4C. \31 D. -V 26.正方体 ABCD AB1GD 1 中，P 、Q 、 过P 、Q 、R 的截面图形是()R 分另【J 是 AB 、AD 、 BG 的中点.那么，正方体的(A)三角形 (B)四边形(C)五边形(D)六边形、填空题：本题共 2小题，每小题9 分.、选择题：本题共 6小题，每小题 9分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1.已知m n 为异面直线, I 芒a ，丨严|卩，则( mL 平面 n 丄平面卩.直线I 满足I 丄m I 丄n,A . a // 卩且 I 〃a a 丄卩且I 丄卩C. a 与卩 相交，且交线垂直于 a 与卩相交，且交线平行于I2.已知正四棱柱 ABC D ABCD 中, AB= 2, CC i2 2 , E 为CC 的中点，则直线AC 与平面A. 2 B. 、3 C .23.过球的一条半径的中点,作垂直于该半,则所得截面的面积与球的表面积的比为A. 16B. C . 3D.169 327.已知矩形ABCD勺顶点都在半径为4的球0的球面上，且AB= 6, BC= Z 3 ,则棱锥OABCD 的体积为_________________ .& a,卩是两个平面，m n是两条直线，有下列四个命题：①如果mb n, ml a, n//卩，那么a丄卩.②如果mb a , n // a,那么m b n.③如果a / 3 , m a ,那么m//卩.④如果m// n, a // 3，那么m与a所成的角和n与卩所成的角相等其中正确的命题有.（填写所有正确命题的编号）三、解答题：9. （本小题满分14分）△ ABC的内角A, B, C的对边分别为a, b, c,已知cos（A—C）+ cos B =1, a= 2c,如图，四棱锥P— ABCD^，底面ABC西菱形，PAL底面ABCD AC 2迈,PA=2, E是PC上的一点，PE= 2EC（1）证明：PC L平面BED⑵设二面角A—PB- C为90°,求PD与平面PBC所成角的大小.10. （本题14分）（本小题满分12分）如图，四棱锥P ABCD中，底面ABCD为矩形，PD底面ABCD , AD PD , E、F别为CD、PB的中点.(I )求证：EF 平面PAB ；(求出所求角的一个三角函数(n )设AB , '2BC，求AC与平面AEF所成的角的大小.值即可)和诚中学2018-2019学年高二数学周练试题（时间：60分钟，满分：100分命题人：）一、选择题：本题共6小题，每小题9分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知m n为异面直线，ml平面a , n丄平面卩.直线I满足I丄m l丄n,1 L—a,I 已，贝叫).A. a// 卩且1//aB. a丄卩且1丄3C. a与卩相交, 且交线垂直于D. a与卩相交, 且交线平行于【答案】：D【解析】因为ml a , I丄m |Q匚a ,所以I //a.同理可得I //卩.又因为m n为异面直线，所以a与卩相交，且I平行于它们的交线.故选 D.2.已知正四棱柱ABC D ABGD中，AB= 2, CG 2丘,E为CC的中点，则直线BED的距离为（）A. 2 B .「3 C .D . 1【答案】D【解析】连结M交肋于点©连结陶又cq二2血_,则良作于点已交加于点庇由磁为&4CC1的中位综知，C^yOE? M为CH的中点.由BD1AC,卫口丄月迅知,，迟D丄面EQG.\CM1BD.面氐也二为直线.4CjiJ平面BDE的距离•AC与平面A 8又A A©为等腰直角三角形，•••CH=2. ••• HM1.3.过球的一条半径的中点 ,作垂直于该半径的平面，则所得截面的面积与球的表面积的比为5.设三棱柱 ABC- A 1B 1C 1的体积为V,P 、Q 分别是侧棱AA 、CG 上的点，且 PA=QC 则四棱锥【解析】：设球半径为E 截面半轻丸rjv f 侄在RTM 阳中卫二亍如〜亍妙 j.j r I 1 在中，——= -AA^-AB. AB 2 2二任RTU4®中显迟一45一A. 216B.9 16C. 38 D. 232^A -4.如图，平面a 丄平面 卩，A € a , B€卩,AB 与两平面 a ,卩所成的角分别为—和一•过A B4 6分别作两平面交线的垂线，垂足为A B'等于A.2 : 1B.3 : 1D.4 : 3【答案】:AC.3 : 2勺体积为（A. 1V B 1V C-V D. 1V6 4 3 2 【答案】C【解析】连接BA-, BC-，在侧面平行四边形AAC-C中，••• PA QC-,四边形APQC勺面积3=四边形PQA1C1的面积S2，记B到面AAC1C的距离为h, --V B APQC-Sh ,3V B PQA I C1…V B APQC V B PQA I C1 ,'V B A1B1C11匚V ,…V B APQC3V B PQA1C1V V32V,.••3VV B APQC二36•正方体ABCD AB-C-D-中，P、Q、R分别是AB、AD、BC-的中点•那么，正方体的过P、Q、R的截面图形是（)（A）三角形（四边形(C)五边形(D)六边形【答案】D【解析】如虱作RG // PQ交CiDi于G连结QP与CB交于屹连结皿交BB1于瓦连结PE、瓯豹截面的咅吩?囑.同理琏结PQ交B于皿连结盹交D6于F,连結QF、面PQERE为六边形一勺体积二、填空题：本题共2小题，每小题9分.为（7.已知矩形ABCD勺顶点都在半径为4的球0的球面上，且AB= 6, BC= ^3，则棱锥OABCD 的体积为. 【答案】8.3【解析】矩形的对角红国长为：胪+口奇=4心」所以球到矩形的K瞎为；以豳―, 所以棱锥O-ABCD旳体积为:ix6x2^>2=8^ .故答秦为:8J3& a,卩是两个平面，m n是两条直线，有下列四个命题：①如果mln, ml a, n//卩，那么a丄卩.②如果ml a , n // a,那么mL n.③如果a / 3 , m a ,那么m卩.④如果m// n, a // 3，那么m与a所成的角和n与卩所成的角相等•其中正确的命题有.（填写所有正确命题的编号）【答案】②③④【解析】试题分析：对于①，膈丄禺™I丄隅则比”的位置关系无袪确忌故错误』对于②厨科忖所以■过直钱川作平面$与平面直相交于宜线6则川匕因为朋丄区所以jn丄匚所以加丄忙故②正确■对于③，由两个平面平行的性质可知正确・对于④，由线面所成角的走哭和等角走理可去嗔正晦故正确的命题有②③④.三、解答题：9. （本小题满分14分）△ ABC的内角A, B, C的对边分别为a, b, c,已知cos（A—C）+ cos B=1, a= 2c,如图，四棱锥P— ABCD^，底面ABCD为菱形，PAL底面ABCD AC 2^2 , PA=2, E是PC上的一点，PE= 2EC⑴证明：P®平面BED⑵设二面角A—PB- C为90°,求PD与平面PBC所成角的大小. 【解析】解法一：⑴ 证明：因为底面ABCD^菱形，所以BDL AC又PAL底面ABCD所以PC L BD设A8 BD=F,连结EF因为AC 2 2 , PA=2, PE=2EC故PC 2 .3 , EC , FC 、2 ,3从而匹,6,也.6,FC ECPC AC因为匚一——，/ FCE=Z PCAFC EC所以△ FC0A PCA / FE（=Z PAC90° ,由此知PC X EFPC与平面BE»两条相交直线BD EF都垂直，所以PC X平面BED⑺在平面期5内过点丄作丄隔G为垂足.因为二面^A-PB-C为帥％所以平面她丄平面？又平面胃婕门平面PBC-PB,故』G丄平面PEG AG±£C.砂与平面PAB内两条相5直线開恥都垂直，故6C丄平面PAB,于是BC1AB,所次底面ABCD为正方形,AD=2J PD =』Pf+ 3 =辺.设刀到平面PBC的距离为也因为ADI/BC,且QX平面PBC t ECC平面PBC f故平面PBC,乩Q两点到平面RBC的亜离相等，即J IG—.谡加与平面PM所成的角为酝则Sifii2t= —=-.PD 2所以PD与平面期C所成的角为30°.10. （本小题14分）（本小题满分12分）如图，四棱锥P ABCD中，底面ABCD为矩形，PD 底面ABCD，AD PD，E、F 分别为CD、PB的中点.（I ）求证：EF 平面PAB ;（II）设AB 2BC，求AC与平面AEF所成的角的大小.（求出所求角的一个三角函数值即可）-11 -【解析】方法一：⑴证明：连结EPTPD丄底面ABCD』DE在平面ABCD内/.PD1DE；又CE=ED, PD-AD-BC /.RlABCE^RriPDE.\PE=BETF为PB的中点二EF 丄PBTDA 丄AB由三垂线定理得PA丄AB二在R IA PAB中PF=AF,又PE=BE=EA/.AEFP^AEFA•\EF1FA••• PB FA为平面PAB内的相交直线••• EF丄平面PAB-12 -QI]解：不妨设EC=1, f?]PI>AD=l J AB-血」AC= ^3 AAPAB^等股直角三角砒且PBT, F为苴斜边中駄BIT目AF丄PE TPB与平面AEF内两条相交直线EF. AF 都垂直J.PB丄平面AEF连结EE交AC于②作GH/；BP交EF干也则GH"平面AEFZGAH为AC与平面AEF所成的角由AEGC<^ABGA可知EG=1GIX，EG=-EB, AG=-AC=^^'■AC与平面AEF所成的角为afc^in-ii --3 -。