重庆市南开中学高考数学模拟试卷(文科)

2006—2007学年度重庆南开中学高三年级第一次模拟考试数学试题（文）第Ⅰ卷（选择题，共50分）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个备选项中，只有一项是符合题目要求的.1．已知向量)3,(),2,4(x ==向量，且∥，则x = （ ）A ．9B ．6C ．5D ．12．已知集合},22|{2R x x x y y M ∈++==，集合})4(log |{2R y x y x N ∈-==，则（ ）A ．N M ⊆B ．M N ⊆C ．φ=N MD ．N N M =3．求以抛物线y 2 = 8x 的焦点为焦点，且离心率为21的椭圆的标准方程为 （ ）A ．1121622=+y x B ．1161222=+y x C ．141622=+y x D ．116422=+y x 4．已知等差数列{a n }满足：30,8531==+S a a ，若等比数列{b n }满足,,4311a b a b ==则 5b 为 （ ）A ．16B ．32C ．64D ．27 5．x x y 52sin 52cos3+=的图象相邻两对称轴之间的距离为 （ ）A ．52πB ．45πC ．25πD ．π56．抛物线y = x 2 + bx + c 在点（1，2）处的切线与其平行直线bx + y + c = 0间的距离是（ ）A ．42 B ．22 C ．223 D ．27．在△OAB （O 为原点）中，)sin 5,cos 5(),sin 2,cos 2(ββαα==，若5-=⋅，则S △AOB 的值为 （ ）A ．3B ．23 C ．35D ．235 8．若函数),()10()(+∞-∞≠>-=-在且a a a ka x f xx是既是奇函数，又是增函数，则 )(l o g )(k x x g a +=的图像是（ ）1 2 2 3 4 3 4 7 7 4 5 11 14 11 59．已知△ABC 的三个角分别为A ，B ，C ，满足4:3:2sin :sin :sin =C B A ，则A sin 的值为（ ）A ．815B ．87 C ．1611 D ．1615 10．设双曲线M ：1222=-y ax ，过点C （0，1）且斜率为1的直线，交双曲线的两渐近线于A ，B 两点，若2|AC | = |CB |，则双曲线的离心度为 （ ）A ．10B ．5C ．310 D ．2511．已知+∈R b a ,，且满足ab b a S b a 2,222++==+设的最大值是 （ ）A ．27 B ．4 C ．29 D ．512．函数))((R x x f y ∈=满足：对一切[)1,0;)(7)1(,0)(,2∈-=+>∈x x f x f x f R x 当 时，,)125(5)250(2)(⎪⎩⎪⎨⎧<≤--<≤+=x x x x f 则=-)32007(f（ ）A ．3322-B ．32-C ．32+D ．2第Ⅱ卷（非选择题，共90分）二、填空题：本大题共4小题，每小题4分，共16分.把答案填写在答题卡相应位置上. 13．以坐标原点为圆心且与直线3x －4y + 5 = 0相切的圆方程为14．已知22)1()1(,2420-++⎪⎩⎪⎨⎧-≥≤+≥-y x x y x y x 则的最小值为15．已知函数)(x f y =的反函数为)10)(1(log 1≠>-+=a a x y a 且，则函数)2(+=x f y 必过定点 16．如右图，它满足①第n 行首尾两数均为n②表中的递推关系如杨辉三角，则第n 行(n ≥2)的第二个数是三、解答题：本大题共6小题，共74分.解答应写出文字说明、证明过程或演算步骤.17．（13分）已知向量x f x x x ⋅=-++=-=)(),3,2cos 2sin 1(),1,tan 1(记 （1）求f (x )的周期； （2）若)42()2()(παα+-=f f a g ，则求)(a g 的最小值.18．（13分）解不等式)00(2log |2log 3|2≠>+<-a a x x a a 且19．（12分）已知偶函数f (x )，对任意R x x ∈21,，恒有12)()()(212121+++=+x x x f x f x x f ，求 （1）f (0)的值； （2）f (x )的表达式； （3）令)10()()(2)]([2≠>=-a a a x F x f x f 且，求),0()(+∞在x F 上的最值.20．（12分）某商场因管理不善及场内设施陈旧，致使年底结算亏损，决定从今年开始投入资金进行整，计划第一个月投入80万元，以后每月投入将比上月减少51。

南开中学高三数学模拟试卷（文科）参考答案一、选择题:（共8小题,每小题5分,共40分）题号 1 2 3 4 5 67 8答案D C D C C A B B二、填空题：（本大题共6小题，每小题5分，共30分）题号9 10 11 12 13 14答案611兀+471?兀292[9,+ 8)三、解答题：（本大题共6小题，共80分）. （15）（本小题满分13分）解:(I) /(兀)=V^sin2兀一cos2x = 2sin(2x --------------- )67T TT S(II ) ill 2k7T + — < 2x ------- < lk7l + —7l伙W z),2 6 271 5得k/r——< x < k7r + — 7r(k e z)3 6n5/r•••单调递减区间为[尿+ =、k兀七—](k ez). ................................... 8分3 6(III)因为-~^x^~，贝ij-兰W2x —兰 W兰，6 4 2 6 3当2x-- = -,即x =-时，/(兀)取得最大值为馆；6 3 4当2%--=--,即兀―仝时,/⑴取得最小值为_2 •.................................. 13分6 2 3（16）（木小题满分13分）解：（I ）由条形图得第七组频率为1-（0.04x2 + 0.08x2 + 0.2x2 + 0.3） = 0.06,0.06x50 = 3 1 分・••第七组的人数为3人组别 1 2 3 4 5 6 7 8 样本中人数 2 4 10 10 15 4 3 2 (II )由条形图得前五组频率为(0.008+0.016+0.04+0.04+0.06)x5=0.82,.......................................................... 4分=71后三组频率为1一0.82=0.18 ................................................... 5分估计这所学校高三年级身高在180cm以上（含180cm）的人数800x0.18=144 （人）. 7分（皿）第二组四人记为a、b、c、d,其中a为男生,b、c、d为女生,第七组三人记为1、2、3,其屮1、2为男生，3为女生，基木事件列表如下：abed1\a \b \c \d22a 2b 2c 2d3 3 a 3b 3c 3d所以基本事件有12个...................................... 10分恰为一男一女的事件有",lc, Id, 2b, 2c, 2d, 3a；共7个..... 12分7因此实验小组中，恰为一男一女的概率是一................... 13分12（17）（本小题满分13分）（I）证明：因为菱形ABCD,所以3D丄AC,又因为平而ACEF丄平面ABCD ,EC丄AC，平面ACEF Q平面ABCD = AC故EC丄平面ABCDEC 丄BD所以BD丄平面ACEF-------------- 5分BDu平面BDE,所以平面BDE丄平面ACEF ；---------------- 6分（II）连结EO, EO//AM ,ZBEO为界面直线BE与AM所成的角或补角，由（I）知，AEOB = 90°,在直角三角形EOB 中，EO = AM=4i,BO = &所以界而直线BE与4M所成的角的正切值心. -------------- 10分2（III）由已知易得BF = FD,BE = ED，所以EO丄BD, FO丄BD,ZEOF为二面角E-BD-F的平而角13分所以二面角E-BD-F为90°.（18）（本小题满分13分）解：（I ）点A （0,2）代入圆C 方程， 得.（2-加尸=9*.* m < 2 ,・*. m = -1 .......... 1 分圆 C ：异+（〉，+ 1）2 =9,圆心（0,-1）・ 设直线的斜率为心，P （3,8）当K 不存在时，PF I ：x = 3,显然不合题意舍去. 当人存在时，PF“ y -8 = k l （x-3）f 即 k }x- y-3« + 8 = 0 .・••号f .解得k }=- ..................................................... 3分W + 1 3 直线 PF ]: 4x-3.y + 12 = 0总线PF 】与x 轴的交点横他标为一3,・・・c=3. F| (—3, 0), F 2(3, 0)............................... 4 分2« = P4F|| + |AF 2|= VB + V13 =2>/13 , a =屈,«2=13, //=4.椭圆E 的方程为：—+ ^- = 1............................. 6分13 4(II)由|丽冃丽|知点A 在线段MN 的垂直平分线上， y = kx-2由]兀2 2 消去y 得(4 + 13/)兀2 一52也=0 (*) —+ —= 1 〔13 4由Id 得方程（*）的A = （52^）2 >0,即方程（*）有两个不相等的实数根…8分 设N （兀2小），线段MN 的中点卩（兀0，儿），26k 4 + 13 衣52k 4 + 13f•宀0,直线仲的斜率为宁=桔由AP 丄MN,得 土竺 xk = _l,解得：k = ±—f……12分13R13・・・存在直线/满足题意，方程为：V5x-V13y-2ji3 =0«KV5x + V13y + 2Vi3 =0 -------------------------------- 13 分 (19) (本小题满分14分)解：(I)方法一：由S 曲=3S “得：数列｛S”｝是等比数列，公比为3,首项为1…2分.•.S” =1・3心=3心 ......... 3分当 n>2 时,a n = S n - S n _{ = 3 心 一 3W '2 = 2 • 3n '2................... 4 分fl (n = 1)•5=\.................. 5 分[2・3心(n > 2)方法一：•** S“+] = 3S“，「. S n = 3S”](M ' 2) 以上两式相减得：Q “+]=3% (n > 2),.................. 2分在 S n+[ = 3S n 中,取 〃 =1 得：a {+a 2= 3a }即 a 2 = 2a } = 2 ,.................. 3 分.・.｛%｝为第二项起的等比数列，公比为3 .................. 4分fl (n = l)/. ci = \.................. 5 分26k 24 + 13p—8 4 + 13/即卩為為)10分2・3宀(n > 2)由(I )知：⑺”｝为第二项起的等比数列，公比为3, s=2t0? + 1)(72 + 2) n(n +1)(/? + 1)(1-/?)① 若r 〉0,则 b n+i -b n <0 HP b n+i < b n (n > 2) .・.数列｛仇｝是从第二项起的递减数列ifij b 、= —, b 2 = — t b 2 >b } 3•••(—b2「 ..................................... 9 分•・•对任意 n e TV * ,都冇 A>/7(Z7 + 1)a“t②若/v0,则b n+} - b n > 0即b n+x > b n (n > 2)・•・数列{仇}是从第二项起的递增数列・・・11 分Ifij/, =-<0,当n >2 时，化=W o't n2r-3w_2b n e (-oo, 0).................. 12 分•• •对任意n e TV * ,都有2>/7(Z7 + 1), > 0 ...................13 分%3综合上面：若/>0,则A>-；若/<0,则A>0o .............................................. 14分t(20) (木小题满分14分)解：(I )当 a = -3ll 寸，/(x) = —x 3 -兀2-3X + 3,所以 广(兀)=x 2 -2x-3 = (x-3)(x + l).令/'(兀) = 0,得 比=_1,兀2=3.当xv-l 时，广(x)〉0,则/(x)在(-oo,-l) ±单调递增； 当一1 v 尢<3时,/'(X )<0 ,则f (x)在(-1,3)上单调递减;・••当心2时,廿2心巴汗畔 “ “ It • 3n_2b n +l ~b n 2r3n-I『•3"10分当x>3时，广(兀)>0 , /(兀)在(3,+00)上单调递增. 所以，当x = -\时，/&)取得极大值为/(-1)=-1-1 + 3 + 3 =—； 当*3时,/(x)取得极小值为/*(3)=丄x27-9-9 + 3 =-6.(II )广(兀)=/-2x + d , △ = 4-4° = 4(1-°) •⑴若dhl,则在心上恒有广(兀)》0,于⑴在R 上单调递增，且值域为R.函 数/(x)的图象少兀轴有且只有一个交点.(2)若a<l,则△>(), /'(%) = 0有两个不等的实根，不妨设为x l9x 2 (x t <x 2).当x 变化吋，广(x)J(x)的取值情况如下表：X(-°°眄)(西，兀2)厶（兀2，+°°）广(刃+—+极大值极小值由兀]2—2 兀]+a = 0 ,得兀]+兀2=2, x l x 2 = a , JL x ）2= 2x, - <7.f （xj = £ 兀1‘ _ X |2 + ax \ 一 a = * £ （2旺 _ d ） — 壬2 + ax }-同理/(x 2) =|［(n-l)x 2-t/_ •函数子(x)的图象与x 轴有且只有一个交点，等价于/(x 2)< f (x,) <0或0</(X2)</(X l)» 即 /(壬)丁(兀2)>0 •又/(西)丁(兀2)=害［(。

南开中学高三数学模拟试卷(文科)说明：1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分，满分150分, 考试时间120分钟.2.请将选择题的答案填涂在答题卡上，填空题、解答题答在答题纸上. 参考公式：・如果事件久〃互斥，那么P(AU〃) = P(4)+P(B) •如果事件右B相互独立,那么関锥侧面积公式S= Tirl其屮厂为底血関半径，/为母线长第I卷(选择题共40分)一.选择题：(本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.頊将等家填徐在登題卡上!)-3-1(1)i是虚数单位，复数一「=l + 2i-l-7i 1(A)l-3i (B) (C) -- + i (D) -1 + i5 5(2)已知集合S = [x\x2<2x]t集合T^Lllogj 则S^T =2(A) (0,1) (B) (1,2) (C) (0,1] (D) (0,2](3)已知a,b,c分别是\ABC的三个内角A,B,C所对的边，若a = 2, b = g , B = 60"则c -(A) 5 (B) 77 (C) 2 (D) 1(4)已知直线厶：2x +紗-7 = 0,若过定点(0,2)与已知直线厶垂直的直线厶与x轴、)，轴正半轴所围成的三角形而积为6,则实数k值为3 2(A) -- (B)-2 32 4(C) -- (D)--（5）阅读如图给出的程序框图，运行相应的程序, 输出的结果S为（A） 1008 （B） 1007（C） -1007 （D） -3022（第5颗）（6）通过随机询问110名性别不同的人学牛是否爱好某项运动，得到如下的列联农:男女总计爱好402060不爱好203050总计6050110〃(加一加)2 争 2 - 110X(40X30-20X20)2 〜(a+b)(c+d)(a+c)(b+d)‘心寸'K =6() X 5() X 6() X 5() 〜附表:P（K?汶）0.0500.0100.001k 3.841 6.63510.828参照附表，得到的正确结论是（）（A）有99%以上的把握认为“爱好该项运动与性别有关”（B）有99%以上的把握认为“爱好该项运动与性别无关”（C）在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别育关”（0）在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”（第7顾）(C)-I3(D)--2（8）己知函数/（x）是定义在［-1,1］上的奇函数，且/（1） = 1 ,当以引-1,1］, a+bHO时有/⑷+ /少）>0・若f（x）tn2- a+ b则实数〃7的取值范围是-2am +1 (m e R,/n h 0)对所有XG[-1 ,1] , ae[-\, 1J 恒成立,(A) (-oo,-2]U(2, + oo)(B) (一oc,-2]U[2, + oo)(C) (YO,—2]U(0,+8)(D) (YO,0)U[2,+ OO)第II卷（非选择题共110分）二.填空题：（本大题共6小题，每小题5分，共30分.请将答案填在答题纸上!）y >0（9）设变量兀,），满足约束条件< % +1 > 0 ,则z = 2x+ y的最大值为________x+y-3<Q分别为A"两点，以4B为直径的圆恰好过双曲线右焦点场，则双曲线的离心率为____________（11）将一个圆柱体挖掉一个圆锥后，所得几何体的（12）如图，已知是圆的-条直径，点C是圆上-点满足"=»,43为圆的切线，C为切点，过点B作切线CZ）的垂线BF,交圆于点E-则线段EF的长为___________ ・（10）已知过双曲线与0~9_21 =1（G > 0』> 0）左焦点F\且垂直于A-轴的直线交双曲线两渐近线三视图如图所示, 则该几何体的萄輻积为___________（第11题）（第12题）I m(13)已知不等式(x + 2y)(—+ —)216对任意止实数x,y恒成立，则止实数血的最小值兀 >?为____ .(14)已知: “ 14一入IW 6 ”，g: "I X-IIW Q”(awR,a>0),若非“是非q的必要不充分条件，则实数。

重庆市南开中学2012届高三5月月考数学(文)试题本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，满分150分，考试时间120分钟．第Ⅰ卷(选择题)一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合1{|3},|2},2x M x x N x MN ⎧⎫=<=>⎨⎬⎭⎩则等于( )A ．φB ．{|13}x x -<<C ．{|03}x x <<D ．{|13}x x <<2．从10名女生与5名男生中选出6名同学组成课外兴趣小组，如果按照性别分层随机抽样，则男生甲的个数为( ) A ．1 B ．2 C ．3 D ．43．已知命题p ：“1xy >”，命题q ：“0x y >>”，则p 是q 的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知sin 4y x π⎛⎫=+ ⎪⎝⎭条对称由是( ) A ．2x π=B ．4x π=C ．34x π=D ．x π=5．已知函数21(0)13(),(),12(0)x x f x f x x x⎧-≥⎪⎪==-⎨⎪<⎪⎩若则实数x 的值为( )A．2-B．34C．324-或D．不存在6．球面有三点A、B、C，任意两点之间的球面距离都等于球大圆周长的四分之一，且||AB=( )A．34πB．3C．D．7．正项数列{}na满足，2211122311111,21,n n nn na a a aa a a a a a++==++++=+则( )8．已知函数231()112()4,(2012)2012f x a og b og x f f=++=且则的值为( )A．—4B．2C．0` D．—29．在直角坐标系,(1,2,3,4),(1,2,3,4) xOy x m m y n n====平面内平行直线与平行直线组成的所有矩形中任取一个矩形，恰好是正方形的概率是( )A．718B．14C．12D．51810．以椭圆的右焦点F2为圆心作一个圆，使此圆过椭圆的中心O并交椭圆于点M、N，若过椭圆的左焦点F1的直线MF1是圆F2的切线，则右准线与圆F2( )A．相交B．相切C．相离D．位置关系随离心率改变第Ⅱ卷(非选择题，共100分)二、填空题：(本大题共5小题，每小题5分，共25分．把答案填写在答题卡相应位置上)11．已知660160123456(2),x a a x a x a a a a a a a-=++++++++=则________12．平面向量a b a a b与的夹角为60,||=2,|b|=1,则|+2|等于________13．已知x，y满足124,31x yx y z x yx-≤⎧⎪+≤=+⎨⎪≥⎩则函数的最大值是________．14．若12,,1,2a b R a ba b+∈+=-且则-的最大值是________．15．6位身高不同的同学拍照，要求分成两排三列，每排3人，则每列后排均比其正前排的同学身村要高的排法有________种．三、解答题(共6小题；共75分，解答应写出文字说明、证明过程或演算步骤．)16．(共13分)已知△ABC的面积为2AB且·2AC =(1)求tan A的值；(2)求22sin2sin cos1222cos()4A A AAπ+--的值．17．(13分)某单位组织4个部门的职工旅游，规定每个部门只能在峨眉山、泰山、华山3个景中任选一个，假设各部门选择每个景区是等可能的．(1)求3个景区都有部门选择的概率；(2)求恰有两个部门选择峨眉山旅游的概率．18．(13分)已知数列{}4 n n n na a≥=+中,前n项和为S,对于任意n1时,3S(1)求数列{}na的通项公式；(2)若数列{}2,{}n n n n n b b S b n T=满足求数列的前项和19．(12分)如图，正三棱柱ABC —A 1B 1C 1的所有棱长都为2，D 为棱CC 1的中点．(1)求证：AB 1⊥平面A 1BD ；(2)求二面角A —A 1D —B 的大小．20．(12分)已知函数321()43cos ,,,0.322f x x x x R πθθθ=-+∈≤≤其中为参数且(1)当θcos =0时,判断函数()f x 是否有极值；(2)要使函数()f x 的极小值大于零，求参数θ的取值范围；(3)若对(Ⅱ)中所求的取值范围内的任意参数θ，函数()f x 在区间(2a －1，a )内都是增函数，求实数a 的取值范围．21．(12分)已知抛物线2:2(0):C x my m l y x m =>=-和直线没有公共点(其中m 为常数)．动点P 是直线l 上的任意一点，过P 点引抛物线C 的两条切线，切点分别为M 、N ，且直线MN 恒过点Q (1，1)．(1)求抛物线C 的方程；(2)已知O 点为原点，连结PQ 交抛物线C 于A 、B 两点，求||||||||PA QA PB QB -的值．参考答案一、选择题：本大题共10小题，每小题5分，共50分． 1—5 CBABC 6—10 BDCDA10．设),,(),,(2211y x M y x P 由于PM 过焦点F ，所以有,41,12121=-=x x y y 再设),(33y x N ，则有22331111(,),(,)44P Q x y x y --，将P 点代入直线方程有,0422=+-c y bx a 两边同乘以2x 有.22,04222222222y x y x y cx y bx a =⇒==+-又 所以,04222=+-a yb cx 同理04233=+-ay b cx ，故所求直线为024=+-a by cx ；故选A ．二、填空题：本大题共5小题，每小题5分，共25分，把答案填写在答题卡相应位置上． 11．31 12．3 13．),3(+∞ 14．3≤a 15．332-15．解：设x AD =，折叠后顶点A 落在线段BC 上的'A 点，则在△'A BD 中，设∠D 'A B =θ，易得：)3π2,6π[∈θ； 在△'A BD 中，由正弦定理有：,sin 1sin θx B x -=即：;sin 2)1(3θ=-xx 又1sin ≤θ， 于是：33212)1(3-≥⇒≤-x xx ，当且仅当2π=θ时取等号．三、解答题：本大题共6小题，共75分．解答应写出文字说明、证明过程或演算步骤．16．(本小题满分13分)解：(Ⅰ)由题可知： ;92n an S n -=又}{n a 为等差数列，设公差和首项分别为,1a d 、且,2=d于是：,)2(212n da n d S n -+=比较可知：1=a ……6分 (Ⅱ)由(Ⅰ)知：|;9|||-==n n S b n n 当;2)17(,91n n S n n -=≤≤时……9分 当10≥n 时，2)91)(9(2)81(8)]9(21[)178(-+-++=-+++++++=n n n S n2)8)(9(36--+=n n ……13分17．(本小题满分13分)解：(Ⅰ)由题可知：;1sin 22cos 2)2πcos(1sin 4)(+=++-⋅=x x x x x f ωωωω 当1=ω时，,1sin 2)(+=x x f 则：π2=T ……7分 (Ⅱ)由(Ⅰ)知：,1sin 2)(+=x x f ω欲使)(x f 在]32π,2π[-上单调递增， 则有：π2π2π2π[,][,]2344ωω-⊆-，于是：3(0,]4ω∈……13分18．(本小题满分13分)解：记“甲在第i 次获胜”为事件21(1,2,,5,6)(),();33i i i A i P A P A =⇒==(Ⅰ)记“经过4次比赛甲获胜”为事件B ，由事件的独立性有： 81163232323132323132)()(43214321=⋅⋅⋅+⋅⋅⋅=+=A A A A A A A A P B P ……6分 (Ⅱ)记“最多经过4次比赛结束”为事件C ，则：432143212121()(A A A A A A A A A A A A P C P +++=8165)43214321=++A A A A A A A A ……13分 19．(本小题满分12分) 解：法一：(Ⅰ)取B 1C 1的中点D ，连结A 1D ，MD ，则A 1D ⊥B 1C 1又由题意可知MD ∥AA 1，所以MD ⊥面A 1B 1C 1，所以MD ⊥B 1C 1，所以B 1C 1⊥面A 1DM ，所以B 1C 1⊥A 1M ……6分 (Ⅱ)过D 作DN ⊥B 1M 于N ，连结A 1N ，由(Ⅰ)可知A 1D ⊥面BB 1C ，由三垂线定理可知∠A 1ND 为二面角C 1－B 1M －A 1的平面角A 1D ,1,23,31===D B MD 在1Rt MDB △中，13311=⋅=MB MD D B DN 所以tan ∠A 1ND 3391333==……12分 法二：如图建立直角坐标，则)1,3,1(),0,3,1(),2,0,2(),0,0,2(),0,0,0(111--C C B B A则)23,23,23(-M (Ⅰ)11133(,)(1,0,22A MBC ⋅=⋅-=∴M A 1⊥11C B ……6分 (Ⅱ)取11C B 的中点)0,23,23(-D ，取面M C B 11的法向量)0,1,3(-设面M B A 11的法向量为),,(z y x =，则⎪⎩⎪⎨⎧⇒=+-=⋅-=⋅==⋅=⋅0232323),,()23,23,23(02),,()0,0,2(111z y x z y x A x z y x n B A )1,3,0(=,434)1,3,0()0,1,3(cos 111=⋅->=--<∴A M B C所以339tan 111>=--<A M B C ……12分 20．(本小题满分12分)解：(Ⅰ)对)(x f 求导得：)1(2)13()('2+++-=a a x a x x f ，代入2=a 有)4)(3()('--=x x x f ；令0)('>x f 得),4(),3,(+∞-∞∈x ； 又令0)('<x f ，得到：),4,3(∈x于是：)(x f 在),4(),3,(+∞-∞上单调递增；)(x f 在)4,3(上单调递减……5分 (Ⅱ)由(Ⅰ)知：)]1()[2()('+--=a x a x x f1)当1<a 时，有：12+<a a ，令0)('>x f 得：);,1(),2,(+∞+-∞∈a a x 再令0)('<x f 得：)1,2(+∈a a x ，故)(x f 在),1(),2,(+∞+-∞a a 上单调递增，在)1,2(+a a 上单调递减；此时可知：)2(a f 为)(x f 的极大值，)1(+a f 为)(x f 的极小值；欲使)(x f y =的图像与x 轴恰有三个交点，则必有：,0)1(0)2(⎩⎨⎧<+>a f a f即是：,06)15()1(0232223⎪⎪⎩⎪⎪⎨⎧<-+>+a a a a 解得：)51,0()0,1()1,3(⋃-⋃--∈a ……9分2)当1>a 时，有：12+>a a ；令0)('>x f 得：),2(),1,(+∞+-∞∈a a x ；再令()0f x '<得：(1,2),x a a ∈+故()f x 在(,1),(2,)a a -∞++∞上单调递增，在)2,1(a a +上单调递减；此时可知：)1(+a f 为)(x f 的极大值，)2(a f 为)(x f 的极小值；欲使)(x f y =的图像与x 轴恰有三个交点，则必有：,0)1(0)2(⎩⎨⎧>+<a f a f即是：3222203,(1)(51)06a a a a a ⎧+<⎪⎪⇒∈∅⎨+-⎪>⎪⎩综上可知：)51,0()0,1()1,3(⋃-⋃--∈a ……12分21．(本小题满分12分)(Ⅰ)由题知点P 到)0,21(F 的距离与它到直线21-=x 的距离相等， 所以点P 的轨迹是抛物线，方程为;22x y =……4分 (Ⅱ)设),0(),,0(),,(00c C b B y x Q ，则x x by b y QB 00:-=-即 0)(000=+--b x y x x b y由直线QB 是圆的切线知1)(||22000=+-+-x b y b x b y 即02)2(0020=-+-x b y b x同理：2000(2)20x c y c x -+-=所以c b ,是方程02)2(0020=-+-x t y t x 的两根2,220000--=--=+∴x xbc x y c b ……8分 0002020024)2(421||21x x x x y x c b S QBC⋅-+-=-=∴∆ 又,|2|202002-=∴=∆x x S x y QBC由题知2,2200200-=-=∴>∆x t x x S x QBC令 则2(2)44448,QBC t S t t t+==++≥+=△当2=t 即40=x 时，取“＝”QBC ∴△面积的最小值为8．……12分。

重庆市南开中学2019-2020下学期高三数学（文科）4月月考考试试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知集合{|0}A x x =>，2{|log (31)2}B x x =-<，则（ ） A ．(0,)A B ⋃=+∞B ．10,3A B ⎛⎤=⎥⎝⎦I C ．A B R ⋃= D ．50,3A B ⎛⎫= ⎪⎝⎭I 2．在ABC ∆中，若23()2||CA AB CB AB AB ⋅+⋅=u u u r u u u r u u u r u u u r u u u r，则1tan tan A B+的最小值为（ ） A ．5 B ．25 C ．6 D ．623．如图，已知四面体ABCD 为正四面体，1AB ＝，E ，F 分别是AD ，BC 中点．若用一个与直线EF 垂直，且与四面体的每一个面都相交的平面α去截该四面体，由此得到一个多边形截面，则该多边形截面面积最大值为（ ）A ．14B ．24C ．34 D ．14．《九章算术》是我国古代内容极为丰富的数学名著，第九章“勾股”，讲述了“勾股定理”及一些应用，还提出了一元二次方程的解法问题直角三角形的三条边长分别称“勾”“股”“弦”．设点F 是抛物线y2=2px 的焦点，l 是该抛物线的准线，过抛物线上一点A 作准线的垂线AB ，垂足为B ，射线AF 交准线l 于点C ，若Rt ABC V 的“勾”3AB =、“股”33CB =，则抛物线方程为（ ）．A ．22y x =B ．23y x = C ．24y x = D ．26y x = 5．已知集合{}|0A x x a =-≤，{}1,2,3B =，若A B φ⋂≠，则a 的取值范围为 A ．(,1]-∞ B ．[1,)+∞ C ．(,3]-∞ D ．[3,)+∞6．某高为4的三棱柱被一个平面截去一部分后得到一个几何体，它的三视图如图所示，则该几何体的体积与原三棱柱的体积之比是（ ）A．34B ．512C ．12D ．387．如图是一个几何体的三视图（侧视图中的弧线是半圆），则该几何体的表面积是（ ）A ．20＋3πB ．24＋3πC ．20＋4πD ．24＋4π8．满足{2018}A ⊆≠⊂{2018,2019,2020}的集合A 的个数为 A ．1B ．2C ．3D ．49．已知x 、y 满足约束条件50{03x y x y x -+≥+≥≤，则24z x y =+的最小值是（ ）A ．6-B ．5C ．10D ．10-10．设P 是椭圆22116925x y +=上一点，M ，N 分别是两圆：()22121x y ++=和()22121x y -+=上的点，则PM PN +的最小值、最大值分别为（ ） A ．18，24B ．16，22C ．24，28D ．20，2611．执行如图所示的程序框图，则输出的值为（ ）A ．5B ．12C ．27D ．5812．函数2πsin12()12xf x x x=-+的零点个数为（ ） A ．0B ．1C ．2D ．4二、填空题：本题共4小题，每小题5分，共20分。

重庆市南开中学高2018级五月末模拟考试试题数学（文科）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分，总共三个大题，22个小题，总分150分，考试时间为120分钟。

第I 卷（选择题，共50分）一、选择题：（每小题5分，共50分。

四个选项中只有一项是符合题目要求的） 1、已知集合{1,2}M =，设集合N 满足NM⊆，则集合N 的个数有（ ）个。

A 、2B 、4C 、6D 、8 2、函数44c o s s inyx x=-图象的一条对称轴方程是（ ）A 、2x π=-B 、4x π=-C 、8x π=D 、4xπ=3、不等式21x x-≥的解集为（）A 、{|21}x x x ><-或B 、{|210}x x x ≥-≤<或 C 、{|021}x x x <<<-或D 、{|210}x x x ≥-<≤或4、已知函数2()lg (1)(0)f x x x =+≤，则1(2)f-的值为（ ）AB、 C、 D、-5、图中阴影部分可用哪一组二元一次不等式表示（ ） A 、1220y x y ≥-⎧⎨-+≥⎩ B 、1220y x y ≥-⎧⎨-+≤⎩C 、01220x y x y ≤⎧⎪≥-⎨⎪-+≥⎩D 、01220x y x y ≤⎧⎪≥-⎨⎪-+≤⎩6、若5250125125(1) (33)mx a a x a x a x a aa+=+++++++=-且，则实数m的值为（ ）A 、3B 、3-C 、32D 、32-7、停车场可以把12辆车停放在一排，当有8辆已停放后，而恰有4个空位连在一起的概率为（ ） A 、8127C B 、8128C C 、8129C D 、81210C8、椭圆22143xy+=的长轴为12A A ，短轴为12BB ，将坐标平面沿y 轴折成一个二面角，使1A 点在平面122BA B 上的射影恰好是该椭圆的右焦点，则此二面角的大小为（ ）A 、30 B 、45 C 、60 D 、759、已知平面上三个向量a 、b 、c 的模均为1，它们相互之间的夹角均为120。

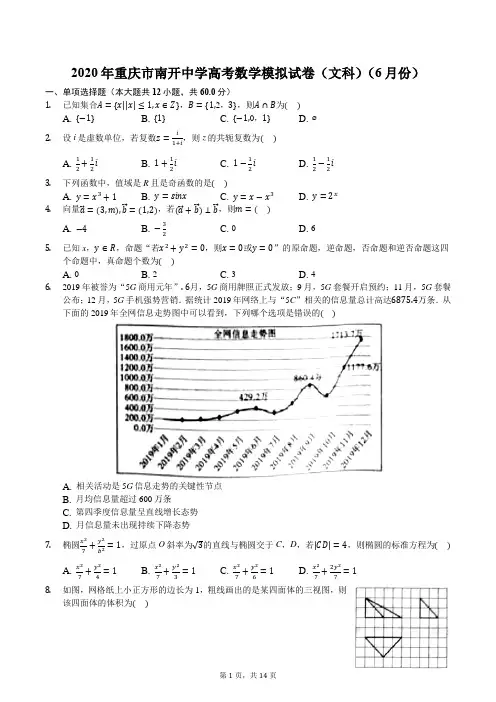
2020年重庆市南开中学高考数学模拟试卷（文科）（6月份）一、单项选择题（本大题共12小题，共60.0分）1.已知集合A={x||x|≤1,x∈Z}，B={1,2，3}，则A∩B为()A. {−1}B. {1}C. {−1,0，1}D. ⌀2.设i是虚数单位，若复数z=i1+i，则z的共轭复数为()A. 12+12i B. 1+12i C. 1−12i D. 12−12i3.下列函数中，值域是R且是奇函数的是()A. y=x3+1B. y=sinxC. y=x−x3D. y=2x4.向量a⃗=(3,m),b⃗ =(1,2)，若(a⃗+b⃗ )⊥b⃗ ，则m=()A. −4B. −32C. 0D. 65.已知x，y∈R，命题“若x2+y2=0，则x=0或y=0”的原命题，逆命题，否命题和逆否命题这四个命题中，真命题个数为()A. 0B. 2C. 3D. 46.2019年被誉为“5G商用元年”.6月，5G商用牌照正式发放；9月，5G套餐开启预约；11月，5G套餐公布；12月，5G手机强势营销．据统计2019年网络上与“5C”相关的信息量总计高达6875.4万条．从下面的2019年全网信息走势图中可以看到，下列哪个选项是错误的()A. 相关活动是5G信息走势的关键性节点B. 月均信息量超过600万条C. 第四季度信息量呈直线增长态势D. 月信息量未出现持续下降态势7.椭圆x27+y2b2=1，过原点O斜率为√3的直线与椭圆交于C，D，若|CD|=4，则椭圆的标准方程为()A. x27+y24=1 B. x27+y23=1 C. x27+y26=1 D. x27+2y27=18.如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的体积为()A. 43B. 83C. 4D. 89.定义在R上的奇函数f(x)满足f(x+1)=f(1−x)，且x∈[0,1]时，f(x)=2x−1，则f(log28)=()A. −1B. 1C. 7D. −1210.点P在函数y=lnx的图象上，若满足到直线y=x+a的距离为√2的点P有且仅有3个，则实数a的值为()A. 1B. −3C. 2D. −2√211.重庆誉为“桥都”，数十座各式各样的大桥横跨长江、嘉陵江两岸，其中朝天门长江大桥是世界第一大拱桥，其主体造型为：桥拱部分(开口向下的抛物线)与主桁(图中粗线)部分(可视为余弦函数一个周期的图象)相结合．已知拱桥部分长552m，两端引桥各有190m，主桁最高处距离桥面89.5m，则将下列函数等比放大后，与主桁形状最相似的是()A. y=0.45cos23x B. y=4.5cos23x C. y=0.9cos32x D. y=9cos32x12.若P是双曲线C：x2a2−y2b2=1(a,b>0)在第一象限上一点，F1，F2为双曲线C的左、右焦点，|PF2|=2b，Q(a2,0)到直线PF1，PF2距离相等，则双曲线C的离心率为()A. 53B. 32C. 43D. 54二、填空题（本大题共3小题，共15.0分）13.若变量x，y满足约束条件{x+y−1≤03x−y+1≥0x−y−1≤0，则z=2x+3y的最大值为______．14.已知△ABC的内角A，B，C的对边分别为a，b，c，若a=2,b=1,c=√7，则BC边上的高为______．15.《九章算术》商功章中研究了一个粮仓的容积计算问题．假设该粮仓近似于由如图的直角梯形以底边AB为轴旋转而成的几何体(图中长度单位为米)，则该粮仓能容纳的体积为______立方米．三、多空题（本大题共1小题，共5.0分）16.已知f(x)=4sinx+3cosx，f(x)向右平移α(0<α<π)个单位后为奇函数，则tanα=(1)，若方程f(x)−m=0在[α,π]上恰有两个不等的根，则m的取值范围是(2)．四、解答题（本大题共7小题，共82.0分）17.正项等比数列{a n}的前n项和为S n，且a1=1，S2+4S4=S6．(1)求{a n}的通项公式；(2)求数列{a n+n}的前n项和T n．18.在中华人民共和国成立70周年，国庆期间三大主旋律大片，集体上映，拉开国庆档电影大幕．据统计《我和我的祖国》票房收入为31.71亿元，《中国机长》票房收入为29.12亿元，《攀登者》票房收入为10.98亿元．已知某城市国庆后统计得知大量市民至少观看了一部国庆档大片，在观看的市民中进行随机抽样调查，抽样100人，其中观看了《我和我的祖国》有49人，《中国机长》有46人，《攀登者》有34人，统计图表如图．(1)计算a，b，c；(2)在恰好观看了两部大片的观众中进行分层抽样访谈，抽取总数为7人．(ⅰ)写出各组中抽取人数；(ⅰ)访谈中有2人表示后面将要看第三部，求这2人中要观看的都是《我和我的祖国》的概率．19.正三棱柱ABC−A1B1C1中，D为CC1中点，AB=2．(1)求证：平面ADB1⊥平面ABB1A1；(2)若AD与平面ABB1A1所成角为π，求四棱锥A−BCDB1的体积．420. 已知圆C ：x 2+(y −3)2=8和动圆P ：(x −a)2+y 2=8交于A ，B 两点．(1)若直线AB 过原点，求a ；(2)若直线AB 交x 轴于Q ，当△PQC 面积最小时，求|AB|． 21. 已知f(x)=−12x 2+x −cosx −k ．(1)若f(x)的一条切线为y =x ，求此时的k ； (2)求使得f(x)>0有解的最大整数k ．22. 在直角坐标系xOy 中，直线l 的参数方程为：{x =tcosαy =2√33+tsinα(t 为参数).在以坐标原点O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C 的极坐标方程为ρ=2(θ∈[0,π]，直线l 与曲线C 交于两不同的点M ，N ．(1)写出直线l 的普通方程与曲线C 的直角坐标方程，并求α的范围； (2)求MN 中点P 轨迹的参数方程．23. 已知对于任意x ≥−1，不等式(1+x)3≥1+3x 成立．(1)求证：对于任意x ≥−1，(1+x)4≥1+4x ； (2)若a >0，b >0，求证：(a +b)4≥a 4+4a 3b.答案和解析1.【答案】B【解析】解：∵集合A={x||x|≤1,x∈Z}={x|−1≤x≤1,x∈Z}={−1,0，1}，B={1,2，3}，∴A∩B={1}．故选：B．求出集合A，B，由此能求出A∩B．本题考查交集的求法，考查交集定义等基础知识，考查运算求解能力，是基础题．2.【答案】D【解析】【分析】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．利用复数代数形式的乘除运算化简，再由共轭复数的概念得答案．【解答】解：∵z=i1+i =i(1−i)(1+i)(1−i)=12+12i，∴z−=12−12i．故选：D．3.【答案】C【解析】解：根据题意，依次分析选项：对于A，y=x3+1，不是奇函数，不符合题意；对于B，y=sinx，为正弦函数，是奇函数，但值域不是R，不符合题意；对于C，y=x−x3，有f(−x)=(−x)−(−x)3=−(x−x3)=−f(x)，为奇函数，其值域为R，符合题意；对于D，y=2x，是指数函数，不是奇函数，不符合题意；故选：C．根据题意，依次分析选项中函数的奇偶性以及值域是否为R，综合即可得答案．本题考查函数的奇偶性的分析判断，涉及函数的值域，属于基础题．4.【答案】A【解析】解：∵向量a⃗=(3,m),b⃗ =(1,2)，∴(a⃗+b⃗ )=(4,m+2)，若(a⃗+b⃗ )⊥b⃗ ，则(a⃗+b⃗ )⋅b⃗ =(4,m+2)⋅(1,2)=4+2m+4=0，则m=−4，故选：A．由题意利用两个向量的数量积公式，两个向量垂直的性质，求出m的值．本题主要考查两个向量的数量积公式，两个向量垂直的性质，属于基础题．5.【答案】B【解析】解：“若x2+y2=0，则x或y=0”，是真命题，其逆命题为：“若x或y=0，则x2+y2=0”是假命题，据互为逆否命题的两个命题真假相同，可知其否命题为假命题、逆否命题是真命题，故真命题的个数为2．故选：B．先写出其命题的逆命题，只要判断原命题和其逆命题的真假即可，根据互为逆否命题的两个命题真假相同，即可判定其否命题、逆否命题的真假．本题考查四种命题及真假判断，注意原命题和其逆否命题同真假，属容易题．6.【答案】B【解析】解：由题知6月、9月、11月、12月活动月的走势均有明显提升，故相关活动是5G信息走势的关键性节点，即A正确；由统计图可知第四季度信息量呈直线增长态势，月信息量未出现持续下降态势，故CD正确；故选：B．根据所给统计图，利用排除法可得答案本题考查统计的相关知识，考查学生合情推理的能力，属于基础题7.【答案】D【解析】【分析】本题考查椭圆方程的求法，主要运用到弦长公式和两点间距离公式，考查学生的运算能力，属于基础题．设点C的坐标为(m,n)，则D(−m,−n)，由弦长公式可知|CD|=√1+(√3)2⋅2|m|=4，由两点间距离公式可知|CD|=2√m2+n2=4，从而解得|m|=1，|n|=√3，代入椭圆方程求出b2的值即可得解．【解答】解：设点C的坐标为(m,n)，则D(−m,−n)，由弦长公式可知，|CD|=√1+(√3)2⋅2|m|=4，∴|m|=1，由两点间距离公式可知，|CD|=√(m+m)2+(n+n)2=2√m2+n2=4．∴|n|=√3，代入椭圆方程有，17+3b2=1，∴b2=72．∴椭圆的方程为x27+2y27=1．故选：D．8.【答案】B【解析】解：根据几何体的三视图转换为直观图为：该几何体为三棱锥体．如图所示：所以：V=13×12×2√2×2√2×2=83．故选：B．首先把三视图转换为直观图，进一步求出几何体的体积．本题考查的知识要点：三视图和直观图之间的转换，几何体的体积公式的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型．9.【答案】A【解析】解：根据题意，log28=3，函数f(x)满足f(x+1)=f(1−x)，令x=2可得：f(2+1)=f(1−2)，即f(3)=f(−1)，又由f(x)为奇函数，则f(−1)=−f(1)=2−1=1，则f(1)=−1，故f(log28)=f(3)=−1；故选：A．根据题意，在f(x+1)=f(1−x)中，令x=2可得f(3)=f(−1)，结合函数的奇偶性与解析式可得f(−1)的值，即可得答案．本题考查函数的奇偶性与周期性的性质以及应用，注意分析函数的周期，属于基础题．10.【答案】B【解析】解：过函数y=lnx的图象上点P(x0,y0)作切线，使得此切线与直线y=x+a平行，又y′=1x ，于是1x0=1，则x0=1，y0=0，∴P(1,0)，当点P到直线y=x+a的距离为√2时，则满足到直线y=x+a的距离为√2的点P有且仅有3个，∴d=√1+1=√2，解得a=1或a=−3，又当a=1时，函数y=lnx的图象与直线y=x+1没有交点，只有两个点到直线距离为√2，所以不满足条件，故a=−3．故选：B．要满足到直线y=x+a的距离为√2的点P有且仅有3个，则需要直线与函数y=lnx的图象相交，而且点P 在函数y=lnx的图象上满足在直线一侧有一个点到直线距离为√2，另外一侧两个点到直线距离为√2，于是就涉及到切线问题，需要求导数，求切点，进一步求出实数a的值．本题考查了两个函数图象位置关系、求曲线切线方程和点到直线距离，考查了学生的转化能力，属于中档题．11.【答案】A【解析】解：由题意，建立平面直角坐标系，如图所示；则f(x)=Acosωx；其中A=89.52≈45，T=552+190+190=932≈900，若按100：1的比例缩小，则A′=0.45，T′=9，ω=2πT′≈2×39=23，所以函数y=0.45cos23x.故选：A．由题意建立平面直角坐标系，设f(x)=Acosωx，求出A、T的值，再按100：1的比例缩小，求出函数y的解析式．本题考查了余弦函数模型的应用问题，也考查了运算求解能力，是中档题．12.【答案】D【解析】解：由题意可知双曲线的图形如图；F1，F2为双曲线C的左、右焦点，|PF2|=2b，则|PF1|=2a+2b，Q到直线PF1，PF2的垂足分别为：N，M，Q(a2,0)到直线PF1，PF2距离相等，可得：MQ=QN，设∠PF2O=θ，所以P的纵坐标：2bsinθ，QM=(c−a2)sinθ，△PF1F2的面积为：12(2a+2b+2b)×(c−a2)sinθ=12×2c×2bsinθ，化简可得：a+2b=2c，即2b=2c−a，所以4(c2−a2)=(2c−a)2，化简可得5a=4c，可得离心率为：e=ac =54．故选：D．画出图形，利用双曲线的定义，结合距离相等，三角形的面积关系．列出方程求解离心率即可．本题考查双曲线的简单性质的应用，是基本知识的考查，中档题．13.【答案】3【解析】解：作出不等式对应的平面区域(阴影部分)，由z=2x+3y，得y=−23x+13z，平移直线y=−23x+13z，由图象可知当直线y=−23x+13z经过点B(0,1)时，直线y=−23x+13z的截距最大，此时z最大．此时z的最大值为z=2×0+3×1=3，故答案为：3．作出不等式对应的平面区域，利用线性规划的知识，通过平移即可求z 的最大值．本题主要考查线性规划的应用，利用数形结合是解决线性规划题目的常用方法．14.【答案】√32【解析】解：由余弦定理可得cosB =a 2+c 2−b 22ac=2×2×√7=2√7 则sinB =√1−cos 2B =√32√7， ∴BC 边上的高为csinB =√7√32√7=√32， 故答案为：√32．先由余弦定理求出cos B ，再根据同角的三角形函数的关系求出sin B ，即可求出BC 边上的高． 本题考查了余弦定理，和同角的三角函数关系，以及解直角三角形，属于基础题． 15.【答案】21π【解析】解：由已知图形可知，粮仓是一个组合体，上半部分为圆锥，下半部分为圆柱，圆锥的底面半径为3，高为1， 圆柱的底面半径为3，高为2．则该粮仓的体积V =13π×32×1+π×32×2=21π．故答案为：21π．由已知图形可知，粮仓是一个组合体，上半部分为圆锥，下半部分为圆柱，圆锥的底面半径为3，高为1，圆柱的底面半径为3，高为2.分别求出圆锥与圆柱的体积，作和得答案． 本题考查圆锥与圆柱体积公式的应用，是基础的计算题．16.【答案】34[245,5)【解析】解：f(x)=4sinx +3cosx =5sin(x +θ)，其中sinθ=35，cosθ=45， 则其向右平移α后f(x)=5sin(x +θ−α)，因为此时函数为奇函数，故f(0)=5sin(θ−α)=0，则θ−α=2kπ或θ−α=π+2kπ，即α=θ−2kπ或α=θ−π−2kπ，k ∈Z ， 因为0<α<π，故只能α=θ，即此时有sinα=sinθ=35，cosα=cosθ=45， 所以tanα=3545=34；方程f(x)−m =0在[α,π]上恰有两个不等的根等价于函数f(x)与y =m 在[α,π]图象有2个不同的交点， 作出函数f(x)的图象如下：由图可得m∈[245,5)．根据平移后函数为奇函数，结合α得范围可得sinα=sinθ=35，cosα=cosθ=45；方程有不等两根等价于函数f(x)与y=m图象有2个交点，数形结合即可．本题考查三角函数相关性质，考查方程根与图象交点个数之间的转化，涉及数形结合思想，属于中档题．17.【答案】解：(1)若公比q=1，2a1+16a1=6a1，不成立；则q≠1，a1(1−q 2)1−q +4a1(1−q4)1−q=a1(1−q6)1−q，由于{a n}为正项等比数列，1−q2≠0，所以1+4(1+q2)=1+q2+q4，即q4−3q2−4=0，解得q2=4，即q=2，所以a n=2n−1，n∈N∗；(2)T n=(1+2+⋯+2n−1)+(1+2+⋯+n)=2n−1+n(n+1)2．【解析】(1)首先判断公比不为1，再由等比数列的求和公式，解方程可得公比，进而得到所求通项公式；(2)可得a n+n=2n−1+n，由数列的分组求和，结合等差数列和等比数列的求和公式，计算可得所求和．本题考查等比数列和等差数列的通项公式和求和公式的运用，考查数列的分组求和，以及方程思想和化简运算能力，属于基础题．18.【答案】解：(1)由题意得：{27+a +b +4=4630+a +c +4=4918+b +c +4=34，解得：{a =9c =6b =6．(2)记“同时观看了《机长》和《祖国》”的为A 组， “同时观看了《机长》和《攀登者》”为B 组， “同时观看《祖国》和《攀登者》“为C 组， ∴按分层抽样，A ，B ，C 组人数分别为3，2，2， 在抽样的7人中，没有观看《祖国》的有2人， 设这七个人分别为A 1，A 2，A 3，B 1，B 2，C 1，C 2， 则还会继续观看第三部的2人可能是：A 1A 2，A 1A 3，A 2A 3B ， 1B 2C 1，C 2A 1，B 1A 1，B 2A 2B ， 1A 2B 3，A 3B 1，A 3B 2，A 1C 1， A 2C 1，A 3C 1，A 1C 2，A 2C 2，A 3C 2，B 1C 1，B 1C 2，B 2C 1，B 2C 2，共21种， 则2人都没有观看《我和我的祖国》的只有B 1B 2一种， ∴这2人中要观看的都是《我和我的祖国》的概率是p =121．【解析】(1)由题意列出方程组，能求出a ，b ，c ．(2)记“同时观看了《机长》和《祖国》”的为A 组，“同时观看了《机长》和《攀登者》”为B 组，“同时观看《祖国》和《攀登者》“为C 组，按分层抽样，A ，B ，C 组人数分别为3，2，2，在抽样的7人中，没有观看《祖国》的有2人，设这七个人分别为A 1，A 2，A 3，B 1，B 2，C 1，C 2，利用列举法能求出这2人中要观看的都是《我和我的祖国》的概率．本题考查概率的求法，考查列举法、古典概型、统计图、分层抽样等基础知识，考查运算求解能力，是基础题．19.【答案】解：(1)证明：取AB 1中点E ，连接DE ，取A 1B 1中点F ，连接EF ，FC 1， 由于三棱柱ABC −A 1B 1C 1是正棱柱，故CC 1⊥面A 1B 1C 1，从而CC 1⊥FC 1， 由于D 为CC 1中点，CC 1⊥AC ，CC 1⊥B 1C 1，所以AD =√22+CD 2,B 1D =√22+C 1D 2AD =B 1D ，则由三线合一性DE ⊥AB 1①， 因为E ，F 分别为AB 1，A 1B 1中点，所以EF//=12AA 1//=DC 1，则四边形EFC 1D 为平行四边形从而DE//FC 1，由于是正棱柱，CC 1⊥面A 1B 1C 1，从而CC 1⊥FC 1，则CC 1⊥DE②， 综合①②可知，DE ⊥面ABB 1A 1，而DE ⊂面ADB 1， 所以平面ADB 1⊥平面ABB 1A 1．(2)解：由DE ⊥面AA 1B 1B 知AD 与平面ABB 1A 1所成角即为∠EAD =π4， 而DE =FC 1=√3，则AD =√6=√4+CD 2，所以CD =√2,CC 1=2√2，所以S BCDB 1=(√2+2√2)⋅12⋅2=3√2，S BCB 1=2√2⋅12⋅2=2√2， 则V A−BCDB 1VA−BCB 1=32，而V A−BCB 1=V C−ABB 1=13S ABB 1⋅CF 1=13⋅2⋅2√2⋅12⋅√3=23√6， 所以四棱锥A −BCDB 1的体积为V A−BCDB 1=23√6⋅32=√6．【解析】(1)取AB 1中点E ，连接DE ，取A 1B 1中点F ，连接EF ，FC 1，推导出CC 1⊥FC 1，CC 1⊥AC ，CC 1⊥B 1C 1，DE ⊥AB 1，CC 1⊥FC 1，CC 1⊥DE ，从而DE ⊥面ABB 1A 1，由此能证明平面ADB 1⊥平面ABB 1A 1． (2)由DE ⊥面AA 1B 1B 知AD 与平面ABB 1A 1所成角即为∠EAD =π4，推导出V A−BCDB 1VA−BCB 1=32，V A−BCB 1=V C−ABB 1=13S ABB 1⋅CF 1，由此能求出四棱锥A −BCDB 1的体积．本题考查面面垂直的证明，考查四棱锥的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．20.【答案】解：(1)由于两圆有两个公共点，则圆心距小于半径之和， 即a 2+9<(4√2)2，解得a ∈(−√23,√23)，两圆相减得公共弦直线AB ：−6y +9=−2ax +a 2， 过原点得，a 2=9，a =±3，检验成立；(2)直线AB ：−6y +9=−2ax +a 2交x 轴，得x Q =12(a −9a )， 则|PQ|=|12(a −9a )−a|=12|a +9a |，S △PQC =12|PQ|⋅3=32|a +9a |≥9 在a =±3时取得最小值，满足a ∈(−√23,√23)，成立，此时直线AB ：y =±x ，圆心到直线距离为√2，弦长为2√8−(√2)2=√14．【解析】(1)根据两圆相交可得圆心距<半径之和，进而求出a 的范围，再代入原点坐标，可得a 的值； (2)表示出点Q 坐标，|PQ|长度，面积表达式，根据弦长公式可求得|AB| 本题考查圆与圆的位置关系，考查相交弦长公式，属于中档题．21.【答案】解：(1)设切点横坐标为t ，f′(t)=−t +1+sint =1，sint −t =0， 令g(x)=sinx −x ，g′(x)=cosx −1≤0，所以g(x)恒单减，而g(0)=0， 所以t =0，从而f(0)=0得k =−1．(2)由题意，要使得−12x 2+x −cosx >k 有解，即求ℎ(x)=−12x 2+x −cosx 的最大值， ℎ′(x)=−x +1+sinx ，ℎ′′(x)=−1+cosx ≤0， 从而ℎ′(x)单减，而ℎ′(π2)=2−π2>0,ℎ′(2π3)=1+√32−2π3<2−2π3<0所以ℎ′(x)在(π2,2π3)有唯一零点x 0，所以ℎ(x)在(−∞,x 0)单增，(x 0,+∞)单减，则ℎ(x)≤ℎ(x 0)=−12x 02+x 0−cosx 0，而ℎ′(x 0)=−x 0+1+sinx 0=0， 所以ℎ(x 0)=−12(1+sinx 0)2+1+sinx 0−cosx 0=−12[1+(sinx 0)2]+1−cosx 0=−12[2−cos 2x 0]+1−cosx 0=12cos 2x 0−cosx 0，由于x 0∈(π2,2π3),cosx 0∈(−12,0)，ℎ(x 0)=12(cosx 0−1)2−12∈(0,34)，所以整数k 最大值为0．【解析】(1)只需令切点处的导数为1，然后结合导数的单调性，确定导数零点的唯一性；(2)分离整数k ，然后利用导数研究函数ℎ(x)=−12x 2+x −cosx 的单调性、零点情况，最终解决问题． 本题研究导数的几何意义及综合应用，通过导数研究函数的单调性，进而研究函数的相关性质，是此类问题的基本路子，属于中档题．22.【答案】解：(1)直线l 的参数方程为：{x =tcosαy =2√33+tsinα(t 为参数).转换为直线l 的普通方程为：sinα⋅x =cosα(y −2√33)；曲线C 的直角坐标方程为：x 2+y 2=4(y ≥0) 直线l 为过(0,23√3)，倾斜角为α的直线， 由于直线l 与曲线C 交于两不同的点M ，N ．所以：当直线的倾斜角的范围在α∈[0,π6]∪[5π6,π)时，直线与曲线有两个交点． (2)直线l 代入曲线C ：t 2+43√3sinα⋅t +43=0,t P =t 1+t 22=−23√3sinα，代入得到中点P 轨迹的参数方程：{x =−2√33sinαcosαy =2√33−2√33sin 2α(α为参数，a ∈[0,π6]∪[5π6,π)).【解析】(1)直接利用转换关系，把参数方程极坐标方程和直角坐标方程之间进行转换． (2)liy9ong 直线和曲线的位置关系式的应用和中点坐标公式的应用求出结果．本题考查的知识要点：参数方程极坐标方程和直角坐标方程之间的转换，一元二次方程根和系数关系式的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型． 23.【答案】证明：(1)∵x ≥−1，∴x +1≥0． 又对于任意x ≥−1，不等式(1+x)3≥1+3x 成立，∴(1+x)4=(1+x)3(1+x)≥(1+3x)(1+x)=1+4x +3x 2≥1+4x ， 即(1+x)4≥1+4x ；(2)欲证(a +b)4≥a 4+4a 3b ， 只需(a+b a)4≥1+4a 3b a 4，即证(1+b a )4≥1+4⋅ba∵a ，b >0，∴ba >0>−1，由(1)知取x =ba 时上式成立，从而原不等式得证．【解析】(1)由x ≥−1，得x +1≥0，结合已知等式再由不等式的可乘积性，即可证明(1+x)4≥1+4x ； (2)欲证(a +b)4≥a 4+4a 3b ，即证(1+ba )4≥1+4⋅ba ，再由ba >−1，结合(1)得结论．本题考查不等式的证明，训练了利用分析法与综合法证明不等式，考查推理论证能力，是中档题．。

2022年重庆市南开中学高考数学模拟试卷一、单项选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）设集合A ＝{x |x ﹣6≤0}，B ＝{x |x ＜2}，则A ∩（∁R B ）＝（ ） A ．[2，6]B ．（﹣∞，2]C ．（2，6]D ．[6，+∞）2．（5分）已知命题P ：“∃x ∈[12，4]，x 2−ax +4＞0”为真命题，则实数a 的取值范围是（ ） A ．a ＜4B ．a ＜172C ．a ＜133D ．a ＞53．（5分）已知tan(θ+π4)=−3，则sin2θ＝（ ） A ．45B ．−45C ．35D ．−354．（5分）已知圆的内接正方形的一条对角线上的两个顶点的坐标分别是（5，6），（3，﹣4），则这个圆的方程为（ ） A ．x 2+y 2+4x ﹣2y +7＝0 B ．x 2+y 2﹣8x ﹣2y ﹣9＝0 C ．x 2+y 2+8x +2y ﹣6＝0D ．x 2+y 2﹣4x +2y ﹣5＝05．（5分）如图，在三棱锥A ﹣BCD 中，AB ＝AC ＝BD ＝CD ＝3，AD ＝BC ＝2，点M ，N 分别为AD ，BC 的中点，则异面直线AN ，CM 所成的角的余弦值是（ ）A ．78B ．−78C ．−725D ．7256．（5分）“杨辉三角”是中国古代数学杰出的研究成果之一．如图所示，由杨辉三角的左腰上的各数出发，引一组平行线，从上往下每条线上各数之和依次为1，1，2，3，5，8，13，……，则下列选项不正确的是（ ）A ．在第9条斜线上，各数之和为55B ．在第n （n ≥5）条斜线上，各数自左往右先增大后减小C ．在第n 条斜线上，共有2n+1−(−1)n4个数D ．在第11条斜线上，最大的数是C 737．（5分）在正方体ABCD ﹣A 1B 1C 1D 1中，|AB |＝3，点E 是线段AB 上靠近点A 的三等分点，在三角形A 1BD 内有一动点P （包括边界），则|P A |+|PE |的最小值是（ ） A ．2B ．2√2C ．3D ．3√38．（5分）已知函数f(x)=e xx 4−klnx ，当x ＞1时，不等式f （x ）≥x +1恒成立，则k 的取值范围是（ ） A ．（﹣∞，﹣e ]B ．（﹣∞，﹣4]C ．（﹣∞，﹣e 2]D ．（﹣∞，0]二、多项选择题：本题共4小题，每小题5分，共20分。

重庆南开中学高2020级一诊模拟考试数学试题卷(文史类)考试说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

满分l50分， 考试时间l20分钟．答题前，务必将自己的姓名、准考证号码填写清楚；选择题必须使用2B 铅笔填涂，非选择题必须使用0.5毫米黑色字迹的签字笔书写， 字体工整，字迹清楚；请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效，在草稿 纸、试题卷上答题无效；保持卡面清洁，不得折叠、不要弄破、弄皱，不准使用涂改液、刮纸刀． 第Ⅰ卷(选择题共50分)一．选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个备选项中，只有一项是符合题目要求的。

1．集合⎭⎬⎫⎩⎨⎧∈≥+-=Z x x x x A ，211的子集个数为( ) A ．2 B ．3 C ．4 D ．52．已知R m ∈，复数i im ++1的实部和虚部相等，则m 的值为( )A ．21B ．0C ．1D ．1-3．下列命题的否定为假命题的是( )A ．0222≤+-∈∃x x R x ， B ．任意一个平面四边形的四个顶点共圆C ．样本的中位数一定在样本中D ．线性回归直线一定经过样本中心点()y x ，4．某工厂从2020件产品中选取l00件抽样检查，若采用下面的方法选取：先用简单随机抽样从2020件产品中剔除15件，剩下的2000件再按系统抽样的方法进行抽取．则每件产品被抽中的概率( )A ．均不相等B ．都相等，且为40320C ．不全相等D ．都相等，且为2015．将函数⎪⎭⎫ ⎝⎛-=3sin 2πx y 的图象向左平移6π个单位，所得函数图象的一条对称轴是( )A ．3π-=x B ．6π-=x C ．6π=x D ．3π=x6．执行如图所示的程序框图，若输10=n ，则输出的=S ( )A ．115B ．1110C ．5536D ．55727．已知圆014222=++-+y x y x C ：，在区间[]64，-上任取整数m ，则直线0=++m y x l ：与圆C 相交所得ABC ∆为钝角三角形(其中B A 、为交点，C 为圆心)的概率为( )A ．52B ．112C ．113D ．1148．已知ABC ∆满足OAB ，4=是ABC ∆所在平面内一点，满足222OC OB OA ==，且R AC OB OA ∈=+λλ，，则BA BO •= ( )A ．28B ．8C ．24D ．49．已知实数y x ，满足可行域⎪⎩⎪⎨⎧≤-+≥+-≥-+09301033y x y x y x D ：，曲线5=+-+Γa y x ：，恰好平分可行域D的面积，则a 的值为( )A ．4-B ．24-C ．6-D ．8-10．已知实数d ，6，c ，d 满足12ln 22=--=c dd b a ，则()()22d b c a -+-的最小值为( )A ．12-B ．22-C ．223-D ．221-第Ⅱ卷(非选择题 共100分)二、填空题：本大题共5小题，每小题5分，共25分。

2020年重庆南开中学高三数学文模拟试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1.设函数，把的图象按平移后得到的函数图象，则函数的对称中心坐标为（）A. B.C. D.参考答案：答案:B2. （5分）（2015?钦州模拟）一个袋子中有号码为1、2、3、4、5大小相同的5个小球，现从袋中任意取出一个球，取出后不放回，然后再从袋中任取一个球，则第一次取得号码为奇数，第二次取得号码为偶数球的概率为（）A．B．C．D．参考答案：D【考点】：列举法计算基本事件数及事件发生的概率．【专题】：概率与统计．【分析】：先求出第一次取得号码为奇数的概率，再求出第二次取得号码为偶数球的概率，根据概率公式计算即可．解：1、2、3、4、5大小相同的5个小球，从袋中任取一个球，则第一次取得号码为奇数的概率为，第二次取得号码为偶数球的概率为=，故第一次取得号码为奇数，第二次取得号码为偶数球的概率为=，故选：D．【点评】：本题考查了条件概率的求法，属于基础题．3. 已知集合，，则=（）A．{0,1,2} B．{1,2} C．{1,2,3} D．{2,3}参考答案：B4. 如图所示的程序框图输出的结果是S＝720，则判断框内应填的条件是( )A．i≤7B．i>7 C．i≤9D．i>9参考答案：B解析：程序框图所示的运算是10×9×8×7×…，若输出结果是S＝720，则应是10×9×8＝720，所以i＝10,9,8时累乘，即当i>7时执行循环体．5. 设a=（），b=（），c=log2，则a，b，c的大小顺序是（）A．b＜a＜c B．c＜b＜a C．c＜a＜b D．b＜c＜a参考答案：B【考点】对数值大小的比较．【专题】数形结合；转化思想；函数的性质及应用．【分析】利用指数函数的单调性即可得出．【解答】解：∵a=（）=＞b=（）＞1，c=log2＜0，∴a＞b＞c．故选：B．【点评】本题考查了指数函数的单调性，考查了推理能力与计算能力，属于基础题．6. 已知集合，.则（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件参考答案：A略7. 下列各对向量中，共线的是（）A.a=（2,3），b=（3，-2）B.a=（2,3）,b=（4，-6）C.a=（，-1），b=（1，)D.a=(1,),b=(,2)参考答案：D略8. 位同学每人从甲、乙、丙门课程中选修门，则恰有人选修课程甲的概率是A. B. C.D.参考答案：A9. 在平面直角坐标系中，过点的直线与椭圆交于、两点，点是线段的中点．设直线的斜率为，直线的斜率为，则的值等于参考答案：答案：10. 设集合，，若，则（）A．B．C．D．参考答案：B略二、填空题:本大题共7小题,每小题4分,共28分11. 己知是虚数单位,若，则__________.参考答案：2+i12. 函数f（x）=的定义域是．参考答案：（1，2）【考点】函数的定义域及其求法．【专题】函数的性质及应用．【分析】根据函数f（x）的解析式，列出使解析式有意义的关于自变量的不等式组，求出解集即可．【解答】解：∵函数f（x）=，∴，解得﹣＜x＜2；∴函数f（x）的定义域是（1，2）．故答案为：（1，2）．【点评】本题考查了求函数定义域的问题，解题的关键是列出使解析式有意义的关于自变量的不等式组，是容易题．13. 若，则的最大值▲。

2020年重庆市南开中学高考数学模拟试卷(文科)(3月份)一、单项选择题（本大题共12小题，共60.0分） 1. 已知复数z =11+i (i 为虚数单位)，则z =( )A.1−i 2B.1+i 2C. 1−iD. 1+i2. 已知函数f (x )=x +ax ，则“a =4”是“函数f (x )在(2,+∞)上为增函数”的( )A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件3. 用六个完全相同的正方形围成的立体图形叫正六面体．已知正六面体ABCD −A 1B 1C 1D 1的棱长为4，则平面AB 1D 1与平面BC 1D 间的距离为( )A. √3B. √63C. 4√33D. 2√34. 已知cos(α−π4)=−13，则sin(−3π+2α)=( )A. 79B. −79C. 35D. −355. 在△ABC 中，角A ，B ，C 所对应的边分别为a ，b ，c ，A =π3，sinB =√33，b =2，则a =( )A. 1B. √3C. 3D. 436. 已知变量x ，y 满足约束条件{y ≤2x +y ≥4x −y ≤1则z =3x +y 的最小值为( )A. 11B. 12C. 8D. 37. 如图是某几何体的三视图，则该几何体的体积为( )A. 12B. 15C. 18D. 218. 在△ABC 中，AD⃗⃗⃗⃗⃗⃗ =2DB ⃗⃗⃗⃗⃗⃗ ，CE ⃗⃗⃗⃗⃗ =2EA ⃗⃗⃗⃗⃗ ，则( ) A. DE ⃗⃗⃗⃗⃗⃗ =13CA ⃗⃗⃗⃗⃗ −23CB ⃗⃗⃗⃗⃗ B. DE ⃗⃗⃗⃗⃗⃗ =13CA ⃗⃗⃗⃗⃗ +23CB ⃗⃗⃗⃗⃗ C. DE ⃗⃗⃗⃗⃗⃗ =23CA ⃗⃗⃗⃗⃗ −13CB ⃗⃗⃗⃗⃗ D. DE ⃗⃗⃗⃗⃗⃗ =23CA ⃗⃗⃗⃗⃗ +13CB ⃗⃗⃗⃗⃗9.执行如图所示框图，则输出S的值为()A. 18B. −18C. √38D. −√3810.已知f′(x)为f(x)的导数，若f′(x)<f(x)对于任意的x∈R都成立，则()A. f(0)<f(2014)e2014B. f(0)>f(2014)e2014C. f(0)=f(2014)e2014D. f(2014)e2014和f(0)的大小关系不确定11.在△ABC中，∠ABC=60°，AB=1，BC=3，则sin∠BAC的值为()A. √314B. 3√314C. √2114D. 3√211412.已知正四棱锥S−ABCD的侧棱长与底面边长都等于2，点E是棱SB的中点，则直线AE与直线SD所成的角的余弦值为()A. √22B. √23C. √32D. √33二、填空题（本大题共4小题，共20.0分）13.已知集合A={x|−2<x<3}，B={x|0<x<4}，则A∪B=_____．14.记数列{a n}的前n项和为S n.若a1=1，S n=2(a1+a n)(n≥2,n∈N∗)，则S n=______ ．15.设F1，F2是椭圆E：x225+y216=1的左右焦点，P是椭圆E上的点，则|PF1|⋅|PF2|的最小值是______..16.先将函数f(x)=sin(2x+π6)的图象向右平移π6个单位，再将所得的图象上所有点的横坐标变为原来的2倍(纵坐标不变)，得到函数g(x)的图象，则函数g(x)的解析式为．三、解答题（本大题共7小题，共82.0分）17.为了调查某厂2000名工人生产某种产品的能力，随机抽查了m位工人某天生产该产品的数量，产品数量的分组区间为[10,15)，[15,20)，[20,25)，[25,30)，[30,35]，频率分布直方图如图所示．已知生产的产品数量在[20,25)之间的工人有6位．(Ⅰ)求m；(Ⅱ)工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训，则这2位工人不在同一组的概率是多少？18.在三棱柱ABC−A1B1C1中，△ABC是边长为2的正三角形，侧面BB1C1C是矩形，D、E分别是线段BB1、AC1的中点．(1)求证：DE//平面A1B1C1；(2)若平面ABC⊥平面BB1C1C，BB1=4，求三棱锥A−DCE的体积．19. 记数列{a n }的前n 项和为T n ，且{a n }满足a 1=1，a n =3n−1+a n−1(n ≥2)．(1)求a 2、a 3的值，并求数列{a n }的通项公式a n ； (2)证明：T n =3 a n −n2．20. 已知抛物线y 2=2px(p >0)，过点(1,0)的直线l 与抛物线交于A ，B 两点，OA ⃗⃗⃗⃗⃗ ⋅OB⃗⃗⃗⃗⃗⃗ =−3． (1)求抛物线的方程；(2)以AB 为斜边作等腰直角三角形ABC ，当点C 在y 轴上时，求△ABC 的面积．21. 已知函数f(x)=ax −lnx −1(a ∈R)．(1)求f(x)的单调区间；(2)若a =0，令g(x)=f(tx +1)+3x+2x+2，若x 1，x 2是g(x)的两个极值点，且g (x 1)+g (x 2)>0，求正实数t 的取值范围．22. 在平面直角坐标系xOy 中，已知曲线C 的参数方程为{x =2cosαy =sinα(α为参数).以直角坐标系原点O 为极点，x 轴的正半轴为极轴建立极坐标系，直线l 1的极坐标方程为ρcos(θ−π4)=√2，直线l 2的极坐标方程为θ=π4，点M 是直线l 1和直线l 2的交点． (1)点P 为曲线C 上的动点，求点P 到直线l 1的距离的最大值； (2)设曲线C 与直线l 1交于点A 、B 两点，求|MA|+|MB|的值．23. 已知函数f(x)=|ax −2|．(1)当a =4时，求不等式f(x)+|4x +2|≥8的解集；(2)若x ∈[2,4]时，不等式f(x)+|x −3|≤x +3成立，求a 的取值范围．【答案与解析】1.答案：A解析：本题考查复数的运算，属于基础题．通过分母实数化即可求出结果．解：z=11+i =1−i(1+i)(1−i)=1−i2．故选A．2.答案：A解析：根据函数单调性的性质，利用充分条件和必要条件烦的定义即可得到结论．解：当a=4时，函数f(x)=x+ax =x+4x在(2,+∞)上为增函数成立，若f(x)=x+ax=x在(2,+∞)上为增函数，a=0也成立，不能推出a=4，∴“a=4”是“函数f(x)在(2,+∞)上为增函数”的充分不必要条件．故答案为A．3.答案：C解析：本题考查空间中点、线、面间的距离计算，考查空间想象能力与思维能力，考查计算能力，是中档题．由题意画出图形，可得A1C⊥平面AB1D1，A1C⊥平面BC1D，求出正方体的棱长，再由等体积法求得|A1E|，则平面AB1D1与平面BC1D间的距离可求．解：由题意正六面体ABCD−A1B1C1D1是棱长为4的正方体，∵AB1//DC1，B1D1//BD，AB1∩B1D1=B1，C1D∩BD=D，∴平面AB1D1//平面BC1D，连接A1C，可得A1C⊥平面AB1D1，A1C⊥平面BC1D.设垂足分别为E，F，则平面AB1D1与平面BC1D间的距离为|EF|．正方体的体对角线长为√42+42+42=4√3．在三棱锥A1−AB1D1中，由等体积法求得：|A1E|=13×12×4×4×413×12×4√2×4√2×√32=4√33．∴平面AB1D1与平面BC1D间的距离为4√3−8√33=4√33．故选：C．4.答案：A解析：解：∵已知cos(α−π4)=−13=sin(α+π4)，即sin(α+π4)=−13，则sin(−3π+2α)=sin(π+2α)=−sin2α=cos(π2+2α)=1−2sin2(π4+α)=1−2×19=79，故选：A．利用诱导公式、二倍角公式进行化简三角函数式，可得结果．本题主要考查利用诱导公式、二倍角公式进行化简三角函数式，属于基础题．5.答案：C解析：本题主要考查了正弦定理的简单应用，属于基础题．由已知结合正弦定理即可求解．解：由正弦定理可得，asinA =bsinB，∴a=bsinAsinB =2×√32√33=3．故选：C．6.答案：C解析：解：由约束条件{y ≤2x +y ≥4x −y ≤1作出可行域如图，联立{y =2x +y =4，解得A(2,2)，化目标函数z =3x +y 为y =−3x +z ，由图可知，当直线y =−3x +z 过A 时，直线在y 轴上的截距最小，z 有最小值为z =3×2+2=8． 故选：C ．作出不等式组对应的平面区域，利用绵竹市的几何意义，通过数形结合即可的得到结论． 本题主要考查线性规划的应用，利用z 的几何意义，通过数形结合是解决本题的关键．7.答案：C解析：本题主要考查由三视图还原几何体，求几何体的体积． 解析：解：由已知中的三视图可得：该几何体是一个长宽高分别为4，3，3的长方体，切去一半得到的， 如图所示：其体积为：12×4×3×3=18， 故选C ．8.答案：A解析：本题考查了平面向量的线性运算，属基础题．由平面向量的加减法得：：DE ⃗⃗⃗⃗⃗⃗ =DA ⃗⃗⃗⃗⃗ +AE ⃗⃗⃗⃗⃗ =23BA ⃗⃗⃗⃗⃗ −13CA ⃗⃗⃗⃗⃗ =23(CA ⃗⃗⃗⃗⃗ −CB ⃗⃗⃗⃗⃗ )−13CA ⃗⃗⃗⃗⃗ =13CA ⃗⃗⃗⃗⃗ −23CB ⃗⃗⃗⃗⃗ ，得解． 解：DE ⃗⃗⃗⃗⃗⃗ =DA ⃗⃗⃗⃗⃗ +AE ⃗⃗⃗⃗⃗ =23BA ⃗⃗⃗⃗⃗ −13CA ⃗⃗⃗⃗⃗ =23(CA ⃗⃗⃗⃗⃗ −CB ⃗⃗⃗⃗⃗ )−13CA ⃗⃗⃗⃗⃗ =13CA ⃗⃗⃗⃗⃗ −23CB ⃗⃗⃗⃗⃗ ， 故选A ．9.答案：D解析：解：执行程序框图，有 k =1，S =1，α=π6 S =√32，α=π3不满足条件k >4，k =3 S =√34，α=2π3不满足条件k >4，k =5 S =−√38，α=4π3满足条件k >4，输出S 的值为−√38． 故选：D ．执行程序框图，写出每次循环得到的S ，α的值，当k =5时，满足条件k >4，输出S 的值为−√38．本题主要考察了程序框图和算法，属于基础题．10.答案：B解析：解：由f′(x)<f(x)得f′(x)−f(x)<0， 构造函数g(x)=f(x)e x， 则g′(x)=f′(x)e x −e x f(x)(e x )2=f′(x)−f(x)e x<0，即函数g(x)单调递减，则g(2014)<g(0)， 即f(2014)e 2014<f(0)e 0， 则f(0)>f(2014)e 2014，故选：B构造函数g(x)=f(x)e x利用导数判断函数的单调性，即可得到结论．本题主要考查函数值的大小比较，根据条件构造函数是解决本题的关键．11.答案：D解析：解：在△ABC中，∵∠ABC=60°，AB=1，BC=3，由余弦定理可得AC2=1+9−2×1×3cos60°=7，∴AC=√7．由正弦定理可得，ACsin∠ABC =BCsin∠BAC，即√7√32=3sin∠BAC，解得：sin∠BAC=3√2114，故选：D．先由条件利用余弦定理求得AC，再利用正弦定理求得sin∠BAC的值即可．本题主要考查正弦定理、余弦定理的应用，属于中档题．12.答案：D解析：解：如图，连接AC，BD，交于O，连接EO，∴EO//SD，则直线AE与直线SD所成的角为∠AEO．∵正四棱锥S−ABCD的侧棱长与底面边长都等于2，∴AO=√2，AE=√3，在Rt△AOE中，EO=√AE2−AO2=√(√3)2−(√2)2=1．∴cos∠AEO=EOAE =√3=√33．故选：D．由题意画出图形，连接AC，BD，交于O，连接EO，可得EO//SD，则∠AEO为直线AE与直线SD 所成的角，求解直角三角形得答案．本题考查异面直线所成的角，关键是由异面直线所成角的定义找出角，是中档题．13.答案：(−2,4)解析：本题考查集合的并集的求法，属于基础题． 根据集合A ，B 直接求出A ∪B 即可．解：因为集合A ={x|−2<x <3}，B ={x|0<x <4}， 所以A ∪B ={x|−2<x <4}． 故答案为(−2,4)．14.答案：2−2n−1解析：解：∵S n =2(a 1+a n )，(n ≥2,n ∈N ∗)， ∴S n−1=2(a 1+a n−1)，(n ≥3,n ∈N ∗)， ∴a n =S n −S n−1=2(a n −a n−1)， ∴a n =2a n−1，(n ≥3)∵S n =2(a 1+a n )(n ≥2,n ∈N ∗)， ∴1+a 2=2(1+a 2)，解得a 2=−1， ∴a n ={1,n =1−1×2n−2,n ≥2，∴S n =1−(1+2+4+⋯+2n−2) =1−1−2n−11−2=2−2n−1．故答案为：2−2n−1．由已知得a n =2a n−1，(n ≥3)，a 2=−1，从而a n ={1,n =1−1×2n−2,n ≥2，由此能求出S n ．本题考查数列的前n 项和的求法，是中档题，解题时要认真审题，注意等比数列性质的合理运用．15.答案：16解析：解：由椭圆E ：x 225+y 216=1，得a 2=25，b 2=16， 则a =5，c =√25−16=3，∵P 是椭圆E 上的点，∴|PF 1|+|PF 2|=2a =10，且5−3=2<|PF 2|<5+3=8， ∴|PF 1|⋅|PF 2|=(10−|PF 2|)⋅|PF 2|=−|PF 2|2+10|PF 2|， ∴当|PF 2|=2或8时，|PF 1|⋅|PF 2|的最小值是16． 故答案为：16．由已知椭圆方程求得a，c的值，可得|PF2|的取值范围，结合椭圆定义把|PF1|⋅|PF2|转化为关于|PF2|的二次函数求最值．本题考查椭圆的简单性质，训练了利用二次函数求最值，是中档题．)16.答案：g(x)=sin (x−π6解析：本题考查三角函数的变换，属于基础题．由函数y=Asin(ωx+φ)的图象变换规律可得答案．解：将函数的图象向右平移个单位长度，可得函数的图象，再把所得图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)得到函数的图象，故答案为．17.答案：解：(Ⅰ)根据直方图可知产品件数在[20,25)内的人数为m×5×0.06=6，则m=20(位).(6分)(Ⅱ)根据直方图可知产品件数在[10,15)，[15,20)，[20,25)组内的人数分别为2，4．设这2位工人不在同一组为A事件，低于20件产品的工人选取2位有C62=15种，这2位工人不在同一组的有2×4=8，则P(A)=8．15.(12分)答：选取这2人不在同组的概率为815，由此计算产品件数在[20,25)内的人数；解析：(1)由频率的意义可知，每小组的频率=频数总人数(2)根据概率公式计算，事件“低于20件产品的工人选取2位”有15种可能，而且这些事件的可能性相同，其中事件“这2位工人不在同一组”可能种数是8，那么即可求得事件A的概率．此题考查了对频数分布直方图的掌握情况，考查的是概率的求法．如果一个事件有n种可能，而且．这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P(A)=mn18.答案：(1)证明：取棱A1C1的中点F，连接EF、B1F，则由EF是△AA1C1的中位线得EF//AA1，EF=12AA1，又DB1//AA1，DB1=12AA1，所以EF//DB1，EF=DB1，故四边形DEFB1是平行四边形，从而DE//B1F，因为B1F⊂平面A1B1C1，DE⊄平面A1B1C1所以DE//平面A1B1C1；(Ⅱ)解：因为E是AC1的中点，所以V A−DCE=V D−ACE=12V A−CDC1，过A作AH⊥BC于H，因为平面ABC⊥平面BB1C1C，平面ABC∩平面BB1C1C=BC 所以AH⊥平面BB1C1C，由已知计算可得AH=√3，△CDC1的面积为矩形面积的一半，所以V A−CDC1=13×12×2×4×√3=4√33，所以V A−DCE=V D−ACE=12V A−CDC1=2√33．解析：本题考查三棱柱的性质、线面及面面平行与垂直的判定定理及其性质定理、三角形中位线定理、四棱锥的体积计算公式，考查了推理能力与计算能力，属于中档题．(1)取棱A1C1的中点F，连接EF、B1F，利用三角形中位线定理，证明四边形DEFB1是平行四边形，从而DE//B1F，利用线面平行的判定定理即可得出．(2)过A作AH⊥BC于H，利用V A−DCE=V D−ACE=12V A−CDC1，即可得出三棱锥A−DCE的体积．19.答案：(1)解：∵{a n}满足a1=1，a n=3n−1+a n−1(n≥2)，∴a2=3+a1=4，a3=32+a2 =13．a n−a n−1=3n−1，∴a n=a1+(a2−a1)+(a3−a2)+⋯+(a n−a n−1)=1+3+32+⋯+3n−1=1−3n1−3=3n2−12．∴数列{a n}的通项公式a n=3n2−12．(2)证明：∵a n=3n2−12，∴T n=12[(3−1)+(32−1)+(33−1)+⋯+(3n−1)]=12[(3+32+33+⋯+3n)−n]=12[3(1−3n)1−3−n]=12[3(3n−1)2−n]=3a n−n2，∴T n=3 a n−n2．解析：(1)由已知依次令n=1和n=2，能求出a2、a3的值，再利用累加法能求出{a n}的通项公式．(2)利用分级求和法结合等比数列前n项和公式能证明T n=3 a n−n2．本题考查数列的通项公式的求法，考查数列前n项和的证明，是中档题，解题时要注意累加法、分组求和法和等比数列的性质的合理运用．20.答案：解：(1)依題意，设直线l方程为x=my+1，A(x1,y1)，B(x2,y2).联立y2=2px，得：y2−2pmy−2p=0．由韦达定理：y1+y2=2pm，y1y2=−2p，又x1x2=y122p ⋅y222p=1，OA⃗⃗⃗⃗⃗ ⋅OB⃗⃗⃗⃗⃗⃗ =x1x2+y1y2=1+y1y2=1−2p=−3，所以p=2.故抛物线方程为y2=4x．(2)设线段AB中点为M(x M,y M)，C(0,y C)由(1)知y M=2m,x M=2m2+1．法一：|AB|=x1+x2+p=2x M+2=4m2+4，|CM|=√1+(−m)2|x M−x C|=√1+m2(2m2+1)．依题意：|AB|=2|CM|，即4(m 2+1)=2√1+m 2(2m 2+1)． 整理得m 2=√32．所以S △ABC =12|AB|⋅|CM|=14|AB|2=14(2√3+4)2=7+4√3． 法二：直线CM 方程为：y −2m =−m(x −2m 2−1)， 即y =−mx +2m 3+3m ． 令x =0，则y C =2m 3+3m ．依题意CA ⃗⃗⃗⃗⃗ ⋅CB ⃗⃗⃗⃗⃗ =x 1x 2+(y 1−y C )(y 2−y C )=x 1x 2+y 1y 2−y C (y 1+y 2)+y C 2=0．代入，整理得4m 6+4m 4−3m 2−3=0， 即(4m 4−3)(m 2+1)=0.所以m 2=√32．又|AB|=x 1+x 2+p =2x M +2=4m 2+4，S △ABC =12|AB|⋅|CM|=14|AB|2=14(2√3+4)2=7+4√3．法三：因为直线l 与x 垂直时，不满足题意．故可设直线l ：y =k(x −1)(k ≠0)，A(x 1y 2)，B(x 2y 2). 线段AB 中点为M(x M ,y M )，C(0,y C ).联立y 2=4x 得：k 2x 2−(2k 2+4)x +k 2=0， 由韦达定理：x 1+x 2=2k 2+4k 2,x 1x 2=1．故y 1+y 2=4k ,y 1y 2=−4，所以M(k 2+2k 2,2k )，线段AB 的垂直平分线为y −2k =−1k (x −1−2k 2)， 可得C(0,3k +2k 3)．依题意CA ⃗⃗⃗⃗⃗ ⋅CB ⃗⃗⃗⃗⃗ =x 1x 2+(y 1−y C )(y 2−y C )=x 1x 2+y 1y 2−y C (y 1+y 2)+y C 2=0． 整理得：ky C 2−4y C −3k =0，代入y C =3k +2k 3，整理得(3k 4−4)(k 2+1)=0.解得k 2=2√33．又|AB|=x 1+x 2+p =4k +4．所以S △ABC =12|AB|⋅|CM|=14|AB|2=14(2√3+4)2=7+4√3．解析：(1)由题意设直线l 的方程与抛物线联立，求出两根之和及两根之积，进而求出OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ 的表达式，再由题意求出p 的值，求出抛物线的方程；(2)用3种方法求出面积，设直线AB 的方程，与抛物线联立求出两根之和及两根之积，进而求出弦长AB 及中点M 的坐标，在y 轴取一点C 使CM =12AB ，且CA ⃗⃗⃗⃗⃗ ⋅CB ⃗⃗⃗⃗⃗ =0，求出参数，进而求出面积． 本题考查直线与抛物线的位置关系，数量积运算，考查弦长问题，面积问题，属于中档题．21.答案：解：(1)x ∈(0,+∞)，f′(x)=a −1x =ax−1x，当a ≤0时，f′(x)<0，f(x)在(0,+∞)上为减函数， 当a >0时，x ∈(0,1a )时，f′(x)<0，f(x)为减函数， x ∈(1a ,+∞)时，f′(x)>0，f(x)为增函数，综上所述，当a ≤0时，f(x)减区间为(0,+∞)，当a >0时，f(x)减区间为(0,1a )，f(x)增区间为(1a ,+∞)． (2)g(x)=f(tx +1)+3x+2x+2=2xx+2−ln(tx +1)，g′(x)=4(x+2)2−t tx+1=−tx 2+4(t−1)(tx+1)(x+2)2，当t ≥1时，g′(x)<0恒成立，故g(x)在x ∈(0,+∞)上为减函数，不成立．∴0<t <1， 令g′(x)=0，得x 1=−2√1−t t，x 2=2√1−t t，∵g(x)有两个极值点，∴g′(x)=0有2个根， 故必有−2√1−t t >−1t 且−2√1−t t≠−2，得0<t <12或12<t <1， 且x 1为极小值点，x 2为极大值点，g(x 1)+g(x 2)=2x 1x 1+2−ln(tx 1+1)+2x 2x 2+2−ln(tx 2+1) =4x 1x 2+4(x 1+x 2)x 1x 2+2(x 1+x 2)+4−ln[t 2x 1x 2+t(x 1+x 2)+1]=4(t−1)2t−1−ln(2t −1)2=2−22t−1−ln(2t −1)2，令u =2t −1，0<t <1且t ≠12，当0<t <12时，−1<u <0，12<t <1时，0<u <1，令ℎ(u)=2−2u −lnu 2(0<t <1且t ≠12)， 当−1<u <0时，ℎ(u)=2−2u −2ln(−u)，ℎ′(u)=2−2u u 2>0，∴ℎ(u)在u ∈(−1,0)上为增函数，∴ℎ(u)>ℎ(−1)=4>0， 故当0<t <12时，g(x 1)+g(x 2)>0成立， 当0<u <1时，ℎ(u)=2−2u −2lnu ，ℎ′(u)=2−2u u 2>0，ℎ(u)在u ∈(0,1)上单调递增，∴ℎ(u)<ℎ(1)=0， 故当12<t <1时，g(x 1)+g(x 2)<0， 综上所述，t ∈(0,12)．解析：本题考查了函数的单调性最值问题，考查导数的应用以及分类讨论思想，转化思想，是一道综合题．(1)求出函数的导数，通过讨论a 的范围，求出函数的单调区间即可；(2)求出0<t <12或12<t <1，得到x 1为极小值点，x 2为极大值点，求出g(x 1)+g(x 2)=2−22t−1−ln(2t −1)2，令u =2t −1，0<t <1且t ≠12，根据函数的单调性求出t 的具体范围即可．22.答案：解：(1)曲线C 的参数方程为{x =2cosαy =sinα(α为参数).点P 为曲线C 上的动点，∴设P(2cosα,sinα)，∵直线l 1的极坐标方程为ρcos(θ−π4)=√2，∴直线l 1的极坐标方程为：√22ρcosθ+√22ρsinθ=√2，∴直线l 1的直角坐标方程为x +y −2=0， ∵点P 到直线l 1的距离d =√2=√5sin(α+θ)−2|√2，∴当sin(α+θ)=−1时，点P 到直线l 1的距离取最大值√5+2√2=√10+2√22． (2)∵曲线C 的参数方程为{x =2cosαy =sinα(α为参数)．∴曲线C 的直角坐标方程为x 24+y 2=1．∵直线l 2的极坐标方程为θ=π4，∴直线l 2的直角坐标方程为y =x ， 联立{y =xx +y −2=0，得M(1,1)，联立{x 24+y 2=1x +y −2=0，得A(2,0)，B(65,45)，∴|MA|+|MB|=√(2−1)2+(0−1)2+√(65−1)2+(45−1)2=6√25．解析：(1)设P(2cosα,sinα)，直线l 1的直角坐标方程为x +y −2=0，求出点P 到直线l 1的距离，由此能求出点P 到直线l 1的距离取最大值． (2)曲线C 的直角坐标方程为x 24+y 2=1.直线l 2的直角坐标方程为y =x ，联立{y =xx +y −2=0，得M(1,1)，由此能求出结果．本题考查点到直线的距离的最大值的求法，两线段和的求法，考查直角坐标方程、参数方程、极坐标方程的互化等基础知识，考查运算求解能力，考查函数与方程思想，是中档题．23.答案：解：(1)当a =4时，原不等式即|4x −2|+|4x +2|≥8，即|2x −1|+|2x +1|≥4，当x ≥12时，原不等式等价于(2x −1)+(2x +1)≥4，解得x ≥1， 当−12<x <12时，原不等式等价于(1−2x)+(2x +1)≥4，不等式无解； 当x ≤−12时，原不等式等价于(1−2x)−(2x +1)≥4，解得x ≤−1． 综上，原不等式的解集为(−∞,−1]∪[1,+∞)(2)由f(x)+|x −3|≤x +3得|ax −2|+|x −3|≤x +3(∗)， 当x ∈[2,3]时，(∗)等价于|ax −2|+3−x ≤x +3， 即|ax −2|≤2x ，即|a −2x |≤2，所以−2+2x ≤a ≤2+2x ， 因为13≤1x ≤12，所以2+2x 的最小值为83，−2+2x 最大值为−1． 所以−1≤a ≤83，当x ∈(3,4]时，原不等式等价于|ax −2|+(x −3)≤x +3， 所以|ax −2|≤6，所以−6≤ax −2≤6，即−4≤ax ≤8．所以−4x ≤a ≤8x ，因为14≤1x ≤13，所以8x 的最小值为2，−4x 的最大值为−1， 所以−1≤a ≤2，综上，a的取值范围是[−1,2]．解析：本题考查了绝对值不等式的解法，绝对值不等式的性质，考查推理论证能力，运算求解能力，化归与转化能力，分类与整合思想，属中档题．(1)分3段去绝对值解不等式，再相并；(2)按照2种情况分类讨论去绝对值可得．。

重庆南开中学高2020级高考模拟考试数学（文科）一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．1．已知集合{|||1,},{1,2,3}A x x x Z B =∈=，则A B ⋂为（） A ．{}1-B ．{}1C ．{1,0,1}- D ．∅2．设i 是虚数单位，若复数1iz i =+，则z 的共轭复数为（） A ．1122i +B ．1122i -C ．112i -D ．112i +3．下列函数中，值域是R 且是奇函数的是（）A ．31y x =+B ．sin y x = C ．3y x x =- D ．2xy = 4．向量(3,),(1,2)a m b ==，若()a b b +⊥，则m =（） A ．4-B ．32-C ．0D ．6 5．已知,x y R ∈，命题“若220x y +=，则0x =或0y =”的原命题，逆命题，否命题和逆否命题这四个命题中，真命题个数为（） A ．0B ．2C ．3D ．46．2019年被誉为“5G 商用元年”．6月，5G 商用牌照正式发放；9月，5G 套餐开启预约；11月，5G 套餐公布；12月，5G 手机强势营销．据统计2019年网络上与“5C ”相关的信息量总计高达6875.4万条．从下面的2019年全网信息走势图中可以看到，下列哪个选项是错误的（）A ．相关活动是5G 信息走势的关键性节点B ．月均信息量超过600万条C ．第四季度信息量呈直线增长态势D ．月信息量未出现持续下降态势7．椭圆22217x y b +=，过原点O C ，D ，若||4CD =，则椭圆的标准方程为（） A ．22174x y +=B ．22173x y += C ．22176x y += D ．222177x y += 8．如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的体积为（）A ．43 B ．83C ．4D ．8 9．定义在R 上的奇函数()f x 满足()()11f x f x +=-，且[0,1]x ∈时，()21xf x =-，则()2log 8f =（）A ．1-B ．1C ．7D ．12-10．点P 在函数ln y x =的图象上，若满足到直线y x a =+P 有且仅有3个，则实数a 的值为（）A ．1B ．3-C ．2D ．-11．重庆誉为“桥都”，数十座各式各样的大桥横跨长江、嘉陵江两岸，其中朝天门长江大桥是世界第一大拱桥，其主体造型为：桥拱部分（开口向下的抛物线）与主桁（图中粗线）部分（可视为余弦函数一个周期的图象）相结合．已知拱桥部分长552m ，两端引桥各有190m ，主桁最高处距离桥面89.5m ，则将下列函数等比放大后，与主桁形状最相似的是（）A ．20.45cos3y x = B ．24.5cos 3y x = C ．30.9cos 2y x = D ．39cos 2y x =12．若P 是双曲线2222:1(,0)x y C a b a b-=>在第一象限上一点，12,F F 为双曲线C 的左右焦点，22PF b =，,02a Q ⎛⎫⎪⎝⎭到直线12,PF PF 距离相等，则双曲线C 的离心率为（） A ．53B ．32C ．43 D ．54二、填空题：本题共4小题，每小题5分，共20分．16题第一空2分，第二空3分．13．若变量x ，y 满足约束条件1031010x y x y x y +-≤⎧⎪-+⎨⎪--⎩，则23z x y =+的最大值为__________．14．已知ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若2,1,a b c ===则BC 边上的高为________．15．《九章算术》商功章中研究了一个粮仓的容积计算问题．假设该粮仓近似于由如图的直角梯形以底边AB 为轴旋转而成的几何体（图中长度单位为米），则该粮仓能容纳的体积为________立方米．16．已知()4sin 3cos f x x x =+，()f x 向右平移(0)ααπ<<个单位后为奇函数，则tan α=________，若方程()0f x m -=在[,]απ上恰有两个不等的根，则m 的取值范围是________． 三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17．（12分）正项等比数列{}n a 的前n 项和为n S ，且12461,4a S S S =+=． （1）求{}n a 的通项公式；（2）求数列{}n a n +的前n 项和n T ． 18．（12分）在中华人民共和国成立70周年，国庆期间三大主旋律大片，集体上映，拉开国庆档电影大幕．据统计《我和我的祖国》票房收入为31.71亿元，《中国机长》票房收入为29.12亿元，《攀登者》票房收入为10.98亿元．已知某城市国庆后统计得知大量市民至少观看了一部国庆档大片，在观看的市民中进行随机抽样调查，抽样100人，其中观看了《我和我的祖国》有49人，《中国机长》有46人，《攀登者》有34人，统计图表如下．（1）计算a ，b ，c ；（2）在恰好观看了两部大片的观众中进行分层抽样访谈，抽取总数为7人． （ⅰ）写出各组中抽取人数；（ⅱ）访谈中有2人表示后面将要看第三部，求这2人中要观看的都是《我和我的祖国》的概率． 19．（12分）正三棱柱111ABC A B C -中，D 为1CC 中点，2AB =．（1）求证：平面1ADB ⊥平面11ABB A ； （2）若AD 与平面11ABB A 所成角为4π，求四棱锥1A BCDB -的体积． 20．（12分）已知圆22:(3)8C x y +-=和动圆22:()8P x a y -+=交于A ，B 两点． （1）若直线AB 过原点，求a ；（2）若直线AB 交x 轴于Q ，当PQC 面积最小时，求||AB ． 21．（12分） 已知21()cos 2f x x x x k =-+--． （1）若()f x 的一条切线为y x =，求此时的k ；（2）求使得()0f x >有解的最大整数k ．请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分．作答时用2B 铅笔在答题卡上把所选题目的题号涂黑．22．（10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中，直线l的参数方程为：cos sin x t y t αα=⎧⎪⎨=+⎪⎩（t 为参数）．在以坐标原点O 为极点，x 轴正半轴为极轴的极坐标系中，曲线C 的极坐标方程为2([0,]ρθπ=∈，直线l 与曲线C 交于两不同的点M ，N ．（1）写出直线l 的普通方程与曲线C 的直角坐标方程，并求α的范围； （2）求MN 中点P 轨迹的参数方程． 23．（10分）选修4-5：不等式选讲 已知对于任意1x -，不等式3(1)13x x ++成立．（1）求证：对于任意1x -，4(1)14x x ++； （2）若0a >，0b >，求证：443()4a b a a b ++．重庆南开中学高2020级高考模拟考试·文科数学参考答案、提示及评分细则一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．二、填空题：本题共4小题，每小题5分，共20分．16题第一空2分，第二空3分． 13．3 14．2 15．21π 16．3424,55⎡⎫⎪⎢⎣⎭三、解答题：共70分．解答应写出文字说明、证明过程或演算步骤． 17．解：（1）若公比1111,2166q a a a =+=，不成立； 1分 则()()()2461111,1411111a a a q q q q q q q≠-+-=---- 由于正项等比数列，210q -≠，所以()2241411q q q ++=++， 3分422340,4,2q q q q --=== 5分所以12n n a -=； 6分（2）()1122(12)n n T n -=+++++++(1)212n n n +=-+12分（每个3分） 18．解：（1）274463044918434a b a c b c +++=⎧⎪+++=⎨⎪+++=⎩解得：966a c b =⎧⎪=⎨⎪=⎩； 4分（2）记“同时观看了《机长》和《祖国》”的为A 组：“同时观看了《机长》和《攀登者》”为B 组；“同时观看《祖国》和《攀登者》“为C 组，∴按分层抽样，A ，B ，C 组人数分别为3，2，2 8分 在抽样的7人中，没有观看《祖国》的有2人，设这七个人分别为1231212A A A B B C C ，则还会继续观看第三部的2人可能是：1213231212111221233132A A A A A A B B C C A B A B A B A B A B A B 11213112223211122122AC A C A C AC A C A C B C B C B C B C共21种， 10分 则2人都没有观看《我和我的祖国》的只有12B B 一种，概率是12112分 19．解：（1）取1AB 中点E ，连接DE ，取11A B 中点F ，连接1,EF FC ， 由于是正棱柱，1CC ⊥面111A B C ，从而11CC FC ⊥ 由于D 为1CC 中点，1111,CC AC CC B C ⊥⊥，所以1AD B D ==1AD B D =，则由三线合一性1DE AB ⊥① 3分因为E ，F 分别为111,AB A B 中点，所以1112EF AA DC ==∥∥，则四边形1EFC D 为平行四边形从而1//DE FC ，由于是正棱柱，1CC ⊥面111A B C ，从而11CC FC ⊥，则1CC DE ⊥ 5分 综合①②可知，DE ⊥面11ABB A ，而DE ⊂面1ADB ，所以平面1ADB ⊥平面11ABB A 6分（2）由DE ⊥面11AA B B 知AD 与平面11ABB A 所成角即为4EAD π∠=，而1DE FC == 7分则AD ==1CD CC ==所以1122BCDB S =⋅⋅=，1122BCB S =⋅=，则1132A BCDB A BCB V V --= 9分而11111112332A BCB C ABB ABB V V S CF --==⋅=⋅⋅= 11分所以132A BCDB V -== 12分 20．解：（1）由于两圆有两个公共点，则圆心距小于半径之和，229a +<，得(a ∈． 1分（也可求出a 后检验是否两圆相交）两圆相减得公共弦直线2:692AB y ax a -+=-+， 3分 过原点得，29,3a a ==±，检验成立 5分 （2）直线2:692AB y ax a -+=-+交x 轴，得192Q x a a ⎛⎫=- ⎪⎝⎭7分 1919||22PQ a a a a a⎛⎫=--=+ ⎪⎝⎭，139||3922PQCS PQ a a=⋅=+≥在3a =±时取得最小值，满足(a ∈，成立 10分此时直线:AB y x == 12分21．解：（1）设切点横坐标为t ，()1sin 1,sin 0f t t t t t '=-++=-= 1分()sin ,()cos 10g x x x g x x '=-=-≤，所以()g x 恒单减，而()00g = 3分所以0t =，从而()00f =得1k =- 4分 （2）由题意，要使得21cos 2x x x k -+->有解，即求21()cos 2h x x x x =-+-的最大值 ()1sin ,()1cos 0h x x x h x x '''=-++=-+≤， 5分从而()h x '单减，而22220,12022333h h πππππ⎛⎫⎛⎫''=->=+-<-<⎪ ⎪⎝⎭⎝⎭所以()h x '在2,23ππ⎛⎫⎪⎝⎭有唯一零点0x ，所以()h x 在()0,x -∞单增，()0,x +∞单减 7分 则()200001()cos 2h x h x x x x ≤=-+-，而()0001sin 0h x x x '=-++= 所以()()2000011sin 1sin cos 2h x x x x =-+++-()2220000001111sin 1cos 2cos 1cos cos cos 222x x x x x x ⎡⎤⎡⎤=-++-=--+-=-⎣⎦⎣⎦ 10分 由于0021,,cos ,0232x x ππ⎛⎫⎛⎫∈∈-⎪ ⎪⎝⎭⎝⎭()()200113cos 10,224h x x ⎛⎫=--∈ ⎪⎝⎭，所以整数k 最大值为0． 12分22．解：（1）直线l的普通方程为：sin cos x y αα⎛⋅=-⎝⎭； 曲线C 的直角坐标方程为：224(0)x y y +=≥ 3分 直线l为过⎛ ⎝，倾斜角α的直线，与曲线C 有两个公共点，作图可知在直线过左右顶点时为临界情况，倾斜角50,,66ππαπ⎡⎤⎡⎫∈⋃⎪⎢⎥⎢⎣⎦⎣⎭5分 （2）直线l 代入曲线C ：21240,32P t t t t t αα++⋅+=== 8分 代入得到中点P 轨迹的参数方程：2cos 3sin 33x y ααα⎧=-⎪⎪⎨⎪=-⎪⎩（α为参数，50,,66a πππ⎡⎤⎡⎫∈⋃⎪⎢⎥⎢⎣⎦⎣⎭） 10分 23．解：（1）因为1x ≥-，所以10x +≥ 1分从而32(1)(1)(13)(1)14314x x x x x x x ++≥++=++≥+，得证 5分 （2）欲证443()4a b a a b +≥+只需43414a b a b a a +⎛⎫≥+ ⎪⎝⎭4114b b a a ⎛⎫⇐+≥+⋅ ⎪⎝⎭（*） 7分由于,0a b >，所以01ba>>-， 8分 由（1）知取bx a=时（*）式成立，从而原不等式得证． 10分。

重庆南开中学高2018级高考模拟考试试题卷数 学（文）数学试题卷（文史类），满分180分。

考试时间180分钟。

注意事项：1、答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2、答选择题时，必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦擦干净后，再选涂其他答案标号。

3、答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4、所有题目必须在答题卡上作答，在试题卷上答题无效。

5、考试结束后，将试题卷和答题卡一并收回。

一、选择题：本大题共18小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、复数1ii+（i 为虚数单位）的模等于（ ）A B 、2 C D 、122、已知全集{}{},21,ln 0x U R A y y B x x ===+=<，则()U C A B = （ ） A 、φ B 、112x x ⎧⎫<≤⎨⎬⎩⎭C 、{}1x x <D 、{}01x x <<3、在等差数列{}n a 中，912162a a =+，则6a =（ ）A 、18B 、18C 、18D 、184、若函数()f x 为偶函数，0x >时，()f x 单调递增，()(),,P f Q f e R fπ=-==，则,,P Q R 的大小为（ ）A 、R Q P >>B 、P Q R >>C 、P R Q >>D 、Q R P >> 5、已知三棱锥的三视图如题（5）图所示，则它的体积为（ ）AB 、3C 、2D6、执行如题（6）图所示程序框图，则输出的S 的值为（ ）A 、21B 、25C 、45D 、93 7、已知函数()2x f x e x a =-+有零点，则实数a 的取值范围是（ ）A 、[)2ln22,-+∞B 、(],2ln22-∞-C 、[)2ln 2,+∞D 、[]2ln22,2ln2- 8、已知(),P x y 是直线()400kx y k ++=>上一动点，PA 是圆22:20C x y y +-=的一条切线，A 是切点，若PA 长度最小值为2，则k 的值为（ ）A 、3B 、2C 、D 、29、已知ABC ∆三个内角,,A B C 对应的边分别为,,a b c ，且满足2,2cos 2a b C c a =+=，3sin 2cos 262A A π⎛⎫++= ⎪⎝⎭，则ABC S ∆=（ ）A 、BCD 、218、已知点A 、B 、C 为椭圆2214x y +=上三点，其中A ⎛ ⎝⎭，且ABC ∆的内切圆圆心在直线1x =上，则ABC ∆三边斜率和为（ ）A 、6- B 、6C 、 D二、填空题：本大题共5小题，每小题5分，共25分。

2016年重庆市南开中学高考数学模拟试卷（文科）一、选择题：（共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．已知集合A={x|x2﹣x=0}，集合B={y|﹣1＜y＜1}，则A∩B=（）A．0 B．∅C．{0}D．{∅}2．已知i为虚数单位，zi=2i﹣z，则复数z在复平面内对应的点位于（）A．第一象限 B．第二象限 C．第三象限 D．第四象限3．从编号为1，2，3，4的四个小球中任选两个球，则选出的两个球数字之和大于等于5的概率为（）A．B．C．D．4．已知△ABC中，内角A，B，C的对边分别为a，b，c，若a2=b2+c2﹣bc，bc=4，则△ABC 的面积为（）A．B．1 C．D．25．已知cos（α+）=，则sin2α=（）A．B．C．D．6．已知F1，F2分别为椭圆+=1（a＞b＞0）的左、右焦点，P为椭圆上一点，且PF2垂直于x轴．若|F1F2|=2|PF2|，则该椭圆的离心率为（）A．B．C．D．7．若执行如图所示的程序框图，则输出的结果s=（）A．8 B．9 C．10 D．118．若定义在R的函数f（x）=ln（ax+）为奇函数，则实数a的值为（）A．1 B．﹣1 C．±1 D．09．如图，在三棱锥V﹣ABC中，V A⊥VC，AB⊥BC，∠V AC=∠ACB=45°，若侧面V AC ⊥底面ABC，则其主视图与左视图面积之比为（）A．2：1 B．2：C．：1 D．1：110．已知抛物线C的顶点是原点O，焦点F在x轴的正半轴上，经过F的直线与抛物线C交于A，B两点，如果•=﹣12，那么抛物线C的方程为（）A．x2=8y B．x2=4y C．y2=8x D．y2=4x11．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上是减函数，若f（ln）+f（ln）﹣2f（1）＜0，则的取值范围是（）A．（0，）B．（，e）C．（e，+∞）D．（0，）∪（e，+∞）12．若存在实数m，n，使得的解集为[m，n]，则a的取值范围为（）A．B．C．D．二、填空题：（本大题共4小题，每小题5分．共20分．）13．已知平面向量=（1，﹣2），2﹣=（﹣1，0），则||=______．14．设x，y满足，则z=x+y的最小值为______．15．已知正方体ABCD﹣A1B1C1D1的各个顶点都在球O的球面上，若球O的表面为12π，则球心O到平面ACD1的距离为______．16．已知函数f（x）=2sin（ωx+）（ω＞0）与函数g（x）=cos（2x+φ）（|φ|＜）的对称轴完全相同，则φ=______．三、解答题：（本大题共5小题，满分60分．解答须写出文字说明，证明过程或演算步骤．）17．数列{a n}的前n项和为A n=n2+bn，数列{b n}是等比数列，公比q＞0，且满足a1=b1=2，b2，a3，b3成等差数列；（1）求数列{a n}和{b n}的通项公式；（2）若数列{c n}满足c n=b n+，求c n的前n项和．18．如图，直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形，E，F分别是BC，CC1的中点．（1）证明：平面AEF⊥平面B1BCC1；（2）设AB的中点为D，且CD=A1D，求三棱锥A1﹣AEF的体积．19．我国大力提倡足球运动，从2013年开始高校的体考生招生也向招收足球项目的考生倾斜，某高校（四年制）为了解近四年学校招收体考生中足球项目考生的情况，做了如下统计，现以2012年为统计起始年，记为x=0，以足球项目考生占所有体考生的比例为y．2012级2013级2014级2015级x 0 1 2 3体考生250 260 300 300足球项目考生35 39 45 48y 0.14 0.15（1）已知y关于变量x的变化关系满足线性回归方程=x+，其中=0.141，求出回归方程；2016级计划足球项目考生60人，根据线性回归方程2016级总的体考生将招收多少人（人数四舍五入）；（2）开学后举行了一次新生足球见面赛，由15级16级的足球项目考生共同组成一支18人足球队，按分层抽样确定15级，16级的足球队员人数．（i）求足球队中，15级和16级的足球队员各有多少人？（ii）比赛上场队员有11人，其余7人在场外替补，已知在场上有6名16级学生，在比赛过程中有2名替补队员被替换上场，求替换上场的选手中恰好有1名16级的新生的概率．20．已知圆F的方程为x2+y2﹣2x=0，与x轴正半轴交于点A，椭圆C的中心在原点，焦点在圆心F，顶点为A．（1）求椭圆的方程；（2）如图D，C是椭圆上关于y轴对称的两点，在x轴上存在点B，使得四边形ABCD为菱形，求B点坐标．21．已知函数f（x）=x+alnx在x=1处的切线与直线x+2y=0垂直，g（x）=f（x）+﹣bx．（1）求实数a的值；（2）设x1，x2（x1＜x2）是函数g（x）的两个极值点，若|g（x1）﹣g（x2）|≥﹣ln2，求b的范围．[选做题：几何选讲]22．如图所示，两个圆相内切于点T，公切线为TN，过内圆上一点M，做内圆的切线，交外圆于C，D两点，TC，TD分别交内圆于A，B两点．（1）证明：AB∥CD；（2）证明：AC•MD=BD•CM．选做题：坐标及参数方程]23．以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为2ρ2cos2θ﹣3ρ2sin2θ=30，圆O的圆心在原点，经过曲线C的右焦点F．（1）求曲线C和圆O的标准方程；（2）已知直线l的参数方程为（t为参数）与圆O交于B，C两点，其中B在第四象限，C在第一象限，若|BC|=5，∠FOC=α，求sin（﹣α）的值．[选做题：不等式选讲]24．已知命题“∀a＞b＞c，”是真命题，记t的最大值为m，命题“∀n∈R，”是假命题，其中．（Ⅰ）求m的值；（Ⅱ）求n的取值范围．2016年重庆市南开中学高考数学模拟试卷（文科）参考答案与试题解析一、选择题：（共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．已知集合A={x|x2﹣x=0}，集合B={y|﹣1＜y＜1}，则A∩B=（）A．0 B．∅C．{0}D．{∅}【考点】交集及其运算．【分析】求出集合的等价条件，根据集合的基本运算进行求解即可．【解答】解：A={x|x2﹣x=0}={0，1}，集合B={y|﹣1＜y＜1}，则A∩B={0}，故选：C2．已知i为虚数单位，zi=2i﹣z，则复数z在复平面内对应的点位于（）A．第一象限 B．第二象限 C．第三象限 D．第四象限【考点】复数代数形式的乘除运算．【分析】把已知的等式变形，然后利用复数代数形式的乘除运算化简得答案．【解答】解：∵zi=2i﹣z，∴z（1+i）=2i，则，∴复数z在复平面内对应的点的坐标为（1，1），位于第一象限．故选：A．3．从编号为1，2，3，4的四个小球中任选两个球，则选出的两个球数字之和大于等于5的概率为（）A．B．C．D．【考点】古典概型及其概率计算公式．【分析】先求出基本事件总数，再用列举法求出选出的两个球数字之和大于等于5包含的基本事件个数，由此能求出选出的两个球数字之和大于等于5的概率．【解答】解：从编号为1，2，3，4的四个小球中任选两个球，基本事件总数n==6，选出的两个球数字之和大于等于5包含的基本事件有：（1，4），（2，3），（2，4），（3，4），共有m=4个，∴选出的两个球数字之和大于等于5的概率p==．故选：B．4．已知△ABC中，内角A，B，C的对边分别为a，b，c，若a2=b2+c2﹣bc，bc=4，则△ABC 的面积为（）A．B．1 C．D．2【考点】余弦定理．【分析】由已知及余弦定理可求cosA，从而可求sinA的值，结合已知由三角形面积公式即可得解．【解答】解：∵a2=b2+c2﹣bc，∴由余弦定理可得：cosA===，又0＜A＜π，∴可得A=60°，sinA=，∵bc=4，=bcsinA==．∴S△ABC故选：C．5．已知cos（α+）=，则sin2α=（）A．B．C．D．【考点】二倍角的正弦；三角函数的化简求值．【分析】利用诱导公式与倍角公式即可得出．【解答】解：∵cos（α+）=，则sin2α=﹣cos=﹣=﹣=﹣，故选：D．6．已知F1，F2分别为椭圆+=1（a＞b＞0）的左、右焦点，P为椭圆上一点，且PF2垂直于x轴．若|F1F2|=2|PF2|，则该椭圆的离心率为（）A．B．C．D．【考点】椭圆的简单性质．【分析】设F1（﹣c，0），F2（c，0），（c＞0），通过|F1F2|=2|PF2|，求出椭圆的离心率e．【解答】解：F1，F2分别为椭圆+=1（a＞b＞0）的左、右焦点，设F1（﹣c，0），F2（c，0），（c＞0），P为椭圆上一点，且PF2垂直于x轴．若|F1F2|=2|PF2|，可得2c=2，即ac=b2=a2﹣c2．可得e2+e﹣1=0．解得e=．故选：D ．7．若执行如图所示的程序框图，则输出的结果s=（ ）A ．8B ．9C ．10D ．11【考点】程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的n ，s ，a 的值，当n=3时，不满足条件n ＜3，输出s 的值为9．【解答】解：模拟执行程序框图，可得 a=1，s=0，n=1 s=1，a=3满足条件n ＜3，n=2，s=4，a=5 满足条件n ＜3，n=3，s=9，a=7不满足条件n ＜3，输出s 的值为9． 故选：B ．8．若定义在R 的函数f （x ）=ln （ax +）为奇函数，则实数a 的值为（ ）A ．1B ．﹣1C ．±1D ．0【考点】函数奇偶性的判断．【分析】根据函数奇偶性的定义建立方程关系进行求解即可得到结论．【解答】解：∵定义在R 的函数f （x ）=ln （ax +）为奇函数，∴f （﹣x ）=﹣f （x ）， 即f （﹣x ）+f （x ）=0，则ln （ax +）+ln （﹣ax +）=ln （ax +）•（﹣ax +）=ln （x 2+1﹣a 2x 2）=0，则x 2+1﹣a 2x 2=1，即x 2﹣a 2x 2=0， 则1﹣a 2=0， 则a=±1，故选：C9．如图，在三棱锥V ﹣ABC 中，V A ⊥VC ，AB ⊥BC ，∠V AC=∠ACB=45°，若侧面V AC ⊥底面ABC ，则其主视图与左视图面积之比为（ ）A ．2：1B ．2：C ．：1 D ．1：1【考点】简单空间图形的三视图．【分析】由条件可知△V AC ，△ABC 为等腰直角三角形，故主视图面积为S △V AC ，左视图面积为S △BOV ．【解答】解：取AC 的中点O ，连接OB ，OV ， ∵VA ⊥VC ，AB ⊥BC ，∠V AC=∠ACB=45°， ∴△V AC ，△ABC 为等腰直角三角形， ∴OV ⊥AC ，OB ⊥AC ，又侧面VAC ⊥底面ABC ，侧面V AC ∩底面ABC=AC ， ∴OV ⊥平面ABC ，OB ⊥平面V AC ．设AC=x ，OV=h ，则OB=．则几何体的主视图面积为S △V AC ==．左视图的面积为S △BOV ==．∴=2．故选：A ．10．已知抛物线C 的顶点是原点O ，焦点F 在x 轴的正半轴上，经过F 的直线与抛物线C交于A ，B 两点，如果•=﹣12，那么抛物线C 的方程为（ ） A ．x 2=8y B ．x 2=4y C ．y 2=8xD ．y 2=4x【考点】轨迹方程．【分析】设抛物线方程为y 2=2px （p ＞0），焦点坐标为（，0），直线AB 的方程为y=k （x﹣），与抛物线方程联立，消去y 整理成关于x 的一元二次方程，设出A （x 1，y 1）、B （x 2，y 2）两点坐标，•=x 1•x 2+y 1•y 2，由韦达定理可以求得答案．【解答】解：设抛物线方程为y2=2px（p＞0），焦点坐标为（，0），∴直线AB的方程为y=k（x﹣），由直线与抛物线方程联立，得k2x2﹣（pk2+2p）x+p2k2=0，设A（x1，y1），B（x2，y2），则x1+x2=p+，x1•x2=p2，y1•y2=k（x1﹣）•k（x2﹣）=k2[x1•x2﹣（x1+x2）+p2]=﹣p2，∴•=x1•x2+y1•y2=p2﹣p2=﹣12，∴p=4，∴抛物线C的方程为y2=8x．故选：C．11．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）上是减函数，若f（ln）+f（ln）﹣2f（1）＜0，则的取值范围是（）A．（0，）B．（，e）C．（e，+∞）D．（0，）∪（e，+∞）【考点】奇偶性与单调性的综合．【分析】由函数为定义在R上的偶函数且在区间[0，+∞）上是单调减函数，则不等式可转化为f（ln）＜f（1），求解对数不等式即可解得答案．【解答】解：∵f（x）定义在R上的偶函数，在区间[0，+∞）上是单调减函数∴f（x）在（﹣∞，0）上是增函数，又f（ln）+f（ln）﹣2f（1）＜0，∴f（ln）＜f（1），∴|ln|＞1，∴ln＞1或ln＜﹣1，可以解得，的取值范围是（0，）∪（e，+∞）．故选：D．12．若存在实数m，n，使得的解集为[m，n]，则a的取值范围为（）A．B．C．D．【考点】其他不等式的解法．【分析】转化为a≤，求出表达式的最大值，以及单调区间，即可得到a的取值范围．【解答】解：ae x≤x（e是自然对数的底数），转化为a≤，令y=，则y′=，令y′=0，可得x=1，当x＞1时，y′＜0，函数y递减；当x＜1时，y′＞0，函数y递增．则当x=1时函数y取得最大值，由于存在实数m、n，使得f（x）≤0的解集为[m，n]，则由右边函数y=的图象可得a的取值范围为（0，）．故选：D．二、填空题：（本大题共4小题，每小题5分．共20分．）13．已知平面向量=（1，﹣2），2﹣=（﹣1，0），则||=5．【考点】向量的模．【分析】设出的坐标，求出2﹣=（2﹣x，﹣4﹣y）=（﹣1，0），根据对应关系求出x，y的值，从而求出向量的模即可．【解答】解：设=（x，y），∵=（1，﹣2），2﹣=（﹣1，0），∴2﹣=（2﹣x，﹣4﹣y）=（﹣1，0），∴，解得：，∴||==5，故答案为：5．14．设x，y满足，则z=x+y的最小值为2．【考点】简单线性规划的应用．【分析】本题考查的知识点是简单线性规划的应用，我们要先画出满足约束条件的平面区域，然后分析平面区域里各个角点，然后将其代入z=x+y中，求出z=x+y的最小值．【解答】解：满足约束条件的平面区域如图示：由图得当过点B（2，0）时，z=x+y有最小值2．故答案为：2．15．已知正方体ABCD﹣A1B1C1D1的各个顶点都在球O的球面上，若球O的表面为12π，则球心O到平面ACD1的距离为．【考点】球内接多面体．【分析】利用球O的表面积为12π，可得球的半径，正方体的对角线长为2，即可求出球心O到平面ACD1的距离．【解答】解：∵球O的表面积为12π，∴4πR2=12π∴R=，∴正方体的对角线长为2，∴球心O到平面ACD1的距离为OD﹣OO1=﹣=．故答案为：．16．已知函数f（x）=2sin（ωx+）（ω＞0）与函数g（x）=cos（2x+φ）（|φ|＜）的对称轴完全相同，则φ=﹣．【考点】正弦函数的对称性；余弦函数的对称性．【分析】由条件利用正弦函数、余弦函数的周期性以及它们的图象的对称性，求得φ的值．【解答】解：∵函数f（x）=2sin（ωx+）（ω＞0）与函数g（x）=cos（2x+φ）（|φ|＜）的对称轴完全相同，∴它们的周期相同，即=，∴ω=2．令2x+=kπ+，可得x=+，k∈Z，即f（x）=2sin（ωx+）的图象的对称轴为x=+，k∈Z．故函数g（x）=cos（2x+φ）（|φ|＜）的图象的对称轴为x=+，k∈Z，即2•（+）+φ=nπ，即kπ++φ=nπ，n∈Z，故φ=﹣，故答案为：﹣．三、解答题：（本大题共5小题，满分60分．解答须写出文字说明，证明过程或演算步骤．）17．数列{a n}的前n项和为A n=n2+bn，数列{b n}是等比数列，公比q＞0，且满足a1=b1=2，b2，a3，b3成等差数列；（1）求数列{a n}和{b n}的通项公式；（2）若数列{c n}满足c n=b n+，求c n的前n项和．【考点】数列的概念及简单表示法．【分析】（1）令n=1得出b，于是a n=A n﹣A n，根据b2，a3，b3成等差数列求出q，从而﹣1得出b n；（2）使用分项求和与列项求和计算c n的前n项和．【解答】解：（1）∵A n=n2+bn，∴当n=1时，a1=1+b=2，∴b=1．=n2+n﹣（n﹣1）2﹣（n﹣1）=2n．∴当n≥2时，a n=A n﹣A n﹣1显然当n=1时，上式仍成立．∴a n=2n．∵数列{b n}是等比数列，公比为q，b1=2．∴b2=2q，b3=2q2．又a3=6，b2，a3，b3成等差数列，∴2q+2q2=12．解得q=2或q=﹣3（舍）．∴b n=2•2n﹣1=2n．（2）c n=2n+=2n+﹣．设{c n}的前n项和为S n，则S n=2+22+23+…+2n+（1﹣）+（）+（）+…+（）=+（1﹣）=2n+1﹣﹣1．18．如图，直三棱柱ABC﹣A1B1C1的底面是边长为2的正三角形，E，F分别是BC，CC1的中点．（1）证明：平面AEF⊥平面B1BCC1；（2）设AB的中点为D，且CD=A1D，求三棱锥A1﹣AEF的体积．【考点】棱柱、棱锥、棱台的体积；平面与平面垂直的判定．【分析】（1）由三棱柱ABC﹣A1B1C1是直三棱柱，可得侧棱垂直于底面，得到AE⊥BB1，再由E是正三角形ABC的边BC的中点，可得AE⊥BC，利用线面垂直的判定得到AE⊥平面B1BCC1，再由面面垂直的判定得答案；（2）△CA1D是等腰直角三角形，解直角三角形得到直三棱柱的高，由三棱锥体积公式，利用等体积转换，即可求得三棱锥A1﹣AEF的体积．【解答】证明：（1）∵三棱柱ABC﹣A1B1C1是直三棱柱，∴B1B⊥底面ABC，则AE⊥BB1，又E是正三角形ABC的边BC的中点，∴AE⊥BC，又B1B∩BC=B，因此AE⊥平面B1BCC1，而AE⊂平面AEF，∴平面AEF⊥平面B1BCC1；解：（2）在正三角形ABC中，由AB=BC=AC=2，得CD=，∵CD=A1D，∴A1D=，在Rt△AA1D中，AA1==，∴三棱锥A1﹣AEF的体积=三棱锥E﹣A1AF的体积==．19．我国大力提倡足球运动，从2013年开始高校的体考生招生也向招收足球项目的考生倾斜，某高校（四年制）为了解近四年学校招收体考生中足球项目考生的情况，做了如下统计，现以2012年为统计起始年，记为x=0，以足球项目考生占所有体考生的比例为y．2012级2013级2014级2015级x 0 1 2 3体考生250 260 300 300足球项目考生35 39 45 48y 0.14 0.15（1）已知y关于变量x的变化关系满足线性回归方程=x+，其中=0.141，求出回归方程；2016级计划足球项目考生60人，根据线性回归方程2016级总的体考生将招收多少人（人数四舍五入）；（2）开学后举行了一次新生足球见面赛，由15级16级的足球项目考生共同组成一支18人足球队，按分层抽样确定15级，16级的足球队员人数．（i）求足球队中，15级和16级的足球队员各有多少人？（ii）比赛上场队员有11人，其余7人在场外替补，已知在场上有6名16级学生，在比赛过程中有2名替补队员被替换上场，求替换上场的选手中恰好有1名16级的新生的概率．【考点】古典概型及其概率计算公式；分层抽样方法．【分析】（1）由已知求出=1.5，=0.15，由线性回归方程=x+0.141过点（1.5，0.15），能求出线性回归方程=0.006x+0.141．根据线性回归方程能求出2016级总的体考生将招收的人数．（2）（i）15级有足球项目考生48人，16级有足球项目考生60人，由15级16级的足球项目考生共同组成一支18人足球队，按分层抽样能确定15级足球队员人数和16级的足球队员人数．（ii）由题意知7名替补队员中有15级学生3名，16级新生4名，由此利用等可能事件概率计算公式能求出替换上场的选手中恰好有1名16级的新生的概率．【解答】解：（1）==1.5，=0.15，∵=0.141，∴=x+0.141，∵线性回归方程=x+0.141过点（1.5，0.15），∴0.15=1.5+0.141，解得=0.006，∴线性回归方程=0.006x+0.141．2016级时，=0.006×4+0.141=0.165，∵2016级计划足球项目考生60人，∴根据线性回归方程2016级总的体考生将招收：≈364（人）．（2）（i）∵15级有足球项目考生48人，16级有足球项目考生60人，由15级16级的足球项目考生共同组成一支18人足球队，∴按分层抽样确定15级足球队员人数为：48×=8人，16级的足球队员人数为：60×=10．（ii）由题意知7名替补队员中有15级学生3名，16级新生4名，在比赛过程中有2名替补队员被替换上场，基本事件总数n==21，替换上场的选手中恰好有1名16级的新生包含的基本事件个数m==12，∴替换上场的选手中恰好有1名16级的新生的概率p===．20．已知圆F的方程为x2+y2﹣2x=0，与x轴正半轴交于点A，椭圆C的中心在原点，焦点在圆心F，顶点为A．（1）求椭圆的方程；（2）如图D，C是椭圆上关于y轴对称的两点，在x轴上存在点B，使得四边形ABCD为菱形，求B点坐标．【考点】直线与圆锥曲线的综合问题；椭圆的标准方程．【分析】（1）圆的方程出A（2，0），圆心F（1，0），设椭圆方程为，（a＞b＞0），则a=2，c=1，由此能求出椭圆方程．（2）设D（m，n），则C（﹣m，n），B（2﹣2m，0），m＞0，n＞0，由题意得，由此能求出点B坐标．【解答】解：（1）∵圆F的方程为x2+y2﹣2x=0，与x轴正半轴交于点A，∴令y=0，得A（2，0），圆心F（1，0），∵椭圆C的中心在原点，焦点在圆心F（1，0），顶点为A（2，0），设椭圆方程为，（a＞b＞0），则a=2，c=1，∴b2=4﹣1=3，∴椭圆方程为．（2）设D（m，n），则C（﹣m，n），B（2﹣2m，0），m＞0，n＞0，由题意得，由m＞0，解得m=.2﹣2m=2﹣=，∴B（，0）．21．已知函数f（x）=x+alnx在x=1处的切线与直线x+2y=0垂直，g（x）=f（x）+﹣bx．（1）求实数a的值；（2）设x1，x2（x1＜x2）是函数g（x）的两个极值点，若|g（x1）﹣g（x2）|≥﹣ln2，求b的范围．【考点】利用导数研究函数的极值；利用导数研究曲线上某点切线方程．【分析】（1）求导数，利用导数的几何意义能求出实数a的值．（2）求出g（x1）﹣g（x2）=ln﹣（﹣），通过换元得到g（x1）﹣g（x2）＞0，得到0＜≤，从而求出b的范围即可．【解答】解：（1）∵f（x）=x+alnx，∴f′（x）=1+，∵f（x）在x=1处的切线l与直线x+2y=0垂直，∴k=f′（x）|x=1=1+a=2，解得a=1．（2）∵g（x）=lnx+x2﹣（b﹣1）x，∴g′（x）==0，∴x1+x2=b﹣1，x1x2=1∴g（x1）﹣g（x2）=ln﹣（﹣）∵0＜x1＜x2，∴设t=，0＜t＜1，令h（t）=lnt﹣（t﹣），0＜t＜1，则h′（t）=﹣＜0，∴h（t）在（0，1）上单调递减，∴h（t）＞h（1）=0，∴g（x1）﹣g（x2）＞0，若|g（x1）﹣g（x2）|≥﹣ln2，即g（x1）﹣g（x2）≥﹣ln2，即lnt﹣（t﹣）≥﹣ln2，∴0＜t≤，∴0＜≤，由x1•x2=1，得：x2=，∴≤，0＜x1≤，而x1+x2=b﹣1即x1+=b﹣1，∴b=+x1+1，（0＜x1＜），令p（x）=x++1，（0＜x＜），p′（x）=1﹣=＜0，p（x）在（0，）递减，∴p（x）＞p（）=1+，故b＞1+．[选做题：几何选讲]22．如图所示，两个圆相内切于点T，公切线为TN，过内圆上一点M，做内圆的切线，交外圆于C，D两点，TC，TD分别交内圆于A，B两点．（1）证明：AB∥CD；（2）证明：AC•MD=BD•CM．【考点】与圆有关的比例线段．【分析】（1）证明∠TCD=∠TAB，即可证明AB∥CD；（2）证明：∠MTD=∠ATM，利用正弦定理证明=，由AB∥CD知=，即可证明AC•MD=BD•CM．【解答】证明：（1）由弦切角定理可知，∠NTB=∠TAB，…同理，∠NTB=∠TCD，所以，∠TCD=∠TAB，所以，AB∥CD．…（2）连接TM、AM，因为CD是切内圆于点M，所以由弦切角定理知，∠CMA=∠ATM，又由（Ⅰ）知AB∥CD，所以，∠CMA=∠MAB，又∠MTD=∠MAB，所以∠MTD=∠ATM．…在△MTD中，由正弦定理知，，在△MTC中，由正弦定理知，，因∠TMC=π﹣∠TMD，所以=，由AB∥CD知=，所以=，即AC•MD=BD•CM．…选做题：坐标及参数方程]23．以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为2ρ2cos2θ﹣3ρ2sin2θ=30，圆O的圆心在原点，经过曲线C的右焦点F．（1）求曲线C和圆O的标准方程；（2）已知直线l的参数方程为（t为参数）与圆O交于B，C两点，其中B在第四象限，C在第一象限，若|BC|=5，∠FOC=α，求sin（﹣α）的值．【考点】简单曲线的极坐标方程；参数方程化成普通方程．【分析】（1）曲线C的极坐标方程为2ρ2cos2θ﹣3ρ2sin2θ=30，把y=ρsinθ，x=ρcosθ代入即可化为标准方程．可得c=5．得到圆O的半径为5，即可得出标准方程．（2）把直线l的参数方程（t为参数），可知：直线l经过点B（4，﹣3），点B在圆O上，而|BC|=5，可得△OBC是等边三角形．得出sin∠xOB即可得出sin（﹣α）．【解答】解：（1）曲线C的极坐标方程为2ρ2cos2θ﹣3ρ2sin2θ=30，把y=ρsinθ，x=ρcosθ代入即可化为2x2﹣3y2=30，∴标准方程为：．∴c==5．可得曲线C的右焦点F（5，0）．∴圆O的标准方程为：x2+y2=25．（2）把直线l的参数方程（t为参数），可知：直线l经过点B（4，﹣3），点B在圆O上，而|BC|=5，∴△OBC是等边三角形．∵sin∠xOB=∴sin（﹣α）=．[选做题：不等式选讲]24．已知命题“∀a＞b＞c，”是真命题，记t的最大值为m，命题“∀n∈R，”是假命题，其中．（Ⅰ）求m的值；（Ⅱ）求n的取值范围．【考点】全称命题．【分析】（Ⅰ）问题转化为，利用基本不等式的性质求出即可；（Ⅱ）问题转化为∃n∈R，”是真命题，根据三角函数以及绝对值的意义求出n的范围即可．【解答】解：（Ⅰ）因为“∀a＞b＞c，”是真命题，所以∀a＞b＞c，恒成立，又a＞b＞c，所以恒成立，所以，．…又因为=，“=”成立当且仅当b﹣c=a﹣b时．因此，t≤4，于是m=4．…（Ⅱ）由（Ⅰ）得，因为“∀n∈R，”是假命题，所以“∃n∈R，”是真命题．…因为|n+sinγ|﹣|n﹣cosγ|=|n+sinγ|﹣|cosγ﹣n|≤|sinγ+cosγ|（），因此，，此时，即时．…∴，由绝对值的意义可知，．…2016年10月5日。

一、选择题（每题5分，共50分）1. 若函数f(x) = 2x^3 - 3x^2 + 4x + 1在x=1处取得极值，则该极值为（）A. 0B. 1C. 2D. 32. 已知等差数列{an}的前n项和为Sn，若a1=1，d=2，则S10等于（）A. 55B. 60C. 65D. 703. 在直角坐标系中，点P(m, n)关于直线y=x的对称点为Q，若P在直线y=2x+1上，则m+n的值为（）A. 1B. 2C. 3D. 44. 若复数z满足|z+1|=|z-1|，则z在复平面上的轨迹是（）A. 圆B. 线段C. 直线D. 点5. 若函数y=Asin(ωx+φ)的图象在x=π/4时取得最小值，则A、ω、φ的取值分别为（）A. A>0, ω>0, φ>π/2B. A>0, ω>0, φ<π/2C. A<0, ω>0, φ>π/2D. A<0, ω>0, φ<π/26. 已知函数f(x) = (x^2 - 1)/(x - 1)，则f(x)的定义域为（）A. (-∞, 1)B. (-∞, 1)∪(1, +∞)C. (-∞, 1)∪(1, +∞)D. (-∞, +∞)7. 在△ABC中，若角A、B、C的对边分别为a、b、c，且a=3，b=4，c=5，则△ABC的面积为（）A. 6B. 8C. 10D. 128. 若函数y=x^3 - 3x在区间[0, 2]上单调递增，则x的取值范围为（）A. (0, 2)B. [0, 2]C. (0, +∞)D. [0, +∞)9. 已知等比数列{an}的公比为q，若a1=2，S5=62，则q的值为（）A. 2B. 1/2C. 1/4D. 410. 在平面直角坐标系中，直线y=kx+b与圆x^2 + y^2 = 1相切，则k^2 + b^2等于（）A. 1B. 2C. 3D. 4二、填空题（每题5分，共25分）11. 函数f(x) = log2(3x - 2)的定义域为______。