中考数学模拟题分类汇编实验及操作.doc

2019-2020 年中考数学模拟试题（含答案）（九年级备课组制）一、选择题（ 3×7=21 分）1．－ 2 的倒数是（）A ．1B ．1C ． 2D ．－ 2222．下列运算正确的是（）A ．x 5 x 5 x 10B ． x 5 ·x 5 x 10C ．( x 5 )5 x 10D ．x 20 x 2x 103．下图中所示的几何体的主视图是（）A ．B ．C ．D ．2x 4 0）4．不等式组0 的解集为（3 xA ．x ＞2 B ．x ＜3C ． x ＞ 2 或 x ＜－3 D ． ＜x ＜32 5、若一次函数 y ax b 的图象经过二、 三、四象限，则二次函数 y ax 2bx 的图象只可能是（ ）A 、B 、C 、D 、O 6、如图， AB 是⊙ O 的弦， OC 是⊙ O 的半径， OC ⊥ AB于点 D ，AB ＝ 16cm ，OD=6cm ，那么⊙ O 的半径是（）D B A 、5 cm B 、10 cmACC 、20 cmD 、12 cm7．如图，小明从点 O 出发，先向西走 40 米，再向南走 30 米到达点 M ，如果点 M 的位置用( － ，－ 30) 表示，那么 (10 ， 表示的位置是（ ）4020)A ．点 A A北 BB ．点 B西C 东OC ．点 CD ．点 DM南 Dc二、填空题（ 7×3=21 分） 1a 8．分解因式： x2 1 ．b 9．如图，直线a，b被直线c所截， 2若 a ∥ b ， 1 60°，则 2 °．10．2010 年我国西南部发生特大干旱，5200 万人饮水困难， 5200 万人用科学记数法表示人．11．函数 y1中，自变量x的取值范围是．x 312．为响应国家要求中小学生每天锻炼 1 小时的号召，某校开展了形式多样的“阳光体育运动” 活动，小明对某班同学参加锻炼的情况进行了统计，并绘制了下面的图 1 和图 2，则图 2 中“乒乓球”部分占（填百分数）．人数2015篮球 40%105其它乒足球乓篮球乓球足球兴趣爱好球其他图 1 图 213．下面是一个简单的数值运算程序，当输入x 的值为2 时，输出的数值是．输入 x ( 2) 4 输出14.如图，点 P 在∠AOB的平分线上，若使△AOP≌△BOP，则需添加的一个条件是． A（只写一个即可，不添加辅助线）PO三、解答题15、（本小题 7 分）先化简，B再求值 :3 m (m 2 5 ), m2 32m 4 m 216．（ 8 分）解分式方程： 2 13 ．x 3 3 x 17、（ 9 的楼顶分）如图， A 点测得楼ABCD和 CD 的楼顶是同一地面上的两座相距 C 的仰角为 45°，楼底36 米的楼房，在楼 ABD 的俯角为 30°。

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）试题1:如图，在△ABC中，AB=AC，D是BA延长线上的一点，点E是AC的中点．（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应字母（保留作图痕迹，不写作法）．①作∠DAC的平分线AM．②连接BE并延长交AM于点F．（2）猜想与证明：试猜想AF与BC有怎样的位置关系和数量关系，并说明理由．试题2:如图，在△ABC中，AB=AC，D是BA延长线上的一点，点E在AC上，且AE=CE。

（1）实践与操作：利用尺规按下列要求作图，并在图中标明相应字母（保留作图痕迹，不写作法）。

①作∠DAC的平分线AM。

②连接BE并延长交AM于点F。

（2）猜想与证明：试猜想AF与BC有怎样的位置关系和数量关系，并说明理由。

评卷人得分试题3:在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为2、2、3，则原直角三角形纸片的斜边长是。

试题4:如图1，将由5个边长为1的小正方形组成的十字形纸板沿虚线剪拼成一个大正方形，需剪4刀。

思考发现：大正方形的面积等于5个小正方形的面积和，大正方形的边长等于_______。

实践操作：如图2，将网格中5个边长为1的小正方形组成的图形纸板剪拼成一个大正方形，要求剪两刀，画出剪拼的痕迹。

智力开发：将网格中的5个边长为1的正方形组成的十字形纸板，要求只剪2刀也拼成一个大正方形。

在图中用虚线画出剪拼的痕迹。

试题5:如图，在菱形纸片ABCD中，∠A=60°，将纸片折叠，点A、D分别落在点A′、D′处，且A′D′经过点B，EF为折痕，当D′F⊥CD时，的值为（）A．B．C．D．试题6:已知矩形纸片ABCD中，AB=1，BC=，将该纸片叠成一个平面图形，折痕EF不经过A点（E、F是该矩形边界上的点），折叠后点A落在A′处，给出以下判断：①当四边形A，CDF为矩形时，EF=；②当EF=时，四边形A′CDF为矩形；③当EF=2时，四边形BA′CD为等腰梯形；④当四边形BA′CD为等腰梯形时，EF=2。

图1图2操作探究一.选择题1．（2015•山东滕州羊庄中学•4月模拟）如图1，⊙O 的半径为1，点O 到直线m 的距离为2，点P 是直线m 上的一个动点，PB 切⊙O 于点B ，则PB 的最小值是A ．1B ．3C ．2D ．5答案：B ；二.填空题1．（2015•山东滕州东沙河中学•二模）如图2，以点P （2，0）为圆心，3为半径作圆，点M （a ，b ）是⊙P 上的一点，则ab的最大值是____．答案：3；三.解答题1.（2015·江苏高邮·一模）（本题满分12分）数学课上，老师和同学们对矩形纸片进行了图形变换的以下探究活动：（1）如图1，若连接矩形ABCD 的对角线AC 、BD 相交于点O ，则Rt △ADC 可由Rt △ABC经过旋转变换得到，这种旋转变换的旋转中心是点▲、旋转角度是▲°；（2）如图2，将矩形纸片ABCD 沿折痕EF 对折、展平．再沿折痕GC 折叠，使点B 落在EF 上的点B ′处，这样能得到∠B ′GC ．求∠B ′GC 的度数．（3）如图3，取AD 边的中点P ，剪下△BPC ，将△BPC 沿着射线BC 的方向依次进行平移变换，每次均移动BC 的长度，得到了△CDE 、△EFG 和△GHI (如图4)．若BH ＝BI ，BC =a ，则：①证明以BD 、BF 、BH 为三边构成的新三角形的是直角三角形；②若这个新三角形面积小于5015，请求出a 的最大整数值．解：（1）点O 、180°……………………2分（2）连接BB'，由题意得EF 垂直平分BC ，故BB'＝B'C ，由翻折可得，AB CDO（图1）EF ADB CB ′G（图2）PBC （图3）B PCIE DG FHa （图4）ADB'C ＝BC ，∴△BB'C 为等边三角形．∴∠B'CB ＝60°，（或由三角函数FC ：B'C ＝1：2求出∠B'CB ＝60°也可以．）∴∠B'CG ＝30°，∴∠B'GC ＝60°……………………4分（3）①分别取CE 、EG 、GI 的中点P 、Q 、R ，连接DP 、FQ 、HR 、AD 、AF 、AH ，∵△ABC 中，BA ＝BC ，根据平移变换的性质，△CDE 、△EFG 和△GHI 都是等腰三角形，∴DM ⊥CE ，FQ ⊥EG ，HN ⊥GI ．在Rt △AHN 中，AH ＝AI ＝4a ，AH 2＝HN 2＋AN 2，HN 2＝154a 2，则DM 2＝FQ 2＝HN 2＝154a 2，AD 2＝AM 2＋DM 2＝6a 2，AF 2＝AQ 2＋FQ 2＝10a 2，新三角形三边长为4a 、6a 、10a ．∵AH 2＝AD 2＋AF 2∴新三角形为直角三角形．……………………4分（或通过转换得新三角形三边就是AD 、DI 、AI ，即求△GAI 的面积或利用△HAI 与△HGI 相似，求△HAI 的面积也可以）②其面积为126a 10a ＝15a 2．∵15a 2＜5015∴a 2＜50∴a 的最大整数值为7．……………………2分2．（2015·江苏江阴·3月月考）提出问题：如图，在“儿童节”前夕，小明和小华分别获得一块分布均匀且形状为等腰梯形和直角梯形的蛋糕（AD ∥BC ），在蛋糕的边缘均匀分布着巧克力，小明和小华决定只切一刀将自己的这块蛋糕平分（要求分得的蛋糕和巧克力质量都一样）．图1AB CD图2ABCD背景介绍：这条分割直线．．既平分了梯形的面积，又平分了梯形的周长，我们称这条线为梯形的“等分积周线”．尝试解决：ABCIEDGFHaMQN（1）小明很快就想到了一条分割直线，而且用尺规作图作出.请你帮小明在图1中作出这条“等分积周线”，从而平分蛋糕．（2）小华觉得小明的方法很好，所以模仿着在自己的蛋糕（图2）中画了一条直线EF 分别交AD 、BC 于点E 、F ．你觉得小华会成功吗？如能成功，说出确定的方法；如不能成功，请说明理由．（3）通过上面的实践，你一定有了更深刻的认识．若图2中AD ∥BC ，∠A =90°，AD <BC ，AB=4cm ，BC =6cm ，CD =5cm .请你找出梯形ABCD 的所有“等分积周线”，并简要的说明确定的方法．答案：解：（1）作线段AD （或BC ）的中垂线即可.（2）小华不会成功．直线平分梯形ABCD 面积，则21(AE +BF )AB=21(ED +CF )AB ∴AE +BF =ED +CF ，又∵AB ＜CD ，∴此时AE +BF +AB ＜ED +CF +CD ∴小华不可能成功（3）可求得：S 梯形ABCD =18，C 梯形ABCD =18，由（2）可知直线分别交AD 、BC 于点E 、F 时不可能，只要分以下几种情况：①当直线分别交AD 、AB 于E 、F 时有S △AEF ≤S △ABD ，又∵S △ABD =6＜9，∴不可能同理，当直线分别交AD 、CD 于E 、F 时S △AEF ≤S △ACD ＜9,∴不可能②当直线分别交AB 、BC 于E 、F 时设BE =x ，则BF =9−x由直线平分梯形面积得：12x (9−x )=9求得：x 1=3，x 2=6＞4（舍去）∴BE =3③当直线分别交CD 、BC 于E 、F 时设CE =x ，可得：S △ECF =12×4x5×(9−x )=92x 2－18x +45=0此方程无解，∴不可能④当直线分别交AB 、CD 于、E 、F 时设CF =x ，可得：S BFEC =12×(3−x 5)(6−3x 5)+6x 225=9∴x1=0，与②同x2=5，BF=−2，舍去综上所述，符合条件的直线共有一条3．（2015·江苏江阴要塞片·一模）对于半径为r的⊙P及一个正方形给出如下定义：若⊙P 上存在到此正方形四条边距离都相等的点，则称⊙P是该正方形的“等距圆”．如图1，在平面直角坐标系xOy中，正方形ABCD的顶点A的坐标为（2，4），顶点C、D在x轴上，且点C 在点D的左侧.（1）当r=①在P1（0，－3），P2（4，6），P3（2）中可以成为正方形ABCD的“等距圆”的圆心的是_______________；②若点P在直线2y x=-+上，且⊙P是正方形ABCD的“等距圆”，则点P的坐标为_______________；（2）如图2，在正方形ABCD所在平面直角坐标系xOy中，正方形EFGH的顶点F的坐标为（6，2），顶点E、H在y轴上，且点H在点E的上方.①若⊙P同时为上述两个正方形的“等距圆”，且与BC所在直线相切，求⊙P在y轴上截得的弦长；②将正方形ABCD绕着点D旋转一周，在旋转的过程中，线段HF上没有一个点能成为它的“等距圆”的圆心，则r的取值范围是_______________．答案：解（1）10×1.5+（18﹣10）×2=31，········2分（2）①当x≤10时，y=1.5x，········3分②当10＜x≤m时，y=10×1.5+（x﹣10）×2=2x﹣5，········4分③当x＞m时，y=10×1.5+（m﹣10）×2+（x﹣m）×3=3x﹣m﹣5，········5分（3）①当40≤m≤50时，此时选择第二种方案，费用=2×40﹣5=75，符合题意，········6分②当20≤m＜40时，此时选择第三种方案，费用=3x﹣m﹣5，则：70≤3x﹣m﹣5≤90，········7分∴25≤m≤45，········9分综合①、②可得m的取值范围为：25≤m≤50．········10分4（2015·福建漳州·一模）动手操作：用两种不同的方法，将下图中一个等腰三角形分割成四个等腰三角形.解：答案：解：每画一个图正确得4分5（2015•山东滕州东沙河中学•二模）如图3，四边形ABCD为矩形，点E在边BC上，四边形AEDF为菱形．（1）求证：ΔABE≌ΔDCE；（2）试探究：当矩形ABCD长宽满足什么关系时，菱形AEDF为正方形?请说明理由答案：解：（1）略（2）AD=2AB．6.（2015•山东滕州羊庄中学•4月模拟）如图4-1，正方形ABCD的对角线AC与BD相交于点M，正方形MNPQ与正方形ABCD全等，将正方形MNPQ绕点M顺时针旋转，在旋转过程中，射线MN与射线MQ分别交正方形ABCD的边于E、F两点。

实验操作专题实验操作型试题是近几年中考数学的热点试题，这类试题就是让同学们在通过实际操作的基础上设计的问题，需要动手操作（包括裁剪、折叠、拼图等），合情猜想和验证，它既考查学生的动手能力，又考查学生的想象能力，不但有利于培养同学们的创新能力和实践能力，更有助于养成实验研究的习惯，体现新课程理念.，符合新课程标准强调的发现式学习、探究式学习和研究式学习，因此，实验与操作问题将成为今后中考的热点题型. 一、折叠类例1 如图1，小娟将一条直角边长为1的一个等腰直角三角形纸片（图①），沿它的对称轴折叠1次后得到一个等腰直角三角形（图②），再将图②的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形（图③），则图③中的等腰直角三角形的一条腰长为________；同上操作，若小娟连续将图①的等腰直角三角形折叠n次后所得到的等腰直角三角形（图n+1）的一条腰长为_______.分析：已知图①的等腰直角三角形的直角边长为1，即112-⎛⎝⎭，则可以利用勾股定理求出其斜边的长为，通过第一次折叠后，图①的等腰直角三角形的斜边的一半即变成图②的直角边，即图②的直角边长为2，即212-⎛⎫⎪⎪⎝⎭，同理，可以得到图③的直角边长为12，即312-⎛⎫⎪⎪⎝⎭，图④的直角边长为4，即412-⎛⎝⎭，由此可以猜想第n个图形中的等腰直角三角形的腰长为12n-⎛⎫⎪⎪⎝⎭，折叠n次后所得到的等腰直角三角形，即如图n+1的一条腰长为11n+-⎝⎭，即n⎝⎭.解：图③中的等腰直角三角形的一条腰长为12；将图①的等腰直角三角形折叠n次后所得到的第n+1个等腰直角三角形的一条腰长为n⎝⎭.①②③n+1图1１２评注：求解本题时，一定要动手操作，经过大胆地猜想、归纳与验证，即可获得正确的结果.跟踪训练:1. 如图，将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线（直角三角形的中位线）剪去上面的小直角三角形.将留下的纸片展开，得到的图形是（ ）2. 如图，将一个长为10cm ，宽为8cm 的矩形纸片对折两次后，沿所得矩形两邻边中点的连线（虚线）剪下，再打开，得到的菱形的面积为（ ）A ．10 cm 2B ．20 cm 2C ．40 cm 2D ．80 cm 2第2题图二、裁剪类例2 如图2，有一块边长为1米的正方形钢板，被裁去长为14米、宽为16米的矩形两角，现要将剩余部分重新裁成一正方形，使其四个顶点在原钢板边缘上，且P 点在裁下的正方形一边上，问：如何剪裁使得该正方形面积最大？最大面积是多少？图2 图3分析：本题是一道与正方形裁剪有关的操作型问题，解决问题首先要画出草图，然后从A B CD 第1题图 A B C D３图形中寻找解决问题的模型．如何剪裁使得该正方形面积最大，实际上是确定正方形顶点的位置，可借助相似三角形的性质构造方程解决．解：如图3，设原正方形为ABCD ，正方形EFGH 是要裁下的正方形，且EH 过点P ．设AH=x ，则BE=AH=x ，AE=1-x ．∵MP∥AH，∴△EMP∽△EAH．∴111641x x x--=-．整理，得12x 2-11x+2=0．解得114x =，223x =． 当14x =时，221151448EFGH S ⎛⎫⎛⎫=+-= ⎪ ⎪⎝⎭⎝⎭正方形．当23x =时，22225513398EFGH S ⎛⎫⎛⎫=+-=< ⎪ ⎪⎝⎭⎝⎭正方形．∴当BE ＝DG ＝14米，BF ＝DH ＝34米时，裁下的正方形面积最大，最大面积为58米2． 评注：解决问题利用相似三角形的性质构造方程，并借助一元二次方程的知识解决，既体现数形结合思想，又体现了方程思想．例3 如图4，将正方形沿图中虚线（其中x ＜y ）剪成①②③④四块图形，用这四块图形恰能拼成一个．．．．．．矩形（非正方形）． （1） 画出拼成的矩形的简图； （2） （2）求xy的值．分析：拼接时抓住相等的边进行拼接（重合），再利用面积相等写出等式，合理整理就可求出（2）的值.解：（1）如图4.（2）解法一：由拼图前后的面积相等，得[(x+y)+y]y=(x+y)2.∵y ≠0，整理,得01)(2=-+yx yx .解得215-=yx （负值不合题意，舍去）.解法二：由拼成的矩形可知yxy y x y x =+++)(.以下同解法一． 跟踪训练：3.如图，△ABC 是一张等腰直角三角形纸板，∠C=90°,AC=BC=2.图4 ②④① ③４（1）要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法（如图①），比较甲、乙两种剪法，哪种剪法所得的正方形面积更大？请说明理由.（2）图①中甲种剪法称为第1次剪取，记所得的正方形面积为S 1；按照甲种剪法，在余下的△ADE 和△BDF 中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形的面积和为S 2 (如图②)，则S 2= ；再在余下的四个三角形中，用同样的方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方第3题图形的面积和为S 3 (如图③)；继续操作下去…则第10次剪取时，S 10= . （3）求第10次剪取后，余下的所有小三角形的面积和.三、探究类例4 如图6，小明将一张矩形纸片沿对角线剪开，得到两张三角形纸片（如图②），量得他们的斜边长为10 cm ，较小锐角为30°，再将这两张三角纸片摆成如图③的形状，但点B ，C ，F ，D 在同一条直线上，且点C 与点F 重合（在图③至图④中统一用F 表示）. 小明在对这两张三角形纸片进行如下操作时遇到了三个问题，请你帮助解决.（1）将图③中的△ABF 沿BD 向右平移到图④的位置，使点B 与点F 重合，请你求出平移的距离；（2）将图③中的△ABF 绕点F 顺时针方向旋转30°到图⑤的位置，A 1F 交DE 于点G ，请你求出线段FG 的长度；（3）将图③中的△ABF 沿直线AF 翻折到图⑥的位置，AB 1交DE 于点H ，请说明AH ＝DH.图6分析：（1）根据题意，由对图形的操作过程可知图形平移的距离就是线段BC 的长. （2）依题意运用勾股定理求解.EBQ④ ⑥ ⑤ ③ ②①５（3）要说明AH ＝DH ，由于∠FAB 1＝∠EDF ＝30°，可知FD ＝FA ，EF ＝FB ＝FB 1，从而得到AE ＝DB 1，可以说明△AHE ≌△DHB 1，问题得解.解：（1）图形平移的距离就是线段BC 的长.∵在Rt△ABC 中，斜边长为10cm ，∠BAC＝30°，∴BC ＝5cm ，即平移的距离为5cm.（2）∵∠A 1FA ＝30°，∴∠GFD＝60°，∠D＝30°.∴∠FGD ＝90°.在Rt △EFD 中，ED ＝10 cm ，∵FD ＝，∴FGcm. （3）在△AHE 与△DHB 1中，∵∠FAB 1＝∠EDF ＝30°，∴FD ＝FA ，EF ＝FB ＝FB 1， ∴FD －FB 1＝FA －FE ，即AE ＝DB 1.又∵∠AHE ＝∠DHB 1，∴△AHE ≌△DHB 1，∴AH ＝DH.评注：动手操作的证明问题，既体现此类题型的动手能力，又能利用几何图形的性质进行全等、相似等证明，同时，从动手操作中学到知识，从操作中得到结论，这些都是借助图形的平移、旋转，读者应注意多加体会.跟踪训练： 4.，我们把这样的矩形叫做黄金矩形．（1）操作：请你在如图所示的黄金矩形ABCD （AB >AD ）中，以短边AD 为一边作正方形AEFD ； （2）探究：在（1）中的四边形EBCF 是不是黄金矩形？若是，请予以证明；若不是，请说明理由；（3）归纳：通过上述操作及探究，请概括出具有一般性的结论（不需要证明）．第4题图参考答案1. 此题我们可以用一张纸按图示过程动手剪一剪，选A.2. 剪下来的图形展开前是一个直角三角形，它的面积是所求菱形面积的四分之一；易知直角三角形的两直角边分别为2，25，∴菱形面积为4S △=4×21×2×25=10，故选A.3.解： (1)如图甲，由题意，得AE=DE=EC.因为AC=2,所以EC=1,S 正方形CFDE=1.如图乙，设MN=x ，则由题意，得AM=MQ=PN=NB=MN=x.33x x ∴==解得，28(39PNMQ S ∴==正方形.６又819>∴甲种剪法所得的正方形的面积更大 注：图甲可另解为：由题意得点D ，E ，F 分别为AB,AC,BC 的中点，112ABCCFDE S S ==正方形.(2)212S =，10912S =. (3)探索规律可知112n n S -=,剩余三角形的面积和为()12109911112212422S S S ⎛⎫-+++=-++++= ⎪⎝⎭. 4．解：（1）如图所示．第4题图（2）四边形EBCF 是黄金矩形．证明：由题意知，215-=AB AD ,所以AD=215-AB ．因为四边形ADFE是正方形，所以AD=AE.所以在四边形EBCF中215215215-=---=-=AB ABAB ADAFAB BC BF ，所以四边形EBCF 是黄金矩形. （3）在黄金矩形内以短边为边作一个正方形后，所得到的另外一个四边形是矩形，而且是黄金矩形．。

中考数学模拟题汇总《操作类试题》专项练习（含答案解析）一、单选题1．如图，在Rt ABC ∆中，90B =∠，以点A 为圆心，适当长为半径画弧，分别交AB AC 、于点,D E ，再分别以点D E 、为圆心，大于12DE 为半径画弧，两弧交于点F ，作射线AF 交边BC 于点1,4BG AC ==，则ACG ∆的面积是（ ）A ．1B ．32 C ．2 D ．522．如图，在ABCD 中，将ADC ∆沿AC 折叠后，点D 恰好落在DC 的延长线上的点E 处．若=60B ︒∠，=3AB ，则ADE ∆的周长为（ ）A ．12B ．15C ．18D ．213．如图，将ABC ∆绕点C 顺时针旋转得到DEC ∆，使点A 的对应点D 恰好落在边AB 上，点B 的对应点为E ，连接BE ．下列结论一定正确的是（ ）A ．AC AD =B ．AB EB ⊥C ．BC DE =D ．A EBC ∠=∠4．如图，菱形ABCD 的对角线AC ，BD 交于点O ，416AC BD ==，，将ABO 沿点A 到点C 的方向平移，得到A B C '''，当点A '与点C 重合时，点A 与点B '之间的距离为( )A ．6B ．8C ．10D ．125．4张长为a 、宽为()b a b >的长方形纸片，按如图的方式拼成一个边长为()a b +的正方形，图中空白部分的面积为1S ，阴影部分的面积为2S ．若122S S =，则a 、b 满足（ ）A ．25a b =B ．23a b =C ．3a b =D ．2a b =6．将一张正方形纸片按如图步骤，通过折叠得到图④，再沿虚线剪去一个角，展开铺平后得到图⑤，其中,FM GN 是折痕．若正方形EFGH 与五边形MCNGF 的面积相等，则FMGF的值是（ ）A B 1-C ．12D 7．如图，矩形ABCD 与菱形的对角线均交于点O ，且//EG BC ，将矩形折叠，使点C 与点O 重合，折痕MN 过点G ．若AB =，2EF =，120H ∠=，则DN 的长为（ ）A -B ．2C D ． 8．如图，直线EF 是矩形ABCD 的对称轴，点P 在CD 边上，将BCP ∆沿BP 折叠，点C 恰好落在线段AP与EF 的交点Q 处，BC =AB 的长是（ ）A ．8B ．C ．D ．109．如图，将ABC ∆沿BC 边上的中线AD 平移到A B C ''∆的位置．已知ABC ∆的面积为16，阴影部分三角形的面积9．若1AA '=，则A D '等于（ ）A ．2B ．3C ．4D ．3210．如图，在△ABC 中，D 是AC 边上的中点，连结BD ，把△BDC ′沿BD 翻折，得到△'BDC ，DC 与AB 交于点E ，连结'AC ，若AD =AC ′=2，BD =3则点D 到BC 的距离为（ ）A ．2B ．7C D 二、填空题11．如图，已知△ABC ，通过测量、计算得△ABC 的面积约为____cm 2.（结果保留一位小数）12．如图，把某矩形纸片ABCD 沿EF 、GH 折叠（点E 、H 在AD 边上，点F 、G 在BC 边上），使得点B 、点C 落在AD 边上同一点P 处，A 点的对称点为A '点，D 点的对称点为D 点，若90FPG ，A EP △的面积为4，D PH △的面积为1，则矩形ABCD 的面积等于_____.13．用一条宽度相等的足够长的纸条打一个结（如图1所示），然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE ．图中，BAC ∠=____度．14．如图，有一张矩形纸片ABCD ，8,6AB AD ==．先将矩形纸片ABCD 折叠，使边AD 落在边AB 上，点D 落在点E 处，折痕为AF ；再将AEF ∆沿EF 翻折，AF 与BC 相交于点G ，则GCF ∆的周长为_____．15．如图，在△ABC 中，∠BAC =90°，AB =AC =10cm ，点D 为△ABC 内一点，∠BAD =15°，AD =6cm ，连接BD ，将△ABD 绕点A 逆时针方向旋转，使AB 与AC 重合，点D 的对应点E ，连接DE ，DE 交AC 于点F ，则CF 的长为________cm .16．如图在正方形ABCD 中，1BE =，将BC 沿CE 翻折，使点B 对应点刚好落在对角线AC 上，将AD 沿AF 翻折，使点D 对应点落在对角线AC 上，求EF =______.17．如图，在Rt ABC ∆中，090C ∠=，以顶点B 为圆心，适当长度为半径画弧，分别交,AB BC 于点,M N ，再分别以点,M N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，作射线BP 交AC 于点D ．若30A ∠=，则BCDABDS S ∆∆=_____．18．七巧板是我国祖先的一项卓越创造，被誉为“东方魔板”.由边长为ABCD 可以制作一副如图1所示的七巧板，现将这副七巧板在正方形EFGH 内拼成如图2所示的“拼搏兔”造型(其中点Q R 、分别与图2中的点E G 、重合，点P 在边EH 上)，则“拼搏兔”所在正方形EFGH 的边长是_____.19．如图，过点C (3,4)的直线2y x b =+交x 轴于点A ，∠ABC =90°，AB =CB ，曲线0ky x x=>（）过点B ，将点A 沿y 轴正方向平移a 个单位长度恰好落在该曲线上，则a 的值为________．20．如图，在每个小正方形的边长为1的网格中，ΔABC 的顶点A 在格点上，B 是小正方形边的中点，ABC 50∠︒=，BAC 30∠︒=，经过点A ，B 的圆的圆心在边AC 上．（Ⅰ）线段AB 的长等于_______________； （Ⅱ）请用无刻度．．．的直尺，在如图所示的网格中，画出一个点P ，使其满足PAC PBC PCB ∠∠∠==，并简要说明点P 的位置是如何找到的（不要求证明）_____．三、解答题21．按要求解答下列各题：（1）如图①，求作一点P ，使点P 到ABC ∠的两边的距离相等，且在ABC △的边AC 上．（用直尺和圆规作图，保留作图痕迹，不写作法和证明）；（2）如图②，B C 、表示两个港口，港口C 在港口B 的正东方向上．海上有一小岛A 在港口B 的北偏东60︒方向上，且在港口C 的北偏西45︒方向上．测得40AB ＝海里，求小岛A 与港口C 之间的距离．（结果可保留根号）22．图①，图②均为44⨯的正方形网格，每个小正方形的顶点称为格点．在图①中已画出线段AB ，在图②中已画出线段CD ，其中A B C D 、、、均为格点，按下列要求画图： ⑴在图①中，以AB 为对角线画一个菱形AEBF ，且,E F 为格点；⑵在图②中，以CD 为对角线画一个对边不相等的四边形CGDH ，且,G H 为格点，090CGD CHD ∠=∠=.23．如图，在76⨯的方格中，ABC △的顶点均在格点上，试按要求画出线段EF （E ,F 均为格点），各画出一条即可．24．按要求作图，不要求写作法，但要保留作图痕迹.（1）如图1，A 为圆E 上一点，请用直尺（不带刻度）和圆规作出圆内接正方形；（2）我们知道，三角形具有性质，三边的垂直平分线相交于同一点，三条角平分线相交于一点，三条中线相交于一点，事实上，三角形还具有性质：三条高交于同一点，请运用上述性质，只用直尺（不带刻度）作图：①如图2，在□ABCD 中，E 为CD 的中点，作BC 的中点F ;②图3，在由小正方形组成的网格中，的顶点都在小正方形的顶点上，作△ABC 的高AH25．如图，将平行四边形纸片ABCD 沿一条直线折叠，使点A 与点C 重合，点D 落在点G 处，折痕为EF ．求证：（1）ECB FCG ∠=∠； （2）EBC FGC ∆≅∆．26．图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A B C D E F 、、、、、均在格点上．在图①、图②、图③中，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法．（1）在图①中以线段AB 为边画一个ABM ∆，使其面积为6． （2）在图②中以线段CD 为边画一个CDN ∆，使其面积为6．（3）在图③中以线段EF 为边画一个四边形EFGH ，使其面积为9，且090EFG ∠=．27．如图，矩形ABCD 中，点E 在边CD 上，将BCE 沿BE 折叠，点C 落在AD 边上的点F 处，过点F 作FG CD 交BE 于点G ，连接CG ． （1）求证：四边形CEFG 是菱形；（2）若6,10AB AD ==，求四边形CEFG 的面积．28．综合与实践 动手操作： 第一步：如图1，正方形纸片ABCD 沿对角线AC 所在直线折叠，展开铺平.在沿过点C 的直线折叠，使点B ，点D 都落在对角线AC 上.此时，点B 与点D 重合，记为点N ，且点E ，点N ，点F 三点在同一直线上，折痕分别为CE ，CF .如图2.第二步：再沿AC 所在的直线折叠，△ACE 与△ACF 重合，得到图3第三步：在图3的基础上继续折叠，使点C 与点F 重合，如图4，展开铺平，连接EF ，FG ，GM ，ME ，如图5，图中的虚线为折痕.问题解决：(1)在图5中，∠BEC 的度数是 ，AEBE的值是 ； (2)在图5中，请判断四边形EMGF 的形状，并说明理由；(3)在不增加字母的条件下，请你以图中5中的字母表示的点为顶点，动手画出一个菱形(正方形除外)，并写出这个菱形： .29．（1）如图1，菱形AEGH 的顶点E 、H 在菱形ABCD 的边上，且60BAD ∠=︒，请直接写出::HD GC EB 的结果（不必写计算过程）（2）将图1中的菱形AEGH 绕点A 旋转一定角度，如图2，求::HD GC EB ； （3）把图2中的菱形都换成矩形，如图3，且::1:2AD AB AH AE ==，此时::HD GC EB 的结果与（2）小题的结果相比有变化吗？如果有变化，直接写出变化后的结果（不必写计算过程）；若无变化，请说明理由．30．如图，等边ABC ∆中，AB =6，点D 在BC 上，BD =4，点E 为边AC 上一动点（不与点C 重合），CDE ∆关于DE 的轴对称图形为FDE ∆.（1）当点F 在AC 上时，求证：DF //AB ；（2）设ACD ∆的面积为S 1，ABF ∆的面积为S 2，记S =S 1-S 2，S 是否存在最大值？若存在，求出S 的最大值；若不存在，请说明理由；（3）当B ，F ，E 三点共线时。

中考数学模拟试题分类汇编中考数学是中学生的必考科目之一，各地的中考数学试题种类繁多。

为了帮助同学们更好地复习和备考，本文将对中考数学模拟试题进行分类汇编，以供大家参考。

一、整数与小数运算试题1：计算[(2.5 + 3) - 1.2] × 5 的结果。

解析：首先计算括号内的运算：2.5 + 3 = 5.5；然后计算减法运算：5.5 - 1.2 = 4.3；最后将结果与5相乘：4.3 × 5 = 21.5。

所以，[(2.5 + 3) - 1.2] × 5 的结果为21.5。

试题2：简化下列表达式：2 × (3 + 4) + 5 × (6 - 2)。

解析：首先计算括号内的加法运算：3 + 4 = 7，6 - 2 = 4；然后计算乘法运算：2 × 7 = 14，5 × 4 = 20；最后将结果相加：14 + 20 = 34。

所以，2 × (3 + 4) + 5 × (6 - 2) 简化后的结果为34。

二、代数式的计算试题1：求解方程式：2x + 5 = 15。

解析：首先将方程式转化为一元一次方程：2x = 15 - 5 = 10；然后将等式两边同时除以2：x = 10 ÷ 2 = 5。

所以，方程2x + 5 = 15的解为x = 5。

试题2：计算：(a + b)²。

解析：根据二次方公式展开：(a + b)² = a² + 2ab + b²。

所以，(a + b)²的展开式为a² + 2ab + b²。

三、几何图形的计算试题1：已知⊙O的直径AB = 4 cm，点C在⊙O上，则△OAC的面积为多少平方厘米？解析：由于OA和OC是半径，所以△OAC为等腰直角三角形，且AC = OC = 2 cm；计算△OAC的面积：面积 = 1/2 ×底 ×高 = 1/2 × 2 × 2 = 2平方厘米。

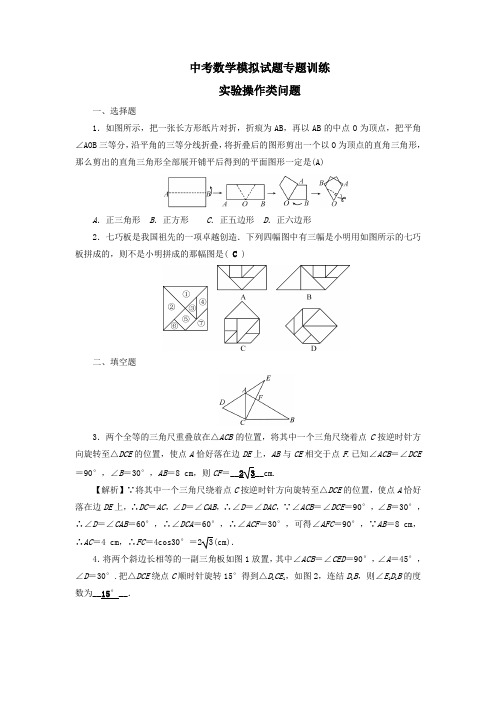
中考数学模拟试题专题训练实验操作类问题一、选择题1．如图所示，把一张长方形纸片对折，折痕为AB，再以AB的中点O为顶点，把平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的直角三角形，那么剪出的直角三角形全部展开铺平后得到的平面图形一定是(A)A．正三角形B．正方形C．正五边形D．正六边形2．七巧板是我国祖先的一项卓越创造．下列四幅图中有三幅是小明用如图所示的七巧板拼成的，则不是小明拼成的那幅图是( C )二、填空题3．两个全等的三角尺重叠放在△ACB的位置，将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置，使点A恰好落在边DE上，AB与CE相交于点F.已知∠ACB＝∠DCE ＝90°，∠B＝30°，AB＝8 cm，则CF＝__23__cm.【解析】∵将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置，使点A恰好落在边DE上，∴DC＝AC，∠D＝∠CAB，∴∠D＝∠DAC，∵∠ACB＝∠DCE＝90°，∠B＝30°，∴∠D＝∠CAB＝60°，∴∠DCA＝60°，∴∠ACF＝30°，可得∠AFC＝90°，∵AB＝8 cm，∴AC＝4 cm，∴FC＝4cos30°＝23(cm)．4．将两个斜边长相等的一副三角板如图1放置，其中∠ACB＝∠CED＝90°，∠A＝45°，∠D＝30°.把△DCE绕点C顺时针旋转15°得到△D1CE1，如图2，连结D1B，则∠E1D1B的度数为__15°__．【解析】设AB 交CD 1于点O ，由于旋转角为15°，由已知条件知∠BCE 1＝15°，∴∠BCD 1＝∠D 1CE 1－∠BCE 1＝45°.易得D 1C ⊥AB 且O 为AB 中点，由△ABC 与△CDE 斜边相等，即AB ＝CD ＝CD 1，∴AB 与CD 1相互垂直平分，易知OD 1＝OB ，∴∠OD 1B ＝45°，∠E 1D 1B ＝∠OD 1B －∠CD 1E 1＝45°－30°＝15°.三、解答题5．如图，一张三角形纸片ABC ，其中∠C ＝90°，AC ＝4，BC ＝3.现小林将纸片做三次折叠：第一次使点A 落在C 处；将纸片展平做第二次折叠，使点B 落在C 处；再将纸片展平做第三次折叠，使点A 落在B 处．这三次折叠的折痕长依次记为a ，b ，c ，求a ∶b ∶c.解：第一次折叠如图1，折痕为DE ，由折叠得：AE ＝EC ＝12AC ＝12×4＝2，DE ⊥AC.∵∠ACB ＝90°，∴DE ∥BC ，∴a ＝DE ＝12BC ＝12×3＝32；第二次折叠如图2，折痕为MN ，由折叠得：BN ＝NC ＝12BC ＝12×3＝32，MN ⊥BC ，∵∠ACB ＝90°，∴MN ∥AC ，∴b ＝MN ＝12AC ＝12×4＝2；第三次折叠如图3，折痕为GH ，由勾股定理得：AB ＝32＋42＝5，由折叠得：AG ＝BG ＝12AB ＝12×5＝52，GH ⊥AB ，∴∠AGH ＝90°∵∠A ＝∠A ，∠AGH ＝∠ACB∴△ACB∽△AGH ，∴AC AG ＝BC GH ，∴452＝3GH ，∴GH ＝158，即c ＝158，a ∶b ∶c ＝12∶16∶156．如图1，边长为4的正方形ABCD 中，点E 在AB 边上(不与点A ，B 重合)，点F 在BC 边上(不与点B ，C 重合)．第一次操作：将线段EF 绕点F 顺时针旋转，当点E 落在正方形上时，记为点G ；第二次操作：将线段FG绕点G顺时针旋转，当点F落在正方形上时，记为点H；依此操作下去……(1)图2中的三角形EFD是经过两次操作后得到的，其形状为__等边三角形__，求此时线段EF的长；(2)若经过三次操作可得到四边形EFGH.①请判断四边形EFGH的形状为__正方形__，此时AE与BF的数量关系是__AE＝BF__．②以①中的结论为前提，设AE的长为x，四边形EFGH的面积为y，求y与x的函数关系式及面积y的取值范围．解：(1)∵四边形ABCD是正方形，∴AD＝CD＝BC＝AB，∠A＝∠B＝∠C＝90°.∵ED＝FD，∴△ADE≌△CDF(HL)，∴AE＝CF，BE＝BF.∴△BEF是等腰直角三角形．设BE的长为x，则EF＝2x，AE＝4－x，∵在Rt△AED中，AE2＋AD2＝DE2，DE＝EF，∴(4－x)2＋42＝(2x)2，解得x1＝－4＋43，x2＝－4－43(不合题意，舍去)，∴EF＝2x＝2(－4＋43)＝－42＋46(2)②∵AE＝x，∴BE＝4－x.∵在Rt△BEF中，EF2＝BF2＋BE2，AE＝BF，∴y＝EF2＝(4－x)2＋x2＝2x2－8x＋16，∵点E不与点A，B重合，点F不与点B，C重合，∴0＜x＜4.∵y＝2x2－8x＋16＝2(x－2)2＋8，∴当x＝2时y有最小值8，当x＝0或4时，有最大值16，∴y的取值范围是8≤y＜16。

2019-2020 年中考数学模拟试题及答案（word 版）班次学号 姓名一、选择题（本大题共 8 小题，每小题 3 分，共 24 分） 1. 5 的倒数是 ( )A ． 5B ．－ 511C ．D ．552. 实数 a 、b 在数轴上的位置如图所示，则a 与b 的大小关系是（）A ． a > bB ．a < bC ． a = bD ． 不能判断ao b第 2 题3. 如图，直线 a 、b 被直线 c 所截，下列说法正确的是（）A ．当∠ 1=∠ 2 时，一定有 a ∥bB ．当 a ∥ b 时，一定有∠ 1= ∠ 2C ．当 a ∥ b 时，一定有∠ 1＋∠ 2=90 °D ．当 a ∥b 时，一定有∠ 1＋∠ 2=180 °第 3题4.下列运算，正确的是( )3＝ a 42﹒ a 3＝a6（ 2）3＝ a 610÷a 2＝a 5A ． a ＋aB ． aC ． aD ． a5.下列命题 ()(1) 等边三角形是中心对称图形;(2) 一组对边平行 , 另一组对边相等的四边形是平行四边形; (3) 两条对角线互相垂直的矩形是正方形;(4)两条对角线互相垂直的四边形是菱形．其中正确命题的个数为 ( A ． 1 个B ． 2 个C ．3 个D ．4 个)6.下列事件是必然事件的是()（ A ）打开电视机屏幕上正在播放天气预报（ B ）到电影院任意买一张电影票，座位号是奇数（ C ）掷一枚均匀的骰子，骰子停止转动后偶数点朝上（ D ）在地球上，抛出去的篮球一定会下落7. 已知⊙ O 1 的半径 r 为 4cm ，⊙ O 2 的半径 的位置关系是 （）A ．相交B ．内含C ．内切R 为 5cm ，两圆的圆心距D ．外切O 1O 2 为6cm ，则这两圆8．一个样本有40 个数据，把它分成 4 个小组，某一组有10 个数据，则这一小组的频率是（）A. 0.05B.0.25C.0.5D.0.6二、填空题（本大题共8 小题，每小题 3 分，共 24 分）9． 2010 年上海世博会共有7300 万人参观，用科学记数法表示7300 万 =3ab 3.10. 分解因式： a b =11．不等式 3 x 4 2 x 的正整数解是.12. 一个角的补角是它的余角的 4 倍，则这个角等于度 .13.将多项式 4 x 2．（只要填1 加上一项后成为一个完全平方式，则这项可以是一个即可）14．如图 , 矩形ABCD的长AB为 5cm，宽BC为 3cm，点P为AB边上的一个动点，则阴影部分的面积为 _____________ cm2．D C6cmA8cm P第 14题 B第15题15.一块直角边分别为6cm 和 8cm 的三角木板，绕6cm 的边旋转一周，则斜边扫过的面积是cm 2 ( 结果用含的式子表示).16．一个口袋中装有 2 个红球、 3 个绿球、 5 个黄球，每个球除颜色外其它都相同，搅均匀后随机从中摸出一个球是绿球的概率是_______.三、解答题（本大题共 6 小题，每小题 6 分，满分36 分）17．计算： 6 2011 0－（1） 1 －8cos60°21 x 418．解不等式组并在数轴上表示出解集： 2 x 3x 2519.如图7，在方格纸中，以格点连线为边的三角形叫格点三角形，⊿ABC就是格点三角形，请在此方格纸上另画一个与⊿ABC相似的格点三角形，并写出它与⊿ABC的相似比．AB C第19 题20． 2010 年 10 月 9 日，国家发改委价格司公布《关于居民生活用电实行阶梯电价的指导意见》提供了两套可供选择的电价方案，向社会公开征求意见：方案一：第一档月均用电量110 度以内，该档内电价不变动；第二档月用电量为110 度至 210 度，提价标准不低于每度 5 分钱；第三档为用电量210 度以上，每度电价上调不低于 0.2 元。

中考数学模拟试题汇编模拟试题一：题目：中考数学模拟试题汇编在中学生备战中考的过程中，数学是其中最重要的科目之一。

合理的模拟试题可以有效帮助学生提高数学水平，增强解题能力。

本文将提供一系列中考数学模拟试题，涵盖不同难度和章节，以帮助学生更好地准备中考。

【模拟试题一】1. 已知三个球形池塘的半径分别是2米、4米和8米，求它们的总体积。

解析：球体的体积公式为V=4/3πr³，其中V表示体积，π约等于3.14，r表示球体的半径。

将三个球体的半径分别代入公式，得到它们的体积分别为：第一个池塘的体积V₁=4/3 × 3.14 × 2³≈33.49立方米；第二个池塘的体积V₂=4/3 × 3.14 × 4³≈268.08立方米；第三个池塘的体积V₃=4/3 × 3.14 × 8³≈2143.57立方米。

所以，三个池塘的总体积为：V₁+V₂+V₃≈33.49+268.08+2143.57≈2445.14立方米。

2. 考虑一个等差数列：2，5，8，11，...，它的第10项是多少？解析：等差数列的通项公式为an=a₁+(n-1)d，其中an表示第n项，a₁表示首项，d表示公差。

根据题目，可以知道a₁=2，d=5-2=3，n=10。

将这些值代入公式，得到第10项的值为a₁₀=2+(10-1)×3=2+9×3=29。

3. 一条带电的纽扣落在地面上，小明用一根非金属棍将纽扣捡起，原因是什么？解析：导体的导电性原理决定了电荷可以在其内部自由移动。

金属是一种良好的导体，当带电物体接触到金属时，电荷会在金属内部迅速传播，从而使整个金属带负电。

而非金属不具备良好的导电性，带电物体接触到非金属时，电荷无法在其中迅速分布，因此不会对纽扣的捡起产生影响。

【模拟试题二】1. 在一个三角形中，若三边分别为3cm、4cm和5cm，那么这个三角形的面积是多少？解析：可以使用海伦公式求解三角形的面积，海伦公式为：S=√[s(s-a)(s-b)(s-c)]，其中S表示面积，a、b、c分别表示三角形的三边长度，s表示半周长，即s=(a+b+c)/2。

实验与操作一、选择题1.（2010年河南省南阳市中考模拟数学试题）将如图①的矩形ABCD 纸片沿EF 折叠得到图②，折叠后DE 与BF 相交于点P ，如果∠BPE=130°，则∠PEF 的度数为( ) A ．60° B ．65° C ．70° D ．75°答：B2.（2010年河南中考模拟题4）分别剪一些边长相同的①正三角形，②正方形，③正五边形，如果用其中一种正多边形镶嵌，可以镶嵌成一个平面图案的有 ( )A.①②B.②③C.①③D.①②③都可以答案：A3.（2010年西湖区月考）有一张矩形纸片ABCD ，其中AD=4cm ，上面有一个以AD 为直径的半园，正好与对边BC 相切，如图(甲).将它沿DE 折叠，是A 点落在BC 上，如图(乙).这时，半圆还露在外面的部分(阴影部分)的面积是（ ）A.（π－32）cm 2B.（21π＋3）cm 2C.（34π－3）cm 2D.（32π＋3）cm 2答案：C4.（2010 河南模拟）某校计划修建一座既是中心对称图形又是轴对称图形的花坛，从学生中征集到的设计方案有正三角形、正五边形、等腰梯形、菱形等四种图案，你认为符合条件的是（ ） A 正三角形 B 正五边形 C 等腰梯形 D 菱形 答案：D5.（2010年广西桂林适应训练）、在1，2，3，4，…，999，1000，这1000个自然数中，数字“0”出现的次数一共是（ ）次．A.182B.189C.192D.194答案：CPFEDCBA FED CB A① ②②①(3)(2)(1)6.（2010年 中考模拟）（大连市）将一张等边三角形纸片按图1－①所示的方式对折，再按图1－②所示的虚线剪去一个小三角形，将余下纸片展开得到的图案是 ( )答案：A二、填空题1.（2010年吉林中考模拟题）将图①中的正方形剪开得到图②，图②中共有4个正方形；将图②中一个正方形剪开得到图③，图③中共有7个正方形；将图③中一个正方形剪开得到图④，图④中共有10个正方形；…；如此下去．则图⑨中共有 个正方形． 答案：252.（2010年河南中考模拟题4）将图（1）所示的正六边形进行分割得到图（2），再将图（2）里的三个小正六边形的其中之一按同样的方式进行分割得到图（3），接着再将图（3）中最小的三个正六边形的其中之一按同样的方式进行分割…，则第n 图形中共有 个六边形．（提示：可设y=an 2+bn+c,把 代入求a,b,c.再求y=?） 答案：3n-23.（2010天水模拟）用一版权法宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边殂ABCDE ，其中∠BAC= 度。

xx学校xx 学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）试题1:把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB=3cm，BC=5cm，则重叠部分△DEF 的面积是（）A．7.5cm2 B．5.1cm2 C．5.2cm2 D．7.2cm2试题2:长为1，宽为a的矩形纸片（＜a＜1），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去，若在第n次操作后，剩下的矩形为正方形，则操作终止．（I）第二次操作时，剪下的正方形的边长为；（Ⅱ）当n=3时，a的值为．（用含a的式子表示）试题3:评卷人得分已知一个矩形纸片OACB，OB＝6，OA＝11，点P为BC边上的动点（点P不与点B、C重合），经过点O折叠该纸片，得折痕OP和点B'，经过点P再次折叠纸片，使点C落在直线PB'上，得折痕PQ和点C'，当点C'恰好落在边OA上时BP的长为．试题4:定义运算“﹡”：规定x﹡y（其中a、b为常数），若1﹡1＝3，1﹡＝1，则1﹡2＝试题5:如图，已知正方形ABCD的顶点A、B在⊙O上，顶点C、D在⊙O内，将正方形ABCD绕点逆时针旋转，使点D落在⊙O上．若正方形ABCD的边长和⊙O的半径均为6cm，则点D运动的路径长为cm．试题6:如图1，一副直角三角板满足AB=BC，AC=DE，∠ABC=∠DEF=90°∠EDF=30°，【操作1】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E旋转，并使边DE与边AB 交于点P，边EF与边BC于点Q．在旋转过程中，如图2，当时，EP与EQ满足怎样的数量关系？并给出证明．【操作2】在旋转过程中，如图3，当时EP与EQ满足怎样的数量关系？，并说明理由．【总结操作】根据你以上的探究结果，试写出当时，EP与EQ满足的数量关系是什么？其中m的取值范围是什么？（直接写出结论，不必证明）m．第1题试题7:如图1，在Rt△ABC中，∠ACB＝90°，∠B＝60°，D为AB的中点，/EDF＝90°，DE交AC于点G，DF经过点C．（1）求/ADE的度数；（2）如图2，将图1中的∠EDF绕点D顺时针方向旋转角α（0°<α<60°），旋转过程中的任意两个位置分别记为∠E1DF1，∠E2DF2，DE1交直线AC于点P，DF1交直线BC于点Q，DE2交直线AC于点M，DF2交直线BC于点N，求的值；（3）若图1中∠B＝β（60°<β<90°），（2）中的其余条件不变，请直接写出的值（用含β的式子表示）．试题8:如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线．（1）用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）（2）设DN与AM交于点F，判断△ADF的形状．（只写结果）试题9:在由m×n（m×n＞1）个小正方形组成的矩形网格中，研究它的一条对角线所穿过的小正方形个数f，（1）当m、n互质（m、n除1外无其他公因数）时，观察下列图形并完成下表：m n m+n f1 2 3 21 3 4 32 3 5 42 5 73 4 7猜想：当m、n互质时，在m×n的矩形网格中，一条对角线所穿过的小正方形的个数f与m、n的关系式是（不需要证明）；（2）当m、n不互质时，请画图验证你猜想的关系式是否依然成立．试题10:如图1，将菱形纸片AB（E）CD（F）沿对角线BD（EF）剪开，得到△ABD和△ECF，固定△ABD，并把△ABD与△ECF叠放在一起．（1）操作：如图2，将△ECF的顶点F固定在△ABD的BD边上的中点处，△ECF绕点F在BD边上方左右旋转，设旋转时FC交BA于点H（H点不与B点重合），FE交DA于点G（G点不与D点重合）．求证：BH•GD=BF2（2）操作：如图3，△ECF的顶点F在△ABD的BD边上滑动（F点不与B、D点重合），且CF始终经过点A，过点A作AG ∥CE，交FE于点G，连接DG．探究：FD+DG= ．请予证明．试题1答案:B【考点】翻折变换（折叠问题）．【专题】计算题．【分析】根据图形折叠前后图形不发生大小变化，得出AE=A′E，再利用勾股定理得出A′E2+A′D2=ED2，从而求出x，进而得出DE的长，再求出△DEF的面积．【解答】解：∵按如图方式折叠，使顶点B和点D重合，折痕为EF，∵AB=3cm，BC=5cm，∴A′D=AB=3cm，假设AE=x，则A′E=xcm，DE=5﹣x（cm），∴A′E2+A′D2=ED2，∴x2+9=（5﹣x）2，解得：x=1.6，∴DE=5﹣1.6=3.4（cm），∴△DEF的面积是：×3.4×3=5.1（cm2）．试题2答案:【考点】翻折变换（折叠问题）．【分析】根据操作步骤，可知每一次操作时所得正方形的边长都等于原矩形的宽．所以首先需要判断矩形相邻的两边中，哪一条边是矩形的宽．当＜a＜1时，矩形的长为1，宽为a，所以第一次操作时所得正方形的边长为a，剩下的矩形相邻的两边分别为1﹣a，a．由1﹣a＜a可知，第二次操作时所得正方形的边长为1﹣a，剩下的矩形相邻的两边分别为1﹣a，a﹣（1﹣a）=2a﹣1．由于（1﹣a）﹣（2a﹣1）=2﹣3a，所以（1﹣a）与（2a﹣1）的大小关系不能确定，需要分情况进行讨论．又因为可以进行三次操作，故分两种情况：①1﹣a＞2a﹣1；②1﹣a＜2a﹣1．对于每一种情况，分别求出操作后剩下的矩形的两边，根据剩下的矩形为正方形，列出方程，求出a的值．【解答】解：由题意，可知当＜a＜1时，第一次操作后剩下的矩形的长为a，宽为1﹣a，所以第二次操作时正方形的边长为1﹣a，第二次操作以后剩下的矩形的两边分别为1﹣a，2a﹣1．故答案为：1﹣a；此时，分两种情况：①如果1﹣a＞2a﹣1，即a＜，那么第三次操作时正方形的边长为2a﹣1．∵经过第三次操作后所得的矩形是正方形，∴矩形的宽等于1﹣a，即2a﹣1=（1﹣a）﹣（2a﹣1），解得a=；②如果1﹣a＜2a﹣1，即a＞，那么第三次操作时正方形的边长为1﹣a．则1﹣a=（2a﹣1）﹣（1﹣a），解得a=．故答案为：或．【点评】本题考查了一元一次方程的应用，解题的关键是分两种情况：①1﹣a＞2a﹣1；②1﹣a＜2a﹣1．分别求出操作后剩下的矩形的两边．试题3答案:试题4答案:4试题5答案:π试题6答案:【考点】相似形综合题．【分析】（操作1）连接BE，根据已知条件得到E是AC的中点，根据等腰直角三角形的性质可以证明DE=CE，∠PBE=∠C．根据等角的余角相等可以证明∠BEP=∠CEQ．即可得到全等三角形，从而证明结论；（操作2）作EM⊥AB，EN⊥BC于M、N，根据两个角对应相等证明△MEP∽△NWQ，发现EP：EQ=EM：EN，再根据等腰直角三角形的性质得到EM：EN=AE：CE；（总结操作）根据（2）中求解的过程，可以直接写出结果；要求m的取值范围，根据交点的位置的限制进行分析．【解答】（操作1）EP=EQ，证明：连接BE，根据E是AC的中点和等腰直角三角形的性质，得：BE=CE，∠PBE=∠C=45°，∵∠BEC=∠FED=90°∴∠BEP=∠CEQ，在△BEP和△CEQ中，∴△BEP≌△CEQ（ASA），∴EP=EQ；如图2，EP：EQ=EM：EN=AE：CE=1：2，理由是：作EM⊥AB，EN⊥BC于M，N，∴∠EMP=∠ENC，∵∠MEP+∠PEN=∠PEN+∠NEF=90°，∴∠MEP=∠NEF，∴△MEP∽△NEQ，∴EP：EQ=EM：EN=AE：CE=1：2；如图3，过E点作EM⊥AB于点M，作EN⊥BC于点N，∵在四边形PEQB中，∠B=∠PEQ=90°，∴∠EPB+∠EQB=180°，又∵∠EPB+∠MPE=180°，∴∠MPE=∠EQN，∴Rt△MEP∽Rt△NEQ，∴=，Rt△AME∽Rt△ENC，∴=m=，∴=1：m=，EP与EQ满足的数量关系式1：m，即EQ=mEP，∴0＜m≤2+，（因为当m＞2+时，EF和BC变成不相交）．【点评】本题考查了相似三角形的性质和判定，全等三角形的性质和判定，主要考查学生运用定理进行推理的能力，证明过程类似．试题7答案:【解答】解：（1）∵∠ACB=90°，D为AB的中点，∴CD=DB，∴∠DCB=∠B.∵∠B=60°，∴∠DCB=∠B=∠CDB=60°∴∠CDA=120°.∵∠EDC=90°，∴∠ADE=30°；（2）∵∠C=90°，∠MDN=90°，∴∠DMC+∠CND=180°.∵∠DMC+∠PMD=180°，∴∠CND=∠PMD.同理∠CPD=∠DQN.∴△PMD∽△QND.过点D分别做DG⊥AC于G，DH⊥BC于H.可知DG，DH分别为△PMD和△QND的高.∴∵DG⊥AC于G，DH⊥BC于H，∴DG∥BC.又∵D为AB中点，∴G为AC中点.∵∠C=90°，∴四边形CGDH为矩形，有CG=DH=AG，Rt△AGD中，.即.（3）=tan（90°﹣β）（=.试题8答案:【考点】等腰三角形的判定与性质；作图—基本作图．【专题】作图题．【分析】（1）以D为圆心，以任意长为半径画弧，交AD于G，交DC于H，分别以G、H为圆心，以大于GH为半径画弧，两弧交于N，作射线DN，交AM于F．（2）求出∠BAD=∠CAD，求出∠FAD=×180°=90°，求出∠CDF=∠AFD=∠ADF，推出AD=AF，即可得出答案．【解答】解：（1）如图所示：（2）△ADF的形状是等腰直角三角形，理由是：∵AB=AC，AD⊥BC，∴∠BAD=∠CAD，∵AF平分∠EAC，∴∠EAF=∠FAC，∵∠FAD=∠FAC+∠DAC=∠EAC+∠BAC=×180°=90°，即△ADF是直角三角形，∵AB=AC，∴∠B=∠ACB，∵∠EAC=2∠EAF=∠B+∠ACB，∴∠EAF=∠B，∴AF∥BC，∴∠AFD=∠FDC，∵DF平分∠ADC，∴∠ADF=∠FDC=∠AFD，∴AD=AF，即直角三角形ADF是等腰直角三角形．【点评】本题考查了作图﹣基本作图，等腰三角形的性质和判定的应用，主要培养学生的动手操作能力和推理能力，题目比较典型，难度也适中．试题9答案:【考点】作图—应用与设计作图；规律型：图形的变化类．【分析】（1）通过观察即可得出当m、n互质时，在m×n的矩形网格中，一条对角线所穿过的小正方形的个数f与m、n 的关系式，（2）当m、n不互质时，画出图即可验证猜想的关系式不成立．【解答】解：（1）表格中分别填6，6m n m+n f1 2 3 21 3 4 32 3 5 42 5 7 63 4 7 6f与m、n的关系式是：f=m+n﹣1．故答案为：f=m+n﹣1．（2）m、n不互质时，猜想的关系式不一定成立，如下图：．【点评】此题考查了作图﹣应用与设计作图，关键是通过观察表格，总结出一条对角线所穿过的小正方形的个数f与m、n的关系式，要注意m、n互质的条件．试题10答案:【考点】相似三角形的判定与性质；全等三角形的判定与性质；菱形的性质；旋转的性质．【专题】压轴题．【分析】（1）根据菱形的性质以及相似三角形的判定得出△BFH∽△DGF，即可得出答案；（2）利用已知以及平行线的性质证明△ABF≌△ADG，即可得出FD+DG的关系．【解答】证明：（1）∵将菱形纸片AB（E）CD（F）沿对角线BD（EF）剪开，∴∠B=∠D，∵将△ECF的顶点F固定在△ABD的BD边上的中点处，△ECF绕点F在BD边上方左右旋转，∴BF=DF，∵∠HFG=∠B，又∵∠HFD=∠HFG+∠GFD=∠B+∠BHF ∴∠GFD=∠BHF，∴△BFH∽△DGF，∴，∴BH•GD=BF2；（2）∵AG∥CE，∴∠FAG=∠C，∵∠CFE=∠CEF，∴∠AGF=∠CFE，∴AF=AG，∵∠BA D=∠C，∴∠BAF=∠DAG，又∵AB=AD，∴△ABF≌△ADG，∴FB=DG，∴FD+DG=BD，故答案为：BD．【点评】此题主要考查了相似三角形的判定以及全等三角形的判定，根据等腰三角形的性质得出∠BAF=∠DAG是解决问题的关键．。

实验应用型问题一、选择题1、（2013江苏扬州弘扬中学二模）如图，在四边形ABCD 中，∠A =90°，AD =4，连接BD ，BD ⊥CD ，∠ADB =∠C ．若P 是BC 边上一动点，则DP 长的最小值为____________.答案：4二、填空题1、如图所示，平面镜I 、II 的夹角是 15，光线从平面镜I 上O 点出发，照射到平面镜II 上的A 点，再经II 反射到B 点，再经C 点反射到D 点,接着沿原线路反射回去，则a ∠的大小为 度. 答案：452．数学家发明了一个魔术盒，当任意实数对()a b ，进入其中时，会得到一个新的实数：21a b ++．例如把(32)-，放入其中，就会得到23(2)18+-+=．现将实数对（m m 2,-）放入其中得到实数4，则m = ．答案：－1或3三、解答题1、在北京举行的2008年奥运会中，某校学生会为了了解全校同学喜欢收看奥运会比赛项目的情况，随机调查了若干名同学（每人只能选其中一项），根据调查结果制作了频数分布表和统计图。

请根据图中提供的信息解答下列问题： （1）补全频数分布表和条形统计图；；（2）根据以上调查，试估计该校1800名学生中，最喜欢收看篮球比赛的人数． （3）根据统计图和统计表，谈谈．．．．．．．．．．．．你的想法。

．．．．．最喜欢收看的项目 频数（人数） 频率足球 20% 篮球 25%排球6 10%乒乓球201题图O DCB AIII a15︒答案：解：（1）最喜欢收看的项目 频数（人数） 频率足球 12（2）最喜欢收看篮球比赛的人数=1800×25%，=450（人）；（3）因为喜欢看乒乓球的人数最多，所以在观看比赛时优先安排看乒乓球．2．（本小题满分8分）如图，甲船从港口A 出发沿北偏东15°方向行驶，同时，乙船也从港口A 出发沿西北方向行驶。

若干小时之后，甲船位于点C 处，乙船位于港口B 的北偏东60°方向，距离岸边BD 10海里的P 处。

2021年中考数学一模分类汇编——实验操作题现场学习、利用旋转变换解决几何计算1.〔西城区〕阅读以下材料：问题：如图1，在正方形ABCD内有一点P，PA=5，PB=2，PC=1，求∠BPC的度数．小明同学的想法是：条件比拟分散，可以通过旋转变换将分散的条件集中在一起，于是他将△BPC绕点B逆时针旋转90°，得到了△BP′A 〔如图2〕，然后连结PP′．请你参考小明同学的思路，解决以下问题：(1) 图2中∠BPC的度数为；(2) 如图3，假设在正六边形ABCDEF内有一点P，且PA=132，PB=4，PC=2，那么∠BPC的度数为，正六边形ABCDEF的边长为．图1 图2 图3图形变换+几何计算2.〔门头沟〕阅读下面材料：小伟遇到这样一个问题：如图1，在正方形ABCD 中，点E 、F 分别为DC 、BC 边上的点，∠EAF =45°，连结EF ，求证：DE +BF =EF ．小伟是这样考虑的：要想解决这个问题，首先应想方法将这些分散的线段集中到同一条线段上．他先后尝试了平移、翻折、旋转的方法，发现通过旋转可以解决此问题．他的方法是将△ADE 绕点A 顺时针旋转90°得到△ABG 〔如F ED AB C B EDA G F D ABC C图1图2图3CDAOBx y图4DADADACDy图2〕，此时GF即是DE+BF．请答复：在图2中，∠GAF的度数是．参考小伟得到的结论和考虑问题的方法，解决以下问题：〔1〕如图3，在直角梯形ABCD中，AD∥BC〔AD＞BC〕，∠D=90°，AD=CD=10，E是CD上一点，假设∠BAE=45°，DE=4，那么BE= ．〔2〕如图4，在平面直角坐标系xOy中，点B是x轴上一动点，且点A〔3-，2〕，连结AB和AO，并以AB为边向上作正方形ABCD含x的代数式表示y，那么y= ．几何作图+图形变换+面积问题3．〔海淀〕阅读下面材料：小明遇到这样一个问题：如图1，△ABO和△CDO均为等腰直角三角形, ∠AOB=∠COD=90︒．假设△BOC的面积为1，试求以AD、BC、OC+OD 的长度为三边长的三角形的面积．图1 图2小明是这样考虑的：要解决这个问题，首先应想方法挪动这些分散的线段，构造一个三角形，再计算其面积即可．他利用图形变换解决了这个问题，其解题思路是延长CO 到E , 使得OE =CO , 连接BE , 可证△OBE ≌△OAD , 从而得到的△BCE 即是以AD 、BC 、OC+OD 的长度为三边长的三角形〔如图2〕．请你答复：图2中△BCE 的面积等于 ． 请你尝试用平移、旋转、翻折的方法，解决以下问题： 如图3，△ABC , 分别以AB 、AC 、BC 为边向外作正方形ABDE 、AGFC 、BCHI , 连接EG 、FH 、ID ．〔1〕在图3中利用图形变换画出并指明以EG 、FH 、ID 的长度为三边长的一个三角形〔保存画图痕迹〕；〔2〕假设△ABC 的面积为1，那么以EG 、FH 、ID 的长度为 三边长的三角形的面积等于 ．图3CBBOCDAI HGF A BCDE几何作图+几何最值4．〔昌平〕 问题探究：〔1〕如图1，在边长为3的正方形ABCD 内〔含边〕画出使∠BPC =90°的一个点P ，保存作图痕迹；〔2〕如图2，在边长为3的正方形ABCD 内〔含边〕画出使∠BPC =60°的所有的点P ，保存作图痕迹并简要说明作法；〔3〕如图3，矩形ABCD ，AB =3，BC =4，在矩形ABCD 内〔含边〕画出使∠BPC=60°，且使△BPC 的面积最大的所有点P ，保存作图痕迹．几何作图+不完全归纳5. 〔燕山〕请你先动笔在草稿纸上画一画，再答复以下问题： 〔1〕平面内两条直线，可以把平面分成几局部？ 〔2〕平面内3条直线，可以把平面分成几局部？图3图2图1A DCBABCDD CB A〔3〕平面内4条直线，可以把平面最多．．分成多少局部？ 〔4〕平面内100条直线，可以把平面最多．．分成多少局部？面积问题6．〔顺义〕问题背景〔1〕如图1，△ABC 中，DE ∥BC 分别交AB ， AC 于D ，E 两点，过点D 作DF ∥AC 交BC 于点F ．请按图示数据填空：四边形DFCE 的面积S = ， △DBF 的面积1S = ， △ADE 的面积2S = ． 探究发现〔2〕在〔1〕中，假设BF a =，FC b =，D Ｇ与BC 间的间隔 为h ．直接写出2S = 〔用含S 、1S 的代数式表示〕． 拓展迁移〔3〕如图2，□DEFG 的四个顶点在△ABC 的三边上，假设△ADG 、△DBE 、△GFC的面积分别为4、8、1，试利用．．．．求□DEFG的面积，直．．〔2．〕中的结论接写出结果．网格问题+面积计算△中，AB、BC、AC7. 〔东城〕在ABC小宝同学在解答这道题时，先建立一个正方形网格〔每个小正方形的边长为1〕，再在网格中画出格点ABC △〔即ABC △三个顶点都在小正方形的顶点处〕，如图1所示．这样不需求ABC △的高，而借用网格就能计算出它的面积．〔1〕请你将ABC △的面积直接填写上在横线上__________________； 思维拓展：〔2〕我们把上述求ABC △面积的方法叫做构图法．．．．假设ABC △三边的长分别为2a 、13a 、17a 〔0a >〕，请利用图2的正方形网格〔每个小正方形的边长为a 〕画出相应的ABC △，并求出它的面积填写上在横线上__________________； 探究创新：〔3〕假设ABC △中有两边的长分别为2a 、10a 〔0a >〕，且ABC△的面积为22a ，试运用构图法．．．在图3的正方形网格〔每个小正方形的边长为a 〕中画出所有符合题意的ABC △(全等的三角形视为同一种情况)，并求出它的第三条边长填写上在横线上__________________．8．〔房山〕阅读下面材料：如图1，线段AB、CD相交于点O，且AB=CD，请你利用所学知识把线段AB、CD转移到同一三角形中．小强同学利用平移知识解决了此问题，详细做法：如图2，延长OD至点E，使DE=CO，延长OA至点F，使AF=OB，联结EF，那么△OEF为所求的三角形．请你仔细体会小强的做法，探究并解答以下问题：如图3，长为2的三条线段AA′，BB′，CC′交于一点O，并且∠B′OA=∠C′OB=∠A′OC=60°；〔1〕请你把三条线段AA′，BB′，CC′转移到同一三角形中．〔简要表达画法〕〔2〕联结AB′、BC′、CA′，如图4，设△AB′O、△BC′O、△CA′O的面积分别为S1、S2、S3，那么S1+S2+S33〔填“>〞或者“<〞或者“=〞〕．图2利用轴对称变换解决几何最值9．〔通州〕小明在学习轴对称的时候，教师留了这样一道考虑题：如图，在直线l的同侧有A、B两点，请你在直线l上确定一点P，使得PA+PB的值最小.小明通过HY考虑，很快得出理解决这个问题的正确方法，他的作法是这样的：①作点A关于直线l的对称点A′.l ABA图3 如图4C②连结A′B ，交直线l 于点P . 那么点P 为所求.请你参考小明的作法解决以下问题：〔1〕如图1，在△ABC 中，点D 、E 分别是AB 、AC 边的中点，BC =6，BC 边上的高为4，请你在BC 边上确定一点P ，使得△PDE 的周长最小.①在图1中作出点P .〔三角板、刻度尺作图，保存作图痕迹，不写作法〕 ②请直接写出△PDE 周长的最小值 .〔2〕如图2在矩形ABCD 中，AB =4，BC =6，G 为边AD 的中点，假设E 、F 为边AB 上的两个动点，点E 在点F 左侧，且EF =1，当四边形CGEF 的周长最小时，请你在图2中确定点E 、F 的位置.〔三角板、刻度尺作图，保存作图痕迹，不写作法〕，并直接写出四边形CGEF周长的最小值 .图１A B图1图2CB A D拼剪问题10．〔丰台〕将矩形纸片分别沿两条不同的直线剪两刀，可以使剪得的三块纸片恰能拼成一个等腰三角形〔不能有重叠和缝隙〕．小明的做法是：如图1所示，在矩形ABCD 中，分别取AD 、AB 、CD 的中点P 、E 、F ，并沿直线PE 、PF 剪两刀，所得的三局部可拼成等腰三角形△PMN (如图2)．〔1〕在图3中画出另一种剪拼成等腰三角形的示意图；〔2〕以矩形ABCD 的顶点B 为原点，BC 所在直线为x 轴建立平面直角坐标系〔如图4〕，矩形ABCD 剪拼后得到等腰三角形△PMN ，点P 在边AD 上〔不与点A 、D 重合〕，点M 、N 在x 轴上〔点M 在N 的左边〕．假如点D 的坐标为(5,8)，直线=y kx b k 的值图1 图2 图3FP D图4 备用11．〔密云、怀柔〕如图①，将一张直角三角形纸片ABC 折叠，使点A 与点C 重合，这时DE 为折痕， △CBE 为等腰三角形；再继续将纸片沿△CBE 的对称轴EF 折叠，这时得到了两个完全重合的矩形〔其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、 无重叠的矩形〕，我们称这样两个矩形为“叠加矩形〞．请完成以下问题：〔1〕如图②，正方形网格中的△ABC 能折叠成“叠加矩形〞吗？假如能，请在图②中画出折痕；〔2〕如图③，在正方形网格中，以给定的BC 为一边，画出一个斜△ABC ，x yDAB CxyD ABC使其顶点A在格点上，且△ABC折成的“叠加矩形〞为正方形；〔3〕假如一个三角形所折成的“叠加矩形〞为正方形，那么他必须满足的条件是．12．〔大兴〕阅读以下材料：小明遇到一个问题：：如图1，在△ABC中，∠BAC=120°,∠ABC=40°，试过△ABC的一个顶点画一条直线，将此三角形分割成两个等腰三角形.他的做法是：如图2，首先保存最小角∠C，然后过三角形顶点A画直线交BC于点D. 将∠BAC分成两个角，使∠DAC=20°，△ABC即可被分割成两个等腰三角形.喜欢动脑筋的小明又继续探究：当三角形内角中的两个角满足怎样的数量关系时，此三角形一定可以被过顶点的一条直线分割成两个等腰三角形.他的做法是：如图3，先画△ADC ，使DA=DC，延长AD到点B，使△BCD也是等腰三角形，假如DC=BC，那么∠CDB =∠ABC，因为∠CDB=2∠A，所以∠ABC= 2∠A．于是小明得到了一个结论：当三角形中有一个角是最小角的2倍时，那么此三角形一定可以被过顶点的一条直线分割成两个等腰三角形．请你参考小明的做法继续探究：直接写出你所探究出的另外两条结论〔不必写出探究过程或者理由〕．折叠问题13．〔石景山〕生活中，有人用纸条可以折成正五边形的形状，折叠过程是将图①中的纸条按图②方式拉紧，压平后可得到图③中的正五边形〔阴影局部表示纸条的反面〕．图①图②图③〔1〕将两端剪掉那么可以得到正五边形，假设将展开，展开后的平面图形是；〔2〕假设原长方形纸条〔图①〕宽为2cm，求〔1〕中展开后平面图形的周长〔可以用三角函数表示〕．14．〔平谷〕如图①，在矩形ABCD中，将矩形折叠，使点B落在AD〔含端点〕上，落点记为E，这时折痕与边BC或者边CD〔含端点〕交于点F.然后再展开铺平，那么以B E F 、、为顶点的BEF △称为矩形ABCD 的“折痕三角形〞．〔1〕由“折痕三角形〞的定义可知，矩形ABCD 的任意一个“折痕BEF △〞一定是一个________三角形；〔2〕如图②，在矩形ABCD 中，24AB BC ==，，当它的“折痕BEF △〞的顶点E 位于边AD 的中点时，画出这个“折痕BEF △〞，并求出点F 的坐标；〔3〕如图③，在矩形ABCD 中，24AB BC ==，.当点F 在OC 上时，在图③中画出该矩形中面积最大的“折痕BEF △〞，并直接写出这个最大面积.图1ACDB图2FOAECD BA现场学习解决几何计算15. 〔延庆〕阅读下面材料：小红遇到这样一个问题，如图1：在△ABC 中，AD ⊥BC ，BD =4，DC =6,且∠BAC =45°,求线段AD 的长.小红是这样想的：作△ABC 的外接圆⊙O ，如图2：利用同弧所对圆周角和圆心角的关系，可以知道∠BOC =90°，然后过O 点作OE ⊥BC 于E ，作OF ⊥AD 于F ，在Rt △BOC 中可以求出⊙O 半径及 OE ，在Rt △AOF 中可以求出AF ,最后利用AD =AF +DF 得以解决此题。

操作探究一.选择题1．〔2021•临安•3 分.〕z 如图，正方形硬纸片ABCD的边长是4，点分别是AB.BC的中点，假设沿左图中的虚线剪开，拼成如图的一座“小别墅〞，那么图中阴影局部的面积是〔〕A．2 B．4 C．8 D．10【分析】此题考察空间想象才能．【解答】解：阴影局部由一个等腰直角三角形和一个直角梯形组成，由第一个图形可知：阴影局部的两局部可构成正方形的四分之一，正方形的面积=4×4=16，∴图中阴影局部的面积是16÷4=4．应选：B．【点评】解决此题的关键是得到阴影局部的组成与原正方形面积之间的关系%@z#step~.co&2. 〔2021••3分〕将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是〔〕A. 〔A〕B. 〔B〕C. 〔C〕D. 〔D〕【答案】A【解析】【分析】根据两次折叠都是沿着正方形的对角线折叠, 展开后所得图形的顶点一定在正方形的对角线上, 根据③的剪法，中间应该是一个正方形.【解答】根据题意，两次折叠都是沿着正方形的对角线折叠的，根据③的剪法，展开后所得图形的顶点一定在正方形的对角线上,而且中间应该是一个正方形.应选A．【点评】关键是要理解折叠的过程，得到关键信息，如此题得到展开后的图形的顶点在正方形的对角线上是解题的关键．3. 〔2021•广西•3分〕如图，矩形纸片ABCD，AB=4，BC=3，点P 在BC 边上，将△C DP 沿DP 折叠，点C 落在点E 处，PE.DE 分别交AB 于点O、F，且OP=OF，那么co s∠ADF 的值是〔〕A．1113B．1315C．1517D．1719【分析】根据折叠的性质可得出 DC=DE.CP=EP，由∠EOF=∠B OP、∠B=∠E.OP=OF 可得出△OE F≌△OBP〔AAS〕，根据全等三角形的性质可得出OE=OB.EF=BP，设EF=x，那么BP=x、DF=4﹣x、BF=PC=3﹣x，进而可得出AF=1+x，在R t△DAF 中，利用勾股定理可求出x 的值，再利用余弦的定义即可求出co s∠A DF 的值．【解答】解：根据折叠，可知：△D CP≌△DE P，∴DC=DE=4，CP=EP．在△O EF 和△O BP 中，EOF BOPB EOP OF∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△O EF ≌△OB P 〔AAS 〕，∴OE=OB ，EF=BP ．设 EF=x ，那么 BP=x ，DF=DE ﹣EF=4﹣x ， 又∵B F=OB+OF=OE+OP=PE=PC ，PC=BC ﹣BP=3﹣x ，∴AF=AB ﹣BF=1+x ．在 Rt △DAF 中，AF 2+AD 2=DF 2，即〔1+x 〕2+32=〔4﹣x 〕2，解得：x=35，∴DF=4﹣x=175，∴co s ∠AD F=ADDF =1517．应选：C ．【点评】此题考察了全等三角形的断定与性质、勾股定理以及解直角三角形，利用勾股定理结合 AF=1+x，求出 AF 的长度是解题的关键．4.〔2021••3分〕如图1，分别沿长方形纸片ABCD 和正方形纸片EFGH 的对角线AC，EG 剪开，拼成如图2 所示的▱KLMN，假设中间空白局部四边形OPQR 恰好是正方形，且▱KLMN 的面积为50，那么正方形EFGH 的面积为〔〕A．24 B．25 C．26D．27【分析】如图，设 PM=PL=NR=AR=a，正方形ORQP 的边长为 b，构建方程即可解决问题；【解答】解：如图，设 PM=PL=NR=AR=a，正方形ORQP 的边长为b．由题意：a 2+b 2+〔a+b 〕〔a ﹣b 〕=50，∴a 2=25，∴正方形 EFGH 的面积=a 2=25， 应选：B ．【点评】此题考察图形的拼剪，矩形的性质，正方形的性质等知识，解题的关键是学会利用 参数构建方程解决问题，学会利用数形结合的思想解决问题，属于中考选择题中的压轴题．二.填空题1. 〔2021••4 分〕折叠矩形纸片 ABCD 时，发现可以进展如下操作：①把△ADE 翻折，点 A 落在 DC 边上的点 F 处，折痕为 DE ，点 E 在 AB 边上；②把纸片展开并铺平；③把△CDG 翻折，点 C 落在直线 AE 上的点 H 处，折痕为 DG ，点 G 在 BC 边上， 假设 AB=AD+2，EH=1，那么 AD= 。

中考数学模拟试题精选汇编数学作为中学教育的一门重要学科，是培养学生逻辑思维和解决问题能力的关键。

中考数学试题的设置旨在考察学生对基本概念、定理和方法的理解和应用能力。

本文将为大家精选一些中考数学模拟试题，旨在帮助学生加深对这些最常见数学题型的认识和理解。

一、选择题1. 已知正整数a和b满足a^b=b^a，那么以下哪个选项是可能的？A. a=2, b=4B. a=3, b=2C. a=4, b=2D. a=5, b=2分析：根据等式a^b=b^a，可得a=b^(1/b)，所以a和b满足对数关系。

根据选项，可以快速得出答案为B。

2. 若正方体的棱长为1，那么过其中一面的对角线长是多少？A. 1B. sqrt(2)C. sqrt(3)D. 2分析：过正方体一面的对角线可看作是正方体的空对角线，根据勾股定理可得其长为sqrt(3)，所以答案为C。

3.在坐标平面上，已知点A(5,3)和点B(-1,1)，则点A关于点B对称的点是：A. (-7,-1)B. (-5,-1)C. (-5,-3)D. (-7,-3)分析：点A关于点B对称的点的横坐标为B的横坐标的两倍减去A的横坐标，纵坐标为B的纵坐标的两倍减去A的纵坐标。

根据计算可得答案为D。

二、填空题1. 三位数中有多少个既是5的倍数又是9的倍数？填写：__分析：三位数中5的倍数的个位数字必为0或5，9的倍数个位数字之和为9或18。

根据这两个条件可得个位数字为5，所填写的答案为1。

2. 已知x=5+sqrt(6)，求x^2的值。

填写：__分析：根据给定的x值可求得x^2的值为11+10sqrt(6)，所填写的答案为11+10sqrt(6)。

三、解答题1. 从1000到9999的所有四位数中，有多少个数的各位上的数字均相同并且除以3余1？解答：首先，对于四位数，其各位上的数字均相同的数有多少个呢？根据各位数字可以选取的情况，共有10个数字可供选择，所以在各位数字相同的情况下，可以选取的数共有10个。