下载文档原格式
1试分别指出以下波形是属于哪种信号？题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示，试作出下列各信号的波形图，并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示，试作出信号x(t)的波形图，并加以标注。
题图1-51- 6 试画出下列信号的波形图：1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图：⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角，并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下，试写出各自系统的输入输出方程。
习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。
因此，公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。
因此，公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数，因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的，基频 =0f 1/π Hz 。
因此，公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解 周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
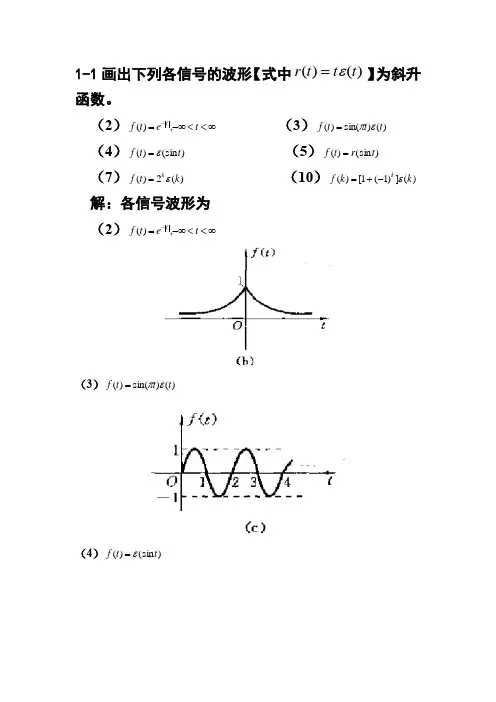
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)f=rt)(sin(t（7）)t=(kf kε(2)（10）)f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是，确定其周期。
（2）)63cos()443cos()(2ππππ+++=k k k f（5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。
信号与系统第三版郑君里课后习题答案第一章习题参考解1，判刑下列信号的类型解：()sin [()];y t A x t = 连续、模拟、周期、功率型信号 。
()()tt y t x ed τττ--∞=⎰连续、模拟、非周期、功率型信号。
()(2y n x n =） 离散、模拟、非周期、功率型信号。
()()y n n x n = 离散、模拟、非周期、功率型信号。
1－6，示意画出下列各信号的波形，并判断其类型。
(1) 0()s in ()x t A t ωθ=+ 连续、模拟、周期、功率型(2) ()t x t A e -= 连续、模拟、非周期、只是一个函数，不是物理量。
(3) ()c o s 0tx t ett -=≥ 连续、模拟、非周期、能量型 (4) ()2112,x t t t =+-≤≤ 连续、模拟、非周期、能量型(5) 4()(),0.5k x k k =≥ 离散、模拟、非周期、能量型(6) 0().j kx k eΩ= 离散、模拟、周期、功率型()s i n [()];()()()(2);()()tt y t A x t y t x ed y n x n y n n x n τττ--∞====⎰1－6题，1－4图。
t=-pi:1/200:pi;y1=1.5*sin(2*t+pi/6);subplot(4,1,1),plot(t,y1),title('1.5sin(2*t+pi/6)'),gridy2=2*exp(-t);subplot(4,1,2),plot(t,y2),title('2exp(-t)'),gridt1=0:1/200:2*pi;y3=10*exp(-t1).*cos(2*pi*t1);subplot(4,1,3),plot(t1,y3),title('10exp(-t1)cos(2*pi*t1)'),grid t2=-1:1/200:2;y4=2*t2+1;subplot(4,1,4),plot(t2,y4),title('2x+1'),grid习题1－6 5－6题n=0:pi/10:2*pi;y=(0.8).^n;subplot(4,1,1),stem(n,y,'fill'),title('(0.8)^n'),gridn1=0:pi/24:2*pi;y1=cos(2*pi*n1);y2=sin(2*pi*n1);subplot(4,1,2),stem3(y1,y2,n1,'fill'),title('exp[2*pi*n1'),gridsubplot(4,1,4),stem(n1,sin(2*pi*n1),'fill'),title('sin2pin1'),gridsubplot(4,1,3),stem(n1,cos(2*pi*n1),'fill'),title('cos2pin1)'),grid1－8，判断下列系统的类型。
一、填空题1．信号()f t 在区间a t a −<<上的功率可表示为 。
2．信号(4)f t −−可将信号()f t ，得到(4)f t −；而后 ，得到(4)f t −−。
3．连续系统的时域框图的基本单元包括积分器、加法器、 和 。
4．单位冲激函数的积分运算可以得到 ；单位阶跃函数的 微分运算可以得到 。
5．根据系统初始状态和激励的不同影响，LTI 连续系统的响应可分为 和 。
6．离散系统可用 方程来描述。
7．LTI 连续系统的零输入响应与 之和可构成LTI 系统的 。
8．时间上是离散的、幅度上是量化的信号称做__________。
二、单项选择题（在每小题的备选答案中，选出一个正确答案，并将正确答案的序号填在括号内。
）1．单位序列在k=（ ）时其数值为1。
A ．1 B ．0 C ．无穷大 D ．无穷小2．已知某连续系统的零状态响应()2()zs y t f t =，则可知系统是（ ）。
A ．不能确定稳定性 B ．稳定的 C ．不稳定的 D ．非因果的3．根据冲激函数的性质，()ate t δ可化简为（ ）。
A ．0B ．1C ．()t δD ．∞4．在LTI 系统中，已知激励信号为()f t 时的零状态响应为()zs y t ，则可知系统在激励信号为(5)f t −时的零状态响应为（ ）。
A ．不能确定B ．()zs y tC ．(5)zs y t −D ．1(1)8zs y t −三．判断题 （下述结论若正确，则在括号内填入√，若错误则填入×）1、离散信号和数字信号的含义相同。
（ ） 2．单位阶跃序列在k=0时取值为1。
（ ）四、画图题1、画出LTI 离散时间系统 )1()1(3)(−=−+k f k y k y 的系统框图。
2．已知信号()f t 的波形如图所示，试画出()(1)(1)g t f t t ε=−−的波形图。
3．已知信号()f t 的波形如图所示，试画出d ()d f t t的波形图。
