精算学作业

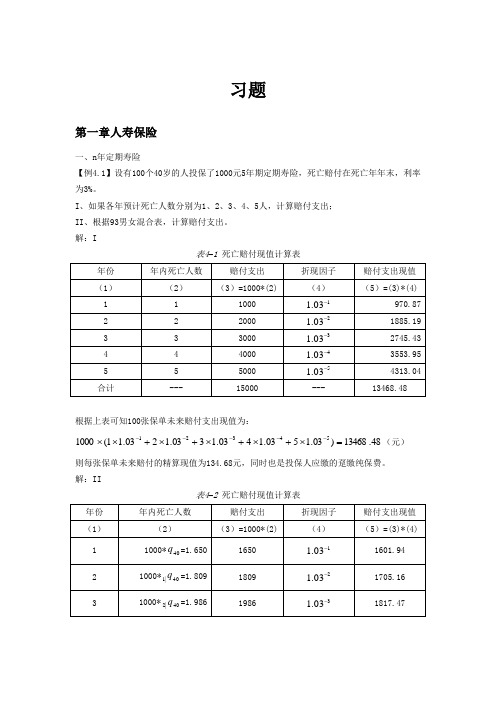
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险，死亡赔付在死亡年年末，利率为3%。

I 、如果各年预计死亡人数分别为1、2、3、4、5人，计算赔付支出； II 、根据93男女混合表，计算赔付支出。

解：I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为：48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----（元）则每张保单未来赔付的精算现值为134.68元，同时也是投保人应缴的趸缴纯保费。

解：II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为：86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q （元）则每张保单未来赔付的精算现值为91.25元，同时也是投保人应缴的趸缴纯保费。

【例4.2】某人在40岁时投保了10000元3年期定期寿险，死亡赔付在死亡年年末，利率为5%。

根据93男女混合表计算：I 、单位趸缴纯保费；II 、单位赔付现值期望的方差；III 、（总）趸缴纯保费； 解：I 、单位趸缴纯保费为，)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=（元）。

II 、单位赔付现值期望的方差为，00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为，28.49100001|3:40=⨯A （元） 【例4.3】某人在50岁时投保了100000元30年期定期寿险，利率为8%。

1．李华1990年1月1日在银行帐户上有5000元存款，（1）在每年10%的单利下，求1994年1月1日的存款额。

（2）在年利率8%的复利下，求1994年5月1日的存款额。

解：（1）5000×（1+4×10%）=7000（元）（2）5000×（1+10%）4.33=7556.8（元）2．把5000元存入银行，前5年的银行利率为8%，后5年年利率为11%，求10年末的存款累计额。

解：5000（1+8%）5×（1+11%）5=12385（元）3．李美1994年1月1日在银行帐户上有10000元存款。

（1）求在复利11%下1990年1月1日的现值。

（2）在11%的折现率下计算1990年1月1日的现值。

解：（1）10000×（1+11%）-4=5934.51（元）（2）10000×（1-11%）4=6274.22（元）4．假设1000元在半年后成为1200元，求⑴ )2(i ，⑵ i, ⑶ )3(d 。

解：⑴ 1200)21(1000)2(=+⨯i ；所以4.0)2(==i ⑵2)2()21(1i i +=+；所以44.0=i ⑶n n m m nd d i m i ---=-=+=+)1()1(1)1()(1)(；所以， 13)3()1()31(-+=-i d ；34335.0)3(=d5．当1>n 时，证明：i idd n n <<<<)()(δ。

证明：①)(n d d <因为，+⋅-⋅+⋅-⋅=-=-3)(32)(2)(10)()()(1)1(1nd C n d C n d C C n d d n n n n n n n n n)(1n d->所以得到，)(n d d <；②δ<)(n d)1()(mn em d δ--=；mm C m C m C m ennnmδδδδδδ->-⋅+⋅-⋅+-=-1)()()(1443322所以，δδ=--<)]1(1[)(mm dn③)(n i <δi n i n n +=+1]1[)(， 即，δ=+=+⋅)1ln()1ln()(i ni n n所以，)1()(-⋅=n n e n i δm m C m C m C m e nnnnδδδδδδ+>+⋅+⋅+⋅++=1)()()(1443322δδ=-+>]1)1[()(nn in④i in <)(i ni nn +=+1]1[)(，)(2)(2)(10)(1)(1]1[n n n n n n n n i n i C n i C C n i +>+⋅+⋅+⋅=+所以，i in <)(6．证明下列等式成立，并进行直观解释：⑴nmm n m a v a a +=+；解：iv a nm nm ++-=1，i v a m m-=1，iv v i v v a v nm m n m nm +-=-=1所以，n m nm m m nmm a ivv v a v a ++=-+-=+1⑵nmm n m s v a a -=-；解：iva nm nm ---=1，iv a mm-=1，iv v s v n m m n m--=-所以，nm nm mmn mma ivv v s v a --=-+-=-1⑶nmm n m a i s s )1(++=+；解：i i smm1)1(-+=，ii i i i i s i m n m n mnm )1()1(1)1()1()1(+-+=-++=++所以，n m mn m m n mms ii i i a i s ++=+-++-+=++)1()1(1)1()1(⑷nmm n m a i s s )1(+-=-。

保险精算试题与答案[注意：本文按照试题格式进行回答]试题一：保险精算的定义和作用是什么？保险精算是指运用数学、统计学和金融学等方法，对保险业务进行量化分析和评估的过程。

其作用主要体现在以下几个方面：1. 风险评估：通过对历史数据和概率模型的分析，保险精算师可以评估保险产品的风险水平，确定保费率和赔付准备金水平，为保险公司提供决策依据。

2. 产品开发与定价：保险精算师可以根据市场需求和风险情况，设计和开发新的保险产品，并确定合理的保费定价策略，以提高保险公司的竞争力和盈利能力。

3. 保险风险管理：保险精算师可以利用精算模型和方法，对保险风险进行全面的管理和控制，降低保险公司的不确定性和风险敞口。

4. 偿付能力评估：通过运用精算方法，保险精算师可以对保险公司的偿付能力进行评估和监测，保证公司能够按时履行合同中对被保险人的赔偿责任。

5. 盈余分配决策：精算师根据保险公司的盈利能力和风险状况，制定合理的盈余分配策略，确保公司的可持续经营和股东利益最大化。

试题二：简述保险精算的核心内容和方法保险精算的核心内容主要包括风险评估、损失模型、资本管理和盈余分配等方面。

1. 风险评估：通过风险测度和量化方法，评估保险产品的风险水平，并制定相应的风险管理策略，保证公司的偿付能力。

2. 损失模型：利用数理统计的方法，分析历史数据和风险模型，构建损失模型，预测未来潜在的赔偿风险，并根据模型结果进行资本分配和准备金计提。

3. 资本管理：通过资本分配和配置，保险精算师可以根据公司的风险状况和盈利能力，确定合理的资本水平和使用策略，提高公司的偿付能力和综合运营效益。

4. 盈余分配：保险精算师基于公司的盈利水平、资本状况和风险状况，制定合理的盈余分配政策，确保公司能够平衡盈利和风险、实现可持续发展。

保险精算的核心方法包括：1. 预测模型：利用历史数据和概率理论，建立预测模型，对未来保险损失进行预测和量化评估。

2. 风险度量方法：通过运用不同的风险测度方法，比如价值-at-Risk、条件VaR等，对保险风险进行度量和分析。

寿险精算习题答案寿险精算习题答案寿险精算作为保险行业中的重要分支，是对寿险产品的风险和收益进行评估和计算的过程。

在寿险精算的学习过程中，习题是不可或缺的一部分，通过解答习题可以帮助我们更好地理解和掌握相关的知识。

下面，我们将一起来解答一些寿险精算的习题。

1. 问题：某寿险公司推出一款定期寿险产品，保险期限为20年，保额为50万，保费为每年1000元。

根据历史数据，该产品的死亡率为1‰。

请计算该产品的预期净保费。

解答：预期净保费是指在考虑风险的情况下，保险公司需要收取的保费。

根据题目给出的数据，我们可以得出以下计算公式：预期净保费 = 保费 - 风险保费风险保费 = 死亡率× 保额代入具体数值进行计算：风险保费= 0.001 × 500000 = 500预期净保费 = 1000 - 500 = 500所以，该产品的预期净保费为500元。

2. 问题：某寿险公司推出一款年金保险产品，保险期限为30年，保险年金为每年2万元，保费为每年5000元。

根据历史数据，该产品的终身年龄为85岁，死亡率为0.5‰。

请计算该产品的预期净保费。

解答：与上一题类似，我们还是需要计算风险保费。

不同之处在于，这是一款年金保险产品，保险期限为30年，但是保险金可能会在30年后一直支付到被保险人去世。

所以，在计算风险保费时，需要考虑被保险人在30年后的存活概率。

风险保费 = 死亡率× 保额× 存活概率存活概率 = 1 - 死亡率× 保险期限代入具体数值进行计算：存活概率 = 1 - 0.0005 × 30 = 0.985风险保费= 0.0005 × 20000 × 0.985 = 9.85预期净保费 = 5000 - 9.85 = 4990.15所以，该产品的预期净保费为4990.15元。

3. 问题：某寿险公司推出一款重大疾病保险产品，保险期限为10年，保额为50万元，保费为每年1000元。

保险精算生命表习题和答案保险精算是保险行业中非常重要的一环，它通过精确的数学模型和统计分析，为保险公司提供风险评估和保费定价等重要数据。

而生命表作为保险精算中的核心工具之一，用于预测人口的寿命和死亡率，对于保险公司的经营和决策具有重要意义。

在这篇文章中，我们将介绍一些保险精算生命表的习题和答案，帮助读者更好地理解和应用这一概念。

首先，我们来看一个简单的习题：假设某个国家的年龄为x的人群的死亡率为qx，那么该国家的生命表中年龄为x的人群的存活率为多少？答案是1-qx。

这是因为存活率是指在某个年龄段内存活下来的人数与初始人数之比，而死亡率则是指在某个年龄段内死亡的人数与初始人数之比。

因此，存活率和死亡率之和必然等于1，即1-qx+qx=1。

接下来，让我们来看一个稍微复杂一些的习题：假设某个国家的生命表中，年龄为x的人群的存活率为px，年龄为x的人群的死亡率为qx，那么该国家的年龄为x的人群的预期寿命是多少？答案是1/qx。

预期寿命是指在某个年龄段内平均还能活多少年，而预期寿命与存活率和死亡率之间存在着密切的关系。

根据生命表的定义，存活率px等于年龄为x的人群在未来一段时间内存活下来的概率，即px=1-qx。

那么，年龄为x的人群在未来一段时间内平均还能活多少年呢？根据概率的性质，我们可以得到以下等式：px*(1+x)+qx*(1+x+1)=1。

将px=1-qx代入该等式，化简可得1+x=qx/(1-qx)，再将qx=1-px代入该等式，化简可得1+x=(1-px)/px，进一步化简可得x=1/px-1。

因此，年龄为x的人群的预期寿命就是1/qx。

除了以上的习题和答案，保险精算生命表还有许多其他的应用和推导。

例如，通过分析不同年龄段的死亡率和存活率，可以预测某个年龄段的人口数量和年龄结构，为社会政策和养老金制度的制定提供参考依据。

此外，保险精算生命表还可以用于评估保险产品的风险和利润，根据不同年龄段的死亡率和存活率，计算出保险公司需要收取的保费，从而确保保险公司的盈利和稳定经营。

保险精算大作业学号：13121271姓名：孔智一、（10分）确定10000元在第3年年末的积累值：1）名义利率为每季度计息一次的年名义利率6%；2）名义贴现率为每4年计息一次的年名义贴现率6%。

解：二、（10分）某人购买一处住宅，价值60万元，缴纳首期付款额后其余部分自下月起每月月初付3000元，共付10年。

年计息12次的年名义利率为8.7%。

计算购房首期付款额。

解：月利率i=8.7%/12=0.725%600000-A = 3000•（1 + v^2 +…+v^119）= 3000•（1 + 1/(1+i)^2 + …+1/(I + i)^119）= 3000•〔1-1/(1 + i)^120〕/〔1-1/(1+i)〕= 241628.61A =358371.39 (元)三、（10分）设01000l=，1990l=，2980l=，…，9910l=，1000l=，求：1）人在70岁至80岁之间死亡的概率；2）30岁的人在70岁至80岁之间死亡的概率；3）30岁的人的取整平均余命。

解：1)(l70-l80)/l0=100/l0=100/1000=0.12)由1)得,30岁的人在70岁至80岁之间死亡的概率为：100/700=1/73)e30=E[K(30)]=∑[k(kP30)] 求和：k=0到k=100=0*0P30+1*1P30+2*2P30+...=(0*l30+1*l31+...)/l30 (设l30=a)=(0*a+1*(a-10)+2*(a-20)...)/a=34.5四、（10分）给出45岁人的取整余命分布如下表：求：1）45岁的人在5年内死亡的概率；2）48岁的人在3年内死亡的概率；3）50岁的人在52岁至55岁之间死亡的概率。

解：假定一个人口基数，然后列出各年人数t x qx lx dx0 45 0.005 100000 5001 46 0.006 99500 5972 47 0.0075 98903 7423 48 0.0095 98161 9334 49 0.012 97229 11675 50 0.013 96062 12496 51 0.0165 94813 15647 52 0.0205 93249 19128 53 0.025 91337 22839 54 0.0300 89054 26721) 等于（500+597+742+933+1167)/100000=0.039382) 等于（933＋1167＋1249）/98161=0.0341083) 等于（1912＋2283＋2672）/96062=0.071481五、（10分）设生存函数为()1100xs x =-，0100x ≤≤，年利率0.10i =。

【解5.1】根据已知条件容易求得1010.0540:10010.112470tA e dt -==⎰110104040:1040:100.6323A A v p =+=100.0540:100707.35470tta e dt --==⎰50.0540:5070 4.27370tta e dt --==⎰则（1）()1140:1040:1040:100.11240.015287.354A P A a ===（2）()40:10540:1040:50.63230.147984.273A P A a ===【解5.2】潜在损失变量为1)20.09 4.250.090.04tttt t x t v L b v P A a v v -=-=-⋅=-它的方差等于()2222()(4.250.09) 4.25() 4.25T T x xVar L Var v Var v A A =-==-因为死亡力恒定()0.06x t μ+=，所以有0.40x A μμδ==+，20.432x A μμδ==+则()22() 4.250.430.4 4.88Var L =⨯-=【解5.3】1130:2030:2030:200.150.0752.0A P a=== 【解5.4】()1130:2030:201130:2030:30:2030:202030:2030:200.0250.0750.50.5759ln1.025i A A A iP A P P aaδδ+===+=⨯+= 【解5.5】（1）亏损现值变量为111(1k k k P PL v Pav d d+++=-=+- 根据净均衡原理有()0E L =（2）根据()0E L =，得到方程3100[(1)]0k k k P Pv q d d+=+-=∑由于014k q =，0,1,2,3k =，等价推导出40.061[(14]04P P a d d+-=求得6.4780.3667PP d=⇒=则1222(1)1222412.36%46%()[(1)](1()2(1)()() 11(1)2(1) () 44 0.17788k k k P PVar L E v d d P P P P E v E v d d d d P P P P a d d d d +++=+-=+-++=+-⨯++=【解5.6】设此险种的趸缴净保费为P,则由净均衡原理可知1120|3020305030:2030:20P P A a P A E a=⋅+=⋅+⋅ 其中1203030:2030:200.20.050.15E A A =-=-=则0.050.1510 1.58P P P =⋅+⨯⇒=【解5.7】未修正之前，赔付变量的精算现值等于2311110000.010.990.020.990.980.0355.631.025 1.025 1.025⎛⎫⨯+⨯⨯+⨯⨯⨯= ⎪⎝⎭所缴保费的精算现值等于21110.990.990.98 2.88931.025 1.025P P ⎛⎫+⋅+⨯⨯= ⎝⎭根据净均衡原理，赔付变量的精算现值等于所缴保费的精算现值，由此求出净均衡保费等于55.6319.2542.8893P ==修正之后，假设保额为B ，则保险赔付的精算现值等于230.020.980.030.980.970.04()0.8281.025 1.025 1.025B B ⨯⨯⨯++=所缴保费的精算现值等于20.980.980.9719.254(1)55.08361.025 1.025⨯++=根据净均衡原理，有0.082855.0836665.26B B =⇒=【解5.8】根据题意，缴费精算现值等于()2220.990.9811 2.89861.025 1.025x x v p v p πππ⎛⎫+⋅+⋅=++= ⎪⎝⎭给付的精算现值等于()()34343431000010000(1) 1.025x x xx v p v k p p p ⋅+⋅+⋅+=++ 因为1x kx k e p ∞==∑，所以34212.10.980.9910.13x x x x x p p e p p ++=--=--= 根据净均衡原则有()343310000100002.898610.1394067.121.025 1.025x x p p π=++=⨯= 由此解出净均衡保费94067.1232452.62.8986π==【解5.9】根据题意，缴费精算现值等于40:10aπ ，而死亡给付额的精算现值分为两部分（1）死亡即刻给付1000元的精算现值：401000A （2）返还所缴保费的精算现值。

保险精算课后习题答案保险精算学是一门应用数学和统计学原理来评估风险和确定保险费率的学科。

它通常包括概率论、统计学、金融数学和经济学的相关知识。

以下是一些保险精算课后习题的答案示例：1. 问题：某保险公司提供一种寿险产品，保险期限为20年。

假设年利率为4%，保险公司需要为每位投保人准备的总金额为100,000元。

请计算每年需要缴纳的保费。

答案：使用等额年金的公式，我们可以计算出每年需要缴纳的保费。

首先计算现值因子PVIFA，公式为：\[ PVIFA = \frac{1 - (1 + r)^{-n}}{r} \]其中，\( r \) 是年利率，\( n \) 是保险期限。

将给定的数值代入：\[ PVIFA = \frac{1 - (1 + 0.04)^{-20}}{0.04} \]计算得到PVIFA后，用总金额除以PVIFA得到每年需要缴纳的保费：\[ \text{年保费} = \frac{100,000}{PVIFA} \]2. 问题：某保险公司希望评估一个30岁男性的寿险风险。

假设该男性的死亡率为0.0015，保险公司希望在10年内每年支付1,000元的保险金。

请计算保险公司需要收取的保费。

答案：首先，我们需要计算10年内该男性死亡的期望值。

这可以通过以下公式计算：\[ \text{期望死亡次数} = 1 \times (1 - (1 - 0.0015)^{10}) \]然后，将期望死亡次数乘以每次死亡的保险金，得到保险公司需要准备的总金额：\[ \text{总保险金} = 1,000 \times \text{期望死亡次数} \]最后，将总保险金除以生存概率的现值因子，得到每年需要收取的保费：\[ \text{年保费} = \frac{\text{总保险金}}{PVIF} \]3. 问题：考虑一个保险公司提供的年金产品，客户在退休后每年领取10,000元，直到去世。

如果客户现在50岁，预期寿命为85岁，年利率为5%，计算客户需要一次性缴纳的保费。

北方工业大学《保险精算学》课程试卷B2013年春季学期开课学院： 理学院考试方式：闭卷考试时间：120 分钟班级 姓名 学号 一、名词解析（本大题共5题，每小题3分，共15分） 1. 人身保险2. 死亡力3. 永续年金4. 现金价值5. 变额寿险订线装二、简答题（本大题共4题，每小题7分，共28分）1. 人身保险精算的原理及内容2. 为什么现金价值要在责任准备金的基础上作出一定的扣除？3. 责任准备金的计算方法有哪些？4. 常见的附加保险费有哪几种？三、证明题（本大题共3题，每小题9分，共27分） 1. 证明等式m a v a a ⋅+=成立2. 证明：1+=x x x a vp a3. 假设死亡在x---x+1岁均匀分布，证明：)(1|1:d vp da x x ---=四、计算题（本大题共3题，每小题10分，共30分）1. 李华1994年1月1日从银行借款1000元，假设年利率为12% （1）1994年5月20日时，他需还银行多少钱（以单利计算）？ （2）1996年1月1日时，他需还银行多少钱（以复利计算）？ （3）几年后需还款1500元（以单、复利计算）？2. 某男在40岁时买了保险额为20 000元的终身寿险，假设他的生存函数可以表示 l x =1 000(1-105x),i=10%，求这一保单的精算现值。

3. 李强在50岁事投保了终身寿险，按照契约规定，若他在投保后第一年内死亡，可获得50 000元的保险金，以后每多活一年后死亡，保险金增加5000元，假定i=0.06，试计算在死亡年末给付的保险精算现值。

（其中A 50=0.2490475，R 50=24280.7261，30.485950 D ）。

第三章：生存模型与生命表1、已知1000X]/4么=2。

在Balducci, UDD和常数死亡力三种假设下对葩么+3/4排序。

°de f pl.52、给定為=0.020,為=0.022,在每一年龄年UDD假设成立，计算幺60：丙=])『几0力。

o 283、给定l x = V100-X,0< X < 100,求幺36：丽和]匚036“36+川。

4> 给定0.5 Px/^x+0.5 =12/ 49 ,在年龄段[x,x+l]Balducci 假设成立，Q x Px。

计算。

x5、给定生存函数S()(/) = l—而,05x5100,则求“25。

1 °6、已知生存分布S^ = ~r—，计算以及(x)的未来生存吋间的屮位数。

1+ x7、设K =曲丄Bcilducc)L= \i3\2i3qQDD),给定l x = 9,Z x+1 = 6,计算K+L。

o8、死亡力遵从de Moivre 法则，©6=42，计算v ar(T(16))o2?9、如果//,=——+ ------- ,()WxW100,求/() = 10 000时，求该生命表中1岁到4岁Z间的死亡人x +1 100 —x数。

10、己知20岁的生存人数为1 000人，21岁的生存人数为998人，22岁的生存人数为992人，求]旳20。

二种假定下的生命表函数函数均匀分布常数死亡力BalluccitQx1-严l-(l-r)-g xtPx 1 -仏严Px1 一(1 一t)q xy Qx+rM X1 fq x1-严 1 - (1 - j - t)q x \ tq x1-(1-Px幺敘) [i - (i - Qg J练习：1、 验证函数S 0(x) = ^2?s x>0可作为生存函数，并给岀 对应的死亡力，T 。

的密度函数与分布函数.2、 设 / =求£◎£(/)忑◎x+13、设 u M = r :t>O^f x (t):F x (t).4已知生存函数S°(x) = ― ,0<x<100 计算 17-P19? 15036 和"(36)。

保险精算习题答案保险精算习题答案保险精算是保险行业中非常重要的一个领域，它涉及到对保险风险的评估和定价。

保险精算师需要通过解决各种习题来提高自己的技能和能力。

在本文中，我将为大家提供一些保险精算习题的答案，并解释一些解题思路和方法。

1. 问题：某保险公司的汽车保险业务在过去的一年中发生了100起事故，总赔款金额为100万美元。

公司共收到了1000份汽车保险合同，每份合同的保费为1000美元。

请计算该保险公司的事故率和平均赔款金额。

答案：事故率是指发生事故的次数与总保单数之比。

在这个例子中，事故率为100/1000 = 0.1，即10%。

平均赔款金额是指总赔款金额与事故次数之比。

在这个例子中，平均赔款金额为100万美元/100 = 10万美元。

2. 问题：某保险公司的寿险业务在过去的一年中发生了50起身故，总赔款金额为500万美元。

公司共收到了10000份寿险合同，每份合同的保费为1000美元。

请计算该保险公司的死亡率和平均赔款金额。

答案：死亡率是指发生身故的次数与总保单数之比。

在这个例子中，死亡率为50/10000 = 0.005，即0.5%。

平均赔款金额为总赔款金额与死亡次数之比。

在这个例子中，平均赔款金额为500万美元/50 = 100万美元。

3. 问题：某保险公司的医疗保险业务在过去的一年中发生了200起医疗事故，总赔款金额为1000万美元。

公司共收到了5000份医疗保险合同，每份合同的保费为2000美元。

请计算该保险公司的事故率和平均赔款金额。

答案：事故率为发生事故的次数与总保单数之比。

在这个例子中，事故率为200/5000 = 0.04，即4%。

平均赔款金额为总赔款金额与事故次数之比。

在这个例子中，平均赔款金额为1000万美元/200 = 50万美元。

通过以上习题的解答，我们可以看出，事故率和平均赔款金额是评估保险风险和定价的重要指标。

保险公司需要根据历史数据和统计分析来确定合理的保费水平，以保证公司的盈利能力和风险控制能力。

【解3.1】因为()()ln ()Pr Pr Pr T z F z Z z e z T δδ-⎛⎫=≤=≤=≥ ⎪-⎝⎭且由条件知剩余寿命服从De Moivre 分布,即()0,70T U ，故70ln ln 1ln ()Pr 17070z z z F z T dt δδδ-⎛⎫=≥==+ ⎪-⎝⎭⎰密度函数等于分布函数求导()ln 117070Z z f z zδδ'⎛⎫=+= ⎪⎝⎭已知0.05δ=，0.6z =代入上式得()0.60.48Z f =【解3.2】（40）的剩余寿命T 服从均匀分布（0，70），其生存函数为407070t tP -=，070t ≤≤由题意，可得ln 70ln ln ()Pr()Pr()Pr()ln 70t z z v F z Z z v z t v-=≤=≤=≥=Z 的90％置信上限即为使()0.9F z =的z 值，即ln 70ln 0.970zv -=解得exp[(70700.9)ln ]0.84z v =-⨯=【解3.3】在恒定死亡力和恒定利息力场合，容易验证趸缴净保费等于x A μδμ=+在调整以前有0.60.05μμ=+则求得0.075μ=调整以后0.0750.020.095μ'=+=，0.04δ'=则调整后的趸缴净保费为0.0950.7040.0950.04x A μμδ'===''++【解3.4】（1）()()tx A E Z E v ==,则()()2200.055001 1.250.031252500.0312522Pr[0]t x T x tt t A e f t dtedte dte Y δ∞-∞--+⎛⎫∞- ⎪⎝⎭====≥⎰⎰⎰其中~( 1.25,25)Y N -，则()1.25Pr(0)Pr(0.25)10.255Y Y +≥=≥=-Φ()0.031252[10.25]0.83x A e =-Φ=（2）因为22()x x Var Z A A =-，其中()()()2220.100.15001 2.50.1252500.12522[10.5]0.70t x T x tt t A e f t dte dte dte ∞-∞--+⎛⎫∞- ⎪⎝⎭====-Φ=⎰⎰⎰所以222()0.700.830.014x x Var Z A A =-=-=【解3.5】给付函数和贴现函数都已知，容易得到现时值函数为1(10.2)t t Z b v t -==+密度函数已知()()40400.02,050T t f t p t t μ=+=≤≤则趸缴净保费等于()()505000ln 10.21110.020.2410.2500.210t E Z dt t +⎛⎫=⨯=== ⎪+⎝⎭⎰两倍利息力下，趸缴净保费等于()()50502200110.020.020.091(10.2)0.210.2E Z dt t t -=⨯=⨯=++⎰所以现值变量的方差等于222()()[()]0.09090.23980.0334Var Z E Z E Z =-=-=【解3.6】一般情况下，如果剩余寿命T 服从()0,ω的均匀分布，即1(),0T f t t ωω=≤≤可以得到()0111t x T tt A e f t dte dtev a δωδωδωωωωδωδω∞---==-=-==⎰⎰本题中，T 服从（0，60）的均匀分布，故所求的净保费为604040100010001000666.76060a A =⨯=⨯=【解3.7】令3z 为()x 岁的人投保期末赔付1的n 年定期生存保险的现时值变量，根据已知条件有3()0.20.450.09n n x E z v p =⋅=⨯=223()0.040.450.018n n x E z v p =⋅=⨯=根据定期两全保险与定期寿险和定期生存险的关系，有213z z z =+则213123()()()()()()0.350.090.26E z E z E z E z E z E z =+⇒=-=-=[][]222213222212322()()()()()()()()0.060.0180.350.1645Var z E z E z E z E z Var z E z E z =+-⇒=-+=-+=推导出()[]2221110.16450.260.0969Var Z E Z E Z ⎡⎤=-=-=⎣⎦【解3.8】因为死亡服从De Moivre 分布，故40岁的人剩余寿命的密度函数为()160T f t =，060t ≤≤由于延期20年，所以赔付现值变量为0,020,2060TT Z e T δ-≤≤⎧=⎨<≤⎩所以，0z =点为重概率点，该点概率值为20201Pr(0)Pr(020)()603T Z T f t dt ==≤≤===⎰【解3.9】该保单可以视为一个10000元的终身寿险和10000元的20年定期寿险的组合，则该保单趸缴净保费为14545:201000010000A A +已知450.25A =，下面求145:20A 的值。

【解2.1】（1）可以被写成=(90−p(r200)18000，又由于达到极限寿命时=0，故=90。

（2）证明：因为，0=1；其次，达到极限寿命=90时，有90=0；且，的导数−110−218000<0,>0。

由此，生存函数的三个条件都被满足。

（3）93333.0)0()10(00010==S S p （4）(030−050)020（5）=−0'(p/0==110+218000−110−2因此，40=0.015833。

【解2.2】作为生存函数的基本属性有：(0)1,S =函数是单调递减的，同时lim ()0x S x →∞=。

（1）由于()exp[0.7(21)](10.72ln 2)xxS x x '=---⨯⨯，(0)0.51480S '=>，说明该函数不满足单调递减的性质。

所以，它不能作为生存函数。

（2）由于(0)1S =,3()2(1)0S x x -'=-+<，21lim ()lim0(1)x x S x x →∞→∞==+。

该函数可以作为生存函数。

（3）由于(0)1S =，()2()(2)0x S x ex -'=-<，lim ()0x S x →∞=。

该函数可以作为生存函数。

【解2.3】（1）4320751001)75(1)75(=--=-=S F （2）20017510040175)()75(=-==-=x x S dx d f （3）501412001)75()75()75(===S f μ【解2.4】(40)40(40)(40)40(40)(40)60(),060(40)60(40)1(),060(40)601()(),06060T t T T t T S t tS t p t S S t t t S t tf x p t t μμ+-===<≤'+=-=<≤+-==<≤【解2.5】()18)100(9)100(6)100(3100)100()100(2)]([2)]([3100)100()100()]([)100()100(222210002221000100022100022x x x x dt x t x t x T E dt p t x T Var xdt x t x dt p x T E x t x l l p xxx t xxx tx t x x t -=---=⎪⎭⎫⎝⎛------=-=-=---==---==⎰⎰⎰⎰----+【解2.6】所有表达式均为非负，因此需要验证是否满足0∞B =∞，使得0)(=∞S （1）∞==∞∞⎰0ln C BC dx BC xx，可以（2）∞=+=+∞∞-⎰001)ln()(x b a dx x b a ，可以（3）21)1(21)1(023=+-=+∞∞-⎰x dx x ，不可以【解2.7】把30.250x q +=代入120.170x q +=式中，得11232120.1700.680x x x x x x q p p q p p ++++++=⋅⋅=⇒=上式与已知条件11210.090x x x q p q+++=⋅=联立求解，解出10.770x p +=，20.117x q +=最后得1212(1)0.230.1170.347x x x x q q p q +++++=-+=+=【解2.8】由()1xS x ω=-，可知~(0,)X U ω，且有(20)~(0,20)T U ω-则[()]2x E T x ω-=，2()[()]12x Var T x ω-=已知020e 40=，即20401002ωω-=⇒=所以2(20)Var[T(20)]533.312ω-==【解2.9】首先计算K 的生存函数k012197k p +1015415则210414()09715151502210422()(21)13509715151513422()()[()]225E K p k k E K k p k k Var K E K E K ==++=∑==+⋅=⋅+⋅+⋅=∑==-=【解2.10】证明：（1）x t x x x t q t T t T p -=<-=≥=1)Pr(1)Pr(（2）xu t x t x x x x ut p p u t T t T u t T t q +-=+≥-≥=+≤≤=)Pr()Pr()Pr(（3）()()()tx u x t t x x x ut p p u T t T p ++⋅=≥⋂≥=Pr 【解2.11】（1）证明：110111111111+∞+∞+-∞∞+=+≤⋅+=+==⎰⎰⎰⎰⎰⎰x x x t x x t x t x t x t x e dt p dtp p dt p dt p dt p dt p e （2）证明：由于是关于的递减函数，因此有K1B≥所以xk x k k k kx tx t x e p dtp dt p e =≥==∑∑⎰⎰∞=+∞=+∞101【解2.12】证明：()()()()()()()t x t x x t S x t f x t S x t x t p p t t S x S x S x μμ+∂∂++-++====∂∂【解2.13】318.02005exp 20025exp 20015exp )5()25()15(200exp 100exp )(2225101020=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛-=-=⎪⎪⎭⎫⎝⎛-=⎭⎬⎫⎩⎨⎧-=⎰S S S q x dt t x S x 【解2.14】[][]8684284p =其中86l 已知，而[][][][][]2848484184841(1)(1)p p p q q ++==--由已知条件推导出[][][]85841848483144508030360.3225550803343640050800.20644556400q q q q q ++-=⋅=⋅=-==⋅⋅=⋅=【解2.15】(1)7[76]=83[76]=1192816608=0.718208(2)6|275+1=82−8475+1=0.084631【解2.16】40+1=40(1−40),40+2=402p [40],43=40+2−40∗2|40,46=43−40+1∗2|340+1.因此343=46/43=1−(1−40)2|340+1/(2p [40]−2|40)=1−(1−0.01608)×0.08964/(0.95977-0.02383)=0.905765【解2.17】151025:2525152540015100.040.04150.06015.40667t t tte p dt p p dtedt eedt--⨯-=+=+=⎰⎰⎰⎰【解2.18】(1)0.752.5=1−53.252.5=1−0.853+0.2540.552+0.553=0.0068381.7|1.252.5=54.2−55.452.5=0.854+0.255−0.655−0.4560.552+0.553=0.022690(2)0.752.5=1−0.5p 52.50.2p 53=1−520.5530.2=0.0068351.7|1.252.5=1.7p 52.51−1.2p 54.2=0.5p 52.5530.2p 541−0.8p 54.20.4p 55=520.553540.21−540.8550.4=0.022668【解2.19】因为{}10102102221exp ()=1exp 2()1exp ()1()1(1)2x x x x x q x t dt x t dt x t dt p q q q μμμ⎡⎤''=--+⎢⎥⎣⎦⎡⎤--+⎢⎥⎣⎦⎡⎤=--+⎢⎥⎣⎦=-=--=-⎰⎰⎰由此推出2x xq q '<。

1、若复利下实际利率为i ，则实际贴现率d 是多少2、已知92094.0]5)60([,1895.0]6)60(5[=>=≤<T P T P ，则65q 是多少3、期末永续年金的现值为|∞a 为多少4、已知21岁的生存人数为1000人，22岁的生存人数为998人，23岁的生存人数为992人，则211q 为多少5、已知年实际利率为10%，求等价的利息强度6、已知,3129,07.08080==d q 求81l 为多少？7、期初永续年金的现值为..|∞a 为多少8、如果,01.0t t =δ求10000元在第12年末的累积值为9、已知30岁的生存人数为1200人，31岁的生存人数为1050人，32岁的生存人数为1000人，则301q 为多少10、简述人寿保险的主要寿险种类，并给出相应的趸缴净保费（精算现值）的计算公式。

11、简述什么是生命表，若x l 表示0l 个新生儿存活到x 岁的人数，给出x t q ，x t p ，x n m q12、简述期末生命年金的主要类型，并给出相应的趸缴净保费（精算现值）的计算公式13、简述什么是精算等价原理及寿险净保费。

14、在以下两种情况下计算投资100元在第2年底的终值：（1）季换算名利率为6%（2）每4年换算一次的名贴现率为6%15已知40岁的死亡率为0.04，41岁的死亡率为0.06，而42岁的人生存至43岁的概率为0.92.如果40岁生存人数为100人，求43岁时的生存人数。

16、老王今年30岁，自今年开始每年年末将收到一笔5000元的年金给付，已知1.0,==i k p x ，该年金精算现值为22500元，试计算k 的值。

17、已知z A y A u A n x n x n x ===+,,1|:|:，用z y u ,,表示x A 18、已知06.0,2.0,46.0,22.01|25:25====+i A A A x x x ，试计算|25:..x a 的值19、若面值为100元的债券在到期前3个月时的买价为96元，计算买方的：（1）季换算名贴现率)4(d （2）年实利率i20、设某群体的初始人数为3000人，20年内的预期死亡人数为240人，第21年和第22年的死亡人数分别为15人和18人。