寿险精算习题及答案

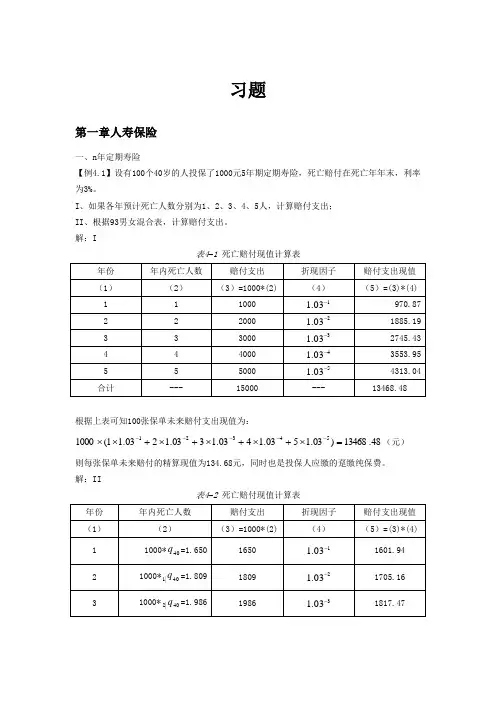
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险，死亡赔付在死亡年年末，利率为3%。

I 、如果各年预计死亡人数分别为1、2、3、4、5人，计算赔付支出； II 、根据93男女混合表，计算赔付支出。

解：I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为：48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----（元）则每张保单未来赔付的精算现值为134.68元，同时也是投保人应缴的趸缴纯保费。

解：II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为：86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q （元）则每张保单未来赔付的精算现值为91.25元，同时也是投保人应缴的趸缴纯保费。

【例4.2】某人在40岁时投保了10000元3年期定期寿险，死亡赔付在死亡年年末，利率为5%。

根据93男女混合表计算：I 、单位趸缴纯保费；II 、单位赔付现值期望的方差；III 、（总）趸缴纯保费； 解：I 、单位趸缴纯保费为，)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=（元）。

II 、单位赔付现值期望的方差为，00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为，28.49100001|3:40=⨯A （元） 【例4.3】某人在50岁时投保了100000元30年期定期寿险，利率为8%。

保险精算（第二版）第一章：利息的基本概念练 习 题1．已知()2a t at b =+，如果在0时投资100元，能在时刻5积累到180元，试确定在时刻5投资300元，在时刻8的积累值。

(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2．(1)假设A(t)=100+10t, 试确定135,,i i i 。

135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯，试确定 135,,i i i 。

135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3．已知投资500元，3年后得到120元的利息，试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。

11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4．已知某笔投资在3年后的积累值为1000元，第1年的利率为 110%i =，第2年的利率为28%i =，第3年的利率为 36%i =，求该笔投资的原始金额。

123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5．确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。

(2)名义贴现率为每4年计息一次的年名义贴现率6%。

(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6．设m ＞1，按从大到小的次序排列()()m m d di i δ<<<<。

【解2.1】（1）可以被写成=(90−p(r200)18000，又由于达到极限寿命时=0，故=90。

（2）证明：因为，0=1；其次，达到极限寿命=90时，有90=0；且，的导数−110−218000<0,>0。

由此，生存函数的三个条件都被满足。

（3）93333.0)0()10(00010==S S p （4）(030−050)020（5）=−0'(p/0==110+218000−110−2因此，40=0.015833。

【解2.2】作为生存函数的基本属性有：(0)1,S =函数是单调递减的，同时lim ()0x S x →∞=。

（1）由于()exp[0.7(21)](10.72ln 2)xxS x x '=---⨯⨯，(0)0.51480S '=>，说明该函数不满足单调递减的性质。

所以，它不能作为生存函数。

（2）由于(0)1S =,3()2(1)0S x x -'=-+<，21lim ()lim0(1)x x S x x →∞→∞==+。

该函数可以作为生存函数。

（3）由于(0)1S =，()2()(2)0x S x ex -'=-<，lim ()0x S x →∞=。

该函数可以作为生存函数。

【解2.3】（1）4320751001)75(1)75(=--=-=S F （2）20017510040175)()75(=-==-=x x S dx d f （3）501412001)75()75()75(===S f μ【解2.4】(40)40(40)(40)40(40)(40)60(),060(40)60(40)1(),060(40)601()(),06060T t T T t T S t tS t p t S S t t t S t tf x p t t μμ+-===<≤'+=-=<≤+-==<≤【解2.5】()18)100(9)100(6)100(3100)100()100(2)]([2)]([3100)100()100()]([)100()100(222210002221000100022100022x x x x dt x t x t x T E dt p t x T Var xdt x t x dt p x T E x t x l l p xxx t xxx tx t x x t -=---=⎪⎭⎫⎝⎛------=-=-=---==---==⎰⎰⎰⎰----+【解2.6】所有表达式均为非负，因此需要验证是否满足0∞B =∞，使得0)(=∞S （1）∞==∞∞⎰0ln C BC dx BC xx，可以（2）∞=+=+∞∞-⎰001)ln()(x b a dx x b a ，可以（3）21)1(21)1(023=+-=+∞∞-⎰x dx x ，不可以【解2.7】把30.250x q +=代入120.170x q +=式中，得11232120.1700.680x x x x x x q p p q p p ++++++=⋅⋅=⇒=上式与已知条件11210.090x x x q p q+++=⋅=联立求解，解出10.770x p +=，20.117x q +=最后得1212(1)0.230.1170.347x x x x q q p q +++++=-+=+=【解2.8】由()1xS x ω=-，可知~(0,)X U ω，且有(20)~(0,20)T U ω-则[()]2x E T x ω-=，2()[()]12x Var T x ω-=已知020e 40=，即20401002ωω-=⇒=所以2(20)Var[T(20)]533.312ω-==【解2.9】首先计算K 的生存函数k012197k p +1015415则210414()09715151502210422()(21)13509715151513422()()[()]225E K p k k E K k p k k Var K E K E K ==++=∑==+⋅=⋅+⋅+⋅=∑==-=【解2.10】证明：（1）x t x x x t q t T t T p -=<-=≥=1)Pr(1)Pr(（2）xu t x t x x x x ut p p u t T t T u t T t q +-=+≥-≥=+≤≤=)Pr()Pr()Pr(（3）()()()tx u x t t x x x ut p p u T t T p ++⋅=≥⋂≥=Pr 【解2.11】（1）证明：110111111111+∞+∞+-∞∞+=+≤⋅+=+==⎰⎰⎰⎰⎰⎰x x x t x x t x t x t x t x e dt p dtp p dt p dt p dt p dt p e （2）证明：由于是关于的递减函数，因此有K1B≥所以xk x k k k kx tx t x e p dtp dt p e =≥==∑∑⎰⎰∞=+∞=+∞101【解2.12】证明：()()()()()()()t x t x x t S x t f x t S x t x t p p t t S x S x S x μμ+∂∂++-++====∂∂【解2.13】318.02005exp 20025exp 20015exp )5()25()15(200exp 100exp )(2225101020=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛-=-=⎪⎪⎭⎫⎝⎛-=⎭⎬⎫⎩⎨⎧-=⎰S S S q x dt t x S x 【解2.14】[][]8684284p =其中86l 已知，而[][][][][]2848484184841(1)(1)p p p q q ++==--由已知条件推导出[][][]85841848483144508030360.3225550803343640050800.20644556400q q q q q ++-=⋅=⋅=-==⋅⋅=⋅=【解2.15】(1)7[76]=83[76]=1192816608=0.718208(2)6|275+1=82−8475+1=0.084631【解2.16】40+1=40(1−40),40+2=402p [40],43=40+2−40∗2|40,46=43−40+1∗2|340+1.因此343=46/43=1−(1−40)2|340+1/(2p [40]−2|40)=1−(1−0.01608)×0.08964/(0.95977-0.02383)=0.905765【解2.17】151025:2525152540015100.040.04150.06015.40667t t tte p dt p p dtedt eedt--⨯-=+=+=⎰⎰⎰⎰【解2.18】(1)0.752.5=1−53.252.5=1−0.853+0.2540.552+0.553=0.0068381.7|1.252.5=54.2−55.452.5=0.854+0.255−0.655−0.4560.552+0.553=0.022690(2)0.752.5=1−0.5p 52.50.2p 53=1−520.5530.2=0.0068351.7|1.252.5=1.7p 52.51−1.2p 54.2=0.5p 52.5530.2p 541−0.8p 54.20.4p 55=520.553540.21−540.8550.4=0.022668【解2.19】因为{}10102102221exp ()=1exp 2()1exp ()1()1(1)2x x x x x q x t dt x t dt x t dt p q q q μμμ⎡⎤''=--+⎢⎥⎣⎦⎡⎤--+⎢⎥⎣⎦⎡⎤=--+⎢⎥⎣⎦=-=--=-⎰⎰⎰由此推出2x xq q '<。

保险精算考试题及答案1. 保险精算中，用于计算未来现金流的现值的公式是：A. 未来值 = 现值× (1 + 利率)^期数B. 现值 = 未来值÷ (1 + 利率)^期数C. 未来值 = 现值× (1 - 利率)^期数D. 现值 = 未来值× (1 - 利率)^期数答案：B2. 在非寿险精算中，用于计算纯保费的公式是：A. 纯保费 = 预期损失 + 预期费用B. 纯保费 = 预期损失 - 预期费用C. 纯保费 = 预期损失× 预期费用D. 纯保费 = 预期损失÷ 预期费用答案：A3. 以下哪项是寿险精算中的生命表的主要组成部分？A. 死亡率表B. 疾病率表C. 残疾率表D. 以上都是答案：A4. 寿险精算中，计算年金现值的公式是：A. 年金现值 = 年金支付额× 利率× (1 - 1/(1 + 利率)^期数)B. 年金现值 = 年金支付额÷ 利率× (1 - 1/(1 + 利率)^期数)C. 年金现值 = 年金支付额× 利率÷ (1 - 1/(1 + 利率)^期数)D. 年金现值 = 年金支付额÷ 利率÷ (1 - 1/(1 + 利率)^期数) 答案：A5. 保险精算中，用于评估保险公司财务稳定性的指标是：A. 偿付能力比率B. 资产负债比率C. 投资回报率D. 以上都是答案：A6. 在精算评估中，用于计算保单持有人未来利益的现值的贴现率是：A. 预定利率B. 市场利率C. 法定利率D. 以上都不是答案：A7. 以下哪项是精算师在评估寿险保单的死亡率风险时常用的方法？A. 蒙特卡洛模拟B. 敏感性分析C. 精算表分析D. 以上都是答案：C8. 保险精算中，用于计算保单持有人未来利益的现值的公式是：A. 未来利益现值 = 未来利益× 利率× (1 - 1/(1 + 利率)^期数)B. 未来利益现值 = 未来利益÷ 利率× (1 - 1/(1 + 利率)^期数)C. 未来利益现值 = 未来利益× 利率÷ (1 - 1/(1 + 利率)^期数)D. 未来利益现值 = 未来利益÷ 利率÷ (1 - 1/(1 + 利率)^期数) 答案：B9. 在保险精算中，用于计算保单的准备金的公式是：A. 准备金 = 未来利益现值 - 已收保费B. 准备金 = 未来利益现值 + 已收保费C. 准备金 = 未来利益现值× 已收保费D. 准备金 = 未来利益现值÷ 已收保费答案：A10. 以下哪项是保险精算中用于评估保单持有人未来利益的不确定性的方法？A. 精算评估B. 风险评估C. 敏感性分析D. 以上都是答案：C。

第一章：利息的基本概念练习题1．已知()2a t at b =+，如果在0时投资100元，能在时刻5积累到180元，试确定在时刻5投资300元，在时刻8的积累值。

(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+=∵2．(1)假设A(t)=100+10t,试确定135,,i i i 。

135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A −−−======(2)假设()()100 1.1nA n =×，试确定135,,i i i 。

135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A −−−======3．已知投资500元，3年后得到120元的利息，试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。

11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4．已知某笔投资在3年后的积累值为1000元，第1年的利率为110%i =，第2年的利率为28%i =，第3年的利率为36%i =，求该笔投资的原始金额。

123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5．确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。

(2)名义贴现率为每4年计息一次的年名义贴现率6%。

(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎞⎜⎟=+=⎜⎟⎜⎟⎝⎠6．设m ＞1，按从大到小的次序排列()()m m d d i i δ<<<<。

第五章【例5.1】某人在40岁时投保了3年期10000元定期寿险，保险金在死亡年年末赔付。

以中国人寿保险业经验生命表（1990-1993）（男女混合）和利率5%，计算趸缴净保费。

解：趸缴净保费为：10000140:3A =10000（v ×40q +2v ×40p ×41q +3v ×402p ×42q ）=3(10.001650)(10.001812)0.0019931.05-⨯-⨯=49.28（元）【例5.2】张某在50岁时投保了一份保额 100000元的30年定期寿险。

假设x l =1000（1-x 105 ），预定利率为0.08，求该保单的趸缴净保费。

解：该生命表的最大年龄是105岁，所以t 的取值范围是0到55，所求的赔付现值是：29(1)150:3050500100000100000 1.08t tt tp qA -++==⨯⨯∑其中5050505555t tt l p+-==505055(54)115555ttt t t tqp++---=-==--故，该保单的趸缴净保费是： 29(1)150:30055110000010000055551.08t t t tA -+=-=⨯⨯-∑ =20468.70（元）【例5.3】假设例5.2中张某50随时购买的是保额为100000元的终身寿险。

已知1000(1)105x xl =-，预定利率为0.08，求该保单的趸缴净保费。

解： 55(1)5050150100000100000 1.08t t tp qA -++==⨯⨯∑=5611000001155 1.081 1.081()1.08-⨯⨯- =22421.91（元）【例5.4】某人在40岁时买了保险额为20000元的终身寿险，假设他的生存函数可以表示为()1105xs x =-，死亡赔付在死亡年年末，i=10%，求这一保单的精算现值。

【解3.1】因为()()ln ()Pr Pr Pr T z F z Z z e z T δδ-⎛⎫=≤=≤=≥ ⎪-⎝⎭且由条件知剩余寿命服从De Moivre 分布,即()0,70T U ，故70ln ln 1ln ()Pr 17070z z z F z T dt δδδ-⎛⎫=≥==+ ⎪-⎝⎭⎰密度函数等于分布函数求导()ln 117070Z z f z zδδ'⎛⎫=+= ⎪⎝⎭已知0.05δ=，0.6z =代入上式得()0.60.48Z f =【解3.2】（40）的剩余寿命T 服从均匀分布（0，70），其生存函数为407070t tP -=，070t ≤≤由题意，可得ln 70ln ln ()Pr()Pr()Pr()ln 70t z z v F z Z z v z t v-=≤=≤=≥=Z 的90％置信上限即为使()0.9F z =的z 值，即ln 70ln 0.970zv -=解得exp[(70700.9)ln ]0.84z v =-⨯=【解3.3】在恒定死亡力和恒定利息力场合，容易验证趸缴净保费等于x A μδμ=+在调整以前有0.60.05μμ=+则求得0.075μ=调整以后0.0750.020.095μ'=+=，0.04δ'=则调整后的趸缴净保费为0.0950.7040.0950.04x A μμδ'===''++【解3.4】（1）()()tx A E Z E v ==,则()()2200.055001 1.250.031252500.0312522Pr[0]t x T x tt t A e f t dtedte dte Y δ∞-∞--+⎛⎫∞- ⎪⎝⎭====≥⎰⎰⎰其中~( 1.25,25)Y N -，则()1.25Pr(0)Pr(0.25)10.255Y Y +≥=≥=-Φ()0.031252[10.25]0.83x A e =-Φ=（2）因为22()x x Var Z A A =-，其中()()()2220.100.15001 2.50.1252500.12522[10.5]0.70t x T x tt t A e f t dte dte dte ∞-∞--+⎛⎫∞- ⎪⎝⎭====-Φ=⎰⎰⎰所以222()0.700.830.014x x Var Z A A =-=-=【解3.5】给付函数和贴现函数都已知，容易得到现时值函数为1(10.2)t t Z b v t -==+密度函数已知()()40400.02,050T t f t p t t μ=+=≤≤则趸缴净保费等于()()505000ln 10.21110.020.2410.2500.210t E Z dt t +⎛⎫=⨯=== ⎪+⎝⎭⎰两倍利息力下，趸缴净保费等于()()50502200110.020.020.091(10.2)0.210.2E Z dt t t -=⨯=⨯=++⎰所以现值变量的方差等于222()()[()]0.09090.23980.0334Var Z E Z E Z =-=-=【解3.6】一般情况下，如果剩余寿命T 服从()0,ω的均匀分布，即1(),0T f t t ωω=≤≤可以得到()0111t x T tt A e f t dte dtev a δωδωδωωωωδωδω∞---==-=-==⎰⎰本题中，T 服从（0，60）的均匀分布，故所求的净保费为604040100010001000666.76060a A =⨯=⨯=【解3.7】令3z 为()x 岁的人投保期末赔付1的n 年定期生存保险的现时值变量，根据已知条件有3()0.20.450.09n n x E z v p =⋅=⨯=223()0.040.450.018n n x E z v p =⋅=⨯=根据定期两全保险与定期寿险和定期生存险的关系，有213z z z =+则213123()()()()()()0.350.090.26E z E z E z E z E z E z =+⇒=-=-=[][]222213222212322()()()()()()()()0.060.0180.350.1645Var z E z E z E z E z Var z E z E z =+-⇒=-+=-+=推导出()[]2221110.16450.260.0969Var Z E Z E Z ⎡⎤=-=-=⎣⎦【解3.8】因为死亡服从De Moivre 分布，故40岁的人剩余寿命的密度函数为()160T f t =，060t ≤≤由于延期20年，所以赔付现值变量为0,020,2060TT Z e T δ-≤≤⎧=⎨<≤⎩所以，0z =点为重概率点，该点概率值为20201Pr(0)Pr(020)()603T Z T f t dt ==≤≤===⎰【解3.9】该保单可以视为一个10000元的终身寿险和10000元的20年定期寿险的组合，则该保单趸缴净保费为14545:201000010000A A +已知450.25A =，下面求145:20A 的值。

寿险精算模拟试题及答案一、选择题1. 寿险精算中，以下哪项是评估保险合同财务影响的基本工具？A. 利率B. 死亡率C. 精算现值D. 保险金额2. 寿险合同的现金价值是指什么？A. 投保人所支付的保费总额B. 保险合同到期时投保人可得到的金额C. 保险合同在某一特定时间点的净值D. 保险公司为保险合同设立的准备金3. 在寿险精算中，以下哪项不是风险评估的基本要素？A. 风险识别B. 风险量化C. 风险规避D. 风险评估二、填空题4. 寿险精算中，_________是指在保险期间内，保险公司为履行保险责任而设立的基金。

5. 寿险精算中，_________是指根据保险合同的条款，计算出的保险金的预期支付额。

三、简答题6. 简述寿险精算中净保费和毛保费的区别。

四、计算题7. 假设某寿险公司销售了一份10年期的寿险合同，年保费为1000元，预定利率为5%，死亡率为0.5%，请计算该合同第一年的净保费。

五、论述题8. 论述寿险精算在保险产品定价中的作用及其重要性。

答案：一、选择题1. C2. C3. C二、填空题4. 准备金5. 预期保险金三、简答题6. 净保费是指在扣除保险公司运营成本和利润后，用于保险风险保障的保费部分。

毛保费则包括了净保费和保险公司的运营成本及利润。

四、计算题7. 净保费计算公式为：净保费 = 毛保费 / (1 + 预定利率) - 死亡率 * 保险金额 / (1 + 预定利率)。

根据题目数据，净保费 = 1000 / (1 + 0.05) - 0.005 * 1000 / (1 + 0.05) = 952.38元。

五、论述题8. 寿险精算在保险产品定价中的作用是确保保险产品的价格既能覆盖风险成本，又能为保险公司带来合理的利润。

精算师通过评估死亡率、利率、费用率等因素，计算出保险产品的净保费，从而确定毛保费。

这一过程对于保险公司的财务稳定和市场竞争力至关重要。

寿险精算基础智慧树知到课后章节答案2023年下山东大学山东大学绪论单元测试1.寿险精算是以概率论和数理统计为工具，研究人寿保险中的寿命分布规律、寿险赔付规律、保险费率厘定、责任准备金的计提、保险现金价值的计算等问题的一门学科。

（）答案:对第一章测试1.现在存入一储蓄账户3万元，第2年底存入1万元，第四年末账户累积到5万元，求此账户实质利率（）答案:6.54%2.下列选项中，已知按季度换算的的年名义利率6%，那么5000元在3年末的积累值为（）元。

答案:5467.23.下列选项中，基金A按实际利率6%计息，基金B按年利率8%计息，在20年的年末两个基金之和为10000，在第10年底基金B金额是基金A的两倍，求第5年底时两个基金账户的价值和为（）答案:3451.54.下列选项中，与按季度换算的年贴现率等价的（每4年换算一次的年名义利率）=（）答案:5.下列选项中，向基金A投资5000元，按积累，基金Y也投资5000元，前3年按照半年换算的年名义利率8%计息，三年以后按年实际利率i计息。

4年末时两个基金账户值相同，求i=（ )答案:0.0786.下列选项中，已知，求 =（）0.05717.下列选项中，年金A月末支付8总共支付3年，年金B每月末支付10共支付1.5年，假设月实际利率为i，两个年金现值相同，求i=（）答案:8%8.下列选项中，永续年金A每年底支付15，等差递增型永续年金B每年末支付1、2、3、…，年金A和B采用相同的年利率i计息，且现值相同，求i=（）答案:7.1%9.张先生从银行贷款20万元，计划每半年还款一次，等额偿还，4年还清。

采用按半年换算的年名义利率7%计息，求每次还款的金额为（）元。

答案:2909510.对于利率为i，已知，则i=（）。

答案:第二章测试1.已知（）答案:0.0012.已知(x)剩余寿命T服从密度函数为的分布，求=（）。

答案:3.已知（）答案:4.下列选项中，假设非整数年龄服从Balducci调和加权平均假设，的正确表达式是（）。

保险精算（第二版）第一章：利息的基本概念练 习 题1．已知()2a t at b =+，如果在0时投资100元，能在时刻5积累到180元，试确定在时刻5投资300元，在时刻8的积累值。

(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2．(1)假设A(t)=100+10t, 试确定135,,i i i 。

135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯，试确定 135,,i i i 。

135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3．已知投资500元，3年后得到120元的利息，试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。

11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4．已知某笔投资在3年后的积累值为1000元，第1年的利率为 110%i =，第2年的利率为28%i =，第3年的利率为 36%i =，求该笔投资的原始金额。

123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5．确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。

(2)名义贴现率为每4年计息一次的年名义贴现率6%。

(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6．设m ＞1，按从大到小的次序排列()()m m d di i δ<<<<。

第四章 人寿保险的精算现值1、（1） 0.092 （2） 0.0552、（1）趸缴纯保费为：12345353637383935:5353535353510001000d d d d d A vv v v v l l l l l ⎛⎫=⋅++++ ⎪⎝⎭（2）自35岁~39岁各年龄的自然保费的总额为：()11111353637383935:136:137:138:139:1353637383910001000d d d d d A A A A A v v v v v l l l l l ⎛⎫++++=⋅++++ ⎪⎝⎭（3）有两个不同之处：第一，各年龄的自然保费的精算现值的时刻点不同，但可以通过()112131412345353637383935:136:137:138:139:1353637383910001000d d d d d A vA v A v A v A v v v v v l l l l l ⎛⎫++++=⋅++++ ⎪⎝⎭解决。

第二，分母不同，即平摊的对象不同，趸交纯保费是期初平摊，分母恒定，自然保费是每年平摊，分母随年龄的增长而减小。

注：因为题目没有给出使用的生命表，所以仅给出公式即可。

下同。

3、（1） 0.05 （2） 0.5注：利用递归公式1112020:20:20:2020x x x x x x x A A E A A A A ++=+=+⋅ 4、略 5、()()()21121100k k kx x kk x x k k k Var Z v p q v p q ++++==⎛⎫=⋅-⋅ ⎪⎝⎭∑∑ ()()2112110.50.50.50.50.1771x x x x x x x x q p q q p q q q ++++=+⋅-+⋅=+-+=10.54x q +⇒=6、0.817、设该保单的保险金额为P ，由130:205000P A ⋅=⇒19113030:203050005000k k k P d A v l ++===⋅∑。

第一章：利息的基本概念练 习 题1．已知()2a t at b =+，如果在0时投资100元，能在时刻5积累到180元，试确定在时刻5投资300元，在时刻8的积累值。

(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=⇒===⇒=+= 2．(1)假设A(t)=100+10t, 试确定135,,i i i 。

135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =⨯，试确定 135,,i i i 。

135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3．已知投资500元，3年后得到120元的利息，试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。

11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=⇒=∴=+==+=⇒=∴=+=4．已知某笔投资在3年后的积累值为1000元，第1年的利率为 110%i =，第2年的利率为28%i =，第3年的利率为 36%i =，求该笔投资的原始金额。

123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++⇒=5．确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。

(2)名义贴现率为每4年计息一次的年名义贴现率6%。

(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=⎛⎫ ⎪=+= ⎪ ⎪⎝⎭6．设m ＞1，按从大到小的次序排列()()m m d di i δ<<<<。

保险精算习题及答案第一章：利息的基本概念练习题1．已知()2a t at b =+，如果在0时投资100元，能在时刻5积累到180元，试确定在时刻5投资300元，在时刻8的积累值。

(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=?===?=+= 2．(1)假设A(t)=100+10t, 试确定135,,i i i 。

135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======(2)假设()()100 1.1nA n =?，试确定 135,,i i i 。

135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3．已知投资500元，3年后得到120元的利息，试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。

11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=?=∴=+==+=?=∴=+=4．已知某笔投资在3年后的积累值为1000元，第1年的利率为110%i =，第2年的利率为28%i =，第3年的利率为 36%i =，求该笔投资的原始金额。

123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++?=5．确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。

(2)名义贴现率为每4年计息一次的年名义贴现率6%。

(4)12341()410000(3)10000(1)11956.18410000(3)10000111750.0814i a i a =+=?? ?=+= ? ???6．设m ＞1，按从大到小的次序排列()()m m d di i δ<<<<。

寿险精算一、填空题1、生命表依据编制对象的不同，可以分为：________和________。

2、根据保险标的的属性不同，保险可分为：________和______________。

3、寿险精算中的基本参数主要有：_________、_______________、_______________。

4、生命表的创始人是___________。

5、生命表方法的实质是_________________________________________________。

6、投保保额为1单位元数的终身寿险，按年度实质贴现率v 复利计息，赔付现值变量为：_____________________。

7、n 年定期两全险是___________和_____________的组合。

8、终身寿险死亡即刻赔付趸缴净保费公式为______________________________。

9、已知05.0,5a ,8a 2===δx x ，则=)(a |T a r V __________.10、1—_______|:n x ad =二、选择题1、世界上第一张简略生命表是（ ）A.1662年约翰•格兰编制的生命表 B ．1693年埃德蒙•哈雷编制的生命表； C ．詹姆斯•道森编制的生命表 D ．1724年亚伯拉罕•棣模佛编制的生命表2、保险精算遵循的最重要原则是（ ）A ．补偿性原则 B．资产负债匹配原则C ．收支平衡原则D ．均衡保费原则3、某10年期确定年金，每4月末给付800元，月利率为2%，则该年金的现值为（ ）。

4、 已知死力µ=0.045，利息力δ=0.055，则每年支付金额1，连续支付的终身生存年金的精算现值为（ ）。

A ．9； B.10； C.11； D.12。

5、下列错误的公式是 （）A.()()x s x s ,x =μB.()()dtP d t x t T =f C.()()()x s t x s x s q x +-=t D.()x s x =p 0 6、设某地新生婴儿未来寿命随机变量Ｘ在区间［0,100］上服从均匀分布，x ∈(0,100) 则（ ）A.s(x)=x/100B.s(x)=1/100C.s(x)=1-x/100D.s(x)=100x7、8、9、下列不是有关分数年龄的假设常用的插值方法的是（）A.线性插值B.调和插值C.几何插值D.牛顿插值10.下列关系不正确的是（） A.x t x t x p l l ∙=+ B.x x x q l d ∙= C.x x xLd m = D.tx x x l l p +=t 三、简答题1.你认为保险精算对保险经营有何重要意义？2.生存年金的定义及分类。

《寿险精算》试题及答案（解答仅供参考）第一套一、名词解释1. 寿险精算：寿险精算是运用数学、统计学、经济学等理论和方法，对人寿保险业务中的风险进行量化分析和评估，以确定保险费率、准备金、利润分配等关键参数的学科。

2. 生命表：生命表是一种记录某一地区或群体在不同年龄阶段死亡率的统计表格，是寿险精算中计算保费和评估风险的重要工具。

3. 保险费率：保险费率是指保险公司为提供保险保障而向被保险人收取的费用比例，它是根据预期损失和运营成本等因素计算得出的。

4. 预定利率：预定利率是指保险公司为未来支付保险金而预先设定的利息率，它是计算保险产品现金价值和准备金的重要参数。

5. 保险准备金：保险准备金是指保险公司为了应对未来的保险责任和赔付风险，按照规定提取并储备的资金。

二、填空题1. 寿险精算的主要任务包括确定______、评估风险、管理资产和负债等。

答案：保险费率2. 在寿险精算中，______是预测未来死亡率的重要工具。

答案：生命表3. 保险产品的现金价值是根据______和已缴保费计算得出的。

答案：预定利率4. 保险公司提取的保险准备金主要包括未到期责任准备金和______。

答案：未决赔款准备金5. 在人寿保险中，______是一种可以在保险期间内改变保险金额和保险费的保险产品。

答案：可变寿险三、单项选择题1. 下列哪一项不属于寿险精算的主要任务？A. 确定保险费率B. 评估风险C. 管理资产和负债D. 制定营销策略答案：D. 制定营销策略2. 生命表中的死亡率通常表示为：A. 每千人的死亡人数B. 每百人的死亡人数C. 每年的死亡人数D. 每年的死亡概率答案：D. 每年的死亡概率3. 下列哪种保险产品的现金价值通常会随着投资收益的变化而变化？A. 定期寿险B. 终身寿险D. 年金保险答案：C. 变额寿险4. 在计算保险准备金时，未决赔款准备金通常是按照以下哪种方法提取的？A. 逐笔认定法B. 平均估算法C. 总和估算法D. 预期损失法答案：A. 逐笔认定法5. 下列哪种保险产品的保险金额和保险费可以在保险期间内进行调整？A. 定期寿险B. 终身寿险C. 变额寿险D. 全残保险答案：C. 变额寿险四、多项选择题1. 下列哪些因素会影响保险费率的确定？A. 预期损失B. 运营成本C. 投资收益D. 市场竞争答案：A、B、C、D2. 下列哪些保险产品具有现金价值？A. 定期寿险C. 变额寿险D. 年金保险答案：B、C、D3. 下列哪些因素可能影响生命表的编制？A. 地理位置B. 种族背景C. 性别D. 社会经济状况答案：A、B、C、D4. 下列哪些保险准备金属于长期准备金？A. 未到期责任准备金B. 未决赔款准备金C. 长期健康保险准备金D. 养老保险准备金答案：C、D5. 下列哪些保险产品具有投资功能？A. 定期寿险B. 终身寿险C. 变额寿险D. 年金保险答案：B、C、D五、判断题1. 寿险精算师只需要具备数学和统计学知识即可。

※<第一章>1．寿险精算与精算的关系答：保险精算包括寿险精算和非寿险精算两大类，而保险精算是精算学中的一个重要分支。

2．什么是精算学？答：精算学是以现代数学和概率数理统计学为基础，从数量方面研究保险业经营管理的各个环节的规律和发展，更好地反映保险机制实质的随机模型。

为保险公司进行科学的决策及提高管理水平提供依据和工具的专门学科。

※<第二章>1．试确定二年期内的常数实际利率，使之等价于第一年5%，第二年6%的实际贴现率。

（5.82%）2．如果20.04(1)t t δ-=+，那么1000元在第20年末的终值是多少？ （1038.8301元）3．试比较δ ，()m i ，i 的大小。

（m>1时，()m i i δ>> ；m=1时，()m i i δ=> ；m<1时，()m i i δ>> ）※<第三章>1．如果实际贴现率为10%，那么8a 为多少？ （5.695327）2．一台新电视机的现金价格为10000元。

某顾客想以月计息一次18%的年利率分期付款购买该台电视，若他在4年内每月月末付款250元，问现付款需要多少？ （1489.3615元）3．王强从银行贷款100000元，计划从第七个月开始每月末等额还款，若银行规定在借款后三年还清本息，设年利率为16%，求每月需还款额。

（4323.9456元）※<第四章>1．已知()1100xS x =-，0100x ≤≤ ，求 201010q 。

（0.125）2．证明：在Balducci 假设下，1(1)x x txq t q μ+=-- ，01t ≤≤3．若 407746l =，417681l = ，计算下列假设下的1404μ的值。

(1)UDD 假设 （2）Balducci 假设 （0.0084091，0.0084446）※<第五章>1．证明：11(1)x x x p a i a --⋅=+2．已知死力 0.04μ=，息力 0.06δ=，求 x a 。