图1
图2
图3
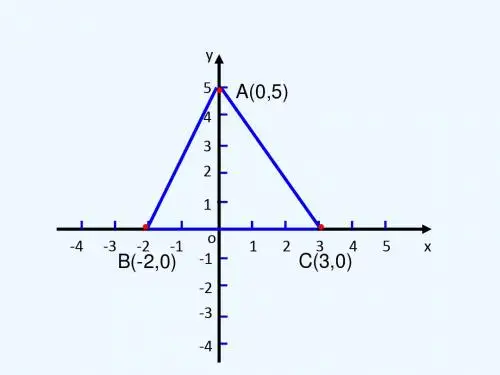
平面直角坐标系中如何求几何图形的面积
一、 求三角形的面积
1、有一边在坐标轴上或平行于坐标轴
例1：如图1，平面直角坐标系中，△ABC 的顶点坐标分别为（-3,0）、（0,3）、（0，-1），你
能求出三角形ABC 的面积吗
2、无边在坐标轴上或平行于坐标轴
例2：如图2，平面直角坐标系中，已知点A （-3，-1）、B （1,3）、C （2，-3），你能求出三角形ABC 的面积吗
归纳：求三角形面积的关键是确定某条边及这条边上的高，如果在坐标系中，某个三角形中有一条边在坐标轴上或平行于坐标轴，则根据这条边的两个顶点的坐标易求出这边的长，根据这条边的相对的顶点可求出他的高。
二、求四边形的面积
例3：如图3，你能求出四边形ABCD 的面积吗
分析：四边形ABCD 是不规则的四边形，面积不能直接求出，我们可以利用分割或补形来求。
归纳：会将图形转化为有边与坐标轴平行的图形进行计算。
怎样确定点的坐标
一、 象限点
解决有关象限点问题的关键是熟记各象限的符号特征，由第一到底四象限点的符号特征分别为（+，+）、 （-，+）、（-，-）、（+，-）。
例1：已知点M （a 3-9,1-a ）在第三象限，且它的坐标都是整数，则a =（ ）
A 、1
B 、2
C 、3
D 、0
二、轴上的点
解决有关轴上点问题的关键是把握“0”的特征，x 轴上点的纵坐标为0，可记为（x ，0）；y 轴上点的横坐标为0，可记为（0，y ）；原点可记为（0,0）。
例2：点P （m+3,m+1）在直角坐标系的x 轴上，则P 点的坐标为（ ）
A 、（0，-2）
B 、（2,0）
C 、（4,0）
D 、（0，-4）
三、象限角平分线上的点 所谓象限角平分线上的点，就是各象限坐标轴夹角平分线上的点。解决这类问题的关键是掌握“y x =”的特征，一、三象限角平分线上点的横、纵坐标相等，可记为（x ，x ）；二、四象限角平分线上的点横、纵坐标互为相反数，可记为（x ，-x ）。
例3：已知点Q （8,4m 22
2++++m m m ）在第一象限的角平分线上，则m=_________.
四、对称点
对称点的横、纵坐标之间有很密切的关系，点P （a ，b ）关于x 轴对称的点的坐标上（a ，-b ）；关于y 轴对称的点的坐标是（-a ，b ）；关于原点对称的点的坐标是（-a ，-b ）；关于一、三象限角平分线对称的点的坐标是（b ，a ）；关于二、四象限角平分线对称的点的坐标是（-b,-a ）.
例4：点（-1,4）关于原点对称的点的坐标是（ ）
A 、（-1，-4）
B 、（1，-4）
C 、（1,4）
D 、（4，-1）
五、平行于坐标轴的直线上的点
平行于x 轴的直线上点的纵坐标相同，平行于y 轴的直线上点的横坐标相同。
例5：点A(4,y)和点B （x ，-3），过A 、B 的直线平
行于x 轴，且AB=5，则x=____,y=_____.
